Как найти наименьшее кратное число. Как найти наименьшее общее кратное, нок для двух и более чисел
Представленный ниже материал является логическим продолжением теории из статьи под заголовком НОК — наименьшее общее кратное, определение, примеры, связь между НОК и НОД . Здесь мы поговорим про нахождение наименьшего общего кратного (НОК) , и особое внимание уделим решению примеров. Сначала покажем, как вычисляется НОК двух чисел через НОД этих чисел. Дальше рассмотрим нахождение наименьшего общего кратного с помощью разложения чисел на простые множители. После этого остановимся на нахождении НОК трех и большего количества чисел, а также уделим внимание вычислению НОК отрицательных чисел.
Навигация по странице.
Вычисление наименьшего общего кратного (НОК) через НОД
Один из способов нахождения наименьшего общего кратного основан на связи между НОК и НОД . Существующая связь между НОК и НОД позволяет вычислять наименьшее общее кратное двух целых положительных чисел через известный наибольший общий делитель. Соответствующая формула имеет вид
Соответствующая формула имеет вид
Пример.
Найдите наименьшее общее кратное двух чисел 126 и 70 .
Решение.
В этом примере a=126 , b=70 . Воспользуемся связью НОК с НОД, выражающуюся формулой НОК(a, b)=a·b:НОД(a, b) . То есть, сначала нам предстоит найти наибольший общий делитель чисел 70 и 126 , после чего мы сможем вычислить НОК этих чисел по записанной формуле.
Найдем НОД(126, 70) , используя алгоритм Евклида: 126=70·1+56 , 70=56·1+14 , 56=14·4 , следовательно, НОД(126, 70)=14 .
Теперь находим требуемое наименьшее общее кратное: НОК(126, 70)=126·70:НОД(126, 70)= 126·70:14=630 .
Ответ:
НОК(126, 70)=630 .
Пример.
Чему равно НОК(68, 34) ?
Решение.
Так как 68 делится нацело на 34 , то НОД(68, 34)=34 . Теперь вычисляем наименьшее общее кратное: НОК(68, 34)=68·34:НОД(68, 34)= 68·34:34=68 .
Ответ:
НОК(68, 34)=68
.
Заметим, что предыдущий пример подходит под следующее правило нахождения НОК для целых положительные чисел a и b : если число a делится на b , то наименьшее общее кратное этих чисел равно a .
Нахождение НОК с помощью разложения чисел на простые множители
Другой способ нахождения наименьшего общего кратного базируется на разложении чисел на простые множители . Если составить произведение из всех простых множителей данных чисел, после чего из этого произведения исключить все общие простые множители, присутствующие в разложениях данных чисел, то полученное произведение будет равно наименьшему общему кратному данных чисел .
Озвученное правило нахождения НОК следует из равенства НОК(a, b)=a·b:НОД(a, b)
. Действительно, произведение чисел a
и b
равно произведению всех множителей, участвующих в разложениях чисел a
и b
. В свою очередь НОД(a, b)
равен произведению всех простых множителей, одновременно присутствующих в разложениях чисел a
и b
(о чем написано в разделе нахождение НОД с помощью разложения чисел на простые множители).
Приведем пример. Пусть мы знаем, что 75=3·5·5 и 210=2·3·5·7 . Составим произведение из всех множителей данных разложений: 2·3·3·5·5·5·7 . Теперь из этого произведения исключим все множители, присутствующие и в разложении числа 75 и в разложении числа 210 (такими множителями являются 3 и 5 ), тогда произведение примет вид 2·3·5·5·7 . Значение этого произведения равно наименьшему общему кратному чисел 75 и 210 , то есть, НОК(75, 210)= 2·3·5·5·7=1 050 .
Пример.
Разложив числа 441 и 700 на простые множители, найдите наименьшее общее кратное этих чисел.
Решение.
Разложим числа 441 и 700 на простые множители:
Получаем 441=3·3·7·7 и 700=2·2·5·5·7 .
Теперь составим произведение из всех множителей, участвующих в разложениях данных чисел: 2·2·3·3·5·5·7·7·7
. Исключим из этого произведения все множители, одновременно присутствующие в обоих разложениях (такой множитель только один – это число 7
): 2·2·3·3·5·5·7·7
. Таким образом, НОК(441, 700)=2·2·3·3·5·5·7·7=44 100
.
Ответ:
НОК(441, 700)= 44 100 .
Правило нахождения НОК с использованием разложения чисел на простые множители можно сформулировать немного иначе. Если ко множителям из разложения числа a добавить недостающие множители из разложения числа b , то значение полученного произведения будет равно наименьшему общему кратному чисел a и b .
Для примера возьмем все те же числа 75 и 210 , их разложения на простые множители таковы: 75=3·5·5 и 210=2·3·5·7 . Ко множителям 3 , 5 и 5 из разложения числа 75 добавляем недостающие множители 2 и 7 из разложения числа 210 , получаем произведение 2·3·5·5·7 , значение которого равно НОК(75, 210) .
Пример.
Найдите наименьшее общее кратное чисел 84 и 648 .
Решение.
Получаем сначала разложения чисел 84
и 648
на простые множители. Они имеют вид 84=2·2·3·7
и 648=2·2·2·3·3·3·3
. К множителям 2
, 2
, 3
и 7
из разложения числа 84
добавляем недостающие множители 2
, 3
, 3
и 3
из разложения числа 648
, получаем произведение 2·2·2·3·3·3·3·7
, которое равно 4 536
. Таким образом, искомое наименьшее общее кратное чисел 84
и 648
равно 4 536
.
Таким образом, искомое наименьшее общее кратное чисел 84
и 648
равно 4 536
.
Ответ:
НОК(84, 648)=4 536 .
Нахождение НОК трех и большего количества чисел
Наименьшее общее кратное трех и большего количества чисел может быть найдено через последовательное нахождение НОК двух чисел. Напомним соответствующую теорему, дающую способ нахождения НОК трех и большего количества чисел.
Теорема.
Пусть даны целые положительные числа a 1 , a 2 , …, a k , наименьшее общее кратное m k этих чисел находится при последовательном вычислении m 2 =НОК(a 1 , a 2) , m 3 =НОК(m 2 , a 3) , …, m k =НОК(m k−1 , a k) .
Рассмотрим применение этой теоремы на примере нахождения наименьшего общего кратного четырех чисел.
Пример.
Найдите НОК четырех чисел 140 , 9 , 54 и 250 .
Решение.
В этом примере a 1 =140 , a 2 =9 , a 3 =54 , a 4 =250 .
Сначала находим m 2 =НОК(a 1 , a 2)=НОК(140, 9)
. Для этого по алгоритму Евклида определяем НОД(140, 9)
, имеем 140=9·15+5
, 9=5·1+4
, 5=4·1+1
, 4=1·4
, следовательно, НОД(140, 9)=1
, откуда НОК(140, 9)=140·9:НОД(140, 9)=
140·9:1=1 260
. То есть, m 2 =1 260
.
То есть, m 2 =1 260
.
Теперь находим m 3 =НОК(m 2 , a 3)=НОК(1 260, 54) . Вычислим его через НОД(1 260, 54) , который также определим по алгоритму Евклида: 1 260=54·23+18 , 54=18·3 . Тогда НОД(1 260, 54)=18 , откуда НОК(1 260, 54)= 1 260·54:НОД(1 260, 54)= 1 260·54:18=3 780 . То есть, m 3 =3 780 .
Осталось найти m 4 =НОК(m 3 , a 4)=НОК(3 780, 250) . Для этого находим НОД(3 780, 250) по алгоритму Евклида: 3 780=250·15+30 , 250=30·8+10 , 30=10·3 . Следовательно, НОД(3 780, 250)=10 , откуда НОК(3 780, 250)= 3 780·250:НОД(3 780, 250)= 3 780·250:10=94 500 . То есть, m 4 =94 500 .
Таким образом, наименьшее общее кратное исходных четырех чисел равно 94 500 .
Ответ:
НОК(140, 9, 54, 250)=94 500 .
Во многих случаях наименьшее общее кратное трех и большего количества чисел удобно находить с использованием разложений данных чисел на простые множители. При этом следует придерживаться следующего правила. Наименьшее общее кратное нескольких чисел равно произведению, которое составляется так: ко всем множителям из разложения первого числа добавляются недостающие множители из разложения второго числа, к полученным множителям добавляются недостающие множители из разложения третьего числа и так далее
.
Рассмотрим пример нахождения наименьшего общего кратного с использованием разложения чисел на простые множители.
Пример.
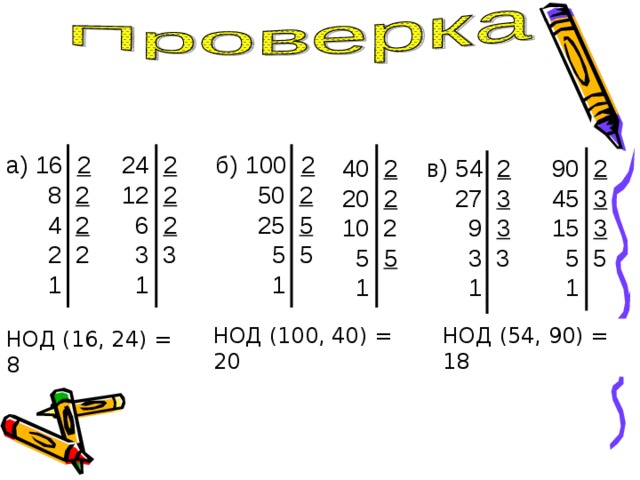
Найдите наименьшее общее кратное пяти чисел 84 , 6 , 48 , 7 , 143 .
Решение.
Сначала получаем разложения данных чисел на простые множители: 84=2·2·3·7 , 6=2·3 , 48=2·2·2·2·3 , 7 (7 – простое число , оно совпадает со своим разложением на простые множители) и 143=11·13 .
Для нахождения НОК данных чисел к множителям первого числа 84
(ими являются 2
, 2
, 3
и 7
) нужно добавить недостающие множители из разложения второго числа 6
. Разложение числа 6
не содержит недостающих множителей, так как и 2
и 3
уже присутствуют в разложении первого числа 84
. Дальше к множителям 2
, 2
, 3
и 7
добавляем недостающие множители 2
и 2
из разложения третьего числа 48
, получаем набор множителей 2
, 2
, 2
, 2
, 3
и 7
. К этому набору на следующем шаге не придется добавлять множителей, так как 7
уже содержится в нем. Наконец, к множителям 2
, 2
, 2
, 2
, 3
и 7
добавляем недостающие множители 11
и 13
из разложения числа 143
.
Наибольший общий делитель и наименьшее общее кратное — ключевые арифметические понятия, которые позволяют без усилий оперировать обыкновенными дробями. НОК и чаще всего используются для поиска общего знаменателя нескольких дробей.
Основные понятия
Делитель целого числа X — это другое целое число Y, на которое X разделяется без остатка. К примеру, делитель 4 — это 2, а 36 — 4, 6, 9. Кратное целого X — это такое число Y, которое делится на X без остатка. К примеру, 3 кратно 15, а 6 — 12.
Для любой пары чисел мы можем найти их общие делители и кратные. К примеру, для 6 и 9 общим кратным является 18, а общим делителем — 3. Очевидно, что делителей и кратных у пар может быть несколько, поэтому при расчетах используется наибольший делитель НОД и наименьшее кратное НОК.
Наименьший делитель не имеет смысла, так как для любого числа это всегда единица. Наибольшее кратное также бессмысленно, так как последовательность кратных устремляется в бесконечность.
Нахождение НОД
Для поиска наибольшего общего делителя существует множество методов, самые известные из которых:
- последовательный перебор делителей, выбор общих для пары и поиск наибольшего из них;
- разложение чисел на неделимые множители;
- алгоритм Евклида;
- бинарный алгоритм.
Сегодня в учебных заведениях наиболее популярными являются методы разложения на простые множители и алгоритм Евклида. Последний в свою очередь используется при решении диофантовых уравнений: поиск НОД требуется для проверки уравнения на возможность разрешения в целых числах.
Нахождение НОК
Наименьшее общее кратное точно также определяется последовательным перебором или разложением на неделимые множители. Кроме того, легко найти НОК, если уже определен наибольший делитель. Для чисел X и Y НОК и НОД связаны следующим соотношением:
НОК (X,Y) = X × Y / НОД(X,Y).
Например, если НОД(15,18) = 3, то НОК(15,18) = 15 × 18 / 3 = 90. Наиболее очевидный пример использования НОК — поиск общего знаменателя, который и является наименьшим общим кратным для заданных дробей.
Взаимно простые числа
Если у пары чисел нет общих делителей, то такая пара называется взаимно простой. НОД для таких пар всегда равен единице, а исходя из связи делителей и кратных, НОК для взаимно простых равен их произведению. К примеру, числа 25 и 28 взаимно просты, ведь у них нет общих делителей, а НОК(25, 28) = 700, что соответствует их произведению. Два любых неделимых числа всегда будут взаимно простыми.
Калькулятор общего делителя и кратного
При помощи нашего калькулятора вы можете вычислить НОД и НОК для произвольного количества чисел на выбор. Задания на вычисление общих делителей и кратных встречаются в арифметике 5, 6 класса, однако НОД и НОК — ключевые понятия математики и используются в теории чисел, планиметрии и коммуникативной алгебре.
Примеры из реальной жизни
Общий знаменатель дробей
Наименьшее общее кратное используется при поиске общего знаменателя нескольких дробей. Пусть в арифметической задаче требуется суммировать 5 дробей:
1/8 + 1/9 + 1/12 + 1/15 + 1/18.
Для сложения дробей выражение необходимо привести к общему знаменателю, что сводится к задаче нахождения НОК. Для этого выберите в калькуляторе 5 чисел и введите значения знаменателей в соответствующие ячейки. Программа вычислит НОК (8, 9, 12, 15, 18) = 360. Теперь необходимо вычислить дополнительные множители для каждой дроби, которые определяются как соотношение НОК к знаменателю. Таким образом, дополнительные множители будут выглядеть как:
- 360/8 = 45
- 360/9 = 40
- 360/12 = 30
- 360/15 = 24
- 360/18 = 20.
После этого умножаем все дроби на соответствующий дополнительный множитель и получаем:
45/360 + 40/360 + 30/360 + 24/360 + 20/360.
Такие дроби мы можем легко суммировать и получить результат в виде 159/360. Сокращаем дробь на 3 и видим окончательный ответ — 53/120.
Решение линейных диофантовых уравнений
Линейные диофантовы уравнения — это выражения вида ax + by = d. Если отношение d / НОД(a, b) есть целое число, то уравнение разрешимо в целых числах. Давайте проверим пару уравнений на возможность целочисленного решения. Сначала проверим уравнение 150x + 8y = 37. При помощи калькулятора находим НОД (150,8) = 2. Делим 37/2 = 18,5. Число не целое, следовательно, уравнение не имеет целочисленных корней.
Давайте проверим пару уравнений на возможность целочисленного решения. Сначала проверим уравнение 150x + 8y = 37. При помощи калькулятора находим НОД (150,8) = 2. Делим 37/2 = 18,5. Число не целое, следовательно, уравнение не имеет целочисленных корней.
Проверим уравнение 1320x + 1760y = 10120. Используем калькулятор для нахождения НОД(1320, 1760) = 440. Разделим 10120/440 = 23. В результате получаем целое число, следовательно, диофантово уравнение разрешимо в целых коэффициентах.
Заключение
НОД и НОК играют большую роль в теории чисел, а сами понятия широко используются в самых разных областях математики. Используйте наш калькулятор для расчета наибольших делителей и наименьших кратных любого количества чисел.
Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы рассмотрим способы нахождения НОК для трех чисел и более, разберем вопрос о том, как найти НОК отрицательного числа.
Yandex.RTB R-A-339285-1
Вычисление наименьшего общего кратного (НОК) через НОД
Мы уже установили связь наименьшего общего кратного с наибольшим общим делителем. Теперь научимся определять НОК через НОД. Сначала разберемся, как делать это для положительных чисел.
Определение 1
Найти наименьшее общее кратное через наибольший общий делитель можно по формуле НОК (a , b) = a · b: НОД (a , b) .
Пример 1
Необходимо найти НОК чисел 126 и 70 .
Решение
Примем a = 126 , b = 70 . Подставим значения в формулу вычисления наименьшего общего кратного через наибольший общий делитель НОК (a , b) = a · b: НОД (a , b) .
Найдет НОД чисел 70 и 126 . Для этого нам понадобится алгоритм Евклида: 126 = 70 · 1 + 56 , 70 = 56 · 1 + 14 , 56 = 14 · 4 , следовательно, НОД (126 , 70) = 14 .
Вычислим НОК: НОК (126 , 70) = 126 · 70: НОД (126 , 70) = 126 · 70: 14 = 630 .
Ответ: НОК (126 , 70) = 630 .
Пример 2
Найдите нок чисел 68 и 34 .
Решение
НОД в данном случае нейти несложно, так как 68 делится на 34 . Вычислим наименьшее общее кратное по формуле: НОК (68 , 34) = 68 · 34: НОД (68 , 34) = 68 · 34: 34 = 68 .
Ответ: НОК (68 , 34) = 68 .
В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b: если первое число делится на второе, что НОК этих чисел будет равно первому числу.
Нахождение НОК с помощью разложения чисел на простые множители
Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители.
Определение 2
Для нахождения наименьшего общего кратного нам понадобится выполнить ряд несложных действий:
- составляем произведение всех простых множителей чисел, для которых нам нужно найти НОК;
- исключаем их полученных произведений все простые множители;
- полученное после исключения общих простых множителей произведение будет равно НОК данных чисел.

Этот способ нахождения наименьшего общего кратного основан на равенстве НОК (a , b) = a · b: НОД (a , b) . Если посмотреть на формулу, то станет понятно: произведение чисел a и b равно произведению всех множителей, которые участвуют в разложении этих двух чисел. При этом НОД двух чисел равен произведению всех простых множителей, которые одновременно присутствуют в разложениях на множители данных двух чисел.
Пример 3
У нас есть два числе 75 и 210 . Мы можем разложить их на множители следующим образом: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . Если составить произведение всех множителей двух исходных чисел, то получится: 2 · 3 · 3 · 5 · 5 · 5 · 7 .
Если исключить общие для обоих чисел множители 3 и 5 , мы получим произведение следующего вида: 2 · 3 · 5 · 5 · 7 = 1050 . Это произведение и будет нашим НОК для чисел 75 и 210 .
Пример 4
Найдите НОК чисел 441 и 700 , разложив оба числа на простые множители.
Решение
Найдем все простые множители чисел, данных в условии:
441 147 49 7 1 3 3 7 7
700 350 175 35 7 1 2 2 5 5 7
Получаем две цепочки чисел: 441 = 3 · 3 · 7 · 7 и 700 = 2 · 2 · 5 · 5 · 7 .
Произведение всех множителей, которые участвовали в разложении данных чисел, будет иметь вид: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 · 7 . Найдем общие множители. Это число 7 . Исключим его из общего произведения: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 . Получается, что НОК (441 , 700) = 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 = 44 100 .
Ответ: НОК (441 , 700) = 44 100 .
Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.
Определение 3
Раньше мы исключали из всего количества множителей общие для обоих чисел. Теперь мы сделаем иначе:
- разложим оба числа на простые множители:
- добавим к произведению простых множителей первого числа недостающие множители второго числа;
- получим произведение, которое и будет искомым НОК двух чисел.

Пример 5
Вернемся к числам 75 и 210 , для которых мы уже искали НОК в одном из прошлых примеров. Разложим их на простые множители: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . К произведению множителей 3 , 5 и 5 числа 75 добавим недостающие множители 2 и 7 числа 210 . Получаем: 2 · 3 · 5 · 5 · 7 . Это и есть НОК чисел 75 и 210 .
Пример 6
Необходимо вычислить НОК чисел 84 и 648 .
Решение
Разложим числа из условия на простые множители: 84 = 2 · 2 · 3 · 7 и 648 = 2 · 2 · 2 · 3 · 3 · 3 · 3 . Добавим к произведению множителей 2 , 2 , 3 и 7 числа 84 недостающие множители 2 , 3 , 3 и
3 числа 648 . Получаем произведение 2 · 2 · 2 · 3 · 3 · 3 · 3 · 7 = 4536 . Это и есть наименьшее общее кратное чисел 84 и 648 .
Ответ: НОК (84 , 648) = 4 536 .
Нахождение НОК трех и большего количества чисел
Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел. На этот случай есть теорема.
На этот случай есть теорема.
Теорема 1
Предположим, что у нас есть целые числа a 1 , a 2 , … , a k . НОК m k этих чисел находится при последовательном вычислении m 2 = НОК (a 1 , a 2) , m 3 = НОК (m 2 , a 3) , … , m k = НОК (m k − 1 , a k) .
Теперь рассмотрим, как можно применять теорему для решения конкретных задач.
Пример 7
Необходимо вычислить наименьшее общее кратное четырех чисел 140 , 9 , 54 и 250 .
Решение
Введем обозначения: a 1 = 140 , a 2 = 9 , a 3 = 54 , a 4 = 250 .
Начнем с того, что вычислим m 2 = НОК (a 1 , a 2) = НОК (140 , 9) . Применим алгоритм Евклида для вычисления НОД чисел 140 и 9: 140 = 9 · 15 + 5 , 9 = 5 · 1 + 4 , 5 = 4 · 1 + 1 , 4 = 1 · 4 . Получаем: НОД (140 , 9) = 1 , НОК (140 , 9) = 140 · 9: НОД (140 , 9) = 140 · 9: 1 = 1 260 . Следовательно, m 2 = 1 260 .
Теперь вычислим по тому е алгоритму m 3 = НОК (m 2 , a 3) = НОК (1 260 , 54) . В ходе вычислений получаем m 3 = 3 780 .
Нам осталось вычислить m 4 = НОК (m 3 , a 4) = НОК (3 780 , 250) . Действуем по тому же алгоритму. Получаем m 4 = 94 500 .
НОК четырех чисел из условия примера равно 94500 .
Ответ: НОК (140 , 9 , 54 , 250) = 94 500 .
Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.
Определение 4
Предлагаем вам следующий алгоритм действий:
- раскладываем все числа на простые множители;
- к произведению множителей первого числа добавляем недостающие множители из произведения второго числа;
- к полученному на предыдущем этапе произведению добавляем недостающие множители третьего числа и т.д.;
- полученное произведение будет наименьшим общим кратным всех чисел из условия.
Пример 8
Необходимо найти НОК пяти чисел 84 , 6 , 48 , 7 , 143 .
Решение
Разложим все пять чисел на простые множители: 84 = 2 · 2 · 3 · 7 , 6 = 2 · 3 , 48 = 2 · 2 · 2 · 2 · 3 , 7 , 143 = 11 · 13 . Простые числа, которым является число 7 , на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.
Простые числа, которым является число 7 , на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.
Теперь возьмем произведение простых множителей 2 , 2 , 3 и 7 числа 84 и добавим к ним недостающие множители второго числа. Мы разложили число 6 на 2 и 3 . Эти множители уже есть в произведении первого числа. Следовательно, их опускаем.
Продолжаем добавлять недостающие множители. Переходим к числу 48 , из произведения простых множителей которого берем 2 и 2 . Затем добавляем простой множитель 7 от четвертого числа и множители 11 и 13 пятого. Получаем: 2 · 2 · 2 · 2 · 3 · 7 · 11 · 13 = 48 048 . Это и есть наименьшее общее кратное пяти исходных чисел.
Ответ: НОК (84 , 6 , 48 , 7 , 143) = 48 048 .
Нахождение наименьшего общего кратного отрицательных чисел
Для того, чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.
Пример 9
НОК (54 , − 34) = НОК (54 , 34) , а НОК (− 622 , − 46 , − 54 , − 888) = НОК (622 , 46 , 54 , 888) .
Такие действия допустимы в связи с тем, что если принять, что a и − a – противоположные числа,
то множество кратных числа a совпадает со множеством кратных числа − a .
Пример 10
Необходимо вычислить НОК отрицательных чисел − 145 и − 45 .
Решение
Произведем замену чисел − 145 и − 45 на противоположные им числа 145 и 45 . Теперь по алгоритму вычислим НОК (145 , 45) = 145 · 45: НОД (145 , 45) = 145 · 45: 5 = 1 305 , предварительно определив НОД по алгоритму Евклида.
Получим, что НОК чисел − 145 и − 45 равно 1 305 .
Ответ: НОК (− 145 , − 45) = 1 305 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.
Например :
Число 12 делится на 1, на 2, на 3, на 4, на 6, на 12;
Число 36 делится на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.
Числа, на которые число делится нацело (для 12 это 1, 2, 3, 4, 6 и 12) называются делителями числа . Делитель натурального числа a — это такое натуральное число, которое делит данное число a без остатка. Натуральное число, которое имеет более двух делителей, называется составным .
Обратите внимание, что числа 12 и 36 имеют общие делители. Это числа: 1, 2, 3, 4, 6, 12. Наибольший из делителей этих чисел — 12. Общий делитель двух данных чисел a и b — это число, на которое делятся без остатка оба данных числа a и b .
Общим кратным нескольких чисел называется число, которое делится на каждое из этих чисел. Например , числа 9, 18 и 45 имеют общее кратное 180. Но 90 и 360 — тоже их общие кратные. Среди всех jбщих кратных всегда есть наименьшее, в данном случае это 90. Это число называется наименьшим общим кратным (НОК) .
Это число называется наименьшим общим кратным (НОК) .
НОК всегда натуральное число, которое должно быть больше самого большого из чисел, для которых оно определяется.
Наименьшее общее кратное (НОК). Свойства.
Коммутативность:
Ассоциативность:
В частности, если и — взаимно-простые числа , то:
Наименьшее общее кратное двух целых чисел m и n является делителем всех других общих кратных m и n . Более того, множество общих кратных m, n совпадает с множеством кратных для НОК(m, n ).
Асимптотики для могут быть выражены через некоторые теоретико-числовые функции.
Так, функция Чебышёва . А также:
Это следует из определения и свойств функции Ландау g(n) .
Что следует из закона распределения простых чисел.
Нахождение наименьшего общего кратного (НОК).
НОК(a, b ) можно вычислить несколькими способами:
1. Если известен наибольший общий делитель , можно использовать его связь с НОК:
2. Пусть известно каноническое разложение обоих чисел на простые множители:
Пусть известно каноническое разложение обоих чисел на простые множители:
где p 1 ,…,p k — различные простые числа, а d 1 ,…,d k и e 1 ,…,e k — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении).
Тогда НОК (a ,b ) вычисляется по формуле:
Другими словами, разложение НОК содержит все простые множители , входящие хотя бы в одно из разложений чисел a, b , причём из двух показателей степени этого множителя берётся наибольший.
Пример :
Вычисление наименьшего общего кратного нескольких чисел может быть сведено к нескольким последовательным вычислениям НОК от двух чисел:
Правило. Чтобы найти НОК ряда чисел, нужно:
— разложить числа на простые множители;
— перенести во множители искомого произведения самое большое разложение (произведение множителей самого большого числа из заданных), а потом добавить множители из разложения других чисел, которые не встречаются в первом числе или стоят в нем меньшее число раз;
— полученное произведение простых множителей будет НОК заданных чисел.
Любые два и более натуральных чисел имеют свое НОК. Если числа не кратны друг другу или не имеют одинаковых множителей в разложении, то их НОК равно произведению этих чисел.
Простые множители числа 28 (2, 2, 7) дополнили множителем 3 (числа 21), полученное произведение (84) будет наименьшим числом, которое делится на 21 и 28 .
Простые множители наибольшего числа 30 дополнили множителем 5 числа 25, полученное произведение 150 больше самого большого числа 30 и делится на все заданные числа без остатка. Это наименьшее произведение из возможных (150, 250, 300…), которому кратны все заданные числа.
Числа 2,3,11,37 — простые, поэтому их НОК равно произведению заданных чисел.
Правило . Чтобы вычислить НОК простых чисел, нужно все эти числа перемножить между собой.
Еще один вариант:
Чтобы найти наименьшее общее кратное (НОК) нескольких чисел нужно:
1) представить каждое число как произведение его простых множителей, например:
504 = 2 · 2 · 2 · 3 · 3 · 7 ,
2) записать степени всех простых множителей:
504 = 2 · 2 · 2 · 3 · 3 · 7 = 2 3 · 3 2 · 7 1 ,
3) выписать все простые делители (множители) каждого из этих чисел;
4) выбрать наибольшую степень каждого из них, встретившуюся во всех разложениях этих чисел;
5) перемножить эти степени.
Пример . Найти НОК чисел: 168, 180 и 3024.
Решение . 168 = 2 · 2 · 2 · 3 · 7 = 2 3 · 3 1 · 7 1 ,
180 = 2 · 2 · 3 · 3 · 5 = 2 2 · 3 2 · 5 1 ,
3024 = 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 = 2 4 · 3 3 · 7 1 .
Выписываем наибольшие степени всех простых делителей и перемножаем их:
НОК = 2 4 · 3 3 · 5 1 · 7 1 = 15120.
Определение. Наибольшее натуральное число, на которое делятся без остатка числа а и b, называют наибольшим общим делителем (НОД) этих чисел.
Найдём наибольший общий делитель чисел 24 и 35.
Делителями 24 будут числа 1, 2, 3, 4, 6, 8, 12, 24, а делителями 35 будут числа 1, 5, 7, 35.
Видим, что числа 24 и 35 имеют только один общий делитель — число 1. Такие числа называют взаимно простыми .
Определение. Натуральные числа называют взаимно простыми , если их наибольший общий делитель (НОД) равен 1.
Наибольший общий делитель (НОД) можно найти, не выписывая всех делителей данных чисел.
Разложим на множители числа 48 и 36, получим:
48 = 2 * 2 * 2 * 2 * 3, 36 = 2 * 2 * 3 * 3.
Из множителей, входящих в разложение первого из этих чисел, вычеркнем те, которые не входят в разложение второго числа
(т. е. две двойки).
Остаются множители 2 * 2 * 3. Их произведение равно 12. Это число и является наибольшим общим делителем чисел 48 и 36.
Так же находят наибольший общий делитель трёх и более чисел.
Чтобы найти наибольший общий делитель
2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
3) найти произ ведение оставшихся множителей.
Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.
Например, наибольшим общим делителем чисел 15, 45, 75 и 180 будет число 15, так как на него делятся все остальные числа: 45, 75 и 180.
Наименьшее общее кратное (НОК)
Определение. Наименьшим общим кратным (НОК) натуральных чисел а и Ь называют наименьшее натуральное число,
которое кратно и a, и b. Наименьшее общее кратное (НОК) чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на
простые множители: 75 = 3 * 5 * 5, а 60 = 2 * 2 * 3 * 5.
Наименьшее общее кратное (НОК) чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на
простые множители: 75 = 3 * 5 * 5, а 60 = 2 * 2 * 3 * 5.
Выпишем множители, входящие в разложение первого из этих чисел, и добавим к ним недостающие множители 2 и 2 из разложения
второго числа (т.е. объединяем множители).
Получаем пять множителей 2 * 2 * 3 * 5 * 5, произведение которых равно 300. Это число является наименьшим общим кратным чисел 75 и 60.
Так же находят наименьшее общее кратное для трёх и более чисел.
Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) выписать множители, входящие в разложение одного из чисел;
3) добавить к ним недостающие множители из разложений остальных чисел;
4) найти произведение получившихся множителей.
Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных
чисел.
Например, наименьшим общим кратным чисел 12, 15, 20 и 60 будет число 60, так как оно делится на все данные числа.
Пифагор (VI в. до н. э.) и его ученики изучали вопрос о делимости чисел. Число, равное сумме всех его делителей (без самого числа),
они называли совершенным числом. Например, числа 6 (6 = 1 + 2 + 3), 28 (28 = 1 + 2 + 4 + 7 + 14) совершенные. Следующие совершенные
числа — 496, 8128, 33 550 336. Пифагорейцы знали только первые три совершенных числа. Четвёртое — 8128 — стало известно в I в. н. э.
Пятое — 33 550 336 — было найдено в XV в. К 1983 г. было известно уже 27 совершенных чисел. Но до сих пор учёные не знают, есть ли
нечётные совершенные числа, есть ли самое большое совершенное число.
Интерес древних математиков к простым числам связан с тем, что любое число либо простое, либо может быть представлено в виде
произведения простых чисел, т. е. простые числа — это как бы кирпичики, из которых строятся остальные натуральные числа.
Вы, наверное, обратили внимание, что простые числа в ряду натуральных чисел встречаются неравномерно — в одних частях ряда их больше,
в других — меньше. Но чем дальше мы продвигаемся по числовому ряду, тем реже встречаются простые числа. Возникает вопрос: существует
ли последнее (самое большое) простое число? Древнегреческий математик Евклид (III в. до н. э.) в своей книге «начала», бывшей на
протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т. е. за каждым простым числом
есть ещё большее простое число.
Но чем дальше мы продвигаемся по числовому ряду, тем реже встречаются простые числа. Возникает вопрос: существует
ли последнее (самое большое) простое число? Древнегреческий математик Евклид (III в. до н. э.) в своей книге «начала», бывшей на
протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т. е. за каждым простым числом
есть ещё большее простое число.
Для отыскания простых чисел другой греческий математик того же времени Эратосфен придумал такой способ. Он записывал все числа
от 1 до какого-то числа, а потом вычёркивал единицу, которая не является ни простым, ни составным числом, затем вычёркивал через
одно все числа, идущие после 2 (числа, кратные 2, т. е. 4, 6, 8 и т. д.). Первым оставшимся числом после 2 было 3. Далее
вычёркивались через два все числа, идущие после 3 (числа, кратные 3, т. е. 6, 9, 12 и т. д.). в конце концов оставались
невычеркнутыми только простые числа.
Наибольший общий делитель. Наименьшее общее кратное.
 Часть 2. НОК (Слупко М.В.) 6 класс онлайн-подготовка на Ростелеком
Часть 2. НОК (Слупко М.В.) 6 класс онлайн-подготовка на РостелекомНаименьшее общее кратное
Числа, которые делятся на 10, мы называем кратными 10. Например, 30 или 50 кратны 10. 28 кратно 14. Числа, которые делятся одновременно и на 10, и на 14, естественно называть общими кратными 10 и 14.
Общих кратных мы можем найти сколько угодно. Например, 140, 280 и т. д.
Естественный вопрос: как найти самое меньшее из общих кратных, наименьшее общее кратное?
Из найденных кратных для 10 и 14 пока наименьшее – это 140. Но является ли оно наименьшим общим кратным?
Разложим наши числа на множители:
Сконструируем такое число, которое делится на 10 и на 14. Чтобы делиться на 10, нужно иметь множители 2 и 5. Чтобы делиться на 14, нужно иметь множители 2 и 7. Но 2 уже есть, осталось добавить 7. Полученное число 70 – это общее кратное для 10 и 14. При этом не получится построить число меньше этого, чтобы оно тоже было общим кратным.
Значит, это и есть наименьшее общее кратное. Для него мы используем обозначение НОК.
Найдем НОД и НОК для чисел 182 и 70.
Примеры для самостоятельного решения
Самостоятельно вычислите:
1.
2.
3.
Проверяем:
1)
2)
3)
Дополнительные сведения
Чтобы понять, что такое НОД и НОК, не обойтись без разложения на множители. Но, когда мы уже поняли, что это такое, уже не обязательно каждый раз раскладывать на множители.
Например:
Вы можете легко убедиться, что для двух чисел, где одно делится на другое, меньшее является их НОДом, а большее – НОКом. Попробуйте сами объяснить, почему это так.
Задача
Длина шага папы – 70 см, а у маленькой дочери – 15 см. Они начинают идти, поставив ноги на одну отметку. Какое расстояние они пройдут, чтобы их ноги опять встали вровень?
Какое расстояние они пройдут, чтобы их ноги опять встали вровень?
Папа и дочь начинают движение. Сначала ноги находятся на одной отметке. Пройдя несколько шагов у них ноги снова встали на одну отметку. Значит, и у папы, и дочери получилось целое количество шагов до этой отметки. Значит, расстояние до нее должно делиться на длину шага и папы, и дочери.
То есть мы должны найти :
То есть это случится через 210 см = 2 м 10 см.
Нетрудно понять, что папа сделает 3 шага, а дочь – 14 (рис. 1).
Рис. 1. Иллюстрация к задаче
НОД и НОК как пересечение и объединение множеств
Задача 1
У Пети в сети «ВКонтакте» 100 друзей, а у Вани – 200. Сколько всего друзей у Пети и Вани вместе, если общих друзей 30?
Ответ 300 – неверный, ведь у них могут быть общие друзья.
Решим эту задачу так. Изобразим множество всех друзей Пети кругом. Изобразим множество друзей Вани другим кругом, побольше.
Эти круги имеют общую часть. Там находятся общие друзья. Эта общая часть называется «пересечение» двух множеств. То есть множество общих друзей – это пересечение множеств друзей каждого.
Рис. 2. Круги множеств друзей
Если общих друзей 30, то слева 70 – это друзья только Петины, а 170 – только Ванины (см. Рис. 2).
Сколько всего?
Всё большое множество, состоящее из двух кругов, называется объединением двух множеств.
На самом деле ВК сам решает за нас задачу пересечения двух множеств, он сразу указывает множество общих друзей, когда вы заходите на страничку другого человека.
Ситуация с НОДом и НОКом двух чисел очень похожа.
Задача 2
Рассмотрим два числа: 126 и 132.
Их простые множители изобразим в кругах (см. Рис. 3).
Рис. 3. Круги с простыми множителями
Пересечение множеств – это общие делители. Из них состоит НОД.
Объединение двух множеств дает нам НОК.
= 2772
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт math-prosto.ru (Источник)
2. Интернет-сайт bymath.net (Источник)
3. Интернет-сайт «Школьный помощник» (Источник)
Домашнее задание
1. В портовом городе начинаются три туристских теплоходных рейса, первый из которых длится 15 суток, второй – 20 и третий – 12 суток. Вернувшись в порт, теплоходы в этот же день снова отправляются в рейс. Сегодня из порта вышли теплоходы по всем трем маршрутам. Через сколько суток они впервые снова вместе уйдут в плавание? Какое количество рейсов сделает каждый теплоход?
В портовом городе начинаются три туристских теплоходных рейса, первый из которых длится 15 суток, второй – 20 и третий – 12 суток. Вернувшись в порт, теплоходы в этот же день снова отправляются в рейс. Сегодня из порта вышли теплоходы по всем трем маршрутам. Через сколько суток они впервые снова вместе уйдут в плавание? Какое количество рейсов сделает каждый теплоход?
2. Найдите НОК чисел:
a) 6 и 8
b) 6 и 9
c) 12 и 30
d) 3 и 4
3. Найдите простые множители наименьшего общего кратного чисел:
, и , если: , , .
НОД и НОК 6 класс презентация, доклад, проект
«НОД и НОК»
Учебная презентация
по математике, 6 класс.
Учитель математики
МБОУ «Новолавельская СОШ №3»
Никифорова Анна Михайловна
Повтори правила
НОД
Разложение на
простые
множители
НОК
НОД – наибольший
общий делитель –
это наибольшее
число, делящее
каждое из данных
чисел.
НОК – наименьшее
общее кратное –
это наименьшее
число, делящееся
на каждое из данных
чисел.
Разложить на простые
множители – представить
число в виде произведения
простых множителей.
Разложение чисел на простые множители
12
2
3
2
6
1
3
12 = 2●2●3
12 = 22●3
3276 = 22 ●32●7●13
3276 = 2●2●3●3●7●13
1
13
13
7
91
3
273
3
819
2
1638
2
3276
Разложение чисел на простые множители
220
2●5
11
2
22
1
11
220 = 22●5●11
8000 = 26●53
1
2
2
2
4
2
8
2●5●2●5●2●5
8000
Разложи числа на простые множители:
16 = 24
18 = 2●32
72 = 23●32
150 = 2●3●52
Проверь себя!
16, 18, 72, 150
= 12
●
●
3
2
2
Нахождение наибольшего общего делителя (НОД) чисел 24 и 36.
12
2
3
2
6
1
3
НОД(24; 36) =
НОД(24; 36) = 22●3
24
2
1
3
3
3
9
2
18
2
36
= 12
24 = 23●3
36 = 22●32
К последнему
слайду
1. Разложить данные числа на простые множители.
2. Выписать все простые множители, которые одновременно входят в каждое из полученных разложений.
Т. е. каждый множитель взять с наименьшим из показателей степени, с которым он входит в разложения данных чисел.
3. Составить произведение из этих множителей и вычислить его.
Алгоритм нахождения наибольшего общего делителя
К последнему
слайду
НОД(16; 12) = 4
НОД(30; 45) = 15
Проверь себя!
НОД(16; 12), НОД(30; 45)
Вычисли:
= 72
= 72
2
3
2
2
Нахождение наименьшего общего кратного (НОК) чисел 24 и 36.
12
2
3
2
6
1
3
НОК (24; 36) =
НОК (24; 36) = 23●32
24
2
1
3
3
3
9
2
18
2
36
2●2●2●3
●3
36 = 22●32
24 = 23●3
К последнему
слайду
1. Разложить данные числа на простые множители.
2. Выписать все простые множители одного числа и добавить те простые множители другого числа, которые не входят в разложение первого числа.
Т. е. каждое из выписанных простых чисел взять с наибольшим из показателей степени, с которым оно входит в разложения данных чисел.
3. Составить произведение из этих множителей и вычислить его.
Алгоритм нахождения наименьшего общего кратного
К последнему
слайду
НОК(18; 12) = 36
НОК(15; 10) = 30
НОК(18; 12), НОК(15; 10)
Проверь себя!
Вычисли:
Я знаю. ..
..
… алгоритм
нахождения
наибольшего
общего делителя
… алгоритм
нахождения
наименьшего
общего кратного
… находить
наименьшее
общее кратное
… находить
наибольший
общий делитель
Я умею…
У меня
получится…
тест
Выход
Ответы:
Ответы:
Ответы:
Ответы:
Тест
12
6
4
НОД (48; 84)
Верно!
У
90
15
60
НОК (45; 30)
Верно!
М
16
20
32
НОД (80; 64)
Верно!
Н
75
5
375
НОК (25; 15)
Верно!
И
Ответы:
24
12
72
НОД (72; 120)
Верно!
Ц
Ответы:
48
16
72
НОК (16; 24)
Верно!
А
К последнему
слайду
Список литературы:
1. «Математика, 6 класс» — учебник. Авторы: И. И. Зубарева, А. Г. Мордкович. Изд. «Мнемозина», Москва, 2010.
«Математика, 6 класс» — учебник. Авторы: И. И. Зубарева, А. Г. Мордкович. Изд. «Мнемозина», Москва, 2010.
2. «Математика, 6 класс» — поурочные планы по учебнику И. И. Зубаревой, А. Г. Мордковича. Автор: Л. А. Тапилина. Изд. «Учитель», Волгоград.
Скачать презентацию
Наименьшее общее кратное — презентация онлайн
1. Наименьшее общее кратное
МОУ СОШ № 46, г. Хабаровск28.01.
Классная работа
Цели урока:
Образовательная: ввести понятие наименьшего
общего
кратного;
формировать
навык
нахождения наибольшего общего делителя;
Воспитательная: формирование интереса к
познавательному процессу; воспитание чувства
взаимопомощи и математической культуры;
Развивающая: развитие логического мышления,
кругозора, внимания, умения систематизировать
и применять полученные знания.
Самостоятельная
работа
1 вариант
2 вариант
Найдите
НОД (55; 88)
НОД (72; 96)
НОД (720; 90)
НОД (15; 25; 35)
Найдите
НОД (44; 99)
НОД (70; 630)
НОД (64; 80)
НОД (15; 27; 33)
4.
 Задача.От одной пристани к другой ходят два катера.
Задача.От одной пристани к другой ходят два катера.Начинают работу одновременно в 8 часов утра.
Первый катер на рейс туда и обратно тратит
2 ч, а второй – 3ч.
Через какое наименьшее время оба катера
опять окажутся на первой пристани, и сколько
рейсов за это время сделает каждый катер?
Сколько раз за сутки эти катера встретятся на
первой пристани, и в какое время это будет
происходить?
5. Решение.
1. Искомое время должно делиться без остаткаи на 2, и на 3, то есть должно быть кратным
числам 2 и 3.
Запишем числа, кратные 2 и 3:
Числа, кратные 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24
Числа, кратные 3:
3, 6, 9, 12, 15, 18, 21, 24
Подчеркните общие кратные чисел 2 и 3
6, 12, 18, 24
6. Решение.
6, 12, 18, 24Назовите наименьшее кратное 2 и 3.
Наименьшее кратное — 6
Значит, через 6 часов после начала работы два
катера одновременно окажутся на первой пристани
7. Решение.
 Сколько рейсов за это время сделает каждый
Сколько рейсов за это время сделает каждыйкатер?
1 катер – 3 рейса, 2 катер – 2 рейса
6 : 2 =3 ( 1 катер – 3 рейса )
6 : 3 = 2 (2 катер – 2 рейса)
8. Решение.
Сколько раз за сутки эти катера встретятся напервой пристани?
24 : 6 = 4 раза
9. Решение.
В какое время это будет происходить?8 + 6 = 14 ч, 14 + 6 = 20 ч, 20 + 6 = 2 ч ночи,
2 + 6 = 8 ч утра.
10. Определение.
• Наименьшее натуральное число,которое делится на каждое из данных
натуральных чисел, называется
наименьшим общим кратным.
• Обозначение: НОК(2; 3) = 6
11. Алгоритм нахождения НОК .
1.2.
3.
Разложить все числа на простые
множители.
Написать разложение одного из чисел
(лучше наибольшего).
Дополнить данное разложение теми
множителями из разложения других
чисел, которые не вошли в написанное
разложение.
12. Найдите НОК.
• НОК (75; 60)• НОК (180; 45; 60)
• НОК (12; 35)
• Сначала надо проверить, не делится ли большее
число на другие числа.

• Если да, то большее число и будет НОК чисел.
13. Домашнее задание
• П. 3.6• № 668(г,д,е)
14. Наименьшее общее кратное.
30.01.Классная работа.
15. Работаем устно.
«Я самый внимательный»
Хлопните в ладоши, если число кратно 2
Покажите фонарики, если число кратно 5
Топайте ногами, если число кратно 10
• 15
435
• 67 226
• 560
539
1000
38
3255
16. Повторение.
Выполните действия:35 * 17 – 35 * 16 + 65 * 99 – 65 * 98=
=(35 * 17 – 35 * 16) + (65 * 99 – 65 * 98)
=35*(17 – 16) + 65*(99 – 98) =
=35 * 1 + 65 * 1 = 35 + 65 = 100
17. Составьте число.
• Составьте четырехзначноечисло, записанное с помощью
цифр 1; 7; 5; 8, кратное 2; 5; 3
• 1578; 1875; 1515
18. Найдите НОК.
• НОК (75; 60)• НОК (180; 45; 60)
• НОК (12; 35)
• Сначала надо проверить, не делится ли большее
число на другие числа.
• Если да, то большее число и будет НОК чисел.

19. Найдите НОК.
• НОК (32; 56)• НОК (132; 72)
• НОК (36; 84; 124)
• НОК (25; 245: 305)
20. Решите уравнения:
• (у – 35) + 12 = 32• 56 – (х + 12) = 24
• 55 – (х – 15) = 30
У=55
Х=20
Х=40
21. Домашнее задание
• Повторить определения делителя,кратного, НОД, НОК, алгоритмы их
нахождения.
• № 676 (а,б,в)
22. Наименьшее общее кратное.
25.01.Классная работа.
23. Цифровой диктант.
Если утверждение верно, пишите 1, если нет – 0.1. Делителем натурального числа а
называют натуральное число, на которое
а делится без остатка.
2. Цифры 0, 2, 4, 6, 8 – называются
нечетными, а цифры 3, 5, 7, 9 – четными.
3. Если сумма цифр делится на 5, то и все
число делится на 5.
24. Цифровой диктант.
Если утверждение верно, пишите 1, если нет – 0.4. Если запись числа оканчивается на 3, то все
число делится на 3.
5. Число 1 является делителем любого числа.

6. Числа, делящиеся на 2 без остатка
называются четными.
7. Любое натуральное число имеет
определенное количество кратных.
25. Цифровой диктант.
Если утверждение верно, пишите 1, если нет – 0.8. Кратным натурального числа а называют
натуральное число, которое делится с остатком на а.
9. Числа, которые при делении на 2 дают остаток 1,
называются нечетными.
10. Если сумма цифр числа делится на 9, то и все число
делится на 9.
11. Число 1 – ни составное, ни простое.
12. Натуральное число называется составным, если оно
имеет только два делителя.
13. Натуральное число называется простым, если
оно имеет только один делитель.
26. Решите уравнения:
• (у – 35) + 12 = 32• 56 – (х + 12) = 24
• 55 – (х – 15) = 30
У=55
Х=20
Х=40
27. Выполните задание.
• Найдите НОД: 24 и 38; 121 и55; 268 и 384
• Найдите НОК: 18 и 27; 7425 и
4455
28. Домашнее задание
• Повторить определения делителя,кратного, НОД, НОК, алгоритмы их
нахождения.

• № 676 (а,б,в)
29. Наименьшее общее кратное.
31.01.Классная работа.
30. Работаем устно.
Найдите НОД и НОК чисел.
НОД = 5; НОК = 15
5 и 15
12 и 9
НОД = 3; НОК = 36
НОД = 8; НОК = 48
16 и 24
НОД = 1; НОК = 15
3и5
16 и 10
НОД = 2; НОК = 80
НОД = 9; НОК = 36
36 и 9
НОД = 3; НОК = 210
21 и 30
12 и 15
НОД = 3; НОК = 60
31. Фронтальный опрос.
• Какие остатки могут получится приделении некоторого числа на 5?
• 1, 2, 3, 4
• Приведите пример числа, которое при
делении на 5 дает остаток 3 и объясните
как вы нашли это число.
• Надо любое натуральное число умножить
на 5 и прибавить 3.
32. Фронтальный опрос.
• Может ли в разложении числа на простыемножители содержаться число 8.
• Нет, оно составное.
• Назовите все четные числа,
расположенные между числами 67 и 76.
• 68, 70, 72, 74
• Шоколадка стоит рубль и ещё
полшоколадки.
 Сколько стоит шоколадка?
Сколько стоит шоколадка?• 2 рубля, потому что полшоколадки не
продается.
33. Задачи на НОД и НОК.
• В одной группе 36 спортсменов, а вдругой 40 спортсменов. Сколько имеется
возможностей для построения
спортсменов так, чтобы группы шли
одна за другой одинаковыми рядами?
• НОД (36; 40) =
4
• Ответ: 4 человека в каждом ряду.
34. Задачи на НОД и НОК.
• Туристические группы возвращаются набазу каждые 16 дней, 10 дней и 20 дней.
Через какое наименьшее количество дней
встретятся инструкторы, если
отправятся в поход одновременно?
• НОК (16; 10; 20) =
• Ответ: через 80 дней.
80
35. Классная работа
• Разложите на простые множителичисло 6552.
• Докажите, что числа 468 и 875
взаимно простые числа.
36. Домашнее задание.
• № 684, 66437. Подготовка к контрольной работе.
01.02.Классная работа.
38. Работаем устно.
Найдите НОД и НОК чисел:
5и9
НОД = 1 НОК =45
НОД = 6 НОК =12
6 и 12
НОД = 1 НОК =24
3и8
НОД = 3 НОК =189
27 и 21
НОД = 1 НОК =11
11 и 1
НОД = 3 НОК =72
24 и 18
39.
 Какие из чисел: 501, 432, 83, 954 – делятся на 3.• Разложите на простые
Какие из чисел: 501, 432, 83, 954 – делятся на 3.• Разложите на простыемножители число 819.
• Какие из чисел: 720, 478,
115, 551 – делятся на 2.
40. Найдите НОД и НОК
• 68 и 51• 72 и 60
41. Повторение.
• Выполните действия:279911
343 * ( 324378 : 54 – 4862 ) + 777
18408 : ( 268 * 75 – 19746 ) + 959
1011
42. Домашнее задание:
• Подготовиться к контрольнойработе
Связь нок и нод
В этой статье всесторонне рассмотрено наименьшее общее кратное (НОК) данных чисел. Сначала дано определение общих кратных, на основании которого дано определение наименьшего общего кратного. После этого введены обозначения НОК, и приведены примеры. Дальше рассмотрена теорема, устанавливающая связь НОК и НОД данных чисел. В заключение показано, как нахождение наименьшего общего кратного трех и большего количества чисел сводится к последовательному вычислению НОК двух чисел.
Навигация по странице.
Общие кратные – определение, примеры
Если знать, что такое кратные числа, то определение общих кратных воспримется очень естественно. Мы будем говорить лишь об общих кратных таких целых чисел, которые отличны от нуля.
Общие кратные данных целых чисел – это такие целые числа, кратные всех данных чисел. Другими словами, общим кратным данных целых чисел называется любое целое число, которое делится на каждое из данных чисел.
Определение общих кратных относится как к двум целым числам, так и к трем, и к большему количеству целых чисел. То есть, мы можем говорить об общих кратных двух, трех, четырех и так далее целых чисел.
Приведем примеры общих кратных.
По определению число 12 является общим кратным двух чисел 2 и 3 , так как 12 кратно и двум и трем. Число 12 также является общим кратным трех чисел 2 , 3 и 4 . Это же число 12 есть общее кратное двенадцати чисел: ±1 , ±2 , ±3 , ±4 , ±6 , ±12 . Все приведенные примеры также имеют место, если вместо 12 взять число −12 .
С другой стороны общее кратное двух чисел 2 и 3 это не только число 12 , целые числа 6 , −24 , 72 , 468 , −100 010 004 также являются общими кратными чисел 2 и 3 . Более того, существуют и другие общие кратные чисел 2 и 3 .
А вот числа 16 , −27 , 5 009 , 27 001 не являются общими кратными чисел 2 и 3 . Действительно, 16 делится на 2 , но не делится на 3 ; число −27 делится на 3 , но не делится на 2 ; а числа 5 009 и 27 001 не делятся ни на 2 , ни на 3 .
Отдельно отметим, что число нуль является общим кратным любого множества ненулевых целых чисел.
Из свойств делимости следует, что если некоторое целое число s является общим кратным данных чисел, то число −s , также является общим кратным данных чисел, так как множества делителей противоположных чисел s и −s совпадают. То есть, общие делители данных чисел могут быть как положительными, так и отрицательными числами. Из выше рассмотренных примеров это отчетливо видно.
Нужно еще обговорить два нюанса, которые мы сформулируем в виде вопросов и дадим на них ответы.
Всегда ли существует общее кратное данных целых чисел»? Да, всегда. Покажем это. Пусть нам даны k целых чисел a1, a2, …, ak . Рассмотрим число, равное произведению a1·a2·…·ak . Свойства делимости позволяют утверждать, что это число делится на каждое из чисел a1, a2, …, ak , следовательно, является общим кратным данных чисел.
А сколько всего общих кратных имеют данные целые числа? Ответ на поставленный вопрос таков: данные целые числа имеют бесконечно много общих кратных. Действительно, выше мы показали, что общее кратное данных чисел всегда существует, пусть это число s . Тогда любое из чисел s·z , где z – любое целое число, является общим кратным данных чисел. А так как целых чисел бесконечно много, то и общих кратных данных чисел бесконечно много.
В заключение этого пункта скажем, что можно ограничиться рассмотрением общих кратных лишь целых положительных (то есть, натуральных) чисел. Это не ограничит общности, и связано с тем, что множество кратных данного числа и множество кратных числа, противоположного данному, совпадают (что следует из свойств делимости).
Это не ограничит общности, и связано с тем, что множество кратных данного числа и множество кратных числа, противоположного данному, совпадают (что следует из свойств делимости).
Наименьшее общее кратное (НОК) – определение, обозначение и примеры
Среди всех кратных данных чисел особый интерес и особую практическую значимость представляет наименьшее общее кратное (понятие наименьшего числа из данного множества чисел мы ввели, когда изучали сравнение целых чисел). Дадим определение наименьшего общего кратного.
Наименьшее общее кратное данных целых чисел – это наименьшее положительное общее кратное этих чисел.
В предыдущем пункте мы сказали, что данные числа всегда имеют общее кратное, причем, если s – общее кратное этих чисел, то и −s , также является общим кратным. Следовательно, наименьшее общее кратное данных чисел всегда существует.
Часто при описании наименьшего общего кратного используют аббревиатуру НОК. Также для краткой записи принято обозначение наименьшего общего кратного чисел a1, a2, …, ak вида НОК(a1, a2, …, ak) . Также в математической литературе можно встретить обозначение наименьшего кратного чисел a1, a2, …, ak вида [a1, a2, …, ak] .
Также в математической литературе можно встретить обозначение наименьшего кратного чисел a1, a2, …, ak вида [a1, a2, …, ak] .
Приведем примеры наименьших общих кратных. Например, НОК двух целых чисел 5 и 6 равно 30 , то есть, НОК(5, 6)=30 , а наименьшее общее кратное четырех чисел 2 , −12 , 15 и −3 равно 60 , то есть, НОК(2, −12, 15, −3)=60 .
Следует отметить, что в предыдущих примерах далеко не очевидно, что указанные числа являются наименьшими общими кратными соответствующих чисел. Этим мы хотим сказать, что в общем случае не удается сразу сказать, чему равен НОК данных чисел, и приходится провести вычисление наименьшего общего кратного.
Связь между НОК и НОД
Наименьшее общее кратное двух чисел непосредственно связано с наибольшим общим делителем этих чисел. Эта связь между НОД и НОК определяется следующей теоремой.
Наименьшее общее кратное двух положительных целых чисел a и b равно произведению чисел a и b , деленному на наибольший общий делитель чисел a и b , то есть, НОК(a, b)=a·b:НОД(a, b) .
Пусть М – какое-нибудь кратное чисел a и b . То есть, М делится на a , и по определению делимости существует некоторое целое число k такое, что справедливо равенство M=a·k . Но М делится и на b , тогда a·k делится на b .
Обозначим НОД(a, b) как d . Тогда можно записать равенства a=a1·d и b=b1·d , причем a1=a:d и b1=b:d будут взаимно простыми числами. Следовательно, полученное в предыдущем абзаце условие, что a·k делится на b , можно переформулировать так: a1·d·k делится на b1·d , а это в силу свойств делимости эквивалентно условию, что a1·k делится на b1 .
В этом случае по свойству взаимно простых чисел, так как a1·k делится на b1 , и a1 не делится на b1 ( a1 и b1 – взаимно простые числа), то на b1 должно делиться k . Тогда должно существовать некоторое целое число t , для которого k=b1·t , а так как b1=b:d , то k=b:d·t . Подставив в равенство M=a·k вместо k его выражение вида b:d·t , приходим к равенству M=a·b:d·t .
Подставив в равенство M=a·k вместо k его выражение вида b:d·t , приходим к равенству M=a·b:d·t .
Так мы получили равенство M=a·b:d·t , которое дает вид всех общих кратных чисел a и b . Из того, что a и b числа положительные по условию следует, что при t=1 мы получим их наименьшее положительное общее кратное, которое равно a·b:d . Этим доказано, что НОК(a, b)=a·b:НОД(a, b) .
Доказанная связь между наименьшим общим кратным и наибольшим общим делителем двух данных чисел позволяет найти НОК через НОД.
Также нужно записать два важных следствия из рассмотренной теоремы.
Общие кратные двух чисел совпадают с кратными их наименьшего общего кратного.
Это действительно так, так как любое общее кратное M чисел a и b определяется равенством M=НОК(a, b)·t при некотором целом значении t .
Наименьшее общее кратное взаимно простых положительных чисел a и b равно их произведению.
Обоснование этого факта достаточно очевидно. Так как a и b взаимно простые, то НОД(a, b)=1 , следовательно, НОК(a, b)=a·b:НОД(a, b)=a·b:1=a·b .
Наименьшее общее кратное трех и большего количества чисел
Нахождение наименьшего общего кратного трех и большего количества чисел можно свести к последовательному нахождению НОК двух чисел. Как это делается, указано в следующей теореме.
Пусть даны целые положительные числа a1, a2, …, ak , наименьшее общее кратное mk этих чисел находится при последовательном вычислении m2=НОК(a1, a2) , m3=НОК(m2, a3) , …, mk=НОК(mk-1, ak) .
Доказательство базируется на первом следствии из теоремы, разобранной в предыдущем пункте. Общие кратные чисел a1 и a2 совпадают с кратными их НОК, то есть, совпадают с кратными числа m2 . Тогда общие кратные чисел a1 , a2 и a3 совпадают с общими кратными чисел m2 и a3 , следовательно, совпадают с кратными числа m3 . И так далее. Общие кратные чисел a1, a2, …, ak совпадают с общими кратными чисел mk-1 и ak , следовательно, совпадают с кратными числа mk . А так как наименьшим положительным кратным числа mk является само число mk , то наименьшим общим кратным чисел a1, a2, …, ak является mk .
И так далее. Общие кратные чисел a1, a2, …, ak совпадают с общими кратными чисел mk-1 и ak , следовательно, совпадают с кратными числа mk . А так как наименьшим положительным кратным числа mk является само число mk , то наименьшим общим кратным чисел a1, a2, …, ak является mk .
Приступим к изучению наименьшего общего кратного двух и более чисел. В разделе мы дадим определение термина, рассмотрим теорему, которая устанавливает связь между наименьшим общим кратным и наибольшим общим делителем, приведем примеры решения задач.
Общие кратные – определение, примеры
В данной теме нас будет интересовать только общие кратные целых чисел, отличных от нуля.
Общее кратное целых чисел – это такое целое число, которое кратно всем данным числам. Фактически, это любое целое число, которое можно разделить на любое из данных чисел.
Определение общих кратных чисел относится к двум, трем и большему количеству целых чисел.
Согласно данному выше определению для числа 12 общими кратными числами будут 3 и 2 . Также число 12 будет общим кратным для чисел 2 , 3 и 4 . Числа 12 и – 12 являются общими кратными числами для чисел ± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 12 .
В то же время общим кратным числом для чисел 2 и 3 будут числа 12 , 6 , − 24 , 72 , 468 , − 100 010 004 и целый ряд любых других.
Если мы возьмем числа, которые делятся на первое число из пары и не делятся на второе, то такие числа не будут общими кратными. Так, для чисел 2 и 3 числа 16 , − 27 , 5 009 , 27 001 не будут общими кратными.
0 является общим кратным для любого множества целых чисел, отличных от нуля.
Если вспомнить свойство делимости относительно противоположных чисел, то получается, что некоторое целое число k будет общим кратным данных чисел точно также, как и число – k . Это значит, что общие делители могут быть как положительными, так и отрицательными.
Для всех ли чисел можно найти НОК?
Общее кратное можно найти для любых целых чисел.
Предположим, что нам даны k целых чисел a 1 , a 2 , … , a k . Число, которое мы получим в ходе умножения чисел a 1 · a 2 · … · a k согласно свойству делимости будет делиться на каждый из множителей, который входил в изначальное произведение. Это значит, что произведение чисел a 1 , a 2 , … , a k является наименьшим общим кратным для этих чисел.
Сколько всего общих кратных могут иметь данные целые числа?
Группа целых чисел может иметь большое количество общих кратных. Фактически, их число бесконечно.
Предположим, что у нас есть некоторое число k . Тогда произведение чисел k · z , где z – это целое число, будет являться общим кратным чисел k и z . С учетом того, что количество чисел бесконечно, то и количество общих кратных бесконечно.
Наименьшее общее кратное (НОК) – определение, обозначение и примеры
Вспомним понятие наименьшего числа из данного множества чисел, которое мы рассматривали в разделе «Сравнение целых чисел». С учетом этого понятия сформулируем определение наименьшего общего кратного, которое имеет среди всех общих кратных наибольшее практическое значение.
С учетом этого понятия сформулируем определение наименьшего общего кратного, которое имеет среди всех общих кратных наибольшее практическое значение.
Наименьшее общее кратное данных целых чисел – это наименьшее положительное общее кратное этих чисел.
Наименьшее общее кратное существует для любого количества данных чисел. Наиболее употребимой для обозначения понятия в справочной литературе является аббревиатура НОК. Краткая запись наименьшего общего кратного для чисел a 1 , a 2 , … , a k будет иметь вид НОК ( a 1 , a 2 , … , a k ) .
Наименьшее общее кратное чисел 6 и 7 – это 42 . Т.е. НОК ( 6 , 7 ) = 42 . Наименьшее общее кратное четырех чисел – 2 , 12 , 15 и 3 будет равно 60 . Краткая запись будет иметь вид НОК ( – 2 , 12 , 15 , 3 ) = 60 .
Не для всех групп данных чисел наименьшее общее кратное очевидно. Часто его приходится вычислять.
Связь между НОК и НОД
Наименьшее общее кратное и наибольший общий делитель связаны между собой. Взаимосвязь между понятиями устанавливает теорема.
Взаимосвязь между понятиями устанавливает теорема.
Наименьшее общее кратное двух положительных целых чисел a и b равно произведению чисел a и b , деленному на наибольший общий делитель чисел a и b , то есть, НОК ( a , b ) = a · b : НОД ( a , b ) .
Предположим, что мы имеем некоторое число M , которое кратно числам a и b . Если число M делится на a , также существует некоторое целое число z , при котором справедливо равенство M = a · k . Согласно определению делимости, если M делится и на b , то тогда a · k делится на b .
Если мы введем новое обозначение для НОД ( a , b ) как d , то сможем использовать равенства a = a 1 · d и b = b 1 · d . При этом оба равенства будут взаимно простыми числами.
Мы уже установили выше, что a · k делится на b . Теперь это условие можно записать следующим образом:
a 1 · d · k делится на b 1 · d , что эквивалентно условию a 1 · k делится на b 1 согласно свойствам делимости.
Согласно свойству взаимно простых чисел, если a 1 и b 1 – взаимно простые числа, a 1 не делится на b 1 при том, что a 1 · k делится на b 1 , то b 1 должно делиться k .
В этом случае уместно будет предположить, что существует число t , для которого k = b 1 · t , а так как b 1 = b : d , то k = b : d · t .
Теперь вместо k подставим в равенство M = a · k выражение вида b : d · t . Это позволяет нам прийти к равенству M = a · b : d · t . При t = 1 мы можем получить наименьшее положительное общее кратное чисел a и b , равное a · b : d , при условии, что числа a и b положительные.
Так мы доказали, что НОК ( a , b ) = a · b : НОД ( a , b ) .
Установление связи между НОК и НОД позволяет находить наименьшее общее кратное через наибольший общий делитель двух и более данных чисел.
Теорема имеет два важных следствия:
- кратные наименьшего общего кратного двух чисел совпадает с общими кратными этих двух чисел;
- наименьшее общее кратное взаимно простых положительных чисел a и b равно их произведению.

Обосновать эти два факта не составляет труда. Любое общее кратное M чисел a и b определяется равенством M = НОК ( a , b ) · t при некотором целом значении t . Так как a и b взаимно простые, то НОД ( a , b ) = 1 , следовательно, НОК ( a , b ) = a · b : НОД ( a , b ) = a · b : 1 = a · b .
Наименьшее общее кратное трех и большего количества чисел
Для того, чтобы найти наименьшее общее кратное нескольких чисел, необходимо последовательно найти НОК двух чисел.
Предположим, что a 1 , a 2 , … , a k – это некоторые целые положительные числа. Для того, чтобы вычислить НОК mk этих чисел, нам необходимо последовательно вычислить m 2 = НОК ( a 1 , a 2 ) , m 3 = НОК ( m 2 , a 3 ) , … , m k = НОК ( m k – 1 , a k ) .
Доказать верность второй теоремы нам поможет первое следствие из первой теоремы, рассмотренной в данной теме. Рассуждения строятся по следующему алгоритму:
- общие кратные чисел a 1 и a 2 совпадают с кратными их НОК, фактически, они совпадают с кратными числа m 2 ;
- общие кратные чисел a 1 , a 2 и a 3 совпадают с общими кратными чисел m 2 и a 3 , следовательно, совпадают с кратными числа m 3 ;
- общие кратные чисел a 1 , a 2 , … , a k совпадают с общими кратными чисел m k – 1 и a k , следовательно, совпадают с кратными числа m k ;
- в связи с тем, что наименьшим положительным кратным числа m k является само число m k , то наименьшим общим кратным чисел a 1 , a 2 , … , a k является m k .

план конспект урока
Скачать:
| Вложение | Размер |
|---|---|
| план конспект | 21.7 КБ |
Предварительный просмотр:
Тема: Решение примеров на нахождение наибольшего общего делителя и наименьшего общего кратного.Связь между НОК и НОД
Тип урока: комбинированный.
- отработка навыков нахождения НОД и НОК;
- применение полученных знаний для решения задач;
- повторение и закрепление признаков делимости, простых и составных чисел.
- наблюдательность, внимание, речь, память, логическое мышление, самостоятельность, интерес к математике через региональный компонент, практическое применение приобретенных знаний, установление межпредметных связей.
- воспитывать у учащихся культуру труда, взаимоуважение, стремление хорошо учиться; воспитывать стремление достигать поставленную цель; уверенности в себе, умение работать в коллективе.

1. Организационный момент Здравствуйте, ребята! Садитесь.
Давайте вспомним, чем мы занимались на предыдущих уроках?
( Мы находили НОД и НОК чисел разными способами и решали задачи)
2. Постановка задачи Сегодня мы с вами обобщим все полученные знания по данной теме. Откройте тетради, запишите число, классная работа, тема: «Нахождение НОД и НОК чисел».
3. Проверка домашнего задания
4. Актуализация знаний Прежде чем приступим к решению заданий, предлагаю вспомнить некоторые правила.
Стратегия «Собери правило» Учащиеся выходят к доске и ставят соответствие нахождения алгоритма НОД и НОК
5. Обобщение и систематизация знаний и умений
Работа в парах Выполнение задания
- НОД (4,12)= Ответ:
- НОД (16,24)= Ответ:
- НОД (30,120)= Ответ:
- НОК (4,12)= Ответ:
- НОК (15,4)= Ответ:
- НОК (22,33)= Ответ:
- НОД (4,16,12)= Ответ:
Связь между НОК и НОД
Наименьшее общее кратное двух чисел непосредственно связано с наибольшим общим делителем этих чисел. Эта связь между НОД и НОК определяется следующей теоремой.
Эта связь между НОД и НОК определяется следующей теоремой.
Наименьшее общее кратное двух положительных целых чисел a и b равно произведению чисел a и b , деленному на наибольший общий делитель чисел a и b , то есть, НОК(a, b)=a·b:НОД(a, b) .
Пусть М – какое-нибудь кратное чисел a и b . То есть, М делится на a , и по определению делимости существует некоторое целое число k такое, что справедливо равенство M=a·k . Но М делится и на b , тогда a·k делится на b .
Обозначим НОД(a, b) как d . Тогда можно записать равенства a=a 1 ·d и b=b 1 ·d , причем a 1 =a:d и b 1 =b:d будут взаимно простыми числами . Следовательно, полученное в предыдущем абзаце условие, что a·k делится на b , можно переформулировать так: a 1 ·d·k делится на b 1 ·d , а это в силу свойств делимости эквивалентно условию, что a 1 ·k делится на b 1 .
В этом случае по свойству взаимно простых чисел , так как a 1 ·k делится на b 1 , и a 1 не делится на b 1 ( a 1 и b 1 – взаимно простые числа), то на b 1 должно делиться k . Тогда должно существовать некоторое целое число t , для которого k=b 1 ·t , а так как b 1 =b:d , то k=b:d·t . Подставив в равенство M=a·k вместо k его выражение вида b:d·t , приходим к равенству M=a·b:d·t .
Тогда должно существовать некоторое целое число t , для которого k=b 1 ·t , а так как b 1 =b:d , то k=b:d·t . Подставив в равенство M=a·k вместо k его выражение вида b:d·t , приходим к равенству M=a·b:d·t .
Так мы получили равенство M=a·b:d·t , которое дает вид всех общих кратных чисел a и b . Из того, что a и b числа положительные по условию следует, что при t=1 мы получим их наименьшее положительное общее кратное, которое равно a·b:d . Этим доказано, что НОК(a, b)=a·b:НОД(a, b) .
Доказанная связь между наименьшим общим кратным и наибольшим общим делителем двух данных чисел позволяет найти НОК через НОД .
Также нужно записать два важных следствия из рассмотренной теоремы.
- Общие кратные двух чисел совпадают с кратными их наименьшего общего кратного.
Это действительно так, так как любое общее кратное M чисел a и b определяется равенством M=НОК(a, b)·t при некотором целом значении t .
- Наименьшее общее кратное взаимно простых положительных чисел a и b равно их произведению.

Обоснование этого факта достаточно очевидно. Так как a и b взаимно простые, то НОД(a, b)=1 , следовательно, НОК(a, b)=a·b:НОД(a, b)=a·b:1=a·b .
7. Решение простейших задач на нахождение НОК и НОД с использованием
Сегодня на уроке мы повторили с вами разложение числа на простые множители, повторили нахождение НОК и НОД чисел.
Последние новости | Национальный океанографический центр
- Медиа-центр
- Последние новости
Ученые теперь могут измерять толщину арктического морского льда круглый годОпубликовано: 21 сентября 2022 Ученые из Национального океанографического центра (НОЦ) вместе с партнерами из UiT Арктического университета Норвегии теперь могут измерять толщину льда в Арктическом море 365 дней в году с помощью спутников. Помимо того, что… |
Начало исследований по мониторингу морской среды в Северном мореОпубликовано: 20 сентября 2022 Национальный океанографический центр (NOC) приступил к проведению исследований с роботизированной подводной лодкой Boaty McBoatface на вышедших из эксплуатации нефтяных месторождениях у побережья Шетландских островов, чтобы помочь отслеживать и защищать морскую среду в Северном море и поддерживать промышленность. |
Выписка Национального океанографического центраОпубликовано: 8 сентября 2022 г. Совместное заявление Джона Херста, CBE, председателя, и профессора Эда Хилла, CBE, исполнительного директора Национального океанографического центра. «Как и вся страна, да и весь мир, мы опечалены смертью Ее Величества Королевы и выражаем соболезнования ее семье…. |
Инновационный подход к измерению геохимии поровой воды in situОпубликовано: 7 сентября 2022 Ученые из Национального океанографического центра (NOC) успешно протестировали новый подход, помогающий улучшить знания о самых глубоких частях океана. Д-р Анна Лихтшлаг и д-р Эллисон Шаап из NOC работают в сотрудничестве с исследователями из центра… |
Презентации и основные доклады на Challenger 150 Опубликовано: 6 сентября 2022 г. Более 70 представителей Национального океанографического центра (НОЦ) обсудят ключевые вопросы океана на конференции Challenger Society Conference 2022, посвященной 150-летию экспедиции Challenger и празднованию рождения международной и междисциплинарной океанографии…. |
Памяти Стюарта РасбиОпубликовано: 2 сентября 2022 г. Национальный океанографический центр глубоко опечален известием о смерти доктора Стюарта Расби (20 октября 1931 г. – 7 июля 2022 г.). Чтобы отметить его значительный вклад в мировое морское сообщество, его дочь вместе с друзьями и коллегами из NOC составила… |
NOC присоединяется к исследованию по оценке воздействия морских ветряных электростанцийОпубликовано: 1 сентября 2022 г. Ученые из Национального центра океанографии, ведущего британского центра океанологических исследований, присоединяются к совместным усилиям по оценке воздействия морских ветряных электростанций на морские экосистемы. Программа стоимостью 7 миллионов фунтов стерлингов позволит экспертам собирать доказательства для информирования морской политики… |
NOC вносит ключевые данные в отчет BAMS о состоянии климата за 2021 годОпубликовано: 1 сентября 2022 г. Отчет BAMS о состоянии климата за 2021 год, опубликованный вчера (31 августа), содержит всестороннюю обновленную информацию о климатических показателях Земли, заметных погодных явлениях и других данных, собранных станциями мониторинга окружающей среды и инструментами, расположенными на суше, воде, льду и в недрах. .. |
Новое исследование помогает информировать о борьбе с солевыми интрузиямиОпубликовано: 25 августа 2022 Ученые из Национального океанографического центра (NOC) сделали важное новое открытие, которое позволяет лучше понять интрузию соленой воды через эстуарии и может помочь в защите жизненно важных пресноводных ресурсов от растущих рисков проникновения соли из-за. |
Scientist Spotlight — погрузитесь в сумеречную зону с доктором Адрианом МартиномОпубликовано: 19 августа 2022 От необычных существ до его решающей роли в том, как океан поглощает и хранит углерод, Сумеречная зона океана является ключевым объектом исследований для ученых всего мира. В этом месяце в разделе «В центре внимания ученых» мы поговорили с доктором Адрианом Мартином из морских систем… |
Northrop Grumman (NOC) — 6 Графики цен 1999-2022 (История)
Хотите наблюдать и анализировать графики цен акций Northrop Grumman Corporation (NOC) для различных временных диапазонов в истории? Этот отчет поможет вам.
РЕКЛАМА
В этом отчете вы найдете 6 полезных разделов. Ниже приведено содержание, которое поможет вам быстро ориентироваться.
- Northrop Grumman Corporation (noc) 20 лет истории акций
- noc Таблица 10-летних акций
- Northrop Grumman Corporation (noc) График акций за 5 лет (Недавняя история)
- noc Акции Трехлетний график Годовой график акций
- noc
- Northrop Grumman Corporation (noc) График акций за 6 месяцев
Примечание: временные рамки анализа этого отчета относятся к 1 ноября 1999 года и 12 сентября 2022 года.
1 Northrop Grumman Corporation (noc) 20-летняя история котировок акций
Во-первых, давайте посмотрим на долгосрочную диаграмму noc. Продолжительность 20 лет между 1901.11.99 и 12.09.2022.
Примечание. Мы построили приведенную ниже диаграмму с использованием среднегодового значения. цены вместо ежедневных цен. Годовой ценовой график можно рассматривать как сглаженную версию дневного ценового графика. Этот тип сглаженного графика даст вам лучшее представление о долгосрочном движении цены Northrop Grumman Corporation (noc).
В таблице ниже приведены среднегодовые данные. Цены корпорации Northrop Grumman (noc), использованные для построения графика выше. Первые два столбца содержат годы и соответствующее среднее значение. цены на акции. Третий и четвертый столбцы помогут вам понять, как изменялись самые высокие и самые низкие годовые цены с течением времени.
| Год | Цена ($) (и изменение по сравнению с прошлым годом %) | Самая высокая дневная цена ($) (и изменение по сравнению с прошлым годом %) | Самая низкая0 дневная цена2 ($ | ) (And Change From Past Year %) |
|---|---|---|---|---|
| 1999 | 14. 93 93 | 16.2278 | 13.665 | |
| 2000 | 19.77 ( 32.42% ) | 26.302 ( 62.08% ) | 12.2552 ( -10.32% ) | |
| 2001 | 25.96 ( 31.31% ) | 31.5686 ( 20.02% ) | 22.1908 ( 81.07% ) | |
| 2002 | 32.57 ( 25.46% ) | 38.8063 ( 22.93% ) | 25.7007 ( 15.82% ) | |
| 2003 | 26.65 ( -18.18% ) | 29.6234 ( -23.66% ) | 23.4158 ( -8,89% ) | |
| 2004 | 31.42 ( 17.9% ) | 35.2842 ( 19.11% ) | 28.435 ( 21.44% ) | |
| 2005 | 33.90 ( 7.89% ) | 37.4078 ( 6.02% ) | 31.3128 ( 10.12% ) | |
| 2006 | 41.46 ( 22.3% ) | 44. 5037 ( 18.97% ) 5037 ( 18.97% ) | 37.1091 ( 18.51% ) | |
| 2007 | 49.02 ( 18.23% ) | 54.3127 ( 22.04% ) | 42.4059 ( 14.27% ) | |
| 2008 | 42.89 ( -12.51% ) | 53.5804 ( -1.35% ) | 22.4414 ( -47.08% ) | |
| 2009 | 32.50 ( -24.22% ) | 39.0353 ( -27.15% ) | 22.9951 ( 2.47% ) | |
| 2010 | 42.59 ( 31.05% ) | 47.9842 ( 22.93% ) | 37.7108 ( 63.99% ) | |
| 2011 | 47.43 ( 11.36% ) | 55.9626 ( 16.63% ) | 39.1969 ( 3.94% ) | |
| 2012 | 52.49 ( 10.67% ) | 59.1779 ( 5.75% ) | 46.9445 ( 19.77% ) | |
| 2013 | 73.61 ( 40. 24% ) 24% ) | 99.5071 ( 68.15% ) | 54.0187 ( 15.07% ) | |
| 2014 | 109.70 ( 49.03% ) | 134.212 ( 34.88% ) | 95.6069 ( 76.99% ) | |
| 2015 | 149.30 ( 36.1% ) | 171.929 ( 28.1% ) | 126.393 ( 32.2% ) | |
| 2016 | 192.21 ( 28.74% ) | 228.967 ( 33.18% ) | 159.996 ( 26.59% ) | |
| 2017 | 243.07 ( 26.46% ) | 287.473 ( 25.55% ) | 207.126 ( 29.46% ) | |
| 2018 | 290.30 ( 19.43% ) | 334.446 ( 16.34% ) | 212.761 ( 2.72% ) | |
| 2019 | 303.20 ( 4.44% ) | 363.752 ( 8.76% ) | 225.636 ( 6.05% ) | |
| 2020 | 314. 50 ( 3.73% ) 50 ( 3.73% ) | 367.716 ( 1.09% ) | 258.773 ( 14.69% ) | |
| 2021 | 342.49 ( 8.9% ) | 400.348 ( 8.87% ) | 278.447 ( 7.6% ) | |
| 2022 | 444.51 ( 29.79% ) | 492.75 ( 23.08% ) | 365,635 ( 31,31% ) |
Интересное наблюдение:
Наибольшее изменение годовой цены акций произошло между 2021 и 2022 годами. Разница составила 102,02 доллара.
РЕКЛАМА
2 noc 10-летняя диаграмма акций
Примечание. Долгосрочные инвесторы придают большое значение долгосрочным диаграммам (обычно охватывающие десятилетия). 10-летний таймфрейм — популярный диапазон анализа, используемый стоимостными инвесторами.
Теперь давайте посмотрим на 10-летний график акций noc. Диапазон графика находится между 2012-09-14 и 2022-09-12.
Приведенный выше график построен с использованием среднего значения. годовые цены корпорации Northrop Grumman (noc).
годовые цены корпорации Northrop Grumman (noc).
3 Northrop Grumman Corporation (noc) График акций за 5 лет
(Недавняя история)Примечание. Как правило, срок инвестирования около 5 лет можно считать среднесрочным. Таким инвесторам, естественно, было бы интересно узнать данные о доходности акций за последние 5 лет. Эти данные вместе со многими другими показателями помогут им проанализировать доходность в течение следующих 5 лет.
Теперь давайте посмотрим на исторический 5-летний график цен корпорации Northrop Grumman (noc). График ниже построен с использованием avg. месячные цены.
В таблице ниже приведены данные о ценах на NOC за 3, 6, 9 и 12 месяцев за каждый год в течение 5 лет, закончившихся 12 сентября 2022 года. Табличные данные помогут вам отследить динамику цен Northrop Grumman Corporation (noc) за 5 лет.
В приведенной ниже таблице второй столбец содержит среднее значение за месяц. цены, последние два столбца содержат дополнительную информацию. Третий столбец содержит самое высокое дневное закрытие за соответствующий месяц, а последний столбец отображает самое низкое дневное закрытие.
Третий столбец содержит самое высокое дневное закрытие за соответствующий месяц, а последний столбец отображает самое низкое дневное закрытие.
| Month-Year | Price ($) | Highest Daily Price ($) | Lowest Daily Price ($) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 9-2017 | 257.07 | 265.542 | 245.21 | ||||||||
| 12 -2017 | 282.40 | 287.473 | 275.696 | ||||||||
| 3-2018 | 320.36 | 329.987 | 314.39 | ||||||||
| 6-2018 | 300.06 | 315.724 | 285.852 | ||||||||
| 9-2018 | 287.54 | 297.344 | 277.798 | ||||||||
| 12-2018 | 237.43 | 254.141 | 212.761 | ||||||||
| 3-2019 | 258.92 | 271.044 | 249.247 | ||||||||
| 6-2019 | 298.27 | 307.126 | 285.226 | ||||||||
| 9-2019 | 351. 14 14 | 363.752 | 351.14 | 363.752 | 351.14 | 363,752 | 351.14 | 363,752 | 351.14 | 363,752 | .0025 |
| 12-2019 | 329.58 | 333.512 | 323.604 | ||||||||
| 3-2020 | 297.92 | 332.715 | 258.773 | ||||||||
| 6-2020 | 309.84 | 335.881 | 290.582 | ||||||||
| 9-2020 | 323.62 | 336.866 | 305.081 | ||||||||
| 12-2020 | 292.52 | 298.479 | 287.88 | ||||||||
| 3-2021 | 301.12 | 315.939 | 286.478 | ||||||||
| 6-2021 | 363.11 | 370.096 | 353.234 | ||||||||
| 9-2021 | 350.61 | 362.619 | 339.816 | ||||||||
| 12-2021 | 369.03 | 382.763 | 342.13 | ||||||||
| 3-2022 | 444. 71 71 | 474.515 | 421.38 | ||||||||
| 6-2022 | 462.96 | 490,338 | 442.377 | ||||||||
| 9-2022 | 484.03 | 491,41 | 476,95 |
. среднее ценности.
4 noc Трехлетний график акций
Теперь давайте посмотрим на трехлетний исторический график noc. Этот график поможет как краткосрочным, так и среднесрочным инвесторам в их анализе.
Примечание. Хотя универсального стандарта не существует, инвестиции на срок менее 3 лет можно считать краткосрочными. А любой срок инвестирования более 3 лет, но в пределах 10 лет можно считать среднесрочным. Следовательно, 3-летняя диаграмма должна помочь обоим.
5 noc Годовой график акций
Самые последние результаты фиксируются на краткосрочных графиках. Теперь давайте посмотрим на годовой график цен Northrop Grumman Corporation (noc). Продолжительность сюжета между 12.09.2021 и 12.09.2022.
Примечание. В отличие от предыдущих разделов, на приведенном ниже графике мы будем использовать среднее значение за неделю. цены вместо месячных или годовых средних. Причина проста. В течение всего 1 года еженедельные цены могут дать сбалансированное представление о движении цен. Цены не будут выглядеть ни слишком волатильными (много взлетов и падений), ни слишком плавными.
В отличие от предыдущих разделов, на приведенном ниже графике мы будем использовать среднее значение за неделю. цены вместо месячных или годовых средних. Причина проста. В течение всего 1 года еженедельные цены могут дать сбалансированное представление о движении цен. Цены не будут выглядеть ни слишком волатильными (много взлетов и падений), ни слишком плавными.
Первые два столбца в приведенной ниже таблице содержат данные, используемые для построения вышеуказанного визуального элемента. Последние несколько столбцов помогут вам отследить тенденцию самых высоких и самых низких недельных цен на Northrop Grumman Corporation (noc) за 1 год.
| Неделя-год | Цена (долл. США) (и изменение по сравнению с прошлой неделей %) | Самая высокая дневная цена (долл. США) (и изменение по сравнению с прошлой неделей %) | ) (и изменение с прошлой недели %) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 37-2021 | 346. 78 78 | 350.253 | 344.267 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38-2021 | 344.42 ( -0.68% ) | 350.214 ( -0.01% ) | 339.816 ( — 1.29% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39-2021 | 354.36 ( 2.89% ) | 357.381 ( 2.05% ) | 351.7 ( 3.5% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40-2021 | 371.24 ( 4,76% ) | 383.709 ( 7.37% ) | 360.03 ( 2.37% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41-2021 | 385.41 ( 3.82% ) | 389.262 ( 1.45% ) | 382.705 ( 6.3 % ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42-2021 | 394.43 ( 2.34% ) | 399.945 ( 2.74% ) | 387.815 ( 1.34% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43-2021 | 375.56 ( — 4,78% ) | 400,348 ( 0.1% ) | 351.71 ( -9.31% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44-2021 | 351.14 ( -6.5% ) | 358. 75 ( -10.39% ) 75 ( -10.39% ) | 347.752 ( -1.13% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45-2021 | 356.31 ( 1.47% ) | 358.898 ( 0.04% ) | 354.103 ( 1.83% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46-2021 | 349.15 ( -2.01 % ) | 354,447 ( -1,24% ) | 346 ( -2.29% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47-2021 | 355.49 ( 1.82% ) | 358.592 ( 1.17% ) | 350.041 ( 1.17% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48-2021 | 348.40 ( -1.99% ) | 353.858 ( -1.32% ) | 342.13 ( -2.26% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49-2021 | 361.86 ( 3.86% ) | 366,931 ( 3,69% ) | 358.634 ( 4.82% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50-2021 | 373.51 ( 3.22% ) | 374.604 ( 2.09% ) | 372.033 ( 3.74% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51-2021 | 373.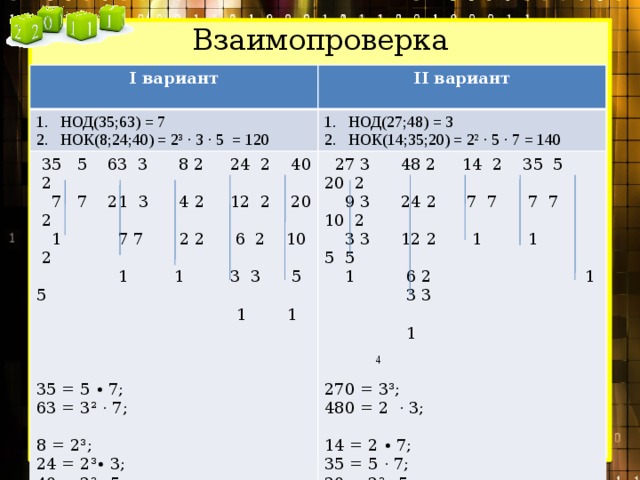 16 ( -0.09% ) 16 ( -0.09% ) | 376.928 ( 0.62% ) | 365.833 ( -1.67% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52-2021 | 380.94 ( 2.08% ) | 382.763 ( 1.55 % ) | 379,935 ( 3.85% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1-2022 | 390.64 ( 2.55% ) | 395.964 ( 3.45% ) | 381.24 ( 0.34% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2-2022 | 395.43 ( 1.23% ) | 398.96 ( 0.76% ) | 391.129 ( 2.59% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3-2022 | 395.43 ( 0% ) | 397.18 ( -0.45% ) | 392,988 ( 0,48% | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4-2022 | 388,36 ( -1,79% ) | 398,743 ( 0,39% ) | 369,828 ( 0,39% ) | 369,828 ( 0,39% ) | 369,828 ( 0,39% ) | 369,828 ( 0,39% ) | 369,828. 5.53% ) | 369.65 ( -7.3% ) | 365. 635 ( -1.13% ) 635 ( -1.13% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6-2022 | 379.37 ( 3.4% ) | 394.876 ( 6.82% ) | 369,007 ( 0,92% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7-2022 | 387.32 ( 2.1% ) | 393.68 ( -0.3% ) | 380.488 ( 3.11% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8-2022 | 391.50 ( 1.08% ) | 406.726 ( 3.31% ) | 381.784 ( 0.34% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9-2022 | 450.72 ( 15.13% ) | 465.202 ( 14.38% ) | 438.962 ( 14.98% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10-2022 | 448.35 ( -0.53% ) | 474.515 ( 2% ) | 433.164 ( -1.32% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11-2022 | 430.96 ( -3.88% ) | 444.602 ( -6.3% ) | 421.38 ( -2.72% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12-2022 | 447.28 ( 3.79% ) | 454.887 ( 2. 31% ) 31% ) | 443.093 ( 5.15% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13-2022 | 446,46 ( -0.18% ) | 451.522 ( -0.74% ) | 443.102 ( 0% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14-2022 | 457.13 ( 2.39% ) | 467.387 ( 3.51% ) | 449.039 ( 1.34% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15-2022 | 460.95 ( 0.84% ) | 463.842 ( -0.76% ) | 458.819 ( 2.18% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16- 2022 | 453,56 ( -1,6% ) | 462.234 ( -0.35% ) | 440.263 ( -4.04% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17-2022 | 439.00 ( -3.21% ) | 441.971 ( -4.38% ) | 436.242 ( -0.91% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18-2022 | 454.27 ( 3.48% ) | 465.332 ( 5.29% ) | 435.468 ( -0.18% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19- 2022 | 447,57 ( -1,47% ) | 450. 717 ( -3.14% ) 717 ( -3.14% ) | 443.271 ( 1.79% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20-2022 | 449.56 ( 0.44% ) | 455.979 ( 1.17% ) | 440.144 ( — 0.71% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21-2022 | 463.73 ( 3.15% ) | 469.113 ( 2.88% ) | 453.487 ( 3.03% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22-2022 | 466.73 ( 0,65% ) | 476,696 ( 1.62% ) | 461.251 ( 1.71% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23-2022 | 472.36 ( 1.21% ) | 490.338 ( 2.86% ) | 461.3 ( 0.01% ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24-2022 | 451,72 ( -4,37% ) | 459,068 ( -6,38% ) | 442.377 (% ) | 442,377 (% ) | 442.377 (% ) | 442,377 (% ) | 442,377 (% ) еженедельные цены составляли 59,22 доллара в период с 8-й по 2022 год по 9-ю неделю.-2022.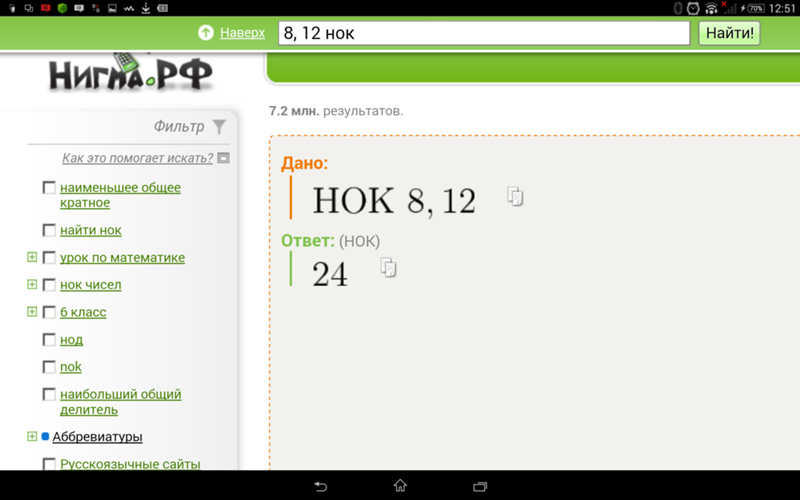 6 Northrop Grumman Corporation (noc) График акций за 6 месяцевТеперь мы подошли к последнему разделу этого отчета. Мы собираемся увидеть 6-месячный исторический график noc. Обычно инвестирование на срок до 6 месяцев не рекомендуется стоимостным инвесторам. Однако график за 6 месяцев может помочь отслеживать движения цен и анализировать соответствующие факторы. Вывод:Картинки говорят лучше слов. Надеемся, что подборка исторических графиков корпорации Northrop Grumman (noc), которую вы только что видели, поможет вам провести глубокий анализ до и во время инвестирования. Каждый хотел бы, чтобы инвестиции со временем росли. В частности, долгосрочные инвесторы ожидают многократного роста. Если вы такой инвестор, вы должны взглянуть на исторический анализ роста noc. Отказ от ответственности: Насколько нам известно, мы проверили данные. Если вы обнаружите неточность данных, пожалуйста, сообщите нам об этом, используя контактную форму, чтобы мы могли действовать оперативно. Черная шляпа США 2022 | Центр управления сетью (NOC) Центр управления сетью Black Hat (NOC) обеспечивает высокую безопасность и доступность сети в одной из самых сложных сред в мире — мероприятии Black Hat. Это достигается с помощью лучших в своем классе поставщиков решений и опытных групп безопасности и инженеров, возглавляемых уважаемыми руководителями групп NOC Black Hat. Вместе эта команда обеспечивает безопасность, стабильность и видимость корпоративной сети мирового класса. Каждый год эта отобранная вручную команда собирается за несколько месяцев до Black Hat, чтобы внедрить новейшие решения в области инфраструктуры и безопасности в работоспособную сетевую структуру. Команда снова собирается всего за несколько дней до Black Hat для сжатого развертывания сети, которая должна быть в рабочем состоянии в день открытия мероприятия. Участники Black Hat могут посетить NOC, чтобы заглянуть в эту ультрасовременную сеть. Программа Black Hat NOC является свидетельством инженерного ноу-хау и командной работы. Часы работыНОК будет транслироваться в прямом эфире на нашем канале Twitch. Часы работы прямой трансляции:
Презентации НОК (Мандалай-Бей — уровень 2 — брейкеры B):
Часы посещения NOC (Mandalay Bay – уровень 2 – Surf E/F)
Лидеры NOCБарт СтампСтарший консультант по безопасностиOptiv Барт Стамп — старший консультант по безопасности, работающий в Optiv из Солт-Лейк-Сити, штат Юта. Нил Р. Уайлер (также известный как Грифтер)Глобальный руководитель отдела активных оценок угрозIBM-X Force Нил Р. Уайлер (он же Грифтер) — инженер по информационной безопасности и исследователь из Солт-Лейк-Сити, штат Юта. Нил в настоящее время работает в IBM-X Force в качестве глобального руководителя отдела оценки активных угроз. Он проработал более 15 лет в качестве специалиста по безопасности, уделяя особое внимание оценке уязвимостей, тестированию на проникновение, физической безопасности и реагированию на инциденты. Он был сотрудником Black Hat Security Briefings более 15 лет и является членом старшего персонала DEF CON. Премиум-партнерыCisco Meraki создает интуитивно понятные технологии для оптимизации и защиты ИТ-опыта с помощью облачной платформы, которая объединяет продукты на основе данных, включая беспроводную связь, коммутацию, безопасность и SD-WAN, интеллектуальные камеры и датчики, открытые API и широкая партнерская экосистема, а также облачные операции. Безопасный и масштабируемый, Meraki Systems Manager закладывает основу для модели безопасности с нулевым доверием с помощью Meraki и других интеграций безопасности Cisco. Узнайте больше на meraki.cisco.com Cisco Secure повышает устойчивость системы безопасности, позволяя организациям защищать целостность своего бизнеса в условиях непредсказуемых угроз или изменений. NetWitness, подразделение RSA, предоставляет комплексные и высокомасштабируемые возможности обнаружения угроз и реагирования на них для организаций по всему миру. Платформа NetWitness обеспечивает полную видимость в сочетании с прикладной аналитикой угроз и аналитикой поведения пользователей для обнаружения, определения приоритетов, исследования угроз и автоматизации реагирования. Это позволяет аналитикам безопасности работать более эффективно и опережать угрозы, влияющие на бизнес. Для получения дополнительной информации перейдите на netwitness.com. Palo Alto Networks, мировой лидер в области кибербезопасности, формирует облачное будущее с помощью технологий, которые меняют способы работы людей и организаций. Партнеры Gigamon помогает ведущим мировым организациям работать быстро, обеспечивать безопасность и внедрять инновации. Мы предоставляем первое в отрасли решение Guided-SaaS NDR (сетевое обнаружение и реагирование), которое закрывает пробел в видимости Центра управления безопасностью (SOC), устраняет ненужные отвлекающие факторы и предоставляет экспертные рекомендации, когда это наиболее важно. Новый Lumen (NYSE: LUMN) руководствуется нашей верой в то, что человечество находится в лучшем состоянии, когда технологии совершенствуют то, как мы живем и работаем. Имея 450 000 миль оптоволоконных маршрутов, обслуживающих клиентов в более чем 60 странах, мы предоставляем самую быструю и безопасную платформу для приложений и данных, чтобы помочь предприятиям, правительству и сообществам предоставлять потрясающие возможности. При поддержкеIronNet — мировой лидер в области кибербезопасности, революционизирующий способы обеспечения безопасности своих предприятий организациями, предоставляя первую в мире масштабируемую платформу коллективной защиты. Наши решения используют наш уникальный наступательный и оборонительный кибер-опыт для обеспечения расширенного поведенческого анализа и коллективного разума для обнаружения известных и неизвестных угроз. Для получения дополнительной информации посетите www.ironnet.com. 15 основных навыков старшего инженера NOC для вашего резюме и карьеры Ниже мы составили список наиболее важных навыков для старшего инженера нокаута. Мы ранжировали лучшие навыки на основе процента резюме старшего инженера, в котором они фигурировали. Например, 18,2% резюме старшего инженера NOC содержали сетевую безопасность как навык. Давайте выясним, какие навыки на самом деле нужны старшему инженеру NOC, чтобы добиться успеха на рабочем месте. 15 основных навыков старшего инженера NOC для вашего резюме и карьерыВот как сетевая безопасность используется в резюме старшего инженера NOC:
Серверы — это компьютеры или системы, которые предоставляют услуги другим компьютерам, известным как клиенты, подключенные к ним через сеть. Это может также относиться к кому-то в ресторане, который доставляет еду посетителям с кухни. Вот как серверы используются в резюме старшего инженера NOC:
Термин OSPF используется для обозначения протокола внутреннего шлюза для сетей интернет-протокола. O Вот как ospf используется в резюме старшего инженера NOC:
И если вы ищете работу, вот пять лучших работодателей, которые сейчас нанимают:
Протокол Border Gateway (BGP) процедура, облегчающая обмен маршрутной информацией между различными сетями, подключенными через Интернет. Вот как bgp используется в резюме старшего инженера NOC:
AD или Active Directory — это технология, разработанная Microsoft, которая используется для управления компьютерами других пользователей. Большинство серверных операционных систем Windows имеют активный каталог. AD помогает в организации пользователей компьютеров или пользователей компании. ИТ-отдел отвечает за управление Active Directory, поскольку он помогает организовать иерархию компании, определить, какие компьютеры используют какую сеть и какие пользователи имеют доступ к хранилищу. Вот как Active Directory используется в резюме старшего инженера NOC:
Системы доменных имен, или сокращенно DNS, — это интернет-система для преобразования удобочитаемого языка, то есть google.com, в машинный язык, то есть 192.168.0. Для простой аналогии некоторые называют это телефонной книгой Интернета. Любой веб-сайт имеет свой IP-адрес, например, 192.168.160. Понятно, что это трудно запомнить. Итак, что делает DNS, так это связывает доменное имя google.com со своим IP-адресом, 192.168.160. Вот как DNS используется в резюме старшего инженера NOC:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



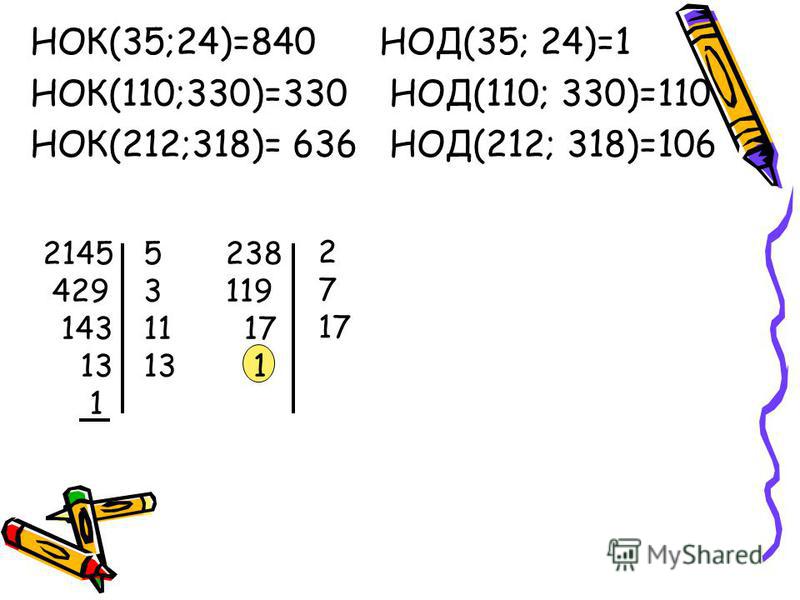



 переход…
переход…

 ..
..

 Он работает в области сетей и безопасности более 14 лет. Он работал на разных должностях, начиная с запуска и проектирования сетевых сред и сред безопасности, заканчивая консультированием, обучением, технической продажей и технической поддержкой. Он был сотрудником Black Hat в течение 12 лет, а также головорезом в DEF CON более 10 лет. Подпишитесь на него в Твиттере @theStump3r.
Он работает в области сетей и безопасности более 14 лет. Он работал на разных должностях, начиная с запуска и проектирования сетевых сред и сред безопасности, заканчивая консультированием, обучением, технической продажей и технической поддержкой. Он был сотрудником Black Hat в течение 12 лет, а также головорезом в DEF CON более 10 лет. Подпишитесь на него в Твиттере @theStump3r. Нил выступал на многочисленных конференциях по безопасности по всему миру, включая Black Hat, DEF CON и RSA Conference. Он был предметом различных интернет-, печатных, кино- и телеинтервью, а также является автором нескольких книг по информационной безопасности. Нил является членом Наблюдательного совета DEF CON CFP и Наблюдательного совета по обучению Black Hat.
Нил выступал на многочисленных конференциях по безопасности по всему миру, включая Black Hat, DEF CON и RSA Conference. Он был предметом различных интернет-, печатных, кино- и телеинтервью, а также является автором нескольких книг по информационной безопасности. Нил является членом Наблюдательного совета DEF CON CFP и Наблюдательного совета по обучению Black Hat. С помощью Cisco Secure организации видят ИТ-среду с несколькими средами, предвидят, что будет дальше, предпринимают правильные действия, устраняют бреши в безопасности и каждый день совершенствуются, чтобы обеспечить успех инвестиций в отказоустойчивость в масштабах всей организации. Узнайте больше на www.cisco.com/go/secure.
С помощью Cisco Secure организации видят ИТ-среду с несколькими средами, предвидят, что будет дальше, предпринимают правильные действия, устраняют бреши в безопасности и каждый день совершенствуются, чтобы обеспечить успех инвестиций в отказоустойчивость в масштабах всей организации. Узнайте больше на www.cisco.com/go/secure. Наша миссия — быть предпочтительным партнером в области кибербезопасности, защищая наш цифровой образ жизни. Мы помогаем решать самые серьезные мировые проблемы безопасности с помощью непрерывных инноваций, которые используют последние достижения в области искусственного интеллекта, аналитики, автоматизации и оркестровки. Предоставляя интегрированную платформу и расширяя возможности растущей экосистемы партнеров, мы находимся в авангарде защиты десятков тысяч организаций в облаках, сетях и на мобильных устройствах. Наше видение — это мир, в котором каждый день безопаснее и надежнее, чем предыдущий. Для получения дополнительной информации посетите сайт www.paloaltonetworks.com.
Наша миссия — быть предпочтительным партнером в области кибербезопасности, защищая наш цифровой образ жизни. Мы помогаем решать самые серьезные мировые проблемы безопасности с помощью непрерывных инноваций, которые используют последние достижения в области искусственного интеллекта, аналитики, автоматизации и оркестровки. Предоставляя интегрированную платформу и расширяя возможности растущей экосистемы партнеров, мы находимся в авангарде защиты десятков тысяч организаций в облаках, сетях и на мобильных устройствах. Наше видение — это мир, в котором каждый день безопаснее и надежнее, чем предыдущий. Для получения дополнительной информации посетите сайт www.paloaltonetworks.com. Имея представление о сетевом трафике во всей своей гибридной облачной инфраструктуре, организации устраняют слепые зоны безопасности, пользуясь рекомендациями экспертов по безопасности Gigamon, помогая повысить эффективность SOC и сократить выгорание своих групп безопасности. Гигамон был награжден более 90 патентует технологии и пользуется доверием клиентов мирового класса в более чем 4000 организаций, в том числе более 80 процентов из списка Fortune 100 и сотни государственных и образовательных организаций по всему миру. Компания Gigamon со штаб-квартирой в Силиконовой долине работает по всему миру. Для получения дополнительной информации посетите сайт www.gigamon.com.
Имея представление о сетевом трафике во всей своей гибридной облачной инфраструктуре, организации устраняют слепые зоны безопасности, пользуясь рекомендациями экспертов по безопасности Gigamon, помогая повысить эффективность SOC и сократить выгорание своих групп безопасности. Гигамон был награжден более 90 патентует технологии и пользуется доверием клиентов мирового класса в более чем 4000 организаций, в том числе более 80 процентов из списка Fortune 100 и сотни государственных и образовательных организаций по всему миру. Компания Gigamon со штаб-квартирой в Силиконовой долине работает по всему миру. Для получения дополнительной информации посетите сайт www.gigamon.com. Посетите Lumen, чтобы узнать больше.
Посетите Lumen, чтобы узнать больше.
 Услуги могут варьироваться от данных, ресурсов, программ или любых других услуг, связанных с вычислениями и компьютерами.
Услуги могут варьироваться от данных, ресурсов, программ или любых других услуг, связанных с вычислениями и компьютерами.
 Это также относится к электронному языку, используемому среди интернет-маршрутизаторов, чтобы определить, как часть информации отправляется от одного маршрутизатора к другому по сети. Этот процесс очень быстрый и занимает всего несколько секунд, что позволяет Интернету работать должным образом.
Это также относится к электронному языку, используемому среди интернет-маршрутизаторов, чтобы определить, как часть информации отправляется от одного маршрутизатора к другому по сети. Этот процесс очень быстрый и занимает всего несколько секунд, что позволяет Интернету работать должным образом.







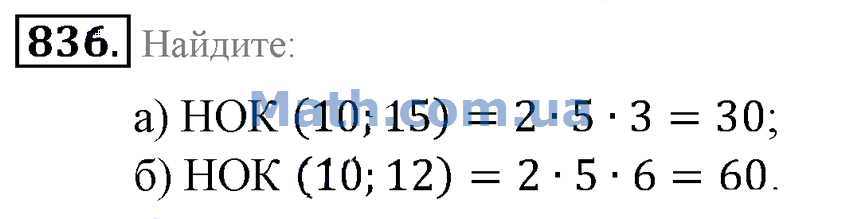
 Это часто делается с помощью кабелей Ethernet, которые подключаются к маршрутизатору или другому порту модема в дополнение к порту компьютера. Поскольку Ethernet соединяет только локальную сеть, существует больше протоколов, касающихся того, как передается информация.
Это часто делается с помощью кабелей Ethernet, которые подключаются к маршрутизатору или другому порту модема в дополнение к порту компьютера. Поскольку Ethernet соединяет только локальную сеть, существует больше протоколов, касающихся того, как передается информация.


 Просмотрите наши примеры резюме, чтобы определить, как лучше всего составить свое резюме. Затем выберите один из 5+ шаблонов резюме, чтобы составить резюме старшего инженера-ночника.
Просмотрите наши примеры резюме, чтобы определить, как лучше всего составить свое резюме. Затем выберите один из 5+ шаблонов резюме, чтобы составить резюме старшего инженера-ночника.
 com
com


 целей, выступая в качестве руководителя VmWare NOC.
целей, выступая в качестве руководителя VmWare NOC.
 Мы нашли несколько онлайн-курсов от Udemy и Coursera, которые помогут вам продвинуться по карьерной лестнице. Поскольку старшим инженерам NOC полезно иметь такие навыки, как сетевая безопасность, серверы и ospf, мы нашли курсы, которые помогут вам улучшить эти навыки.
Мы нашли несколько онлайн-курсов от Udemy и Coursera, которые помогут вам продвинуться по карьерной лестнице. Поскольку старшим инженерам NOC полезно иметь такие навыки, как сетевая безопасность, серверы и ospf, мы нашли курсы, которые помогут вам улучшить эти навыки. ..
.. .. План разработки (2022 г.)
.. План разработки (2022 г.) ..
..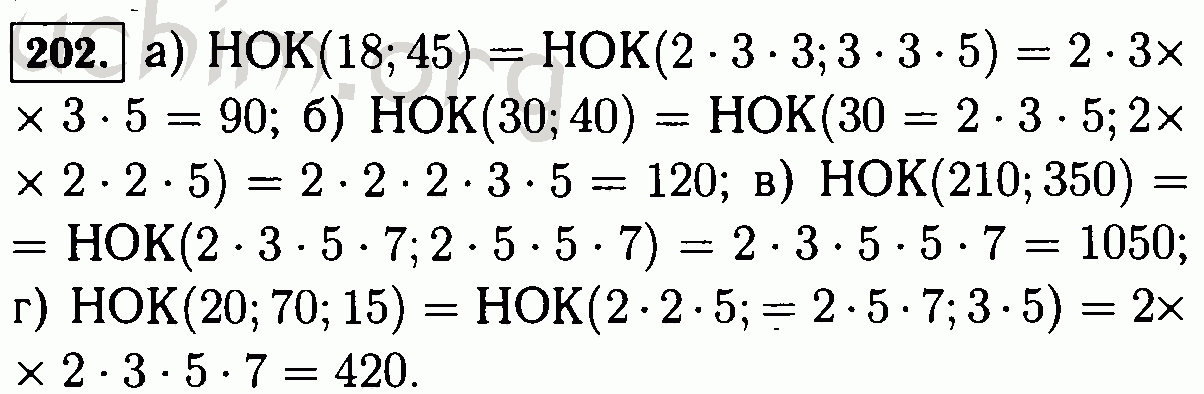 ..
.. .. Инженеры
.. Инженеры 11.2022
11.2022 06.2022
06.2022 07.2022
07.2022 07.2022
07.2022 02.2022
02.2022 02.2022
02.2022 Риаза, машинист поезда, DMTCL
Риаза, машинист поезда, DMTCL 02.2022
02.2022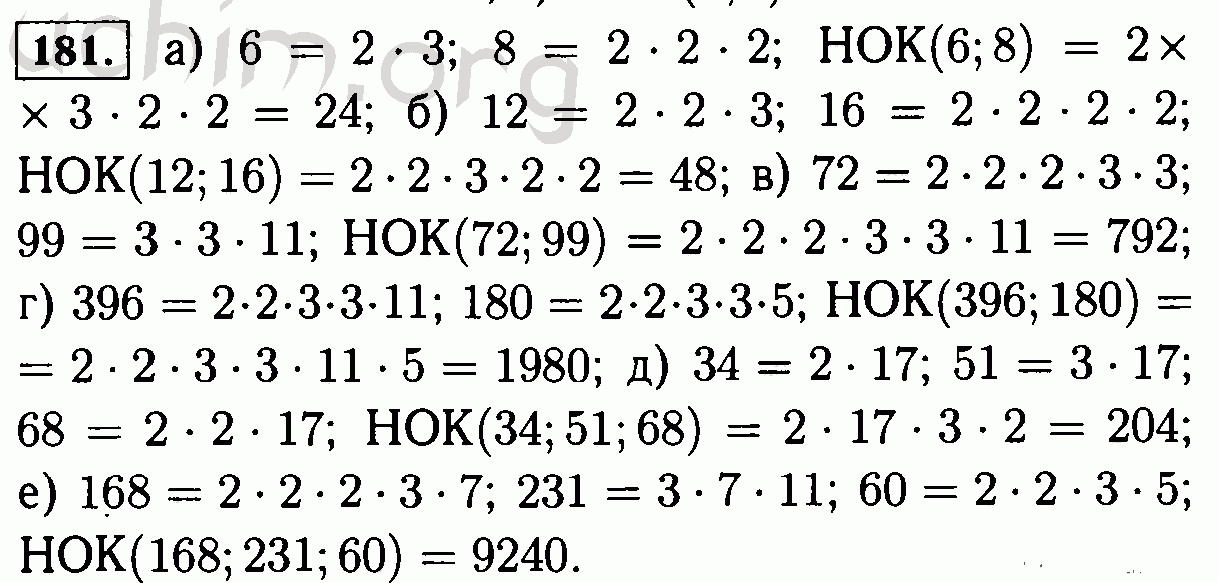 02.2022
02.2022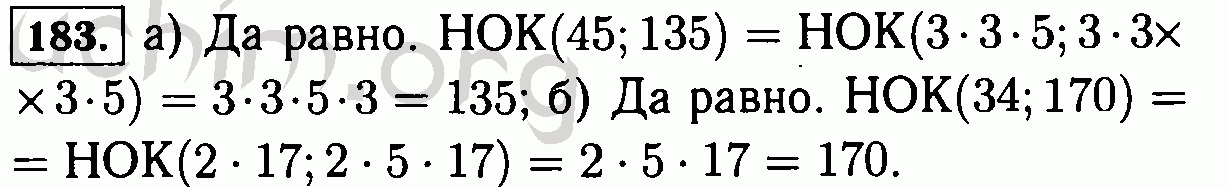 11.2021
11.2021 09.2021
09.2021 05.2021
05.2021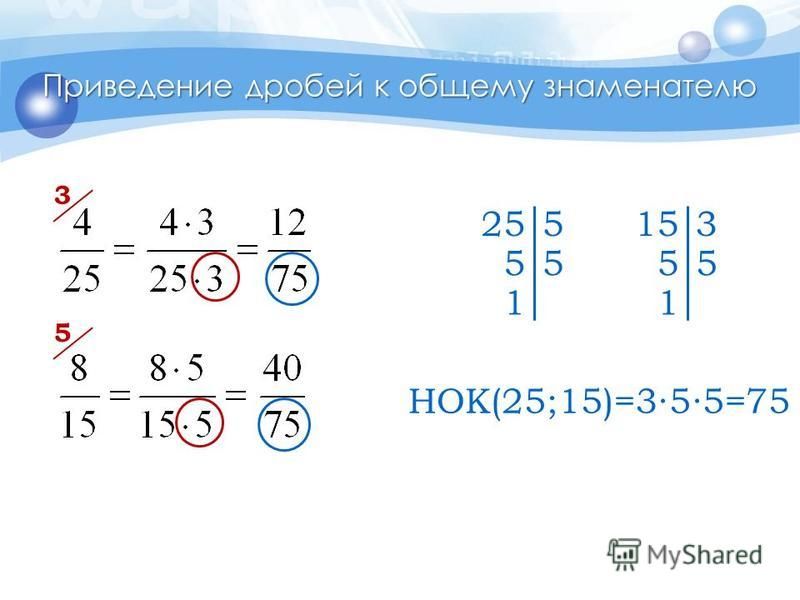 03.2021
03.2021 03.2021
03.2021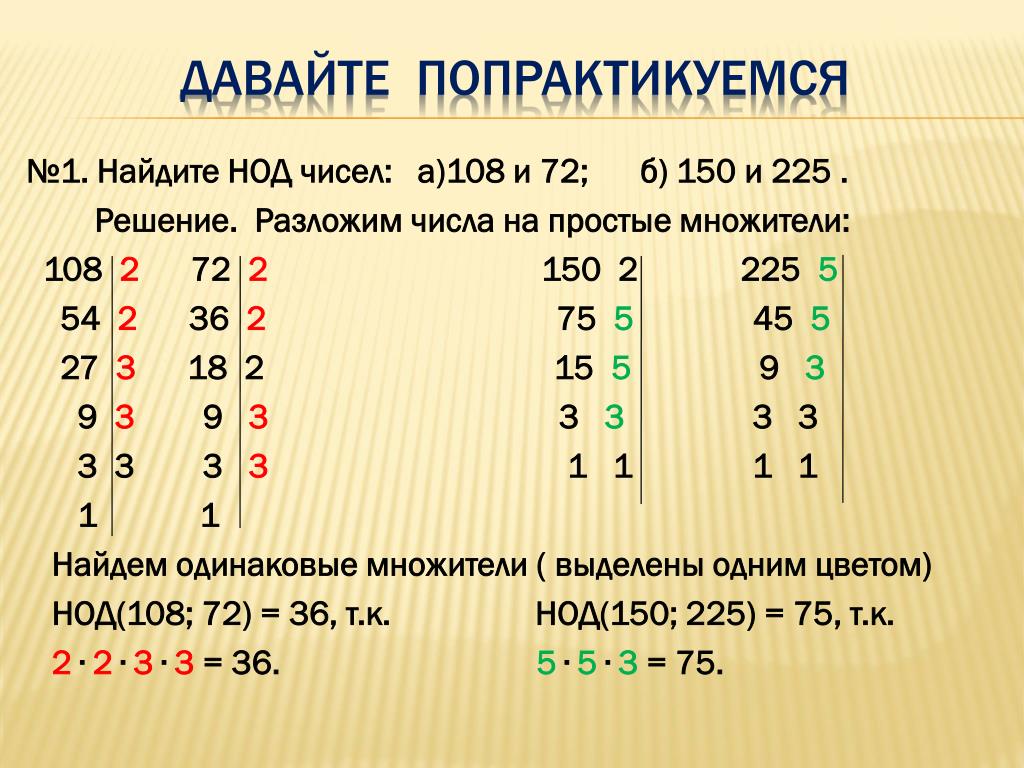 03.2021
03.2021 03.2021
03.2021 Аслам Хоссейн, диспетчер станции, DMTCL
Аслам Хоссейн, диспетчер станции, DMTCL 11.2021
11.2021 07.2020
07.2020 04.2019
04.2019
 030
030 16.12.21
16.12.21 16.09.20
16.09.20 ..
..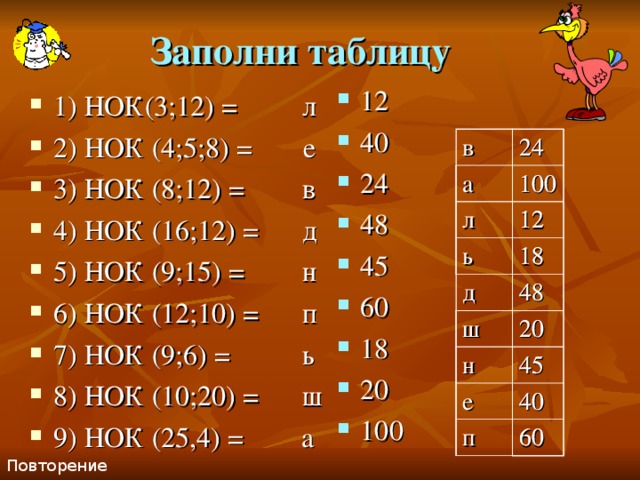 320
320 11/14/18
11/14/18 100
100 16, 20175/16/17
16, 20175/16/17