Нок 36 и 48: НАЙДИТЕ. НОК(36,48).. — ответ на Uchi.ru

alexxlab / / Разное

Содержание

Whaleblue

Начать решать задания

Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.

Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, при этом оно должно быть максимально маленьким.

Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.

Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:

Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12.

Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.

Из определения понятно, что НОК это наименьшее число, которое делится без остатка на 9 и на 12. Этот НОК требуется найти.

Для нахождения наименьшего общего кратного (НОК) можно пользоваться двумя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.

В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9. Итак, начнём. Кратные будем выделять красным цветом:

9 × 1 = 9

9 × 2 = 18

9 × 3 = 27

9 × 4 = 36

9 × 5 = 45

9 × 6 = 54

9 × 7 = 63

9 × 8 = 72

9 × 9 = 81

Теперь находим кратные для числа 12. Для этого, поочерёдно умножаем 12 на все числа 1 до 12:

12 × 1 = 12

12 × 2 = 24

12 × 3 = 36

12 × 4 = 48

12 × 5 = 60

12 × 6 = 72

12 × 7 = 84

12 × 8 = 96

12 × 9 = 108

12 × 10 = 120

12 × 11 = 132

12 × 12 = 144

Теперь выпишем кратные обоих чисел:

Кратные 9 это числа { 9, 18, 27, 36, 45, 54, 63, 72 }

Кратные 12 это числа { 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144 }

Теперь находим общие кратные для обоих чисел. Найдя, сразу закрасим их синим цветом:

Кратные 9 { 9 18 27 36 45 54 63 72 }

Кратные 12 { 12 24 36 48 60 72 84 96 108 120 132 144 }

Общими кратными для чисел 9 и 12 являются числа { 36, 72 }. Теперь среди найденных общих кратных находим наименьшее. Очевидно, это число 36.

Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

НОК (9 и 12) = 36

36 : 9 = 4

36 : 12 = 3

Второй способ нахождения НОК
Второй способ заключается в том, что числа, для которых ищется НОК раскладываются на простые множители. Затем, выписываются множители входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.

Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.

Разложим на множители число 9

разложение на множители числа 9

Разложим на множители число 12

Разложение на множители числа 12

Выпишем первое разложение:

3 × 3

Теперь допишем множители из второго разложения, которых нет первом разложении.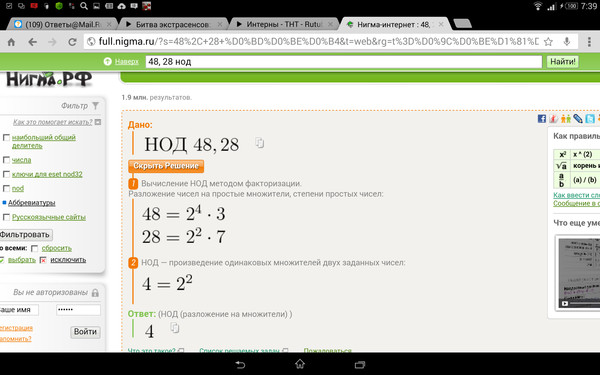 В первом разложении нет двух двоек. Их и допишем:

3 × 3 × 2 × 2

Теперь перемножаем эти множители:

3 × 3 × 2 × 2 = 36

Получили ответ 36. Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

36 : 9 = 4

36 : 12 = 3

НОК (9 и 12) = 36

line

Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.

Наша задача состояла в том, чтобы организовать новое разложение куда входило бы и разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входит и разложение числа 9 и разложение числа 12

Разложение чисел 9 и 12

Пример 2.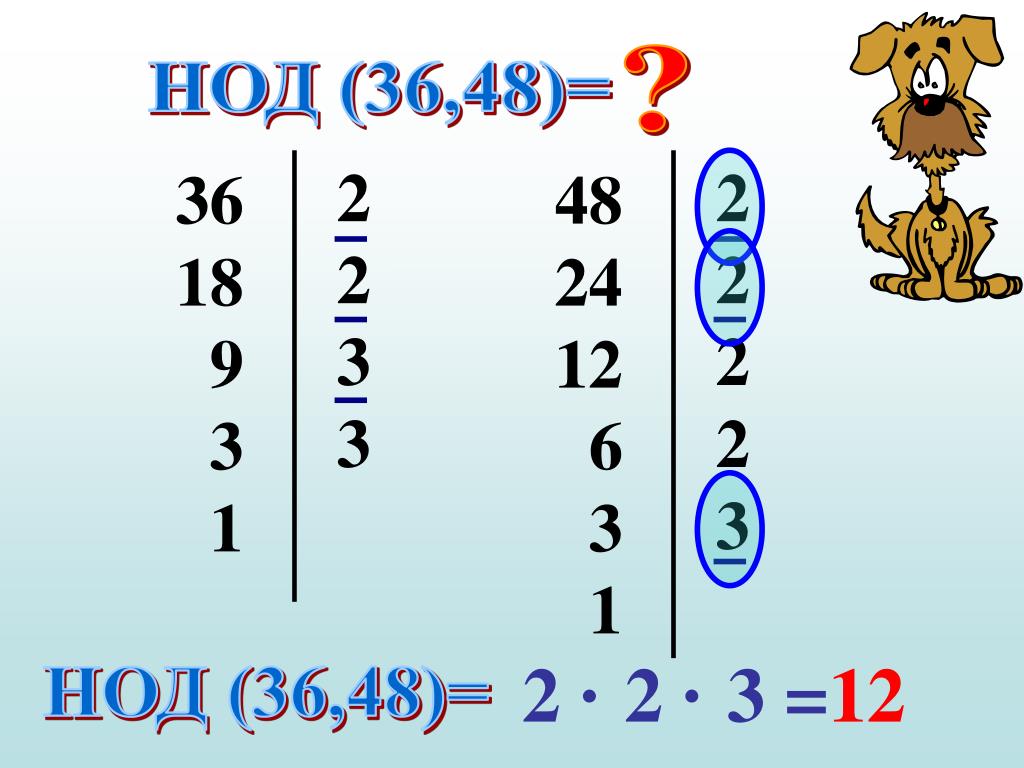

Найти НОК чисел 50 и 180

Разложим на множители число 50

разложение на множители числа 50

Разложим на множители число 180

Разложение на множители числа 180

Выпишем первое разложение:

2 × 5 × 5

Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:

2 × 5 × 5 × 2 × 3 × 3

Теперь перемножаем эти множители:

2 × 5 × 5 × 2 × 3 × 3 = 900

Получили ответ 900. Значит наименьшее общее кратное для чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:

900 : 50 = 18

900 : 180 = 5

НОК (50 и 180) = 900

Пример 3. Найти НОК чисел 8, 15 и 33

Разложим на множители число 8

Разложение на множители числа 8

Разложим на множители число 15

разложение на множители числа 15

Разложим на множители число 33

Разложение на множители числа 33

Выпишем первое разложение:

2 × 2 × 2

Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:

2 × 2 × 2 × 3 × 5 × 11

Теперь перемножаем эти множители:

2 × 2 × 2 × 3 × 5 × 11 = 1320

Получили ответ 1320. Значит наименьшее общее кратное для чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:

1320 : 8 = 165

1320 : 15 = 88

1320 : 33 = 40

НОК (8, 15 и 33) = 1320

Третий способ нахождения НОК
Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.

Данный способ разумнее использовать, когда одновременно нужно найти и НОД и НОК двух чисел.

К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:

нок для 24 и 12 для второго способа нахождения НОК step 1

Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.

Итак, перемножим числа 24 и 12

нок для 24 и 12 для второго способа нахождения НОК step 2

Разделим полученное число 288 на НОД чисел 24 и 12

нок для 24 и 12 для второго способа нахождения НОК step 3

Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24

НОК (24 и 12) = 24

Пример 2. Найти НОД и НОК чисел 36 и 48

Найдем НОД чисел 36 и 48

нок для 36 и 48 для второго способа нахождения НОК step 1

Перемножим числа 36 и 48

нок для 36 и 48 для второго способа нахождения НОК step 2

Разделим 1728 на НОД чисел 36 и 48

нок для 36 и 48 для второго способа нахождения НОК step 3

Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144

НОК(36 и 48) = 144

Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделаем правильно, то снова должны получить 144

Начать решать задания

Найдите наименьшее общее кратное » задачи

НОД и НОК »

  • Найдите наименьшее общее кратное чисел aиb если:

    а) а=5*5*7*13, b=5*7*7*13
    б) a=504,b=540

    Решение: A = 5 * 5 * 7 * 13 = 2 275 b = 5 * 7 * 7 * 13 = 3 185
    НОК (a; b) = 5 * 5 * 7 * 7 * 13 = 15 925 — наименьшее общее кратное
    15 925 : 2 275 = 7 15 925 : 3 185 = 5
    а = 504 = 2 * 2 * 2 * 3 * 3 * 7 b = 540 = 2 * 2 * 3 * 3 * 3 * 5
    НОК (a; b) = 2 * 2 * 2 * 3 * 3 * 3 * 5 * 7 = 7 560 — наименьшее общее кратное
    7 560 : 504 = 15 7 560 : 540 = 14
  • Найдите наименьшее общее кратное чисел : 54, 90 и 135

    Решение: Наименьшее общее красное чисел- это число, которое разделится на представленные числа без остатка. Искать легче всего для большего числа. 135- не подходит, далее умножаем его на 2 получаем 270, это и есть наш ответ, потому что делится и на 135, и на 90, и на 54 без остатка. Ответ 270.
  • Являются ли данные числа взаимно простыми? Найдите наименьшее общее кратное этих чисел. г )50 и 51 д)11 и 48 е) 39 и 50.

    Решение: Нок(50,51)=нок(2*5*5, 3*17)=2*3*5*5*7=1050
    Нок(11,48)=нок(11, 2*2*2*2*3)=2*2*2*2*3*11=528
    Нок(39,50)=нок(3*13, 2*5*5)=2*3*5*5*13=975
    Взаимно простые числа — несколько целых чисел, которые не имеют никаких общих делителей, кроме ±1. Все даные пары чисел в примерах являются взаимно простыми, так как не имеют одинаковых множителей

    ДА ВСЕ ЯВЛЯЮТСЯ ВЗАИМНО ПРОСТЫМИ ЧИСЛАМИ

  • Найдите наименьшее общее кратное и наибольший общий делитель числителя и знаменателя следующих дробей:13/26;5/112;36/84

    Решение: Представь как будто это написано в столбик 😉 13|13=1, 26|2=13|13=1 НОД(13,26)=1, НОК(13,26)=1*2*13=26; 5|5=1, 112|2=56|2=28|2=14|7=2|2=1 НОД(5,12)= — НОК(5,12)=5*2*2*2*7*2=560; 36|2=18|2=9|3=3|3=1, 84|2=42|2=21|7=3|3=1 НОД(36,84)=2*2*3=12 НОК(36,84)=2*2*3*3*7=252.
  • Найдите наименьшее общее кратное чисел удобным способом: 6 и 8; 4и 7; 9и 15; 5,16 и 20; 15,30, и 45; 10,14и 35;

    Решение: НОК (6; 8)-3*2*4=24
    6|3 8|4
    2|2 2|2
    1|  1|
    НОК (4; 7)-2*2*7=28
    4|2 7|7
    2|2 1|
    1|
    НОК (9; 15)-3*3*5=45
    9|3 15|5
    3|3 3|3
    1| 1|
    НОК (5; 16; 20)-5*8*2*10=800
    5|5 16|8 20|10
    1| 2|2 2|2
      1| 1|
    НОК (15; 30; 45)-5*3*10*9=1350
    15|5 30|10 45|9
     3|3 3|3 5|5
     1| 1| 1|
    НОК (10; 14; 35)-5*2*7=70
    10|5 14|7 35|7
     2|2 7|7 5|5
     1| 1| 1|
  • Найдите наименьшее общее кратное и нок

    6 и 8
    72 и 99
    34. 51 и68
    Решение: НОК-НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ.
    Раскладываем 6 и 8 на простые множители.
    6=2*3
    8=2*2*2
    НОК(8,6)=6*2*2=24
    Раскладываем 72 и 99 на простые множители.
    72=2*2*2*3*3
    99=3*3*11
    НОК(72,99)=72*11=792
    Раскладываем 34,51 и 68 на простые множители.
    34=2*17
    51=3*17
    68=2*2*17
    НОК(34,51,68)=34*3*2=204
  • Найдите наименьшее общее кратное чисел методом разложения на простые множители:

    28,35
    16,56
    21,100
    18,162
    264,300
    360,1020
    72,90 и 96
    58,87 и 435
    Решение: 28, 35 это 4*7 и 5*7 наименьшее общее кратное 7
    16,56 это 2*8 и 2*28 наименьшее общее кратное 2
    21,100 или ошибка или 1
    18,162 это 2*9 и  2*81 наименьшее общее кратное 2
    264,300 это 2*132 и 2*150 наименьшее общее кратное 2
    360,1020 это 2*180 и 2*510 наименьшее общее кратное 2
    72,90 и 96 это 2*36, 2*45, 2*48 наименьшее общее кратное 2
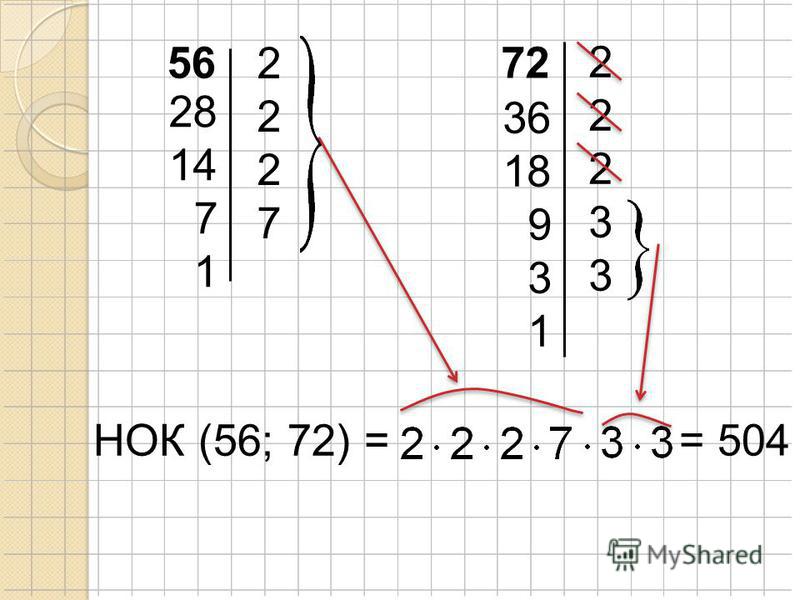
    58,87 и 435 это 2*29, 3*29, 15*29 наименьшее общее кратное 29
  • Найдите наименьшее общее кратное чисел 56 и 72

    3375 и 2250
    Решение: 56 = 2 * 2 * 2 * 7

    72 = 2 * 2 * 2 * 3 * 3

    НОК (56; 72) = 2 * 2 * 2 * 3 * 3 * 7 = 504 — наименьшее общее кратное

    504 : 56 = 9             504 : 72 = 7

    3375 = 3 * 3 * 3 * 5 * 5 * 5

    2250 = 2 * 3 * 3 * 5 * 5 * 5

    НОК (3375; 2250) = 2 * 3 * 3 * 3 * 5 * 5 * 5 = 6750 — наименьшее общее кратное

    6750 : 3375 = 2          6750 : 2250 = 3

    Чтобы найти НОК, нужно разложить данные числа на простые множители и найти произведение всех простых множителей, взятых с наибольшим показателем степени.

  • Найдите наименьшее общее кратное чисел 18 и 45, 30 и 40, 210 и 350, 20 70 и 15

    Решение: Наименьшее общее кратное (НОК) : НОК натуральных чисел a и b называю наименьшее натуральное число, которое кратно и a, и b. (Иными словами если это число делить на a или b, то ответ будет целое число). Решают так:1) разложим числа на простые множители:18 = 2 Х 3 Х 345 = 3 Х 3 Х 52) выпишем множители входящие в разложение одного из чиселну без разницы, например: 3 Х 3 Х 53) добавить к ним недостающие множители из разложения остальных чисел (просто НОК можно искать для двух, трех и более чисел) так, чего нам не хваает? а! одной двойки, получимНОК (18, 45) = 3 Х 3 Х 5 х 2 = 9030 = 2 Х 3 Х 540 = 2 Х 2 Х 2 Х 5НОК (30, 40) = 2 Х 2 Х 2 Х 5 Х 3 = 120210 = 2 Х 3 Х 5 Х 7350 = 2 Х 5 Х 5 Х 7НОК (210, 350) = 2 Х 5 Х 5 Х 7 Х 3 = 105020 = 2 Х 2 Х 570 = 2 Х 5 Х 715 = 3 Х 5НОК (20, 70, 15) = 2 Х 2 Х 5 Х 7 Х 3 = 420
  • Найдите наименьшее общее кратное чисел 18и45 210и350

    Решение: 1) НОК 18 и 45 чтобы найти наименьшее общее кратное нужно разделить оба числа на простые множители и перемножить их взяв каждый в наименьшей степени, получим 90
    2) НОК 210 и 350 Наименьшее Общее кратное этих чисел — 2100

    18*5=90
    45*2=90
    наименьшее общее кратное чисел 18и45 является 90
    210*5=1050
    350*3=1050
    наименьшее общее кратное чисел 210и350 является 1050

121314 15 > >>

Command Watch — Ресурсы центра обработки данных

Консольная мебель для диспетчерской круглосуточной работы 7 дней в неделю со встроенным питанием, кабельным управлением и местом для хранения.

Мебель консоли Command Watch предназначена для оптимизации площади пола и линий обзора видеодисплеев. Уменьшенная глубина и низкопрофильная конструкция делают его идеальным для использования с ЖК-мониторами. Столешница глубиной 24 дюйма обеспечивает достаточную рабочую зону. За этой рабочей поверхностью находится 10-дюймовый монитор. Кроме того, ниша для монитора регулируется по высоте, что позволяет расположить мониторы так, чтобы максимально увеличить линию обзора. 10-дюймовая решетчатая стена позволяет устанавливать ЖК-мониторы, папки, телефоны и другие аксессуары. Одной из дополнительных ключевых особенностей часов Command Watch является уникальная выдвижная полка. Полка выдвигается в обоих направлениях и вращается, обеспечивая легкий доступ как для операторов, так и для техников. Наконец, встроенные разветвители питания и система управления кабелями делают его полноценным решением для вашей диспетчерской.

Стандартные модули упрощают настройку Command Watch. Стандартные длины 24″, 36″, 48″, 60″ и 72″. Доступны нестандартные длины консоли. Угловые модули включают секции 22,5, 45, 90, обратные 22,5 и обратные 45 градусов. В продукте Command Watch используется конструкция из ламината высокого давления, обеспечивающая долгий срок службы. Корпус из ламината и декоративная окантовка, подходящая к любой цветовой гамме интерьера, делают Command Watch красивым и впечатляющим мебельным решением. Доступны специальные материалы рабочей поверхности, такие как фенольная смола и нержавеющая сталь.