Нок чисел 75 и 45: НОД и НОК для 45 и 75 (с решением)

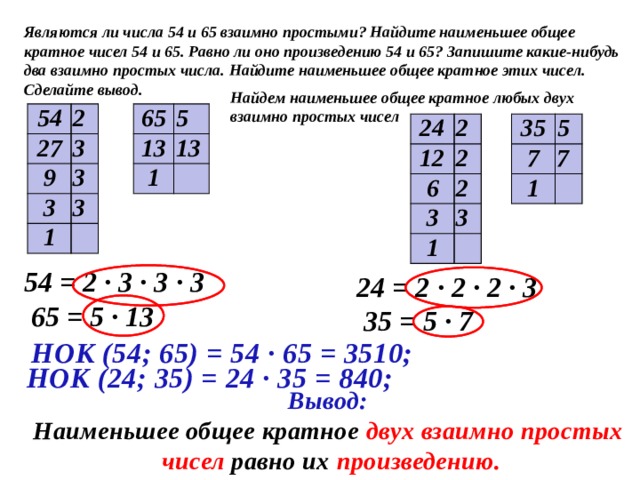
Наименьшее общее кратное 45 и 75

Калькулятор «Наименьшее общее кратное»

Какое наименьшее общее кратное (НОК) у чисел 45 и 75?

Ответ: НОК чисел 45 и 75 это 225

(двести двадцать пять)

Нахождение наименьшего общего кратного для чисел 45 и 75 используя НОД этих чисел

Первый способ нахождения НОК для чисел 45 и 75 — через нахождение наибольшего общего делителя (НОД) этих чисел. Формула:

НОК = (Число1 × Число2) ÷ НОД

НОД чисел 45 и 75 равняется 15, следовательно

НОК = (45 × 75) ÷ 15

НОК = 3375 ÷ 15

НОК = 225

Нахождение наименьшего общего кратного для чисел 45 и 75 используя перечисление кратных

Второй способ нахождения НОК для чисел 45 и 75 заключается в перечислении всех кратных для обоих чисел и выбор первого совпадающего:

Кратные числа 45: 45, 90, 135, 180, 225, 270, 315

Кратные числа 75: 75, 150, 225, 300, 375

Следовательно, НОК для 45 и 75 равняется 225

Нахождение наименьшего общего кратного для чисел 45 и 75 используя разложение чисел на простые множители

Еще один способ нахождения НОК чисел 45 and 75 — это нахождение всех простых множителей для обоих чисел и перемножение самых больших экспоненциальных форм

Все простые множители числа 45: 3, 3, 5 (экспоненциальная форма: 3², 5¹)

Все простые множители числа 75: 3, 5, 5 (экспоненциальная форма: 3¹, 5²)

3² × 5² = 225

Поделитесь текущим расчетом

Печать

https://calculat. io/ru/number/least-common-multiple-lcm-of/45—75

<a href=»https://calculat.io/ru/number/least-common-multiple-lcm-of/45—75″>Наименьшее общее кратное 45 и 75 — Calculatio</a>

О калькуляторе «Наименьшее общее кратное»

Данный калькулятор поможет найти Наименьшее общее кратное двух чисел. Например, он может помочь узнать какое наименьшее общее кратное (НОК) у чисел 45 и 75? Выберите первое число (например ’45’) и второе число (например ’75’). После чего нажмите кнопку ‘Посчитать’.

Наименьшее общее кратное (НОК) для двух чисел - это наименьшее натуральное число, которое делится на оба числа без остатка

Калькулятор «Наименьшее общее кратное»

Таблица Наименьших общих кратных

Число 1	Число 2	НОК
30	75	150
31	75	2325
32	75	2400
33	75	825
34	75	2550
35	75	525
36	75	900
37	75	2775
38	75	2850
39	75	975
40	75	600
41	75	3075
42	75	1050
43	75	3225
44	75	3300
45	75	225
46	75	3450
47	75	3525
48	75	1200
49	75	3675
50	75	150
51	75	1275
52	75	3900
53	75	3975
54	75	1350
55	75	825
56	75	4200
57	75	1425
58	75	4350
59	75	4425

Наименьшее общее кратное 4 чисел.

Нод и нок чисел

Наибольший общий делитель и наименьшее общее кратное — ключевые арифметические понятия, которые позволяют без усилий оперировать обыкновенными дробями. НОК и чаще всего используются для поиска общего знаменателя нескольких дробей.

Основные понятия

Делитель целого числа X — это другое целое число Y, на которое X разделяется без остатка. К примеру, делитель 4 — это 2, а 36 — 4, 6, 9. Кратное целого X — это такое число Y, которое делится на X без остатка. К примеру, 3 кратно 15, а 6 — 12.

Для любой пары чисел мы можем найти их общие делители и кратные. К примеру, для 6 и 9 общим кратным является 18, а общим делителем — 3. Очевидно, что делителей и кратных у пар может быть несколько, поэтому при расчетах используется наибольший делитель НОД и наименьшее кратное НОК.

Наименьший делитель не имеет смысла, так как для любого числа это всегда единица. Наибольшее кратное также бессмысленно, так как последовательность кратных устремляется в бесконечность.

Нахождение НОД

Для поиска наибольшего общего делителя существует множество методов, самые известные из которых:

• последовательный перебор делителей, выбор общих для пары и поиск наибольшего из них;
• разложение чисел на неделимые множители;
• алгоритм Евклида;
• бинарный алгоритм.

Сегодня в учебных заведениях наиболее популярными являются методы разложения на простые множители и алгоритм Евклида. Последний в свою очередь используется при решении диофантовых уравнений: поиск НОД требуется для проверки уравнения на возможность разрешения в целых числах.

Нахождение НОК

Наименьшее общее кратное точно также определяется последовательным перебором или разложением на неделимые множители. Кроме того, легко найти НОК, если уже определен наибольший делитель. Для чисел X и Y НОК и НОД связаны следующим соотношением:

НОК (X,Y) = X × Y / НОД(X,Y).

Например, если НОД(15,18) = 3, то НОК(15,18) = 15 × 18 / 3 = 90. Наиболее очевидный пример использования НОК — поиск общего знаменателя, который и является наименьшим общим кратным для заданных дробей.

Взаимно простые числа

Если у пары чисел нет общих делителей, то такая пара называется взаимно простой. НОД для таких пар всегда равен единице, а исходя из связи делителей и кратных, НОК для взаимно простых равен их произведению. К примеру, числа 25 и 28 взаимно просты, ведь у них нет общих делителей, а НОК(25, 28) = 700, что соответствует их произведению. Два любых неделимых числа всегда будут взаимно простыми.

Калькулятор общего делителя и кратного

При помощи нашего калькулятора вы можете вычислить НОД и НОК для произвольного количества чисел на выбор. Задания на вычисление общих делителей и кратных встречаются в арифметике 5, 6 класса, однако НОД и НОК — ключевые понятия математики и используются в теории чисел, планиметрии и коммуникативной алгебре.

Примеры из реальной жизни

Общий знаменатель дробей

Наименьшее общее кратное используется при поиске общего знаменателя нескольких дробей. Пусть в арифметической задаче требуется суммировать 5 дробей:

1/8 + 1/9 + 1/12 + 1/15 + 1/18.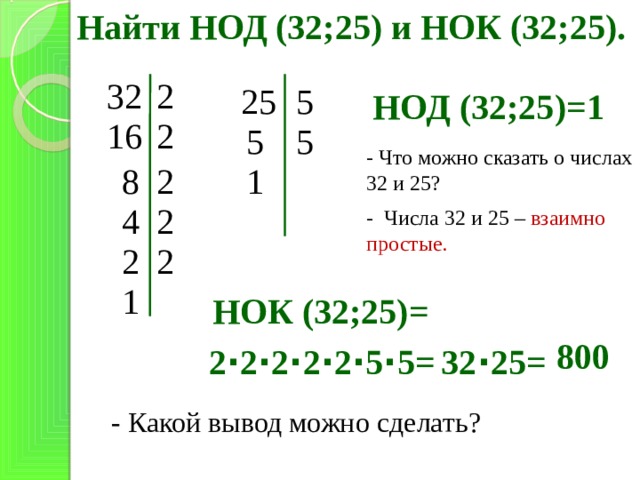

Для сложения дробей выражение необходимо привести к общему знаменателю, что сводится к задаче нахождения НОК. Для этого выберите в калькуляторе 5 чисел и введите значения знаменателей в соответствующие ячейки. Программа вычислит НОК (8, 9, 12, 15, 18) = 360. Теперь необходимо вычислить дополнительные множители для каждой дроби, которые определяются как соотношение НОК к знаменателю. Таким образом, дополнительные множители будут выглядеть как:

• 360/8 = 45
• 360/9 = 40
• 360/12 = 30
• 360/15 = 24
• 360/18 = 20.

После этого умножаем все дроби на соответствующий дополнительный множитель и получаем:

45/360 + 40/360 + 30/360 + 24/360 + 20/360.

Такие дроби мы можем легко суммировать и получить результат в виде 159/360. Сокращаем дробь на 3 и видим окончательный ответ — 53/120.

Решение линейных диофантовых уравнений

Линейные диофантовы уравнения — это выражения вида ax + by = d. Если отношение d / НОД(a, b) есть целое число, то уравнение разрешимо в целых числах. Давайте проверим пару уравнений на возможность целочисленного решения. Сначала проверим уравнение 150x + 8y = 37. При помощи калькулятора находим НОД (150,8) = 2. Делим 37/2 = 18,5. Число не целое, следовательно, уравнение не имеет целочисленных корней.

Проверим уравнение 1320x + 1760y = 10120. Используем калькулятор для нахождения НОД(1320, 1760) = 440. Разделим 10120/440 = 23. В результате получаем целое число, следовательно, диофантово уравнение разрешимо в целых коэффициентах.

Заключение

НОД и НОК играют большую роль в теории чисел, а сами понятия широко используются в самых разных областях математики. Используйте наш калькулятор для расчета наибольших делителей и наименьших кратных любого количества чисел.

Математические выражения и задачи требуют множества дополнительных знаний. НОК — это одно из основных, особенно часто применяемое в Тема изучается в средней школе, при этом не является особо сложным в понимании материалом, человеку знакомому со степенями и таблицей умножения не составит труда выделить необходимые числа и обнаружить результат.

Определение

Общее кратное — число, способное нацело разделиться на два числа одновременно (а и b). Чаще всего, это число получают методом перемножения исходных чисел a и b. Число обязано делиться сразу на оба числа, без отклонений.

НОК — это принятое для обозначения краткое название, собранной из первых букв.

Способы получения числа

Для нахождения НОК не всегда подходит способ перемножения чисел, он гораздо лучше подходит для простых однозначных или двухзначных чисел. принято разделять на множители, чем больше число, тем больше множителей будет.

Пример № 1

Для простейшего примера в школах обычно берутся простые, однозначные или двухзначные числа. Например, необходимо решить следующее задание, найти наименьшее общее кратное от чисел 7 и 3, решение достаточно простое, просто их перемножить. В итоге имеется число 21, меньшего числа просто нет.

Пример № 2

Второй вариант задания гораздо сложнее. Даны числа 300 и 1260, нахождение НОК — обязательно. Для решения задания предполагаются следующие действия:

Разложение первого и второго чисел на простейшие множители. 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7. Первый этап завершен.

Второй этап предполагает работу с уже полученными данными. Каждое из полученных чисел обязано участвовать в вычислении итогового результата. Для каждого множителя из состава исходных чисел берется самое большое число вхождений. НОК — это общее число, поэтому множители из чисел должны в нем повторятся все до единого, даже те, которые присутствуют в одном экземпляре. Оба изначальных числа имеют в своем составе числа 2, 3 и 5, в разных степенях, 7 есть только в одном случае.

Для вычисления итогового результата необходимо взять каждое число в наибольшей их представленных степеней, в уравнение. Остается только перемножить и получить ответ, при правильном заполнении задача укладывается в два действия без пояснений:

1) 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7.

2) НОК = 6300.

Вот и вся задача, если попробовать вычислить нужное число посредством перемножения, то ответ однозначно не будет верным, так как 300 * 1260 = 378 000.

Проверка:

6300 / 300 = 21 — верно;

6300 / 1260 = 5 — верно.

Правильность полученного результата определяется посредством проверки — деления НОК на оба исходных числа, если число целое в обоих случаях, то ответ верен.

Что значит НОК в математике

Как известно, в математике нет ни одной бесполезной функции, эта — не исключение. Самым распространенным предназначением этого числа является приведение дробей к общему знаменателю. Что изучают обычно в 5-6 классах средней школы. Также дополнительно является общим делителем для всех кратных чисел, если такие условия стоят в задаче. Подобное выражение может найти кратное не только к двум числам, но и к гораздо большему количестве — трем, пяти и так далее. Чем больше чисел — тем больше действий в задаче, но сложность от этого не увеличивается.

Например, даны числа 250, 600 и 1500, необходимо найти их общее НОК:

1) 250 = 25 * 10 = 5 2 *5 * 2 = 5 3 * 2 — на этом примере детально описано разложение на множители, без сокращения.

2) 600 = 60 * 10 = 3 * 2 3 *5 2 ;

3) 1500 = 15 * 100 = 33 * 5 3 *2 2 ;

Для того чтобы составить выражение, требуется упомянуть все множители, в этом случае даны 2, 5, 3, — для всех этих чисел требуется определить максимальную степень.

Внимание: все множители необходимо доводить до полного упрощения, по возможности, раскладывая до уровня однозначных.

Проверка:

1) 3000 / 250 = 12 — верно;

2) 3000 / 600 = 5 — верно;

3) 3000 / 1500 = 2 — верно.

Данный метод не требует каких-либо ухищрений или способностей уровня гения, все просто и понятно.

Еще один способ

В математике многое связано, многое можно решить двумя и более способами, то же самое касается поиска наименьшего общего кратного, НОК. Следующий способ можно использовать в случае с простыми двузначными и однозначными числами. Составляется таблица, в которую вносятся по вертикали множимое, по горизонтали множитель, а в пересекающихся клетках столбца указывается произведение.

Можно отразить таблицу посредством строчки, берется число и в ряд записываются результаты умножения этого числа на целые числа, от 1 до бесконечности, иногда хватает и 3-5 пунктов, второе и последующие числа подвергаются тому же вычислительному процессу. Все происходит вплоть до того, как найдется общее кратное.

Даны числа 30, 35, 42 необходимо найти НОК, связывающий все числа:

1) Кратные 30: 60, 90, 120, 150, 180, 210, 250 и т. д.

2) Кратные 35: 70, 105, 140, 175, 210, 245 и т. д.

3) Кратные 42: 84, 126, 168, 210, 252 и т. д.

Заметно, что все числа достаточно разные, единственное общее среди них число 210, вот оно и будет НОК. Среди связанных с этим вычислением процессов есть также наибольший общий делитель, вычисляющийся по похожим принципам и часто встречающийся в соседствующих задачах. Различие невелико, но достаточно значимо, НОК предполагает вычисление числа, которое делится на все данные исходные значения, а НОД предполагает под собой вычисление наибольшего значение на которое делятся исходные числа.

Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы рассмотрим способы нахождения НОК для трех чисел и более, разберем вопрос о том, как найти НОК отрицательного числа.

Yandex.RTB R-A-339285-1

Вычисление наименьшего общего кратного (НОК) через НОД

Мы уже установили связь наименьшего общего кратного с наибольшим общим делителем. Теперь научимся определять НОК через НОД. Сначала разберемся, как делать это для положительных чисел.

Определение 1

Найти наименьшее общее кратное через наибольший общий делитель можно по формуле НОК (a , b) = a · b: НОД (a , b) .

Пример 1

Необходимо найти НОК чисел 126 и 70 .

Решение

Примем a = 126 , b = 70 . Подставим значения в формулу вычисления наименьшего общего кратного через наибольший общий делитель НОК (a , b) = a · b: НОД (a , b) .

Найдет НОД чисел 70 и 126 . Для этого нам понадобится алгоритм Евклида: 126 = 70 · 1 + 56 , 70 = 56 · 1 + 14 , 56 = 14 · 4 , следовательно, НОД (126 , 70) = 14 .

Вычислим НОК: НОК (126 , 70) = 126 · 70: НОД (126 , 70) = 126 · 70: 14 = 630 .

Ответ: НОК (126 , 70) = 630 .

Пример 2

Найдите нок чисел 68 и 34 .

Решение

НОД в данном случае нейти несложно, так как 68 делится на 34 . Вычислим наименьшее общее кратное по формуле: НОК (68 , 34) = 68 · 34: НОД (68 , 34) = 68 · 34: 34 = 68 .

Ответ: НОК (68 , 34) = 68 .

В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b: если первое число делится на второе, что НОК этих чисел будет равно первому числу.

Нахождение НОК с помощью разложения чисел на простые множители

Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители.

Определение 2

Для нахождения наименьшего общего кратного нам понадобится выполнить ряд несложных действий:

• составляем произведение всех простых множителей чисел, для которых нам нужно найти НОК;
• исключаем их полученных произведений все простые множители;
• полученное после исключения общих простых множителей произведение будет равно НОК данных чисел.

Этот способ нахождения наименьшего общего кратного основан на равенстве НОК (a , b) = a · b: НОД (a , b) . Если посмотреть на формулу, то станет понятно: произведение чисел a и b равно произведению всех множителей, которые участвуют в разложении этих двух чисел. При этом НОД двух чисел равен произведению всех простых множителей, которые одновременно присутствуют в разложениях на множители данных двух чисел.

Пример 3

У нас есть два числе 75 и 210 . Мы можем разложить их на множители следующим образом: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . Если составить произведение всех множителей двух исходных чисел, то получится: 2 · 3 · 3 · 5 · 5 · 5 · 7 .

Если исключить общие для обоих чисел множители 3 и 5 , мы получим произведение следующего вида: 2 · 3 · 5 · 5 · 7 = 1050 . Это произведение и будет нашим НОК для чисел 75 и 210 .

Пример 4

Найдите НОК чисел 441 и 700 , разложив оба числа на простые множители.

Решение

Найдем все простые множители чисел, данных в условии:

441 147 49 7 1 3 3 7 7

700 350 175 35 7 1 2 2 5 5 7

Получаем две цепочки чисел: 441 = 3 · 3 · 7 · 7 и 700 = 2 · 2 · 5 · 5 · 7 .

Произведение всех множителей, которые участвовали в разложении данных чисел, будет иметь вид: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 · 7 . Найдем общие множители. Это число 7 . Исключим его из общего произведения: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 . Получается, что НОК (441 , 700) = 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 = 44 100 .

Ответ: НОК (441 , 700) = 44 100 .

Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.

Определение 3

Раньше мы исключали из всего количества множителей общие для обоих чисел. Теперь мы сделаем иначе:

• разложим оба числа на простые множители:
• добавим к произведению простых множителей первого числа недостающие множители второго числа;
• получим произведение, которое и будет искомым НОК двух чисел.

Пример 5

Вернемся к числам 75 и 210 , для которых мы уже искали НОК в одном из прошлых примеров. Разложим их на простые множители: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . К произведению множителей 3 , 5 и 5 числа 75 добавим недостающие множители 2 и 7 числа 210 . Получаем: 2 · 3 · 5 · 5 · 7 . Это и есть НОК чисел 75 и 210 .

Пример 6

Необходимо вычислить НОК чисел 84 и 648 .

Решение

Разложим числа из условия на простые множители: 84 = 2 · 2 · 3 · 7 и 648 = 2 · 2 · 2 · 3 · 3 · 3 · 3 . Добавим к произведению множителей 2 , 2 , 3 и 7 числа 84 недостающие множители 2 , 3 , 3 и
3 числа 648 . Получаем произведение 2 · 2 · 2 · 3 · 3 · 3 · 3 · 7 = 4536 . Это и есть наименьшее общее кратное чисел 84 и 648 ​​​​​​ ​.

Ответ: НОК (84 , 648) = 4 536 .

Нахождение НОК трех и большего количества чисел

Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел. На этот случай есть теорема.

Теорема 1

Предположим, что у нас есть целые числа a 1 , a 2 , … , a k . НОК m k этих чисел находится при последовательном вычислении m 2 = НОК (a 1 , a 2) , m 3 = НОК (m 2 , a 3) , … , m k = НОК (m k − 1 , a k) .

Теперь рассмотрим, как можно применять теорему для решения конкретных задач.

Пример 7

Необходимо вычислить наименьшее общее кратное четырех чисел 140 , 9 , 54 и 250 .

Решение

Введем обозначения: a 1 = 140 , a 2 = 9 , a 3 = 54 , a 4 = 250 .

Начнем с того, что вычислим m 2 = НОК (a 1 , a 2) = НОК (140 , 9) . Применим алгоритм Евклида для вычисления НОД чисел 140 и 9: 140 = 9 · 15 + 5 , 9 = 5 · 1 + 4 , 5 = 4 · 1 + 1 , 4 = 1 · 4 . Получаем: НОД (140 , 9) = 1 , НОК (140 , 9) = 140 · 9: НОД (140 , 9) = 140 · 9: 1 = 1 260 . Следовательно, m 2 = 1 260 .

Теперь вычислим по тому е алгоритму m 3 = НОК (m 2 , a 3) = НОК (1 260 , 54) . В ходе вычислений получаем m 3 = 3 780 .

Нам осталось вычислить m 4 = НОК (m 3 , a 4) = НОК (3 780 , 250) . Действуем по тому же алгоритму. Получаем m 4 = 94 500 .

НОК четырех чисел из условия примера равно 94500 .

Ответ: НОК (140 , 9 , 54 , 250) = 94 500 .

Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.

Определение 4

Предлагаем вам следующий алгоритм действий:

• раскладываем все числа на простые множители;
• к произведению множителей первого числа добавляем недостающие множители из произведения второго числа;
• к полученному на предыдущем этапе произведению добавляем недостающие множители третьего числа и т.д.;
• полученное произведение будет наименьшим общим кратным всех чисел из условия.

Пример 8

Необходимо найти НОК пяти чисел 84 , 6 , 48 , 7 , 143 .

Решение

Разложим все пять чисел на простые множители: 84 = 2 · 2 · 3 · 7 , 6 = 2 · 3 , 48 = 2 · 2 · 2 · 2 · 3 , 7 , 143 = 11 · 13 . Простые числа, которым является число 7 , на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.

Теперь возьмем произведение простых множителей 2 , 2 , 3 и 7 числа 84 и добавим к ним недостающие множители второго числа. Мы разложили число 6 на 2 и 3 . Эти множители уже есть в произведении первого числа. Следовательно, их опускаем.

Продолжаем добавлять недостающие множители. Переходим к числу 48 , из произведения простых множителей которого берем 2 и 2 . Затем добавляем простой множитель 7 от четвертого числа и множители 11 и 13 пятого. Получаем: 2 · 2 · 2 · 2 · 3 · 7 · 11 · 13 = 48 048 . Это и есть наименьшее общее кратное пяти исходных чисел.

Ответ: НОК (84 , 6 , 48 , 7 , 143) = 48 048 .

Нахождение наименьшего общего кратного отрицательных чисел

Для того, чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.

Пример 9

НОК (54 , − 34) = НОК (54 , 34) , а НОК (− 622 , − 46 , − 54 , − 888) = НОК (622 , 46 , 54 , 888) .

Такие действия допустимы в связи с тем, что если принять, что a и − a – противоположные числа,
то множество кратных числа a совпадает со множеством кратных числа − a .

Пример 10

Необходимо вычислить НОК отрицательных чисел − 145 и − 45 .

Решение

Произведем замену чисел − 145 и − 45 на противоположные им числа 145 и 45 . Теперь по алгоритму вычислим НОК (145 , 45) = 145 · 45: НОД (145 , 45) = 145 · 45: 5 = 1 305 , предварительно определив НОД по алгоритму Евклида.

Получим, что НОК чисел − 145 и − 45 равно 1 305 .

Ответ: НОК (− 145 , − 45) = 1 305 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

CD178 (Fas-лиганд) Моноклональное антитело (NOK-1), PE (12-9919-42)

CHMP2A регулирует чувствительность опухоли к цитотоксичности, опосредованной естественными клетками-киллерами.

Nature Communications

Bernareggi D, Xie Q, Prager BC, Yun J, Cruz LS, Pham TV, Kim W, Lee X, Coffey M, Zalfa C, Azmoon P, Zhu H, Tamayo P, Rich JN, Kaufman DS

Опубликованный рисунок с использованием моноклонального антитела CD178 (Fas-лиганд) (номер продукта 12-9919-42) в проточной цитометрии0003

Интерлейкин-24 регулирует активность Т-клеток у пациентов с колоректальной аденокарциномой.

Frontiers in Oncology

Zhang Y, Liu Y, Xu Y

12-9919-42 использовали в проточной цитометрии, чтобы показать, что IL-24 может регулировать функцию Т-клеток дозозависимым образом.

Ср 30 сен 00:00:00 EDT 2020

Сайленсинг гена растворимой эпоксидгидролазы 2 уменьшает H ₂ O ₂ -индуцированное окислительное повреждение в эпителиальных клетках IEC-6 кишечника крыс посредством активации сигнального пути PI3K/Akt/GSK3β.

Cytotechnology

Li J,Luo J,Zhang Y,Tang C,Wang J,Chen C

12-9919 использовали в Вестерн-блоттинге для изучения эффектов и молекулярного механизма siEPHX2 на индуцированное h3O2 окислительное повреждение эпителия кишечника крыс. Ячейки IEC-6.

Сб 01 февраля 00:00:00 EST 2020

Трансмембранный TNF-α способствует индуцированной активацией гибели клеток посредством прямой и обратной передачи сигналов.

Oncotarget

Zhang M, Wang J, Jia L, Huang J, He C, Hu F, Yuan L, Wang G, Yu M, Li Z

Опубликованный рисунок с использованием моноклонального антитела CD178 (Fas-лиганд) (номер продукта 12-9919-42) в проточной цитометрии

IL12-опосредованная сенсибилизация Т-клеточного рецептор-зависимого и независимого уничтожения опухолевых клеток.

Онкоиммунология

Braun M, Ress ML, Yoo YE, Scholz CJ, Eyrich M, Schlegel PG, Wölfl M

12-9919 использовали в проточной цитометрии/сортировке клеток для изучения того, как IL12 и другие воспалительные цитокины формируют эффекторные функции Т-клеток человека.

Пт 01 июля 00:00:00 по восточному времени 2016

Долгосрочное влияние терапии интерфероном-α на естественные клетки-киллеры на исходы инфекции ВГС.

Журнал исследований интерферона и цитокинов: официальный журнал Международного общества исследований интерферона и цитокинов

Hu X, Jiang Y, Li X, Gao Y, Guo X, Chi X, Yan H, Feng J, Zhong J, Sun B, Shao X, Xiao W, Pan Y, Niu J

12-9919 использовали в проточной цитометрии/сортировке клеток для исследования динамических изменений частоты различных субпопуляций естественных клеток-киллеров после лечения у xx пациентов с хроническим гепатитом C.

Чт 01 мая 00:00:00 по восточноевропейскому летнему времени 2014

Fas-опосредованное уничтожение клеток первичного рака предстательной железы усиливается митоксантроном и доцетакселом.

Молекулярная терапия рака

Symes JC, Kurin M, Fleshner NE, Medin JA

12-9919 использовали в проточной цитометрии/сортировке клеток для исследования восприимчивости культивируемых первичных клеток простаты к Fas-опосредованному апоптозу.

Пн 01 сен 00:00:00 по восточноевропейскому времени 2008

Siva-1 отрицательно регулирует активность NF-kappaB: влияние на гибель клеток, опосредованную активацией Т-клеточного рецептора (AICD).

Oncogene

Gudi R, Barkinge J, Hawkins S, Chu F, Manicassamy S, Sun Z, Duke-Cohan JS, Prasad KV

12-9919 использовали в Вестерн-блоттинге, чтобы продемонстрировать значительную роль эндогенного Siva-1, благодаря его ингибирующему действию на активность NF-kappaB при TCR-опосредованной гибели клеток, индуцированной активацией (AICD).

Чт 08 июня 00:00:00 по восточноевропейскому времени 2006

c-FLIP ингибирует гибель клеток колоректального рака, вызванную химиотерапией.

Oncogene

Longley DB, Wilson TR, McEwan M, Allen WL, McDermott U, Galligan L, Johnston PG

12-9919 использовали в проточной цитометрии/сортировке клеток для изучения влияния c-FLIP на апоптотический ответ на химиотерапию, применяемую при колоректальном раке.

Чт, 9 февраля, 00:00:00 EST 2006

Что они означают и почему важны

Запутались в номерах удобрений? Мы не виним вас! Зайдите в любой магазин садовых принадлежностей, и вы увидите полки, заполненные разнообразными удобрениями с разными ингредиентами, но, что более важно, с тремя цифрами, которые могут показаться пугающими.

Понимание этих трех чисел не должно быть таким сложным, и мы здесь, чтобы избавить садоводство от догадок, чтобы у вас были красивые, пышные зеленые газоны и здоровые растения.

Эта статья не только объяснит, что это за числа, но и даст вам отличные практические правила, чтобы вы могли легко ориентироваться в проходах, чтобы найти подходящее удобрение для ваших приключений на заднем дворе!

Содержание

Что означают номера удобрений?

Каждое удобрение, которое вы встретите, будет выделено тремя цифрами жирным шрифтом. Это соотношение N-P-K растения, и оно всегда будет в таком порядке. Эта этикетка также известна как сорт удобрения, что является национальным стандартом.

Эти три числа соответствуют трем наиболее важным макроэлементам для растений, а именно азоту (N), фосфору (P) и калию (K). Хотя существует 16 питательных веществ, которые необходимы для здоровья растений, эти три являются наиболее важными.

Таким образом, первое число всегда означает количество азота (N), второе число — количество фосфата (P2O5), а третье число — количество калия (K2O). Вместе они представляют основные питательные вещества, в которых нуждается ваше растение: азот (N) – фосфор (P) – калий (K).

Цифры на нашем универсальном удобрении, например, 5-5-5. Это массовый процент азота, фосфора и калия, содержащихся в удобрении.

Разбивка номеров удобрений Далее

Давайте упростим некоторые числа, чтобы понять содержание питательных веществ, скажем, в 100 фунтах универсального удобрения с соотношением NPK 5-5-5.

Это означает, что он содержит 5 процентов азота, 5 процентов фосфора и 5 процентов калия.

Рассчитать точное количество питательных веществ в фунтах очень просто.

N: 5% от 100 фунтов (0,05 x 100), что составляет 5 фунтов

P: 5% от 100 фунтов (0,05 x 100), что составляет 5 фунтов

K: 5% от 100 фунтов (0,05 x 100), что составляет 5 фунтов

3 Остальную часть удобрения составляет наполнитель, которым обычно является песок или гранулированный известняк.

Таким образом, вы можете рассчитать точное количество питательных веществ практически в любом удобрении, если знаете вес и соотношение NPK.

Почему азот (N), фосфор (P) и калий (K) так важны?

Но подождите, что такого важного в азоте, фосфоре и калии? Выше мы упоминали, что это три самых важных макроэлемента, но давайте разберемся, для чего полезен каждый из них:

Азот (N)

Азот (N), вероятно, является наиболее широко известным питательным веществом, известным прежде всего своей способностью «озеленять» газоны. Азот в основном влияет на вегетативный рост и общее состояние здоровья. И именно поэтому вы заметите, что многие удобрения для газонов содержат большое количество азота, что способствует росту листьев.

Хлорофилл, зеленое вещество растений, отвечающее за фотосинтез, в основном состоит из азота. Он также активно используется в новых побегах, почках и листьях.

Воздух содержит около 78% азота, но атмосферный азот недоступен для растений. Они должны впитать его через почву.

Все эти питательные вещества бывают в органической и синтетической (химической) формах. Аммиачная селитра, мочевина и сульфат аммония являются легкодоступными формами азота, и именно они обычно используются в химических удобрениях и сильно и быстро вымываются из почвы.

Азот также можно вносить органически разными способами, включая кровяную муку, перьевую муку и различные жидкие удобрения, такие как Alaska Fish Fertilizer. Имейте в виду, что многие органические сухие удобрения являются медленно высвобождаемыми, помогая долгосрочному содержанию азота и накапливая органические вещества в почве.

Дефицит азота определяется по пожелтению старых листьев, замедлению или остановке роста. Листья могут опадать раньше, чем ожидалось. Избыток азота проявляется в чрезвычайно быстром росте, в результате чего появляются длинные, веретенообразные, слабые побеги с темно-зелеными листьями.

Фосфор (P)

Фосфор (P) важен для здоровых корней и используется в большей степени во время цветения и завязывания семян. Фосфор легко становится недоступным для растений, когда рН немного несбалансирован. Он высвобождается в почве при разложении органических веществ.

Дефицит фосфора определяется по тускло-зеленым листьям и пурпурным стеблям. Растение в целом нездоровое, иногда желтеет.

Отсутствие цветения с пышной зеленой листвой также может свидетельствовать о недостатке фосфора. Органический фосфор можно найти в каменном фосфате, костной муке и различных жидких органических удобрениях, таких как Neptune’s Harvest Fish & Seaweed.

Калий (K)

Калий (K), иногда называемый калием, важен для общего здоровья растений. Он играет ключевую роль в образовании хлорофилла и других растительных соединений. Также известно, что калий помогает с устойчивостью к болезням.

Дефицит калия трудно выявить, но растения, как правило, болезненны, с мелкими плодами, пожелтением от старых листьев вверх и болезненными цветками.

Источниками органического калия являются sul-po-mag (сульфат калийной магнезии), зола пальмовых связок и жидкие удобрения, такие как Earth Juice Meta-K.

Какие другие питательные вещества важны для здоровья растений?

Выше мы упоминали, что существует 16 питательных веществ, которые необходимы для общего здоровья и роста растений. Мы уже рассмотрели три основных макроэлемента, но что насчет остальных?

Три из оставшихся 13 растений получают из воздуха и воды: водород, кислород и углерод.

Осталось 10. Из них три считаются вторичными питательными веществами. Это означает, что, хотя они важны для растений, они необходимы в меньших количествах, чем N, P и K. Это:

• Кальций (Ca): кальций помогает растениям в формировании клеточных стенок и клеточных мембран, и даже играет важную роль в структуре почвы. Признаки дефицита кальция у растений включают скручивание листьев, обесцвечивание, медленный рост и даже различные виды гнили.
• Магний (Mg): Магний помогает растениям усваивать питательные вещества и даже необходим для метаболизма фосфатов. Это помогает придать листьям зеленый цвет. Когда растениям не хватает магния, желтизна начинает пробиваться по жилкам и по краям листьев. Старые листья обычно страдают первыми и со временем отмирают, если не обеспечить должный уход.
• Сера (S): Сера необходима для образования хлорофилла, который помогает им поддерживать темно-зеленый цвет и способствует правильному росту. Растения, испытывающие дефицит серы, часто бывают бледно-зелеными, желтовато-зелеными, а иногда даже полностью желтыми. Эти признаки проявляются в первую очередь на молодых листьях.

Остальные питательные вещества, в которых нуждаются растения, известны как микроэлементы или микроэлементы, поскольку они необходимы в гораздо меньших количествах. К ним относятся железо, марганец, цинк, медь, бор, молибден и хлор.

Удобрения могут содержать некоторые или все микроэлементы, но ваш сад может не нуждаться в них в большем количестве. Чрезмерное внесение удобрений сопряжено со множеством проблем, поэтому проведение анализа почвы — лучший способ выяснить, каких питательных веществ не хватает в вашей почве.

Проверьте свою почву, чтобы выбрать правильное удобрение

Лучший способ узнать, достаточно ли питательных веществ в почве вашего сада, — это протестировать ее. Результаты испытаний почвы включают анализ вашей текущей почвы, а также рекомендации по удобрению, которое следует использовать для устранения недостатков, которые могут быть в вашей почве.

Несмотря на то, что доступны домашние тестовые наборы, лабораторные тесты дают наиболее полные и надежные результаты. В каждом штате США есть совместная служба распространения знаний, связанная с его университетской системой. Анализ почвы обычно стоит от 15 до 20 долларов, и получение результатов занимает около месяца.

Почва постоянно меняется, поэтому рекомендуется проверять почву каждые 2-3 года и вести записи результатов испытаний, внесения удобрений и любых поправок, которые вы можете использовать.

Вот и все, что вам нужно знать о количестве удобрений и о том, как вы можете использовать их, чтобы иметь растения, урожай и сад вашей мечты.

Эрик Винье

Веб-сайт | + posts

Эрик Винье основал Planet Natural вместе со своим отцом Уэйном в 1991 году. Сначала он занимался доставкой по почте приманки для кузнечиков из гаража.

Эрик сейчас на пенсии, но по-прежнему является известным садовником, известным своим опытом компостирования, органического садоводства и борьбы с вредителями, используя варианты без пестицидов, такие как полезные насекомые.