Обозначение длины вектора: Длина (модуль) вектора, формулы и онлайн калькуляторы

Тест по теме «Векторы»

Тест по теме «Векторы»

Вариант 1

1. Отрезок, для которого указано, какой из его концов является началом, а какой – концом, называется:

А. луч

Б. прямая

В. вектор

Г. нет верного варианта ответа

1. Два ненулевых вектора, лежащие на одной прямой или на параллельных прямых, называются:

А. сонаправленными

Б. коллинеарными

В. противоположно направленными

Г. равными

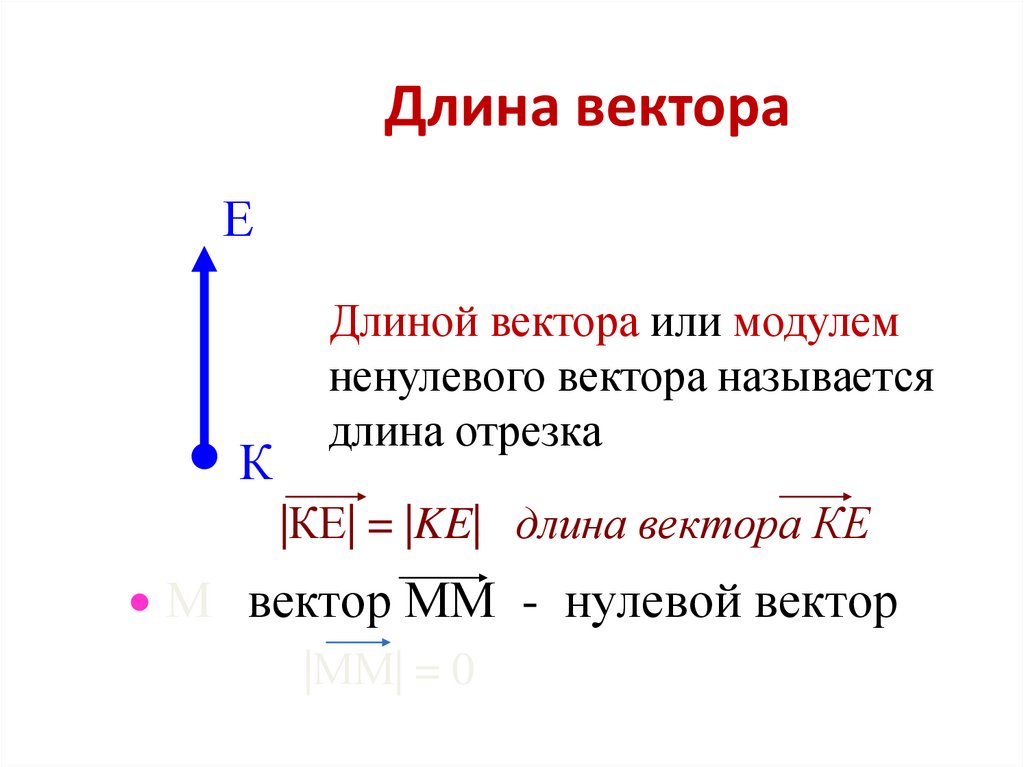
1. Длиной ненулевого вектора  называется:

А. длина луча

Б. длина отрезка AB

В. длина прямой

Г. нет верного варианта ответа

1. Выберите верное обозначение сонаправленных векторов.

А.

Б.

В.

Г. нет верного варианта ответа

1. Векторы называются равными, если:

А. они коллинеарны

Б. их длины равны

В. они сонаправлены

Г. они сонаправлены и их длины равны

1. – это формула:

А. разности вектора

Б. сочетательного закона

В. нет верного варианта ответа

Г. переместительного закона

1. Выберите пары противоположно направленных векторов.

А. и , и

Б. и , и

В. и , и

Г. и , и

1. Выберите пары равных векторов.

А. и , и

Б. и , и

В. и , и

Г. и , и

1. Верны ли следующие суждения?

а. Направленный отрезок (вектор), длина которого равна нулю, – это нулевой вектор.

б. От любой точки можно отложить вектор, равным данному, и притом только один.

А. верно только а

Б. верно только б

В. оба суждения верны

Г. оба суждения неверны

1. Верны ли следующие суждения?

а.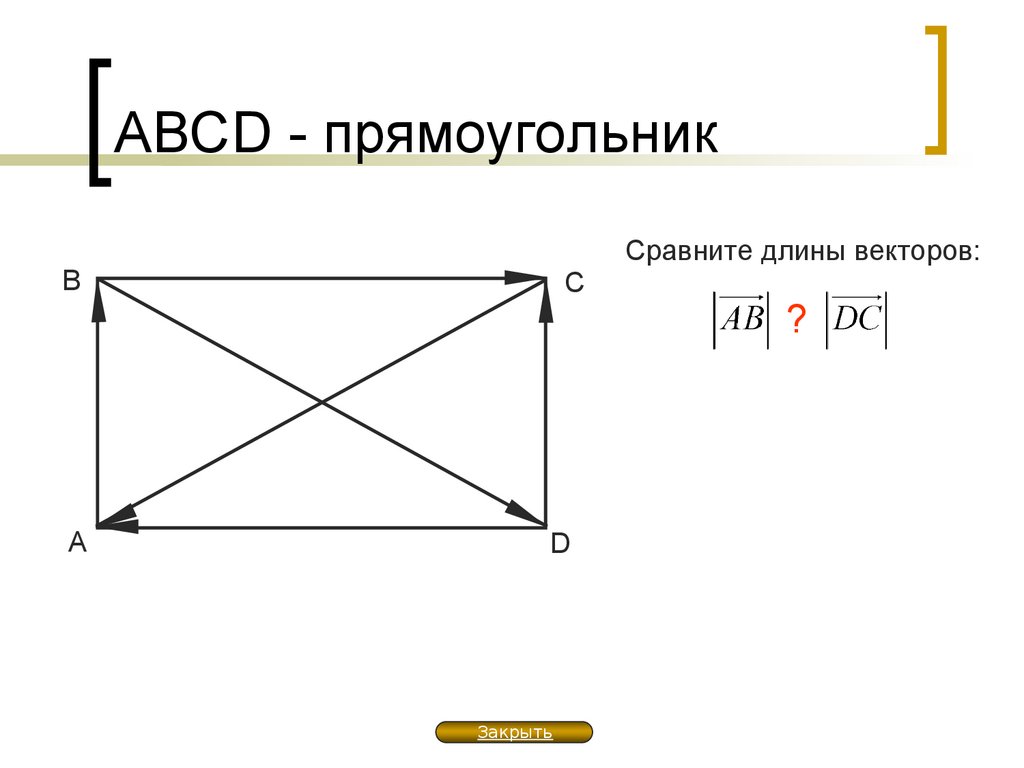 – формула сочетательного закона

б. – формула правила треугольника

А. верно только а

Б. верно только б

В. оба суждения верны

Г. оба суждения неверны

1. Дан треугольник OEH. Найдите сумму векторов  и .

1. Дан параллелограмм RSTV. Найдите сумму векторов  и .

Тест по теме «Векторы»

Вариант 2

1. Любая точка пространства может рассматриваться как вектор. Такой вектор называется:

А. коллинеарным

Б. сонаправленным

В. нулевым

Г. ненулевым

1. Какие слова пропущены в предложении?

Если два ненулевых вектора коллинеарны, то они могут быть направлены либо одинаково (тогда их называют …), либо противоположно (тогда их называют …).

А. сонаправленные; разнонаправленные

Б. противоположно направленные: сонаправленные

В. сонаправленные: противоположно направленные

Г.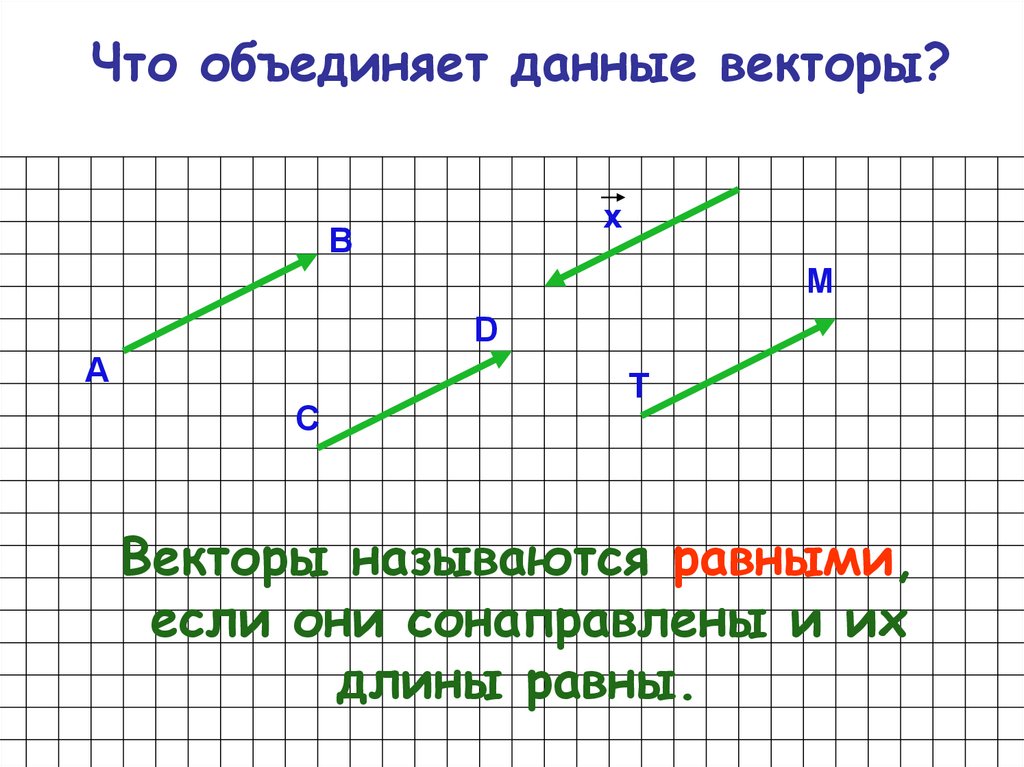 нет верного варианта ответа

1. Выберите верное обозначение длины вектора 

А.

Б.

В.

Г.

1. Выберите верное обозначение противоположно направленных векторов.

А.

Б.

В.

Г. нет верного варианта ответа

1. Векторы называются равными, если:

А. они сонаправлены

Б. они сонаправлены и их длины равны

В. они коллинеарны

Г. их длины равны

1. Выберите верную формулу сочетательного закона.

А.

Б.

В. (

Г.

1. Выберите пары сонаправленных векторов.

А. и , и

Б. и , и

В. и , и

Г. и , и

1. Выберите пары равных векторов.

А. и , и

Б. и и

В. и , и

Г. и , и

1. Верны ли следующие суждения?

а.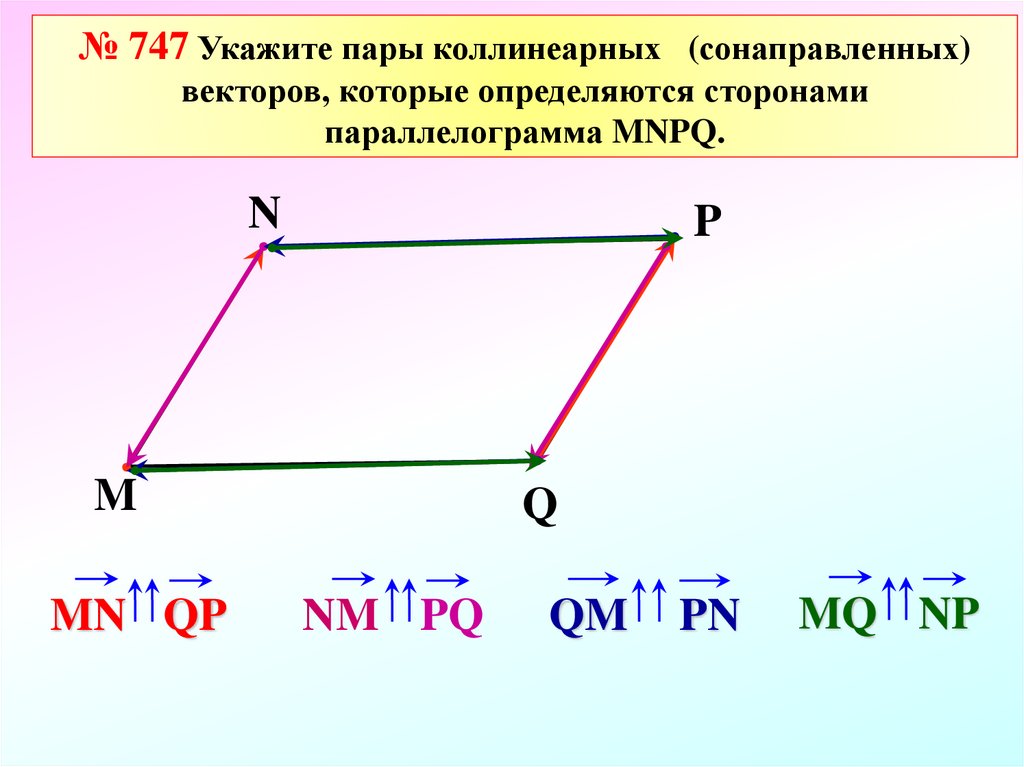 Векторы называются равными, если они коллинеарные и их длины равны.

б. Длиной ненулевого вектора   является длина отрезка CD.

А. верно только а

Б. верно только б

В. оба суждения верны

Г. оба суждения неверны

1. Верны ли следующие суждения?

а. Вектор называется нулевым, если его начальная и конечная точка совпадает.

б. Модулем вектора называется длина вектора, выраженная числовым выражением.

А. верно только а

Б. верно только б

В. оба суждения верны

Г. оба суждения неверны

1. Дан треугольник OEH. Найдите сумму векторов  и .

12. Дан параллелограмм RSTV. Найдите сумму векторов  и .

Ответы:

	Вариант 1	Вариант 2
1	В	В
2	Б	В
3	Б	А
4	А	Б
5	Г	Б
6	Г	В
7	А	В
8	Г	А
9	В	Б
10	Б	В
11	ОЕ	EO
12	SV	TR

Векторы плоскости.

Координаты вектора — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Тема: «Векторы плоскости»

Выполнил: Календарев Равиль 9 «Г»

2. Определение вектора

Определение. Вектор — это направленный
отрезок, то есть отрезок, имеющий длину и
определенное направление. Графически
вектора изображаются в виде направленных
отрезков прямой определенной длины.

3. Обозначение вектора

Вектор началом которого
есть точка А, а концом точка В,
обозначается AB. Также
вектора обозначают одной
маленькой буквой,
например a.

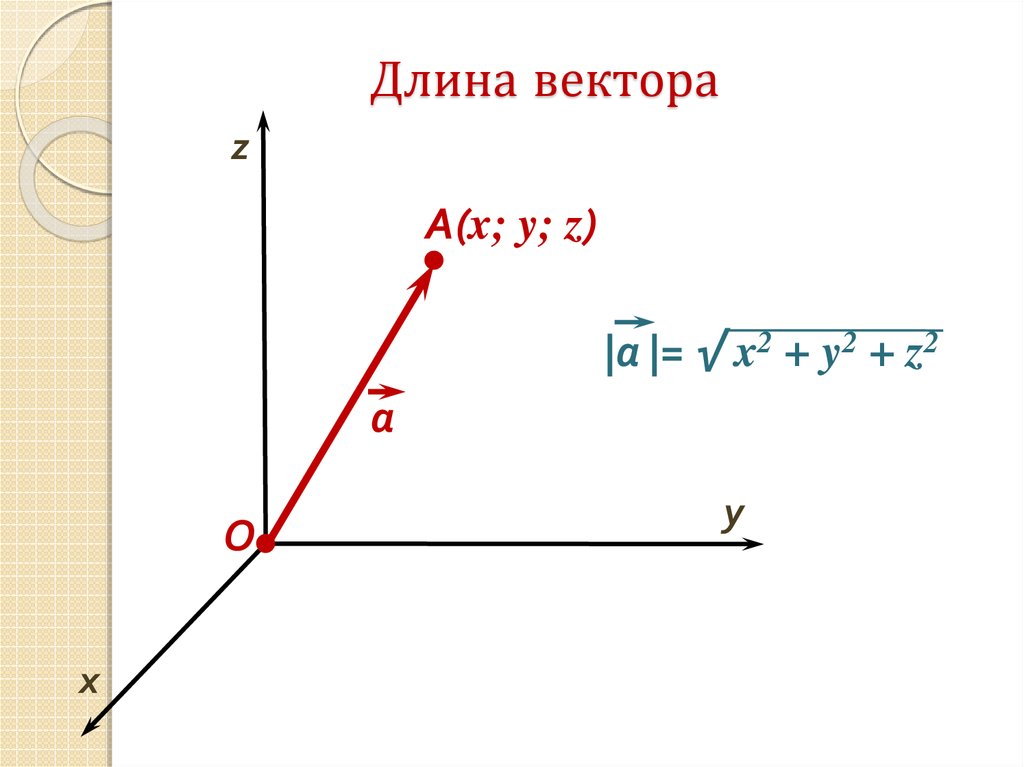
4. Длина вектора

Определение. Длина направленного отрезка
определяет числовое значение вектора и
называется длиной вектораили модулем
вектора AB.
Для обозначения длины вектора используются
две вертикальные линии слева и справа |AB|.

5. Нулевой вектор

Определение. Нулевым
вектором называется вектор, у
которого начальная и конечная
точка совпадают.
Нулевой вектор обычно
обозначается как 0.
Длина нулевого вектора равна
нулю.

6. Коллинеарные вектора

Определение. Вектора, параллельные одной
прямой или лежащие на одной прямой
называют коллинеарными векторами.

7. Сонаправленные вектора

Определение. Два коллинеарных
вектора a и b называются сонаправленными
векторами, если их направления
совпадают: a↑↑b

8. Противоположно направленные вектора

Определение. Два коллинеарных
вектора a и b называются противоположно
направленными векторами, если их
направления противоположны: a↑↓b

9.

Равные вектораОпределение. Вектора a и b называются
равными, если они лежат на одной или
параллельных прямых, их направления
совпадают, а длины равны.

10.  Сложение векторов

Сложение векторов
Определение.
Сложение векторов (сумма
векторов) a + b есть операция вычисления
вектора c, все элементы которого равны
попарной сумме соответствующих
элементов векторов a и b, то есть каждый
элемент вектора c равен:
с i = ai + b i

11. Вычитание векторов

Определение.
Вычитание векторов (разность
векторов) a — b есть операция вычисления
вектора c, все элементы которого равны
попарной разности соответствующих
элементов векторов a и b, то есть каждый
элемент вектора c равен:
с i = ai — b i

12. Сумма и разность векторов

Сумма
Разность
AB AC CB
AB BC AC
C
a b
A
a
b
B
C
b
A
a
a b
B

13. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ

Определение. Векторным
произведением вектора a на
вектор b называется вектор c, длина которого
численно равна площади параллелограмма
построенного на векторах a и b,
перпендикулярный к плоскости этих векторов
и направленный так, чтоб наименьшее
вращение от a к b вокруг
вектора c осуществлялось против часовой
стрелки, если смотреть с конца вектора c

14.

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ

15. Угол между векторами

Определение. Углом между двумя векторами,
отложенными от одной точки, называется
кратчайший угол, на который нужно повернуть
один из векторов вокруг своего начала до
положения сонаправленности с другим
вектором.
Основное соотношение. Косинус угла между
векторами равен скалярному произведению
векторов, поделенному на произведение модулей
векторов.
Формула вычисления угла между векторами
cos α =
a·b
| a|·|b|

17. Скалярное произведение

Скалярным произведением двух ненулевых
векторов и называется число, равное
произведению длин этих векторов на косинус
угла между ними:

18. Свойства скалярного произведения. Угол между векторами

19. КООРДИНАТЫ ВЕКТОРА

Основное соотношение. Чтобы найти
координаты вектора AB, зная координаты его
начальной точек А и конечной точки В,
необходимо из координат конечной точки
вычесть соответствующие координаты
начальной точки.

English     Русский Правила

Обозначение

Математические объекты

92\$

Пример	Значение	Латекс
$P$	Точки и позиции обозначаются прописными курсивными буквами.	\$П\$
$(4, 5, -2)$	Координаты позиции задаются в виде кортежа, поэтому $P$ находится в точке $(4, 5, -2)$ — это то же самое, что сказать, что $P$ имеет координаты $x = 4$, $y = 5$, $ г = -2$. Обратите внимание на отличие от векторных компонентов с помощью квадратных скобок.	\$(4, 5, -2)\$
$\boldsymbol{v}$	Векторы в наборном материале выделены жирным шрифтом. 2}$.	\$\|\boldsymbol{v}\|\$, \$v\$
$\шляпа{\boldsymbol{v}}$	В единичных векторах используется верхняя шляпа, поэтому $\hat{\boldsymbol{v}} = \frac{\boldsymbol{v}}{\|\boldsymbol{v}\|}$.	\$\шляпа{\boldsymbol{v}}\$
$\шляпа{\boldsymbol{\imath}}$, $\шляпа{\boldsymbol{\jmath}}$, $\шляпа{\boldsymbol{k}}$	декартовы базисные векторы, поэтому мы пишем $\boldsymbol{v} = 3\hat{\boldsymbol{\imath}} + \hat{\boldsymbol{\jmath}} + 7\hat{\boldsymbol{k}}$.	\$\шляпа{\boldsymbol{\imath}}\$, \$\шляпа{\boldsymbol{\jmath}}\$, \$\шляпа{\boldsymbol{k}}\$
$[3, 1, 7]$	Компоненты вектора используют квадратные скобки, поэтому мы пишем $[\boldsymbol{v}]_R = [3, 1, 7] = 3\hat{\boldsymbol{\imath}} + \hat{\boldsymbol{\jmath}} + 7\шляпа{\boldsymbol{k}}$. Если базис ясен, то будем писать $\boldsymbol{v} = [3, 1, 7]$.	\$[3, 1, 7]\$
$[\boldsymbol{v}]_R$	Компоненты вектора в базисе $R$. Стандартные имена базиса: $R$ для прямоугольного (декартова), $P$ для полярного, $C$ для цилиндрического, $S$ для сферического.	\$[\boldsymbol{v}]_R\$
$v_x, v_y, v_z$	Компоненты вектора выделены нежирным шрифтом с нижними индексами, поэтому $\boldsymbol{v} = [v_x, v_y, v_z] = v_x\,\hat{\boldsymbol{\imath}} + v_y\,\hat{\boldsymbol{\ jmath}} + v_z\,\hat{\boldsymbol{k}}$.	\$v_x, v_y, v_z\$
$v$ против $v_x$	Величина (положительная) — это простая буква $v$, а знаковый компонент — $v_x$.	\$v\$ против \$v_x\$
$\шляпа{\boldsymbol{e}}_r, \шляпа{\boldsymbol{e}}_\theta$	Полярные базисные векторы. Может быть, нам следует изменить это на $\hat{\boldsymbol{r}}, \hat{\boldsymbol\theta}$?	\$\шляпа{е}_r\$, \$\шляпа{е}_\тета\$
$\boldsymbol{r}$, $\boldsymbol{r}_P$, $\boldsymbol{r}_{OP}$, $\overrightarrow{OP}$	Вектор положения точки $P$ из начала координат $O$. Происхождением и/или точкой можно пренебречь, если это очевидно из контекста.	\$\boldsymbol{r}\$, \$\boldsymbol{r}_P\$, \$\boldsymbol{r}_{OP}\$, \$\overrightarrow{OP}\$
$\boldsymbol{\rm A}$	Матрицы выделены прямым (римским) жирным шрифтом.

Элементы диаграммы

Элемент	Значение	Латекс
$\mathcal{B}_1$	Кузов номер 1. Используйте номера 1,2,3 для тел.	\$\mathcal{B}_1\$
$m_1, \omega_1, \alpha_1$	Масса, угловая скорость и угловое ускорение тела $\mathcal{B}_1$. Используйте индексы для количеств, связанных с телами.	\$m_1, \omega_1, \alpha_1\$
$П, К$	Точки $P$ и $Q$. Используйте курсив заглавными буквами для пунктов.	\$Р, Q\$
$\boldsymbol{r}_P, \boldsymbol{v}_P, \boldsymbol{a}_P$	Векторы положения, скорости и ускорения точки $P$. Используйте подстрочные прописные курсивные буквы для количеств, связанных с точками.	\$\boldsymbol{r}_P, \boldsymbol{v}_P, \boldsymbol{a}_P\$
$I_{1,P,z}$	Момент инерции тела $\mathcal{B}_1$ относительно точки $P$ вокруг оси $z$. Любым из нижних индексов можно пренебречь, если они очевидны из контекста, хотя, по крайней мере, точка обычно должна быть включена.	\$I_{1,P,z}\$

Цветовая схема для диаграмм

По возможности используйте бледно-желтый (или коричневый) фон с светло-серая (или светло-зеленая) квадратная сетка, как традиционная инженерная бумага. Также можно использовать пустой белый фон.

Цвет	Значение
Черный	Координатные оси и объекты.
Серый	Измерения, углы, другие примечания.
Синий	Векторы положения.
Зеленый	Скорости и угловые скорости.
Голубой	Ускорения и угловые ускорения.
Красный	Сил.
Фиолетовый	мгновений.

Пример диаграммы с цветными элементами.

Видео: Введение в нотацию векторов

Стенограмма видео

В этом видео мы поговорим о том, что такое векторы и какие обозначения мы используем для их представления.

Теперь это немного отличается от страны к стране. Итак, мы собираемся показать вам очень разные способы отображения одного и того же, используя разные обозначения. И вам просто нужно выбрать вариант нотации, который работает там, где вы находитесь.

𝐴 вектор — это набор чисел, который может быть представлен в подходящем пространстве отрезком прямой с определенной длиной и направлением. В этом случае у нас есть двумерный вектор, который представляет сдвиг на три единицы в направлении 𝑥, поэтому мы идем на три положительные единицы по оси 𝑥 и на две отрицательные единицы в направлении 𝑦, поэтому мы собираемся

минус три [минус два] в 𝑦-направлении. Итак, чтобы перейти от 𝐴 к 𝐵, мы делаем три в 𝑥-направлении и минус два в 𝑦-направлении.

Векторы использовались астрономами еще в семнадцатом веке как способ записи и отслеживания движения планет в ночном небе. Само слово происходит от латинского, что означает носитель. Так что попытайтесь думать о векторах как о значении того, в каком направлении и как далеко я должен двигаться, если я хочу, чтобы меня перенесло из 𝐴 в 𝐵 по прямой линии. Теперь подумайте, что этот набор инструкций можно применить к любому начальному положению, чтобы воспроизвести одно и то же относительное движение.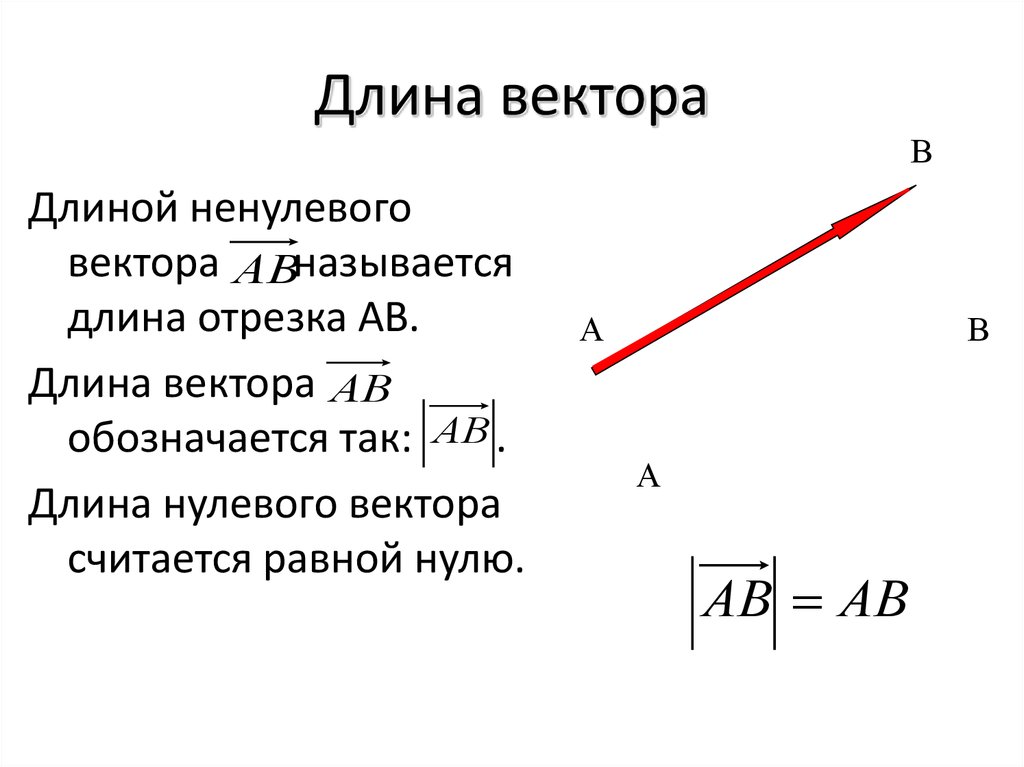 Итак, в этом случае мы только что переместились на определенное расстояние в 𝑥-направлении, не сильно изменившись в 𝑦-направлении. Таким образом, один и тот же набор инструкций можно было применять с разных стартовых и финишных позиций.

Когда мы рисуем векторы, мы используем отрезок линии определенной длины и стрелку, чтобы мы могли видеть подразумеваемое направление движения. В определениях вы часто будете видеть, что у векторов есть начальная точка и конечная точка. Но помните, что вы можете взять вектор и поместить его в любое место в пространстве, чтобы представить одно и то же относительное движение, если вы убедитесь, что он имеет одинаковую длину и ориентацию. Так что фактически начальная точка и конечная точка на самом деле не фиксированы. Они просто помогают вам рассчитать направление и расстояние движения. Поэтому, если я добавлю координаты 𝐴 и 𝐵 к своей диаграмме, я увижу, что двигался четыре раза в направлении 𝑥 и два в направлении 𝑦. Таким образом, вектор представляет собой комбинацию этих двух компонентов: 𝑥-компонента и 𝑦-компонента.

Теперь мы увидим, что означают все эти числа, и через мгновение мы более глубоко подумаем о векторах. Но прежде всего давайте зададимся вопросом, почему мы вообще должны использовать векторы. Мы можем количественно оценить множество вещей, используя только число, а иногда и единицу измерения. Например, масса, площадь, объем, длина — все они могут быть представлены числом, а иногда и единицей. Например, десять килограммов, двенадцать квадратных сантиметров, тысяча кубических сантиметров и так далее. Все они называются скалярными величинами. Теперь у векторных величин есть дополнительный аспект — направление. Таким образом, они могли бы описать, например, перемещение определенной величины в определенном направлении. Так перевод из точки 𝐴 в точку 𝐵, например. Они также могут представлять, скажем, скорость определенной скорости в определенном направлении. Точно так же их можно использовать для обозначения ускорения или даже силы, приложенной в определенном направлении. Таким образом, векторные величины — это ситуации, когда нам нужно число для представления величины чего-то, но нам также нужно знать конкретное направление, в котором оно работает.

Итак, какие обозначения мы используем для векторов? Ну, мы видели это графически, мы можем использовать отрезок линии определенной длины, ориентированный в определенном направлении. Но мы также можем использовать буквы и цифры для представления векторов, хотя существует несколько различных соглашений, в зависимости от того, где вы живете. Итак, давайте для начала подумаем о двухмерном пространстве, но его можно легко расширить до трехмерного или даже более высокого измерения, просто добавив дополнительные числа.

Итак, один из способов называется формой компонента. Здесь мы сначала пишем объем перевода в 𝑥-направлении, затем объем перевода в 𝑦-направлении. К сожалению, есть три популярных формата. У одного есть угловые скобки, у другого формат вертикального вектора-столбца, а еще один выглядит как аннотация координат. Если мы хотим дать нашим векторам имя, то одно популярное и полезное обозначение состоит в том, чтобы пометить его, используя его начальную и конечную точки, со стрелкой над ней, показывающей, что есть что. Буквы обычно заглавные, начальная точка первая, а конечная точка вторая. В зависимости от того, где вы живете, вы будете использовать либо стрелу, либо полустрелу в стиле гарпуна выше. Итак, давайте посмотрим на них сейчас.

Таким образом, для этих двух, обычно в узком письменном формате, у вас будут заглавные буквы 𝐴 и 𝐵, выделенные курсивом, со стрелкой в ​​​​стиле гарпуна над ними. А для обозначения вектора-столбца это обычно связано с некурсивными прописными буквами с обычной стрелкой, показывающей направление от 𝐴 к 𝐵. Надеюсь, вы узнаете систему, которая используется в вашем районе, из ваших учебников или школьных работ. Итак, если бы мы хотели представить вектор, идущий от 𝐵 к 𝐴, мы могли бы использовать любой из этих форматов здесь слева. 𝐵𝐴 — это минус три, минус четыре, бутог, потому что, чтобы перейти от 𝐵 к 𝐴, нам нужно было пройти минус три в 𝑥-направлении и минус четыре в 𝑦-направлении. Таким образом, порядок букв, направление стрелки, знак числа имеют решающее значение, когда дело доходит до записи наших векторов.

Теперь, чтобы добавить путаницы, если мы просто хотим присвоить конкретную букву вектору a-a, а не указывать его начальную и конечную точки, мы можем сделать и это. Но опять же, существует множество различных соглашений, которые мы можем использовать. Это на самом деле довольно сложно, когда вы записываете это, чтобы представить это на экране. Но, как правило, вы можете использовать вариант этой буквы жирным шрифтом, может быть в верхнем регистре, может быть в нижнем регистре. Итак, если бы мы назвали наш вектор 𝑣, он был бы жирным 𝐯 или курсивом 𝑣, равным трем, четырем в этой конкретной системе обозначений.

Теперь люди, использующие нотацию вектора-столбца, также используют полужирную букву для представления имени вектора. Поэтому, если бы мы хотели назвать вектор 𝑣, это была бы жирная буква шрифта. Но когда мы пишем это от руки, мы можем написать это как обычную букву 𝑣 от руки, но с подчеркиванием под ней, чтобы показать, что это вектор. Так что это просто способ помочь вам записать векторы в рукописной записи.

И люди, которые используют координатную нотацию для векторов, опять же, использовали бы полужирную букву, но они помещают одну из этих маленьких гарпунных стрелок над буквой, чтобы обозначить тот факт, что это вектор. Или они могут даже использовать курсивную версию этой буквы с гарпуном над ней для обозначения вектора, иногда.

Так что это звучит немного запутанно, когда мы говорим об этом вот так. Но из контекста вопросов, которые вы рассматриваете, вы узнаете, какие обозначения они используют и что они означают векторы. Итак, давайте взглянем на пару примеров векторов.

Таким образом, вектор 𝐴𝐵 таков: мы движемся на пять в 𝑥-направлении, чтобы попасть из 𝐴 в 𝐵, и мы двигаемся на положительную тройку в 𝑦-направлении, поэтому наш вектор будет задан как пять [пять, три ]. Итак, есть три разных способа написать это путешествие от 𝐴 к 𝐵. Во всех случаях мы добавляем пять к 𝑥-координате, которая у нас была в точке 𝐴, чтобы получить координату, которую мы имели в точке 𝐵. И мы добавляем три к ac-координате, которая у нас была в 𝐴, чтобы получить 𝑦-координату, которая у нас есть в 𝐵. Так что перевод пять, три.

Итак, теперь давайте рассмотрим вектор в обратном направлении от 𝐵 к 𝐴. Как бы это выглядело? На этот раз мы делаем минус пять в 𝑥-направлении и минус три в 𝑦-направлении. Идем налево и вниз. Поэтому мы бы написали, что 𝐵𝐴 — это минус пять, минус три в любом из тех форматов, которые вы выберете. Теперь, поскольку каждый компонент нашего вектора 𝐵𝐴 является отрицательным значением компонента, который мы имели в соответствующем векторе 𝐴𝐵, мы можем сказать, что 𝐵𝐴 равно отрицательному 𝐴𝐵, или 𝐵𝐴 отрицательно 𝐴𝐵 в этом формате. Итак, мы видим отрицание вектора; мы проходим точно такое же расстояние, но женимся, мы делаем это в совершенно противоположном направлении.

И помните, у нас также была возможность обозначить наш вектор одной буквой. Таким образом, у нас мог бы быть жирный 𝑢, или подчеркнутый 𝑢, или жирный 𝑢 с маленькой стрелкой-гарпуном сверху. Таким образом, вместо того, чтобы использовать эту нотацию, мы могли бы использовать наши отдельные буквы. Все означает одно и то же, и все они, скорее всего, будут теми вещами, с которыми вы столкнетесь в вопросах, когда будете смотреть на векторы.

Теперь в этом примере перевод из 𝐶 в 𝐷 включает добавление шести к 𝑥-координате, но вычитание четырех из 𝑦-координаты, чтобы получить из 𝐶-координаты 𝑦-координаты 𝐷-координаты 𝑦. Итак, вот три разных обозначения: угловые скобки, векторы-столбцы и то, что выглядит как обозначение координат — шесть, минус четыре — и разные способы записи 𝐶𝐷 с разными стрелками или стрелками-гарпунами над ними. В качестве альтернативы мы могли бы пометить 𝐶𝐷 отдельной буквой либо полужирным 𝑣, либо подчеркнутым 𝑣, либо полужирным 𝑣 с гарпуном над ним. И мы могли бы заменить наши 𝐶𝐷 этими буквами. Так что жирный 𝑣 доступен во всех случаях. Иногда вы можете просто написать нежирный 𝑣 с подчеркиванием, а иногда вам нужен жирный 𝑣 с небольшим гарпуном поверх него.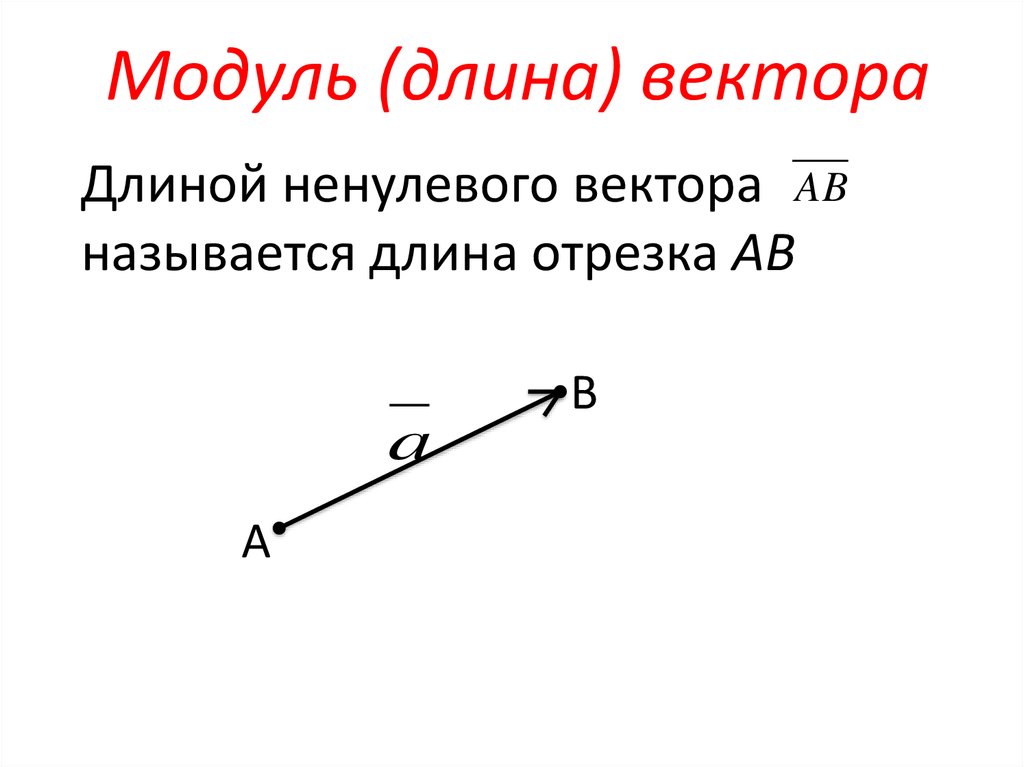

Итак, теперь мы можем представлять векторы различными способами. Давайте также подумаем о кратных векторах. Вектор 𝑤 представляет собой перемещение числа три, положительное число три, в направлении 𝑥 и отрицательное число два, в направлении 𝑦. Тогда два 𝑤 будут просто вдвое большим переводом в каждом направлении. Таким образом, вы можете представить это как две 𝑤, поставленные встык друг за другом. И все, что мы сделали, потому что у нас есть две 𝑤, мы удваиваем 𝑥-компоненту, мы удваиваем 𝑦-компоненты. Получается шесть, минус четыре в каждом из этих форматов. А три 𝑤 будут просто тремя копиями вектора, расположенными встык. Таким образом, мы получили бы девять минус шесть.

И снова, с отрицательным 𝑤, мы берем отрицательное значение каждого компонента. Итак, отрицательное число три равно отрицательному числу три, отрицательное значение числа два равно положительному числу два. Таким образом, в своем компонентном формате отрицательное 𝑤 равно отрицательному числу три, два.