Ноль факториал чему равен: 0! = 1? или почему факториал нуля равен единице / Хабр

Почему нулевой факториал равен единице?

Нулевой факториал — это математическое выражение для количества способов упорядочить набор данных без значений, равный единице.В общем, факториал числа является кратким способом записи выражения умножения, в котором число умножается на каждое число меньше его, но больше нуля. 4! Например, = 24 — это то же самое, что и запись 4 x 3 x 2 x 1 = 24, где каждый использует восклицательный знак справа от факторного числа (четыре), чтобы выразить то же уравнение.

Из этих примеров довольно ясно, как рассчитать факториал любого целого числа, большего или равного единице, но почему значение факториала равно нулю, несмотря на математическое правило, согласно которому все, умноженное на ноль, равно нулю?

Определение факториала утверждает, что 0! = 1. Это обычно смущает людей в первый раз, когда они видят это уравнение, но мы увидим в примерах ниже, почему это имеет смысл, если вы посмотрите на определение, перестановки и формулы для нулевого факториала.

Определение нулевого факториала

Первая причина того, почему нулевой факториал равен единице, заключается в том, что именно так оно и должно быть в определении, что является математически правильным, если не несколько неудовлетворительным объяснением. Тем не менее, следует помнить, что определение факториала — это произведение всех целых чисел, равных или меньших по значению на исходное число — другими словами, это факториал — это число возможных комбинаций с числами, меньшими или равными этому числу.,

Поскольку ноль не имеет меньших чисел, но все еще сам по себе является числом, существует еще одна возможная комбинация того, как этот набор данных может быть организован: он не может. Это по-прежнему считается одним из способов его организации, поэтому по определению нулевой факториал равен единице, равно как 1! равен единице, потому что существует только одно возможное расположение этого набора данных.

Для лучшего понимания того, как это имеет смысл математически, важно отметить, что факториалы, подобные этим, используются для определения возможных порядков информации в последовательности, также известной как перестановки, которые могут быть полезны для понимания того, что, хотя в пустой или нулевой набор, есть еще один способ, которым этот набор организован.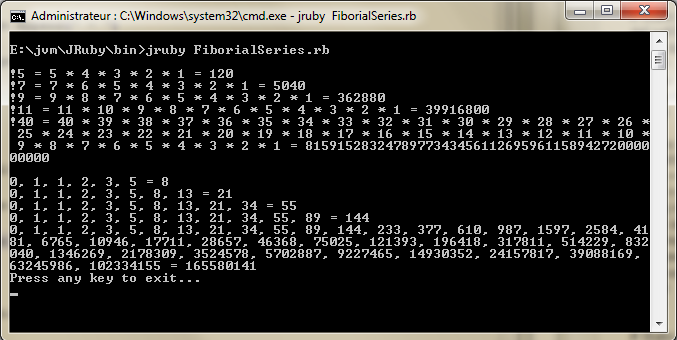

Перестановки и Факториалы

Перестановка — это особый, уникальный порядок элементов в наборе. Например, существует шесть перестановок множества {1, 2, 3}, которое содержит три элемента, поскольку мы можем записать эти элементы следующими шестью способами:

• 1, 2, 3
• 1, 3, 2
• 2, 3, 1
• 2, 1, 3
• 3, 2, 1
• 3, 1, 2

Мы также можем констатировать этот факт с помощью уравнения 3! = 6, который является факториальным представлением полного набора перестановок. Аналогичным образом, есть 4! = 24 перестановки набора из четырех элементов и 5! = 120 перестановок набора из пяти элементов. Таким образом, альтернативный способ думать о факториале состоит в том, чтобы N быть натуральным числом и сказать, что N ! число перестановок для набора с N элементы.

При таком подходе к факториалу давайте рассмотрим еще пару примеров. Набор из двух элементов имеет две перестановки: {a, b} можно расположить как a, b или как b, a. Это соответствует 2! = 2. Множество с одним элементом имеет одну перестановку, поскольку элемент 1 в наборе {1} можно упорядочить только одним способом.

Это подводит нас к нулю факториала. Множество с нулевыми элементами называется пустым множеством. Чтобы найти значение нулевого факториала, мы спрашиваем: «Сколько способов мы можем заказать набор без элементов?». Здесь нам нужно немного расширить мышление. Несмотря на то, что нет ничего, чтобы навести порядок, есть один способ сделать это. Таким образом, мы имеем это 0! = 1

Формулы и другие проверки

Еще одна причина для определения 0! = 1 имеет отношение к формулам, которые мы используем для перестановок и комбинаций. Это не объясняет, почему нулевой факториал равен единице, но показывает, почему установка 0! = 1 хорошая идея.

Комбинация — это группировка элементов набора без учета порядка. Например, рассмотрим набор {1, 2, 3}, в котором есть одна комбинация, состоящая из всех трех элементов. Независимо от того, в каком порядке мы расположим эти элементы, мы получим одну и ту же комбинацию.

Мы используем формулу для комбинаций, при этом комбинация из трех элементов берется по три одновременно, и мы видим, что 1 = С (3, 3) = 3! / (3! 0!) И если рассматривать 0! как неизвестное количество и решить алгебраически, мы видим, что 3! 0! = 3! и так 0! = 1

Есть и другие причины, почему определение 0! = 1 правильно, но причины, приведенные выше, являются наиболее простыми. Общая идея в математике заключается в том, что когда создаются новые идеи и определения, они остаются совместимыми с другой математикой, и это именно то, что мы видим в определении нулевого факториала, равного единице.

Сколько нулей в конце факториала 100?

Факториал одной сотни записывается как 100! Это произведение всех натуральных чисел до ста включительно. Иногда запись факториала имеет такой вид:

100 х 99 х 98 х 97 х … х 4 х 3 х 2 х 1

Для ответа на вопрос задачи вам не обязательно находить результат умножения. От вас ждут, чтобы вы лишь определили число нулей в конце произведения, не зная, каким именно оно будет. Для решения этой задачи потребуется сформулировать несколько правил. Одно из них вы уже знаете. Взгляните на следующее выражение.

387 000 х 12 900 = 5 027 131 727

Вам не кажется, что здесь есть что-то забавное? Ведь при перемножении двух круглых чисел, то есть тех, которые оканчиваются на нули, невозможно получить некруглое число. Это нарушило бы закон сохранения конечных нулей (закон, который я только что вывел, но, тем не менее, он является верным). Произведение всегда унаследует нулевые окончания своих составляющих. Вот несколько верных примеров этого:

10 х 10 = 100
7 х 20 = 140
30 х 400 = 12 000

Из сомножителей факториала 100 десять заканчиваются на ноль: 10, 20, 30, 40, 50, 60, 70, 80, 90 и 100 (заканчивается на два 0). Это дает уже как минимум одиннадцать конечных нулей, которые 100! обязательно унаследует.
Предупреждение: следование только этому правилу иногда побуждает некоторых кандидатов в своем ответе заявить, что в конце факториала 100 стоят одиннадцать нулей. Такой ответ является неверным. Иногда можно умножить два числа, не заканчивающихся на ноль, и получить произведение, имеющее в конце один или несколько нулей. Вот несколько примеров этого рода:

2 х 5 = 10
5 х 8 = 40
6 х 15 = 90
8 х 125 = 1000

Все, кроме последней пары, входят в сотню составляющих факториала 100. Поэтому ваша работа не закончилась. Теперь мы подходим к закону «сосисок и булочек». Представьте себе ситуацию, когда на пикник одни люди приносят сосиски (в упаковках по десять штук), другие — булочки (упакованные по восемь штук), а некоторые — и то, и другое. Есть единственный способ, позволяющий определить, сколько хотдогов из этих продуктов можно приготовить. Сосчитайте сосиски, сосчитайте булочки и выберите меньшее число из двух.

Тот же самый закон следует использовать и отвечая на наш вопрос. Для этого надо заменить «сосиски» и «булочки» на «сомножители на 2» и «сомножители на 5».

В каждом из приведенных выше уравнений число, которое делится на 2, умножается на число, которое делится на 5. Сомножители на 2 и на 5 при их перемножении «совместно» дают идеальную десятку, что добавляет еще один ноль к общему произведению. Посмотрите на последний пример, где в конце, можно сказать, из воздуха возникает три нуля.

8 х 125 = (2 х 2 х 2) х (5 х 5 х 5)
= (2 х 5) х (2 х 5) х (2 х 5)
= 10 х 10 х 10
= 1000

Поэтому надо составить пары из двоек и пятерок. Возьмем, к примеру, число, равное 692 978 456 718 000 000.

Оно оканчивается на шесть нулей. Это означает, что его можно записать следующим образом:

692 978 456 718 х 10 х 10 х 10 х 10 х 10 х 10,

или так:

692 978 456 718 х (2 х 5) х (2 х 5) х (2 х 5) х (2 х 5) х (2 х 5) х (2 х 5).

Первая часть, 692 978 456 718, не делится на 10. В ином случае она бы оканчивалась на ноль, и можно было бы эту часть уменьшить еще в 10 раз. К тому же здесь есть шесть сомножителей, равных 10 (или 2 х 5), что соответствует шести нулям в конце числа 692 978 456 718 000 000. Ну как, убедительно?

Это дает нам надежную систему для определения количества нулей в конце любого большого числа. Выделите сомножители 2 и 5. Составьте из них пары и перемножьте их: (2 х 5) х (2 х 5) х (2 х 5) х … Число пар из двоек и пятерок равно количеству нулей в конце. Закройте глаза на все, что осталось слева.

В целом слева у вас останется двойка или пятерка, для которых не нашлось пары. Обычно это двойки. Более того, когда вы имеете дело с факториалом, это всегда двойки. (В факториалах имеется больше четных множителей, чем множителей, которые делятся на 5.) Поэтому узким местом является число пятерок. Из этого следует, что вопрос можно сформулировать по-другому: сколько раз 100! можно разделить без остатка на 5?

Эту арифметическую операцию можно легко проделать даже в голове. В диапазоне от 1 до 100 есть 20 чисел, которые делятся на пятерку: 5, 10, 15, …, 95, 100. Обратите внимание, что 25 дает 2 множителя, равные 5 (25 = 5 х 5), и к тому же в этой группе есть еще три числа, в состав которых входит 25: 50, 75 и 100. В совокупности это добавляет еще четыре пятерки, а всего их 24. 24 множителя на пять дают 24 пары с равным числом двоек, в результате чего получается 24 множителя на 10 (оставляя слева еще множество двоек, для которых не оказалось пары). Таким образом, в конце 100! будет 24 нуля.

Если вам любопытно узнать точный ответ, то значение факториала 100 равно:

93 326 215 443 944 152 681 699 238 856 266 700 490 715 968 264 381 621 468 592 963 895 217 599 993 229 915 608 941 463 976 156 518 286 253 697 920 827 223 758 251 185 210 916 864 000 000 000 000 000 000 000 000.

Разбор по книге «Действительно ли Вы достаточно умны, чтобы работать в Google?»

Почему нулевой фактор равен единице?

Автор Тимохин Александр На чтение 4 мин. Просмотров 349 Опубликовано 03.10.2021

Нулевой факториал — это математическое выражение для количества способов упорядочить набор данных без значений в нем, равный единице. В общем, факториал числа — это сокращенный способ записать выражение умножения, в котором число умножается на каждое число, меньшее его, но большее нуля. 4! = 24, например, то же самое, что и запись 4 x 3 x 2 x 1 = 24, но для выражения того же уравнения справа от факториала (четыре) используется восклицательный знак.

Из этих примеров довольно ясно, как вычислить факториал любого целого числа, большего или равного единице, но почему значение факториала равно нулю, несмотря на математическое правило, что все умножается нулем равно нулю?

Определение факториала утверждает, что 0! = 1. Это обычно сбивает людей с толку в первый раз, когда они видят это уравнение, но мы увидим в приведенных ниже примерах, почему это имеет смысл, когда вы посмотрите на определение, перестановки и формулы для нулевого факториала.

Содержание

1. Определение нулевого факториала
2. Перестановки и факториалы
3. Формулы и другие проверки

Определение нулевого факториала

Первая причина, по которой нулевой факториал равен единице, заключается в том, что это то, что по определению должно быть, что является математически правильным объяснением (хотя и несколько неудовлетворительным). Тем не менее, нужно помнить, что определение факториала — это произведение всех целых чисел, равных или меньших по значению исходному числу, другими словами, факториал — это количество возможных комбинаций с числами, меньшими или равными этому числу.

Поскольку ноль не имеет меньших чисел, но все же сам по себе является числом, существует только одна возможная комбинация того, как этот набор данных может быть организован : оно не может. Это по-прежнему считается способом упорядочения, поэтому по определению нулевой факториал равен единице, как и 1! равно единице, потому что существует только одно возможное расположение этого набора данных.

Для лучшего понимания того, как это имеет математический смысл, важно отметить что факториалы, подобные этим, используются для определения возможных порядков информации в последовательности, также известных как перестановки, которые могут быть полезны для понимания того, что даже если в пустом или нулевом наборе нет значений, все же существует один способ упорядочения набора .

Перестановки и факториалы

Перестановка — это особый уникальный порядок элементов в наборе. Например, существует шесть перестановок набора {1, 2, 3}, который содержит три элемента, поскольку мы можем записать эти элементы следующими шестью способами:

• 1, 2, 3
• 1, 3, 2
• 2, 3, 1
• 2, 1, 3
• 3, 2, 1
• 3, 1, 2

Мы также можем констатировать этот факт с помощью уравнения 3! = 6, что является факториальным представлением полного набора перестановок. Аналогично есть 4! = 24 перестановки набора из четырех элементов и 5! = 120 перестановок набора из пяти элементов. Таким образом, альтернативный способ подумать о факториале — позволить

n быть натуральным числом и сказать, что n ! — это количество перестановок для набора с n элементами.

Рассматривая факториал таким образом, давайте посмотрим еще пара примеров. Набор из двух элементов имеет две перестановки: {a, b} могут быть расположены как a, b или как b, a. Это соответствует 2! = 2. Набор с одним элементом имеет единственную перестановку, так как элемент 1 в наборе {1} может быть упорядочен только одним способом.

Это приводит нас к нулевому факториалу. Набор с нулевыми элементами называется пустым набором. Чтобы найти значение нулевого факториала, мы спрашиваем: «Сколько способов мы можем упорядочить набор без элементов?» Здесь нам нужно немного расширить наше мышление. Несмотря на то, что навести порядок нечего, есть один способ сделать это. Таким образом, мы имеем 0! = 1.

Формулы и другие проверки

Еще одна причина для определения 0! = 1 имеет отношение к формулам, которые мы используем для перестановок и комбинаций. Это не объясняет, почему нулевой факториал равен единице, но показывает, почему установка 0! = 1 — хорошая идея.

Комбинация — это группировка элементов набора без учета порядка. Например, рассмотрим набор {1, 2, 3}, в котором есть одна комбинация, состоящая из всех трех элементов. Независимо от того, как мы расположим эти элементы, мы получим одну и ту же комбинацию.

Мы используем формулу для комбинаций с комбинацией из трех элементов, взятых по три за один раз и увидим, что 1 = C (3, 3) = 3!/(3! 0!), и если мы обработаем 0! как неизвестную величину и решаем алгебраически, мы видим, что 3! 0! = 3! и так 0! = 1.

Есть и другие причины, по которым определение 0! = 1 правильно, но причины, указанные выше, наиболее очевидны. Общая идея математики состоит в том, что при построении новых идей и определений они остаются согласованными с другой математикой, и это именно то, что мы видим в определении нулевого факториала, равного единице.

Факториал | это… Что такое Факториал?

Факториа́л числа n (лат. factorialis — действующий, производящий умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно:

Например:

По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.

Последовательность факториалов неотрицательных целых чисел начинается так:

1, 1, 2, 6, 24, 120, 720, 5040, 40 320, 362 880, 3 628 800, 39 916 800, 479 001 600, 6 227 020 800, 87 178 291 200, 1 307 674 368 000, 20 922 789 888 000, 355 687 428 096 000, 6 402 373 705 728 000, 121 645 100 408 832 000, 2 432 902 008 176 640 000, … (последовательность A000142 в OEIS)

Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.

Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция ).

Содержание 1 Свойства 1.1 Рекуррентная формула 1.2 Комбинаторная интерпретация 1.3 Связь с гамма-функцией 1.4 Формула Стирлинга 1.5 Разложение на простые числа 1. 6 Другие свойства 2 Обобщения 2.1 Двойной факториал 2.2 Кратный факториал 2.3 Убывающий факториал 2.4 Возрастающий факториал 2.5 Праймориал или примориал 2.6 Суперфакториалы 2.7 Субфакториал 3 Ссылки 4 См. также 5 Примечания

Свойства

Рекуррентная формула

Комбинаторная интерпретация

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, т. к. пустое множество упорядочено единственным способом.

Связь с гамма-функцией

Амплитуда и фаза факториала комплексного аргумента.

Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.

Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при

Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.

Более непосредственным обобщением факториала на множество вещественных (и комплексных) чисел является пи-функция, определяемая как

Поскольку то пи-функция натурального числа совпадает с его факториалом: Как факториал, пи-функция удовлетворяет рекурсивному соотношению

Формула Стирлинга

Основная статья: Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).

Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:

При этом можно утверждать, что

Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Так, с помощью формулы Стирлинга легко подсчитать, что

• 100! ≈ 9,33×10¹⁵⁷;
• 1000! ≈ 4,02×10²⁵⁶⁷;
• 10 000! ≈ 2,85×10^35 659.

Разложение на простые числа

Каждое простое число p входит в разложение n! на простые множители в степени

Таким образом,

где произведение берётся по всем простым числам. Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n.

Другие свойства

• Для натурального числа n

Обобщения

Двойной факториал

Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,

По определению полагают 0!! = 1.

Последовательность значений n!! начинается так:

1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, … (последовательность A006882 в OEIS).

Кратный факториал

m-Кратный факториал числа n обозначается и определяется следующим образом:

Пусть число n представимо в виде где Тогда^[1]

Двойной факториал является частным случаем m-кратного факториала для m = 2.

Кратный факториал связан с гамма-функцией следующим соотношением^[2]:

Убывающий факториал

Убывающим факториалом (или неполным факториалом) называется выражение

Убывающий факториал даёт число размещений из n по k.

Возрастающий факториал

Возрастающим факториалом называется выражение

Праймориал или примориал

Праймориал или примориал (англ. primorial) числа n обозначается n# и определяется как произведение всех простых чисел, не превышающих n. Например,

11# = 12# = 2 · 3 · 5 · 7 · 11 = 2310.

Последовательность праймориалов (включая ) начинается так:

1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 410, 32 589 158 477 190 044 730, 1 922 760 350 154 212 639 070, … (последовательность A002110 в OEIS).

Суперфакториалы

Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырёх равен

(поскольку устоявшегося обозначения нет, используется функциональное).

В общем

Последовательность суперфакториалов чисел n⩾0 начинается так:

1, 1, 2, 12, 288, 34 560, 24 883 200, … (последовательность A000178 в OEIS).

Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Superduperfactorial), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел n⩾0 начинается так:

1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 125 411 328 000, 5 056 584 744 960 000, 1 834 933 472 251 084 800 000, 6 658 606 584 104 736 522 240 000 000, 265 790 267 296 391 946 810 949 632 000 000 000, 127 313 963 299 399 416 749 559 771 247 411 200 000 000 000 … (последовательность A055462 в OEIS)

Продолжая рекуррентно, можно определить факториал кратного уровня, или m-уровневый факториал числа n, как произведение первых n (m−1)-уровневых факториалов, то есть

где для и

Субфакториал

Основная статья: Субфакториал

Субфакториал !n определяется как количество беспорядков порядка n, то есть перестановок n-элементного множества без неподвижных точек.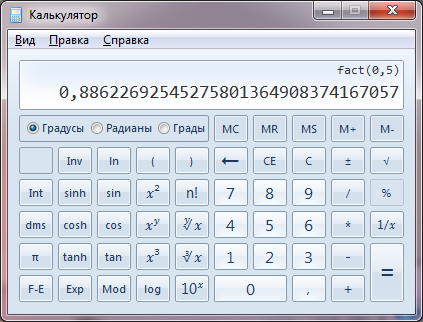

Ссылки

• Онлайн Калькулятор Факториалов

См. также

• Факторион

Примечания

1. ↑ «Энциклопедия для детей» Аванта+. Математика.
2. ↑ wolframalpha.com.

Вычисление факториала числа онлайн | BBF.RU

Факториал натурального числа n — это произведение последовательных натуральных чисел от 1 до n. Факториалы естественным образом возникают во многих областях математики, а «родиной» факториала считается комбинаторика.

Основная информация

Сначала заметим, что математически факториал записывается при помощи восклицательного знака. Такая запись выглядит как n!, а читается как эн-факториал. Математический смысл факториала состоит в произведении последовательных натуральных чисел от 1 до n:

n! = 1 × 2 × 3 … (n − 2) × (n − 1) × n,

где n — заданное количество натуральных чисел.

Первые значения n! выглядят так:

• 1! = 1
• 2! = 2
• 3! = 6
• 4! = 24
• 5! = 120

Факториал очень быстро растущая функция, если 5! эквивалентно 120, то 15! составляет уже 1 307 674 368 000, а 50! имеет в своем составе 64 нуля. Факториал возник в комбинаторике при расчете количества перестановок множества из n-ного количества элементов. К примеру, для трехэлементного множества Z = {A, B, C} существует 3! = 6 вариантов перестановок:

• ABC;
• ACB;
• BAC;
• BCA;
• CAB;
• CBA.

Теоретико-множественное обоснование смысла факториала позволило доказать парадоксальное на первый взгляд утверждение, что 0! = 1. Ноль-факториал, по сути, представляет собой 0 × 1, а каждый пятиклассник знает, что при умножении на ноль в результате также будет ноль. Пустое же множество, не содержащее элементов, может быть упорядоченно одним единственным способом, поэтому факториал нуля равен единице. В целом факториал находит широкое применение в теории чисел, теории вероятностей, функциональном анализе, комбинаторике, а также при разложении функций в ряд Тейлора.

Вычисление n!

Вычисление факториала для натуральных чисел меньше 10 не представляет особой сложности, однако молниеносный рост функции делает крайне затруднительным вычисление факториалов по мере роста чисел. В компьютерных вычислениях основной сложностью становится отображение и хранение результата расчета функции n!. Прямое умножение натуральных чисел для вычисления факториала для n > 20 не используется.

Формула Стирлинга

Формула Стирлинга позволяет вычислить приблизительное значение факториала любого числа n, оперируя при этом только числом n и постоянными коэффициентами. Данная формула позволяет избежать огромных промежуточных вычислений. Для точного вычисления значения формула Стирлинга содержит 7 слагаемых, однако в большинстве случаев эти слагаемые опускаются, а факториал рассчитывается приближенно:

n! ≈ sqrt(2pi × n ) × (n/e)ⁿ,

где e — экспонента.

Наш калькулятор рассчитывает факториал именно по формуле Стирлинга, поэтому для небольших чисел значение факториала будет выглядеть необычно. Например, 2! ≈ 1,919, а 3! ≈ 5,836. Не пугайтесь такого представления результата, просто округлите число до ближайшего целого в большую сторону и вы получите правильный ответ. Для больших чисел результат будет представлен в виде мантиссы и порядка. Например, 100! ≈ 9,325e+157. Это означает, что 100! ≈ 9,325 × 10¹⁵⁷.

Другие виды факториалов

Помимо стандартного n! для ряда натуральных чисел существуют также экзотические виды факториала, которые рассчитываются для четных/нечетных или простых чисел. Последний называется праймориал и рассчитывается для последовательности простых чисел меньших или равных заданному. К примеру, праймориал первых 7 простых чисел представляет собой:

p7 = 2 × 3 × 5 × 7 × 11 × 13 × 17 = 510 510

Кроме того, существует суперфакториал, который представляет собой произведение первых n факториалов. Например, суперфакториал 5 равен:

sf(5) = 1! × 2! × 3! × 4! × 5! = 1 × 2 × 6 × 24 × 120 = 34 560

Очевидно, что последовательность суперфакториалов является самой быстрорастущей.

Наша программа использует формулу Стирлинга для вычисления сколь угодно больших факториалов. Для небольших чисел не забывайте округлять результат до целого в большую сторону, так как факториал — это всегда целое число.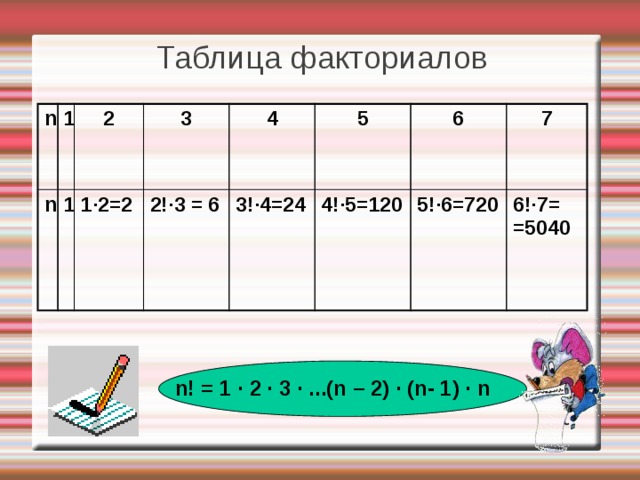

Рассмотрим пример из комбинаторики

Лотерея

Всем известны различные лотереи, где игрокам требуется угадать комбинацию 6 чисел из 52 возможных. Правила могут отличаться, иногда требуется угадать 5 чисел из 60 или 6 из 90. Пусть вы купили билет классической лотереи «Спортлото» и для выигрыша вам требуется угадать комбинацию 6 чисел из 49 возможных. Какова вероятность выиграть главный приз? К нам на помощь приходит комбинаторика и факториалы. Общее количество возможных комбинаций для данного примера рассчитывается по формуле:

Общее количество 6 из 49 = 49! / (6! × 43!)

Воспользуемся калькулятором и по отдельности вычислим значения факториалов:

Общее количество 6 из 49 = 6,072e+62 / 720 × 6,030e+52 = 13 985 627.

Это означает, существует приблизительно 14 миллионов шестиэлементных комбинаций, образованных из 49 чисел. Следовательно, вероятность выигрыша в «Спортлото» составляет 1 к 14 миллионам.

Заключение

Факториалы естественным образом возникают в комбинаторике, теории чисел и теории вероятностей. Используйте нашу программу для подсчета приблизительных значений факториалов сколько угодно больших чисел.

Факториал Суперфакториалы гиперфакториал примориал Дискретная математика. Теория…

Привет, сегодня поговорим про факториал, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое факториал, суперфакториал, гиперфакториал, примориал , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

факториал числа n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральныхчисел от 1 до n включительно:

Например:

.

По договоренности: . Также это равенство выполняется естественным образом:

Факториал определен только для целых неотрицательных чисел.

Последовательность факториалов неотрицательных целых чисел начинается так:

Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.

Факториал является чрезвычайно быстро растущей функцией. Он растет быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция ).

В математике существует около десятка различных факториалов, рассмотрим их

1. Факториал

пример 5! = 1*2*3*4*5

Возникает естественным образом в комбинаторике — науке, в которой изучаются задачи, связанные с выбором и расположением различных элементов чаще всего конечных множеств.

2. Двойной факториал

пример 7!! = 7*5*3*1

общий случай n!!= если n четное , то = n(n-2) * … * 4 * 2 или

если n — не четное , то = n(n-2) * … * 3 * 1

Этот факториал имеет просто громадное количество приложений в комбинаторике и достоин отдельного материала.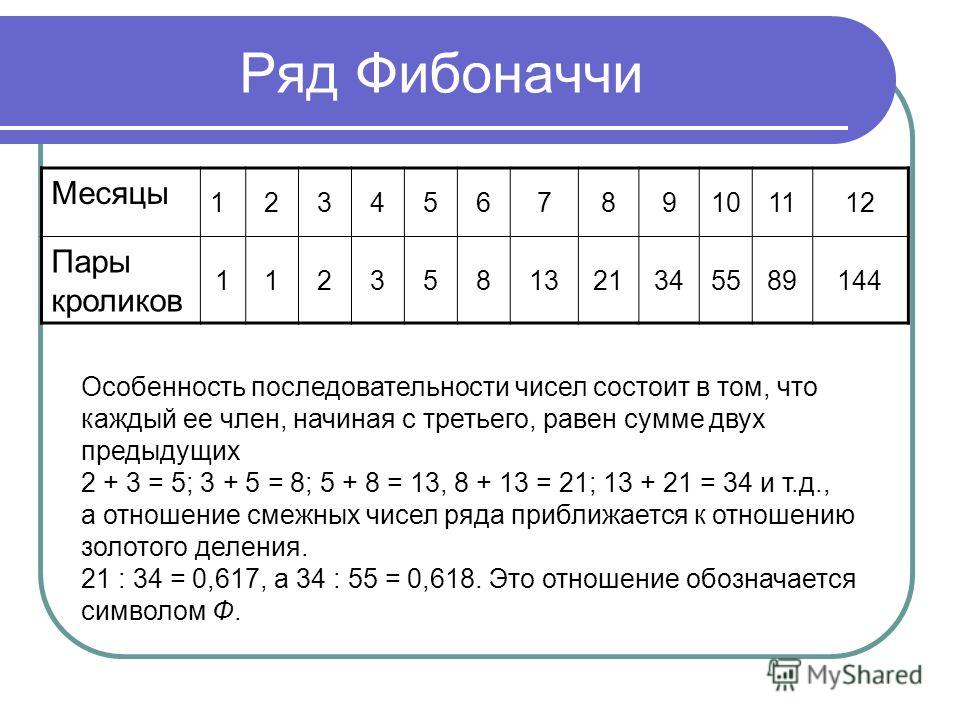 Впервые он использовался при выводе замечательного произведения Уоллиса, связывающего натуральные числа и число π:

3. Субфакториал

Этот представитель семейства в отличие от обычного факториала, который определяет количество перестановок, определяет количество беспорядков.

4. Праймориал

Определяется как произведение простых чисел, меньших или равных данному.

5. суперфакториал Слоуна

Название дано создателем уникальной в своем роде Онлайн Энциклопедии Целочисленных Последовательностей (OEIS). Определяется как произведение факториалов чисел, меньших или равных заданному.

6. Суперфакториал Пиковера

Запись показателя степени слева сверху от числа определяет особенную математическую операцию — тетрацию

удивительно быстрорастущая функция. Для числа 3 — это уже вот такая невообразимая башня:

Степени «схлопываются» справа-налево

7.

Экспоненциальный факториал

По сравнению с предыдущим представителем растет «медленно» . Об этом говорит сайт https://intellect.icu . Например, для выражения выше — это 262144. Конечно, для числа 6 в результате уже нулей.

8. гиперфакториал

Растет еще медленнее, чем предшествующие два. Только лишь на 14 шаге число нулей приближается к гуголу.

9. Фиббоначиал

Равняется произведению первых n чисел Фибоначчи.

10. Другие факториалы

Кроме вышеописанных существуют еще возрастающие и убывающие факториалы, но они являются частным случаем факториала обычного.

А также факториал дробного числа.

Факториал дробного числа — факториал вычисляемый от аргумента —

Вычисляется по формуле:

где [x] — целая часть чиcла x, {x} — дробная часть числа x.

Например, для x=11,2 будем иметь log(11,2!) = log(11!) + 0,2*log(12)

Вычисляемое таким способом значение факториала дробного числа является приближенным. Для точных расчетов необходимо использовать гамма-функцию.

Факториалы нецелых (дробных) чисел появляются при статистическом описании нейросетевых преобразователей биометрия/код ключа доступа биномиальным законом распределения зависмимых биометрических данных.

История факториала

Факториалы использовались для подсчета перестановок, по крайней мере, еще в 12 веке индийскими учеными. В 1677 году Фабиан Стедман описал факториалы применительно к смене звонков (сигналов вызова) , музыкальному искусству, включающему звон многих настроенных колоколов. После описания рекурсивного подхода Стедман дает утверждение факториала (используя язык оригинала):

Теперь природа этих методов такова, что изменения на одном числе охватывают [включают] изменения на всех меньших числах … настолько, что полный Пил(звон) изменений на одном числе, по-видимому, формируется путем объединения завершенных Пилсов(серии звонков) на всех меньшие числа в одно целое тело.

Обозначения п ! был введен французским математиком Кристианом Крампом в 1808 году.

Свойства факториала

Рекуррентная формула

Комбинаторная интерпретация

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, так как пустое множество упорядочено единственным способом.

Связь с гамма-функцией

Амплитуда и фаза факториала комплексного аргумента.

Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.

Путем аналитического продолжения ее также расширяют и на всю комплексную плоскость, исключаяособые точки при .

Пи-функция, определенная для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.

Более непосредственным обобщением факториала на множество вещественных (и комплексных) чисел является пи-функция, определяемая как

.

Поскольку то пи-функция натурального числа совпадает с его факториалом: Как факториал, пи-функция удовлетворяет рекурсивному соотношению

Формула Стирлинга

Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

см. O-большое .

Во многих случаях для приближенного значения факториала достаточно рассматривать только главный член формулы Стирлинга:

При этом можно утверждать, что

Формула Стирлинга позволяет получить приближенные значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Так, с помощью формулы Стирлинга легко подсчитать, что

​

Разложение на простые числа

Каждое простое число p входит в разложение n! на простые множители в степени

Таким образом,

где произведение берется по всем простым числам.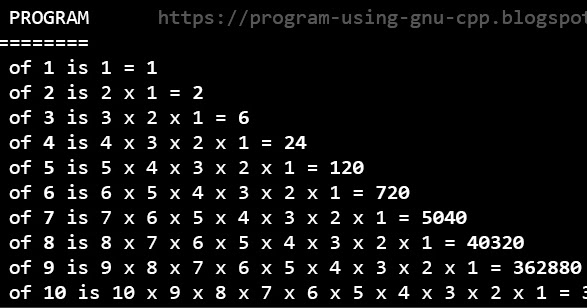 Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n.

Связь с производной от степенной функции

Для целого неотрицательного числа n:

Например:

Другие свойства

• Для натурального числа n:

Обобщения

Двойной факториал

Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же четность, что и n.

• Для четного n:

• Для нечетного n:

Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.

• Для четного n:

• Для нечетного n:

Выведение формул

Осуществив замену для четного n и для нечетного n соответственно, где — целое неотрицательное число, получим:

• для четного числа:

• для нечетного числа:

По договоренности: . Также это равенство выполняется естественным образом:

Двойной факториал, также как и обычный факториал, определен только для целых неотрицательных чисел.

Последовательность значений n!! начинается так:

1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, … .

Кратный факториал

m-кратный факториал числа n обозначается и определяется следующим образом. Пусть число n представимо в виде где Тогда

Обычный и двойной факториалы являются частными случаями m-кратного факториала для m = 1 и m = 2 соответственно.

Кратный факториал связан с гамма-функцией следующим соотношением :

Неполный факториал

Убывающий факториал

Убывающим факториалом называется выражение

.

Например:

n = 7; k = 4,

(n − k) + 1 = 4,

3k = 7 • 6 • 5 • 4 = 840.

Убывающий факториал дает число размещений из n по k.

Возрастающий факториал

Возрастающим факториалом называется выражение

Праймориал или примориал

Сюда перенаправляется запрос «Праймориал». На эту тему нужна отдельная статья.

Праймориал или примориал (англ. primorial) числа n обозначается pn# и определяется как произведение n первых простых чисел. Например,

.

Иногда праймориалом называют число , определяемое как произведение всех простых чисел, не превышающих заданное n.

Последовательность праймориалов (включая ) начинается так:

1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 410, 32 589 158 477 190 044 730, 1 922 760 350 154 212 639 070, … .

Суперфакториалы

Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырех равен

(поскольку устоявшегося обозначения нет, используется функциональное).

В общем

Последовательность суперфакториалов чисел начинается так: 1, 1, 2, 12, 288, 34 560, 24 883 200, … .

Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Superduperfactorial), которые являются произведением первых nсуперфакториалов. Последовательность гиперфакториалов чисел начинается так:

1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 745 453 331 864 786 829 312 000 000, 3 769 447 945 987 085 350 501 386 572 267 520 000 000 000, 6 916 686 207 999 802 072 984 424 331 678 589 933 649 915 805 696 000 000 000 000 000 … .

Продолжая рекуррентно, можно определить факториал кратного уровня, или m-уровневый факториал числа n, как произведение первых n (m−1)-уровневых факториалов, то есть

где для и

Субфакториал

Субфакториал !n определяется как количество беспорядков порядка n, то есть перестановок n-элементного множества без неподвижных точек.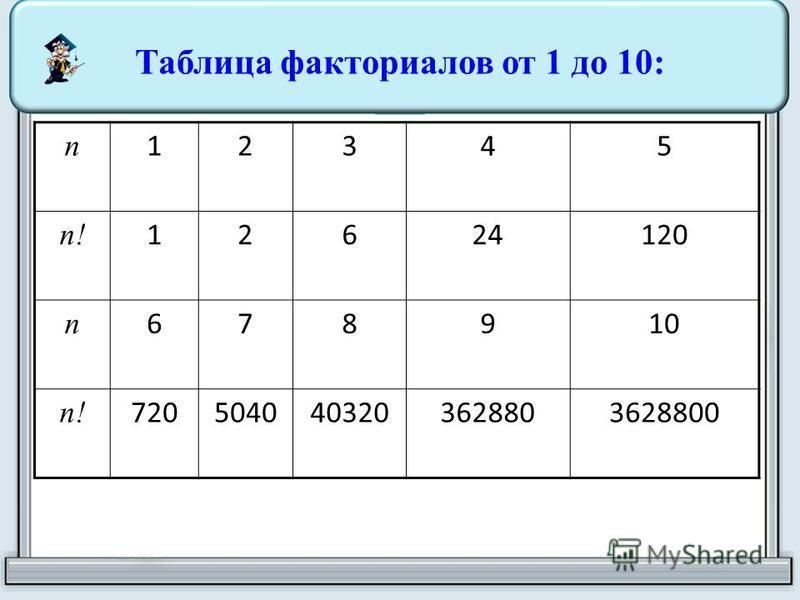

Субфакториал числа n (обозначение: !n) определяется как количество беспорядков порядка n, то есть перестановок порядка n без неподвижных точек. Название субфакториал происходит из аналогии с факториалом, определяющим общее количество перестановок.

В частности, !n есть число способов положить n писем в n конвертов (по одному в каждый), чтобы ни одно не попало в соответствующий конверт (так называемая Задача о письмах).

«Примеры реализации функции факториал»

• Факторион — натуральное число, которое равно сумме факториалов своих цифр.

Список факторионов

Примечания

1. ↑ последовательность A000142 в OEIS
2. ↑ Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS(знаменатели)
3. ↑ последовательность A006882 в OEIS
4. ↑ «Энциклопедия для детей» Аванта+. Математика.
5. ↑ последовательность A002110 в OEIS
6. ↑ последовательность A000178 в OEIS
7. ↑ последовательность A055462 в OEIS

Напиши свое отношение про факториал. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое факториал, суперфакториал, гиперфакториал, примориал и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.

Определение нулевого факториала

Вещи определяются такими, какие они есть, по уважительным причинам. Сейчас это кажется совершенно очевидным, но когда я узнал об этом на первом курсе колледжа, это открыло мне глаза. Наш профессор Майк Старберд попросил нас вернуться домой и подумать о том, как определить сходимость ряда. Не то, как определяется , а то, как следует определять . Мы должны были не искать определение, а думать о том, каким оно должно быть. На следующий день мы предложили свои определения. В хорошей сократовской манере Starbird показала нам недостатки каждого из них и привела нас к стандартному определению.

Это упражнение дало мне уверенность в том, что математические определения были созданы простыми смертными, такими как я. Это также положило начало моей привычке внимательно изучать определения, чтобы понять, чем они мотивированы.

Часто возникает вопрос, почему нулевой факториал равен 1. Педантичный ответ: «Потому что так определено». Сам по себе этот ответ не очень полезен, но он приводит к более тонкому вопросу: почему 0! определяется как 1?

Ответ на пересмотренный вопрос заключается в том, что многие формулы упрощаются, если мы определяем 0! быть 1. Если бы мы определили 0! чтобы быть равным 0, например, бесчисленные формулы должны были бы добавлять дисквалификаторы, такие как «кроме случаев, когда n равно нулю».

Например, биномиальные коэффициенты определяются как

C ( n , k ) = n ! / k !( n – k )!.

Биномиальный коэффициент C ( n , k ) говорит нам, сколькими способами можно взять набор из n предметов и выбрать k из них. Например, число способов сдачи пяти карт из колоды 52 равно 9.0013 С (52, 5) = 52! / 5! 47! = 2 598 960.

Сколькими способами можно раздать руку из 52 карт из колоды из 52 карт? Очевидно одно: колода — это рука. Но наша формула говорит, что ответ

C (52, 52) = 52! / 52! 0!,

и формула верна только если 0! = 1. Если 0! были определены как что-то еще, мы должны были бы сказать: «Количество способов раздать руку из k карт из колоды из n карт равно C ( n , k ), , кроме , когда k = 0 или k = n , и в этом случае ответ равен 1». (Подробности см. в [1] ниже.)

Приведенный выше пример, конечно, не единственный, где удобно определить 0! быть 1. Бесчисленные теоремы было бы более неудобно формулировать, если бы 0! определялись как-то иначе.

Иногда люди обращаются к гамма-функции для обоснования того, что 0! должно быть определено равным 1. Гамма-функция расширяет факториал до действительных чисел, а значение гамма-функции связано с 0! равно 1. (Подробно, п ! = Γ( n +1) для положительных целых чисел n и Γ(1) = 1.) Это обнадеживает, но поднимает другой вопрос: почему гамма-функция должна быть авторитетной?

Действительно, существует множество способов расширения факториала до нецелочисленных значений, и исторически было предложено множество способов . Однако гамма-функция победила, а ее конкуренты канули в лету. Так почему же оно победило? По аналогии с приведенным выше обсуждением мы могли бы сказать, что гамма-функция победила, потому что просто с этим определением работает больше формул, чем с другими. То есть можно очень часто заменить п ! с Γ( n + 1) в формуле, истинной для положительных целых значений n , и получить новую формулу, действительную для действительных или даже комплексных значений n .

Есть еще одна причина, по которой победила гамма, и это теорема Бора–Моллерупа. В нем говорится, что если вы ищете функцию f ( x ), определенную для x > 0, которая удовлетворяет f (1) = 1 и f ( x +1) = x f ( x ), то гамма-функция является единственным логарифмически выпуклым решением. Почему мы должны искать логарифмически выпуклые функции? Поскольку факториал логарифмически выпукл, это естественное свойство, требуемое от его расширения.

Обновление : Иногда я слышу, как кто-то говорит, что гамма-функция (со сдвигом ее аргумента на 1) является единственной аналитической функцией, которая расширяет факториал до комплексной плоскости, но это не так. Например, если вы добавите sin(πx) к гамма-функции, вы получите еще одну аналитическую функцию, которая принимает те же значения, что и гамма, для положительных целых аргументов.

• Почему пустые продукты 1?
• Почему натуральные логарифмы натуральные?
• Еще одна причина, по которой натуральные логарифмы являются натуральными

* * *

[1] Теоремы о биномиальных коэффициентах должны накладывать некоторые ограничения на аргументы. Полную информацию см. в этих примечаниях. Но в случае раздачи карт единственными необходимыми ограничениями являются естественных : мы предполагаем, что количество карт в колоде и количество, которое мы хотим получить в руке, являются неотрицательными целыми числами, и что мы не пытаемся возьмите больше карт для руки, чем есть в колоде. Определение 0! поскольку 1 избавляет нас от необходимости делать любые неестественные уточнения типа «если только вы не раздаете всю колоду».

Факториал нуля: почему он равен единице?

Поделиться на

Хотите «обмануть» в исчислении? Ознакомьтесь с нашим справочником «Практическое исчисление с мошенничеством» , в котором вы найдете сотни простых ответов в удобной электронной книге.

Функция факториала >

Если вам интересно, почему нулевой факториал равен 1, вы не одиноки. Это одна из величайших головоломок математики, которая кажется совершенно неинтуитивной. Есть несколько разных способов показать, что 0! = 1 должно быть верно:

1. С определением,
2. С формулой комбинаций (из статистики),
3. С ограничениями (исчисление).

причина почему 0! = 1 равно , потому что так определено.

«…ноль факториал равен 1, 0! = 1 [и] 1! = 1. Однако нельзя аналогичным образом заключить, что 0 = 1, потому что один результат получен соглашением , а другой результат является математическим фактом . Как и во всех соглашениях, при арифметических операциях с нулями необходимо соблюдать определенные протоколы и правила.0004 » [1]

Если у вас возникли проблемы с обдумыванием этого утверждения, вы не одиноки. На протяжении тысячелетий математики спорили о том, существует ли вообще нуль (даже без факториала )! [2] В римской системе счисления не было нулей, и только после введения десятичной системы в 13 веке «ноль» действительно стал вещью. Тем не менее, работа с «0» приводит к множеству проблем, включая неинтуитивную идею о том, что 0! = 1,

Примечание : Вы можете прочитать «Что такое факториал?» первый.

Мы хотим показать, что есть только один способ выбора нулевых элементов (что нулевой факториал равен единице) с помощью формулы комбинаций из статистики:

• _n C _r = n! / ((п – р)! г!)

Где:

• n = количество предметов.
• r = Сколько предметов берется за раз.

Давайте начнем с трех элементов и двигаемся назад, чтобы посмотреть, есть ли логическая закономерность.

Допустим, у вас на полке было три романа, и вы хотели выбрать сразу три. Сколькими разными способами вы могли бы захватить все три сразу? По логике можно сказать, что есть только один способ схватить все три. Но это можно показать с помощью формулы комбинаций. У нас есть n = 3 и r = 3, поэтому:

₃ C ₃ = 3! / ((3 – 3)! 3!) = 1.

Это ожидаемый ответ. Теперь попробуем две книги:

₃ C ₃ = 2! / (2 – 2)! 2! = 1.

Вы видите закономерность? Пока вы берете все предметы одновременно (нам все равно, в каком порядке они расположены), она всегда будет равна 1. Вы можете ввести 99 999 или 1 миллион, и вы все равно получите: 1

Теперь мы установили логику, внимательно рассмотрим один пример:

• = 2! / (2 – 2)! 2!
• = 2 / (0)!*2

Мы знаем, что это уравнение должно равняться двум. Единственный способ сделать это, если 0! = 1. В противном случае у вас было бы деление на ноль, которое не определено.

Что произойдет, если мы последуем нашей первоначальной интуиции и решим, что 0! = 0? Это означает, что количество способов выбрать 3 книги из набора из трех книг было бы неопределенным:

• = 3! / (3 – 3)! 3!
• = 6 / (0)*3 = не определено.

Следующее объяснение [3] довольно легко понять с помощью некоторых основных понятий исчисления.

1. Давайте определим факториал для элементов, равных или превышающих единицу (на мгновение мы проигнорируем 0!).
   Определение : Факториал n определяется как n ! = ( n )( n – 1)…(3) (2) (1) для всех n ≥ 1.
2. Нижняя граница для [1] должна быть равна 1, потому что 1 ⁿ = (1) (1) (1) … → 1 ≤ n .
3. Мы можем определить верхнюю границу таким же образом: n! ≤ (n) (n) (n) … = n ⁿ .
4. Складывая (2) и (3), получаем: 1 ≤ n! ≤ п ^п .
5. Верхняя граница в (4) верна для n > 0, поэтому возьмем предел при n → 0 ⁺ : Этот предел неопределен, поскольку 0 ⁿ = 0 для любого n > 0 и n ⁰ = 1 для любого n ≠ 0,
6. Из (5) мы можем сказать, что
   
7. Используя Правило Лопиталя , мы имеем предел n ln n (при n→ 0 ⁺ )

= 0. Мы можем сделать вывод, что:


8. Если мы допустим предел n! в (7) равно нулю, получаем: 1 ≤ 0! ≤ 1, откуда следует, что 0! = 1,

Ссылки

[1] Ноль в четырех измерениях: культурная, историческая, математическая и психологическая перспективы.
[2] Сейфе, К. (2000). Зеро: Биография опасной идеи. Книги пингвинов.
[3] Махмуд, М. и Махмуд, И. (2015). Простая демонстрация нулевого факториала равна единице. Международный журнал математического образования 47(6):1-2

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Нулевой факториал: почему он равен единице?» От CalculusHowTo.com : Исчисление для всех нас! https://www.calculushowto.com/zero-factorial-why-does-it-equal-one/

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

ИсчислениеHowTo.com

• ← Обратное дифференцирование
• Интеграл TI 89: пошаговые примеры →

Почему факториал нуля равен единице?

12 сентября 2022 г. по

Факториал ничего — это числовое выражение для множества способов упорядочить данный stage_set без значений в нем, что равно единице. Как правило, факториал phone_number — это сокращенный способ написания формулировки генерации, в которой число умножается на каждую проблему меньше его, но больше нуля. 4! = 24, например, является лаппом, как запись 4 десять 3 адам 2 десять 1 = 24, но для выражения уравнения лаппа в правом поле факториала (четыре) используется маркер экфонезис.

Из этих примеров достаточно ясно, как вычислить факториал любого неповрежденного числа, большего или равного единице, но почему приз ничего факториала равен единице, несмотря на числовое соглашение, согласно которому любое произведение, умноженное на ничто, адекватно нулю?

Определение факториала гласит, что 0! = 1. Это обычно сбивает людей с толку в начале clock_time, когда они видят это уравнение, но мы увидим в примерах ниже, почему это имеет здравый смысл, когда вы выражаете определение, перестановки и формулы для ничего факториала.

Содержание

Определение нулевого факториала

Рациональность first_base, почему ни один факториал не равен единице, заключается в том, что определение говорит, что это должно быть так, что является математически правильным объяснением (хотя и немного разочаровывающим). Тем не менее, следует помнить, что определение факториала — это совокупность всех целых чисел, соответствующих или меньших по отношению к главному числу — в первых словах факториал — это подсчет возможных комбинаций с числами, меньшими или равными этому числу.

Поскольку ноль не имеет чисел, меньших его, но сам по себе является числом, существует только одна потенциальная комбинация того, как можно упорядочить это искривленное данное: он не может. Эта винокурня считается средством ее организации, так как по определению нулевой факториал адекватен единице, равен 1! является равным одному, потому что существует только одно потенциальное согласие этого набора данных.

Для лучшего понимания того, как это выглядит математически, важно отметить, что факториалы, подобные этим, используются для определения потенциальных порядков данных в последовательности, помимо известных как перестановки, которые могут быть утилитарными по симпатии в тот вечер, хотя в них нет значений. свободный или нулевой набор, есть спокойное одно направление, которое устроено закаливание.

Перестановки и факториалы

Подстановка — это конкретное, единственное упорядочение элементов в наборе. Например, существует шесть перестановок комбинации {1, 2, 3}, которая содержит три элемента, поскольку мы можем записать эти элементы шестью способами:

• 1, 2, 3
• 1, 3, 2
• 2, 3, 1
• 2, 1, 3
• 3, 2, 1
• 3, 1, 2

Мы могли бы помимо state_of_matter обосновать этот факт через равенство 3! = 6, что является факториальным театральным представлением полнолуния, определяющим перестановки. Точно так же их 4! = 24 перестановки спецификации с четырьмя элементами и 5! = 120 перестановок исправления с пятью элементами. Таким образом, суррогатная комната для размышлений о факториале — это позволить азоту быть реалистичным действием и сказать, что n! это phone_number перестановок для расположения с северными элементами.

При таком способе мышления о факториале давайте приведем еще примеры. Растение с двумя элементами имеет две перестановки: {а, Ь} можно расположить как а, бацилла или как Ь, а. Это соответствует 2! = 2. Желе с одним компонентом имеет индивидуальную перестановку, так как компонент 1 в наборе {1} может быть заказан только одним способом.

Это приводит нас к нулевому факториалу. Сик с нулевыми элементами называется эвакуационным множеством. Чтобы найти меру нулевого факториала, мы спрашиваем: «Сколькими способами мы можем упорядочить место без элементов?» здесь нам нужно немного расширить наше мышление. вечер, хоть и нечего приводить в порядок, есть одно средство сделать это. ладана у нас 0! = 1.

Формулы и ранние валидации

Еще одна причина для определения 0! = 1 имеет отношение к формулам, которые мы используем для перестановок и комбинаций. Это не объясняет, почему нулевой факториал равен единице, но показывает, почему установка 0! = 1 — товарная идея.

Комбинация — это группа элементов рига без соблюдения порядка. Например, рассмотрим set_up {1, 2, 3}, в котором есть одна комбинация, состоящая из всех трех элементов. Нет темы, как мы расположим эти элементы, в итоге мы получим одинаковое сочетание.

Мы используем рецепт комбинаций с комбинацией трех элементов, взятых по три в четвертом_измерении, и видим, что 1 = C (3, 3) = 3!/(3! 0!), а если рассматривать 0! как незнакомую меру и решить алгебраически, мы видим, что 3! 0! = 3! и поэтому 0! = 1.

Есть ранние причины, по которым определение 0! = 1 правильно, но причины, приведенные выше, самые простые. Общий смысл математики заключается в том, что когда создаются свежие идеи и определения, они остаются воспроизводимыми с другой математикой, и это именно то, что мы видим в определении нулевого факториала, адекватного единице.

Факториал — определение, расчет | Факториал сотен и 0

Факториал целого числа n определяется как произведение этого числа на каждое целое число, меньшее или равное n, до 1. Например, факториал числа 4 равен 4 × 3 × 2 × 1, что равно 24. Оно представляется с помощью символа ‘!’ Итак, 24 — это значение 4!. В 1677 году британский автор Фабиан Стедман определил факториал как эквивалент звонка сдачи. Перезвон был частью музыкального представления, когда музыканты звонили в несколько настроенных колокольчиков. И было это в 1808 году, когда математик из Франции Кристиан Крамп придумал символ факториала: n!. Изучение факториалов лежит в основе нескольких тем математики, таких как теория чисел, алгебра, геометрия, вероятность, статистика, теория графов, дискретная математика и т. д.

Думаете о том, как вычислить факториал числа? Давай учить.

1.	Что такое факториал?
2.	n Факториальная формула
3.	0 Факториал
4.	Факториал сотен
5.	Факториал отрицательных чисел
6.	Использование Факториала
7.	Расчет факториала
8.	Часто задаваемые вопросы о Факториале

Что такое факториал?

Факториал целого числа — это функция, которая умножает число на каждое натуральное число под ним. Символически факториал можно представить с помощью символа «!». Таким образом, «n факториал» является произведением первых n натуральных чисел и представляется как n!

Итак, н! или «n факториал» означает:

• n! = 1 · 2 · 3 · … · n = Произведение первых n натуральных чисел = n(n-1)(n-2)…………………….(3)(2)(1)

Например, 4 факториал, то есть 5! можно записать как: 5! = 5 × 4 × 3 × 2 × 1 = 120.

Обратите внимание на числа и их значения факториалов, указанные в следующей таблице. Чтобы найти факториал числа, умножьте это число на значение факториала предыдущего числа. Например, чтобы узнать значение 6! умножьте 120 (факториал 5) на 6 и получите 720. За 7! умножьте 720 (значение факториала 6) на 7, получите 5040. т. е. n! = п × (п — 1)!

нет	н! (n-факториал)	н! = п × (п — 1)!	Результат
1	1	1	1
2	2 × 1	= 2 × 1!	= 2
3	3 × 2 × 1	= 3 × 2!	= 6
4	4 × 3 × 2 × 1	= 4 × 3!	= 24
5	5 × 4 × 3 × 2 × 1	= 5 × 4!	= 120

n Факториальная формула

Формула для n-факториала: n! = п × (п — 1)!

• н! = п × (п — 1)!

Это означает, что факториал любого числа равен данному числу, умноженному на факториал предыдущего числа. Итак, 8! = 8 × 7!. ….. И 9! = 9 × 8!…… Факториал 10 будет 10! = 10 × 9!….. Вот так, если у нас есть (n+1) факториал, то его можно записать как (n+1)! = (n+1) × n! . Давайте посмотрим на некоторые примеры.

5 Факториал

Значение 5 факториала равно 5×4×3×2×1, что равно 120. Мы также можем вычислить его, используя формулу факториала. 5! = 5 × 4! = 5 × 24 = 120,

10 Факториал

10 факториал есть не что иное, как 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3 628 800.

0 Факториал

Нулевой факториал интересен, и его значение равно 1, т.е. 0! = 1 . Да, значение факториала 0 НЕ 0, а 1.

Давайте посмотрим, как это работает:

1! = 1
2! = 2 × 1 = 2
3! = 3 × 2 × 1 = 3 × 2! = 6
4! = 4 × 3 × 2 × 1 = 4 × 3! = 24

Перейдем к основной формуле факториала n! = п × (п — 1)! Как найти 3! То, что вы делаете, это 4! / 4. Аналогично, 2! это 3! / 3 и так далее. Теперь давайте посмотрим на образец:

Таким образом, мы можем доказать, что 0 факториал равен 1.

Альтернативный способ доказательства 0! = 1

В перестановках мы изучили бы, что n! есть количество способов упорядочить «n» разных вещей между собой. Если мы посмотрим на факториал таким образом, 1! = 1, так как возможна только 1 аранжировка с 1 вещью. Точно так же 0! = 1,

Факториал сотен

100 факториал = 100 × 99 × 98 × …. × 3 × 2 × 1 = 9,332621544 E+157. Этот продукт слишком велик для расчета вручную, поэтому используется калькулятор. Вот некоторые факты о факториале сотни:

• 100 факториал имеет 24 нуля в конце.
• Общее количество цифр в 100! 158.
• Точное значение факториала 100 равно 93, 326, 215, 443, 944, 152, 681, 699, 238, 856, 266, 700, 49.0, 715, 968, 264, 381, 621, 468, 592, 963, 895, 217, 599, 993, 229, 915, 608, 941, 463, 976, 156, 518, 286, 253, 697, 920, 827, 223, 758, 251, 185, 210, 916, 864, 000, 000, 000, 000, 000, 000, 000, 000 (всего 158 цифр).

Факториал отрицательных чисел

Можем ли мы иметь факториалы для таких чисел, как −1, −2 и т. д.? Начнем с 3! = 3 × 2 × 1 = 6

3! = 3 × 2 × 1 = 6
2! = 3! / 3 = 6 / 3 = 2
1! = 2! / 2 = 2 / 2 = 1
0! = 1! / 1 = 1 / 1 = 1
(- 1)! = 0! / 0 = 1 / 0 = деление на ноль не определено

И с этого момента все целочисленные факториалы не определены. Таким образом, отрицательные целочисленные факториалы не определены.

Использование Факториала

Одной из областей, где факториалы обычно используются, являются перестановки и комбинации.

• Перестановка — это упорядоченное расположение результатов, которое можно рассчитать по формуле: ⁿ P _r = n! / (н — р)!
• Комбинация — это группировка исходов, порядок которых не имеет значения. Его можно рассчитать по формуле: ⁿ C _r = n! / [(н — р)! р!]

В обеих этих формулах «n» — это общее количество доступных вещей, а «r» — это количество вещей, которые нужно выбрать. Поясним это на следующих примерах.

Пример 1: В группе из 10 человек разыгрываются призы 200, 100 и 50 долларов. Сколькими способами можно распределить призы?

Решение:

Это перестановка, потому что здесь имеет значение порядок распределения призов. Его можно рассчитать как ¹⁰ P ₃ способов.

¹⁰ P ₃ = (10!) / (10 — 3)! = 10! / 7! = (10 × 9 × 8 × 7!) / 7! = 10 × 9 × 8 = 720 способов.

Пример 2: Три приза по 50 долларов должны быть распределены в группе из 10 человек. Сколькими способами можно распределить призы?

Решение:

Это комбинация, потому что здесь порядок распределения призов не имеет значения (поскольку все призы имеют одинаковую ценность). Его можно рассчитать, используя ¹⁰ C ₃ .

¹⁰ С ₃ = (10!) / [ 3! (10 — 3)!] = 10! / (3! 7!) = (10 × 9 × 8 × 7!) / [(3 × 2 × 1) 7!] = 120 способов.

Расчет факториала

Факториал n обозначается n! и рассчитывается путем умножения целых чисел от 1 до n. Формула для n факториала равна н! = n × (n — 1)!.

Пример: Если 8! 40 320, тогда что такое 9!?

Решение:

9! = 9 × 8! = 9 × 40 320 = 362 880

Теперь давайте посмотрим на приведенную ниже таблицу факториалов, которая показывает значения факториала для первых 15 натуральных чисел:

n	н!
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40 320
9	362 880
10	3 628 800
11	39 916 800
12	479 001 600
13	6 227 020 800
14	8 717 8291 200
15	1 307 674 368 000

☛ Связанные темы:

• Факторный калькулятор
• Что такое факториал числа 9?
• Что такое факториал числа 20?

Важные замечания по факториалу:

• Факториал любого целого числа можно вычислить с помощью n! = n × (n — 1)!.
• Значение нулевого факториала равно единице, т. е. 0! = 1,
• Отрицательные целочисленные факториалы не определены.
• Перестановку и комбинацию можно рассчитать с помощью факториалов: ⁿ P _r = n! / (н — р)! & ⁿ C _r =n! / [(н — р)! р!].

 

Факториальные примеры

1. Пример 1: Вычислите выражение с факториалами: 10!/(4! × 6!).

   Решение:

   10!/(4! × 6!) = (10 × 9 × 8 × 7 × 6!) / (4! × 6!)
   = (10 × 9 × 8 × 7) / (4 × 3 × 2 × 1)
   = 210

   Ответ: Следовательно, значение выражения 10!/(4! × 6!) равно 210.

2. Пример 2: Найдите значение 5! (6 — 3)!.

   Решение:

   5! (6−3)! = 5! × 3!

   Теперь мы вычислим эти факториалы.

   = (5 × 4 × 3 × 2 × 1)(3 × 2 × 1)

   = 120 × 6

   = 720

   Ответ: Следовательно, значение 5! (6 — 3)! 720.

3. Пример 3: Сколько пятизначных чисел можно составить из цифр 1, 2, 5, 7 и 8, в каждом из которых не повторяется ни одна цифра?

   Решение:

   Данные 5 цифр (1, 2, 5, 7 и 8) нужно переставить между собой, чтобы получить все возможные 5-значные числа.

   Количество способов сделать это можно с помощью факториала.

   5! = 5 × 4 × 3 × 2 × 1 = 120

   Ответ: Следовательно, искомое количество пятизначных чисел равно 120.

4. Пример 4: Сколькими способами восемь человек могут выстроиться слева направо для группового фото?

   Решение:

   Количество способов, которыми 8 человек могут выстроиться в очередь, равно количеству способов, которыми они могут расположиться между собой, и это не что иное, как факториал 8.

   8! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 40 320

   Ответ: Следовательно, восемь человек могут выстроиться в очередь 40 320 способами.

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду

Хотите создать прочную основу в математике?

Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.

Записаться на бесплатный пробный урок

Практические вопросы по факториалу

 

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы о Факториале

Где мы используем факториалы?

Факториал — это функция, которая используется для нахождения количества возможных способов, которыми можно расположить выбранное количество объектов между собой. Эта концепция факториала используется для поиска перестановок и комбинаций чисел и событий.

Что означает факториал числа?

Факториал в математике — это одна из операций (обозначается символом «!»), а факториал числа — это произведение числа на все положительные целые числа, меньшие этого числа. Например 8! (читается как факториал 8) = 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1 = 40 320.

Что такое факториал n+1?

Факториал n+1 можно вычислить как (n+1)! = (n+1)n!.

Что такое символ факториала?

Для обозначения факториала используется символ ‘ ! ‘. Например «9factorial» записывается как 9!.

Что такое факториал 100?

Факториал 100 записывается как 100! и его значение равно 100 · 99 · 98 · … · 2 · 1 = 9,332621544 E+157.

Что такое факториал числа 10?

10! можно вычислить как 10 = 10 × 9! = 10 × 362 880 = 3 628 800. число означает умножение числа на каждое положительное целое число, меньшее этого. Итак, n!= n × (n-1) × (n-2) × (n-3) × ….. × 3 × 2 × 1.

Каково применение факториалов?

Факториалы используются для нахождения числа образов, решения задач перестановки и комбинации, определения вероятности событий и т. д.

Что такое факториальная запись?

Факторная запись представляет собой запись произведения последовательных целых чисел в виде факториала. Итак, 3 × 2 × 1 = 3! (3 факториала), 6 × 5 × 4 × 3 × 2 × 1 = 6! (6 факториал) и так далее.

✉️ Почему 0! = 1 (ноль факториал равен единице)? – 🥇 Приложение Scalar Scientific Calculator, графики и сценарии

Недавно я думал о различных обоснованиях определения 0! (факториал нуля), что равно

$$0!=1$$

Предполагаемое значение 1 может показаться вполне очевидным, если вы рассмотрите рекурсивную формулу. Однако «математически» меня это не удовлетворило. Вот почему я решил написать эти несколько предложений. Я приведу мотивации для менее продвинутых, но будут и мотивации для чуть более инсайдеров.

⭐️Факториал в скалярном калькуляторе

⭐️ Факториал и повторение

Для целых n > 0 факториал определяется следующим образом:

$$n!=n\times (n-1)\times (n-2)\times \ldots \times 2\times 1 $$

Легко видеть, что приведенная ниже рекурсивная формула следует за

$$n!=n\times (n-1)!$$

$$1!=1$$

⭐️ 0! = 1 – мотивация на основе повторяемости

Малая трансформация

$$n!=n\times (n-1)!$$

дает

$$(n-1)!=\frac{n!} {n}$$

Подставляя n = 1

$$(1-1)!=\frac{1!}{1}$$

$$0!=1!=1$$

Это объяснение, хотя и простое, не дает (на мой взгляд) достаточно глубокое понимание того, «почему это должно быть лучшим вариантом».

⭐️ Факториал! подсчитывает возможные различные последовательности n различных объектов (перестановок)

Предположим, что у нас есть множество, содержащее n элементов

$$\{1,2,\ldots,n\}$$

Теперь давайте подсчитаем возможные порядки элементов это множество

• n способов выбора первого элемента (поскольку у нас есть весь набор)
• n-1 способов выбора второго элемента (поскольку первый уже выбран, осталось n-1)
• n-2 способов выбора выбор третьего элемента (поскольку два уже выбраны, осталось n-2)
• …
• n- (k-1) способов выбора элемента с номером k (поскольку k-1 уже выбраны, n- (k -1) осталось)
• 2 способа выбора элемента с номером n-1 (поскольку было выбрано n-2, осталось 2)
• 1 способ выбора элемента с номером n (так как были выбраны n-1, остался только один)

Наконец, посчитав все возможные способы, получим

$$n\times (n-1)\times ( n-2)\times \ldots \times 2\times 1=n!$$

Вывод: Факториал n считает количество перестановок множества, состоящего из n элементов.

⭐️ k-перестановки n, иногда называемые частичными перестановками или вариациями

k-перестановки n — это различные упорядоченные расположения k-элементного подмножества n-множества. Количество таких k-перестановок n равно 9n=n!$$

$$n! = \frac{n!}{(n-n)!} = \frac{n!}{0!}$$

Следующее понимание того, почему 0!=1 является правильным определением, исходит из того, что для любого n > 0 мы должны есть

$$0! \ раз н! = n!$$

⭐️ Функция как отображение множеств

Функция

$$f:A\to B$$

Функция f : A → B, где для каждого a ∈ A существует f(a) = b ∈ B, определяет связь между элементами a и b. Можно сказать, что элементы a ∈ A и b ∈ B находятся в отношении «f» тогда и только тогда, когда f(a) = b.

⭐️ Функция как подмножество декартова произведения

Функция представляет собой бинарное отношение, то есть функция может быть выражена подмножеством декартова произведения.

$$(a,b)\in f \subseteq A\times B \iff f(a)=b$$

⭐️ Инъективная функция

Инъективная функция — это функция, которая сохраняет различимость: она никогда не отображает различные элементы своего домена к тому же элементу своего кодового домена. Вскоре

$$x\neq y \Rightarrow f(x) \neq f(y)$$

⭐️ Сюръективная функция

Функция f сюръективна (или онто), если для каждого элемента b в кодовой области существует по крайней мере один элемент a в области такой, что f(a)=b . Не требуется, чтобы x был уникальным.

$$f:A\to B$$

$${\large \displaystyle\forall_{b \in B} \quad\displaystyle\exists_{a\in A}\quad}f(a)=b $$

⭐️ Биективная функция

Биективная функция, или однозначное соответствие, — это функция, в которой каждый элемент одного множества сопряжен ровно с одним элементом другого множества, а каждый элемент другого множества соединен с ровно один элемент первого множества. Непарных элементов нет.

С математической точки зрения, биективная функция является как инъективным, так и сюръективным отображением множества A в множество B.

⭐️ Биективная функция против перестановки n-элементный набор {1, 2, …, n}, тогда перестановка будет функцией

$$p:\{1, 2, …, n\}\to\{1, 2, …, n\}$ $

удовлетворяющих условию биективной функции.

Задавая вопрос о количестве перестановок, мы можем также спросить о количестве различных биекций данного множества в себя.

⭐️ Пустая функция

Пустая функция — это любая функция, областью определения которой является пустое множество.

$$f:\emptyset\to B$$

Пустая функция «chart» является пустым множеством, поскольку декартово произведение домена и кодомена пусто.

$$\emptyset\times B = \emptyset$$

Пустая функция сохраняет отчетливость (инъективна), так как в области определения (пустом множестве) нет двух различных элементов, для которых значение функции равно .

⭐️ Частный случай пустой функции

Давайте проанализируем функцию, которая отображает пустое в пустое множество

$$f:\emptyset\to\emptyset$$

Такая функция является биекцией, поскольку она является инъективной функцией (как показано выше), и в домене кода нет элемента (домен кода — это пустой набор), который не был бы связан с элементами в домене.

Обратите внимание, что существует ровно одна такая биекция, которая является результатом того, что функция является подмножеством декартова произведения домена и кодомена. В данном случае это только один из возможных наборов.

$$f:\emptyset\to\emptyset$$

$$\emptyset\times\emptyset = \emptyset$$

Пустое множество имеет ровно одно подмножество, которое является пустым множеством – таким образом, такая биекция однозначно определено.

⭐️ 0! = 1 vs Пустая функция

Выше я писал, что количество перестановок n-элементного множества равно количеству различных биективных функций из этого множества в себя.

Далее – перестановка 0-элементного множества соответствует биекции из пустого множества в пустое множество/ 9{t}dt$$

После

$$\Gamma(n+1)=n!$$

$$0! = \Gamma(1) = 1$$

⭐️ Скалярная поддержка функции Gamma

Функции в скалярном калькуляторе, поддерживающие специальную функцию Gamma

• Gamma(x) – специальная функция Gamma Γ(s)
• sgnGamma(x) – Специальная функция Signum Gamma, Γ(s)
• logGamma(x) – Специальная функция Log Gamma, lnΓ(s)
• diGamma(x) – Функция Digamma как логарифмическая производная специальной функции Gamma, ψ(x)
• GammaL(s,x) – Нижняя неполная специальная функция гаммы, γ(s,x)
• GammaU(s,x) – Верхняя неполная специальная функция гаммы, Γ(s,x) (s,x) , GammaRegL(s,x) – Нижняя регуляризованная специальная функция P-гаммы, P(s,x)
• GammaQ(s,x), GammaRegU(s,x) – Верхняя регуляризованная специальная функция Q-гаммы функция, Q(s,x)

Гамма-функция

Гамма-функция в сравнении с факториальной диаграммой

⭐️ Число e и отношение факториала 9\infty\frac{1}{n!}=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3! }+\ldots$$

Сходимость последовательности

Это увлекательно, так как показывает еще более сильную связь факториала с e

Спасибо за чтение! Всего наилучшего 🙂

? Скаляр в действии

? Скаляр Lite (бесплатно)

? Scalar Pro

Что это такое и как им пользоваться

Цифра 0 уже давно ставит в тупик людей, изучающих математические понятия. Ноль это число? Как мы это используем? Хотя все мы на каком-то уровне знаем, что ноль означает ничего или ничего, это не всегда помогает нам включить его в математические задачи. Ниже мы рассмотрим несколько основных функций нуля и способы решения уравнений, содержащих ноль, с использованием этих функций.

 

Что такое число 0?

Является ли ноль числом? Ноль или 0 — это число , а цифра, используемая для представления числа 0 , широко используется в математике и может использоваться как самостоятельное число или как заполнитель в уравнениях.

 

История

Число 0 использовалось для обозначения идеи «ничто» со времен древнего шумерского общества, которое использовало его для обозначения отсутствия числа при записи чисел и уравнений.

Овальная форма , известная нам сегодня как 0, появилась в арабском языке в конце 700-х годов . Зеро не появлялся в европейском обществе до конца 12 века.

 

Современное использование

Ноль обычно используется в языке для выражения концепции отсутствия, а в математике используется как целое число. Число 0 в сегодняшней математике может быть сложным; зачем что-то вычислять, когда на самом деле там ничего нет? Но ноль можно использовать в различных математических задачах, и важно знать, что делать с нулем, когда вы его видите.

 

Операции с 0

Хотя этот список функций с использованием нуля не охватывает все математические функции , эти основные арифметические инструкции с использованием нуля помогут вам решать задачи на тестах и, возможно, даже в реальном мире.

 

Сложение

Тождество Закон сложения гласит, что любое число, добавленное к 0, равно самому себе .

Таким образом, вы можете добавить любое число и получить ту же сумму. Таким образом, вы можете добавить 0 к 1, 107 и 1 000 000 и все равно получить то же число, с которого вы начали.

 

Вычитание

Как и при сложении, если вычесть 0 из любого числа, вы получите ту же сумму. Например, 12-0 = 12.

Если вы вычитаете, вам может понадобиться заимствование для решения проблемы. Заимствование — это метод, используемый для вычитания чисел, состоящих более чем из одной цифры.

Вот пример заимствования (разберусь как форматировать):

1572-125 = х

В этой задаче из 2 нельзя вычесть 5. Значит, надо заимствовать из 7.

70 это 7 десятков. Итак, вы можете убрать десятку, и 7 станет 2; затем 2 становится 12. Теперь вам нужно вычесть 5 из 12.

12-5 равно 7.

6-2 равно 4.

5-1 равно 4.

1-0 (пустое место) равно 1.

Следовательно, ответ равен 1447.

Итак, если 0 — это ничто, как мы можем заимствовать его в задаче на вычитание? Ключ заключается в том, чтобы заимствовать из следующей цифры слева. Вы можете идти так далеко влево, как вам нужно.

Итак, если бы вы сделали 306-98 вы должны сначала позаимствовать из 3, чтобы сделать 0 равным 10. Затем вы можете позаимствовать из 10, чтобы сделать 6 равным 16. Таким образом, ваша задача будет выглядеть так: 16-8=8.

9-9=0.

2-0=2.

Таким образом, ваш ответ 208.

 

Не стесняйтесь заниматься математикой с помощью , добавив в свою жизнь котят

 

Умножение

Умножение на 0 на самом деле является одной из самых простых функций. , ответ всегда 0.

12 × 0 = 0

255 × 0 = 0

1679 × 0=0

И знаете что? 123596395539 x ​​0 = 0

 

Деление

Число 0, деленное на любое число, равно нулю. Подумайте об этом так: деление означает деление или разделение вещей поровну, верно ? Если у вас есть коробка с 8 кексами и за вашим столом 4 человека, вы разделите 8 на 4 и обнаружите, что каждый получает по два кекса. Но если у вас за столом 4 человека и в коробке 0 кексов, вам фактически нечего делить. Каждый получает 0 кексов.

К сожалению, деление числа на ноль не столь очевидно логично. Любое число, деленное на ноль, считается неопределенным; если вы поместите его в свой калькулятор прямо сейчас, вы, вероятно, получите сообщение об ошибке.

При делении вы всегда можете перепроверить свой ответ, умножив частное (ответ на задачу о делении) на делимое . В нашей задаче о кексах это 2 x 4. Число должно равняться нашему первоначальному делителю, 8.

Однако это помогает нам понять, почему мы не можем разделить число на 0. Поскольку мы знаем из наших правил умножения, что все, что умножается на 0, равно 0, изложенная выше концепция не работает, если 0 является делимым, потому что ответ всегда будет 0, даже если это не исходный делитель.

Если по какой-то причине вы встретили 0 как делимое в задаче, вы можете выразить его как 1, даже если ответ технически не определен .

 

Возведение в степень

Как и в делении, 0 в экспоненте считается неопределенным. Однако, когда вы решаете задачи и сталкиваетесь с чем-то, что равно 0 в степени другого числа или числу в степени 0, помните о правиле степени 0

Правило степени 0 гласит, что любое основание с показателем степени 0 или 0 равно 1. Итак, x¹ = 1,

Между тем, 0 в любой степени равно 0. Таким образом, 0² = 0.

 

 

Факториал нуля

Факториал — это математическое выражение, выражаемое как ! равно числу, полученному путем умножения всех чисел между 1 и заданным целым числом.

Итак, 2! означает, что мы умножаем все числа от 1 до 2. Это означает, что 2! = 2×1 = 2 и, следовательно, 2! = 24

6! означает, что мы умножаем все числа от 1 до 6. Итак, 6! = 1×2×3×4×5×6 = 720 и, следовательно, 6! = 720

Нулевой факториал, часто записывается как 0! Определяется как равный 1. По сути, поскольку факториал представляет собой выражение произведения всех целых чисел между заданными числами и 1, это единственный технически правильный ответ для 0! потому что единственное число между 0 и 1 — это 1.

 

Использовать число ноль может быть сложно, но есть несколько правил, которые помогут вам правильно выполнять математические операции, когда речь идет о нуле. Обязательно придерживайтесь этих правил и помните, что ноль вам не враг. Если вы знаете, как работать с числом ноль, использовать его будет проще простого.

 

Что дальше?

Очарованы числом ноль? Узнайте, сколько нулей в миллиарде и сколько нулей в гуголе и гуголплексе.

Нужна дополнительная помощь по математике? Узнайте, как преобразовывать десятичные дроби в дроби, складывать и вычитать дроби, а также все о составных и рациональных числах. И не забудьте нашу удобную таблицу умножения.

 

Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!

Наша проверенная база данных репетиторов включает ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают в исчислении.