Нормальное распределение это: Нормальное распределение (Normal Distribution) · Loginom Wiki

Нормальное распределение

Одномерное нормальное распределение

Графики плотности нормального распределения

Вычисления процентных точек нормального распределения

Двумерное нормальное распределение 

Графики плотности двумерного распределения

Нормальное распределение (normal distribution) – играет важную роль в анализе данных.

Иногда вместо термина нормальное распределение употребляют термин гауссовское распределение в честь К. Гаусса (более старые термины, практически не употребляемые в настоящее время: закон Гаусса, Гаусса-Лапласа распределение).

Одномерное нормальное распределение

Нормальное распределение имеет плотность::

      (*)

В этой формуле ,  фиксированные параметры,  – среднее

, – стандартное отклонение.

Графики плотности при различных параметрах приведены ниже.

Характеристическая функция нормального распределения имеет вид:

Дифференцируя характеристическую функцию и полагая t = 0, получаем моменты любого порядка.

Кривая плотности нормального распределения симметрична относительно  и имеет в этой точке единственный максимум, равный 

Параметр стандартного отклонения  меняется в пределах от 0 до ∞.

Среднее  меняется в пределах от -∞ до +∞.

При увеличении параметра  кривая растекается вдоль оси х, при стремлении  к 0 сжимается вокруг среднего значения (параметр  характеризует разброс, рассеяние).

При изменении  кривая сдвигается вдоль оси х (см. графики).

Варьируя параметры  и , мы получаем разнообразные модели случайных величин, возникающие в телефонии.

Типичное применение нормального закона в анализе, например, телекоммуникационных данных – моделирование сигналов, описание шумов, помех, ошибок, трафика.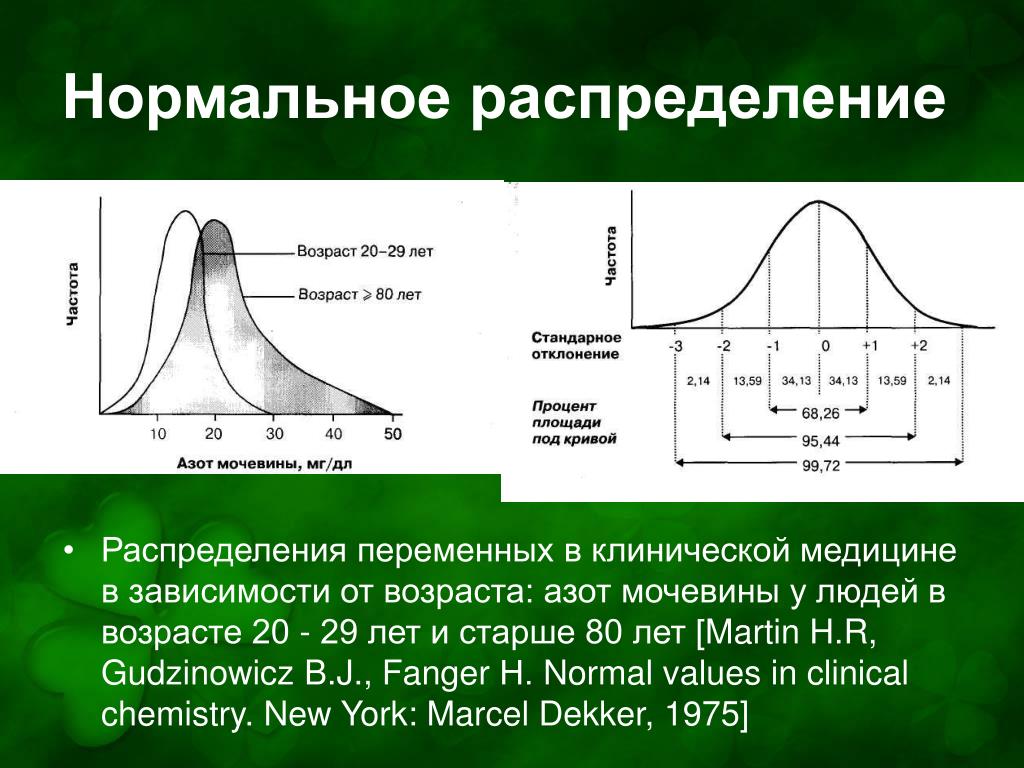

Графики одномерного нормального распределения

Рисунок 1. График плотности нормального распределения: среднее равно 0, стандартное отклонение 1

Рисунок 2. График плотности стандартного нормального распределения с областями, содержащими 68% и 95% всех наблюдений

Рисунок 3. Графики плотностей нормальных распределений c нулевым средним и разными отклонениями (=0.5, =1, =2)

Рисунок 4 Графики двух нормальных распределений N(-2,2) и N(3,2).

Заметьте, центр распределения сдвинулся при изменении параметра .

Замечание

В программе STATISTICA под обозначением N(3,2) понимается нормальный или гауссов закон с параметрами: среднее  = 3 и стандартное отклонение =2.

В литературе иногда второй параметр трактуется как дисперсия, т.е. квадрат стандартного отклонения.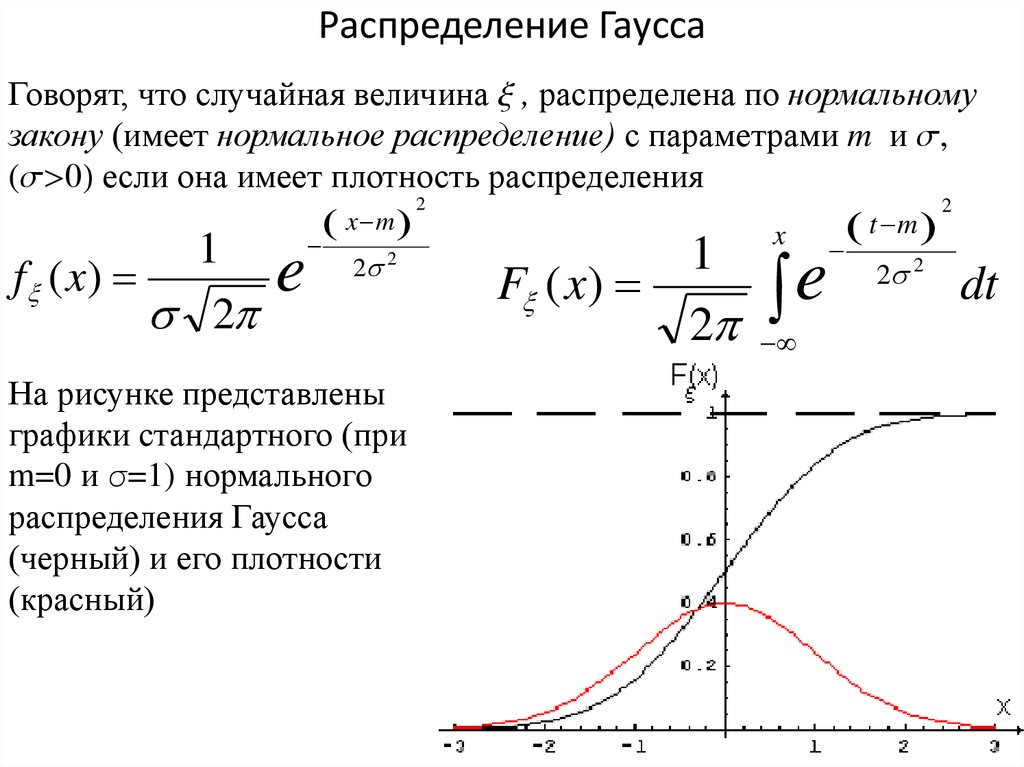

Вычисления процентных точек нормального распределения с помощью вероятностного калькулятора

STATISTICA

С помощью вероятностного калькулятора STATISTICA можно вычислить различные характеристики распределений, не прибегая к громоздким таблицам, используемым в старых книгах.

Шаг 1. Запускаем Анализ / Вероятностный калькулятор / Распределения.

В разделе распределения выберем нормальное.

Рисунок 5. Запуск калькулятора вероятностных распределений

Шаг 2.

Указываем интересующие нас параметры.

Например, мы хотим вычислить 95% квантиль нормального распределения со средним 0 и стандартным отклонением 1.

Укажем эти параметры в полях калькулятора (см. поля калькулятора среднее и стандартное отклонение).

Введем параметр p=0,95.

Галочка «Обратная ф.р». отобразится автоматически. Поставим галочку «График».

Нажмем кнопку «Вычислить» в правом верхнем углу.

Рисунок 6. Настройка параметров

Шаг 3. В поле Z получаем результат: значение квантиля равно 1,64 (см. следующее окно).

Рисунок 7. Просмотр результата работы калькулятора

Далее автоматически появится окно с графиками плотности и функции распределения нормального закона:

Рисунок 8. Графики плотности и функции распределения. Прямая x=1,644485

  

  

Рисунок 9. Графики функции нормального распределения. Вертикальные пунктирные прямые- x=-1.5, x=-1, x=-0.5, x=0

     

Рисунок 10. Графики функции нормального распределения. Вертикальные пунктирные прямые- x=0.5, x=1, x=1.5, x=2 

Оценка параметров нормального распределения

Значения нормального распределения можно вычислить с помощью интерактивного калькулятора.

Двумерное нормальное распределение

Одномерное нормальное распределение естественно обобщается на двумерное нормальное распределение.

Например, если вы рассматриваете сигнал только в одной точке, то вам достаточно одномерного распределения, в двух точках – двумерного, в трех точках – трехмерного и т.д.

Общая формула для двумерного нормального распределения имеет вид:

Где  – парная корреляция между X₁ и X₂;

– среднее и стандартное отклонение переменной X₁соответственно;

– среднее и стандартное отклонение переменной X₂соответственно.

Если случайные величины Х₁ и Х₂ независимы, то корреляция равна 0,  = 0,  соответственно средний член в экспоненте зануляется, и мы имеем:

f(x₁,x₂) = f(x₁)*f(x₂)

Для независимых величин двумерная плотность распадается в произведение двух одномерных плотностей.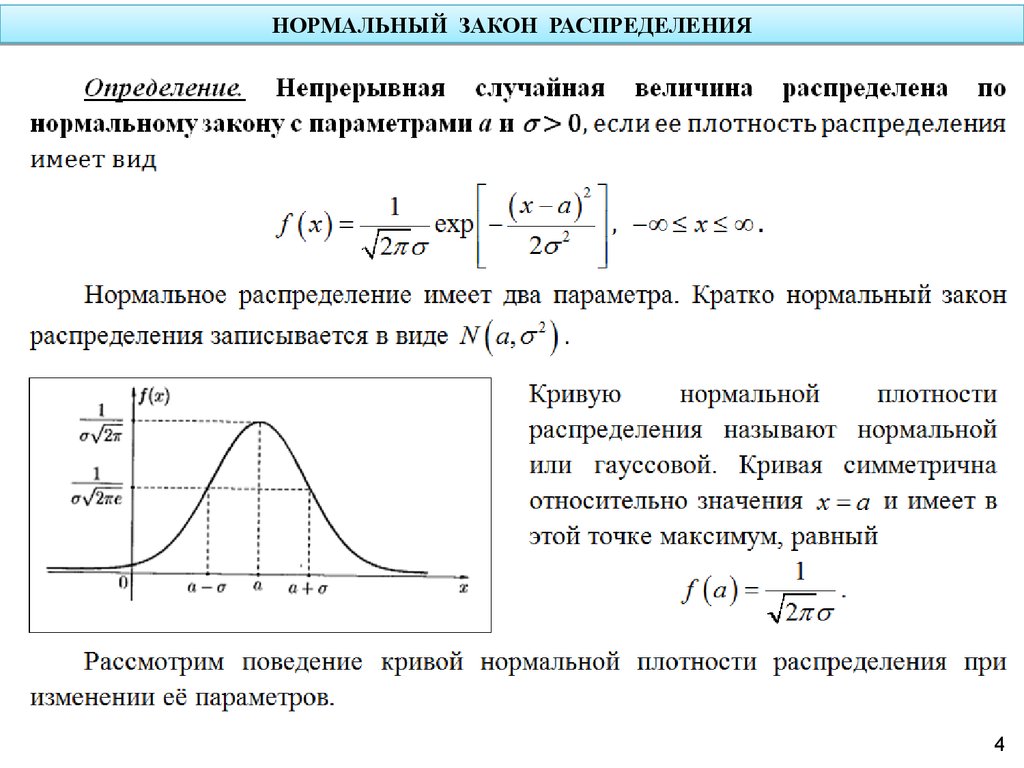

Графики плотности двумерного нормального распределения

Рисунок 11. График плотности двумерного нормального распределения (нулевой вектор средних, единичная ковариационная матрица)

Рисунок 12. Сечение графика плотности двумерного нормального распределения плоскостью z=0.05

Рисунок 13. График плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и 0.5 на побочной)

Рисунок 14. Сечение графика плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и 0.5 на побочной) плоскостью z= 0.05

Рисунок 15. График плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и -0.

5 на побочной)

Рисунок 16. Сечение графика плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и -0.5 на побочной) плоскостью z=0.05

Рисунок 17. Сечения графиков плотностей двумерного нормального распределения плоскостью z=0.05

Для лучшего понимания двумерного нормального распределения попробуйте решить следующую задачу.

Задача. Посмотрите на график двумерного нормального распределения. Подумайте, можно ли его представить, как вращение графика одномерного нормального распределения? Когда нужно применить прием деформации?

Читайте далее — многомерное нормальное распределение

Связанные определения:
Cтандартное нормальное распределение
Критерий Колмогорова-Смирнова
Нормальное распределение
Шапиро-Уилка W критерий

В начало

Содержание портала

Нормальное распределение

Одномерное нормальное распределение

Графики плотности нормального распределения

Вычисления процентных точек нормального распределения

Двумерное нормальное распределение 

Графики плотности двумерного распределения

Нормальное распределение (normal distribution) – играет важную роль в анализе данных.

Иногда вместо термина нормальное распределение употребляют термин гауссовское распределение в честь К. Гаусса (более старые термины, практически не употребляемые в настоящее время: закон Гаусса, Гаусса-Лапласа распределение).

Одномерное нормальное распределение

Нормальное распределение имеет плотность::

      (*)

В этой формуле ,  фиксированные параметры,  – среднее, – стандартное отклонение.

Графики плотности при различных параметрах приведены ниже.

Характеристическая функция нормального распределения имеет вид:

Дифференцируя характеристическую функцию и полагая t = 0, получаем моменты любого порядка.

Кривая плотности нормального распределения симметрична относительно  и имеет в этой точке единственный максимум, равный 

Параметр стандартного отклонения  меняется в пределах от 0 до ∞.

Среднее  меняется в пределах от -∞ до +∞.

При увеличении параметра  кривая растекается вдоль оси х, при стремлении  к 0 сжимается вокруг среднего значения (параметр  характеризует разброс, рассеяние).

При изменении  кривая сдвигается вдоль оси х (см. графики).

Варьируя параметры  и , мы получаем разнообразные модели случайных величин, возникающие в телефонии.

Типичное применение нормального закона в анализе, например, телекоммуникационных данных – моделирование сигналов, описание шумов, помех, ошибок, трафика.

Графики одномерного нормального распределения

Рисунок 1. График плотности нормального распределения: среднее равно 0, стандартное отклонение 1

Рисунок 2. График плотности стандартного нормального распределения с областями, содержащими 68% и 95% всех наблюдений

Рисунок 3. Графики плотностей нормальных распределений c нулевым средним и разными отклонениями (=0. 5, =1, =2)

Рисунок 4 Графики двух нормальных распределений N(-2,2) и N(3,2).

Заметьте, центр распределения сдвинулся при изменении параметра .

Замечание

В программе STATISTICA под обозначением N(3,2) понимается нормальный или гауссов закон с параметрами: среднее  = 3 и стандартное отклонение =2.

В литературе иногда второй параметр трактуется как дисперсия, т.е. квадрат стандартного отклонения.

Вычисления процентных точек нормального распределения с помощью вероятностного калькулятора

STATISTICA

С помощью вероятностного калькулятора STATISTICA можно вычислить различные характеристики распределений, не прибегая к громоздким таблицам, используемым в старых книгах.

Шаг 1. Запускаем Анализ / Вероятностный калькулятор / Распределения.

В разделе распределения выберем нормальное.

Рисунок 5. Запуск калькулятора вероятностных распределений

Шаг 2. Указываем интересующие нас параметры.

Например, мы хотим вычислить 95% квантиль нормального распределения со средним 0 и стандартным отклонением 1.

Укажем эти параметры в полях калькулятора (см. поля калькулятора среднее и стандартное отклонение).

Введем параметр p=0,95.

Галочка «Обратная ф.р». отобразится автоматически. Поставим галочку «График».

Нажмем кнопку «Вычислить» в правом верхнем углу.

Рисунок 6. Настройка параметров

Шаг 3. В поле Z получаем результат: значение квантиля равно 1,64 (см. следующее окно).

Рисунок 7. Просмотр результата работы калькулятора

Далее автоматически появится окно с графиками плотности и функции распределения нормального закона:

Рисунок 8.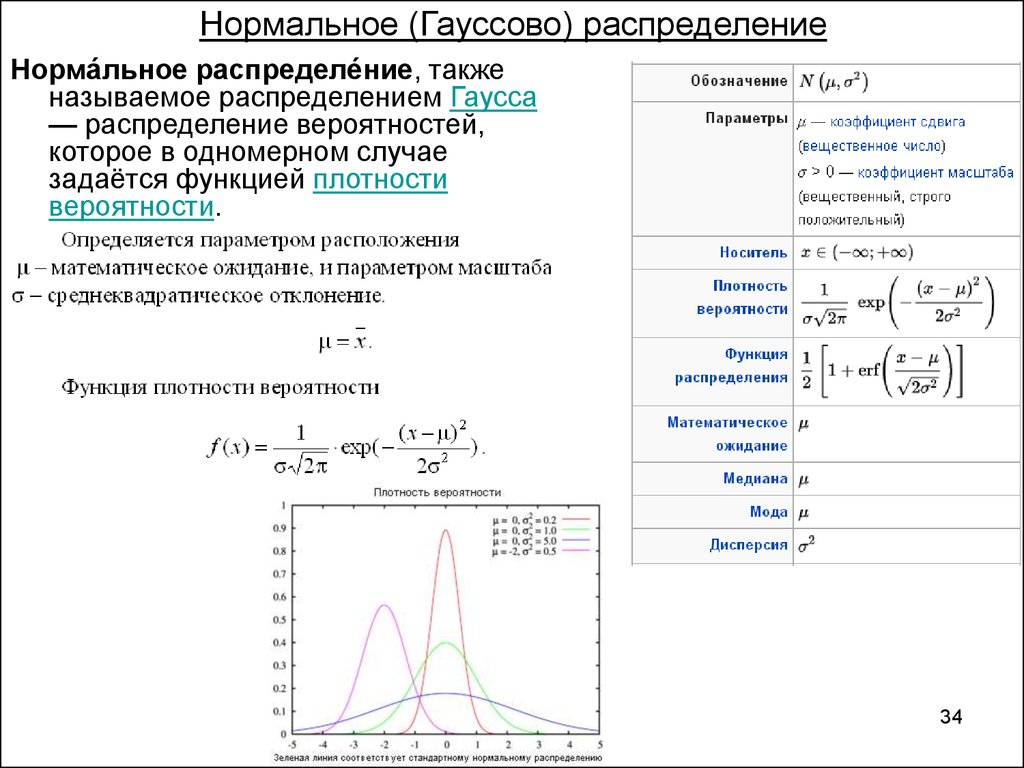 Графики плотности и функции распределения. Прямая x=1,644485

  

  

Рисунок 9. Графики функции нормального распределения. Вертикальные пунктирные прямые- x=-1.5, x=-1, x=-0.5, x=0

     

Рисунок 10. Графики функции нормального распределения. Вертикальные пунктирные прямые- x=0.5, x=1, x=1.5, x=2 

Оценка параметров нормального распределения

Значения нормального распределения можно вычислить с помощью интерактивного калькулятора.

Двумерное нормальное распределение

Одномерное нормальное распределение естественно обобщается на двумерное нормальное распределение.

Например, если вы рассматриваете сигнал только в одной точке, то вам достаточно одномерного распределения, в двух точках – двумерного, в трех точках – трехмерного и т.д.

Общая формула для двумерного нормального распределения имеет вид:

Где  – парная корреляция между X₁ и X₂;

– среднее и стандартное отклонение переменной X₁соответственно;

– среднее и стандартное отклонение переменной X₂соответственно.

Если случайные величины Х₁ и Х₂ независимы, то корреляция равна 0,  = 0,  соответственно средний член в экспоненте зануляется, и мы имеем:

f(x₁,x₂) = f(x₁)*f(x₂)

Для независимых величин двумерная плотность распадается в произведение двух одномерных плотностей.

Графики плотности двумерного нормального распределения

Рисунок 11. График плотности двумерного нормального распределения (нулевой вектор средних, единичная ковариационная матрица)

Рисунок 12. Сечение графика плотности двумерного нормального распределения плоскостью z=0.05

Рисунок 13. График плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и 0.5 на побочной)

Рисунок 14.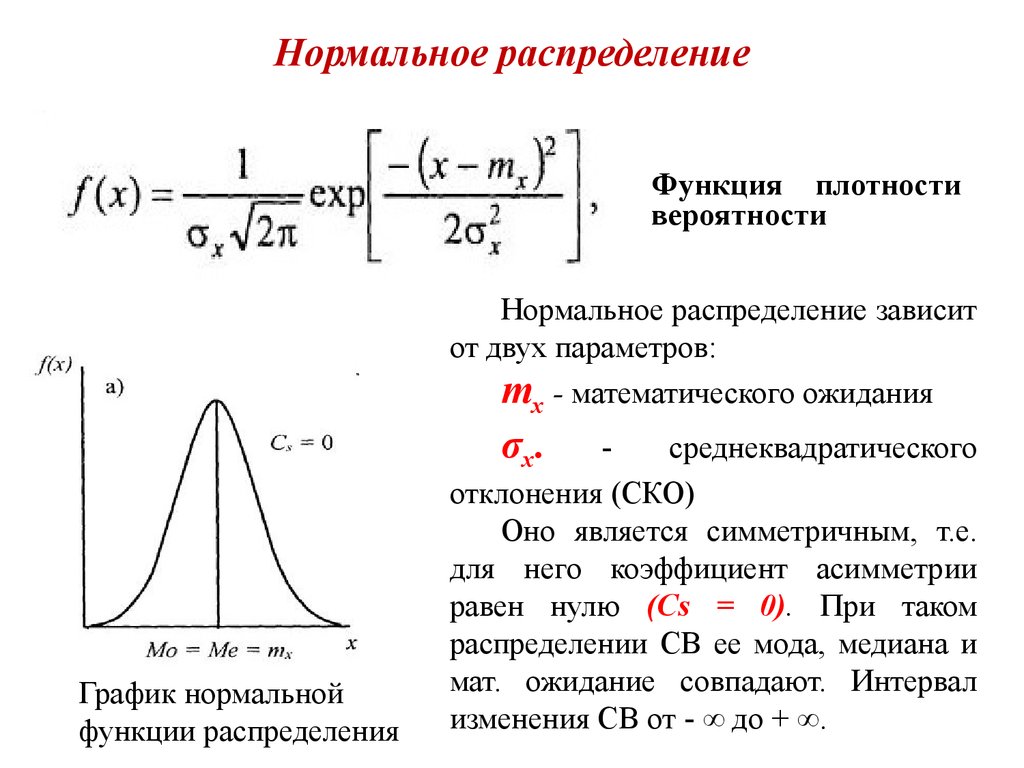 Сечение графика плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и 0.5 на побочной) плоскостью z= 0.05

Рисунок 15. График плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и -0.5 на побочной)

Рисунок 16. Сечение графика плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и -0.5 на побочной) плоскостью z=0.05

Рисунок 17. Сечения графиков плотностей двумерного нормального распределения плоскостью z=0.05

Для лучшего понимания двумерного нормального распределения попробуйте решить следующую задачу.

Задача. Посмотрите на график двумерного нормального распределения. Подумайте, можно ли его представить, как вращение графика одномерного нормального распределения? Когда нужно применить прием деформации?

Читайте далее — многомерное нормальное распределение

Связанные определения:
Cтандартное нормальное распределение
Критерий Колмогорова-Смирнова
Нормальное распределение
Шапиро-Уилка W критерий

В начало

Содержание портала

Что это такое, свойства, применение и формула

Что такое нормальное распределение?

Нормальное распределение, также известное как распределение Гаусса, представляет собой распределение вероятностей, симметричное относительно среднего значения, показывающее, что данные, близкие к среднему, встречаются чаще, чем данные, далекие от среднего.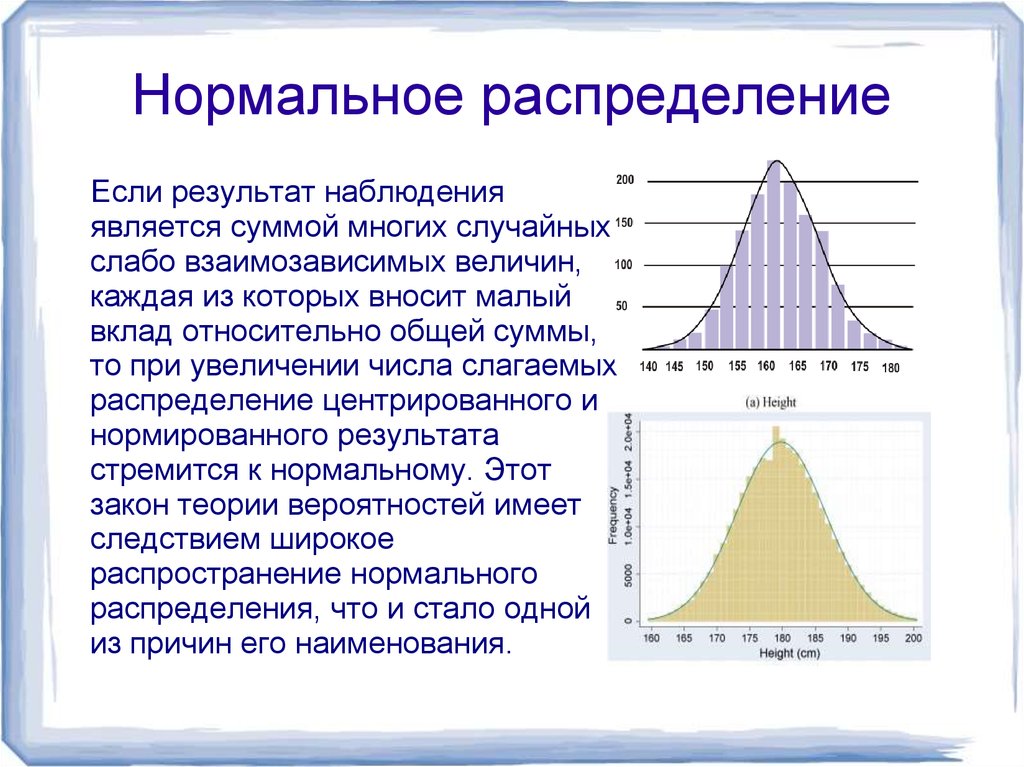

В графической форме нормальное распределение выглядит как «гауссова кривая».

Основные выводы

• Нормальное распределение — это правильный термин для колоколообразной кривой вероятности.
• В нормальном распределении среднее значение равно нулю, а стандартное отклонение равно 1. Оно имеет нулевую асимметрию и эксцесс 3.
• Нормальные распределения симметричны, но не все симметричные распределения являются нормальными.
• Многие естественные явления имеют тенденцию приближаться к нормальному распределению.
• Однако в финансах большинство распределений цен не являются совершенно нормальными.

Нормальное распределение

Понимание нормального распределения

Нормальное распределение является наиболее распространенным типом распределения, используемым в техническом анализе фондового рынка и в других видах статистического анализа. Стандартное нормальное распределение имеет два параметра: среднее значение и стандартное отклонение.

Модель нормального распределения важна в статистике и является ключом к Центральной предельной теореме (ЦПТ). Эта теория утверждает, что средние значения, рассчитанные для независимых, одинаково распределенных случайных величин, имеют приблизительно нормальное распределение, независимо от типа распределения, из которого взяты переменные (при условии, что оно имеет конечную дисперсию).

Нормальное распределение является одним из видов симметричного распределения. Симметричные распределения возникают, когда разделительная линия дает два зеркальных изображения. Не все симметричные распределения являются нормальными, поскольку некоторые данные могут выглядеть как два горба или ряд холмов в дополнение к кривой нормального распределения, указывающей на нормальное распределение.

Свойства нормального распределения

Нормальное распределение имеет несколько ключевых особенностей и свойств, которые его определяют.

Во-первых, его среднее (среднее), медиана (средняя точка) и мода (наиболее частое наблюдение) равны друг другу. Более того, все эти значения представляют собой пик или наивысшую точку распределения. Затем распределение падает симметрично вокруг среднего значения, ширина которого определяется стандартным отклонением.

Все нормальные распределения можно описать всего двумя параметрами: средним значением и стандартным отклонением.

Эмпирическое правило

Для всех нормальных распределений 68,2% наблюдений будут находиться в пределах плюс-минус одно стандартное отклонение от среднего значения; 95,4% наблюдений будут находиться в пределах +/- двух стандартных отклонений; и 99,7% в пределах +/- трех стандартных отклонений. Этот факт иногда называют «эмпирическим правилом» — эвристикой, описывающей, где будет появляться большая часть данных в нормальном распределении.

Это означает, что данные, выходящие за пределы трех стандартных отклонений («3-сигма»), будут означать редкие случаи.

Инвестопедия / Сабрина Цзян

Асимметрия

Асимметрия измеряет степень симметрии распределения. Нормальное распределение симметрично и имеет нулевую асимметрию.

Если вместо этого распределение набора данных имеет асимметрию меньше нуля или отрицательную асимметрию (асимметрию влево), то левый хвост распределения длиннее правого; положительная асимметрия (правая асимметрия) означает, что правый хвост распределения длиннее левого.

Эксцесс

Эксцесс измеряет толщину хвостов распределения по отношению к хвостам распределения. Нормальное распределение имеет эксцесс, равный 3,0.

Распределения с большим эксцессом более 3,0 демонстрируют хвостовые данные, превышающие хвосты нормального распределения (например, пять или более стандартных отклонений от среднего). Этот избыточный эксцесс известен в статистике как лептокуртик, но в просторечии он известен как «толстые хвосты». Возникновение толстых хвостов на финансовых рынках описывает так называемый хвостовой риск.

Распределения с низким эксцессом менее 3,0 (платикуртик) демонстрируют хвосты, которые обычно менее экстремальны («более тонкие»), чем хвосты нормального распределения.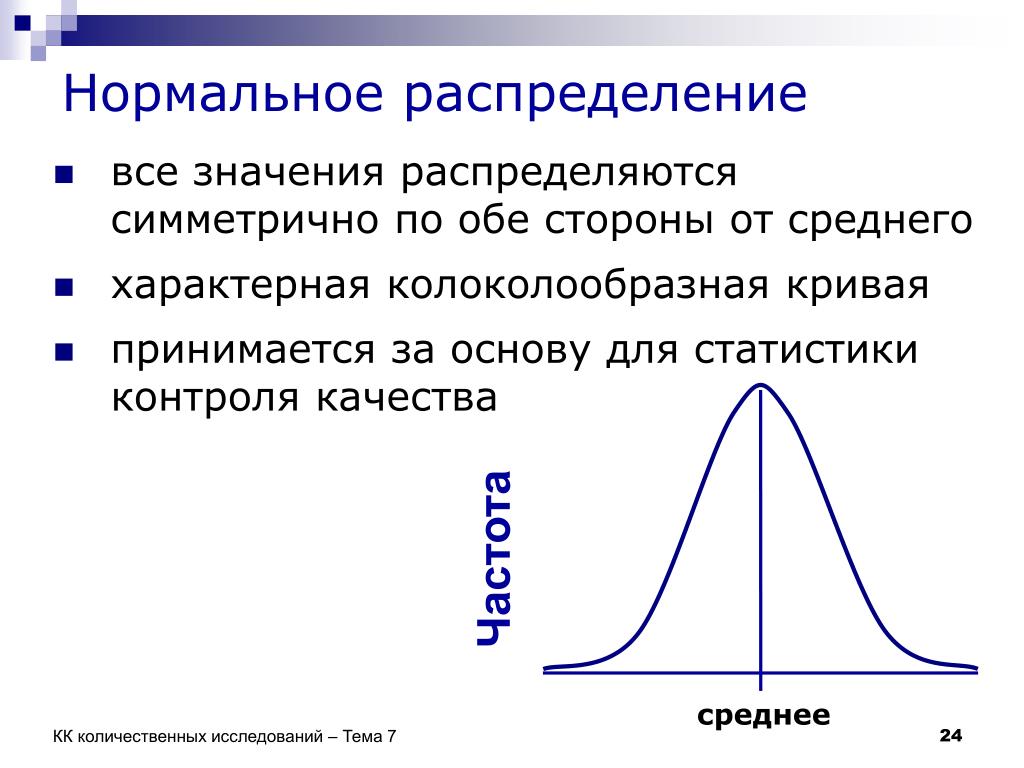

Формула нормального распределения

Нормальное распределение подчиняется следующей формуле. Обратите внимание, что необходимы только значения среднего (μ) и стандартного отклонения (σ).

Формула нормального распределения.

где:

• x  = значение исследуемой переменной или данных и f(x) функция вероятности
• μ = среднее значение
• σ = стандартное отклонение

Как нормальное распределение используется в финансах

Предположение о нормальном распределении применяется как к ценам активов, так и к ценовому действию. Трейдеры могут отображать ценовые точки с течением времени, чтобы подогнать недавнее ценовое движение к нормальному распределению. Чем дальше цена движется от среднего значения, в этом случае тем выше вероятность того, что актив переоценен или недооценен. Трейдеры могут использовать стандартные отклонения, чтобы предлагать потенциальные сделки. Этот тип торговли, как правило, осуществляется на очень коротких временных интервалах, поскольку большие временные масштабы затрудняют выбор точек входа и выхода.

Точно так же многие статистические теории пытаются моделировать цены на активы в предположении, что они подчиняются нормальному распределению. В действительности, ценовые распределения, как правило, имеют толстые хвосты и, следовательно, имеют эксцесс больше трех. Цены на такие активы превышали среднее значение более чем на три стандартных отклонения чаще, чем можно было бы ожидать, исходя из предположения о нормальном распределении. Даже если актив прошел через длительный период, в течение которого он соответствует нормальному распределению, нет никакой гарантии, что прошлые результаты действительно влияют на будущие перспективы.

Пример нормального распределения

Многие естественные явления кажутся нормально распределенными. Возьмем, к примеру, распределение роста людей. Средний рост составляет примерно 175 см (5 футов 9 дюймов), считая как мужчин, так и женщин.

Как показано на приведенной ниже диаграмме, большинство людей соответствуют этому среднему показателю.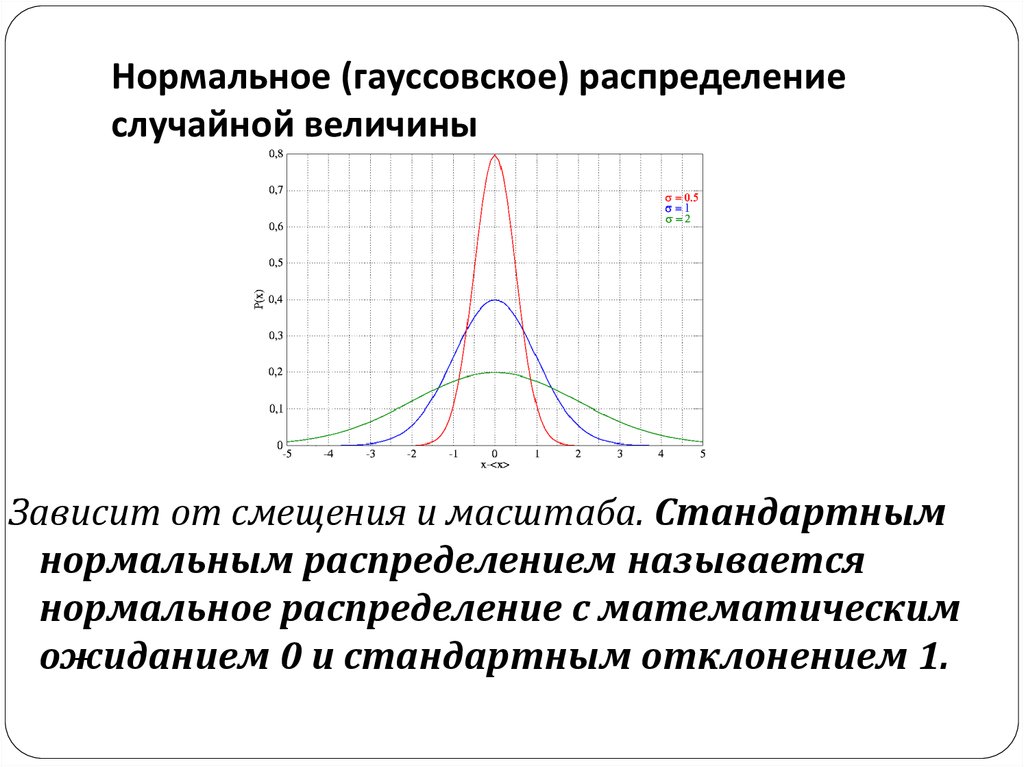 Между тем, более высокие и низкие люди существуют, но их частота в популяции снижается. Согласно эмпирическому правилу, 99,7 % всех людей упадут с +/- тремя стандартными отклонениями от среднего или между 154 см (5 футов 0 дюймов) и 19 см.6 см (6 футов 5 дюймов). Те, кто выше и ниже, были бы довольно редки (всего 0,15% населения каждый).

Что подразумевается под нормальным распределением?

Нормальное распределение описывает симметричный график данных относительно среднего значения, где ширина кривой определяется стандартным отклонением. Визуально это изображается как «гауссовая кривая».

Почему нормальное распределение называется «нормальным»?

Нормальное распределение технически известно как распределение Гаусса, однако оно получило терминологию «нормальный» после научных публикаций в 19^-й -й век, показывающий, что многие природные явления, по-видимому, «нормально отклоняются» от среднего значения. Эта идея «нормальной изменчивости» стала популярной как «нормальная кривая» натуралиста сэра Фрэнсиса Гальтона в его работе 1889 года « Natural Inheritance».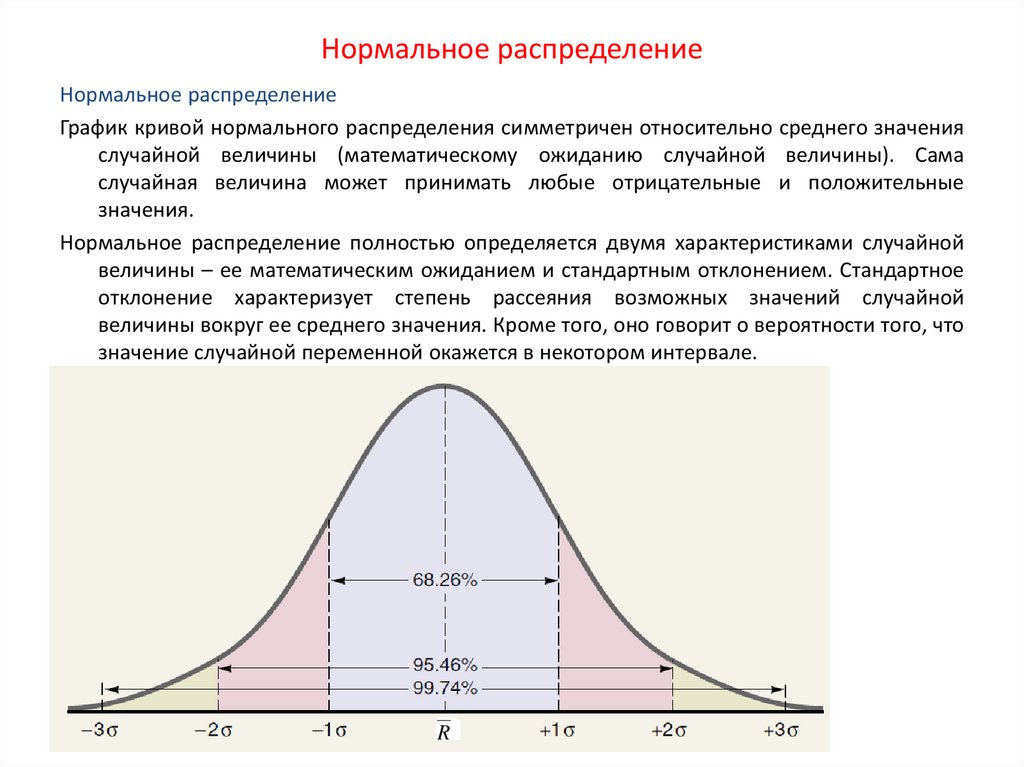

Каковы ограничения нормального распределения в финансах?

Хотя нормальное распределение является чрезвычайно важным статистическим понятием, его применение в финансах может быть ограничено, поскольку финансовые явления, такие как ожидаемая доходность фондового рынка, не подпадают под нормальное распределение. На самом деле цены, как правило, следуют логарифмически нормальному распределению, которое смещено вправо и имеет более толстые хвосты. Следовательно, слишком сильно полагаться на кривую нормального распределения при прогнозировании этих событий может привести к ненадежным результатам. Хотя большинству аналитиков хорошо известно об этом ограничении, преодолеть этот недостаток довольно сложно, поскольку часто неясно, какое статистическое распределение использовать в качестве альтернативы.

Нормальное распределение Значение Пример в финансах

Что такое кривая нормального распределения?

Колоколообразная кривая — это распространенный тип распределения переменной, также известный как нормальное распределение. Термин «колоколообразная кривая» происходит от того факта, что график, используемый для изображения нормального распределения, состоит из симметричной колоколообразной кривой.

Самая высокая точка на кривой или вершина колокола представляет собой наиболее вероятное событие в ряду данных (его среднее значение, мода и медиана в данном случае), в то время как все другие возможные события симметрично распределяются вокруг среднего значения, создавая наклонную вниз кривую с каждой стороны от пика. Ширина колоколообразной кривой описывается ее стандартным отклонением.

Ключевые выводы

• Колоколообразная кривая — это график, изображающий нормальное распределение, форма которого напоминает колокол.
• В верхней части кривой показаны среднее, мода и медиана собранных данных.
• Его стандартное отклонение отображает относительную ширину кривой нормального распределения вокруг среднего значения.
• Кривые Белла (нормальные распределения) обычно используются в статистике, в том числе при анализе экономических и финансовых данных.

Кривая нормального распределения

Понимание кривой нормального распределения

Термин «кривая колокола» используется для описания графического изображения нормального распределения вероятностей, основные стандартные отклонения которого от среднего значения создают изогнутую форму колокола. Стандартное отклонение — это измерение, используемое для количественной оценки изменчивости дисперсии данных в наборе заданных значений вокруг среднего. Среднее, в свою очередь, относится к среднему значению всех точек данных в наборе данных или последовательности и будет найдено в самой высокой точке на кривой нормального распределения.

Финансовые аналитики и инвесторы часто используют нормальное распределение вероятностей при анализе доходности ценной бумаги или общей чувствительности рынка. В финансах стандартные отклонения, отражающие доходность ценной бумаги, известны как волатильность.

Например, акции, отображающие колоколообразную кривую, обычно представляют собой акции «голубых фишек» и акции с более низкой волатильностью и более предсказуемыми поведенческими паттернами. Инвесторы используют нормальное распределение вероятностей прошлой доходности акции, чтобы делать предположения относительно ожидаемой будущей доходности.

Помимо учителей, которые используют кривую нормального распределения при сравнении результатов тестов, кривая нормального распределения часто также используется в мире статистики, где она может широко применяться. Кривые Белла также иногда используются в управлении эффективностью, помещая сотрудников, выполняющих свою работу в среднем, в нормальное распределение графика. По обеим сторонам падающего наклона представлены самые высокие и самые низкие показатели. Он может быть полезен крупным компаниям при оценке эффективности или при принятии управленческих решений.

Инвестопедия / Джули Бэнг

Пример кривой распределения

Ширина колоколообразной кривой определяется ее стандартным отклонением, которое рассчитывается как уровень вариации данных в выборке вокруг среднего значения. Используя эмпирическое правило, например, если 100 тестовых результатов собираются и используются в нормальном распределении вероятностей, 68% этих тестовых результатов должны находиться в пределах одного стандартного отклонения выше или ниже среднего. Перемещение двух стандартных отклонений от среднего значения должно включать 95% из 100 набранных тестовых баллов. Отклонение от среднего значения на три стандартных отклонения должно составлять 99,7% баллов (см. рисунок выше).

Результаты тестов, которые являются крайними выбросами, например, 100 или 0, будут считаться точками данных с длинным хвостом, которые, следовательно, лежат прямо за пределами трех диапазонов стандартных отклонений.

Кривая нормального распределения в сравнении с ненормальным распределением

Однако предположение о нормальном распределении вероятностей не всегда верно в финансовом мире. Акции и другие ценные бумаги могут иногда демонстрировать ненормальное распределение, которое не похоже на кривую нормального распределения.

Ненормальные распределения имеют более толстые хвосты, чем распределение кривой нормального распределения (нормальная вероятность). Более толстый хвост искажает негативные сигналы для инвесторов о большей вероятности отрицательной доходности.

Ограничения кривой нормального распределения

Оценка или оценка производительности с использованием кривой нормального распределения заставляет группы людей быть классифицированными как плохие, средние или хорошие. Для небольших групп необходимость категоризировать определенное количество людей в каждой категории, чтобы соответствовать кривой нормального распределения, окажет людям медвежью услугу. Как иногда, все они могут быть просто средними или даже хорошими работниками или студентами, но, учитывая необходимость подогнать свой рейтинг или оценки к кривой нормального распределения, некоторые люди вынуждены попасть в группу бедняков. На самом деле данные не совсем нормальные. Иногда существует асимметрия или отсутствие симметрии между тем, что находится выше и ниже среднего. В других случаях есть толстые хвосты (избыточный эксцесс), что делает события хвоста более вероятными, чем можно было бы предсказать при нормальном распределении.

Каковы характеристики кривой нормального распределения?

Колоколообразная кривая — это симметричная кривая, центрированная вокруг среднего или среднего значения всех измеряемых точек данных. Ширина колоколообразной кривой определяется стандартным отклонением: 68 % точек данных находятся в пределах одного стандартного отклонения от среднего, 95 % данных находятся в пределах двух стандартных отклонений и 99,7 % точек данных находятся в пределах трех стандартных отклонений. отклонения среднего.

Как кривая Белла используется в финансах?

Аналитики часто используют кривые нормального распределения и другие статистические распределения при моделировании различных потенциальных результатов, имеющих отношение к инвестированию. В зависимости от проводимого анализа они могут включать будущие цены на акции, темпы роста будущих доходов, потенциальные уровни дефолтов или другие важные явления. Прежде чем использовать кривую нормального распределения в своем анализе, инвесторы должны тщательно взвесить, действительно ли изучаемые результаты имеют нормальное распределение. В противном случае точность полученной модели может быть серьезно подорвана.

Каковы ограничения кривой нормального распределения?

Хотя колоколообразная кривая является очень полезным статистическим понятием, ее применение в финансах может быть ограничено, поскольку финансовые явления, такие как ожидаемая доходность фондового рынка, не подпадают под нормальное распределение.