Нормированный вектор это: Нормированный вектор — Большая Энциклопедия Нефти и Газа, статья, страница 1

2.2. Ортогональный и орто-нормированный базисы в пространстве е

В линейном пространстве у нас нет оснований предпочесть одни базисы другим. Там все базисы равноправны. В евклидовом пространстве существуют наиболее удобные базисы, а именно, ортогональные базисы. Они играют здесь ту же роль, что и прямоугольные системы координат в аналитической геометрии.

ОПРЕДЕЛЕНИЕ 5. Будем говорить, что n векторов ни один из которых не равен нулю, образуютортогональный базис в n-мерном евклидовом пространстве , если они попарно ортогональны, то есть:

при .

ОПРЕДЕЛЕНИЕ 6. Векторы ни один из которых не равен нулю, образуютортогональный нормированный базис, если они попарно ортогональны и имеют каждый длину равную единице, то есть, если выполняется равенство:

(9)

Для того, чтобы данное нами определение ортогонального и ортонормированных базисов было корректным, необходимо доказать, что входящие в определение векторы действительно образуют базис, то есть являются линейно независимыми.

Докажем, что равенство

(10)

возможно лишь, если , то есть является тривиальным. Умножим обе части равенства (10) скалярно на. Получим:

.

Но по определению ортогонального базиса

при .

Следовательно, Аналогично, умножая (10) на , получим₂=0 и т. д. Таким образом, соотношение (10) выполнено, если , то есть векторыявляются независимы, что и доказывает корректность утверждения.

Чтобы доказать существование ортогональных базисов в евклидовом пространстве , воспользуемся, так называемым, процессом ортогонализации.

Процесс ортогонализации состоит в том, что из не ортогональных, но линейно независимых векторов , можно построить систему попарно ортогональных векторов. Опишем процесс их построения. Пусть даны

n линейно независимых векторов . По этим векторам построимn попарно ортогональных векторов . Сначала положим. Векторбудем искать в виде:, где число₁ подберем таким образом, чтобы выполнялось условие .

Имеем:

(11)

Предположим, что построена система попарно ортогональных и отличных от нуля векторов . Далее векторбудем определять так:

, (12)

то есть вектор мы получаем из векторапутем «исправления» его с помощью линейной комбинации уже построенных векторов.

Коэффициенты находим из условия ортогональности векторак векторам. Последовательно умножим соотношение (12) на, затем наи т.д. Имеем

( 13)

Так как векторы попарно ортогональны, то равенства (13) запишутся так:

Отсюда находим:

(14)

До сих пор не было использовано то, что векторы линейно независимы. Это будем использовать при доказательстве того, что построенный векторотличен от нуля. Заметим предварительно, что векторесть линейная комбинация векторов. Но, с другой стороны, вектор можно заменить линейной комбинацией и векторов . В итоге, векторзаписывается в виде:

. (15)

Теперь ясно, что .Так как, в противном случае, правая часть равенства (15) была бы нулем, что противоречит линейной независимости векторов.

Итак, доказано, что .

Мы построили по векторам ивектор. Таким же образом пои мы построим и т.д.

Продолжая этот процесс до тех пор, пока не будут исчерпаны заданные векторы . Получаемn отличных от нуля и попарно ортогональных векторов , которые образуют ортогональный базис в исходном евклидовом пространстве.

Т е о р е м а 4. Во всяком n-мерном евклидовом пространстве существует ортогональный базис.

Д о к а з а т е л ь с т в о. По определению n-мерного пространства в нем существует базис линейно независимых векторов. С помощью процесса ортогонализации из векторовможно построить ортогональный базис, что и доказывает теорему.

Немного об арифметике / Хабр

Вы когда-нибудь задумывались о том, как мы считаем? Как устроен счет на низком уровне? Например, как выглядят на прямой единичные отрезки в выражении

1 + 1 = 2

. Или что такое квадратный корень из .

Счет появился не просто чтобы считать, а чтобы посчитать какие-то объекты. Например, количество яблок или антилоп в стаде. То есть всегда есть единица измерения.

Можно считать на пальцах или палочках, то есть задать некоторое соответствие между единицами измерения. Одна антилопа — одна палочка. Так как любые другие единицы можно заменить на палочки, то будем рассматривать только их. Палочка это абстрактная единица измерения.

Простые действия

Надо заметить, что счет идет в порядке возрастания. Такая счетная палочка сама по себе подразумевает наличие следующей палочки. То есть единица измерения имеет направление. А значит это единичный вектор.

Добавляя один единичный вектор в конец другого, мы будем перемещаться по числовой прямой, получая новые значения.

И тут появляется 4 варианта.

Как выглядят концы единичного отрезка? Какой вариант лучше моделирует реальный счет?

Первый не подходит. Двигаясь таким образом, мы никогда не попадем в целое число. Вроде досчитали до 1, а ни первому ни второму вектору оно не принадлежит.

Четвертый тоже не подходит. Если мы в точке 1, то непонятно, это первый вектор или второй. Когда мы считаем овечек, прыгающих через забор, у них нет общих точек.

Второй выглядит самым правильным. Дошли до точки 1 — значит отсчитали 1 объект. Каждая точка принадлежит одному вектору. Его мы и будем использовать в дальнейшем.

Третий тоже выглядит подходящим. Но у него есть особенность — точка 0 принадлежит первому вектору. Когда еще ничего нет, мы считаем что что-то уже есть. Это не похоже на реальный счет. Зато похоже на счет, используемый в компьютерах. Первая 32-разрядная ячейка в оперативной памяти занимает байты с адресами 0, 1, 2, 3. Чтобы было похоже на счет реальных объектов, надо было бы отсчитывать от адреса 1*4 и брать байты со смещением 0, -1, -2, -3.

Значит, второй вариант.

Обратите внимание, ноля здесь нет. Если просто считать по порядку, то не совсем очевидно, что точка отсчета не первая единица, а что-то до нее. Возможно поэтому ноль появился позже появления собственно счета.

Результат сложения можно представить в виде одного вектора из начальной точки в конечную.

Как сделать вычитание? Для этого надо добавить в рассмотрение вектор, направленный в обратную сторону.

Будем считать, что закрашенная точка означает стрелочку, то есть показывает направление вектора.

Чтобы различать эти вектора, назовем их соответственно положительным и отрицательным.

Можно ввести операцию изменения направления. После применения ее к положительному вектору получается отрицательный.

После применения ее 2 раза получается исходный вектор. По-другому ее можно назвать «унарный минус» или «смена знака».

Отрицательные вектора тоже образуют последовательность.

Если бы мы рассматривали только отрицательное направление, можно было бы использовать те же числа, что и для положительного, то есть без знака. Но мы рассматриваем оба, и надо отличать отсчеты в положительном и отрицательном направлении. Поэтому у чисел в отрицательном направлении стоит знак «минус». Можно и положительные числа обозначить знаком «плюс», но это необязательно, отличие и так есть.

Что это означает? Что есть положительный и отрицательный 0. Геометрически они находятся в одной точке. Это связывает положительный и отрицательный луч направления счета.

Ноль можно рисовать закрашенным, но для этого надо ввести особый вектор нулевой длины, к которому и прибавлять единичные. Его можно получить из единичных векторов.

3 + -3 = 0

Технически у него левый край тоже не включен, но правый край находится в той же точке. То есть вектор превращается в точку, или по-другому, точка это частный случай вектора.

Интересный момент, мы можем подойти к нулю слева или справа. Соответственно и знак у него будет положительный или отрицательный. Что-то похожее упоминается здесь.

Раз точка 0 это вектор нулевой длины, то можно сказать, что и отдельно взятая на прямой точка 1, или 2, или 3, это тоже вектор нулевой длины. Получается, есть нулевые векторы, которые связаны ненулевыми. Это решает вопрос, почему отрезок ненулевой длины состоит из бесконечного числа точек нулевой длины. Потому что точки всегда соединены ненулевыми векторами. Это две противоположности, которые образуют систему. Как 0 и 1 в двоичной системе счисления.

С умножением все просто — берем целиком второй вектор столько раз, сколько единиц в первом векторе.

С делением сложнее. Так же как вычитание это сложение со сменой знака, так и деление это умножение на обратное число. То есть надо задать способ получения вектора 1/N. Так как он меньше единичного вектора, надо ввести более мелкую единицу измерения.

Например, как разделить вектор длиной 12 на 10 частей? Вводим новый вектор некоторой длины и задаем условие, что этот вектор, повторенный 10 раз, дает исходный единичный вектор. В результате снова получаем вычисления в целых числах. 120 мелких векторов делим на 10 частей, получаем 12 мелких или 1.2 единичного.

Как выразить через такие векторы число пи? Никак. Точное выражение через единицы измерения означает точную десятичную запись. Точно так же нельзя выразить ими число = 0.333(3). Иначе надо будет до бесконечности вводить все более мелкие единицы измерения. Можно только обозначить эти числа другим способом — буквой или выражением.

Число = 0.5 можно выразить, но только потому что основание нашей системы счисления кратно этому числу. В десятичной системе все дроби периодические, кроме тех, знаменатели у которых кратны 2 или 5. Это может быть не совсем очевидно, так как мы чаще работаем с конечными дробями

Выходим за границы

Как попасть в эту точку?

Двигаясь только по прямой мы не можем в нее попасть. Значит, надо ввести еще один единичный вектор, перпендикулярный первому. Ввести положительное и отрицательное направление, определить правила сложения и вычитания между всеми видами векторов. Получается слишком сложно. Много сущностей и заданных правил, к тому же похожих друг на друга.

Что если подойти с другой стороны? Что надо сделать, чтобы попасть в точку в стороне от основного направления? Надо повернуть.

Повернули один вектор и складываем с другим.

Нетрудно заметить, что поворот положительного единичного вектора 2 раза дает отрицательный вектор.

Ничего не напоминает? Да ведь это умножение на мнимую единицу.

Значит что получается. это не вектор, перпендикулярный вещественному направлению. это поворот на прямой угол. Это не единица направления, а единица поворота. Умножение вектора на означает поворот вектора на через комплексное пространство. Смена знака это поворот 2 раза.

«Комплексное пространство» означает что если мы рассматриваем двумерный график функции , то мнимая часть находится в плоскости, перпендикулярной поверхности графика. Для ее отображения понадобится третье измерение, а мнимая часть потребует уже четвертого. Для одномерной числовой прямой достаточно второго.

А что такое квадратный корень из ? Видимо это такое значение, что умножение единичного вектора на него 2 раза дает вектор .
Раз умножение на это поворот на , то умножение на корень из это поворот на .

Проверим в Wolfram Alpha.

Ага, так и есть.

Любое выражение вида можно представить в виде , где это длина вектора, а задает угол поворота как коэффициент для .

При умножении чисел длины перемножаются, а углы складываются.

4 умножения на i возвращают вектор в исходное состояние. График умножения на с изменением степени по 0.1 дает обычную единичную окружность. Если развернуть ее по оси , получим обычные синус и косинус. Как думаете, как выглядят синус и косинус в 3D? Это спираль.

Здесь период целочисленный, так как по отсчитываются обороты, а не длина окружности.

Картинки кликабельные, по ссылкам интерактивная страница с графиками. В блоке «Axis mappping» определяется, какие 3 из 4 осей показываются в 3D. В поле «Function 1» и «Function 2» находится javascript-код, из которого создается объект типа Function.
В URL хэш, в хэше base64, в base64 json, в json значения полей.
Подписи относятся не к центральным осям, а к линиям, по которым откладываются цифры.
Расчеты в комплексных числах выполняются с помощью math.js, графики сделаны с помощью plotly.js.

А что если умножать не на , а на ? Вместо окружности получится расходящаяся логарифмическая спираль.

Вернемся ненадолго к делению. Обратное число это степень -1. Это связано с движением по этой логарифмической спирали.

Это график функции . Длина вектора изменяется от до 2.

График длины радиуса это обычный экспоненциальный график вида .

Особый случай

Рассмотрим график функции

Тождество Эйлера выглядит так:

Это особый случай формулы Эйлера. (1/2)

Также есть объекты Plotly и math, которые добавляются библиотеками.

Зачем нужна нормализация вектора?

Чтение документации Godot Game Engine об единичном векторе, нормализации и скалярном произведении действительно имеет большой смысл. Вот статья:

Единичные векторы

Итак, мы знаем, что такое вектор. У него есть направление и величина. Мы также знаем, как использовать их в Godot. Следующий шаг — изучение единичных векторов. Любой вектор с величиной длины 1 считается единичным вектором. В 2D представьте, что вы рисуете круг радиусом один. Этот круг содержит все единичные векторы, существующие для двух измерений:

Итак, что такого особенного в единичных векторах? Единичные векторы удивительны. Другими словами, единичные векторы обладают несколькими очень полезными свойствами.

Не терпится узнать больше о фантастических свойствах единичных векторов, но шаг за шагом. Итак, как из обычного вектора создается единичный вектор?

Нормализация

Взятие любого вектора и уменьшение его величины до 1,0 при сохранении его направления называется нормализацией. Нормализация выполняется путем деления компонентов x и y (и z в 3D) вектора на его величину:

 переменная а = вектор2(2,4)
var m = sqrt(a.x*a.x + a.y*a.y)
х / = м
ау /= м
 

Как вы могли догадаться, если вектор имеет величину 0 (имеется в виду, что это не вектор, а начало координат, также называемое нулевым вектором), происходит деление на ноль, и Вселенная проходит через второй Большой взрыв, за исключением обратной полярности и потом обратно. В результате человечество в безопасности, но Годо напечатает ошибку. Запомнить! Вектор(0,0) не может быть нормализован!.

Конечно, Vector2 и Vector3 уже предоставляют метод для этого:

 а = а.нормализованный()
 

Скалярное произведение

Итак, скалярное произведение — самая важная часть векторной математики.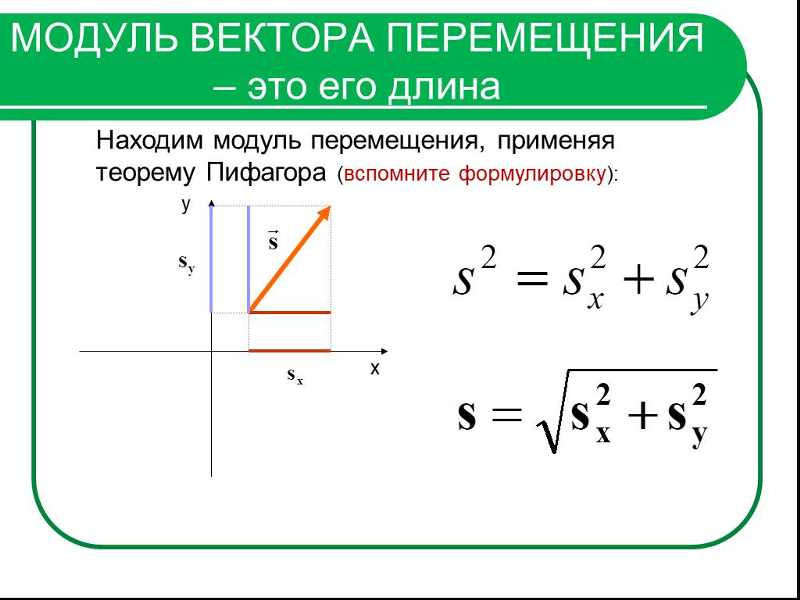 Без скалярного произведения Quake никогда бы не был создан. Это самый важный раздел учебника, поэтому обязательно усвойте его правильно. Большинство людей, пытающихся понять векторную математику, сдаются здесь, потому что, несмотря на то, насколько она проста, они не могут понять из нее орел или решку. Почему? Вот почему, потому что…

Скалярное произведение берет два вектора и возвращает скаляр:

 вар с = а.х*б.х + а.у*б.у
 

Да, почти так. Умножьте x из вектора a на x из вектора b. Сделайте то же самое с y и сложите его вместе. В 3D почти то же самое:

 var s = a.x*b.x + a.y*b.y + a.z*b.z
 

Я знаю, это совершенно бессмысленно! Вы даже можете сделать это с помощью встроенной функции:

 var s = a.dot(b)
 

Порядок двух векторов не имеет значения, a.dot(b) возвращает то же значение, что и b.dot(a) .

Здесь начинается отчаяние, и книги и учебники показывают вам эту формулу:

A ⋅ B = ∥A∥ ∥B∥ cos(θ)

И вы понимаете, что пришло время отказаться от создания 3D-игр или сложных 2D-игр. . Как что-то такое простое может быть таким сложным? Кто-то другой должен будет сделать следующую Zelda или Call of Duty. В конце концов, ролевые игры с видом сверху выглядят не так уж и плохо. Да, я слышал, что кто-то сделал красивую волю с одним из них в Steam…

Итак, это ваш момент, это ваше время, чтобы сиять. НЕ СДАВАЙСЯ! На этом этапе этот учебник сделает крутой поворот и сосредоточится на том, что делает точечный продукт полезным. Вот почему это полезно. Мы сосредоточимся один за другим на вариантах использования точечного продукта с реальными приложениями. Нет больше формул, которые не имеют никакого смысла. Формулы обретут смысл, как только вы узнаете, для чего они полезны.

Сайдинг Первым полезным и наиболее важным свойством скалярного произведения является проверка того, на что смотрит побочный материал. Давайте представим, что у нас есть любые два вектора, a и b. Любое направление или величина (ни происхождение). Неважно, какие они, но давайте представим, что мы вычисляем скалярное произведение между ними.

 var s = a.dot(b)
 

Операция вернет одно число с плавающей запятой (но поскольку мы находимся в мире векторов, мы называем их скалярными, и впредь будем использовать этот термин). Это число скажет нам следующее:

Если число больше нуля, оба смотрят в одном направлении (угол между ними < 90° градусов). Если число меньше нуля, оба смотрят в противоположном направлении (угол между ними > 90° градусов). Если число равно нулю, векторы имеют форму буквы L (угол между ними равен 90° градусов).

Итак, давайте подумаем о реальном сценарии использования. Представьте, что Змей идет по лесу, а тут рядом враг. Как мы можем быстро определить, видел ли противник обнаруженную Змею? Чтобы обнаружить его, противник должен иметь возможность видеть Снейка. Скажем, тогда что:

Змея находится в положении А. Противник находится на позиции B. Враг смотрит в сторону вектора направления F.

Итак, давайте создадим новый вектор BA, который идет от охранника (B) к Змее (A), вычитая два:

 var BA = A - B
 

В идеале, если бы охранник смотрел прямо на змею, чтобы установить зрительный контакт, он делал бы это в том же направлении, что и вектор BA.

Если скалярное произведение между F и BA больше 0, будет обнаружена Змея. Это происходит потому, что мы сможем сказать, что охранник смотрит на него:

, если (BA.dot(F) > 0):
    Распечатать("!")
 

Похоже, Снейк пока в безопасности.

Сайдинг с единичными векторами Итак, теперь мы знаем, что скалярное произведение между двумя векторами позволит нам узнать, смотрят ли они в одну и ту же сторону, в противоположные стороны или просто перпендикулярны друг другу.

Это работает одинаково со всеми векторами, независимо от величины, поэтому единичные векторы не являются исключением. Однако использование того же свойства с единичными векторами дает еще более интересный результат, поскольку добавляется дополнительное свойство:

Если оба вектора обращены в одном и том же направлении (параллельно друг другу, угол между ними равен 0°), результирующая скалярная величина равна 1. Если оба вектора обращены в прямо противоположном направлении (параллельно друг другу, но угол между ними равен 180 °), результирующая скалярная величина равна -1. Это означает, что скалярное произведение между единичными векторами всегда находится в диапазоне от 1 до -1. Итак, еще раз…

Если их угол равен 0°, скалярное произведение равно 1. Если их угол равен 90°, то скалярное произведение равно 0. Если их угол равен 180°, то скалярное произведение равно -1. Э-э.. это странно знакомо… видел это раньше… где?

Возьмем два единичных вектора. Первый направлен вверх, второй тоже, но мы будем вращать его сверху (0°) вниз (180° градусов)…

Пока строим результирующий скаляр!

Ага! Теперь все имеет смысл, это функция косинуса!

Мы можем сказать, что тогда, как правило…

Скалярное произведение двух единичных векторов равно косинусу угла между этими двумя векторами. Итак, чтобы получить угол между двумя векторами, мы должны сделать:

 var angle_in_radians = acos( a.dot(b))
 

Для чего это нужно? Ну, получение угла напрямую, вероятно, не так полезно, но просто возможность определить угол полезна для справки.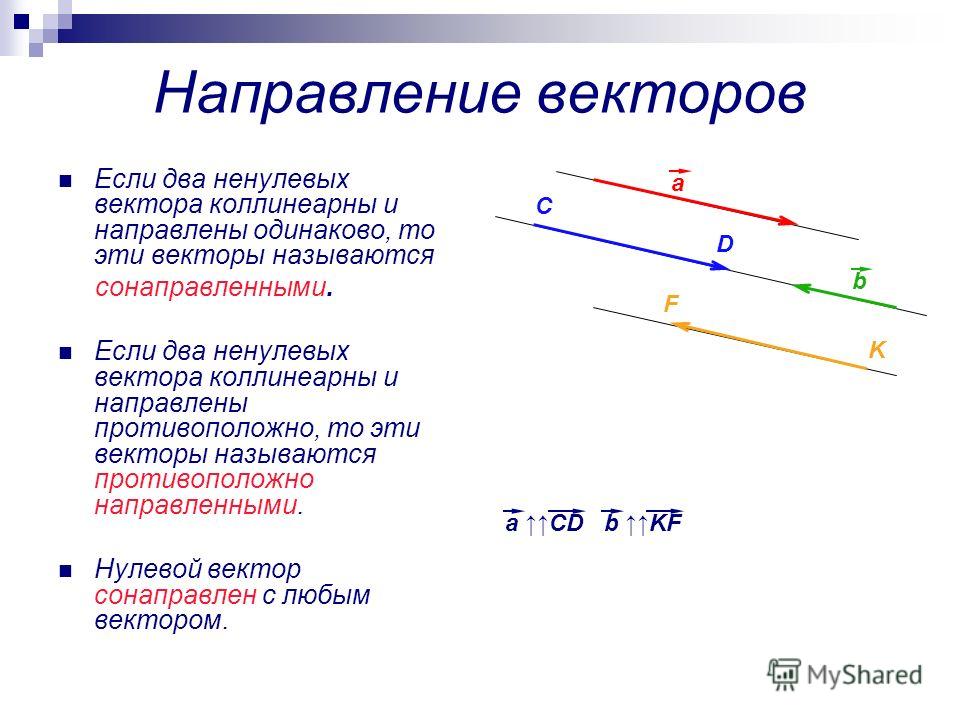 Одним из примеров является демонстрация кинематического персонажа, когда персонаж движется в определенном направлении, мы ударяем по объекту. Как узнать, попали ли мы в пол?

Путем сравнения нормали точки столкновения с ранее вычисленным углом.

Прелесть в том, что один и тот же код работает точно так же и без изменений в 3D. Векторная математика в значительной степени не зависит от размерности, поэтому добавление или удаление оси лишь немного усложняет задачу.

opengl — Что значит нормализовать значение?

спросил 10 лет, 4 месяца назад

Изменено 1 год, 8 месяцев назад

Просмотрено 43к раз

В настоящее время я изучаю освещение в OpenGL, в котором используется функция GLSL, называемая нормализацией. Согласно документам OpenGL, в нем говорится, что он «вычисляет нормализованное произведение двух векторов». Однако это все еще не объясняет, что означает «нормализованный». Я попытался найти нормализованный продукт в Google, однако ничего не могу найти об этом. Может ли кто-нибудь объяснить, что означает нормализация, и привести несколько примеров нормализованного значения?

• opengl
• gsl
• нормализация

9

Я думаю, что путаница возникает из-за идеи нормализации «значения», а не «вектора»; если вы просто думаете об одном числе как о значении, нормализация не имеет никакого смысла. Нормализация полезна только при применении к вектору.

Вектор — это последовательность чисел; в 3D-графике это обычно координата, выраженная как .2) Это в основном длина линии от начала координат <0,0,0> до точки, выраженной вектором.

Вектор является нормальным , если его длина равна 1. Вот и все!

Нормализация вектора означает изменить его так, чтобы он указывал в том же направлении (вспомните эту линию от начала координат), но его длина была равна единице.

Основная причина, по которой мы используем векторы нормалей, — это представление направления; например, если вы моделируете источник света, который находится на бесконечном расстоянии, вы не можете указать для него точные координаты. Но вы можете указать, где найти его из конкретной точки, используя вектор нормали.

4

Это математический термин, и эта ссылка очень просто объясняет его значение:

Операции в 2D и 3D компьютерной графике часто выполняются с использованием копий нормализованных векторов, т.е. преобразованы в единичные векторы… Нормализация вектора включает два шага:

1. вычислить его длину, затем
2. разделить каждый из его ( xy или xyz ) компонентов на его длину…

Это сложно объяснить, если вы не слишком много знаете о векторах или даже о векторной алгебре. (Вы можете проверить эту статью об общих понятиях, таких как вектор, вектор нормали или даже процедура нормализации.