16. Плоские прямоугольные координаты
Плоскими прямоугольными координатами в топографии называются линейные величины – абсцисса х и ордината у, определяющие положение точки на плоскости (карте), на которой отображена по определенному математическому закону (в проекции Гаусса) поверхность земного эллипсоида. Эти координаты несколько отличаются от принятых в математике декартовых координат на плоскости. За положительное направление осей координат принято для оси абсцисс (осевого меридиана зоны) направление на север, для оси ординат (экватора эллипсоида) на восток.
Применение
системы плоских прямоугольных координат
в топографии имеет некоторые особенности,
вызванные шарообразной формой Земли,
которая не может быть изображена на
плоскости без разрывов и искажений.
Поэтому ее условно разделили на равные
части, ограниченные меридианами с
разностью долгот 6° (рис. 30), которые
назвали координатными зонами. Счет зон
ведется от 1 до 60 от Гринвичского
(начального) меридиана к востоку.
x x x
Рис. 30. Координатные зоны и их нумерация
Оси координат делят шестиградусную зону на четыре четверти (рис. 31), счет которых ведется по ходу часовой стрелки от положительного направления оси абсцисс X.
Положение любой точки в каждой зоне относительно начала координат, например точки М, определяется кратчайшими расстояниями до осей координат, то есть перпендикулярами. Таким образом, при одних и тех же абсолютных значениях х и у точка М в зависимости от знаков координат может занимать в координатной зоне четыре различных положения. Ширина любой координатной зоны составляет на экваторе примерно 670 км, на широте 40° – 510 км, на широте 50° – 430 км.
Рис. 31.Координатная зона и плоские прямоугольные координаты
В Северном полушарии Земли (I и IV четверти зон) знаки абсцисс положительные.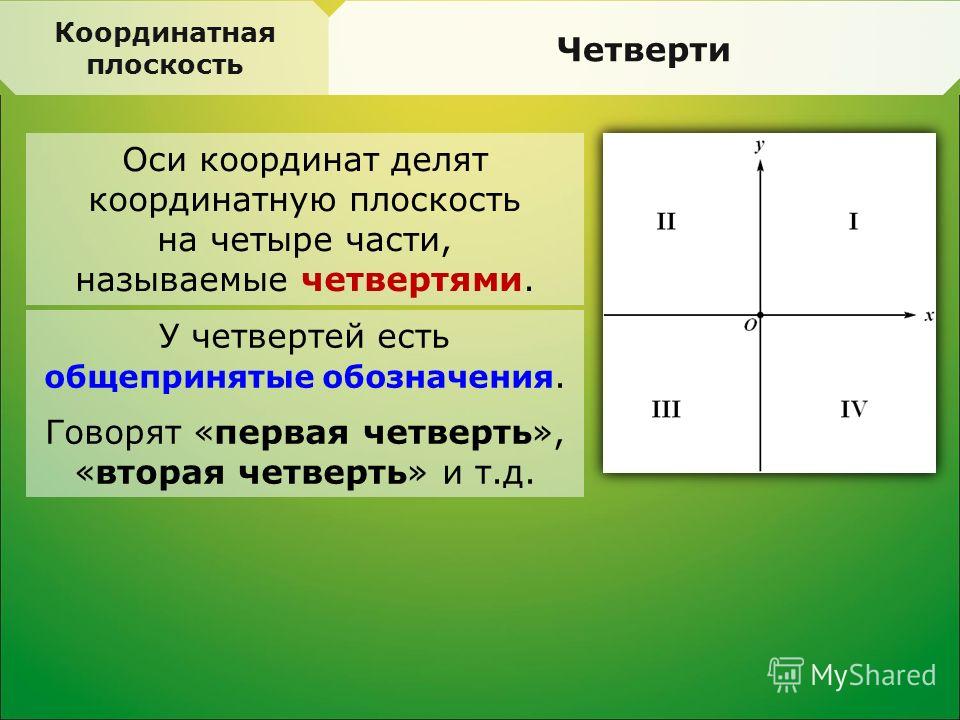
Знак
ординаты в IV четверти отрицательный.
Чтобы не иметь отрицательных значений
ординат при работе с топографическими
картами, в точке начала координат каждой
зоны величина ординаты принята равной
500 км. Таким образом, ось X как бы
переносится к западу от осевого меридиана
на 500 км.В этом случае ордината любой точки, расположенной к западу от осевого меридиана зоны, будет всегда положительной и по абсолютному значению меньше 500 км, а ордината точки, расположенной к востоку от осевого меридиана, будет всегда больше 500 км.
Для связи ординат между зонами слева от записи ординаты точки приписывают номер зоны, в которой находится эта точка. Полученные таким образом координаты точки называются полными. Например, полные прямоугольные координаты точки х = 2 567 845,
Это
означает, что точка находится в 2567 км
845 м к северу от экватора, в 36-й зоне и в
123 км 550 м к западу от осевого меридиана
этой зоны (500 000 – 376 450 = 123 550).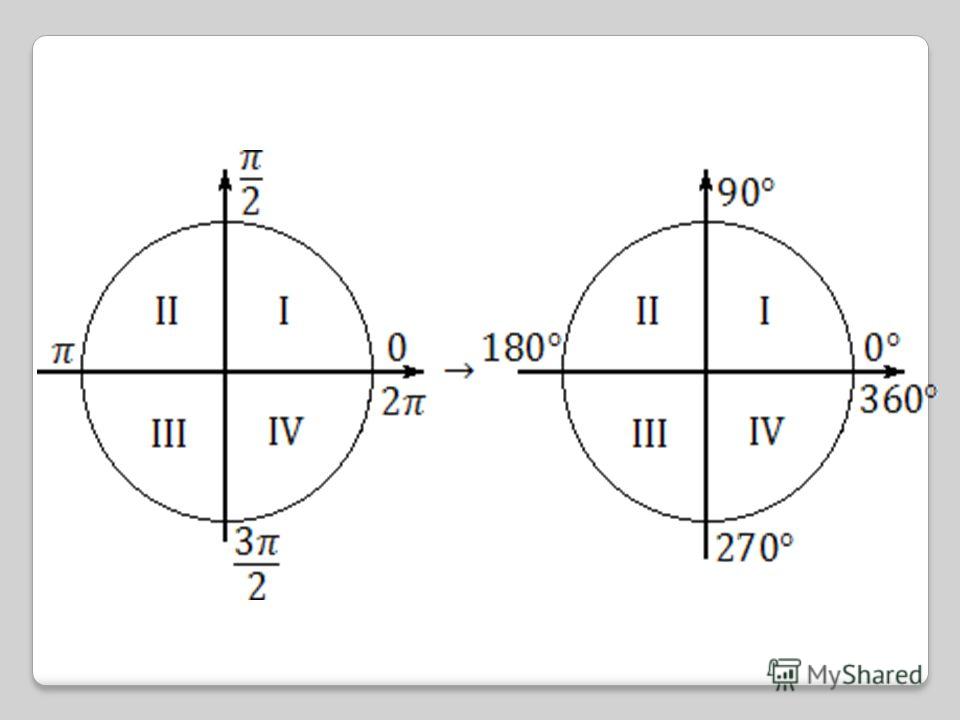
Прямоугольная координатная сетка на топографических картах. В каждой координатной зоне строится координатная сетка. Она представляет собой сетку квадратов, образованных линиями, параллельными координатным осям зоны. Линии сетки проводятся через целое число километров. Поэтому координатную сетку называют также километровой сеткой, а ее линии – километровыми. Если изображение одной зоны с нанесенной на ней сеткой квадратов разделить на отдельные листы карты, то каждый лист будет покрыт координатной сеткой, составляющей часть разграфки, общей для всей зоны.
На
карте масштаба 1:25 000 линии, образующие
координатную сетку, проводятся через
4 см, то есть через 1 км на местности
(рис.2), а на картах масштабов 1:50 000,
1:100 000, 1:200 000 – через 2 см (1, 2 и 4 км на
местности соответственно). На карте
масштаба 1:500 000 наносятся лишь выходы
линий координатной сетки на внутренней
рамке каждого листа через 2 см (10 км на
местности). При необходимости по этим
выходам координатные линии могут быть
нанесены на карту.
Оцифровка линий координатной сетки. Координатная сетка каждой зоны имеет оцифровку, которая одинакова во всех зонах. На рис. 32 даны подписи значений абсцисс и ординат координатных линий, проведенных через 100 км. Таким образом, в каждой координатной зоне имеется множество точек, численные значения координат которых одинаковы с численными значениями координат точек других зон. Например, точка
Чтобы
однозначно определять положение точки,
необходимо всегда слева от значения ее
ординаты, как отмечалось ранее, указывать
номер зоны.При работе на ограниченной территории, изображенной, например, на одном листе карты, используют сокращенные координаты. В этом случае при определении прямоугольных координат по карте указывают десятки и единицы километров, сотни, десятки и единицы метров. Тогда точка А будет иметь сокращенные координаты х = 10850, у = 20600. На топографических картах значения абсцисс и ординат координатных линий подписывают у выходов линий за внутренней рамкой листа и в девяти местах на каждом листе карты.
Полные
значения абсцисс и ординат в километрах
подписывают около ближайших к углам
рамки карты координатных линий, около
линий, ограничивающих квадраты
координатной сетки по сто километров,
и около ближайшего к северо-западному
углу пересечения координатных линий.
Остальные координатные линии подписывают
сокращенно двумя цифрами (десятки и
единицы километров).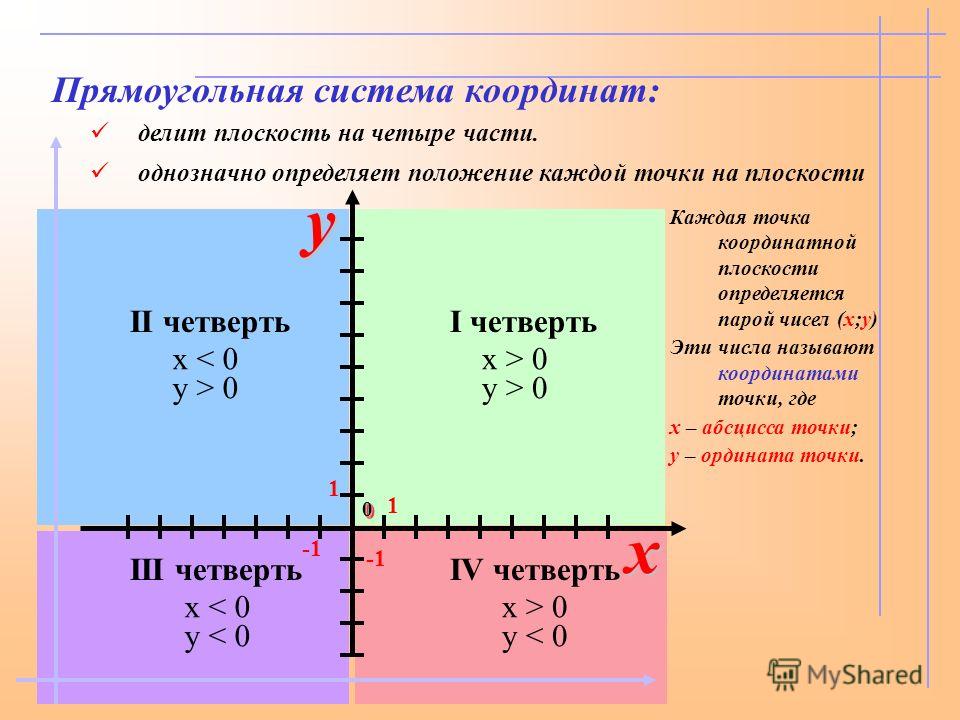
Подписи около
горизонтальных линий координатной
сетки соответствуют расстояниям от оси
ординат в километрах.
Подписи около вертикальных линий обозначают номер зоны (одна или две первые цифры) и расстояние в километрах (всегда три цифры) от начала координат, условно перенесенного к западу от осевого меридиана зоны на 500 км. Например, подпись 6740 означает: 6 – номер зоны, 740 – расстояние от условного начала координат в километрах.
Дополнительная километровая сетка на стыке двух координатных зон
Так как вертикальные километровые линии параллельны осевому меридиану своей зоны, а осевые меридианы соседних зон между собой непараллельны, то при смыкании сеток двух зон линии одной из них расположатся под углом к линиям другой (рис. 33).
Вследствие
этого при работе на стыке двух зон могут
возникнуть затруднения с использованием
координатных сеток, так как они будут
относиться к разным осям координат.
Рис. 33. Взаимное расположение километровых линий на стыке смежных зон
Чтобы устранить это неудобство, в каждой зоне все листы карт, расположенные в пределах 2° к востоку и западу от границы зоны, имеют помимо своей координатной сетки еще дополнительную, являющуюся продолжением сетки соседней зоны (рис. 34). Оцифровка дополнительной координатной сетки составляет продолжение нумерации линий смежной зоны. Она подписывается за внешней рамкой листа.
Рис. 34. Обозначение дополнительной сетки за рамкой карты
Если
работа ведется с листами карты на стыке
двух зон и требуется пользоваться на
всех этих листах единой системой
координат, надо на листах карты одной
зоны соединить карандашом по линейке
противоположные концы одноименных
километровых линий сетки соседней зоны
(вертикальных и горизонтальных). В
дальнейшем при работе на этих листах
следует пользоваться лишь новой
дополнительной сеткой.
Урок по математике «Координатная плоскость»; 6 класс (VI вид) — К уроку — Математика, алгебра, геометрия
Интегрированный урок + презентация по теме «Координатная плоскость». Математика 6 класс.
Щербакова Ирина Михайловна, учитель математики, II квалификационная категория, ГКОУ РО школа-интернат VIвида г.Волгодонск.
Ведь, если звезды зажигают –
Значит – это кому-нибудь нужно?
Значит – кто-то хочет, чтобы они были?
Тип урока:. Интегрированный урок
Цель — более глубокое усвоение знаний, высокий уровень обобщения, систематизации знаний по теме.
Задачи:
— образовательные: выявить качество и уровень овладения знаниями и умениями, полученными на предыдущих уроках по теме Координатная плоскость, обобщить материал как систему знаний.
—
воспитательные: воспитывать
общую культуру, эстетическое восприятие
окружающего; создать условия для реальной
самооценки учащихся, реализации его
как личности.
— развивающие: развивать пространственное мышление, умение классифицировать, выявлять связи, формулировать выводы; развивать коммуникативные навыки при работе в группах, развивать познавательный интерес.
Ход урока:
Организация начала урока.
Звучат первые два куплета песни «Маленький принц» в исполнении Валерии.
Слайды 1-5
«У меня есть серьезные основания полагать, что Маленький принц прилетел с планетки, которая называется «астероид В-612». Этот астероид был замечен в телескоп лишь один раз, в 1909 году, одним турецким
астрономом.
Астроном доложил тогда о своем замечательном открытии на Международном астрономическом конгрессе. Но никто ему не поверил, а все потому, что он был одет по-турецки. Уж такой народ эти взрослые!
К
счастью для репутации астероида
В-612, турецкий султан велел своим
подданным под страхом смерти носить
европейское платье. В 1920 году тот
астроном снова доложил о своем открытии.
На этот раз он был
одет по последней моде, — и все с ним согласились.
Я вам рассказала так подробно об астероиде В-612 и даже сообщила его номер только из-за взрослых. Взрослые очень любят цифры. Когда рассказываешь им, что у тебя появился новый друг, они никогда не
спросят о самом главном. Никогда они не скажут: «А какой у него голос? В какие игры он любит играть? Ловит ли он бабочек?» Они спрашивают: «Сколько ему лет? Сколько у него братьев? Сколько он весит? Сколько зарабатывает его отец?» И после этого воображают, что узнали человека.
Точно так же, если им сказать: «Вот доказательства, что Маленький принц на самом деле существовал: он был очень, очень славный, он смеялся, и ему хотелось иметь барашка. А кто хочет барашка, тот, безусловно, существует. Уж такой народ эти взрослые. Не стоит на них сердиться. Дети должны быть очень снисходительны к взрослым.
Но
мы, те, кто понимает, что такое жизнь,
мы, конечно, смеемся над номерами и
цифрами! Я охотно начала бы эту
повесть как волшебную сказку.
Я хотела
бы начать так:
«Жил да был Маленький принц. Он жил на планете, которая была чуть побольше его самого, и ему очень не хватало друга…».
Ребята, я начала наш урок с отрывка сказки «Маленький принц» написанной замечательным французским писателем, летчиком Антуаном де Сент Экзюпери. Я приглашаю вас сегодня в космическое путешествие на планету Маленького принца, и мне очень хотелось чтобы вы подружились бы с ним, ведь у Маленького принца совсем нет друзей.
Я, к сожалению, не волшебник, и мы с вами современные люди. Поэтому для космического путешествия нам нужен космический корабль и карта с космическим маршрутом. Вам предлагается на этом уроке стать космическими конструкторами, штурманами, летчиками.
Слайд 6 (звучит музыка группы Спейс «Волшебное путешествие»)
Перед
вами карта нашего космического пути.
Ваша задача самостоятельно определить
координаты звезд и проложить наш путь
к звезде Маленького принца. (Самостоятельная
работа по заполнению таблицы, обмениваются
работами, проверка по слайду).
Слайд 7
Правильно выполнившие всю работу образуют группу конструкторов, остальные – авиокосмические инженеры.
Группе конструкторов предлагается по готовому чертежу ракеты определить координаты основных узлов и записать их для группы инженеров.
В это время у группы инженеров проверяется знание техники безопасности и проверяется предполетная готовность по слайду.
Слайд 8
Отвечают на вопросы
1.Что такое координатная плоскость?
2. Чье имя носит данная система координат?
3. Как называется ось ОХ?
4. Как называется ось ОУ?
5. Какова нумерация координатных четвертей?
6. В каких четвертях лежат точки у которых: (х>0; y>0), (х>0; y<0), (х<0; y>0), (х<0; y<0)?
7. Какие координаты имеет точка пересечения осей координат?
8. Где лежат точки с координатами (0;у)?
9. Где лежат точки с координатами (х;0)?
После
ответов на вопросы группа авиокосмических
инженеров под наблюдением конструкторов
на интерактивной доске строят космическую
ракету (Чертеж готовой ракеты находится
на слайде 10 за «шторкой» на интерактивной
доске.
По нему проводят окончательную
проверку и докладывают учителю о
готовности к полету).
Итак, мои маленькие космонавты, мы отправляемся в космическое путешествие на планету Маленького принца! Пока мы совершаем перелет, я хочу рассказать вам об этой планете.
«На планете Маленького принца есть ужасные, зловредные семена… это семена баобабов. Почва планеты вся заражена ими. А если баобаб не распознать вовремя, потом от него уже не избавишься. Он завладеет всей планетой. Он пронижет ее насквозь своими корнями. И если планета очень маленькая, а баобабов много, они разорвут ее на клочки. У Маленького принца есть твердое правило:
— Встал поутру, умылся, привел себя в порядок — и сразу же приведи в порядок свою планету. Непременно надо каждый день выпалывать баобабы. Это очень скучная работа, но совсем не трудная.»
И еще на его планете растет капризная роза, которую он поливает, прячет от лучей солнца, выпалывает сорняки. Может вам покажется, что это самая обычная роза, но не спешите, остановитесь и задумайтесь!
«У
людей уже не хватает времени что-либо
узнавать.
Они покупают вещи
готовыми в магазинах. Но ведь нет таких магазинов, где торговали бы
друзьями, и потому люди больше не имеют друзей. Если хочешь, чтобы у
тебя был друг, приручи его!
Вот секрет Маленького принца, он очень прост: зорко одно лишь сердце. Самого главного глазами не увидишь.
Люди забыли эту истину, но ты не забывай: ты навсегда в ответе за всех, кого приручил»
В добрый путь друзья, к новым планетам, к новым открытиям!
Звучит песня Маленький принц и показываются слайды 12,13.
Итог урока: выставляются оценки, даются рекомендации прочесть всю сказку «Маленький принц»
Источники информации.
Антуаном де Сент Экзюпери «Маленький принц».
http://images.search.conduit.com – картинки звездного неба и Маленького принца.
В банке монет есть 37 долларов, состоящих из четвертаков и десяти центов. Десятицентов в 10 раз больше, чем в 2 раза больше четвертаков.
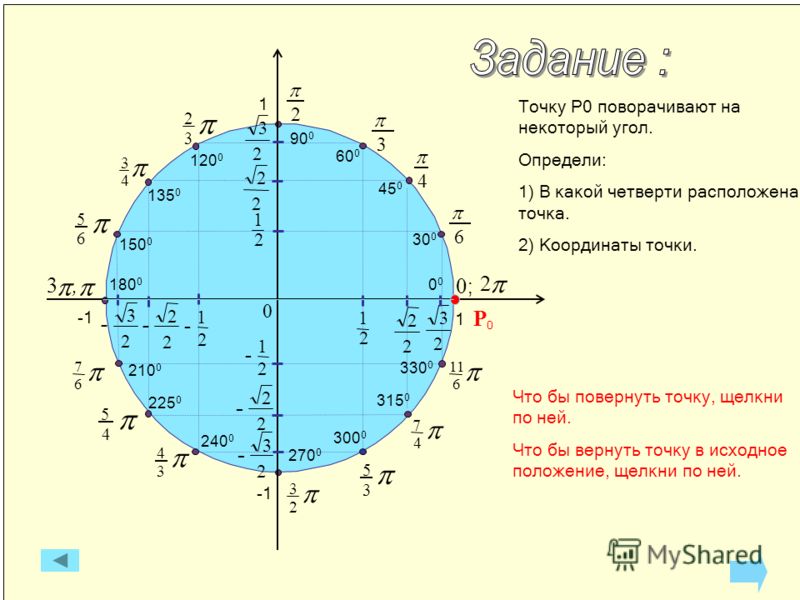сколько четвертаков и десятицентовиков РЕШЕНИЕ: В банке монет есть 37 долларов, состоящих из четвертаков и десятицентовиков. Десятицентов в 10 раз больше, чем в 2 раза больше четвертаков. сколько четвертаков и десятицентовиковАлгебра -> Системы координат и линейные уравнения -> РЕШЕНИЕ: В банке монет есть 37 долларов, состоящих из четвертаков и десяти центов. Десятицентов в 10 раз больше, чем в 2 раза больше четвертаков. сколько четвертаков и десятицентовиков Войти
|
Десятицентов в 10 раз больше, чем в 2 раза больше четвертаков. сколько четвертаков и десятицентовиков 
com. Ищите «Базовая, промежуточная и студенческая алгебра: шаг за шагом». Выберите «Основы алгебры» и найдите соответствующую тему в «Главе 1». Это удобное объяснение с интегрированными в него примерами и упражнениями. ВСЕ мои ученики говорят мне, что это легче понять, чем традиционные учебники! См. также мои страницы «МАТЕТИКА В ЖИВОМ ЦВЕТЕ», где многие из этих упражнений решены в «Живом цвете».
92 Резюме: Точки и линии на координатной плоскости
Резюме: Точки и линии на координатной плоскости
Ключевые понятия
- оси x- и смещения от у- ось.
- Уравнение можно изобразить на плоскости, создав таблицу значений и точек графика.
- Использование графического калькулятора или компьютерной программы делает графические уравнения более быстрыми и точными.
