Ньютона треугольник: Бином Ньютона и треугольник Паскаля

Бином Ньютона. Треугольник Паскаля — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Контрольные вопросы
1.
2.
3.
4.
5.
6.
7.
8.
Что в теории многочленов называют биномами?
Запишите биноминальную формулу Ньютона.
Для чего предназначен треугольник Паскаля?
Что представляет собой треугольник Паскаля? Опишите
схему его составления.
Перечислите основные свойства бинома Ньютона.

Рассмотрите и запишите решения примеров 1,2, 3.
Запишите формулу для вычисления общего члена
бинома Ньютона.
Рассмотрите и запишите решение примера 4.
НЬЮТОН — английский
математик, механик, астроном и
физик, создатель классической
механики. Разработал
дифференциальное и
интегральное исчисления.
Открыл дисперсию света,
исследовал интерференцию и
дифракцию, развивал
корпускулярную теорию света.
Построил зеркальный телескоп.
Сформулировал основные
законы классической механики.
Открыл закон всемирного
тяготения, создал теорию
движения небесных тел, создав
основы небесной механики.
1643-1727 г.г.

4. В теории многочленов двучлены часто называют биномами

5. Биномиальная формула Ньютона

1 n 1
n
2 n 2 2
n
(a b) a C a b C a b …
n
k n k k
n
n
C a b … b
n
Биномиальные коэффициенты легко находить с помощью треугольника
Паскаля.
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая
треугольную форму. Биноминальные коэффициенты можно вычислить, применяя только
сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы.
Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа
в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта
схема называется треугольником Паскаля:
1
1
1
1
1
1
1
1
7
2
3
4
5
6
1
3
6
10
15
21
1
4
10
20
35
1
1
5
15
35
1
6
21
1
7
1
1623-1662 г.г.
ПАСКАЛЬ–
французский
математик, физик,
религиозный философ
и писатель. Работы по
арифметике, теории
чисел, алгебре,
геометрии, теории
вероятностей. В 1641г.
сконструировал
суммирующую машину.
n
k
0
0
3
4
5
6
7
8
9
10
2
3
4
5
6
7
8
9
10
1
1
2
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
1
8
28
56
70
56
28
8
1
1
9
36
84
126 126 84
36
9
1
10
45
120 210 252 210 120 45
1
10
1
1. Число слагаемых на 1 больше степени бинома.
2. Коэффициенты находятся по треугольнику Паскаля.
3.Коэффициенты симметричны.
4.Если в скобке знак минус, то знаки + и – чередуются.
Все четные члены разложения имеют знак «минус»
5.Сумма степеней каждого слагаемого равна степени
бинома.
Данные свойства часто используют для проверки
результата разложения бинома.
Пример 1. Представить в виде многочлена
Согласно треугольнику Паскаля, в случае четвертой
степени биноминальные коэффициенты многочлена будут
равны 1, 4, 6, 4, 1.
И, действительно
Пример 2. Найдите коэффициент бинома Ньютона для
шестого члена разложения выражения
.
В нашем примере n=10, k=6-1=5. Таким образом, мы
можем вычислить требуемый биномиальный
коэффициент:

12. Воспользуемся свойством 4 бинома Ньютона

3
Пример 3. Вычислить: 1 a 3 b 1 a 3 3 1 a 2 3 b 3 1 a 3 b
4
8
4
4
2 4
2
Воспользуемся свойством 4 бинома Ньютона
3
2
3
1 2 3
1 3 3 1 3 1 2
1 2 27 3
1 3 1 3
a
b
a
3
a
b
3
a
b
b
a
a
b
ab b
4
4
2 4 4 8
16
32
64
2 4 8

13.

Формула общего члена бинома Ньютона Т n 1 C a
n
m
m n
b
n
6
(
a
2
b
)
Пример 4. Найдите пятый член разложения
Воспользуемся формулой:
Т n 1 C a
n
m
Получаем:
Т 4 1 C64 a 6 4b 4
m n
b
n
6! 2 4 5 6 2 Т4 15a 2b 4
a b5
Т5
a bТ 5
2
4!2!

English     Русский Правила

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Справочник по математике

Алгебра

Формулы сокращенного умножения

Формула бинома Ньютона

Связь бинома Ньютона с треугольником Паскаля

Свойства биномиальных коэффициентов

Формула бинома Ньютона

      В Таблице 1 из раздела «Формулы сокращенного умножения» приведены формулы для натуральных степеней бинома

(x + y)ⁿ

в случаях, когда   n = 1, 2, 3, 4, 5, 6.

      В настоящем разделе рассматривается общий случай этой формулы, т.е. случай произвольного натурального значения  n .

      Материал настоящего раздела близко связан с материалом разделов «Формулы сокращенного умножения: степень суммы и степень разности», «Треугольник Паскаля» и «Комбинаторика: размещения и сочетания».

      Утверждение. Для любого натурального числа   n   и любых чисел  x  и  y  справедлива формула бинома Ньютона:

где

(2)

– числа сочетаний из  n  элементов по  k  элементов.

      В формуле (1) слагаемые

называют членами разложения бинома Ньютона, а числа сочетаний  – коэффициентами разложения или биномиальными коэффициентами.

      Если в формуле (1) заменить   y   на   – y ,   то мы получим формулу для   n — ой степени разности:

Связь бинома Ньютона с треугольником Паскаля

      Напомним, что треугольник Паскаля имеет следующий вид:

№	Треугольник Паскаля
0	1
1	1     1
2	1     2     1
3	1     3     3     1
4	1     4     6     4     1
5	1     5     10     10     5     1
6	1     6     15     20     15     6     1
…	…

      Поскольку числа, составляющие треугольник Паскаля, являются биномиальными коэффициентами, то треугольник Паскаля можно переписать в другом виде:

№	Треугольник Паскаля
0
1
2
3
4
5
6
…	…

Треугольник Паскаля

…

Треугольник Паскаля

…

Свойства биномиальных коэффициентов

      Для биномиальных коэффициентов справедливы равенства:

к доказательству которых мы сейчас и переходим.

      Докажем сначала равенство 1.

      Это равенство отражает основное свойство треугольника Паскаля, заключающееся в том, что в каждой из строк треугольника Паскаля, начиная со строки с номером   2 ,   между числами   1   стоят числа, каждое из которых равно сумме двух чисел, стоящих над ним в предыдущей строке.

      Для доказательства равенства 1 воспользуемся формулой (2):

что и требовалось.

      Для доказательства равенства 2 положим в формуле бинома Ньютона (1)    x = 1,   y = 1.

      Если же в формуле бинома Ньютона (1) взять   x = 1,   y = –1, то получится равенство 3.

      Перейдем к доказательству равенства 4. С этой целью положим в формуле бинома Ньютона (1)    y = 1

(3)

      Воспользовавшись очевидным равенством

перепишем формулу (3) в другом виде

(4)

      Если теперь перемножить формулы (3) и (4), то мы получим равенство:

(5)

      Если к левой части формулы (5) применить формулу бинома Ньютона, а затем, раскрыв в правой части скобки и приведя подобные члены, приравнять коэффициенты при   xⁿ в левой и в правой частях, то мы получим следующее равенство:

что и требовалось.

Time Speed ​​and Distance: Formula & Triangle

Вы заметили, как на автомобильных выставках всегда говорят о времени, которое требуется автомобилю, чтобы разогнаться с нуля до 60 миль в час? Они также говорят о так называемой максимальной скорости. Итак, что это значит, когда автомобиль движется со скоростью 100 миль в час? Можем ли мы связать этот термин с расстоянием, которое он может преодолеть за определенное время? Ну, краткий ответ — да. В следующей статье мы рассмотрим определения скорости, расстояния, времени и отношения между ними. Мы также рассмотрим, как мы можем использовать треугольник для представления отношений между тремя. Наконец, мы будем использовать несколько примеров для расчета скорости различных объектов.

Определение расстояния, скорости и времени

Прежде чем мы перейдем к взаимосвязи между расстоянием, скоростью и временем, нам нужно понять, что означает каждый из этих терминов в физике. Во-первых, мы смотрим на определение расстояния. Поскольку это одно из наиболее часто используемых слов в словаре, большинство людей должны знать, что означает расстояние.

Расстояние — это мера площади земли, покрытой объектом. Единицей расстояния в системе СИ является метр (м).

Расстояние — это скалярная величина . Когда мы говорим о расстоянии, пройденном объектом, мы не говорим о направлении, в котором движется объект. Величины, которые имеют как величину, так и направление, называются векторными величинами.

А время? Как физика может усложнить определение такой простой вещи, как время? Что ж, как бы просто это ни было, это было одной из самых интересных областей исследований для таких ученых, как Альберт Эйнштейн.

Время определяется как развитие события из прошлого в настоящее и будущее. Единицей времени в системе СИ является секунда (секунды).

Наконец, теперь, когда мы знаем определение расстояния и времени в контексте физики, мы можем посмотреть, как они используются для определения одной из самых важных величин в области физики, скорости.

Скоростью называется расстояние, пройденное объектом за заданный период времени.

Единица скорости в системе СИ в метрах/секундах (м/с). В имперской системе мы используем мили в час для измерения скорости. Например, когда мы говорим, что объект движется со скоростью 60 миль в час, мы имеем в виду, что этот объект преодолеет расстояние в 60 миль, если продолжит двигаться с этой скоростью в течение следующего часа. Точно так же мы можем определить скорость 1 м/с как скорость, с которой движется объект, когда он проходит 1 метр за 1 секунду.

Время, скорость и формула расстояния

Давайте посмотрим на взаимосвязь между расстоянием, временем и скоростью. Если объект движется с постоянной скоростью по прямой, то его скорость определяется следующим уравнением:

Скорость = пройденное расстояние и время

Эту простую формулу можно изменить двумя способами для расчета времени и расстояния. Это изображается с помощью треугольника скорости. Треугольник поможет вам запомнить три формулы, включая приведенное выше уравнение.

Time=DistanceSpeedDistance=Speed×Time

Или в символах:

s=vt

Где пройденное расстояние, скорость и время, затраченное на преодоление расстояния.

Расстояние, скорость и треугольник времени

Вышеупомянутые соотношения можно показать с помощью так называемого треугольника скорости, как показано ниже. Это простой способ запомнить формулу. Разделите треугольник на три части и поместите расстояние D вверху, скорость S в левом поле и время T в правом поле. Этот треугольник поможет нам запомнить различные формулы, которые можно вывести из треугольника.

Скорость, расстояние и временной треугольник можно использовать для расчета одной из этих трех переменных, StudySmarter

Время, скорость и этапы расчета расстояния

Давайте посмотрим, как мы можем использовать расстояние, скорость и временной треугольник, чтобы получить формулы для каждой из переменные.

Расчет скорости

Сэнди каждое воскресенье пробегает 5 км. Она проходит это за 40 минут. Вычислите ее скорость в м/с, если она может поддерживать одну и ту же скорость на протяжении всего бега.

Преобразование единиц измерения

5 км=5000 м,40 мин=60×40 с=2400 с

Треугольник скорости для расчета скорости, Nidhish-StudySmarter

Теперь возьмите треугольник скорости и закройте член, который вам нужно рассчитать. В данном случае это скорость. если вы закроете скорость, то формула будет выглядеть следующим образом:

Скорость = Пройденное расстояние и время Скорость = 5000 м 2400 с = 2,083 м/с

Расчет времени

Представьте, что Сэнди из приведенного выше примера пробежала 7 км, поддерживая скорость 2,083 м/с. За сколько часов она преодолеет это расстояние?

Треугольник скорости для расчета времени, StudySmarter

Перевод единиц измерения

7 км = 7000 м, скорость = 2,083 м/с

Накройте коробку со временем. Теперь у вас осталась формула зависимости расстояния от скорости:

Time=DistanceSpeed=7000m2.083m/s=3360.5s

Преобразование секунд в минуты

3360.5s=3360.5s60s/min=56min

Calc расстояние

Из приведенных выше примеров мы знаем, что Сэнди любит бегать. Какое расстояние она могла бы преодолеть, если бы бежала изо всех сил со скоростью 8 м/с за 25 с?

Треугольник скорости для расчета расстояния, Nidhish-StudySmarter

Используя треугольник скорости, закройте коробку, в которой указано расстояние. Теперь у нас осталось произведение скорости и времени.

Расстояние=Время×Скорость=25с×8м/с=200м

Сэнди сможет преодолеть расстояние 200мин25с! Как вы думаете, вы можете обогнать ее?

Время, скорость и расстояние — ключевые выводы

• Расстояние — это мера площади, пройденной объектом, когда он движется независимо от направления движения. Его единица СИ — 9 метров.0122
• Время определяется как развитие события из прошлого в настоящее и будущее. Его единицей СИ являются секунды
• Скорость относится к расстоянию, пройденному объектом в заданный период времени.
• Между временем, скоростью и пройденным расстоянием существуют следующие соотношения: Скорость=РасстояниеВремя,Время=РасстояниеСкорость,Расстояние=СкоростьxВремя
• Треугольник скорости может помочь вам запомнить три формулы.
• Разделите треугольник на три части и поставьте расстояние D вверху, скорость S в левом поле и время T в правом поле.
• Включите величину, которую вы хотите измерить, в треугольник скорости, и формула для ее расчета откроется сама собой.

Набросков Подсказка Леонардо да Винчи постиг гравитацию на столетие раньше Ньютона : ScienceAlert

Диаграммы, показывающие исследование Леонардо гравитации. (Gharib et al., Leonardo, 2022)

Исааку Ньютону приписывают первую формулировку теории гравитации во второй половине 17-го века, очевидно вдохновленную падением яблока с дерева, но фундаментальные аспекты гравитационного притяжения также были новое исследование объясняет Леонардо да Винчи более ста лет назад.

В ходе исследования были проанализированы диаграммы в уже оцифрованных записных книжках Леонардо, в том числе наброски треугольников, которые показывают взаимосвязь между естественным движением, направленным движением и выравниванием движения — признание того, что гравитация является своего рода ускорением.

В случае с Леонардо это включало в себя размышления о песке, высыпаемом из кувшина. Эрудит понял, что если кувшин тянуть по горизонтальной плоскости с той же скоростью, что и сила, тянущая песчинки вниз, песок образует гипотенузу треугольника. Это осознание изменения скорости падающего объекта с течением времени является решающим шагом на пути к нахождению гравитационной постоянной на Земле.

Треугольник, установленный Леонардо. (Gharib et al., Leonardo, 2022)

«Около 500 лет назад Леонардо да Винчи пытался раскрыть тайну гравитации и ее связь с ускорением с помощью серии остроумных экспериментов, руководствуясь только своим воображением и искусными экспериментальными методами», — пишут исследователи в своей опубликованной статье.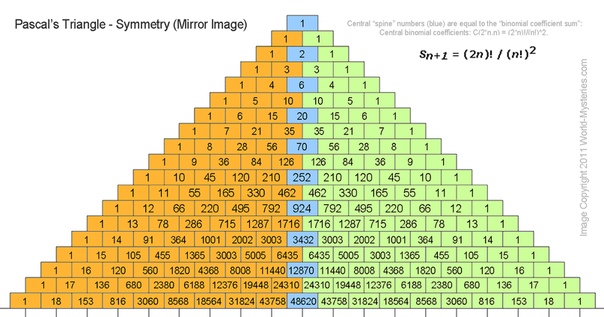

Эта гравитационная постоянная позже использовалась Ньютоном для определения его законов движения (включая гравитацию) и Альбертом Эйнштейном в его общей теории относительности. Леонардо знал, что он что-то нашел, но не был уверен, что именно.

Частично эта неуверенность была вызвана тем, что Леонардо разделял идею Аристотеля о непрерывной силе, известной как импетус, которая наполняет снаряды и дает им возможность двигаться против гравитации. Принцип инерции, когда объекты просто продолжают двигаться в одном направлении, пока не встретятся с противодействующей силой, еще не был установлен в науке того времени.

Проведение экспериментов Леонардо в современной лаборатории. (Калифорнийский технологический институт)

Гравитация, тем временем, объяснялась Аристотелем как склонность материалов располагаться в соответствии с естественным порядком. Другими словами, гравитация и летающие снаряды объяснялись двумя очень разными теориями.

Хотя в его расчетах были ошибки, воссоздание экспериментов Леонардо в лаборатории показало, что его алгоритм рассчитал неуловимую гравитационную постоянную («g») с точностью 97% по сравнению с современными методами и уравнениями.

«Разработав подход геометрической эквивалентности для демонстрации законов движения, Леонардо продемонстрировал замечательное понимание динамики падающих объектов, избегая необходимости знать точное значение «g», пока мы предполагаем, что «g» представляет собой скорость изменения скорости или ускорения», — пишут исследователи.

«Если бы он провел эксперимент, который описал в своей рукописи, то он мог бы быть первым человеком, который сознательно создал эффект перегрузки, не находясь в состоянии свободного падения.»

Особое впечатление на исследователей произвели методы Леонардо, использующие то, что было ему доступно в то время, в первую очередь геометрию, и применяя это для исследования чего-то неизвестного. То же самое новшество все еще может быть применено к науке сегодня.

Ньютон не сам придумал свой закон всемирного тяготения: Галилей признал связь между движением свободного падения и временем в 1604 году, в то время как сам Ньютон полагался на открытия Буллиальда и Борелли в своих теориях.