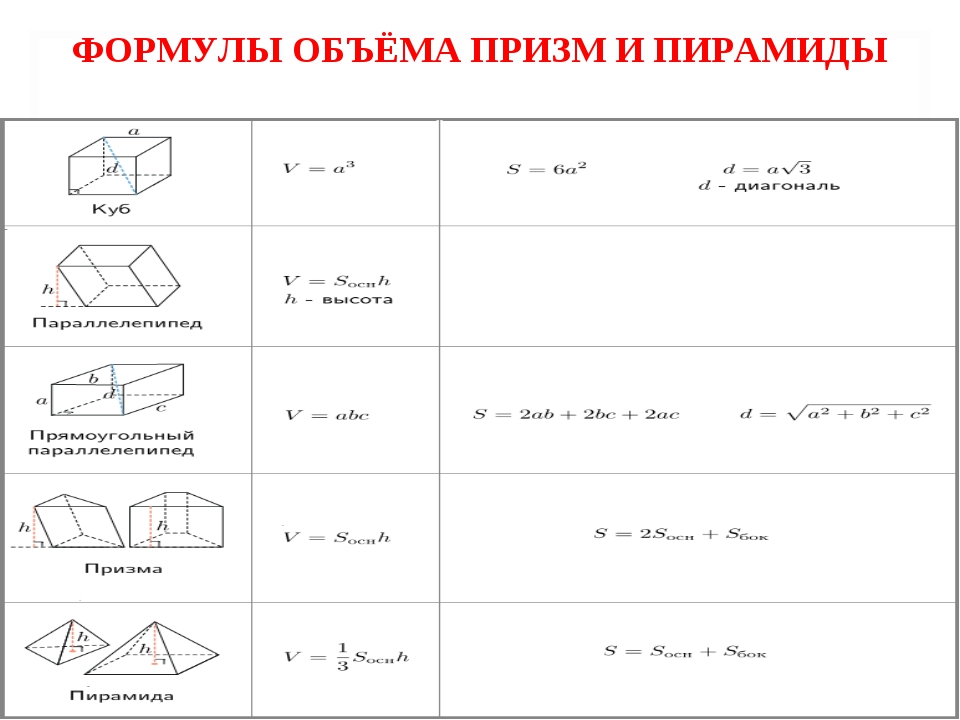
Формулы объема и площади поверхности многогранников: призма, пирамида, куб, параллелепипед
Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:
- Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
- Элементарная логика.
Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.
| Куб | диагональ | |
| Параллелепипед | высота | |
| Прямоугольный параллелепипед | | |
| Призма | ||
| Пирамида |
Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».
Вот, оказывается, откуда берётся выражение «возвести в куб».
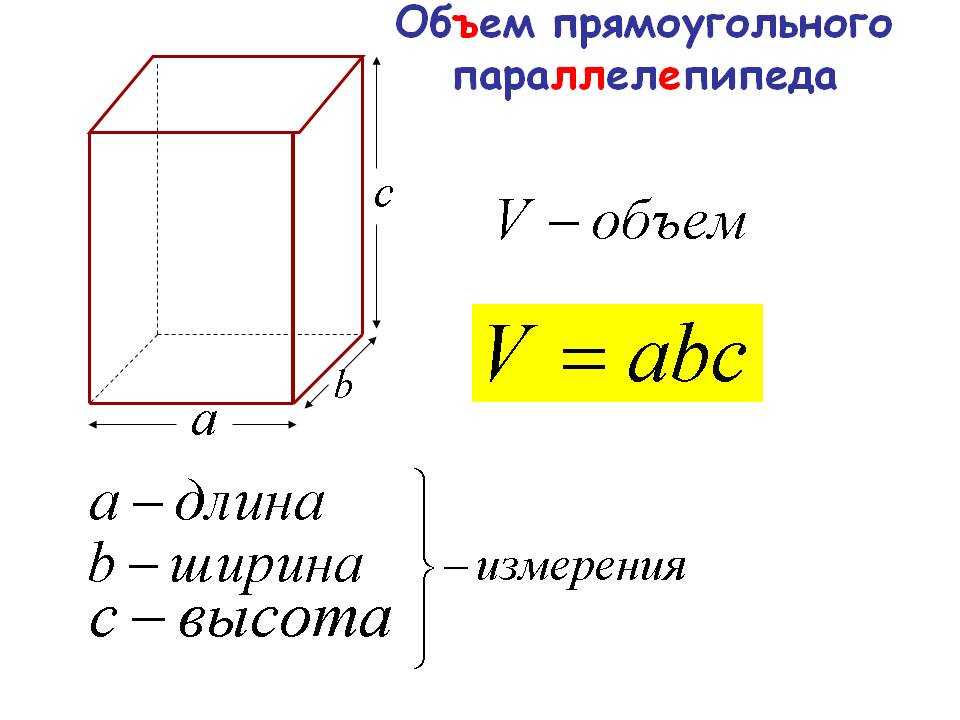
Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.
Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.
Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.
Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.
Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение:
Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 🙂
Очевидно, их 6, поскольку у куба 6 граней.
Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.
А дальше — читайте о приемах решения задач по стереометрии.
Разберем задачи, где требуется найти площадь поверхности многогранника.
Мы рассмотрим призмы и пирамиды. Начнем с призмы.
Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.
Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Многогранник на рисунке – это прямая призма с высотой 12.
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
(больший квадрат), (маленький прямоугольник),
Подставим все данные в формулу: и найдем площадь поверхности многогранника:
Ответ: 424.
Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение.
Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:
(большой прямоугольник), (маленький прямоугольник).
Найдем площадь полной поверхности:
Ответ: 54
Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Покажем еще один способ решения задачи.
Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.
И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:
Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело.
Ответ: 42
Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.
Решение.
Пусть АВ = 5 см, ВС = 3 см, тогда
Из по теореме косинусов найдем ребро АС:
Отрезок АС – большая сторона , следовательно, большая боковая грань призмы.
Поэтому или откуда
Ответ: 75
Теперь две задачи на площадь боковой поверхности пирамиды.
Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.
Решение.
Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.
Проведем , тогда (по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.
– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.
Из прямоугольного получим:
Из прямоугольного имеем:
(по двум катетам), тогда следовательно
Ответ: 192
Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.
Решение:
Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.
Площадь поверхности пирамиды равна
где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.
Значит, полупериметр основания .
Апофему найдем по теореме Пифагора:
Ответ: 2256
Как решать задачи на нахождение объема многогранника сложной формы?
Покажем два способа.
Первый способ
1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.
Второй способ.
1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.
Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
1) Достроим составной многогранник до параллелепипеда.
2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:
3) Найдем объем лишней части, то есть маленького параллелепипеда.
Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем
4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
Ответ: 220.
Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.
Объем призмы равен , а так как призма прямая, то ее боковое ребро является и высотой, то есть
Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания
Ответ: 126
Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.
Решение.
Объем призмы равен
Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.
Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.
Объем воды не изменился, Так как высота воды должна быть в 81 раз меньше, чем Она равна (см).
Ответ: 4
Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды
Решение.
Опустим из вершины высоту Н на основание
Диагональ основания делит его на два равных треугольника, следовательно,
Имеем:
Ответ: 3,5
Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна
Решение.
По формуле объема пирамиды, .
В основании пирамиды лежит правильный треугольник. Его площадь равна
Объем пирамиды
Ответ: 96
Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру.
Решение.
По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.
Пусть тогда
Так как точки М и К – середины АD и DС соответственно, то
Площадь треугольника MDK, лежащего в основании новой призмы, составляет часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен
Ответ: 4
Докажем полезную теорему.
Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство:
Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.
Больше задач на формулы объема и площади поверхности здесь.
Объемы тел. Основные формулы.
Объем пирамиды.
| Формула | Рисунок | Расшифровка формулы |
|
Sосн — площадь основания, h — высота. Основание может быть n-угольником, где n=3; 4; 5; … . |
||
|
h — высота усеченной пирамиды, Sниж — площадь нижнего основания, Sверх — площадь верхнего основания. Формула применима только для усеченной пирамиды. Другой способ нахождения объема: из объема полной пирамиды вычесть объем ее отсеченной части. |
Объем конуса.
| Формула | Рисунок | Расшифровка формулы |
| R — радиус основания, H — высота конуса | ||
|
R, r — радиусы оснований, Н — высота. Формула применима только для усеченного конуса. Другой способ нахождения объема: из объема полного конуса вычесть объем его отсеченной части. |
Объем цилиндра.
| Формула | Рисунок | Расшифровка формулы |
|
r — радиус, h — высота |
Объем сферы, шара.
| Формула | Рисунок | Расшифровка формулы |
| R — радиус |
Объем параллелепипеда и куба.
| Формула | Рисунок | Расшифровка формулы |
|
а, b — стороны основания, с — боковое ребро. Формула применяется для прямоугольного параллелепипеда. |
||
|
а, b — стороны основания, h — высота. Общая формула для нахождения объема параллелепипеда. |
||
| а — сторона куба. |
| ||||||||||||||||||
| ||||||||||||||||||
Оценка диапазона Mildot | ||||||||||||||||||
| ||||||||||||||||||
Оценка дальности — ключевой навык снайпера. В прошлые годы базовая сетка для плесневых грибов выпускалась в двух вариантах. Вы можете получить круглые точки или «футбольные мячи». В последнее время футбольные мячи исчезли. Их заменило множество линий, кружков и точек. Основная предпосылка, которую мы собираемся продемонстрировать здесь, будет работать для любой сетки с милрадианами.
| ||||||||||||||||||
| Мил Формула отношения | ||||||||||||||||||
В основе оценки дальности прицела винтовки лежит математическая задача, известная как «Формула отношения Миля». Это берет высоту цели в дюймах, умножает ее на константу, а затем делит на число мил, считанное в области. Базовая формула выглядит так: 27,77 является «константой».
| ||||||||||||||||||
| Измерение в милах | ||||||||||||||||||
Самая сложная часть оценки дальности по формуле отношения Миля – это фактическое измерение цели. Чтобы быть точным, вам нужно тренировать свой глаз, чтобы измерять с точностью до десятых, мил или 0,1 мил. Большинство опытных снайперов могут измерять до пяти сотых мил или 0,05. Все, что нужно, это практика. Первая фокальная плоскость против второй фокальной плоскости: Прицелы обычно бывают двух видов. First Focal Plane набирают популярность в США. Их преимущество заключается в том, что прицельная сетка считывается правильно при любой настройке мощности. Когда вы смотрите в прицел на цель и поворачиваете кольцо селектора мощности, прицельная сетка будет увеличиваться или уменьшаться с той же скоростью, что и цель. Недостатком этого является то, что толщина сетки становится компромиссом. Слишком толстая сетка скроет слишком большую часть цели при большом увеличении. Проверка шкалы сетки: Прежде чем использовать сетку Mil, прежде всего убедитесь, что шкала показывает правильно и при каком увеличении. Это довольно простое упражнение. Сначала найдите большой кусок картона. Нарисуйте на нем вертикальную линию жирным черным маркером. С помощью очень точной линейки нанесите горизонтальные штрихи через вертикальную линию через каждые 3,6 дюйма. Будьте осторожны при измерении. Установите картон на расстоянии 100 ярдов и выровняйте центр сетки по самой нижней штриховой отметке на картоне. Каждый мил в вашем прицеле должны совпадать с каждой решеткой на картоне.Если вы используете прицел типа мидот, то решетка должна делить точки пополам.Если вы используете сетку линейного типа, такую как сетка GAP, то решетка должна совпадать с полными решетками mil в сетке. Что делать, если не совпадает? Если ваш прицел является прицелом второй фокальной плоскости, поэкспериментируйте с различными настройками мощности, пока не найдете тот, который подходит. Когда вы это сделаете, возьмите серебряный маркер и сделайте отметку на кольце и корпусе прицела, чтобы вы могли быстро найти правильную настройку в поле. Если у вас прицел первой фокальной плоскости и вы уверены, что правильно измерили при укладке вашей платы, то вам необходимо обратиться к производителю для гарантийного обслуживания. Фрезерование мишени. Надеюсь, к вашему прицелу прилагалась литература, показывающая масштаб различных частей вашей сетки. В любой сетке, основанной на милах, расстояние от центра до центра наиболее заметных меток должно составлять один мил. Все остальные измерения доступны для захвата. Вот пара обычных прицелов: | ||||||||||||||||||
В большинстве наших примеров мы будем использовать Mildots типа «Армия». Чтобы поразить цель с точностью до десятой доли миля, нам нужно занять устойчивую позицию, как если бы мы собирались выстрелить вниз. Любой тремор вызовет проблемы. Поместите сетку над мишенью и сосчитайте, сколько полных мил приращений. | ||||||||||||||||||
| На изображении выше мы видим, что рост бойца Талибана составляет 4 мила. Поскольку наш S2 проинформировал нас, что эта выбранная цель составляет 5 футов 8 дюймов (68 дюймов), мы можем подставить эти цифры в нашу формулу. | ||||||||||||||||||
Высота 68 дюймов, умноженная на 27,77 (наша постоянная), деленная на число мил, измеренное в прицеле (4). Теперь давайте немного усложним задачу.
| ||||||||||||||||||
На этом изображении мы видим, что наши невинные маленькие друзья гуляют. Наш погрузчик больше двух с половиной милов в высоту, но этого недостаточно.
| ||||||||||||||||||
Если мы внимательно посмотрим, где его нога падает выше третьей точки мельницы, мы можем начать ломать ее. Своим мысленным взором разделите эту милоту пополам. Эта половина милдо имеет размер 0,1 мил. Теперь вы не можете втиснуть эту половинку милдо между его ногой и верхом целой милоты, так что мы снова разбираем ее. Это дает нам 0,05 мил. Теперь добавьте это к «половине» мидота, и мы получим 0,15 мил между центром точки и основанием стопы нашего джихадиста. Если из 1 вычесть 0,15 мил, получится 0,85 мил.
| ||||||||||||||||||
Если бы мы не утруждали себя его разбивкой и округляли до 3 мил, мы бы получили 592,42 ярда до цели. В данном случае это привело бы к ошибке возвышения около 12 дюймов с M118LR. Уменьшение точки до 0,05 даст вам повышенную точность, но не требуется для целей с более близкого расстояния. Когда цель не будет стоять на месте, или вы не знаете высоту вашей цели, вы можете использовать предметы поблизости. В городе это довольно просто. В лесу немного сложнее. Если у вас есть несколько объектов в поле зрения, сначала выберите самый крупный. Большие цели, как правило, дадут вам большую точность. Ранжирование нескольких целей и получение среднего значения также уменьшит вашу ошибку. Через некоторое время вы можете заметить закономерности в своих ошибках. Если вы работаете со наблюдателем, вы оба должны сделать расчеты независимо друг от друга, а затем взять среднее значение. Милдот — дальнобойность — отличный навык, но точность зависит от вас. Кроме того, он медленный и его трудно использовать на движущихся объектах. В этом превосходит лазерный дальномер. Однако аккумуляторы умирают, а электроника выходит из строя. Хорошо иметь навыки резервного копирования.
| ||||||||||||||||||
| Дополнительные формулы | ||||||||||||||||||
| ||||||||||||||||||
| Обычные предметы | ||||||||||||||||||
Все размеры являются приблизительными и должны быть проверены пользователем.
| ||||||||||||||||||
| Другие сетки | ||||||||||||||||||
| ||||||||||||||||||
Вернуться к статьям | ||||||||||||||||||
Использование диспетчера имен в Excel
Используйте диалоговое окно Name Manager для работы со всеми определенными именами и именами таблиц в книге. Например, вам может понадобиться найти имена с ошибками, подтвердить значение и ссылку на имя, просмотреть или отредактировать описательные комментарии или определить область действия. Вы также можете сортировать и фильтровать список имен, а также легко добавлять, изменять или удалять имена из одного места.
Чтобы открыть диалоговое окно Диспетчер имен , на вкладке Формулы в группе Определенные имена щелкните Диспетчер имен .
В диалоговом окне Name Manager отображается следующая информация о каждом имени в списке:
Имя столбца | Описание |
|---|---|
Имя | Один из следующих:
|
Значение | Текущее значение имени, например результат формулы, строковая константа, диапазон ячеек, ошибка, массив значений или заполнитель, если формулу невозможно вычислить. Ниже приведены репрезентативные примеры:
3.1459 |
Относится к | Текущая ссылка на имя. Ниже приведены репрезентативные примеры: |
Объем |
Имя рабочего листа, если областью действия является локальный уровень рабочего листа. |
Комментарий | Дополнительная информация об имени до 255 символов. Ниже приведены типичные примеры:
На основе номеров сертификационных экзаменов ISO. |
Относится к: | Ссылка для выбранного имени. Вы можете быстро изменить диапазон имени, изменив данные в поле Относится к . После внесения изменений вы можете нажать Подтвердить , чтобы сохранить изменения, или нажать Отменить , чтобы отменить изменения. |
Примечания:
Вы не можете использовать диалоговое окно Диспетчер имен при изменении содержимого ячейки.
В диалоговом окне Name Manager не отображаются имена, определенные в Visual Basic для приложений (VBA), или скрытые имена (для свойства Visible имени установлено значение False).

На вкладке Формулы в группе Определенные имена щелкните Определить имя .
В диалоговом окне New Name в поле Name введите имя, которое вы хотите использовать для справки.
Примечание. Имена могут содержать до 255 символов.
Область действия автоматически устанавливается по умолчанию на Workbook . Чтобы изменить область действия имени, в раскрывающемся списке Scope выберите имя рабочего листа.
org/ListItem»>В поле Относится к выполните одно из следующих действий:
Щелкните Свернуть диалоговое окно (что временно свернет диалоговое окно), выберите ячейки на листе и нажмите Развернуть диалоговое окно .
Чтобы ввести константу, введите = (знак равенства), а затем введите значение константы.
Чтобы ввести формулу, введите = и введите формулу.

Советы:
Будьте осторожны при использовании абсолютных или относительных ссылок в формуле. Если вы создадите ссылку, щелкнув ячейку, на которую хотите сослаться, Excel создаст абсолютную ссылку, например «Лист1!$B$1». Если вы вводите ссылку, например «B1», это относительная ссылка. Если при определении имени вашей активной ячейкой является A1, то ссылка на «B1» действительно означает «ячейка в следующем столбце». Если вы используете определенное имя в формуле в ячейке, ссылка будет на ячейку в следующем столбце относительно того места, где вы вводите формулу. Например, если вы введете формулу в C10, ссылка будет D10, а не B1.
Дополнительная информация – Переключение между относительными, абсолютными и смешанными ссылками
org/ListItem»>
При необходимости в поле Комментарий введите описательный комментарий длиной до 255 символов.
Чтобы закончить и вернуться к рабочему листу, нажмите OK .
Примечание: Чтобы сделать Новое имя Диалоговое окно шире или длиннее, щелкните и перетащите ручку захвата внизу.
Если изменить определенное имя или имя таблицы, все варианты использования этого имени в рабочей книге также будут изменены.
На вкладке Формулы в группе Определенные имена щелкните Диспетчер имен .
В диспетчере имен дважды щелкните имя, которое нужно изменить, или щелкните имя, которое нужно изменить, а затем щелкните Изменить .
org/ListItem»>В поле Относится к измените ссылку и нажмите OK .
В диалоговом окне Name Manager в поле Относится к измените ячейку, формулу или константу, представленную именем.
В диалоговом окне Edit Name в поле Name введите новое имя для ссылки.
На вкладке Формулы в группе Определенные имена щелкните Диспетчер имен .
org/ListItem»>Выберите одно или несколько имен, выполнив одно из следующих действий:
Чтобы выбрать имя, щелкните его.
Чтобы выбрать более одного имени в непрерывной группе, щелкните и перетащите имена или нажмите SHIFT и щелкните кнопкой мыши для каждого имени в группе.
Чтобы выбрать более одного имени в несмежной группе, нажмите клавишу CTRL и щелкните кнопкой мыши для каждого имени в группе.

Нажмите Удалить .
Нажмите OK , чтобы подтвердить удаление.
В диалоговом окне Name Manager щелкните имя, которое хотите изменить.
Используйте команды из раскрывающегося списка Фильтр для быстрого отображения подмножества имен. Выбор каждой команды включает или выключает операцию фильтрации, что позволяет легко комбинировать или удалять различные операции фильтрации для получения желаемых результатов.
Можно фильтровать по следующим параметрам:
Выберите | — |
|---|---|
Имена, включенные в рабочий лист | Отображать только те имена, которые являются локальными для рабочего листа. |
Имена, включенные в рабочую книгу | Отображать только те имена, которые являются глобальными для книги. |
Имена с ошибками | Отображать только те имена, значения которых содержат ошибки (например, #ССЫЛКА, #ЗНАЧ или #ИМЯ). |
Имена без ошибок | Отображать только те имена, значения которых не содержат ошибок. |
Определенные имена | Отображать только имена, определенные вами или программой Excel, например область печати. |


 Если вы не знаете, как далеко находится ваша цель, у вас мало шансов поразить ее с первого выстрела. Один выстрел, одно убийство… верно? Существует много методов определения диапазона цели. В рамках этого периода обучения мы рассмотрим оценку дальности с помощью сетки мильдо и ее вариантов.
Если вы не знаете, как далеко находится ваша цель, у вас мало шансов поразить ее с первого выстрела. Один выстрел, одно убийство… верно? Существует много методов определения диапазона цели. В рамках этого периода обучения мы рассмотрим оценку дальности с помощью сетки мильдо и ее вариантов. Иногда это выражается в 27,78, что является математически правильным округленным числом. Большинство морских пехотинцев будут использовать калибр 27,77, потому что нас так учили. Любой из них подведет вас достаточно близко, чтобы нанести удар в первом раунде. Доступны и другие формулы для преобразования диапазона в метры или для начала с высоты цели в другой единице измерения. Я предпочитаю эту формулу, потому что ее легко запомнить и в ней используются единицы, знакомые большинству из нас в Соединенных Штатах.
Иногда это выражается в 27,78, что является математически правильным округленным числом. Большинство морских пехотинцев будут использовать калибр 27,77, потому что нас так учили. Любой из них подведет вас достаточно близко, чтобы нанести удар в первом раунде. Доступны и другие формулы для преобразования диапазона в метры или для начала с высоты цели в другой единице измерения. Я предпочитаю эту формулу, потому что ее легко запомнить и в ней используются единицы, знакомые большинству из нас в Соединенных Штатах. Наиболее распространена сетка во второй фокальной плоскости. В этом типе сетка покрывает большую или меньшую часть цели в зависимости от настройки увеличения прицела. Если вы смотрите на цель через оптический прицел и поворачиваете кольцо селектора мощности, прицельная сетка остается того же размера по мере увеличения масштаба цели. Это вызывает пару проблем. Во-первых, сетка будет точной только для дальности при одной настройке мощности. Во-вторых, прицельная сетка будет корректной только для удержания при одной настройке мощности.
Наиболее распространена сетка во второй фокальной плоскости. В этом типе сетка покрывает большую или меньшую часть цели в зависимости от настройки увеличения прицела. Если вы смотрите на цель через оптический прицел и поворачиваете кольцо селектора мощности, прицельная сетка остается того же размера по мере увеличения масштаба цели. Это вызывает пару проблем. Во-первых, сетка будет точной только для дальности при одной настройке мощности. Во-вторых, прицельная сетка будет корректной только для удержания при одной настройке мощности. Слишком тонкий и он станет незаметным при малой мощности. Сетку также легко потерять на заднем плане при малой мощности при слабом освещении, если она не освещена.
Слишком тонкий и он станет незаметным при малой мощности. Сетку также легко потерять на заднем плане при малой мощности при слабом освещении, если она не освещена.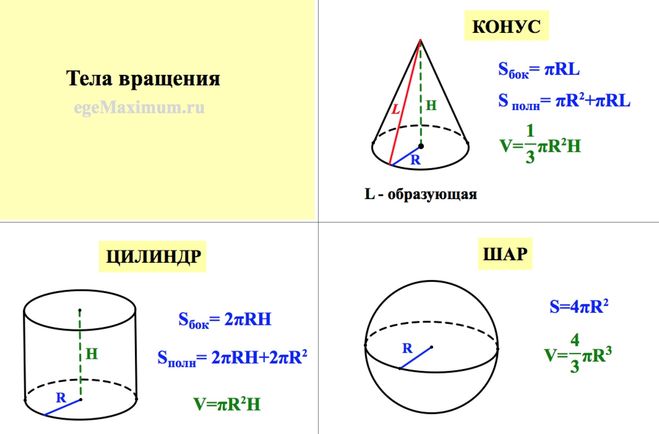
 Они наиболее распространены и встречаются в прицелах Leupold, а также во многих других марках прицелов. Мне неизвестно о каких-либо новых прицелах, использующих USMC Mildot. Я включаю их сюда на тот случай, если кто-нибудь наткнется на старый прицел морской пехоты США.
Они наиболее распространены и встречаются в прицелах Leupold, а также во многих других марках прицелов. Мне неизвестно о каких-либо новых прицелах, использующих USMC Mildot. Я включаю их сюда на тот случай, если кто-нибудь наткнется на старый прицел морской пехоты США. Прокрутите это через свой калькулятор, и вы увидите, что наша цель находится в 472 ярдах.
Прокрутите это через свой калькулятор, и вы увидите, что наша цель находится в 472 ярдах. Добавьте обратно два мила выше этого, и мы получим измеренную высоту 2,85 мила. Давайте предположим, что наш боевик имеет рост 64 дюйма (согласно нашим разведданным). Подставим это в нашу формулу.0013
Добавьте обратно два мила выше этого, и мы получим измеренную высоту 2,85 мила. Давайте предположим, что наш боевик имеет рост 64 дюйма (согласно нашим разведданным). Подставим это в нашу формулу.0013 Это хорошо отметить, чтобы в будущем вы могли принять их во внимание. Лазерный дальномер — отличный инструмент для подтверждения ваших расчетов, когда вы учитесь читать милы.
Это хорошо отметить, чтобы в будущем вы могли принять их во внимание. Лазерный дальномер — отличный инструмент для подтверждения ваших расчетов, когда вы учитесь читать милы. Когда это возможно, вам действительно стоит выйти в те места, где вы работаете, и измерить обычные предметы. Если вы часто оказываетесь в одних и тех же жилых проектах, измерьте некоторые окна и двери. Они могут пригодиться однажды ночью, если ваш LRF умрет.
Когда это возможно, вам действительно стоит выйти в те места, где вы работаете, и измерить обычные предметы. Если вы часто оказываетесь в одних и тех же жилых проектах, измерьте некоторые окна и двери. Они могут пригодиться однажды ночью, если ваш LRF умрет. Эта сетка используется в прицелах Falcon Menace FFP первого поколения. Сетка хорошо работает на максимальном увеличении. При уменьшении мощности сетку становится трудно увидеть при тусклом свете или на загроможденном фоне.
Эта сетка используется в прицелах Falcon Menace FFP первого поколения. Сетка хорошо работает на максимальном увеличении. При уменьшении мощности сетку становится трудно увидеть при тусклом свете или на загроможденном фоне. Имя таблицы — это имя таблицы Excel, представляющей собой набор данных о конкретном предмете, хранящихся в записях (строках) и полях (столбцах). Excel создает имя таблицы Excel по умолчанию Table1, Table2 и т. д. каждый раз, когда вы вставляете таблицу Excel. Вы можете изменить имя таблицы, чтобы сделать его более понятным. Дополнительные сведения о таблицах Excel см. в разделе Использование структурированных ссылок с таблицами Excel.
Имя таблицы — это имя таблицы Excel, представляющей собой набор данных о конкретном предмете, хранящихся в записях (строках) и полях (столбцах). Excel создает имя таблицы Excel по умолчанию Table1, Table2 и т. д. каждый раз, когда вы вставляете таблицу Excel. Вы можете изменить имя таблицы, чтобы сделать его более понятным. Дополнительные сведения о таблицах Excel см. в разделе Использование структурированных ссылок с таблицами Excel.