Объем сферы – Объем шара | Мозган калькулятор онлайн

Статьи по теме:

Инструкция

Используйте классическую формулу объема (V) сферы, если из условий известен ее радиус (r) — возведите радиус в третью степень, умножьте на число Пи, а результат увеличьте еще на треть. Записать эту формулу можно так: V=4*π*r³/3.

Если есть возможность измерить диаметр (d) сферы, то поделите его пополам и используйте как радиус в формуле из предыдущего шага. Или найдите одну шестую часть от возведенного в куб диаметра, умноженного на число Пи: V=π*d³/6.

Используйте принцип измерения, противоположный описанному в предыдущем шаге, если тело в форме сферы нельзя наполнить жидкостью, но можно погрузить в нее. Заполните мерный сосуд водой, отметьте уровень, погрузите измеряемое сферическое тело в жидкость и по разнице уровней определите количество вытесненной воды. Затем переведите полученный результат из литров в кубометры так же, как это описано в предыдущем шаге.

Видео по теме

Источники:

• объем полусферы

Совет полезен?

Статьи по теме:

Не получили ответ на свой вопрос?
Спросите нашего эксперта:

www.kakprosto.ru

Как рассчитать объем оболочки сферы, толщиной 60 мм?

Объем внутренней сферы: 4/3*Pi*r^3, объем внешней 4/3*Pi*R^3, разность между ними даст объем оболочки: 4/3*Pi*(R^3-r^3) = 4/3*Pi*(R-r)*(R^2+R*r + r^2) -> (R-r) = 60 mm -> 4/3*Pi*60*(R^2+R*r+r^2) = 80*Pi*(R^2+R*r+r^2) кубических миллиметров. Если R и r выражены в миллиметрах.

Формула объема шара: V1 = 4/3 * π * R3 — для наружной и V2 = 4/3 * π * r3 — для внутренней сфер. Искомый объем: V = V1 — V2 или V = 4/3 * π * R3 — 4/3 * π * r3 = 4/3 * π * (R3 — r3) Так что без знания радиусов внешней и внутренней сфер расчет невозможен.. . Если уж так надо, чтобы в формуле фигурировала толщина, обратимся к формуле разности кубов. Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат суммы. Отсюда: V = 4/3 * π * (R — r) * (R2 + R*r + r2) или V = 4/3 * π * 60 mm * (R2 + R*r + r2) Или V = 80 * π * (R2 + R*r + r2)

Формула Площади сферы такова: S = 4 П R^2. Умножаем полученную площадь на толщину. И вот объем остальные решения не рациональны.

как высчитать объем сферы? если его длина равна 180 см а высота 180 см, а внутреняя оболочка сферы имеет размеры 90 см длина и 90 см ширина. Где ставить точку отчета радиуса? от основной сферы ее или от внутренней оболочки сферы? мне нужно вычислить объем внешней сферы 180 см от внутренней 90 см, то есть пространство которое остается между ними. <img src=»//otvet.imgsmail.ru/download/67093210_0ee0d7fdd551d304599334fbed7eaad3_800.jpg» alt=»» data-lsrc=»//otvet.imgsmail.ru/download/67093210_0ee0d7fdd551d304599334fbed7eaad3_120x120.jpg» data-big=»1″>

touch.otvet.mail.ru

Объем и площадь n-мерной сферы

На основании размерности для объема n-мерной сферы радиусом r, для объема шарового слоя толщиной dr и для площади сферы получаем

,

,

.

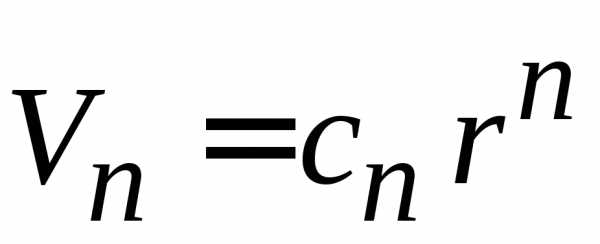Найдем постоянную 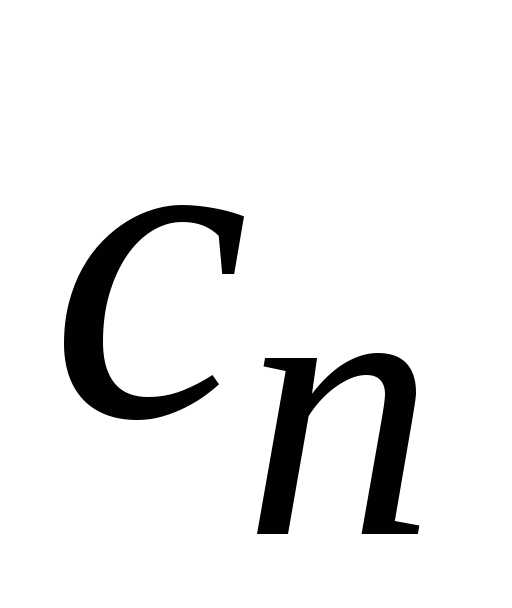, вычислив сходящийся интеграл

по всему пространству в декартовых и сферических координатах.

В декартовых координатах

,

,

тогда

,

где использован интеграл Пуассона (доказывается в курсе ММФ)

.

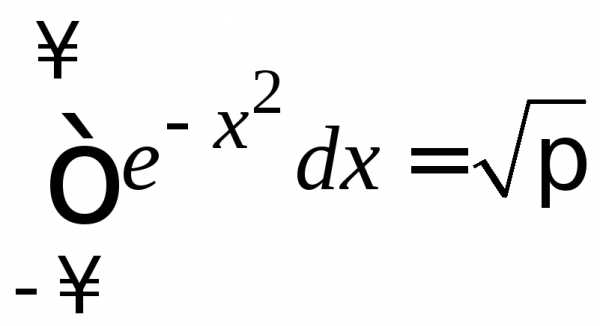В сферических координатах

,

тогда

,

где использовано

.

Гамма-функция вычисляется по формулам

Г(n + 1) = n!, ,

Г(z + 1) = z Г(z),

,

,

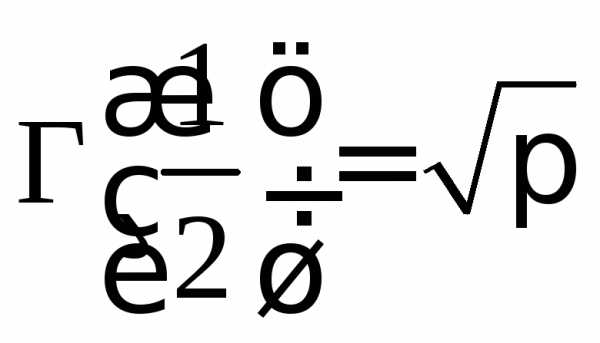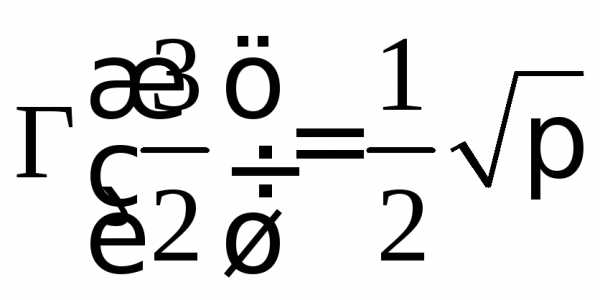
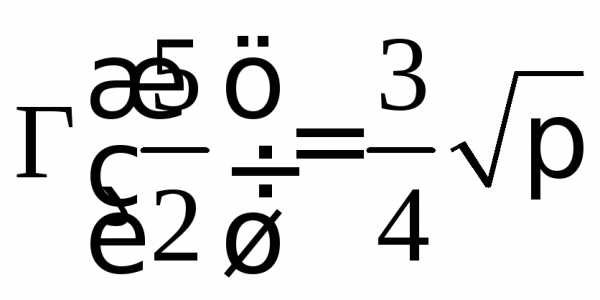при .

Сравниваем результаты в декартовых координатах

и в сферических координатах

,

находим

.

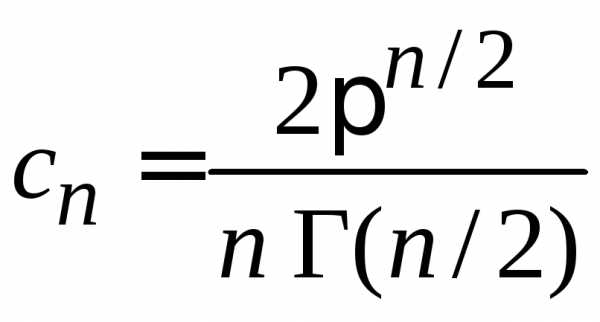В результате объем n-мерного шара, шарового слоя и площадь сферы

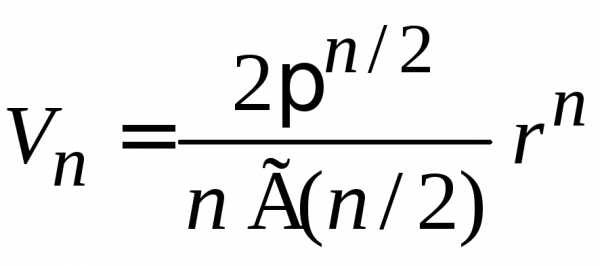, (П.2.1)

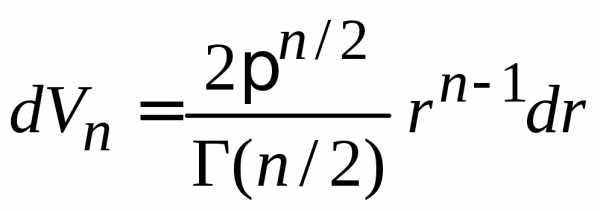. (П.2.2)

. (П.2.3)

В частности при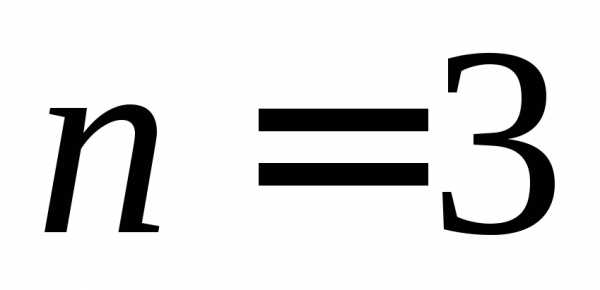

, ,.

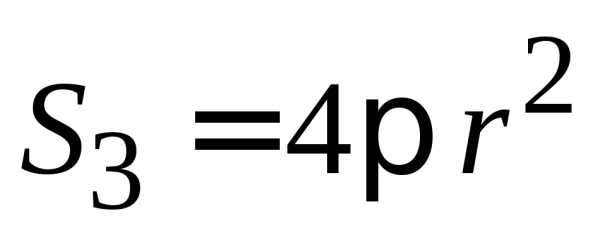Эллипсоид с полуосями удовлетворяет уравнению

.

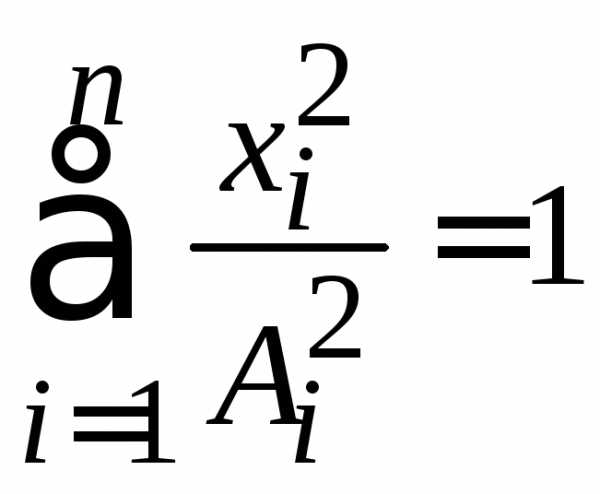Сравниваем с уравнением сферы

,

обобщаем (П.2.1)

,

находим объем n-мерного эллипсоида

. (П.2.1а)

Фазовая траектория

С течением времени система изменяет свое микросостояние за счет движения частиц, и точка X перемещается по фазовой траектории согласно уравнениям Гамильтона (2.1)

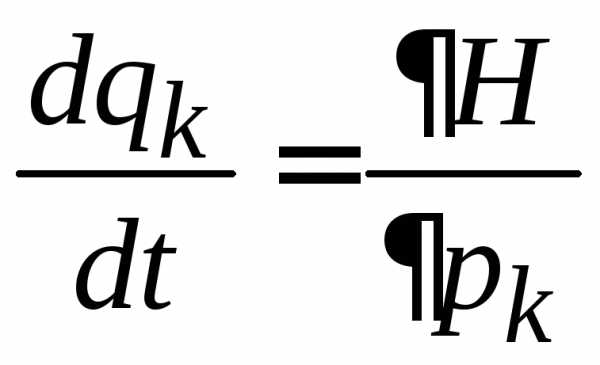
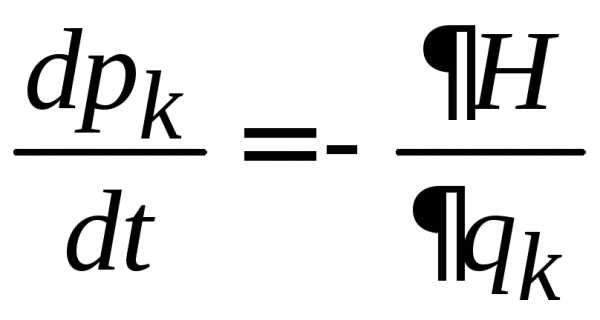Фазовый ансамбль

Макросостояние системы характеризуется макроскопическими и термодинамическими величинами, в частности: числом частиц N, температурой T, объемом V, давлением P, внутренней энергией U, свободной энергией F, энтропией S. Одному макросостоянию соответствует множество различных микросостояний, меняющих свое положение в фазовом пространстве с течением времени. Все они находятся в пределах некоторой области фазового пространства, границы которой зависят от макрохарактеристик. Фазовые траектории микросостояний не выходят за пределы указанной области. По истечении некоторого времени микросостояние возвращается в свое начальное положение со сколь угодно высокой точностью. Фазовый ансамбль есть множество микросостояний с одинаковыми макрохарактеристиками, эти состояния относятся к одному макросостоянию.

Точка X фазового пространства описывает микросостояние системы. В бесконечно малом безразмерном объеме

около точки X вероятность реализации микросостояния равна 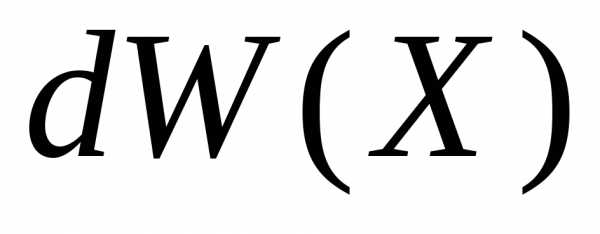. Вероятность реализации в единичном объеме около точкиX называется функцией распределения, или плотностью вероятности

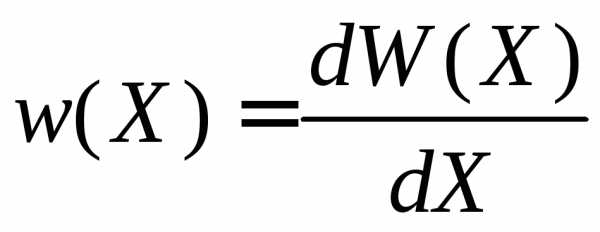. (2.3)

Вероятность нахождения системы в интервале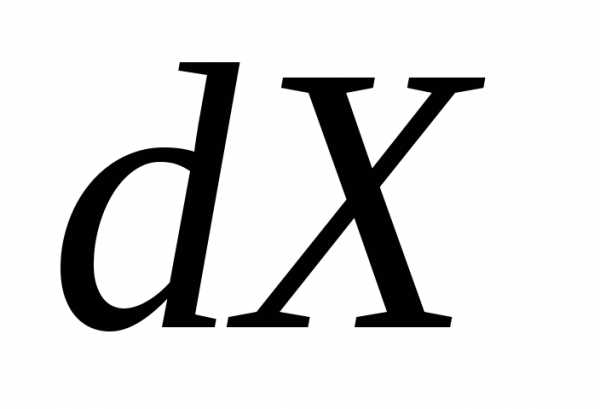

(2.3а)

удовлетворяет условию нормировки

, (2.4)

где интегрирование ведется по всему фазовому пространству.

Макроскопической характеристикой является среднее по фазовому ансамблю величины 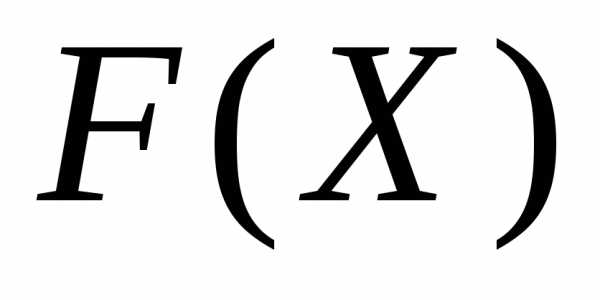, зависящей от микроскопических переменныхX

. (2.4а)

Задача статистической физики состоит в том, чтобы для фиксированного макросостояния системы найти функцию распределения микросостояний по фазовому пространству 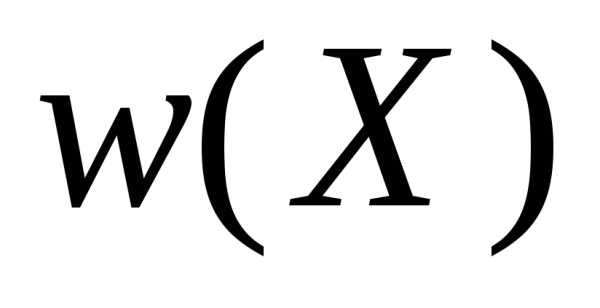и вычислить макрохарактеристики системы.

Эргодическая гипотеза утверждает, что среднее по фазовому ансамблю равно среднему по времени. Если приготовить множество одинаковых систем в одном и том же макроскопическом состоянии и найти среднее по их микросостояниям в один момент времени, то результат совпадает с усреднением по микросостояниям, которые принимает одна системы с течением времени. Следовательно, усреднение по фазовому ансамблю и по фазовой траектории дают одинаковый результат.

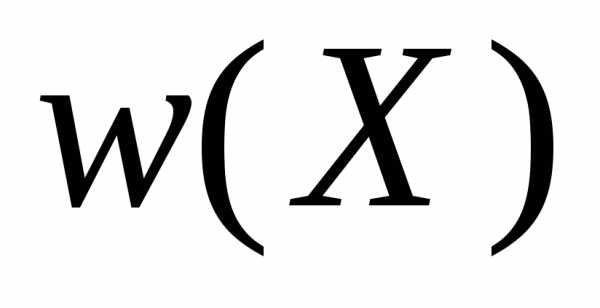Плотность вероятности пропорциональначислу реализованных микросостояний в единице объема фазового пространства, т. е. плотности микросостояний. Установим общие свойства , используя теорему Лиувилля.

studfiles.net