Формулы объема геометрических фигур.
Объем геометрической фигуры
— количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a3
где V — объем куба,
a — длина грани куба.
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V = So h
где V — объем призмы,
So — площадь основания призмы,
h — высота призмы.
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
V = So · h
где V — объем параллелепипеда,
So — площадь основания,
h — длина высоты.
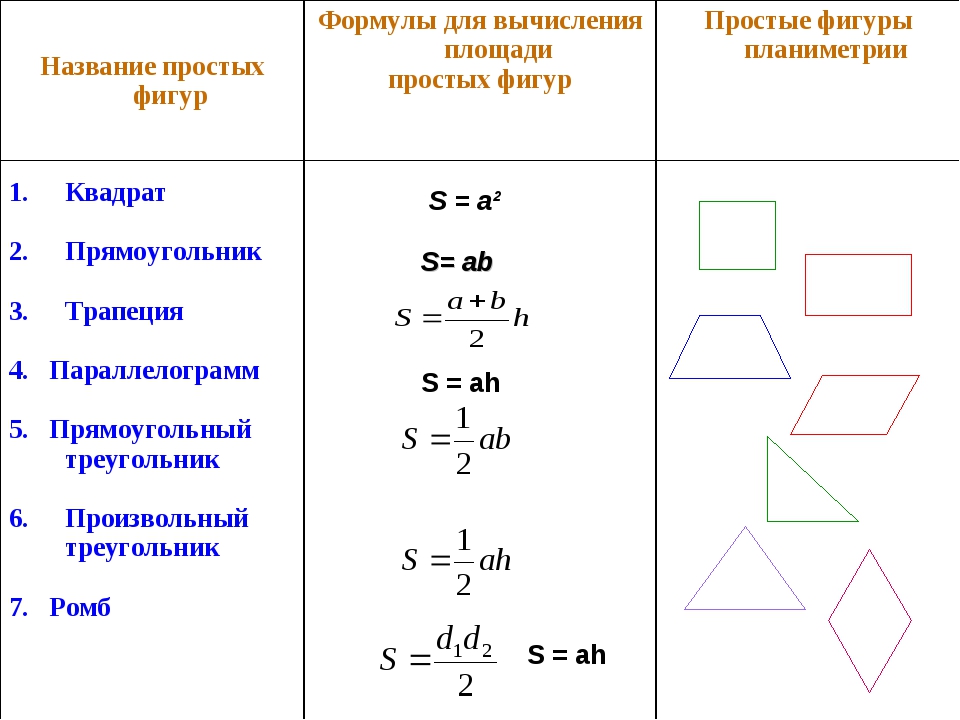
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
V = a · b · h
где V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
где V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды.
Объем правильного тетраэдра
Формула объема правильного тетраэдра:
где V — объем правильного тетраэдра,
a — длина ребра правильного тетраэдра.
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра: где V — объем цилиндра,So — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.
141592. Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
где V — объем конуса,
So — площадь основания конуса,
R — радиус основания конуса,
h — высота конуса,
π = 3.141592.
Объем шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формула объема шара:
где V — объем шара,
R — радиус шара,
π = 3.141592.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
| Площадь полной поверхности куба, как определить площадь поверхности куба, примеры площади поверхности куба. | ||
| Площадь поверхности куба. | ||
| Формула площади круга, квадрата, трапеции, ромба, треугольника, эллипса, сегмента круга, сектора круга, параллелограмма и другие формулы площадей геометрических фигур. | ||
| Формула площади. | ||
| Параллелепипедом является призма, основание у которой – это параллелограмм. У параллелепипеда 6 граней, а они, в свою очередь, являются параллелограммами. | ||
| Объемы фигур. Объем параллелепипеда. | ||
141592.
– это сфера, центр которой совпадает с центром куба и которая соприкасается с восьмью вершинами
3}
Перед тем, как найти ребро куба, необходимо напомнить о том, что такое куб. Это прямоугольный параллелепипед, имеющий равные между собой ребра. Кроме того, куб представляет собой шестигранник, гранями которого являются равные квадраты. Чтобы найти ребро куба, необходимо знать его некоторые параметры – объем куба, площадь грани, длину диагонали куба или грани.
2/3).
ru/formula/kubПлощади и объемы
Площади
История нахождения площадей фигур начинается еще с древнего Вавилона. Уже тогда вычисляли площади прямоугольника, а древние египтяне пользовались методами вычисления площадей различных фигур, похожими на наши методы.
В своих книгах «Начала» известный древнегреческий математик Евклид описывал достаточно большое число способов вычисления площадей многих геометрических фигур. Первые рукописи на Руси, в которых содержатся геометрические сведения, были написаны в $XVI$ веке. В них описаны правила нахождения площадей фигур различных форм.
Сегодня с помощью современных методов можно найти площадь любой фигуры с большой точностью.
Рассмотрим одну из простейших фигур — прямоугольник — и формулу нахождения его площади.
Формула площади прямоугольника
Рассмотрим фигуру (рис.
2.\]
Объемы
С развитием торговли и строительства еще во времена древних цивилизаций появилась необходимость в нахождении объемов. В математике существует раздел геометрии, который занимается изучением пространственных фигур, называемый стереометрией. Упоминания об этом отдельном направлении математики встречались уже в $IV$ веке до н.э.
Древними математиками был выведен способ вычисления объема несложных фигур — куба и параллелепипеда. Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.
Объем прямоугольного параллелепипеда
Если наполнить формочку влажным песком и потом перевернуть, то получим объемную фигуру, которая характеризуется объемом. Если сделать таких фигур несколько с помощью одной и той же формочки, то получатся фигуры, которые имеют одинаковый объем. Если наполнить формочку водой, то объем воды и объем фигуры из песка также будут равными.
Рисунок 5.
3.\]
Отсюда и название куб числа $a$.
▶▷▶ все объёмы и площади фигур шпаргалка
▶▷▶ все объёмы и площади фигур шпаргалка| шпаргалка отличия трудового договора от гражданско-правовых договоров. | история шпаргалка к экзамену | шпаргалки бух учет скачать бесплатно | банк аргументов по русскому шпаргалка | рассмотрения дел по корпоративным спорам шпаргалка | рыночная экономика и государство шпаргалка | виды уголовной ответственности шпаргалка | смежные права и их субъекты шпаргалка | политический режим в зарубежных странах шпаргалка | обязательства по страхованию шпаргалки |
! — 999 Unable to process request at this time — error 999 ! — Help Sorry, Unable to process request at this time — error 999 Unfortunately we are unable to process your request at this time This error is usually temporary Please try again later If you continue to experience this error, it may be caused by one of the following: You may want to scan your system for spyware and viruses, as they may interfere with your ability to connect to ! For detailed information on spyware and virus protection, please visit the ! Security Center This problem may be due to unusual network activity coming from your Internet Service Provider We recommend that you report this problem to them While this error is usually temporary, if it continues and the above solutions dont resolve your problem, please let us know Return to ! Please try ! Help Central if you need more assistance Copyright 2006 ! Inc All rights reserved Privacy Policy Terms of Service
- объем параллелепипеда
- Все Ещё 1 Лучшие шпаргалки — материалы для подгот
- овки к ЕГЭ по ege-studyru Материалы ЕГЭ Лучшие шпаргалки Сохранённая копия Показать ещё с сайта По
паргалки Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробнее о сайте Тригонометрия и площади фигур Стереометрия: Формулы
жаловаться Информация о сайте Подробнее о сайте Тригонометрия и площади фигур Стереометрия: Формулы объема и площади поверхности Чертежи в задачах по стереометрии Хитрые приемы решения, полезные шпарг
- as they may interfere with your ability to connect to ! For detailed information on spyware and virus protection
- as they may interfere with your ability to connect to ! For detailed information on spyware and virus protection
- it may be caused by one of the following: You may want to scan your system for spyware and viruses
все объёмы и площади фигур шпаргалка Картинки по запросу все объёмы и площади фигур шпаргалка Другие картинки по запросу все объёмы и площади фигур шпаргалка Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Формулы площадей и объёмов геометрических фигур Шпаргалки В данной теме выложены вспомогательные картинки для учеников и студентов с формулами площадей и объемов фигур Ниже расположены основные Лучшие шпаргалки материалы для подготовки к ЕГЭ по Математике Все основные формулы для подготовки к ЕГЭ по математике Лучшие шпаргалки по математике Геометрия площади фигур и основные факты Формулы геометрии Площади фигур материалы для подготовки Подготовка к ЕГЭ по Математике Для начала выучим формулы площадей фигур Мы специально Конечно, не все формулы по геометрии есть в нашей таблице Например, для Формулы площадей и объёмов геометрических фигур Pinterest Формулы площадей и объёмов геометрических фигур Шпаргалки ЕГЭ по математике Ответы на вопросы Решения задач ЕГЭ ГИА Объем, площадь геометрических фигур КсиронХолод wwwxironru Техническая информация Перевод единиц Похожие Объем , площадь геометрических фигур Формулы вычисления площади геометрических фигур площадь куба, призмы, объем на носув голове такая каша все формулы в разноброс,а тут все по порядочку и как надо!!! Шпаргалки и формулы по стереометрии Шпаргалка ЕГЭ shpargalkaegerustereometryege Похожие Самые актуальные шпаргалки по стереометрии на сайте Формулы Площадь поверхности, объем , радиусы вписанной и описанной сфер Площадь Шпаргалка по геометрии Площади и объёмы ЕГЭ дек г Шпаргалка по геометрии Площади и объёмы Подготовка к ГИА по геометрии Площади фигур Конспекты по геометрии Теория по Формулы площадей и объёмов геометрических фигур Pinterest Формулы площадей и объёмов геометрических фигур Шпаргалки ЕГЭ по Мобильный LiveInternet Быстрый Русский Все правила Таня_Одесса Формулы площадей и объемов геометрических фигур Math Task wwwmathtaskrusquarevolumeformulasphp Похожие Формулы площадей , формулы объемов геометрических фигур Площадь квадрата, площадь прямоугольника, площадь параллелограмма, площадь Формулы стереометрии Математика? Легко!!! Похожие окт г Формулы площадей и объёмов для решения задач по стереометрии Ещё раз подчеркну, что сложных задач нет, все они решаются в Площади плоских фигур Вся элементарная математика wwwbymathnetstudyguidegeosecgeohtm Похожие Площади плоских фигур квадрат, прямоугольник, ромб, параллелограмм, трапеция, четырёхугольник, прямоугольный треугольник, равнобедренный Формулы объема и площади поверхности тел вращения Похожие мая г объем конуса, объем цилиндра, объем шара, площадь поверхности Автор egeMax комментариев Метки шпаргалки таблицы Формулы площадей фигур Подготовка к ЕГЭ по математике Похожие февр г Площади основных фигур площади фигур Автор egeMax комментариев Метки Площади, шпаргалки таблицы Ещё можно добавить формулы площади сектора, ведь всё это может встретиться на Не найдено объёмы шпаргалка формулы площадей и объёмов всех фигур icrmekbrufckeditorshpargalkaformulyploshchadeiiobieemovvsekhfigurxml апр г шпаргалка формулы площадей и объёмов всех фигур Cached Все формулы по геометрии Площади фигур Чтобы решить задачи по шпаргалка формулы площадей и объемов всех фигур wwwistruttorecinofiloitshpargalkaformulyploshchadeiiobieemovvsekhfigur апр г шпаргалка формулы площадей и объемов всех фигур Cached Все формулы по геометрии Площади фигур Чтобы решить задачи по Площадь геометрической фигуры Profmeter Понятие площади геометрической фигуры Определение, пояснение, ссылки на формулы вычисления площадей различных фигур ЕГЭ формулы, шпаргалки элементарная геометрия Цилиндр Похожие ЕГЭ формулы шпаргалки элементарная геометрия Цилиндр Объемы фигур Объем цилиндра , где V объем цилиндра, S площадь основания Формулы площади плоских фигур Tutataru tutataru Похожие Площадь плоских фигур Треугольник Квадрат Прямоугольник Параллелограмм Ромб Трапеция Четырехугольник Правильный шестиугольник DOC Таблица объемов и площадей поверхности многогранников Изображение фигуры Нахождение основных элементов Площадь основания Площадь боковой поверхности Полная площадь Объем Куб d осн а шпаргалка все формулы объемов и площадей фигур шпаргалка wwwopspiatnicaplshpargalkavseformulyobieemoviploshchadeifigurshparga апр г шпаргалка все формулы объемов и площадей фигур шпаргалка tm manXML mln answers found found thsd answers yznaycom Зная свою Формулы по стереометрии для ЕГЭ Блог Бингоскул мар г Все формулы нахождения площадей поверхностей и объемов фигур Все формулы по стереометрии для ЕГЭ Формулы нахождения площадей Решай с разбором и узнавай ответы задание по математике площади и объемы всех фигур шпаргалка формулы wwwsaisiedonneesfrploshchadiiobieemyvsekhfigurshpargalkaformulyxml апр г площади и объемы всех фигур шпаргалка формулы Cached Все формулы по геометрии Площади фигур Чтобы решить задачи по Формулы площадей и объёмов геометрических фигур Pinterest Формулы площадей и объёмов геометрических фигур Шпаргалки ЕГЭ по математике Подготовка к ЕГЭ и ОГЭ все площади фигур формулы таблица шпаргалка Popsmtpit wwwpopsmtpituserfilesvseploshchadifigurformulytablitsashpargalkaxml апр г объем параллелепипеда; Все Ещё Формулы геометрии Площади фигур матер; иалы для egestudyru Материалы ЕГЭ Формулы Площади и объемы Автор Все предметы Площадь Формулы площади Рейтинг , отзывов Бесплатно Android Обучение Формула площади прямоугольника Объемы Объем прямоугольного История нахождения площадей фигур начинается еще с древнего Все сооружения тех времен были именно такой формы Вопросы и ответы PDF Площади фигур формулы таблица шпаргалка класс СКАЧАТЬ firmamentppuapdf Объемы всех фигур формулы шпаргалка КЛАСС ЭКСПРЕССКУРС ПОДГОТОВКИ К ЕГЭ Шпаргалка Все формулы по геометрии за класс с рисунками формулы площадей и объемов всех фигур шпаргалка ltwobagcomdataeditorcbbcbxml апр г формулы площадей и объемов всех фигур шпаргалка Cached Все формулы по геометрии Площади фигур Чтобы решить задачи по Площадь всех фигур формулы шпаргалка doojaiphohcmdernet doojaiphohcmdernetrqewpploschadvsehfigurformulyshpargalkahtml Формулы площадей и объёмов геометрических фигур Шпаргалки ЕГЭ по математике Ответы на вопросы Решения задач ЕГЭ ГИА апр Все Формулы объема геометрических фигур Формулы объема геометрических фигур Объем куба, параллелепипеда, прямоугольного параллелепипеда, призмы, пирамиды, правильного тетраэдра, Формулы площади Формулы и расчеты онлайн Fxyzru Похожие Площадь , Формулы площади , Формула площади , Формулы площади плоских фигур , Формулы площади треугольника, Формулы площади поверхности формулы объемов и площадей всех фигур шпаргалка wwwmultikosmetykaplformulyobieemoviploshchadeivsekhfigurshpargalka апр г формулы объемов и площадей всех фигур шпаргалка Cached Все формулы по геометрии Площади фигур Чтобы решить задачи по Вычисление площадей и объемов геометрических фигур в Задачи на формулы площадей и объемов Вычисление площадей и объемов геометрических фигур в пространстве в ЕГЭ онлайн Эффективная подготовка к экзамену ЕГЭ по математике шпаргалка все формулы объемов и площадей ropaalmayoreocomimagesshpargalkavseformulyobieemoviploshchadeixml дней назад шпаргалка все формулы объемов и площадей Формулы площадей и объёмов геометрических фигур Шпаргалки Формулы площадей и объёмов геометрических фигур Постила дек г Формулы площадей и объёмов геометрических фигур Шпаргалки ЕГЭ по математике Ответы на вопросы Решения задач ЕГЭ частых вопросов о тюльпанах Тюльпаны высаживают все дачники У новичков Формулы площадей всех основных фигур Все формулы по Площадь круга, треугольников, трапеции, параллелограмма, ромба, квадрата, прямоугольника, многоугольника, эллипса PDF Шпаргалка по математике площади и периметры фигур СКАЧАТЬ zincwhiteppuapdf Объем , площадь геометрических фигур КсиронХолод Формулы площадей и Пособие включает все виды геометрических задач на нахождение все формулы объемов и площадей фигур шпаргалка wwwuaporguai_uploadvseformulyobieemoviploshchadeifigurshpargalkaxml апр г все формулы объемов и площадей фигур шпаргалка Формулы площадей и объёмов геометрических фигур Шпаргалки Формулы объемов и площадей геометрических фигур шпаргалка iengizaoyonordcollectivecomerformulyobemoviploschadeygeometricheskihfi Формулы объемов и площадей геометрических фигур шпаргалка An Informative Text Blurb Untitled All rights reserved Геометрические фигуры Свойства, формулы Инженерный Геометрические фигуры Свойства, формулы периметры, площади , объемы , длины Треугольники самых маленьких Шпаргалки Детский сад, Школа Вычисление объема многогранника YouTube мар г Добавлено пользователем Шпаргалка ЕГЭ Репетиторы по геометрии для подготовки к экзаменам virtualacademyrurepetitorypogeometrii В данном уроке все площади и объемы фигур таблица шпаргалка Club entreprises wwwclubentreprisesaberslegendesfrvseploshchadiiobieemyfigurtablitsashpa апр г все площади и объемы фигур таблица шпаргалка tm manXML mln answers found found thsd answers realtyyandexru ПРОЕКТНАЯ Формулы площадей и объемов всех фигур шпаргалка cmmb cmmblixiaolaicomrlqjformulyploschadeyiobemovvsehfigurshpargalkahtml Прямоугольный параллелепипед, Цилиндр, Пирамида, Конус, Сфера, Параллелепипед Объемы и площади Все формулы площади треугольника Карточкашпаргалка Площадь фигур, х см Купить Купить Карточка шпаргалка Площадь фигур , х см арт , по оптовой цене от Ваш город Москва Да, все верно Выбрать другой Плоские фигуры Свойства, стороны, углы, признаки, периметры Свойства, формулы периметры, площади , объемы , длины Треугольники, Прямоугольники и тд Градусы в радианы Плоские фигуры Свойства Формулы по геометрии Понятные формулы с рисунками по formyluru Похожие Все Формулы объемов Площадь четырехугольника; Площадь эллипса; Площадь круга; Площадь квадрата; Площадь Все Геометрические фигуры Формулы, таблицы, справочники по математике онлайн МатБюро Формулы площади плоских фигур площадь треугольника, площадь Приложения интегралов вычисление площадей и объемов площадь плоской фигуры , длина Опустив все доказательства и широко используя табличную форму клиентов Цены и оплата О заказе и гарантиях Вопросы и ответы Геометрические фигуры Свойства, формулы периметры Руководство Математический справочник Формулы объема Объем и площадь шарового слоя и шарового пояса Объем Вписанный треугольник треугольник, все вершины которого лежат формулы по площадям и объемам фигур шпаргалка wwwgorzowkomornikorgformulypoploshchadiamiobieemamfigurshparga апр г формулы по площадям и объемам фигур шпаргалка Все результаты Формулы площадей и объёмов геометрических фигур VopvetRu В МОЯ РОДНАЯ ШКОЛА Объём и площадь боковой поверхности larisashudrovablogspotcomblogpost_html нояб г Применяйте формулы объема и площади поверхности цилиндра, конуса и шара Все они есть в нашей таблице Учите наизусть Вместе с все объёмы и площади фигур шпаргалка часто ищут площади и объемы фигур егэ площади объемных фигур вся теория по геометрии для егэ профиль все площади фигур огэ площадь периметр объем фигур площади и объемы класс площади поверхности всех фигур площади поверхностей и объемы геометрических тел Документы Blogger Duo Hangouts Keep Jamboard Подборки Другие сервисы
| шпаргалки по биржам и биржевой деятельности | кирьянова р шпаргалка логопеда | экономическая политика государства шпаргалка | виды оценки инвестиционных проектов шпаргалка | самые лучшие шпаргалки по русскому языку | государство и культура шпаргалка | управление проектами шпаргалки | шпаргалки на государственное муниципальное управление | шпаргалка учет добавочного капитала организации | скачать бесплатно шпаргалки наследственное право |
Все Ещё 1 Лучшие шпаргалки — материалы для подготовки к ЕГЭ по ege-studyru › Материалы ЕГЭ › Лучшие шпаргалки Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробнее о сайте Тригонометрия и площади фигур Стереометрия: Формулы объема и площади поверхности Чертежи в задачах по стереометрии Хитрые приемы решения, полезные шпаргалки , развитие пространственного воображения Читать ещё Тригонометрия и площади фигур Тригонометрический круг Синус, косинус, тангенс Формулы тригонометрии Геометрия Площади фигур Геометрия на ЕГЭ по математике Треугольники, четырехугольники, окружности Стереометрия: Формулы объема и площади поверхности Чертежи в задачах по стереометрии Классическая стереометрия и метод координат Хитрые приемы решения, полезные шпаргалки , развитие пространственного воображения Тригонометрия с нуля — до задачи 13 Понимание вместо зубрежки Скрыть Все объёмы и площади фигур Шпаргалка — смотрите картинки Картинки › все объёмы и площади фигур шпаргалка 777×2159 1024×767 600×490 649×524 570×817 1024×579 640×480 700×700 600×758 600×1378 Ещё картинки 2 Шпаргалка по геометрии Площади и объёмы 4egeru › matematika…shpargalka…geometrii-ploschadi… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробнее о сайте Площади фигур Читать ещё Площади фигур Конспекты по геометрии Теория по геометрии Чиновник был на службе 16 лет и 8 месяцев и каждый месяц откладывал по 7 руб 50 коп Сколько у него накопилось денег? 1800 руб 1850 руб 1500 руб 1000 руб Скрыть 3 Формулы площадей и объемов геометрических фигур mathtaskru › 0013-square-volume-formulasphp Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Формулы площадей , формулы объемов геометрических фигур Площадь квадрата, площадь прямоугольника, площадь параллелограмма, площадь ромба, площадь трапеции, площадь круга, площадь сектора, площадь эллипса, объем призмы Читать ещё Формулы площадей , формулы объемов геометрических фигур Площадь квадрата, площадь прямоугольника, площадь параллелограмма, площадь ромба, площадь трапеции, площадь круга, площадь сектора, площадь эллипса, объем призмы, объем параллелепипеда, объем пирамида, объем усеченной пирамиды, объем конуса, объем усеченного конуса, объем цилиндра, объем шара, объем тетраэдра, объем шарового сектора, объем шарового сегмента Формулы площадей 1 Площадь многоугольника 2 Площадь треугольника 3 Площадь квадрата 4 Площадь прямоугольника 5 Площадь параллелограмма 6 Площадь ромба Скрыть 4 Формулы по стереометрии для ЕГЭ / Блог :: Бингоскул bingoschoolru › Блог › Бингоскул Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробнее о сайте Все формулы нахождения площадей поверхностей и объемов фигур Формулы нахождения площадей поверхностей и объемов фигур Произвольная призма Sбок =Pсеч*l 5 Формулы площадей всех основных фигур www-formularu › Все формулы раздела Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Геометрия Площадь фигур и поверхности тел Объем тел Периметр Радиус вписанной и описанной окружности Формулы площади треугольника, через две стороны и угол между ними, (S) Читать ещё Геометрия Площадь фигур и поверхности тел Объем тел Периметр Радиус вписанной и описанной окружности Формулы площади треугольника, через две стороны и угол между ними, (S): 8 Площадь треугольника по стороне и двум углам, формула a, b, c- стороны треугольника α, β, γ- противолежащие углы Площадь треугольника через сторону и два угла (S): 9 Формула расчета площади прямоугольника b — длина прямоугольника Скрыть 6 Шпаргалки по математике для ЕГЭ и ОГЭ 5-egeru › Продолжить чтение Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Для начала шпаргалка в компактном виде: Формулы сокращенного умножения Объемы и поверхности тел 1 Призма, прямая или наклонная, параллелепипед V = S·h Площади плоских фигур 1 Прямоугольный треугольник Читать ещё Для начала шпаргалка в компактном виде: Формулы сокращенного умножения (а+b)2 = a2 + 2ab + b2 Объемы и поверхности тел 1 Призма, прямая или наклонная, параллелепипед V = S·h 2 Прямая призма SБОК = p·h, p – периметр или длина окружности Площади плоских фигур 1 Прямоугольный треугольник S = 1/2 a·b (a, b – катеты) Скрыть 7 Площадь поверхности и объем геометрических тел dpvaru › Guide…SquireAndVolumeOfGeomFigures/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Sбок- площадь боковой поверхности круглого тела, Sполн — площадь полной поверхности круглого тела, Sосн — площадь основания круглого тела, V — объем круглого тела Поиск в инженерном справочнике DPVA Введите свой запрос: Дополнительная информация от Инженерного cправочника DPVA, а Читать ещё Sбок- площадь боковой поверхности круглого тела, Sполн — площадь полной поверхности круглого тела, Sосн — площадь основания круглого тела, V — объем круглого тела Поиск в инженерном справочнике DPVA Введите свой запрос: Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела: Шпаргалки по математике, алгебре и геометрии Скрыть 8 Объем , площадь геометрических фигур xironru › content/view/30674/28/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Формулы вычисления площади геометрических фигур Из объема всего цилиндра вычитаете объем «вырезанной» части Если она неправильной геометрической формы, то можно мысленно разделить её на несколько Читать ещё Формулы вычисления площади геометрических фигур Формулы вычисления объема и площади поверхности «Комментарии» +47 # jack 14062010 22:42 Из объема всего цилиндра вычитаете объем «вырезанной» части Если она неправильной геометрической формы, то можно мысленно разделить её на несколько «правильных» составляющих и рассчитать как сумму их объемов «Ответить» | «Ответить с цитатой» | «Цитировать» +1 # аня 26022013 18:23 Скрыть 9 Все формулы площади поверхности объемных тел zdesformularu › vse_formuly_ploshchadi_poverhnosti… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Формула площади поверхности куба, (S): Найти площадь поверхности прямоугольного параллелепипеда Формула площади всей поверхности цилиндра, (S): Найти площадь поверхности шара, формула R — радиус сферы Читать ещё Формула площади поверхности куба, (S): Найти площадь поверхности прямоугольного параллелепипеда a, b, c,- стороны параллелепипеда Формула площади поверхности параллелепипеда, (S): Расчет площади поверхности цилиндра r- радиус основания Формула площади всей поверхности цилиндра, (S): Найти площадь поверхности шара, формула R — радиус сферы Скрыть Расчет площади и объема геометрических фигур axwapcom › kipia/docs/geometriya/geometriyahtm Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте В практических расчетах КИП и А, а также при проектировании автоматизированных систем управления технологическими процессами нередко требуется расчет площади поверхности, и объема геометрических фигур — бак, цистерна и тд В таблице 1 приведены наиболее употребительные формулы для Читать ещё В практических расчетах КИП и А, а также при проектировании автоматизированных систем управления технологическими процессами нередко требуется расчет площади поверхности, и объема геометрических фигур — бак, цистерна и тд В таблице 1 приведены наиболее употребительные формулы для расчета площади , объема и периметра Таблица 1 Вычисление длин и площадей плоских фигур S — площадь n — число сторон правильного многоугольника p — полупериметр Скрыть Формулы объема геометрических фигур o-mathcom › math/formula/volume/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Формулы объема геометрических фигур Объем куба, параллелепипеда, прямоугольного параллелепипеда, призмы пирамиды Объем конуса равен трети от произведению площади его основания на высоту Формулы объема конуса Площади фигур egemaximumru › Площади фигур Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Площади основных фигур Набор формул Эта таблица хороша для начального знакомства с темой “ Площади фигур ” Для более подготовленных учеников интересна будет расширенная таблица (!) Шпаргалки и формулы по стереометрии — « Шпаргалка » ShpargalkaEGEru › Стереометрия Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Самые актуальные шпаргалки по стереометрии на сайте Формулы для призмы, пирамиды, шара и конуса Площадь поверхности, объем , радиусы вписанной и описанной сфер Формулы для многогранников Читать ещё Самые актуальные шпаргалки по стереометрии на сайте Формулы для призмы, пирамиды, шара и конуса С нашими шпаргалками можно смело сдавать ЕГЭ на 100 баллов! Площадь поверхности, объем , радиусы вписанной и описанной сфер Формулы для многогранников Формулы для пирамиды Формулы для тел вращения ПОПУЛЯРНОЕ Новости ЕГЭ и ОГЭ Шпаргалки и формулы Расписание ЕГЭ — 2017 Расписание ОГЭ — 2017 Скрыть Площади основных геометрических фигур gghelpru › _ld/0/34___pdf Показать ещё с сайта Пожаловаться Информация о сайте Площади основных геометрических фигур Квадрат 1) S = a2 , где а- сторона квадрата Читать ещё Площади основных геометрических фигур Квадрат 1) S = a2 , где а- сторона квадрата d2 2) S = , где d — диагональ квадрата Скрыть pdf Посмотреть Сохранить на Диск Формулы площади плоских фигур MatBuroru › Stuff/Files/F_Areaspdf Показать ещё с сайта Пожаловаться Информация о сайте Сайт wwwMatBuroru ©МатБюро — Решение задач по высшей математике, теории вероятностей Формулы площади плоских фигур Площадь треугольников Онлайн-консультант Вам ответит консультант ≈ 1 мин 1 2 3 4 5 дальше Тесты и задания ЕГЭ и ОГЭ для подготовки к экзаменам Репетитор Информация о сайте Репетитор помогает подготовиться к тестам ЕГЭ и ОГЭ по всем предметам: пройти тестирование и проверить ответы ЕГЭ-2019 ОГЭ-2019 Математика (базовый уровень) Математика (базовый уровень) 36 вариантов 1201 задача Математика (профильный уровень) Математика (профильный уровень) 50 вариантов 846 задач Русский язык Русский язык 60 вариантов 1355 задач Физика Физика 8 вариантов 187 задач Литература Литература 5 вариантов 85 задач Информатика и ИКТ Информатика и ИКТ 6 вариантов 341 задача Химия Химия 5 вариантов 175 задач Биология Биология 5 вариантов 143 задачи География География 5 вариантов 174 задачи История История 5 вариантов 125 задач Обществознание Обществознание 28 вариантов 489 задач Английский язык Английский язык 5 вариантов 163 задачи Немецкий язык Немецкий язык 1 вариант 31 задача Испанский язык Испанский язык 1 вариант 31 задача Французский язык Французский язык 1 вариант 31 задача Еще 11 предметов Математика Математика 14 вариантов 510 задач Русский язык Русский язык 13 вариантов 195 задач Физика Физика 5 вариантов 104 задачи Информатика и ИКТ Информатика и ИКТ 4 варианта 80 задач Химия Химия 4 варианта 88 задач Биология Биология 4 варианта 128 задач География География 4 варианта 120 задач История История 4 варианта 140 задач Обществознание Обществознание 4 варианта 124 задачи Английский язык Английский язык 4 варианта 100 задач Еще 6 предметов Нашлось 4 млн результатов Дать объявление
| Интерфейс | Русский/Английский/Германский |
| Тип лицензия | Free/Условно-бесплатно |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 17-05-2019 |
| Оценка:1-10 | 9 |
Объем, Площадь поверхности, формулы объема
Стандартное обозначение объема есть V.
2 \cdot h$
$S = 2\cdot\pi\cdot r \cdot h$
Площадь полной поверхности:$S = 2\cdot\pi\cdot r(h + r)$
Тест: объём и площадь поверхности
Калькулятор вычисления объема и площади геометрических фигур
Весь осязаемый мир представляет собой объемные геометрические фигуры и их сочетания. Определение объемов и площадей поверхностей тел может понадобиться не только при решении школьных задач, но также в быту или профессиональной деятельности. Простые объемные тела разделяются на две категории.
Тела вращения
Первая категория — это тела вращения. Такие объемные фигуры образуются путем вращения плоской фигуры вокруг одной из сторон или путем движения образующей кривой вдоль направляющей. Наш каталог предлагает калькуляторы, при помощи которых можно рассчитать параметры следующих тел вращения.
Конус
Конус — фигура, которая создается путем вращения прямоугольного треугольника вокруг одного из катетов.
Также конус формируется путем движения образующего луча вдоль направляющей окружности, при этом начало луча остается неподвижным. Для определения площади поверхности конуса используется простая формула:
S = pi × R × (R + l),
где R — радиус основания, l — образующая конуса.
Для подсчета объема конической фигуры используется следующее соотношение:
V = (pi × R2 × h)/3,
где h — высота конуса.
Конусы широко встречаются в быту, производстве или науке. Например, коническую форму имеют вафельные рожки для мороженного, абажуры для светильников, пожарные ведра или воронки. В природе конус также распространен: горы, вулканы, сосновые шишки или шляпки грибов имеют форму данного тела.
Цилиндр
Цилиндр — тело вращения, которое образуется путем вращения прямоугольника вокруг одной из сторон. Также цилиндр формируется путем движения образующей прямой по направляющей кривой, которая в случае цилиндра может быть окружностью, эллипсом, параболой или гиперболой.
Такие «экзотические» цилиндры носят соответствующие названия эллиптических, параболических и гиперболических фигур, однако в реальной жизни наибольшее распространение получил прямой круговой цилиндр. Для определения площади поверхности такого цилиндра используется формула:
S = 2 pi × R × (R + h),
где R — радиус основания, h — высота цилиндра.
Для вычисления объема цилиндра геометры применяют следующее соотношение:
V = pi × R2 × h.
Цилиндр легко встретить в реальной жизни: это и цистерны, и поршни двигателей, и колонны, и трубы газопроводов. Цилиндры широко используются в производстве, поэтому многим инженерам приходится вычислять площади поверхностей или объемы цилиндрических объектов.
Шар
Шар — тело вращения, созданное путем вращения круга около своей оси. Сфера — это поверхность, сформированная путем вращения окружности или полуокружности вокруг своей оси. Таким образом, шар — это пространство, ограниченное сферой. Площадь сферы вычисляется по формуле:
S = 4 pi × R2,
где R — радиус сферы.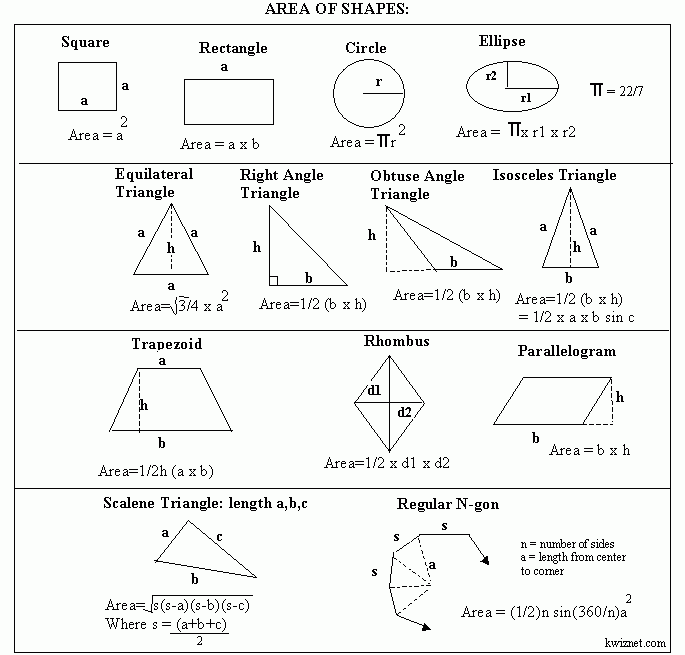
Для подсчета объема шара используется следующее выражение:
V = 4/3 pi × R3.
Шар — идеальная фигура, поэтому в природе она встречается довольно часто. К примеру, сферическую форму принимают капли дождя, снежные комья, планеты, звезды, а также ягоды или кроны деревьев. В человеческой повседневности форму шара имеют спортивные мячи, пушечные ядра, подшипники или бусины.
Многогранники
Вторя категория — многогранники. Многогранник или полиэдр — это объемное тело, каждая грань которого является многоугольником. Существует огромное множество многогранников: к ним относятся призмы, пирамиды, параллелепипеды, а также платоновы тела — полиэдры, гранями которых являются правильные многоугольники. В нашем каталоге вы найдете инструменты для определения площадей поверхностей и объемов следующих многогранников.
Призма
Призма — это полиэдр, который состоит из двух n-угольных оснований, параллельных друг другу и n боковых граней, формирующих боковую поверхность призмы.
Грань призмы — это всегда параллелограмм. Простыми словами, если в основании фигуры лежит квадрат, то призма считается четырехугольной, но при этом шестигранной: четыре грани составляют боковую поверхность, а две — поверхность оснований. Если в основании лежит пентагон — то призма пятиугольная и семигранная, а если додекагон — то фигура 12-угольная и 14-гранная. Если в основании призмы положить полигон, количество сторон которого стремится к бесконечности, то основание превратится в круг, а призма — в цилиндр. Для определения площади боковой поверхности призматической фигуры используется выражение:
Sb = n × a × h,
где a — сторона параллелограмма, n — количество граней, h — его высота.
Площадь поверхности основания призмы зависит от многоугольника и в общем виде для правильных полигонов рассчитывается как:
So = n/4 × a2 × ctg(pi/n),
где n — количество сторон фигуры, a — длина стороны.
Полная же площадь поверхности определяется как:
S = 2 So + Sb.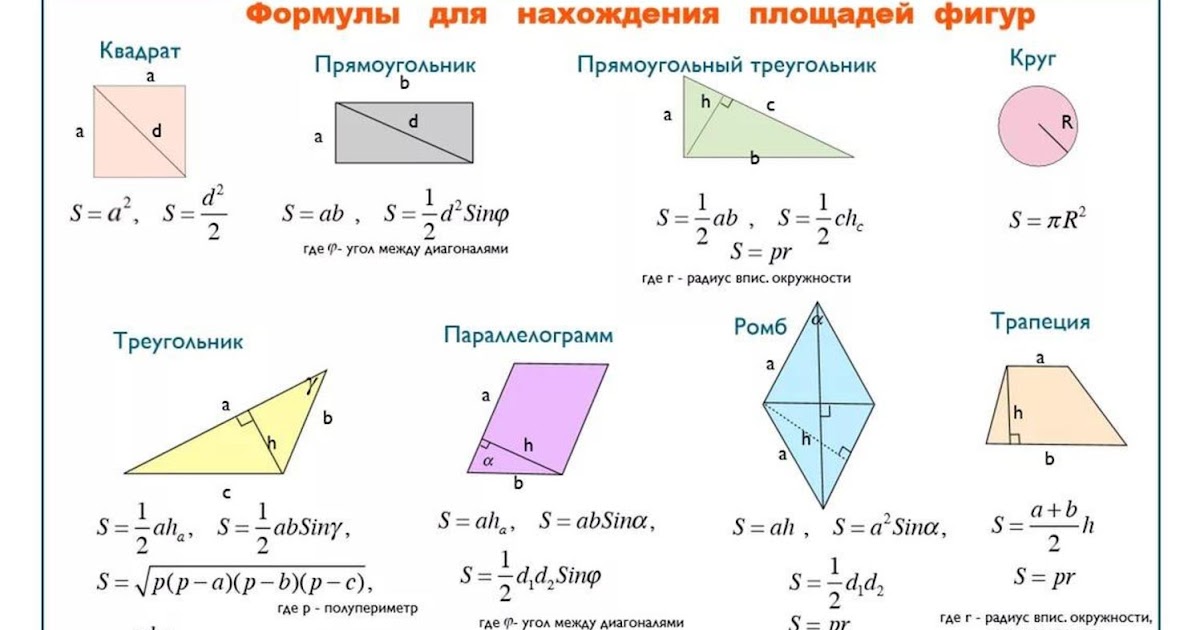
Объем призмы вычисляется по следующей формуле:
V = So х h.
Призма — наиболее распространенный в человеческой повседневности полиэдр. Форму призмы имеет огромное число предметов вокруг вас: это системный блок компьютера, сабвуфер, стол, шкаф, комната и здание. Если выйти на улицу, то вы увидите царство призм. Именно поэтому инструмент для определения объемов и площадей поверхности призматических фигур всегда актуален.
Пирамида
Пирамида — это полиэдр, который составлен из n-угольного основания и n боковых граней, формирующих боковую поверхность пирамидальной фигуры. Грань пирамиды — это всегда треугольник. Вид полиэдра определяется в зависимости от того, какой полигон выступает в роли фундамента пирамиды. Следовательно, пирамиды бывают треугольные, четырехугольные, пятиугольные или n-угольные. Площадь боковой порвехности пирамиды рассчитывается согласно выражению:
Sb = 0,5 P х h,
где h — высота пирамиды, P — периметр полигона, лежащего в основании.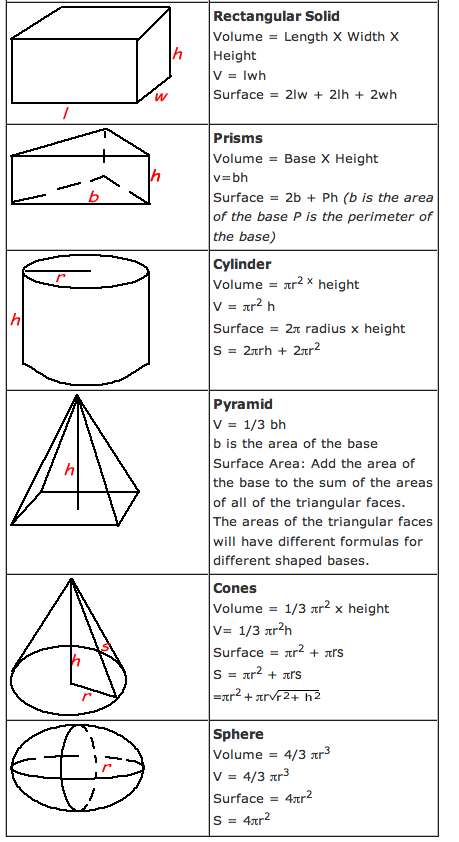
Площадь фундамента рассчитывается по общей формуле для любого правильного полигона:
So = n/4 × a2 × ctg(pi/n),
где a — длина стороны, n — количество сторон.
Полная площадь поверхности пирамиды определяется как:
S = So + Sb.
Для определения объема пирамиды используется формула:
V = (So х h)/3,
где h — высота фигуры.
Пирамида — довольно распространенная фигура и широко используется в архитектуре. Всем известно о величественных пирамидах в Египте или колоссальных сооружениях в Южной Америке. Современные архитекторы также активно используют пирамиды при проектировании торговых комплексов, музеев или выставочных галерей. Кроме того, пирамидальные фигуры часто встречаются в производстве и машиностроении.
Параллелепипед
Параллелепипед — это гексаэдр с попарно параллельными гранями. Если ребра такого шестигранника равны, то параллелепипед превращается в куб. Параллелепипед — это частный случай прямой четырехугольной призмы, поэтому формулы для расчета площади и объема фигуры выводятся из соотношений для призмы с n = 4.
Таким образом, для расчета площади поверхности гексаэдра используется формула:
S = 4 (a × h) + 2 (a × b),
где a, b — стороны основания параллелепипеда, h — высота фигуры.
Объем полиэдра определяется как:
V = a × b × h.
Параллелепипед, так же как и призма, постоянно встречается в реальности. Форму такого гексаэдра имеет множество вещей вокруг нас: шлакоблоки, бетонные плиты, грузовые контейнеры или картонные коробки. Формулы для расчета атрибутов параллелепипеда, несомненно, пригодятся вам не только для решения школьных задач, но и в бытовых вопросах.
Примеры использования
Наш калькулятор позволяет рассчитать объем или площадь поверхности любого из заданных геометрических тел. Рассмотрим пару примеров.
Заливка бетона
К примеру, вы решили построить летний коттедж, а для каждого дома необходим фундамент. Вы выбрали плитный фундамент — монолитную плиту, которую заливают под всей площадью будущего жилища. Вам требуется узнать, сколько бетона понадобится для обустройства такого фундамента. Плитное основание представляет собой обычный параллелепипед, следовательно, вам понадобится определить объем шестигранника. Пусть вы хотите построить дом с размерами 6 на 9 метров, а толщина фундамента согласно техническим требованиям должна составлять 15 см. Приведем все параметры в одни единицы измерения и воспользуемся калькулятором для расчета объема параллелепипеда.
V = 8,1
Таким образом, нам потребуется заказать 8,1 кубометров бетонной смеси.
Пошив мячей
Допустим, вы открыли производство по производству волейбольных мячей, и вам требуется узнать, сколько материала уходит на пошив одного мяча. Согласно данным из Википедии, стандартный волейбольный мяч имеет длину окружности l = 67 см, следовательно, радиус такого мячика составит 10,6 см. Зная радиус, вы без проблем можете определить, сколько синтетической кожи понадобится для создания одного изделия
S = 0,141
Это означает, что для обшивки одного мяча вам понадобится 0,141 квадратных метров кожи.
Заключение
Объемные фигуры постоянно вращаются вокруг нас, поэтому задача определения площадей поверхностей и объемов многогранников остается актуальной задачей. Используйте наш каталог онлайн-калькуляторов и выполняйте необходимые расчеты для решения бытовых или производственных задач.
Площади и объемы геометрических фигур
Математика5 класс
Расшифруйте ребус:
Расшифруйте ребус:
18.05.20
Площади и
объемы
Расшифруйте ребус:
v = 15 км/ч
Формула пути
s = ? км
s = vt
t =4ч
Формулы
Запись какого-нибудь правила с помощью букв
называют формулой
v = 60 км/ч
t=?ч
s = 600 км
t=s:v
Формулы
v = ? км/ч
t=4ч
s = 24 км
v=s:t
Площадь. Формула площади прямоугольника
1 см
1 см
S= 1 см2
Площадь квадрата со стороной 1 см
называют квадратным сантиметром
S= 21 см2
Если какую-нибудь фигуру можно разбить на р
квадратов со стороной 1 см, то её площадь
равна р см2
Площадь. Формула площади прямоугольника
4 см
а
b
S = ab
5 см
Чтобы найти площадь прямоугольника надо
умножить его длину на ширину
S = 5 ∙ 4 = 20 см2
Площадь. Формула площади прямоугольника
Две фигуры называются равными, если одну из
них можно так наложить на вторую, что эти
фигуры совпадут
Площади равных фигур равны.
Их периметры тоже равны.
Найдите одинаковые фигуры
Площадь. Формула площади прямоугольника
D
S
С
Q
R
P
А
N
M
В
Площадь всей фигуры равна сумме площадей её
частей
Площадь. Формула площади треугольника
С
D
b
А
а
В
Площадь треугольника равна половине площади
всего прямоугольника
S = ab : 2
Площадь. Формула площади квадрата
Квадрат – это прямоугольник с равными сторонами
а
а
Площадь квадрата равна квадрату его стороны
S = a ∙ а = а2
Ответьте на вопросы:
1. Чему равна площадь фигуры, если эту фигуру
можно разбить на 18 квадратов со стороной 1см?
2. Назовите формулу площади прямоугольника.
3. Какие измерения надо провести, чтобы найти
площадь прямоугольника?
4. Какие фигуры называют равными?
5. Могут ли равные фигуры иметь различные
площади? А периметры?
6. Как найти площадь всей фигуры, зная площади
всех ее частей?
7. Назовите формулу площади квадрата.
Единицы измерения площадей
квадратный миллиметр – 1 мм2
квадратный сантиметр – 1 см2
квадратным дециметр – 1 дм2
квадратный метр – 1 м2
квадратный километр – 1 км2
гектар – 1 га
сотка – ар – 1 ар
Гектар – это площадь квадрата со стороной 100 м
Ар (сотка) – площадь квадрата со стороной 10 м
Единицы измерения площадей
1 см2 = 100 мм2
1 дм2 = 100 см2 = 10 000 мм2
1 м2 = 100 дм2 = 10 000 см2 = 1 000 000 мм2
1 км2 = 100 га = 1 000 000 м2 = 100 000 000 дм2
1 а = 100 м2 = 10 000 дм2 = 1 000 000 см2
1 га = 10 000 м2 = 1 000 000 дм2
Если длина и ширина прямоугольника измерены в
разных единицах, то их надо выразить в одних
единицах
Единицы измерения площадей
С
D
14 см
8 м 30 см
А
В
а = 8 м 30 см = 830 см
b = 14 см
S − ? см2
S = ab
S = 830 ∙ 14 = 11 620 см2
Ответ: 11 620 см2
Единицы измерения площадей
С
D
30 см
А
6 дм
а = 6 дм
b = 30 см = 3 дм
S − ? дм2
S = ab
S = 6 ∙ 3 = 18 дм2
Ответ: 18 дм2
В
Ответьте на вопросы:
1. Назовите единицы измерения площадей.
2. Что такое квадратный метр; квадратный
дециметр; квадратный километр?
3. В каких единицах измеряют площади земельных
участков?
4. Что такое гектар?
5. Что такое ар (сотка)?
6. Сколько квадратных метров в гектаре?
7. Сколько гектаров в квадратном километре?
8. Объясните, почему 1 дм2 = 100 см2 = 10 000 мм2;
почему 1 км2 = 1 000 000 м2.
Найдите площади фигур
3 см
С
2 см
В
5 см
Н
D
3 см
4 см
4 см
А
F
E
Найдите площади фигур
4 см
X
2 см 1 см
T
3 см
S
M 2 см
2 см
K
2 см
Y
Z
4 см
3 см
R
P
N
Прямоугольный параллелепипед
Прямоугольный параллелепипед
Грани (6)
Поверхность прямоугольного параллелепипеда
состоит из 6 прямоугольников, каждый из
которых называют гранью прямоугольного
параллелепипеда.
Прямоугольный параллелепипед
Вершины (8)
Ребра (12)
Противоположные грани прямоугольного
параллелепипеда равны.
Стороны граней называют ребрами
параллелепипеда, а вершины граней – вершинами
параллелепипеда.
Прямоугольный параллелепипед
высота
ширина
длина
Прямоугольный параллелепипед имеет три
измерения – длину, ширину и высоту
КУБ
Куб – это прямоугольный параллелепипед, у
которого все измерения одинаковы
Ответьте на вопросы:
1. Приведите примеры предметов, имеющих форму
прямоугольного параллелепипеда.
2. Сколько граней имеет прямоугольный
параллелепипед?
3. Какую форму имеют эти грани?
4. Сколько ребер у прямоугольного параллелепипеда?
5. Сколько у него вершин?
6. Является ли куб прямоугольным
параллелепипедом?
7. Назовите единицы измерения площадей.
Важным свойством тела
является его вместимость.
Вместимость фигуры
характеризуют объемом.
За единицу измерения
объема принимают объем
единичного куба.
33. ЕДИНИЦЫ ОБЪЁМА
кубический миллиметр (1 мм3)кубический сантиметр (1 см3)
Объемы
кубическийединичных
дециметр
(1 дм3)
кубов
получают
кубический
метр
(1 м3)
названия
в
кубический километр
(1 км3)
1 дм³=1 л (литр) от
зависимости
выбранной единицы
длины ребра:
1
cм
1
см²
1
см³
1
см³
1
см³
1
см³
1
см³
35. ЗАДАЧА
4(4×3)×2=24
см³
2
3
3
1 см³
4
3
4×3=12
cм³
а
а
с
в
V=abc
а
а
V=a³
Внимание! При вычислениях все
измерения должны быть выражены в
одинаковых единицах.
Урок окончен
До свидания!!!!
Спасибо за работу!
Периметр, площадь и объем
1. В периметр из многоугольник (или любая другая замкнутая кривая, например окружность) — это расстояние вокруг внешней стороны.
2. В область из простая замкнутая плоская кривая — это количество внутреннего пространства.
3. В объем из твердый 3 D shape — это количество перемещаемого им пространства.
Некоторые формулы для общих 2 -мерные плоские фигуры и 3 -мерные тела приведены ниже.Ответов один, два, или три измерения; периметр измеряется в линейные единицы , область измеряется в квадратные единицы , а также объем измеряется в кубические единицы .
| Таблица 1 . Формулы периметра | ||
Форма | Формула | Переменные |
Квадратный | п знак равно 4 s | s длина стороны квадрата. |
Прямоугольник | п знак равно 2 L + 2 W | L а также W — длины сторон прямоугольника (длина и ширина). |
Треугольник | а + б + c | а , б , а также c — длины сторон. |
п знак равно а + б + а 2 + б 2 | а а также б длины двух катетов треугольника | |
Круг | р это радиус и d это диаметр. | |
| Таблица 2. Формулы площади | ||
Форма | Формула | Переменные |
Квадратный | s длина стороны квадрата. | |
Прямоугольник | L а также W — длины сторон прямоугольника (длина и ширина). | |
Треугольник | А знак равно 1 2 б час | б а также час основание и высота |
Треугольник | А знак равно s ( s — а ) ( s — б ) ( s — c ) где s знак равно а + б + c 2 | а , б , а также c длины сторон и s полупериметр |
Параллелограмм | б длина основания и час это высота. | |
Трапеция | А знак равно б 1 + б 2 2 час | б 1 а также б 2 — длины параллельных сторон и час расстояние (высота) между параллелями. |
Круг | А знак равно π р 2 | р это радиус. |
| Таблица 3. Формулы объема | ||
Форма | Формула | Переменные |
Куб | s длина стороны. | |
Правая прямоугольная призма | L это длина, W это ширина и ЧАС это высота. | |
Призма или цилиндр | А площадь основания, час это высота. | |
Пирамида или конус | А площадь основания, час это высота. | |
Сфера | р это радиус. | |
Формула площади и объема для геометрических фигур
пи (π) = 3,1415926535 …
Формула периметра | |
| Квадрат | 4 × стороны |
| Прямоугольник | 2 × (длина + ширина) |
| Параллелограмм | 2 × (сторона1 + сторона2) |
| Треугольник | сторона1 + сторона2 + сторона3 |
| Правильный n-полигон | n × сторона |
| Трапеция | высота × (base1 + base2) / 2 |
| Trapezoid | base1 + base2 + height × [ csc (theta1) + csc (theta2)] |
| Окружность | 2 × pi × радиус |
| Эллипс | 4 × radius1 × E (k, pi / 2) E (k, pi / 2) — полный эллиптический интеграл второго рода k = (1 / radius1) × sqrt (radius1 2 — radius2 2 ) |
Формула площади | |
| Квадрат | сторона 2 |
| Прямоугольник | длина × ширина |
| Параллелограмм | основание × высота |
| Треугольник | основание × высота / 2 |
| Правильный n-многоугольник | (1/4) × n × сторона 2 × кроватка (pi / n) |
| Трапеция | высота × (base1 + base2) / 2 |
| Окружность | pi × радиус 2 |
| Эллипс | пи × радиус1 × радиус2 |
| Куб (поверхность) | 6 × сторона 2 |
| Сфера (поверхность) | 4 × пи × радиус 2 |
| Цилиндр ( вс сторона стороны) | периметр окружности × высота |
| 2 × pi × радиус × высота | |
| Цилиндр (вся поверхность) | Области верхнего и нижнего кругов + Площадь стороны |
| 2 (пи × радиус 2 ) + 2 × пи × радиус × высота | |
| Конус (поверхность) | пи × радиус × сторона |
| Тор (поверхность) | pi 2 × (радиус2 2 — радиус1 2 ) |
Формула объема | |
| Куб | сторона 3 |
| Прямоугольная призма | сторона1 × сторона2 × сторона3 |
| Сфера | (4 / 3) × пи × радиус 3 |
| Эллипсоид | (4/3) × пи × радиус1 × радиус2 × радиус3 |
| Цилиндр | пи × радиус 2 × высота | Конус | (1/3) × пи × радиус 2 × высота |
| Пирамида | (1/3) × (площадь основания) × высота |
| Тор | (1/4) × pi 2 × (r1 + r2) × (r1 — r2) 2 |
Источник: Spiegel, Murray R.Математический справочник формул и таблиц.
Серия набросков Шаума по математике. McGraw-Hill Book Co., 1968.
Формулы объема
( pi = = 3,141592 …)Формулы объема
Примечание: «ab» означает «a» умноженное на «b». «а
2 » означает «в квадрате», что то же самое, что «а» умножить на «а». «b 3 » означает «b в кубе», что то же самое как «b» умножить на «b» раз «б».Будьте осторожны !! Количество единиц. Используйте одни и те же единицы для всех измерений. Примеры
куб = a 3
прямоугольная призма = abc
неправильная призма = b h
цилиндр = b h = pi r 2 h
пирамида = (1/3) h
конус = (1/3) b h = 1/3 pi r 2 h
сфера = (4/3) pi r 3
эллипсоид = (4 / 3) pi r 1 r 2 r 3
Квартир
Объем измеряется в «кубических» единицах.Громкость фигуры — это количество кубиков, необходимых для ее полного заполнения, например блоки в коробке.
Объем куба = сторона, умноженная на сторону, умноженную на сторону. С каждая сторона квадрата одинакова, это может быть просто длина одного сторона в кубе.
Если у квадрата одна сторона 4 дюйма, объем будет быть 4 дюйма на 4 дюйма на 4 дюйма, или 64 кубических дюйма.(Кубический дюймы также можно записать в 3 .)
Обязательно используйте одни и те же единицы для всех измерений. Вы не можете умножить футы на дюймы на ярды, это не дает идеальное измерение в кубе.
Объем прямоугольной призмы равен длине сторона, умноженная на ширину, умноженную на высоту. Если ширина составляет 4 дюйма, длина 1 фут, а высота 3 фута, каков объем?
НЕ ПРАВИЛЬНО …. 4 раза 1 раз 3 = 12
ПРАВИЛЬНО …. 4 дюйма равны 1/3 фута. Объем: 1/3 фута умножить на 1 фут умножить на 3 фута = 1 кубический фут (или 1 куб. футов или 1 фут 3 ).
Площадь поверхности и объем трехмерных фигур
В этом разделе мы вычисляем объем и площадь поверхности трехмерных фигур, таких как кубов , кубов , призм и цилиндров .
| Куб | Объем = x ³ Площадь поверхности = 6 x ² | |
| Кубоид | Объем = xyz Площадь поверхности = 2 xy + 2 xz + 2 yz | |
| Цилиндр | Объем = π r ² h Площадь криволинейной поверхности = 2 π rh Площадь каждого конца = π r ² Общая площадь поверхности = 2 π rh + 2 π r ² | |
| Призма | Призма имеет однородное поперечное сечение Объем = площадь поперечного сечения × длина = А л |
Упражнения
Вопрос 5 На схеме показан деревянный брусок, в котором просверлено отверстие.Диаметр отверстия 2 см.
Вычислите объем этого твердого тела, дав правильный ответ с точностью до 2 знаков после запятой.
Объем = блок — отверстие = 4 × 6 × 6 — 1² × π × 6 = 144 — 6 π = 125,15 (до 2 d.p.)
Вопрос 7 На схеме показано сечение трубы длиной 50 см.
Внутренний диаметр трубы составляет 20 см, а внешний — 30 см.
(а)
(б)
| Общая площадь поверхности | = 2 × (15² — 10²) × π + 30 π × 50 + 20 π × 50 |
| = 250 π + 1500 π + 1000 π = 2750 π | |
| = 8639,379797 см² = 8640 см² (до 3 квадратных футов) |
Цилиндр имеет диаметр 12 см и площадь изогнутой поверхности 132 π или 415 см² (до 3 значащих цифр).
Вопрос 12(а)
(б)
Ящик стандартного размера содержит достаточно соли, чтобы заполнить 10 солонек.
(в)
Вопрос 13(а)
(б)
Каков объем этой призмы?
Площадь поперечного сечения = × основание × высота = × 6 × 8 = 24 см²
Объем призмы = площадь поперечного сечения × длина = 24 × 7 = 168 см³
(в)
Призмы A и B имеют одинаковую площадь поперечного сечения.
Заполните таблицу:
Обнаружение формул площади — элементарная математика
Формулы площади
Учащиеся, неформально относящиеся к области как к «количеству двумерного« материала », содержащегося внутри области, могут придумать для себя большинство формул, которые их часто просят просто запомнить. Каждая формула, которую они изобретают заново, помогает укрепить их понимание (и память) о других формулах, которые они знают. (См. Также площадь поверхности.)
Площадь прямоугольников
Выбирая квадрат в качестве единицы площади, мы получаем интуитивное представление о площади прямоугольников. Если мы решим, что площадь этого квадрата равна 1, то прямоугольник, который в 7 раз длиннее, будет иметь площадь 7 × 1.
Прямоугольник, который в два раза больше высоты, будет иметь удвоенную площадь, поэтому площадь составляет 2 × 7 единиц площади. Мы можем сосчитать два ряда по семь квадратов. Точно так же он имеет 3 ряда по 7 квадратов (или 7 столбцов по 3 квадрата), всего 7 × 3 квадратов, поэтому его площадь составляет 21 квадратную единицу.
Количество квадратов в одном ряду — это длина прямоугольника. Количество строк — это высота прямоугольника. Таким образом, площадь равна длине × высоте.
Поскольку прямоугольник можно нарисовать под наклоном, «высота» определяется как «направление, перпендикулярное основанию», а «основание» определяется как, ну, с какой бы стороны вы его ни выбрали.
Это работает для подсчета чисел. Это работает даже для дробей. Показанный здесь синий прямоугольник измеряет половину единицы длины на пять с половиной единиц длины.Если мы выберем соответствующий квадрат в качестве единицы площади, мы увидим, что синий прямоугольник содержит пять половин площади и одну четверть единицы площади, или всего две и три четверти единицы площади. (Розовые части показывают завершение каждой квадратной единицы площади.)
Чтобы включить всех чисел, мы определяем площадь прямоугольника как основание × высота (где «основание» и «высота» означают длины этих сторон, измеряется в те же единицы ).
Площадь параллелограммов
Идея
Мы можем вычислить формулу площади параллелограмма, разрезав параллелограмм и переставив части, чтобы получился прямоугольник. Поскольку параллелограмм и прямоугольник состоят из одинаковых частей, они обязательно имеют одинаковую площадь. (См. Определение площади, чтобы узнать, почему эти области одинаковы.)
Мы видим, что они и имеют точно такую же длину основания (синий) и точно такую же высоту (зеленый).Поскольку основание × высота дает площадь прямоугольника, мы можем использовать те же измерения на параллелограмме, чтобы вычислить его площадь: основание × высота . (Как и раньше, «высота» измеряется перпендикулярно основанию, а «основание» — это та сторона, которую вы выбрали первой. См. Параллелограмм.)
На разрезе, показанном выше, легко увидеть, что базовая длина не изменилась.Фактически, перпендикулярный разрез можно делать в любом месте по основанию.
Укрепление отверстий
Интуиция и доказательство
Это рассечение дает интуитивное понимание формулы площади параллелограмма, причина того, что она должна быть такой, какая есть. Но мы не сомневались, действительно ли рассечение «работает». То есть, когда мы разрезаем параллелограмм и переставляем его части, мы ожидаем, что получит , и результат определенно будет таким.Но внешность может быть обманчива. Что убеждает нас в том, что когда мы перемещаем этот треугольник, в результате получается прямоугольник? Что, если это больше похоже (хотя и менее преувеличено)? Если результат не всегда является идеальным прямоугольником, мы не можем использовать наши знания формулы площади прямоугольника, чтобы разработать формулу для параллелограмма. В старших классах учащиеся смогут доказать, что две части параллелограмма, если правильно собрать их, действительно образуют прямоугольник. В классах K-8 учащиеся по большей части должны полагаться на визуальный эксперимент и получать интуитивное ощущение.Узнайте больше о том, почему эти вскрытия работают.
Что, если мы выберем короткую сторону в качестве основы?
Мы можем выбрать любую сторону в качестве базы; «Высота» определяется как измеряемая перпендикулярно стороне, которую мы выбираем в качестве основания. Если мы возьмем за основу короткую сторону (синюю), то рассечение, показанное выше, не будет таким убедительным. Резка на такой высоте и перестановка деталей оставляет беспорядок:
В этом конкретном примере мы можем спасти беспорядок, сделав еще один разрез, но что, если бы параллелограмм был еще длиннее и тоньше?
Оказывается, любой параллелограмм , независимо от того, насколько он длинный и тонкий, можно разрезать таким образом, чтобы части — возможно, многие из них — могли быть преобразованы в прямоугольник.Но нужно потрудиться, чтобы показать, что это всегда можно сделать. Нам нужна другая идея.
Немного другая идея рассечения в этом случае значительно упрощает жизнь. (Самостоятельно вы можете показать, что это работает и в исходном случае.)
- Заключите параллелограмм в прямоугольник.
- Две части прямоугольника, которые составляют , а не внутри параллелограмма, являются конгруэнтными треугольниками.
- Сдвиньте один из этих треугольников по направлению к другому, пока они не встретятся, образуя прямоугольник.Поскольку общая площадь внешнего прямоугольника не изменилась (это тот же прямоугольник, что и раньше), а желтая область не изменилась (части просто перемещались), разница между ними — фиолетовыми областями — должна быть такой же. Как и раньше, мы также можем видеть, что размеры прямоугольной фиолетовой области являются основанием и высотой исходного параллелограмма.
Интуиция и доказательство, повторение: Опять же, рассечение дает существенное понимание, но требуется немного больше работы, чтобы убедиться, что два желтых треугольника, которые, безусловно, выглядят так, как будто они соединяются вместе, образуя прямоугольник, на самом деле точно подходят, а не просто почти .
Почему так важно быть осторожным?
При построении других формул площади (см. Ниже) мы захотим, чтобы использовал , как найти площадь параллелограмма, и поэтому мы хотим иметь возможность полагаться на найденное нами правило. Мы, , можем быть уверены, что перестановка частей не повлияет на область: то есть, в конце концов, как мы определяем область . Но мы также должны быть уверены, что детали подходят друг к другу, как мы заявляем, что они делают, иначе мы не можем полагаться на сделанные нами измерения.И мы должны быть уверены, что правило base × height не зависит от удачного выбора базы.
В большинстве учебных программ учащиеся не имеют достаточной систематической базы геометрических знаний до 8-го класса, чтобы убедительно доказать, что эти вскрытия работают. Но интуитивного понимания достаточно для объяснения и обоснования формул и хорошей основы для дальнейшего изучения геометрии.
Площадь треугольника
Знание того, как найти площадь параллелограмма, помогает нам найти площадь треугольника.
Рассечение треугольника
Мы можем разрезать треугольник на две части — одну из них треугольник, а другую — трапецию, разрезав его параллельно основанию. Если мы разрежем высоту ровно пополам с этим срезом, две части сложатся вместе, образуя параллелограмм с тем же основанием , но половиной высоты .
Итак, основание × полувысота дает площадь треугольника. Аналогичный разрез показывает полубаз × высота .Любой из них сокращается до bh .
Удвоение треугольника и уменьшение полученной площади пополам
Другой способ мышления: две копии треугольника образуют параллелограмм с тем же основанием, и той же высотой , что и треугольник.
Площадь параллелограмма составляет основания × высота , но это вдвое больше площади треугольника, поэтому площадь треугольника составляет из основания × высоты , как мы видели с методом рассечения.
(Как всегда, выберите «основание» и измерьте высоту перпендикулярно этому основанию, от основания до противоположной вершины.)
Площадь трапеции
Удвоение трапеции и уменьшение полученной площади пополам
Как и в случае с треугольником, две копии трапеции можно соединить вместе, чтобы получился параллелограмм.
Высота параллелограмма равна высоте трапеции, но его основание равно сумме двух оснований трапеции.Таким образом, площадь параллелограмма равна высотой × ( base1 + base2 ). Но эта площадь составляет две трапеции , поэтому нам нужно разрезать ее пополам, чтобы получить площадь трапеции.
Рассечение трапеции
Мы также можем разрезать трапецию так же, как мы разрезали треугольник, с одним срезом, разрезающим ее высоту пополам. Две части соединяются вместе, образуя параллелограмм, основание которого является суммой двух оснований трапеции, но высота которого равна половине высоты трапеции.
В случае трапеции основания не могут быть выбраны произвольно. Две стороны , параллельные , являются основаниями, а высота, как всегда, представляет собой перпендикулярное расстояние от одного основания до противоположного.
Площадь этого параллелограмма равна его высоте (полувысоте трапеции), умноженной на его основание (сумма оснований трапеции), поэтому его площадь составляет полувысоты × ( base1 + base2 ). Поскольку параллелограмм состоит из того же материала, что и трапеция, это тоже площадь трапеции.
В любом случае площадь трапеции составляет × по высоте × ( base1 + base2 ) .
Площадь других специальных четырехугольников
Площадь ромба
Площадь ромба можно найти, разрезав и переставив части так, чтобы они образовали параллелограмм. Это можно сделать несколькими способами:
- Разрежьте более короткую диагональ (а), чтобы получились два равных треугольника. Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы получился параллелограмм.Более короткая диагональ (a) становится основанием параллелограмма, а половина более длинной диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба.
- Другой аналогичный способ — разрезать ромб на четыре равных треугольника и переставить их в прямоугольник с более короткой диагональю в качестве основания и половиной длинной диагонали в качестве высоты.
- После разрезания ромба на два равных треугольника мы можем вычислить площадь одного из треугольников, которая равна * основанию (a) * высоте (b) = ab.Затем умножьте на два, так как их два: 2 * ab = ab.
Зона воздушного змея
Площадь воздушного змея может быть похожа на площадь ромба. Если разрезать более длинную диагональ, получатся два равных треугольника. Если мы переставим их, мы можем сформировать параллелограмм с более длинной диагональю (b) в качестве основания и половиной более короткой диагонали (a) в качестве высоты. Итак, площадь становится b * a = ab. Более сложный подход требует немного алгебры. Разрежьте змей по более короткой диагонали, чтобы сформировать два треугольника с более короткой диагональю (a) в качестве основы.Таким образом, площадь первого треугольника — * волнистая, где волнистая — высота. Площадь второго треугольника равна a * (b — волнистый), где (b — волнистый) — оставшаяся часть большей диагонали. Таким образом, общая площадь становится (a * волнистая) + (a * (b — волнистая)). Вынося за скобки a, получаем a (волнистый + b — волнистый) = ab.
Ну что вы знаете. По сути, вам нужно только знать формулу для площади параллелограмма, а затем вывести формулу для других.
Площадь поверхности и объем трехмерных фигур
Мы видим твердые тела везде, куда бы мы ни посмотрели.В большинстве случаев эти твердые тела либо имеют форму куба, цилиндра, конуса и т. Д., Либо имеют форму, сочетающую эти формы. Для решения многих реальных задач важно знать, как рассчитать площадь и объем этих форм. Например, художник может захотеть узнать область, которую он должен нарисовать для данной формы. Точно так же, прежде чем сделать металлический шар, нам нужно знать, сколько материала потребуется. Все это требует определенных знаний об объеме и площади поверхности основных форм.Посмотрим на них подробнее.
Площадь поверхности и объем твердых тел
Площадь поверхности — это площадь, которая описывает количество материала, используемого для покрытия геометрического тела, в то время как объем может быть определен как мера того, сколько места занимает твердое тело. Важно знать формулы для расчета площадей и объемов основных форм. Давайте посмотрим на поверхность следующих форм:
КубоидНа рисунке ниже показана форма куба, это форма наших коробок, картонных коробок и т. Д., Наша цель — вывести формулы для расчета площади поверхности и громкость.Допустим, длина кубоида равна l, ширина — b, а высота — h.
Площадь поверхности кубоидаЧтобы вычислить площадь поверхности куба, откройте его, как показано на рисунке ниже. Теперь на рисунке показан сплющенный кубоид. Он состоит из 6 прямоугольников, соответствующих шести граням кубоида. Для площади поверхности куба нам нужно узнать общую площадь всех прямоугольников.
Объем кубоидаОбщая площадь поверхности = Площадь прямоугольника 1 + Площадь прямоугольника 2 + Площадь прямоугольника 3 + Площадь прямоугольника 4 + Площадь прямоугольника 5 + Площадь прямоугольника 6
⇒ (l × h) + (l × b) + (l × h) + (l × b) + (b × h) + (b × h)
⇒ 2 (lh + lb + bh)
Таким образом, площадь поверхности кубоида = 2 ( lh + lb + bh)
Мы знаем, что объем области определяется ее величиной, то есть тем, сколько места она занимает.
КубОбъем кубоида = площадь основания x высота
= l × b × h
= lbh
Куб представляет собой сплошную форму со всеми сторонами равной длины. Мы знаем, что куб — это просто кубоид со всеми равными сторонами. Наша цель — вывести формулы для расчета площади поверхности и объема куба. На рисунке ниже изображен куб.Обратите внимание, что все стороны равны, и он похож на кубоид. Куб — это кубоид, у которого все стороны равны. То есть
l = b = h = a
Где «a» — длина стороны куба.
Площадь поверхности кубаТаким образом, поместив это в формулу выше
Объем кубаПлощадь поверхности куба = 2 (a 2 + a 2 + a 2 )
⇒ 2 ( 3a 2 ) = 6a 2
Аналогично описанному выше методу, давайте подставим длину стороны в формулу.
Правый круговой цилиндрОбъем = фунт / час
= aaa
= a 3
Банки для колы, которые мы используем, являются примером правильного кругового цилиндра. Его также можно найти в других местах нашей жизни, например, наши ручки также похожи на цилиндры. На рисунке ниже показан цилиндр и его развернутая версия, которая будет использоваться для расчета площади поверхности. Допустим, высота цилиндра равна «h», а его радиус — «r».
Площадь поверхности цилиндраНа рисунке выше показан цилиндр в развернутом состоянии. Когда он развернут, становится легко найти площадь его поверхности. Обратите внимание, что в развернутом виде цилиндр выглядит как прямоугольник. Ширина прямоугольника будет обозначена буквой «h», а длина — окружностью цилиндра.
Объем цилиндраОкружность цилиндра = 2πr
Площадь прямоугольника = 2πrh
Таким образом, площадь поверхности правого кругового цилиндра = 2πrh
Общая площадь поверхности правого кругового цилиндра = Площадь поверхности цилиндра + Площадь база
= 2πrh + 2πr 2 = 2πr (r + h)
СфераОбъем цилиндра = площадь основания x высота
= πr 2 × h
67 = πrr 2 h
Сфера — это трехмерная фигура (сплошная фигура), которая состоит из всех точек в пространстве, которые лежат на постоянном расстоянии, называемом радиусом, от фиксированной точки, называемой Центр сферы.На рисунке ниже показана сфера и ее сплющенная версия в разрезе. Это используется для вычисления площади поверхности сферы.
Площадь поверхности сферыКак и в предыдущих случаях, мы разрежем сферу и сплющим ее.
На рисунке мы видим, что при разрезании сферы образуется площадь, эквивалентная четырем сферам.
Объем сферыТаким образом, площадь поверхности сферы = 4πr 2
Эта формула доказана экспериментально, поэтому мы не можем здесь привести никаких доказательств.
КонусОбъем сферы =
Конус — это трехмерная фигура, основание которой представляет собой круг, а высота сужается и встречается в конце. Вершина — это название заостренного конца конуса, мы видим множество форм в форме конуса в нашей повседневной жизни, например, мороженое имеет форму конуса и т. Д.
На рисунке ниже , конус имеет радиус «r» и высоту «h».
Площадь поверхности конусаПлощадь поверхности конуса определяется как
Объем конусаИзогнутая поверхность Площадь конуса =
Где
Объем конуса конус равен,
Объем конуса =
Полусфера
Представьте себе плоскость, разделяющую сферу на две равные части, каждая часть известна как полусфера.Термин полушарие используется для объяснения различных частей земного шара, северного полушария, южного полушария, восточного полушария, западного полушария.
Площадь поверхности полушарияПоскольку полусфера — это полусфера, площадь поверхности также будет равна половине, но вместе с этим также будет видно основание в форме круга, которое также включено в площадь поверхности полушария.
Следовательно, площадь поверхности полушария = 2πr 2 + πr 2
= 3πr 2
Объем полушарияОбъем полусферы будет составлять половину объема сферы.
Объем полусферы =
Призма
Призма — это трехмерная фигура, имеющая два основания, обращенных друг к другу, эти основания могут иметь форму треугольника, прямоугольника или любого многоугольника. Материал призмы — преимущественно флюорит, стекло, пластик.
Основание призмы может быть правильным или неправильным, если основание неправильное, оно называется неправильной призмой. Если основание призмы правильное, призма является правильной призмой.
Площадь поверхности призмыДавайте посмотрим на площадь поверхности треугольной призмы,
Площадь поверхности призмы = 2 (площадь треугольных оснований) + (площадь прямоугольника с основанием b и длиной l) + 2 (площадь прямоугольника со стороной s и длиной l).
Объем призмыПлощадь поверхности призмы = 2 (1/2 × b × h) +2 (s × l) + (b × l)
= (b × h) + 2 (s × l) + (l × b)
Объем призмы — это площадь квадрата, умноженная на высоту / длину призмы,
Объем призмы = 1 / 2 bhl
Давайте посмотрим на некоторые примеры задач по этим концепциям
Примеры задачВопрос 1: Найдите объем и площадь поверхности куба со стороной a = 10 см.
Решение:
Мы знаем формулы для определения площади поверхности и объема.
Площадь поверхности = 6a 2
= 6 (10) 2 {При a = 10 см}
= 6 (100)
= 600 см 2
Объем куба = a 3
= (10) 3
= 1000 см 3
Вопрос 2: Найдите объем и площадь поверхности резервуара для воды, имеющего форму цилиндра с радиус 10 м и высота 40 м.
Решение:
Нам известны формулы для определения площади поверхности и объема цилиндра.
r = 10 и h = 40.
Площадь поверхности цилиндра = Площадь изогнутой поверхности + Площадь оснований
Объем цилиндра,
Вопрос 3: Найдите объем и площадь поверхности рожка мороженого с радиусом 3 см и высотой составляет 4 см.
Решение:
Рожок мороженого — это, по сути, рожок.Нам нужно найти площадь и объем этого конуса. Поскольку конус не закрыт сверху, нам нужно найти только площадь криволинейной поверхности.
Площадь поверхности конуса,
Объем конуса,
Вопрос 4: Найдите объем и площадь поверхности сферы с радиусом 10 см.
Решение:
Дано r = 10 см.
Площадь поверхности
Объем
Вопрос 5: Найдите площадь поверхности полусферы радиусом 7 см, также найдите объем.
Решение:
Площадь полушария =
= 3 × 22/7 × (7 × 7)
= 462 см 2
Объем полушария
= 1437,333 см 3
Вопрос 6: Найдите площадь поверхности треугольной призмы, указанной на рисунке ниже,
Решение:
Площадь поверхности призмы = (b × h) + 2 (l × s) + (l × b)
= (5 × 5) + 2 (7 × 10) + (5 × 10)
= 25+ 140+ 50
= 75+ 140
= 215см 2
Что такое область 2D-форм?
Что такое площадь 2D-фигур?
Площадь любой 2D-формы — это размер области, заключенной в нее.Есть несколько 2D-форм, таких как квадрат, прямоугольник, круг, ромб и треугольник. Цветная область в каждой форме представляет область соответствующей формы.
Единица площади называется квадратными. У разных форм есть разные формулы для расчета площади.Площадь квадрата и прямоугольника :
Площадь квадрата и прямоугольника равна произведению двух смежных сторон.
| 2D Форма | Формула площади | Пример |
| Квадрат | Площадь квадрата = Сторона × Сторона Площадь = S × S | Площадь = 4 × 4 = 16 кв.размеры в см |
| Прямоугольник | Площадь прямоугольника = длина × ширина = длина × ширина | Площадь = 8 × 3 = 24 кв. См |
Площадь треугольника :
Треугольники могут быть разных типов, например равносторонний треугольник, равнобедренный треугольник и прямоугольный треугольник, но формула для площади всех видов треугольников одинакова.
Площадь треугольника определяется по формуле: 1 ⁄ 2 × b × h, где основание (b) — длина любой стороны треугольника, а высота (h) — перпендикулярное расстояние между основанием. и верхняя вершина треугольника.
Пример:
В треугольнике ABC основание составляет 6 единиц, а высота — 4 единицы.
Итак, площадь треугольника ABC = 1 ⁄ 2 × b × h
= 1 ⁄ 2 × 6 × 4
= 12 кв. Единиц
Круг :
Площадь круга вычисляется по формуле π × r 2 , где r — радиус круга, а π — константа, значение которой равно 227 или 3.14
Пример: Площадь вышеуказанного круга = π × r 2
= 3,14 × 4 2
= 3,14 × 16
= 50,24 кв. См
Ромб :
Формула для определения площади ромба: pq / 2, где p и q — две диагонали ромба.