Тригонометрическая и алгебраическая форма комплексного числа – Формы записи комплексного числа: алгебраическая, тригонометрическая и показательная

Формы записи комплексных чисел, определения и примеры

Существует три формы записи комплексных чисел: алгебраическая, тригонометрическая и показательная. Каждая форма записи удобна для решения своих задач, соответственно вы можете переводить комплексное число из одной формы в другую, в зависимости от решаемой задачи.

Алгебраическая форма комплексного числа

Например:

1. Комплексное число и его сопряженное число записаны в алгебраической форме.
2. Мнимое число записано в алгебраической форме.

Подробнее про алгебраическую форму читайте в отдельной статье: Алгебраическая форма комплексного числа.

Тригонометрическая форма комплексного числа

ОПРЕДЕЛЕНИЕ Тригонометрической формой комплексного числа , не равного нулю, называется запись где — модуль комплексного числа .

Ниже мы подробно распишем, как вычислять модуль и аргумент комплексного числа и приведем примеры.

Подробнее про тригонометрическую форму читайте в отдельной статье: Тригонометрическая форма комплексного числа.

Модуль и аргумент комплексного числа

ОПРЕДЕЛЕНИЕ Модулем комплексного числа называется выражение .

Если является действительным числом, то его модуль равен абсолютной величине этого действительного числа.

Например.

Показательная форма комплексного числа

ОПРЕДЕЛЕНИЕ Показательной формой комплексного числа называется выражение , где — модуль комплексного числа, — расширение экспоненты на случай, когда показатель степени является комплексным числом.

Подробнее про показательную форму читайте в отдельной статье: Показательная форма комплексного числа.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Лекция 4 — Комплексные числа. Алгебраическая и тригонометрическая форма записи комплексного числа. Действия над комплексными числами в алгебраической и тригонометрической форме.

Страница 1 из 3

Комплексные числа

Прежде чем, мы перейдем к рассмотрению комплексных чисел, дам важный совет: не пытайтесь представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве.

Если хотите, комплексное число – это двумерное число. Оно имеет вид , где и – действительные числа, – так называемая мнимая единица. Число называется действительной частью () комплексного числа , число называется мнимой частью () комплексного числа .

– это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: или переставить мнимую единицу: – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке

:

Чтобы всё было понятнее, сразу приведу геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости:

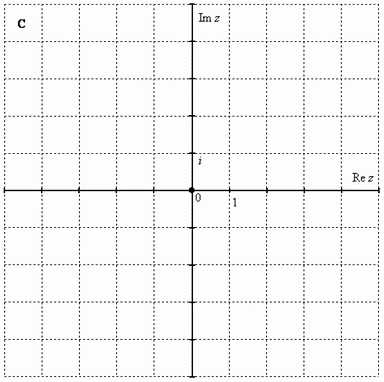
Как упоминалось выше, буквой принято обозначать множество действительных чисел. Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой . Поэтому на чертеже следует поставить букву , обозначая тот факт, что у нас комплексная плоскость.

Комплексная плоскость состоит из двух осей:

– действительная ось

– мнимая ось

Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат. По осям нужно задать масштаб, отмечаем:

ноль;

единицу по действительной оси;

мнимую единицу по мнимой оси.

Не нужно проставлять все значения: …–3, –2, –1, 0, 1, 2, 3,… и .

Да чего тут мелочиться, рассмотрим чисел десять.

Построим на комплексной плоскости следующие комплексные числа:

, ,
, ,
, , ,

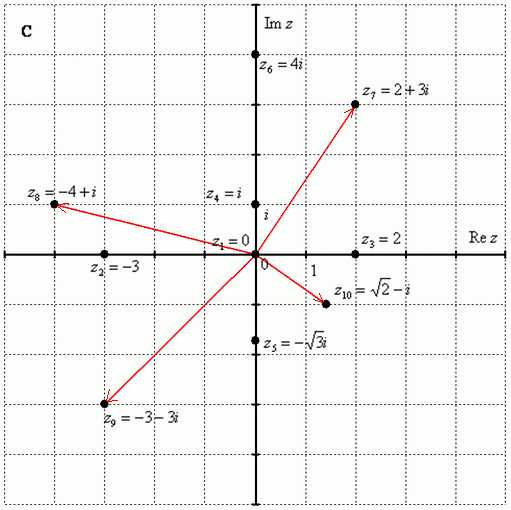
По какому принципу отмечены числа на комплексной плоскости, думаю, очевидно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.

Рассмотрим следующие комплексные числа: , , . Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось обозначает в точности множество действительных чисел , то есть на оси сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел является подмножеством множества комплексных чисел .

Числа , , – это комплексные числа с нулевой мнимой частью.

Числа , , – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси .

В числах , , , и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому что они сливаются с осями.

 

grishko.esy.es

Алгебраическая форма комплексного числа

ОПРЕДЕЛЕНИЕ Алгебраической формой комплексного числа называется запись комплексного числа в виде , где и – действительные числа, – мнимая единица, удовлетворяющая соотношению .

Число называется действительной частью комплексного числа и имеет обозначение .

Число называется мнимой частью комплексного числа и имеет обозначение .

Например:

1. Комплексное число и его сопряженное число записаны в алгебраической форме.
2. Мнимое число записано в алгебраической форме.

Также, в зависимости от решаемой задачи, вы можете перевести комплексное число в тригонометрическую или показательную форму.

ПРИМЕР

Задание	Записать число в алгебраической форме, найти его действительную и мнимую части, а также сопряженное число.
Решение	Применяя почленное деление дроби и правило сложения дробей, получаем:     Следовательно, действительной частью комплексного числа является число , мнимой частью является число . Сопряженное число имеет вид: .
Ответ

Действия над комплексными числами в алгебраической форме

Сравнение

Два комплексных числа и называются равными, если , т.е. равны их действительные и мнимые части.

ПРИМЕР

Задание	Определить, при каких и два комплексных числа и являются равными.
Решение	По определению два комплексных числа являются равными, если равны их действительные и мнимые части, т.е. .
Ответ

Сложение

Сложение комплексных чисел и выполняется непосредственным суммированием действительных и мнимых частей:

   

ПРИМЕР

Задание	Найти сумму комплексных чисел .
Решение	Действительной частью комплексного числа является число , мнимой частью является число . Действительная и мнимая части комплексного числа равны и , соответственно. Следовательно, сумма комплексных чисел равна:
Ответ

Подробнее про сложение комплексных числе читайте в отдельной статье: Сложение комплексных чисел.

Вычитание

Вычитание комплексных чисел и выполняется непосредственным вычитанием действительных и мнимых частей:

   

ПРИМЕР

Задание	Найти разность комплексных чисел .
Решение	Найдем действительные и мнимые части комплексных чисел :         Следовательно, разность комплексных чисел равна:
Ответ

Умножение

Умножение комплексных чисел и выполняется непосредственным произведением чисел в алгебраической форме, учитывая свойство мнимой единицы :

   

   

ПРИМЕР

Задание	Найти произведение комплексных чисел .
Решение	Произведение комплексных чисел равно:
Ответ

Подробнее про умножение комплексных чисел читайте в отдельной статье: Умножение комплексных чисел.

Деление

Частное комплексных чисел и находится путем домножения числителя и знаменателя на сопряженное число к знаменателю:

   

ПРИМЕР

Задание	Разделить число 1 на комплексное число .
Решение	Поскольку мнимая часть вещественного числа 1 равна нулю, частное чисел равно:
Ответ

Подробнее про деление комплексных чисел читайте в отдельной статье: Деление комплексных чисел.

Читайте также:

Все формы записи комплексных чисел

Тригонометрическая форма КЧ

Показательная форма КЧ

Мнимая часть комплексного числа

Комплексно сопряженные числа

Операции над комплексными числами

ru.solverbook.com

1.Комплексные числа. Свойства. Формы записи.

БИЛЕТ1

Комплексным числом называется выражение вида , где— действительные числа;— число, квадрат которого равен минус единице; число обозначается.

Свойства комплексных чисел:

1) комплексные числа коммутативны по сложению и по умножению.

2) комплексные числа ассоциативны по сложению и по умножению.

3) комплексные числа дистрибутивны.

Для комплексных чисел операция деления определена как операция обратная операции умножения. Если , то z является решением уравнения . Решим это уравнение, домножив левую и правую часть на и разделив обе части на квадрат модуля. Получим, что

Формы записи:

Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи.

Алгебраическая форма — это  такая форма записи комплексных чисел, при которой комплексное число  z, заданное парой вещественных чисел   (x , y), записывается в виде

где использован символ   i , называемый мнимой единицей. Число x называют вещественной (реальной) частью комплексного числа   z = x + i y   и обозначают   Re z. Число y называют мнимой частью комплексного числа   z = x + i y   и обозначают   Im z.

Тригонометрическая форма записи комплексного числа

      Из формулы вытекает, что любое отличное от нуля комплексное число   z = x + i y   может быть записано в виде

z = r (cos φ + i sin φ) ,

(5)

где   r  и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству  r > 0.

Формула Эйлера. Экспоненциальная форма записи комплексного числа

Формула Эйлера: cos φ + i sin φ = e ^iφ.

Из формулы Эйлера и тригонометрической формы записи комплексного числа вытекает, что любое отличное от нуля комплексное число z = x + i y   может быть записано в виде

где   r  и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству  r > 0.

БИЛЕТ 2.

2.Интегрирование простейших рациональных функций

Для интегрирования рациональной функции , где P(x) и Q(x) — полиномы, используется следующая последовательность шагов:

1)Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение; 2)Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений; 3)Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;

4)Вычислить интегралы от простейших дробей.

Рассмотрим указанные шаги более подробно. 

Шаг 1. Преобразование неправильной рациональной дроби

Если дробь неправильная (т.е. степень числителя P(x) больше степени знаменателя Q(x)), разделим многочленP(x) на Q(x). Получим следующее выражение:

где — правильная рациональная дробь. 

Шаг 2. Разложение знаменателя на простейшие дроби

Запишем многочлен знаменателя Q(x) в виде

где квадратичные функции являются несократимыми, то есть не имеющими действительных корней. 

Шаг 3. Разложение рациональной дроби на сумму простейших дробей.

Запишем рациональную функцию в следующем виде:

Общее число неопределенных коэффициентов A_i , B_i , K_i , L_i , M_i , N_i , … должно быть равно степени знаменателя Q(x).  Затем умножим обе части полученного уравнения на знаменатель Q(x) и приравняем коэффициенты при слагаемых с одинаковыми степенями x. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов A_i , B_i , K_i , L_i , M_i , N_i , …. Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов. 

Шаг 4. Интегрирование простейших рациональных дробей.

Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул:

У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат:

где Затем применяются следующие формулы:

Интеграл может быть вычислен за k шагов с помощью формулы редукции

БИЛЕТ 3

studfiles.net

Тема 18 тригонометрическая форма комплексного числа. Действия над комплексными числами в тригонометрической форме конспект 18.

18.1 Тригонометрическая форма комплексного числа

Любое комплексное число (кроме нуля) можно записать в тригонометрической форме:, где– этомодуль комплексного числа, а–аргумент комплексного числа. Изобразим на комплексной плоскости число. Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что: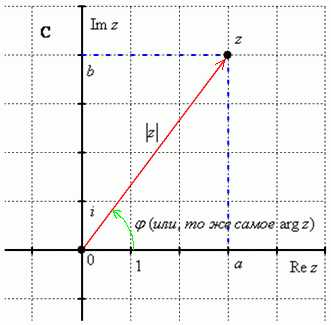

Напоминаю, модулем комплексного числаназывается расстояние от начала координат до соответствующей точки комплексной плоскости.

Модуль комплексного числа стандартно обозначают:или

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедливадля любыхзначений «а» и «бэ».

Аргументом комплексного числаназываетсяугол междуположительной полуосьюдействительной осии радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:.

Аргумент комплексного числа стандартно обозначают:или

Из геометрических соображений получается следующая формула для нахождения аргумента: .Внимание!Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем.

Но сначала рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях.

Пример 1

Представить в тригонометрической форме комплексные числа: ,,,.

На самом деле задание устное. Для наглядности перепишу тригонометрическую форму комплексного числа:

Запомним намертво, модуль – длина(которая всегданеотрицательна), аргумент –угол.

1) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что. Формальный расчет по формуле:. Очевидно, что(число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме:.

Ясно, как день, обратное проверочное действие:

2) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что. Формальный расчет по формуле:. Очевидно, что(или 90 градусов). На чертеже угол обозначен красным цветом. Таким образом, число в тригонометрической форме:.

Используя таблицу значений тригонометрических функций, легко обратно получить алгебраическую форму числа (заодно выполнив проверку):

3) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что. Формальный расчет по формуле:. Очевидно, что(или 180 градусов). На чертеже угол обозначен синим цветом. Таким образом, число в тригонометрической форме:.

Проверка:

4) И четвёртый интересный случай. Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что. Формальный расчет по формуле:.

Аргумент можно записать двумя способами: Первый способ: (270 градусов), и, соответственно:. Проверка:

18.2 ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ В ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ

Частное комплексных чисел

Произведение комплексных чисел

Возведение комплексных чисел в степень

формула Муавра

Пример 2

найти.

 

Тогда, по формуле Муавра:

Упаси боже, не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря,  нужно избавиться от лишних оборотов. Один оборот составляетрадиан или 360 градусов. Смотрим сколько у нас оборотов в аргументе:оборотов, в данном случае можно убавить один оборот:. Надеюсь всем понятно, чтои– это один и тот же угол.

Таким образом, окончательный ответ запишется так:

Любители стандартов везде и во всём могут переписать ответ в виде: (т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).

Хотя – ни в коем случае не ошибка.

ПРАКТИКУМ 18

ЗАДАНИЕ N 1Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

Решение:Для представления комплексного числа в тригонометрической форме записи необходимо найти его модуль и аргумент. Используя формулу, где– действительная, а– мнимая часть комплексного числа, получим:По формуламинайдем аргументкомплексного числа. Обращаем внимание, что под аргументомпонимается его главное значение, то есть значение, удовлетворяющее условиюТак кактоЗная, что тригонометрическая форма комплексного числа имеет видполучим:

ЗАДАНИЕ N 2Тема: Тригонометрическая форма комплексного числаПроизведение комплексных чиселиравно …

Решение:Воспользуемся формулой:Получим:

ЗАДАНИЕ N 3Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

Решение:Для представления комплексного числа в тригонометрической форме записи необходимо найти его модуль и аргумент. Заметим, что мнимая часть данного комплексного числа равна нулю, поэтомуТочка, изображающая это число, принадлежит положительной части действительной оси, значит,Зная, что тригонометрическая форма комплексного числа имеет видполучим:

ЗАДАНИЕ N 4Тема: Тригонометрическая форма комплексного числаЧастноекомплексных чиселиравно …

Решение:Воспользуемся формулой:Получим:

ЗАДАНИЕ N 5Тема: Тригонометрическая форма комплексного числаСтепень комплексного числаравна …

Решение:Согласно формуле Муавранаходим:

САМОСТОЯТЕЛЬНАЯ РАБОТА 18

ЗАДАНИЕ N 1Тема: Тригонометрическая форма комплексного числаСтепень комплексного числаравна …

ЗАДАНИЕ N 2Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

ЗАДАНИЕ N 3Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

ЗАДАНИЕ N 4Тема: Тригонометрическая форма комплексного числаЧастноекомплексных чиселиравно …

ЗАДАНИЕ N 5Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

 ЗАДАНИЕ N 6Тема: Тригонометрическая форма комплексного числаЧастноекомплексных чиселиравно …

ЗАДАНИЕ N 7Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

 

ЗАДАНИЕ N 8Тема: Тригонометрическая форма комплексного числаСтепень комплексного числаравна …

ЗАДАНИЕ N 9Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

ЗАДАНИЕ N 10Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

ЗАДАНИЕ N 11Тема: Тригонометрическая форма комплексного числаЧастноекомплексных чиселиравно …

ЗАДАНИЕ N 12Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

ЗАДАНИЕ N 13Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

ЗАДАНИЕ N 14Тема: Тригонометрическая форма комплексного числаПроизведение комплексных чиселиравно …

studfiles.net

Комплексные числа. Алгебраическая, тригонометрическая и показательная форма комплексных чисел

Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i² = –1. Число aназывается действительной частью, а число b — мнимой частьюкомплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.

Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i² = –1). Число = a – bi называется комплексно-сопряженнымк z = a + bi. Равенство z · = a² + b² позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:

.

(Например, .)

Алгебраическая форма комплексного числа

 

Запись комплексного числа z в виде , где a и b — действительные числа, называется алгебраической формой комплексного числа.

 

Например .

 

Тригонометрическая форма комплексного числа

 

Если  — модуль комплексного числа , а  — его аргумент, то тригонометрической формой комплексного числа z называется выражение

 

Показательная форма комплексного числа

 

Показательной формой комплексного числа  называется выражение

 

 

Метод координат на плоскости. Основные задачи на метод координат

Основная идея метода координат на плоскости состоит в том, что геометрические свойства линии L выясняются путем изучения аналитическими и алгебраическими средствами свойств уравнения F(x, y) = 0 этой линии. Например, геометрический вопрос о числе точек пересечения прямой и окружности сводится к аналитическому вопросу о числе решений алгебраической системы уравнений прямой и окружности.

В аналитической геометрии на плоскости систематически исследуются так называемые алгебраические линии 1 — го и 2 — го порядков; эти линии в декартовых прямоугольных координатах определяются соответственно алгебраическими уравнениями 1 — й и 2 — й степеней. Линии 1 — го порядка суть прямые и обратно, каждая прямая определяется алгебраическим уравнением 1 — й степени Ax + By + C = 0. Линии 2 — го порядка определяются уравнениями вида Ax² + Bxy + Cy² + Dx + Ey + F = 0. Основной метод исследования и классификации этих линий заключается в подборе такой декартовой прямоугольной системы координат, в которой уравнение линии имеет наиболее простой вид, и последующем исследовании этого простого уравнения.

В аналитической геометрии в пространстве декартовы прямоугольные координаты x, y, z (абсцисса, ордината и аппликата) точки М вводятся в полной аналогии с плоским случаем. Каждой поверхности S в пространстве можно сопоставить ее уравнение F(x, y, z) = 0относительно системы координат Oxyz. При этом геометрические свойства поверхности S выясняются путем изучения аналитическими и алгебраическими средствами свойств уравнения этой поверхности. Линию L в пространстве задают как линию пересечения двух поверхностей S₁ и S₂. Если F₁(x, y, z) = 0 и F₂(x, y, z) = 0 — уравнения S₁ и S₂, то пара этих уравнений, рассматриваемая совместно, представляет собой уравнение линии L. Например, прямую в пространстве можно рассматривать как линию пересечения двух плоскостей. В аналитической геометрии в пространстве систематически исследуются так называемые алгебраические поверхности 1 — го и 2 — г порядков. Выясняется, что алгебраическими поверхностями 1 — го порядка являются лишь плоскости. Поверхности 2 — го порядка определяются уравнениями вида: Ax² + By² + Cz² + Dxy + Eyz + Fzx + Gx + Hy + Mz + N = 0.

Основной метод исследования и классификации этих поверхностей заключается в подборе такой декартовой прямоугольной системы координат, в которой уравнение поверхности имеет наиболее простой вид, и последующем исследовании этого простого уравнения.

 

studopedia.net

Тригонометрическая форма записи комплексного числа » Аналитическая геометрия f(x)dx.Ru

п.4. Тригонометрическая форма записи комплексного числа.

   Если точка z комплексной плоскости имеет декартовые координаты (х, у), т.е.  и полярные , то они связаны соотношением (1):

                             .

По определению,  и из (1) получаем:

                             .                                   (9)

Подставляя в алгебраическую форму записи числа z получаем: . Или

                                             (10)

Определение. Запись комплексного числа в виде (3) называется его тригонометрической формой.

Замечание. Поскольку одну букву писать экономнее нежели несколько, то чаще всего тригонометрическую форму комплексного числа пишут в виде:

                          ,                                (11)

где .

Теорема. (О равенстве комплексных чисел в тригонометрической форме.)

Два комплексных числа равны тогда и только тогда, когда равны их модули и аргументы.

   Доказательство. Так как между всеми комплексными числами и всеми точками комплексной плоскости существует взаимно однозначное соответствие, то равные комплексные числа отождествляются на комплексной плоскости с одной и той же точкой, следовательно, имеют одни и те же полярные координаты, т.е. полярный радиус, который по определению равен модулю комплексного числа, и полярный угол, который по определению равен аргументу комплексного числа. Обратно, если комплексные числа имеют равные модули и аргументы, то они изображаются на комплексной плоскости одной точкой и, следовательно, равны.

Теорема доказана.

   Используя соотношения, которые связывают полярные и декартовые координаты точки плоскости, можно найти модуль и аргумент комплексного числа зная его действительную и мнимую части.

   Пусть , т.е. , . Тогда

                                    ,                               (12)

, если точка z лежит в первой или четвертой четверти или , если точка z лежит во второй или третьей четверти. Также можно пользоваться формулами (6) – (8) п.1, где .

Пример. Найти тригонометрическую форму записи комплексного числа z, если:

а) ;  б) ;  в) ;  г) ;  д) .

Решение. а) , .

 , .

Ответ: .

б) , , , .

Ответ: .

в) , , , .

Ответ: .

г) , , , .

Ответ: .

д) , , ,

.

Ответ: , где .

Замечание. В некоторых случаях удобнее не пользоваться формулами, а изображать на чертеже соответствующую точку на комплексной плоскости и находить модуль и аргумент комплексного числа пользуясь чертежом. Например, найдем тригонометрическую форму комплексного числа .

   Число  соответствует на комплексной плоскости точке . Отметим ее на координатной плоскости:

                   

                                       рис.5.

   Из рис.5 мы сразу же видим, что  и . Отсюда, .

Найдем, далее тригонометрическую форму числа комплексно сопряженного числу , т.е. .

Из рис.5 мы видим, что ,  и

 или .

   Замечание. Несмотря на то, что , а , форма записи комплексного числа z с аргументом  в виде  не является тригонометрической, т.к. . В этом случае правильной записью тригонометрической формы комплексного числа будет:

 или .

Возможно найдутся ответы здесь:

fxdx.ru