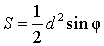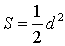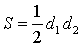Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
S = ab,
которая позволяет найти площадь прямоугольникапрямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник |  | S = ab | a и b – смежные стороны |
 |
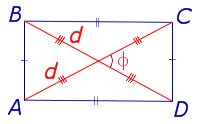Посмотреть вывод формулы | d – диагональ, | |
 | S = 2R2 sin φ Получается из верхней формулы подстановкой d=2R | R – радиус описанной окружности, | |
| Параллелограмм |  | S = a ha Посмотреть вывод формулы | a – сторона, |
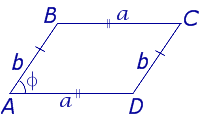 | S = absin φ Посмотреть вывод формулы | a и b – смежные стороны, | |
 |
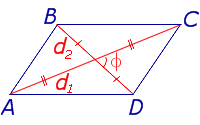Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | |
| Квадрат | 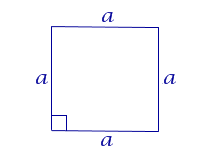 | S = a2 | a – сторона квадрата |
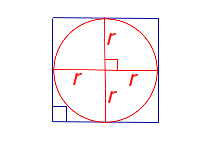 | S = 4r2 | r – радиус вписанной окружности | |
 |
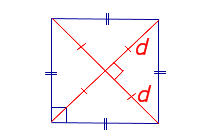Посмотреть вывод формулы | d – диагональ квадрата | |
 | S = 2R2 Получается из верхней формулы подстановкой d = 2R | R – радиус описанной окружности | |
| Ромб |  | S = a ha Посмотреть вывод формулы | a – сторона, |
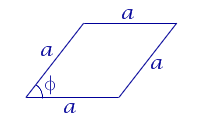 | S = a2 sin φ Посмотреть вывод формулы | a – сторона, | |
 |
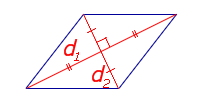Посмотреть вывод формулы | d1, d2 – диагонали | |
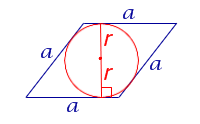 | S = 2ar Посмотреть вывод формулы | a – сторона, | |
 |
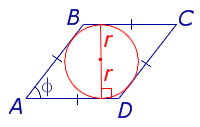Посмотреть вывод формулы | r – радиус вписанной окружности, | |
| Трапеция |  |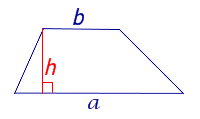
Посмотреть вывод формулы | a и b – основания, |
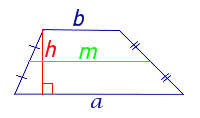 | S = m h | m – средняя линия, | |
 |
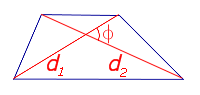Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | |
 |
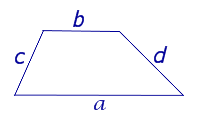Посмотреть вывод формулы | a и b – основания, | |
| Дельтоид | 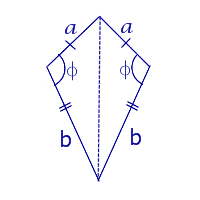 | S = ab sin φ | a и b – неравные стороны, |
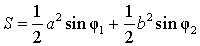 |  | a и b – неравные стороны, | |
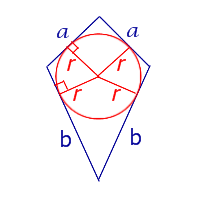 | S = (a + b) r Посмотреть вывод формулы | a и b – неравные стороны, | |
 |
Посмотреть вывод формулы | d1, d2 – диагонали | |
| Произвольный выпуклый четырёхугольник |  |
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними |
| Вписанный четырёхугольник |  |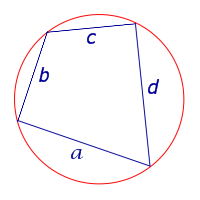
Посмотреть вывод формулы Брахмагупты | a, b, c, d – длины сторон четырёхугольника, Формулу называют «Формула Брахмагупты» |
| Прямоугольник | |
| S = ab где |
|
где Посмотреть вывод формулы |
| S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R |
| Параллелограмм | |
| S = a ha где Посмотреть вывод формулы |
| S = absin φ где Посмотреть вывод формулы |
|
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Квадрат | |
| S = a2 где |
| S = 4r2 где |
|
где Посмотреть вывод формулы |
| S = 2R2 где Получается из верхней формулы подстановкой d = 2R |
| Ромб | |
| S = a ha где Посмотреть вывод формулы |
| S = a2 sin φ где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
| S = 2ar где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
| Трапеция | |
|
где Посмотреть вывод формулы |
| S = m h где |
|
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
| Дельтоид | |
| S = ab sin φ где |
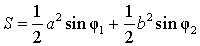| где |
| S = (a + b) r где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
| Произвольный выпуклый четырёхугольник | |
|
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Вписанный четырёхугольник | |
|
где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты |
| Прямоугольник |
S = ab где |
где Посмотреть вывод формулы |
S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R |
| Параллелограмм |
S = a ha где Посмотреть вывод формулы |
S = absin φ где Посмотреть вывод формулы |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Квадрат |
S = a2 где |
S = 4r2 где |
где Посмотреть вывод формулы |
S = 2R2 где Получается из верхней формулы подстановкой d = 2R |
| Ромб |
S = a ha где Посмотреть вывод формулы |
S = a2 sin φ где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
S = 2ar где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Трапеция |
где Посмотреть вывод формулы |
S = m h где |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
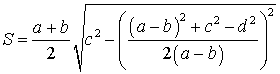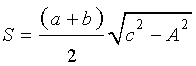  где Посмотреть вывод формулы |
| Дельтоид |
S = ab sin φ где |
где |
S = (a + b) r где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Произвольный выпуклый четырёхугольник |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Вписанный четырёхугольник |
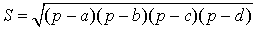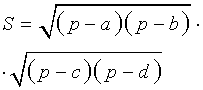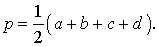   где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты |
Вывод формул для площадей четырехугольников
Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле
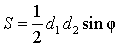
где d1 и d2 – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис. 1).
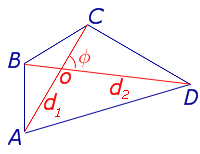
Рис. 1
Доказательство. В соответствии с рисунком 1 справедливо равенство:
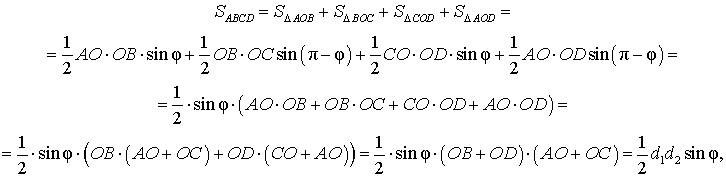
что и требовалось доказать.
Утверждение 2. Площадь параллелограммапараллелограмма можно найти по формуле
S = a ha ,
где a – сторона параллелограмма, а ha – высотавысотавысота, опущенная на эту сторону (рис. 2).
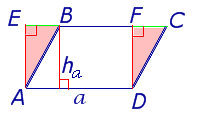
Рис. 2
Доказательство. Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
SABCD = SAEFD = a ha ,
что и требовалось доказать.
Утверждение 3.Площадь параллелограмма параллелограмма можно найти по формуле
S = ab sin φ,
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
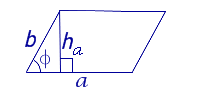
Рис. 3
Доказательство. Поскольку
ha = b sin φ,
то, в силу утверждения 2, справедлива формула
S = a ha = ab sin φ,
что и требовалось доказать.
Утверждение 4. Площадь ромбаромба можно найти по формуле
,
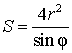где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
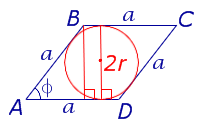
Рис. 4
Доказательство. Поскольку каждая из диагоналей ромба является биссектрисой угла, а каждая точка биссектрисы угла равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена от всех сторон ромба и является центром вписанной в ромб окружности. Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
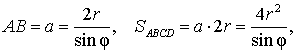
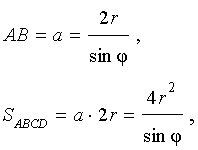
что и требовалось доказать.
Утверждение 5. Площадь трапеции можно найти по формуле
,
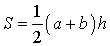где a и b – основания трапеции, а h – высотавысотавысота (рис.5).
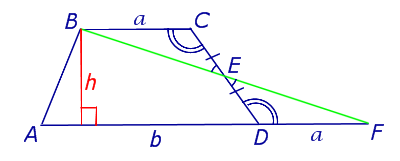
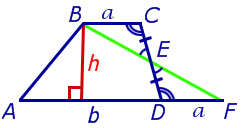
Рис. 5
Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF. Поэтому
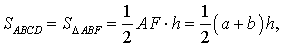
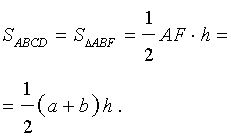
что и требовалось доказать.
Утверждение 6. Площадь трапеции трапеции можно найти по формуле
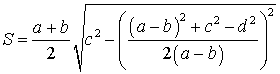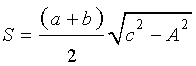
,где a и b – основания, а c и d – боковые стороны трапеции,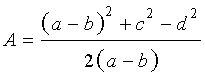
(рис.6).
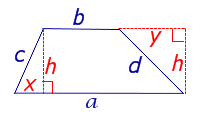
Рис. 6
Доказательство. Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
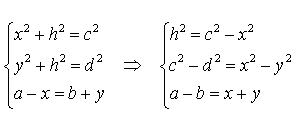
Следовательно,
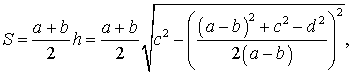
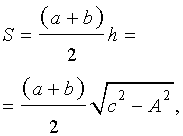
где
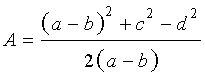,что и требовалось доказать.
Утверждение 7. Площадь дельтоида, дельтоида, можно найти по формуле:
S = (a + b) r,
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
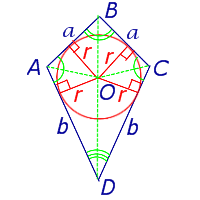
Рис. 7
Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
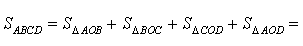
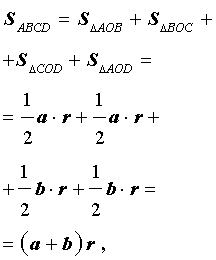
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Площади параллелограмма и ромба – методическая разработка для учителей, Айтмуханова Жанна Абаевна
|
Цели урока: |
Учащийся будет: |
|
Критерии оценивания: |
Учащийся: |
|
Языковые цели: |
Учащиеся будут:
Предметная лексика и терминология:
Серия полезных фраз для диалога/ письма:
|
|
Привитие ценностей: |
Уважение к себе и другим, сотрудничество через работу в паре и в группе, открытость – учащиеся самостоятельно могут определить цели урока и уровень сложности работы. |
|
Межпредметные связи: |
Взаимосвязь с алгеброй. Взаимосвязь с жизнью, через решение практических задач. Взаимосвязь с культурой. |
|
Предварительные знания: |
Знание единиц измерения, формул площади квадрата, площади прямоугольника. |
Ход урока
|
Запланированные этапы урока |
Запланированная деятельность на уроке |
Ресурсы |
|
Начало урока
0–3 мин
4–6 мин |
1. Организационный момент. Учащихся рассадить по группам по методу «Атомы и молекулы». — Сегодня на уроке мы продолжаем разговор о нахождении площадей многоугольников. Повторим известные нам свойства площадей, изученные формулы площадей некоторых видов многоугольников, применение их при решении задач. Продолжим исследование одного из видов многоугольников, а в частности параллелограмма и ромба, с целью вычисления их площадей. 2. Актуализация опорных знаний. Проверка домашнего задания. Учащиеся просматривают видео о вычислении площади, используя интернет ресурсы.
Работа в группе на логику: Посчитайте сколько ромбов изображено на рисунке. (24) |
https://bilimland.kz/ru/courses/math-ru/geometriya/planimetriya/chetyrexugolniki/lesson/ploshadi-pryamougolnika-parallelogramma-i-trapeczii Приложение 1 |
|
Середина урока 7–9 мин |
Ребята формулируют этапы решения задачи? 1.Необходимо знать площадь кухни S общ 2.Знать площадь одной плитки S одной плитки. 3.Площадь кухни поделить на площадь одной плитки: N = S общ : S одной плитки и узнать сколько таких плиток понадобиться. |
Презентация |
|
Середина урока 10–13 мин |
|
https://bilimland.kz/ru/subject/geometriya/8-klass/ploshad-parallelogramma-trapeczii |
|
Разминка 14–15 |
Австралийский дождь: — В Австралии поднялся ветер. (ведущий трет ладони) — Начинает капать дождь. (клацание пальцами) — Дождь усиливается. (поочередные хлопки ладонями по груди) — Начинается настоящий ливень. (хлопки по бедрам) — А вот и град – настоящая буря. (топот ногами) — Но что это? Буря стихает. (хлопки по бедрам) — Редкие капли падают на землю. (клацание пальцами) — Тихий шелест ветра. (ведущий трет ладони) — Солнце! (руки вверх) |
|
|
Середина урока 16–28 мин |
Работа в группе. Стратегия «Жигсо» Каждому участнику группы даются номерки с номером от 1 до 4. Затем все 1 собираются за 1 столом, 2 – за 2 столом, 3 – за 3 столом, 4 – за 4 столом. Каждая группа разбирает 1 задачу в течении 5 мин. Затем все возвращаются в свои группы и там рассказывают решение своей задачи. |
Приложение 2 |
|
Работа в группе 29-34 |
Групповая работа (3-4 человека). Стратегия «Репродукция картины».Для закрепления навыков применения формул вычисления площади учащимся предлагается собрать репродукции картин, например, работы Абильхана Кастеева (казахстанский художник). Для организации работы необходимо следующее. 1. Панно, на которое Учащиеся будут: крепить части репродукции, разделив его схематично на несколько частей, обозначив каждую часть номером.
2. Карточки с заданиями в соответствии с количеством ячеек на панно. Для составления карточек с заданиями можно использовать задачи на готовых чертежах. 3. Репродукция картины разрезается в соответствии со схемой заданий и на оборотной стороне пишутся ответы ко всем карточкам, не указывая номера заданий. 4. Разрезанные части репродукции перемешиваются с ответами. 5. Объединив учащихся в группы (по количеству репродукций или по количеству заданий), ученикам предоставляется панно для сбора репродукции, карточки с заданиями и части картины, на которых написаны ответы. Работая в группе, учащиеся выполняют задания, находят к ним части картины с соответствующими ответами и крепят найденные части картины к панно, тем самым собирая картину.
|
Приложение 3 |
|
Конец урока
35–40 мин |
Учащиеся заполняют лист самооценки ученика об успешности своего участия в коллективной работе группы и сдают учителю.
Рефлексия вывешивается перед выходом из класса и учащиеся прикрепляют стикер со своим именем: Я весь урок решал Я добросовестно выполнял Я принимал эти непонятные задачи всю работу на уроке участие в умножении своих знаний Домашнее задание: найти какие предметы окружающего мира имеют форму параллелограмма. |
Приложение 4 |
|
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? |
Здоровье и соблюдение техники безопасности. Связи с ИКТ. |
|
На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости). |
В ходе деятельности при решении задач, оцениваются знание известных формул, необходимых для вычисления площадей, умение применять их при практической работе. Предусмотрена самопроверка, в ходе которой ученики оценивают умение применять теоретические знания. |
Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, необходимо обеспечить безопасность. Следить за осанкой учащихся. |
Приложение 1
Приложение 2
1 группа:
Дан параллелограмм. S=96см2, ha= 8 см, hb=6 см. Найти P-периметр.
Решение.
1) S=ahа, отсюда a=S/hа;
S=bhb, отсюда b=S/hb.
2) а= 12 (см.)
b= 16 (см)
3) P=2(a+b).
P= 56 (см)
Ответ: 56 см.
2 группа:
Дан периметр параллелограмма ABCD равный 80 см, высота, проведенная к большей стороне равна 3 см. А стороны относятся как 2:3. Найдите площадь параллелограмма.
Решение:
- 2х+3х=80
5х=80
х=16
- 16*3=48 большая сторона
- S=48*3=144 см2
Ответ: 144 см2
3 группа:
Найти площадь ромба, если его сторона равна 5 см, а большая диагональ – 8 см.
Решение: 1) д2= 25-16=9 по т. Пифагора
2) S=12∙6∙8=24 см2
4 группа:
Периметр ромба равен 20 см, меньшая диагональ равна 6 см. Вычислите площадь ромба.
Решение: 1) а=20:4=5 см с- сторона ромба.
2) д2= 25-9=16=4 по т.Пифагора
3) ) S=12∙8∙6=24 см2
Приложение 3
Ответ к приложению 3:
Приложение 4
ФИ учащегося____________________________________
Поставьте «+» в одной из ячеек напротив каждого утверждения.
| отлично | хорошо |
удовлетворительно |
|
|
Я помогал группе при решении задачи. |
|||
|
Я оценил знания, которые уже имею. |
|||
|
Я подготовился к выступлению в группе. |
|||
|
Я учусь говорить четко и понятно, чтобы успешно выступить. |
|||
|
Я ответил на все вопросы, задаваемые участниками группы. |
|||
|
Я внимательно слушаю, когда рассказывают другие ученики. |
|||
|
Наблюдая за собой, я понял(а), каких знаний мне не хватает. |
|||
|
Я понял(а) какую информацию мне удалось получить в ходе работы и как я смогу применить ее на практике. |
Площадь параллелограмма, треугольника и трапеции — урок. Геометрия, 8 класс.
Площадь параллелограмма
Необходимо определить, что такое высота параллелограмма.
Это перпендикуляр, проведённый из любой точки стороны параллелограмма к прямой, содержащей противоположную параллельную сторону. Обычно высоту проводят из вершины параллелограмма. Так как параллелограмм имеет две пары параллельных сторон, то он имеет высоты двух различных длин.
Высота \(BE\), проведённая между длинными сторонами, короче высоты \(BF\), проведённой между короткими сторонами.
Так как стороны ромба одинаковы, то высоты ромба также одинаковы: \(BE = BF\).
Площадь произвольного параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.
Проведём высоты из двух вершин \(B\) и \(C\) к стороне \(AD\) .
Прямоугольные треугольники \(ABE\) и \(DCF\) равны (равные гипотенузы как противоположные стороны параллелограмма и равные катеты как расстояние между параллельными прямыми).
Параллелограмм \(ABCD\) и прямоугольник \(EBCF\) — равновеликие, так как состоят из равных фигур:
SABCD=SABE+SEBCD;SEBCF=SEBCD+SDCF.
Значит, площадь параллелограмма определяется так же, как площадь прямоугольника:
SEBCF=BE⋅BC;SABCD=BE⋅BC=BE⋅AD.
Если обозначить сторону через \(a\), высоту — через \(h\), то:
Sп−гр=a⋅h.
Для определения площади параллелограмма можно использовать короткую сторону и высоту, проведённую к короткой стороне.
Площадь ромба
Диагонали ромба в точке пересечения делятся пополам, они перпендикулярны и делят ромб на четыре равных прямоугольных треугольника.
SABCD=4⋅SABO=4⋅BO⋅AO2=2⋅BO⋅AO.
Формула определения площади ромба:
Sромба=d1⋅d22.
Эта формула справедлива для определения площади любого четырёхугольника, если его диагонали перпендикулярны.
Так как диагонали квадрата равны, то для определения площади квадрата в формуле достаточно длины одной диагонали:
Sквадрата=d22.
Площадь произвольного треугольника
Так как диагональ параллелограмма делит его на два равных треугольника, то площадь треугольника равна половине площади параллелограмма.
Sтреуг=aha2, где \(h\) — высота (на рисунке — \(BE\)), проведённая к стороне \(a\) (на рисунке — \(AD\)).
Для определения площади треугольника можно использовать любую сторону и высоту, проведённую к этой стороне.
Удобно иногда использовать формулу Герона, если известны длины всех трёх сторон треугольника.
SΔ=pp−ap−bp−c;p=a+b+c2
— формула Герона, где \(a\), \(b\) и \(c\) — стороны треугольника, \(p\) — полупериметр треугольника.
Площадь прямоугольного треугольника
Так как катеты прямоугольного треугольника взаимно перпендикулярны, то один катет может быть высотой, а другой катет — стороной, к которой проведена высота. Получаем формулу:
S=a⋅b2, где \(a\) и \(b\) — катеты.
Для прямоугольного треугольника также можно применять формулы площади произвольного треугольника.
Пример:
1. вычислим площадь треугольника со сторонами \(17\) см, \(39\) см, \(44\) см.
Решение:
p=17+39+442=50;SΔ=50⋅50−17⋅50−39⋅50−44=50⋅33⋅11⋅6==25⋅2⋅3⋅11⋅11⋅2⋅3=5⋅2⋅3⋅11=330см2.
Чтобы легче было вычислить корень, необходимо не перемножать все числа, а раскладывать их на множители: a⋅a=a.
Формулу Герона можно использовать для вычисления высоты треугольника.Пример:
2. вычислим меньшую высоту треугольника, стороны которого равны \(15\) см, \(13\) см, \(4\) см.
Решение:
используем две формулы вычисления площади: SΔ=aha2 и SΔ=pp−ap−bp−c.
Меньшая высота в треугольнике — та, которая проведена к большей стороне, поэтому \(a =\) \(15\) см.
SΔ=pp−ap−bp−c=16⋅1⋅3⋅12=24см2.
Составляем уравнение:
15⋅h3=24⋅215⋅h=48;h=4815=3,2(см).
Иногда формула Герона используется для вычисления площади параллелограмма, если даны стороны параллелограмма и его диагональ.
Пример:
3. дан параллелограмм со сторонами \(17\) см и \(39\) см, длина диагонали равна \(44\) см. Вычислим площадь параллелограмма.
Решение:
диагональ делит параллелограмм на два равных треугольника. Используем результат, полученный в первом примере:
Sпараллелограмма=2⋅SΔ=2⋅330=660(см2).
Площадь трапеции
Трапеция имеет одну пару параллельных сторон, следовательно, имеет одну высоту — перпендикуляр, проведённый между параллельными сторонами.
Чаще всего высоту трапеции проводят из вершин или через точку пересечения диагоналей.
Площадь трапеции определим как сумму площадей треугольников, на которые трапецию делит диагональ.
SABCD=SABD+SDBC;SABCD=AD⋅BE2+BC⋅DF2=AD⋅BE2+BC⋅BE2==AD+BC⋅BE2.
Если обозначить параллельные стороны (основания) трапеции через \(a\) и \(b\), высоту через \(h\), то:
Sтрап=a+b2⋅h.
Обрати внимание!
Важные следствия:
1. если высоты треугольников равны, то их площади относятся как длины оснований.
2. Если основания треугольников равны, то их площади относятся как длины высот.
3. Если высоты треугольников равны и их основания равны, то они равновелики, например, медиана делит треугольник на две равновеликие части.
Площадь параллелограмма
Площадь параллелограмма, формулы и калькулятор для вычисления площади в режиме онлайн.
Для вычисления площади параллелограмма применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади в режиме онлайн.
Площадь параллелограмма – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.
Таблица с формулами площади параллелограмма (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
1
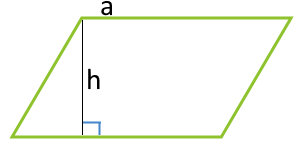
Площадь параллелограмма по основанию и высоте параллелограмма
… подготовка …
a — сторона
h — высота
2
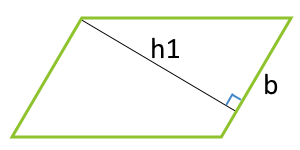
Площадь параллелограмма по стороне и высоте, опущенной на эту сторону
… подготовка …
b — сторона
hb — высота
3
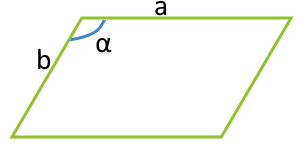
Площадь параллелограмма по двум сторонам и углу между ними
… подготовка …
a — сторона
b — сторона
α° — угол между сторонами
4
Площадь параллелограмма по двум диагоналям и углу между этими диагоналями
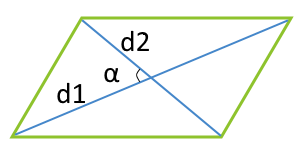
… подготовка …
d1 — диагональ
d2 — диагональ
α° — угол между диагоналями
5
Площадь параллелограмма по вписанной окружности и стороне
Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.
… подготовка …
a — сторона
r — радиус вписанной окружности
6
Площадь параллелограмма по вписанной окружности и углу между сторонами
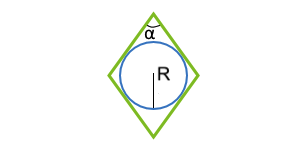
Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.
… подготовка …
r — радиус вписанной окружности
α° — угол между сторонами
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади параллелограмма
Определения
Параллелограмм — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.
Высота параллелограмма – это отрезок проведенный из вершины параллелограмма к противоположной стороне под углом в 90 градусов.
Некоторые свойства параллелограмма:
- Сумма углов параллелограмма равна 360 градусов
- Сумма углов, прилегающих к любой из сторон равна 180 градусов
- Противоположные стороны параллельны и имеют одинаковую длину
- Противолежащие углы равны
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Вывод формулы площади параллелограмма
Построим параллелограмм ABCD. Проведем в нем диагонали и обозначим точку их пересечения точкой О.
Рассмотрим треугольники AOD и СОВ. Эти треугольники равны между собой, а значит и площади их также равны.
Найдем сумму площадей этих двух треугольников:
Рассмотрим треугольники AOB и СОD. Эти треугольники равны между собой, а значит и площади их также равны.
Найдем сумму площадей этих двух треугольников:
Площадь параллелограмма можно найти как сумму площадей рассмотренных четырех треугольников:
Вынесем общие множители за скобки:
Сумма отрезков OD и ОВ дает диагональ параллелограмма BD, поэтому формулу перепишем в виде:
Известно, что у параллелограмма диагонали при их пересечении делятся пополам. Получаем, что отрезок АО равен половине диагонали АС. Таким образом, получим:
Итак, получена формула площади параллелограмма через его диагонали и угол между ними:
Все формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
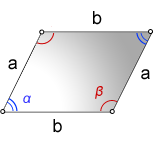
a, b — стороны параллелограмма
α, β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):
Калькулятор — вычислить, найти площадь параллелограмма:
a(сторона)=
b(сторона)=
α или β (угол в градусах)= ( sin α=sin β )
S=
2. Формула площади параллелограмма через сторону и высоту
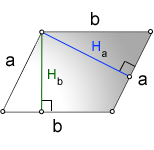
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
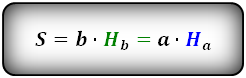
3. Формула площади параллелограмма через диагонали и угол между ними
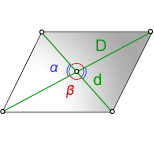
D — большая диагональ
d —меньшая диагональ
α, β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
Калькулятор — вычислить, найти площадь параллелограмма:
D (большая диагональ)=
d (меньшая диагональ )=
α или β (угол в градусах)= ( sin α=sin β )
S=
Формулы для параллелограмма:
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Острый угол и тупой угол параллелограмма
Углы между диагоналями параллелограмма
Формула суммы квадратов диагоналей параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Периметр параллелограмма
Все формулы по геометрии
Как найти площадь параллелограмма abcd: формула через стороны, диагонали
Параллелограмм – это геометрическая фигура; четырехугольник, у которого противоположные стороны равны и параллельны.
Формула вычисления площади
1. По длине стороны и высоте:
Площадь параллелограмма (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a * h
2. По двум сторонам и углу между ними:
Площадь параллелограмма находится путем умножения длин его обеих сторон и синуса угла между ними:
S = a * b * sin α
3. По двум диагоналям и углу между ними:
Площадь параллелограмма равна одной второй произведения длин его диагоналей, умноженного на синус угла между ними:
S = 1/2 * d1 *d2 * sin α
Примеры задач
Задание 1
Найдите площадь параллелограмма, если длина его стороны равняется 7 см, а высоты – 4 см.
Решение:
Используем первую формулу, в которой задействованы известные нам по условиям задания значения: S = 4 см * 7 см = 28 см2.
Задание 2
Найдите площадь параллелограмма, если его стороны равны 6 и 8 см, а угол между ними – 30°.
Решение:
Применим вторую формулу, рассмотренную выше: S = 6 см * 8 см * sin 30° = 24 см2.
Задание 3
Найдите площадь параллелограмма с диагоналями, равными 4 и 6 см. Угол между ними составляет 90°.
Решение:
Воспользуемся формулой, в которой фигурируют диагонали: S = 1/2 * 4 см * 6 см * sin 90° = 12 см2.
Площадь ромба Формула
Площадь формулы ромба — периметр и площадь ромба
СМОТРЕТЬ БОЛЬШЕ
Ромб — это параллелограмм, в котором смежные стороны равны (следовательно, все стороны равны).Диагонали ромба делят друг друга пополам, как параллелограмм, но они также перпендикулярны друг другу. Мы можем использовать этот факт, чтобы вывести простую и интересную формулу для площади ромба. На следующем рисунке показан ромб с известной длиной диагонали, скажем, $ {d_1} $ и $ {d_2} $.Мы знаем, что диагональ ромба делит его на два конгруэнтных треугольника, и, следовательно, эти два треугольника имеют равные площади. Поскольку диагонали ромба делят друг друга пополам под углом 90 ° , мы можем вычислить высоту и основание одного из этих треугольников и умножить результат на два, чтобы получить площадь ромба.
$ \ begin {gather}
AO = \ frac {{AC}} {2} = \ frac {{{d_2}}} {2} \ hfill \\
{\ text {area}} \ left ({\ Дельта ADB} \ right) = \ frac {1} {2} \ times DB \ times AO = \ frac {1} {2} \ times {d_1} \ times \ frac {{{d_2}}} {2} = \ frac {{{d_1} {d_2}}} {4} \ hfill \\
{\ text {area}} \, {\ text {of}} \, {\ text {rhombus}} = 2 \ times площадь \ left ({\ Delta ADB} \ right) = 2 \ times \ frac {{{d_1} {d_2}}} {4} = \ frac {{{d_1} {d_2}}} {2} \ hfill \\
\ end {gather} $
Давайте теперь рассмотрим пример.
Вопрос:
Если периметр ромба 20 см, а длина одной из диагоналей 6 см, рассчитайте его площадь.2}, $ найти длины двух его диагоналей.
Опции:
(a) $ 4 \, cm, \, \, 7 \, cm $
(b) $ 3 \, cm, \, \, 6 \, cm $
(c) $ 4.2 \, cm, \, \, 7.2 \, cm $
(d) ни один из этих
Ans wer : (a)
Решение:
$ {d_1} = x \, cm \ Rightarrow {d_2 } = \ left ({x + 3} \ right) \, см $
$ \ begin {gather}
{\ text {area}} = \ frac {{{d_1} {d_2}}} {2} = \ frac {{x \ left ({x + 3} \ right)}} {2} = 14 \ Rightarrow {x ^ 2} + 3x — 28 = 0 \ hfill \\
{x ^ 2} + 7x — 4x — 28 = 0 \ Rightarrow \ left ({x + 7} \ right) \ left ({x — 4} \ right) = 0 \ Rightarrow x = — 7, \, 4 \ hfill \\
\ end {в собранном виде } $
Поскольку длина отрезка не может быть отрицательной, $ {d_1} = x = 4 \, см \ Rightarrow {d_2} = 4 + 3 = 7 \, см $
Площадь параллелограмма (определение, формулы и примеры)
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
- BNAT 000 NC
- 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- 000 NC Книги
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательность и серия
- Таблицы умножения
- Детерминанты и матрицы
- Pr
- BNAT 000 NC
- Классы
Определение площади ромба
Ромб — это параллелограмм, стороны которого равны. Диагонали ромба перпендикулярны друг другу. Они также делят друг друга пополам. В этом посте мы собираемся найти общую формулу для определения площади ромба с использованием этих свойств. Мы собираемся изучить два метода.
Метод 1
Рассмотрим ромб ниже.
Мы можем разделить его на два равных треугольника, используя диагональ.Поскольку диагонали ромба перпендикулярны друг другу, мы можем использовать как основание и половину как высоту верхнего треугольника (Почему?). Если принять за площадь верхнего треугольника, то, вычислив его площадь, получим
.
Теперь мы рассчитали только площадь верхнего треугольника. Так как площадь ромба в два раза больше площади верхнего треугольника, умножаем на 2. То есть
.
Метод 2
Второй способ — заключить ромб в прямоугольник.Это можно сделать, проведя линии, параллельные диагоналям и проходящие через вершины (см. Рисунок ниже).
Две диагонали делят ромб на четыре треугольника. Обратите внимание, что если мы переместим два треугольника, как показано стрелкой на рисунке выше, то превратит параллелограмм в прямоугольник.
Теперь длина прямоугольника равна, а ширина равна. Площадь прямоугольника равна произведению его длины и ширины, поэтому
.
Используя два вышеупомянутых метода, мы показали, что площадь ромба равна половине произведения длины двух его диагоналей.
.Разница между ромбом и параллелограммом (со сравнительной таблицей)
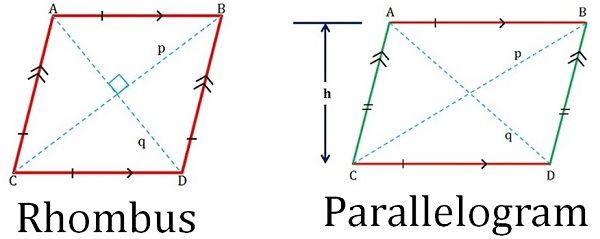В геометрии существует множество типов четырехугольника, например параллелограмм, ромб, квадрат, прямоугольник, трапеция и воздушный змей, которые имеют общие характеристики, из-за которых люди сталкиваются с проблемами в понимание этих цифр. Ромб можно назвать косым квадратом, у которого смежные стороны равны. Напротив, параллелограмм представляет собой наклонный прямоугольник с двумя наборами параллельных противоположных сторон.
Основное различие между ромбом и параллелограммом заключается в их свойствах, то есть все стороны ромба имеют одинаковую длину, а параллелограмм — это прямолинейная фигура, противоположные стороны которой параллельны.
Содержание: ромб против параллелограмма
- Сравнительная таблица
- Определение
- Ключевые отличия
- Заключение
Таблица сравнения
| Основа для сравнения | Ромб | Параллелограмм |
|---|---|---|
| Значение | Ромб обозначает плоскую четырехгранную фигуру, все стороны которой совпадают. | Параллелограмм — это четырехгранная плоская фигура, противоположные стороны которой параллельны друг другу. |
| Равные стороны | Все четыре стороны имеют одинаковую длину. | Противоположные стороны имеют одинаковую длину. |
| Диагонали | Диагонали делят друг друга пополам под прямым углом, образуя разносторонний треугольник. | Диагонали пересекают друг друга пополам, образуя два равных треугольника. |
| Площадь | (pq) / 2, где p и q — диагонали | bh, где b = основание и h = высота |
| Периметр | 4 a, где a = сторона | 2 (a + b), где a = сторона, b = основание |
Определение ромба
Четырехугольник, длины сторон которого совпадают, называется ромбом.Он имеет плоскую форму и четыре стороны; при этом обращенные стороны параллельны друг другу (см. рисунок ниже).
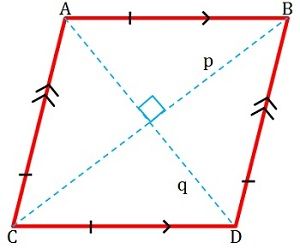Противоположные углы ромба равны, т.е. одного градуса. Его диагонали пересекаются под углом 90 градусов (прямой угол), поэтому перпендикулярны друг другу и образуют два равносторонних треугольника. Его смежные стороны являются дополнительными, а это значит, что сумма их меры равна 180 градусам. Он также известен как равносторонний параллелограмм.
Определение параллелограмма
Параллелограмм, как следует из его названия, описывается как фигура плоской формы, имеющая четыре стороны, множество противоположных сторон которых параллельны и конгруэнтны (см. Рисунок ниже).
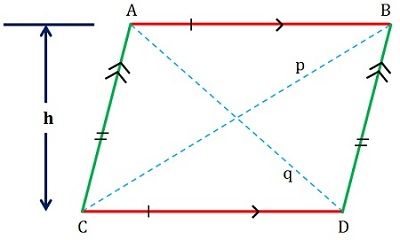Мера углов его облицовки одинакова, а следующие друг за другом углы являются дополнительными, т.е. сумма их меры равна 180 градусам. Его диагонали пересекают друг друга, образуя два равных треугольника.
Ключевые различия между ромбом и параллелограммом
Разницу между ромбом и параллелограммом можно ясно провести по следующим признакам:
- Мы определяем ромб как плоский четырехугольник с четырьмя сторонами, длина всех сторон которого одинакова.Параллелограмм — это четырехгранная плоская фигура, противоположные стороны которой параллельны друг другу.
- Все стороны ромба равны по длине, в то время как равны только противоположные стороны параллелограмма.
- Диагонали ромба пересекают друг друга под прямым углом, образуя два разносторонних треугольника. В отличие от параллелограмма, диагонали которого делят друг друга пополам, образуя два конгруэнтных треугольника.
- Математическая формула для вычисления площади ромба: (pq) / 2, где p и q — диагонали.И наоборот, площадь параллелограмма можно вычислить, умножив основание и высоту.
- Периметр ромба можно рассчитать по следующей формуле — 4 a, где a = сторона ромба. Напротив, периметр параллелограмма можно вычислить, сложив основание и высоту и умножив полученную сумму на 2.
Заключение
Параллелограмм и ромб — четырехугольники, у которых лицевые стороны параллельны, противоположные углы равны, сумма внутренних углов составляет 360 градусов.Сам ромб — это особый вид параллелограмма. Следовательно, можно сказать, что каждый ромб — это параллелограмм, но обратное невозможно.
.