32. Область истинности предикатов
Множество тех значений, принадлежащих области определения M, для которых P(x)=1, называется множеством истинности предиката P(x). Обозначается «Т».
33. Операции над предикатами
Конъюнкцией двух предикатов А(х) и В(х) называется новый предикат , который принимает значение «истина» при тех и только тех значениях х Т, при которых каждый из предикатов принимает значение «истина», и принимает значение «ложь» во всех остальных случаях. Множеством истинности Т предиката А(х) В(х), х Х является пересечение множеств истинности предикатов А(х) – Т1 и В(х) – Т2, т.е. Т= Т1 ∩Т2. Например: А(х): «х – четное число», В(х): « х кратно 3». А(х) В(х) – «х – четное число и х кратно 3». Т.е. предикат «х делится на 6».
Дизъюнкцией двух предикатов А(х) и В(х) называется
новый предикат
,
который принимает значение «ложь» при
тех и только тех значениях х Т, при
которых каждый из предикатов принимает
значение «ложь» и принимает значение
«истина» во всех остальных случаях.
Отрицанием предиката А(х) называется новый предикат , который принимает значение «истина» при всех значениях х Т, при которых предикат А(х) принимает значение «ложь», и принимает значение «ложь», если А(х) принимает значение «истина». Множеством истинности предиката , х Х является дополнение Т’ к множеству Т в множестве Х.
Импликацией предикатов А(х) и В(х) называется новый предикат А(х) В(х), который является ложным при тех и только тех значениях х Т, при которых А(х) принимает значение «истина», а В(х) – значение «ложь» и принимает значение «истина» во всех остальных случаях. Читают: «Если А(х), то В(х)». Например. А(х): «Натуральное число х делится на 3». В(х): «Натуральное число х делится на 4», можно составить предикат: «Если натуральное число х делится на 3, то оно делится и на 4». Множеством истинности предиката А(х) В(х) является объединение множества Т2 – истинности предиката В(х) и дополнения к множеству Т1 истинности предиката А(х)
34.
 Предикатная формула
Предикатная формула— 35. Формализация предложения
—
36. Кванторы и кванторные операции над предикатами.
Квантор – общее название для логических операций, ограничивающих область истинности какого-либо предиката.
Квантор всеобщности — ) (читается как «для каждого», «для любого», «для всех»)
Квантор существования – ( Ǝ ) (читается как «существует», «найдётся»)
xP(x) означает, что область значений переменной x включает область истинности P(x) («При всех значения (х) утверждение верно»)
Ǝ xP(x) означает, что область истинности предиката P(x) не пуста («существует такой (х) при котором утверждение верно»)
37.
 Исчисление предикатов и аксиомы исчисления предикатов.
Исчисление предикатов и аксиомы исчисления предикатов.Перенос квантора через отрицание.
; ;
Вынесение квантора за скобки.
; ;
; ;
3) Перестановка одноименных кванторов.
; ;
Переименование связанных переменных. Если заменить связанную переменную формулы другой переменной, не входящей в эту формулу, в кванторе и всюду в области действия квантора получаем формулу, равносильную .
Исчисление предикатов базируется на приведенных выше свойствах и правилах, называемых аксиомами.
Какими бы ни были формулы А и В для них справедливы следующие аксиомы:
1) ;
2)
3)
4) , где формула не содержит переменной .
5) , где формула не содержит переменной .
§18. Алгебра логики | Предикаты и их множества истинности (курс фгос 34 ч.)
Планирование уроков на учебный год (ФГОС)
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 10 классы | Планирование уроков на учебный год (ФГОС) | Алгебра логики
Содержание урока:
18. 1. Логические высказывания и переменные
1. Логические высказывания и переменные
18.2. Логические операции
18.3. Логические выражения
18.4. Предикаты и их множества истинности
САМОЕ ГЛАВНОЕ. Вопросы и задания
Материалы к уроку
| 18.4. Предикаты и их множества истинности |
||||
| 18.3. Логические выражения | САМОЕ ГЛАВНОЕ Вопросы и задания |
18.4. Предикаты и их множества истинности
Равенства, неравенства и другие предложения, содержащие переменные, высказываниями не являются, но они становятся высказываниями при замене переменной каким-нибудь конкретным значением. Например, предложение х < 12 становится истинным высказыванием при х = 5 (5 < 12 — истина) и ложным при x: = 15 (15 < 12 — ложь). Предложения такого рода называют высказывательными формами или предикатами.
Предложения такого рода называют высказывательными формами или предикатами.
Предикат — это утверждение, содержащее одну или несколько переменных.
Выделим некоторый предикат Р(х) и рассмотрим множество всевозможных объектов I, к которым он относится, — область определения предиката. Можно выделить такое подмножество Р множества I, что на всех его элементах предикат Р(х) будет превращаться в истинное высказывание. Определённое таким образом Р называется множеством истинности предиката Р(х).
Рассмотрим множество учеников некоторого класса. Известно, что в этом классе два отличника — Иван и Саша. Предикат «Он отличник» будет истинным высказыванием только по отношению к этим двум ученикам и ложным по отношению ко всем остальным.
Предикаты позволяют задать множество, не перечисляя всех его элементов. Например, множество истинности предиката Р(х) = (х < 0) — множество отрицательных чисел; множество истинности предиката Р(х, у) = (х2 + у2 = 1) — множество точек окружности единичного радиуса с центром в начале координат. Следует отметить, что многие задания, выполняемые вами на уроках математики, прямо связаны с предикатами. Например, стандартное задание «Решить квадратное уравнение x
Следует отметить, что многие задания, выполняемые вами на уроках математики, прямо связаны с предикатами. Например, стандартное задание «Решить квадратное уравнение x
Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.
Пусть А и В соответственно являются множествами истинности предикатов А(х) и В(х). Тогда пересечение множеств А и В будет являться множеством истинности для предиката А(х) & В(х), а объединение множеств А и В будет множеством истинности для предиката А(х) ∨ В(х).
Пример 5. Найдём все целые числа 2, превращающие предикат
P(z) = (z > 5) & (z — 2 < 15) в
истинное высказывание. Другими словами, требуется найти множество истинности предиката P(z), заданного на множестве целых чисел I.
Предикат P(z) состоит из двух предикатов, соединённых операцией конъюнкции: P(z) = A(z) & B(z).
Множеством истинности предиката A(z) = (z > 5) являются целые числа 6, 7, 8 и т. д. Множеством истинности предиката В(z) = (z — 2 < 15) являются все целые числа, меньшие 17.
Множество истинности исходного предиката — пересечение (общие элементы) множеств истинности образующих его предикатов:
Р = А ∩ В = {6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16}.
Его мощность |Р| = 11.
Пример 6. Рассмотрим предикат (50 < х2) → (50 > (х + 1)2), определённый на множестве целых чисел. Найдём множество истинности этого предиката.
Зачастую задания такого рода формулируют несколько иначе.
Например, так: «Найдите все целые числа х, для которых истинно высказывание (50 < х2) → (50 > (х + 1)2)».
Проанализируем отдельно каждый из элементарных предикатов (50 < х2) и (50 > (x + 1)2), решив соответствующие неравенства:
Определим значение исходного предиката на каждом из полученных подмножеств, причём отдельно рассмотрим значение х = -8 (оно попадает в два подмножества) и значение х = 7 (оно не попадает ни в одно подмножество):
Итак, множеством истинности исходного предиката являются целые числа, принадлежащие отрезку [-8; 7]. Наименьшим элементом этого множества является число -8, наибольшим — число 7; мощность множества равна 16.
Наименьшим элементом этого множества является число -8, наибольшим — число 7; мощность множества равна 16.
Cкачать материалы урока
предикатов и подлежащих | Истина и др.: Шесть лекций по древней логике
Фильтр поиска панели навигации Oxford Academic Truth и др. Шесть лекций по древней логикеДревняя философияФилософия языкаФилософия математики и логикиКнигиЖурналы Мобильный телефон Введите поисковый запрос
Закрыть
Фильтр поиска панели навигации Oxford Academic Truth и др. Шесть лекций по древней логикеДревняя философияФилософия языкаФилософия математики и логикиКнигиЖурналы Введите поисковый запрос
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
Укажите
Барнс, Джонатан, «Предикаты и субъекты»,  д. Шесть лекций по древней логике (
д. Шесть лекций по древней логике (
, 2009; онлайн-издание, Oxford Academic, 3 октября 2011 г.), https://doi.org/10.1093/ acprof:oso/9780199568178.003.0002, по состоянию на 5 марта 2023 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford Academic Truth и др. Шесть лекций по древней логикеДревняя философияФилософия языкаФилософия математики и логикиКнигиЖурналы Мобильный телефон Введите поисковый запрос
Закрыть
Фильтр поиска панели навигации Oxford Academic Truth и др. Шесть лекций по древней логикеДревняя философияФилософия языкаФилософия математики и логикиКнигиЖурналы Введите поисковый запрос
Advanced Search
Abstract
Когда Готлоб Фреге решил отказаться от подлежащих и предикатов и начать новую жизнь с аргументами и функциями, он утверждал, что подлежащие и предикаты были среди тех нескольких нездоровых понятий, которые грамматика навязала логике. Он не утверждал, что подлежащие и предикаты были элементами, подобными флогистону и светоносному эфиру; но он был уверен, что они в лучшем случае предназначены только для глаз грамматика. Это, пожалуй, единственная точка зрения, которую Фреге разделял с Фридрихом Ницше. Это различие чуждо лингвистике: это одно из нескольких неуместных понятий, которые логика навязала грамматике. Несомненно, подлежащие и предикаты имеют некоторую логическую полезность; но на самом деле они не представляют никакой пользы или интереса для грамматика.
Он не утверждал, что подлежащие и предикаты были элементами, подобными флогистону и светоносному эфиру; но он был уверен, что они в лучшем случае предназначены только для глаз грамматика. Это, пожалуй, единственная точка зрения, которую Фреге разделял с Фридрихом Ницше. Это различие чуждо лингвистике: это одно из нескольких неуместных понятий, которые логика навязала грамматике. Несомненно, подлежащие и предикаты имеют некоторую логическую полезность; но на самом деле они не представляют никакой пользы или интереса для грамматика.
Ключевые слова: Готтлоб Фреге, предметы, предикаты, аргументы, функции, грамматика, лингвистика, логика
Предмет
Философия языкаДревняя философияФилософия математики и логики
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Щелкните Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.

- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Покупка
Наши книги можно приобрести по подписке или купить в библиотеках и учреждениях.
Информация о покупке
Понятие подлежащего содержит понятие сказуемого | Континуанты: их деятельность, их бытие и их идентичность
Фильтр поиска панели навигации Oxford AcademicContinuants: Их деятельность, их существование и их идентичностьМетафизикаКнигиЖурналы Мобильный телефон Введите поисковый запрос
Закрыть
Фильтр поиска панели навигации Oxford AcademicContinuants: Их деятельность, их существование и их идентичностьМетафизикаКнигиЖурналы Введите поисковый запрос
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
Укажите
Виггинс, Дэвид, «Концепция субъекта содержит концепцию сказуемого», Continuants: Их активность, их существование и их идентичность (
Oxford, 2016; онлайн-издание, Oxford Academic, 22 декабря 2016 г. ), https://doi.org/10.1093/acprof:oso/9780198716624.003.0007, по состоянию на 5 марта 2023 г.
), https://doi.org/10.1093/acprof:oso/9780198716624.003.0007, по состоянию на 5 марта 2023 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford AcademicContinuants: Их деятельность, их существование и их идентичностьМетафизикаКнигиЖурналы Мобильный телефон Введите поисковый запрос
Закрыть
Фильтр поиска панели навигации Oxford AcademicContinuants: Их деятельность, их существование и их идентичностьМетафизикаКнигиЖурналы Введите поисковый запрос
Advanced Search
Abstract
В «Рассуждение о метафизике» Лейбниц говорит, что предложение истинно тогда и только тогда, когда понятие субъекта содержит понятие предиката.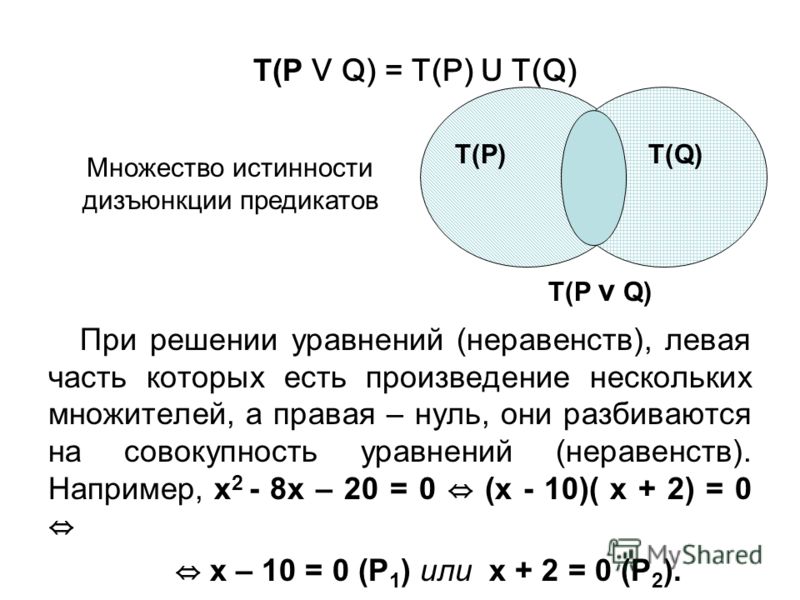 Он применяет это в равной степени к необходимым и случайным предложениям. Философам было трудно понять, как Лейбниц мог предположить, что это был хороший принцип истины для случайных предложений. Эта глава призвана объяснить, почему Лейбниц рекомендовал этот принцип и как он оставляет место для непредвиденных обстоятельств, утверждая, что проблема, обнаруженная некоторыми современными учеными в отношении этого принципа, может быть решена путем ссылки на предложения, которые сам Лейбниц делает в Беседа о метафизике . Это также предполагает, что Лейбниц впоследствии либо уточняет принцип, либо отказывается от него из-за сложности управления логикой общности. Цель этой главы также состоит в том, чтобы сказать кое-что о проблеме, которую, по мнению самого Лейбница, он видел в приспосабливании к непредвиденным обстоятельствам.
Он применяет это в равной степени к необходимым и случайным предложениям. Философам было трудно понять, как Лейбниц мог предположить, что это был хороший принцип истины для случайных предложений. Эта глава призвана объяснить, почему Лейбниц рекомендовал этот принцип и как он оставляет место для непредвиденных обстоятельств, утверждая, что проблема, обнаруженная некоторыми современными учеными в отношении этого принципа, может быть решена путем ссылки на предложения, которые сам Лейбниц делает в Беседа о метафизике . Это также предполагает, что Лейбниц впоследствии либо уточняет принцип, либо отказывается от него из-за сложности управления логикой общности. Цель этой главы также состоит в том, чтобы сказать кое-что о проблеме, которую, по мнению самого Лейбница, он видел в приспосабливании к непредвиденным обстоятельствам.
Ключевые слова: Лейбниц, необходимость, случайность, субъект, предикат, вмещаемость, истина
Предмет
Метафизика
В настоящее время у вас нет доступа к этой главе.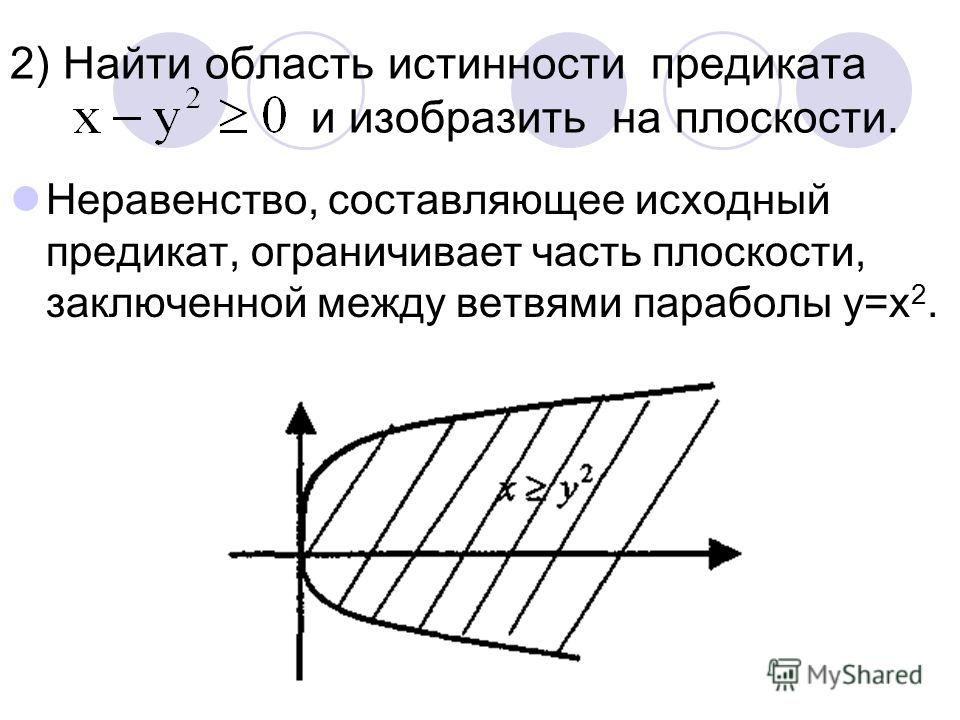
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.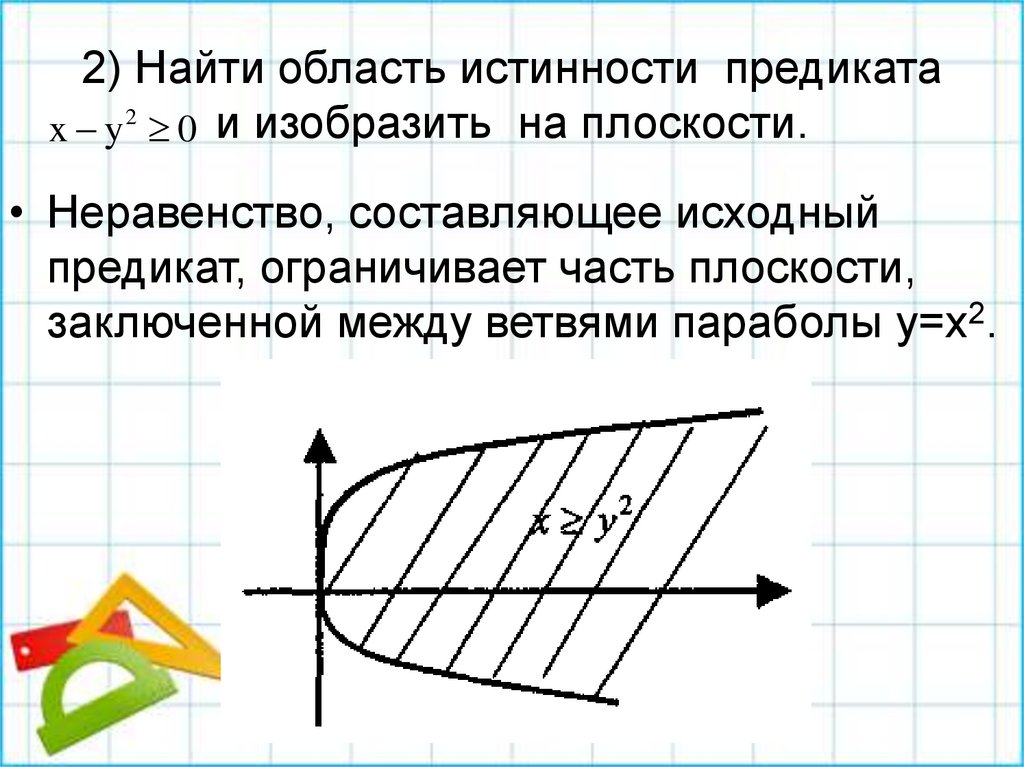
- Щелкните Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т.

 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic.