По двум точкам построить прямую: Уравнение прямой по двум точкам

alexxlab / / Разное

Содержание

Уравнение прямой по двум точкам

Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.

Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнения прямой, проходящей через две точки могут быть следующих видов:

  • каноническое уравнение,
  • параметрическое уравнение,
  • общее уравнение прямой,
  • уравнение прямой с угловым коэффициентом,
  • уравнение прямой в полярных координатах и другие.

Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.

Каноническое уравнение прямой на плоскости

{\dfrac{x-x_a}{x_b-x_a} = \dfrac{y-y_a}{y_b-y_a}}

xa и

ya — координаты первой точки A,

xb и yb — координаты второй точки B

Параметрическое уравнение прямой на плоскости

{\begin{cases} x=l \cdot t + x_a \\ y=m \cdot t + y_a \end{cases}}

xa, ya — координаты точки, лежащей на прямой,

{l;m} — координаты направляющего вектора прямой,

t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.

Каноническое уравнение прямой в пространстве

{\dfrac{x-x_a}{x_b-x_a} = \dfrac{y-y_a}{y_b-y_a} = \dfrac{z-z_a}{z_b-z_a}}

xa, ya и za — координаты первой точки A,

xb, yb и zb — координаты второй точки B

Параметрическое уравнение прямой в пространстве

{ \begin{cases} x=l \cdot t + x_a \\ y=m \cdot t + y_a \\ z=n \cdot t + z_a \end{cases} }

xa, ya и za — координаты точки, лежащей на прямой,

{l;m;n} — координаты направляющего вектора прямой,

t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.

Пример нахождения уравнения прямой, проходящей через две точки

Найдем уравнения прямой, проходящей через точки A(1,2) и B(3,8).

Каноническое уравнение прямой

Каноническое уравнение прямой, проходящей через две точки имеет вид {\dfrac{x-x_a}{x_b-x_a} = \dfrac{y-y_a}{y_b-y_a}}

Подставим в формулу координаты точек A и B: {\dfrac{x-1}{3-1} = \dfrac{y-2}{8-2}}

Получаем каноническое уравнение прямой: {\dfrac{x-1}{2} = \dfrac{y-2}{4}}

Уравнение прямой с угловым коэффициентом

Из канонического уравнения получаем уравнение прямой с угловым коэффициентом: {y=3x-1}

Параметрическое уравнение прямой

Параметрическое уравнение прямой имеет вид:

{ \begin{cases} x=l \cdot t + x_a \\ y=m \cdot t + y_a \end{cases} }

где {x_a, y_b} — координаты точки, лежащей на прямой, {\{l;m\}} — координаты направляющего вектора прямой, t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении. В качестве координат используем координаты точки {A(x_a, y_b)}.

Найдем координаты направляющего вектора:

\overline{AB} = \{x_b — x_a; y_b — y_a\} = \{3-1; 8-2\} = \{2; 6\}

Получаем параметрическое уравнение:

\begin{cases} x=2 t + 1 \\ y=6 t + 2 \end{cases}

Используем калькулятор для проверки полученного ответа.

Уравнение прямой, проходящей через две точки

Получить уравнение прямой по двум точкам бывает необходимо, когда мы решаем задачи, связанные с анализом различных фигур на плоскости. В этом случае бывает полезно знать уравнение прямой, проходящей через две точки. Например, составляя такое уравнение мы уже знаем – как проходит прямая, с какие углом наклона к осям координат и можем рассчитать расположение прямой по отношению к другим прямым или к фигурам.

Содержание

Составляем уравнение прямой по двум точкам

Итак, пусть нам даны две точки и . Наша прямая проходит через две эти точки, давайте получим уравнение этой прямой. Уравнение пучка прямых, проходящих через точку с координатами имеет вид:

   

То есть если прямая проходит через две точки и она – одна из этого пучка прямых, проходящих через точку и эта прямая имеет определенный коэффициент . Значит, координаты точки должны удовлетворять уравнению (1), то есть

   

.

Находим из (2) :

   

и подставим в уравнение (1):

   

.

Преобразовывая уравнение (3) получим:

   

Это и есть уравнение прямой, проходящей через две точки и .

Примечание: если точки и лежат на прямой, которая параллельна оси или оси , то уравнение прямой будет иметь вид или соответственно.

Зная координаты любых двух точек прямой, мы всегда сможем определить угловой коэффициент прямой:

   

Геометрический вывод уравнения прямой

Действительно, давайте нарисуем прямую в системе координат и отметим на прямой две точки и , координаты которых известны и и отметим на этой прямой произвольную точку .

Из подобия треугольников и находим:

   

Из рисунка видно, что:

   

   

   

   

,

Таким образом, получаем уравнение прямой по двум точкам:

   

Задача

Составим уравнение прямой, проходящей через две точки и .

Решение: Имеем , , , . Подставим эти значения в уравнение прямой, проходящей через две заданные точки:

   

   

Умножим левую и правую части уравнения на 5, получим:

– получившееся уравнение прямой.

Давайте сделаем проверку – если мы все решили правильно, то при подстановке координат точек и мы получим верное равенство. Итак, подставим сначала координаты точки :

Теперь координаты точки :

Значит, уравнение прямой мы нашли верно.

Ответ:

Условие прохождения прямой через три заданные точки

Если нам в задаче нужно убедиться, что три точки с заданными координатами лежат на одной прямой, можно рассуждать так:

  1. Если две точки с заданными координатами образуют прямую, то их координаты удовлетворяют уравнению прямой, проходящей через две точки.
  2. Если третья точка также лежит на этой прямой, то и ее координаты будут удовлетворять этому уравнению.

Таким образом, если нам даны три точки , и , лежащие на одной прямой, то их координаты будут удовлетворять условию:

   

Теперь вы легко сможете составить уравнение прямой по двум точкам, а также найти угловой коэффициент прямой и проверить – принадлежит ли третья точка этой прямой.

Как нарисовать линию, которая пересекает две точки, но пересекает направление X, используя Plotly Python?

Я построил свечную диаграмму (ось X — временной ряд, ось Y — цены акций) с сегментом (синий), который начинался с точки данных и заканчивался другой точкой данных.

 импортировать plotly.graph_objects как есть
импортировать панд как pd
df = pd.read_csv('https://raw.githubusercontent.com/plotly/datasets/master/finance-charts-apple.csv')
печать (len (df ['Дата']))
fig = go.Figure(data=[go.Candlestick(x=df['Date'],
                открыть=df['AAPL.Открыть'],
                высокий=df['AAPL.Высокий'],
                низкий=df['AAPL.Низкий'],
                закрыть=df['AAPL.Закрыть'])])
fig.add_shape (тип = 'линия',
              x0=df['Дата'][200], y0=df['AAPL.Open'][200],
              x1=df['Дата'][400], y1=df['AAPL.Open'][400],
              линия = dict (цвет = 'синий', ширина = 3),
              xref='x', yref='y')
fig.update_layout (xaxis_rangeslider_visible = ложь)
рис.
 
 шоу()

Теперь я хочу превратить сегмент в линию, т. е. он по-прежнему пересекает те же две точки данных, но теперь он начинается слева от области графика и заканчивается справа от области графика (фиолетовый).

Моя первая попытка состояла в том, чтобы узнать координаты точек данных на холсте, поэтому я могу придумать уравнение формулы линии, таким образом вычислив начальную точку и конечную точку более длинной линии, но я не могу найти такой метод, которым я могу передать необработанные данные (например,

x — время, y — цена этого времени) и дайте мне координату холста этого набора данных ( x — 0~1, а y — 0~1 или что-то еще).

Есть ли лучший способ построить линию через две точки данных? Спасибо!

  • питон
  • сюжетный питон

2

Вы можете продолжить поиск готового решения или создать его самостоятельно.
Дата и время обычно преобразуются вашим графическим инструментом в целое число. Чаще всего это «секунды с 1 января 1970 года». Вы можете вычислить его с помощью python datetime.datetime.timestamp().

Прямая линия определяется уравнением y = m * x + b.
Ваши 2 точки данных принадлежат линии, поэтому вы можете вычислить m=(y2-y1)/(x2-x1), а затем b = y2 / (m*x2).

Найдите координаты X границ вашего графика и вычислите:
y3 = m * x3 + b и y4 = m * x4 + b

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Плагины

qgis — нарисуйте линию между двумя точками и увеличьте масштаб нового слоя — PyQGIS

спросил

Изменено 3 года, 2 месяца назад

Просмотрено 929 раз

В моем подключаемом модуле QGIS3 у меня есть этот код для рисования линии между двумя точками.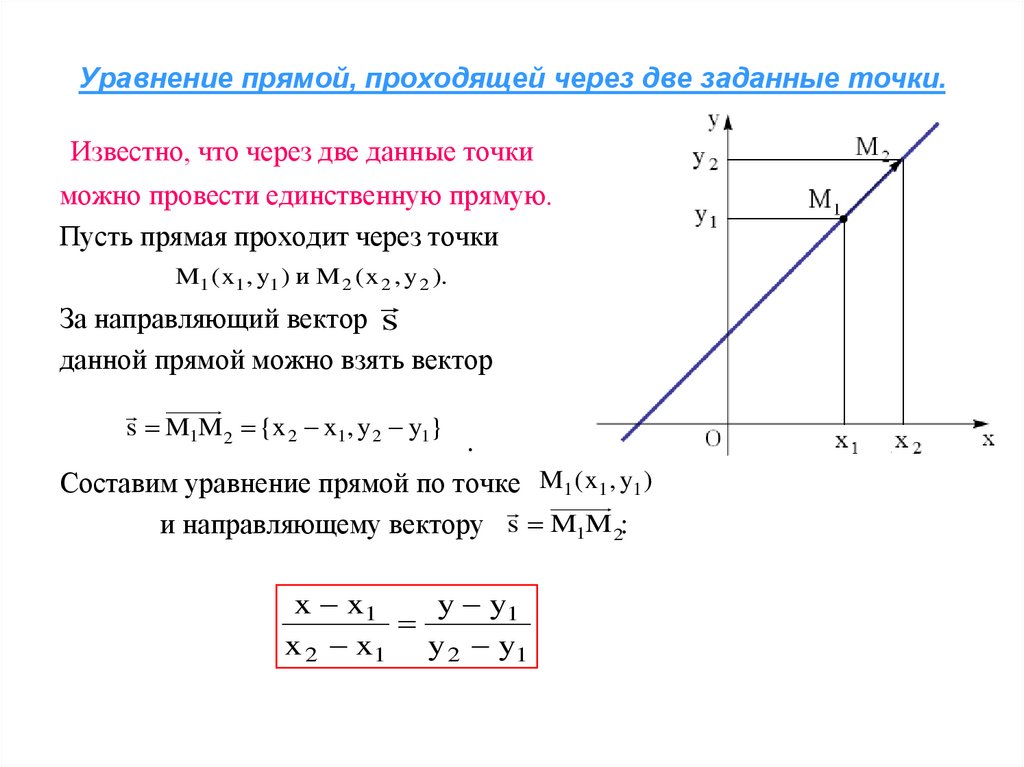 Код работает, но после его запуска QGIS масштабируется где-то посередине Тихого океана, когда я хочу увеличить масштаб нового слоя («линии»). Проблема возникает в последней строке этого кода, когда я вызываю addMapLayers() .

 def drawLine(self, line_start, line_end):
  start_point = QgsPoint(line_start.asPoint())
  end_point = QgsPoint(line_end.asPoint())
  v_layer = QgsVectorLayer("LineString", "строка", "память")
  пр = v_layer.dataProvider()
  сегмент = QgsFeature()
  seg.setGeometry(QgsGeometry.fromPolyline([начальная_точка, конечная_точка]))
  pr.addFeatures([seg])
  v_layer.updateExtents()
  crs = v_layer.crs()
  crs.createFromId (4326)
  v_layer.setCrs(crs)
  QgsProject.instance().addMapLayers([v_layer])

Я попытался добавить iface.zoomToActiveLayer() , но ничего не изменилось. Как я могу увеличить этот новый слой, чтобы избежать проблемы с Тихим океаном?

  • pyqgis
  • qgis-plugins
  • qgis-3

Попробуйте указать CRS при создании объекта QgsVectorLayer , например.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *