Область определения | это… Что такое Область определения?
ТолкованиеПеревод
- Область определения
- Запрос «Отображение» перенаправляется сюда. Cм. также другие значения.
В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое понятие числовой функции, являющееся частным случаем математической функции.
Содержание
- 1 Определения
- 2 Обозначения
- 3 Связанные определения
- 4 Свойства
- 4.1 Свойства прообразов и образов
- 5 Классы функций
- 6 Вариации и обобщения
- 6.1 Функции нескольких аргументов
- 7 Примечания
- 8 См. также
- 9 Литература
Определения
- Нестрогое определение: функция — это «закон», по которому каждому значению элемента

- Строгое определение: функция или отображе́ние — это бинарное отношение, обладающее свойством:
- Функция называется инъективной, если
Обозначения
- , или для отображения F множества X в множество Y;
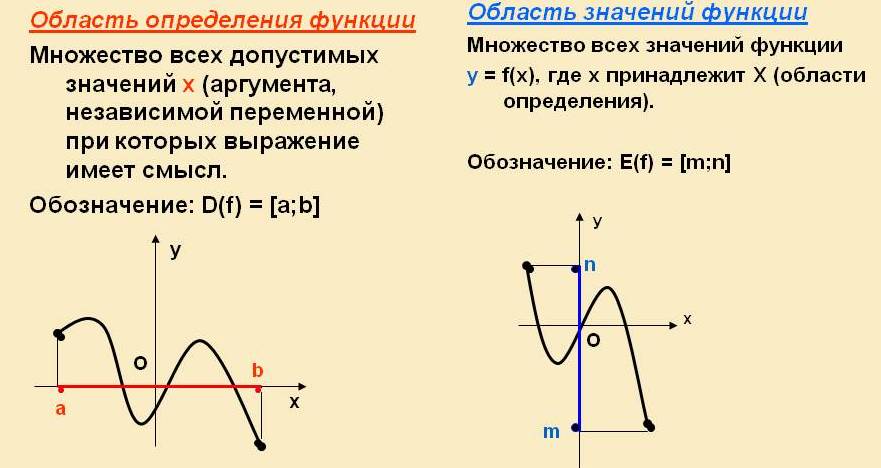
- Множество X называется о́бластью определе́ния отображения F (обозначается D(F), или .).
- Множество Y называется о́бластью значе́ний отображения F.(обозначается E(F), или ).
- , y = F(x) или или . Используется также обратная польская запись: y = xF, а иногда y = xF.
- Элементы x называют аргументами функции , а соответствующие элементы y — значениями функции.
Связанные определения
- Пусть дано отображение , и . Тогда суже́нием функции F на M называется функция , определяемая равенством
- .

- Это определение подчёркивает, что фиксация области определения является частью определения функции.
- .
- F является продолжением функции на множество . Можно рассматривать продолжения, обладающие различными свойствами, например аналитическое продолжение.
- Пусть . Тогда о́бразом множества M
- .
- Множество F(X) называется образом отображения F и обозначается .
- Пусть задано отображение , и y = F(x). Тогда x называется проо́бразом y, а y называется о́бразом x. Согласно определению отображения, каждый элемент должен иметь ровно один образ, но элемент может не иметь прообразов либо иметь один или несколько.
- Например, пусть дана функция , где F(x) = x2.
 Тогда
Тогда- y = − 1 не имеет прообразов;
- y = 0 имеет единственный прообраз x = 0;
- y = 1 имеет два прообраза: x1 = 1 и x2 = − 1.
- Например, пусть дана функция , где F(x) = x2.
- Пусть задано отображение , и . Тогда множество называется по́лным проо́бразом элемента y. Полный прообраз обозначается F — 1(y).
- Например, пусть , и F(x) = sinx. Тогда
- .
- Например, пусть , и F(x) = sinx. Тогда
- Пусть . Тогда проо́бразом множества N называется подмножество множества X, определяемое равенством
- .
- Например, пусть , и F(x) = cosx. Тогда
- ,
- .
Свойства
Свойства прообразов и образов
- ;
- ;
- ;
- . Заметим отсутствие равенства в этом случае.
Классы функций
При необходимости можно различать отображения в зависимости от природы множеств X и Y.
 Если X и Y — числовые множества, такие, как или , то отображение называют функцией. Если X или Y многомерны, например, или , то отображение называют ве́ктор-фу́нкцией
Если X и Y — числовые множества, такие, как или , то отображение называют функцией. Если X или Y многомерны, например, или , то отображение называют ве́ктор-фу́нкциейВариации и обобщения
- многозначная функция
Функции нескольких аргументов
Определение функции легко обобщить на случай функции многих аргументов.
Пусть даны множества и множество Y, тогда упорядоченное множество всех кортежей называется функцией n аргументов тогда и только тогда, когда для любых и из следует, что .[1]
Примечания
- ↑ Кудрявцев Л. Д. Курс математического анализа. — том 1. — М.: Высшая школа, 1981. — с. 8.
См. также
- Композиция функций
- График функции
- Сюръективность
- Инъективность
- Биективность
- Функция с множеством значений {0, 1}
- Функциональное уравнение
Литература
- Функция.
 Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
Wikimedia Foundation. 2010.
Поможем сделать НИР
- Область датского права
- Область переписи населения
Полезное
Область определения произведения функций — Студопедия
Поделись
Если функция f — это произведение n функций (основных элементарных или элементарных) f1, f2, …, fn, то есть, функция f задается формулой , то областью определения функции f является пересечение областей определения функций f1, f2, …, fn. Итак, .
Пример.
Найдите область определения функции .
Решение.
Запишем заданную функцию в следующем виде , f1 – это постоянная функция, 
Нам известно, что и . Тогда
Ответ:
областью определения функции является множество всех действительных положительных чисел.
Отдельно остановимся на нахождении области определения функции, заданной формулой , где С – некоторое действительное число. Легко показать, что область определения этой функции совпадает с областью определения функции f. Действительно, функция – это произведение постоянной функции и функции f. Областью определения постоянной функции является множество всех действительных чисел, а область определения функции f есть . Тогда область определения функции есть , что и требовалось показать.
Итак, области определения функций y=f(x) и , где С – некоторое действительное число, совпадают.
В частности, области определения функций y=f(x) и y=-f(x) совпадают и можно утверждать, что область определения разности функций находится так же, как и область определения суммы n функций.
Пример.
Найдите область определения функции .
Решение.
Данную функцию f будем рассматривать как разность двух функций и . Тогда .
Сначала найдем область определения функции f1.
Эта функция сложная, ее можно представить в виде , где f3 – логарифмическая функция с основанием 3, а . Тогда область определения сложной функции f1 найдем, решив систему неравенств вида . Определив и , вернемся к этой системе.
Мы знаем, что . Найдем .
Функция f4 – это разность двух функций и
Продолжим нахождение области определения функции f1 и подставим полученные и в систему . Имеем
Имеем
Таким образом, .
Теперь найдем область определения функции f2.
Область определения этой функции совпадает с областью определения показательной функции с основанием 2, то есть, .
Наконец мы можем найти область определения исходной функции: .
Ответ:
.
Озвучим и докажем еще одно очень важное утверждение: область определения целой рациональной функции – это множество всех действительных чисел.
Рассмотрим целую рациональную функцию , где n – некоторое натуральное число, а — некоторые действительные числа. Она представляет собой сумму (n+1)-ой функции. Очевидно, что область определения каждой из функций – это множество всех действительных чисел, следовательно, областью определения исходной целой рациональной функции также является множество всех действительных чисел.
Пример.
Какова область определения функции ?
Решение.
Исходная функция (обозначим ее f) — это разность двух функций и . Функция f1 – это целая рациональная функция, областью ее определения является множество всех действительных чисел. Область определения функции f2 совпадает с областью определения степенной функции с показателем
Функция f1 – это целая рациональная функция, областью ее определения является множество всех действительных чисел. Область определения функции f2 совпадает с областью определения степенной функции с показателем
Тогда .
Ответ:
.
К началу страницы
Домен и диапазон
Домен и диапазон функции — это все возможные значения независимой переменной x, для которых определено y. Диапазон функции — это все возможные значения зависимой переменной y.
В приведенном ниже примере показаны два различных способа представления функции: в виде таблицы функций и в виде набора координат.
| 3 |
Несмотря на то, что они представлены по-разному, приведенные выше функции являются одной и той же функцией, и домен функции равен x = {2, 3, 5, 6, 8}, а диапазон равен y = {4, 8, 2, 9, 3}. Вот как вы можете определить домен и диапазон для дискретных функций. Порядок, в котором вы перечисляете значения, не имеет значения. Но как определить домен и диапазон для функций, которые не являются дискретными?
Вот как вы можете определить домен и диапазон для дискретных функций. Порядок, в котором вы перечисляете значения, не имеет значения. Но как определить домен и диапазон для функций, которые не являются дискретными?
Пример:
f(x) = x 2
Функция f(x) = x 2 имеет область определения всех действительных чисел (x может быть любым) и диапазон, который больше или равен до нуля.
Два способа записи области определения и диапазона функции: интервальная запись и запись множества.
Интервальная запись
При использовании интервальной записи домен и диапазон записываются как интервалы значений. Для f(x) = x 2 домен в интервальной нотации:
D: (-∞, ∞)
D указывает, что вы говорите о домене, а (-∞, ∞), читается как от отрицательной бесконечности до положительной бесконечности, это еще один способ сказать, что домен «полностью реален». числа».
Диапазон f(x) = x 2 в интервальной записи:
R: [0, ∞)
R указывает, что вы говорите о диапазоне. Обратите внимание, что скобка используется для 0 вместо круглой скобки. Это связано с тем, что диапазон функции включает 0 при x = 0. Диапазон функции исключает ∞ (каждая функция делает), поэтому мы используем круглую скобку.
Обратите внимание, что скобка используется для 0 вместо круглой скобки. Это связано с тем, что диапазон функции включает 0 при x = 0. Диапазон функции исключает ∞ (каждая функция делает), поэтому мы используем круглую скобку.
На графике вы знаете, когда функция включает или исключает конечную точку, потому что конечная точка будет открытой или закрытой.
Нотация набора
При использовании нотации набора мы используем символы неравенства для описания домена и диапазона как набора значений. Домены и диапазоны, использованные в примерах дискретных функций, были упрощенными версиями обозначений множеств. Существует множество различных символов, используемых в системе обозначений, но здесь будут представлены только самые основные структуры.
Область определения f(x) = x 2 в системе обозначений:
D: {x | x∈ℝ}
Опять же, D указывает домен. «|» означает «такой, что», символ ∈ означает «элемент», а «ℝ» означает «все действительные числа».
Собрав все вместе, это утверждение можно прочитать как «область определения — это множество всех x, таких что x является элементом всех действительных чисел».
Диапазон f(x) = x 2 в системе обозначений:
R: {y | y ≥ 0}
R указывает диапазон. При использовании обозначения набора символы неравенства, такие как ≥, используются для описания домена и диапазона. Следовательно, это утверждение можно прочитать как «диапазон — это набор всех y, таких, что y больше или равен нулю».
Отношения и определение того, является ли отношение функцией — Задача 1
Домен — это набор всех значений «x», а диапазон — это набор всех значений «y» в наборе упорядоченных пар. Помните, что упорядоченные пары записываются как (x, y). При просмотре набора упорядоченных пар найдите домен, перечислив все значения x из отношения. Найдите диапазон, перечислив все значения y из упорядоченных пар. Повторяющиеся значения в домене или диапазоне не обязательно указывать более одного раза. Чтобы отношение было функцией, каждый x должен соответствовать только одному значению y. Если со значением x связано более одного значения y, например, в отношении {(4, 1), (4,2)} значение x 4 имеет значение y, равное 1, и 2, поэтому этот набор упорядоченных пар не является функцией. Если каждому значению x соответствует только одно значение y, то отношение является функцией.
Чтобы отношение было функцией, каждый x должен соответствовать только одному значению y. Если со значением x связано более одного значения y, например, в отношении {(4, 1), (4,2)} значение x 4 имеет значение y, равное 1, и 2, поэтому этот набор упорядоченных пар не является функцией. Если каждому значению x соответствует только одно значение y, то отношение является функцией.
домен диапазон вход выход функция отношение
Когда вы работаете с доменом, диапазоном, отношениями и функциями, очень важно держать весь этот словарь прямо в голове. Имейте в виду, что домен — это набор всех X, диапазон — это набор всех Y, и чтобы быть функцией, каждый x должен иметь ровно один y.
Итак, давайте проверим эту проблему. Найдите домен и диапазон, определите, является ли отношение функцией. Итак, первое, что я собираюсь сделать, это найти домен, домен — это набор всех x чисел. Итак, когда это настроено в упорядоченных парах, вы, ребята, знаете, что числа x идут первыми. Таким образом, мой домен будет 6, 4, 1 и 4, только мне не нужно писать это 4 дважды. Так что это будет 6, 4 и 1, хотя у меня есть 4 точки, у меня есть только 3 разных значения, и я собираюсь написать их с помощью этих маленьких фигурных скобок, потому что это то, что мы называем набором обозначений в математике. Это станет более важным, когда вы пройдете курсы.
Найдите домен и диапазон, определите, является ли отношение функцией. Итак, первое, что я собираюсь сделать, это найти домен, домен — это набор всех x чисел. Итак, когда это настроено в упорядоченных парах, вы, ребята, знаете, что числа x идут первыми. Таким образом, мой домен будет 6, 4, 1 и 4, только мне не нужно писать это 4 дважды. Так что это будет 6, 4 и 1, хотя у меня есть 4 точки, у меня есть только 3 разных значения, и я собираюсь написать их с помощью этих маленьких фигурных скобок, потому что это то, что мы называем набором обозначений в математике. Это станет более важным, когда вы пройдете курсы.
Диапазон выглядит следующим образом -1, 3 и 2. Опять же, это значения y -1, 3, 1 и 2. Итак, я нашел свой домен в диапазоне. Это была первая часть проблемы.
Следующее, что нам нужно сделать, это определить, является ли отношение функцией, и будет ли отношение функцией, если каждый x имеет ровно один y. Итак, давайте посмотрим, что 6 имеет -1, хорошо, держите это в голове, 4 идет с 3, хорошо, 1 идет с о, о, 4 идет с 3 там и 4 идет с 2 там? Это похоже на два разных значения y для одного и того же x.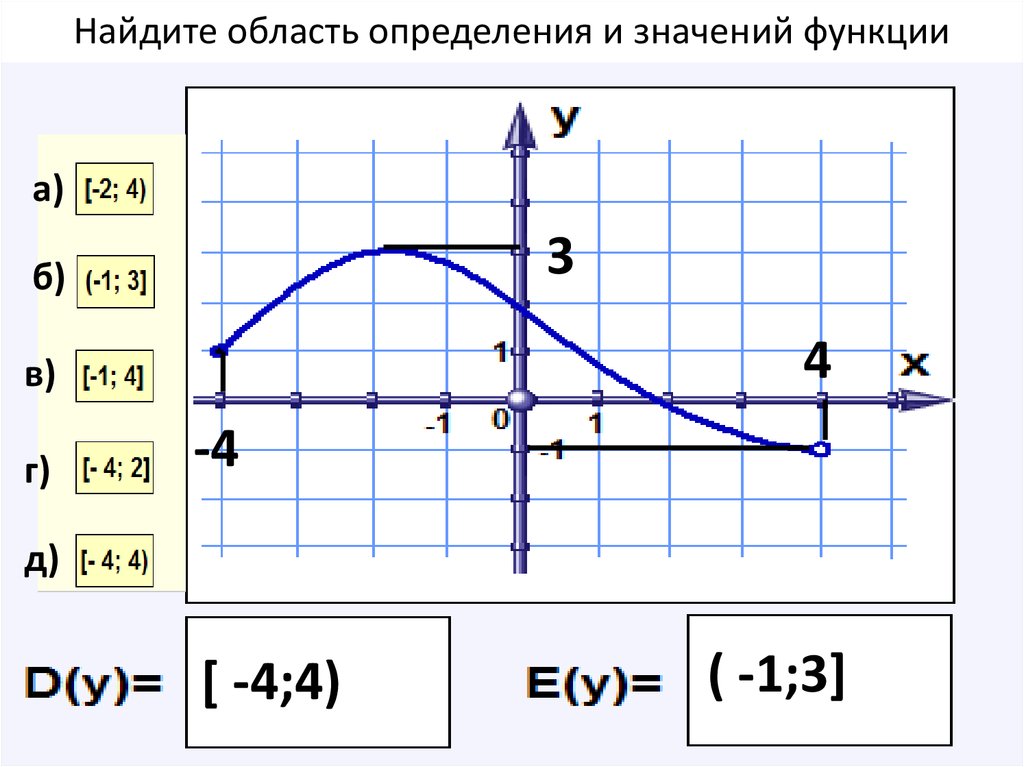


 Тогда
Тогда Если X и Y — числовые множества, такие, как или , то отображение называют функцией. Если X или Y многомерны, например, или , то отображение называют ве́ктор-фу́нкцией
Если X и Y — числовые множества, такие, как или , то отображение называют функцией. Если X или Y многомерны, например, или , то отображение называют ве́ктор-фу́нкцией Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.