Как найти область определения функции?
Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
- Например, область значений функции y = x2 — это все числа больше либо равные нулю. Это можно записать так: Е (у): у ≥ 0.
Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin)
— область определения функции арксинус.Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
|
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.
Множество значений такой функции состоит из одного единственного элемента.
Например:
- Область определения постоянной функции y = -3 — это множество всех действительных чисел: D(f) = (−∞, +∞) или D(f) = R.
- Область определения функции y = 3√9 является множество R.
Еще больше примеров — в современной онлайн-школе Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
Приходите на бесплатный вводный урок математики и начните заниматься эффективно и в удовольствие!
Область определения функции с корнем
Функцию с корнем можно определить так: y = n√x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
- Если n — четное число, то есть, n = 2m, где m ∈ N, то ее область определения есть множество всех неотрицательных действительных чисел:
- Если показатель корня нечетное число больше единицы, то есть, n = 2m+1, то область определения корня — множество всех действительных чисел:
Значит, область определения каждой из функций y = √x, y = 4√x, y = 6√x,… есть числовое множество [0, +∞). А область определения функций y = 3√x, y = 5√x, y = 7√x,… — множество (−∞, +∞).
А область определения функций y = 3√x, y = 5√x, y = 7√x,… — множество (−∞, +∞).
Пример
Найти область определения функции:
Как решаем:
Так как подкоренное выражение должно быть положительным, то решим неравенство x2 + 4x + 3 > 0.
Разложим квадратный трёхчлен на множители:
x2 + 4x + 3 > 0
D = 16 — 12 = 4 > 0
Дискриминант положительный. Ищем корни:
Значит парабола a(x) = x2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x2 + 4x + 3 < 0), а другая часть — выше оси (неравенство x2 + 4x + 3 > 0).
Поскольку коэффициент a = 1 > 0, то ветви параболы смотрят вверх. Можно сделать вывод, что на интервалах (−∞, -3) ∪ (−1, +∞) выполнено неравенство x2 + 4x + 3 > 0 (ветви параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке (-3; -1) ниже оси абсцисс, что соответствует неравенству x
Ответ: область определения: D(f) = (−∞, -3) ∪ (−1, +∞).
Область определения степенной функции
Степенная функция выглядит так: y = xa, то есть, f(x) = xa, где x — переменная в основании степени, a — некоторое число в показателе степени.
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
- Если a — положительное целое число, то область определения функции есть множество действительных чисел: (−∞, +∞).
- Для нецелых действительных положительных показателей степени: D(f) = [0, +∞).
- Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).
- Для остальных действительных отрицательных a область определения степенной функции — числовой промежуток (0, +∞).
При a = 0 степенная функция y = xa определена для всех действительных значений x, кроме x = 0. Это связано с тем, что мы не определяли 00. А любое отличное от нуля число в нулевой степени равно единице. То есть, при a = 0 функция приобретает вид y = x0 = 1 на области определения (−∞, 0) ∪ (0, +∞).
Это связано с тем, что мы не определяли 00. А любое отличное от нуля число в нулевой степени равно единице. То есть, при a = 0 функция приобретает вид y = x0 = 1 на области определения (−∞, 0) ∪ (0, +∞).
Рассмотрим несколько примеров.
- Область определения функций y = x5, y = x12 — множество R, так как показатели степени целые положительные.
- Степенные функции определены на интервале [0, +∞), так как их показатели положительные, но не целые.
- Область определения функции y = x−2, как и функции y = x−5 — это множество (−∞, 0) ∪ (0, +∞), так как показатели степени целые отрицательные.
- Область определения степенных функций y = x
Область определения показательной функции
Показательную функцию можно задать формулой y = ax, где переменная x — показатель степени, а — больше нуля и не равно единице.
Область определения показательной функции — это множество R.
Примеры показательных функций:
- y = ex
- y = (√15)x
- y = 13x.
Область определения каждой из них (−∞, +∞).
Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
- D (ln) = (0, +∞) и D (lg) = (0, +∞).
Рассмотрим примеры логарифмических функций:
- y = log7x
- y = lnx
Область определения этих функций есть множество (0, +∞).
Пример
Укажите область определения функции:
Как решаем:
Составим и решим систему:
Графическое решение:
Ответ: область определения: D(f) = (−3, -2) ∪ (−2, +∞).
Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
- Функция, которая задается формулой y = sinx, называется синусом, обозначается sin и определяется на множестве всех действительных чисел. Область определения синуса — это множество всех действительных чисел, то есть, D(sin) = R.
- Функция, которая задана формулой
- Функции, которые заданы формулами y = tgx и y = ctgx, называются тангенсом и котангенсом и обозначаются tg и ctg. Область определения тангенса — это множество всех действительных чисел, кроме чисел . Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что и x ∈ r, x ≠ πk, k ∈ Z соответственно.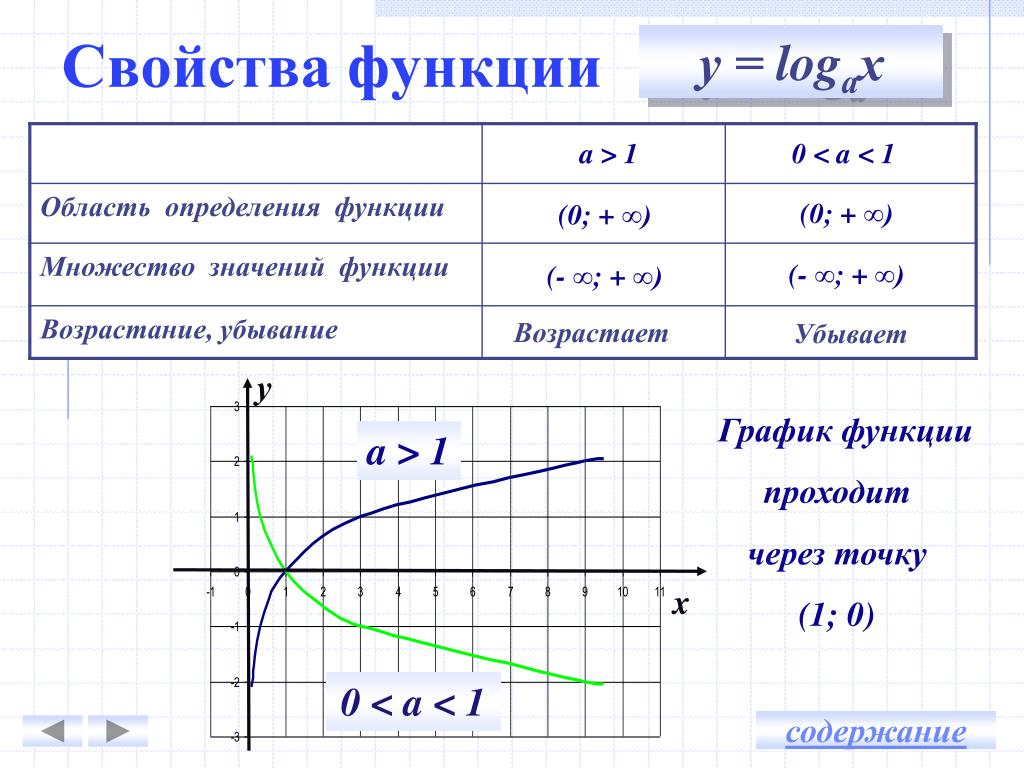
Пример
Найдите область определения функции f(x) = tg2x.
Как решаем:
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате . Отразим графически:
Ответ: область определения: .
Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
- Функция, которая задается формулой y = arcsinx и рассматривается на отрезке [−1, 1], называется арксинусом и обозначается arcsin.
Область определения арксинуса — это множество [−1, 1], то есть, D(arcsin) = [−1, 1].
- Функция, которая задается формулой y = arccosx и рассматривается на отрезке [−1, 1], называется арккосинусом и обозначается arccos.
Область определения функции арккосинус — отрезок [−1, 1], то есть, D(arccos) = [−1, 1].
- Функции, которые задаются формулами вида y = arctgx и y = arcctgx и рассматриваются на множестве всех действительных чисел, называются арктангенсом и арккотангенсом и обозначаются arctg и arcctg.

Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.
Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Функция | Область определения функции |
Постоянная y = C | R |
Корень y = n√x | [0 ; +∞) , если n — четное; (-∞; +∞) , если n — нечетное. |
Степенная y = xa | (-∞; +∞) , если a > 0, a ∈ Z; [0 ; +∞), если a > 0, a ∈ R, a ∉ Z; (-∞; 0) ∪ (0; +∞) , если a < 0, a ∈ Z; (0; +∞), если a ∈ R, a ≠ Z; (-∞; 0) ∪ (0, +∞), если a = 0. |
Показательная y = ax | R |
Логарифмическая y = lognx | (0; +∞) |
Тригонометрические y = sinxy y = cosxy y = tgxy y = ctgx | R R x ∈ R, x ≠ π/2 + πk, k ∈ Z x ∈ R, x ≠ πk, k ∈ Z |
Обратные тригонометрические y = arcsinxy y = arccosxy y = arctgxy y = arcctgx | [-1; 1] [-1; 1] R R |
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в современную школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
А еще помогут догнать сверстников и справиться со сложной контрольной.
Как найти область определения функции?
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно углубить знания данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y=x+x-2 или y=5·x2+1·x3, y=xx-5 или y=x-15-3. Рассмотрим теорию и решим несколько примеров с подобными заданиями.
Что значит найти область определения
После того, как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Ограничение области определения
Область определения рассматривается еще в школьной курсе. у действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально определить ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
у действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально определить ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
- при имеющемся знаменателе необходимо производить деление такого типа функции как y=x+2·xx4-1;
- при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа y=x+1 или y=23·x+3x;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y=5·(x+1)-3, y=-1+x113, y=(x3-x+1)2, которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y=lnx2+x4 или y=1+logx-1(x+1) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y=x3+tg2·x+5 или y=ctg(3·x3-1), так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y=arcsin(x+2)+2·x2, y=arccosx-1+x, область определения которых определяется ни интервале от -1 до 1.

При отсутствии хотя бы одного признака, область определения приходится искать другим образом. Рассмотрим пример функции вида y=x4+2·x2-x+12+223·x. Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y=2·x+1. Для вычисления ее значения можем определить x. Из выражения 2·x+1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y=3x-1, а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3x-1знаменатель равняется нулю при х=1, поэтому искомая область определения данной функции примет вид (−∞, 1)∪(1, +∞) и считается числовым множеством.
На рассмотрении примера y=x2-5·x+6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю. Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно, чтобы имело место следующее утверждение:
Когда функция ff считается суммой n функций f1, f2, …, fn, иначе говоря, эта функция задается при помощи формулы y=f1(x)+f2(x)+…+fn(x), тогда ее область определения считается пересечением областей определения функций f1, f2, …, fn. Данное утверждение можно записать как:
D(f)=D(f1)D(f2)…D(fn)
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом для понимания перечисления числовых множеств.
Найти область определения функции вида y=x7+x+5+tgx.
Решение
Заданная функция представляется как сумма четырех: степенной с показателем 7,степенной с показателем 1, постоянной, функции тангенса.
По таблице определения видим, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞), D(f3)=(−∞, +∞), причем область определения тангенса включает в себя все действительные числа, кроме π2+π·k, k∈Z.
Областью определения заданной функции f является пересечение областей определения f1, f2, f3 и f4. То есть для функции существует такое количество действительных чисел, куда не входит π2+π·k, k∈Z.
Ответ: все действительные числа кроме π2+π·k, k∈Z.
Для нахождения области определения произведения функций необходимо применять правило:
Определение 2Когда функция f считается произведением n функций f1, f2, f3 и fn, тогда существует такая функция f, которую можно задать при помощи формулы y=f1(x)·f2(x)·…·fn(x), тогда ее область определения считается областью определения для всех функций.
Запишется D(f)=D(f1)D(f2)…D(fn)
Пример 2Найти область определения функции y=3·arctg x·ln x.
Решение
Правая часть формулы рассматривается как f1(x)·f2(x)·f3(x), где за f1является постоянной функцией, f2является арктангенсом, f3– логарифмической функцией с основанием e. По условию имеем, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞) и D(f3)=(0, +∞). Мы получаем, что
D(f)=D(f1)D(f2)D(fn)=(-∞, +∞)(-∞, +∞)D(0, +∞)=(0, +∞)
Ответ: область определения y=3·arctg x·ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y=C·f(x), где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y=C·f(x)– произведение постоянной функции и f. Область определения – это все действительные числа области определения D(f). Отсюда видим, что область определения функции y=C·f(x)является -∞, +∞D(f)=D(f).
Получили, что область определения y=f(x) и y=C·f(x), где C является некоторое действительное число, совпадают. Это видно на примере определения корня y=x считается [0, +∞), потому как область определения функции y=-5·x — [0, +∞).
Области определения y=f(x) и y=−f(x)совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Пример 3Найти область определения функции y=log3x−3·2x.
Решение
Необходимо рассмотреть как разность двух функций f1 и f2.
f1(x)=log3x и f2(x)=3·2x. Тогда получим, что D(f)=D(f1)D(f2).
Область определения записывается как D(f1)=(0, +∞). Приступим к области определения f2 . в данном случае она совпадает с областью определения показательной, тогда получаем, что D(f2)=(−∞, +∞).
Для нахождения области определения функции y=log3x−3·2x получим, что
D(f)=D(f1)D(f2)=(0, +∞)-∞, +∞
Ответ: (0, +∞).
Необходимо озвучить утверждение о том, что областью определения y=anxn+an-1xn-1+…+a1x+a0 является множество действительных чисел.
Рассмотрим y=anxn+an-1xn-1+…+a1x+a0, где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы (n+1)-ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R.
Пример 4Найти область определения f1(x)=x5+7×3-2×2+12.
Решение
Примем обозначение f за разность двух функций, тогда получим, что f1(x)=x5+7×3-2×2+12 и f2(x)=3·x-ln 5. Выше было показано, что D(f1)=R. Область определения для f2 является совпадающей со степенной при показателе –ln5, иначе говоря, что D(f2)=(0, +∞).
Получаем, что D(f)=D(f1)D(f2)=-∞, +∞(0, +∞)=(0, +∞).
Ответ: (0, +∞).
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y=f1(f2(x)). Известно, что D(f)является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Известно, что D(f)является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Видно, что область определения сложной функции вида y=f1(f2(x)) находится на пересечении двух множеств таких, где x∈D(f2) и f2(x)∈D(f1). В стандартном обозначении это примет вид
x∈D(f2)f2(x)∈D(f1)
Рассмотрим решение нескольких примеров.
Пример 5Найти область определения y=ln x2.
Решение
Данную функцию представляем в виде y=f1(f2(x)), где имеем, что f1 является логарифмом с основанием e, а f2 – степенная функция с показателем 2.
Для решения необходимо использовать известные области определения D(f1)=(0, +∞) и D(f2)=(−∞, +∞).
Тогда получим систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-∞, +∞x2∈(0, +∞)⇔⇔x∈(-∞, +∞)x2>0⇔x∈(-∞, +∞)x∈(-∞, 0)∪(0, +∞)⇔⇔x∈(-∞, 0)∪(0, +∞)
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Ответ: (−∞, 0)∪(0, +∞).
Пример 6Найти область определения функции y=(arcsin x)-12.
Решение
Так как дана сложная функция, необходимо рассматривать ее как y=f1(f2(x)), где f1 является степенной функцией с показателем -12, а f2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D(f1)=(0, +∞) и D(f2)=[−1, 1]. Теперь найдем все множества значений x, где x∈D(f2) и f2(x)∈D(f1). Получаем систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-1, 1arcsin x∈(0, +∞)⇔⇔x∈-1, 1arcsin x>0
Для решения arcsin x>0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [−1, 1], причем обращается в ноль при х=0, значит, что arcsin x>0 из определения x принадлежит промежутку (0, 1].
Преобразуем систему вида
x∈-1, 1arcsin x>0⇔x∈-1, 1x∈(0, 1]⇔x∈(0, 1]
Область определения искомой функции имеет интервал равный (0, 1].
Ответ: (0, 1].
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y=f1(f2(…fn(x)))). Область определения такой функции ищется из x∈D(fn)fn(x)∈D(fn-1)fn-1(fn(x))∈D(fn-2)…f2(f3(…(fn(x)))∈D(f1).
Пример 7Найти область определения y=sin(lg x4).
Решение
Заданная функция может быть расписана, как y=f1(f2(f3(x))), где имеем f1 – функция синуса, f2 – функция с корнем 4 степени, f3– логарифмическая функция.
Имеем, что по условию D(f1)=(−∞, +∞), D(f2)=[0, +∞), D(f3)=(0, +∞). Тогда областью определения функции – это пересечение множеств таких значений, где x∈D(f3), f3(x)∈D(f2), f2(f3(x))∈D(f1). Получаем, что
x∈D(f3)f3(x)∈D(f2)f2(f3(x))∈D(f1)⇔x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞
Условие lg x4∈-∞, +∞ аналогично условию lg x∈[0, +∞), значит
x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞⇔x∈(0, +∞)lg x∈[0, +∞)lg x∈[0, +∞)⇔⇔x∈(0, +∞)lg x∈[0, +∞)⇔x∈(0, +∞)lg x≥0⇔⇔x∈(0, +∞)lg x≥lg 1⇔x∈(0, +∞)x≥1⇔⇔x∈[1, +∞)
Ответ: [1, +∞).
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f1(x)f2(x). Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f2(х) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x∈D(f1)x∈D(f2)f2(x)≠0.
Запишем функцию y=f1(x)f2(x) в виде y=f1(x)·(f2(x))-1. Тогда получим произведение функций вида y=f1(x) с y=(f2(x))-1. Областью определения функции y=f1(x) является множество D(f1), а для сложной y=(f2(x))-1 определим из системы вида x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f2)f2(x)≠0.
Значит, x∈D(f1)x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f1)x∈D(f2)f2(x)≠0.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 8Найти область определения y=tg(2·x+1)x2-x-6.
Решение
Заданная функция дробная, поэтому f1 – сложная функция, где y=tg(2·x+1) и f2 – целая рациональная функция, где y=x2−x−6, а область определения считается множеством всех чисел. Можно записать это в виде
x∈D(f1)x∈D(f2)f2(x)≠0
Представление сложной функции y=f3(f4(x)), где f3–это функция тангенс, где в область определения включены все числа, кроме π2+π·k, k∈Z, а f4– это целая рациональная функция y=2·x+1 с областью определения D(f4)=(−∞, +∞). После чего приступаем к нахождению области определения f1:
x∈D(f4)2·x+1∈D(f3)⇔x∈(-∞, +∞)2x+1≠π2+π·k, k∈Z⇔x≠π4-12+π2·k, k∈Z
Еще необходимо рассмотреть нижнюю область определения y=tg(2·x+1)x2-x-6. Тогда получаем, что
x∈D(f1)x∈D(f2)f2(x)≠0⇔x≠π4-12+π2·k, k∈Zx∈-∞, +∞x2-x-6≠0⇔⇔x≠π4-12+π2·k, k∈Zx≠-2x≠3
Ответ: множество действительных чисел, кроме -2, 3 и π4-12+π2·k, k∈Z.
Область определения логарифма с переменной в основании
Определение 3Определение логарифма существует для положительных оснований не равных 1. Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
А аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y=logaf1(x)logaf2(x), a>0, a≠1. После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y=logaf1(x) и y=logaf2(x) можно определить из получившейся системы вида x∈D(f1)f1(x)>0 и x∈D(f2)f2(x)>0. Иначе эту область можно записать в виде y=logaf1(x)logaf2(x), a>0, a≠1, что означает нахождение y=logf2(x)f1(x) из самой системы вида
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0logaf2(x)≠0=x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
Пример 9Обозначить область определения функции y=log2·x(x2-6x+5).
Решение
Следует принять обозначения f1(x)=x2−6·x+5 и f2(x)=2·x, отсюда D(f1)=(−∞, +∞) и D(f2)=(−∞, +∞). Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
x∈(-∞, +∞)x2-6x+5>0x∈(-∞, +∞)2·x>02·x≠1⇔x∈(-∞, +∞)x∈(-∞, 1)∪(5, +∞)x∈(-∞, +∞)x>0x≠12⇔⇔x∈0, 12∪12, 1∪(5, +∞)
Отсюда видим, что искомой областью функции y=log2·x(x2-6x+5) считается множнство, удовлетворяющее условию 0, 12∪12, 1∪(5, +∞).
Ответ: 0, 12∪12, 1∪(5, +∞).
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y=(f1(x))f2(x). Ее область определения включает в себя такие значения x, которые удовлетворяют системе x∈D(f1)x∈D(f2)f1(x)>0.
Эта область позволяет переходить от показательно-степенной к сложной вида y=aloga(f1(x))f2(x)=af2(x)·logaf1(x), где где a>0, a≠1.
Пример 10Найти область определения показательно-степенной функции y=(x2-1)x3-9·x.
Решение
Примем за обозначение f1(x)=x2−1 и f2(x)=x3-9·x.
Функция f1определена на множестве действительных чисел, тогда получаем область определения вида D(f1)=(−∞, +∞). Функция f2является сложной, поэтому ее представление примет вид y=f3(f4(x)), а f3 – квадратным корнем с областью определения D(f3)=[0, +∞), а функция f4 – целой рациональной,D(f4)=(−∞, +∞). Получаем систему вида
x∈D(f4)f4(x)∈D(f3)⇔x∈(-∞, +∞)x3-9·x≥0⇔⇔x∈(-∞, +∞)x∈-3, 0∪[3, +∞)⇔x∈-3, 0∪[3, +∞)
Значит, область определения для функции f2имеет вид D(f2)=[−3, 0]∪[3, +∞). После чего необходимо найти область определения показательно-степенной функции по условию x∈D(f1)x∈D(f2)f1(x)>0.
Получаем систему вида x∈-∞, +∞x∈-3, 0∪[3, +∞)x2-1>0⇔x∈-∞, +∞x∈-3, 0∪[3, +∞)x∈(-∞, -1)∪(1, +∞)⇔⇔x∈-3, -1∪[3, +∞)
Ответ: [−3, −1)∪[3, +∞)
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.Ф
| Функция | Ее область определения |
Сумма, разность, произведение функций f1, f2,…, fn | Пересечение множеств D(f1), D(f2), …, D(fn) |
Сложная функция y=f1(f2(f3(…fn(x))))
В частности, y=f1(f2(x)) | Множество всех x, одновременно удовлетворяющих условиям x∈D(fn),fn(x)∈D(fn-1),fn-1(fn(x))∈D(fn-2),… ,f2(f3(…fn(x)))∈D(f1)
x∈D(f2),f2(x)∈D(f1) |
Расположим функции и их области определения.
| Функция | Ее область определения |
Прямая пропорциональность y=k·x | R |
| Линейная y=k·x+b | R |
Обратная пропорциональность y=kx | -∞, 0∪0, +∞ |
| Квадратичная y=a·x2+b·x+c | R |
| y=anxn+an-1xn-1+…+a1x+a0 | R |
| Целая рациональная | R |
| y=C·f(x), где C — число | D(f) |
Дробная y=f1(x)f2(x)
В частности, если f1(x), f2(x) — многочлены | Множество всех x, которые одновременно удовлетворяют условиям
f2(x)≠0 |
| y=f(x)n, где n — четное | x∈D(f1), f(x)≥0 |
y=logf2(x)f1(x)
В частности, y=logaf1(x)
В частности, y=logf2(x)a | x∈D(f1), f1(x)>0,x∈D(f2), f2(x)>0, f2(x)≠1
x∈D(f1), f1(x)>0
x∈D(f2), f2>0, f2(x)≠1 |
| Показательно-степенная y=(f1(x))f2(x) | x∈D(f1), x∈D(f2), f1(x)>0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
Урок 37. Тема урока: «Функция. Область определения функции.учитель Леонова Л.М.
ФОРМУЛА КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ
Методическая разработка по алгебре (8 класс) ФОРМУЛА КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ Амосова Галина Владимировна, учитель математики и информатики ГБОУ СОШ 2 Василеостровского района Санкт-Петербурга «Метод
ПодробнееПояснительная записка
Пояснительная записка Рабочая программа по алгебре для 8 класса разработана в соответствии с Примерной программой основного общего образования по математике, с учетом требований федерального компонента
ПодробнееКомментарий пояснение.

методическая разработка урока с использованием ИКТ Учебный предмет алгебра Тема урока Линейная функция 7 класс Муниципальное общеобразовательное учреждение средняя общеобразовательная школа 10 г. Сочи
ПодробнееПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ В результате изучения курса алгебры в 8АВ, 8 ГД (группа А) классе учащийся научится знать/понимать: значение математической науки для решения задач, возникающих в теории и практике;
ПодробнееКонспект урока по теме:
Муниципальное общеобразовательное бюджетное учреждение «Лицей 5» Конспект урока по теме: «Функции y = x 1 и y = x 2» Учитель: Сагарда И.В. г. Оренбург 2016 г. Аннотация к уроку Данный урок разработан в
ПодробнееУчебно- методический комплекс
Учебно- методический комплекс курсов «АЛГЕБРА» класса 11 «Б» учителя (Ф. И.О.) Зверевой Елены Станиславовны государственного бюджетного общеобразовательного учреждение Самарской области «Школа-интернат
И.О.) Зверевой Елены Станиславовны государственного бюджетного общеобразовательного учреждение Самарской области «Школа-интернат
Пояснительная записка
Пояснительная записка Рабочая учебная программа по алгебре в 9 классе составлена на основе следующих документов: 1. Федеральный государственный образовательный стандарт основного общего образования (приказ
ПодробнееРАБОЧАЯ ПРОГРАММА по алгебре 9 класс
Муниципальное бюджетное общеобразовательное учреждение «Школа 120» «Рассмотрено» на заседании школьного методического объединения Председатель: Прохоренко Н. Н. Протокол 1 30.08.2017 «Согласовано» заместитель
ПодробнееРАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ 8 КЛАСС
РАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ 8 КЛАСС Пояснительная записка Рабочая программа составлена на основе: — Федерального компонента государственного образовательного стандарта основного общего образования по
ПодробнееББК Б94 ISBN
ББК 74. 262.21 Б94 Б94 Буцко Е.В. Алгебра : 7 класс : методическое пособие / Е.В. Буцко, А.Г. Мерзляк, В.Б. Полонский и др. М. : Вентана-Граф, 2017. 104 с. : ил. ISBN 978-5-360-08673-4 Пособие содержит
262.21 Б94 Б94 Буцко Е.В. Алгебра : 7 класс : методическое пособие / Е.В. Буцко, А.Г. Мерзляк, В.Б. Полонский и др. М. : Вентана-Граф, 2017. 104 с. : ил. ISBN 978-5-360-08673-4 Пособие содержит
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
РАБОЧАЯ ПРОГРАММА ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Курс математики в 9 классе состоит из двух разделов: «Алгебра», «Геометрия». На изучение алгебры в 9 классе отведено 102 часа за год На изучение геометрии отведено
ПодробнееПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа по алгебре для 8 класса разработана и составлена в соответствии с федеральным компонентом государственного стандарта начального общего, основного общего и среднего
ПодробнееКиселёва Ольга Львовна. Ход урока.
1.Организация класса. ( Слайд 1) Ход урока. Начинается урок. Он пойдёт ребятам впрок 2. Первичная актуализация. (Слайд 2) — Ребята, нужны ли нам умения решать задачи на движение? — Зачем они нам необходимы?
Начинается урок. Он пойдёт ребятам впрок 2. Первичная актуализация. (Слайд 2) — Ребята, нужны ли нам умения решать задачи на движение? — Зачем они нам необходимы?
Ход урока: 1 Организационный момент.
Цель: Организовать деятельность учащихся по закреплению графического метода решения уравнений с параметром, проводить исследование на наличие корней уравнения для каждого значения параметра. Задачи: 1.
ПодробнееУравнения и неравенства с параметрами
Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа 7» Уравнения и неравенства с параметрами программа элективного курса для учащихся 9 классов Обсуждено на заседании
ПодробнееПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Цели обучения. Школьное математическое образование ставит следующие цели обучения: овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности,
Школьное математическое образование ставит следующие цели обучения: овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности,
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа по математике для 7 класса составлена на основе следующих документов: 1. Федеральный компонент государственного стандарта основного общего образования по математике.
ПодробнееУДК :512 ББК 22.14я721.6 М52
УДК 373.167.1:512 ББК 22.14я721.6 М52 Мерзляк, А.Г. М52 Алгебра : 9 класс : cамостоятельные и контрольные работы : пособие для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, Е.М.
ПодробнееРабочая программа по алгебре
МОУ: Наименование образовательного учреждения Рабочая программа по алгебре 8 класс Учитель Местонахождение образовательного учреждения 00-00 учебный год ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Школьное математическое образование
ПодробнееСодержание.
 1. Пояснительная записка
1. Пояснительная запискаСодержание. Пояснительная записка стр. описание места учебного предмета в учебном плане учебно-методический комплект планируемые результаты освоения предмета формы контроля. Содержание тем учебного предмета
ПодробнееРабочая программа по алгебре
Муниципальное казенное образовательное учреждение «Ревякинская средняя общеобразовательная школа» Ясногорского района Тульской области УТВЕРЖДЕНО на заседании педагогического совета (протокол от 27.08.2014
ПодробнееПояснительная записка.
Пояснительная записка. Рабочая программа составлена на основании: Учебного плана МБОУ «Средняя школа 15» на 2016/2017 учебный год. Положения о рабочей программе учебных предметов и курсов внеурочной деятельности
ПодробнееТема: Решение систем уравнений
Цель урока: МОУ гимназия 11 г. Елец Липецкой области Разработчик: учитель информатики Губина Т.Н. Методическая разработка системы интегрированных уроков по информатике и математике в 10 классе Урок 7 Тема:
Елец Липецкой области Разработчик: учитель информатики Губина Т.Н. Методическая разработка системы интегрированных уроков по информатике и математике в 10 классе Урок 7 Тема:
Пояснительная записка.
Пояснительная записка. Данная рабочая программа ориентирована на учащихся 8 класса и реализуется на основе следующих документов:. Государственный стандарт начального общего, основного общего и среднего
ПодробнееМесто предмета в учебном плане Цели курса
Алгебра 7 класс Рабочая программа по алгебре для обучающихся 7 класса составлена в соответствии с требованиями федерального государственного образовательного стандарта основного общего образования и примерной
ПодробнееПланируемые результаты
Повторение 7 часов. п/п Дата Тема урока Тип урока Основные вопросы 1. Повторение. Преобразование алгебраических дробей. 2. Повторение. Преобразование алгебраических дробей. 3 Повторение. Степени. Степень
Повторение. Преобразование алгебраических дробей. 2. Повторение. Преобразование алгебраических дробей. 3 Повторение. Степени. Степень
Рабочая программа по алгебре 7 класс
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ Государственное бюджетное общеобразовательное учреждение города Москвы «Школа 830» 125362, г. Москва, ул. Большая Набережная, д.23, тел./факс: 8-495-491-13-45 ИНН/КПП
ПодробнееЧто такое функция.
В материале представлено самое первое знакомство с функцией. Дано определение, приведены примеры функций, а также введены понятия области определения и области значений функций.
Просмотр содержимого документа
«Что такое функция.
 »
»
7 класс.
Что такое функция.
Функцией называется такая зависимость переменной у от переменной х, что каждому значению переменной х соответствует только одно значение переменной у. Переменная х называется независимой (или аргументом), а переменная у – зависимой (или значением функции).
Например, .
Каждая функция имеет область определения и область значений. Разберёмся, что это такое.
Областью определения функции называется множество всех значений, которые может принимать независимая переменная х (аргумент). Обозначается она так: .
Например, рассмотрим функцию . Нам нужно определить, какие значения может принимать х. Так как на 2 мы можем умножить любое число и от любого результата можем отнять 1, то х может принимать абсолютно любые значения. Значит, – любое число.
Так как на 2 мы можем умножить любое число и от любого результата можем отнять 1, то х может принимать абсолютно любые значения. Значит, – любое число.
Рассмотрим теперь функцию . Здесь мы замечаем, что х находится в знаменателе, а всем известно, что на 0 делить нельзя. Поэтому, мы находим число, при котором знаменатель станет равным 0. Это число . Значит, х может принимать любые значения, кроме . Поэтому, – любое число, кроме .
Областью значений функции называется множество всех значений, которые может принимать зависимая переменная у (значение функции). Обозначается она так: .
Как находить область значений функции мы рассмотрим, когда будем изучать тему «Графики функций».
Функция может выражаться не только переменными х и у. Если рассматривать задачу о нахождении периметра квадрата со стороной а см, то формула, по которой находится этот периметр также является функцией. Здесь а – независимая переменная, а P – зависимая переменная, так как понятно, что периметр зависит от стороны квадрата, т.е. каждому значению а соответствует только одно значение P.
Здесь а – независимая переменная, а P – зависимая переменная, так как понятно, что периметр зависит от стороны квадрата, т.е. каждому значению а соответствует только одно значение P.
В начале нагревания температура воды была . При нагревании температура воды повышалась на в минуту. Задайте функцию зависимости температуры воды от времени нагревания .
Турист отошёл от лагеря на 8 км и остановился отдохнуть. Потом он продолжил движение со скоростью 6 км/ч. Задайте функцию зависимости расстояния , пройденного туристом, от времени , которое отсчитывается после отдыха.
Закипев при температуре , вода начала охлаждаться. Каждую минуту её температура понижалась на . Задайте функцию зависимости температуры воды от времени её охлаждения .
Поезд находится на расстоянии 50 км от города и удаляется от него со скоростью 40 км/ч.
 Задайте функцию зависимости расстояния (км) от между городом и поездом от времени (ч) движения поезда.
Задайте функцию зависимости расстояния (км) от между городом и поездом от времени (ч) движения поезда.Поезд находится на расстоянии 70 км от города и удаляется от него со скоростью 50 км/ч. Задайте функцию зависимости расстояния (км) от между городом и поездом от времени (ч) движения поезда.
Периметр прямоугольника равен 16 см, длина одной его стороны равна х см. Задайте функцию зависимости площади от стороны х.
Периметр прямоугольника равен 24 см, длина одной его стороны равна х см. Задайте функцию зависимости площади от стороны х.
Расстояние между поездами 150 км, и они удаляются друг от друга, двигаясь в противоположных направлениях, со скоростями 40 км/ч и 50 км/ч. Задайте функцию зависимости расстояния (км) между поездами от времени (ч) движения поездов.
Расстояние между поездами 180 км, и они удаляются друг от друга, двигаясь в противоположных направлениях, со скоростями 50 км/ч и 60 км/ч.
 Задайте функцию зависимости расстояния (км) между поездами от времени (ч) движения поездов.
Задайте функцию зависимости расстояния (км) между поездами от времени (ч) движения поездов.Одна из сторон прямоугольника равна х см, а периметр равен см. Задайте функцию зависимости площади этого прямоугольника от стороны х.
Одна из сторон прямоугольника равна х см, а периметр равен см. Задайте функцию зависимости площади этого прямоугольника от стороны х.
Из равенства найдите зависимость переменной у от переменной х.
Из равенства найдите зависимость переменной у от переменной х.
Из равенства найдите зависимость переменной у от переменной х.
Из равенства найдите зависимость переменной у от переменной х.
Дана функция . Найдите зависимость переменной х от переменной у.

Дана функция . Найдите зависимость переменной х от переменной у.
Дана функция . Найдите зависимость переменной х от переменной у.
Дана функция . Найдите зависимость переменной х от переменной у.
Найдите область определения функций:
Задайте формулой функцию, если известно, что:
значения функции противоположны значениям аргумента;
значения функции в 2 раза больше значений аргумента;
значения функции на 3 меньше, чем удвоенные значения аргумента;
значения функции равны значениям аргумента;
значения функции в 2 раза меньше значений аргумента;
значения функции на 1 больше, чем утроенные значения аргумента.

2
Что такое функция, или Функция рядом с нами. 7-й класс
Самые простые наблюдения подчас приводят к очень важным выводам. Ход истории показал, что выводы из наблюдений за различными процессами сыграли фундаментальную роль в развитии науки и техники.
Тема «Функция» в школьной программе обширна и многогранна в своих приложениях. Эта тема является одной из важнейших для всего курса математики.Она вплотную связана с решением уравнений, неравенств, текстовых задач и др. Мы не думаем, что все выпускники школы в будущем станут математиками, но мы уверены, что будущие абитуриенты высших учебных заведенийдолжны уверенно владеть понятием функциональной зависимости, свободно строить графики функций, находить области определения и т.д. Поэтому так важно сформировать основные понятия,связанные с данной темой у семиклассников уже на первых этапах ее изучения.
Урок «Что такое функция или функции вокруг нас» — первый в изучении темы «Функция». Необходимо заинтересовать и замотивировать ребят к дальнейшей плодотворной работе. Поэтому наглядность играет большую роль. Вследствие этого – презентация к уроку, плакаты с основными понятиями, раздаточный материал.
Необходимо заинтересовать и замотивировать ребят к дальнейшей плодотворной работе. Поэтому наглядность играет большую роль. Вследствие этого – презентация к уроку, плакаты с основными понятиями, раздаточный материал.
В подготовке уроков мне всегда является огромным методическим подспорьем личный, систематизированный по темам, архив Приложения Математика газеты «Первое сентября». В данном случае есть целая подборка материала по теме «Функция», откуда взят материал [8]. К сожалению, некоторые статьи, из которых тоже заимствована часть материала к уроку, отксерокопированы давно без указания номера газеты или журнала и года издания.Полный список использованных источников указан в конце статьи.
Цели и задачи:
- Привести учащихся к пониманию самого понятия функции и ее значения в жизни человека.
- Развитие умения решения задач по теме.
- Содействовать развитию у учащихся умений исследовать познавательные объекты, сравнивать, находить соответствия и делать выводы.

Сценарий урока (2 часа) (форма урока – ЛЕКЦИЯ с практической работой)
Техническое оснащение урока: компьютер, проектор, экран, магнитная дока.
Дидактические материалы:
- Раздаточная папка «Функции и их графики»
- Плакаты формата А4 с эпиграфом к уроку, с основными определениями, с формулами функций для устной работы.
- Тетрадь с пропечатанной основой (ТПО) «Задания для обучения и развития учащихся, Алгебра, 7 класс», Лебединцева Е.А., Беленкова Е.Ю. [9].
- Карточки с домашним заданием.
Рисунок 1
Лекционная частьУчитель: Если мы будем рисовать ряд окружностей, все более и более увеличивая радиус, то и сама окружность будет увеличиваться. Следовательно, длина окружности зависит от радиуса. В математике всякое правило, устанавливающее подобное соответствие, называется функцией.
Большинство математических понятий прошли долгий путь развития. Сложный путь прошло и понятие функции. Оно уходит корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Они еще не умели считать, но уже знали, что чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода; чем сильнее натянута тетива лука, тем дальше полетит стрела; чем дольше горит костер, тем теплее будет в пещере.
С развитием скотоводства, земледелия, ремесел и обмена увеличилось количество известных людям зависимостей между величинами.
Мы тоже являемся функцией многих переменных, одна из которых – время. Проходят годы, и мы меняемся. Мы также зависим от своей наследственности, от книг, которые мы читаем, от температуры окружающей нас среды и от многих других факторов. И поэтому тему нашего с вами УРОКА я обозначила так:
«Что же такое функция или функции рядом с нами».
Эпиграфом предлагаю взять следующие слова:
«Математическими портретами закономерностей природы служат функции»
Презентация – 1 часть: ИСТОРИЯ РАЗВИТИЯ ПОНЯТИЯ ФУНКЦИИ (слайды 2-10)
Работа с раздаточным материалом «Что такое функция?»:
ЧТО ТАКОЕ ФУНКЦИЯ?
Общее определение функции, которое мы называем теперь «классическим», сформировалось в математике не очень давно – лишь в начале прошлого века. И хотя математики имели дело с различными конкретными функциями почти на каждом шагу многовекового развития науки, все же должен был быть пройден долгий путь постепенной кристаллизации элементарных понятий и их обобщений, пока ученые пришли к необходимости общего определения функции и нашли его.
И хотя математики имели дело с различными конкретными функциями почти на каждом шагу многовекового развития науки, все же должен был быть пройден долгий путь постепенной кристаллизации элементарных понятий и их обобщений, пока ученые пришли к необходимости общего определения функции и нашли его.
Впервые в печати формулировка определения функции как аналитического выражения или «функции вообще» появилась в одной работе ученика и сотрудника Готфрида Вильгельма Лейбница, Иоганна Бернулли в 1718 году.
С проблемой общего определения функции в середине XVIII века столкнулись крупнейшие математики того времени, Жан ле Рон Даламбер и Леонард Эйлер, в решении задачи о колебаниях струны. В спор с ними ввязался молодой математик, сын Иоганна Бернулли, Даниил Бернулли. Но в их формулировках еще ничего не говорилось о допустимом характере зависимости «первых» величин от «вторых», они оставались достаточно расплывчатыми, так что каждый из последующих математиков был волен истолковывать их на свой лад.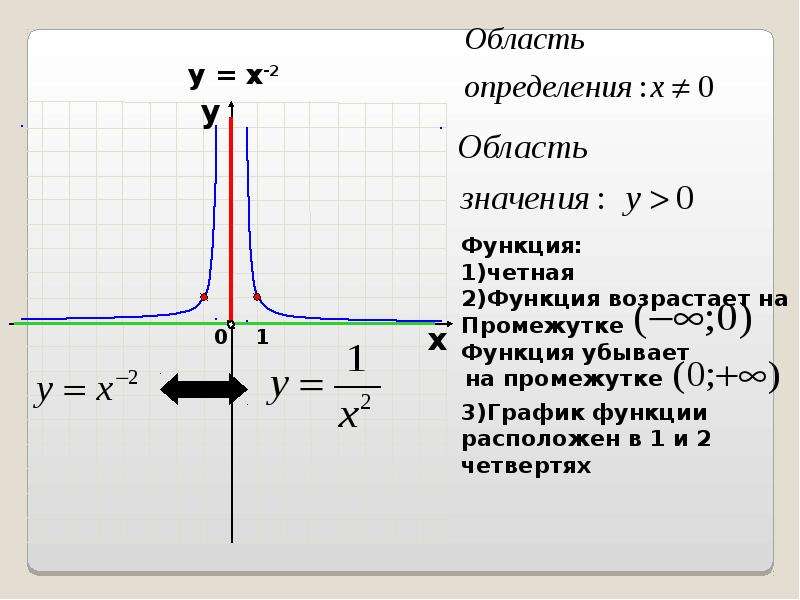 Свою лепту внесли Сильвестр Франсуа Лакруа, Жозеф Фурье, Коши, Николай Иванович Лобачевский, Петер Лежен Дирихле. Математики даже разбились на два лагеря – сторонников определения функции «по Дирихле», не требующих обязательного правила, и сторонников определения функции «по Лобачевскому», требующих обязательного правила из конечного числа слов.
Свою лепту внесли Сильвестр Франсуа Лакруа, Жозеф Фурье, Коши, Николай Иванович Лобачевский, Петер Лежен Дирихле. Математики даже разбились на два лагеря – сторонников определения функции «по Дирихле», не требующих обязательного правила, и сторонников определения функции «по Лобачевскому», требующих обязательного правила из конечного числа слов.
В конце двадцатых годов прошлого века над определением функции возникла новая угроза, теперь уже со стороны физиков. Теория явлений в физике микромира, новая эпоха в развитии новой физики, потребовала введения нового объекта – «дельта-функции». Здесь возникли очень серьезные разногласия между физиками и математиками, и тем значительнее представляется заслуга советского математика С.Л. Соболева, который открыл класс объектов, удовлетворяющих всем выдвинутым требованиям; впоследствии они были названы «обобщенными функциями».
Последняя форма определения функции еще не означает конца ее истории. Можно не сомневаться, что в дальнейшем под воздействием новых требований как самой математики, так и других наук – физики, биологии, науки об обществе, определение функции будет изменяться и каждое следующее изменение будет открывать новые горизонты науки и приводить к важным открытиям.
Можно не сомневаться, что в дальнейшем под воздействием новых требований как самой математики, так и других наук – физики, биологии, науки об обществе, определение функции будет изменяться и каждое следующее изменение будет открывать новые горизонты науки и приводить к важным открытиям.
ОПРЕДЕЛЕНИЯ ФУНКЦИИ
Функция переменной величины есть аналитическое выражение, составленное из этой величины и постоянных. И. Бернулли, 1718.
Функция есть кривая, начертанная свободным влечением руки. Л. Эйлер, 1748.
Когда некоторые количества зависят от других таким образом, что при изменении последних изменяются и первые, то первые называются функциями вторых. Л. Эйлер, 1755.
Всякое количество, значение которого зависит от одного или многих других количеств, называется функцией этих последних, независимо от того, известно или нет, какие операции нужно произвести, чтобы перейти от них к первому.
С. Лакруа, 1797.
Функция от x есть число, которое дается для каждого x и вместе с x постепенно изменяется. Значение функции может быть дано и аналитическим выражением, или условием, которое подает средство испытывать все числа. Зависимость может существовать и оставаться неизвестной. Н.И. Лобачевский, 1834.
Y есть функция от x, если всякому значению x соответствует вполне определенное значение y, причем совершенно неважно, каким именно способом установлено указанное соответствие. П. Дирихле, 1837.
Презентация – 2 часть: ФУНКЦИИ РЯДОМ С НАМИ (слайды 11-19)
Слайд 13 «Знание законов природы…» — в продолжении рассказ русского математика Игнатьева:
«Как-то проездом через некий уездный городок он узнал, что в городе есть своего рода чудо-математик. Тот решал всякую предложенную ему задачу чрезвычайно быстро, почти не думая, при помощи всего-навсего обыкновенной шахматной доски. Удивительно! Но, быть может, секрет этого доморощенного математика окажется не столь уж загадочным, если сообразить, на что похожа шахматная доска? Это та же бумага в клетку, удобная для построения графиков!»
Тот решал всякую предложенную ему задачу чрезвычайно быстро, почти не думая, при помощи всего-навсего обыкновенной шахматной доски. Удивительно! Но, быть может, секрет этого доморощенного математика окажется не столь уж загадочным, если сообразить, на что похожа шахматная доска? Это та же бумага в клетку, удобная для построения графиков!»
Слайды 14-16.
Давайте теперь рассмотрим еще один интересный вопрос. Этот вопрос обсуждают персонажи знаменитого трактата Галилея «Беседы и математические доказательства, касающихся двух новых отраслей науки»:
«Почему не бывает животных какой угодно величины? Почему, например, нет слонов в три раза большего роста, чем существуют, но тех же пропорций?
Ответ таков: стань слон в три раза больше, вес его бы увеличился в 27 раз, как куб размера, а площадь сечения костей и, следовательно, их прочность – только в 9 раз, как квадрат размера. Прочности костей не хватило бы выдержать увеличившийся вес. Такой слон был бы раздавлен собственной тяжестью. Рассуждение вполне строгое и убедительное.
Рассуждение вполне строгое и убедительное.
Строгость и убедительность ему придало знание собеседниками двух функциональных зависимостей: первая устанавливает соответствие между размерами подобных тел и их объемами – объем изменяется как куб размера; вторая связывает размеры подобных фигур и их площади – площадь изменяется как квадрат размера.
Говоря на математическом языке, линейный размер играет роль независимой переменной или аргумента, а объем и площадь являются зависимыми переменными или функциями.»
Запишем в тетради определения функции и графика функции.
(Слайды 10 и 16)
Практическая часть1. Слайд 17 «Чтобы наглядно проиллюстрировать…»
Третий лист раздаточной папки «Функции рядом с нами» — обсуждение с классом.
Функции рядом с нами.
Знание законов природы дало человеку возможность объяснять и предсказывать ее разнообразнейшие явления. «Математическими портретами» закономерностей природы и служит функция. Чтобы наглядно проиллюстрировать характерные свойства функции, обратимся к пословицам. Ведь пословицы – это тоже отражение устойчивых закономерностей, выверенных многовековым опытом народа.
«Математическими портретами» закономерностей природы и служит функция. Чтобы наглядно проиллюстрировать характерные свойства функции, обратимся к пословицам. Ведь пословицы – это тоже отражение устойчивых закономерностей, выверенных многовековым опытом народа.
- «Чем дальше в лес, тем больше дров». Изобразим графиком, как нарастает количество дров по мере продвижения в глубь леса – от опушки (S), где давным-давно все собрано, до чащобы, куда еще не ступала нога заготовителя.
- «Каши маслом не испортишь». Количество каши можно рассматривать, как функцию количества масла в ней. Согласно пословице, качество каши не понижается с добавкой масла. Подобного рода функции называются монотонно не убывающими.
- «Дальше от кумы – меньше греха». Функция, которая показывает, как изменяется мера греха по мере удаления от кумы, – монотонно убывающая функция.
- «Выше меры конь не скачет». Если изобразить траекторию скачущего коня, то высота скачков в полном соответствии с пословицей будет ограничена сверху некоторой «мерой».

- «Пересев хуже недосева». Вековой опыт свидетельствует: урожай лишь до некоторой поры растет вместе с плотностью посева, а далее он снижается, потому что при чрезмерной густоте ростки начинают «глушить» друг друга. В виде графика урожай максимален, когда поле засеяно в меру. Максимум – это наибольшее значение функции по сравнению с ее значениями во всех соседних точках. Это как бы «вершина горы», с которой все дороги ведут вниз, куда ни шагни.
- «Не круто начиная, круто кончай». Эта пословица может быть включена в правила научной организации труда. Повелительное звучание пословицы явно рассчитано на борьбу с противоположной, весьма распространенной манерой работы. На нее есть тоже своя пословица: «Горяч на почине, да скоро остыл». Обе функции, зависимы от времени, возрастающие. Но, как свидетельствуют кривые, «расти» можно по-разному.
- Сказка «про белого бычка». Если изобразить на графике эту сказку, мы получим периодическую функцию.
 Еще одним примером периодической функции является прибаутка: «У попа была собака – он ее любил…» и т.п. Что такое периодичность? Периодичностью в обычной речи называют чуть ли не всякую повторяемость. Однако повторяемость может быть более или менее строгой, достаточно сравнить между собой приведенные тексты.
Еще одним примером периодической функции является прибаутка: «У попа была собака – он ее любил…» и т.п. Что такое периодичность? Периодичностью в обычной речи называют чуть ли не всякую повторяемость. Однако повторяемость может быть более или менее строгой, достаточно сравнить между собой приведенные тексты.
2. Разминка (устная работа):
ТПО, стр. 30-31, № 38-39
3. Первая – вторая страница раздаточной папки (Приложение 1 и Приложение 2).
Ну, а теперь попробуем найти вот такие соответствия:
Каждой из следующих ситуаций соотнесите график функции, который описывает ее.
1 – н
2 – г
3 – ж
4 – а
5 – б
6 – з
7 – е
8 – д
9 – м
10 – и
11 – к
12 – л
Перемена.
4. ТПО стр. 29, №37
Функция задана таблицей. Заполним пропуски. Обратить внимание учащихся как обозначается область определения и область значений функции. Построим график, из чего он состоит – обратить внимание учащихся на определение графика и определение самой функции.
Построим график, из чего он состоит – обратить внимание учащихся на определение графика и определение самой функции.
5. Работа с учебником (Макарычев Ю.Н. Алгебра. 7 класс : для углубленного изучения алгебры). Стр. 196-198[10]
Разбор определений функции, зависимой переменной, независимой переменной или аргумента, области определения функции и области значения функции, числовой функции.
6. Работа с классом – обобщение.
Пример соответствия двух множеств: множество действительных чисел и множество натуральных чисел, являющихся их квадратами. Запись формулы, таблицы значений.
Вопрос: Как можно задать функцию? – исходим из того, что делали, какие задания были. Запись способов задания функции.
7. У меня есть три каточки с формулами функций и три карточки с графиками. Кто попробует установить соответствие между ними?
(Карточки на магнитах на доске – функции у=x, y= х2, y= х3 и их графики. )
)
Проверяем работу ученика и обсуждаем.
Объясняю, что аналогичная работа будет и дома в ТПО№168, надо упростить формулы функций, преобразовав выражения в правой стороне заданных функций и найти соответствие на предложенных графиках, определив, какая из данных линий может быть использована для создания графика каждой из них. К тому же, надо еще и достроить оси координат. Обратить внимание на карточки с формулами и графиками на доске, для которых искали соответствие.
8. Дома я предлагаю продолжить работу по данной тематике (раздаю отпечатанные карточки):
Домашнее задание:
а) глава 7 учебника, § 14 – прочитать, внимательно рассмотреть примеры: будем обсуждать, № 980
б) ТПО №168, стр. 140
в) предлагаю на выбор следующие творческие задания:
- составить практическую задачу, решение которой можно иллюстрировать с помощью графика функций;
- самим найти пословицы, которые можно интерпретировать с помощью графиков функций.

- с помощью графиков функций проиллюстрировать смысл найденных пословиц и пословиц, предложенных на уроке.
9. Итог урока.
Учитель: Итог нашего урока я выразила с помощью презентации «Функции в нашей жизни».
Слайды 20-32.
Учитель: Любоваться природой можно и не зная математики. Но понять ее, увидеть ее, то, что скрыто за внешними образами явлений можно лишь с помощью точной науки. Только она позволяет заметить, что в явлениях природы есть формы и ритмы, недоступные глазу созерцателя, но открытые глазу аналитика.
Урок закончен, спасибо за урок.
Использованная литература и интернет-ресурсы:
- Глейзер Г.И. История математики в школе: 7-8 класс. / Г.И. Глейзер. — М.: Просвещение. — 1982.
- Чистяков В.Д. Исторические экскурсы на уроках математики в средней школе. / В.Д. Чистяков. – Минск: “Народная освета”.
 — 1969.
— 1969. - Малыгин К.А. Элементы историзма в преподавании математики в средней школе. / К.А. Малыгин. — М.:Учпедгиз. — 1958.
- Математический энциклопедический словарь. — М.: Сов.энциклопедия. — 1988.
- Энциклопедический словарь юного математика. — М.: Педагогика. — 1989.
- https://urok.1sept.ru/authors/103-256-737/Нагоева Эльвира Германовна, учитель информатики
- Крамор В. С. Повторяем и систематизируем школьный курс алгебры и начал анализа. / В.С. Крамор. – М. : Просвещение, 1990.
- Григорьева В. Лекция «Функции рядом с нами». // Приложение Математика, №4. – М. : из-во Первое сентября, 2003. – с. 1-4, 6.
- Лебединцева Е.А., Беленкова Е.Ю. Алгебра 7 класс.Задания для обучения и развития учащихся. / Е.А.Лебединцева, Е.Ю.Беленкова.– М. : Интеллект-центр, 2005.
- Макарычев Ю.Н. Алгебра. 7 класс : для углубленного изучения алгебры. / Ю.Н. Макарычев, Г.
 Н. Миднюк, И.Е. Феоктистов. – 8-е изд. – М. : Мнемозина, 2008.
Н. Миднюк, И.Е. Феоктистов. – 8-е изд. – М. : Мнемозина, 2008.
Функция в 7 классе
Алгебра. 7 класс. Параграф 5. Тест 1.
Вариант I.
1. Найти область определения функции, заданной формулой у=2х2+5.
A) х ≠ 0; B) х — любое число; C) х ≠ -2,5; D) х ≠ -5.
2. Найти область определения функции, заданной формулой
A) х ≠ -3; B) х — любое число; C) х ≠ 4; D) х ≠ 0.
3. Найти область определения функции, заданной формулой
A) х ≠ 0; B) х — любое число; C) х ≠ 5; D) х ≠ -4.
4. Найти область определения функции, заданной формулой
A) х ≠ 0; B) х — любое число; C) х ≠ 1; D) х ≠ 0, х ≠ 1.
5. Функция задана формулой у = -3х. Найти значение этой функции для аргумента, равного (-12).
A) 4; B) 36; C) 32; D) -36.
6. Функция задана формулой у = 2х + 7. Найти значение этой функции для аргумента, равного (-8).
A) -7,5; B) -23; C) -9; D) 9.
7. Функция задана формулой
Найти значение этой функции для аргумента, равного 10.
A) -1,4; B) -140; C) 0,7; D) -14.
8. Функция задана формулой
Найти значение этой функции для аргумента, равного 5.
A) -0,2; B) 0,4; C) 0,2; D) 5.
9. Функция задана формулой у = -4х. Найдите значение аргумента, при котором значение функции равно 0,32.
A) -0,8; B) -0,08; C) -12,8; D) 0,08.
10. Функция задана формулой у = 0,8х+5. Найдите значение аргумента, при котором значение функции равно 7,4.
A) 0,3; B) 30; C) -3; D) 3.
11. Функция задана формулой
Найдите значение аргумента, при котором значение функции равно 4,5.
A) 2; B) 20; C) -2; D) 4,5.
12. Функция задана формулой
Найдите значение аргумента, при котором значение функции равно 3.
A) 3; B) 4; C) -2; D) 2.
Вариант II.
1. Найти область определения функции, заданной формулой:
A) х ≠ 0; B) х — любое число; C) х ≠ -2; D) х ≠ 2.
2. Найти область определения функции, заданной формулой:
у=-х2+4х-1.
A) х ≠ -1; B) х — любое число; C) х ≠ 4; D) х ≠ 0.
3. Найти область определения функции, заданной формулой:
A) х ≠ -1; B) х — любое число; C) х ≠ 1; D) х ≠ 0.
4. Найти область определения функции, заданной формулой:
A) х ≠ 0; B) х — любое число; C) х ≠ -4; х ≠ 0; D) х ≠ -4.
5. Функция задана формулой у = 2х+1. Найти значение этой функции для аргумента, равного (-6).
A) -14; B) -10; C) -11; D) -16.
6. Функция задана формулой у = -4х. Найти значение этой функции для аргумента, равного 5.
A) -20; B) -21; C) -20; D) -18.
7. Функция задана формулой у =8/x. Найти значение этой функции для аргумента, равного 1,6.
A) 6; B) 4; C) 7; D) 5.
8. Функция задана формулой:
Найти значение этой функции для аргумента, равного (-3).
A) -0,12; B) -0,25; C) -0,3; D) -0,5.
9. Функция задана формулой у = -7х. Найдите значение аргумента, при котором значение функции равно 2,8.
A) -19,6; B) -0,35; C) -0,4; D) -0,8.
10. Функция задана формулой у = 0,6х-5. Найдите значение аргумента, при котором значение функции равно (-2,4).
A) 3; B) 6; C) 4; D) 5.
11. Функция задана формулой y=12/x. Найдите значение аргумента, при котором значение функции равно 1,5.
A) 6; B) 10; C) 8; D) 7,5.
12. Функция задана формулой:
Найдите значение аргумента, при котором значение функции равно 2.
А) -4; B) 4; C) -1,6; D) -2.
Справочные материалы.
Зависимость, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной, называется функциональной зависимостью или функцией. Записывают: y = f(x). Независимую переменную x называют аргументом. Зависимую переменную y называют функцией.
Множество значений, которые принимает независимая переменная (аргумент), называют областью определения функции y=f(x) и обозначают D(f) или D(у).
Множество всех значений функции y=f(x) называют областью значений функции и обозначают Е(f) или Е(у).
Функцию можно задать графическим, словесным, табличным или аналитическим способом. Аналитический способ задания функции означает, что зависимость между переменными x и y задается посредством формулы (выражения).
Сверить ответы.
Поделиться новостью в соцсетях Метки: алгебра 7 класс, функция
Тест Область значения функции по алгебре (10 класс)
Сложность: эксперт.Последний раз тест пройден 12 часов назад.
Вопрос 1 из 10
Найдите область значений функции g(x) = 2sinx – 1
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 57% участников
- 43% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветитьВопрос 2 из 10
Найдите область значений функции h(x) = 3 + lgx
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 58% участников
- 42% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 3 из 10
Укажите функцию, областью значений которой является множество (-∞; +∞)
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 53% участников
- 47% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 4 из 10
Функция y = f(x) задана графиком на отрезке [-4; 3].
 Укажите область ее значений.
Укажите область ее значений.- Правильный ответ
- Неправильный ответ
- Вы и еще 50% ответили правильно
- 50% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 5 из 10
Найдите область значений функции y= 4cos2x
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 52% участников
- 48% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 6 из 10
Найдите наибольшее целочисленное значение функцииy = 3,9cosx
- Правильный ответ
- Неправильный ответ
- Вы и еще 51% ответили правильно
- 51% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 7 из 10
Найдите область значений функции y=
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 68% участников
- 32% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 8 из 10
Найдите область значений функции y = — 0,2sin5x
- Правильный ответ
- Неправильный ответ
- Вы и еще 54% ответили правильно
- 54% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 9 из 10
Укажите функцию, областью значений которой является промежуток (0; +∞)
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 81% участников
- 19% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 10 из 10
Найдите наибольшее целочисленное значение функцииy = 6,5sinx
- Правильный ответ
- Неправильный ответ
- Вы и еще 69% ответили правильно
- 69% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
При изучении алгебры большое внимание уделяется определению области значений функции как одному из важнейших базовых навыков, поэтому тест «Область значения функции» (10 класс) будет полезен всем, кто стремится к твердым знаниям. Эта разработка включает в себя десять заданий, при выполнении которых школьники смогут повторить весь необходимый теоретический материал и отработать все практические навыки.
Тесты по алгебре «Область определения функции» адресованы всем, кто изучает алгебру и начала анализа: и десятиклассникам, стремящимся успешно написать контрольную работу, и выпускникам, самостоятельно готовящимся к сдаче ЕГЭ.
Рейтинг теста
Средняя оценка: 3.6. Всего получено оценок: 191.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Объем и контекст объяснены в Swift — LearnAppMaking
Главная »Разработка приложений» Объем и контекст, объясненные в Swift
Написано Рейндером де Фризом 25 марта 2021 г. в разделе «Разработка приложений», Swift
в разделе «Разработка приложений», Swift
Что такое «объем» в программировании на Swift? Концепция области гласит, что если вы объявили переменную в одном «месте» кода, вы не можете использовать ее за пределами этого места. Это неявное, но важное правило программирования, которое поначалу может быть непросто для понимания.
В этом руководстве мы сосредоточимся на изучении scope и его значения для практической разработки под iOS.
Вот что мы обсудим:
- Как решить проблему Не удается найти «x» в области видимости Ошибка
- Каков объем и чем он отличается от контекста?
- Типы области действия: глобальная, локальная, функция, закрытие, блок и т. Д.
- Работа со сферой в практической разработке iOS
Готовы? Пошли.
- Что такое Scope в Swift?
- Глобальный, локальный, функция и область действия класса
- Область практической разработки под iOS
- Как исправить «ошибку: не удается найти« x »в области видимости»
- Дополнительная литература
Что такое объем в Swift?
Мы начнем с примера, демонстрирующего различные области видимости.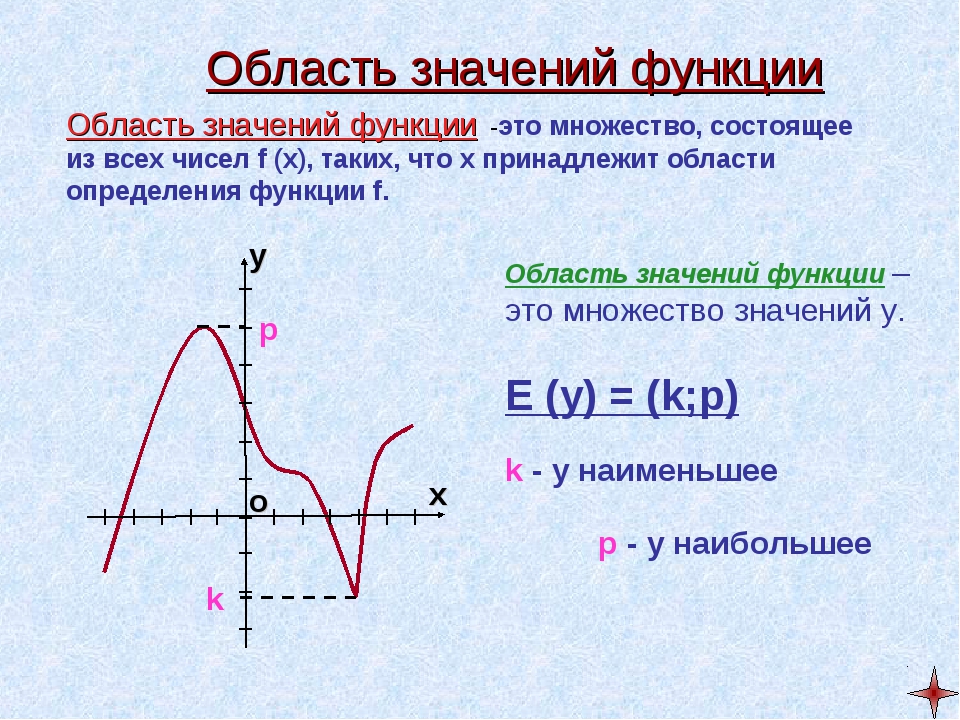 Проверьте следующий код Swift:
Проверьте следующий код Swift:
Найдите минутку, чтобы прочитать код. Можете ли вы без обмана угадать, каковы значения age и anotherAge ?
В этом примере вы работаете с двумя видами области : глобальной и локальной.
- Локальная область видимости присутствует в функции
getAge (), поэтому ее часто называют областью действия . К таким переменным, какage, которые объявлены как внутри функции, нельзя получить доступ за пределами этой функции. - Глобальная осциллограф присутствует повсюду — поэтому она называется global . Переменные, определенные на самом высоком уровне кода, то есть вне функций, классов и т. Д., Могут использоваться где угодно. (Хотя бывают исключения.)
А теперь давайте еще раз посмотрим на этот код. Переменная age определяется внутри функцией getAge () . Мы не можем получить доступ к той же переменной за пределами функции. Это важное правило при работе с прицелами.
Мы не можем получить доступ к той же переменной за пределами функции. Это важное правило при работе с прицелами.
Мы также не можем повторно объявить переменную с тем же именем в той же области видимости, потому что имена переменных должны быть уникальными в пределах своей области видимости. Что мы сделали, так это определили другую переменную с таким же именем в другой области видимости . Посмотри, какой?
- Переменная
ageопределена внутри функцииgetAge ()сvar age = 42в первой строке функции. - Переменная
ageопределена вне (ниже) функцииgetAge ()сvar age = 99.
У этих двух переменных одинаковое имя, но они объявлены в разных областях. У них есть 2 разных значения. Их «области» кода — их область действия — не конфликтуют друг с другом. Вот почему мы можем использовать их оба, с одним и тем же именем, но с разными значениями, по отдельности!
Вот как работает приведенный выше код, строка за строкой:
При запуске кода переменная age инициализируется значением 99 . Затем мы инициализируем переменную с именем
Затем мы инициализируем переменную с именем anotherAge значением, возвращаемым функцией getAge () , то есть 43 (42 + 1).Затем это значение увеличивается на единицу с , другое возраст + = 1 .
Наконец, мы распечатываем значения этих переменных. Значение age равно 99 , потому что оно не изменилось. Значение anotherAge составляет 44 . Он инициализируется как 42 , увеличивается внутри функции и увеличивается вне ее. Несмотря на то, что две из этих трех переменных имеют одинаковое имя, они не конфликтуют друг с другом, поскольку объявлены в разных областях.
Начинаете разбираться с прицелом ? Это не что иное, как «регион» или место, в котором у вас есть доступ к определенным переменным. Мы также определили 2 основных правила:
- Вы не можете использовать переменную за пределами области, объявленной в
- Имена переменных должны быть уникальными в пределах своей собственной области действия
Есть исключения из этих правил, как вы скоро увидите. Например, свойство из области видимости класса может иметь то же имя, что и переменная в области действия функции, но для доступа к первому вам потребуется использовать self.
Например, свойство из области видимости класса может иметь то же имя, что и переменная в области действия функции, но для доступа к первому вам потребуется использовать self.
Проще всего представить себе оптический прицел как настоящий оптический прицел, вы знаете, тот, который вы найдете на вершине винтовки, или как видоискатель в вашей фотоаппарате, или в бинокле. Когда вы смотрите в прицел, вы не видите то, что находится за пределами вашего поля зрения!
Локальная область видимости — это область, в которой вы находитесь в данный момент, т.е. вводите этот блок кода между волнистыми скобками {} . Если вы хотите попрактиковаться в области видимости, просто отслеживайте текущую локальную область видимости, а также переменные, типы и т. Д.у вас есть доступ.
В Swift функции находятся на самом глубоком уровне области видимости, поэтому локальная область видимости часто совпадает с областью действия функции. Замыкания находятся на более глубоком уровне, чем функции, но закрытия могут «закрывать» , что делает их особенными. Подробнее об этом позже!
Подробнее об этом позже!
Глобальный, локальный, функциональный и классовый
До сих пор мы рассматривали только глобальные и локальные масштабы. Есть еще что-то, что называется областью действия, и у классов тоже есть область видимости.Фактически, фреймворки, модули и файлы Swift сами по себе имеют область действия. Области видимости имеют уровни, они иерархичны, и типы тоже имеют область видимости. Пфу! С чего бы нам вообще начать !?
Начнем с простого класса. Как это:
класс Изделие
{
}
Насколько мы видим, этот класс определен в глобальной области . Теперь мы собираемся добавить в этот класс перечисление в виде вложенного типа . Как это:
класс Изделие
{
var kind = Добрый.вещь
enum Kind {
чехол для еды
дело вещь
}
}
В приведенном выше коде мы определили перечисление с именем Kind . У него 2 варианта: в данном примере мы рассматриваем любой продукт либо продукт , (можно его есть), либо предмет , (нельзя его есть). Мы также добавили свойство экземпляра
Мы также добавили свойство экземпляра kind типа Kind , которое по умолчанию инициализируется значением перечисления .thing .
Давайте обсудим этот пример с точки зрения объема.Что это за прицел и все такое? Вот что:
- Объем продукта
класса— глобальный . Он определен глобально, поэтому мы можем создавать объектыProductв любом месте кода. - Область действия перечисления
Kindограничена классом . Мы можем использоватьKindtype внутри класса , а не вне его (см. Ниже). - Объем свойства
видатакже ограничен классом .Мы можем использовать это свойство внутри класса с self.
Однако происходит кое-что еще. Мы можем использовать Product в глобальной области, и поскольку перечисление Kind имеет внутреннее управление доступом по умолчанию, мы можем использовать его как Product. type в любом месте кода . Kind
Kind
Приведенный ниже код можно использовать в любом месте кода. Мы можем достичь Kind вложенного типа через Product class:
let banana = Продукт ()
если банан.kind == Product.Kind.food {
print («банан - это еда»)
}
Точно так же свойство типа определено в области класса, но поскольку оно также общедоступно, мы можем получить доступ к этому свойству для любого объекта типа Product .
пусть посудомоечная машина = Товар ()
посудомоечная машина.kind = .thing
Важным отличием здесь является то, что класс Product и переменная посудомоечной машины объявлены и, следовательно, доступны в глобальной области видимости.Вот почему мы можем использовать их в приведенном выше фрагменте кода.
Давайте вернемся к этим различным типам прицелов. Посмотрите приведенный ниже код Swift. Мы добавляем функцию
Мы добавляем функцию canEat () в класс Product :
класс Изделие
{
var kind = Kind.thing
enum Kind {
чехол для еды
дело вещь
}
func canEat () -> Bool {
вернуть вид ==. еда
}
}
Здесь мы имеем дело с 3 уровнями охвата:
- Глобальная область , в которой определен класс
Product - Область действия класса , в которой определены свойство
kind, перечислениеKindи функцияcanEat () - Область видимости функции внутри функции
canEat (), в которой мы используем значение свойстваkindтекущего экземпляра класса.
Класс Product определен в глобальной области, поэтому мы можем использовать его в любом месте модуля приложения.Свойство kind определено в области действия класса, поэтому мы можем использовать его в классе Product . То же самое касается перечисления
То же самое касается перечисления Kind и функции canEat () .
Мы используем свойство kind внутри функции canEat () . Это означает, что у областей есть иерархия, потому что мы можем получить доступ к свойству из области класса внутри области функции .
Однако, если мы определили локальную переменную внутри canEat () , мы не сможем использовать эту переменную в другой функции того же класса, потому что у них разные области действия.
func canEat () -> Bool {
пусть голодный = ···
}
func isThing () -> Bool {
печать (вид)
печать (голодный)
}
Вот краткое обозначение иерархии областей видимости:
- Глобальная область (также, область файла / модуля)
Чтобы прочитать эту иерархию, нужно понять, что у вас есть доступ к глобальной области (высшей) в области закрытия (наименьшей), но не наоборот. Вы можете получить доступ к тому, что выше на более низких уровнях, но не к тому, что ниже на более высоких уровнях.
Итак, резюмируем:
- Каждая область вашего кода, заключенная в квадратные скобки, имеет область действия: глобальную область действия, область действия класса, область действия функции и т. Д.
- Обычно мы различаем локальную и глобальную область видимости, чтобы показать, есть ли у нас доступ к определенной переменной, свойству или типу. Области
- являются иерархическими, что означает, что мы можем получить доступ к
Kindчерез продукт. Kind, если мы находимся в глобальной области - Области видимости являются иерархическими, что означает, что мы можем получить доступ к свойству класса внутри функции класса, потому что функция имеет доступ к области видимости класса
Видимость типа, переменной, свойства и т. Д.определяет, доступен ли он. Это называется контроля доступа . У нас есть 5 различных уровней доступа: открытый , открытый , внутренний , частный файл и частный .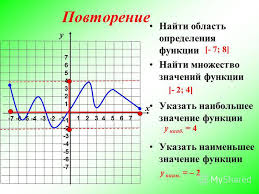 В общем, мы сокращаем это до «общедоступно?» или «это частное лицо?» , потому что так быстрее. Вы можете узнать больше об управлении доступом в Swift в этом руководстве: Управление доступом в Swift
В общем, мы сокращаем это до «общедоступно?» или «это частное лицо?» , потому что так быстрее. Вы можете узнать больше об управлении доступом в Swift в этом руководстве: Управление доступом в Swift
Область практической разработки под iOS
Scope используется повсюду в повседневной практической разработке iOS.Когда вы передаете значения в своем приложении, отслеживание того, какие переменные, типы и т. Д. У вас есть, является постоянным действием.
Скорее всего, если вы относительно новичок в разработке iOS, вы уже включили scope в свои рассуждения о своем коде, даже не подозревая об этом! «К какой переменной и где я могу получить доступ?»
Интересный случай области применения — это закрытие. Как вы, возможно, знаете, замыкание — это блок кода, который можно передавать по вашему коду.Это похоже на функцию, за исключением того, что сам код является значением. Вы можете назначить закрытие переменной, передать его в функцию, после чего оно окажется в другой части вашей программы.
часто используются как так называемые обработчики завершения . Допустим, мы асинхронно загружаем изображение из Интернета. Когда загрузка завершится, в будущем мы хотим выполнить некоторый код, чтобы показать изображение. Мы определяем этот код в закрытии и передаем его функции, загружающей изображение.Затем эта функция выполняет закрытие после завершения загрузки.
Вот, посмотрите:
класс DetailViewController: UIViewController
{
@IBOutlet weak var imageView: UIImageView?
функция viewDidLoad ()
{
network.downloadImage (url, completingHandler: {изображение в
imageView? .image = изображение
})
}
}
Примечание. Scope — это концепция независимо от того, используете ли вы UIKit или SwiftUI.Если вам нравится SwiftUI, не игнорируйте приведенный выше пример только потому, что он использует контроллер представления. Суть этого раздела, как вы скоро увидите, заключается в том, как использовать свойство imageView внутри области закрытия. Это относится и к SwiftUI, и к другим компонентам!
Это относится и к SwiftUI, и к другим компонентам!
В приведенном выше коде мы создали класс контроллера представления со свойством imageView . Внутри функции мы вызываем гипотетическую функцию downloadImage (_: completionHandler :) .Его второй параметр, обработчик завершения, заключенный между самыми внутренними волнистыми скобками, является закрытием. Когда загрузка изображения завершена, мы присваиваем загруженному изображению значение свойству image объекта imageView , которое будет отображать изображение.
Закрытие называется закрытием, потому что оно «закрывает» любые значения, на которые ссылается закрытие. Поскольку замыкания могут передаваться через ваш код как значения, замыканию требуется способ ссылки на значения, которые используются внутри замыкания.Этот принцип называется , закрывающим , или , захватывающим .
В приведенном выше примере кода замыкание удерживает ссылку на свойство imageView .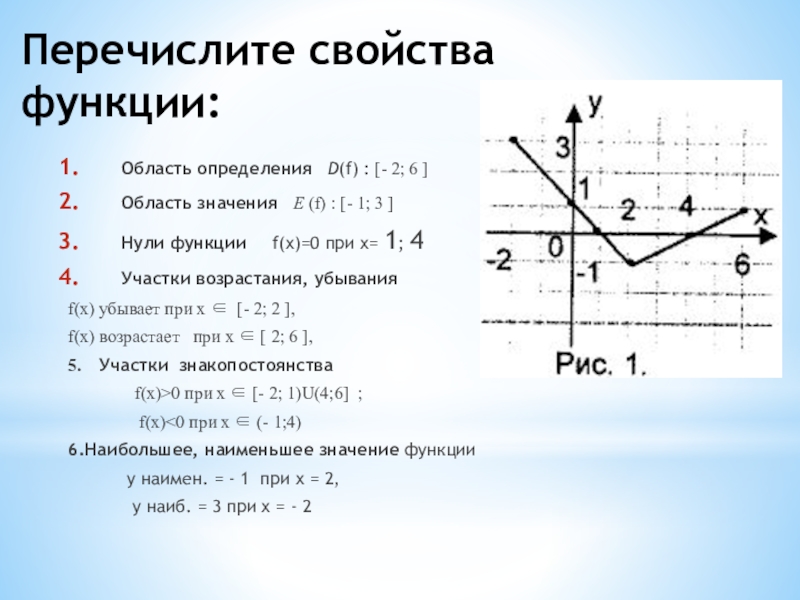 Это свойство понадобится позже, чтобы установить изображение. Когда закрытие завершает выполнение, эта ссылка освобождается.
Это свойство понадобится позже, чтобы установить изображение. Когда закрытие завершает выполнение, эта ссылка освобождается.
Этот захват работает только в том случае, если замыкание имеет доступ к тому же уровню области видимости, что и функция, в которой оно определено. Несмотря на то, что замыкание является отдельной сущностью, оно может получить доступ к свойству imageView , поскольку функция viewDidLoad () имеет доступ к этой области.Замыкание имеет ту же область видимости, что и объект, в котором оно определено, и в данном случае это область действия функции. То же самое верно для наблюдателей свойств, вычисляемых свойств и другого блочного кода.
Интересно, правда? Понимание захвата — это окончательная проверка вашего понимания области действия. Вам нужно будет выяснить, , почему закрытие, которое выполняется в будущем , как видно из контекста функции viewDidLoad () , может иметь доступ к свойству imageView .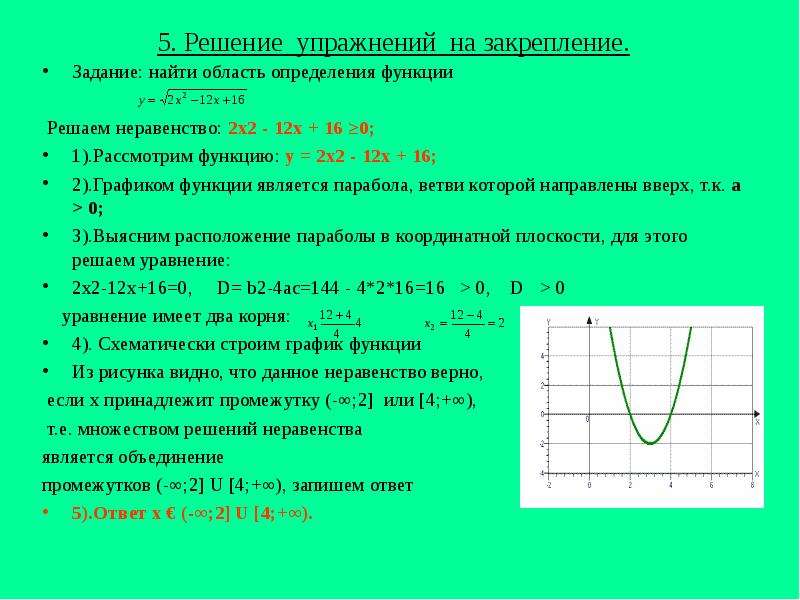 Это потому, что замыкание имеет доступ к области, в которой оно определено!
Это потому, что замыкание имеет доступ к области, в которой оно определено!
Область действия и контекст часто путают. Область видимости фиксирована, потому что код, который вы пишете, фиксирован. Контекст изменчив и зависит от выполнения вашего кода. Таким образом, у вас может быть доступ к свойству, потому что оно в области действия , но из-за контекста вашего кода, то есть его точки выполнения, это свойство пусто. Вы можете видеть область как ваш код (фиксированный) и контекст как то, что ваш код делает в любой заданный момент времени выполнения (текучая среда).Думайте об этом, как о езде на мотоцикле: у мотоцикла 2 колеса (прицел), и крутятся они или нет, зависит от того, ездите вы на велосипеде (контекст).
Как исправить «ошибку: не удается найти« x »в области видимости»
Теперь, когда мы обсудили, что такое осциллограф и как она работает, давайте сосредоточимся на наиболее распространенной ошибке, которую вы обнаружите при работе с осциллографами. Это:
Это:
ошибка: не удается найти «…» в области видимости
Это ошибка времени компиляции, поэтому она появляется, когда вы пытаетесь скомпилировать код, приводящий к этой ошибке.Как вы уже догадались, смысл этого прост: имя переменной, на которую вы ссылаетесь, не существует!
Проверьте это:
Когда вы запустите приведенный выше код, вы получите следующую ошибку:
ошибка: не удается найти «текст» в области видимости
Что здесь происходит? Мы явно где-то ошиблись. Несмотря на то, что строка для c в тексте имеет смысл — перебирать каждый символ в текст — переменная текст не существует.Это понятная опечатка: текст должен быть строкой , которая является входным параметром для функции reverse () .
В целом можно с уверенностью предположить, что «Не удается найти«… »в области видимости» относится к переменной, функции, типу или другому символу, который не существует . Если вы хотите решить эту ошибку и исправить ошибку, начните с того, чего не существует, и продолжайте работать оттуда (например, текст
Если вы хотите решить эту ошибку и исправить ошибку, начните с того, чего не существует, и продолжайте работать оттуда (например, текст ).
Приятно знать, что ошибка «Не удается найти«… »в области действия» является признаком , поэтому она не является основной причиной.Например, в приведенном выше коде ссылка на «текст» была опечаткой. Совершенно не поможет, если мы создадим новую переменную text только для устранения ошибки, а позже обнаружим, что функция reverse () больше не работает.
Какие еще проблемы могут вызвать ошибку «Не удается найти«… »в области действия»?
- Отсутствует импорт: Обратите внимание, что эта ошибка также может быть вызвана отсутствующим типом , а не только неправильным написанием имен переменных.Например, если вам не хватает типа
View, вам, вероятно, потребуетсяимпортировать SwiftUI. В этом вам может помочь документация iOS SDK.
- Отсутствующие модули: Допустим, вы добавили библиотеку в свой проект, но она содержит ошибку. Эта ошибка препятствует компиляции библиотеки. В результате библиотека, которую вы импортируете, и ее типы отсутствуют. Вы видите ошибку как «Не удается найти…», но основная причина — ошибка в библиотеке!
- Xcode Проблема: К сожалению, Xcode иногда дает сбой и начинает выдавать ошибки, когда их нет.Может случиться так, что происходит сбой автозаполнения или компилятор Swift, и в результате библиотека, тип, переменная и т. Д., О которых вы знаете, , существует , по-видимому, отсутствует. Выполните или нажмите Command + Option + Shift + K , чтобы очистить папку сборки вашего проекта, и снова запустите код.
- Измененный код: Большая часть кода, от которого вы зависите — библиотеки, фреймворки, SDK — находится в постоянном движении. У нас есть семантическое управление версиями, теги выпуска, закрепление версий и т.
 Д., Но в какой-то момент вам придется обновить приложение с библиотеки v1.0 до 2.0. Между тем, API для этой библиотеки изменился, и они переименовали какой-то класс, который вы используете. Что происходит? Не могу найти… в объеме. В этом сценарии важно помнить о своих предположениях — потому что вы собираетесь искать тот класс, который наверняка существовал в v1.0!
Д., Но в какой-то момент вам придется обновить приложение с библиотеки v1.0 до 2.0. Между тем, API для этой библиотеки изменился, и они переименовали какой-то класс, который вы используете. Что происходит? Не могу найти… в объеме. В этом сценарии важно помнить о своих предположениях — потому что вы собираетесь искать тот класс, который наверняка существовал в v1.0! - Отсутствует переменная: Это, конечно, наиболее частая причина: вы неправильно ввели имя переменной, имя функции, тип или что-то еще. Легко пропустить опечатку: строчные буквы вместо прописных, где-то точка или
ULRSessionвместоURLSession.Не волнуйся! Это случается с лучшими из нас (больше, чем мы хотели бы признать). Если сомневаетесь, спите на нем или прогуляйтесь, а потом посмотрите на него свежим взглядом.
Дополнительная литература
Область действия — это концепция, которую сложно описать правилами и словами, но как только вы освоите ее, она станет вашей второй натурой. Вы все время работали с прицелом, возможно, даже не подозревая об этом. Область действия — это ответ на вопрос: «Могу ли я использовать здесь эту переменную?» Аккуратно!
Вы все время работали с прицелом, возможно, даже не подозревая об этом. Область действия — это ответ на вопрос: «Могу ли я использовать здесь эту переменную?» Аккуратно!
Хотите узнать больше? Ознакомьтесь с этими ресурсами:
Область действия переменной в TypeScript: глобальная, локальная и функция
Переменные имеют область действия или видимость.Объем переменной определяет, какая часть программы может получить к ней доступ. Мы можем определить переменную тремя способами, чтобы ограничить их видимость. Одна из них — это локальная переменная или переменная блока, которая имеет область действия блока кода (область действия блока или локальную область действия). Второй — это функциональная переменная или переменная класса, имеющая область видимости функции / класса. Последняя — это глобальная переменная, к которой можно получить доступ в любом месте программы (глобальная область видимости).
Объем важен. без осциллографов переменные будут видны повсюду. Это заставляет нас отслеживать имена всех объявленных переменных, чтобы случайно не использовать их повторно. И если переменная имеет неправильное значение, вам придется сканировать всю базу кода на предмет ошибки, потому что значение могло быть изменено любым оператором.
Это заставляет нас отслеживать имена всех объявленных переменных, чтобы случайно не использовать их повторно. И если переменная имеет неправильное значение, вам придется сканировать всю базу кода на предмет ошибки, потому что значение могло быть изменено любым оператором.
Область действия переменной
Переменная Typescript может иметь три области действия в зависимости от того, как и где вы их определили.
- Глобальная область действия
- Область действия функции или область действия класса
- Локальная область действия или область действия блока
Глобальная область действия
Определите глобальную переменную вне какой-либо функции / класса или блока кода, и они станут частью глобальной области действия.Мы можем использовать их где угодно в программе.
В следующем примере показана переменная globalVar , определенная вне какой-либо функции или блока кода. Вы можете получить к нему доступ в любом месте кода.
1 2 3 4 5 6 7 8 9 10 11 000316 17 18 19 20 21 22 23 24 25 26 27 28 30 / определяется глобально.вне какой-либо функции или блока кода// Вы можете получить к нему доступ из любого места, включая функцию, блок кода, вложенную функцию и т. д. let GlobalVar = 100; function someFn () {// function console.log (GlobalVar) if (true) {// кодовый блок console.log (GlobalVar) } function nested () {// вложенная функция в консоли someFn1 .log (GlobalVar) } } for (let c = 0; c <3; c ++) {// блок кода console.log (GlobalVar); } function someOtherFn1 () {// другая функция console. } console.log (GlobalVar) // вне какой-либо функции / блока кода |
Область действия функции
Переменные функции или класса, определенные внутри функции / класса и т. Д., Имеют область действия.Их можно использовать в любом месте функции. Вы не можете использовать их вне функции.
В следующем примере переменная fnVar определена внутри функции someFn . Это делает его функцию ограниченной. Вы можете получить к нему доступ из someFn . Вы также можете получить к нему доступ из кодового блока или вложенной функции в someFn
1 2 3 4 5 6 7 8 10 11 12 13 14 15 16 17 18 19 20 21 22 000 000 2627 28 29 30 31 32 | функция someFn () { // Переменная, определенная внутри функции. // можно получить доступ из любого места внутри функции // включая вложенную функцию или блок кода let fnVar = 10 console.log (fnVar) // можно получить здесь if (true) { console.log (fnVar) // здесь } function nested () { console.log (fnVar) // здесь } } function someOtherFn () { console.log (fnVar) // здесь нет доступа } for (let c = 0; c <3; c ++) { console.log (fnVar); // здесь нет доступа } console.log (fnVar) // здесь нет доступа |
Вложенная функция
В приведенном ниже примере определяется fnNestedVar внутри вложенной функции. Мы можем получить доступ к этой переменной только внутри вложенной функции и ее вложенных функций и блоков кода.Но не из родительской функции или где-либо вне вложенной функции.
1 2 3 4 5 6 7 8 9 10 11 0003 1617 18 19 20 21 22 23 24 25 26 27 | функция { ) {функция if (true) { } function nested () { // определено внутри вложенной функции // доступно только внутри вложенной функции и ее вложенных функций и блоков кода let fnNestedVar = 100 консоль.log (fnNestedVar) } console.log (fnNestedVar) // здесь недоступен } function someOtherFn () { console.log (fnNestedVar) // здесь недоступен } для (пусть c = 0; c <3; c ++) { console.log (fnNestedVar); // здесь нет доступа } console. |
Локальная область или область действия блока
Локальные переменные объявляются внутри блока кода.Они также известны по переменной блока имен
Блок кода - это часть исходного кода, четко обозначенная фигурными скобками. Например, внутри блока if / try / catch / while / for.
В приведенном ниже примере показана localVar , объявленная внутри условия if . Область localVar заканчивается там, где заканчиваются фигурные скобки условия if. Вне блока кода вы не можете получить к нему доступ.
1 2 3 4 5 6 7 8 9 10 11 0003 1617 18 19 20 21 22 23 24 25 26 27 28 27 28 293 {if (true) { // определено локально // Его область действия заканчивается там, где заканчиваются фигурные скобки let localVar = 1000 console. } console.log (localVar) // Ошибка function nested () { console.log (localVar) // Ошибка } } для (пусть c = 0; c <3; c ++) { console.log (localVar); // Ошибка } function someOtherFn () { console.log (localVar) // Ошибка } console.log (localVar) // Ошибка |
var является исключением
Ключевое слово var является исключением из приведенного выше правила. var поддерживает только глобальные и функциональные области. Таким образом, если вы определяете переменную внутри блока кода, она ограничивается охватывающей функцией, а не блоком кода.
Это основная причина, по которой позволяет существовать . Чтобы перенести локальную область видимости в Javascript. let является частью спецификации ES2015 или ES6.
Например, возьмите приведенный выше пример и измените let на var . Вы можете видеть, что localVar недоступен вне блока кода, а также во вложенной функции.
1 2 3 4 5 6 7 8 9 10 11 000316 17 18 19 20 21 22 23 24 25 26 27 28 30 0000002 29000 | function someFn () { if (true) { // определяется локально с помощью var, которая имеет область видимости функции // Вы можете получить к нему доступ из любого места в пределах someFn // Это основное различие между var & let var localVar = 1000 console.log (localVar) // ok } console. function nested () { console.log (localVar) // ok } } для (пусть c = 0; c <3; c ++) { console.log (localVar); // Ошибка } function someOtherFn () { console.log (localVar) // Ошибка } console.log (localVar) // Ошибка |
Объявление переменной
Есть три ключевых слова, которые вы можете использовать для объявления переменной в Typescript. Это ключевое слово let , var или const . Правила определения объема работ между ними различаются.
var поддерживает функции и глобальные области, как показано в примере выше.
let и const поддерживают все три осциллографа.
Ниже показано использование всех трех прицелов. В первом примере для определения используется var , а во втором примере - let .
Пример области применения var
1 2 3 4 5 6 7 8 9 10 110003 11 14 15 16 17 18 19 20 21 22 23 24 | var GlobalScope = 1; function someFunc () { var FunctionScope = 2; if (true) { var BlockScope = 3; консоль.журнал (GlobalScope); console.log (FunctionScope); console.log (BlockScope); } console.log (GlobalScope); console.log (FunctionScope); console.log (BlockScope); // Ошибки нет } console.log (GlobalScope); console.log (FunctionScope); // ошибка console.log (BlockScope); // ошибка |
Пример области действия let
1 2 3 4 5 6 7 9 100003 12 13 14 15 16 17 18 19 20 21 22 23 24 2 глобальныйfunction someFunc () { let FunctionScope = 2; if (true) { let BlockScope = 3; консоль. console.log (FunctionScope); console.log (BlockScope); } console.log (GlobalScope); console.log (FunctionScope); console.log (BlockScope); // ошибка } console.log (GlobalScope); console.log (FunctionScope); // ошибка console.log (BlockScope); // ошибка |
Пример использования цикла for
В следующем примере мы используем ключевое слово var для объявления переменной i , которая находится внутри блока кода.Но поскольку var является функциональной областью, мы можем получить доступ к i даже вне цикла for. Следовательно, он доступен в console.log, который находится за пределами
function countMe () { for (var i = 0; i <10; i ++) { console.log (i) } console.log ('Подсчитано:', i); // Ошибки нет } countMe (); |
Теперь замените var на let . Компилятор выдает ошибку TS2304: Не удается найти имя «i».
Компилятор выдает ошибку TS2304: Не удается найти имя «i».
function countMe () { for (let i = 0; i <10; i ++) { console.log (i) } console.log ('Подсчитано: ', i); // приводит к ошибке } countMe (); |
Сводка
Переменные Typescript имеют три области действия. Глобальный, функциональный и локальный.Используя var , вы можете создать глобальную и функциональную переменную. В то время как мы используем , пусть и const для всех трех.
Разрешение имен в вашем коде - Real Python
Концепция области определяет, как переменные и имена ищутся в вашем коде. Он определяет видимость переменной в коде. Объем имени или переменной зависит от того места в коде, где вы создаете эту переменную. Концепция области действия Python обычно представлена с использованием правила, известного как правило LEGB .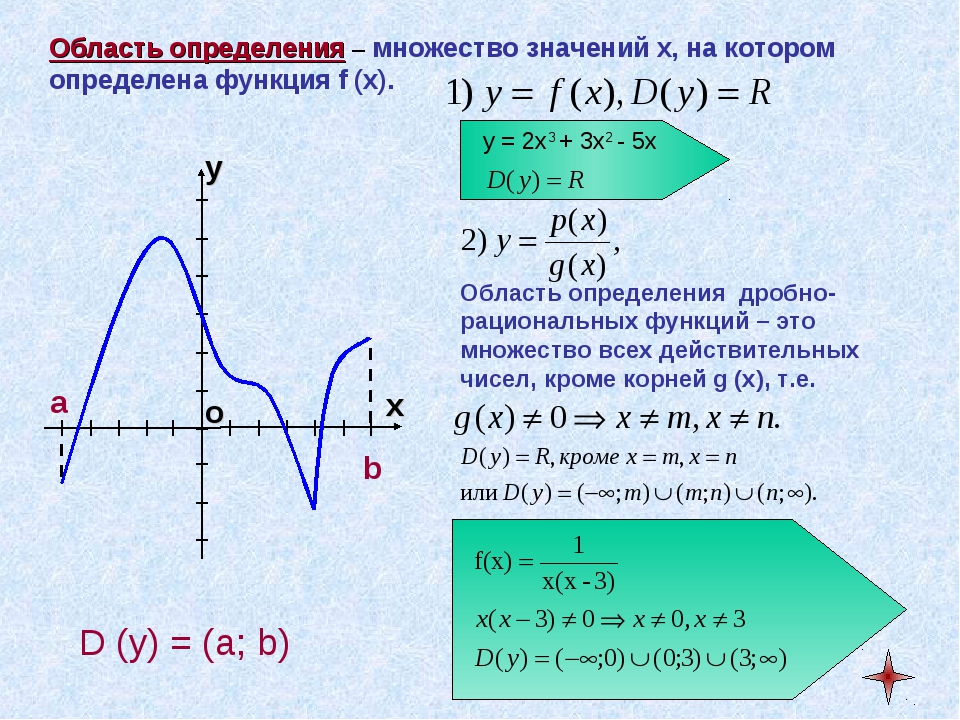
Буквы в аббревиатуре LEGB обозначают локальную, охватывающую, глобальную и встроенную осциллографы . Это суммирует не только уровни области видимости Python, но и последовательность шагов, которые выполняет Python при разрешении имен в программе.
Обладая этими знаниями, вы можете использовать возможности Python для написания более надежных и поддерживаемых программ. Использование области Python поможет вам избежать или минимизировать ошибки, связанные с конфликтом имен, а также с неправильным использованием глобальных имен в ваших программах.
Общие сведения об объеме
В программировании область имени определяет область программы, в которой вы можете однозначно получить доступ к этому имени, например, к переменным, функциям, объектам и так далее. Имя будет видно и доступно только коду в его области видимости. Некоторые языки программирования используют возможности для предотвращения конфликтов имен и непредсказуемого поведения. Чаще всего вы различаете две общие области действия:
Чаще всего вы различаете две общие области действия:
Глобальная область: Имена, которые вы определяете в этой области, доступны для всего вашего кода.
Локальная область: Имена, которые вы определяете в этой области, доступны или видны только коду в этой области.
Scope возникла потому, что ранние языки программирования (такие как BASIC) имели только глобальное имя . С таким именем любая часть программы могла изменить любую переменную в любое время, поэтому обслуживание и отладка больших программ могли стать настоящим кошмаром. Чтобы работать с глобальными именами, вам нужно помнить весь код одновременно, чтобы знать, каково значение данного имени в любое время.Это был важный побочный эффект отсутствия прицелов.
Некоторые языки, такие как Python, используют область видимости , чтобы избежать подобных проблем. Когда вы используете язык, реализующий область видимости, у вас нет возможности получить доступ ко всем переменным в программе во всех местах этой программы. В этом случае ваша возможность получить доступ к данному имени будет зависеть от того, где вы задали это имя.
В этом случае ваша возможность получить доступ к данному имени будет зависеть от того, где вы задали это имя.
Примечание: Вы будете использовать термин имя для обозначения идентификаторов переменных, констант, функций, классов или любого другого объекта, которому можно присвоить имя.
Имена в ваших программах будут иметь объем блока кода, в котором вы их определяете. Когда вы можете получить доступ к значению данного имени где-нибудь в вашем коде, вы скажете, что имя в области видимости . Если вы не можете получить доступ к имени, вы скажете, что имя вне области .
Имена и области в Python
Поскольку Python - это язык с динамической типизацией, переменные в Python возникают, когда вы впервые присваиваете им значение.С другой стороны, функции и классы доступны после их определения с помощью def или class соответственно. Наконец, модули существуют после того, как вы их импортируете.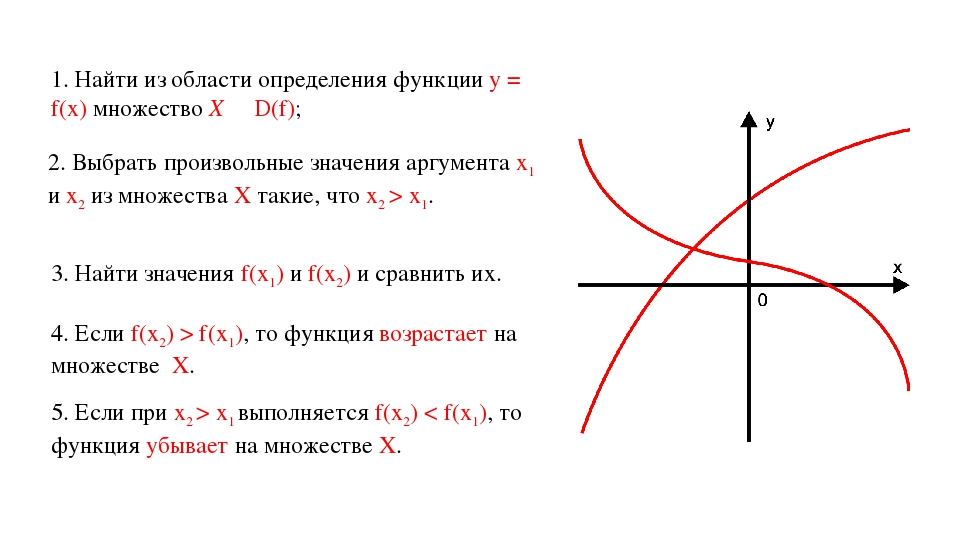 Подводя итог, вы можете создать имена Python с помощью одной из следующих операций:
Подводя итог, вы можете создать имена Python с помощью одной из следующих операций:
| Эксплуатация | Заявление |
|---|---|
| Назначения | x = значение |
| Импортные операции | импортировать модуль или из имени импорта модуля |
| Определения функций | def my_func ():... |
| Определения аргументов в контексте функций | def my_func (arg1, arg2, ... argN): ... |
| Определения классов | класс MyClass: ... |
Все эти операции создают или, в случае присваивания, обновляют новые имена Python, потому что все они присваивают имя переменной, константе, функции, классу, экземпляру, модулю или другому объекту Python.
Примечание: Существует важное различие между операциями присваивания и операциями обращения или доступа . Когда вы ссылаетесь на имя, вы просто получаете его содержание или значение. Когда вы назначаете имя, вы либо создаете это имя, либо изменяете его.
Когда вы ссылаетесь на имя, вы просто получаете его содержание или значение. Когда вы назначаете имя, вы либо создаете это имя, либо изменяете его.
Python использует расположение присвоения или определения имени, чтобы связать его с определенной областью действия. Другими словами, то, где вы назначаете или определяете имя в своем коде, определяет объем или видимость этого имени.
Например, если вы присваиваете значение имени внутри функции, то это имя будет иметь локальную область видимости Python .Напротив, если вы присваиваете значение имени вне всех функций - скажем, на верхнем уровне модуля - тогда это имя будет иметь глобальную область видимости Python .
Область действия Python и пространство имен
В Python концепция области видимости тесно связана с концепцией пространства имен. Как вы уже узнали, область действия Python определяет, где в вашей программе отображается имя. Области действия Python реализованы в виде словарей, которые сопоставляют имена с объектами. Эти словари обычно называются пространствами имен .Это конкретные механизмы, которые Python использует для хранения имен. Они хранятся в специальном атрибуте
Эти словари обычно называются пространствами имен .Это конкретные механизмы, которые Python использует для хранения имен. Они хранятся в специальном атрибуте .__ dict__ .
Имена на верхнем уровне модуля хранятся в пространстве имен модуля. Другими словами, они хранятся в атрибуте модуля .__ dict__ . Взгляните на следующий код:
>>> import sys
>>> sys .__ dict __. keys ()
dict_keys (['__ name__', '__doc__', '__package __', ..., 'argv', 'ps1', 'ps2'])
После импорта sys можно использовать .keys () для проверки ключей sys .__ dict__ . Это возвращает список со всеми именами, определенными на верхнем уровне модуля. В этом случае можно сказать, что .__ dict__ содержит пространство имен sys и является конкретным представлением области видимости модуля.
Примечание: Выходные данные некоторых примеров в этом руководстве были сокращены ( .) для экономии места. Результат может отличаться в зависимости от вашей платформы, версии Python или даже от того, как долго вы используете текущий интерактивный сеанс Python. ..
..
В качестве дополнительного примера предположим, что вам нужно использовать имя ps1 , которое определено в sys . Если вы знаете, как .__ dict__ и пространства имен работают в Python, вы можете ссылаться на ps1 как минимум двумя разными способами:
- Использование точечной записи в имени модуля в виде
module.name - Использование операции подписки на
.__ dict__в формеmodule .__ dict __ ['name']
Обратите внимание на следующий код:
>>> >>> sys.ps1
'>>>'
>>> sys .__ dict __ ['ps1']
'>>>'
После того, как вы импортировали sys , вы можете получить доступ к ps1 , используя точечную нотацию на sys . Вы также можете получить доступ к
Вы также можете получить доступ к ps1 , используя поиск по словарю с ключом 'ps1' . Оба действия возвращают один и тот же результат: '>>>' .
Примечание. ps1 - это строка, определяющая основное приглашение интерпретатора Python. ps1 определяется только в том случае, если интерпретатор находится в интерактивном режиме и его начальное значение - '>>>' .
Каждый раз, когда вы используете имя, такое как имя переменной или функции, Python просматривает различные уровни области (или пространства имен), чтобы определить, существует ли имя или нет. Если имя существует, вы всегда получите первое его появление. В противном случае вы получите сообщение об ошибке. Об этом поисковом механизме вы расскажете в следующем разделе.
Использование правила LEGB для области действия Python
Python разрешает имена с помощью так называемого правила LEGB , которое названо в честь области Python для имен.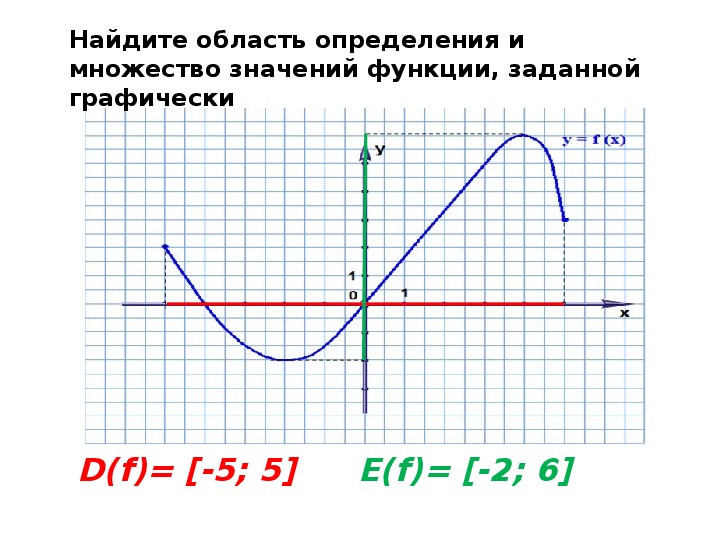 Буквы в LEGB обозначают локальный, закрывающий, глобальный и встроенный. Вот краткий обзор значений этих терминов:
Буквы в LEGB обозначают локальный, закрывающий, глобальный и встроенный. Вот краткий обзор значений этих терминов:
Локальная (или функция) область видимости - это блок кода или тело любой функции Python или
лямбда-выражения. Эта область Python содержит имена, которые вы определяете внутри функции. Эти имена будут видны только из кода функции. Он создается при вызове функции, а не , а не при определении функции, поэтому у вас будет столько же различных локальных областей, сколько и при вызовах функций.Это верно, даже если вы вызываете одну и ту же функцию несколько раз или рекурсивно. Каждый вызов приведет к созданию новой локальной области.Вложенная (или нелокальная) область видимости - это специальная область видимости, которая существует только для вложенных функций. Если локальная область видимости является внутренней или вложенной функцией, тогда охватывающая область видимости является областью внешней или включающей функции.
 Эта область содержит имена, которые вы определяете во включающей функции. Имена в охватывающей области видны из кода внутренних и включающих функций.
Эта область содержит имена, которые вы определяете во включающей функции. Имена в охватывающей области видны из кода внутренних и включающих функций.Глобальная (или модульная) область видимости - это самая верхняя область в программе, скрипте или модуле Python. Эта область Python содержит все имена, которые вы определяете на верхнем уровне программы или модуля. Имена в этой области Python видны повсюду в вашем коде.
Встроенная область видимости - это специальная область действия Python, которая создается или загружается всякий раз, когда вы запускаете сценарий или открываете интерактивный сеанс. Эта область содержит имена, такие как ключевые слова, функции, исключения и другие атрибуты, встроенные в Python.Имена в этой области Python также доступны повсюду в вашем коде. Он автоматически загружается Python при запуске программы или сценария.
Правило LEGB - это своего рода процедура поиска имени, которая определяет порядок, в котором Python ищет имена. Например, если вы ссылаетесь на заданное имя, Python будет искать это имя последовательно в локальной, включающей, глобальной и встроенной области. Если имя существует, вы получите первое его появление. В противном случае вы получите сообщение об ошибке.
Например, если вы ссылаетесь на заданное имя, Python будет искать это имя последовательно в локальной, включающей, глобальной и встроенной области. Если имя существует, вы получите первое его появление. В противном случае вы получите сообщение об ошибке.
Примечание: Обратите внимание, что поиск в локальной и включающей области Python выполняется только в том случае, если вы используете имя внутри функции (локальная область видимости) или вложенной или внутренней функции (локальная и включающая область видимости).
Таким образом, когда вы используете вложенные функции, имена разрешаются путем первой проверки локальной области видимости или локальной области видимости самой внутренней функции. Затем Python просматривает все охватывающие области внешних функций от самой внутренней до самой внешней. Если совпадений не найдено, Python просматривает глобальную и встроенную области видимости.Если он не может найти имя, вы получите сообщение об ошибке.
В любой момент времени во время выполнения у вас будет не более четырех активных областей действия Python - локальной, включающей, глобальной и встроенной - в зависимости от того, где вы находитесь в коде. С другой стороны, у вас всегда будет как минимум две активные области: глобальная и встроенная. Эти два прицела всегда будут вам доступны.
С другой стороны, у вас всегда будет как минимум две активные области: глобальная и встроенная. Эти два прицела всегда будут вам доступны.
Функции: локальная область действия
Локальная область видимости или область действия функции - это область действия Python, созданная при вызове функции.Каждый раз, когда вы вызываете функцию, вы также создаете новую локальную область видимости. С другой стороны, вы можете рассматривать каждый оператор def и выражение lambda как образец для новых локальных областей видимости. Эти локальные области будут появляться всякий раз, когда вы вызываете функцию под рукой.
По умолчанию параметры и имена, которые вы назначаете внутри функции, существуют только в пределах функции или локальной области, связанной с вызовом функции. Когда функция возвращается, локальная область видимости уничтожается, а имена забываются.Вот как это работает:
>>> >>> def квадрат (основание):
. .. результат = база ** 2
... print (f'Квадрат {base}: {result} ')
...
>>> квадрат (10)
Квадрат 10 составляет: 100
>>> result # Недоступен извне square ()
Отслеживание (последний вызов последний):
Файл "
.. результат = база ** 2
... print (f'Квадрат {base}: {result} ')
...
>>> квадрат (10)
Квадрат 10 составляет: 100
>>> result # Недоступен извне square ()
Отслеживание (последний вызов последний):
Файл "", строка 1, в
результат
NameError: имя 'результат' не определено
>>> base # Недоступен извне square ()
Отслеживание (последний вызов последний):
Файл "", строка 1, в
база
NameError: имя base не определено
>>> квадрат (20)
Площадь 20 составляет: 400.
square () - это функция, которая вычисляет квадрат заданного числа, по основанию .Когда вы вызываете функцию, Python создает локальную область видимости, содержащую имена base (аргумент) и result (локальная переменная). После первого вызова square () , основание содержит значение 10 , а результат содержит значение 100 . Во второй раз локальные имена не запомнят значения, которые были сохранены в них при первом вызове функции. Обратите внимание, что
Обратите внимание, что base теперь содержит значение 20 , а результат содержит 400 .
Примечание: Если вы попытаетесь получить доступ к результату или base после вызова функции, вы получите NameError , потому что они существуют только в локальной области, созданной вызовом square () . Всякий раз, когда вы пытаетесь получить доступ к имени, которое не определено ни в одной области Python, вы получите NameError . В сообщении об ошибке будет указано имя, которое не удалось найти.
Поскольку вы не можете получить доступ к локальным именам из операторов, находящихся вне функции, разные функции могут определять объекты с одинаковыми именами.Посмотрите этот пример:
>>> >>> def cube (base):
... результат = база ** 3
... print (f'Куб {base}: {result} ')
...
>>> куб (30)
В кубе 30 получается: 27000
Обратите внимание, что вы определяете cube () с использованием той же переменной и параметра, которые вы использовали в square () . Однако, поскольку
Однако, поскольку cube () не может видеть имена внутри локальной области видимости square () и наоборот, обе функции работают должным образом без какого-либо конфликта имен.
Вы можете избежать конфликтов имен в своих программах, правильно используя локальную область видимости Python. Это также делает функции более самодостаточными и создает поддерживаемые программные модули. Кроме того, поскольку вы не можете изменять локальные имена из удаленных мест в коде, ваши программы будет легче отлаживать, читать и изменять.
Вы можете проверить имена и параметры функции с помощью .__ code__ , который является атрибутом, содержащим информацию о внутреннем коде функции.Взгляните на код ниже:
>>> квадрат .__ код __. Co_varnames
('база', 'результат')
>>> квадрат .__ код __. co_argcount
1
>>> квадрат .__ код __. co_consts
(Нет, 2, 'Квадрат', 'равен:')
>>> квадрат .__ код __. co_name
'квадратный'
В этом примере кода вы проверяете . на 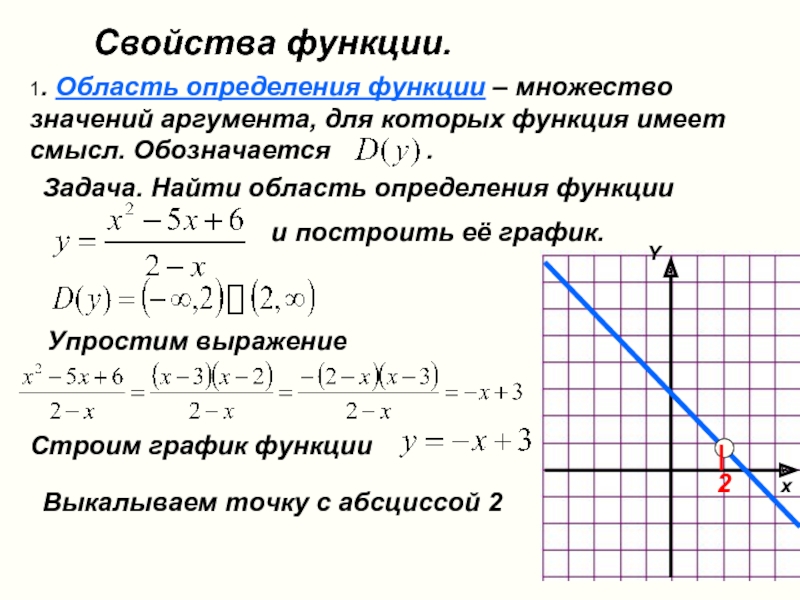 __ code__
__ code__ square () . Это специальный атрибут, содержащий информацию о коде функции Python. В этом случае вы видите, что .co_varnames содержит кортеж, содержащий имена, которые вы определяете внутри square () .
Вложенные функции: закрывающая область
Вложенная или нелокальная область видимости наблюдается, когда вы вкладываете функции внутрь других функций. Вложенная область видимости была добавлена в Python 2.2. Он принимает форму локальной области видимости любой включающей функции. Имена, которые вы определяете во включающей области Python, обычно известны как нелокальные имена . Рассмотрим следующий код:
>>> >>> def outer_func ():
... # Этот блок является локальной областью outer_func ()
... var = 100 # нелокальная переменная
... # Это также область действия inner_func ()
... def inner_func ():
... # Этот блок является локальной областью inner_func ()
.. . print (f "Печать переменной из inner_func (): {var}")
...
... inner_func ()
... print (f "Печать переменной из outer_func (): {var}")
...
>>> outer_func ()
Печать var из inner_func (): 100
Печать var из outer_func (): 100
>>> inner_func ()
Отслеживание (последний вызов последний):
Файл "
. print (f "Печать переменной из inner_func (): {var}")
...
... inner_func ()
... print (f "Печать переменной из outer_func (): {var}")
...
>>> outer_func ()
Печать var из inner_func (): 100
Печать var из outer_func (): 100
>>> inner_func ()
Отслеживание (последний вызов последний):
Файл "", строка 1, в
NameError: имя 'inner_func' не определено
Когда вы вызываете outer_func () , вы также создаете локальную область видимости.Локальная область видимости outer_func () одновременно является охватывающей областью inner_func () . Изнутри inner_func () эта область не является ни глобальной, ни локальной. Это специальный прицел, который находится между этими двумя прицелами и известен как закрывающий прицел .
Примечание: В некотором смысле, inner_func () - это временная функция, которая оживает только во время выполнения ее включающей функции outer_func () . Обратите внимание, что
Обратите внимание, что inner_func () виден только коду в outer_func () .
Все имена, которые вы создаете во внешней области видимости, видны изнутри inner_func () , за исключением имен, созданных после вызова inner_func () . Вот новая версия outer_fun () , которая показывает эту точку:
>>> def outer_func ():
... var = 100
... def inner_func ():
... print (f "Печать переменной из inner_func (): {var}")
... print (f "Печать another_var из inner_func (): {another_var}")
...
... inner_func ()
... another_var = 200 # Это определяется после вызова inner_func ()
... print (f "Печать переменной из outer_func (): {var}")
...
>>> outer_func ()
Печать var из inner_func (): 100
Отслеживание (последний вызов последний):
Файл "", строка 1, в
external_func ()
Файл "", строка 7, в outer_func
inner_func ()
Файл "", строка 5, в inner_func
print (f "Печать another_var из inner_func (): {another_var}")
NameError: свободная переменная 'another_var', на которую ссылается перед присваиванием во вложении
сфера
Когда вы вызываете outer_func () , код работает до точки, в которой вы вызываете inner_func () .Последний оператор inner_func () пытается получить доступ к another_var . На данный момент another_var еще не определен, поэтому Python вызывает NameError , потому что не может найти имя, которое вы пытаетесь использовать.
И последнее, но не менее важное: вы не можете изменять имена во включающей области изнутри вложенной функции, если не объявите их как нелокальный во вложенной функции. Вы узнаете, как использовать нелокальный позже в этом руководстве.
: глобальный охват
С момента запуска программы Python вы находитесь в глобальной области действия Python. Внутренне Python превращает основной скрипт вашей программы в модуль с именем __main__ , чтобы удерживать выполнение основной программы. Пространство имен этого модуля - это основная глобальная область видимости вашей программы.
Примечание: В Python понятия глобальной области видимости и глобальных имен тесно связаны с файлами модулей. Например, если вы определяете имя на верхнем уровне любого модуля Python, то это имя считается глобальным для модуля.По этой причине этот вид области также называют областью модуля .
Если вы работаете в интерактивном сеансе Python, вы заметите, что '__main__' также является именем его основного модуля. Чтобы убедиться в этом, откройте интерактивный сеанс и введите следующее:
>>> __name__
'__основной__'
Каждый раз, когда вы запускаете программу Python или интерактивный сеанс, как в приведенном выше коде, интерпретатор выполняет код в модуле или скрипте, который служит точкой входа в вашу программу.Этот модуль или скрипт загружается со специальным именем __main__ . С этого момента вы можете сказать, что ваша основная глобальная область видимости - это область __main__ .
Чтобы проверить имена в пределах вашей основной глобальной области видимости, вы можете использовать dir () . Если вы вызовете dir () без аргументов, вы получите список имен, которые находятся в вашей текущей глобальной области видимости. Взгляните на этот код:
>>> dir ()
['__annotations__', '__builtins__' ,..., '__package__', '__spec__']
>>> var = 100 # Назначить var на верхнем уровне __main__
>>> dir ()
['__annotations__', '__builtins __', ..., '__package__', '__spec__', 'var']
Когда вы вызываете dir () без аргументов, вы получаете список имен, доступных в вашей основной глобальной области Python. Обратите внимание: если вы назначите новое имя (например, var здесь) на верхнем уровне модуля (здесь это __main__ ), то это имя будет добавлено в список, возвращаемый функцией dir () .
Примечание: Более подробно dir () будет рассмотрено позже в этом руководстве.
Существует только одна глобальная область действия Python на выполнение программы. Эта область сохраняется до тех пор, пока программа не завершится и все ее имена не будут забыты. В противном случае при следующем запуске программы имена будут помнить свои значения из предыдущего запуска.
Вы можете получить доступ к значению любого глобального имени или сослаться на него из любого места в вашем коде. Сюда входят функции и классы.Вот пример, поясняющий эти моменты:
>>> >>> var = 100
>>> def func ():
... return var # Вы можете получить доступ к var из func ()
...
>>> func ()
100
>>> var # Остается без изменений
100
Внутри функции func () вы можете свободно обращаться к значению var или ссылаться на него. Это не влияет на ваше глобальное имя var , но показывает, что к var можно получить свободный доступ из func () .С другой стороны, вы не можете назначать глобальные имена внутри функций, если вы явно не объявите их как глобальные имена с помощью оператора global , который вы увидите позже.
Каждый раз, когда вы присваиваете значение имени в Python, может произойти одно из двух:
- Вы создаете новое имя
- Вы обновите существующее имя
Конкретное поведение будет зависеть от области Python, в которой вы назначаете имя.Если вы попытаетесь присвоить значение глобальному имени внутри функции, вы создадите это имя в локальной области видимости функции, затеняя или замещая глобальное имя. Это означает, что вы не сможете изменить большинство переменных, определенных вне функции, изнутри функции.
Если вы последуете этой логике, то поймете, что следующий код не будет работать так, как вы могли ожидать:
>>> >>> var = 100 # Глобальная переменная
>>> def increment ():
... var = var + 1 # Попробуйте обновить глобальную переменную
...
>>> инкремент ()
Отслеживание (последний вызов последний):
Файл "", строка 1, в
инкремент ()
Файл "", строка 2, в приращении
var = var + 1
UnboundLocalError: локальная переменная 'var', на которую ссылается перед назначением
В пределах increment () вы пытаетесь увеличить глобальную переменную var . Поскольку var не объявляется global внутри increment () , Python создает новую локальную переменную с тем же именем, var , внутри функции.В процессе Python понимает, что вы пытаетесь использовать локальную var перед его первым назначением ( var + 1 ), поэтому он вызывает UnboundLocalError .
Вот еще один пример:
>>> >>> var = 100 # Глобальная переменная
>>> def func ():
... print (var) # Ссылка на глобальную переменную var
... var = 200 # Определить новую локальную переменную с тем же именем var
...
>>> func ()
Отслеживание (последний вызов последний):
Файл "", строка 1, в
func ()
Файл "", строка 2, в функции
печать (var)
UnboundLocalError: локальная переменная 'var', на которую ссылается перед назначением
Вы, вероятно, ожидаете, что сможете распечатать глобальную var и обновить var позже, но снова вы получите UnboundLocalError .Здесь происходит следующее: когда вы запускаете тело func () , Python решает, что var является локальной переменной, поскольку она назначается в области видимости функции. Это не ошибка, а выбор дизайна. Python предполагает, что имена, присвоенные в теле функции, являются локальными для этой функции.
Примечание. Глобальные имена могут быть обновлены или изменены из любого места в вашей глобальной области Python. Кроме того, оператор global может использоваться для изменения глобальных имен практически из любого места в вашем коде, как вы увидите в заявлении global .
Изменение глобальных имен обычно считается плохой практикой программирования, потому что это может привести к получению кода следующего вида:
- Сложно отладить: Практически любой оператор в программе может изменить значение глобального имени.
- Трудно понять: Вы должны знать все операторы, которые обращаются к глобальным именам и изменяют их.
- Невозможно повторно использовать: Код зависит от глобальных имен, специфичных для конкретной программы.
Хорошая практика программирования рекомендует использовать локальные имена, а не глобальные. Вот несколько советов:
- Напишите автономных функций, которые полагаются на локальные имена, а не на глобальные.
- Попробуйте использовать уникальные имена объектов, независимо от того, в какой области вы находитесь.
- Избегайте изменения глобального имени в ваших программах.
- Избегайте изменения имени кросс-модуля .
- Используйте глобальные имена как константы, которые не изменяются во время выполнения вашей программы.
К этому моменту вы рассмотрели три области действия Python. В следующем примере показано, где они расположены в вашем коде и как Python ищет имена через них:
>>> >>> # Эта область является глобальной или модульной областью
>>> число = 100
>>> def outer_func ():
... # Этот блок является локальной областью external_func ()
... # Это также область действия inner_func ()
... def inner_func ():
... # Этот блок является локальной областью действия inner_func ()
... печать (число)
...
... inner_func ()
...
>>> outer_func ()
100
Когда вы вызываете outer_func () , вы получаете 100 , напечатанное на вашем экране. Но как Python в этом случае ищет имя номер ? Следуя правилу LEGB, вы будете искать номер в следующих местах:
- Внутри
inner_func (): Это локальная область видимости, нономертам не существует. - Внутри
outer_func (): Это охватывающая область, нономертам тоже не определен. - В области действия модуля: Это глобальная область, и вы найдете там
номер, так что вы можете вывести на экранномер.
Если номер не определен внутри глобальной области видимости, Python продолжает поиск, просматривая встроенную область видимости. Это последний компонент правила LEGB, как вы увидите в следующем разделе.
встроенных : встроенная область Встроенная область видимости - это специальная область видимости Python, которая реализована в виде стандартного библиотечного модуля с именем builtins в Python 3.Икс. Все встроенные объекты Python находятся в этом модуле. Они автоматически загружаются во встроенную область видимости, когда вы запускаете интерпретатор Python. Python ищет встроенных файлов последним в своем поиске LEGB, поэтому вы получаете все имена, которые он определяет, бесплатно. Это означает, что вы можете использовать их без импорта какого-либо модуля.
Обратите внимание, что имена во встроенных командах всегда загружаются в вашу глобальную область Python со специальным именем __builtins__ , как вы можете видеть в следующем коде:
>>> dir ()
['__annotations__', '__builtins__' ,..., '__package__', '__spec__']
>>> директория (__ builtins__)
['ArithmeticError', 'AssertionError', ..., 'кортеж', 'тип', 'vars', 'zip']
В выводе первого вызова dir () вы можете видеть, что __builtins__ всегда присутствует в глобальной области Python. Если вы проверите сам __builtins__ с помощью dir () , то получите весь список встроенных имен Python.
Встроенная область видимости добавляет более 150 имен в вашу текущую глобальную область действия Python.Например, в Python 3.8 вы можете узнать точное количество имен следующим образом:
>>> >>> len (dir (__ builtins__))
152
При вызове len () вы получаете количество элементов в списке , возвращенное функцией dir () . Это возвращает 152 имени, которые включают исключения, функции, типы, специальные атрибуты и другие встроенные объекты Python.
Несмотря на то, что вы можете получить доступ ко всем этим встроенным объектам Python бесплатно (без какого-либо импорта), вы также можете явно импортировать встроенных объектов и получить доступ к именам, используя точечную нотацию.Вот как это работает:
>>> import builtins # Импортировать встроенные модули как обычный модуль
>>> dir (встроенные)
['ArithmeticError', 'AssertionError', ..., 'кортеж', 'тип', 'vars', 'zip']
>>> builtins.sum ([1, 2, 3, 4, 5])
15
>>> builtins.max ([1, 5, 8, 7, 3])
8
>>> builtins.sorted ([1, 5, 8, 7, 3])
[1, 3, 5, 7, 8]
>>> builtins.pow (10, 2)
100
Вы можете импортировать встроенных модулей , как и любой другой модуль Python.С этого момента вы можете получить доступ ко всем именам в builtins , используя поиск атрибутов с точками или полностью определенные имена. Это может быть весьма полезно, если вы хотите убедиться, что у вас не будет конфликта имен, если какое-либо из ваших глобальных имен переопределяет любое встроенное имя.
Вы можете переопределить или переопределить любое встроенное имя в вашей глобальной области видимости. Если вы это сделаете, имейте в виду, что это повлияет на весь ваш код. Взгляните на следующий пример:
>>> >>> abs (-15) # Стандартное использование встроенной функции
15
>>> abs = 20 # Переопределить встроенное имя в глобальной области видимости
>>> абс (-15)
Отслеживание (последний вызов последний):
Файл "", строка 1, в
TypeError: объект int не вызывается
Если вы переопределите или повторно назначите abs , то исходный встроенный abs () повлияет на весь ваш код.Теперь предположим, что вам нужно вызвать исходный abs () и вы забыли, что вы переназначили имя. В этом случае, когда вы снова вызовете abs () , вы получите TypeError , потому что abs теперь содержит ссылку на целое число, которое нельзя вызвать.
Примечание: Случайное или непреднамеренное переопределение или переопределение встроенных имен в вашей глобальной области действия может быть источником опасных и трудно обнаруживаемых ошибок. Лучше постараться избегать такой практики.
Если вы экспериментируете с каким-то кодом и случайно повторно назначаете встроенное имя в интерактивном запросе, вы можете либо перезапустить сеанс, либо запустить del name , чтобы удалить переопределение из вашей глобальной области Python. Таким образом вы восстанавливаете исходное имя во встроенной области. Если вы еще раз вернетесь к примеру abs () , вы можете сделать что-то вроде этого:
>>> del abs # Удалите переопределенный abs из вашей глобальной области видимости
>>> abs (-15) # Восстановить исходный abs ()
15
Когда вы удаляете пользовательское имя abs , вы удаляете это имя из глобальной области видимости.Это позволяет снова получить доступ к исходному abs () во встроенном прицеле.
Чтобы обойти такую ситуацию, вы можете явно импортировать встроенных модулей , а затем использовать полностью определенные имена, как в следующем фрагменте кода:
>>> импорт встроенных
>>> builtins.abs (-15)
15
После того, как вы явно импортируете встроенных модулей , у вас будет имя модуля, доступное в вашей глобальной области Python. С этого момента вы можете использовать полностью определенные имена, чтобы однозначно получать нужные имена из встроенных команд , точно так же, как вы это делали со встроенными командами .abs () в приведенном выше примере.
В качестве краткого обзора некоторые значения области действия Python показаны в следующей таблице:
| Действие | Глобальный код | Местный код | Код вложенной функции |
|---|---|---|---|
| Имена доступа или ссылки, которые находятся в глобальной области действия | Есть | Есть | Есть |
| Изменить или обновить имена, которые находятся в глобальной области | Есть | Нет (если не заявлено global ) | Нет (если не заявлено global ) |
| Имена доступа или ссылки, которые находятся в локальной области | № | Да (собственная локальная область действия), Нет (другая локальная область действия) | Да (собственная локальная область действия), Нет (другая локальная область действия) |
| Переопределить имена во встроенной области | Есть | Да (во время выполнения функции) | Да (во время выполнения функции) |
| Имена доступа или ссылки, которые находятся в их охватывающей области | НЕТ | НЕТ | Есть |
| Изменить или обновить имена, которые находятся в их охватывающей области | НЕТ | НЕТ | Нет (если не заявлено нелокальное ) |
Кроме того, код в разных областях может использовать одно и то же имя для разных объектов.Таким образом, вы можете использовать локальную переменную с именем spam , а также глобальную переменную с тем же именем, spam . Однако это считается плохой практикой программирования.
Изменение поведения области действия Python
До сих пор вы узнали, как работает область видимости Python и как она ограничивает видимость переменных, функций, классов и других объектов Python определенными частями вашего кода. Теперь вы знаете, что вы можете обращаться к глобальным именам или ссылаться на них из любого места в вашем коде, но они могут быть изменены или обновлены изнутри глобальной области Python.
Вы также знаете, что вы можете получить доступ к локальным именам только изнутри локальной области Python, в которой они были созданы, или изнутри вложенной функции, но вы не можете получить к ним доступ из глобальной области Python или из других локальных областей. Кроме того, вы узнали, что нелокальное имя может быть доступно из вложенных функций, но не может быть изменено или обновлено оттуда.
Несмотря на то, что области Python по умолчанию следуют этим общим правилам, есть способы изменить это стандартное поведение.Python предоставляет два ключевых слова, которые позволяют изменять содержимое глобальных и нелокальных имен. Эти два ключевых слова:
-
по всему миру -
нелокальный
В следующих двух разделах вы узнаете, как использовать эти ключевые слова Python для изменения стандартного поведения областей действия Python.
The
global Заявление Вы уже знаете, что когда вы пытаетесь присвоить значение глобальному имени внутри функции, вы создаете новое локальное имя в области действия функции.Чтобы изменить это поведение, вы можете использовать оператор global . С помощью этого оператора вы можете определить список имен, которые будут обрабатываться как глобальные имена.
Оператор состоит из ключевого слова global , за которым следует одно или несколько имен, разделенных запятыми. Вы также можете использовать несколько операторов global с именем (или списком имен). Все имена, которые вы перечисляете в глобальном операторе , будут сопоставлены с глобальной областью или областью модуля, в которой вы их определяете.
Вот пример, когда вы пытаетесь обновить глобальную переменную из функции:
>>> >>> counter = 0 # Глобальное имя
>>> def update_counter ():
... counter = counter + 1 # Ошибка обновления счетчика
...
>>> update_counter ()
Отслеживание (последний вызов последний):
Файл "", строка 1, в
Файл "", строка 2, в update_counter
UnboundLocalError: локальная переменная counter, на которую ссылается перед присваиванием
Когда вы пытаетесь назначить счетчик внутри update_counter () , Python предполагает, что счетчик является локальным для update_counter () и вызывает UnboundLocalError , потому что вы пытаетесь получить доступ к имени, которое не определено еще.
Если вы хотите, чтобы этот код работал так, как вы ожидаете, вы можете использовать глобальный оператор следующим образом:
>>> counter = 0 # Глобальное имя
>>> def update_counter ():
... global counter # Объявить счетчик как глобальный
... counter = counter + 1 # Успешно обновить счетчик
...
>>> update_counter ()
>>> счетчик
1
>>> update_counter ()
>>> счетчик
2
>>> update_counter ()
>>> счетчик
3
В этой новой версии update_counter () вы добавляете оператор global counter в тело функции прямо перед попыткой изменить counter .С помощью этого крошечного изменения вы сопоставляете имя счетчика в области действия функции с тем же именем в глобальной области или области модуля. С этого момента вы можете свободно изменять counter внутри update_counter () . Все изменения отразятся в глобальной переменной.
С помощью оператора global counter вы говорите Python искать в глобальной области видимости имя counter . Таким образом, выражение counter = counter + 1 не создает новое имя в области действия функции, а обновляет его в глобальной области.
Примечание: Использование global в целом считается плохой практикой. Если вы обнаружите, что используете global для решения проблем, подобных описанной выше, остановитесь и подумайте, есть ли лучший способ написать свой код.
Например, вы можете попытаться написать автономную функцию, которая полагается на локальные имена, а не на глобальные имена, следующим образом:
>>> >>> global_counter = 0 # Глобальное имя
>>> def update_counter (счетчик):
... return counter + 1 # Использовать локальное имя
...
>>> global_counter = update_counter (global_counter)
>>> global_counter
1
>>> global_counter = update_counter (global_counter)
>>> global_counter
2
>>> global_counter = update_counter (global_counter)
>>> global_counter
3
Эта реализация update_counter () определяет счетчик как параметр и возвращает его значение, увеличенное на 1 единиц каждый раз, когда вызывается функция.Таким образом, результат update_counter () зависит от счетчика , который вы используете в качестве входных данных, а не от изменений, которые другие функции (или фрагменты кода) могут выполнять в глобальной переменной global_counter .
Вы также можете использовать глобальный оператор для создания ленивых глобальных имен, объявив их внутри функции. Взгляните на следующий код:
>>> def create_lazy_name ():
... global lazy # Создайте глобальное имя, lazy
... ленивый = 100
... вернуться ленивым
...
>>> create_lazy_name ()
100
>>> lazy # Имя теперь доступно в глобальной области видимости
100
>>> dir ()
['__annotations__', '__builtins __', ..., 'create_lazy_name', 'lazy']
Когда вы вызываете create_lazy_name () , вы также создаете глобальную переменную с именем lazy . Обратите внимание, что после вызова функции имя lazy становится доступным в глобальной области Python. Если вы проверите глобальное пространство имен с помощью dir () , вы увидите, что lazy появляется последним в списке.
Примечание: Даже если вы можете использовать глобальный оператор для создания ленивых глобальных имен, это может быть опасной практикой, которая может привести к ошибкам в коде. Так что лучше избегать подобных вещей в своем коде.
Например, предположим, что вы пытаетесь получить доступ к одному из этих ленивых имен, и по какой-то причине ваш код еще не вызвал функцию, создающую это имя. В этом случае вы получите ошибку NameError , и ваша программа выйдет из строя.
Наконец, стоит отметить, что вы можете использовать global изнутри любой функции или вложенной функции, и перечисленные имена всегда будут сопоставляться с именами в глобальной области Python.
Также обратите внимание, что, хотя использование оператора global на верхнем уровне модуля является законным, это не имеет особого смысла, потому что любое имя, присвоенное в глобальной области видимости, уже является глобальным именем по определению. Взгляните на следующий код:
>>> имя = 100
>>> dir ()
['__annotations__', '__builtins __', ..., '__spec__', 'name']
>>> глобальное имя
>>> dir ()
['__annotations__', '__builtins __', ..., '__spec__', 'name']
Использование оператора global , такого как глобальное имя , ничего не меняет в вашей текущей глобальной области, как вы можете видеть в выходных данных dir () .Имя переменной является глобальной переменной независимо от того, используете ли вы global или нет.
Нелокальный
Заявление Подобно глобальным именам, нелокальные имена могут быть доступны из внутренних функций, но не могут быть назначены или обновлены. Если вы хотите их изменить, вам необходимо использовать нелокальный оператор . С помощью оператора nonlocal вы можете определить список имен, которые будут обрабатываться как нелокальные.
Оператор нелокального состоит из ключевого слова нелокального , за которым следует одно или несколько имен, разделенных запятыми.Эти имена будут ссылаться на те же имена во входящей области Python. В следующем примере показано, как использовать нелокальный для изменения переменной, определенной во включающей или нелокальной области:
>>> def func ():
... var = 100 # нелокальная переменная
... def nested ():
... nonlocal var # Объявить var нелокальным
... var + = 100
...
... вложенный ()
... печать (var)
...
>>> func ()
200
С помощью оператора nonlocal var вы сообщаете Python, что вы измените var внутри nested () .Затем вы увеличиваете var с помощью операции расширенного присваивания. Это изменение отражено в нелокальном имени var , которое теперь имеет значение 200 .
В отличие от global , вы не можете использовать нелокальный вне вложенной или закрытой функции. Чтобы быть более точным, вы не можете использовать нелокальный оператор ни в глобальной, ни в локальной области. Вот пример:
>>> nonlocal my_var # Попробуйте использовать нелокальное значение в глобальной области видимости
Файл "", строка 1
SyntaxError: нелокальное объявление недопустимо на уровне модуля
>>> def func ():
... nonlocal var # Попробуйте использовать нелокальную переменную в локальной области видимости
... печать (var)
...
Файл "", строка 2
SyntaxError: привязка для нелокальной 'var' не найдена
Здесь вы сначала пытаетесь использовать нелокальный оператор в глобальной области Python. Поскольку нелокальный работает только внутри внутренней или вложенной функции, вы получаете SyntaxError , говорящую о том, что вы не можете использовать нелокальный в области видимости модуля. Обратите внимание, что нелокальный также не работает внутри локальной области.
В отличие от global , вы не можете использовать нелокальный для создания ленивых нелокальных имен. Имена должны уже существовать во включающей области Python, если вы хотите использовать их как нелокальные имена. Это означает, что вы не можете создавать нелокальные имена, объявляя их в операторе nonlocal во вложенной функции. Взгляните на следующий пример кода:
>>> def func ():
... def nested ():
... nonlocal lazy_var # Попробуйте создать нелокальное ленивое имя
...
Файл "", строка 3
SyntaxError: привязка для нелокальной 'lazy_var' не найдена
В этом примере, когда вы пытаетесь определить нелокальное имя с помощью nonlocal lazy_var , Python немедленно вызывает SyntaxError , потому что lazy_var не существует во включающей области nested () .
Использование охватывающих областей как замыканий
Замыкания — это особый вариант использования охватывающей области Python. Когда вы обрабатываете вложенную функцию как данные, операторы, составляющие эту функцию, упаковываются вместе со средой, в которой они выполняются.Результирующий объект называется закрытием. Другими словами, замыкание — это внутренняя или вложенная функция, которая несет информацию о своей охватывающей области, даже если эта область завершила свое выполнение.
Примечание: Вы также можете вызвать этот вид функции фабрикой , фабричной функцией или, чтобы быть более точной, фабрикой замыкания , чтобы указать, что функция создает и возвращает замыкания (внутренняя функция) , а не классы или экземпляры.
Замыканияпозволяют сохранять информацию о состоянии между вызовами функций. Это может быть полезно, если вы хотите написать код, основанный на концепции ленивого или отложенного вычисления. Взгляните на следующий код, чтобы увидеть, как работают замыкания и как вы можете использовать их в Python:
>>> >>> def power_factory (exp):
... степень защиты (базовая):
... вернуть базу ** exp
... вернуть мощность
...
>>> квадрат = power_factory (2)
>>> квадрат (10)
100
>>> cube = power_factory (3)
>>> куб (10)
1000
>>> куб (5)
125
>>> квадрат (15)
225
Ваша функция фабрики закрытия power_factory () принимает аргумент с именем exp .Вы можете использовать эту функцию для создания замыканий, которые запускают различные операции с питанием. Это работает, потому что каждый вызов power_factory () получает свой собственный набор информации о состоянии. Другими словами, он получает свое значение exp .
Примечание: Такие переменные, как exp , называются свободными переменными . Это переменные, которые используются в блоке кода, но не определены там. Свободные переменные — это механизм, который закрытие использует для сохранения информации о состоянии между вызовами.
В приведенном выше примере внутренняя функция power () сначала назначается квадрату . В этом случае функция запоминает, что exp равно 2 . Во втором примере вы вызываете power_factory () , используя 3 в качестве аргумента. Таким образом, куб содержит функциональный объект, который запоминает, что exp — это 3 . Обратите внимание, что вы можете свободно повторно использовать square и cube , потому что они не забывают информацию о своем состоянии.
В качестве последнего примера использования замыканий предположим, что вам нужно вычислить среднее значение некоторых выборочных данных. Вы собираете данные посредством потока последовательных измерений анализируемого параметра. В этом случае вы можете использовать фабрику укупорки, чтобы сгенерировать укупорку, которая запоминает предыдущие измерения в образце. Взгляните на следующий код:
>>> >>> def mean ():
... образец = []
... def _mean (число):
... образец.добавить (число)
... вернуть сумму (образец) / len (образец)
... вернуть _mean
...
>>> current_mean = среднее ()
>>> current_mean (10)
10.0
>>> current_mean (15)
12,5
>>> current_mean (12)
12,333333333333334
>>> current_mean (11)
12.0
>>> current_mean (13)
12.2
Замыкание, которое вы создаете в приведенном выше коде, запоминает информацию о состоянии образца между вызовами current_mean . Таким образом, вы можете решить проблему элегантным и питоническим способом.
Обратите внимание, что если ваш поток данных становится слишком большим, эта функция может стать проблемой с точки зрения использования памяти. Это потому, что с каждым вызовом current_mean , образец будет содержать все больший и больший список значений. Взгляните на следующий код для альтернативной реализации с использованием нелокального :
>>> def mean ():
... всего = 0
... длина = 0
... def _mean (число):
... нелокальный итог, длина
... итог + = число
... длина + = 1
... вернуть итог / длину
... вернуть _mean
...
>>> current_mean = среднее ()
>>> current_mean (10)
10.0
>>> current_mean (15)
12,5
>>> current_mean (12)
12,333333333333334
>>> current_mean (11)
12.0
>>> current_mean (13)
12.2
Несмотря на то, что это решение более подробное, у вас больше нет бесконечно растущего списка. Теперь у вас есть одно значение для всего и длины .Эта реализация намного эффективнее с точки зрения потребления памяти, чем предыдущее решение.
Наконец, вы можете найти несколько примеров использования замыканий в стандартной библиотеке Python. Например, functools предоставляет функцию с именем partial () , которая использует метод закрытия для создания новых объектов функций, которые могут быть вызваны с использованием предопределенных аргументов. Вот пример:
>>> from functools import partial
>>> def power (exp, base):
... возвратная база ** exp
...
>>> квадрат = частичный (степень, 2)
>>> квадрат (10)
100
Вы используете частичный для создания функционального объекта, который запоминает информацию о состоянии, где exp = 2 . Затем вы вызываете этот объект, чтобы выполнить операцию питания и получить окончательный результат.
Осуществление имен с помощью импорта
Когда вы пишете программу Python, вы обычно разбиваете код на несколько модулей. Чтобы ваша программа работала, вам необходимо перенести имена этих отдельных модулей в модуль __main__ .Для этого вам нужно явно импортировать модули или имена. Это единственный способ использовать эти имена в основной глобальной области Python.
Взгляните на следующий код, чтобы увидеть пример того, что происходит, когда вы импортируете некоторые стандартные модули и имена:
>>> >>> dir ()
['__annotations__', '__builtins __', ..., '__spec__']
>>> import sys
>>> dir ()
['__annotations__', '__builtins __', ..., '__spec__', 'sys']
>>> import os
>>> dir ()
['__annotations__', '__builtins__' ,..., '__spec__', 'os', 'sys']
>>> from functools import partial
>>> dir ()
['__annotations__', '__builtins __', ..., '__spec__', 'os', 'partial', 'sys']
Сначала вы импортируете sys и os из стандартной библиотеки Python. Вызвав dir () без аргументов, вы увидите, что эти модули теперь доступны вам как имена в вашей текущей глобальной области видимости. Таким образом, вы можете использовать точечную нотацию, чтобы получить доступ к именам, которые определены в sys и os .
В последней операции import вы используете форму из . Таким образом, вы можете использовать импортированное имя прямо в коде. Другими словами, вам не нужно явно использовать точечную нотацию.
Обнаружение необычных областей видимости Python
Вы найдете некоторые структуры Python, в которых разрешение имен не соответствует правилу LEGB для областей действия Python. Эти структуры включают:
В следующих нескольких разделах вы узнаете, как область видимости Python работает с этими тремя структурами.Обладая этими знаниями, вы сможете избежать тонких ошибок, связанных с использованием имен в подобных структурах Python.
Объем переменных понимания
Первая структура, которую вы рассмотрите, — это понимание . Понимание — это компактный способ обработки всех или части элементов в коллекции или последовательности. Вы можете использовать понимания для создания списков, словарей и наборов.
Понятия состоят из пары скобок ( [] ) или фигурных скобок ( {} ), содержащих выражение, за которым следуют один или несколько для предложений и затем ноль или один , если предложение на для предложения . .
Предложение для в понимании работает аналогично традиционному циклу для . Переменная цикла в понимании является локальной по отношению к структуре. Обратите внимание на следующий код:
>>> [элемент для элемента в диапазоне (5)]
[0, 1, 2, 3, 4]
>>> item # Попробуйте получить доступ к переменной понимания
Отслеживание (последний вызов последний):
Файл "", строка 1, в
пункт
NameError: имя 'item' не определено
После запуска анализа списка переменная item будет забыта, и вы больше не сможете получить доступ к ее значению.Маловероятно, что вам понадобится использовать эту переменную вне понимания, но, тем не менее, Python гарантирует, что ее значение больше не доступно после завершения понимания.
Обратите внимание, что это относится только к пониманию. Когда дело доходит до обычных для циклов , переменная цикла содержит последнее значение, обработанное циклом:
>>> для элемента в диапазоне (5):
... печать (элемент)
...
0
1
2
3
4
>>> item # Доступ к переменной цикла
4
После завершения цикла вы можете получить свободный доступ к переменной цикла , элемент .Здесь переменная цикла содержит последнее значение, обработанное циклом, которое в этом примере составляет 4 .
Область действия переменных исключения
Еще один нетипичный случай области видимости Python, с которым вы столкнетесь, — это случай переменной исключения . Переменная исключения — это переменная, которая содержит ссылку на исключение, вызванное оператором try . В Python 3.x такие переменные являются локальными для , за исключением блока , и забываются, когда блок заканчивается.Обратите внимание на следующий код:
>>> lst = [1, 2, 3]
>>> попробуйте:
... lst [4]
... кроме IndexError как err:
... # Переменная err является локальной для этого блока
... # Здесь вы можете делать что угодно с помощью err
... печать (ошибка)
...
индекс списка вне допустимого диапазона
>>> err # Выходит за рамки
Отслеживание (последний вызов последний):
Файл "", строка 1, в
ошибаться
NameError: имя 'err' не определено
err содержит ссылку на исключение, вызванное предложением try .Вы можете использовать err только внутри кодового блока , за исключением предложения . Таким образом, вы можете сказать, что область Python для переменной исключения является локальной для , за исключением блока кода . Также обратите внимание, что если вы попытаетесь получить доступ к err извне , кроме блока , то получите NameError . Это потому, что как только блок , за исключением , заканчивается, имя больше не существует.
Чтобы обойти это поведение, вы можете определить вспомогательную переменную из оператора try , а затем назначить исключение этой переменной внутри , кроме блока .Посмотрите на следующий пример:
>>> lst = [1, 2, 3]
>>> ex = Нет
>>> попробуйте:
... lst [4]
... кроме IndexError как err:
... ex = err
... печать (ошибка)
...
индекс списка вне допустимого диапазона
>>> err # Выходит за рамки
Отслеживание (последний вызов последний):
Файл "", строка 1, в
NameError: имя 'err' не определено
>>> ex # Содержит ссылку на исключение
индекс списка вне допустимого диапазона
Вы используете ex в качестве вспомогательной переменной для хранения ссылки на исключение, вызванное предложением try .Это может быть полезно, когда вам нужно что-то сделать с объектом исключения после завершения блока кода. Обратите внимание, что если исключение не возникает, то ex остается None .
Область действия атрибутов класса и экземпляра
Когда вы определяете класс, вы создаете новую локальную область Python. Имена, присвоенные на верхнем уровне класса, живут в этой локальной области. Имена, которые вы присвоили в инструкции class , не конфликтуют с именами в других местах.Можно сказать, что эти имена следуют правилу LEGB, где блок класса представляет уровень L .
В отличие от функций, локальная область видимости класса создается не во время вызова, а во время выполнения. Каждый объект класса имеет свой собственный атрибут .__ dict__ , который содержит область действия класса или пространство имен, в котором находятся все атрибуты класса . Посмотрите этот код:
>>> класс А:
... attr = 100
...
>>> A .__ dict __. Keys ()
dict_keys (['__ module__', 'attr', '__dict__', '__weakref__', '__doc__'])
При осмотре ключей .__dict__ вы увидите, что attr находится в списке вместе с другими специальными именами. Этот словарь представляет собой локальную область видимости класса. Имена в этой области видны всем экземплярам класса и самому классу.
Чтобы получить доступ к атрибуту класса извне класса, вам необходимо использовать точечную нотацию следующим образом:
>>> >>> класс А:
... attr = 100
... print (attr) # Доступ к атрибутам класса напрямую
...
100
>>> А.attr # Доступ к атрибуту класса извне класса
100
>>> attr # Не определен вне A
Отслеживание (последний вызов последний):
Файл "", строка 1, в
attr
NameError: имя attr не определено
Внутри локальной области видимости A вы можете получить доступ к атрибутам класса напрямую, как вы это делали в операторе print (attr) . Чтобы получить доступ к любому атрибуту класса после выполнения блока кода класса, вам нужно будет использовать точечную нотацию или ссылку на атрибут, как вы это делали с A.attr . В противном случае вы получите NameError , потому что атрибут attr является локальным для блока класса.
С другой стороны, если вы попытаетесь получить доступ к атрибуту, который не определен внутри класса, вы получите AttributeError . Посмотрите на следующий пример:
>>> A.undefined # Пытаться получить доступ к неопределенному атрибуту класса
Отслеживание (последний вызов последний):
Файл "", строка 1, в
А.неопределенный
AttributeError: объект типа A не имеет атрибута undefined
В этом примере вы пытаетесь получить доступ к атрибуту undefined . Поскольку этого атрибута нет в A , вы получите ошибку AttributeError , сообщающую, что A не имеет атрибута с именем undefined .
Вы также можете получить доступ к любому атрибуту класса, используя экземпляр класса следующим образом:
>>> >>> obj = A ()
>>> объект.attr
100
Когда у вас есть экземпляр, вы можете получить доступ к атрибутам класса, используя точечную нотацию, как вы сделали здесь с obj.attr . Атрибуты класса специфичны для объекта класса, но вы можете получить к ним доступ из любых экземпляров класса. Стоит отметить, что атрибуты класса являются общими для всех экземпляров класса. Если вы измените атрибут класса, то изменения будут видны во всех экземплярах класса.
Примечание: Думайте о точечной нотации, как если бы вы говорили Python: «Найдите атрибут с именем attr в obj .Если найдешь, отдай мне ».
Каждый раз, когда вы вызываете класс, вы создаете новый экземпляр этого класса. У экземпляров есть собственный атрибут .__ dict__ , который содержит имена в локальной области или пространстве имен экземпляра. Эти имена обычно называются атрибутами экземпляра и являются локальными и специфичными для каждого экземпляра. Это означает, что если вы измените атрибут экземпляра, то изменения будут видны только этому конкретному экземпляру.
Чтобы создать, обновить или получить доступ к любому атрибуту экземпляра изнутри класса, вам необходимо использовать self вместе с точечной нотацией.Здесь self — это специальный атрибут, представляющий текущий экземпляр. С другой стороны, чтобы обновить или получить доступ к любому атрибуту экземпляра извне класса, вам необходимо создать экземпляр, а затем использовать точечную нотацию. Вот как это работает:
>>> класс А:
... def __init __ (self, var):
... self.var = var # Создать новый атрибут экземпляра
... self.var * = 2 # Обновить атрибут экземпляра
...
>>> obj = A (100)
>>> объект.__dict__
{'var': 200}
>>> obj.var
200
Класс A принимает аргумент с именем var , который автоматически удваивается внутри .__ init __ () с использованием операции присваивания self.var * = 2 . Обратите внимание, что когда вы проверяете .__ dict__ на obj , вы получаете словарь, содержащий все атрибуты экземпляра. В этом случае словарь содержит только имя var , значение которого теперь 200 .
Несмотря на то, что вы можете создавать атрибуты экземпляра в любом методе класса, рекомендуется создавать и инициализировать их внутри .__ init __ () . Взгляните на эту новую версию A :
>>> класс А:
... def __init __ (self, var):
... self.var = var
...
... def duplicate_var (self):
... вернуть self.var * 2
...
>>> obj = A (100)
>>> obj.var
100
>>> obj.duplicate_var ()
200
>>> А.вар
Отслеживание (последний вызов последний):
Файл "", строка 1, в
А.вар
AttributeError: объект типа A не имеет атрибута var
Здесь вы изменяете A , чтобы добавить новый метод с именем duplicate_var () . Затем вы создаете экземпляр A , передавая 100 инициализатору класса. После этого теперь вы можете вызвать duplicate_var () на obj , чтобы дублировать значение, хранящееся в self.var .Наконец, если вы попытаетесь получить доступ к var , используя объект класса вместо экземпляра, вы получите AttributeError , потому что к атрибутам экземпляра нельзя получить доступ с помощью объектов класса.
Как правило, когда вы пишете объектно-ориентированный код на Python и пытаетесь получить доступ к атрибуту, ваша программа выполняет следующие шаги:
- Сначала проверьте локальную область видимости или пространство имен экземпляра .
- Если атрибут там не найден, проверьте локальную область видимости или пространство имен class .
- Если имя не существует в пространстве имен класса, вы получите
AttributeError.
Это основной механизм, с помощью которого Python разрешает имена в классах и экземплярах.
Хотя классы определяют локальную область видимости или пространство имен класса, они не создают охватывающую область для методов. Следовательно, когда вы реализуете класс, ссылки на атрибуты и методы должны выполняться с использованием точечной записи:
>>> >>> класс А:
... var = 100
... def print_var (self):
... print (var) # Попытка получить доступ к атрибуту класса напрямую
...
>>> A (). Print_var ()
Отслеживание (последний вызов последний):
Файл "", строка 1, в
A (). Print_var ()
Файл "", строка 4, в print_var
печать (var)
NameError: имя 'var' не определено
Поскольку классы не создают закрывающую область для методов, вы не можете получить доступ к var непосредственно из print_var () , как вы пытаетесь сделать здесь.Чтобы получить доступ к атрибутам класса изнутри любого метода, вам необходимо использовать точечную нотацию. Чтобы устранить проблему в этом примере, измените оператор print (var) внутри print_var () на print (A.var) и посмотрите, что произойдет.
Вы можете переопределить атрибут класса атрибутом экземпляра, который изменит общее поведение вашего класса. Однако вы можете получить доступ к обоим атрибутам однозначно, используя точечную нотацию, как в следующем примере:
>>> >>> класс А:
... var = 100
... def __init __ (сам):
... self.var = 200
...
... def access_attr (self):
... # Используйте точечную нотацию для доступа к атрибутам класса и экземпляра
... print (f'Атрибут экземпляра: {self.var} ')
... print (f'Атрибут класса: {A.var} ')
...
>>> obj = A ()
>>> obj.access_attr ()
Атрибут экземпляра: 200
Атрибут класса: 100
>>> A.var # Атрибуты класса доступа
100
>>> A (). Var # Доступ к атрибутам экземпляра
200
>>> А.__dict __. ключи ()
dict_keys (['__ module__', 'var', '__init __', ..., '__getattribute__'])
>>> A () .__ dict __. Keys ()
dict_keys (['var'])
Вышеупомянутый класс имеет атрибут экземпляра и атрибут класса с тем же именем var . Вы можете использовать следующий код для доступа к каждому из них:
- Экземпляр: Используйте
self.varдля доступа к этому атрибуту. - Класс: Используйте
A.varдля доступа к этому атрибуту.
Поскольку в обоих случаях используется точечная запись, проблем с конфликтом имен не возникает.
Примечание: В общем, хорошие практики ООП рекомендуют не дублировать атрибуты класса с атрибутами экземпляра, которые имеют разные обязанности или выполняют разные действия. Это может привести к незаметным и труднодоступным ошибкам.
Наконец, обратите внимание, что класс .__ dict__ и экземпляр .__ dict__ — это совершенно разные и независимые словари. Вот почему атрибуты класса доступны сразу после запуска или импорта модуля, в котором был определен класс.Напротив, атрибуты экземпляра оживают только после создания объекта или экземпляра.
Заключение
Область видимости переменной или имени определяет ее видимость во всем вашем коде. В Python область видимости реализована как локальная, охватывающая, глобальная или встроенная. Когда вы используете переменную или имя, Python последовательно выполняет поиск в этих областях, чтобы решить эту проблему. Если имя не найдено, вы получите сообщение об ошибке. Это общий механизм, который Python использует для разрешения имен и известен как правило LEGB .
Теперь вы можете:
- Воспользуйтесь областью действия Python, чтобы избежать или минимизировать ошибки, связанные с конфликтом имен
- Используйте как глобальные, так и локальные имена в своих программах, чтобы улучшить ремонтопригодность кода
- Используйте согласованную стратегию для доступа, изменения или обновления имен во всем вашем коде Python
Кроме того, вы рассмотрели некоторые связанные с областью действия инструменты и методы, которые предлагает Python, и то, как вы можете использовать их для сбора информации об именах, которые существуют в данной области, или для изменения стандартного поведения области действия Python.Конечно, есть еще кое-что, выходящее за рамки данного руководства, так что продолжайте заниматься разрешением имен в Python!
Демистифицируем область действия переменных JavaScript и поднимаем их вверх
Сохранение значений в переменных — фундаментальная концепция в программировании. «Область действия» переменной определяет, когда она доступна, а когда нет в вашей программе. Понимание области видимости переменных в JavaScript — один из ключей к созданию прочной основы языка.
В этой статье объясняется, как работает система определения области видимости JavaScript. Вы узнаете о различных способах объявления переменных, различиях между локальной и глобальной областью видимости, а также о чем-то, что называется «подъем» — уловке JavaScript, которая может превратить невинно выглядящее объявление переменной в тонкую ошибку.
Диапазон изменения
В JavaScript область действия переменной контролируется местоположением объявления переменной и определяет часть программы, в которой доступна конкретная переменная.
В настоящее время существует три способа объявления переменной в JavaScript: с помощью старого ключевого слова var и с помощью нового ключевого слова let и const . До ES6 использование ключевого слова var было единственным способом объявления переменной, но теперь мы можем использовать let и const , которые имеют более строгие правила и делают код менее подверженным ошибкам. Ниже мы рассмотрим различия между всеми тремя ключевыми словами.
Правила определения объема варьируются от языка к языку.JavaScript имеет две области : глобальную и локальную . Локальная область видимости имеет два варианта: старая область видимости функций и новая область видимости блока , представленная в ES6. Стоит отметить, что область видимости функции на самом деле является особым типом области видимости блока.
Глобальный охват
В сценарии самая внешняя область видимости — это глобальная область. Любые переменные, объявленные в этой области, становятся глобальными переменными и доступны из любой точки программы:
const name = "Моник";
function sayHi () {
приставка.журнал (`Привет, $ {name}`);
}
скажи привет();
Как показывает этот простой пример, переменная имя является глобальной. Он определен в глобальной области видимости и доступен во всей программе.
Но как бы удобно это ни казалось, использование глобальных переменных в JavaScript не приветствуется. Это, например, связано с тем, что они потенциально могут быть перезаписаны другими сценариями или откуда-то еще в вашей программе.
Локальная область действия
Любые переменные, объявленные внутри блока, принадлежат этому конкретному блоку и становятся локальными переменными.
Функция в JavaScript определяет область для переменных, объявленных с использованием var , let и const . Любая переменная, объявленная в этой функции, доступна только из этой функции и любых вложенных функций.
Блок кода ( для , для и т. Д.) Определяет область только для переменных, объявленных с помощью ключевых слов let и const . Ключевое слово var ограничено областью действия функции, что означает, что новая область действия может быть создана только внутри функций.
Ключевые слова let и const имеют область видимости блока, которая создает новую локальную область видимости для любого блока, в котором они объявлены. Вы также можете определять отдельные блоки кода в JavaScript, и они аналогичным образом ограничивают область действия:
{
}
Области действия функций и блоков могут быть вложенными. В такой ситуации с несколькими вложенными областями видимости переменная доступна в пределах своей собственной области или из внутренней области. Но за пределами области действия переменная недоступна.
Простой пример, помогающий визуализировать область действия
Чтобы прояснить ситуацию, давайте воспользуемся простой метафорой. У каждой страны в нашем мире есть границы. Все, что находится внутри этих границ, относится к сфере действия страны. В каждой стране есть много городов, и каждый из них имеет свой городской масштаб. Страны и города подобны функциям или блокам JavaScript. У них свои локальные прицелы. То же самое и с континентами. Хотя они огромны по размеру, их также можно определить как локали.
С другой стороны, мировые океаны нельзя определить как имеющие локальную область действия, потому что они фактически охватывают все локальные объекты — континенты, страны и города — и, таким образом, их область действия определяется как глобальная. Давайте представим это в следующем примере:
var locales = {
европа: функция () {
var myFriend = "Моник";
var france = function () {
var paris = function () {
console.log (myFriend);
};
Париж();
};
Франция();
}
};
локации.европа ();
См. Pen
Variable Scope: 1 от SitePoint (@SitePoint)
на CodePen.
Здесь переменная myFriend доступна из функции paris , как она была определена во внешней области видимости функции france . Если мы поменяем местами переменную myFriend и оператор консоли, мы получим ReferenceError: myFriend не определен как , потому что мы не можем достичь внутренней области из внешней области.
Теперь, когда мы понимаем, что такое локальные и глобальные области видимости и как они создаются, пора узнать, как интерпретатор JavaScript использует их для поиска конкретной переменной.
Возвращаясь к данной метафоре, допустим, я хочу найти своего друга по имени Моник. Я знаю, что она живет в Париже, поэтому и начинаю поиски оттуда. Когда я не могу найти ее в Париже, я поднимаюсь на один уровень выше и расширяю свой поиск по всей Франции. Но опять же, ее там нет. Затем я снова расширяю свой поиск, поднимаясь на другой уровень выше. Наконец, я нахожу ее в Италии, которая в нашем случае является локальным размахом Европы.
В предыдущем примере мой друг Моник представлен переменной myFriend .В последней строке мы вызываем функцию europe () , которая вызывает france () , и, наконец, когда вызывается функция paris () , начинается поиск. Интерпретатор JavaScript работает в текущей области видимости и работает до тех пор, пока не найдет нужную переменную. Если переменная не найдена ни в одной области, создается исключение.
Этот тип поиска называется лексической (статической) областью видимости. Статическая структура программы определяет область видимости переменной.Область действия переменной определяется ее местоположением в исходном коде, а вложенные функции имеют доступ к переменным, объявленным во внешней области. Независимо от того, откуда вызывается функция или даже как она вызывается, ее лексическая область видимости зависит только от того, где функция была объявлена.
Теперь посмотрим, как работает новая область видимости блока:
function testScope (n) {
если правда) {
константное приветствие = 'Привет';
пусть имя = п;
console.log (приветствие + "" + имя);
}
приставка.журнал (приветствие + "" + имя);
}
testScope ('Дэвид');
См. Pen
Variable Scope: 2 от SitePoint (@SitePoint)
на CodePen.
В этом примере мы видим, что приветствие и именуют переменные , объявленные с const и let , недоступны за пределами блока if .
Давайте теперь заменим const и let на var и посмотрим, что произойдет:
function testScope (n) {
если правда) {
var приветствие = 'Привет';
var name = n;
приставка.журнал (приветствие + "" + имя);
}
console.log (приветствие + "" + имя);
}
testScope ('Дэвид');
См. Pen
Variable Scope: 3 от SitePoint (@SitePoint)
на CodePen.
Как видите, когда мы используем ключевое слово var , переменные достижимы во всей области действия функции.
В JavaScript переменные с одинаковыми именами могут быть указаны на нескольких уровнях вложенной области видимости. В такой ситуации локальные переменные имеют приоритет над глобальными.Если вы объявляете локальную переменную и глобальную переменную с тем же именем, локальная переменная будет иметь приоритет, когда вы используете ее внутри функции или блока. Этот тип поведения называется затенение . Проще говоря, внутренняя переменная затеняет внешнюю.
Это точный механизм, используемый, когда интерпретатор JavaScript пытается найти определенную переменную. Он начинается с самой внутренней области, выполняемой в данный момент, и продолжается до тех пор, пока не будет найдено первое совпадение, независимо от того, есть ли другие переменные с тем же именем на внешних уровнях или нет.Давайте посмотрим на пример:
var test = «Я глобальный»;
function testScope () {
var test = "Я местный";
console.log (тест);
}
testScope ();
console.log (тест);
См. Pen
Variable Scope: 4 от SitePoint (@SitePoint)
на CodePen.
Даже с тем же именем локальная переменная не перезаписывает глобальную после выполнения функции testScope () . Но так бывает не всегда. Давайте посмотрим на это:
var test = «Я глобальный»;
function testScope () {
test = "Я местный";
приставка.журнал (тест);
}
console.log (тест);
testScope ();
console.log (тест);
См. Pen
Variable Scope: 5 от SitePoint (@SitePoint)
на CodePen.
На этот раз локальная переменная test перезаписывает глобальную переменную с тем же именем. Когда мы запускаем код внутри функции testScope () , глобальная переменная переназначается. Если локальная переменная назначается без предварительного объявления с ключевым словом var , она становится глобальной переменной.Чтобы избежать такого нежелательного поведения, вы всегда должны объявлять свои локальные переменные перед их использованием. Любая переменная, объявленная с ключевым словом var внутри функции, является локальной переменной. Рекомендуется объявлять переменные.
Примечание. В строгом режиме будет ошибкой присвоить значение переменной без предварительного объявления переменной.
Подъемник
Интерпретатор JavaScript выполняет множество операций за кулисами, и одна из них — «подъем».Если вы не подозреваете об этом «скрытом» поведении, это может вызвать большую путаницу. Лучший способ думать о поведении переменных JavaScript — всегда визуализировать их как состоящие из двух частей: объявления и инициализации / присвоения:
var состояние;
состояние = "готово";
var state = "готово";
В приведенном выше коде мы сначала объявляем переменную state , а затем присваиваем ей значение "готово" . И в последней строке кода мы видим, что эти два шага можно комбинировать.Но вам нужно иметь в виду, что, хотя они кажутся одним оператором, на практике движок JavaScript обрабатывает этот единственный оператор как два отдельных оператора, как и в первых двух строках примера.
Мы уже знаем, что любая переменная, объявленная в области видимости, принадлежит этой области. Но чего мы пока не знаем, так это того, что независимо от того, где переменные объявлены в определенной области, все объявления переменных перемещаются в верхнюю часть своей области (глобальной или локальной).Это называется поднятием , поскольку объявления переменных поднимаются в верхнюю часть области видимости. Обратите внимание, что подъем перемещает только объявление. Любые назначения остаются на месте. Давайте посмотрим на пример:
console.log (состояние);
var state = "готово";
См. Pen
Variable Scope: 6 от SitePoint (@SitePoint)
на CodePen.
Как вы можете видеть, когда мы регистрируем значение состояния , на выходе получается undefined , потому что мы ссылаемся на него до фактического присвоения.Вы могли ожидать, что будет выброшено ReferenceError , потому что состояние еще не объявлено. Но вы не знаете, что переменная объявлена и инициализирована значением по умолчанию undefined за сценой. Вот как код интерпретируется движком JavaScript:
var состояние;
console.log (состояние);
состояние = "готово";
Важно отметить, что переменная не перемещается физически.Подъем — это всего лишь модель, описывающая, что JS-движок делает за кулисами.
Теперь давайте посмотрим, как работает подъем с переменными let :
{
console.log (состояние);
пусть состояние = "готово";
}
См. Pen
Variable Scope: 7 от SitePoint (@SitePoint)
на CodePen.
В этом примере вывод консоли — это не undefined , но выдается справочная ошибка. Почему? Переменные let , в отличие от переменных var , не могут быть прочитаны / записаны, пока они не будут полностью инициализированы.Они полностью инициализируются только там, где они фактически объявлены в коде. Итак, объявление переменной let поднимается, но не инициализируется значением undefined , как в случае с переменными var . Участок от начала блока до фактического объявления переменной называется временной мертвой зоной . Это механизм, который обеспечивает лучшую практику программирования, заставляя вас объявлять переменную перед ее использованием. Если мы переместим консольный оператор из TDZ, мы получим ожидаемый результат: готов .
{
пусть состояние = "готово";
console.log (состояние);
}
См. Pen
Variable Scope: 8 от SitePoint (@SitePoint)
на CodePen.
Переменные, объявленные с ключевым словом const , имеют то же поведение, что и переменные let .
Функции
Подъем также влияет на объявления функций. Но прежде чем мы рассмотрим несколько примеров, давайте сначала узнаем разницу между объявлением функции и выражением функции:
function showState () {}
var showState = function () {};
Самый простой способ отличить объявление функции от выражения функции — это проверить позицию слова функция в операторе.Если функция является самым первым в операторе, то это объявление функции. В противном случае это выражение функции.
Объявления функций полностью подняты. Это означает, что тело всей функции перемещается наверх. Это позволяет вызывать функцию до ее объявления:
showState ();
function showState () {
console.log («Готово»);
}
var showState = function () {
console.log («Ожидание»);
};
См. Pen
Variable Scope: 9 от SitePoint (@SitePoint)
на CodePen.
Причина, по которой предыдущий код работает, заключается в том, что движок JavaScript перемещает объявление функции showState () и все ее содержимое в начало области. Код интерпретируется так:
function showState () {
console.log («Готово»);
}
var showState;
showState ();
showState = function () {
console.log («Ожидание»);
};
Как вы могли заметить, поднимается только объявление функции, а выражение функции — нет.Когда функция назначается переменной, правила те же, что и для подъема переменной (перемещается только объявление, а присваивание остается на месте).
В приведенном выше коде мы видели, что объявление функции имеет приоритет над объявлением переменной. А в следующем примере мы увидим, что когда у нас есть объявление функции, а не присвоение переменной, последнее имеет приоритет:
var showState = function () {
console.log («Ожидание»);
};
function showState () {
приставка.журнал («Готово»);
}
showState ();
См. Pen
Variable Scope: 10 от SitePoint (@SitePoint)
на CodePen.
На этот раз мы вызываем функцию showState () в последней строке кода, что меняет ситуацию. Теперь получаем на выходе "Idle" . Вот как это выглядит при интерпретации движком JavaScript:
function showState () {
console.log («Готово»);
}
var showState;
showState = function () {
приставка.журнал ("Ожидание");
};
showState ();
Примечание: стрелочные функции работают идентично функциональным выражениям.
Классы
Объявления классов также поднимаются аналогично переменным, объявленным с помощью оператора let :
var user = new Person ('Дэвид', 33);
class Person {
конструктор (имя, возраст) {
this.name = имя;
this.age = возраст;
}
}
См. Pen
Variable Scope: 11 от SitePoint (@SitePoint)
на CodePen.
В этом примере мы видим, что использование класса Person перед объявлением вызывает ошибку ссылки, аналогичную той, что была в переменной let . Чтобы исправить это, мы должны использовать класс Person после объявления:
class Person {
конструктор (имя, возраст) {
this.name = имя;
this.age = возраст;
}
}
var user = new Person ('Дэвид', 33);
console.log (пользователь);
См. Pen
Variable Scope: 12 от SitePoint (@SitePoint)
на CodePen.
Классы также могут быть созданы с использованием выражения класса, используя var , let или const операторы объявления переменных:
console.log (typeof Person);
var user = new Person ('Дэвид', 33);
var Person = class {
конструктор (имя, возраст) {
this.name = имя;
this.age = возраст;
}
};
См. Pen
Variable Scope: 13 от SitePoint (@SitePoint)
на CodePen.
В этом примере мы видим, что класс Person поднимается как выражение функции, но его нельзя использовать, поскольку его значение — undefined .Опять же, чтобы исправить это, мы должны использовать класс Person после объявления:
console.log (typeof Person);
var Person = class {
конструктор (имя, возраст) {
this.name = имя;
this.age = возраст;
}
};
var user = new Person ('Дэвид', 33);
console.log (пользователь);
См. Pen
Variable Scope: 14 от SitePoint (@SitePoint)
на CodePen.
Что нужно помнить
-
varпеременные имеют функциональную область видимости. -
letиconst.имеют область видимости блока (это также включает функции). - Все объявления — классы, функции и переменные — поднимаются в верхнюю часть содержащей их области до того, как будет выполнена какая-либо часть вашего кода.
- Сначала поднимаются функции, затем переменные.
- Объявления функций имеют приоритет перед объявлениями переменных, но не перед назначениями переменных.
Объем — cppreference.com
Каждое имя, которое появляется в программе C ++, допустимо только в некоторых, возможно, несмежных Часть исходного кода называется областью .
В пределах области неквалифицированный поиск имени может использоваться для связывания имени с его объявлением.
[править] Объем блока
Возможная область видимости переменной, представленной объявлением в блоке (составной оператор), начинается в точке объявления и заканчивается в конце блока. Фактическая область действия такая же, как и потенциальная область, если только не существует вложенного блока с объявлением, которое вводит идентичное имя (в этом случае вся потенциальная область вложенного объявления исключается из области внешнего объявления)
int main ()
{
int a = 0; // начинается область видимости первой 'а'
++ a; // имя 'a' находится в области видимости и относится к первому 'a'
{
int a = 1; // начинается область действия второй 'а'
// область видимости первой 'а' прерывается
а = 42; // 'a' находится в области видимости и относится ко второму 'a'
} // блок заканчивается, область действия второго 'а' заканчивается
// возобновляется область действия первого 'а'
} // блок заканчивается, область действия первого 'а' заканчивается
int b = a; // Ошибка: имя 'a' не входит в область видимости Потенциальная область действия имени, объявленного в обработчике исключений, начинается в точке объявления и заканчивается, когда обработчик исключений завершается, и не входит в область действия другого обработчика исключений или во включающем блоке.
try {
f ();
} catch (const std :: runtime_error & re) {// начинается область повторного выполнения
int n = 1; // начинается область n
std :: cout << re.what (); // re находится в области видимости
} // область действия заканчивается, область действия n заканчивается
catch (std :: exception & e) {
std :: cout << re.what (); // ошибка: re не входит в область видимости
++ n; // ошибка: n не входит в область видимости
} Потенциальная область видимости имени, объявленного в init-заявлении цикла for, в условии for цикла, в range_declaration цикла range for, в init-заявлении Оператор if или оператор switch (начиная с C ++ 17), в условии , оператора if, цикл while или оператор switch начинается в точке объявления и заканчивается в конце управляемого оператора.
Base * bp = new Derived;
if (Производное * dp = dynamic_cast <Производное *> (bp))
{
dp-> f (); // dp находится в области видимости
} // область действия заканчивается
for (int n = 0; // начинается область n
n <10; // n находится в области видимости
++ n) // n находится в области видимости
{
std :: cout << n << ''; // n находится в области видимости
} // объем n заканчивается [править] Объем параметра функции
Возможная область действия параметра функции (включая параметры лямбда-выражения) или предопределенной переменной, локальной для функции, начинается с точки ее объявления.
- Если ближайший декларатор включающей функции не является декларатором определения функции, его потенциальная область действия заканчивается в конце этого декларатора функции.
- В противном случае его потенциальная область действия заканчивается в конце последнего обработчика исключений блока try-функции или в конце тела функции, если блок try функции не использовался.
const int n = 3;
int f1 (int n, // область глобального 'n' прервана,
// начинается область действия параметра 'n'
int y = n); // ошибка: аргумент по умолчанию ссылается на параметр
int (* (* f2) (int n)) [n]; // ОК: область действия параметра функции 'n'
// заканчивается в конце декларатора своей функции
// в деклараторе массива глобальное n находится в области видимости
// (объявляется указатель на функцию, возвращающую указатель на массив из 3 int
// напротив
авто (* f3) (int n) -> int (*) [n]; // ошибка: параметр 'n' как привязанный к массиву
int f (int n = 2) // начинается область видимости 'n'
try // функция try block
{// тело функции начинается
++ n; // 'n' находится в области видимости и относится к параметру функции
{
int n = 2; // начинается область видимости локальной переменной 'n'
// область действия параметра функции 'n' прервана
++ n; // 'n' относится к локальной переменной в этом блоке
} // область локальной переменной 'n' заканчивается
// область действия параметра функции 'n' возобновляется
} ловить(...) {
++ n; // n находится в области видимости и относится к параметру функции
бросать;
} // последний обработчик исключений завершается, область действия параметра функции 'n' заканчивается
int a = n; // ОК: глобальное 'n' находится в области [править] Область пространства имен
Имя, объявленное в пространстве имен, становится видимым в местоположении его первого объявления и входит в область видимости во всех определениях пространства имен для того же пространства имен, которые следуют ниже, плюс для любой директивы using, которая вводит это имя или все его пространство имен в другую область, остальная часть этого объема.
Область верхнего уровня единицы трансляции ("область файла" или "глобальная область") также является пространством имен и правильно называется "областью глобального пространства имен". Любое имя, объявленное в области видимости глобального пространства имен, становится видимым в местоположении его первого объявления и остается в области видимости до конца единицы трансляции.
Имя, объявленное в безымянном пространстве имен или во встроенном пространстве имен, отображается во включающем пространстве имен.
namespace N {// начинается область N (как член глобального пространства имен)
int i; // начинается область действия i
int g (int a) {вернуть; } // начинается область действия g
int j (); // начинается область j
void q (); // начинается область видимости q
namespace {
int x; // область видимости x начинается
} // объем x не заканчивается
inline namespace inl {// начинается область inl
int y; // начинается область видимости y
} // объем y не заканчивается
} // область видимости i, g, j, q, inl, x, y прервана
namespace {
int l = 1; // начинается область l
} // область l не заканчивается (это член безымянного пространства имен)
namespace N {// область видимости i, g, j, q, inl, x, y продолжается
int g (char a) {// перегружает N :: g (int)
вернуть l + a; // l из безымянного пространства имен находится в области видимости
}
int i; // ошибка: повторяющееся определение (i уже в области видимости)
int j (); // ОК: повторное объявление функции разрешено
int j () {// ОК: определение ранее объявленного N :: j ()
вернуть g (i); // вызывает N :: g (int)
}
int q (); // ошибка: q уже находится в области видимости с другим типом возврата
} // область видимости i, g, j, q, inl, x, y прервана
int main () {
используя пространство имен N; // область видимости i, g, j, q, inl, x, y возобновляется
я = 1; // N :: i находится в области видимости
х = 1; // N: :( анонимно) :: x находится в области видимости
у = 1; // N :: inl :: y находится в области видимости
inl :: y = 2; // N :: inl также входит в область видимости
} // область видимости i, g, j, q, inl, x, y прервана Имя также может быть видно в единицах перевода, которые импортировали текущую единицу перевода. | (начиная с C ++ 20) |
[править] Область действия класса
Потенциальная область видимости имени, объявленного в классе, начинается в точке объявления и включает в себя остальную часть тела класса и все тела функций (даже если они определены вне определения класса или до объявления имени), аргументы по умолчанию, исключение спецификации, внутриклассовые инициализаторы скобок или равенства и все эти вещи во вложенных классах рекурсивно.
класс X {
int f (int a = n) {// X :: n находится в области видимости внутри параметра по умолчанию
вернуть a * n; // X :: n находится в области видимости внутри тела функции
}
используя r = int;
г г ();
int я = п * 2; // X :: n находится в области видимости внутри инициализатора
// int x [n]; // Ошибка: n не входит в область видимости в теле класса
статическая константа int n = 1;
int x [n]; // ОК: n теперь находится в области видимости в теле класса
};
// r X :: g () {// Ошибка: r находится вне области видимости вне тела функции-члена
auto X :: g () -> r {// ОК: конечный возвращаемый тип X :: r находится в области видимости
return n; // X :: n находится в области видимости в теле внеклассовой функции-члена
} Если имя используется в теле класса до его объявления, а другое объявление для этого имени находится в области видимости, программа имеет неправильный формат, диагностика не требуется.
typedef int c; // :: c
перечисление {я = 1}; // :: я
class X {
char v [i]; // Ошибка: здесь i ссылается на :: i
// но есть еще X :: i
int f () {
return sizeof (c); // ОК: X :: c, а не :: c находится в области видимости внутри функции-члена
}
char c; // X :: c
перечисление {я = 2}; // X :: i
};
typedef char * T;
struct Y {
Т а; // Ошибка: в этот момент T относится к :: T
// но есть еще Y :: T
typedef long T;
Т б;
}; Имена членов класса могут использоваться в следующих контекстах:
- в своей собственной области класса или в области класса производного класса
- после
.оператор, примененный к выражению типа его класса или класса, производного от него - после оператора
->, примененного к выражению типа указателя на его класс или указателей на производный от него класс - после применения оператора
::к имени его класса или имени производного от него класса
[править] Область перечисления
Имя перечислителя, введенного в перечисление с ограниченной областью действия, начинается в точке объявления и заканчивается в конце спецификатора перечисления (напротив, перечислители без области действия находятся в области после конца спецификатора перечисления)
enum e1_t {// перечисление без области видимости
А,
В = А * 2
}; // область действия A и B не заканчивается
enum class e2_t {// перечисление с ограниченной областью видимости
SA,
SB = SA * 2 // SA входит в область видимости
}; // область действия SA и SB заканчивается
e1_t e1 = B; // ОК, B находится в области видимости
// e2_t e2 = SB; // Ошибка: SB не входит в область видимости
e2_t e2 = e2_t :: SB; // ОК [править] Область параметров шаблона
Потенциальная область действия имени параметра шаблона начинается сразу в точке объявления и продолжается до конца наименьшего объявления шаблона, в котором он был введен.В частности, параметр шаблона может использоваться в объявлениях последующих параметров шаблона и в спецификациях базовых классов, но не может использоваться в объявлениях предыдущих параметров шаблона.
templateclass X: public Array // T может использоваться в имени базового класса { // T можно использовать и внутри тела }; // области действия T и U заканчиваются, область действия X продолжается
Потенциальная область действия имени параметра параметра шаблона шаблона - это наименьший список параметров шаблона, в котором появляется это имя.
template // границы Y и G заканчиваются
класс Т,
// typename U = Y // Ошибка: Y не входит в область видимости
typename U
>
класс X
{
}; // объемы T и U конец Подобно другим вложенным областям видимости, имя параметра шаблона скрывает одно и то же имя из внешней области на время своей собственной:
typedef int N; templateclass T // N здесь параметр шаблона, а не int > структура A;
[править] Пункт декларации
Как правило, имя отображается после местоположения его первого объявления, которое расположено следующим образом:
Для переменных и других имен, представленных простыми объявлениями, локус находится сразу после декларатора этого имени и перед его инициализатором, если таковой имеется:
беззнаковый символ x = 32; // первый 'x' становится видимым
{
беззнаковый символ x = x; // второй 'x' становится видимым перед инициализатором (= x)
// это не инициализирует второй 'x' значением 32,
// это инициализирует второй 'x' своим собственным,
// неопределенное значение
}
std :: function f = [&] (int n) {return n> 1? п * ж (п-1): п;};
// имя функции 'f' находится в области видимости лямбда и может
// быть правильно захваченным по ссылке, давая рекурсивную функцию const int x = 2; // первый 'x' становится видимым
{
int x [x] = {}; // второй x становится видимым перед инициализатором (= {})
// но после декларатора (x [x]).Внутри декларатора внешний
// 'x' все еще в области видимости. Это объявляет массив из 2 int.
} Местоположение объявления класса или шаблона класса находится сразу после идентификатора, который называет класс (или идентификатора шаблона, который называет специализацию шаблона), появляется в его заголовке класса. Имя класса или шаблона класса уже находится в области видимости в списке базовых классов:
// имя 'S' сразу после появления, // чтобы его можно было использовать в списке базовых классов структура S: std :: enable_shared_from_this{ };
Местоположение спецификатора перечисления или объявления непрозрачного перечисления находится сразу после идентификатора, который называет перечисление:
enum E: int {// E уже находится в области видимости
A = sizeof (E)
}; Местоположение псевдонима типа или объявления шаблона псевдонима находится сразу после идентификатора типа, на который ссылается псевдоним:
, используя T = int; // точка объявления T находится в точке с запятой
{
используя T = T *; // то же, что и T = int *
} Место для декларатора в объявлении using, которое не называет конструктор, находится сразу после декларатора:
шаблонclass base { защищено: статическая константа int next = N + 1; static const int value = N; }; производная структура: основание <0>, основание <1>, основание <2> { using base <0> :: next, // next теперь в области видимости base :: value; // производное :: значение равно 1 };
Местоположение перечислителя находится сразу после его определения (не перед инициализатором, как для переменных):
const int x = 12;
{
enum {x = x + 1, // точка объявления находится в запятой, x инициализируется значением 13
y = x + 1 // перечислитель x теперь в области видимости, y инициализируется значением 14
};
} Локус для введенного-имени-класса следует сразу за открывающей фигурной скобкой в определении его класса (или шаблона класса):
шаблонstruct Array //: std :: enable_shared_from_this // Ошибка: имя внедренного класса не входит в область видимости : std :: enable_shared_from_this > // ОК: массив имени шаблона находится в области видимости {// массив имени внедренного класса теперь находится в области видимости, как если бы имя открытого члена Массив * p; // указатель на массив };
Местоположение неявного объявления для локальной предопределенной переменной __func__ находится непосредственно перед телом функции определения функции. | (начиная с C ++ 11) |
Местоположение объявления структурированной привязки находится сразу после списка идентификаторов, но инициализаторам структурированной привязки запрещено ссылаться на любое из вводимых имен. | (начиная с C ++ 17) |
Локус для переменной или структурированных привязок (начиная с C ++ 17), объявленных в range_declaration оператора for на основе диапазона, находится сразу после выражения range_expression: std :: vector | (начиная с C ++ 11) |
Локус для параметра шаблона находится сразу после его полного параметра шаблона (включая необязательный аргумент по умолчанию):
typedef unsigned char T;
шаблон <класс T
= T // поиск находит имя typedef беззнакового символа
, T // поиск находит параметр шаблона
N = 0> структура A {}; Место определения понятия находится сразу после имени понятия, но в определениях понятий запрещается ссылаться на вводимое имя понятия. | (начиная с C ++ 20) |
Локус определения именованного пространства имен находится сразу после имени пространства имен.
[править] Ссылки
- Стандарт C ++ 17 (ISO / IEC 14882: 2017):
- Стандарт C ++ 14 (ISO / IEC 14882: 2014):
- Стандарт C ++ 11 (ISO / IEC 14882: 2011):
- Стандарт C ++ 98 (ISO / IEC 14882: 1998):
- 3.3 Декларативные области и области [basic.scope]
[править] См. Также
об областях применения - PowerShell | Документы Microsoft
- 16 минут для чтения
В этой статье
Краткое описание
Объясняет концепцию области в PowerShell и показывает, как устанавливать и изменять объем элементов.
Длинное описание
PowerShell защищает доступ к переменным, псевдонимам, функциям и PowerShell дисков (PSDrives), ограничивая места их чтения и изменения. PowerShell использует правила области действия, чтобы гарантировать, что вы случайно не измените элемент, который не следует менять.
Ниже приведены основные правила области применения:
Области могут быть вложенными. Внешняя область видимости называется родительской. Любые вложенные области - это дочерние области этого родителя.
Элемент виден в области, в которой он был создан, и в любом дочернем элементе области, если вы явно не сделаете его закрытым. Вы можете размещать переменные, псевдонимы, функции или диски PowerShell в одной или нескольких областях.
Элемент, созданный вами в области действия, может быть изменен только в области действия в который был создан, если вы явно не укажете другую область.
Если вы создаете элемент в области действия, и этот элемент разделяет свое имя с элементом в другой объем, исходный элемент может быть скрыт под новым элементом, но он не отменяется и не изменяется.
Области действия PowerShell
PowerShell поддерживает следующие области:
Global: область действия, которая действует при запуске PowerShell или при создании новый сеанс или пространство выполнения. Переменные и функции, которые присутствуют при Запуск PowerShell был создан в глобальной области, такой как автоматический переменные и переменные предпочтений. Переменные, псевдонимы и функции в ваши профили PowerShell также создаются в глобальной области. Глобальный scope - это корневая родительская область в сеансе.
Локальный: текущий объем. Локальная область видимости может быть глобальной или любой другой. другой объем.
Сценарий: область, которая создается во время выполнения файла сценария. Только команды в сценарии, запущенном в области сценария. К командам в сценарии область действия сценария - это локальная область.
Примечание
Частный не является областью действия. Это вариант, который меняет видимость элемента за пределами области, в которой этот элемент определен.
Родительские и дочерние области
Вы можете создать новую дочернюю область, вызвав сценарий или функцию. Вызов scope - это родительская область. Вызываемый скрипт или функция является дочерней областью. Вызываемые вами функции или скрипты могут вызывать другие функции, создавая иерархия дочерних областей видимости, корневой областью которой является глобальная область.
Если вы явно не сделаете элементы закрытыми, элементы в родительской области доступны для дочерней области. Однако элементы, которые вы создаете и изменяете в дочерняя область не влияет на родительскую область, если вы явно не укажете объем при создании предметов.
Примечание
Функции модуля не выполняются в дочерней области вызывающей области. У модулей есть собственное состояние сеанса, связанное с глобальной областью видимости. Весь код модуля выполняется в специфичной для модуля иерархии областей видимости, которая имеет свои собственная корневая область видимости.
Наследование
Дочерняя область не наследует переменные, псевдонимы и функции из родительская область. Если элемент не является частным, дочерняя область может просматривать элементы в родительская область. И он может изменить элементы, явно указав родительская область, но элементы не являются частью дочерней области.
Однако дочерняя область создается с набором элементов. Обычно в него входят все псевдонимы, у которых есть опция AllScope . Этот вариант обсуждается позже в этой статье. Он включает в себя все переменные, которые есть у AllScope вариант плюс несколько автоматических переменных.
Чтобы найти элементы в определенной области, используйте параметр Scope в Get-Variable или Get-Alias .
Например, чтобы получить все переменные в локальной области, введите:
Get-Variable -Scope local
Чтобы получить все переменные в глобальной области, введите:
Get-Variable -Scope global
Модификаторы прицела
Имя переменной, псевдонима или функции может включать любое из следующих необязательные модификаторы области действия:
global:- указывает, что имя существует в области Global .local:- указывает, что имя существует в области Local . Электрический ток областью всегда является область Local .private:- указывает, что имя - Private и отображается только для текущий объем.сценарий:- указывает, что имя существует в области сценария . Script область видимости ближайшего родительского файла сценария или Global , если нет файла сценария ближайшего предка.using:- Используется для доступа к переменным, определенным в другой области во время работы сценарии с помощью командлетов, таких какStart-JobиInvoke-Command.рабочий процесс:- указывает, что имя существует в рабочем процессе. Примечание: Рабочие процессы не поддерживаются в PowerShell Core.<пространство имен переменных>- модификатор, созданный поставщиком PowerShell PSDrive. Например:Пространство имен Описание Псевдоним:Псевдонимы, определенные в текущей области Env:Переменные среды, определенные в текущей области Функция:Функции, определенные в текущей области Переменная:Переменные, определенные в текущей области
Область по умолчанию для сценариев - это область сценария.Область действия по умолчанию для функции и псевдонимы - это локальная область видимости, даже если они определены в сценарий.
Использование модификаторов области видимости
Чтобы указать область действия новой переменной, псевдонима или функции, используйте область видимости. модификатор.
Синтаксис модификатора области в переменной:
$ [<модификатор области>:] <имя> = <значение>
Синтаксис модификатора области в функции:
функция [<модификатор-области>:] <имя> {<тело-функции>}
Следующая команда, которая не использует модификатор области видимости, создает переменную в текущем или местном масштабе :
$ a = "один"
Чтобы создать такую же переменную в глобальной области , используйте область global: модификатор:
$ global: a = "one"
Чтобы создать такую же переменную в области сценария , используйте сценарий : область модификатор:
$ скрипт: a = "one"
Вы также можете использовать модификатор области с функциями.Следующая функция Определение создает функцию в глобальной области :
function global: Hello {
Write-Host "Hello, World"
}
Вы также можете использовать модификаторы области для ссылки на переменную в другой области.
Следующая команда относится к переменной $ test , первой в локальной области.
а затем в глобальном масштабе:
$ тест
$ global: test
The
Использование: модификатор области действия Использование - это специальный модификатор области видимости, который идентифицирует локальную переменную в удаленном команда.Без модификатора PowerShell ожидает переменные в удаленных командах быть определенным в удаленном сеансе.
Модификатор области Использование представлен в PowerShell 3.0.
Для любого сценария или команды, которые выполняются вне сеанса, вам понадобится Использование модификатор области видимости для встраивания значений переменных из области видимости вызывающего сеанса, чтобы
вне сеансового кода может получить к ним доступ. Модификатор области с использованием поддерживается в
следующие контексты:
- Удаленно выполняемые команды, запускаемые с помощью
Invoke-Commandс использованием ComputerName , HostName , SSHConnection или Параметры сеанса (удаленный сеанс) - Фоновые задания, запущенные с
Start-Job(внепроцессный сеанс) - потоковых заданий, запускаемых через
Start-ThreadJobилиForEach-Object -Parallel(отдельный сеанс потока)
В зависимости от контекста значения встроенных переменных являются независимыми. копии данных в вызывающей области или ссылки на нее.В удаленных и внепроцессные сеансы, они всегда являются независимыми копиями.
Для получения дополнительной информации см. About_Remote_Variables.
В сеансах потоков они передаются по ссылке. Это означает, что можно изменить переменные области вызова в другом потоке. Для безопасного изменения переменных требуется синхронизация потоков.
Для получения дополнительной информации см .:
Сериализация значений переменных
Удаленно выполняемые команды и фоновые задания выполняются вне процесса.Внепроцессные сеансы используют сериализацию и десериализацию на основе XML для создания значения переменных, доступные через границы процесса. В процесс сериализации преобразует объекты в PSObject , который содержит исходные свойства объекта, но не его методы.
Для ограниченного набора типов десериализация восстанавливает объекты обратно в оригинальный тип. Регидратированный объект - это копия исходного экземпляра объекта. Он имеет свойства типа и методы. Для простых типов, таких как Система .Версия , копия точная. Для сложных типов копия несовершенный. Например, объекты регидратированного сертификата не включают закрытый ключ.
Экземпляры всех остальных типов - это экземпляры PSObject . PSTypeNames свойство содержит исходное имя типа с префиксом Deserialized , для например, Deserialized.System.Data.DataTable
Опция AllScope
Переменные и псевдонимы имеют свойство Option , которое может принимать значение AllScope .Элементы, имеющие свойство AllScope , становятся частью любого дочернего элемента. области, которые вы создаете, хотя они не наследуются задним числом родительскими объемы.
Элемент, имеющий свойство AllScope , отображается в дочерней области и это часть этой области. Изменения элемента в любом объеме влияют на все области, в которых определена переменная.
Управляющий объем
Некоторые командлеты имеют параметр Scope , который позволяет получить или установить (создать и изменить) элементы в определенной области.Используйте следующую команду, чтобы найти все командлеты в сеансе с параметром Scope :
Get-Help * -Объем параметров
Чтобы найти переменные, которые видны в определенной области, используйте Scope параметр Get-Variable . Видимые переменные включают глобальные переменные,
переменные в родительской области и переменные в текущей области.
Например, следующая команда получает переменные, которые видны в локальный охват:
Get-Variable -Scope local
Чтобы создать переменную в определенной области, используйте модификатор области действия или Область действия параметр Set-Variable .Следующая команда создает переменную
в мировом масштабе:
New-Variable -Scope global -Name a -Value "One"
Вы также можете использовать параметр Scope для New-Alias , Set-Alias или Get-Alias командлеты для указания области. Следующая команда создает
псевдоним в глобальной области видимости:
New-Alias -Scope global -Name np -Value Notepad.exe
Чтобы получить функции в определенной области, используйте командлет Get-Item , когда вы
входят в сферу охвата.Командлет Get-Item не имеет параметра Scope .
Примечание
Для командлетов, использующих параметр Scope , вы также можете обратиться к прицелы по номеру. Число описывает относительное положение одного прицела относительно Другой. Область 0 представляет текущую или локальную область. Область 1 указывает непосредственная родительская область. Область 2 указывает на родительскую область родительской области, и так далее. Пронумерованные области полезны, если вы создали много рекурсивных объемы.
Использование нотации источника с осциллографом
Скрипты и функции подчиняются всем правилам области видимости. Вы создаете их в определенная область, и они влияют только на эту область, если вы не используете командлет параметр или модификатор области, чтобы изменить эту область.
Но вы можете добавить скрипт или функцию в текущую область, используя точечный источник обозначение. Затем, когда скрипт запускается в текущей области, любые функции, псевдонимы и переменные, которые создает скрипт, доступны в текущем сфера.
Чтобы добавить функцию в текущую область, введите точку (.) И пробел перед путь и имя функции в вызове функции.
Например, чтобы запустить сценарий Sample.ps1 из каталога C: \ Scripts в область сценария (по умолчанию для сценариев), используйте следующую команду:
c: \ scripts \ sample.ps1
Чтобы запустить сценарий Sample.ps1 в локальной области, используйте следующую команду:
. c: \ scripts.sample.ps1
Когда вы используете оператор вызова (&) для запуска функции или скрипта, это не добавлен в текущую область.В следующем примере используется оператор вызова:
& c: \ scripts.sample.ps1
Подробнее об операторе вызова можно прочитать в about_operators.
Любые псевдонимы, функции или переменные, создаваемые скриптом Sample.ps1, являются недоступно в текущей области.
Ограничение без ограничения
Некоторые концепции PowerShell похожи на область действия или взаимодействуют с областью действия. Эти концепции могут быть перепутаны с областью действия или поведением области действия.
Сеансы, модули и вложенные приглашения являются автономными средами, но они не являются дочерними областями глобальной области в сеансе.
Сессий
Сеанс - это среда, в которой работает PowerShell. Когда вы создаете сеанс на удаленном компьютере PowerShell устанавливает постоянное соединение с удаленный компьютер. Постоянное соединение позволяет использовать сеанс для несколько связанных команд.
Поскольку сеанс является изолированной средой, у него есть собственная область действия, но session не является дочерней областью сеанса, в котором он был создан. В сеанс начинается с его собственной глобальной области видимости. Этот объем не зависит от глобальная область видимости сеанса.Вы можете создавать дочерние области в сеансе. Для Например, вы можете запустить сценарий для создания дочерней области в сеансе.
Модули
Вы можете использовать модуль PowerShell для совместного использования и доставки инструментов PowerShell. Модуль это блок, который может содержать командлеты, скрипты, функции, переменные, псевдонимы и другие полезные предметы. Если явно не указано иное, элементы в модуле не доступны вне модуля. Таким образом, вы можете добавить модуль в свой сеанс и использовать общедоступные элементы, не беспокоясь о том, что другие элементы могут переопределить командлеты, сценарии, функции и другие элементы вашего сеанса.
По умолчанию модули загружаются на верхний уровень текущего сеанса состояние , а не текущая область . Текущее состояние сеанса может быть модулем
состояние сеанса или глобальное состояние сеанса. Добавление модуля в сеанс делает
не менять масштаб. Если вы находитесь в глобальной области видимости, то модули загружаются
в состояние глобального сеанса. Любой экспорт помещается в глобальные таблицы.
Если вы загружаете module2 из в module1, module2 загружается в сеанс
состояние module1, а не глобальное состояние сеанса.Любой экспорт из module2
помещается в верхнюю часть состояния сеанса module1. Если вы используете Import-Module -Scope local , затем экспорт помещается в текущий
объект области, а не на верхнем уровне. Если вы в модуле и используете Import-Module -Scope global (или Import-Module -Global ) для загрузки другого
модуль, этот модуль и его экспорт загружаются в глобальное состояние сеанса
вместо локального состояния сеанса модуля. Эта функция была разработана для
написание модуля, управляющего модулями.Модуль WindowsCompatibility делает это для импорта модулей прокси в состояние глобального сеанса.
В состоянии сеанса модули имеют свою собственную область действия. Рассмотрим следующие
модуль C: \ temp \ mod1.psm1 :
$ a = "Привет"
function foo {
"` $ a = $ a "
"` $ global: a = $ global: a "
}
Теперь мы создаем глобальную переменную $ a , присваиваем ей значение и вызываем функцию foo .
$ a = "До свидания"
фу
Модуль объявляет переменную $ a в области видимости модуля, затем функцию foo выводит значение переменной в обеих областях.
$ a = Здравствуйте
$ global: a = До свидания
Вложенные запросы
Вложенные подсказки не имеют собственной области действия. Когда вы входите во вложенный приглашение, вложенное приглашение является подмножеством среды. Но ты остаешься в пределах местного масштаба.
У скриптов есть своя область действия. Если вы отлаживаете сценарий и достигли точка останова в сценарии, вы вводите область действия сценария.
Частный вариант
Псевдонимы и переменные имеют свойство Option , которое может принимать значение Рядовой .Элементы с опцией Private можно просматривать и изменять. в том объеме, в котором они созданы, но их нельзя просмотреть или изменить за пределами этой области.
Например, если вы создаете переменную с частной опцией в глобальном
области, а затем запустить сценарий, команды Get-Variable в сценарии не
отобразить частную переменную. Использование модификатора глобальной области видимости в этом случае
не отображает частную переменную.
Вы можете использовать параметр Option в New-Variable , Set-Variable ,
Командлеты New-Alias и Set-Alias для установки значения свойства Option на
Частный.
Видимость
Свойство Visibility переменной или псевдонима определяет, можете ли вы увидеть элемент вне контейнера, в котором он был создан. Контейнер мог быть модулем, скриптом или оснасткой. Видимость предназначена для контейнеров в так же, как значение Private свойства Option предназначено для объемы.
Свойство Visibility принимает значения Public и Private .Предметы которые имеют частную видимость, могут быть просмотрены и изменены только в контейнере в которые они были созданы. Если контейнер добавлен или импортирован, элементы, которые имеют частную видимость, не могут быть просмотрены или изменены.
Поскольку видимость предназначена для контейнеров, она работает по-другому в области видимости.
- Если вы создаете элемент, который имеет частную видимость в глобальной области, вы не может просматривать или изменять элемент в любой области.
- Если вы попытаетесь просмотреть или изменить значение переменной, имеющей частный видимость, PowerShell возвращает сообщение об ошибке.
Для создания переменной можно использовать командлеты New-Variable и Set-Variable .
который имеет частную видимость.
Примеры
Пример 1. Изменение значения переменной только в скрипте
Следующая команда изменяет значение переменной $ ConfirmPreference в
скрипт. Изменение не влияет на глобальную область видимости.
Во-первых, чтобы отобразить значение переменной $ ConfirmPreference в локальном
области, используйте следующую команду:
PS> $ ConfirmPreference
Высокая
Создайте область действия.ps1 скрипт, содержащий следующие команды:
$ ConfirmPreference = "Низкий"
«Значение $ ConfirmPreference равно $ ConfirmPreference».
Запустите сценарий. Скрипт меняет значение $ ConfirmPreference переменная, а затем сообщает ее значение в области сценария. Результат должен
напоминать следующий вывод:
Значение $ ConfirmPreference низкое.
Затем проверьте текущее значение переменной $ ConfirmPreference в текущем
сфера.
PS> $ ConfirmPreference
Высокая
В этом примере показано, что изменяется значение переменной в области сценария. не влияет на значение переменной в родительской области.
Пример 2. Просмотр значения переменной в разных областях
Вы можете использовать модификаторы области видимости для просмотра значения переменной в локальной области видимости. и в родительской области.
Сначала определите переменную $ test в глобальной области видимости.
$ test = "Global"
Затем создайте образец.ps1, который определяет переменную $ test . в
скрипт используйте модификатор области для ссылки на глобальную или локальную версию
переменной $ test .
в Sample.ps1:
$ test = "Локально"
"Локальное значение $ test равно $ test."
"Глобальное значение` $ test равно $ global: test ".
При запуске Sample.ps1 вывод должен напоминать следующий вывод:
Локальное значение $ test - Local.
Глобальное значение $ test - Global. Когда сценарий завершен, только глобальное значение $ test определяется в
сеанс.
PS> $ test
Глобальный
Пример 3. Изменение значения переменной в родительской области
Если вы не защитите элемент с помощью параметра "Личное" или другого метода, вы может просматривать и изменять значение переменной в родительской области.
Сначала определите переменную $ test в глобальной области видимости.
$ test = "Global"
Затем создайте образец.ps1, который определяет переменную $ test . в
скрипт используйте модификатор области для ссылки на глобальную или локальную версию
переменной $ test .
в Sample.ps1:
$ global: test = "Local"
"Глобальное значение` $ test равно $ global: test ".
По завершении сценария глобальное значение $ test изменяется.
PS> $ test
Местный
Пример 4: Создание частной переменной
Частная переменная - это переменная, имеющая свойство Option , которое имеет стоимость Частный . Частные переменные наследуются дочерней областью, но их можно просматривать или изменять только в том объеме, в котором они были созданы.
Следующая команда создает частную переменную с именем $ ptest в локальном
сфера.
New-Variable -Name ptest -Value 1 -Option private
Вы можете отображать и изменять значение $ ptest в локальной области.
PS> $ ptest
1
PS> $ ptest = 2
PS> $ ptest
2
Затем создайте образец.ps1, содержащий следующие команды. В
Команда пытается отобразить и изменить значение $ ptest .
в Sample.ps1:
"Значение $ Ptest равно $ Ptest."
«Значение $ Ptest равно $ global: Ptest».
Переменная $ ptest не отображается в области сценария, вывод
пустой.
"Значение $ Ptest равно."
"Значение $ Ptest равно."
Пример 5: Использование локальной переменной в удаленной команде
Для переменных в удаленной команде, созданной в локальном сеансе, используйте Использование модификатор области видимости.PowerShell предполагает, что переменные в удаленных командах были
создан в удаленном сеансе.
Синтаксис:
$ Использование:
Например, следующие команды создают переменную $ Cred в локальном
сеанс, а затем используйте переменную $ Cred в удаленной команде:
$ Кредит = Get-Credential
Invoke-Command $ s {Remove-Item. \ Test * .ps1 -Credential $ Using: Cred}
Область использования была представлена в PowerShell 3.0. В PowerShell 2.0 для указать, что переменная была создана в локальном сеансе, используйте следующие формат команды.
$ Кредит = Get-Credential
Invoke-Command $ s {
параметр ($ c)
Remove-Item. \ Test * .ps1 -Credential $ c
} -ArgumentList $ Cred
См. Также
about_Variables
about_Environment_Variables
about_Functions
about_Script_Blocks
Начало-ThreadJob
Вложенная функция, объем переменных и замыканий в Python
В этом посте сначала представлены вложенные функции, а затем различные области применения переменных, такие как глобальные переменные, локальные переменные в функциях и т. Д.и, наконец, замыкания с использованием вложенной функции в Python.
Вы можете узнать о функциях Python из нашего курса Python и из этого поста.
Вложенная функция
Подобно вложенным циклам, у нас могут быть вложенные функции в Python. Мы просто создаем функцию, используя def внутри другой функции, чтобы вложить две функции. Например,
def f1 (): #outer функция
print ("Привет")
def f2 (): # внутренняя функция
print ("мир")
f2 ()
f1 ()
Выход
Привет
мир
def f1 (): #outer функция
x = 1 # переменная, определенная в функции f1
def f2 (a): # внутренняя функция
print (a + x) # позволяет получить доступ к переменной внешней функции
f2 (2)
f1 ()
Выход
3
Это кажется довольно простым.Вы можете видеть, что мы также получили доступ к переменным внешней функции из внутренней функции. Итак, попробуем поменять переменные внешней функции на внутреннюю.
def f1 (): #outer функция
x = 1 # переменная, определенная во внешней функции
def f2 (a): # внутренняя функция
# создаст новую переменную во внутренней функции
# вместо изменения значения x внешней функции
х = 4
печать (а + х)
print (x) # выводит значение x внешней функции
f2 (2)
f1 ()
Выход
1
6
Из двух приведенных выше примеров вы можете видеть, что мы можем распечатать переменные внешней функции из внутренней, но не можем ее изменить. x = 4 создал новую переменную с именем «x» внутри функции f2 вместо изменения значения переменной «x» функции f1. Поэтому, прежде чем перейти к дальнейшим обсуждениям вложенных функций, давайте сначала узнаем об объеме переменных в Python, то есть о том, где находятся переменные и откуда мы можем получить к ним доступ.
Объем переменных
Место, где мы можем найти переменную, а также при необходимости получить к ней доступ, называется областью действия переменной. Итак, давайте узнаем, что это за прицелы.
Локальные и глобальные переменные
Переменная в функции в Python является локальной переменной, если она не объявлена как что-то еще. Доступ к локальной переменной можно получить только локально, т.е. переменная, определенная внутри функции, доступна только для этой функции и не может использоваться вне функции.
def f1 ():
а = 5
f1 ()
#a недоступен вне функции f1
print (a) # выдаст ошибку
Выход
Отслеживание (последний вызов последний):
Файл "a.py ", строка 5, в
print x # выдаст ошибку
NameError: имя 'x' не определено
Вы можете видеть, что переменная 'a', созданная внутри функции, является локальной переменной и недоступна вне функции.
Кроме того, мы можем получить доступ из функции к переменным, которые определены вне этой функции, но не можем их изменять.
а = 5
def f1 ():
print (a) # напечатает 5
f1 ()
Выход
5
Мы можем вывести глобальную переменную 'a'.Сначала Python искал переменную с именем «a» внутри функции, а когда она не была найдена, он просматривал глобальную область видимости и печатал глобальное значение «a».
а = 1
def f1 ():
а = 5
print (a) # напечатает 5
print (a) # напечатает 1
f1 ()
Выход
1
5
Вы можете видеть, что объявление a = 5 создает новую локальную переменную внутри функции вместо изменения существующей глобальной переменной 'a'.Это связано с тем, что Python предполагает, что переменная является локальной, если она явно не объявлена глобальной.
Чтобы сообщить Python, что мы хотим использовать глобальную переменную внутри функции, нам нужно использовать ключевое слово global . Пример приведен ниже.
а = 1
def f1 ():
global a # using глобальная переменная a
a = 5 # глобальная переменная изменена на 5
print (a) # напечатает 5
f1 ()
print (a) # напечатает 5
Выход
5
5
Обратите внимание, что в отличие от других языков, таких как C, Python не имеет отдельной области видимости для циклов, if / else и т. Д.Таким образом, изменение переменных внутри цикла также изменит глобальную переменную.
а = 1
если правда:
а = 2
печать (а)
Выход
2
а = 1
для i в диапазоне (1,10):
а = я
печать (а)
Выход
9
После понимания глобальных и локальных переменных, давайте углубимся в область видимости переменных во вложенных функциях.
Объем переменных во вложенной функции
Мы уже знаем, как получить доступ к глобальной переменной из функции.
В этом разделе мы узнаем о доступе и изменении переменных внешней функции из внутренней. Итак, сначала попробуем вывести переменную внешней функции из внутренней.
def f1 (): #outer функция
а = 1
def f2 (): # внутренняя функция
print (a) # напечатает 1
f2 ()
f1 ()
Выход
1
Как видите, мы можем распечатать переменную внешней функции. Это похоже на печать глобальной переменной из функции.
Попробуем изменить значение переменной внешней функции.
def f1 (): #outer функция
а = 1
def f2 (): #outer функция
а = 2
print (а) # отпечатки 2
f2 ()
print (а) # отпечатки 1
f1 ()
Выход
2
1
Как видите, мы не можем изменить значение переменной внешней функции из внутренней. a = 2 создал новую локальную переменную функции f2 вместо изменения значения 'a' из функции f1.
Есть разные способы изменить значение локальной переменной внешней функции из внутренней функции. Первый способ - использовать итерацию.
def f1 (): #outer функция
а = [1]
def f2 (): #outer функция
а [0] = 2
print (a [0]) # отпечатки 2
f2 ()
print (a [0]) # отпечатки 2
f1 ()
Выход
2
2
Мы также можем изменить значение переменной, как показано в следующем примере.
def f1 (): #outer функция
f1.а = 1
def f2 (): #outer функция
f1.a = 2
print (f1.a) # отпечатки 2
f2 ()
print (f1.a) # отпечатки 2
f1 ()
Выход
2
2
Третий способ - использовать ключевое слово nonlocal. Обратите внимание, что ключевое слово nonlocal работает только с Python3. Вы можете использовать любой из двух способов, упомянутых выше, чтобы изменить значение переменной в Python2.
Мы можем использовать ключевое слово nonlocal для изменения значения переменной внешней функции аналогично использованию ключевого слова global для изменения значения глобальных переменных.
def f1 (): #outer функция
а = 1
def f2 (): #outer функция
нелокальный
а = 2
print (а) # отпечатки 2
f2 ()
print (а) # отпечатки 2
f1 ()
Выход
2
2
Когда вы разобрались с концепциями областей действия переменных, давайте узнаем о замыканиях в Python.
Закрытие
Замыкание - это, по сути, запись функции в среде. Например, если мы вызываем функцию с аргументом (foo (1)), то она должна вести запись среды с этим аргументом, чтобы использовать ее позже в программе.Это будет видно из примеров, приведенных ниже.
def f1 (a):
def f2 (b):
вернуть a + b
вернуть f2
а = f1 (1)
б = f1 (100)
печать (a (2))
печать (b (2))
Выход
3
102
Вы можете видеть, что среда, созданная f1 (1), отличается от среды f1 (100), и обе они были запомнены Python, таким образом выводя разные значения для a (2) и b (2).




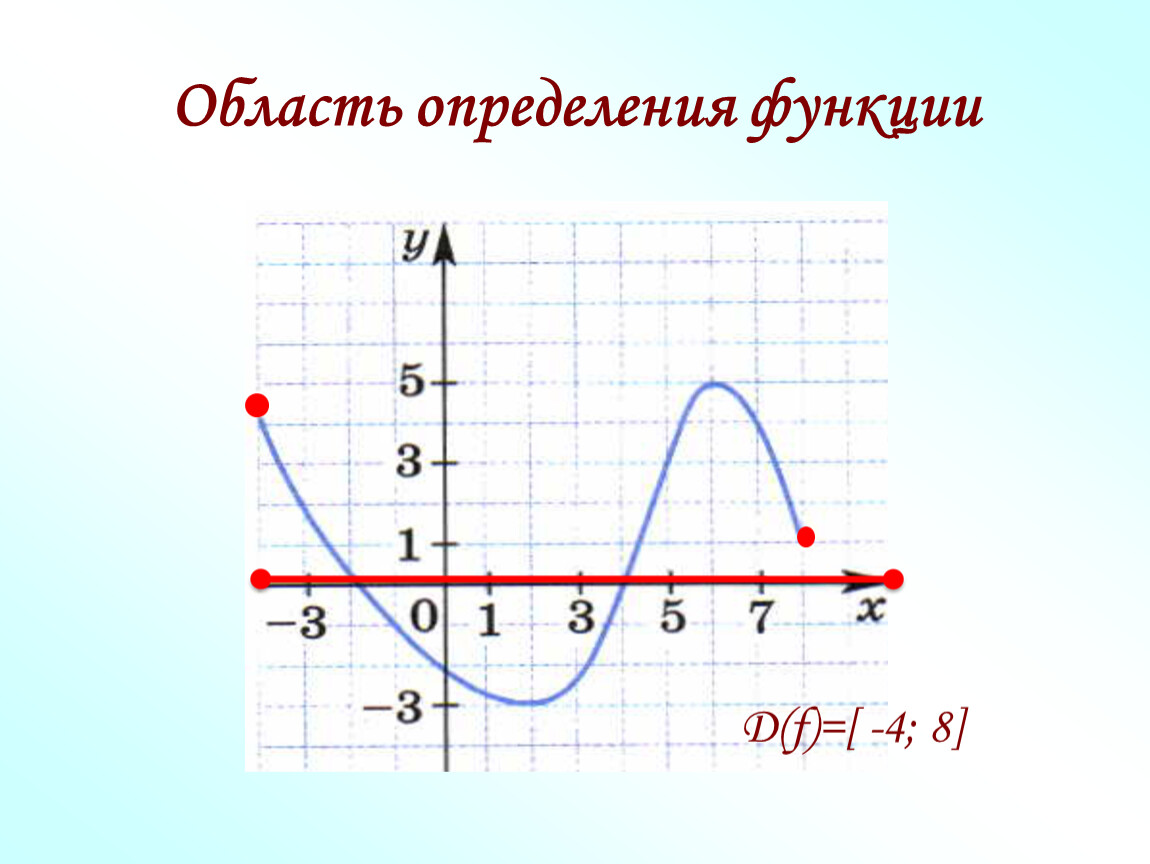 Задайте функцию зависимости расстояния (км) от между городом и поездом от времени (ч) движения поезда.
Задайте функцию зависимости расстояния (км) от между городом и поездом от времени (ч) движения поезда. Задайте функцию зависимости расстояния (км) между поездами от времени (ч) движения поездов.
Задайте функцию зависимости расстояния (км) между поездами от времени (ч) движения поездов.



 Еще одним примером периодической функции является прибаутка: «У попа была собака – он ее любил…» и т.п. Что такое периодичность? Периодичностью в обычной речи называют чуть ли не всякую повторяемость. Однако повторяемость может быть более или менее строгой, достаточно сравнить между собой приведенные тексты.
Еще одним примером периодической функции является прибаутка: «У попа была собака – он ее любил…» и т.п. Что такое периодичность? Периодичностью в обычной речи называют чуть ли не всякую повторяемость. Однако повторяемость может быть более или менее строгой, достаточно сравнить между собой приведенные тексты.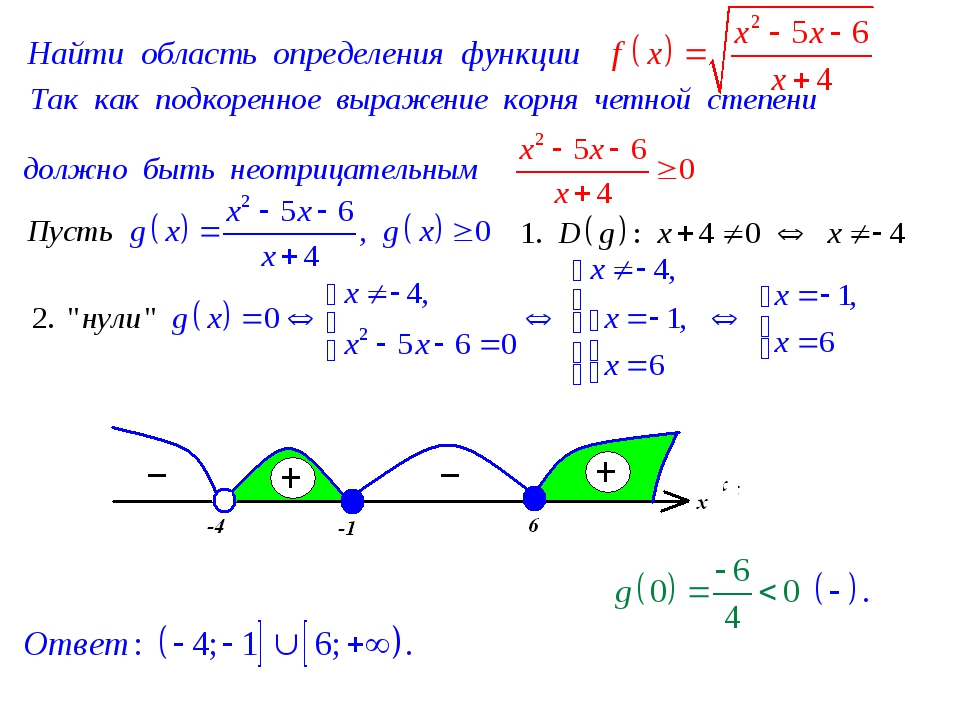
 — 1969.
— 1969. Н. Миднюк, И.Е. Феоктистов. – 8-е изд. – М. : Мнемозина, 2008.
Н. Миднюк, И.Е. Феоктистов. – 8-е изд. – М. : Мнемозина, 2008. Укажите область ее значений.
Укажите область ее значений.
 Д., Но в какой-то момент вам придется обновить приложение с библиотеки v1.0 до 2.0. Между тем, API для этой библиотеки изменился, и они переименовали какой-то класс, который вы используете. Что происходит? Не могу найти… в объеме. В этом сценарии важно помнить о своих предположениях — потому что вы собираетесь искать тот класс, который наверняка существовал в v1.0!
Д., Но в какой-то момент вам придется обновить приложение с библиотеки v1.0 до 2.0. Между тем, API для этой библиотеки изменился, и они переименовали какой-то класс, который вы используете. Что происходит? Не могу найти… в объеме. В этом сценарии важно помнить о своих предположениях — потому что вы собираетесь искать тот класс, который наверняка существовал в v1.0! log (GlobalVar)
log (GlobalVar)
 log (fnNestedVar) // здесь нет доступа
log (fnNestedVar) // здесь нет доступа log (localVar) // ok
log (localVar) // ok log (localVar) // ok
log (localVar) // ok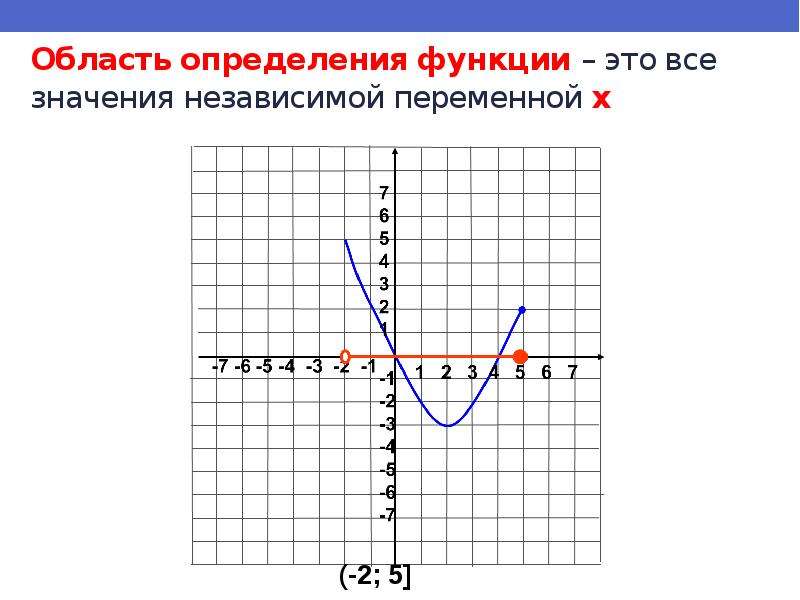 журнал (GlobalScope);
журнал (GlobalScope);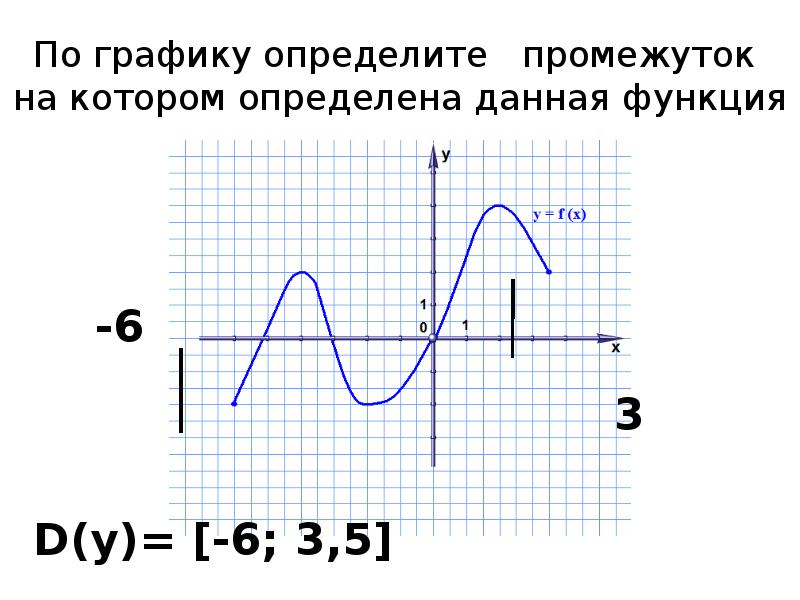 Эта область содержит имена, которые вы определяете во включающей функции. Имена в охватывающей области видны из кода внутренних и включающих функций.
Эта область содержит имена, которые вы определяете во включающей функции. Имена в охватывающей области видны из кода внутренних и включающих функций.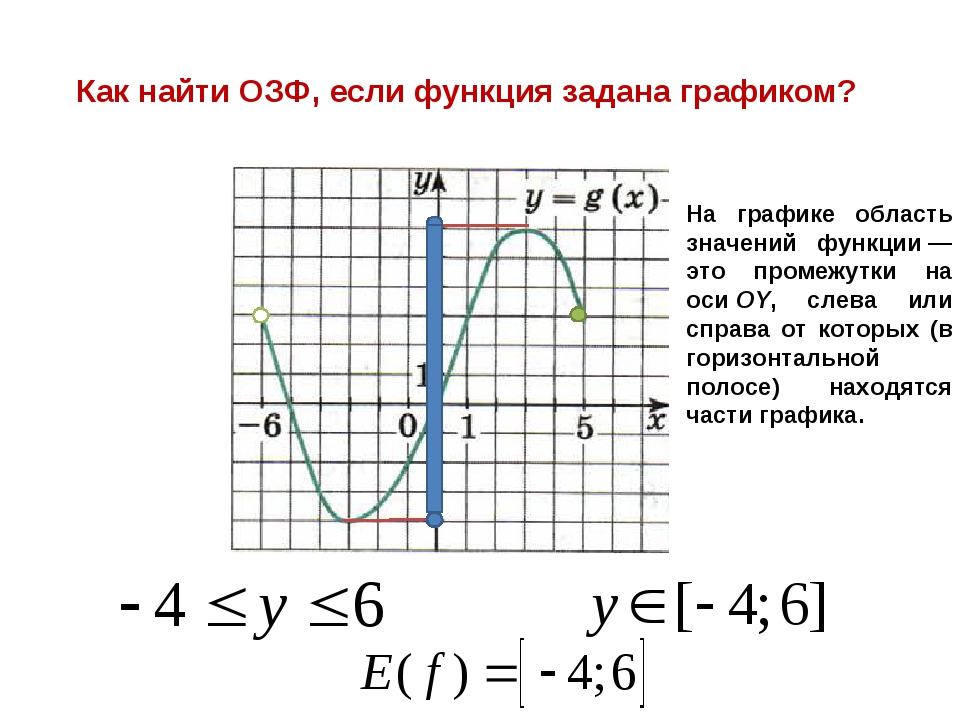 .. результат = база ** 2
... print (f'Квадрат {base}: {result} ')
...
>>> квадрат (10)
Квадрат 10 составляет: 100
>>> result # Недоступен извне square ()
Отслеживание (последний вызов последний):
Файл "
.. результат = база ** 2
... print (f'Квадрат {base}: {result} ')
...
>>> квадрат (10)
Квадрат 10 составляет: 100
>>> result # Недоступен извне square ()
Отслеживание (последний вызов последний):
Файл " . print (f "Печать переменной из inner_func (): {var}")
...
... inner_func ()
... print (f "Печать переменной из outer_func (): {var}")
...
>>> outer_func ()
Печать var из inner_func (): 100
Печать var из outer_func (): 100
>>> inner_func ()
Отслеживание (последний вызов последний):
Файл "
. print (f "Печать переменной из inner_func (): {var}")
...
... inner_func ()
... print (f "Печать переменной из outer_func (): {var}")
...
>>> outer_func ()
Печать var из inner_func (): 100
Печать var из outer_func (): 100
>>> inner_func ()
Отслеживание (последний вызов последний):
Файл "