Длина дуги окружности. Центральный угол окружности. Дуга большого круга.
В той статье мы узнаем что такое дуга окружности, центральный угол, измерение дуги окружности.
Дуга окружности
Дуга — это любая связанная часть окружности круга. На рисунке ниже часть окружности от \(M\) до \(N\) образует дугу. Она называется \(\smile\) \(MN\).
Дуга может быть малой дугой, полукругом или большой дугой. Полукруг — это дуга, равная половине круга. Малая дуга — это дуга, которая меньше полукруга. Большая дуга — это дуга, которая больше полукруга.
Центральный угол
Центральный угол — это угол, вершина которого находится в центре окружности. Например угол \(∠NAM\):
Дуга круга, угол
На приведенной выше диаграмме центральный угол для дуги \(MN\) равен \(45°\).
Сумма центральных углов в любой окружности равна \(360°\). Мера полуокружности равна \(180°\).
Мера малой дуги равна мере центрального угла, который перехватывает дугу. Можно также сказать, что мера малой дуги равна мере центрального угла, который подтягивается дугой. На диаграмме ниже мера дуги \(MN\) равна \(45°\):
Мера главной дуги равна \(360°\).
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
Геометрия. Урок 5. Окружность — ЁП
Содержание страницы:
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности.
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности (d=2R).
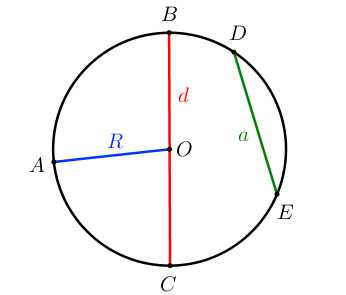
OA — радиус, DE — хорда, BC — диаметр.
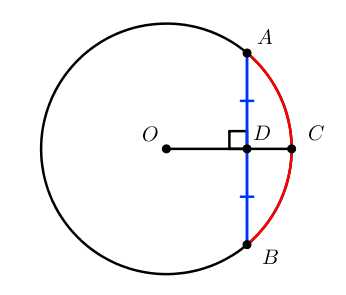
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
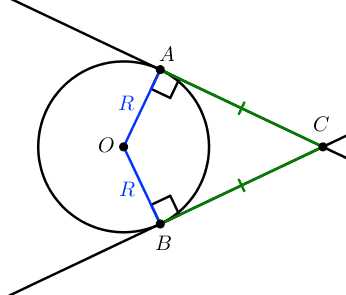
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Часть окружности, заключенная между двумя точками, называется дугой окружности.
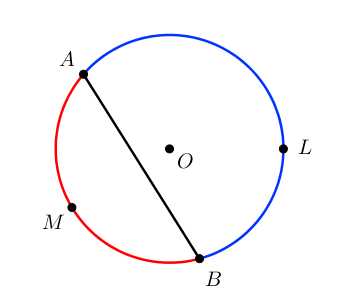
Например, хорда AB стягивает две дуги: ∪AMB и ∪ALB.
Теорема 4:
Равные хорды стягивают равные дуги.
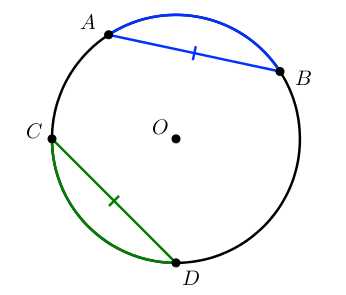
Если AB=CD, то ∪AB=∪CD
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠AOB — центральный.
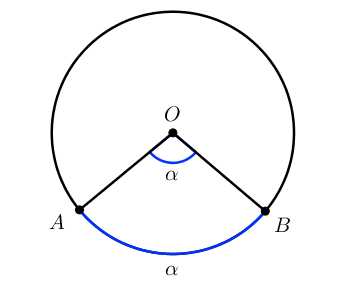
Центральный угол равен градусной мере дуги, на которую он опирается
. ∪AB=∠AOB=αЕсли провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360°.
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ACB — вписанный.
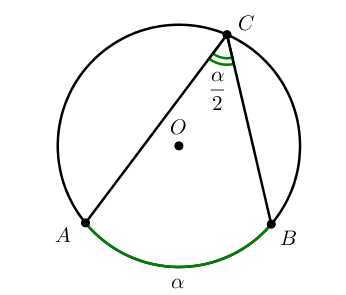
Вписанный угол равен половине градусной меры дуги, на которую он опирается. ∠ACB=∪AB2=α2∪AB=2⋅∠ACB=α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
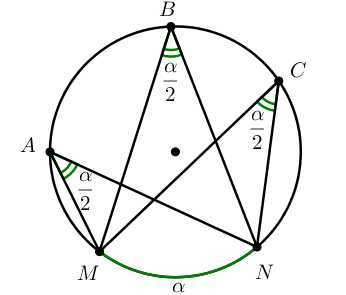
∠MAN=∠MBN=∠MCN=∪MN2=α2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен
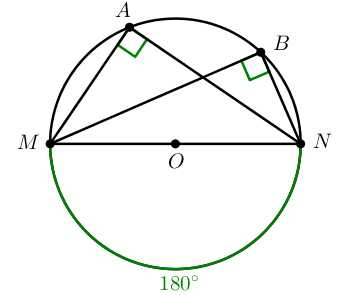
MN — диаметр.
∠MAN=∠MBN=∪MN2=180°2=90°
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги — это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α.
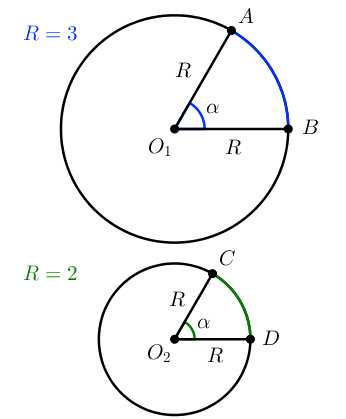
Градусная мера дуги ∪AB равна градусной мере дуги ∪CD и равна α.
∪AB=∪CD=α
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
l=2πR
Длина дуги окружности, на которую опирается центральный угол α равна:
lα=πR180∘⋅α
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг — часть пространства, которая находится внутри окружности.
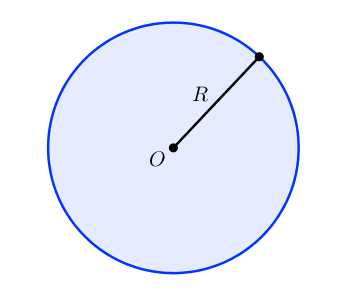
Иными словами, окружность — это граница, а круг — это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S=πR2
Сектор — это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
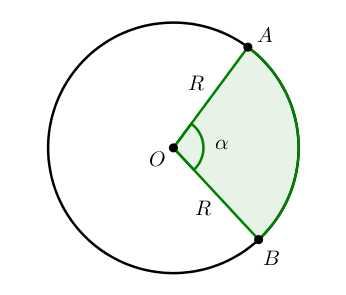
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: Sα=πR2360°⋅α
Сегмент — это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
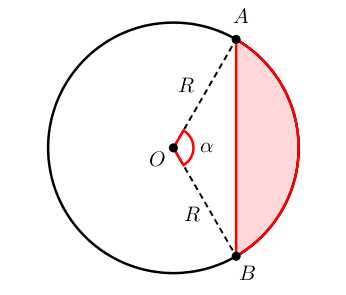
Примеры сектора в реальной жизни: мармелад «лимонная долька», лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S=πR2180°⋅α−12R2sinα
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
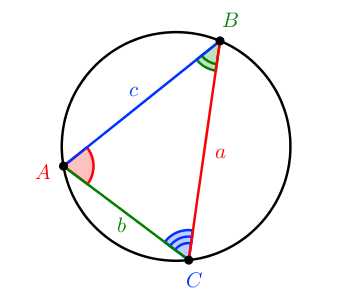
asin∠A=bsin∠B=csin∠C=2R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Модуль геометрия: задания, связанные с окружностями.
epmat.ru
дуга окружности — это… Что такое дуга окружности?
- дуга окружности
- arc of circle, circular arc
Большой англо-русский и русско-английский словарь. 2001.
- дуга меридиана
- дуга пантографа
Смотреть что такое «дуга окружности» в других словарях:
Дуга окружности — Дуга одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки A и B окружности разбивают ее на две части; каждая из этих частей называется дугой. Если A и B – концы диаметра (т … Википедия
дуга окружности — apskritimo lankas statusas T sritis fizika atitikmenys: angl. circular arc vok. Kreisbogen, m rus. дуга окружности, f pranc. arc de cercle, m … Fizikos terminų žodynas
Дуга — Дуга: В математике Дуга (геометрия) участок кривой между двумя её точками. Дуга окружности кривая линия, лежащая на окружности и ограниченная двумя точками. Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия
ДУГА — жен. согнутая линия, черта или вещь, образующая кривизну, погиб; часть окружности круга или другой кривой черты, и пр. элипса, параболы. | ·стар. и сев. радуга. | В оглобельной упряжи, деревянная, согнутая крутым лучком тугая распорка между… … Толковый словарь Даля
ДУГА НАБЛЮДЕНИЯ — наименьшее расстояние от Солнца, на котором планета видима, когда Солнце находится под горизонтом. Дневная дуга дуга, которую Солнце проходит от Восхода до Заката. В Равноденствие она составляет 180 градусов или 12 часов правого восхождения. С… … Астрологическая энциклопедия
дуга — и; мн. дуги; ж. 1. Часть окружности или какой л. другой кривой линии в виде полукруга. Ракета описала в небе дугу. Соединить дугой. // О том, что имеет форму кривой, изогнутой линии. Д. лука. Тёмные дуги бровей. Радуга дуга. На повороте река… … Энциклопедический словарь
ДУГА — ДУГА, дуги, мн. дуги, дугам, жен. 1. Принадлежность упряжи из круто изогнутого ствола тонкого дерева, концы которого вдеваются в гужи для скрепления оглобель с хомутом. «Дуги гнут с терпеньем и не вдруг.» Крылов. 2. Часть окружности круга или… … Толковый словарь Ушакова
Дуга — I ж. 1. Изогнутая часть какого либо предмета. 2. Часть окружности или какой либо изогнутой линии. отт. устар. Название линии меридиана или параллели. 3. Часть конской упряжи из тонкого, круто изогнутого ствола дерева, служащая для прикрепления… … Современный толковый словарь русского языка Ефремовой
ДУГА БОЛЬШОГО КРУГА — часть окружности, получаемой при сечении шара плоскостью, проходящей через его центр. Под термином прямое направление жел. дор. линии понимают направление по Д. б. к. между конечными или промежуточными опорными точками жел. дор. линии. Для целей… … Технический железнодорожный словарь
Дуга (геометрия) — Дуга связное подмножество окружности.Свойства*Длина дуги L радиуса R с центральным углом alpha, измеренным в радианах, вычисляется по формуле: L=Ralpha … Википедия
дуга — ДУГА, и, мн дуги, ж Линия в виде полукруга, часть кривой, изогнутой линии или окружности, заключенная между двумя ее точками. Ракета описала в небе дугу … Толковый словарь русских существительных
dic.academic.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Планиметрия
Вписанные и центральные углы
Определение 1. Центральным угломназывают угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Рис. 1
Определение 2. Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Рис. 2
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3. Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема |
| Вписанный угол | Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство | |
| Вписанный угол | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |
| Вписанный угол | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |
| Вписанный угол | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды | |
| Вписанный угол | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |
| Окружность, описанная около прямоугольного треугольника | Середина гипотенузы прямоугольного треугольника является центром описанной Посмотреть доказательство |
| Вписанный угол |
Теорема: Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство |
Теорема: Вписанные углы, опирающиеся на одну и ту же дугу равны. |
Теорема: Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды |
Теорема: Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды |
Теорема: Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр |
| Окружность, описанная около прямоугольного треугольника |
Теорема: Середина гипотенузы прямоугольного треугольника является центром описанной Посмотреть доказательство |
Теоремы об углах, образованных хордами, касательными и секущими
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами | Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство | ||
| Угол, образованный секущими, которые пересекаются вне круга | Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство | ||
| Угол, образованный касательной и хордой, проходящей через точку касания | Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство | ||
| Угол, образованный касательной и секущей | Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство | ||
| Угол, образованный двумя касательными к окружности | Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный пересекающимися хордами хордами |
| Формула: |
Теорема Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство |
| Угол, образованный секущими секущими, которые пересекаются вне круга |
| Формула: |
Теорема Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный касательной и хордой хордой, проходящей через точку касания |
| Формула: |
Теорема Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство |
| Угол, образованный касательной и секущей касательной и секущей |
| Формула: |
Теорема Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный двумя касательными касательными к окружности |
| Формулы: |
Теорема Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
Доказательства теорем об углах, связанных с окружностью
Теорема 1. Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Доказательство. Рассмотрим сначала вписанный угол ABC, сторона BC которого является диаметром окружности диаметром окружности, и центральный угол AOC (рис. 5).
Рис. 5
Так как отрезки AO и BO являются радиусами окружности радиусами окружности, то треугольник AOB – равнобедренный, и угол ABO равен углу OAB. Поскольку угол AOC является внешним углом треугольника AOB, то справедливы равенства
Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.
Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).
Рис. 6
В этом случае справедливы равенства

и теорема 1 в этом случае доказана.
Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).
Рис. 7
В этом случае справедливы равенства

что и завершает доказательство теоремы 1.
Теорема 2. Величина угла, образованного пересекающимися хордами хордами, равна половине суммы величин дуг, заключённых между его сторонами.
Доказательство. Рассмотрим рисунок 8.
Рис. 8
Нас интересует величина угла AED, образованного пересекающимися в точке E хордами AB и CD. Поскольку угол AED – внешний угол треугольника BED, а углы CDB и ABD являются вписанными углами, то справедливы равенства
что и требовалось доказать.
Теорема 3. Величина угла, образованного секущими секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство. Рассмотрим рисунок 9.
Рис. 9
Нас интересует величина угла BED, образованного пересекающимися в точке E секущими AB и CD. Поскольку угол ADC – внешний угол треугольника ADE, а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства
что и требовалось доказать.
Теорема 4. Величина угла, образованного касательной и хордой касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.
Доказательство. Рассмотрим рисунок 10.
Рис. 10
Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр, проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства
что и требовалось доказать
Теорема 5. Величина угла, образованного касательной и секущей касательной и секущей, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство. Рассмотрим рисунок 11.
Рис. 11
Нас интересует величина угла BED, образованного касательной AB и секущей CD. Заметим, что угол BDC – внешний угол треугольника DBE, а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB, в силу теоремы 4, равны. Поэтому справедливы равенства
что и требовалось доказать.
Теорема 6.Величина угла, образованного двумя касательными к окружности касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами.
Доказательство. Рассмотрим рисунок 12.
Рис. 12
Нас интересует величина угла BED, образованного касательными AB и CD. Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство
α = π – γ .
Далее получаем
что и требовалось доказать.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
дуга окружности — с русского на английский
См. также в других словарях:
Дуга окружности — Дуга одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки A и B окружности разбивают ее на две части; каждая из этих частей называется дугой. Если A и B – концы диаметра (т … Википедия
дуга окружности — apskritimo lankas statusas T sritis fizika atitikmenys: angl. circular arc vok. Kreisbogen, m rus. дуга окружности, f pranc. arc de cercle, m … Fizikos terminų žodynas
Дуга — Дуга: В математике Дуга (геометрия) участок кривой между двумя её точками. Дуга окружности кривая линия, лежащая на окружности и ограниченная двумя точками. Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия
ДУГА — жен. согнутая линия, черта или вещь, образующая кривизну, погиб; часть окружности круга или другой кривой черты, и пр. элипса, параболы. | ·стар. и сев. радуга. | В оглобельной упряжи, деревянная, согнутая крутым лучком тугая распорка между… … Толковый словарь Даля
ДУГА НАБЛЮДЕНИЯ — наименьшее расстояние от Солнца, на котором планета видима, когда Солнце находится под горизонтом. Дневная дуга дуга, которую Солнце проходит от Восхода до Заката. В Равноденствие она составляет 180 градусов или 12 часов правого восхождения. С… … Астрологическая энциклопедия
дуга — и; мн. дуги; ж. 1. Часть окружности или какой л. другой кривой линии в виде полукруга. Ракета описала в небе дугу. Соединить дугой. // О том, что имеет форму кривой, изогнутой линии. Д. лука. Тёмные дуги бровей. Радуга дуга. На повороте река… … Энциклопедический словарь
ДУГА — ДУГА, дуги, мн. дуги, дугам, жен. 1. Принадлежность упряжи из круто изогнутого ствола тонкого дерева, концы которого вдеваются в гужи для скрепления оглобель с хомутом. «Дуги гнут с терпеньем и не вдруг.» Крылов. 2. Часть окружности круга или… … Толковый словарь Ушакова
Дуга — I ж. 1. Изогнутая часть какого либо предмета. 2. Часть окружности или какой либо изогнутой линии. отт. устар. Название линии меридиана или параллели. 3. Часть конской упряжи из тонкого, круто изогнутого ствола дерева, служащая для прикрепления… … Современный толковый словарь русского языка Ефремовой
ДУГА БОЛЬШОГО КРУГА — часть окружности, получаемой при сечении шара плоскостью, проходящей через его центр. Под термином прямое направление жел. дор. линии понимают направление по Д. б. к. между конечными или промежуточными опорными точками жел. дор. линии. Для целей… … Технический железнодорожный словарь
Дуга (геометрия) — Дуга связное подмножество окружности.Свойства*Длина дуги L радиуса R с центральным углом alpha, измеренным в радианах, вычисляется по формуле: L=Ralpha … Википедия
дуга — ДУГА, и, мн дуги, ж Линия в виде полукруга, часть кривой, изогнутой линии или окружности, заключенная между двумя ее точками. Ракета описала в небе дугу … Толковый словарь русских существительных
translate.academic.ru
Значение словосочетания ДУГА ОКРУЖНОСТИ. Что такое ДУГА ОКРУЖНОСТИ?
- Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки A и B окружности разбивают её на две части; каждая из этих частей называется дугой. Если A и B – концы диаметра (т.е. центральный угол AOB развернутый), то они определяют две равные дуги, называемые полуокружностями. Если угол AOB не развернутый, то одна из двух дуг AB – это часть окружности, лежащая внутри угла AOB; говорят, что она меньше полуокружности, и что вторая дуга больше полуокружности. Их называют дополнительными. Дуги можно измерять в угловых единицах. Следует заметить, что равные по углам дуги необязательно равны по длине, равны только при равенстве радиусов окружностей.
Источник: Википедия
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: сматывать — это что-то нейтральное, положительное или отрицательное?
Положительное
Отрицательное
kartaslov.ru
Дуга окружности — с русского на все языки
См. также в других словарях:
Дуга окружности — Дуга одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки A и B окружности разбивают ее на две части; каждая из этих частей называется дугой. Если A и B – концы диаметра (т … Википедия
дуга окружности — apskritimo lankas statusas T sritis fizika atitikmenys: angl. circular arc vok. Kreisbogen, m rus. дуга окружности, f pranc. arc de cercle, m … Fizikos terminų žodynas
Дуга — Дуга: В математике Дуга (геометрия) участок кривой между двумя её точками. Дуга окружности кривая линия, лежащая на окружности и ограниченная двумя точками. Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия
ДУГА — жен. согнутая линия, черта или вещь, образующая кривизну, погиб; часть окружности круга или другой кривой черты, и пр. элипса, параболы. | ·стар. и сев. радуга. | В оглобельной упряжи, деревянная, согнутая крутым лучком тугая распорка между… … Толковый словарь Даля
ДУГА НАБЛЮДЕНИЯ — наименьшее расстояние от Солнца, на котором планета видима, когда Солнце находится под горизонтом. Дневная дуга дуга, которую Солнце проходит от Восхода до Заката. В Равноденствие она составляет 180 градусов или 12 часов правого восхождения. С… … Астрологическая энциклопедия
дуга — и; мн. дуги; ж. 1. Часть окружности или какой л. другой кривой линии в виде полукруга. Ракета описала в небе дугу. Соединить дугой. // О том, что имеет форму кривой, изогнутой линии. Д. лука. Тёмные дуги бровей. Радуга дуга. На повороте река… … Энциклопедический словарь
ДУГА — ДУГА, дуги, мн. дуги, дугам, жен. 1. Принадлежность упряжи из круто изогнутого ствола тонкого дерева, концы которого вдеваются в гужи для скрепления оглобель с хомутом. «Дуги гнут с терпеньем и не вдруг.» Крылов. 2. Часть окружности круга или… … Толковый словарь Ушакова
Дуга — I ж. 1. Изогнутая часть какого либо предмета. 2. Часть окружности или какой либо изогнутой линии. отт. устар. Название линии меридиана или параллели. 3. Часть конской упряжи из тонкого, круто изогнутого ствола дерева, служащая для прикрепления… … Современный толковый словарь русского языка Ефремовой
ДУГА БОЛЬШОГО КРУГА — часть окружности, получаемой при сечении шара плоскостью, проходящей через его центр. Под термином прямое направление жел. дор. линии понимают направление по Д. б. к. между конечными или промежуточными опорными точками жел. дор. линии. Для целей… … Технический железнодорожный словарь
Дуга (геометрия) — Дуга связное подмножество окружности.Свойства*Длина дуги L радиуса R с центральным углом alpha, измеренным в радианах, вычисляется по формуле: L=Ralpha … Википедия
дуга — ДУГА, и, мн дуги, ж Линия в виде полукруга, часть кривой, изогнутой линии или окружности, заключенная между двумя ее точками. Ракета описала в небе дугу … Толковый словарь русских существительных
translate.academic.ru
