Функции. Область определения и множество значений; график функции, построение графиков функции, заданных различными способами. Свойства функции. | План-конспект занятия по алгебре (10, 11 класс):
Тема: Функции. Область определения и множество значений; график функции, построение графиков функции, заданных различными способами. Свойства функции.
Цель:
- дать определение понятий «функция», «область определения», «область значений», «график функции»;
- рассмотреть способы задания функций;
- рассмотреть свойства функций (нули функций, промежутки знакопостоянства, промежутки возрастания и убывания функции, четность и нечетность функции)
- рассмотреть свойства некоторых элементарных функций
Теоретическая часть
Функция — одно из важнейших математических понятий. Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции.
Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: y=f(x). (Читают: у равно f от х.) Символом f(x) обозначают значение функции, соответствующее значению аргумента, равному х.
Все значения независимой переменной образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.
Способы задания функции:
1. аналитический способ (функция задается с помощью математической формулы;
2. табличный способ (функция задается с помощью таблицы)
3. описательный способ (функция задается словесным описанием)
описательный способ (функция задается словесным описанием)
4. графический способ (функция задается с помощью графика).
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
1. Нули функции
Нуль функции – такое значение аргумента, при котором значение функции равно нулю .
2. Промежутки знакопостоянства функции
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
3. Возрастание (убывание) функции.
Возрастающая в некотором промежутке функция — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Функция у = f (x) называется возрастающей на интервале (а; b), если для любых x1 и x2 из этого интервала таких, что x1
Убывающая в некотором промежутке функция — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Функция у =f (x) называется убывающей на интервале (а; b), если для любых x1 и x2 из этого интервала таких, что x1f(x2).
4. Четность (нечетность) функции
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Например, у = х2 — четная функция.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.
Например: у = х3 — нечетная функция.
Функция общего вида не является четной или нечетной (у = х2+х).
Свойства некоторых функций и их графики
1. Линейной функцией называется функция вида , где k и b – числа.
Область определения линейной функции – множество R действительных чисел.
Графиком линейной функции у = kx + b (k ≠ 0) является прямая проходящая через точку (0; b) и параллельная прямой у = kx.
Прямая, не параллельная оси Оу, является графиком линейной функции.
Свойства линейной функции.
1. При k > 0 функция у = kx + b возрастающая в области определения.
2. При k
3. Множеством значений функции y = kx + b(k ≠ 0) является вся числовая прямая, т.е. множество R действительных чисел.
При k = 0 множество значений функции у = kx + b состоит из одного числа b.
3. При b = 0 и k = 0 функция не является ни четной, ни нечетной.
При k = 0 линейная функция имеет вид у = b и при b ≠ 0 она является четной.
При k = 0 и b = 0 линейная функция имеет вид у = 0 и являете одновременно четной и нечетной.
Графиком линейной функции у = b является прямая, проходящая через точку (0; b) и параллельная оси Ох. Заметим, что при b = 0 график функции у = b совпадаете осью Ох.
5. При k > 0 имеем, что у > 0, если и у 0, если и у
2. Функция y = x2
Функция y = x2
Область определения этой функции — множество R действительных чисел.
Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле y = x2 , изображаем график функции.
График функции y = x2 называется параболой.
Свойства функции у = х2.
1. Если х = 0, то у = 0, т.е. парабола имеет с осями координат общую точку (0; 0) — начало координат.
2. Если х ≠ 0, то у > 0, т.е. все точки параболы, кроме начала координат, лежат над осью абсцисс.
3. Множеством значений функции у = х2 является промежуток [0; + ∞).
4. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. парабола симметрична относительно оси ординат (функция у = х2 — четная).
5. На промежутке [0; + ∞) функция у = х2 возрастает.
6. На промежутке (-∞; 0] функция у = х2 убывает.
7. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.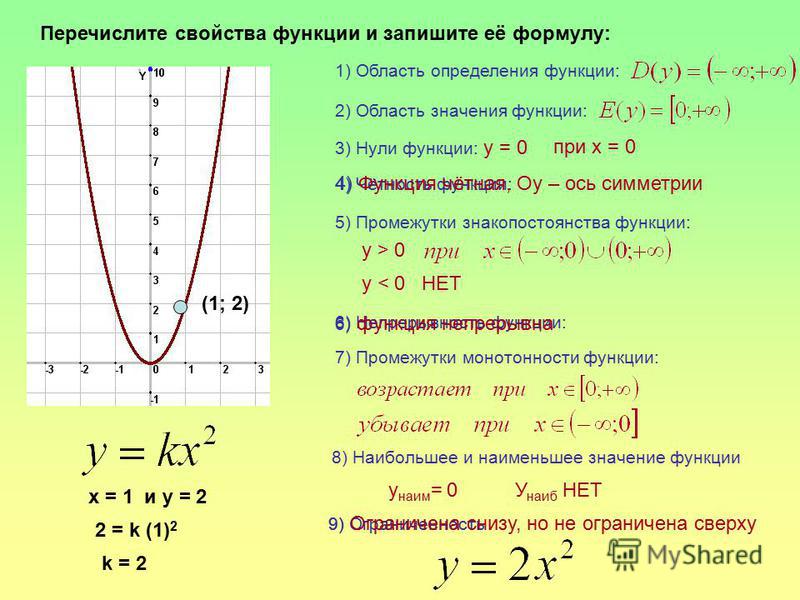
3.Фунуция
Область определения этой функции — промежуток [0;+∞), т. е. все неотрицательные числа.
Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле , изображаем график функции.
Свойства функции.
1. Если х = 0, то у = 0, т.е. график функции имеет с осями координат общую точку (0; 0) — начало координат.
2. Если х > 0, то у > 0, т.е. все точки графика функции, кроме начала координат, лежат над осью абсцисс.
3. Множеством значений функции является промежуток [0;+∞).
4. Функция не является ни четной, ни нечетной.
5. Функция возрастающая в области определения.
6. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.
4. Функция y = x3
Область определения этой функции — множество R действительных чисел,
Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле у = х3, изображаем график функции.
График функции у= х3 называется кубической параболой.
Свойства функции y = x3.
1. Если х = 0, то у = 0, т.е. кубическая парабола пересекает оси координат в точке (0; 0) — начале координат.
2. Если х > 0, то у > 0, а если х
3. Множеством значений функции у = х3 является вся числовая прямая.
4. Если значения аргумента отличаются только знаком, то и значения функции отличаются только знаком, т.е. кубическая парабола симметрична относительно начала координат (функция у = х3 — нечетная).
4. Функция у = х3 возрастающая в области определения.
5. Функция y = |x|
Область определения этой функции — множество R действительных чисел.
Пользуясь определением модуля числа х при х > О получим у = х, а при х
График функции состоит из двух частей: части прямой у = х при х ≥ 0 и из части прямой у =- х при х
Свойства функции
1. Если х = 0, то у = 0, т.е. график пересекает оси координат в точке (0; 0) — начале координат.
2. Если х ≠ 0, то у > 0, т.е. все точки графика функции y = |x|, кроме начала координат, лежат над осью абсцисс.
3. Множеством значений функции y = |x| является промежуток [0;+∞).
4. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. график функции симметричен относительно ординат (функция y = |x| — четная).
5. На промежутке [0;+∞) функция y = |x| возрастает.
6. На промежутке (-∞;0] функция y = |x| убывает.
7. Наименьшее значение функция принимает в точке х, оно равно 0. Наибольшего значения не существует.
6. Функция
Область определения функции: .
Область значений функции: .
График — гипербола.
1. Нули функции.
у ≠ 0, нулей нет.
2. Промежутки знакопостоянства,
Если k > 0, то у > 0 при х > 0; у
Если k 0; у > 0 при х
3. Промежутки возрастания и убывания.
Если k > 0, то функция убывает при .
Если k
4. Четность (нечетность) функции.
Функция нечетная.
Практическая часть:
- Найдите область определения функции
- При каких значениях функция принимает положительные значения?
Постройте график функции
- Постройте график функции и укажите координаты точек пересечения этих графиков.
- Постройте график функции
Проходит ли график через точку А(-35, -65)?
Домашнее задание
- Вычислите координаты точек пересечения параболы и прямой
- Какая из прямых у = 3х — 1, у = 2х + 4 или у = -2х проходит через начало координат? Постройте график этой функции.
Алгебра Функция. Область определения и область значений
Материалы к уроку
Конспект урока
Функцией называется зависимость переменной игрек от переменной икс, при которой каждому значению переменной икс соответствует единственное значение переменной игрек.
Икс называется независимой переменной или аргументом. Игрек называется зависимой переменной, значением функции или просто функцией.
Если зависимость переменной игрек от переменной икс является функцией, то коротко записывают так: игрек равно эф от икс. Этим символом обозначают также значение функции, соответствующее значению аргумента икс.
Пусть функция задана формулой игрек равно три икс квадрат минус пять. Тогда можно записать, что эф от икс равно три икс квадрат минус пять. Найдем значения функции эф для значений икс, равных двум и минус пяти. Они будут равны семи и семидесяти.
Заметим, что в записи игрек равно эф от икс вместо эф можно употреблять и другие буквы: же, фи и так далее.
Все значения икс образуют область определения функции. Все значения, которые принимает игрек, образуют область значений функции.
Функция считается заданной, если указана её область определения и правило, согласно которому каждому значению икс поставлено в соответствие единственное значение игрек.
Если функция игрек равно эф от икс задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений переменной икс, при которых выражение эф от икс имеет смысл…
Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
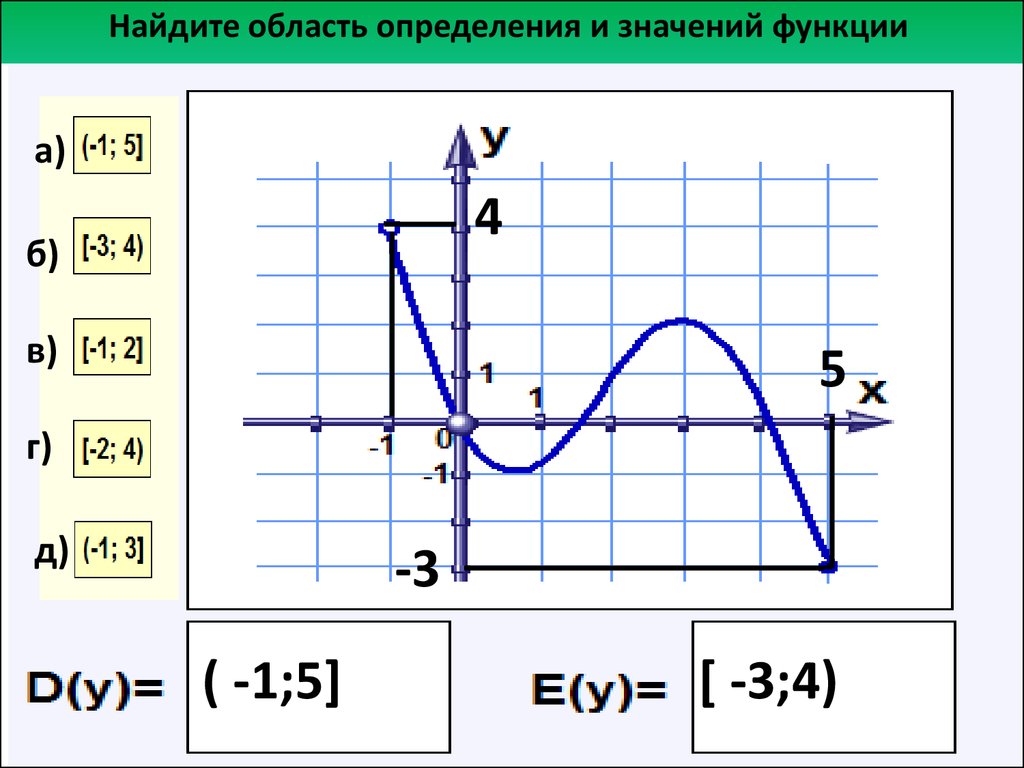
На рисунке изображен график функции игрек равно эф от икс, областью определения которой является отрезок от единицы до пяти. С помощью графика можно найти, например, что функция от числа один равна минус трем, функция от двух равна двум, функция от числа четыре равна минус двум, функция от числа пять равна минус четырем. Наименьшее значение функции равно минус четырем, а наибольшее – двум. При этом любое число от минус четырех до двух, включая эти числа, является значением данной функции. Таким образом, областью значений функции игрек равно эф от икс является отрезок от минус четырех до двух.
Ранее нами уже были изучены некоторые виды функций:
- Линейная функция, задаваемая формулой игрек равно ка икс плюс бэ, где ка и бэ – некоторые числа;
- Прямая пропорциональность – частный случай линейной функции, она задается формулой игрек равно ка икс, где ка не равно нулю;
- Обратная пропорциональность – функция игрек равно ка деленное на икс, где ка не равно нулю.
Графиком функции игрек равно ка икс плюс бэ является прямая. Область определения этой функции — множество всех чисел. Областью значений этой функции при ка не равном нулю является множество всех чисел, а при ка равном нулю ее область значений состоит из одного числа бэ.
График функции игрек равно ка деленное на икс называется гиперболой.
На рисунке изображен график функции игрек равно ка деленное на икс, для ка большего нуля. Областью определения этой функции является множество всех чисел, кроме нуля. Это множество является и областью ее значений…
Функциями описываются многие реальные процессы и закономерности. Например, прямой пропорциональностью является зависимость массы тела от его объема при постоянной плотности; зависимость длины окружности от ее радиуса. Обратной пропорциональностью является зависимость силы тока на участке цепи от сопротивления проводника при постоянном напряжении; зависимость времени, которое затрачивает равномерно движущееся тело на прохождение заданного пути, от скорости движения.
Например, прямой пропорциональностью является зависимость массы тела от его объема при постоянной плотности; зависимость длины окружности от ее радиуса. Обратной пропорциональностью является зависимость силы тока на участке цепи от сопротивления проводника при постоянном напряжении; зависимость времени, которое затрачивает равномерно движущееся тело на прохождение заданного пути, от скорости движения.
Изучались также функции, заданные формулами игрек равно икс квадрат, игрек равно икс куб, игрек равно корень квадратный из икс.
Рассмотрим функцию, заданную формулой игрек равно модуль икс.
Так как выражение модуль икс имеет смысл при любом икс, то областью определения этой функции является множество всех чисел. По определению модуль икс равен икс, если икс больше либо равен нулю, и минус икс, если икс меньше нуля. Поэтому функцию игрек равно модуль икс можно задать следующей системой.
График рассматриваемой функции в промежутке от нуля до плюс бесконечности, включая ноль, совпадает с графиком функции игрек равно икс, а в промежутке от минус бесконечности до нуля – с графиком функции игрек равно минус икс.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Домен и диапазон функции
Доля на
Содержание:
- Что такое домен и диапазон функции?
- Как найти область определения и область значений функции
- Диапазон (Статистика)
- Закрытый домен
- Кодовый домен
- Частотный диапазон
- Домен интеграции
- Интервальный домен
- Домен — это набор значений x, которые можно поместить в функцию.
 Другими словами, это набор всех возможных значений независимой переменной.
Другими словами, это набор всех возможных значений независимой переменной. - Диапазон — это набор значений y, которые выводятся для домена.
- Кодовый домен похож на диапазон, но с одним большим отличием: кодовый домен может содержать все возможных выходных данных , а не только те, которые действительно появляются.
Посмотрите видео для краткого обзора:
Домен и область действия
Посмотрите это видео на YouTube.
- Проверка известных доменов/диапазонов,
- Угадай и проверь,
- Графика,
- Таблица значений.
Сначала посмотрите, сможете ли вы выяснить, какой тип функции у вас есть (это не всегда ясно).
Многие функции имеют бесконечный набор для домена. «Бесконечное множество» — это просто множество всех возможных чисел. Например, вы можете ввести любое число в функцию y = x 2 , и она все равно выдаст вам результат. Но как насчет диапазона? Отрицательное число никогда не будет отображаться для этой функции; отрицательный раз отрицательный всегда будет положительным. Если вы поставите, например, -10, вы получите:
Но как насчет диапазона? Отрицательное число никогда не будет отображаться для этой функции; отрицательный раз отрицательный всегда будет положительным. Если вы поставите, например, -10, вы получите:
Имеет смысл, что диапазон для x 2 равен 0 > ∞.
Некоторые функции имеют определенные домены и диапазоны. Краткое описание приведено ниже или просмотрите наш плейлист на YouTube, в котором есть серия очень коротких видеороликов о поиске доменов и диапазонов для различных функций.
- Линейные функции обычно имеют область определения и диапазон всех действительных чисел. См.: Линейные функции (видео).
- Полиномиальные функции имеют область определения всех действительных чисел. Диапазон зависит от степени и старшего коэффициента. См.: Полиномиальные функции.
- Квадратичные (квадратичные) функции имеют область определения всех действительных чисел.
 Диапазон зависит от знака старшего коэффициента: y ≥ min (+) или y ≥ max, (-). См.: Квадратичные функции.
Диапазон зависит от знака старшего коэффициента: y ≥ min (+) или y ≥ max, (-). См.: Квадратичные функции. - Функции абсолютного значения имеют область определения всех действительных чисел. Диапазон зависит от вершины и знака выражения абсолютного значения. См.: Функция абсолютного значения.
- Функция квадратного корня имеет область значений x ≥ 0 и диапазон y ≥ 0. Информацию о других функциях квадратного корня, таких как √(x – 5), см.: Функции квадратного корня и радикальные функции.
- Рациональные функции f(x) = 1/x имеют область определения x ≠ 0 и диапазон значений x ≠ 0. Если у вас есть более сложная форма, например f(x) = 1 / (x – 5), вы можете найти домен и диапазон с помощью обратной функции или графика. См. Рациональные функции.
- Синусоидальные функции и функции косинуса имеют область определения всех действительных чисел и диапазон -1 ≤ y ≤ 1.
Совет: Ознакомьтесь с формами основных функций, таких как синус/косинус и многочлены. Таким образом, вы сможете разумно найти область определения и диапазон функции, просто взглянув на уравнение.
Таким образом, вы сможете разумно найти область определения и диапазон функции, просто взглянув на уравнение.
Если у вас нет сильных навыков алгебры, вы можете пропустить этот метод и вместо этого попробовать графические или табличные методы.
По сути, используйте свои навыки алгебры, чтобы найти домен и диапазон для функции, угадывая и проверяя! Несколько общих советов:
- Деление на ноль запрещено ). В качестве примера предположим, что у вас есть функция:
f(x) = 1/(x 2 – 9).
Вы можете исключить любые значения x (домен), которые делают знаменатель равным нулю. - Для домена число под знаком квадратного корня не может быть отрицательным . Например, вы не можете найти домен для √-10, потому что решение — мнимое число.
- Попробуйте ввести в функцию разные x-значения для y, чтобы посмотреть, что произойдет. Ищите такие тенденции, как: всегда положительные, всегда отрицательные или наборы чисел, которые не работают.
 Попробуйте ввести очень большое (например, миллион) или очень маленькое (например, отрицательное значение миллиона) и посмотрите, сработает ли это.
Попробуйте ввести очень большое (например, миллион) или очень маленькое (например, отрицательное значение миллиона) и посмотрите, сработает ли это.
Найти область определения и диапазон для:
Область определения:
- Числитель имеет квадратный корень; числа под этим не могут быть отрицательными (см. № 2 выше). Таким образом, у вас могут быть только числа для x, большие или равные -2.
- Знаменатель : Вы не можете разделить на ноль, вы не можете получить -3 + 3, так как это даст ноль. Например, 3
Домен для этой конкретной функции: x > -2, x ≠ 3.
Диапазон
Диапазон для этой функции — это набор всех значений f(x), исключая F(x) = 0. Вот где ваш навыки алгебры получить тренировку!
- Числитель : Глядя на функцию, вы должны сразу увидеть, что числитель становится равным 0, когда x = -2:
√(2 + 2) = √0 = 0, - Знаменатель:
- Работая с -2 по-прежнему, знаменатель становится: (-2) 2 – 9 = 5.
 Таким образом, f(-2) = 0/-5 = 0,
Таким образом, f(-2) = 0/-5 = 0, - Если вы вставите несколько значений x между 2 и 3 в (x 2 – 9), вы увидите, что функция приближается к отрицательной бесконечности.
- Вставьте еще несколько значений x, превышающих x = 3, обратите внимание, что функция стремится к положительной бесконечности.
- Чем больше становятся значения x, тем меньше становятся значения функции (но на самом деле они никогда не достигают нуля).
- Работая с -2 по-прежнему, знаменатель становится: (-2) 2 – 9 = 5.
Постройте график функции и посмотрите, где лежат ваши значения x и y. Большинство графических калькуляторов помогут вам увидеть домен функции (или указать, какие значения могут быть недопустимы). Например, если вы нарисуете x 2 , будет ясно, что домен не может включать отрицательные числа. Если у вас нет графического калькулятора, попробуйте этот бесплатный онлайн-калькулятор. Всегда увеличивайте и уменьшайте масштаб графика, чтобы проверить непрерывность или отсутствующие области.
График x 2 и 4x 2 +25 (используя онлайн-калькулятор HRW.
Из приведенного выше графика видно, что диапазон для x 2 (зеленый) и 4x 2 +25 (красный график) является положительным; На этом этапе вы можете предположить, что это набор из всех положительных действительных чисел, основываясь на графике
Составьте таблицу значений на вашем графическом калькуляторе ( См. : Как сделать таблицу значений на TI89)
Включите ввод x от -10 до 10, затем несколько больших чисел (например, один миллион). Используйте калькулятор, чтобы найти значения y для значений x. Если калькулятор говорит вам, что значения или не определены, или что значения могут достигать предела (число, к которому функция приближается, но никогда не достигает), это должно помочь вам определить диапазон.
В статистике диапазон является мерой разброса: это разница между самым высоким и самым низким значением в наборе данных. Чтобы найти его, вычтите наименьшее число из наибольшего.
Чтобы найти его, вычтите наименьшее число из наибольшего.
Несколько конкретных примеров поиска статистических диапазонов см. в разделе Как найти диапазон в статистике.
Другие значения «Диапазона»
В исчислении диапазоном являются все выходные значения функции . В некоторых областях математики диапазон может — что может сбивать с толку — также означать просто весь диапазон чисел — например, диапазон цен на мобильные телефоны может составлять от 40 до 550 долларов. Эванс и др. коллеги (2000, стр. 5) и Феллер (1968, стр. 200) используют термин «диапазон» для обозначения «области».
Закрытый домен — это домен, содержащий все его граничные точки. Если домен содержит набор всех внутренних точек (исключая границу), домен является открытым доменом . Незакрытый домен (что не то же самое, что открытый домен) содержит некоторые граничные точки, но не все.
Если домен содержит все точки в пределах ограниченного расстояния от начала координат, он называется ограниченным доменом . Неограниченная область имеет точки, не находящиеся внутри границы; Другими словами, они находятся на произвольном расстоянии от начала координат.
Неограниченная область имеет точки, не находящиеся внутри границы; Другими словами, они находятся на произвольном расстоянии от начала координат.
Непрерывная функция в ограниченной закрытой области D будет иметь максимальное значение и минимальное значение в D.
Закрытая область в других контекстах
конкретная система ответа на вопрос (QA). Например, система под названием САМОЛЕТ может хорошо отвечать на вопросы о воздушной скорости, ускорении и грузоподъемности конкретного самолета, но не очень хороша за пределами этой конкретной области. С другой стороны, QA с открытым доменом может просеивать неограниченный домен, чтобы найти ответ на вопрос.
В разработке программного обеспечения закрытый домен — это просто домен, все границы которого закрыты. Открытый домен — это домен, в котором открыты все границы.
Целостно замкнутые области находятся в коммутативной алгебре. Целостно замкнутая область A — это область целостности (ненулевое коммутативное кольцо, в котором произведение любых двух ненулевых элементов также не равно нулю), интегральное замыкание которой в своем поле частных есть само A.
Кодовый домен A (или целевой набор) содержит все значения (выходные данные) функции.
Когда мы говорим, что функция f: X → Y (что означает «набор значений X выводит набор значений Y»), кодовый домен — это Y . Другими словами, выходные данные функции ограничены доменом кода.
Диапазон аналогичен, но разница в том, что диапазон представляет собой набор фактических значений функции (фактических выходов). Кодовый домен или целевой набор могут содержать все возможных выходных данных , а не только те, которые появляются на самом деле. Например, вы можете указать, что кодовый домен — это «набор всех действительных чисел (ℝ)». Однако это не означает, что все действительные числа являются выводами для вашей функции.
Графическое представление кода домена
На приведенном ниже изображении показана взаимосвязь между доменом, совместным доменом и диапазоном.
- Красный овал — домен .
 Каждый вход для функции f является членом этой области и может быть представлен x.
Каждый вход для функции f является членом этой области и может быть представлен x. - Синий овал (рассматриваемый в целом, включая желтый подраздел) — это кодовый домен . Это представляет все возможные числа, которые могут быть получены на выходе. Каждый экземпляр домена отображается функцией f в этот кодовый домен.
- Желтый овал, — подмножество этого целевого домена, — диапазон , содержащий все фактические экземпляры f(x).
Примеры кода домена
Возьмем функцию f(x) = x 2 , ограниченную вещественными числами, поэтому f: ℝ → ℝ.
Здесь целевым набором f являются все действительные числа (ℝ), но поскольку все значения x 2 положительны*, фактическое изображение или диапазон f равен ℝ + 0 .
*Любой отрицательный ввод приведет к положительному результату (например, -2 * -2 = +4).
Целевые наборы и композиция
Целевые наборы приобретают решающее значение, когда мы начинаем обсуждать композиции функций. Композиция «f∘g» читается как «f из g» или «f после g» и представляет собой составную функцию, которая включает в себя взятие члена домена g, отправку его через функцию g и передачу этого вывода через f. .
Композиция действительна тогда и только тогда, когда область определения второй функции совпадает с областью определения первой функции. В нашем примере композиция действительна только в том случае, если кодовый домен g совпадает с доменом f.
Анализ частотной области — это когда сигнал изучается относительно частоты , а не относительно времени . Исследуемые данные нанесены с частотой по оси x и амплитудой по оси y; это показывает, как энергия сигнала распределяется в зависимости от частоты.
Функция может быть представлена либо временной областью , либо частотной областью; каждый полезен для разных целей. Представление сигнала во временной области может быть преобразовано в частотное представление с использованием преобразования Фурье или аналогичных манипуляций.
Представление сигнала во временной области может быть преобразовано в частотное представление с использованием преобразования Фурье или аналогичных манипуляций.
Преобразование Фурье преобразует представление во временной области (красный) в частотную область (синий). Пики в области представляют частоты компонентов.
Важность и использование анализа в частотной области
Термин впервые появился в 1953 году в технике связи. Однако сегодня этот анализ используется во многих различных областях, в том числе:
- Геология,
- Химия,
- Дистанционное зондирование,
- Обработка изображений,
- Электротехника,
- Связь.
Анализ в частотной области называют краеугольным камнем системной инженерии и важной частью набора инструментов почти любого ученого, инженера или статистика.
Это представление часто позволяет охарактеризовать сигнал или серию сигналов с помощью простой алгебры, в отличие от сложных дифференциальных уравнений, которые используются для представления сигнала во временной области. Простые вычисления, связанные с обработкой этих сигналов, делают его особенно полезным для инженеров. Возможно, что более важно, частотный анализ позволяет вам увидеть циклическое поведение, которое могло бы быть не сразу очевидным в представлении во временной области.
Простые вычисления, связанные с обработкой этих сигналов, делают его особенно полезным для инженеров. Возможно, что более важно, частотный анализ позволяет вам увидеть циклическое поведение, которое могло бы быть не сразу очевидным в представлении во временной области.
При интегрировании по замкнутому интервалу [a, b] некоторой функции этот интервал называется областью интегрирования . Например:
Областью интегрирования этой функции является отрезок [1, 3].
Область интегрирования может быть бесконечной (т. е. от -∞ до ∞), как показывает следующий несобственный интеграл:
Пример несобственного интеграла с бесконечной областью интегрирования.
Несобственные интегралы нельзя вычислить напрямую; Они вычисляются как пределы обычных интегралов.
В трех измерениях все становится немного сложнее, но в большинстве случаев областью основания объекта является область интеграции.
Область интегрирования на 3D-форме обычно является базой (показана красными линиями на этом изображении).
Как нарисовать область интегрирования
Начертить область для любого интеграла легко, если у вас есть только один интеграл (см. пример в шаге 1 ниже). Для нескольких интегралов, если вы разбиваете их на шаги, это становится намного менее сложным.
Пример задачи: Нарисуйте область интегрирования для следующего повторного интеграла:
Решение:
Шаг 1: Нарисуйте границы интегрирования для первого интеграла. Границы задаются как x = от 0 до 1, поэтому:
Шаг 2: Нарисуйте границы второго интеграла на том же графике из шага 1. Примечание. Если границы интегрирования не являются целыми числами (второй интеграл здесь есть e, число Эйлера), вы можете использовать графический калькулятор (я использовал калькулятор на Desmos.com, чтобы нарисовать этот график), чтобы вам было легче набросать форму.
Шаг 3: Найдите заштрихованную область, соответствующую определению обоих интегралов. В этом примере вы затеняете только область от 0 до 1, которая также находится в пределах [e, e x ].
В этом примере вы затеняете только область от 0 до 1, которая также находится в пределах [e, e x ].
Вот и все!
Вообще говоря, интервальный домен — это домен, ограниченный интервалом [1]. Например, входные данные (например, значения x) для конкретной функции могут быть ограничены интервалом [0, 1]. Интервалы могут быть закрытыми, открытыми или полузакрытыми/полуоткрытыми.
Функция, определенная на полуоткрытом интервале «область интервала» [5.5, 10].
Интервальная область в теории доменов
В теории областей термин «интервальная область», впервые предложенный Д. С. Скоттом в 1972 г. [2], представляет собой способ аппроксимации действительных чисел. Он получил свое название, потому что реалы разделены на интервалы для вычислений.
Аппроксимации иногда необходимы для вычислений над неисчисляемыми пространствами, такими как действительные числа (ℝ) или некоторые функциональные пространства. Области интервалов не так просто определить, как «интервалы», с которыми вы сталкиваетесь в исчислении; Алгебраические структуры, состоящие из набора плюс одна или несколько бинарных операций, удовлетворяющих определенным аксиомам, необходимы для демонстрации различий между многими эквивалентными (и неэквивалентными) версиями интервальной области [3].
Области интервалов не так просто определить, как «интервалы», с которыми вы сталкиваетесь в исчислении; Алгебраические структуры, состоящие из набора плюс одна или несколько бинарных операций, удовлетворяющих определенным аксиомам, необходимы для демонстрации различий между многими эквивалентными (и неэквивалентными) версиями интервальной области [3].
Теоретическая основа Скотта для дифференциального исчисления изначально была разработана для функций с одной переменной. Недавно он был распространен на функции нескольких переменных [3]. Это расширение переводит интервальную область в аппроксимации кривых и поверхностей [4].
Теория доменов и алгебраические структуры выходят за рамки этой статьи, но если вам интересно, прочитайте статью Джесс Бланк в Computer Journal Интервальные домены и вычислимые последовательности: пример редукции доменов [5].
Область интервалов: ссылки
[1] Klippert, J. (1989). Расширенное расширенное исчисление: подсчет разрывов функции с действительным знаком с интервальной областью. Журнал «Математика»
Журнал «Математика»
Том. 62, № 1 (февраль 1989 г.), стр. 43-48 (6 страниц)
[2] Скотт, Д. С. (1972) Теория решеток, типы данных и семантика. В
Растин, Р. (редактор), Формальная семантика языков программирования,
стр. 65
[3] Эдалат, А. (1995a) Теория предметной области и интеграция. Теоретическая информатика 151 163–193.
[4] Edalat, A. & Lieutier, A. (2004). Теория доменов и дифференциальное исчисление (функции одной переменной). Мат. Структура в Комп. Наука, том. 14, стр. 771–802. c2004 Cambridge University PressDOI: 10.1017/S0960129504004359 Напечатано в Соединенном Королевстве
[5] Blanck, J. (2012). Интервальные домены и вычислимые последовательности: пример сокращения доменов. Компьютерный журнал (5 сентября).
Домен и диапазон: другие ссылки
Кэссиди, Стив. COMP449 Примечания к курсу. Распознавание речи: Глава 6. Частотный Дом. Анализ. Получено с http://web.science.mq.edu.au/~cassidy/comp449/html/ch06.html 15 июня 2018 г.
Кулкарни. Частота Дом. и преобразования Фурье. Получено с https://www.princeton.edu/~cuff/ele201/kulkarni_text/frequency.pdf 16 июня 2018 г.
Частота Дом. и преобразования Фурье. Получено с https://www.princeton.edu/~cuff/ele201/kulkarni_text/frequency.pdf 16 июня 2018 г.
Лю, Г. Исчисление нескольких переменных. Получено 31 августа 2020 г. с: https://www.math.ucla.edu/~azhou/teaching/18W/hw-solutions.pdf
, факультет машиностроения Массачусетского технологического института. 2.14 Раздаточный материал; Введение в частоту. Обработка домена. Получено с http://web.mit.edu/2.14/www/Handouts/FreqDom.pdf 16 июня 2018 г.
Ци, П. (2019). Ответы на сложные открытые вопросы в масштабе. Получено 7 января 2020 г. с: http://ai.stanford.edu/blog/answering-complex-questions/
Rogawski, J. (2007). Многомерное исчисление. WH Freeman.
Тиан, Дж. Инженерия качества программного обеспечения: тестирование, обеспечение качества и количественное улучшение.
Чжоу, А. Проблема. Получено 31 августа 2020 г. с: https://www.math.ucla.edu/~azhou/teaching/18W/hw-problems.pdf
ЦИФРОВАТЬ ЭТО КАК:
Stephanie Glen . «Область и диапазон функции» из CalculusHowTo.com : Исчисление для всех нас! https://www.calculushowto.com/types-of-functions/domain-and-range-of-a-function/
«Область и диапазон функции» из CalculusHowTo.com : Исчисление для всех нас! https://www.calculushowto.com/types-of-functions/domain-and-range-of-a-function/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
ИсчислениеHowTo.com
Домен и диапазон функции
Домен и диапазон функции
Что такое факты о домене и диапазоне функции?
- Домен — это набор значений x, которые можно поместить в функцию.
- Диапазон — это количество значений y, которые нужно вернуть для домена.
- Кодовый домен похож на область с одним большим отличием: кодовый домен может содержать все возможные выходные данные, а не только те, которые действительно появляются.

Как вы описываете домен и диапазон функции?
Диапазон функции соответствует всем возможным значениям xs упорядоченных пар, а диапазон функции соответствует всем возможным значениям ys упорядоченных пар. Вы можете легко найти их, построив функции или упорядоченные пары.
Как вычислить область определения функции?
Чтобы найти диапазон функции, вы должны сначала оценить члены уравнения. Квадратичная функция имеет вид ax 2 + bx + c: f(x) = 2x 2 + 3x + 4. Примеры функций с дробями: f(x) = (1/x), f(x) = (x + 1) / (x1) и т. д.
Как найти область определения графической функции?
- Нарисовать график
- Найдите возможные значения x, где определено f(x). Здесь значения x начинаются с 2 и заканчиваются на 2.
- Возможные значения x — это диапазон функции.
Что важнее домен или диапазон?
В своей простейшей форме домен — это все значения, которые вписываются в функцию, а область — все значения, которые вписываются в функцию.
На самом деле, они очень важны при определении функции.
Как вычислить область определения и диапазон функции?
Найдите площадь и размер функции f(x) = 2/x. Установите знаменатель равным нулю. Следовательно, доменом являются все действительные числа, кроме 0. Диапазоном являются все допустимые значения x, кроме 0. Найдите домен и диапазон следующей функции. Приравняйте знаменатель к нулю и найдите х.
Какое определение термина домен является лучшим?
Ключевые понятия 1 Домен: набор значений (баллов), которые может получить функция. 2 Домен: совокупность всех точек, в которых определена функция. Функция 3: Любая математическая формула, которая возвращает один результат для каждого входа.
Что такое диапазон и кодовый домен функции?
Кодовый домен — это набор значений, которые могут в конечном итоге появиться. Кодовый домен на самом деле является частью определения функции. А диапазон — это количество реально полученных значений. Пример: вы можете определить функцию f(x) = 2x с доменом и доменом целых чисел (потому что так говорят).
Пример: вы можете определить функцию f(x) = 2x с доменом и доменом целых чисел (потому что так говорят).
Что такое область определения и область значений функции калькулятора
Первое, что вы узнаете об этой концепции, это то, что переменная X используется для определения области действия функции, в то время как область действия функции определяется переменная Y. Область видимости — это множество входных значений X, а диапазон — множество выходных значений Y.
Каково определение домена и диапазона?
Объем и объем — это термины, которые применяются к математике, особенно к естественным наукам, которые состоят из функций. Размер и степень являются основными факторами, определяющими применимость математических функций. Математическая функция описывает отношения между двумя группами переменных.
Как определить диапазон функции?
Найдите размер функции отношения. Напишите отношение. Перечислите y-координаты отношения. Удалите все повторяющиеся координаты, чтобы у вас была только одна координата для каждого y. Запишите степень родства в порядке возрастания. Убедитесь, что отношения являются особенностью.
Удалите все повторяющиеся координаты, чтобы у вас была только одна координата для каждого y. Запишите степень родства в порядке возрастания. Убедитесь, что отношения являются особенностью.
Как решить для домена?
Примечание. Найдите диапазон функции, записанной в виде уравнения, содержащего дробь. Определите входные значения. Определите ограничения доступа. Если формула функции содержит знаменатель, установите знаменатель равным нулю и найдите x x. Зарегистрируйте домен как область действия и убедитесь, что все ограниченные значения исключены из домена.
Как узнать домен этой функции?
Часть 1 из 3: Определение функциональной области Определите тип функции, с которой вы работаете. Диапазон функции — это все значения x (горизонтальная ось), которые дают ей допустимые значения y. Запишите домен в правильном формате. При записи области определения функции используются квадратные скобки и квадратные скобки (,). Нарисуйте график квадратного уравнения.
Домен и диапазон функционального графика
Домен — это все значения x x x или входы функции, а диапазон — все значения y и y или выходы функции. Если посмотреть на график, домен соответствует всем значениям на графике слева направо. В диапазон входят все значения на графике снизу вверх.
Как найти область определения и область значений функции?
Используйте диаграммы, чтобы найти район и пляж. Другой способ определить функциональную область и объем функций — использовать диаграммы. Поскольку домен относится к набору возможных входных значений, домен графика состоит из всех входных значений, отображаемых на оси X. Диапазон — это количество возможных выходных данных, показанных на оси Y.
Как узнать домен и диапазон этого?
- Проверить известные домены/области Сначала проверьте их роль (это не всегда очевидно).
- Угадывание и тестирование Если вы плохо понимаете алгебру, вы можете пропустить этот метод и попробовать вместо него графические или табличные методы.
- Графика
В чем разница между доменом и диапазоном?
Домен — это то, что вставляется в функцию, а диапазон — это результат функции со значением домена. 1. Область применения и область применения являются основными факторами, определяющими применимость математических функций. 2. Диапазон является независимой переменной, а диапазон — зависимой переменной.
Могут ли домен и диапазон совпадать?
Могут ли домен и набор функций совпадать? Да сэр. Например, и диапазон, и диапазон функции кубического корня представляют собой набор всех действительных чисел.
Что такое домен и диапазон в алгебре?
Домен представляет собой совокупность всех первых элементов упорядоченных пар (координаты x). Площадь — это множество всех вторых элементов упорядоченных пар (координаты y). Только элементы, используемые отношением или функцией, составляют область действия. Домен: все значения x, которые будут использоваться (независимые значения).
Что такое факты о предметной области и диапазоне рабочих листов функций
Объем и объем функций Рабочие листы — отличный способ определить входы и выходы с помощью упорядоченных пар упражнений, таблиц, картографических таблиц, диаграмм и многого другого. Какие отношения являются функциями?
Рабочая таблица доменов и диапазонов
Таблица диапазонов и диапазонов Для функции y = f(x) диапазон функции представляет собой набор допустимых входных данных, а диапазон — результирующий набор выходных данных. Домены можно найти алгебраически, домены часто можно найти алгебраически и графически. Фермы и пляжи группируются. Поэтому необходимо использовать правильное обозначение множества.
Что такое домен и диапазон доменов?
В своей простейшей форме домен — это все значения, которые вписываются в функцию, а область — все значения, которые вписываются в функцию. На самом деле, они очень важны при определении функции.
Что такое диапазон и функция домена?
Предмет и сфера деятельности. Диапазон функции соответствует всем возможным значениям xs упорядоченных пар, а диапазон функции соответствует всем возможным значениям ys упорядоченных пар. Вы можете легко найти их, построив функции или упорядоченные пары.
Является ли домен значением X или Y?
Область описывает значения x на графике, область описывает значения y. Домен является независимым значением, что делает диапазон зависимым значением.
Как описать область определения и область значений калькулятора функций
Область значений функций — это набор переменных, не зависящих от x, а диапазон — это набор переменных, зависящих от y. Чтобы найти диапазон функции, просто подставьте значения x в квадратную формулу, чтобы получить результат. Чтобы найти диапазон функции, сначала найдите значение x и значение y вершины, используя формулу x = b / 2a.
Каковы область определения и область значений линейной функции?
Диапазон и диапазон линейных функций являются действительными числами или от отрицательной бесконечности до положительной бесконечности. Однако иногда объем и область действия линейной функции могут быть ограничены в зависимости от информации, которую она представляет.
Как вы описываете домен и диапазон функционального графика
Область состоит из всех значений x x x или входных данных функции, а область состоит из всех значений y и y или выходных данных функции. Если посмотреть на график, домен соответствует всем значениям на графике слева направо. В диапазон входят все значения на графике снизу вверх. Привет!
Как вы описываете домен и диапазон рабочего листа функции
Чтобы найти область действия функции, вам нужно найти значения x, для которых определена данная функция. Вышеупомянутая функция определена для всех действительных значений x.
Следовательно, область определения данной функции состоит из всех действительных значений или R-значений. Чтобы определить область определения функции, вы должны сначала найти обратную y.
Как найти домен заданной функции?
Чтобы найти область определения функции, необходимо перечислить все возможные числа, которым удовлетворяет функция, или все значения x. Перепишите уравнение, заменив f(x) на y. Это приводит уравнение к согласованной форме и упрощает обработку.
Какая связь между доменом и функцией?
Функция однозначно связывает элементы области с элементами области, так что только одно значение y присваивается области для каждого значения x в области. Область определения и степень функции образуют ряд упорядоченных пар, порожденных по правилу y = f(x).
Какова разумная область определения функции?
Разумный диапазон и диапазон — это набор значений, существующих для функции. Неправильные суммы не считаются объемом и объемом.
Разумная область: {x | R, x 3}, потому что в выражении квадратного корня не может быть отрицательного значения.
Как определить область определения функции калькулятора
Чтобы найти диапазон этого типа функции, установите наименьшее значение равным нулю и исключите значение x, найденное при решении уравнения. Функция с переменной внутри радикала. Чтобы найти область действия такого рода функции, установите для членов главного героя значение > 0 и найдите значения, которые работают для x.
Какова практическая область применения функции?
Диапазон функции — это набор значений x для вашей функции, и значения x вводятся. Практическая область посвящена числам, которые реалистичны в проблемной ситуации.
Какие значения находятся в области определения функции?
Диапазон функции — это набор чисел, которые могут быть включены в конкретную функцию. Другими словами, это набор значений x, которые вы можете подставить в данное уравнение. Множество возможных значений y называется диапазоном. Если вы хотите узнать, как найти домен роли в различных ситуациях, выполните следующие действия.
Множество возможных значений y называется диапазоном. Если вы хотите узнать, как найти домен роли в различных ситуациях, выполните следующие действия.
Как найти наибольшую область определения функции
Нахождение области определения функции с помощью графика — самый простой способ найти область определения. Область определения функции на графике — это множество всех возможных значений x на оси x. Для области они должны выяснить, где начинается и заканчивается значение x, часть оси x, где определяется f(x).
Как найти домен?
Определение диапазона функции с помощью графика Посмотрите на график. Проверьте значения x на графике. Это может быть легче сказать, чем сделать, но вот несколько советов: Одно правило. Введите свой домен. Просто укажите диапазон в зависимости от типа диаграммы, с которой вы работаете.
Как определить домен формулы функции
Домен функции — это набор допустимых значений для входной переменной. Диапазон — это набор значений функции (то есть значений выходных переменных), которые соответствуют значениям домена.
Используя термины «площадь» и «площадь», они переформулировали определение функции следующим образом.
Какова область определения дробной функции?
Объем дроби относится ко всем действительным числам, которые могут быть независимой переменной дроби. Если вы знаете математические истины о действительных числах и решаете несколько простых алгебраических уравнений, вы можете найти диапазон любого регулярного выражения. Посмотрите на знаменатель дроби. Знаменатель – это наименьшее число дроби.
Как определить домен рабочего листа функции
Единственный способ сделать это — использовать формулу из столбца «Найти домен» рабочего листа «Функция с ответами». Нажмите знак «+» в поле формулы, и вы увидите формулу на листе формул. Просто введите термин для домена роли, и появится ваша ячейка.
Что такое функция диапазона доменов?
Область определения функции — это полный набор возможных значений независимой переменной.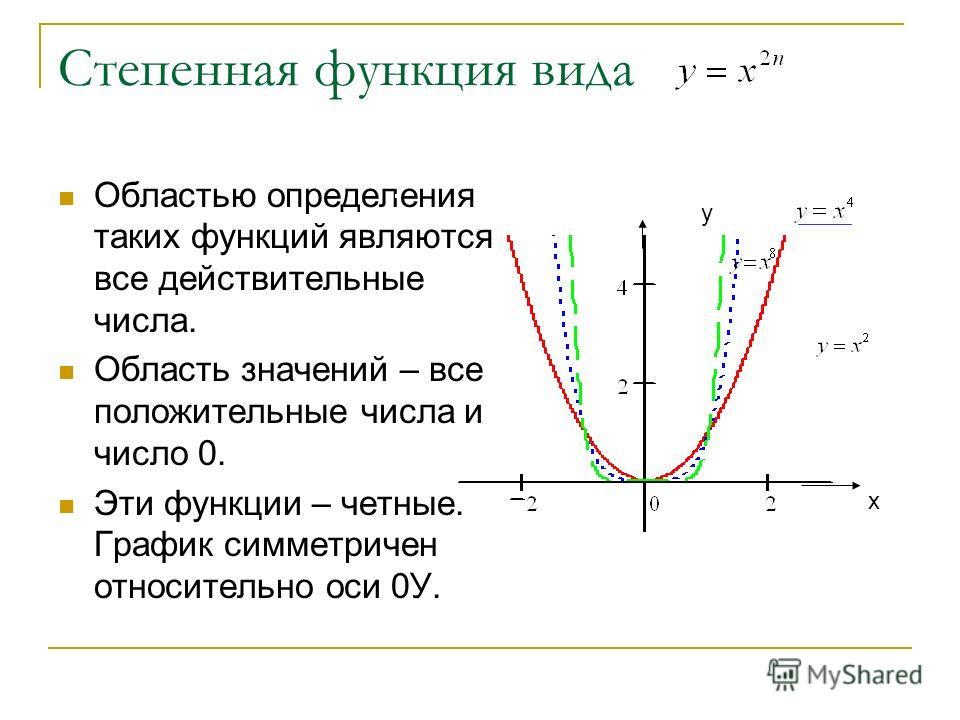 Это определение ясно означает: домен — это набор всех возможных значений x, которые заставляют функцию работать и генерировать реальные значения y.
Это определение ясно означает: домен — это набор всех возможных значений x, которые заставляют функцию работать и генерировать реальные значения y.
Каков диапазон доменов графа?
Поскольку домен относится к набору возможных входных значений, домен графика состоит из всех входных значений, отображаемых на оси x. Диапазон — это количество возможных выходных данных, показанных на оси Y.
Как найти наибольшую область определения функционального уравнения
Объем функции — это набор всех возможных входных данных для функции. Например, диапазон f(x) = x² состоит из всех действительных чисел, а диапазон g(x) = 1 / x состоит из всех действительных чисел, кроме x = 0. Вы также можете определить специальные функции, применение которых более ограничено. Класс Google Facebook Twitter. Адрес электронной почты.
Как получить домен адреса электронной почты?
Чтобы извлечь домен из адреса электронной почты, вы можете использовать формулу, основанную на функциях ПРАВО, ДЛСТР и НАЙТИ. В приведенной выше общей форме электронная почта — это адрес электронной почты, с которым вы работаете. В показанном примере формула E4 выглядит так:
В приведенной выше общей форме электронная почта — это адрес электронной почты, с которым вы работаете. В показанном примере формула E4 выглядит так:
Как найти диапазон других функций?
Самый простой способ определить диапазон других функций, таких как корни и дроби, — построить график функции с помощью графического калькулятора. Найдите значение x вершины функции. Вершина квадратичной функции является вершиной параболы. Помните, что квадратное уравнение равно ax 2 + bx + c.
Что является областью определения квадратного уравнения?
Квадратные уравнения образуют параболический график, направленный вверх или вниз. Поскольку парабола будет бесконечно продолжаться вдоль оси x, площадь самой квадратичной функции — это все действительные числа.
Какова функция домена?
Важной функцией доменных имен является обеспечение легко узнаваемых и запоминающихся имен для интернет-ресурсов с цифровой адресацией.
Эта абстракция позволяет перемещать любой ресурс в другое физическое место в топологии сетевых адресов либо глобально, либо локально в интрасети.
Как найти максимально возможный домен в терминах?
Ваша первая функция определена для всех вещественных значений x, поэтому максимально возможный диапазон является вещественным. Таким образом, вы можете получить максимально широкий диапазон, заметив, что часть косинуса идет от -1 до 1 и добавляет к нему 1.
Какова область определения большинства квадратичных функций?
Поскольку парабола будет бесконечно продолжаться вдоль оси x, площадь самой квадратичной функции — это все действительные числа. Другими словами, квадратное уравнение включает в себя все значения x на числовой прямой и образует диапазон R (символ всех действительных чисел).
Какова область определения функции h?
Итак, домен, здесь домен, домен h — это буквально две действительные записи, где x может быть 3, а pi. Это единственные действительные записи. Это единственные два числа, для которых фактически определена эта функция.
Это единственные действительные записи. Это единственные два числа, для которых фактически определена эта функция.
Каковы возможные значения Дома?
Возможными значениями dom являются действительные и комплексные числа. По умолчанию это реально. Когда dom действителен, все переменные, параметры, константы и значения функций проверяются. Недостатками являются уравнения, неравенства или их логические комбинации.
Когда использовать символ бесконечности в домене?
Вы можете использовать столько символов U, сколько хотите, если в домене есть несколько пробелов. Используйте символы бесконечности и отрицательной бесконечности, чтобы указать, что область простирается бесконечно в обоих направлениях. Всегда используйте (), а не , с бесконечным количеством символов. Обратите внимание, что эта классификация может варьироваться в зависимости от того, где вы живете.
Когда исключать значения в домене функции?
Во-вторых, если уравнение функции содержит знаменатель, исключить из диапазона те значения, у которых знаменатель равен нулю.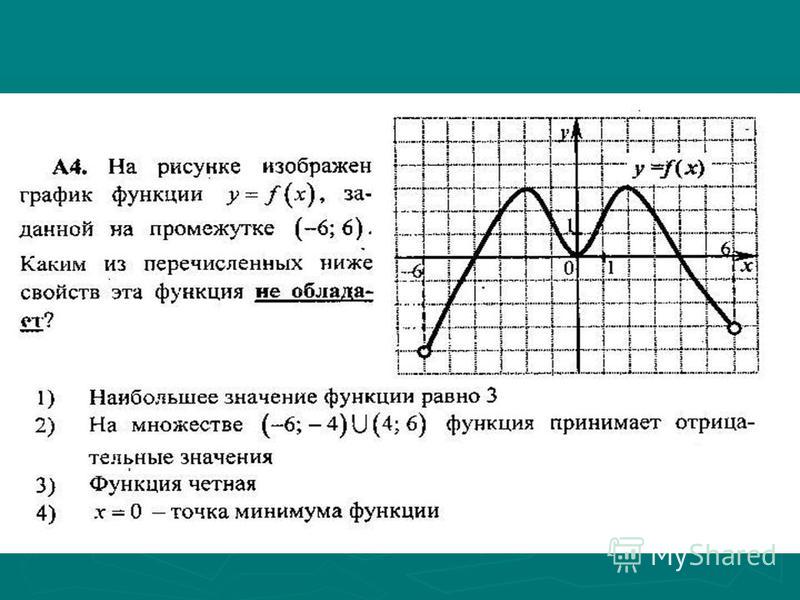 В-третьих, если есть четный корень, вы должны исключить значения, которые сделали бы корневое выражение отрицательным. Прежде чем они начнут, давайте взглянем на соглашения об интервалах:.
В-третьих, если есть четный корень, вы должны исключить значения, которые сделали бы корневое выражение отрицательным. Прежде чем они начнут, давайте взглянем на соглашения об интервалах:.
Можно ли включить четный корень в домен?
Например, они не могут содержать входное значение, вызывающее извлечение четного корня из отрицательного числа, если домен и диапазон являются действительными числами. Или в функции, выраженной в виде формулы, они не могут содержать входное значение в поле, которое привело бы к делению на 0.
Как найти наибольшую область определения графика функции
То же самое касается размера графика по вертикали, поэтому диапазон и диапазон охватывают все действительные числа. Для обратной функции f (x) = 1 x f (x) = 1 x вы не можете делить на 0, поэтому вы должны исключить из диапазона. Кроме того, 1, деленная на любое значение, никогда не может равняться 0, поэтому диапазон не содержит 0.
Как узнать домен и диапазон f f?
Определите диапазон определения и размер функции f f. Вы можете заметить, что размер графика по горизонтали составляет от –3 до 1, поэтому диапазон ff равен (– 3, 1] (– 3, 1). Размер графика по вертикали равен 4–4, поэтому диапазон равен
Вы можете заметить, что размер графика по горизонтали составляет от –3 до 1, поэтому диапазон ff равен (– 3, 1] (– 3, 1). Размер графика по вертикали равен 4–4, поэтому диапазон равен
Область определения и область значений кубической функции — все действительные числа?
Для кубической функции f(x) = x3 f(x) = x3 диапазон состоит из всех действительных чисел, поскольку горизонтальное расширение графика представляет собой полную цепочку действительных чисел. То же самое касается размера графика по вертикали, поэтому диапазон и диапазон охватывают все действительные числа.
Как найти самый большой домен рабочего листа функции
Найти область и область действия функции: Чтобы найти область действия функции, вам нужно найти значения x, для которых функция определена. Знаменатель становится равным нулю, и функция не определена для x = 2. Следовательно, указанная выше функция определена для всех действительных значений x, кроме 2.
Как рабочие листы доменов и диапазонов используются в средней школе?
Эта коллекция рабочих листов по областям и областям в формате PDF дает даже восьмиклассникам аккуратную визуализацию в виде диаграмм и таблиц.
Как проверить свои навыки домена и диапазона?
Проверьте свои навыки с помощью этих распечатываемых таблиц диапазонов и проверок диапазонов, которые предлагают комбинацию абсолютной f(x), квадратного корня, квадратного корня и обратных функций. Определите диапазон (x) и заполните возможные значения x, чтобы найти диапазон (y).
Как найти наибольший домен таблицы функций
Ваша первая функция определена для всех действительных значений x, поэтому максимально возможный диапазон является действительным. Таким образом, вы можете получить максимально широкий диапазон, заметив, что часть косинуса идет от -1 до 1 и добавляет к нему 1.
Как найти максимально возможную область определения в функциях?
Ваша первая функция определена для всех действительных $ x $, поэтому максимально возможный диапазон включает все действительные значения.
Затем вы можете получить максимально широкий диапазон, заметив, что часть косинуса идет от 1 доллара к 1 доллару и добавляет 1 доллар.
Как найти область определения функции в Mathway?
Шаг 1 : Введите функцию, которую вы хотите оборудовать в редакторе. Калькулятор домена позволяет использовать простую или сложную функцию и мгновенно найти домен, как в интервале, так и в определенном формате.
Шаг 2 : Нажмите синюю стрелку, чтобы отправить и посмотреть результат.
Что является примером области определения функции?
Функции влияют на выходы и входы. Область действия функции — это совокупность всех возможных входных данных для функции. Например, диапазон f(x) = x² состоит из всех действительных чисел, а диапазон g(x) = 1 / x состоит из всех действительных чисел, кроме x = 0. Вы также можете определить специальные функции, применение которых более ограничено.
Как найти область определения дробной функции?
Когда вы находите диапазон функции дроби, вы должны исключить любое значение x, которое делает знаменатель равным нулю, потому что вы никогда не сможете делить на ноль. Итак, запишите знаменатель в виде уравнения и установите его равным 0. Вот как это сделать: f(x) = 2x / (x 2 4).
Итак, запишите знаменатель в виде уравнения и установите его равным 0. Вот как это сделать: f(x) = 2x / (x 2 4).
Как написать область определения уравнения?
Определите ограничения на запись и исключите эти значения из домена. Если возможно, укажите домен в качестве интервала. Найдите диапазон функции f(x) = x2 −1 f(x) = x 2 − 1. Входное значение, представленное переменной xx в уравнении, возводится в квадрат, затем результат уменьшается на единицу.
Когда исключать значения из области определения функции?
Во-вторых, если уравнение функции содержит знаменатель, исключить значения, при которых знаменатель равен нулю. В-третьих, при наличии четного корня следует рассмотреть возможность исключения значений, которые сделали бы корневое выражение отрицательным.
Как найти наибольшую область определения функции пример
Посмотрите на квадратурную функцию. При работе с действительными числами максимально возможным диапазоном для функции f(x) = x 2 является R, множество всех действительных чисел. Однако в этой области квадратурная функция имеет досадный недостаток.
Однако в этой области квадратурная функция имеет досадный недостаток.
Домен и диапазон рабочего листа функции
Объем и объем функций Рабочие листы — это отличный способ определить входы и выходы с помощью упорядоченных пар упражнений, таблиц, картографических таблиц, диаграмм и многого другого.
Как определить стоимость домена?
- Запишите проблему.
- Поместите в круглые скобки термины больше нуля.
- Просто отметьте переменную x, добавив 8 к каждой стороне.
- Введите свой домен. Покажите, что область определения этого уравнения равна всем числам от 8 до бесконечности.
Каков диапазон данного домена?
Домен — это числа слева или числа со значением x. Диапазон — это числа справа или числа со значением y.
Встроенная функция Python range(). Давайте разберемся с основами range()… | Автор Tanu N Prabhu
Давайте разберемся с основами функции range() в Python.
Теперь давайте разберемся с концепцией range function() в python. Ниже показаны концепции вместе с примерами, которые помогут вам, ребята, понять range() понятным образом. Кроме того, посетите мой репозиторий GitHub, чтобы найти более подробную информацию о функции диапазона ниже:
Tanu-N-Prabhu/Python
Вы не можете выполнить это действие в данный момент. Вы вошли в другую вкладку или окно. Вы вышли из системы на другой вкладке или…
github.com
Функция range() — это встроенная функция, используемая в python, она используется для генерации последовательности чисел . Если пользователь хочет сгенерировать последовательность чисел с заданными начальным и конечным значениями, он может указать эти значения в качестве параметров функции range(). Затем функция range() сгенерирует последовательность чисел в соответствии с требованиями пользователя.
Ниже показан синтаксис функции range():
range(start, stop, step)
Внутри range() есть три параметра: start, stop и step .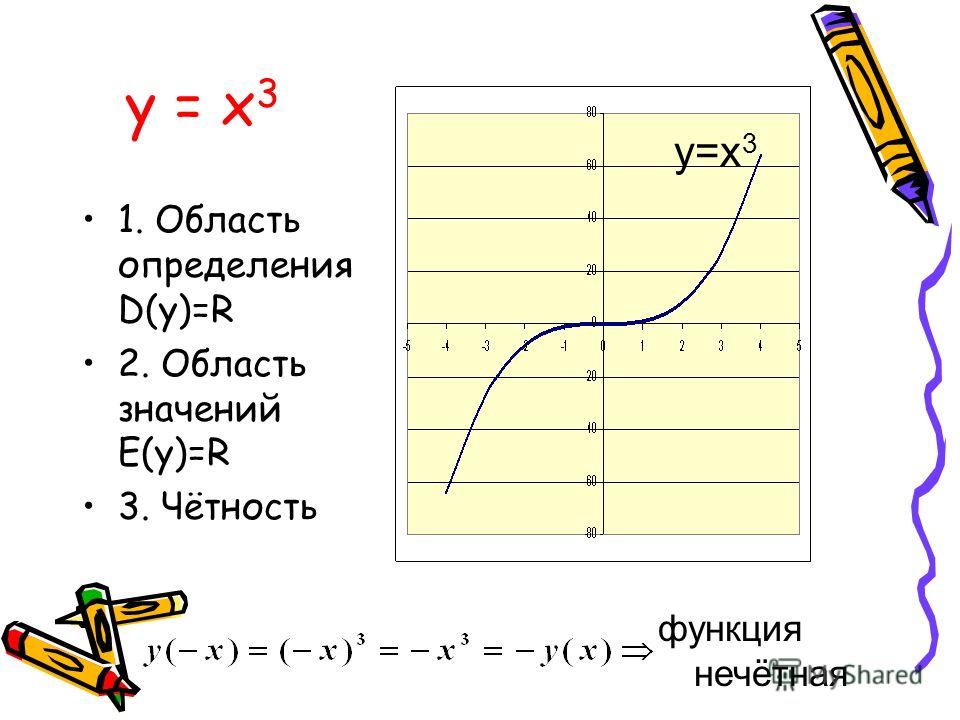 Когда вы думаете об этих трех параметрах, это напоминает реальный сценарий, который будет обсуждаться ниже.
Когда вы думаете об этих трех параметрах, это напоминает реальный сценарий, который будет обсуждаться ниже.
Начало: Необязательный — целое число, указывающее, где начать (значение по умолчанию — 0). Шаг: Необязательный — целое число, указывающее, на сколько увеличить число (значение по умолчанию — 1)
Возвращаемое значение функции диапазона — это последовательность чисел, зависящая от определенных параметров.
1. Давайте посмотрим, что происходит, когда мы просто печатаем функцию диапазона со значением 10. значение 10 указывает конечное значение для функции диапазона, а значение 0 по умолчанию добавляется в качестве начального значения.
2. Давайте посмотрим, что произойдет, если мы поместим функцию диапазона в цикл for.
x = диапазон (10)
для I в x:
Печать (I) 0
1
2
3
4
5
6
7
8
Теперь, как видно выше, мы можем получить значения от 0 до 10, но исключая 10, потому что конечное значение функции диапазона всегда возвращает значение -1 . Отсюда значения 0–10.
Отсюда значения 0–10.
3. Давайте посмотрим, что произойдет, если мы зададим начальное и конечное значение функции диапазона.
x = range(1, 10)
for i in x:
print(i) 1
2
3
4
5
6
7
8
9 6 от 1 до 9, потому что начальное значение определено как 1.4. Давайте посмотрим, что произойдет, когда мы зададим значение шага функции диапазона.
x = диапазон (1, 10, 2)
для i в x:
print(i) 1
3
5
7
9Как показано выше, шаг используется для увеличения чисел, в в этом случае шаг равен 2, поэтому число увеличивается на 2.
В общем, представьте, что функция диапазона похожа на реальный сценарий:
- Вы начинаете идти — начинаете
- Вы делаете свои шаги (шаги) — шаг
- Вы останавливаетесь, чтобы идти, потому что вы достигли пункта назначения — остановка .

Даже если вы не объявляете переменную шага, в этом случае вы будете делать один шаг за раз. Очевидно, что никто не делает два шага за раз.
Да, функция диапазона — это класс, потому что когда вы проверяете тип функции диапазона с помощью type(), вы получаете ответ.
x = range(10)
print(type(x))Функция диапазона не работает для значений с плавающей запятой, так как в соответствии с функцией диапазона плавающий объект не может быть интерпретирован как целое число. Следовательно, сделайте это общим правилом, которое всегда указывает целые значения внутри функции диапазона.
x = диапазон (10,0, 100,5)
для i в x:
print(i) ---------------------------- ------------------------------------------------------ TypeError Traceback (самый последний вызов последним)in () TypeError : объект 'float' не может быть интерпретирован как целое число
----> 1 x = диапазон (10.0, 100.5)
2 for i in x:
3 print(i)Если вам вообще нужно его решить, вы можете преобразовать его в целое число, как показано ниже:
x = range(int(10.0), int(100.5))
для i в x:
print(i) 10
11
12
13
14
-
-
-
-
99Чтобы поддержать этот контекст, я провел некоторое исследование StackOverflow, а затем увидел там проблему, которая была сформулирована как «, я хочу выполнить цикл от 0 до 100, но с шагом 1/2 ». это не простая проблема, потому что для этого применяется приведенная выше концепция, поэтому вам нужно использовать некоторую логику, теперь я использовал какую-то свою логику для решения этой проблемы, как показано ниже:
x = диапазон (0, 100 * 2 )
для i в x:
print(i * 0,5) 0,0
0,5
1.0
1.5
2.0
-
-
-
99.5Вы можете решить вышеуказанную проблему с помощью своей логики и предоставить решение в разделе комментариев ниже.
Это также встроенная функция в python. Я думаю, что это также работает так же, как и range(), когда я попытался выполнить его, я получил странную ошибку:
x = xrange(1, 5)
для i в x:
print(i) ------------------------------------------------------ ----------------------------- NameError Traceback (последний последний вызов)в () NameError: имя 'xrange' не определено
----> 1 x = xrange(1, 5)
2 для i в x:
3 print(i)Затем, после тщательного исследования, я узнал, что xrange является инкрементной версией диапазона в соответствии с переполнением стека. Один из них сказал, что Python2 использует xrange(), а Python3 использует диапазон, поэтому вам не нужно об этом беспокоиться.
Функции диапазона также можно использовать в списке Python. Простой способ сделать это показан ниже:
name = ['Индия', 'Канада', 'Соединенные Штаты', 'Великобритания']
for i in range(1, len(names)):
print (имена[i]) Канада
США
ВеликобританияДумаю, к этому времени вы уже знаете, как это сделать. Но в любом случае я бы предложил решение этой проблемы. В этом случае вам нужно просто поиграть с параметром шага .
Увеличение
x = диапазон (1, 10, 2)
для I в x:
Print (I) 1
3
5
7
Уменьшение
1. 10, 1, -2)
for i in x:
print(i) 10
8
6
4
2Это все, что вам нужно знать о функции диапазона в Python, я рекомендую вам прочитать Официальное руководство Python:
Встроенные функции — Документация Python 3.8.0
Интерпретатор Python имеет ряд встроенных функций и типов, которые всегда доступны.
Они перечислены…
docs.python.org
Спасибо, ребята, за чтение этого краткого руководства, я надеюсь, вам понравилось, дайте мне знать о своем мнении, и если у вас есть какие-либо сомнения, раздел комментариев полностью ваш.
Вложенная функция, область действия переменной и замыкания в Python
В этом посте сначала представлены вложенные функции, затем различные области действия переменных, такие как глобальные переменные, локальные переменные в функциях и т. д., и, наконец, замыкания с использованием вложенной функции в Python.
Вы можете узнать о функциях Python из нашего курса Python и из этого поста.
Вложенная функция
Как и вложенные циклы, в Python также могут быть вложенные функции. Мы просто создаем функцию, используя def внутри другой функции, чтобы вложить две функции. Например,
def f1(): #внешняя функция печать ("Привет") def f2(): #внутренняя функция печать ("мир") f2() f1()Выход
Привет
мир
def f1(): #внешняя функция x = 1 #переменная, определенная в функции f1 def f2(a): #внутренняя функция print (a+x) #доступ к переменной внешней функции f2(2) f1()Вывод
3Это кажется довольно простым.
Вы можете видеть, что мы также получили доступ к переменным внешней функции из внутренней функции. Итак, попробуем заменить переменные внешней функции на переменные внутренней.
def f1(): #внешняя функция x = 1 # переменная, определенная во внешней функции def f2(a): #внутренняя функция # создаст новую переменную во внутренней функции #вместо изменения значения x внешней функции х = 4 напечатать (а+х) print (x) # печатает значение x внешней функции f2(2) f1()Выход
1
6Из приведенных выше двух примеров видно, что мы можем вывести переменные внешней функции из внутренней, но не можем их изменить.
x=4создал новую переменную с именем 'x' внутри функции f2 вместо изменения значения переменной 'x' функции f1. Поэтому, прежде чем перейти к более подробному обсуждению вложенных функций, давайте сначала узнаем об области видимости переменных в Python, т.е. о том, где находятся переменные и откуда мы можем получить к ним доступ.
Область видимости переменных
Место, где мы можем найти переменную и при необходимости получить к ней доступ, называется областью видимости переменной. Итак, давайте узнаем, что это за прицелы.
Локальные и глобальные переменные
Переменная в функции в Python является локальной переменной, если она не объявлена как-то иначе. Доступ к локальной переменной возможен только локально, т. е. переменная, определенная внутри функции, доступна только для этой функции и не может использоваться вне функции.
защита f1(): а = 5 f1() #a не может быть доступен вне функции f1 print (a) # выдаст ошибкуВыход
Трассировка (последний последний вызов):
Файл "a.py", строка 5, в
print x # выдастerror
NameError: имя 'x' не определеноВы можете видеть, что переменная 'a', созданная внутри функции, является локальной переменной и недоступна вне функции.
Кроме того, мы можем получить доступ из функции к переменным, которые определены вне этой функции, но не можем их изменить.
а = 5 защита f1(): print (a) # напечатает 5 f1()Вывод
5Мы можем вывести глобальную переменную 'a'. Python сначала искал переменную с именем «a» внутри функции, а когда она не была найдена, он искал в глобальной области видимости и печатал глобальное значение «a».
а = 1 защита f1(): а = 5 print (a) #будет печатать 5 print (a) #будет печатать 1 f1()Выход
1
5Вы можете видеть, что объявление
a = 5, создал новую локальную переменную внутри функции вместо изменения существующей глобальной переменной «a». Это связано с тем, что Python предполагает, что переменная является локальной, если она явно не объявлена глобальной.Чтобы сообщить Python, что мы хотим использовать глобальную переменную внутри функции, нам нужно использовать ключевое слово
global.Пример приведен ниже.
а = 1 защита f1(): global a #используя глобальную переменную a a = 5 # глобальная переменная изменена на 5 print (a) #будет печатать 5 f1() print (a) #будет печатать 5Выход
5
5Обратите внимание, что в отличие от других языков, таких как C, Python не имеет отдельной области видимости для циклов, if/else и т. д. Таким образом, изменение переменных внутри цикла также изменит глобальную переменную.
а = 1 если правда: а = 2 печать (а)Выход
2а = 1 для я в диапазоне (1,10): а = я печать (а)Выход
9Разобравшись с глобальными и локальными переменными, давайте углубимся в область действия переменных во вложенных функциях.
Область действия переменных во вложенной функции
Мы уже знаем, как получить доступ к глобальной переменной из функции.

В этом разделе мы узнаем о доступе и изменении переменных внешней функции из внутренней. Итак, сначала попробуем вывести переменную внешней функции из внутренней.def f1(): #внешняя функция а = 1 def f2(): #внутренняя функция print (a) #будет печатать 1 f2() f1()Вывод
1Как видите, мы можем напечатать переменную внешней функции. Это похоже на печать глобальной переменной из функции.
Попробуем изменить значение переменной внешней функции.
def f1(): #внешняя функция а = 1 def f2(): #внешняя функция а = 2 печать (а) # печатает 2 f2() print (а) #prints 1 f1()Выход
2
1Как видите, мы не можем изменить значение переменной внешней функции от внутренней.
a=2создал новую локальную переменную функции f2 вместо изменения значения 'a' из функции f1.Существуют разные способы изменить значение локальной переменной внешней функции из внутренней функции.
Первый способ — использовать итерируемый объект.
def f1(): #внешняя функция а = [1] def f2(): #внешняя функция а[0] = 2 print (a[0]) #выводит 2 f2() print (a[0]) #выводит 2 f1()Выход
2
2Мы также можем изменить значение переменной, как показано в следующем примере.
def f1(): #внешняя функция f1.а = 1 def f2(): #внешняя функция f1.а = 2 печать (f1.a) # печатает 2 f2() печать (f1.a) # печатает 2 f1()
Выход
2
2Третий способ — использовать ключевое слово nonlocal. Обратите внимание, что
нелокальный 9Ключевое слово 1159 работает только с Python3. Вы можете использовать любой из двух способов, упомянутых выше, чтобы изменить значение переменной в Python2.Мы можем использовать ключевое слово
nonlocalдля изменения значения переменной внешней функции аналогично использованию ключевого словаglobalдля изменения значения глобальных переменных.def f1(): #внешняя функция а = 1 def f2(): #внешняя функция нелокальный а а = 2 печать (а) # печатает 2 f2() печать (а) # печатает 2 f1()Выход
2
2Когда вы разобрались с концепциями областей действия переменных, давайте узнаем о замыканиях в Python.
Закрытие
Закрытие, по сути, ведет учет функции в среде. Например, если мы вызываем функцию с аргументом (foo(1)), то она должна хранить запись об окружении с этим аргументом для последующего использования в программе. Это будет понятно из приведенных ниже примеров.
по умолч. f1(a): защита f2(b): вернуть а+б вернуть f2 а = f1(1) б = f1(100) распечатать (а(2)) печать (б(2))Выход
3
102Вы можете видеть, что среда, созданная f1(1), отличается от среды f1(100), и обе они были запомнены Python, поэтому печатаются разные значения для a(2) и b(2).
Вот что такое закрытие.
Таким образом, функция (объект), которая запоминает среду, в которой она была создана, является замыканием.
Замыкание также является ответом на вопрос - "Какая польза от вложенной функции". Но это также ставит перед нами другой вопрос: «Какая польза от замыканий?»
Классы более гибкие, чем замыкания, но замыкания работают быстрее. Можно создавать замыкания для обработки простых случаев, когда создание класса на самом деле не требуется.
Функция ПУСТЬ
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Больше...Меньше
Функция LET присваивает имена результатам вычислений. Это позволяет сохранять промежуточные вычисления, значения или определять имена внутри формулы. Эти имена применяются только в рамках функции LET. Подобно переменным в программировании, оператор LET реализуется с помощью собственного синтаксиса формул Excel.
Чтобы использовать функцию ПУСТЬ в Excel, вы определяете пары имен и связанных значений, а также расчет, который использует их все.
Вы должны определить по крайней мере одну пару имя/значение (переменную), а LET поддерживает до 126.
Преимущества
Повышенная производительность Если одно и то же выражение вводится в формулу несколько раз, Excel вычисляет этот результат несколько раз. LET позволяет вызывать выражение по имени и для Excel вычислять его один раз.
Легкое чтение и составление Больше не нужно помнить, на что ссылается конкретный диапазон/ссылка на ячейку, что делает ваш расчет или копировать/вставлять одно и то же выражение. Имея возможность объявлять и называть переменные, вы можете дать значимый контекст себе и потребителям вашей формулы.
=LET(имя1, имя_значение1, вычисление_или_имя2, [имя_значение2, вычисление_или_имя3...])
Аргумент
Описание
имя1
Обязательно
Первое имя для назначения. Должен начинаться с буквы. Не может быть результатом формулы или конфликтовать с синтаксисом диапазона.
имя_значение1
Обязательно
Значение, присвоенное имени1.
расчет_или_имя2
Обязательно
Один из следующих:
Вычисление, в котором используются все имена в функции LET. Это должен быть последний аргумент в функции LET.
Второе имя для присвоения второму значению name_value. Если указано имя, становятся обязательными имя_значение2 и вычисление_или_имя3.
имя_значение2
Дополнительно
Значение, назначенное для вычисления_или_имя2.
расчет_или_имя3
Дополнительно
Один из следующих:
Вычисление, в котором используются все имена в функции LET. Последний аргумент в функции LET должен быть вычислением.
Третье имя для присвоения третьему значению name_value. Если указано имя, становятся обязательными имя_значение3 и вычисление_или_имя4.
Примечания:
org/ListItem">
Последний аргумент должен быть вычислением, возвращающим результат.
Имена переменных совпадают с допустимыми именами, которые можно использовать в диспетчере имен. Например. «a» допустимо, а «c» — нет, потому что оно конфликтует со ссылками на стиль R1C1.
Примеры
Пример 1
Рассмотрим простое выражение "СУММ(x, 1)", где x – это именованная переменная, которой можно присвоить значение (в данном случае x присваивается значение 5).
=ЛЕТ(х, 5, СУММ(х, 1))
Когда эта формула вводится в ячейку, она возвращает значение 6.
Пример 2
Предположим, у вас есть необработанные данные о продажах, и вы хотите отфильтровать эти данные, чтобы показать одного человека, и добавить тире к любым пустым ячейкам.
Нефильтрованные данные
Отфильтрованные данные
Хотя описанное выше можно выполнить и без LET, использование LET улучшает читаемость формулы и вычисляет в два раза быстрее, чем без LET.
Пример данных
Скопируйте следующую таблицу в ячейку A1 пустого рабочего листа, если хотите самостоятельно выполнить этот пример.
Респ.
Регион
Продукт
Прибыль
Эми
Восток
Яблоко
1,33 $
Фред
Юг
Банан
$0,09
Эми
Запад
Манго
1,85 $
Фред
Север
0,82 $
Фред
Запад
Банан
1,25 $
Эми
Восток
Яблоко
0,72 $
Фред
Север
Манго
$0,54
Оригинальная формула
=ЕСЛИ(ЕСПУСТО(ФИЛЬТР(A2:D8,A2:A8="Фред")),"-", ФИЛЬТР(A2:D8,A2:A8="Фред"))
Формула с использованием LET
=LET( filterCriteria , «Фред» , filteredRange , FILTER(A2:D8,A2:A8= filterCriteria ), IF(ISBLANK( filterRange ", 6 9edRange)"-1"-1 )
Шлем | Flow Control
Структуры управления (называемые «действиями» на языке шаблонов) предоставляют вам, автор шаблона, с возможностью контролировать поток шаблона поколение.
Язык шаблонов Helm предоставляет следующие управляющие структуры:
if/elseдля создания условных блоковсдля указания области действиядиапазон, который обеспечивает цикл в стиле «для каждого» несколько действий для объявления и использования named сегменты шаблона:
определитьобъявляет новый именованный шаблон внутри вашего шаблонашаблонимпортирует именованный шаблонблокобъявляет специальный вид заполняемой области шаблонаВ этом разделе мы поговорим о
if,сидиапазоне. Остальные рассматривается в разделе «Именованные шаблоны» далее в этом руководстве.If/Else
Первая управляющая структура, которую мы рассмотрим, предназначена для условного включения блоков. текста в шаблоне. Это блок
, если/, иначе.Базовая структура условного предложения выглядит следующим образом:
{{ если ТРУБОПРОВОД }} # Сделай что-нибудь {{ иначе, если ДРУГОЙ КОНТРОЛЛЕР }} # Сделайте что-нибудь еще {{ еще }} # Случай по умолчанию {{ конец }}Обратите внимание, что сейчас мы говорим о конвейерах вместо значений. Причина для того, чтобы было ясно, что управляющие структуры могут выполнять всю конвейер, а не просто оценивать значение.
Конвейер оценивается как false , если значение:
- логическое значение false
- числовой ноль
- Пустая строка
- A
Nil(пустая или нулевая)- Пустая коллекция (
MAP,Slice,Tuple,DICT,Array). условие верно.
Давайте добавим простое условие в нашу ConfigMap.
Мы добавим еще один параметр, если напиток настроен на кофе:
apiVersion: v1 вид: карта конфигурации метаданные: имя: {{ .Release.Name }}-configmap данные: мое значение: "Привет, мир" напиток: {{ .Values.favorite.drink | по умолчанию "чай" | цитировать }} еда: {{ .Values.favorite.food | верхний | цитировать }} {{ if eq .Values.favorite.drink "coffee" }}mug: "true"{{ end }}Так как мы закомментировали
drink: coffeeв нашем последнем примере, вывод должен не включает кружку: «истинный» флаг. Но если мы добавим эту строку обратно в нашvalues.yamlвывод должен выглядеть так:# Источник: mychart/templates/configmap.yaml апиВерсия: v1 вид: карта конфигурации метаданные: имя: очевидец-элк-configmap данные: мое значение: "Привет, мир" пить кофе" еда: "ПИЦЦА" кружка: "правда"Управление пробелами
Пока мы смотрим на условные операторы, мы должны бросить беглый взгляд на то, как пробелы контролируются в шаблонах.
Возьмем предыдущий пример и отформатируйте его, чтобы его было немного легче читать:
apiVersion: v1 вид: карта конфигурации метаданные: имя: {{ .Release.Name }}-configmap данные: мое значение: "Привет, мир" напиток: {{ .Values.favorite.drink | по умолчанию "чай" | цитировать }} еда: {{ .Values.favorite.food | верхний | цитировать }} {{ if eq .Values.favorite.drink "кофе" }} кружка: "правда" {{ конец }}Поначалу все выглядит хорошо. Но если мы пропустим его через механизм шаблонов, мы получить печальный результат:
$ helm install --dry-run --debug ./mychart СЕРВЕР: "локальный: 44134" ПУТЬ К ДИАГРАМЕ: /Users/mattbutcher/Code/Go/src/helm.sh/helm/_scratch/mychart Ошибка: ошибка синтаксического анализа YAML в mychart/templates/configmap.yaml: ошибка преобразования YAML в JSON: yaml: строка 9: не найден ожидаемый ключЧто случилось? Мы сгенерировали неправильный YAML из-за пробелов выше.
# Источник: mychart/templates/configmap.yaml апиВерсия: v1 вид: карта конфигурации метаданные: имя: очевидец-элк-configmap данные: мое значение: "Привет, мир" пить кофе" еда: "ПИЦЦА" кружка: "правда"
кружкаимеет неправильный отступ. Давайте просто удалим эту строку и запустим снова:apiVersion: v1 вид: карта конфигурации метаданные: имя: {{ .Release.Name }}-configmap данные: мое значение: "Привет, мир" напиток: {{ .Values.favorite.drink | по умолчанию "чай" | цитировать }} еда: {{ .Values.favorite.food | верхний | цитировать }} {{ if eq .Values.favorite.drink "кофе" }} кружка: "правда" {{ конец }}Когда мы отправим это, мы получим YAML, который действителен, но все еще выглядит немного забавно:
# Источник: mychart/templates/configmap.yaml апиВерсия: v1 вид: карта конфигурации метаданные: имя: говоря-шимпанзе-configmap данные: мое значение: "Привет, мир" пить кофе" еда: "ПИЦЦА" кружка: "правда"Обратите внимание, что мы получили несколько пустых строк в нашем YAML.
Почему? Когда шаблон двигатель работает, он удаляет содержимое внутри
{{и}}, но оставляет остальные пробелы в точности как есть.YAML приписывает значение пробелам, поэтому управление пробелами становится довольно удобным. важный. К счастью, в шаблонах Helm есть несколько полезных инструментов.
Во-первых, синтаксис объявлений шаблонов с фигурными скобками можно изменить с помощью специальные символы, чтобы указать механизму шаблонов уничтожать пробелы.
{{-(с добавлены тире и пробел) указывает, что пробелы должны быть оставлены, в то время как-}}означает, что пробел справа должен быть использован. Будьте осторожны! Новые строки - это пробел!Убедитесь, что между
-и остальной частью директивы есть пробел.{{- 3 }}означает "обрезать левый пробел и напечатать 3", а{{-3 }}означает "печать -3".Используя этот синтаксис, мы можем изменить наш шаблон, чтобы избавиться от этих новых строк:
apiVersion: v1 вид: карта конфигурации метаданные: имя: {{ .Release.Name }}-configmap данные: мое значение: "Привет, мир" напиток: {{ .Values.favorite.drink | по умолчанию "чай" | цитировать }} еда: {{ .Values.favorite.food | верхний | цитировать }} {{- if eq .Values.favorite.drink "кофе" }} кружка: "правда" {{- конец }}
Просто чтобы прояснить этот момент, давайте скорректируем вышеизложенное и замените
*для каждого пробела, который будет удален в соответствии с этим правилом.*в конце строки указывает на символ новой строки, который будет удаленоAPIVersion: v1 вид: карта конфигурации метаданные: имя: {{ .Release.Name }}-configmap данные: мое значение: "Привет, мир" напиток: {{ .Values.favorite.drink | по умолчанию "чай" | цитировать }} еда: {{ .Values.favorite.food | верхний | цитировать }}* **{{- if eq .Values.favorite.drink "кофе" }} кружка: "правда"* **{{- конец }}Имея это в виду, мы можем запустить наш шаблон через Helm и увидеть результат:
# Источник: mychart/templates/configmap.yaml апиВерсия: v1 вид: карта конфигурации метаданные: имя: clunky-cat-configmap данные: мое значение: "Привет, мир" пить кофе" еда: "ПИЦЦА" кружка: "правда"
Будьте осторожны с модификаторами жевания. Легко сделать что-то случайно вот так:
food: {{ .Values.favorite.food | верхний | цитировать }} {{- if eq .Values.favorite.drink "coffee" -}} кружка: "правда" {{- конец -}}Это будет производить еду
: кружка "ПИЦЦА": "true", потому что она потребляла новые строки на обоих стороны.Подробнее об управлении пробелами в шаблонах см. Официальный документация по шаблону
Наконец, иногда проще указать системе шаблонов, как сделать отступ за вас вместо того, чтобы пытаться освоить интервал директив шаблона. По этой причине, иногда может оказаться полезным использовать функцию
indent({{ indent 2 "mug:true" }}).Изменение прицела с помощью
сСледующей структурой управления, на которую следует обратить внимание, является
с действием.Это контролирует переменная область видимости. Напомним, что
.является ссылкой на текущую область . Так.Values указывает шаблону найти объектValues в текущей области.Синтаксис для
саналогичен простому операторуif:{{ with PIPELINE }} # ограниченная область действия {{ конец }}Область действия может быть изменена.
сможет позволить вам установить текущую область (.) на конкретный объект. Например, мы работали с.Values.favorite. Давайте перепишем нашу ConfigMap, чтобы изменить.область, на которую нужно указать.Values.favorite:apiVersion: v1 вид: карта конфигурации метаданные: имя: {{ .Release.Name }}-configmap данные: мое значение: "Привет, мир" {{- с .Values.favorite }} напиток: {{ .drink | по умолчанию "чай" | цитировать }} еда: {{ .еда | верхний | цитировать }} {{- конец }}
Обратите внимание, что мы удалили условие
ifиз предыдущего упражнения. потому что теперь это не нужно - блок послестолько выполняется если значениеPIPELINEне пусто.Обратите внимание, что теперь мы можем ссылаться на
.drinkи.foodбез их уточнения. Это потому, что операторс операторомустанавливает., чтобы указать на.Values.favorite..сбрасывается до предыдущей области действия через{{конец}}.Но вот предостережение! Внутри ограниченной области вы не будете возможность доступа к другим объектам из родительской области с помощью
.. Это, для например, не получится:{{- с .Values.favorite }} напиток: {{ .drink | по умолчанию "чай" | цитировать }} еда: {{ .еда | верхний | цитировать }} релиз: {{ .Release.Name }} {{- конец }}Произойдет ошибка, поскольку
Release.не входит в ограниченный объем наName
.. Однако, если мы поменяем местами последние две строки, все будет работать как положено. потому что область сбрасывается после{{ end }}.{{- с .Values.favorite }} напиток: {{ .drink | по умолчанию "чай" | цитировать }} еда: {{ .еда | верхний | цитировать }} {{- конец }} релиз: {{ .Release.Name }}Или мы можем использовать
$для доступа к объектуRelease.Nameот родителя сфера.$сопоставляется с корневой областью, когда начинается выполнение шаблона, и это не изменяется во время выполнения шаблона. Следующее также будет работать:{{- с .Values.favorite }} напиток: {{ .drink | по умолчанию "чай" | цитировать }} еда: {{ .еда | верхний | цитировать }} релиз: {{ $.Release.Name }} {{- конец }}После просмотра диапазона
мы рассмотрим переменные шаблона, которые предлагают одно решение проблемы определения области выше.Зацикливание с диапазоном
действиеМногие языки программирования поддерживают циклы с использованием
дляциклов,foreachпетли или аналогичные функциональные механизмы. В языке шаблонов Helm способ итерация по коллекции заключается в использованиидиапазоноператор.Для начала добавим список начинок для пиццы в наш файл
values.yaml:избранное: пить кофе еда: пицца пиццаНачинки: - грибы - сыр - перец - лукТеперь у нас есть список (называемый в шаблонах ломтиком
) изначинок пиццы. Мы можем измените наш шаблон, чтобы распечатать этот список в нашей ConfigMap:apiVersion: v1 вид: карта конфигурации метаданные: имя: {{ .Release.Name }}-configmap данные: мое значение: "Привет, мир" {{- с .Values.favorite }} напиток: {{ .drink | по умолчанию "чай" | цитировать }} еда: {{ .еда | верхний | цитировать }} {{- конец }} начинки: |- {{- диапазон .Values.pizzaToppings }} - {{ . | название | цитировать }} {{- конец }}
Мы можем использовать
$для доступа к спискуValues.pizzaToppingsот родителя сфера.$сопоставляется с корневой областью, когда начинается выполнение шаблона, и это не изменяется во время выполнения шаблона. Также будет работать следующее:apiVersion: v1 вид: карта конфигурации метаданные: имя: {{ .Release.Name }}-configmap данные: мое значение: "Привет, мир" {{- с .Values.favorite }} напиток: {{ .drink | по умолчанию "чай" | цитировать }} еда: {{ .еда | верхний | цитировать }} начинки: |- {{- диапазон $.Values.pizzaToppings }} - {{ . | название | цитировать }} {{- конец }} {{- конец }}Давайте подробнее рассмотрим начинку
: список. Функция диапазонабудет «перебрать» (перебрать) списокpizzaToppings.Но сейчас что-то интересно бывает. Точно так же, как
с, устанавливает область действия., так же как и диапазоноператор. Каждый раз в цикле.устанавливается на текущую начинку для пиццы. То есть в первый раз.устанавливается нагрибов. Вторая итерация это установить насыри так далее.Мы можем отправить значение
.прямо по конвейеру, поэтому, когда мы делаем{{ . | название | цитата }}, он отправляет. отдозаголовок(функция регистра заглавий), а затем вцитата. Если мы запустим этот шаблон, вывод будет:# Источник: mychart/templates/configmap.yaml апиВерсия: v1 вид: карта конфигурации метаданные: имя: острая-стрекоза-configmap данные: мое значение: "Привет, мир" пить кофе" еда: "ПИЦЦА" начинки: |- - «Грибы» - "Сыр" - «Перцы» - "Лук"В этом примере мы сделали кое-что хитрое.
Начинка
: |- строкаобъявление многострочной строки. Так что наш список начинок на самом деле не YAML. список. Это большая струна. Зачем нам это делать? Поскольку данные в ConfigMapsданныесостоят из пар ключ/значение, где и ключ, и значение простые струны. Чтобы понять, почему это так, взгляните на Документы Kubernetes ConfigMap. Впрочем, для нас эта деталь не имеет большого значения.Маркер
|-в YAML принимает многострочную строку. Это может быть полезным метод встраивания больших блоков данных в ваши манифесты, как проиллюстрировано здесь.Иногда полезно иметь возможность быстро составить список внутри вашего шаблона, а затем перебрать этот список. В шаблонах Helm есть функция, позволяющая сделать это легко:
кортеж. В информатике кортеж — это набор фиксированных значений в виде списка. размер, но с произвольными типами данных. Это примерно передает способкортежесть использовал.

 Другими словами, это набор всех возможных значений независимой переменной.
Другими словами, это набор всех возможных значений независимой переменной. Диапазон зависит от знака старшего коэффициента: y ≥ min (+) или y ≥ max, (-). См.: Квадратичные функции.
Диапазон зависит от знака старшего коэффициента: y ≥ min (+) или y ≥ max, (-). См.: Квадратичные функции. Попробуйте ввести очень большое (например, миллион) или очень маленькое (например, отрицательное значение миллиона) и посмотрите, сработает ли это.
Попробуйте ввести очень большое (например, миллион) или очень маленькое (например, отрицательное значение миллиона) и посмотрите, сработает ли это. Таким образом, f(-2) = 0/-5 = 0,
Таким образом, f(-2) = 0/-5 = 0,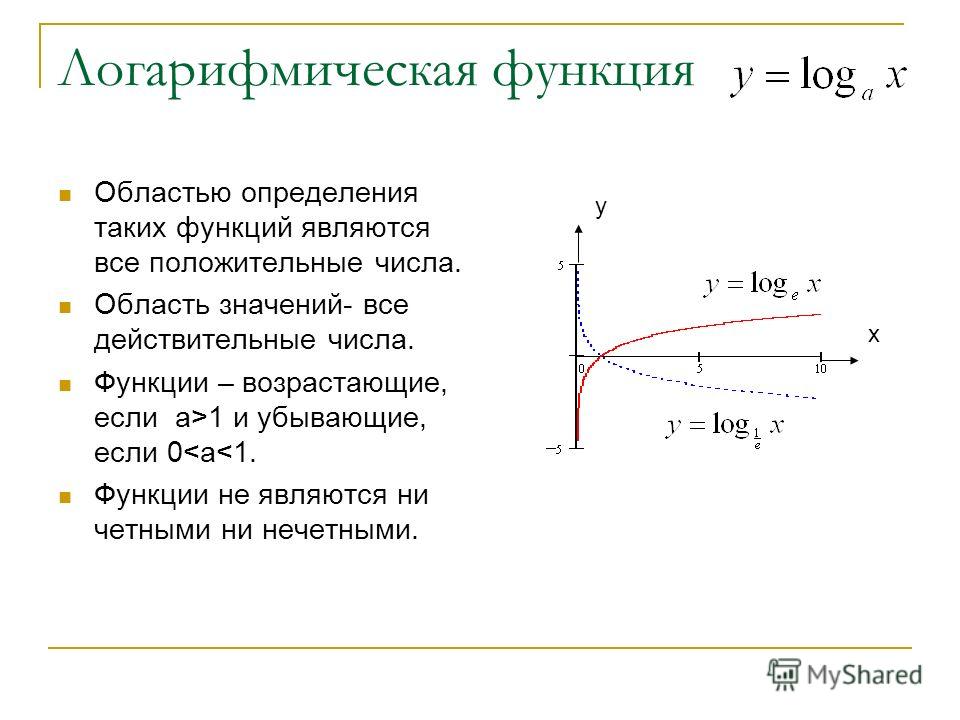 Каждый вход для функции f является членом этой области и может быть представлен x.
Каждый вход для функции f является членом этой области и может быть представлен x.
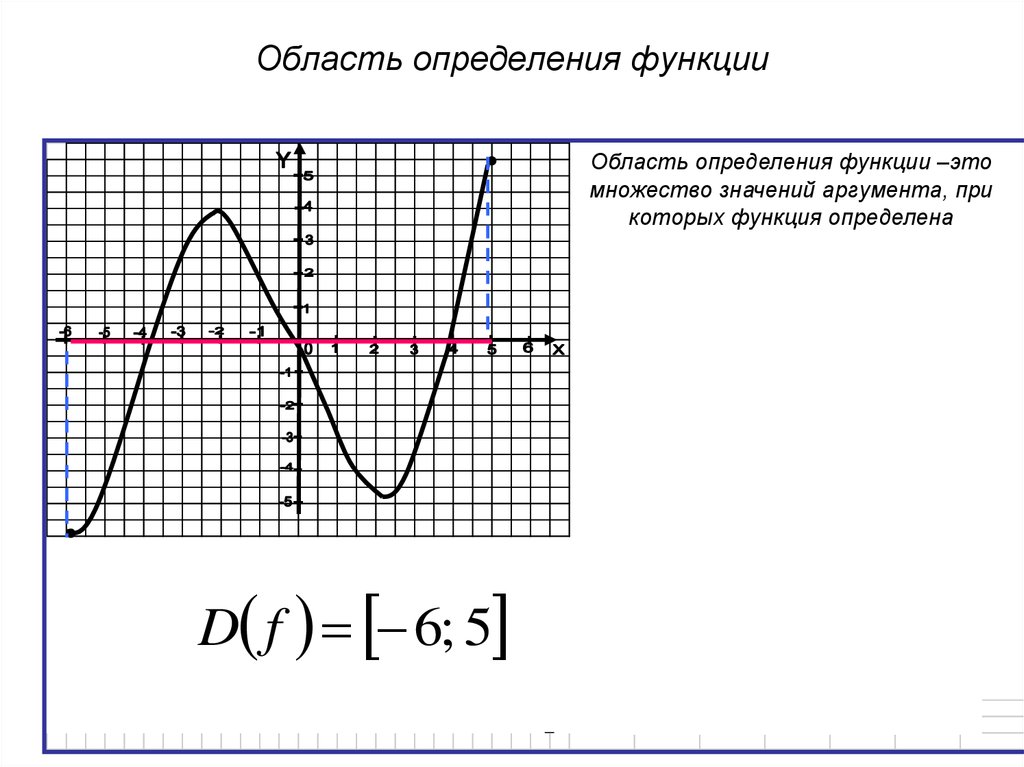 На самом деле, они очень важны при определении функции.
На самом деле, они очень важны при определении функции.



 Следовательно, область определения данной функции состоит из всех действительных значений или R-значений. Чтобы определить область определения функции, вы должны сначала найти обратную y.
Следовательно, область определения данной функции состоит из всех действительных значений или R-значений. Чтобы определить область определения функции, вы должны сначала найти обратную y. Разумная область: {x | R, x 3}, потому что в выражении квадратного корня не может быть отрицательного значения.
Разумная область: {x | R, x 3}, потому что в выражении квадратного корня не может быть отрицательного значения.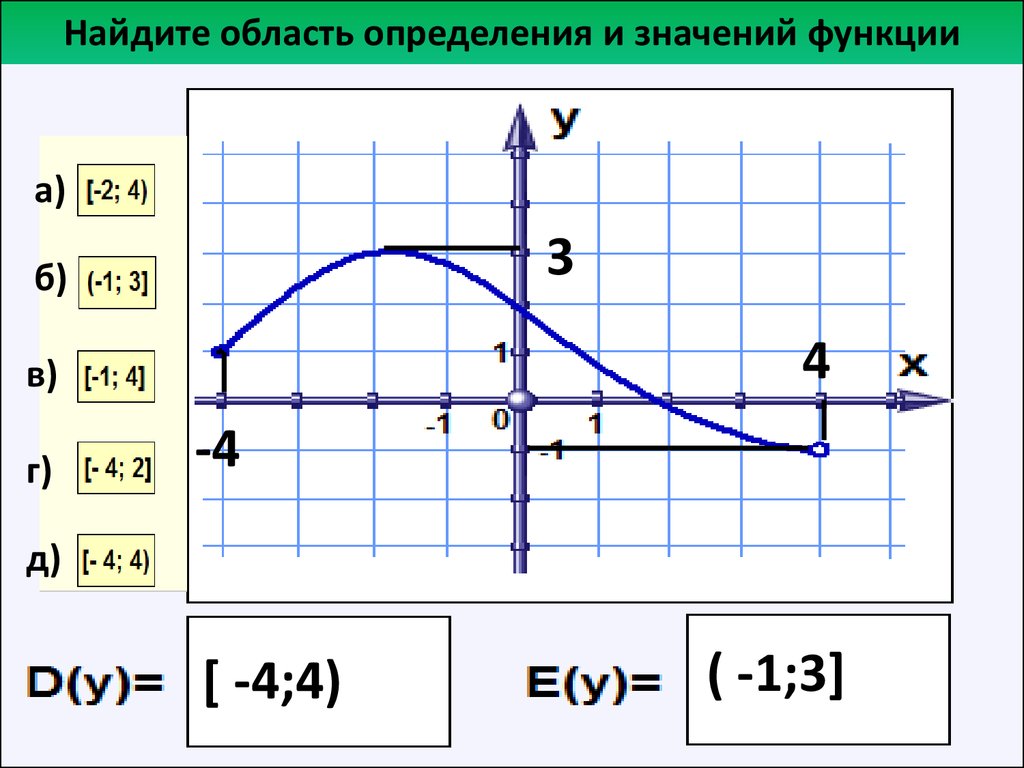 Используя термины «площадь» и «площадь», они переформулировали определение функции следующим образом.
Используя термины «площадь» и «площадь», они переформулировали определение функции следующим образом.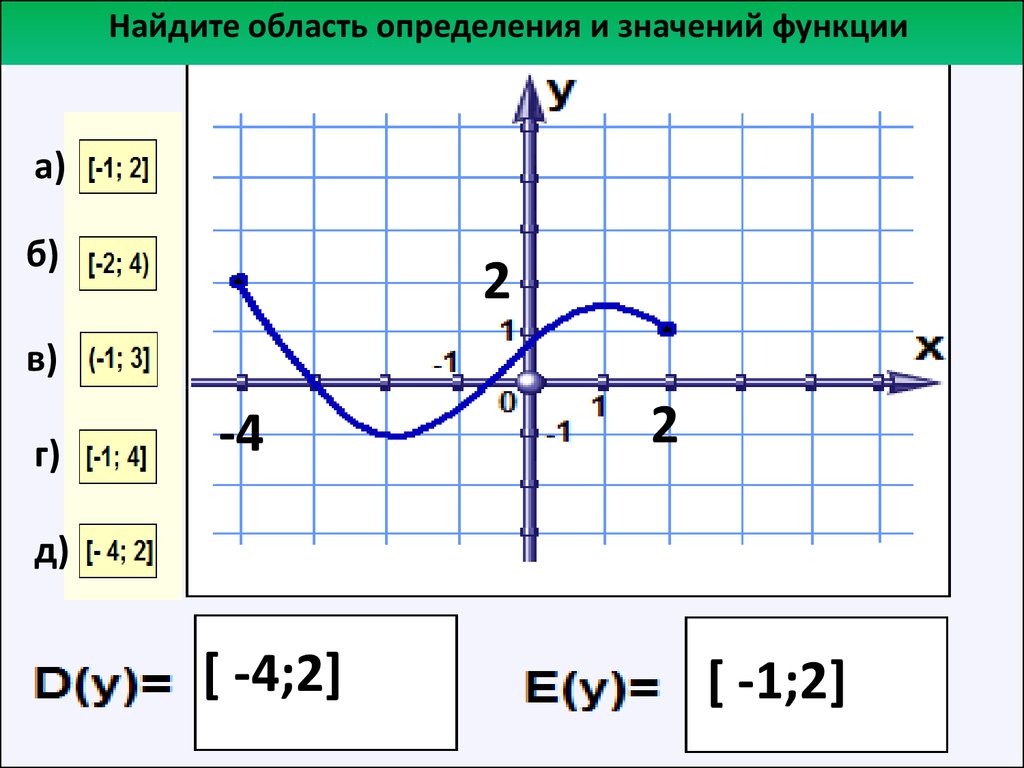 Эта абстракция позволяет перемещать любой ресурс в другое физическое место в топологии сетевых адресов либо глобально, либо локально в интрасети.
Эта абстракция позволяет перемещать любой ресурс в другое физическое место в топологии сетевых адресов либо глобально, либо локально в интрасети.
 Затем вы можете получить максимально широкий диапазон, заметив, что часть косинуса идет от 1 доллара к 1 доллару и добавляет 1 доллар.
Затем вы можете получить максимально широкий диапазон, заметив, что часть косинуса идет от 1 доллара к 1 доллару и добавляет 1 доллар.
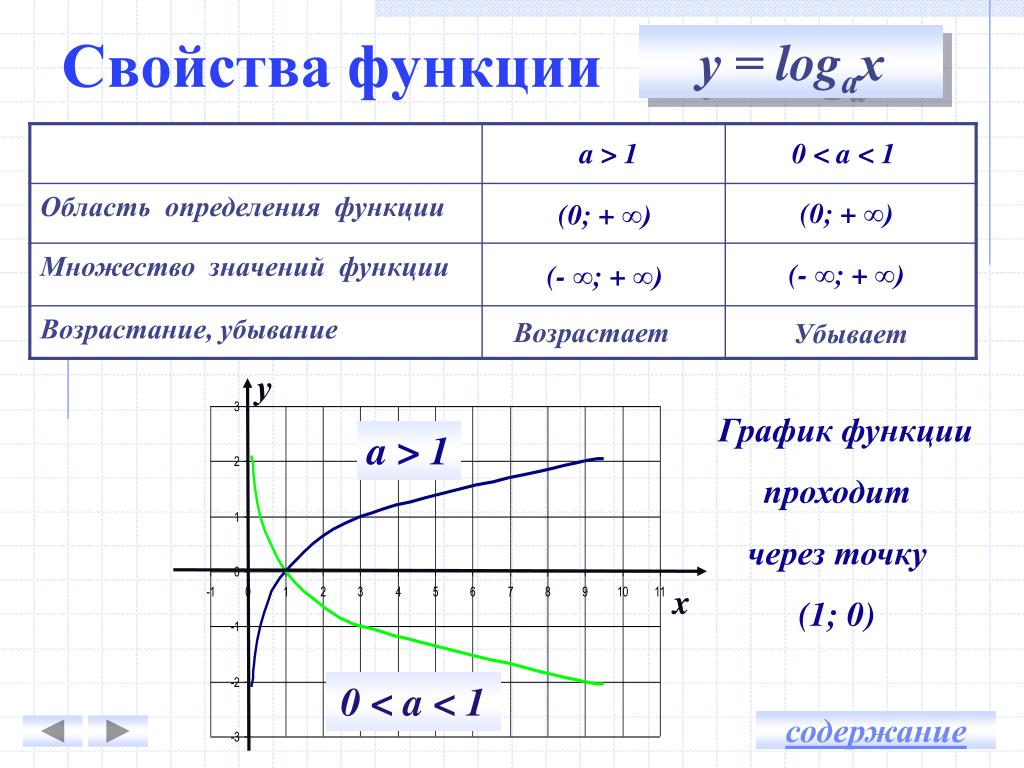 0, 100.5)
0, 100.5)  0
0 
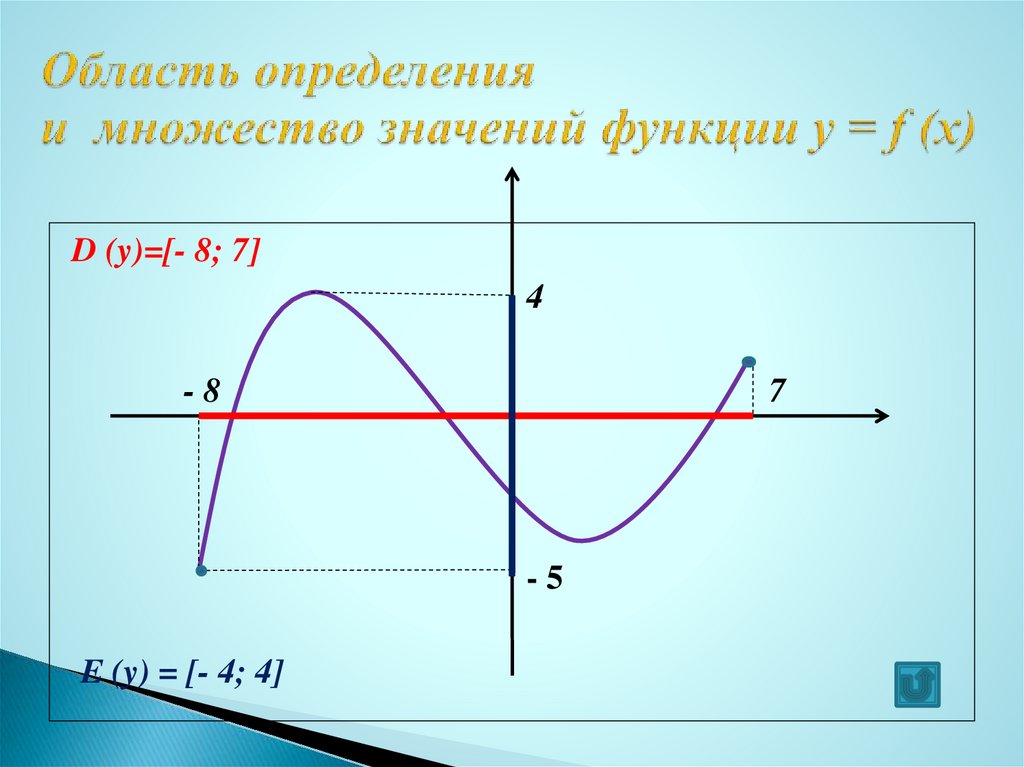 Они перечислены…
Они перечислены…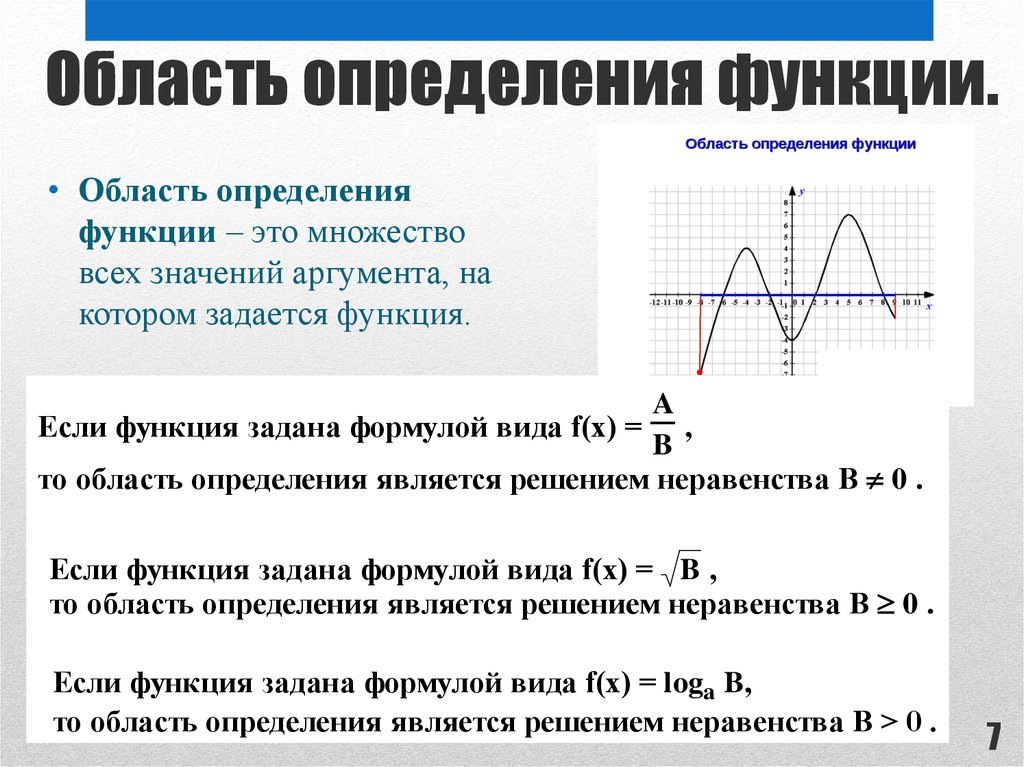 Вы можете видеть, что мы также получили доступ к переменным внешней функции из внутренней функции. Итак, попробуем заменить переменные внешней функции на переменные внутренней.
Вы можете видеть, что мы также получили доступ к переменным внешней функции из внутренней функции. Итак, попробуем заменить переменные внешней функции на переменные внутренней.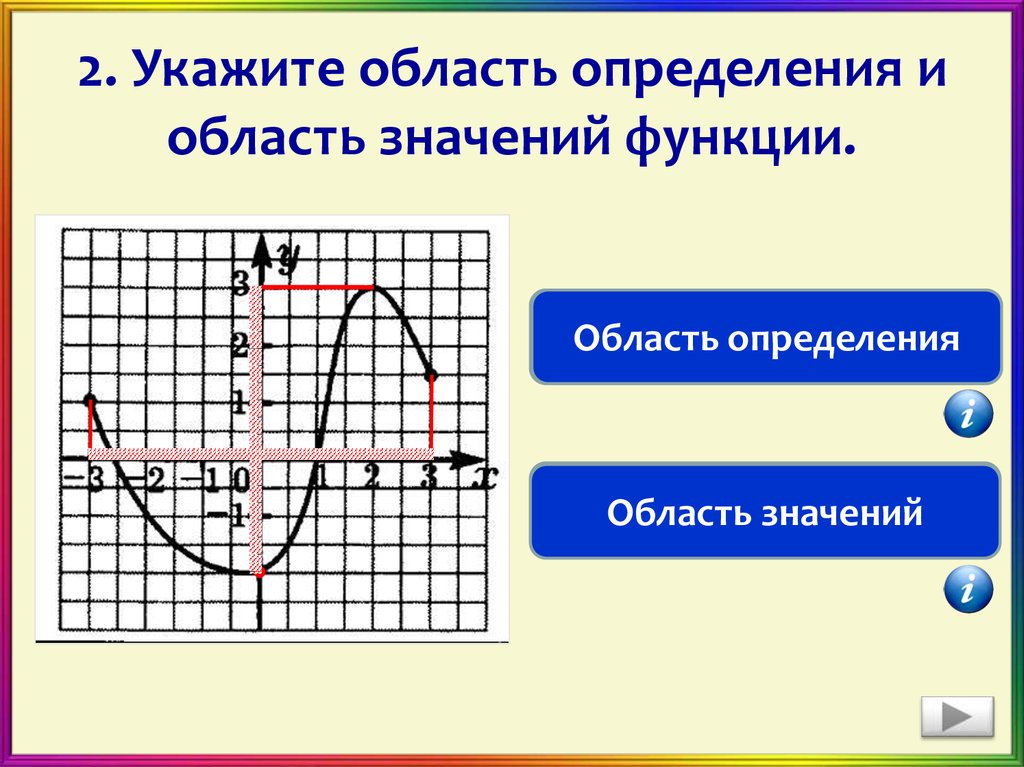 е. о том, где находятся переменные и откуда мы можем получить к ним доступ.
е. о том, где находятся переменные и откуда мы можем получить к ним доступ.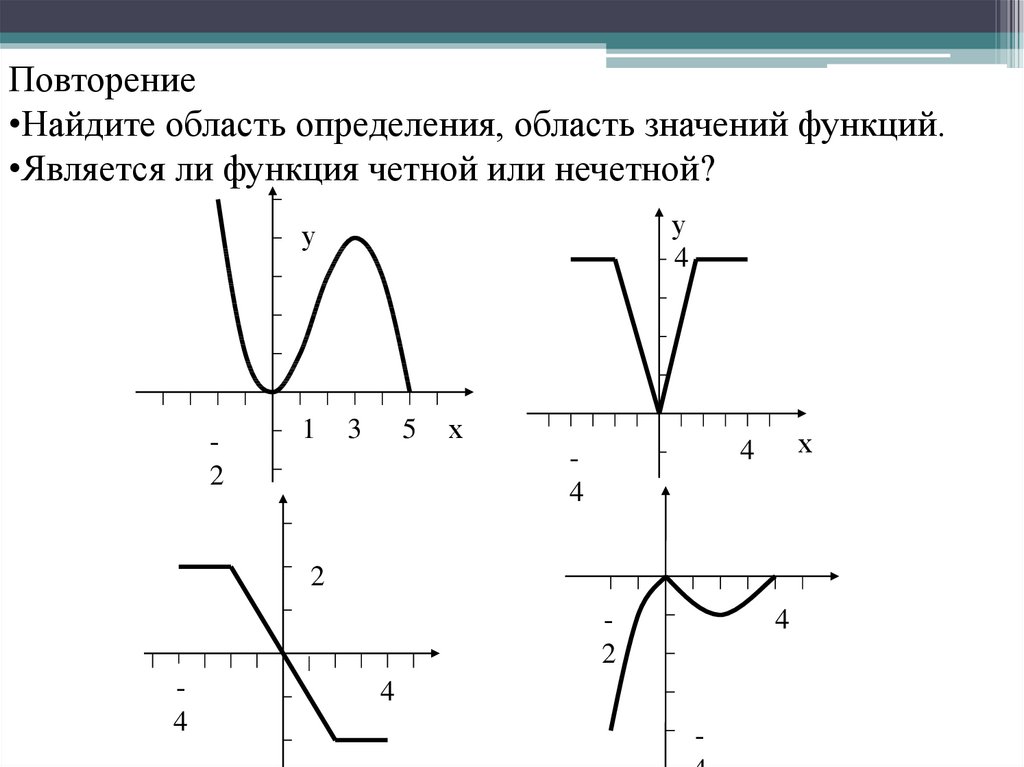
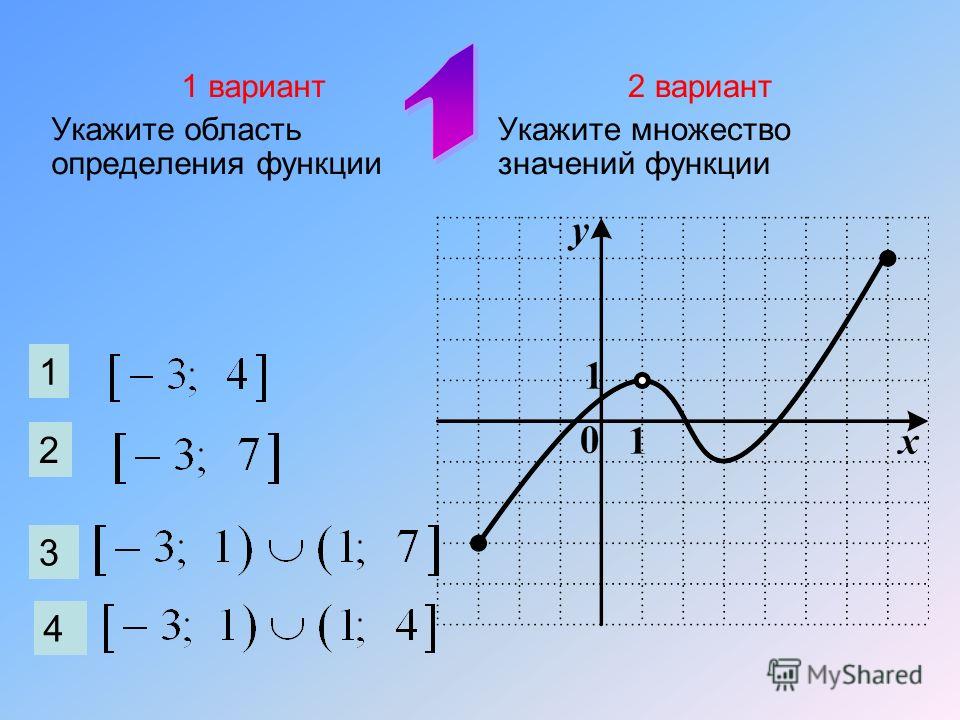 Пример приведен ниже.
Пример приведен ниже.
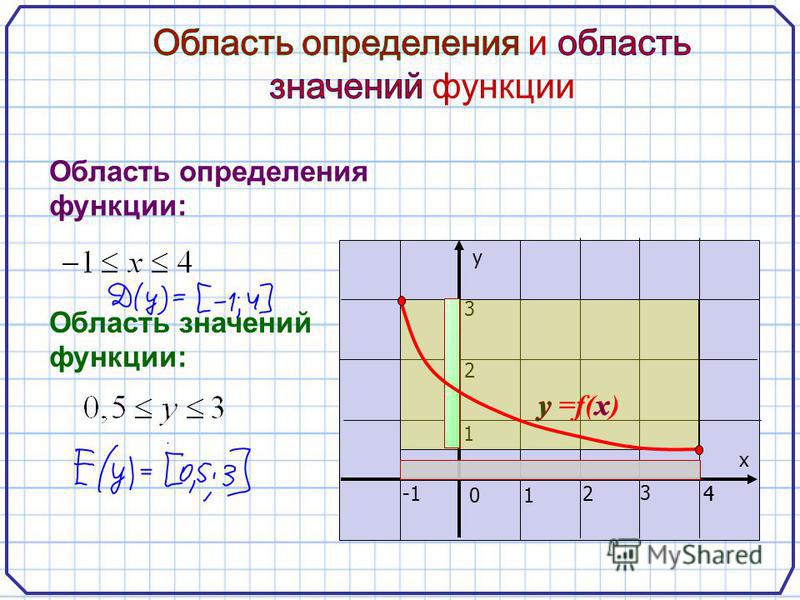 Первый способ — использовать итерируемый объект.
Первый способ — использовать итерируемый объект.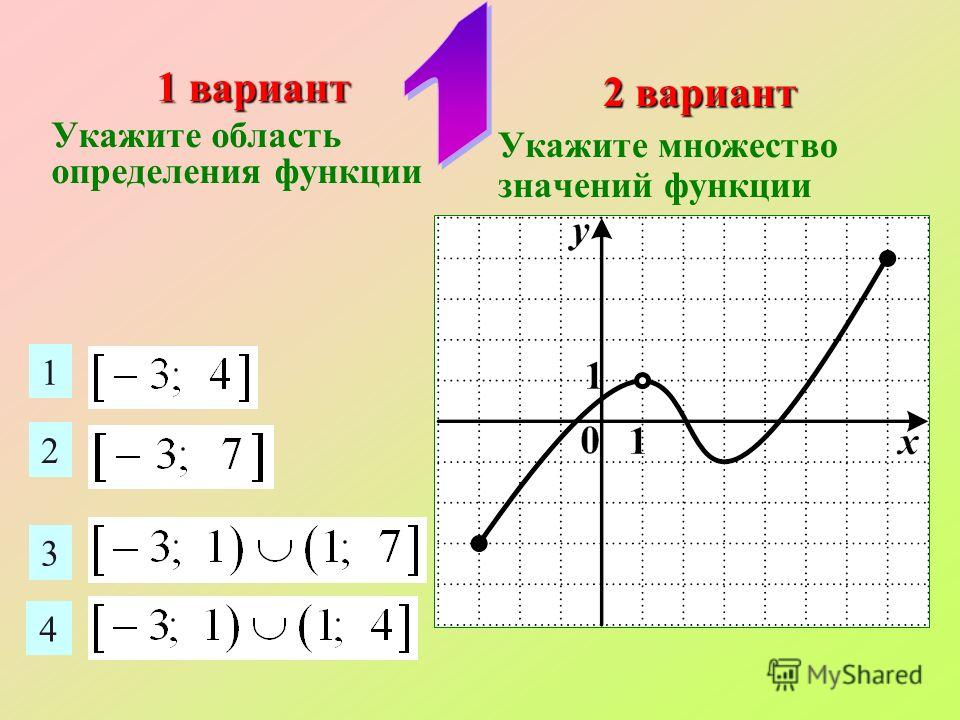
 Вот что такое закрытие.
Вот что такое закрытие. Вы должны определить по крайней мере одну пару имя/значение (переменную), а LET поддерживает до 126.
Вы должны определить по крайней мере одну пару имя/значение (переменную), а LET поддерживает до 126.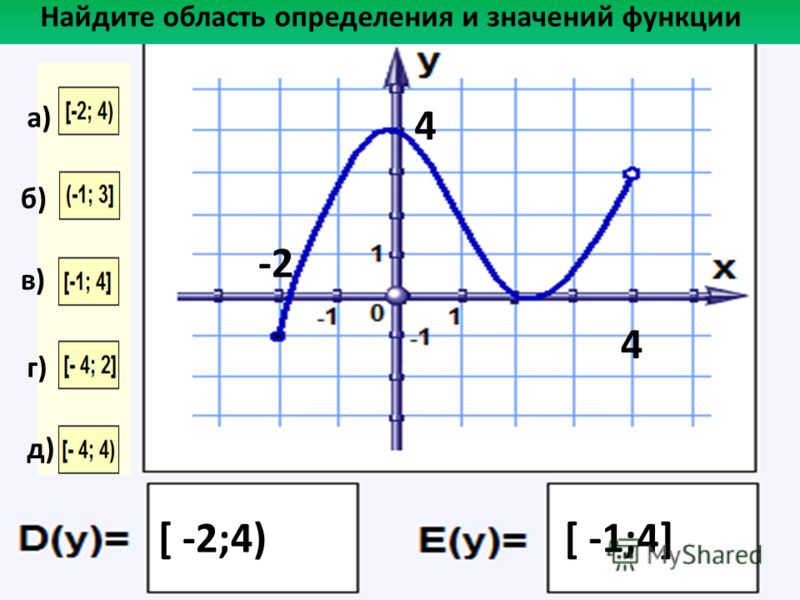



 Язык шаблонов Helm предоставляет следующие управляющие структуры:
Язык шаблонов Helm предоставляет следующие управляющие структуры: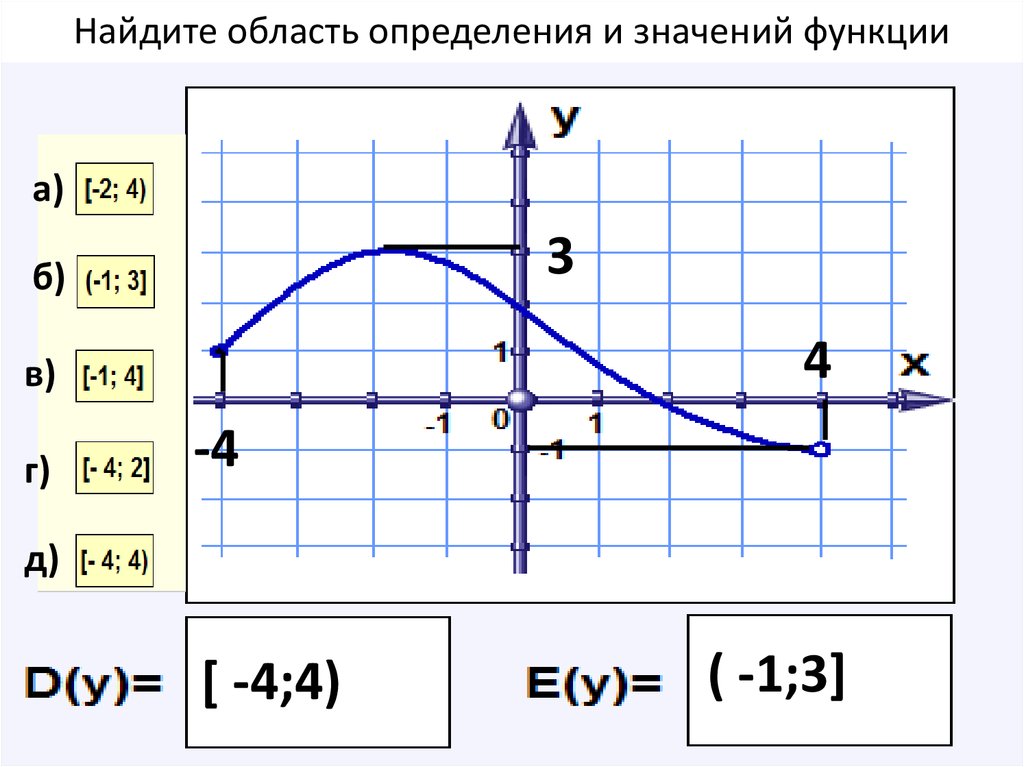
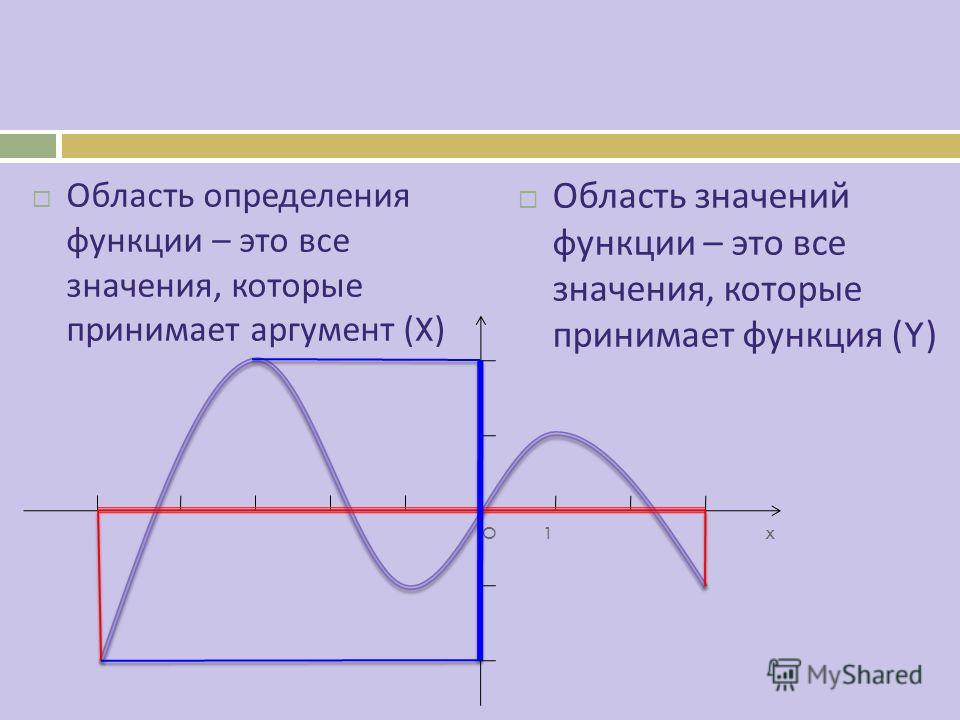 Мы добавим еще один параметр, если
напиток настроен на кофе:
Мы добавим еще один параметр, если
напиток настроен на кофе: Возьмем предыдущий пример и
отформатируйте его, чтобы его было немного легче читать:
Возьмем предыдущий пример и
отформатируйте его, чтобы его было немного легче читать: yaml
апиВерсия: v1
вид: карта конфигурации
метаданные:
имя: очевидец-элк-configmap
данные:
мое значение: "Привет, мир"
пить кофе"
еда: "ПИЦЦА"
кружка: "правда"
yaml
апиВерсия: v1
вид: карта конфигурации
метаданные:
имя: очевидец-элк-configmap
данные:
мое значение: "Привет, мир"
пить кофе"
еда: "ПИЦЦА"
кружка: "правда"
 Почему? Когда шаблон
двигатель работает, он удаляет содержимое внутри
Почему? Когда шаблон
двигатель работает, он удаляет содержимое внутри  Release.Name }}-configmap
данные:
мое значение: "Привет, мир"
напиток: {{ .Values.favorite.drink | по умолчанию "чай" | цитировать }}
еда: {{ .Values.favorite.food | верхний | цитировать }}
{{- if eq .Values.favorite.drink "кофе" }}
кружка: "правда"
{{- конец }}
Release.Name }}-configmap
данные:
мое значение: "Привет, мир"
напиток: {{ .Values.favorite.drink | по умолчанию "чай" | цитировать }}
еда: {{ .Values.favorite.food | верхний | цитировать }}
{{- if eq .Values.favorite.drink "кофе" }}
кружка: "правда"
{{- конец }}
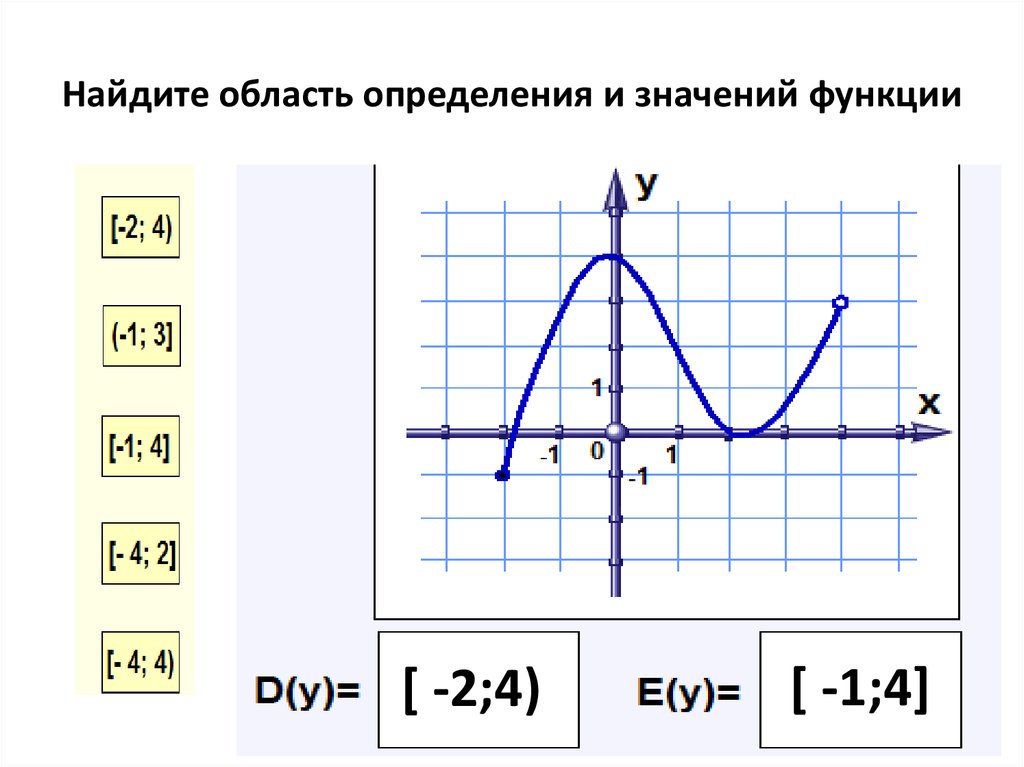 yaml
апиВерсия: v1
вид: карта конфигурации
метаданные:
имя: clunky-cat-configmap
данные:
мое значение: "Привет, мир"
пить кофе"
еда: "ПИЦЦА"
кружка: "правда"
yaml
апиВерсия: v1
вид: карта конфигурации
метаданные:
имя: clunky-cat-configmap
данные:
мое значение: "Привет, мир"
пить кофе"
еда: "ПИЦЦА"
кружка: "правда"
 Это контролирует
переменная область видимости. Напомним, что
Это контролирует
переменная область видимости. Напомним, что  еда | верхний | цитировать }}
{{- конец }}
еда | верхний | цитировать }}
{{- конец }}
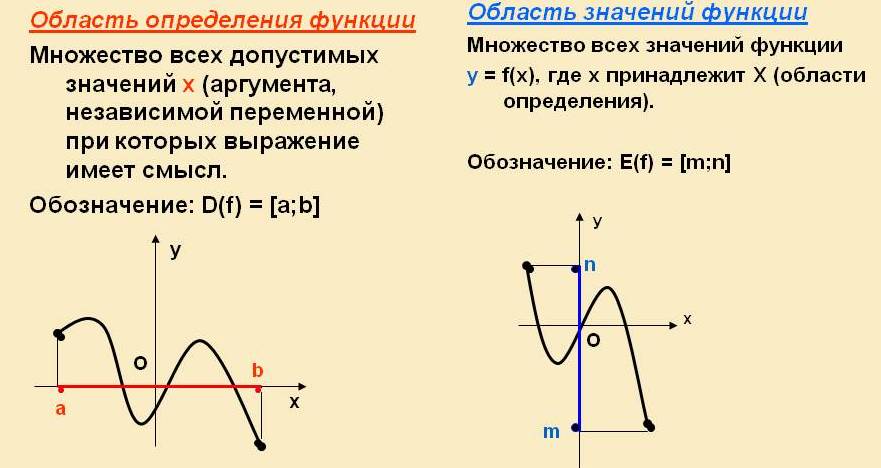 Name
Name 
 еда | верхний | цитировать }}
{{- конец }}
начинки: |-
{{- диапазон .Values.pizzaToppings }}
- {{ . | название | цитировать }}
{{- конец }}
еда | верхний | цитировать }}
{{- конец }}
начинки: |-
{{- диапазон .Values.pizzaToppings }}
- {{ . | название | цитировать }}
{{- конец }}
 Но сейчас что-то
интересно бывает. Точно так же, как
Но сейчас что-то
интересно бывает. Точно так же, как 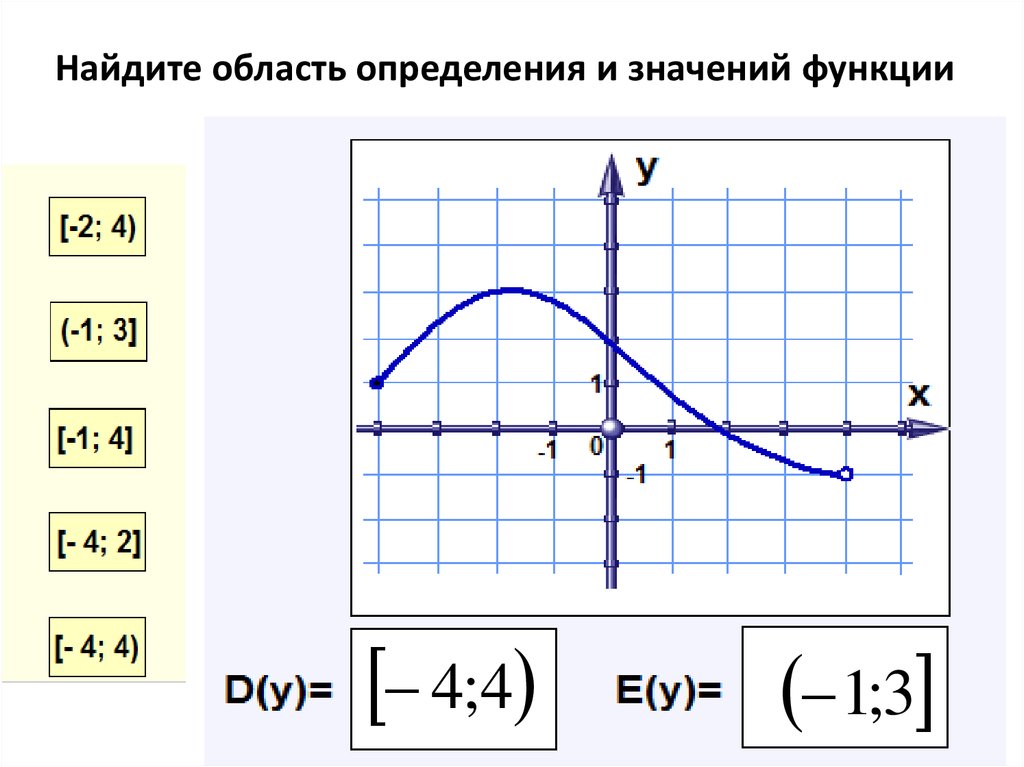 Начинка
Начинка