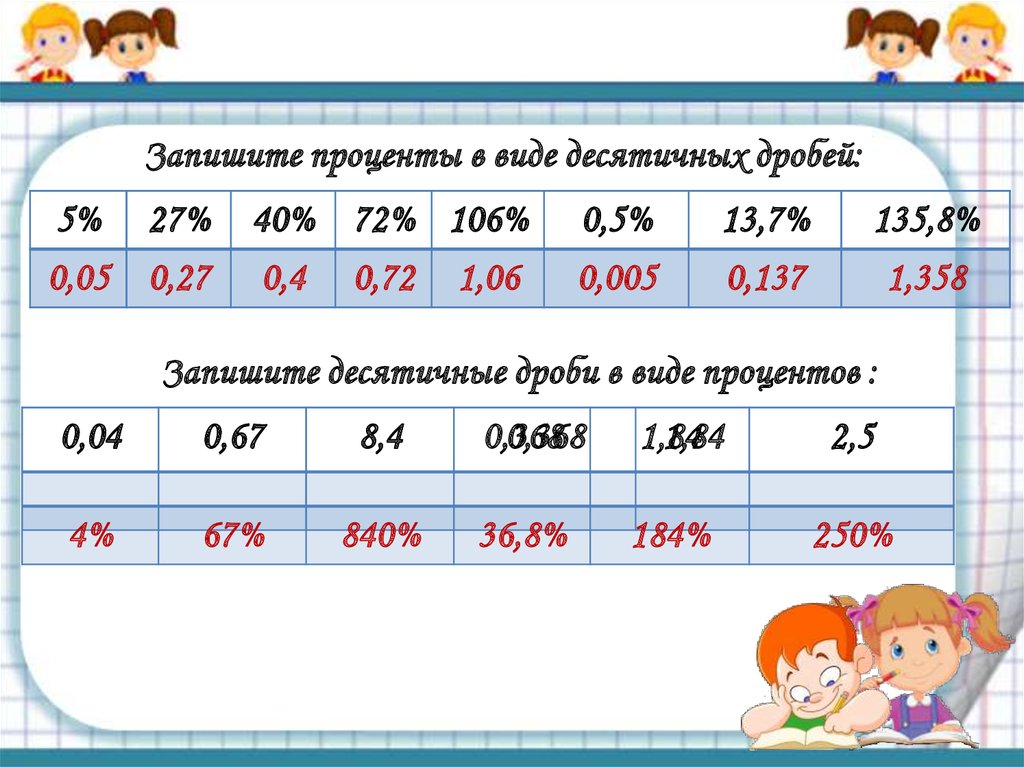
Как перевести обыкновенную дробь в десятичную?
Что такое дробь: понятие
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 5/9 или (1,5 — 0,2)/15.
- Алгебраические — состоят из переменных. Например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как «пять целых одна четвертая», а записывается — 5 1\4.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Что такое десятичная дробь
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,8
- 7,42
- 9,932
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».
Обучение на курсах математики в Skysmart поможет улучшить оценки в школе и подготовиться к выпускным экзаменам!
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
Обыкновенная и десятичная дробь — давние друзья. Вот как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.

- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Как перевести обычную дробь в десятичную
Прежде чем узнать, как от обычной записи перейти к десятичной, вспомним различия двух видов дробей и сформулируем важное правило.
Десятичные дроби — это конструкции вида 0,5; 2,16 и -7,42. А так выглядят эти же числа в форме обыкновенных дробей:
Обыкновенную дробь можно перевести в конечную десятичную дробь только при условии, что её знаменатель можно разложить на простые множители 2 и 5 любое количество раз. Например:
Например:
Дробь 11/40 можно преобразовать в конечную десятичную, потому что знаменатель раскладывается на множители 2 и 5.
Дробь 17/60 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3.
А теперь перейдем к самому главному вопросу: рассмотрим несколько алгоритмов перевода обыкновенной дроби в десятичную.
Способ 1. Превращаем знаменатель в 10, 100 или 1000
Чтобы превратить дробь в десятичную, нужно числитель и знаменатель умножить на одно и то же число так, чтобы в знаменателе получилось 10, 100, 1000 и т.д. Но прежде, чем приступать к вычислениям, нужно проверить, можно ли вообще превратить данную дробь в десятичную.
Для примера возьмем дробь 3/20. Ее можно привести в конечную десятичную, потому что её знаменатель раскладывается на множители 2 и 5.
Мы можем получить в нижней части 100: достаточно умножить 20 на 5. Про верхнюю часть тоже не забываем: получаем 15.
Теперь запишем числитель отдельно. Отсчитываем справа столько же знаков, сколько нулей стоит в знаменателе, и ставим запятую. В нашем примере в знаменателе 100 (у него два нуля), значит ставим запятую после отсчета двух знаков и получаем 0,15. Преобразование готово.
Отсчитываем справа столько же знаков, сколько нулей стоит в знаменателе, и ставим запятую. В нашем примере в знаменателе 100 (у него два нуля), значит ставим запятую после отсчета двух знаков и получаем 0,15. Преобразование готово.
Еще пример:
Способ 2. Делим числитель на знаменатель
Чтобы перевести обыкновенную дробь в десятичную, достаточно разделить ее верхнюю часть на нижнюю. Проще всего это сделать, конечно же, на калькуляторе — но на контрольных им пользоваться не разрешают, поэтому учимся по-другому.
Для примера возьмем дробь 78/100. Убедимся, что дробь можно привести в конечную десятичную.
Делим столбиком числитель на знаменатель — преобразование готово:
Если при делении уголком стало ясно, что процесс не заканчивается и после запятой выстраиваются повторяющиеся цифры — эту дробь нельзя перевести в конечную десятичную. Ответ можно записать в виде периодической дроби — для этого нужно записать повторяющееся число в скобки, вот так: 1/3 = 0,3333. . = 0,(3).
. = 0,(3).
Для удобства мы собрали табличку дробей со знаменателями, которые чаще всего встречаются в заданиях по математике. Скачайте ее на гаджет или распечатайте и храните в учебнике как закладку:
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед. По сути, алгоритм превращения десятичной дроби в обыкновенную противоположен тем, что мы разобрали в предыдущей части. Вот, как это выглядит в обратную сторону:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.

- 2,34 = 234/100 = 117/50 = 2 17/50.
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
| Еще алгоритм: как преобразовать десятичную дробь в обыкновенную
|
Вот и всё! Эта схема значительно проще и быстрее. Проверим:
Как видим, в дроби 0,55 после запятой стоит две цифры — 5 и 5.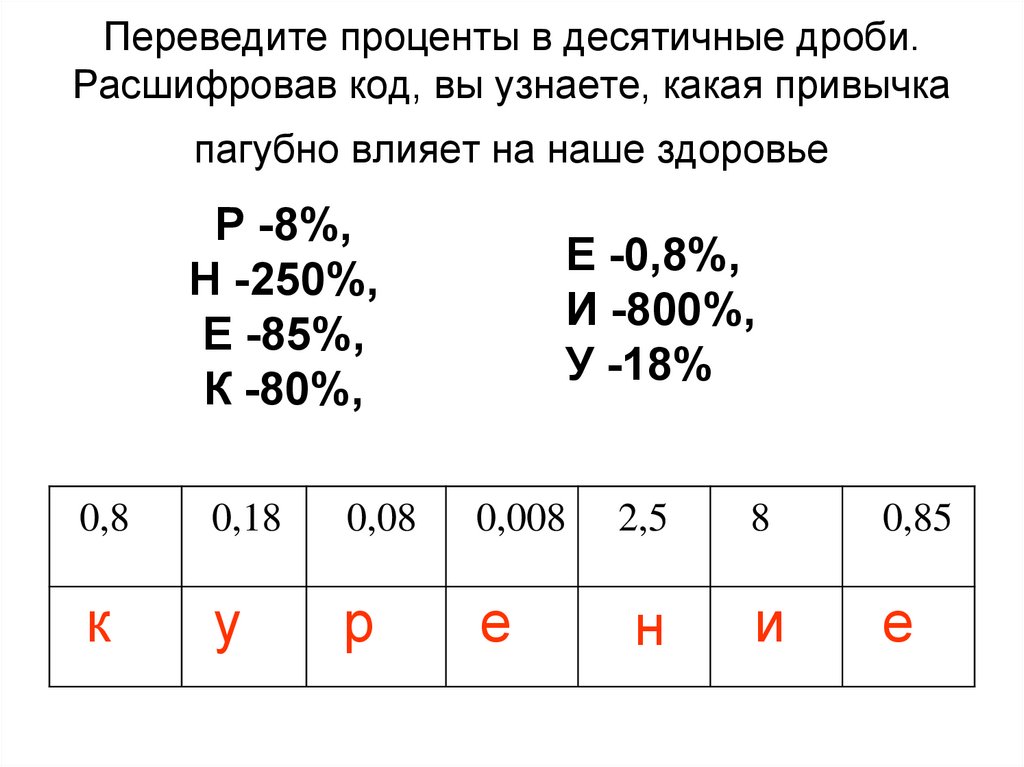
Десятичные дроби. Классы десятичных дробей. «Альфа-школа».
- Альфашкола
- Статьи
- Десятичные дроби
Десятичные дроби — это вид дроби, в которой \(m\) – простое число, а \(n\) в какой-либо степени \(10\). Рассмотрим примеры: \(\frac{1}{10},\frac{1}{100},\frac{1}{1000}\)- в десятой, в сотой и в тысячной части соответственно. Дробь семь пятидесятых \(\frac{7}{50}\) можно записать в виде десятичного числа, умножив числитель и знаменатель на \(2\), получаем \(\frac{14}{100}\), то есть \(0,14\), \(\frac{6}{1000}\) произносится как шесть тысячных и записывается в десятичном виде как \(0,006\).
Дробь четыре пятых \(\frac{4}{5}\) можно написать как восемь десятых \(\frac{8}{10}\).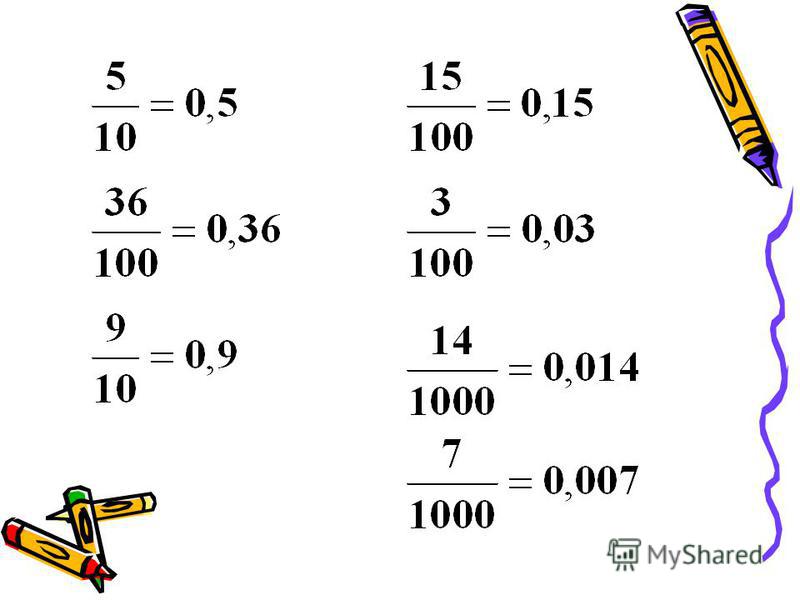
По каким правилам обыкновенная дробь переводится в десятичную?
- \(\frac{1}{5}=0,2\)
- \(\frac{2}{5}=0,4\)
- \(\frac{3}{5}=0,6\)
Первый способ.
Чтобы перевести дробь в десятичную нужно числитель и знаменатель умножить на одно и то же число, чтобы в знаменателе получилось \(10,100,1000,10 000\) и т.д.
Второй способ.
Второй способ более сложный, но применяется чаще первого. Для его использования, нужно вспомнить деление уголком:
- Десятичная дробь не поменяет свое значение, если у нее отнять справа несколько нулей, если они есть;
- Десятичная дробь не поменяет свое значение, если к ней прибавить справа несколько нулей;
- Дробь со знаменателем \(10\) в степени n можно записать в виде десятичной дроби;
- Дробная и целая часть разделяется запятой;
- Если дробь содержит конечное число цифр, то дробь называется конечной;
- Если дробь имеет бесконечное число цифр, то дробь называется бесконечной;
Пример бесконечной дроби:
- Повторяющиеся цифры после запятой, называется периодом этой бесконечной десятичной дроби;
- Бесконечные десятичные дроби существуют двух видов: периодические и непериодические дроби;
Можно ли перевести любую дробь в конечную десятичную?
- Если знаменатель обыкновенной дроби раскладывается на простые множители
\(2\) и \(5\), то она является конечной:
- Если знаменатель обыкновенной дроби, раскладывается на простые множители не только на \(2\) и \(5\),
то она является бесконечной.
Десятичные дроби применяются в единицах измерения длины.
\(1\) км \(=1000\) м \(=10000\) дм \(=100000\)см \(=1000000\) мм
\(1\) мм -\(1\) одна миллионная км,\(0,000001\)
\(1\) см — \(1\) стотысячная км, \(0,00001\)
\(1\) дм — \(1\) десятитысячная км \(0,0001\)
\(1\) м — \(1\) одна тысячная км \(0,001\)
Задача: выразите \(2,250\) метра в километрах, в десятичной дроби.
Решение:
1)убираем ноль с правой части, получаем \(2,25\)
2) в одном км — \(1000\) м значит делим на \(1000 :0,00225\) км
Ответ: \(0,00225\) км.
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Ирина Евгеньевна Русакова
Репетитор по математике
Стаж (лет)
Образование:
Пермский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-11 классов и информатике для 1-11 классов.
Дарина Юрьевна Дивнова
Репетитор по математике
Стаж (лет)
Образование:
Брестский государственный университет им. А.С. Пушкина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов. Объясню простым языком даже самую сложную тему. Люблю математику и покажу как она прекрасна. Считаю, что всему можно научить, нужно лишь желание, время и преподаватель, способный заинтересовать ребенка.
Объясню простым языком даже самую сложную тему. Люблю математику и покажу как она прекрасна. Считаю, что всему можно научить, нужно лишь желание, время и преподаватель, способный заинтересовать ребенка.
Зарема Юсуповна Висаева
Репетитор по математике
Стаж (лет)
Образование:
ФГБОУ ВО
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку для 7-11 классов. Подготовка к ОГЭ, ВПР. Магистр. Знание русского языка очень важно в нашей повседневной жизни. Он помогает нам общаться между собой, понимать друг друга, передавать свои мысли, чувства и эмоции. Он безмерно богат разнообразной лексикой, различными афоризмами, крылатыми выражениями, пословицами и поговорками. Знание русского языка позволяет нам достигать поставленных целей в жизни, заводить новых друзей, умственно и культурно развиваться.
В преподавании русского языка я применяю различные методики в зависимости от индивидуальных особенностей обучающегося.
Дабы разнообразить скучные монотонные уроки, в рамках занятий я часто использую такие игровые элементы, как кроссворды, загадки, ребусы, викторины. Использую также различные наглядные пособия, видео и фотоматериалы, презентации.
Привожу интересные факты по изучаемой теме, которых не встретишь в обычных школьных учебниках, применяя тем самым прием под названием «Яркое пятно».
Также в процессе обучения я использую и многие другие интересные приемы преподавания, например прием «Ассоциаций», который позволяет лучше усвоить и запомнить новый материал; прием «Подводящего диалога», который способствует развитию логического мышления у обучающихся; прием «Толстые и тонкие вопросы», выявляя с его помощью проблемные моменты, акцентируя на них особое внимание; различные творческие задания, развивая с их помощью и воображение, кругозор обучающихся.
Он помогает нам общаться между собой, понимать друг друга, передавать свои мысли, чувства и эмоции. Он безмерно богат разнообразной лексикой, различными афоризмами, крылатыми выражениями, пословицами и поговорками. Знание русского языка позволяет нам достигать поставленных целей в жизни, заводить новых друзей, умственно и культурно развиваться.
В преподавании русского языка я применяю различные методики в зависимости от индивидуальных особенностей обучающегося.
Дабы разнообразить скучные монотонные уроки, в рамках занятий я часто использую такие игровые элементы, как кроссворды, загадки, ребусы, викторины. Использую также различные наглядные пособия, видео и фотоматериалы, презентации.
Привожу интересные факты по изучаемой теме, которых не встретишь в обычных школьных учебниках, применяя тем самым прием под названием «Яркое пятно».
Также в процессе обучения я использую и многие другие интересные приемы преподавания, например прием «Ассоциаций», который позволяет лучше усвоить и запомнить новый материал; прием «Подводящего диалога», который способствует развитию логического мышления у обучающихся; прием «Толстые и тонкие вопросы», выявляя с его помощью проблемные моменты, акцентируя на них особое внимание; различные творческие задания, развивая с их помощью и воображение, кругозор обучающихся. 3 года являюсь преподавателем русского языка и литературы в колледже.
В 2021 году являлась экспертом по проверке ВПР по русскому языку студентов СПО.
Имеется опыт успешной подготовки детей ко Всероссийским олимпиадам, конкурсам сочинений, ОГЭ.
Владею четырьмя языками:
русский — в совершенстве,
казахский — средний,
чеченский — средний,
английский — базовый.
Обладаю такими важными человеческими качествами, как доброжелательность, терпеливость, тактичность, ответственность, честность, стрессоустойчивость, умение подстраиваться под нестандартные ситуации.
Выбирая меня в качестве репетитора, Вы можете быть уверены в положительном результате своего обучения.
3 года являюсь преподавателем русского языка и литературы в колледже.
В 2021 году являлась экспертом по проверке ВПР по русскому языку студентов СПО.
Имеется опыт успешной подготовки детей ко Всероссийским олимпиадам, конкурсам сочинений, ОГЭ.
Владею четырьмя языками:
русский — в совершенстве,
казахский — средний,
чеченский — средний,
английский — базовый.
Обладаю такими важными человеческими качествами, как доброжелательность, терпеливость, тактичность, ответственность, честность, стрессоустойчивость, умение подстраиваться под нестандартные ситуации.
Выбирая меня в качестве репетитора, Вы можете быть уверены в положительном результате своего обучения.
Похожие статьи
- Как найти делитель?
- РУДН: факультет математики
- Площадь трапеции
- ЕГЭ по математике, профильный уровень.
 Задачи по планиметрии
Задачи по планиметрии - ЕГЭ по математике, базовый уровень. Задачи на координатной решетке
- Задачи на движение по воде
- Коэфициент адаптивности: что такое AQ, как помочь ребенку его развить
- Что такое снег, как появляется и зачем он нужен?
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Калькулятор десятичных дробей — перевести обыкновенную дробь в десятичную
Калькулятор десятичных дробей — перевести обыкновенную дробь в десятичнуюКалькулятор позволит перевести обыкновенную дробь (числитель/знаменатель) в десятичную. Или Вам нужно наоборот перевести десятичную дробь в обыкновенную (тогда переходите по ссылке).
Смешанные дроби Обыкновенные дроби
Дробь:
Рассчитать Сбросить
Результат:
Графически:
Решение:
Как преобразовать дробь в десятичную?
Способ № 1
Разложите знаменатель до степени 10.
Пример № 1
3/5 расширяется до 6/10 путем умножения числителя на 2 и знаменателя на 2:
| 3 | = | 3×2 | = | 6 | = | 0.6 |
| 5 | 5×2 | 10 |
Пример № 2
3/4 расширяется до 75/100 путем умножения числителя на 25 и знаменателя на 25:
| 3 | = | 3×25 | = | 75 | = | 0.75 |
| 4 | 4×25 | 100 |
Пример № 3
5/8 расширен до 625/1000 путем умножения числителя на 125 и знаменателя на 125:
| 5 | = | 5×125 | = | 625 | = | 0.625 |
| 8 | 8×125 | 1000 |
Способ № 2
— Используйте калькулятор, чтобы разделить числитель дроби на знаменатель.
— Для смешанных чисел добавьте целое число.
Пример № 1
2/5 = 2÷5 = 0.4
Пример № 2
1 2/5 = 1+2÷5 = 1.4
Способ № 3
Используйте длинное деление, чтобы разделить числитель дроби на знаменатель дроби.
Пример № 1
Рассчитайте 3/4 длинным делением 3 на 4:
| 0.75 | |
| 4 | 3 |
| 0 | |
| 30 | |
| 28 | |
| 20 | |
| 20 | |
| 0 |
Таблица преобразования в десятичную дробь
| Дробь | Десятичная дробь |
|---|---|
| 1/2 | 0.5 |
| 1/3 | 0.33333333 |
| 2/3 | 0.66666667 |
| 1/4 | 0.25 |
| 2/4 | 0.5 |
| 3/4 | 0.75 |
| 1/5 | 0. 2 2 |
| 2/5 | 0.4 |
| 3/5 | 0.6 |
| 4/5 | 0.8 |
| 1/6 | 0.16666667 |
| 2/6 | 0.33333333 |
| 3/6 | 0.5 |
| 4/6 | 0.66666667 |
| 5/6 | 0.83333333 |
| 1/7 | 0.14285714 |
| 2/7 | 0.28571429 |
| 3/7 | 0.42857143 |
| 4/7 | 0.57142858 |
| 5/7 | 0.71428571 |
| 6/7 | 0.85714286 |
| 1/8 | 0.125 |
| 2/8 | 0.25 |
| 3/8 | 0.375 |
| 4/8 | 0.5 |
| 5/8 | 0.625 |
| 6/8 | 0.75 |
| 7/8 | 0.875 |
| 1/9 | 0.11111111 |
| 2/9 | 0. 22222222 22222222 |
| 3/9 | 0.33333333 |
| 4/9 | 0.44444444 |
| 5/9 | 0.55555556 |
| 6/9 | 0.66666667 |
| 7/9 | 0.77777778 |
| 8/9 | 0.88888889 |
| 1/10 | 0.1 |
| 2/10 | 0.2 |
| 3/10 | 0.3 |
| 4/10 | 0.4 |
| 5/10 | 0.5 |
| 6/10 | 0.6 |
| 7/10 | 0.7 |
| 8/10 | 0.8 |
| 9/10 | 0.9 |
| 1/11 | 0.09090909 |
| 2/11 | 0.18181818 |
| 3/11 | 0.27272727 |
| 4/11 | 0.36363636 |
| 5/11 | 0.45454545 |
| 6/11 | 0.54545454 |
| 7/11 | 0.63636363 |
| 8/11 | 0. 72727272 72727272 |
| 9/11 | 0.81818181 |
| 10/11 | 0.90909091 |
Другие калькуляторы дробей:
Калькулятор обыкновенных дробей — сложение, вычитание, умножение, деление Калькулятор десятичных дробей — сложение, вычитание, умножение, деление Перевести обыкновенную дробь в десятичную Перевести десятичную дробь в обыкновенную Калькулятор сокращения дробей Калькулятор преобразование дробей в проценты Калькулятор преобразование процентов в дробь Калькулятор процентов
Перевести десятичное число в дробь онлайн. Перевод обыкновенной дроби в десятичную дробь и обратно, правила, примеры
В самом начале нужно все-таки узнать, что такое дробь и каких видов она бывает. А бывает она трех видов. И первый из них это обыкновенная дробь, например ½, 3/7,3/432 и т. д. Эти числа также можно записывать при помощи горизонтальной черточки. И первое, и второе будет одинаково верно. Цифра сверху называется числительным, а снизу знаменателем. Есть даже поговорка, для тех людей, кто постоянно путает эти два названия. Она звучит так: «Зззззапомни! Зззззнаменатель — внизззззу! ». Это поможет не запутаться. Обыкновенная дробь это всего лишь два числа, которые делятся друг на друга. Черточка в них и обозначает знак деления. Ее можно заменить знаком двоеточие. Если стоит вопрос «как дробь перевести в число», то это очень просто. Следует всего лишь числитель поделить на знаменатель. И все. Дробь переведена.
Есть даже поговорка, для тех людей, кто постоянно путает эти два названия. Она звучит так: «Зззззапомни! Зззззнаменатель — внизззззу! ». Это поможет не запутаться. Обыкновенная дробь это всего лишь два числа, которые делятся друг на друга. Черточка в них и обозначает знак деления. Ее можно заменить знаком двоеточие. Если стоит вопрос «как дробь перевести в число», то это очень просто. Следует всего лишь числитель поделить на знаменатель. И все. Дробь переведена.
Второй вид дробей называется десятичным. Это ряд цифр с запятой. К примеру, 0,5, 3,5 и т. д. Назвали их десятичными, только потому, что после запетой первая цифра обозначает «десятки», вторая в десять раз больше «сотни» и так далее. А первые цифра до запятой, называются целыми. Например, число 2,4 звучит так, двенадцать целых и двести тридцать четыре тысячных. Такие дроби появляются в основном из-за того, что поделив два числа без остатка не получается. И большинство обыкновенных дробей, во время того как их будут переводить в числа, в конечном итоге имеют вид десятичной дроби. Например, одна вторая ровняется ноль целым пяти десятым.
Например, одна вторая ровняется ноль целым пяти десятым.
И заключительный третий вид. Это смешанные числа. Пример этого можно привести такой, как 2½. Звучит так, две целых и одна вторая. В старших классов такой вид дробей уже не используются. Их наверняка необходимо будет приводить или в обыкновенный вид дроби, или в десятичный. Сделать это так же легко. Просто целое число нужно умножить на знаменатель и, полученное обозначение, сложить с числительным. Возьмем наш пример 2½. Два умножается на два, получается четыре. Четыре плюс один, равно пяти. И дробь формой 2½ образуется в 5/2. А пять, поделив на два можно получить десятичную дробь. 2½=5/2=2,5. Уже стало понятно, как переводить дроби в числа. Следует всего лишь разделить числитель на знаменатель. Если числа большие можно воспользоваться калькулятором.
Если на нем получается не целые числа и после запятой идет очень много цифр, то тогда данное значение можно округлить. Округляется все очень просто. Сначала следует определиться, к какой цифре нужно округлить. Следует рассмотреть пример. Человеку нужно округлить число ноль целых, девять тысяч семьсот пятьдесят шесть десятитысячных или в цифровом значении 0,6. Округление необходимо сделать до сотых. Это означает, что в данный момент до семи сотых. После цифры семь в дроби идет пять. Теперь нужно использовать правила для округления. Цифры больше пяти округляются в большую сторону, а меньшие – в меньшую. В примере у человека — пять, она стоит на пограничье, но считается, что округление происходит в большую сторону. Значит, все цифры после семерки убираем и к ней прибавляем единицу. Получается 0,8.
Следует рассмотреть пример. Человеку нужно округлить число ноль целых, девять тысяч семьсот пятьдесят шесть десятитысячных или в цифровом значении 0,6. Округление необходимо сделать до сотых. Это означает, что в данный момент до семи сотых. После цифры семь в дроби идет пять. Теперь нужно использовать правила для округления. Цифры больше пяти округляются в большую сторону, а меньшие – в меньшую. В примере у человека — пять, она стоит на пограничье, но считается, что округление происходит в большую сторону. Значит, все цифры после семерки убираем и к ней прибавляем единицу. Получается 0,8.
Также возникают ситуации, когда человеку необходимо быстро перевести обыкновенную дробь в число, а калькулятора рядом нет. Для этого стоит применить деление столбиком. Первым делом следует на листке написать рядом друг с другом числитель и знаменатель. Между ними ставится уголок деления, он похож на букву «Т», только лежащую на боку. Для примера можно взять дробь десять шестых. И так, десять следует поделить на шесть.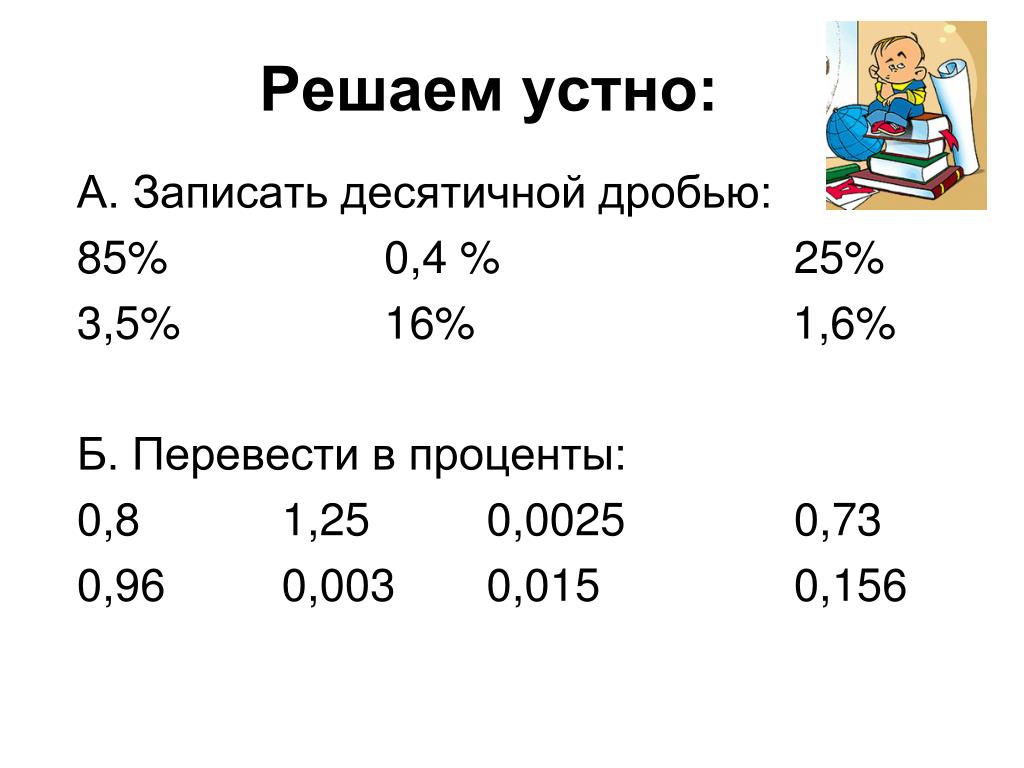 Сколько шестерок может вместиться в десятке, только одна. Единица записывается под уголком. Десять отнять шесть получится четыре. Сколько шестерок будет в четверке, несколько. Значит, в ответе после единицы ставится запятая, а четверка умножается на десять. В сорока шесть шестерок. В ответе дописывается шестерка, а от сорока отнимается тридцать шесть. Получается опять четыре.
Сколько шестерок может вместиться в десятке, только одна. Единица записывается под уголком. Десять отнять шесть получится четыре. Сколько шестерок будет в четверке, несколько. Значит, в ответе после единицы ставится запятая, а четверка умножается на десять. В сорока шесть шестерок. В ответе дописывается шестерка, а от сорока отнимается тридцать шесть. Получается опять четыре.
В данном примере произошло зацикливание, если продолжить делать все точно также получится ответ 1,6(6) Цифру шесть продолжается для бесконечности, но применив правило округления, можно привести получение число к 1,7. Что намного удобней. Из этого можно сделать вывод, что не все обыкновенные дроби можно перевести в десятичные. В некоторых происходит зацикливание. Но зато любую десятичную дробь можно перевести в простую. Здесь поможет элементарное правило, как слышится, так и пишется. Например, число 1,5, слышится, как одна целых двадцать пять сотых. Так и нужно записать, одна целая, двадцать пять поделить на сто. Одна целая это сто, а значит, простая дробь будет сто двадцать пять на сто (125/100) . Все также просто и понятно.
Одна целая это сто, а значит, простая дробь будет сто двадцать пять на сто (125/100) . Все также просто и понятно.
Вот и было разобраны самые основные правила и преобразования, которые связанны с дробями. Все они несложные, но знать их следует. В повседневную жизнь уже давно вошли дроби, особенно десятичные. Это хорошо видно на ценниках в магазинах. Круглые цены уже давно не кто не пишет, а с дробями цена кажется визуально на много дешевле. Также одна из теорий гласит, что человечество отвернулось от римских цифр и приняла в оборот арабские, только потому, что в римских не было дробей. И многие ученые соглашаются с этим предположением. Ведь с дробями можно вести подсчеты более точней. А в наш век космических технологий, точность в расчетах нужна как никогда. Так что изучать дроби в школе по математики жизненно необходимо для понимания многих наук и технических достижений.
Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления. В таких случаях говорят, что выполнено деление с остатком , и решение записывают в таком виде:
В таких случаях говорят, что выполнено деление с остатком , и решение записывают в таком виде:
497: 4 = 124 (1 остаток).
Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое , 4 — делитель . Результат деления при делении с остатком называют неполным частным . В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток . В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело . Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64: 32 = 2, то проверку можно сделать так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.
Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление . Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \(\frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:
\(m:n = \frac{m}{n} \)
Верны следующие правила:
Чтобы получить дробь \(\frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.
Чтобы получить дробь \(\frac{m}{n} \), надо число m разделить на число n.
Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на
знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)
Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a: m}{b: m} \)
Это свойство называют основным свойством дроби .
Два последних преобразования называют сокращением дроби .
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю .
Правильные и неправильные дроби. Смешанные числа
Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например,
дробь \(\frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались
для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими
дробями, как, например, \(\frac{5}{5} \) или \(\frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби,
у которых числитель больше знаменателя или равен ему, называют неправильными дробями . Остальные дроби, т. е. дроби, у которых
числитель меньше знаменателя, называют правильными дробями .
Наверное, поэтому такие дроби,
у которых числитель больше знаменателя или равен ему, называют неправильными дробями . Остальные дроби, т. е. дроби, у которых
числитель меньше знаменателя, называют правильными дробями .
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие дроби называются смешанными .
Например:
\(5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \(\frac{2}{3} \) — дробная часть.
Если числитель дроби \(\frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:
\(\large \frac{a}{b} : n = \frac{a:n}{b} \)
Если числитель дроби \(\frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:
\(\large \frac{a}{b} : n = \frac{a}{bn} \)
Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Действия с дробями. Сложение дробей.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \(\frac{2}{7} \) и \(\frac{3}{7} \). Легко понять, что \(\frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\(\large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)
Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\(\large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Сложение смешанных дробей
Такие записи, как \(2\frac{2}{3} \), называют смешанными дробями . При этом число 2 называют целой частью смешанной дроби, а число \(\frac{2}{3} \) — ее дробной частью . Запись \(2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \(\frac{8}{3} \) и \(2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \(\frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \(\frac{8}{3} \) представлена в виде смешанной дроби \(2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть .
Вычитание дробей (дробных чисел)
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:
\(\frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \(\frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)
Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.
С помощью букв это правило записывается так:
\(\large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)
Умножение дробей
Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.
С помощью букв правило умножения дробей можно записать так:
\(\large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)
Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.
Деление дробей
Возьмем дробь \(\frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \(\frac{3}{2} \).
Эту дробь называют обратной дроби \(\frac{2}{3} \).
Получим дробь \(\frac{3}{2} \).
Эту дробь называют обратной дроби \(\frac{2}{3} \).
Если мы теперь «перевернем» дробь \(\frac{3}{2} \), то получим исходную дробь \(\frac{2}{3} \). Поэтому такие дроби, как \(\frac{2}{3} \) и \(\frac{3}{2} \) называют взаимно обратными .
Взаимно обратными являются, например, дроби \(\frac{6}{5} \) и \(\frac{5}{6} \), \(\frac{7}{18} \) и \(\frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \(\frac{a}{b} \) и \(\frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1 . Например: \(\frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Используя буквы, правило деления дробей можно записать так:
\(\large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)
Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления
дробей, его надо предварительно представить в виде неправильной дроби.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Дроби в старших классах не сильно досаждают. До поры до времени. Пока не столкнётесь со степенями с рациональными показателями да логарифмами. А вот там…. Давишь, давишь калькулятор, а он все полное табло каких-то циферок кажет. Приходится головой думать, как в третьем классе.
Давайте уже разберёмся с дробями, наконец! Ну сколько можно в них путаться!? Тем более, это всё просто и логично. Итак, какие бывают дроби?
Виды дробей. Преобразования.
Дроби бывают трёх видов.
1. Обыкновенные дроби , например:
Иногда вместо горизонтальной чёрточки ставят наклонную черту: 1/2, 3/4, 19/5, ну, и так далее. Здесь мы часто будем таким написанием пользоваться. Верхнее число называется числителем , нижнее — знаменателем. Если вы постоянно путаете эти названия (бывает. ..), скажите себе с выражением фразу: «Ззззз апомни! Ззззз наменатель — вниззззз у!» Глядишь, всё и ззззапомнится.)
..), скажите себе с выражением фразу: «Ззззз апомни! Ззззз наменатель — вниззззз у!» Глядишь, всё и ззззапомнится.)
Чёрточка, что горизонтальная, что наклонная, означает деление верхнего числа (числителя) на нижнее (знаменатель). И всё! Вместо чёрточки вполне можно поставить знак деления — две точки.
Когда деление возможно нацело, это надо делать. Так, вместо дроби «32/8» гораздо приятнее написать число «4». Т.е. 32 просто поделить на 8.
32/8 = 32: 8 = 4
Я уж и не говорю про дробь «4/1». Которая тоже просто «4». А если уж не делится нацело, так и оставляем, в виде дроби. Иногда приходится обратную операцию проделывать. Делать из целого числа дробь. Но об этом далее.
2. Десятичные дроби , например:
Именно в таком виде нужно будет записывать ответы на задания «В».
3. Смешанные числа , например:
Смешанные числа практически не используются в старших классах. Для того, чтобы с ними работать, их всяко надо переводить в обыкновенные дроби. Но это точно надо уметь делать! А то попадётся такое число в задачке и зависните… На пустом месте. Но мы-то вспомним эту процедуру! Чуть ниже.
Но это точно надо уметь делать! А то попадётся такое число в задачке и зависните… На пустом месте. Но мы-то вспомним эту процедуру! Чуть ниже.
Наиболее универсальны обыкновенные дроби . С них и начнём. Кстати, если в дроби стоят всякие логарифмы, синусы и прочие буковки, это ничего не меняет. В том смысле что все действия с дробными выражениями ничем не отличаются от действий с обыкновенными дробями !
Основное свойство дроби.
Итак, поехали! Для начала я вас удивлю. Всё многообразие преобразований дробей обеспечивается одним-единственным свойством! Оно так и называется, основное свойство дроби . Запоминайте: если числитель и знаменатель дроби умножить (разделить) на одно и то же число, дробь не изменится. Т.е:
Понятно, что писать можно дальше, до посинения. Синусы и логарифмы пусть вас не смущают, с ними дальше разберёмся. Главное понять, что все эти разнообразные выражения есть одна и та же дробь . 2/3.
А оно нам надо, все эти превращения? Ещё как! Сейчас сами увидите. Для начала употребим основное свойство дроби для сокращения дробей . Казалось бы, вещь элементарная. Делим числитель и знаменатель на одно и то же число и все дела! Ошибиться невозможно! Но… человек — существо творческое. Ошибиться везде может! Особенно, если приходится сокращать не дробь типа 5/10, а дробное выражение со всякими буковками.
Для начала употребим основное свойство дроби для сокращения дробей . Казалось бы, вещь элементарная. Делим числитель и знаменатель на одно и то же число и все дела! Ошибиться невозможно! Но… человек — существо творческое. Ошибиться везде может! Особенно, если приходится сокращать не дробь типа 5/10, а дробное выражение со всякими буковками.
Как правильно и быстро сокращать дроби, не делая лишней работы, можно прочитать в особом Разделе 555 .
Нормальный ученик не заморачивается делением числителя и знаменателя на одно и то же число (или выражение)! Он просто зачеркивает всё одинаковое сверху и снизу! Здесь-то и таится типичная ошибка, ляп, если хотите.
Например, надо упростить выражение:
Тут и думать нечего, зачеркиваем букву «а» сверху и двойку снизу! Получаем:
Все правильно. Но реально вы поделили весь числитель и весь знаменатель на «а». Если вы привыкли просто зачеркивать, то, впопыхах, можете зачеркнуть «а» в выражении
и получить снова
Что будет категорически неверно. Потому что здесь весь числитель на «а» уже не делится ! Эту дробь сократить нельзя. Кстати, такое сокращение – это, гм… серьезный вызов преподавателю. Такого не прощают! Запомнили? При сокращении делить надо весь числитель и весь знаменатель!
Потому что здесь весь числитель на «а» уже не делится ! Эту дробь сократить нельзя. Кстати, такое сокращение – это, гм… серьезный вызов преподавателю. Такого не прощают! Запомнили? При сокращении делить надо весь числитель и весь знаменатель!
Сокращение дробей сильно облегчает жизнь. Получится где-нибудь у вас дробь, к примеру 375/1000. И как теперь с ней дальше работать? Без калькулятора? Умножать, скажем, складывать, в квадрат возводить!? А если не полениться, да аккуратненько сократить на пять, да ещё на пять, да ещё… пока сокращается, короче. Получим 3/8! Куда приятнее, правда?
Основное свойство дроби позволяет переводить обыкновенные дроби в десятичные и наоборот без калькулятора ! Это важно на ЕГЭ, верно?
Как переводить дроби из одного вида в другой.
С десятичными дробями всё просто. Как слышится, так и пишется! Скажем, 0,25. Это ноль целых, двадцать пять сотых. Так и пишем: 25/100. Сокращаем (делим числитель и знаменатель на 25), получаем обычную дробь: 1/4. Всё. Бывает, и не сокращается ничего. Типа 0,3. Это три десятых, т.е. 3/10.
Всё. Бывает, и не сокращается ничего. Типа 0,3. Это три десятых, т.е. 3/10.
А если целых — не ноль? Ничего страшного. Записываем всю дробь без всяких запятых в числитель, а в знаменатель — то, что слышится. Например: 3,17. Это три целых, семнадцать сотых. Пишем в числитель 317, а в знаменатель 100. Получаем 317/100. Ничего не сокращается, значит всё. Это ответ. Элементарно, Ватсон! Из всего сказанного полезный вывод: любую десятичную дробь можно превратить в обыкновенную .
А вот обратное преобразование, обыкновенной в десятичную, некоторые без калькулятора не могут сделать. А надо! Как вы ответ записывать будете на ЕГЭ!? Внимательно читаем и осваиваем этот процесс.
Десятичная дробь чем характерна? У неё в знаменателе всегда стоит 10, или 100, или 1000, или 10000 и так далее. Если ваша обычная дробь имеет такой знаменатель, проблем нет. Например, 4/10 = 0,4. Или 7/100 = 0,07. Или 12/10 = 1,2. А если в ответе на задание раздела «В» получилось 1/2? Что в ответ писать будем? Там десятичные требуются. ..
..
Вспоминаем основное свойство дроби ! Математика благосклонно позволяет умножать числитель и знаменатель на одно и то же число. На любое, между прочим! Кроме нуля, разумеется. Вот и применим это свойство себе на пользу! На что можно умножить знаменатель, т.е. 2 чтобы он стал 10, или 100, или 1000 (поменьше лучше, конечно…)? На 5, очевидно. Смело умножаем знаменатель (это нам надо) на 5. Но, тогда и числитель надо умножить тоже на 5. Это уже математика требует! Получим 1/2 = 1х5/2х5 = 5/10 = 0,5. Вот и всё.
Однако, знаменатели всякие попадаются. Попадётся, например дробь 3/16. Попробуй, сообрази тут, на что 16 умножить, чтоб 100 получилось, или 1000… Не получается? Тогда можно просто разделить 3 на 16. За отсутствием калькулятора делить придётся уголком, на бумажке, как в младших классах учили. Получим 0,1875.
А бывают и совсем скверные знаменатели. Например, дробь 1/3 ну никак не превратишь в хорошую десятичную. И на калькуляторе, и на бумажке, мы получим 0,3333333. .. Это значит, что 1/3 в точную десятичную дробь не переводится . Так же, как и 1/7, 5/6 и так далее. Много их, непереводимых. Отсюда ещё один полезный вывод. Не каждая обыкновенная дробь переводится в десятичную !
.. Это значит, что 1/3 в точную десятичную дробь не переводится . Так же, как и 1/7, 5/6 и так далее. Много их, непереводимых. Отсюда ещё один полезный вывод. Не каждая обыкновенная дробь переводится в десятичную !
Кстати, это полезная информация для самопроверки. В разделе «В» в ответ надо десятичную дробь записывать. А у вас получилось, например, 4/3. Эта дробь не переводится в десятичную. Это означает, что где-то вы ошиблись по дороге! Вернитесь, проверьте решение.
Итак, с обыкновенными и десятичными дробями разобрались. Осталось разобраться со смешанными числами. Для работы с ними их всяко нужно перевести в обыкновенные дроби. Как это сделать? Можно поймать шестиклассника и спросить у него. Но не всегда шестиклассник окажется под руками… Придётся самим. Это несложно. Надо знаменатель дробной части умножить на целую часть и прибавить числитель дробной части. Это будет числитель обычной дроби. А знаменатель? Знаменатель останется тем же самым. Звучит сложно, но на деле всё элементарно. Смотрим пример.
Смотрим пример.
Пусть в задачке вы с ужасом увидели число:
Спокойно, без паники соображаем. Целая часть — это 1. Единица. Дробная часть — 3/7. Стало быть, знаменатель дробной части — 7. Этот знаменатель и будет знаменателем обыкновенной дроби. Считаем числитель. 7 умножаем на 1 (целая часть) и прибавляем 3 (числитель дробной части). Получим 10. Это будет числитель обыкновенной дроби. Вот и всё. Еще проще это выглядит в математической записи:
Ясненько? Тогда закрепите успех! Переведите в обыкновенные дроби. У вас должно получится 10/7, 7/2, 23/10 и 21/4.
Обратная операция — перевод неправильной дроби в смешанное число — в старших классах редко требуется. Ну если уж… И если Вы — не в старших классах — можете заглянуть в особый Раздел 555 . Там же, кстати, и про неправильные дроби узнаете.
Ну вот, практически и всё. Вы вспомнили виды дробей и поняли, как переводить их из одного вида в другой. Остаётся вопрос: зачем это делать? Где и когда применять эти глубокие познания?
Отвечаю. Любой пример сам подсказывает необходимые действия. Если в примере смешались в кучу обыкновенные дроби, десятичные, да ещё и смешанные числа, переводим всё в обыкновенные дроби. Это всегда можно сделать . Ну а если написано, что-нибудь типа 0,8 + 0,3, то так и считаем, безо всякого перевода. Зачем нам лишняя работа? Мы выбираем тот путь решения, который удобен нам !
Любой пример сам подсказывает необходимые действия. Если в примере смешались в кучу обыкновенные дроби, десятичные, да ещё и смешанные числа, переводим всё в обыкновенные дроби. Это всегда можно сделать . Ну а если написано, что-нибудь типа 0,8 + 0,3, то так и считаем, безо всякого перевода. Зачем нам лишняя работа? Мы выбираем тот путь решения, который удобен нам !
Если в задании сплошь десятичные дроби, но гм… злые какие-то, перейдите к обыкновенным, попробуйте! Глядишь, всё и наладится. Например, придется в квадрат возводить число 0,125. Не так-то просто, если от калькулятора не отвыкли! Мало того, что числа перемножать столбиком надо, так ещё думай, куда запятую вставить! В уме точно не получится! А если перейти к обыкновенной дроби?
0,125 = 125/1000. Сокращаем на 5 (это для начала). Получаем 25/200. Ещё раз на 5. Получаем 5/40. О, ещё сокращается! Снова на 5! Получаем 1/8. Легко возводим в квадрат (в уме!) и получаем 1/64. Всё!
Подведём итоги этого урока.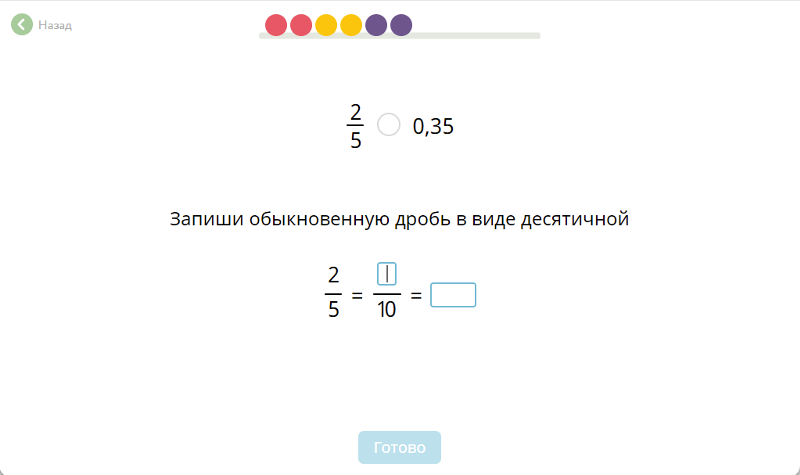
1. Дроби бывают трёх видов. Обыкновенные, десятичные и смешанные числа.
2. Десятичные дроби и смешанные числа всегда можно перевести в обыкновенные дроби. Обратный перевод не всегда возможен.
3. Выбор вида дробей для работы с заданием зависит от этого самого задания. При наличии разных видов дробей в одном задании, самое надёжное — перейти к обыкновенным дробям.
Теперь можно потренироваться. Для начала переведите эти десятичные дроби в обыкновенные:
3,8; 0,75; 0,15; 1,4; 0,725; 0,012
Должны получиться вот такие ответы (в беспорядке!):
На этом и завершим. В этом уроке мы освежили в памяти ключевые моменты по дробям. Бывает, правда, что освежать особо нечего…) Если уж кто совсем крепко забыл, или ещё не освоил… Тем можно пройти в особый Раздел 555 . Там все основы подробненько расписаны. Многие вдруг всё понимать начинают. И решают дроби с лёту).
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас. )
)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Десятичная дробь состоит из двух частей, которые разделены запятыми. Первая часть — это целая единица, вторая часть — это десятки (если число после запятой одно), сотни (два числа после запятой, как два нуля в ста), тысячные итд. Посмотрим на примеры десятичной дроби: 0, 2; 7, 54; 235,448; 5,1; 6,32; 0,5. Всё это — десятичные дроби. Как же перевести десятичную дробь в обыкновенную?
Пример первый
У нас есть дробь, к примеру, 0,5. Как уже выше писалось, она состоит из двух частей. Первое число 0, показывает, сколько целых единиц у дроби. В нашем случае их нет. Второе число показывает десятки. Дробь даже читается ноль целых пять десятых. Десятичное число перевести в дробь теперь не составит труда, пишем 5/10. Если видите, что у цифр есть общий делитель, можете сократить дробь. У нас это число 5, поделив обе части дроби на 5, получаем — 1/2.
У нас это число 5, поделив обе части дроби на 5, получаем — 1/2.
Пример второй
Возьмем более сложную дробь — 2,25. Читается она так — две целых и двадцать пять сотых. Обратите внимание — сотых, так как чисел после запятой две. Теперь можно перевести в обыкновенную дробь. Записываем — 2 25/100. Целая часть — 2, дробная 25/100. Как и в первом примере, эту часть можно сократить. Общим делителем для цифр 25 и 100 является число 25. Заметьте, что мы всегда подбираем наибольший общий делитель. Разделив обе части дроби на НОД, получили 1/4. Итак, 2, 25 это 2 1/4.
Пример третий
И для закрепления материала возьмем десятичную дробь 4,112 — четыре целых и сто двенадцать тысячных. Почему тысячных, думаю, ясно. Записываем теперь 4 112/1000. По алгоритму находим НОД чисел 112 и 1000. В нашем случае — это число 6. Получаем 4 14/125.
Вывод
- Разбиваем дробь на целую и дробную части.
- Смотрим, сколько цифр после запятой. Если одна — это десятки, две — сотни, три -тысячные итд.

- Записываем дробь в обыкновенном виде.
- Сокращаем числитель и знаменатель дроби.
- Записываем полученную дробь.
- Выполняем проверку, делим верхнюю часть дроби на нижнюю. Если есть целая часть, прибавляем к полученной десятичной дроби. Получился исходный вариант — замечательно, значит, вы все сделали правильно.
На примерах я показала, как можно перевести десятичную дробь в обыкновенную. Как видите, сделать это очень легко и просто.
То нажмите на кнопки, и задача выполнена. В результате у вас получится либо целое число, либо десятичная дробь. Десятичная дробь может получится с длинным остатком после . В этом случае дробь нужно округлить до определенного, нужного вам разряда, используя округления (цифры до 5 округляются в меньшую сторону, от 5 включительно и более — в большую сторону).
Если калькулятора под рукой не , но придется . Напишите числитель дроби со знаменателем, между ними уголочек, означающий . К примеру, переведите в число дробь 10/6. Для начала 10 разделите на 6. Получится 1. Запишите результат по уголком. Перемножьте 1 на 6, получится 6. Вычтите 6 из 10. Получится остаток 4. Остаток нужно снова разделить на 6. Допишите к 4 цифру 0, и разделите 40 на 6. Получится 6. Запишите 6 в результат, после запятой. Перемножьте 6 на 6. Получится 36. Вычтите 36 из 40. Получится вновь остаток 4. Далее можно не продолжать, поскольку становится очевидным, что результатом будет число 1,66(6). Округлите данную дробь до того разряда, который вам необходим. Например, 1,67. Это и есть окончательный результат.
Для начала 10 разделите на 6. Получится 1. Запишите результат по уголком. Перемножьте 1 на 6, получится 6. Вычтите 6 из 10. Получится остаток 4. Остаток нужно снова разделить на 6. Допишите к 4 цифру 0, и разделите 40 на 6. Получится 6. Запишите 6 в результат, после запятой. Перемножьте 6 на 6. Получится 36. Вычтите 36 из 40. Получится вновь остаток 4. Далее можно не продолжать, поскольку становится очевидным, что результатом будет число 1,66(6). Округлите данную дробь до того разряда, который вам необходим. Например, 1,67. Это и есть окончательный результат.
Связанная статья
Источники:
- перевод дробей с целым числом
Дроби нужны для обозначения чисел, которые состоят из одной или нескольких частей единицы. Термин «дробь» произошел от латинского fractura, которое имеет значение «дробить, ломать». Различаются обыкновенные и десятичные дроби. При этом в обыкновенных дробях единицу можно разделить на любое количество частей, а в десятичной — это количество должно быть кратно 10. Любая дробь может иметь быть как обычной, так и десятичной.
Любая дробь может иметь быть как обычной, так и десятичной.
Вам понадобится
- Для подсчета результата вам понадобится калькулятор или листок и ручка.
Инструкция
Итак, для начала возьмите обыкновенную дробь и разделите ее на части. Например, 2 1\8, в которой 2 — это целая часть, а 1\8 дробь. Из нее можно увидеть, что число разделили на 8 , но взяли лишь одну. Часть, которую взяли, числитель, а количество частей, на которое делят, — знаменатель.
Обратите внимание
Зачастую встречаются дроби, которые нельзя полностью перевести в десятичные. В этом случае на помощь приходит округление. Если вы хотите округлить до тысячных, то посмотрите на четвертое число после запятой. Если оно меньше 5, то запишите в ответ, первые три цифры после запятой без изменения, в противном случае к последней цифре из трех необходимо прибавить единицу. Например, 0, 89643123 можно записать как 0,896, а вот 0, 89663123 — 0,897.
Полезный совет
Если вы подсчитываете результат вручную, то перед делением дробь лучше максимально сократить, а также выделить из нее целые части.
Источники:
- как перевести дроби
Дробь является одним из элементов формул, для ввода которых в текстовом процессоре Word существует инструмент Microsoft Equation. С помощью него можно вводить любые сложные математические или физические формулы, уравнения и другие элементы, включающие в себя специальные символы.
Инструкция
Чтобы запустить инструмент Microsoft Equation необходимо пройти по адресу: «Вставка» -> «Объект», в открывшемся диалоговом окне, на первой вкладке из списка нужно выбрать Microsoft Equation и нажать «Ок» или два раза кликнуть на выбранном пункте. После запуска редактора , перед вами откроется панель инструментов и в отобразится поле для ввода : прямоугольник в пунктирной . Панель инструментов разделена на секции, в каждой из них находится набор знаков действий или выражений. При нажатии на одну из секций, развернется список находящихся в ней инструментов. Из открывшегося списка необходимо выбрать нужный символ и кликнуть на нем. После выбора, указанный символ появится в выделенном прямоугольнике в документе.
После выбора, указанный символ появится в выделенном прямоугольнике в документе.
Секция, в которой располагаются элементы для написания дробей, находится во второй строке панели инструментов. При наведении на нее курсора мыши, вы увидите подсказку «Шаблоны дробей и радикалов». Кликните секцию один раз и разверните список. В выпавшем меню есть шаблоны для дробей с горизонтальной и косой . Среди появившихся вариантов вы можете выбрать тот, который подходит для вашей задачи. Кликните на нужном варианте. После нажатия, в поле для ввода, которое открылось в документе, появится символ дроби и места для ввода числителя и знаменателя, обрамленные пунктирной линией. Курсор по умолчанию автоматически устанавливается в поле для ввода числителя. Введите числитель. Помимо цифр можно так же вводить символы, буквы или знаки действий. Их можно вводить как с клавиатуры, так и из соответствующих секций панели инструментов Microsoft Equation. После вода числителя, нажатием клавиши TAB, перейдите к знаменателю. Перейти можно и кликнув мышью в поле для ввода знаменателя. Как только написана, кликните указателем мыши в любом месте документа, панель инструментов закроется, ввод дроби будет завершен. Чтобы отредактировать , дважды нажмите на ней левой кнопкой мыши.
Перейти можно и кликнув мышью в поле для ввода знаменателя. Как только написана, кликните указателем мыши в любом месте документа, панель инструментов закроется, ввод дроби будет завершен. Чтобы отредактировать , дважды нажмите на ней левой кнопкой мыши.
Если при открытии меню «Вставка» -> «Объект», в списке вы не обнаружили инструмента Microsoft Equation, его необходимо установить. Запустите установочный диск, образ диска или файл дистрибутива Word. В появившемся окне инсталлятора выберите «Добавить или удалить компоненты. Добавление или удаление отдельных компонентов» и нажмите «Далее». В следующем окне отметьте пункт «Расширенная настройка приложений». Нажмите «Далее». В следующем окне найдите пункт списка «Средства Office» и нажмите на плюсик слева. В развернувшемся списке, нас интересует пункт «Редактор формул». Кликните на значок рядом с надписью «Редактор формул» и, в открывшемся меню, нажмите «Запускать с компьютера». После этого нажмите «Обновить» и дождитесь пока пройдет установка необходимого компонента.
правила, примеры, решения, как целое число разделить на десятичную дробь
В этой статье мы разберем такое важное действие с десятичными дробями, как деление. Сначала сформулируем общие принципы, затем разберем, как правильно выполнять деление десятичных дробей столбиком как на другие дроби, так и на натуральные числа. Далее мы разберем деление обыкновенных дробей на десятичные и наоборот, а в конце посмотрим, как правильно выполнять деление дробей, заканчивающихся на 0,1, 0,01, 100, 10 и др.
Здесь мы возьмем только случаи с положительными дробями. Если же перед дробью стоит минус, то для действия с ней нужно изучить материал о делении рациональных и действительных чисел.
Основы деления десятичных дробей
Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами.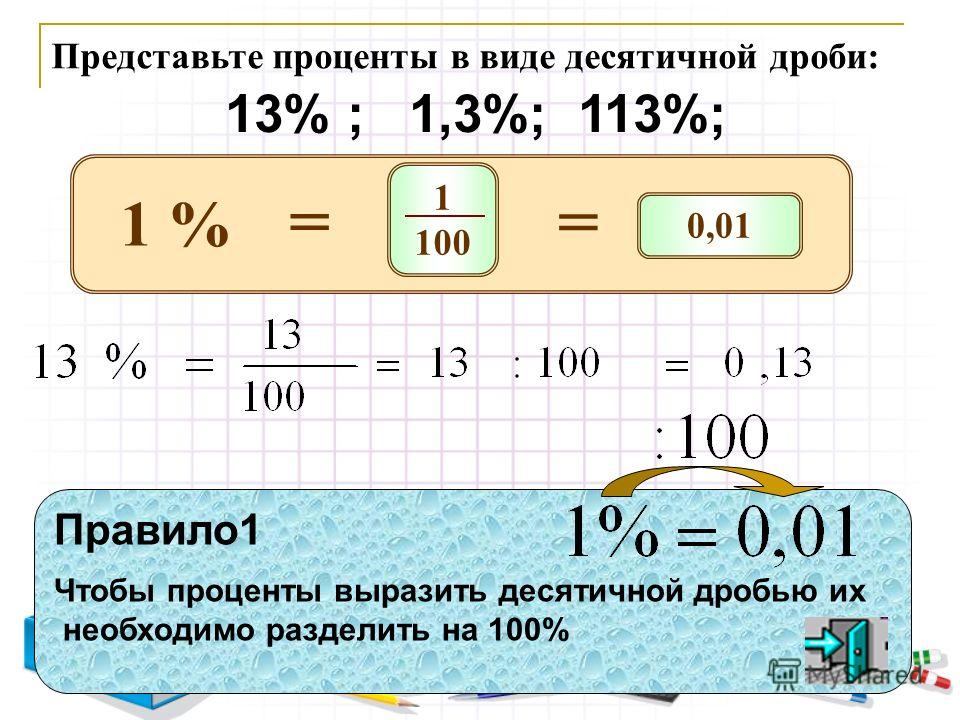 Возьмем конкретный пример.
Возьмем конкретный пример.
Разделите 1,2 на 0,48.
Решение
Запишем десятичные дроби в виде обыкновенных. У нас получится:
1,2=1210=65
0,48=48100=1225.
Таким образом, нам надо разделить 65 на 1225. Считаем:
1,2:0,48=62:1225=65·2512=6·255·12=52
Из получившейся в итоге неправильной дроби можно выделить целую часть и получить смешанное число 212, а можно представить ее в виде десятичной дроби, чтобы она соответствовала исходным цифрам: 52=2,5. О том, как это сделать, мы уже писали ранее.
Ответ: 1,2:0,48=2,5.
Пример 2Посчитайте, сколько будет 0,(504)0,56.
Решение
Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.
0,(504)=0,5041-0,001=0,5040,999=504999=56111
После этого конечную десятичную дробь также переведем в другой вид: 0,56=56100. Теперь у нас есть два числа, с которыми нам будет легко провести необходимые вычисления:
0,(504):1,11=56111:56100=56111·10056=100111
У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:
Для этого разделим числитель на знаменатель, используя метод столбика:
Ответ: 0,(504):0,56=0,(900).
Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.
Пример 3Найдите, сколько будет 0,779…/1,5602.
Решение
Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:
0,779…≈0,78
1,5602≈1,56
Можем продолжить подсчеты и получить примерный результат: 0,779…:1,5602≈0,78:1,56=78100:156100=78100·100156=78156=12=0,5.
Точность результата будет зависеть от степени округления.
Ответ: 0,779…:1,5602≈0,5.
Как разделить натуральное число на десятичную дробь и наоборот
Подход к делению в этом случае практически аналогичен: конечные и периодические дроби заменяем обыкновенными, а бесконечные непериодические округляем. Возьмем для начала пример деления с натуральным числом и десятичной дробью.
Пример 4Разделите 2,5 на 45.
Решение
Приведем 2,5 к виду обыкновенной дроби: 25510=512. Далее нам надо просто разделить ее на натуральное число. Делать это мы уже умеем:
25,5:45=512:45=512·145=1730
Если перевести результат в десятичную запись, то мы получим 0,5 (6).
Ответ: 25,5:45=0,5(6).
Как разделить десятичную дробь на натуральное число столбиком
Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.
Определение 1Для деления столбиком десятичных дробей на натуральные числа необходимо:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.
Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.
Пример 5Вычислите, сколько будет 65,144.
Решение
Используем метод столбика. Для этого допишем к дроби два нуля и получим десятичную дробь 65,1400, которая будет равна исходной. Теперь пишем столбик для деления на 4:
Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:
Ставим запятую, отделяя ее, и продолжаем:
Мы добрались до нулевого остатка, следовательно, процесс деления завершен.
Ответ: 65,14:4=16,285.
Пример 6Разделите 164,5 на 27.
Решение
Делим сначала дробную часть и получаем:
Отделяем полученную цифру запятой и продолжаем делить:
Мы видим, что остатки стали периодически повторяться, и в частном стали чередоваться цифры девять, два и пять. На этом мы остановимся и запишем ответ в виде периодической дроби 6,0(925).
Ответ: 164,5:27=6,0(925).
Как разделить столбиком одну десятичную дробь на другую
Такое деление можно свести к уже описанному выше процессу нахождения частного десятичной дроби и натурального числа. Для этого нам потребуется умножить делимое и делитель на 10, 100 и др. так, чтобы делитель превратился в натуральное число. Дальше выполняем описанную выше последовательность действий. Такой подход возможен благодаря свойствам деления и умножения.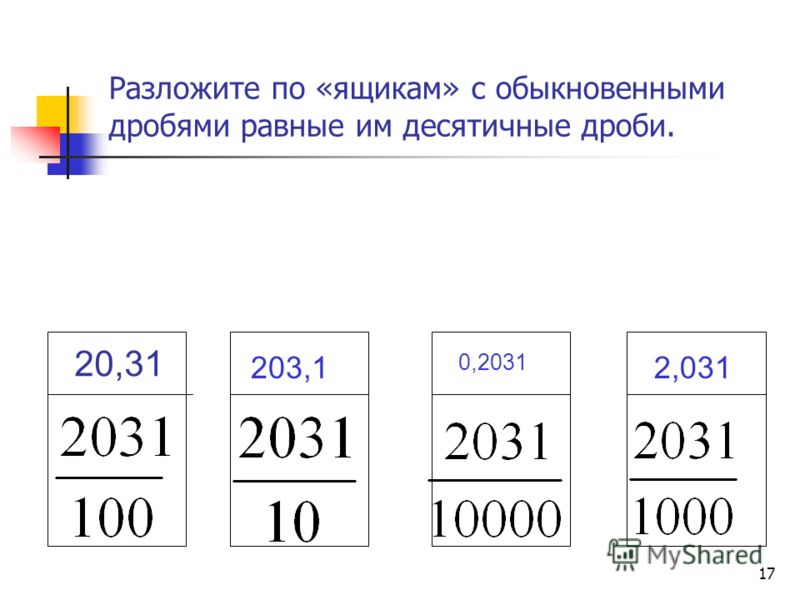 В буквенном виде мы записывали их так:
В буквенном виде мы записывали их так:
a:b=(a·10):(b·10), a:b=(a·100):(b·100) и так далее.
Сформулируем правило:
Определение 2Для деления одной конечной десятичной дроби на другую необходимо:
1. Перенести запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, допишем в него нули с правой стороны.
2. После этого делим дробь столбиком на получившееся натуральное число.
Разберем конкретную задачу.
Пример 7Разделите 7,287 на 2,1.
Решение: Чтобы делитель стал натуральным числом, нам надо перенести запятую на один знак вправо. Так мы перешли к делению десятичной дроби 72,87 на 21. Запишем полученные числа столбиком и вычислим
Ответ: 7,287:2,1=3,47
Пример 8Вычислите 16,30,021.
Решение
Нам придется переносить запятую на три знака. В делителе для этого не хватит цифр, значит, нужно воспользоваться дополнительными нулями. Считаем, что получится в итоге:
Считаем, что получится в итоге:
Видим периодическое повторение остатков 4, 19, 1, 10, 16, 13. В частном повторяются 1, 9, 0, 4, 7 и 5. Тогда наш результат является периодической десятичной дробью 776,(190476).
Ответ: 16,3:0,021=776,(190476)
Описанный нами метод позволяет делать и наоборот, то есть делить натуральное число на конечную десятичную дробь. Посмотрим, как это делается.
Пример 9Подсчитайте, сколько будет 3 5,4.
Решение
Очевидно, что нам придется перенести запятую вправо на один знак. После этого мы можем приступить к делению 30,0 на 54. Запишем данные столбиком и вычислим результат:
Повторение остатка дает нам в итоге число 0,(5), которое является периодической десятичной дробью.
Ответ: 3:5,4=0,(5).
Как разделить десятичные дроби на 1000, 100, 10 и др.
Согласно уже изученным правилам деления обыкновенных дробей, деление дроби на десятки, сотни, тысячи аналогично ее умножению на 1/1000, 1/100, 1/10 и др.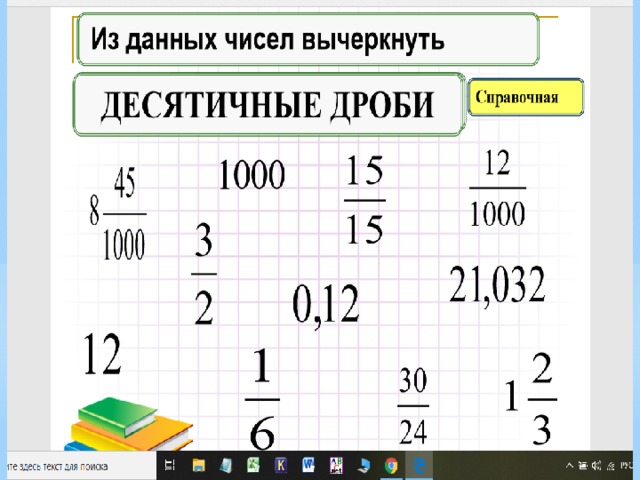 Получается, чтобы выполнить деление, в данном случае достаточно просто перенести запятую на нужное количество цифр. Если значений в числе не хватит для переноса, нужно дописать нужное количество нулей.
Получается, чтобы выполнить деление, в данном случае достаточно просто перенести запятую на нужное количество цифр. Если значений в числе не хватит для переноса, нужно дописать нужное количество нулей.
Так, 56,21:10=5,621, а 0,32:100 000=0,0000032.
В случае с бесконечными десятичными дробями мы поступаем таким же образом.
Пример 11Например, 3,(56):1 000=0,003(56) и 593,374…:100=5,93374….
Как разделить десятичные дроби на 0,001, 0,01, 0,1 и др.
Воспользовавшись тем же правилом, мы можем так же разделить дроби на указанные значения. Это действие будет аналогично умножению на 1000, 100, 10 соответственно. Для этого мы переносим запятую на одну, две или три цифры в зависимости от условий задачи и дописываем нули, если цифр в числе окажется недостаточно.
Пример 12К примеру, 5,739:0,1=57,39 и 0,21:0,00001=21 000.
Это правило действует и в случае с бесконечными десятичными дробями. Советуем только быть внимательными с периодом дроби, которая получается в ответе.
Так, 7,5(716):0,01=757,(167), поскольку после того, как мы перенесли запятую в записи десятичной дроби 7,5716716716… на два знака вправо, у нас получилось 757,167167….
Если же у нас в примере непериодические дроби, то все обстоит проще: 394,38283…:0,001=394382,83….
Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот
Это действие мы также сводим к операциям с обыкновенными дробями. Для этого надо заменить десятичные числа соответствующими обыкновенными дробями, а смешанное число записать в виде неправильной дроби.
Если мы делим непериодическую дробь на обыкновенную либо на смешанное число, нужно поступить наоборот, заменив обыкновенную дробь или смешанное число соответствующей им десятичной дробью.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Что такое 2/5 в виде десятичной дроби? (Преобразовать 2/5 в десятичную)
Преобразование 2/5 в десятичную, возможно, одно из самых простых вычислений, которые вы можете сделать. В этом (очень коротком) руководстве мы покажем вам, как превратить любую дробь в десятичную менее чем за 3 секунды! Вот так!
В этом (очень коротком) руководстве мы покажем вам, как превратить любую дробь в десятичную менее чем за 3 секунды! Вот так!
Хотите быстро узнать или показать учащимся, как преобразовать 2/5 в десятичную дробь? Включи это очень быстрое и веселое видео прямо сейчас!
Прежде всего, если вы не знаете, что такое числитель и знаменатель в дроби, нам нужно повторить это:
2 (числитель) / 5 (знаменатель)
Вот небольшой секрет, с помощью которого можно мгновенно преобразовать любую дробь в десятичную: Просто разделите числитель на знаменатель:
= 2/5
= 2 ÷ 5
= 0,4
3
Вот буквально все! 2/5 в виде десятичной дроби равно 0,4.Хотел бы я рассказать вам больше о преобразовании дроби в десятичную, но это действительно так просто, и мне больше нечего сказать об этом.
Если вы хотите потренироваться, возьмите ручку и блокнот и попробуйте самостоятельно вычислить некоторые дроби в десятичном формате. Если вы действительно чувствуете себя ленивым , вы можете вместо этого использовать наш калькулятор ниже!
Почему вы хотите преобразовать 2/5 в десятичную дробь?
Отличный вопрос. У нас есть много расчетов на этом сайте о преобразовании дроби в десятичную, но зачем вам вообще это нужно?
У нас есть много расчетов на этом сайте о преобразовании дроби в десятичную, но зачем вам вообще это нужно?
Ну, во-первых, это просто хороший способ представить дробь в лучшем виде, который позволяет вам выполнять с ними обычные арифметические действия (такие как сложение, вычитание, деление и умножение).
В реальной жизни мы в основном имеем дело с десятичными дробями (например, с валютой), и, поскольку наш мозг с юных лет приучен понимать и сравнивать десятичные дроби чаще, чем дроби, проще понимать и сравнивать дроби, если они сначала преобразовать в десятичную!
Вот небольшой пример из реальной жизни преобразования дроби в десятичную при использовании количества. Допустим, вы готовите, и обычно вы можете видеть, сколько ингредиента осталось в упаковке. Однако электронные весы измеряют вес в десятичных дробях, а не в долях оставшегося ингредиента. Это делает преобразование между дробями и десятичными дробями полезным навыком в кулинарии.
Надеюсь, это руководство помогло вам понять, как преобразовать дробь в десятичное число. Теперь вы можете идти вперед и преобразовывать дроби в десятичные столько, сколько пожелает ваше маленькое сердце!
Теперь вы можете идти вперед и преобразовывать дроби в десятичные столько, сколько пожелает ваше маленькое сердце!
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
«Что такое 2/5 в виде десятичной дроби?». VisualFractions.com . По состоянию на 23 сентября 2022 г. http://visualfractions.com/calculator/fraction-as-decimal/what-is-2-5-as-a-decimal/.
«Что такое 2/5 в виде десятичной дроби?». VisualFractions.com , http://visualfractions.com/calculator/fraction-as-decimal/what-is-2-5-as-a-decimal/. По состоянию на 23 сентября 2022 г.

Что такое 2/5 в виде десятичной дроби?. VisualFractions.com. Получено с http://visualfractions.com/calculator/fraction-as-decimal/what-is-2-5-as-a-decimal/.
Калькулятор преобразования дроби в десятичную дробь
Дробь в виде десятичной дроби
Введите числитель и знаменатель
Вычисление следующей дроби в десятичную дробь
- Что такое 2/6 в виде десятичной дроби?
Случайные дроби в десятичные числа
Если вы добрались до этого конца страницы, значит, вы ДЕЙСТВИТЕЛЬНО любите преобразовывать дроби в десятичные? Ниже приведена куча случайно сгенерированных вычислений для вашего удовольствия от десятичной любви:
Что такое 325/464 как десятичная
Десятичное число 501/623
Десятичное число 429/636
Десятичное число 570/902
Десятичное число 902/965
Десятичное число 6
Десятичное число 69/91
Десятичное число 407/797
Десятичное число 530/659
Десятичное число 260/540
Десятичное число 873/96
Что такое 668/894 в виде десятичного числа
Что такое 677/790 в виде десятичного числа
Десятичное число 623/758
Десятичное число 170/260
Десятичное число 202/739
Десятичное число 161/966
Десятичное число 162/76
Десятичное число 682/767
Десятичное число 372/506
Десятичное число 72/269
Десятичное число 948/971
Десятичное число 6 a 494/81
Что такое 74/249 в виде десятичного числа
Что такое 105/280 в виде десятичного числа
Десятичное число 83/305
Десятичное число 312/601
Десятичное число 528/890
Десятичное число 580/617
Десятичное число 626/99
Десятичное число 923/962
Десятичное число 90/694
Десятичное число 485/697
Десятичное число 45/87
Десятичное число 660/82
Что такое 621/970 в виде десятичного числа
Что такое 242/695 в виде десятичного числа
Десятичное число 207/709
Десятичное число 133/955
Десятичное число 730/834
Десятичное число 663/790
Десятичное число 311/989 03
Десятичное число 915/985
Десятичное число 468/905
Десятичное число 306/827
Десятичное число 681/702
Десятичное число 710/729 0
Что такое 924/959 в виде десятичного числа
Что такое 865/930 в виде десятичного числа
Десятичное число 304/568
Десятичное число 685/790
Десятичное число 399/729
Десятичное число 937/945
Десятичное число 512/8690 03
Десятичное число 862/879
Десятичное число 726/860
Десятичное число 910/914
Десятичное число 358/626
Десятичное число 817/979 0
Что такое 60/199 в виде десятичного числа
Что такое 408/564 в виде десятичного числа
Десятичное число 555/609
Десятичное число 788/956
Десятичное число 906/919
Десятичное число 716/752
Десятичное число 932/9790
Десятичное число 512/588
Десятичное число 247/733
Десятичное число 908/954
Десятичное число 503/796
Десятичное число 226/6490
Что такое 291/698 в виде десятичного числа
Что такое 993/996 в виде десятичного числа
Десятичное число 750/852
Десятичное число 380/452
Десятичное число 183/730
Десятичное число 767/924
Десятичное число 84/864 03
Что такое десятичное число 26/81
Что такое десятичное число 749/772
Что такое десятичное число 52/434
Что такое десятичное число 295/347
Что такое десятичное число 607/772 902
Что такое 587/659 в виде десятичного числа
Что такое 128/833 в виде десятичного числа
Что такое 565/949 в виде десятичного числа
Что такое 727/960 в виде десятичного числа
Что такое 290/333 в виде десятичного числа
Что такое 829/836 в виде десятичного числа
Что такое 186/238 в виде десятичного числа Что такое
930 в виде десятичного числа
Что такое 355/651 в виде десятичного числа
Что такое 368/880 в виде десятичного числа
Что такое 861/968 в виде десятичного числа
Что такое 834/985 в виде десятичного числа
23
32 998 в виде десятичного числа
Что такое 509/765 в виде десятичного числа
Что такое 567/999 в виде десятичного числа
Что такое 984/996 в виде десятичного числа
Что такое 270/484 в виде десятичного числа
Что такое 373/623 в виде десятичного числа
Что такое 2 5/16 в виде десятичного числа
16 равно 2,3125 в десятичной форме. Используйте наш калькулятор преобразования дроби в десятичную, чтобы преобразовать любую дробь в десятичную и узнать, является ли она завершающей или повторяющейся (повторяющейся) десятичной дробью.
Используйте наш калькулятор преобразования дроби в десятичную, чтобы преобразовать любую дробь в десятичную и узнать, является ли она завершающей или повторяющейся (повторяющейся) десятичной дробью.
Калькулятор / конвертер дробей в десятичные дроби
Введите дробное значение: Пример: 1/2, 2 1/2, 5/3 и т. д. Обратите внимание, что 2 1/2 означает два с половиной = 2 + 1/2 = 2,5
Ответ:
Пошаговое решение:
Цитаты
См. также:
- Калькулятор дробей
- Калькулятор десятичной дроби
- Калькулятор доли в процентах
- Фракции Simplifier/Reducer
- Калькулятор эквивалентных дробей
Таблица преобразования: дробь в десятичные дюймы и эквивалент в миллиметрах
Чтобы преобразовать дроби в десятичные дроби и миллиметры и наоборот, используйте эту формулу:
1 дюйм = 25,4 мм точно, поэтому . ..
..
Чтобы преобразовать из дюймов в миллиметры умножьте значение в дюймах на 25,4.
Чтобы преобразовать миллиметры в дюймы, разделите значение в миллиметрах на 25,4.
Проще всего это сделать с помощью приведенной ниже таблицы. Как?
Пример 1
Преобразование 1 1/32 дюйма в миллиметры:
Найдите 1 1/32 и прочитайте справа под столбцом мм! Вы найдете 26,1938. форма).
fraction decimal mm 1/64 0.0156 0.3969 1/32 0.0313 0.7938 3/64 0.0469 1.1906 1/16 0.0625 1.5875 5/64 0.0781 1.9844 3/32 0.0938 2.3813 7/64 0.1094 2.7781 1/8 0.1250 3. 1750
1750 9/64 0.1406 3.5719 5/32 0.1563 3.9688 11/64 0.1719 4.3656 3/16 0.1875 4.7625 13/64 0.2031 5.1594 7/32 0.2188 5.5563 15/64 0.2344 5.9531 1/4 0.2500 6.3500 17/64 0.2656 6.7469 9/32 0.2813 7.1438 19/64 0.2969 7.5406 5/16 0.3125 7.9375 21/64 0.3281 8.3344 11/32 0.3438 8.7313 23/64 0. 3594
3594 9.1281 3/8 0.3750 9.5250 25/64 0.3906 9.9219 13/32 0.4063 10.3188 27/64 0.4219 10.7156 7/16 0.4375 11.1125 29/64 0.4531 11.5094 15/32 0.4688 11.9063 31/64 0.4844 12.3031 1/2 0.5000 12.7000 33/64 0.5156 13.0969 17/32 0.5313 13.4938 35/64 0.5469 13.8906 9/16 0.5625 14.2875 37/64 0.5781 14.6844 19/32 0. 5938
5938 15.0813 39/64 0.6094 15.4781 5/8 0.6250 15.8750 41/64 0.6406 16.2719 21/32 0.6563 16.6688 43/64 0.6719 17.0656 11/16 0.6875 17.4625 45/64 0.7031 17.8594 23/32 0.7188 18.2563 47/64 0.7344 18.6531 3/4 0.7500 19.0500 49/64 0.7656 19.4469 25/32 0.7813 19.8438 51/64 0.7969 20.2406 13/ 16 0.8125 20.6375 53/64 0. 8281
8281 21.0344 27/32 0.8438 21.4313 55/64 0.8594 21.8281 7/8 0.8750 22.2250 57/64 0.8906 22.6219 29/32 0.9063 23.0188 59 /64 0.9219 23.4156 15/16 0.9375 23.8125 61/64 0.9531 24.2094 31/32 0.9688 24.6063 63/64 0.9844 25.0031 1 1.0000 25.4000
fraction decimal mm 1 1/64 1.0156 25.7969 1 1/32 1. 0313
0313 26.1938 1 3/64 1.0469 26.5906 1 1/16 1.0625 26.9875 1 5/64 1.0781 27.3844 1 3/32 1.0938 27.7813 1 7/64 1.1094 28.1781 1 1/8 1.1250 28.5750 1 9/64 1.1406 28.9719 1 5/32 1.1563 29.3688 1 11/64 1.1719 29.7656 1 3/16 1.1875 30.1625 1 13/64 1.2031 30.5594 1 7/32 1.2188 30.9563 1 15/64 1.2344 31.3531 1 1/4 1.2500 31. 7500
7500 1 17/64 1.2656 32.1469 1 9/32 1.2813 32.5438 1 19/64 1.2969 32.9406 1 5/16 1.3125 33.3375 1 21/64 1.3281 33.7344 1 11/32 1.3438 34.1313 1 23/64 1.3594 34.5281 1 3/8 1.3750 34.9250 1 25/64 1.3906 35.3219 1 13/32 1.4063 35.7188 1 27 /64 1.4219 36.1156 1 7/16 1.4375 36.5125 1 29/64 1.4531 36.9094 1 15/32 1.4688 37. 3063
3063 1 31/64 1.4844 37.7031 1 1/2 1.5000 38.1000 1 33/64 1.5156 38.4969 1 17/32 1.5313 38.8938 1 35/64 1.5469 39.2906 1 9/16 1.5625 39.6875 1 37/64 1.5781 40.0844 1 19/32 1.5938 40.4813 1 39/64 1.6094 40.8781 1 5/8 1.6250 41.2750 1 41/64 1.6406 41.6719 1 21/32 1.6563 42.0688 1 43/64 1.6719 42.4656 1 11/16 1.6875 42. 8625
8625 1 45/64 1.7031 43.2594 1 23/32 1.7188 43.6563 1 47/64 1.7344 44.0531 1 3/4 1.7500 44.4500 1 49/64 1.7656 44.8469 1 25/32 1.7813 45.2438 1 51/64 1.7969 45.6406 1 13/16 1.8125 46.0375 1 53/64 1.8281 46.4344 1 27/32 1.8438 46.8313 1 55/64 1.8594 47.2281 1 7/8 1.8750 47.6250 1 57/64 1.8906 48.0219 1 29/32 1.9063 48. 4188
4188 1 59/64 1.9219 48.8156 1 15/16 1.9375 49.2125 1 61/64 1.9531 49.6094 1 31/32 1.9688 50.0063 1 63/64 1.9844 50.4031 2 2.0000 50.8000
fraction decimal mm 2 1/64 2.0156 51.1969 2 1/ 32 2.0313 51.5938 2 3/64 2.0469 51.9906 2 1/16 2.0625 52.3875 2 5/64 2.0781 52.7844 2 3/32 2.0938 53.1813 2 7/64 2. 1094
1094 53.5781 2 1/8 2.1250 53.9750 2 9/64 2.1406 54.3719 2 5/32 2.1563 54.7688 2 11/64 2.1719 55.1656 2 3/16 2.1875 55.5625 2 13/64 2.2031 55.9594 2 7/32 2.2188 56.3563 2 15/64 2.2344 56.7531 2 1/4 2.2500 57.1500 2 17/64 2.2656 57.5469 2 9/32 2.2813 57.9438 2 19/64 2.2969 58.3406 2 5/16 2.3125 58.7375 2 21/64 2.3281 59. 1344
1344 2 11/32 2.3438 59.5313 2 23/64 2.3594 59.9281 2 3/8 2.3750 60.3250 2 25/64 2.3906 60.7219 2 13/32 2.4063 61.1188 2 27/64 2.4219 61.5156 2 7/16 2.4375 61.9125 2 29/64 2.4531 62.3094 2 15/32 2.4688 62.7063 2 31/64 2.4844 63.1031 2 1/2 2.5000 63.5000 2 33/64 2.5156 63.8969 2 17/32 2.5313 64.2938 2 35/64 2.5469 64. 6906
6906 2 9/16 2.5625 65.0875 2 37/64 2.5781 65.4844 2 19/32 2.5938 65.8813 2 39/64 2.6094 66.2781 2 5/8 2.6250 66.6750 2 41/64 2.6406 67.0719 2 21/32 2.6563 67.4688 2 43/64 2.6719 67.8656 2 11/16 2.6875 68.2625 2 45/64 2.7031 68.6594 2 23/32 2.7188 69.0563 2 47/64 2.7344 69.4531 2 3/4 2.7500 69.8500 2 49/64 2.7656 70. 2469
2469 2 25/32 2.7813 70.6438 2 51/64 2.7969 71.0406 2 13/16 2.8125 71.4375 2 53/64 2.8281 71.8344 2 27/32 2.8438 72.2313 2 55/64 2.8594 72.6281 2 7/8 2.8750 73.0250 2 57/64 2.8906 73.4219 2 29/32 2.9063 73.8188 2 59/64 2.9219 74.2156 2 15/16 2.9375 74.6125 2 61/64 2.9531 75.0094 2 31/32 2.9688 75.4063 2 63/64 2.9844 75. 8031
8031 3 3.0000 76.2000
Fraction to Decimal Calculator
Ссылка на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
Фракция выборки до десятичных расчетов
- 1 96/30 до десятичного десятичного от
- 1/86 до десятичного детью
- 25/92 до десятичного деть. 8 до десятичной
- 2 90/43 до десятичной
- 2 25/32 до десятичной
- 1 61/7 до десятичной
- 61/30 до десятичной
- 2 31/59 до десятичного десятичного. сделано для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за любые ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
Как преобразовать футы/дюймы/дроби в десятичный формат
Калькуляторы Спайка
Множество чисел, с которыми нужно иметь дело, и нет, не очень полезные для выбора лотерейных номеров. Но если вы понимаете основные понятия, это избавляет вас от необходимости конвертировать эти числа, и вы обязательно станете победителем.
Но если вы понимаете основные понятия, это избавляет вас от необходимости конвертировать эти числа, и вы обязательно станете победителем.
Дюйм Десятичный фут 1 дюйм 0,0833 2 дюйма0299 0.167 3 inches 0.25 4 inches 0.333 5 inches 0.417 6 inches 0.5 7 inches 0.583 8 дюймов 0,667 9 дюймов 0,75 10 дюймов 0,939 9032 11 inches 0.917 12 inches 1
Fraction Decimal Value of an Inch 1/16 0.0625 1/8 0. 125
125 3/16 0.1875 1/4 0.25 5/16 0.3125 3/8 0.375 7/16 0.4375 1/2 0.5 9.16 0.5625 5/8 0.625 11 /16 0.6875 3/4 0.75 13/16 0.8125 7/8 0.875 15/16 0,9375
Пример
Преобразование 7′-4 3/4″ в десятичное число.
- Если вы похожи на меня, я бы сказал, что 7′ пока остается 7′.
- Смотрю на диаграммы 4″ = 0,333 3/4″ = 0,75
- 0,333 + 0,75 = 1,083 дюйма + 7 дюймов = 8,083
- , и я бы написал все это как 8,083 в десятичном формате.

Конечно, вы не можете добавить десятичное значение фута к десятичному значению дюйма без преобразования десятичного значения дроби в дюймах в десятичное значение фута.
Попробуем еще раз:
Преобразование 7′- 4 3/4″ в десятичное число.
- 7′ пока остается 7′.
- 4″ = 0,333 (преобразовать в десятичное значение в футах: 4 ÷ 12)
- 3/4″ = 0,75 (перевести дробь в десятичную, разделив числитель на знаменатель 3 ÷ 4)
- 0,75 = 0,0625 (преобразование в десятичное число футов путем деления 0,75 на 12)
- 0,333 + 0,0625 = 0,3955 + 7′ = 7,3955
Запишите 7′- 4 3/4″ в десятичной форме = 7,3955
1/16 0.0625 0.005208 1/8 0.125 0.01042 3/16 0.1875 0.015625 1/4 0. 25
25 0.020883 5/16 0.3125 0.026004 3/8 0.375 0.03125 7/16 0.4375 0.036458 1/2 0.5 0.041666 9.16 0.5625 0.046875 5/8 0.625 0.05208 11/16 0.6875 0.057291 3/4 0.75 0.0625 13/16 0.8125 0.0677 7/8 0.875 0.072916 15/16 0.9375 0.078125 1 inch 12/12 1 0. 0833
0833 2 inches 24/12 2 0.167 3 inches 36/12 3 0.25 4 inches 48/12 4 0.333 5 inches 60/12 5 0.417 6 inches 72/ 12 6 0.5 7 inches 84/12 7 0.583 8 inches 96/12 8 0.667 9 inches 108/12 9 0.75 10 inches 120/12 10 0.833 11 inches 132/12 11 0,917 12 дюймов 144/12 12 1
Разделите количество дюймов на 12
Пример:
2 дюйма ÷ 12 = 0,16667
5 дюймов ÷ 12 = 0,41667
Преобразование дюймов плюс дробь в десятичную дробь
Преобразуйте дюйм в дробь, используя тот же знаменатель, что и дробь, прибавьте дробь к этой сумме и разделите числитель на знаменатель.
2 1/4″
8/4 + 1/4= 9/4″
9/4 = 2,25″
3 11/16″
48/16 + 11/16= 59/16″
59/16 = 3,6875″
Воспользуйтесь нашим калькулятором для преобразования футов/дюймов/дробей в десятичный формат
Если у вас есть какие-либо вопросы или комментарии, пожалуйста
Связаться с нами
Политика конфиденциальности
© 1998, VmNet.
Преобразование процентов, десятичных знаков и дробей
Урок 4. Преобразование процентов, десятичных знаков и дробей
/en/percents/percentages-in-real-life/content/
Преобразование дробей, десятичных знаков и процентов мы говорим, мы часто используем разные слова, чтобы выразить одно и то же. Например, мы могли бы описать тот же автомобиль как
крошечный или маленький или маленький . Все эти слова означают, что машина не большая. Дроби, десятичные числа и проценты похожи на слова крошечный , маленький и маленький . Все они просто разные способы выражения частей целого .
Дроби, десятичные числа и проценты похожи на слова крошечный , маленький и маленький . Все они просто разные способы выражения частей целого . На этом изображении в каждой мерной чашке одинаковое количество сока. Но мы выразили эту сумму тремя способами: в виде дроби, в процентах и в виде десятичной дроби. Поскольку они выражают одно и то же количество, мы знаем, что 1/2, 50% и 0,5 равны друг другу. Каждый раз, когда мы видим 1/2, мы знаем, что это также может означать 50% или 0,5.
Иногда полезно преобразовать один вид числа в другой. Например, гораздо проще сложить 1/4 и 0,5, если превратить 0,5 в дробь. Изучение того, как преобразовывать дроби, десятичные числа и проценты, также поможет вам в изучении более сложной математики.
Дроби и десятичные числа
Каждая дробь может быть записана как десятичная и наоборот. Возможно, вы не будете делать это очень часто, но преобразование десятичных и дробных чисел может помочь вам в математике. Например, проще вычесть 1/6 из 0,52, если сначала превратить 1/6 в десятичную дробь.
Например, проще вычесть 1/6 из 0,52, если сначала превратить 1/6 в десятичную дробь.
Преобразование дроби в десятичную
Преобразование дроби в десятичную. Мы будем использовать математический навык, который вы уже изучили: длинное деление. Чтобы освежить в памяти этот навык, вы можете просмотреть наш урок «Длинная дивизия».
Щелкните слайд-шоу, чтобы узнать, как преобразовать дробь в десятичную.
Давайте посмотрим, как мы можем преобразовать 1/4 в десятичную дробь.
Чтобы преобразовать дробь в десятичную, мы просто разделим числитель…
Чтобы преобразовать дробь в десятичную, мы просто разделим числитель… на знаменатель.
В нашем примере мы разделим 1 на 4.
1 разделить на 4 будет 0. 1.
Мы также добавим десятичную точку после 0 сверху.
Теперь мы можем разделить 10 на 4.
10 разделить на 4 равно 2.
Теперь умножим 4 на 2.
4 умножить на 2 равно 8. Итак, мы вычтем 8 из 10.
Поскольку 2 больше 0, мы еще не закончили деление. Мы добавим еще один 0 после запятой и уменьшим его.
Теперь поделим 20 на 4.
20 разделить на 4 равно 5.
Теперь умножим. 4 умножить на 5 равно 20.
Когда мы вычитаем 20 из 20, мы получаем 0. 0 означает, что мы закончили деление.
1 разделить на 4 равно 0,25.
Итак, 1/4 равно 0,25.
Попробуйте!
Преобразуйте каждую из этих дробей в десятичное число .
Преобразование десятичного числа в дробь
Теперь сделаем это в обратном порядке. Преобразуем десятичную дробь в дробь.
Щелкните слайд-шоу, чтобы узнать, как преобразовать десятичную дробь в дробь.
Мы перепишем 0,85 в виде дроби. Чтобы преобразовать десятичную дробь в дробь, мы будем использовать разрядных значений .
В десятичных дробях число сразу справа от запятой находится в десятых разрядах.
Место справа от десятого разряда — это сотый разряд .
Чтобы преобразовать десятичное число, сначала мы проверим разрядное значение последнего числа справа.
В 0,85 5 стоит на сотых.
Это означает, что наша десятичная дробь равна 85 сотым. 85 сотых также можно записать как 85/100.
Теперь у нас есть дробь. Но всегда полезно сокращать дроби, когда это возможно, — это облегчает их чтение.
Чтобы уменьшить, нам нужно найти наибольшее число, которое будет равномерно входить как в 85, так и в 100. дробь на 5,
Сначала разделим числитель. 85 разделить на 5 равно 17.
Теперь разделим знаменатель. 100 разделить на 5 равно 20. Это означает, что 85/100 можно уменьшить до 17/20.
Итак, 0,85 равно 17/20.
Уменьшение дроби может показаться ненужным при преобразовании десятичной дроби. Но это важно, если вы собираетесь использовать дробь в математической задаче. Если вы добавляете две дроби, вам может даже понадобиться уменьшить или изменить обе дроби так, чтобы у них был общий знаменатель .
Попробуй!
Преобразуйте эти десятичные дроби в дроби. Обязательно уменьшите каждую дробь до простейшей формы!
Проценты и десятичные дроби
Знание того, как преобразовывать проценты и десятичные дроби, поможет вам рассчитать такие вещи, как налог с продаж и скидки. Чтобы узнать, как это сделать, ознакомьтесь с нашим уроком «Проценты в реальной жизни».
Преобразование процентов в десятичные
Преобразование процентов в десятичные числа на удивление просто. Это займет всего несколько простых шагов.
Щелкните слайд-шоу, чтобы узнать, как преобразовать проценты в десятичные дроби.
Мы собираемся преобразовать 17% в десятичную дробь.
Сначала возьмем знак процента…
Сначала возьмем знак процента… и превратим его в десятичную точку.
Далее мы переместим десятичную точку два пробелов до осталось .
Теперь мы переместим десятичную точку на два пробела до слева .
Мы преобразовали наши проценты в десятичную дробь. 17% равно 0,17.
Давайте рассмотрим другой пример. На этот раз мы превратим 78% в десятичную дробь.
Во-первых, мы заменим знак процента на десятичную точку .
Затем мы переместим десятичную точку два пробела до слева .
Затем мы переместим десятичную точку на два пробела до слева .
78% равно 0,78.
Давайте рассмотрим другой пример. На этот раз мы превратим 8% в десятичную.
Во-первых, мы заменим знак процента на десятичную точку .
Затем мы переместим десятичную точку на два пробела в осталось .
Затем мы переместим десятичную точку на два пробела до слева .
Обратите внимание, что рядом с цифрой 8 есть дополнительный пробел. Мы не можем просто оставить пустое место, в котором ничего нет. Поскольку ноль ничему не равен, мы заменим пробел на ноль .
Обратите внимание, что рядом с цифрой 8 есть дополнительный пробел. Мы не можем просто оставить пустое место, в котором ничего нет. Так как ноль ничему не равен, мы заменим пробел на ноль .
8% равно 0,08
Почему это работает?
Преобразование процентов в десятичные дроби настолько просто, что вам может показаться, что вы что-то упустили. Но не волнуйтесь — это действительно так просто! Вот почему метод, который мы вам показали, работает.
Но не волнуйтесь — это действительно так просто! Вот почему метод, который мы вам показали, работает.
Когда мы превращаем процент в десятичную дробь, мы фактически делаем два шага. Сначала мы конвертируем наш процент в дробь. Поскольку все проценты выходят за пределы 100, мы просто помещаем проценты больше 100, например:
78% = 78/100
На втором этапе мы преобразуем 78/100 в десятичное число. Вы уже знаете, что это означает, что мы разделим числитель на знаменатель , вот так:
78 ÷ 100 = 0,78
Так почему же мы не показали эти шаги в слайд-шоу? Потому что вы можете получить ответ и без них. Вы знаете, что все проценты не равны 100, поэтому можете не превращать проценты в дроби. Вы должны разделить процент на 100, чтобы получить десятичную дробь, но есть быстрый способ сделать это. Просто переместите запятую на две позиции влево! Таким образом, вы можете получить тот же ответ всего за один простой шаг.
Попробуй!
Преобразуйте эти проценты в десятичные дроби.
Преобразование десятичной дроби в проценты
Теперь обратим то, что вы только что узнали. Преобразуем десятичную дробь в проценты.
Щелкните слайд-шоу, чтобы узнать, как преобразовать десятичную дробь в проценты.
Мы собираемся преобразовать 0,45 в проценты.
Повторим то, что мы сделали в предыдущем разделе. На этот раз мы переместим десятичную точку на два разряда в 9.0011 справа .
Повторим то, что мы сделали в предыдущем разделе. На этот раз мы переместим запятую на два знака справа от .
Теперь заменим десятичную точку знаком процента.
Мы закончили преобразование нашей десятичной дроби в проценты. 0,45 равно 45%.
Давайте попробуем другой пример. На этот раз наша десятичная дробь имеет три числа справа от запятой.
Но мы все равно переместим десятичную точку на два деления вправо.
Но мы по-прежнему собираемся переместить десятичную точку на два пробела вправо.
У нас еще есть число справа от запятой. Число не равно 0, поэтому мы не можем его отбросить.
Вместо мы сохраним десятичную точку, а добавим знак процента в конце числа.
Итак, 0,635 равно 63,5%.
Попробуйте!
Вычислите эти десятичные дроби в процентах.
Проценты и дроби
Умение записывать проценты в виде дробей и наоборот может помочь вам в повседневной жизни. Например, предположим, что вы получили оценку 80% на тесте. Вы можете преобразовать 80% в дробь, чтобы узнать, сколько из ваших ответов были правильными. Когда ваш учитель оценивает тест, он может поступить наоборот. Если учащийся правильно ответил на 8 из 10 вопросов, учитель может преобразовать 8/10 в проценты, чтобы поставить учащемуся оценку.
Преобразование процентов в дроби
При преобразовании процентов в дроби полезно помнить, что проценты всегда выходят за пределы 100. Вы можете попрактиковаться с процентами в нашем уроке «Введение в проценты».
Щелкните слайд-шоу, чтобы узнать, как преобразовать проценты в дроби.
Преобразуем 30% в дробь.
В разделе «Введение в проценты» вы узнали, что все проценты выражаются из 100. На самом деле это то, что означает слово 9.0011 процентов означает.
Таким образом, любой процент равен самому себе больше 100. В нашем примере 30% равно 30/100.
Теперь мы преобразовали 30% в дробь, но нам еще нужно ее уменьшить.
10 — наибольшее число, которое равномерно делится на 30 и 100. Значит, мы можем разделить обе части дроби на 10.
Сначала разделим числитель дроби. 30 разделить на 10 равно 3.
Теперь разделим знаменатель. 100 разделить на 10 равно 10.
Итак, 30% равно 3/10.
Попробуйте!
Запишите эти проценты в виде дробей. Убедитесь, что уменьшите каждую дробь до простейшей формы.
Преобразование дроби в проценты
Преобразование дроби требует двух навыков, которые вы только что изучили: записи дроби в виде десятичной дроби и записи десятичной дроби в виде процентов . Давайте посмотрим, как мы можем использовать эти навыки для преобразования дроби в проценты.
Щелкните слайд-шоу, чтобы узнать, как преобразовать дробь в проценты.
Преобразуем 3/6 в проценты.
Точно так же, как при преобразовании дроби в десятичную, мы разделим числитель на знаменатель .
3 разделить на 6 равно 0,5.
Мы превратили нашу дробь в десятичную.
Теперь мы превратим десятичную дробь в проценты, переместив запятую на две позиции вправо.
Теперь мы превратим десятичную дробь в проценты, переместив запятую на две позиции вправо.
Мы также изменим десятичную точку на знак процента. 0,50 равно 50%.
Итак, 3/6 равно 50%.
Попробуйте!
Преобразуйте эти дроби в проценты.
Вернуться к учебнику
Предыдущий: Проценты в реальной жизни
Далее:Вернуться к плейлисту: Проценты
Что такое 2/5 как целое число?
Числительные — это математические числа, используемые в финансовой, профессиональной, а также в социальной сфере в социальном мире. Цифры и разрядное значение в числе и основание системы счисления определяют значение числа. Числа используются в различных математических операциях, таких как суммирование, вычитание, умножение, деление, процент и т. д., которые используются в нашей повседневной деятельности и торговой деятельности.
д., которые используются в нашей повседневной деятельности и торговой деятельности.
Что такое числа?
Числа используются в различных арифметических значениях, применимых для выполнения различных арифметических операций, таких как сложение, вычитание, умножение и т. д., которые применяются в повседневной жизни для целей вычислений. Значение числа определяется цифрой, ее разрядностью в числе и основанием системы счисления.
Числа , также известные как цифры, представляют собой математические значения, используемые для подсчета, измерения, маркировки и измерения основных величин.
Числа — это математические значения или цифры, используемые для измерения или вычисления величин. Он представлен цифрами 2, 4, 7 и т. д. Примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.
Типы чисел
Существуют различные типы чисел, разделенные на наборы по системе счисления. Типы описаны ниже:
Типы описаны ниже:
- Натуральные числа: Натуральные числа — это положительные числа, которые считаются от 1 до бесконечности. Подмножество не включает дробные или десятичные значения. Множество натуральных чисел представлено ‘ Н ’. Это числа, которые мы обычно используем для счета. Набор натуральных чисел может быть представлен как N=1,2,3,4,5,6,7,……………
- Целые числа: Целые числа — это положительные натуральные числа, включая ноль, который отсчитывается от 0 до бесконечности. Целые числа не включают дроби или десятичные дроби. Набор целых чисел представлен как « W ». Набор может быть представлен как W=0,1,2,3,4,5,………………
- Целые числа: Целые числа представляют собой набор чисел, включающий все положительные счетные числа, ноль, а также все отрицательные числа, которые считают от отрицательной бесконечности до положительной бесконечности. В наборе нет дробей и десятичных знаков.
 Набор целых чисел обозначается ‘ З ’. Набор целых чисел можно представить в виде Z=………..,-5.-4,-3,-2,-1,0,1,2,3,4,5,………….
Набор целых чисел обозначается ‘ З ’. Набор целых чисел можно представить в виде Z=………..,-5.-4,-3,-2,-1,0,1,2,3,4,5,…………. - Десятичные числа: Любое числовое значение, состоящее из десятичной точки, является десятичным числом. В некоторых случаях он также может быть выражен в дробной форме. Его можно выразить как 2,5, 0,567 и т. д.
- Действительное число: Действительные числа — это заданные числа, не содержащие мнимых значений. Он включает в себя все положительные целые числа, отрицательные целые числа, дроби и десятичные значения. Обычно обозначается ‘ Р ».
- Комплексное число: Комплексные числа — это набор чисел, включающий мнимые числа. Его можно выразить как a+bi, где «a» и «b» — действительные числа. Обозначается « C ».
- Рациональные числа: Рациональные числа — это числа, которые можно выразить как отношение двух целых чисел.
 Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается ‘ Q ’.
Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается ‘ Q ’. - Иррациональные числа: Иррациональные числа — это числа, которые не могут быть выражены в дробях или отношениях целых чисел. Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Обозначается ‘ P ’.
Что такое целые числа?
Целые числа — это числа без дробей, представляющие собой набор положительных целых чисел от 0 до бесконечности. Все целые числа существуют в числовых рядах. Все целые числа являются действительными числами, но мы не можем сказать, что все действительные числа являются целыми числами. Целые числа не могут быть отрицательными. Целые числа представлены символом «W».
Примеры целых чисел
Натуральные числа также известны как счетные числа, в том числе ноль является частью целых чисел, таких как 0,1,2,3,4,5 и т. д., за исключением целых отрицательных чисел, дробей и десятичных дробей. .
д., за исключением целых отрицательных чисел, дробей и десятичных дробей. .
0, 15, 16, 76, 110 и т. д. — все это примеры целых чисел.
Что такое 2/5 целого числа?
Ответ:
Число 2/5, которое также можно записать как 0,4. Следовательно, число 2/5 не является целым числом, так как оно имеет дробную форму, а целые числа не включают в себя дроби или десятичные дроби.
Однако, если необходимо преобразовать 2/5 в целое число, 0,4 можно либо округлить до 1 как целое число, либо округлить до 0 как целое число.
Объяснение:
Целые числа — это числа, начинающиеся с нуля.
Рассмотрим число 2/5 как Y.
Y = 2/5
Разделив 2/5, мы получим целое число,
, так что получим
Y = 2/5
Y = 0,4
3 Теперь, округлив до ближайшего целого числа, мы получим 0 при округлении в меньшую сторону.
Также при округлении до ближайшего целого числа получается 1.
Следовательно, 2/5 как целое число будет 0 или 1.
Аналогичные вопросы
Вопрос 1. Что такое 44/10 как целое число?
Ответ:
Дано: Число равно 44/10
Объяснение:
Целые числа — это числа, начинающиеся с нуля.
Рассмотрим число 44/10 как Y.
Y = 44/10
Разделив 44/10, мы получим целое число,
получаем,
Y = 44/10
Y = 4,4
Округляя до ближайшего целого числа, получаем 4.
Следовательно, целое число 44/10 равно 4
Вопрос 2. Что такое 146/4 как целое число?
Ответ:
Дано: Число равно 146/4
Объяснение:
Целые числа — это числа, начинающиеся с нуля.
Рассмотрим число 146/4 как Y.
Y = 146/4
Разделим 146/4, чтобы получить целое число,
, получим
Y = 146/4
Y = 36,5
Округлим до ближайшего целого числа, получим 37, потому что значение после запятой равно 5, поэтому оно будет округлено до 37.
Следовательно, целое число 146/4 равно 37.
Вопрос 3. Что такое 40/5 как целое число?
Ответ:
Дано: Число 40/5
Объяснение:
Целые числа — это числа, начинающиеся с нуля.
Рассмотрим число 40/5 как Y.
Y = 40/5
Разделив 40/5, мы получим целое число,
, так что получим
Y = 40/5
Y = 8
3
3 Следовательно, целое число 40/5 равно 8.
Что такое десятичная дробь? [Определение, факты и примеры]
Определение десятичных дробей
Необходимым условием для понимания десятичных дробей является понимание нормальных дробей. Вы должны знать, что дробь состоит из числителя (верхняя часть) и знаменателя (нижняя часть). Правильный способ записи дроби —
X — числитель в этом примере, а y — знаменатель.
Десятичные дроби — это дроби, в которых знаменатель (y на изображении) должен быть равен 10 или кратен 10, например 100, 1000, 10000 и т. д. Числитель может быть любым целым числом (от -бесконечности до +бесконечности). Эти десятичные дроби обычно выражаются десятичными числами (числа с десятичной точкой).
д. Числитель может быть любым целым числом (от -бесконечности до +бесконечности). Эти десятичные дроби обычно выражаются десятичными числами (числа с десятичной точкой).
В алгебре десятичная дробь — это число, имеющее 10 или степени 10, такие как 10¹, 10², 10³ и т. д. в знаменателе.
Примеры десятичных дробей
- 7/10000 — десятичная дробь, записанная в десятичной форме как 0,0007.
- 19/10 — десятичная дробь, записанная в десятичной форме как 1,9.
- 39/1000 — десятичная дробь, записанная как 0,039.
Примеры десятичных дробей
Другие дроби, в знаменателе которых не десять чисел, не являются десятичными дробями. Это:
- 37/8
- 2/1083
- 83/145
Чтение десятичных дробей
Рассмотрим сценарий, в котором 1 стоит в числителе. Мы будем рассматривать разные знаменатели, чтобы понять, как эти термины читаются с этим числителем.
- 1/10 читается как одна десятая.

- 1/100 читается как одна сотая.
- 1/1000 читается как тысячная.
Когда значение числителя больше единицы, мы добавляем к имени букву «s». Так, например, 3/10 читается как три десятых.
История десятичных дробей
Китайцы впервые разработали и использовали десятичные дроби в конце 4-го века до нашей эры, которые распространились на Ближний Восток, прежде чем достигли Европы.
Преобразование в десятичные дроби
1. Преобразование из дробей в десятичные дроби :
- Рассмотрим пример дроби 3/2.
- Первым шагом будет рассмотрение числа, которое дает 10 или кратно 10 при умножении на знаменатель. В этом случае 5, умноженное на 2, дает 10.
- Теперь умножьте числитель и знаменатель на одно и то же число, чтобы получить десятичную дробь. Здесь 3 x 5/2 x 5 дает 15/10.
- Таким образом, десятичная дробь 3/2 равна 15/10.
2. Преобразование смешанных чисел в десятичные дроби :
Преобразование смешанных чисел в десятичные дроби :
- Преобразование смешанной дроби в нормальную дробь.
- Выполните шаги по преобразованию дробей в десятичные дроби.
3. Преобразование десятичных чисел в десятичные дроби :
- Запишите исходное десятичное число в форме числителя и знаменателя, поставив 1 в знаменателе: 4,3/1.
- Для каждого места, на которое вы перемещаете десятичную точку, добавьте ноль рядом с 1 в знаменателе: 43/10 (Как мы видим, на один сдвиг десятичного знака нужно добавить один 0 к знаменателю).
4,3/1
43,0/10
- Поскольку число в числителе не является десятичным, вы получили десятичную дробь: 4,3 = 43/10.
Применение десятичных дробей в реальной жизни
Десятичные дроби используются для понимания точных величин вместо целых чисел. Вы также будете использовать их для выражения процентов. Например, 97% можно записать как 97/100 для простоты вычисления.
Например, 97% можно записать как 97/100 для простоты вычисления.
Вот несколько ситуаций, в которых вы можете столкнуться с десятичными дробями:
- Монеты (доли рупий)
- Взвешивание продуктов
- Измерение ингредиентов во время приготовления
Решаемые примеры
Пример 1
Преобразуйте 2 ½ в десятичную дробь.
= 2 ½
= 5/2
= 5 x 5 / 2 x 5
= 25 / 10
Пример 2
= 5,4/1
= 54/10
Пример 3
Преобразуйте 8 ⅕ в десятичную дробь.
= 8 ⅕
= 41/5
= 41 x 2 / 5 x 2
= 82/10
Заключение
Десятичные дроби побуждают учащихся изучать точные величины. Это поможет им понять вес, например, 3,2 кг, и расстояние, например, 7,85 км. Первым шагом к лучшему пониманию десятичных чисел является ежедневное выполнение задач с десятичными дробями. Идея взять ручку и бумагу для решения задач скучна и неинтересна для учащихся. Им нужны развлекательные способы, чтобы побудить их к практике сумм.
Им нужны развлекательные способы, чтобы побудить их к практике сумм.
SplashLearn делает процесс изучения десятичных чисел увлекательным и интерактивным для детей. С десятками игр с десятичными дробями у вашего ребенка никогда не будет недостатка в вариантах для занятий математикой. Вместо этого обучение становится увлекательным благодаря интересным играм, которые привлекают ваших детей к решению задач.
Давайте сделаем это!
Вместо того, чтобы учить детей десятичным дробям и раздавать практические задания, попросите их найти и составить десятичные дроби из десятичных дробей, которые вы называете.
Практические задачи
634/100
634/10
6.34/100
6.34/10
Правильный ответ: 634/100
, так как есть два места после десятичной точки, десятичная фракция 6.34 будет будет быть 634/100.
4/2
4/10
45/100
45/10
Правильный ответ: 45/10
4 ½ можно записать как 4,5, а так как после запятой только один знак, то десятичная дробь будет 45/10. 16/10 125/10
16/10 125/10
125/100
25/20
5/4
Правильный ответ: 125/100 92 и др.) в знаменателе. Эти числа записываются в десятичной форме для удобства решения математических сумм. Например, 4/1000 — это десятичная дробь, записываемая десятичными знаками как 0,004.
Как записать десятичную дробь?
Десятичная дробь записывается как любое число в числителе с 10 и кратным 10 в знаменателе.
Что такое десятичная дробь в простейшем виде?
Простейшей формой десятичной дроби является основная неделимая дробь, полученная делением числителя на знаменатель. Например, простейшая форма десятичной дроби 4/10 — это 2/5.
Все ли проценты могут быть выражены десятичными дробями? Приведите пример.
Да. Все проценты могут быть выражены в виде десятичных дробей. Например, 80% записывается как 80/100 в форме десятичной дроби. Это можно разделить, чтобы получить простейшую форму 4/5 десятичной формы.
 Используйте наш калькулятор преобразования дроби в десятичную, чтобы преобразовать любую дробь в десятичную и узнать, является ли она завершающей или повторяющейся (повторяющейся) десятичной дробью.
Используйте наш калькулятор преобразования дроби в десятичную, чтобы преобразовать любую дробь в десятичную и узнать, является ли она завершающей или повторяющейся (повторяющейся) десятичной дробью.Пример: 1/2, 2 1/2, 5/3 и т. д. Обратите внимание, что 2 1/2 означает два с половиной = 2 + 1/2 = 2,5
Ответ:
Пошаговое решение:
 ..
.. 1750
1750 3594
3594 5938
5938 8281
8281 0313
0313 7500
7500 3063
3063 8625
8625 4188
4188 1094
1094 1344
1344 6906
6906 2469
2469 8031
8031Как преобразовать футы/дюймы/дроби в десятичный формат
Калькуляторы Спайка
Множество чисел, с которыми нужно иметь дело, и нет, не очень полезные для выбора лотерейных номеров. Но если вы понимаете основные понятия, это избавляет вас от необходимости конвертировать эти числа, и вы обязательно станете победителем.
Но если вы понимаете основные понятия, это избавляет вас от необходимости конвертировать эти числа, и вы обязательно станете победителем.
| Дюйм | Десятичный фут |
| 1 дюйм | 0,0833 |
| 2 дюйма0299 | 0.167 |
| 3 inches | 0.25 |
| 4 inches | 0.333 |
| 5 inches | 0.417 |
| 6 inches | 0.5 |
| 7 inches | 0.583 |
| 8 дюймов | 0,667 |
| 9 дюймов | 0,75 |
| 10 дюймов | 0,939 9032 |
| 11 inches | 0.917 |
| 12 inches | 1 |
| Fraction | Decimal Value of an Inch |
| 1/16 | 0.0625 |
| 1/8 | 0.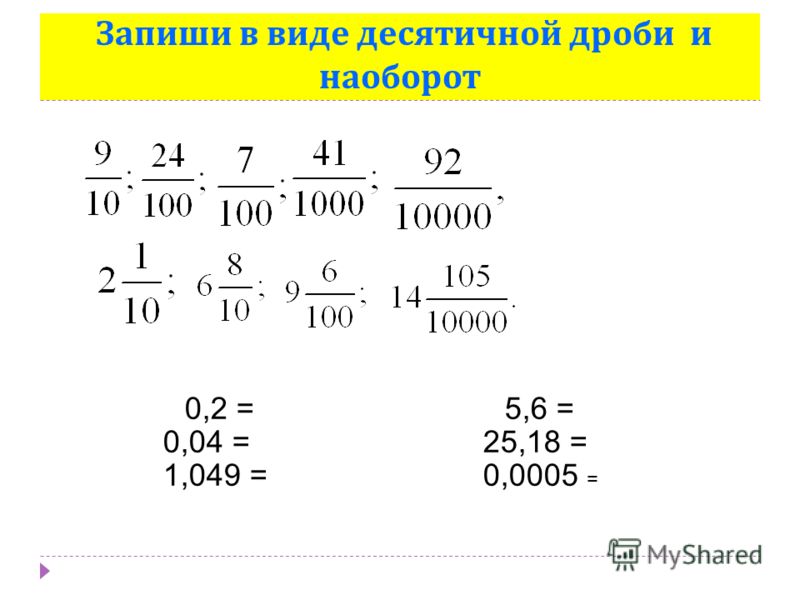 125 125 |
| 3/16 | 0.1875 |
| 1/4 | 0.25 |
| 5/16 | 0.3125 |
| 3/8 | 0.375 |
| 7/16 | 0.4375 |
| 1/2 | 0.5 |
| 9.16 | 0.5625 |
| 5/8 | 0.625 |
| 11 /16 | 0.6875 |
| 3/4 | 0.75 |
| 13/16 | 0.8125 |
| 7/8 | 0.875 |
| 15/16 | 0,9375 |
Пример
Преобразование 7′-4 3/4″ в десятичное число.
- Если вы похожи на меня, я бы сказал, что 7′ пока остается 7′.
- Смотрю на диаграммы 4″ = 0,333 3/4″ = 0,75
- 0,333 + 0,75 = 1,083 дюйма + 7 дюймов = 8,083
- , и я бы написал все это как 8,083 в десятичном формате.

Конечно, вы не можете добавить десятичное значение фута к десятичному значению дюйма без преобразования десятичного значения дроби в дюймах в десятичное значение фута.
Попробуем еще раз:
Преобразование 7′- 4 3/4″ в десятичное число.
- 7′ пока остается 7′.
- 4″ = 0,333 (преобразовать в десятичное значение в футах: 4 ÷ 12)
- 3/4″ = 0,75 (перевести дробь в десятичную, разделив числитель на знаменатель 3 ÷ 4)
- 0,75 = 0,0625 (преобразование в десятичное число футов путем деления 0,75 на 12)
- 0,333 + 0,0625 = 0,3955 + 7′ = 7,3955
Запишите 7′- 4 3/4″ в десятичной форме = 7,3955
| 1/16 | 0.0625 | 0.005208 | |
| 1/8 | 0.125 | 0.01042 | |
| 3/16 | 0.1875 | 0.015625 | |
| 1/4 | 0. 25 25 | 0.020883 | |
| 5/16 | 0.3125 | 0.026004 | |
| 3/8 | 0.375 | 0.03125 | |
| 7/16 | 0.4375 | 0.036458 | |
| 1/2 | 0.5 | 0.041666 | |
| 9.16 | 0.5625 | 0.046875 | |
| 5/8 | 0.625 | 0.05208 | |
| 11/16 | 0.6875 | 0.057291 | |
| 3/4 | 0.75 | 0.0625 | |
| 13/16 | 0.8125 | 0.0677 | |
| 7/8 | 0.875 | 0.072916 | |
| 15/16 | 0.9375 | 0.078125 | |
| 1 inch | 12/12 | 1 | 0. 0833 0833 |
| 2 inches | 24/12 | 2 | 0.167 |
| 3 inches | 36/12 | 3 | 0.25 |
| 4 inches | 48/12 | 4 | 0.333 |
| 5 inches | 60/12 | 5 | 0.417 |
| 6 inches | 72/ 12 | 6 | 0.5 |
| 7 inches | 84/12 | 7 | 0.583 |
| 8 inches | 96/12 | 8 | 0.667 |
| 9 inches | 108/12 | 9 | 0.75 |
| 10 inches | 120/12 | 10 | 0.833 |
| 11 inches | 132/12 | 11 | 0,917 |
| 12 дюймов | 144/12 | 12 | 1 |
Разделите количество дюймов на 12
Пример:
2 дюйма ÷ 12 = 0,16667 5 дюймов ÷ 12 = 0,41667
Преобразование дюймов плюс дробь в десятичную дробь
Преобразуйте дюйм в дробь, используя тот же знаменатель, что и дробь, прибавьте дробь к этой сумме и разделите числитель на знаменатель.
2 1/4″
8/4 + 1/4= 9/4″
9/4 = 2,25″
3 11/16″
48/16 + 11/16= 59/16″
59/16 = 3,6875″
Воспользуйтесь нашим калькулятором для преобразования футов/дюймов/дробей в десятичный формат
Если у вас есть какие-либо вопросы или комментарии, пожалуйста
Связаться с нами
Политика конфиденциальности
© 1998, VmNet.
Преобразование процентов, десятичных знаков и дробей
Урок 4. Преобразование процентов, десятичных знаков и дробей
/en/percents/percentages-in-real-life/content/
Преобразование дробей, десятичных знаков и процентов мы говорим, мы часто используем разные слова, чтобы выразить одно и то же. Например, мы могли бы описать тот же автомобиль как
крошечный или маленький или маленький . Все эти слова означают, что машина не большая.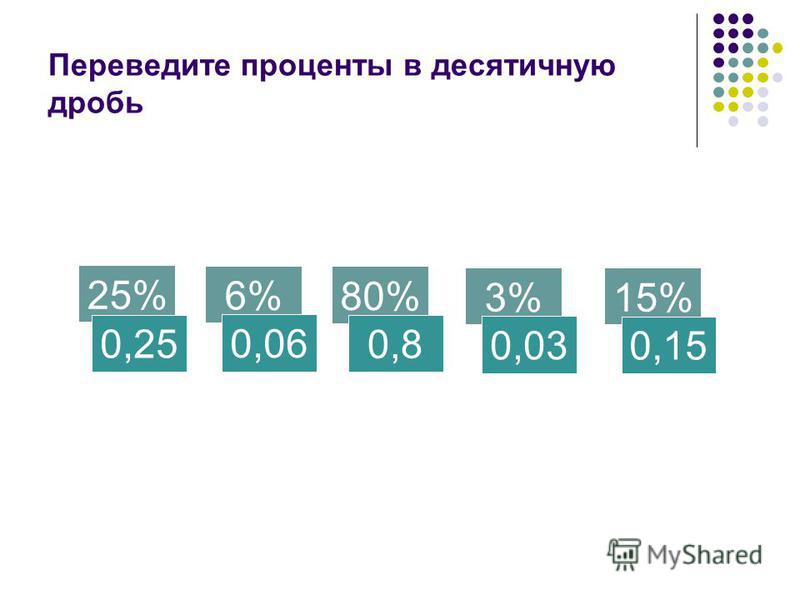 Дроби, десятичные числа и проценты похожи на слова крошечный , маленький и маленький . Все они просто разные способы выражения частей целого .
Дроби, десятичные числа и проценты похожи на слова крошечный , маленький и маленький . Все они просто разные способы выражения частей целого .На этом изображении в каждой мерной чашке одинаковое количество сока. Но мы выразили эту сумму тремя способами: в виде дроби, в процентах и в виде десятичной дроби. Поскольку они выражают одно и то же количество, мы знаем, что 1/2, 50% и 0,5 равны друг другу. Каждый раз, когда мы видим 1/2, мы знаем, что это также может означать 50% или 0,5.
Иногда полезно преобразовать один вид числа в другой. Например, гораздо проще сложить 1/4 и 0,5, если превратить 0,5 в дробь. Изучение того, как преобразовывать дроби, десятичные числа и проценты, также поможет вам в изучении более сложной математики.
Дроби и десятичные числа
Каждая дробь может быть записана как десятичная и наоборот. Возможно, вы не будете делать это очень часто, но преобразование десятичных и дробных чисел может помочь вам в математике. Например, проще вычесть 1/6 из 0,52, если сначала превратить 1/6 в десятичную дробь.
Например, проще вычесть 1/6 из 0,52, если сначала превратить 1/6 в десятичную дробь.
Преобразование дроби в десятичную
Преобразование дроби в десятичную. Мы будем использовать математический навык, который вы уже изучили: длинное деление. Чтобы освежить в памяти этот навык, вы можете просмотреть наш урок «Длинная дивизия».
Щелкните слайд-шоу, чтобы узнать, как преобразовать дробь в десятичную.
Давайте посмотрим, как мы можем преобразовать 1/4 в десятичную дробь.
Чтобы преобразовать дробь в десятичную, мы просто разделим числитель…
Чтобы преобразовать дробь в десятичную, мы просто разделим числитель… на знаменатель.
В нашем примере мы разделим 1 на 4.
1 разделить на 4 будет 0. 1.
Мы также добавим десятичную точку после 0 сверху.
Теперь мы можем разделить 10 на 4.
10 разделить на 4 равно 2.
Теперь умножим 4 на 2.

4 умножить на 2 равно 8. Итак, мы вычтем 8 из 10.
Поскольку 2 больше 0, мы еще не закончили деление. Мы добавим еще один 0 после запятой и уменьшим его.
Теперь поделим 20 на 4.
20 разделить на 4 равно 5.
Теперь умножим. 4 умножить на 5 равно 20.
Когда мы вычитаем 20 из 20, мы получаем 0. 0 означает, что мы закончили деление.
1 разделить на 4 равно 0,25.
Итак, 1/4 равно 0,25.
Попробуйте!
Преобразуйте каждую из этих дробей в десятичное число .
Преобразование десятичного числа в дробь
Теперь сделаем это в обратном порядке. Преобразуем десятичную дробь в дробь.
Щелкните слайд-шоу, чтобы узнать, как преобразовать десятичную дробь в дробь.
Мы перепишем 0,85 в виде дроби. Чтобы преобразовать десятичную дробь в дробь, мы будем использовать разрядных значений .

В десятичных дробях число сразу справа от запятой находится в десятых разрядах.
Место справа от десятого разряда — это сотый разряд .
Чтобы преобразовать десятичное число, сначала мы проверим разрядное значение последнего числа справа.
В 0,85 5 стоит на сотых.
Это означает, что наша десятичная дробь равна 85 сотым. 85 сотых также можно записать как 85/100.
Теперь у нас есть дробь. Но всегда полезно сокращать дроби, когда это возможно, — это облегчает их чтение.
Чтобы уменьшить, нам нужно найти наибольшее число, которое будет равномерно входить как в 85, так и в 100. дробь на 5,
Сначала разделим числитель. 85 разделить на 5 равно 17.
Теперь разделим знаменатель. 100 разделить на 5 равно 20. Это означает, что 85/100 можно уменьшить до 17/20.
Итак, 0,85 равно 17/20.

Уменьшение дроби может показаться ненужным при преобразовании десятичной дроби. Но это важно, если вы собираетесь использовать дробь в математической задаче. Если вы добавляете две дроби, вам может даже понадобиться уменьшить или изменить обе дроби так, чтобы у них был общий знаменатель .
Попробуй!
Преобразуйте эти десятичные дроби в дроби. Обязательно уменьшите каждую дробь до простейшей формы!
Проценты и десятичные дроби
Знание того, как преобразовывать проценты и десятичные дроби, поможет вам рассчитать такие вещи, как налог с продаж и скидки. Чтобы узнать, как это сделать, ознакомьтесь с нашим уроком «Проценты в реальной жизни».
Преобразование процентов в десятичные
Преобразование процентов в десятичные числа на удивление просто. Это займет всего несколько простых шагов.
Щелкните слайд-шоу, чтобы узнать, как преобразовать проценты в десятичные дроби.
Мы собираемся преобразовать 17% в десятичную дробь.
Сначала возьмем знак процента…
Сначала возьмем знак процента… и превратим его в десятичную точку.
Далее мы переместим десятичную точку два пробелов до осталось .
Теперь мы переместим десятичную точку на два пробела до слева .
Мы преобразовали наши проценты в десятичную дробь. 17% равно 0,17.
Давайте рассмотрим другой пример. На этот раз мы превратим 78% в десятичную дробь.
Во-первых, мы заменим знак процента на десятичную точку .
Затем мы переместим десятичную точку два пробела до слева .
Затем мы переместим десятичную точку на два пробела до слева .

78% равно 0,78.
Давайте рассмотрим другой пример. На этот раз мы превратим 8% в десятичную.
Во-первых, мы заменим знак процента на десятичную точку .
Затем мы переместим десятичную точку на два пробела в осталось .
Затем мы переместим десятичную точку на два пробела до слева .
Обратите внимание, что рядом с цифрой 8 есть дополнительный пробел. Мы не можем просто оставить пустое место, в котором ничего нет. Поскольку ноль ничему не равен, мы заменим пробел на ноль .
Обратите внимание, что рядом с цифрой 8 есть дополнительный пробел. Мы не можем просто оставить пустое место, в котором ничего нет. Так как ноль ничему не равен, мы заменим пробел на ноль .
8% равно 0,08
Почему это работает?
Преобразование процентов в десятичные дроби настолько просто, что вам может показаться, что вы что-то упустили. Но не волнуйтесь — это действительно так просто! Вот почему метод, который мы вам показали, работает.
Но не волнуйтесь — это действительно так просто! Вот почему метод, который мы вам показали, работает.
Когда мы превращаем процент в десятичную дробь, мы фактически делаем два шага. Сначала мы конвертируем наш процент в дробь. Поскольку все проценты выходят за пределы 100, мы просто помещаем проценты больше 100, например:
78% = 78/100
На втором этапе мы преобразуем 78/100 в десятичное число. Вы уже знаете, что это означает, что мы разделим числитель на знаменатель , вот так:
78 ÷ 100 = 0,78
Так почему же мы не показали эти шаги в слайд-шоу? Потому что вы можете получить ответ и без них. Вы знаете, что все проценты не равны 100, поэтому можете не превращать проценты в дроби. Вы должны разделить процент на 100, чтобы получить десятичную дробь, но есть быстрый способ сделать это. Просто переместите запятую на две позиции влево! Таким образом, вы можете получить тот же ответ всего за один простой шаг.
Попробуй!
Преобразуйте эти проценты в десятичные дроби.
Преобразование десятичной дроби в проценты
Теперь обратим то, что вы только что узнали. Преобразуем десятичную дробь в проценты.
Щелкните слайд-шоу, чтобы узнать, как преобразовать десятичную дробь в проценты.
Мы собираемся преобразовать 0,45 в проценты.
Повторим то, что мы сделали в предыдущем разделе. На этот раз мы переместим десятичную точку на два разряда в 9.0011 справа .
Повторим то, что мы сделали в предыдущем разделе. На этот раз мы переместим запятую на два знака справа от .
Теперь заменим десятичную точку знаком процента.
Мы закончили преобразование нашей десятичной дроби в проценты. 0,45 равно 45%.
Давайте попробуем другой пример. На этот раз наша десятичная дробь имеет три числа справа от запятой.
Но мы все равно переместим десятичную точку на два деления вправо.

Но мы по-прежнему собираемся переместить десятичную точку на два пробела вправо.
У нас еще есть число справа от запятой. Число не равно 0, поэтому мы не можем его отбросить.
Вместо мы сохраним десятичную точку, а добавим знак процента в конце числа.
Итак, 0,635 равно 63,5%.
Попробуйте!
Вычислите эти десятичные дроби в процентах.
Проценты и дроби
Умение записывать проценты в виде дробей и наоборот может помочь вам в повседневной жизни. Например, предположим, что вы получили оценку 80% на тесте. Вы можете преобразовать 80% в дробь, чтобы узнать, сколько из ваших ответов были правильными. Когда ваш учитель оценивает тест, он может поступить наоборот. Если учащийся правильно ответил на 8 из 10 вопросов, учитель может преобразовать 8/10 в проценты, чтобы поставить учащемуся оценку.
Преобразование процентов в дроби
При преобразовании процентов в дроби полезно помнить, что проценты всегда выходят за пределы 100. Вы можете попрактиковаться с процентами в нашем уроке «Введение в проценты».
Щелкните слайд-шоу, чтобы узнать, как преобразовать проценты в дроби.
Преобразуем 30% в дробь.
В разделе «Введение в проценты» вы узнали, что все проценты выражаются из 100. На самом деле это то, что означает слово 9.0011 процентов означает.
Таким образом, любой процент равен самому себе больше 100. В нашем примере 30% равно 30/100.
Теперь мы преобразовали 30% в дробь, но нам еще нужно ее уменьшить.
10 — наибольшее число, которое равномерно делится на 30 и 100. Значит, мы можем разделить обе части дроби на 10.
Сначала разделим числитель дроби. 30 разделить на 10 равно 3.
Теперь разделим знаменатель. 100 разделить на 10 равно 10.

Итак, 30% равно 3/10.
Попробуйте!
Запишите эти проценты в виде дробей. Убедитесь, что уменьшите каждую дробь до простейшей формы.
Преобразование дроби в проценты
Преобразование дроби требует двух навыков, которые вы только что изучили: записи дроби в виде десятичной дроби и записи десятичной дроби в виде процентов . Давайте посмотрим, как мы можем использовать эти навыки для преобразования дроби в проценты.
Щелкните слайд-шоу, чтобы узнать, как преобразовать дробь в проценты.
Преобразуем 3/6 в проценты.
Точно так же, как при преобразовании дроби в десятичную, мы разделим числитель на знаменатель .
3 разделить на 6 равно 0,5.
Мы превратили нашу дробь в десятичную.
Теперь мы превратим десятичную дробь в проценты, переместив запятую на две позиции вправо.

Теперь мы превратим десятичную дробь в проценты, переместив запятую на две позиции вправо.
Мы также изменим десятичную точку на знак процента. 0,50 равно 50%.
Итак, 3/6 равно 50%.
Попробуйте!
Преобразуйте эти дроби в проценты.
Вернуться к учебнику
Предыдущий: Проценты в реальной жизни
Далее:Вернуться к плейлисту: Проценты
Что такое 2/5 как целое число?
Числительные — это математические числа, используемые в финансовой, профессиональной, а также в социальной сфере в социальном мире. Цифры и разрядное значение в числе и основание системы счисления определяют значение числа. Числа используются в различных математических операциях, таких как суммирование, вычитание, умножение, деление, процент и т. д., которые используются в нашей повседневной деятельности и торговой деятельности.
д., которые используются в нашей повседневной деятельности и торговой деятельности.
Что такое числа?
Числа используются в различных арифметических значениях, применимых для выполнения различных арифметических операций, таких как сложение, вычитание, умножение и т. д., которые применяются в повседневной жизни для целей вычислений. Значение числа определяется цифрой, ее разрядностью в числе и основанием системы счисления.
Числа , также известные как цифры, представляют собой математические значения, используемые для подсчета, измерения, маркировки и измерения основных величин.
Числа — это математические значения или цифры, используемые для измерения или вычисления величин. Он представлен цифрами 2, 4, 7 и т. д. Примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.
Типы чисел
Существуют различные типы чисел, разделенные на наборы по системе счисления. Типы описаны ниже:
Типы описаны ниже:
- Натуральные числа: Натуральные числа — это положительные числа, которые считаются от 1 до бесконечности. Подмножество не включает дробные или десятичные значения. Множество натуральных чисел представлено ‘ Н ’. Это числа, которые мы обычно используем для счета. Набор натуральных чисел может быть представлен как N=1,2,3,4,5,6,7,……………
- Целые числа: Целые числа — это положительные натуральные числа, включая ноль, который отсчитывается от 0 до бесконечности. Целые числа не включают дроби или десятичные дроби. Набор целых чисел представлен как « W ». Набор может быть представлен как W=0,1,2,3,4,5,………………
- Целые числа: Целые числа представляют собой набор чисел, включающий все положительные счетные числа, ноль, а также все отрицательные числа, которые считают от отрицательной бесконечности до положительной бесконечности. В наборе нет дробей и десятичных знаков.
 Набор целых чисел обозначается ‘ З ’. Набор целых чисел можно представить в виде Z=………..,-5.-4,-3,-2,-1,0,1,2,3,4,5,………….
Набор целых чисел обозначается ‘ З ’. Набор целых чисел можно представить в виде Z=………..,-5.-4,-3,-2,-1,0,1,2,3,4,5,…………. - Десятичные числа: Любое числовое значение, состоящее из десятичной точки, является десятичным числом. В некоторых случаях он также может быть выражен в дробной форме. Его можно выразить как 2,5, 0,567 и т. д.
- Действительное число: Действительные числа — это заданные числа, не содержащие мнимых значений. Он включает в себя все положительные целые числа, отрицательные целые числа, дроби и десятичные значения. Обычно обозначается ‘ Р ».
- Комплексное число: Комплексные числа — это набор чисел, включающий мнимые числа. Его можно выразить как a+bi, где «a» и «b» — действительные числа. Обозначается « C ».
- Рациональные числа: Рациональные числа — это числа, которые можно выразить как отношение двух целых чисел.
 Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается ‘ Q ’.
Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается ‘ Q ’. - Иррациональные числа: Иррациональные числа — это числа, которые не могут быть выражены в дробях или отношениях целых чисел. Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Обозначается ‘ P ’.
Что такое целые числа?
Целые числа — это числа без дробей, представляющие собой набор положительных целых чисел от 0 до бесконечности. Все целые числа существуют в числовых рядах. Все целые числа являются действительными числами, но мы не можем сказать, что все действительные числа являются целыми числами. Целые числа не могут быть отрицательными. Целые числа представлены символом «W».
Примеры целых чисел
Натуральные числа также известны как счетные числа, в том числе ноль является частью целых чисел, таких как 0,1,2,3,4,5 и т. д., за исключением целых отрицательных чисел, дробей и десятичных дробей. .
д., за исключением целых отрицательных чисел, дробей и десятичных дробей. .
0, 15, 16, 76, 110 и т. д. — все это примеры целых чисел.
Что такое 2/5 целого числа?
Ответ:
Число 2/5, которое также можно записать как 0,4. Следовательно, число 2/5 не является целым числом, так как оно имеет дробную форму, а целые числа не включают в себя дроби или десятичные дроби.
Однако, если необходимо преобразовать 2/5 в целое число, 0,4 можно либо округлить до 1 как целое число, либо округлить до 0 как целое число.
Объяснение:
Целые числа — это числа, начинающиеся с нуля.
Рассмотрим число 2/5 как Y.
Y = 2/5
Разделив 2/5, мы получим целое число,
, так что получим
Y = 2/5
Y = 0,4
3 Теперь, округлив до ближайшего целого числа, мы получим 0 при округлении в меньшую сторону.
Также при округлении до ближайшего целого числа получается 1.
Следовательно, 2/5 как целое число будет 0 или 1.
Аналогичные вопросы
Вопрос 1. Что такое 44/10 как целое число?
Ответ:
Дано: Число равно 44/10
Объяснение:
Целые числа — это числа, начинающиеся с нуля.
Рассмотрим число 44/10 как Y.
Y = 44/10
Разделив 44/10, мы получим целое число,
получаем,
Y = 44/10
Y = 4,4
Округляя до ближайшего целого числа, получаем 4.
Следовательно, целое число 44/10 равно 4
Вопрос 2. Что такое 146/4 как целое число?
Ответ:
Дано: Число равно 146/4
Объяснение:
Целые числа — это числа, начинающиеся с нуля.
Рассмотрим число 146/4 как Y.
Y = 146/4
Разделим 146/4, чтобы получить целое число,
, получим
Y = 146/4
Y = 36,5
Округлим до ближайшего целого числа, получим 37, потому что значение после запятой равно 5, поэтому оно будет округлено до 37.
Следовательно, целое число 146/4 равно 37.
Вопрос 3. Что такое 40/5 как целое число?
Ответ:
Дано: Число 40/5
Объяснение:
Целые числа — это числа, начинающиеся с нуля.
Рассмотрим число 40/5 как Y.
Y = 40/5
Разделив 40/5, мы получим целое число,
, так что получим
Y = 40/5
Y = 8
3
3 Следовательно, целое число 40/5 равно 8.
Что такое десятичная дробь? [Определение, факты и примеры]
Определение десятичных дробей
Необходимым условием для понимания десятичных дробей является понимание нормальных дробей. Вы должны знать, что дробь состоит из числителя (верхняя часть) и знаменателя (нижняя часть). Правильный способ записи дроби —
X — числитель в этом примере, а y — знаменатель.
Десятичные дроби — это дроби, в которых знаменатель (y на изображении) должен быть равен 10 или кратен 10, например 100, 1000, 10000 и т. д. Числитель может быть любым целым числом (от -бесконечности до +бесконечности). Эти десятичные дроби обычно выражаются десятичными числами (числа с десятичной точкой).
д. Числитель может быть любым целым числом (от -бесконечности до +бесконечности). Эти десятичные дроби обычно выражаются десятичными числами (числа с десятичной точкой).
В алгебре десятичная дробь — это число, имеющее 10 или степени 10, такие как 10¹, 10², 10³ и т. д. в знаменателе.
Примеры десятичных дробей
- 7/10000 — десятичная дробь, записанная в десятичной форме как 0,0007.
- 19/10 — десятичная дробь, записанная в десятичной форме как 1,9.
- 39/1000 — десятичная дробь, записанная как 0,039.
Примеры десятичных дробей
Другие дроби, в знаменателе которых не десять чисел, не являются десятичными дробями. Это:
- 37/8
- 2/1083
- 83/145
Чтение десятичных дробей
Рассмотрим сценарий, в котором 1 стоит в числителе. Мы будем рассматривать разные знаменатели, чтобы понять, как эти термины читаются с этим числителем.
- 1/10 читается как одна десятая.

- 1/100 читается как одна сотая.
- 1/1000 читается как тысячная.
Когда значение числителя больше единицы, мы добавляем к имени букву «s». Так, например, 3/10 читается как три десятых.
История десятичных дробей
Китайцы впервые разработали и использовали десятичные дроби в конце 4-го века до нашей эры, которые распространились на Ближний Восток, прежде чем достигли Европы.
Преобразование в десятичные дроби
1. Преобразование из дробей в десятичные дроби :
- Рассмотрим пример дроби 3/2.
- Первым шагом будет рассмотрение числа, которое дает 10 или кратно 10 при умножении на знаменатель. В этом случае 5, умноженное на 2, дает 10.
- Теперь умножьте числитель и знаменатель на одно и то же число, чтобы получить десятичную дробь. Здесь 3 x 5/2 x 5 дает 15/10.
- Таким образом, десятичная дробь 3/2 равна 15/10.
2. Преобразование смешанных чисел в десятичные дроби :
Преобразование смешанных чисел в десятичные дроби :
- Преобразование смешанной дроби в нормальную дробь.
- Выполните шаги по преобразованию дробей в десятичные дроби.
3. Преобразование десятичных чисел в десятичные дроби :
- Запишите исходное десятичное число в форме числителя и знаменателя, поставив 1 в знаменателе: 4,3/1.
- Для каждого места, на которое вы перемещаете десятичную точку, добавьте ноль рядом с 1 в знаменателе: 43/10 (Как мы видим, на один сдвиг десятичного знака нужно добавить один 0 к знаменателю).
4,3/1
43,0/10
- Поскольку число в числителе не является десятичным, вы получили десятичную дробь: 4,3 = 43/10.
Применение десятичных дробей в реальной жизни
Десятичные дроби используются для понимания точных величин вместо целых чисел. Вы также будете использовать их для выражения процентов. Например, 97% можно записать как 97/100 для простоты вычисления.
Например, 97% можно записать как 97/100 для простоты вычисления.
Вот несколько ситуаций, в которых вы можете столкнуться с десятичными дробями:
- Монеты (доли рупий)
- Взвешивание продуктов
- Измерение ингредиентов во время приготовления
Решаемые примеры
Пример 1
Преобразуйте 2 ½ в десятичную дробь.
= 2 ½
= 5/2
= 5 x 5 / 2 x 5
= 25 / 10
Пример 2
= 5,4/1
= 54/10
Пример 3
Преобразуйте 8 ⅕ в десятичную дробь.
= 8 ⅕
= 41/5
= 41 x 2 / 5 x 2
= 82/10
Заключение
Десятичные дроби побуждают учащихся изучать точные величины. Это поможет им понять вес, например, 3,2 кг, и расстояние, например, 7,85 км. Первым шагом к лучшему пониманию десятичных чисел является ежедневное выполнение задач с десятичными дробями. Идея взять ручку и бумагу для решения задач скучна и неинтересна для учащихся. Им нужны развлекательные способы, чтобы побудить их к практике сумм.
Им нужны развлекательные способы, чтобы побудить их к практике сумм.
SplashLearn делает процесс изучения десятичных чисел увлекательным и интерактивным для детей. С десятками игр с десятичными дробями у вашего ребенка никогда не будет недостатка в вариантах для занятий математикой. Вместо этого обучение становится увлекательным благодаря интересным играм, которые привлекают ваших детей к решению задач.
Давайте сделаем это!
Вместо того, чтобы учить детей десятичным дробям и раздавать практические задания, попросите их найти и составить десятичные дроби из десятичных дробей, которые вы называете.
Практические задачи
634/100
634/10
6.34/100
6.34/10
Правильный ответ: 634/100
, так как есть два места после десятичной точки, десятичная фракция 6.34 будет будет быть 634/100.
4/2
4/10
45/100
45/10
Правильный ответ: 45/10
4 ½ можно записать как 4,5, а так как после запятой только один знак, то десятичная дробь будет 45/10.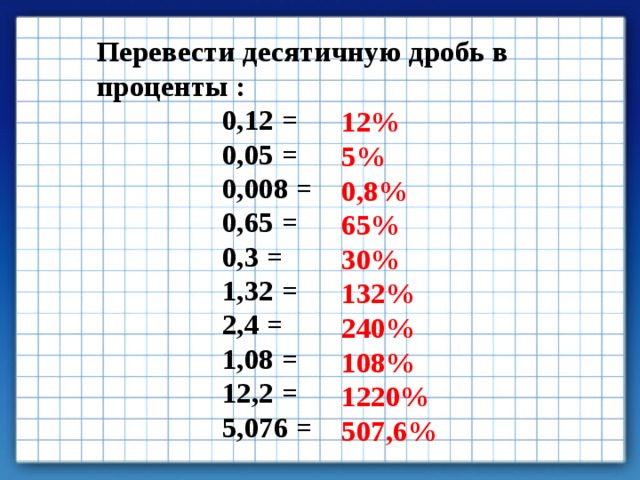 16/10 125/10
16/10 125/10
125/100
25/20
5/4
Правильный ответ: 125/100 92 и др.) в знаменателе. Эти числа записываются в десятичной форме для удобства решения математических сумм. Например, 4/1000 — это десятичная дробь, записываемая десятичными знаками как 0,004.
Как записать десятичную дробь?
Десятичная дробь записывается как любое число в числителе с 10 и кратным 10 в знаменателе.
Что такое десятичная дробь в простейшем виде?
Простейшей формой десятичной дроби является основная неделимая дробь, полученная делением числителя на знаменатель. Например, простейшая форма десятичной дроби 4/10 — это 2/5.
Все ли проценты могут быть выражены десятичными дробями? Приведите пример.
Да. Все проценты могут быть выражены в виде десятичных дробей. Например, 80% записывается как 80/100 в форме десятичной дроби. Это можно разделить, чтобы получить простейшую форму 4/5 десятичной формы.



 Задачи по планиметрии
Задачи по планиметрии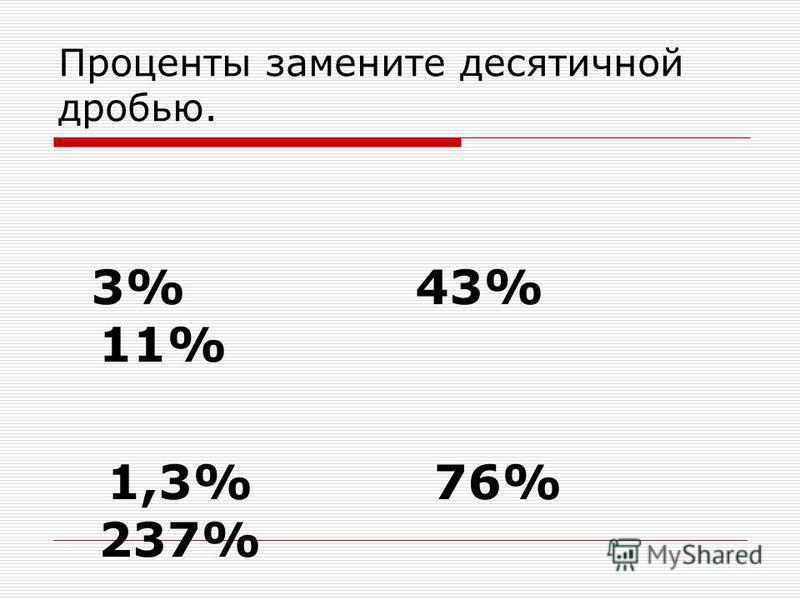









 Набор целых чисел обозначается ‘ З ’. Набор целых чисел можно представить в виде Z=………..,-5.-4,-3,-2,-1,0,1,2,3,4,5,………….
Набор целых чисел обозначается ‘ З ’. Набор целых чисел можно представить в виде Z=………..,-5.-4,-3,-2,-1,0,1,2,3,4,5,…………. Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается ‘ Q ’.
Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается ‘ Q ’.