дробные системы уравнений онлайн
дробные системы уравнений онлайнВы искали дробные системы уравнений онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор для решения систем уравнений, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «дробные системы уравнений онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как дробные системы уравнений онлайн,калькулятор для решения систем уравнений,калькулятор линейных уравнений с двумя переменными,калькулятор онлайн решение линейных уравнений с одной переменной,калькулятор онлайн решение систем уравнений,калькулятор онлайн решение систем уравнений с двумя переменными,калькулятор онлайн систем,калькулятор онлайн система,калькулятор решение систем уравнений,калькулятор решений систем уравнений,калькулятор решения систем,калькулятор решения систем уравнений,калькулятор решения систем уравнений онлайн,калькулятор решите систему уравнений,калькулятор решить однородную систему линейных алгебраических уравнений,калькулятор решить систему уравнений,калькулятор систем уравнений,калькулятор систем уравнений с решением,калькулятор систем уравнения,калькулятор система онлайн,калькулятор системы онлайн,калькулятор уравнений с двумя неизвестными,калькулятор уравнения системы,линейные уравнения онлайн,найти базисные решения системы линейных уравнений онлайн,найти общее решение однородной системы линейных уравнений онлайн,найти общее решение слау онлайн калькулятор,найти фср онлайн,найти фундаментальную систему решений онлайн калькулятор,общее решение системы линейных уравнений онлайн,онлайн как решить систему уравнений,онлайн калькулятор решение системы уравнений,онлайн калькулятор решения систем уравнений,онлайн калькулятор система,онлайн калькулятор системы,онлайн калькулятор уравнение линейное,онлайн калькулятор уравнение с двумя неизвестными,онлайн калькулятор фундаментальная система решений,онлайн найти общее решение системы линейных уравнений,онлайн общее решение системы линейных уравнений,онлайн решение нелинейных систем уравнений,онлайн решение однородной системы линейных уравнений,онлайн решение однородных систем линейных уравнений,онлайн решение систем квадратных уравнений,онлайн решение систем однородных уравнений,онлайн решение систем показательных уравнений,онлайн решение систем с решением,онлайн решение систем уравнений квадратных,онлайн решение систем уравнений методом подстановки,онлайн решение систем уравнений с двумя переменными,онлайн решение системы нелинейных уравнений,онлайн решение уравнений с 3 неизвестными,онлайн решение уравнений с двумя неизвестными,онлайн решение уравнений с двумя переменными,онлайн решение уравнения с двумя неизвестными,онлайн решения линейных уравнений с одной переменной,онлайн решить однородную систему линейных алгебраических уравнений,онлайн решить систему из трех уравнений,онлайн решить систему уравнений методом подстановки,онлайн решить систему уравнений с решением,онлайн систем,онлайн система уравнений с двумя неизвестными,онлайн система уравнений с двумя переменными,онлайн уравнение с 2 неизвестными,решатель систем уравнений,решение квадратных систем уравнений онлайн,решение квадратных систем уравнений онлайн с подробным решением,решение квадратных системы уравнений онлайн,решение линейных уравнений с одной переменной онлайн,решение нелинейных систем уравнений онлайн,решение однородной системы линейных уравнений онлайн,решение однородных систем уравнений онлайн,решение систем калькулятор,решение систем квадратных уравнений онлайн,решение систем квадратных уравнений онлайн с подробным решением,решение систем линейных,решение систем линейных однородных уравнений онлайн,решение систем нелинейных уравнений онлайн,решение систем однородных линейных уравнений онлайн,решение систем однородных уравнений онлайн,решение систем онлайн,решение систем уравнений второй степени онлайн,решение систем уравнений калькулятор,решение систем уравнений квадратных онлайн,решение систем уравнений квадратных онлайн с подробным решением,решение систем уравнений методом подстановки онлайн,решение систем уравнений онлайн квадратных,решение систем уравнений онлайн методом подстановки,решение систем уравнений онлайн с двумя переменными,решение систем уравнений с двумя переменными онлайн,решение систем уравнений с двумя переменными онлайн калькулятор,решение системы двух уравнений онлайн,решение системы квадратных уравнений с двумя неизвестными онлайн,решение системы нелинейных уравнений онлайн,решение системы уравнений калькулятор,решение системы уравнений калькулятор онлайн,решение системы уравнений квадратных онлайн,решение системы уравнений онлайн квадратных,решение системы уравнений онлайн с двумя неизвестными,решение системы уравнений с двумя неизвестными калькулятор онлайн,решение системы уравнений с двумя неизвестными онлайн,решение системы уравнений с двумя неизвестными онлайн калькулятор,решение системы уравнений с решением онлайн,решение уравнений онлайн с 2 неизвестными,решение уравнений онлайн с двумя неизвестными онлайн калькулятор,решение уравнений онлайн с двумя переменными,решение уравнений онлайн с тремя неизвестными,решение уравнений с 2 неизвестными онлайн,решение уравнений с двумя неизвестными онлайн,решение уравнений с двумя переменными онлайн,решение уравнений с тремя неизвестными онлайн,решение уравнения онлайн с двумя неизвестными,решение уравнения с двумя неизвестными онлайн,решение уравнения с двумя неизвестными онлайн калькулятор,решения линейных уравнений с одной переменной онлайн,решения систем линейных уравнений калькулятор,решения систем уравнений калькулятор,решения систем уравнений онлайн,решения систем уравнений онлайн калькулятор,решения системы уравнений онлайн,решите систему уравнений калькулятор,решите систему уравнений онлайн,решить методом подстановки систему уравнений онлайн,решить однородную систему алгебраических линейных уравнений онлайн,решить однородную систему линейных алгебраических уравнений калькулятор,решить однородную систему линейных алгебраических уравнений онлайн,решить однородную систему линейных уравнений онлайн,решить однородную систему уравнений онлайн,решить однородную систему уравнений онлайн с подробным решением,решить онлайн однородную систему уравнений,решить онлайн систему с решением,решить онлайн систему уравнений методом подстановки,решить онлайн систему уравнения,решить онлайн уравнение с 2 неизвестными,решить систему 3 уравнений онлайн,решить систему из 3 уравнений онлайн,решить систему квадратных уравнений онлайн с подробным решением,решить систему нелинейных уравнений онлайн,решить систему онлайн,решить систему онлайн с решением,решить систему уравнение онлайн,решить систему уравнение с решением онлайн,решить систему уравнений калькулятор,решить систему уравнений методом подстановки онлайн,решить систему уравнений онлайн,решить систему уравнений онлайн калькулятор,решить систему уравнений онлайн квадратных,решить систему уравнений онлайн методом подстановки,решить систему уравнений онлайн методом сложения онлайн,решить систему уравнений онлайн с двумя неизвестными,решить систему уравнений онлайн с подробным решением 9 класс,решить систему уравнений онлайн способом сложения онлайн,решить систему уравнений с двумя неизвестными онлайн,решить систему уравнений с решением онлайн,решить системы линейных уравнений,решить уравнение онлайн с 2 неизвестными,решить уравнение онлайн с двумя переменными,решить уравнение онлайн систему,решить уравнение с двумя неизвестными онлайн,решить уравнение с двумя неизвестными онлайн калькулятор с решением,решить уравнение с двумя переменными онлайн,решить уравнение систему онлайн,розв язати систему лінійних рівнянь,система 3 уравнений с 3 неизвестными онлайн,система калькулятор онлайн,система онлайн,система уравнение онлайн,система уравнений онлайн,система уравнений с двумя неизвестными онлайн,система уравнений с двумя переменными онлайн,системы калькулятор онлайн,системы линейных уравнений решить,системы онлайн,системы уравнений онлайн решение методом подстановки,системы уравнений решить онлайн,системы уравнения калькулятор,сколько решений имеет система уравнений онлайн,совместность системы линейных уравнений онлайн,уравнение онлайн система,уравнение с 2 неизвестными онлайн,уравнение с двумя неизвестными онлайн,уравнение с двумя неизвестными онлайн калькулятор,уравнение с тремя неизвестными решить онлайн,уравнение система онлайн,уравнения система онлайн.
Решить задачу дробные системы уравнений онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Системы уравнений с параметром
1. Системы линейных уравнений с параметром
Системы линейных уравнений с параметром решаются теми же основными методами, что и обычные системы уравнений: метод подстановки, метод сложения уравнений и графический метод.
Знание графической интерпретации линейных систем позволяет легко ответить на вопрос о количестве корней и их существовании.
Пример 1.
Найти все значения для параметра а, при которых система уравнений не имеет решений.
{х + (а2 – 3)у = а,
{х + у = 2.
Решение.
Рассмотрим несколько способов решения данного задания.
1 способ. Используем свойство: система не имеет решений, если отношение коэффициентов перед х равно отношению коэффициентов перед у, но не равно отношению свободных членов (а/а
1/1 = (а2 – 3)/1 ≠ а/2 или систему
{а2 – 3 = 1,
{а ≠ 2.
Из первого уравнения а2 = 4, поэтому с учетом условия, что а ≠ 2, получаем ответ.
Ответ: а = -2.
2 способ. Решаем методом подстановки.
{2 – у + (а2 – 3)у = а,
{х = 2 – у,
или
{(а2 – 3)у – у = а – 2,
{х = 2 – у.
После вынесения в первом уравнении общего множителя у за скобки, получим:
{(а2 – 4)у = а – 2,
{х = 2 – у.
Система не имеет решений, если первое уравнение не будет иметь решений, то есть
{а2 – 4 = 0,
{а – 2 ≠ 0.
Очевидно, что а = ±2, но с учетом второго условия в ответ идет только ответ с минусом.
Ответ: а = -2.
Пример 2.
Найти все значения для параметра а, при которых система уравнений имеет бесконечное множество решений.
{8х + ау = 2,
{ах + 2у = 1.
Решение.
По свойству, если отношение коэффициентов при х и у одинаковое, и равно отношению свободных членов системы, то она имеет бесконечное множество решений (т. е. а/а1 = b/b1 = c/c1). Следовательно 8/а = а/2 = 2/1. Решая каждое из полученных уравнений находим, что а = 4 – ответ в данном примере.
Ответ: а = 4.
2. Системы рациональных уравнений с параметром
Пример 3.
Найти все значения параметра а, при которых система уравнений имеет единственное решение.
{3|х| + у = 2,
{|х| + 2у = a.
Решение.
Умножим первое уравнение системы на 2:
{6|х| + 2у = 4,
{|х| + 2у = a.
Вычтем из первого второе уравнение, получим 5|х| = 4 – а. Это уравнение будет иметь единственное решение при а = 4. В других случаях это уравнение будет иметь два решения (при а < 4) или ни одного (при а > 4).
Ответ: а = 4.
Пример 4.
Найти все значения параметра а, при которых система уравнений имеет единственное решение.
{х + у = а,
{у – х2 = 1.
Решение.
Данную систему решим с использованием графического метода. Так, графиком второго уравнения системы является парабола, поднятая по оси Оу вверх на один единичный отрезок.
Первое уравнение задает множество прямых, параллельных прямой y = -x (рисунок 1). Из рисунка хорошо видно, что система имеет решение, если прямая у = -х + а является касательной к параболе в точке с координатами (-0,5; 1,25). Подставив в уравнение прямой вместо х и у эти координаты, находим значение параметра а:
1,25 = 0,5 + а;
а = 0,75.
Ответ: а = 0,75.
Пример 5.
Используя метод подстановки, выясните, при каком значении параметра а, система имеет единственное решение.
{ах – у = а + 1,
{ах + (а + 2)у = 2.
Решение.
Из первого уравнения выразим у и подставим во второе:
{у = ах – а – 1,
{ах + (а + 2)(ах – а – 1) = 2.
Приведем второе уравнение к виду kx = b, которое будет иметь единственное решение при k ≠ 0. Имеем:
ах + а2х – а2 – а + 2ах – 2а – 2 = 2;
а2х + 3ах = 2 + а2 + 3а + 2.
Квадратный трехчлен а2 + 3а + 2 представим в виде произведения скобок
(а + 2)(а + 1), а слева вынесем х за скобки:
(а2 + 3а)х = 2 + (а + 2)(а + 1).
Очевидно, что а2 + 3а не должно быть равным нулю, поэтому,
а2 + 3а ≠ 0, а(а + 3) ≠ 0, а значит а ≠ 0 и ≠ -3.
Ответ: а ≠ 0; ≠ -3.
Пример 6.
Используя графический метод решения, определите, при каком значении параметра а, система имеет единственное решение.
{х2 + у2 = 9,
{у – |х| = а.
Решение.
Исходя из условия, строим окружность с центром в начале координат и радиусом 3 единичных отрезка, именно ее задает первое уравнение системы
х2 + у2 = 9. Второе уравнение системы (у = |х| + а) – ломаная. С помощью рисунка 2 рассматриваем все возможные случаи ее расположения относительно окружности.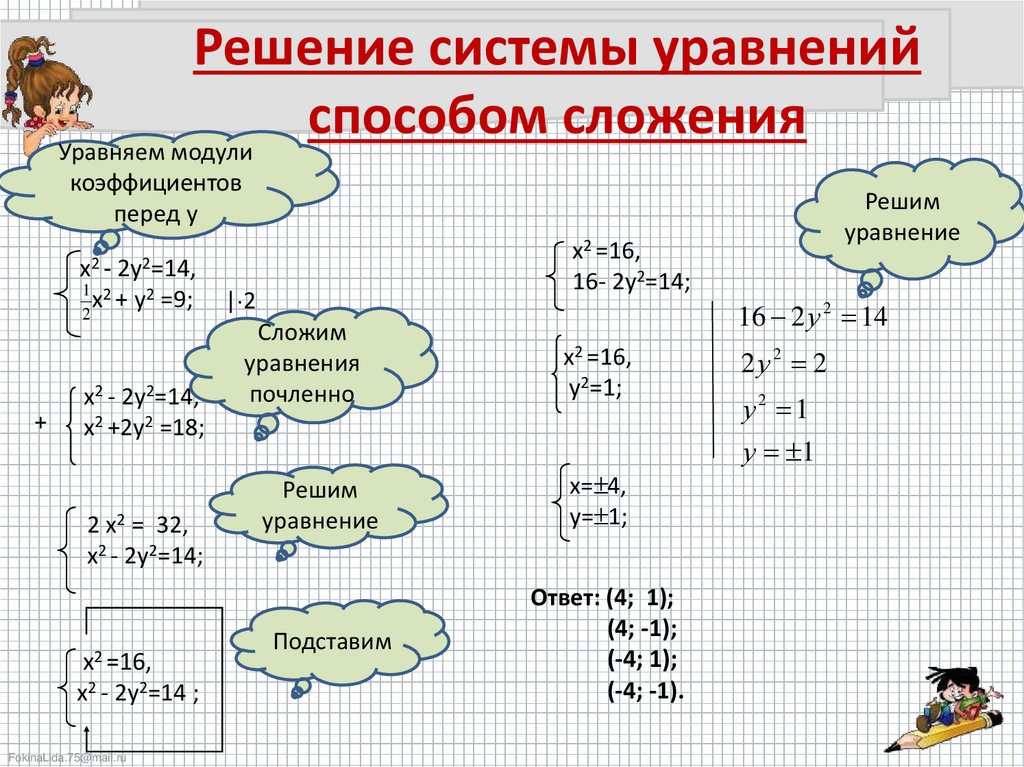
Легко видеть, что а = 3.
Ответ: а = 3.
Остались вопросы? Не знаете, как решать системы уравнений?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Решить уравнения, тригонометрию, производные и интегралы онлайн
Сервис на данной странице позволяет решить математику онлайн, выполнить:
онлайн решение задач;
решение уравнений онлайн;
решение неравенств онлайн;
решение интегралов онлайн;
решение логарифмов онлайн;
решение пределов онлайн;
нахождение производных онлайн;
исследование функции онлайн;
и много-много чего еще.
возведение в степень solve решение уравнений, неравенств,
систем уравнений и неравенствexpand раскрытие скобок factor разложение на множители sum вычисление суммы членов последовательности derivative дифференцирование (производная) integrate интеграл lim предел inf бесконечность plot построить график функции log (a, b) логарифм по основанию a числа b sin, cos, tg, ctg синус, косинус, тангенс, котангенс sqrt корень квадратный pi число «пи» (3,1415926535. 2), {x, 0.5, 2}- Правообладателям
- Карта сайта
Решите систему — уравнения с несколькими неизвестными
Решение уравнений, расчет онлайн
Summary :
Решатель систем линейных уравнений позволяет решать уравнения с несколькими неизвестными: система уравнений с 2 неизвестными, система уравнений с 3 неизвестными, система с n неизвестными.
решить_уравнения онлайн
Описание :
Решение уравнений с несколькими неизвестными другими словами, решение системы уравнений онлайн возможно за счет использования функцииsolve_equations калькулятора. Калькулятор допускает разрешение системы онлайн нескольких типов, это возможно:
- по решать системы уравнений с двумя неизвестными онлайн ,
- — решать системы уравнений с тремя неизвестными онлайн ,
- и, в более общем смысле, разрешение онлайн-систем, уравнение с несколькими неизвестными.
Обладая способностью к алгебре, калькулятор может решить уравнений с двумя неизвестными или решить уравнения с 3 неизвестными с участием букв (буквальный расчет).
Калькулятор представляет собой решатель системы уравнений , который использует очень простой синтаксис для решения систем линейных уравнений, допускающих единственное решение.
Решение системы 2 уравнений с 2 неизвестными
Существует несколько методов решения системы 2 уравнений с 2 неизвестными: метод замещения , комбинированный метод , графический метод , метод Крамера .
- Комбинированный метод заключается в исключении одной из переменных благодаря арифметическим операциям над уравнениями;
- Метод подстановки состоит в выражении одной из переменных как функции другой и последующей замене для получения уравнения с одним неизвестным;
- Метод графического решения позволяет предположить решение, которое необходимо будет проверить вычислением, графический метод состоит в изображении прямых линий, соответствующих уравнениям, а затем «чтении» координат точки пересечения, графический калькулятор позволяет выполнять этот тип операции;
- Метод Крамера использует определители.
Калькулятор может использовать эти методы для решения уравнений с 2 неизвестными
Чтобы решить систему 2 уравнений с 2 неизвестными согласно x+y=18 и 3*y+2*x=46, необходимо войти solve_equations(`[x+y=18;3*y+2*x=46];[x;y]`), после вычисления возвращается результат [x=8;y=10].
Решение системы 3-х уравнений с 3-мя неизвестными
Чтобы найти решения системы 3-х уравнений с 3-мя неизвестными , калькулятор может использовать метод подстановки, комбинированный метод или метод Крамера.
Так, например, для решения линейной системы уравнений по x+y+z=1, x-y+z=3, x-y-z=1 необходимо ввести solve_equations(`[x+y+z=1;x-y+z=3;x-y-z=1];[x;y;z]`) , после вычисления результат [x=1;y=-1; z=1] возвращается.
Синтаксис:
решить_уравнения([уравнение1;уравнение2;…;уравнениеN];[переменная1;переменная2…переменнаяN])
Примеры:
- x+y=18
- 3*у+2*х=46
solve_equations(`[x+y=18;3*y+2*x=46];[x;y]`), возвращает[x=8;y=10] Рассчитайте онлайн с помощьюsolve_equations (решите систему линейных уравнений)
См.
такжеСписок связанных калькуляторов:
- Решение квадратного уравнения с комплексным числом : complexe_solve. Калькулятор уравнений комплексных чисел возвращает комплексные значения, для которых квадратное уравнение равно нулю.
- Расчет дискриминанта онлайн: дискриминант. Калькулятор, который позволяет вычислить дискриминант квадратного уравнения онлайн.
- Найти уравнение прямой линии из двух точек: уравнение_прямой_линии. Калькулятор уравнения прямой позволяет рассчитать уравнение прямой по координатам двух точек с пошаговым расчетом.
- Найдите уравнение касательной линии: уравнение_касательной_линии. Калькулятор уравнения касательной используется для расчета уравнения касательной к кривой в заданной точке абсцисс с поэтапным вычислением.
- Калькулятор теоремы Пифагора: пифагорейский. Калькулятор использует теорему Пифагора, чтобы проверить прямоугольность треугольника или найти длину одной стороны прямоугольного треугольника.
- Калькулятор решения для x: уравнение_решателя. Решатель уравнений позволяет решать уравнения с неизвестным с шагами расчета: линейное уравнение,
квадратное уравнение, логарифмическое уравнение, дифференциальное уравнение.
- Калькулятор неравенства: неравенство_решатель. Решатель неравенств, который решает неравенство с деталями расчета: линейное неравенство, квадратное неравенство.
- Решение системы линейных уравнений :solve_equations. Решатель систем линейных уравнений позволяет решать уравнения с несколькими неизвестными: система уравнений с 2 неизвестными, система уравнений с 3 неизвестными, система с n неизвестными.
- Решатель обратного отсчета: arithmetic_solver. Этот решатель обратного отсчета позволяет найти целевое число из набора целых чисел с помощью арифметических операций.
Список связанных упражнений:
- Решите систему двух уравнений с двумя неизвестными. Целью этого исправленного математического упражнения является решение системы двух уравнений с двумя неизвестными.
- Использование системы уравнений для решения задачи. Целью этого упражнения является использование системы двух уравнений с двумя неизвестными для решения задачи.
Напоминания о курсах, калькуляторы, упражнения и игры: уравнения, матрицы
Калькулятор системы уравнений — факты, примеры
Калькулятор системы уравнений помогает определить значение переменных в данном наборе уравнений. Когда одно или несколько линейных уравнений используются для нахождения значений набора переменных, это называется системой линейных уравнений. Их также называют одновременными уравнениями.
Что такое калькулятор системы уравнений?
Калькулятор системы уравнений — это онлайн-инструмент, который помогает найти значение трех переменных, x, y, z, с помощью заданных уравнений. Многие вычислительные алгоритмы основаны на системе линейных уравнений. Они широко применяются в инженерии, физике, химии и т.
д. Чтобы использовать систему калькулятор уравнений , введите значения в поля ввода.Калькулятор системы уравнений
ПРИМЕЧАНИЕ: Вводите числа длиной до 3 цифр.
Как пользоваться калькулятором системы уравнений?
Выполните следующие действия, чтобы найти значения переменных с помощью калькулятора системы уравнений:
- Шаг 1: Перейдите к онлайн-калькулятору системы уравнений Cuemath.
- Шаг 2: Введите значения в поля ввода.
- Шаг 3: Нажмите кнопку «Решить» , чтобы найти x, y, z.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает калькулятор системы уравнений?
Существует множество методов решения системы линейных уравнений. Один из широко используемых методов — это использование матриц для решения одновременных уравнений.
Это широко известно как правило Крамера. Ниже приведены шаги для решения системы уравнений с использованием этой техники.Предположим, что система уравнений имеет вид:
\(a_{1}x + b_{1}y + c_{1}z = d_{1}\)
\(a_{2}x + b_{2}y + c_{2}z = d_{2}\)
\(a_{3}x + b_{3}y + c_{3}z = d_{3}\)Шаг 1: Найдите различные определители, как показано ниже:
D = \(\begin{vmatrix } a_{1} &b_{1} & c_{1}\\ a_{2} &b_{2} & c_{2}\\ a_{3} &b_{3} & c_{3} \end{vmatrix}\ )
\(D_{x}\) = \(\begin{vmatrix} d_{1} &b_{1} & c_{1}\\ d_{2} &b_{2} & c_{2}\\ d_ {3} &b_{3} & c_{3} \end{vmatrix}\)
\(D_{y}\) = \(\begin{vmatrix} a_{1} &d_{1} & c_{1}\\ a_{2} &d_{2} & c_{2}\\ a_{ 3} &d_{3} & c_{3} \end{vmatrix}\)
\(D_{z}\) = \(\begin{vmatrix} a_{1} &b_{1} & d_{1}\ \ a_{2} &b_{2} & d_{2}\\ a_{3} &b_{3} & d_{3} \end{vmatrix}\)
Шаг 2 : Используя эти определители, найдите значение переменные следующим образом:
x = \(D_{x}\) / D
y = \(D_{y}\) / D
z = \(D_{z}\) / D
Чтобы упростить процесс нахождения значения каждого определителя, можно использовать преобразования строк и столбцов.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Запись на бесплатный пробный урок
Решенные примеры на калькуляторе системы уравнений
Пример 1:
Найдите значения x, y, z в заданном уравнении: \( \begin{matrix} 5x\;+ \;2y\;+\;1z \;=\;4\\ 2x\;+\;3y\;+\;1z \;=\;4\\ 2x\;+\;2y\;+\; 1z \;=\;2\конец{матрица} \)
Решение:
D = \(\begin{vmatrix} 5 & 2 & 1\\ 2 & 3 & 1\\ 2 & 3 & 1 \end{vmatrix}\)
\(D_{x }\) = \(\begin{vmatrix} 4 & 2 & 1\\ 4 & 3 & 1\\ 2 & 3 & 1 \end{vmatrix}\)
\(D_{y}\) = \( \begin{vmatrix} 5 & 4 & 1\\ 2 & 4 & 1\\ 2 & 2 & 1 \end{vmatrix}\)
\(D_{z}\) = \(\begin{vmatrix} 5 & 2 & 4\\ 2 & 3 & 4\\ 2 & 2 & 2 \end{vmatrix}\)
x = \(D_{x}\) / D = 0,667
y = \(D_{y}\) / D = 2
z = \(D_{z}\) / D = -3,333
Пример 2:
Найдите значения x, y, z в данном уравнении: \( \begin{matrix} 1x\;+\;1y\;-\;1z \;=\; 6\\ 3x \;-\;2y\;+\;1z \;=\;-5\\ 1x\;+\;3y\;-\;2z \;=\;14\end{matrix} \)
Решение:
D = \(\begin{vmatrix} 1 & 1 & -1\\ 3 & -2 & 1\\ 1 & 3 & -2 \end{vmatrix}\)
\(D_{x }\) = \(\begin{vmatrix} 6 & 1 & -1\\ -5 & -2 & 1\\ 14 & 3 & -2 \end{vmatrix}\)
\(D_{y}\) = \(\begin{vmatrix} 1 & 6 & -1\\ 3 & -5 & 1\\ 1 & 15 & -2 \end{vmatrix}\)
\ (D_{z}\) = \(\begin{vmatrix} 1 & 1 & 6\\ 3 & -2 & -5\\ 1 & 3 & 14 \end{vmatrix}\)
x = \(D_ {x}\) / D = 1
y = \(D_{y}\) / D = 3
z = \(D_{z}\) / D = 2
Аналогично можно попробовать систему калькулятора уравнений и найти значения x,y,z
- \( \begin{matrix} 2x\;+\;2y\;+\;5z \;=\; 4\\ x\;+\; 3y\;+\;1z \;=\;4\\ 2x\;+\;4y\;+\;1z \;=\;2\end{matrix} \)
- \( \begin{matrix} x\;-\;3y\;+\;7z \;=\; 13\\ x\;+\;y\;+\;z \;=\; 1\\ х\;-\;2у\;+\;3z \;=\;4\конец{матрица} \)
- Линейные уравнения
- Система уравнений
Дифференциальные уравнения — Системы ДУ
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.До сих пор мы рассматривали только решение одиночных дифференциальных уравнений. Однако многие ситуации «реальной жизни» описываются системой дифференциальных уравнений. Рассмотрим проблемы населения, которые мы рассмотрели в разделе моделирования в главе о дифференциальных уравнениях первого порядка. В этих задачах мы рассматривали только популяцию одного вида, однако задача также содержала некоторую информацию о хищниках вида. Мы предполагали, что любое хищничество в этих случаях будет постоянным. Однако в большинстве случаев уровень хищничества также будет зависеть от популяции хищника. Итак, чтобы быть более реалистично, у нас также должно быть второе дифференциальное уравнение, которое давало бы популяцию хищников.
Также обратите внимание, что популяция хищника будет каким-то образом зависеть и от популяции жертвы. Другими словами, нам нужно знать что-то об одной популяции, чтобы найти другую популяцию. Таким образом, чтобы найти популяцию жертвы или хищника, нам нужно решить систему по крайней мере из двух дифференциальных уравнений.Следующая тема для обсуждения — как решать системы дифференциальных уравнений. Однако, прежде чем сделать это, нам сначала нужно сделать краткий обзор линейной алгебры. Многое из того, что мы будем делать в этой главе, будет зависеть от тем из линейной алгебры. Этот обзор не предназначен для того, чтобы полностью научить вас предмету линейной алгебры, так как это тема для полного курса. Краткий обзор предназначен для того, чтобы вы достаточно ознакомились с некоторыми основными темами, чтобы вы могли выполнять необходимую работу, как только мы приступим к решению систем дифференциальных уравнений.
Вот краткий перечень тем, затронутых в этой главе.
Обзор: Системы уравнений.
В этом разделе мы дадим обзор традиционной отправной точки для класса линейной алгебры. Мы будем использовать методы линейной алгебры для решения системы уравнений, а также приведем несколько полезных фактов о количестве решений, которые может иметь система уравнений.Обзор: Матрицы и векторы. В этом разделе мы дадим краткий обзор матриц и векторов. Мы рассмотрим арифметику с использованием матриц и векторов, нахождение обратной матрицы, вычисление определителя матрицы, линейно зависимые/независимые векторы и преобразование систем уравнений в матричную форму.
Обзор: Собственные значения и собственные векторы. В этом разделе мы познакомимся с понятием собственных значений и собственных векторов матрицы. Мы определяем характеристический многочлен и показываем, как его можно использовать для нахождения собственных значений матрицы. Получив собственные значения матрицы, мы также покажем, как найти соответствующие собственные значения матрицы.
Системы дифференциальных уравнений.
{ \text{th}}\) в систему дифференциальных уравнений.Решения систем. В этом разделе мы кратко рассмотрим, как мы решаем системы дифференциальных уравнений в матричной форме. Мы также определяем вронскиан для систем дифференциальных уравнений и показываем, как его можно использовать для определения наличия общего решения системы дифференциальных уравнений.
Фазовая плоскость. В этом разделе мы дадим краткое введение в фазовую плоскость и фазовые портреты. Мы определяем равновесное решение/точку для однородной системы дифференциальных уравнений и то, как можно использовать фазовые портреты для определения устойчивости равновесного решения. Мы также показываем формальный метод построения фазовых портретов.
Вещественные собственные значения. В этом разделе мы будем решать системы двух линейных дифференциальных уравнений, в которых собственные значения являются различными действительными числами. Мы также покажем, как рисовать фазовые портреты, связанные с реальными различными собственными значениями (седловыми точками и узлами).
Комплексные собственные значения. В этом разделе мы будем решать системы двух линейных дифференциальных уравнений, в которых собственные значения являются комплексными числами. Это будет включать в себя иллюстрацию того, как получить решение, которое не включает комплексные числа, которые мы обычно ищем в этих случаях. Мы также покажем, как рисовать фазовые портреты, связанные со сложными собственными значениями (центрами и спиралями).
Повторяющиеся собственные значения. В этом разделе мы будем решать системы двух линейных дифференциальных уравнений, в которых собственные значения являются вещественными повторяющимися (в данном случае двойными) числами. Это будет включать получение второго линейно независимого решения, которое нам понадобится для формирования общего решения системы. Мы также покажем, как рисовать фазовые портреты, связанные с реальными повторяющимися собственными значениями (неправильными узлами).
Неоднородные системы. В этом разделе мы рассмотрим быстрые примеры, иллюстрирующие использование неопределенных коэффициентов и вариаций параметров для решения неоднородных систем дифференциальных уравнений.
Метод неопределенных коэффициентов будет работать почти так же, как и для дифференциальных уравнений n-го порядка, в то время как изменение параметров потребует дополнительной работы по выводу, чтобы получить формулу/процесс, который мы можем использовать в системах.Преобразования Лапласа. В этом разделе мы рассмотрим быстрый пример, иллюстрирующий, как можно использовать преобразования Лапласа для решения системы двух линейных дифференциальных уравнений.
Моделирование. В этом разделе мы кратко рассмотрим некоторые расширения некоторых методов моделирования, которые мы использовали в предыдущих главах и которые приводят к системам дифференциальных уравнений. В частности, мы рассмотрим задачи смешивания, в которых у нас есть два соединенных резервуара с водой, задачу хищник-жертва, в которой учитываются популяции обоих, и задачу о механических вибрациях с двумя массами, соединенными с пружиной, каждая из которых связана с стена с пружиной.
Онлайн-калькулятор нелинейной системы уравнений
- Экспрессия
- Уравнение
- Неравенство
- Связаться с US
- Упрощение
- Фактор
- Expand
- GCF
- LCM
- Система
- Решение
- График
- Система
- Математический решатель на вашем сайте
- 9.
VIND- 6799467VER
- 67776799467VE0027
онлайн-калькулятор нелинейная система уравнений
Связанные темы:
экспоненциальные функции и рабочий лист уравнений решить и проверить | место математики | решатель многочленов деления на мономы | онлайн алгебра 1а для 9-х классов | решить следующее, разложив на множители и составив соответствующие таблицы знаков | метод лестницы с наименьшим общим фактором | наклон матлаб числовойАвтор Сообщение AzNBjNaYBoJ Зарегистрирован: 10.06.2003
От:Размещено: Суббота, 30 декабря, 12:07 Привет, ребята, мне интересно, может ли кто-нибудь объяснить нелинейную систему уравнений онлайн-калькулятора? У меня есть крупный проект, который нужно завершить через пару месяцев, и для этого мне нужно глубокое понимание решения проблем в таких темах, как радикальные неравенства, такие как знаменатели и формулы алгебры. Я не могу начать свой проект, пока не получу четкое представление о нелинейной системе уравнений онлайн-калькулятора, поскольку большинство расчетов будут так или иначе напрямую связаны с ней. У меня есть набор проблем, которые, если бы кто-то помог мне решить, очень помог бы мне.Наверх кфир Зарегистрирован: 07.05.2006
Откуда: ЕгипетРазмещено: Суббота, 30 декабря, 14:39 Вы можете попробовать Алгебратор. Это буквально помогает вам очень быстро решать вопросы по алгебре. Вы можете добавить вопросы, и этот продукт шаг за шагом пройдет их вместе с вами, чтобы вы могли лучше понять их по мере их решения. Доступно несколько демонстраций, так что вы также можете узнать, насколько невероятно полезна программа. Я уверен, что здесь ваш онлайн-калькулятор нелинейной системы уравнений решит быстрее.Наверх Коэм Зарегистрирован: 22.10.2001
Откуда: ШвецияРазмещено: Понедельник, 01 января, 07:28 Приятно знать, что вы хотите улучшить свою математику и прилагаете усилия для этого. Я думаю, вам стоит попробовать Алгебратор. Это не совсем обучающее программное обеспечение, но оно предлагает решения математических задач в очень описательной форме. И самое лучшее в этом продукте то, что он очень удобен в использовании. Есть много примеров, приведенных по различным темам, которые весьма полезны для изучения предмета. Попробуйте и желаю вам удачи в математике.Наверх Mibxrus Зарегистрирован: 19.10.2002
Откуда: Ванкувер, КанадаРазмещено: Понедельник, 01 января, 11:13 свойства уравнений, lcf и расстояние между точками были для меня кошмаром, пока я не нашел Algebrator, действительно лучшую математическую программу, с которой я когда-либо сталкивался. Я использовал его на нескольких уроках математики — Pre Algebra, Basic Math и Basic Math. Просто введите задачу по алгебре и нажмите «Решить», Алгебратор сгенерирует пошаговое решение задачи, и моя домашняя работа по математике будет готова. Программу искренне рекомендую.Наверх NejhdLimks Дата регистрации: 18.08.2005
Откуда: Бронкс, Нью-ЙоркРазмещено: Понедельник, 01 января, 16:05 Друзья, большое спасибо за советы, которые вы дали. Я только что взглянул на Алгебратор, доступный по адресу: https://алгебра-equation.com/equations.html. Лучшее, что мне понравилось, это гарантия окупаемости, которую они там продлевают. Я пошел дальше и купил Algebrator. Это действительно удобно для пользователя и оказывается замечательным инструментом для предварительной алгебры.Наверх Такси Зарегистрирован: 05.12.2002
Откуда: Бостон, Массачусетс, СШАРазмещено: вторник, 02 января, 09:11 Вот, пожалуйста, нажмите на эту ссылку — https://алгебра-equation. com/plane-curves-parametric-equation.html. Я лично считаю, что это действительно хорошее программное обеспечение, и тот факт, что они даже предлагают неограниченную гарантию возврата денег, делает его выгодным, вы не можете его пропустить.Наверх Решатель систем уравнений онлайн
Примеры систем уравнений
- Система двух уравнений с двумя неизвестными
2х - у = 5 3х - у = 7
х - у = 1 у - 2х = 1
- Система трех уравнений с тремя переменными
х1 - 2х2 + 3*х3 = 14 2x1 + 3x2 - 4x3 = 0
- Метод Гаусса
х - у - 1 = 0 х + у + 2 = 0
- Метод Крамера
2*х - 3*у = 5 5*х + у = 4
- Прямой метод
2*х - у = 3 2*х + у = 9
92 = 2 + х - Система четырех уравнений
х1 + 2х2 + 3х3 - 2х4 = 1 2х1 - х2 - 2х3 - 3х4 = 2 3х1 + 2х2 - х3 + 2х4 = -5 2x1 - 3x2 + 2x3 + x4 = 11
- Система линейных уравнений с четырьмя неизвестными
2x + 4y + 6z + 8v = 100 3х + 5у + 7з + 9в = 116 3х - 5у + 7з - 9в = -40 -2x + 4y - 6z + 8v = 36
- Система из трех нелинейных уравнений с квадратом или дробью 912
Что умеет калькулятор?
- Решает системы уравнений различными методами:
- Метод Крамера
- Метод Гаусса
- Численное решение
- Графический метод
- Подробное решение тремя способами:
- Методы Крамера и Гаусса
- Простая замена переменных
Приведенные выше примеры также содержат:
- модуль или абсолютное значение: absolute(x) или |x|
- квадратные корни sqrt(x),
кубических корня cbrt(x) - тригонометрические функции:
sinus sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - экспоненциальные функции и показатели exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс acot(x) - натуральные логарифмы ln(x),
десятичные логарифмы log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x), гиперболический арктангенс ath(x), гиперболический арккотангенс acoth(x) - другие тригонометрические и гиперболические функции:
секанс сек(х), косеканс csc(x), арксеканс asec(x), арккосеканс acsc(x), гиперболический секанс sech(x), гиперболический косеканс csch(x), гиперболический арксикансек asech(x), гиперболический арккосеканс acsch(x) - функции округления:
округление вниз по полу(x), округление вверх по потолку(x) - знак числа:
знак(х) - по теории вероятностей:
функция ошибок erf(x) (интеграл вероятности), Функция Лапласа laplace(x) - Факториал x :
x! или факториал(х) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
- Тригонометрические интегралы: Si(x), Ci(х), Ши(х), Чи(х)
Правила вставки
Следующие операции могут быть выполнены 95
- — возведение в степень
- х + 7
- — дополнение
- х — 6
- — вычитание
- Реальные числа
- вставка как 7,5 , № 7,5
Константы
- Пи
- — число Пи
- и
- — основание натурального логарифма
- и
- — комплексный номер
- оо
- — символ бесконечности
Решатель полярных уравнений онлайн
Дом Рациональные выражения Графики рациональных функций Решение двухшаговых уравнений Умножение, деление; экспоненты; Квадратные корни; и решение уравнений Линейные уравнения Решение квадратного уравнения Системы линейных уравнений Введение Уравнения и неравенства Решение уравнений 2-й степени Обзор решения квадратных уравнений Система уравнений Решение уравнений и неравенств Функции линейных уравнений, нули и приложения Рациональные выражения и функции Линейные уравнения с двумя переменными План урока по сравнению и упорядочению рациональных чисел Линейные уравнения Решение уравнений Радикалы и рациональные показатели Решение линейных уравнений Системы линейных уравнений Решение экспоненциальных и логарифмических уравнений Решение систем линейных уравнений РАССТОЯНИЕ, КРУГИ И КВАДРАТНЫЕ УРАВНЕНИЯ Решение квадратных уравнений Квадратичное и рациональное неравенство Приложения систем линейных уравнений в двух Переменные Системы линейных уравнений Описание теста для RATIONAL EX Экспоненциальные и логарифмические уравнения Системы линейных уравнений: правило Крамера Введение в системы линейных уравнений Буквенные уравнения и формулы Уравнения и неравенства с абсолютным значением Рациональные выражения РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТИЧНЫХ УРАВНЕНИЙ Самый крутой спуск для решения линейных уравнений Квадратное уравнение Линейные уравнения с двумя переменными - Выражение
- Уравнение
- Неравенство
- Contact us
- Simplify
- Factor
- Expand
- GCF
- LCM
- Solve
- Graph
- System
- Solve
- Graph
- System
- Math solver on ваш сайт
онлайн-решатель полярных уравнений
Связанные темы:
решение линейных уравнений java | как наклон используется в прикладной алгебре | учебник помощь с задачами по алгебре 1 | листы линейных уравнений | код для решения системы нелинейных уравнений | комплексный номер теста Java | «www . shodor.org ./interactive/activities/алгебраатор» |
Java-программа для переворачивания числа и вывода его суммы |
примеры наклона алгебры десятый класс |
-/+ более компактное уравнение |
решение вопросов бесплатная помощь шаг за шагом |
алгебраическая диаграмма факторов |
рабочий лист для 6-х классов |
онлайн-решатель задач по алгебре в колледжеАвтор Сообщение InjoyМЕРВАНО! Зарегистрирован: 18.04.2005
Откуда: ГерманияРазмещено: Суббота, 30 декабря, 13:50 Здравствуй, математический гений. Я в настоящем беспорядке. просто не знаю что делать. Знаете, у меня проблемы с математикой, и мне нужна помощь с онлайн-решателем полярных уравнений. Вы знаете кого-нибудь, кто может спасти меня, добавляя матрицы, сложные дроби и вычитая дроби? Я пытался найти репетитора, но не смог. Их трудно найти, и они чертовски дороги. Также сложно найти кого-то достаточно быстро, а у меня скоро экзамен. Любые советы о том, что я должен делать? Буду очень признателен за быстрый ответ.Наверх oc_rana Зарегистрирован: 08.03.2007
Откуда: Египет, АлександрияРазмещено: Воскресенье, 31 декабря, 08:52 Вы можете найти много ссылок в Интернете, если будете искать по ключевому слову онлайн-решатель полярных уравнений. Однако большая часть информации предназначена для читателей, которые уже имеют некоторые знания по этому вопросу. Если вы полный новичок, вам следует использовать Algebrator. Это легко понять и очень полезно.Наверх Долкнанки Зарегистрирован: 24.10.2003
Откуда: Где текут форельные ручьи и воздух приятныйРазмещено: Воскресенье, 31 декабря, 17:02. Я попробовал каждый из них сам, и именно тогда я наткнулся на Algebrator. Я нашел его особенно подходящим для линейных уравнений, десятичных дробей и эквивалентных дробей. На самом деле это была детская игра, чтобы начать это делать. Как только вы вводите проблему, программа ведет вас к ответу, проясняя каждый шаг на своем пути. Вот что делает его великолепным. К тому времени, когда вы придете к ответу, вы уже знаете, как решать проблемы. Мне было полезно научиться решать задачи по алгебре 1, предварительной алгебре и алгебре 2 по алгебре. Я также уверен, что вам тоже понравится эта программа, как и мне. Разве вы не хотите попробовать это?Наверх Вильд Зарегистрирован: 03.07.2001
Откуда: Сакраменто, КалифорнияРазмещено: Понедельник, 01 января, 10:48 перпендикулярные линии, десятичные дроби и графики были для меня кошмаром, пока я не нашел Algebrator, который действительно является лучшей программой алгебры, с которой я когда-либо сталкивался. Я часто использовал его на нескольких занятиях по алгебре — «Основная математика», «Алгебра 1» и «Алгебра 1». Просто введите задачу по алгебре и нажмите «Решить», Алгебратор сгенерирует пошаговое решение задачи, и моя домашняя работа по математике будет готова. Я действительно рекомендую программу.Наверх jni Зарегистрирован: 24.01.2004
Откуда: ВеликобританияРазмещено: вторник, 02 января, 18:49 Спасибо за подробную инструкцию, звучит круто. Я хотел что-то вроде Алгебратора, потому что мне не нужна программа, которая только решает задачу и дает окончательный результат, мне нужно что-то, что действительно может показать мне, как нужно решать задачу. Так я смогу понять это и в следующий раз решить самостоятельно, а не просто копировать ответы. Где я могу найти программное обеспечение?Наверх Мов Зарегистрирован: 15.05.2002
От:Размещено: Четверг, 04 января, 11:09 Попробуйте эту ссылку: https://rational-equations.
2), {x, 0.5, 2}
также
Калькулятор уравнений комплексных чисел возвращает комплексные значения, для которых квадратное уравнение равно нулю.
Целью этого упражнения является использование системы двух уравнений с двумя неизвестными для решения задачи.
д. Чтобы использовать систему калькулятор уравнений , введите значения в поля ввода.
Это широко известно как правило Крамера. Ниже приведены шаги для решения системы уравнений с использованием этой техники.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Также обратите внимание, что популяция хищника будет каким-то образом зависеть и от популяции жертвы. Другими словами, нам нужно знать что-то об одной популяции, чтобы найти другую популяцию. Таким образом, чтобы найти популяцию жертвы или хищника, нам нужно решить систему по крайней мере из двух дифференциальных уравнений.
В этом разделе мы дадим обзор традиционной отправной точки для класса линейной алгебры. Мы будем использовать методы линейной алгебры для решения системы уравнений, а также приведем несколько полезных фактов о количестве решений, которые может иметь система уравнений.
{ \text{th}}\) в систему дифференциальных уравнений.
Метод неопределенных коэффициентов будет работать почти так же, как и для дифференциальных уравнений n-го порядка, в то время как изменение параметров потребует дополнительной работы по выводу, чтобы получить формулу/процесс, который мы можем использовать в системах.
VIND
Я не могу начать свой проект, пока не получу четкое представление о нелинейной системе уравнений онлайн-калькулятора, поскольку большинство расчетов будут так или иначе напрямую связаны с ней. У меня есть набор проблем, которые, если бы кто-то помог мне решить, очень помог бы мне.
Это буквально помогает вам очень быстро решать вопросы по алгебре. Вы можете добавить вопросы, и этот продукт шаг за шагом пройдет их вместе с вами, чтобы вы могли лучше понять их по мере их решения. Доступно несколько демонстраций, так что вы также можете узнать, насколько невероятно полезна программа. Я уверен, что здесь ваш онлайн-калькулятор нелинейной системы уравнений решит быстрее.
Я думаю, вам стоит попробовать Алгебратор. Это не совсем обучающее программное обеспечение, но оно предлагает решения математических задач в очень описательной форме. И самое лучшее в этом продукте то, что он очень удобен в использовании. Есть много примеров, приведенных по различным темам, которые весьма полезны для изучения предмета. Попробуйте и желаю вам удачи в математике.
Я использовал его на нескольких уроках математики — Pre Algebra, Basic Math и Basic Math. Просто введите задачу по алгебре и нажмите «Решить», Алгебратор сгенерирует пошаговое решение задачи, и моя домашняя работа по математике будет готова. Программу искренне рекомендую.
Я только что взглянул на Алгебратор, доступный по адресу: https://алгебра-equation.com/equations.html. Лучшее, что мне понравилось, это гарантия окупаемости, которую они там продлевают. Я пошел дальше и купил Algebrator. Это действительно удобно для пользователя и оказывается замечательным инструментом для предварительной алгебры.
com/plane-curves-parametric-equation.html. Я лично считаю, что это действительно хорошее программное обеспечение, и тот факт, что они даже предлагают неограниченную гарантию возврата денег, делает его выгодным, вы не можете его пропустить.
shodor.org ./interactive/activities/алгебраатор» |
Java-программа для переворачивания числа и вывода его суммы |
примеры наклона алгебры десятый класс |
-/+ более компактное уравнение |
решение вопросов бесплатная помощь шаг за шагом |
алгебраическая диаграмма факторов |
рабочий лист для 6-х классов |
онлайн-решатель задач по алгебре в колледже
Я в настоящем беспорядке. просто не знаю что делать. Знаете, у меня проблемы с математикой, и мне нужна помощь с онлайн-решателем полярных уравнений. Вы знаете кого-нибудь, кто может спасти меня, добавляя матрицы, сложные дроби и вычитая дроби? Я пытался найти репетитора, но не смог. Их трудно найти, и они чертовски дороги. Также сложно найти кого-то достаточно быстро, а у меня скоро экзамен. Любые советы о том, что я должен делать? Буду очень признателен за быстрый ответ.
Однако большая часть информации предназначена для читателей, которые уже имеют некоторые знания по этому вопросу. Если вы полный новичок, вам следует использовать Algebrator. Это легко понять и очень полезно.
Я нашел его особенно подходящим для линейных уравнений, десятичных дробей и эквивалентных дробей. На самом деле это была детская игра, чтобы начать это делать. Как только вы вводите проблему, программа ведет вас к ответу, проясняя каждый шаг на своем пути. Вот что делает его великолепным. К тому времени, когда вы придете к ответу, вы уже знаете, как решать проблемы. Мне было полезно научиться решать задачи по алгебре 1, предварительной алгебре и алгебре 2 по алгебре. Я также уверен, что вам тоже понравится эта программа, как и мне. Разве вы не хотите попробовать это?
Я часто использовал его на нескольких занятиях по алгебре — «Основная математика», «Алгебра 1» и «Алгебра 1». Просто введите задачу по алгебре и нажмите «Решить», Алгебратор сгенерирует пошаговое решение задачи, и моя домашняя работа по математике будет готова. Я действительно рекомендую программу.
Я хотел что-то вроде Алгебратора, потому что мне не нужна программа, которая только решает задачу и дает окончательный результат, мне нужно что-то, что действительно может показать мне, как нужно решать задачу. Так я смогу понять это и в следующий раз решить самостоятельно, а не просто копировать ответы. Где я могу найти программное обеспечение?