Область определения функции линейной функции: Функция. Область определения и область значений функции

Линейная функция — область определения и значения. Свойства, примеры и график

Функцию, которую можно задать формулой вида y = kx + b, где  k и b — некоторые числа, х — независимая переменная, называют линейной. Рассмотрим несколько примеров.

В бассейне было 200 л. воды. В течении t мин. в бассейн каждую минуту поступало 80 л. воды. Тогда объем V воды в бассейне вычисляется по формуле: V = 80t + 200, где t ≥ 0. Эта формула задает функциональную зависимость переменной V от переменной t.

Первая бригада собрала 25 ящиков яблок; каждый рабочий второй бригады собрал по 2 ящика. Пусть во второй бригаде было х рабочих. Обозначим число всех ящиков, собранных двумя бригадами, буквой y. Тогда зависимость переменной y от переменной х выражается формулой y = 2x + 25, где х — натуральное число. Важно заметить, что областью определения линейной функции являются все действительные числа.

Построим график функции y = -2x + 1.

Первым делом составим таблицу значений этой функции для некоторых значений аргумента.

х	-3	-2	-1	0	1	2	3
y	7	5	3	1	-1	-3	-5

Точки А(-3;7), В(-2;5), С(-1;3), Е(0;1), Т(1;-1), М(2;-3), К(3;-5) принадлежат искомому графику.

Все эти точки лежат на одной прямой, которая и является графиком функции y = -2x + 1.

Заметим, что вертикальная прямая, т. е. прямая перпендикулярная оси абсцисс не может служить графиком функции. Поскольку прямая однозначно задается любыми двумя своими точками, то то для построения графика линейной функции достаточно выбрать два произвольных значения аргумента и составить таблицу значений функции, имеющую лишь два столбца.  Рассмотрим пример.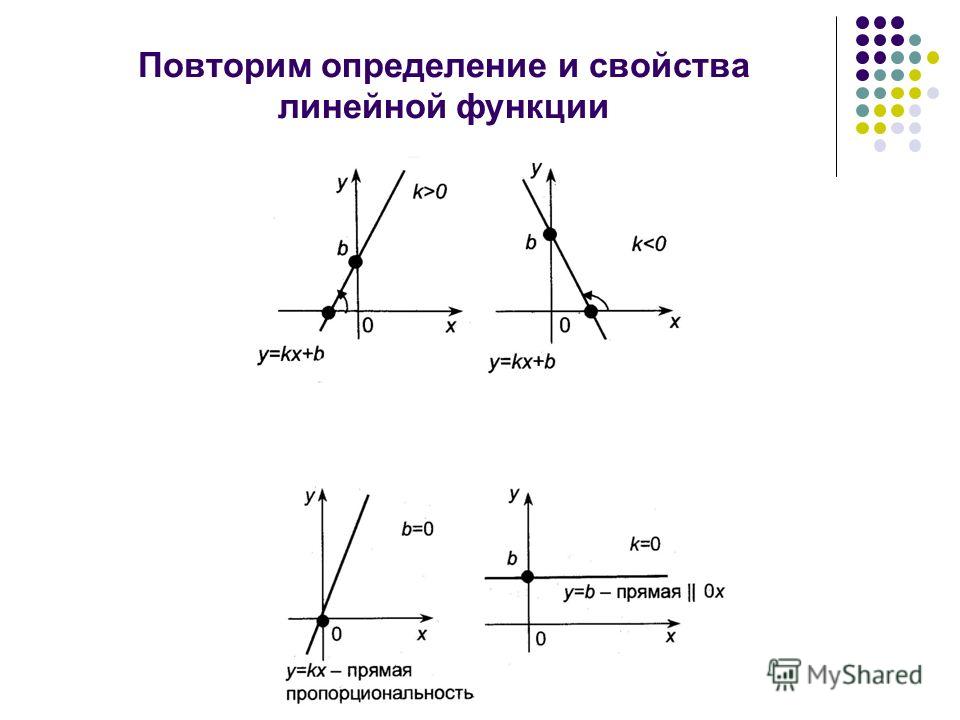

Построим график функции y = — 3x + 2, составим таблицу значений данной функции для двух произвольных значений аргумента.

х	0	1
y	2	-1

Отметим на координатной плоскости точки (0;2) и (1;-1) и проведём через них прямую линию.

Эта прямая является графиком линейной функции y = — 3x + 2.

В формуле y = kx + b, задающей линейную функцию, не исключены случаи, когда k = 0 или b = 0. Рассмотрим случай, когда b = 0 и k ≠ 0. Тогда формула приобретает вид y = kx. Отсюда для всех не равных нулю значений аргумента можно записать, что y/x = k. Эта формула показывает, что для функции 

y = kx при x ≠ 0 отношение соответствующих значений зависимой и независимой переменных остается постоянным и равно k. Такую зависимость называют прямой прямой пропорциональностью. Поэтому линейную функцию, которую задают формулой y = kx, где k ≠ 0, называют прямой пропорциональностью.                 Функции y = 2x, y = x, y = — x, y = —1/3x — примеры прямых пропорциональностей. Поскольку прямая пропорциональность — частный случай линейной функции, то её график — прямая. Особенностью является то, что эта прямая при любом значении k проходит через точку О(0;0). Действительно, если в формуле y = kx предположить что x = 0, то получим y = 0. Поэтому для построения графика прямой пропорциональности достаточно указать какую-нибудь точку графика, отличающуюся от начала координат, и провести прямую через эту точку и начало координат О(0;0). Для примера изобразим графики прямых пропорциональностей которые приводились выше.

Рассмотрим еще один частный случай линейной функции. В формуле y = kx + b предположим k = 0. Получим y = b. Ясно, что в этом случае значения функции будут оставаться неизменными при любых изменениях значений аргумента. Рассмотрим пример, построим график функции y = 2. Как и для построения графика любой линейной функции, нужно знать две принадлежащие ему точки. Эти точки будут иметь одинаковые ординаты, равные 2. Их абсциссы выберем произвольно, например равные -2 и 0. Остается провести прямую через точки А(-2;2) и В(0;2), эта прямая будет параллельна оси абсцисс.

Важно, графиком функции y = 0 является ось абсцисс. Графиком функции y = b, где b

 ≠ 0, является прямая, параллельная оси абсцисс.

Рассмотрим пример, задайте формулой линейную функцию, график которой изображен на рисунке ниже.

График данной функции пересекает ось ординат в точке (0;4). Подставив координаты этой точки в формулу y = kx + b, получаем 4 = k0 + b, откуда b = 4. Так как данный график пересекает ось абсцисс в точке (3;0), то подставив её координаты в формулу y = kx + 4, получим: 3k + 4 = 0, k = —4/3. в ответе получаем уравнение y = -4/3x + 4.

 

Алгебра Функция. Область определения и область значений

Материалы к уроку

Конспект урока

Функцией называется зависимость переменной игрек от переменной икс, при которой каждому значению переменной икс соответствует единственное значение переменной игрек.

Икс называется независимой переменной или аргументом. Игрек называется зависимой переменной, значением функции или просто функцией.

Если зависимость переменной игрек от переменной икс является функцией, то коротко записывают так: игрек равно эф от икс. Этим символом обозначают также значение функции, соответствующее значению аргумента икс.

Пусть функция задана формулой игрек равно три икс квадрат минус пять. Тогда можно записать, что эф от икс равно три икс квадрат минус пять. Найдем значения функции эф для значений икс, равных двум и минус пяти. Они будут равны семи и семидесяти.

Заметим, что в записи игрек равно эф от икс вместо эф можно употреблять и другие буквы: же, фи и так далее.

Все значения икс образуют область определения функции. Все значения, которые принимает игрек, образуют область значений функции.

Функция считается заданной, если указана её область определения и правило, согласно которому каждому значению икс поставлено в соответствие единственное значение игрек.

Если функция игрек равно эф от икс задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений переменной икс, при которых выражение эф от икс имеет смысл…

Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.

На рисунке изображен график функции игрек равно эф от икс, областью определения которой является отрезок от единицы до пяти. С помощью графика можно найти, например, что функция от числа один равна минус трем, функция от двух равна двум, функция от числа четыре равна минус двум, функция от числа пять равна минус четырем. Наименьшее значение функции равно минус четырем, а наибольшее – двум. При этом любое число от минус четырех до двух, включая эти числа, является значением данной функции. Таким образом, областью значений функции игрек равно эф от икс является отрезок от минус четырех до двух.

Ранее нами уже были изучены некоторые виды функций:

• Линейная функция, задаваемая формулой игрек равно ка икс плюс бэ, где ка и бэ – некоторые числа;
• Прямая пропорциональность – частный случай линейной функции, она задается формулой игрек равно ка икс, где ка не равно нулю;
• Обратная пропорциональность – функция игрек равно ка деленное на икс, где ка не равно нулю.

Графиком функции игрек равно ка икс плюс бэ является прямая. Область определения этой функции — множество всех чисел. Областью значений этой функции при ка не равном нулю является множество всех чисел, а при ка равном нулю ее область значений состоит из одного числа бэ.

График функции игрек равно ка деленное на икс называется гиперболой. 

На рисунке изображен график функции игрек равно ка деленное на икс, для ка большего нуля. Областью определения этой функции является множество всех чисел, кроме нуля. Это множество является и областью ее значений…

Функциями описываются многие реальные процессы и закономерности. Например, прямой пропорциональностью является зависимость массы тела от его объема при постоянной плотности; зависимость длины окружности от ее радиуса. Обратной пропорциональностью является зависимость силы тока на участке цепи от сопротивления проводника при постоянном напряжении; зависимость времени, которое затрачивает равномерно движущееся тело на прохождение заданного пути, от скорости движения.

Изучались также функции, заданные формулами игрек равно икс квадрат, игрек равно икс куб, игрек равно корень квадратный из икс.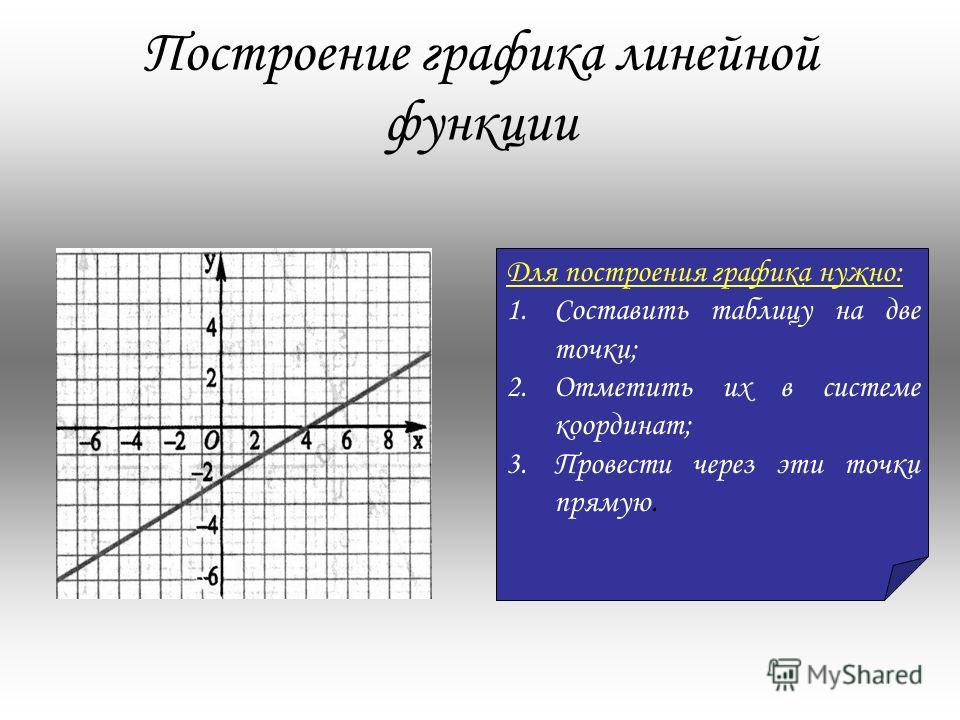

Рассмотрим функцию, заданную формулой игрек равно модуль икс.

Так как выражение модуль икс имеет смысл при любом икс, то областью определения этой функции является множество всех чисел. По определению модуль икс равен икс, если икс больше либо равен нулю, и минус икс, если икс меньше нуля. Поэтому функцию игрек равно модуль икс можно задать следующей системой.

График рассматриваемой функции в промежутке от нуля до плюс бесконечности, включая ноль, совпадает с графиком функции игрек равно икс, а в промежутке от минус бесконечности до нуля – с графиком функции игрек равно минус икс. График функции игрек равно модуль икс состоит из двух лучей, которые исходят из начала координат и являются биссектрисами первого и второго координатных углов.

 

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитораОставить заявку на подбор

Что такое линейная функция? — Уравнение, график, определение

Линейная функция представляет собой прямую линию на координатной плоскости.

Например, y = 3x — 2 представляет собой прямую линию на координатной плоскости и, следовательно, представляет собой линейную функцию. Поскольку y можно заменить на f(x), эту функцию можно записать в виде f(x) = 3x — 2.

В этой статье мы изучим определение линейной функции вместе с ее графиком, областью определения, и диапазон. Мы также узнаем, как идентифицировать линейную функцию и как найти ее обратную.

1.	Что такое линейная функция?
2.	Уравнение линейной функции
3.	Идентификация линейной функции
4.	График линейной функции
5.	Область и диапазон линейной функции
6.	Обратная линейная функция
7.	Кусочно-линейная функция
8.	Часто задаваемые вопросы о линейной функции

Что такое линейная функция?

Линейная функция имеет вид f(x) = mx + b, где m и b — действительные числа. Разве это не похоже на форму пересечения наклона линии, которая выражается как y = mx + b? Да, это потому, что линейная функция представляет собой линию, т. е. ее график является линией. Здесь,

• ‘м’ — наклон линии
• ‘b’ — точка пересечения по оси y линии
.
• ‘x’ — независимая переменная
• ‘y’ (или f(x)) является зависимой переменной

Линейная функция — это алгебраическая функция. Это потому, что он включает только алгебраические операции.

Уравнение линейной функции

Родительская линейная функция f(x) = x, которая представляет собой прямую, проходящую через начало координат. В общем случае уравнение линейной функции имеет вид f(x) = mx + b, и вот несколько примеров.

• f(x) = 3x — 2
• f(x) = -5x — 0,5
• f(x) = 3

Пример линейной функции из реальной жизни

Вот несколько реальных применений линейной функции.

• Служба потоковой передачи фильмов взимает ежемесячную плату в размере 4,50 доллара США и дополнительную плату в размере 0,35 доллара США за каждый загруженный фильм. Теперь общая ежемесячная плата представлена ​​линейной функцией f(x) = 0,35x + 4,50, где x — количество фильмов, скачанных за месяц.
• Компания по производству футболок взимает единовременную плату в размере 50 и 7 долларов США за каждую футболку за печать логотипов на футболках. Таким образом, общий сбор выражается линейной функцией f(x) = 7x + 50, где x — количество футболок.
• Линейная функция используется для представления целевой функции в задачах линейного программирования, чтобы помочь минимизировать закрытие или максимизировать прибыль.

Как найти линейную функцию?

Мы используем форму пересечения наклона или форму точки-наклона, чтобы найти линейную функцию. Процесс нахождения линейной функции аналогичен процессу нахождения уравнения прямой и объясняется на примере.

Пример: Найдите линейную функцию, на которой есть две точки (-1, 15) и (2, 27).

Решение:

Даны точки (x ₁ , y ₁ ) = (-1, 15) и (x₂, y₂) = (2, 27).

Шаг 1: Найдите наклон функции по формуле: -1)) = 12/3 = 4.

Шаг 2: Найдите уравнение линейной функции, используя форму точечного наклона.

у — у ₁ = m (х — х ₁ )

у — 15 = 4 (х — (-1))

у — 15 = 4 (х + 1)

у — 15 = 4x ​​+ 4

y = 4x + 19

Следовательно, уравнение линейной функции: f(x) = 4x + 19.

Идентификация линейной функции

Если информация о функции представлена ​​в виде графика, то она является линейной, если график представляет собой линию. Если информация о функции дана в алгебраической форме, то она линейна, если имеет вид f(x) = mx + b. Но чтобы увидеть, представляют ли данные в табличном формате линейную функцию:

• Вычислить разницу в значениях x.
• Вычислить разницу значений y
• Проверить, всегда ли постоянно отношение разницы значений y к разнице значений x.

Пример: Определите, представляют ли следующие данные из следующей таблицы линейную функцию.

х	г
3	15
5	23
7	31
11	47
13	55

Решение:

Мы будем вычислять разность значений x, разность значений y и отношение (разница y)/(разность x) каждый раз и смотреть, является ли это отношение константой.

Поскольку все числа в последнем столбце равны константе, данные в данной таблице представляют собой линейную функцию.

График линейной функции

Мы знаем, что для построения линии нам достаточно любых двух точек на ней. Если мы найдем две точки, то мы можем просто соединить их линией и продолжить ее в обе стороны. График линейной функции f(x) = mx + b

• является возрастающей линией при m > 0
• убывающая линия, когда m < 0
• горизонтальная линия при m = 0

Есть два способа построения графика линейной функции.

• Найдя на нем две точки.
• Используя наклон и точку пересечения по оси Y.

Построение графика линейной функции путем нахождения двух точек

Чтобы найти любые две точки на линейной функции (линии) f(x) = mx + b, мы просто принимаем некоторые случайные значения для ‘x’ и подставляем эти значения в функцию найти соответствующие значения для y. Процесс объясняется на примере, где мы собираемся построить график функции f(x) = 3x + 5,9.0005

• Шаг 1: Найдите две точки на прямой, взяв несколько случайных значений.
  Будем считать, что x = -1 и x = 0,
• Шаг 2: Подставьте каждое из этих значений в функцию, чтобы найти соответствующие значения y.
  Вот таблица линейной функции y = 3x + 5.

  х	г
  -1	3(-1)+5 = 2
  0	3(0)+5 = 5

  Следовательно, две точки на прямой — это (-1, 2) и (0, 5).
• Шаг 3: Нанесите точки на график и соедините их линией. Также продлите линию с обеих сторон.

   

График линейной функции с использованием наклона и точки пересечения с осью y

Чтобы построить график линейной функции f(x) = mx + b, мы можем использовать ее наклон ‘m’ и точку пересечения с осью y ‘b’. Процесс снова объясняется путем построения графика той же линейной функции f (x) = 3x + 5. Ее наклон равен m = 3, а ее точка пересечения по оси y равна (0, b) = (0, 5).

• Шаг 1: Постройте точку пересечения по оси y (0, b).
  Здесь мы наносим точку (0, 5).
• Шаг 2: Запишите наклон в виде доли подъема/набега и определите «нарастание» и «набег».
  Здесь наклон = 3 = 3/1 = подъем/разбег.
  Итак, подъем = 3 и бег = 1.
• Шаг 3: Поднимите точку пересечения по оси y по вертикали с помощью команды «подъем», а затем выполните горизонтальное перемещение с помощью команды «бег». Это приводит к новой точке.
  (Обратите внимание, что если «подъем» положительный, мы идем вверх, а если «подъем» отрицательный, мы идем вниз. Кроме того, если «бег» положительный, мы идем вправо, а если «бег» отрицательный, мы идем влево. )
  Здесь мы поднимаемся на 3 единицы вверх от точки пересечения y и, таким образом, идем вправо на 1 единицу.
• Шаг 4: Соедините точки Шаг 1 и Шаг 2 линией и продолжите линию с обеих сторон.
  

Область и диапазон линейной функции

Область определения линейной функции — это множество всех действительных чисел, а диапазон линейной функции — это также множество всех действительных чисел. На следующем рисунке показано, как f(x) = 2x + 3 и g(x) = 4−x отложены на одних и тех же осях.

Обратите внимание, что обе функции принимают действительные значения для всех значений x, а это означает, что областью определения каждой функции является множество всех действительных чисел (R).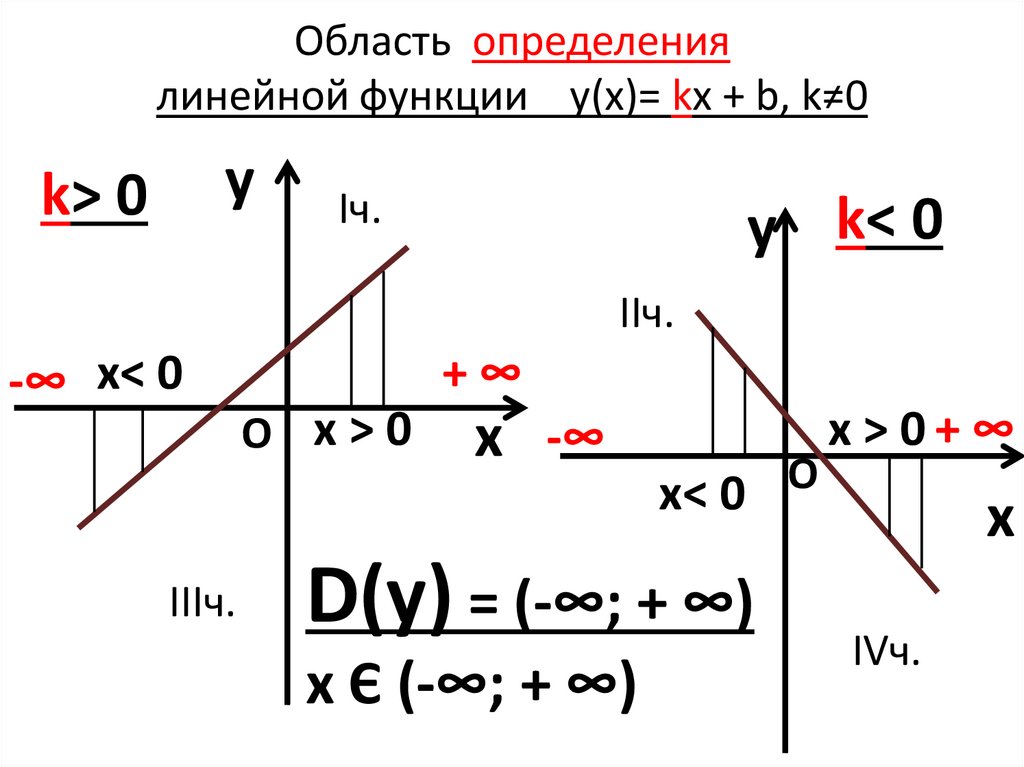 Посмотрите вдоль оси X, чтобы убедиться в этом. Для каждого значения x у нас есть точка на графике.

Кроме того, выходной сигнал для каждой функции постоянно находится в диапазоне от отрицательной бесконечности до положительной бесконечности, что означает, что диапазон любой функции также равен R. Это можно подтвердить, взглянув вдоль оси Y, которая ясно показывает, что существует точка на каждом графике для каждого значения y. Таким образом, при наклоне m ≠ 0,

• Область определения линейной функции = R
• Диапазон линейной функции = R

Примечание:

(i) Область определения и область значений линейной функции равна R, если в задаче не упоминается какая-либо конкретная область или область значений.

(ii) Когда наклон m = 0, то линейная функция f(x) = b является горизонтальной линией, и в этом случае домен = R, а диапазон = {b}.

Обратная линейная функция

Обратная линейная функция f(x) = ax + b представлена ​​функцией f ^-1 (x) такой, что f(f ^-1 (x)) = f ^-1 (f (х)) = х. Процесс поиска обратной линейной функции объясняется на примере, где мы собираемся найти обратную функцию f(x) = 3x + 5.

• Шаг 1: Запишите y вместо f(x ).
  Тогда приведенное выше уравнение принимает вид y = 3x + 5,
.
• Шаг 2: Поменять местами переменные x и y.
  Тогда мы получаем x = 3y + 5,
• Шаг 3: Решите приведенное выше уравнение для y.
  х — 5 = 3 года
  у = (х — 5)/3
• Шаг 4: Замените y на f ^-1 (x), и это будет функция, обратная f(x).
  f ^-1 (х) = (х — 5)/3

Обратите внимание, что f(x) и f ^-1 (x) всегда симметричны относительно прямой y = x. Построим линейную функцию f(x) = 3x + 5 и обратную ей f ^-1 (x) = (x — 5)/3 и посмотреть, симметричны ли они относительно y = x. Кроме того, когда (x, y) лежит на f(x), то (y, x) лежит на f ^-1 (x). Например, на следующем графике (-1, 2) лежит на f(x), тогда как (2, -1) лежит на f ^-1 (x).

Кусочно-линейная функция

Иногда линейная функция не может быть определена единообразно во всей области определения. Он может быть определен двумя или более способами, поскольку его домен разделен на две или более частей. В таких случаях это называется кусочно-линейная функция. Вот пример.

Пример: Постройте график следующей кусочно-линейной функции.

\(f(x)=\left\{\begin{массив}{ll}
х+2, & х \in[-2,1) \\
2 x-3 и x \in[1,2]
\end{array}\right.\)

Решение:

Эта кусочная функция линейна в обеих указанных частях своей области определения. Найдем концы прямой в каждом случае.

Когда x ∈ [-2, 1):

x	г
-2	-2 + 2 = 0
1 (дырка в данном случае как 1 ∉ [-2, 1))	1 + 2 = 3

При x ∈ [1, 2]:

x	г
1	2(1) — 3 = -1
2	2(2) — 3 = 1

Соответствующий график показан ниже:

Важные замечания о линейных функциях:

• Линейная функция имеет вид f(x) = mx + b, поэтому ее график представляет собой линию.
• Линейная функция f(x) = mx + b представляет собой горизонтальную линию, когда ее наклон равен 0, и в этом случае она известна как постоянная функция.
• Область определения и область значений линейной функции f(x) = ax + b равна R (все действительные числа), тогда как область значений постоянной функции f(x) = b равна {b}.
• Эти линейные функции полезны для представления целевой функции в линейном программировании.
• Постоянная функция не имеет обратной, поскольку она НЕ является однозначной функцией.
• Две линейные функции параллельны, если их наклоны равны.
• Две линейные функции перпендикулярны, если произведение их наклонов равно -1.
• Вертикальная линия НЕ является линейной функцией, так как она не проходит тест вертикальной линии.

☛ Связанные темы:

• Калькулятор линейных функций
• Формула линейной функции
• Квадратичная функция
• Графические функции

Часто задаваемые вопросы о линейной функции

Что такое определение линейной функции?

Линейная функция — это функция, график которой представляет собой линию.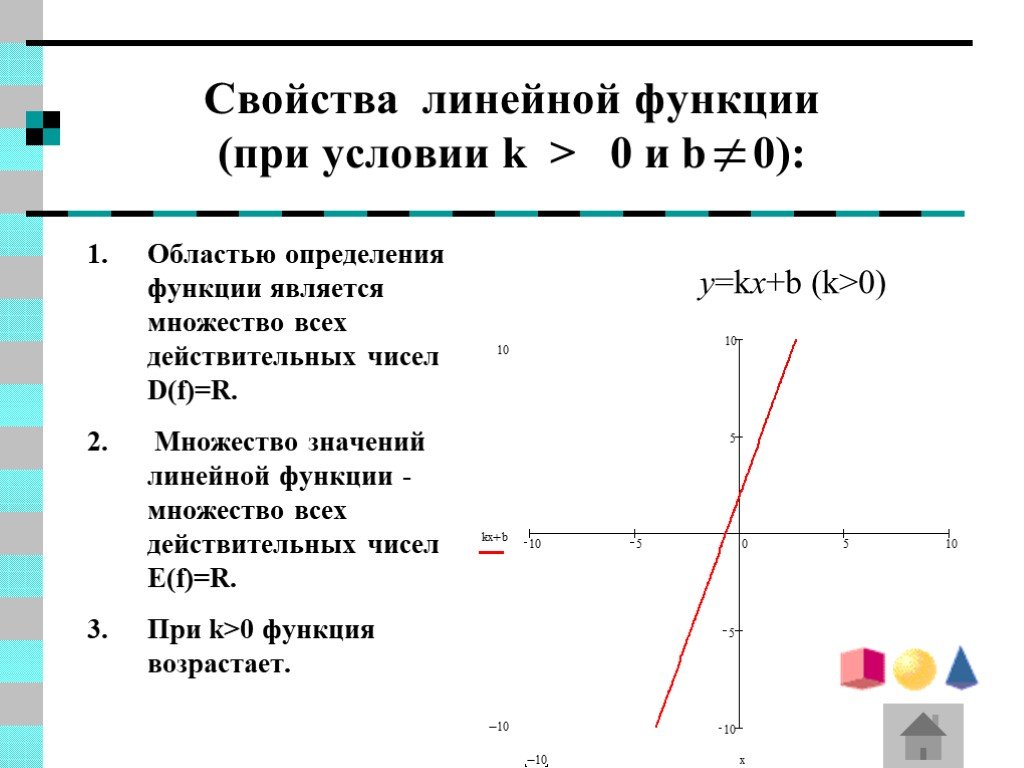 Таким образом, оно имеет вид f(x) = mx + b, где m и b — действительные числа. Здесь «m» — это наклон, а «b» — точка пересечения с осью y линейной функции.

По какой формуле найти линейную функцию?

Поскольку линейная функция представляет собой прямую, все формулы, используемые для нахождения уравнения прямой, можно использовать для нахождения уравнения линейной функции. Таким образом, формулы линейной функции:

• Стандартная форма: ax + by + c = 0
• Форма пересечения наклона: y = mx + b
• Форма точки-наклона: y — y ₁ = m (x — x ₁ )
• Форма перехвата: x/a + y/b = 1

Обратите внимание, что y можно заменить на f(x) во всех этих формулах.

Что такое таблица линейных функций?

Иногда данные, представляющие линейную функцию, представляются в виде таблицы с двумя столбцами, где первый столбец дает данные независимой переменной, а второй столбец дает соответствующие данные зависимой переменной.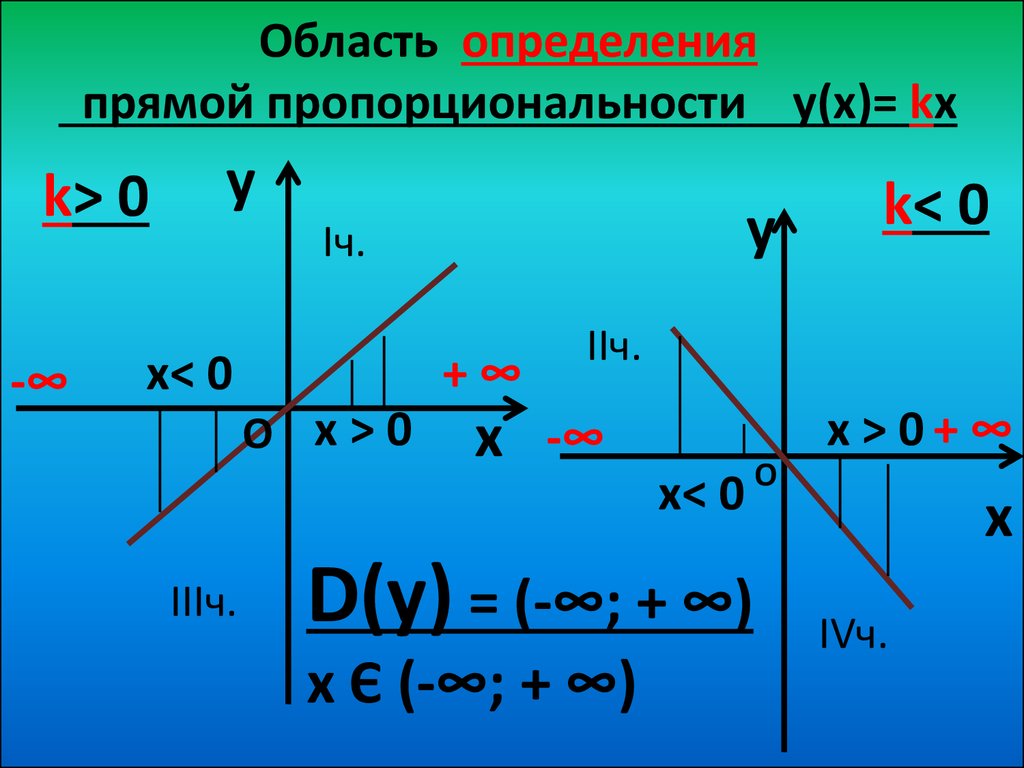 Это называется таблицей линейных функций.

В чем разница между линейной функцией и нелинейной функцией?

График линейной функции представляет собой линию, тогда как график нелинейной функции НЕ является линией. Уравнение линейной функции имеет вид f(x) = ax + b (т. е. является линейным выражением), тогда как уравнение нелинейной функции может быть любого другого вида, кроме ax + b.

Как построить график линейной функции?

Чтобы построить график линейной функции, найдите на ней любые две точки, приняв несколько случайных чисел либо за зависимую, либо за независимую переменную, и найдите соответствующие значения другой переменной. Просто нанесите эти две точки и соедините их прямой линией, продлив линию с обеих сторон.

Что такое область определения и диапазон линейной функции?

Область определения и область значений линейной функции f(x) = ax + b, где a ≠ 0 — множество всех действительных чисел. Если a = 0, домен по-прежнему является набором всех действительных чисел, но диапазоном является набор {b}. Иногда область и диапазон в задаче могут быть ограничены некоторым интервалом.

Что такое уравнение линейной функции?

Уравнение линейной функции представляет собой форму пересечения наклона. Таким образом, это выражается как f(x) = mx + b, где m — наклон, а b — точка пересечения линии по оси y.

Что такое примеры линейных функций?

f(x) = 2x + 3, f(x) = (1/5) x — 7 — некоторые примеры линейной функции. Для реальных примеров линейной функции нажмите здесь.

Как определить линейную функцию?

Мы можем определить линейную функцию следующими способами.

• Если дано уравнение функции, то оно линейно, если оно имеет вид f(x) = ax + b.
• Если задан график функции, то он линейный, если представляет собой прямую.
• Если дана таблица значений, представляющая функцию, то она является линейной, если отношение разности значений y к разнице значений x всегда является константой.

Линейные функции.

Определение, примеры, правила

Ключевые понятия

• Функции в представлении функций.
• Правило линейной функции.
• График линейной функции.
• Решение задач, связанных с линейной функцией.

Функции, домен и диапазон 

Функция

Отношение, в котором каждый вход имеет один выход.

Домен и диапазон являются важными значениями, которые помогают определить отношение. Домен принимает все возможные входные значения из действительных чисел смещения, а диапазон принимает все выходные значения функции.

Вопрос 1: Для показанного набора упорядоченных пар определите домен и диапазон. Представляет ли отношение функцию?

{(1, 8), (5, 3), (7, 6), (2, 2), (8, 4), (3, 9), (5, 7)}{1, 8, 5, 3, 7, 6,2, 2, 8, 4, 3, 9, (5, 7)}

Решение:  

Дана упорядоченная пара : {(1, 8), (5, 3), (7, 6), (2, 2), (8, 4), (3, 9), (5, 7)}{1, 8, 5 , 3, 7, 6,2, 2, 8, 4, 3, 9, (5, 7)}

Домен: {1, 5, 7, 2, 8, 3, 5}{1, 5, 7 , 2, 8, 3, 5}

Диапазон: {8, 3, 6, 2, 4, 9, 7}{8, 3, 6, 2, 4, 9, 7}

Отношение представляет функцию потому что каждый вход имеет другой выход.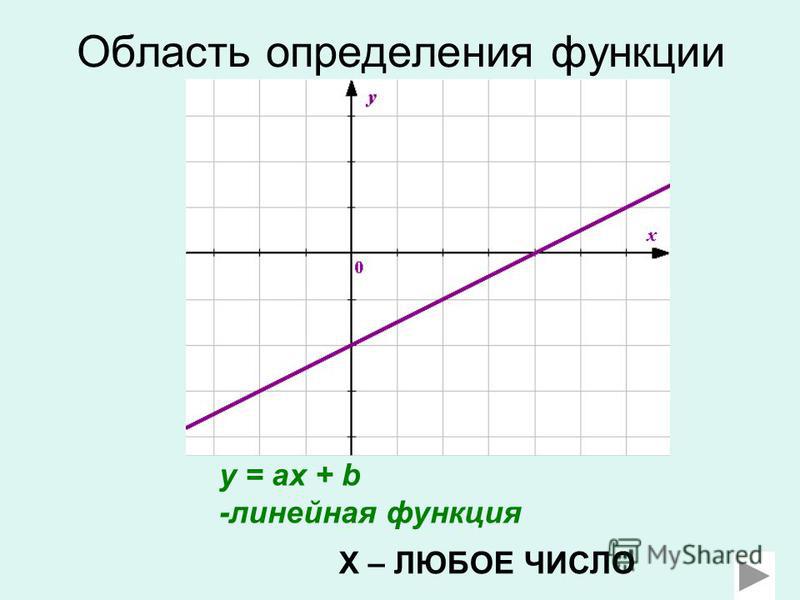

Вопрос 2: Блок-схема показывает этапы математической головоломки. Запишите и заполните результат в табличной колонке. Сделайте прогноз о том, каким будет окончательное число для любого числа. Объяснять.

Решение:   

Из блок-схемы подумайте о числах 1, 2, 3, 4 и 5 и заполните приведенную ниже таблицу:

Из таблицы каждый выход кратен 2. число/значение x, выход будет в 2 раза больше входного значения.

Обозначение функций

Обозначение функций — это метод записи переменных как функций других переменных.

Переменная y становится функцией x. Переменная x используется для нахождения значения y.

Обозначение функций помогает различать различные функции.

В обозначении функций могут использоваться буквы, отличные от f. Другими часто используемыми буквами являются g и h.

Рассмотрим уравнение y = 3x−2.

Запишите уравнение y = 3x−2

, используя функциональную запись.

Функция f определяется в виде функции f(x) = 3x−2

Пример 1:  

Каково значение h(x) = 7x+1, когда x = 5?

Решение:

Вычислите h(x) = 7x+1 при x = 5

Если h(x) = 7x+1, то h(5) = 36

Пример 2:

Что такое значение g(x) = 5−3x, когда x = 2?

Решение:

Оценить g(x)= 5−3x для x = 2.

Если g(x) = 5−3x, то g(2) = −1

Правило линейной функции

Пример 1:   

Стоимость изготовления 4 браслетов указана в таблице.

Определите стоимость изготовления любого количества браслетов.

Решение:

Шаг 1:

Зависимость линейная.

Шаг 2:   

Напишите функцию, используя для правила форму пересечения наклона.

f(x) = mx+b

f(x) = 15x+b

Шаг 3:   

Найдите значение b

Подставьте любую упорядоченную пару из таблицы.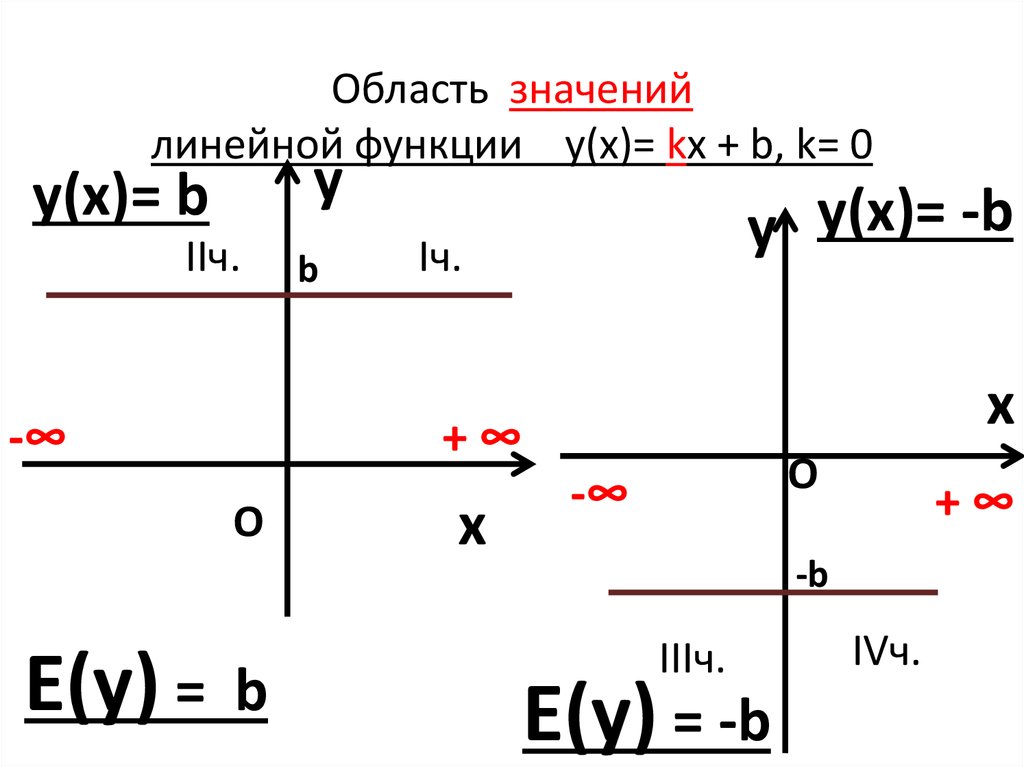

17 = 15(1)+b

2=b

Итак, функция

f(x) = 15x+2

Пример 2:   

Запишите линейную функцию для данных в таблице, используя функциональную запись.

Решение:

Шаг 1:

Связь линейная.

Шаг 2:   

Напишите функцию, используя для правила форму пересечения наклона.

f(x) = mx+b

f(x) = 4x+b

Шаг 3:

Найдите значение b, подставив любую упорядоченную пару из таблицы.

15 = 4(3)+b

3 = b

Итак, линейная функция равна

f(x) = 4x+3

Анализ линейной функции

температура наружного воздуха в 6:00 утра. Температура наружного воздуха увеличивается на 2°F каждый час в течение следующих 6 часов. Если температура продолжит повышаться с той же скоростью, какой будет температура в 14:00?

Решение:

Шаг 1:

Напишите функцию, моделирующую ситуацию:  

f(x) = mx+c

Поскольку температура в 6:00 утра. равна −3

, а температура увеличивается со скоростью 2°F каждый час.

Итак,

c = −3 & m = 2

f(x) = 2x−3

Шаг 2:  

Нарисуйте график функции.

Шаг 3:

Найдите значение y при x = 8. 00 вечера будет 13°F.

График функции f(x) = 2x−3 представляет собой линию.

Использование линейных функций для решения задач 

Вопрос:  

Кресельная канатная дорога начинается на высоте 0,8 мили над основанием горы и поднимается вверх с постоянной скоростью. Как далеко от подножия горы находится кресельный подъемник через 10 минут?

Решение:  

Шаг 1:  

Линейная функция для представления расстояния, на которое кресельный подъемник движется от подножия горы.

Пусть время (в минутах) равно t

Учитывая, что скорость кресельного подъемника выражается в милях в час, переведите скорость в мили в минуту.