Функции. Область определения функции. Алгебра 9 класс
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Функции. Область определения функции.
АЛГЕБРА9 КЛАСС
2. На рисунках показаны графики некоторых функций. Укажите название функции, название графика и формулу, задающую данную функцию.
уу = k/x
(k > 0)
у
y = ах + b
(a > 0)
у
y = ах + b
b
(a = 0)
O
х
Гипербола
Функция обратная
пропорциональность
b
х
O
Прямая
Линейная
функция
O
х
Прямая
Линейная
функция
3.
 На рисунках показаны графики некоторых функций. Укажите название графика и формулу, задающую данную функцию.у
На рисунках показаны графики некоторых функций. Укажите название графика и формулу, задающую данную функцию.уу
у
y = x2
y = x3
у
х
O
O
Парабола
х
O
Кубическая
парабола
Ветвь параболы
вдоль оси ОХ
х
4. Функция задана формулой у = 2×2 – 6. Можно записать, что f(x)= 2×2 – 6. Найдите f(2,5) и f(-3). Решение. f(2,5) = 2*2,52 – 6 =
6,5;f(-3) = 2*(-3)2 – 6 =12.
5. Правило 1. Если функция представлена в виде многочлена, то областью её определения является множество действительных чисел.
Пример.Областью определения функции
f(x) = 5×2 + 6x – 4
является множество всех действительных чисел,
т.к. 5×2 + 6x – 4 – многочлен.
6. Правило 2. Если функция представлена в виде дроби, то областью её определения является множество действительных чисел, при
которыхзнаменатель отличен от нуля.
Пример. Найдите область определения функции,
заданной формулой: у =
Решение.
 Так как в области действительных чисел
Так как в области действительных чиселделить на нуль нельзя, то область определения функции
найдем из условия: знаменатель не равен нулю.
х2 — 6х + 8 ≠ 0, отсюда х ≠ 2. х ≠ 4.
Ответ: множество действительных чисел, кроме х = 2 и
х = 4.
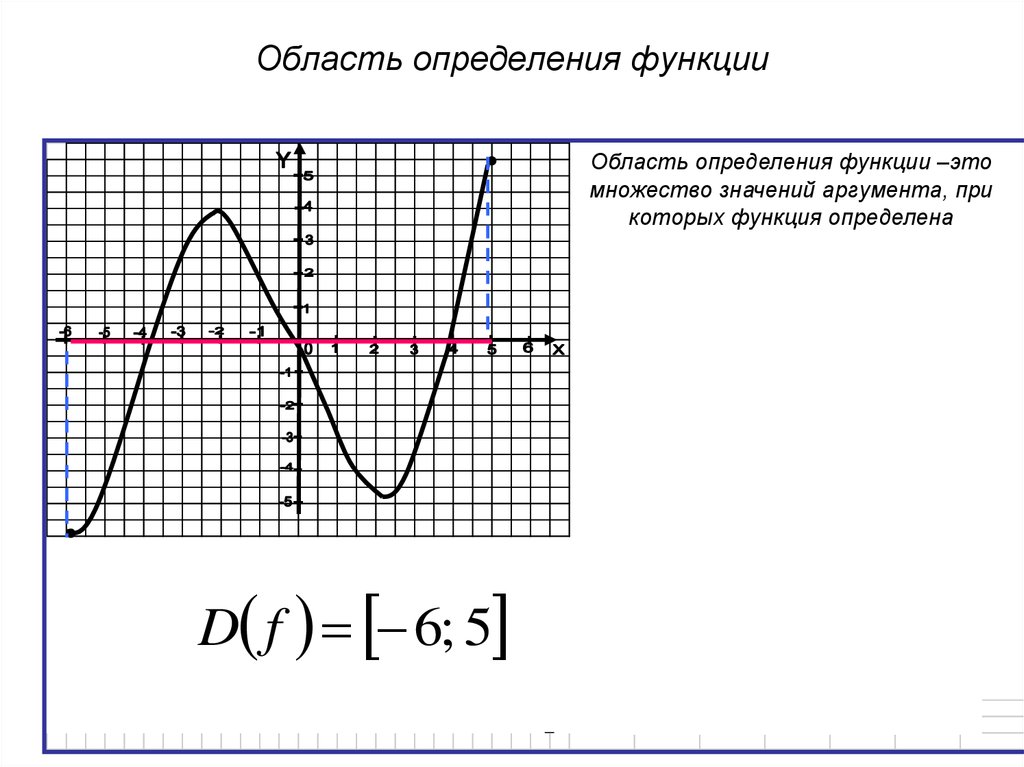
7. Правило 3. Если функция представлена в виде корня четной степени из выражения с переменной, то областью её определения является
множестводействительных чисел, при которых подкоренное
выражение неотрицательно.
Пример. Найдите область определения функции, заданной
формулой: у =
Решение. Так как в области действительных чисел под
знаком квадратного корня может находиться только
неотрицательное число, то область определения
функции найдем из условия: подкоренное выражение
больше либо равно нуля.
-6х + 8 ≥ 0, отсюда х ≤ .
Ответ: (-
8. Найдите область определения функции:
Вариант 2Вариант 1
а) у = х2 – 3х + 4
Решение. х2 – 3х + 4 – многочлен,
значит областью определения
функции является множество
всех действительных чисел.

б) у =
Решение. Так как в области
действительных чисел делить на
нуль нельзя, то область
определения функции найдем из
условия: знаменатель не равен
нулю. х – 2 ≠ 0, отсюда х ≠ 2..
Ответ: множество
действительных чисел, кроме
х = 2.
а) у = х2 – 5х
Решение. х2 – 5х – многочлен,
значит областью определения
функции является множество
всех действительных чисел.
б) у =
Решение. Так как в области
действительных чисел делить на
нуль нельзя, то область
определения функции найдем из
условия: знаменатель не равен
нулю. 2х – 3 ≠ 0, отсюда х ≠ 1,5
Ответ: множество
действительных чисел, кроме
х = 1,5.
9. Найдите область определения функции:
Вариант 2Вариант 1
у=
Решение. Учитывая, что в
области действительных
чисел под знаком квадратного
корня может находиться
только неотрицательное число и
делить на нуль нельзя, то
область
определения
функции найдем из условия:
подкоренное выражение
больше нуля.
6 – 3х > 0, -3х > -6, х < 2
Ответ: х < 2.
у=
Решение. Так как в области
действительных чисел под знаком
квадратного корня может
находиться только
неотрицательное число, то область
определения функции найдем из
условия: подкоренное выражение
больше либо равно нуля.
8х + 5 ≥ 0, отсюда х ≥ — 0,625 .
Ответ: х ≥ — 0,625 .
10. Используемая литература
1.Алгебра. 9 класс: учеб. для общеобразоват. организаций /[Ю.Н.Макарычев, Н.Г.Миндюк, К.И. Нешков, С.Б.Суворова] ;
под ред. С.А.Теляковского.- М. : Просвещение, 2014.
2.Алгебра. 9 класс. Самостоятельные работы для учащихся
Общеобразовательных учреждений : к учебнику А.Г.Мордковича,
П.В.Семенова / Л.А.Александрова ; под ред. А.Г.Мордковича. – 10-е изд.,
English Русский Правила
Найти одз функции онлайн калькулятор. Как найти область определения функции? Примеры решений
Функция-это модель. Определим X, как множество значений независимой переменной // независимая -значит любая. 2. (наз. парабола)
2. (наз. парабола)
3.у=3х+7. (наз. прямая)
4. у= √ х. (наз. ветвь параболы)
Независимая переменная (кот. мы обозначаем х) имеет название аргумент функции.
Область определения функции
Множество всех значений, которые принимает аргумент функции, называется областью определения функции и обозначается D (f) или D (y).
Рассмотрим D (у) для 1.,2.,3.,4.
1. D (у)= (∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.
2. D (у)= (∞; +∞)//всё мн-во действит.чисел
3. D (у)= (∞; +∞)//всё мн-во действит.чисел
4. D (у)=
. Остается найти пересечение множеств таких значений x
, что x∈D(f 2)
и f 2 (x)∈D(f 1)
:
Чтобы arcsinx>0 вспомним свойства функции арксинус . Арксинус возрастает на всей области определения [−1, 1] и обращается в ноль при x=0 , следовательно, arcsinx>0 для любого x из промежутка (0, 1] .
Вернемся к системе:
Таким образом, искомая область определения функции есть полуинтервал (0, 1]
.
Ответ:
(0, 1] .
Теперь давайте перейдем к сложным функциям общего вида y=f 1 (f 2 (…f n (x)))) . Область определения функции f в этом случае находится как .
Пример.
Найти область определения функции .
Решение.
Заданную сложную функцию можно расписать как y=f 1 (f 2 (f 3 (x))) , где f 1 – sin , f 2 – функция корень четвертой степени, f 3 – lg .
Нам известно, что D(f 1)=(−∞, +∞) , D(f 2)= .
Все это говорит о том, как важно наличие ОДЗ.
Пример 3
Найти ОДЗ выражения x 3 + 2 · x · y − 4 .
Решение
В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.
Ответ: x и y – любые значения.
Пример 4
Найти ОДЗ выражения 1 3 — x + 1 0 .
Решение
Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль.
Ответ: ∅ .
Пример 5
Найти ОДЗ заданного выражения x + 2 · y + 3 — 5 · x .
Решение
Наличие квадратного корня говорит о том, что это выражение обязательно должно быть больше или равно нулю. При отрицательном значении оно не имеет смысла. Значит, необходимо записать неравенство вида x + 2 · y + 3 ≥ 0 . То есть это и есть искомая область допустимых значений.
Ответ: множество x и y , где x + 2 · y + 3 ≥ 0 .
Пример 6
Определить ОДЗ выражения вида 1 x + 1 — 1 + log x + 8 (x 2 + 3) .
Решение
По условию имеем дробь, поэтому ее знаменатель не должен равняться нулю. Получаем, что x + 1 — 1 ≠ 0 . Подкоренное выражение всегда имеет смысл, когда больше или равно нулю, то есть x + 1 ≥ 0 . Так как имеет логарифм, то его выражение должно быть строго положительным, то есть x 2 + 3 > 0 . Основание логарифма также должно иметь положительное значение и отличное от 1 , тогда добавляем еще условия x + 8 > 0 и x + 8 ≠ 1 .
x + 1 — 1 ≠ 0 , x + 1 ≥ 0 , x 2 + 3 > 0 , x + 8 > 0 , x + 8 ≠ 1
Иначе говоря, называют системой неравенств с одной переменной. Решение приведет к такой записи ОДЗ [ − 1 , 0) ∪ (0 , + ∞) .
Ответ: [ − 1 , 0) ∪ (0 , + ∞)
Почему важно учитывать ОДЗ при проведении преобразований?
При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.
Тождественные преобразования:
- могут не влиять на ОДЗ;
- могут привести в расширению или дополнению ОДЗ;
- могут сузить ОДЗ.
Рассмотрим на примере.
Пример 7
Если имеем выражение вида x 2 + x + 3 · x , тогда его ОДЗ определено на всей области определения. Даже при приведении подобных слагаемых и упрощении выражения ОДЗ не меняется.
Пример 8
Если взять пример выражения x + 3 x − 3 x , то дела обстоят иначе. У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид (− ∞ , 0) ∪ (0 , + ∞) . Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.
У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид (− ∞ , 0) ∪ (0 , + ∞) . Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.
Рассмотрим пример с наличием подкоренного выражения.
Пример 9
Если имеется x — 1 · x — 3 , тогда следует обратить внимание на ОДЗ, так как его необходимо записать в виде неравенства (x − 1) · (x − 3) ≥ 0 . Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид (− ∞ , 1 ] ∪ [ 3 , + ∞) . После преобразования x — 1 · x — 3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x — 1 ≥ 0 , x — 3 ≥ 0 . При ее решении получаем, что [ 3 , + ∞) . Значит, ОДЗ полностью записывается так: (− ∞ , 1 ] ∪ [ 3 , + ∞) .
Нужно избегать преобразований, которые сужают ОДЗ.
Пример 10
Рассмотрим пример выражения x — 1 · x — 3 , когда х = — 1 . При подстановке получим, что — 1 — 1 · — 1 — 3 = 8 = 2 2 . Если это выражение преобразовать и привести к виду x — 1 · x — 3 , тогда при вычислении получим, что 2 — 1 · 2 — 3 выражение смысла не имеет, так как подкоренное выражение не должно быть отрицательным.
Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.
Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.
Пример 11
Рассмотрим на примере дроби вида x x 3 + x . Если сократить на x , тогда получаем, что 1 x 2 + 1 . Тогда ОДЗ расширяется и становится (− ∞ 0) ∪ (0 , + ∞) . Причем при вычислении уже работаем со второй упрощенной дробью.
При наличии логарифмов дело обстоит немного иначе.
Пример 12
Если имеется выражение вида ln x + ln (x + 3) , его заменяют на ln (x · (x + 3)) , опираясь на свойство логарифма. Отсюда видно, что ОДЗ с (0 , + ∞) до (− ∞ , − 3) ∪ (0 , + ∞) . Поэтому для определения ОДЗ ln (x · (x + 3)) необходимо производить вычисления на ОДЗ, то есть (0 , + ∞) множества.
При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
|
Каталог Поиск книг Электронные приложения Авторизация Подписка на рассылкуСтихи о нас Богатство Трудности эти уже превратились в смыслы. Тивикова С.К., зав. каф. начального образования НИРО Обратная связь Отправить сообщение с сайта Партнёры |
Введение Презентация «Информатика 9 класс. Введение» Презентация «Информатика 9 класс. Введение» (Open Document Format) Ссылки на ресурсы ЕК ЦОР
Глава 1. Моделирование и формализация 1.1. Моделирование как метод познания Презентация «Моделирование как метод познания» Презентация «Моделирование как метод познания» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
Ссылки на ресурсы ФЦИОР:
Ресурсы сети Интернет: Планета Земля § 1.2. Знаковые модели Презентация «Знаковые модели» Презентация «Знаковые модели» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР
Ссылки на ресурсы ФЦИОР:
§ 1.3. Графические информационные модели Презентация «Графические модели» Презентация «Графические модели» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР
§ 1.4. Табличные информационные модели Презентация «Табличные информационные модели» Презентация «Табличные информационные модели» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР
§ 1.5. База данных как модель предметной области Презентация «База данных как модель предметной области» Презентация «База данных как модель предметной области» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР
§ 1.6. Система управления базами данных Презентация «Система управления базами данных» Презентация «Система управления базами данных» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
Интерактивный тест «Моделирование и формализация» Тест 1 Глава 2. Алгоритмизация и программирование § 2.1. Решение задач на компьютере Презентация «Программирование как этап решения задачи на компьютере» Презентация «Программирование как этап решения задачи на компьютере» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР
§ 2.2. Одномерные массивы целых чисел Презентация «Одномерные массивы целых чисел» Презентация «Одномерные массивы целых чисел» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР
Ссылки на ресурсы ФЦИОР:
Ссылки на свободно распространяемое программное обеспечение:
§ 2.3. Конструирование алгоритмов Презентация «Конструирование алгоритмов» Презентация «Конструирование алгоритмов» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
Ссылки на свободно распространяемое программное обеспечение:
§ 2. Презентация «Запись вспомогательных алгоритмов на языке Паскаль» Презентация «Запись вспомогательных алгоритмов на языке Паскаль» (Open Document Format) Интерактивные тесты
Ссылки на свободно распространяемое программное обеспечение:
§ 2.5. Алгоритмы управления Презентация «Алгоритмы управления» Презентация «Алгоритмы управления» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
Интерактивный тест «Алгоритмизация и программирование» Тест 2 Глава 3. § 3.1. Электронные таблицы Презентация «Электронные таблицы» Презентация «Электронные таблицы» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
§ 3.2. Организация вычислений в электронных таблицах Презентация «Организация вычислений в электронных таблицах» Презентация «Организация вычислений в электронных таблицах» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
§ 3. Презентация «Средства анализа и визуализации данных» Презентация «Средства анализа и визуализации данных» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
Ссылки на ресурсы ФЦИОР:
Тест 3 Глава 4. § 4.1. Локальные и глобальные компьютерные сети Презентация «Локальные и глобальные компьютерные сети» Презентация «Локальные и глобальные компьютерные сети» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
Ссылки на ресурсы ФЦИОР:
§ 4. Презентация «Всемирная компьютерная сеть Интернет» Презентация «Всемирная компьютерная сеть Интернет» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
§ 4.3. Информационные ресурсы и сервисы Интернета Презентация «Информационные ресурсы и сервисы Интернета» Презентация «Информационные ресурсы и сервисы Интернета» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
§ 4.4. Создание Web-сайта Презентация «Создание Web-сайта» Презентация «Создание Web-сайта» (Open Document Format) Интерактивные тесты
Интерактивный тест «Коммуникационные технологии» Тест 4 Ссылки на ресурсы ЕК ЦОР:
|
Домен и область действия
Область функции представляет собой набор всех ее допустимых входов.
Соглашение о домене гласит, что если домен функции не указан, то
предполагается, что это набор всех действительных чисел, для которых определена функция.
Диапазон функции представляет собой набор всех ее выходов, поскольку входы варьируются в зависимости от весь домен.
Область определения функции $\,f\,$ обозначается через $\,\text{dom}(f)\,$.
Область значений функции $\,f\,$ обозначается $\,\text{ran}(f)\,$.
Поскольку домен и диапазон представляют собой наборов , при сообщении о них необходимо использовать правильное обозначение набора.
Может оказаться полезным просмотреть интервалы и обозначения списка.
Помните, что символ
$\,\mathbb{R}\,$
обозначает множество действительных чисел.
Область определения функции обычно довольно легко определяется по формуле для функции.
Числа, вызывающие деление на ноль, должны быть исключены из домена.
Все, что находится внутри четного корня (квадратный корень, корень четвертой степени и т. д.), должно быть больше или равно нулю.
Диапазон функции обычно труднее определить по формуле.
Часто гораздо проще получить диапазон из графика функции
(это тема будущего раздела).
В этом упражнении вас просят найти диапазон только для очень простых функций.
ПРИМЕРЫ:
Вопрос:
Какова область определения функции $\,f\,$, определяемой равенством $\,f(x) = \sqrt{x+2}\,$?
Решение:
Поскольку любое число внутри квадратного корня должно быть неотрицательным,
мы должны иметь: $\,x+2\ge 0$
Вычитая $\,2\,$ с обеих сторон:
$\,x\ge -2\,$
Таким образом, областью определения является множество всех действительных чисел, которые больше или равны $\,-2\,$.
Использование записи интервала и написание полного математического предложения, чтобы сообщить ответ:
$\,\cssId{s33}{\text{dom}(f)}
\cssId{s34}{= [-2,\infty)}\,$
Вопрос:
Какова область определения функции $\,f\,$, определяемой $\,f(x) = 3\, $?
Решение:
Это постоянная функция!
Независимо от входных данных, на выходе будет число $\,3\,$.
Например:
- $\,f(0) = 3\,$
- $\,f(-2,79) = 3\,$
- $\,f(\pi) = 3\,$
Все действительные числа могут быть входными данными.
Таким образом, используя обозначение интервала,
$\,\cssId{s46}{\text{dom}(f)}
\cssId{s47}{= (-\infty,\infty)}\,$.
В качестве альтернативы вы можете написать
$\,\cssId{s49}{\текст{дом}(е)}
\cssId{s50}{= \mathbb{R}}\,$.
Вопрос:
Каков диапазон функции $\,f\,$, определяемой $\,f(x) = 3\,$?
Решение:
Независимо от входных данных, на выходе будет число $\,3\,$.
Таким образом, диапазон содержит только одно число, $\,3\,$.
Используя нотацию списка,
$\,\cssId{s57}{\text{ран}(f)}
\cssId{s58}{= \{3\}}\,$.
Вопрос:
Каков диапазон функции $\,g\,$, определяемой равенством $\,g(x) = \sqrt{x}\,$?
Решение:
Выходы квадратных корней всегда неотрицательны (больше или равны нулю).
А можно получить 92}}
\cssId{s69}{= 1,528}\,$
Используя запись интервала,
$\,\cssId{s71}{\текст{ран}(г)}
\cssId{s72}{= [0,\infty)}\,$.
Вопрос:
Какова область определения функции $\,f\,$
определяется как $\displaystyle\,f(x) = \frac{-2}{3x+5}\,$?
Решение:
Знаменатель не может быть равен нулю; это единственное ограничение.
Таким образом, мы должны исключить любое значение $\,x\,$, для которого $\,3x + 5 = 0\,$:
$3x + 5 = 0$
$3x = -5$
$x = -\frac53$
Итак, областью определения является множество всех действительных чисел , кроме $\,-\frac53\,$.
То есть мы хотим, чтобы все действительные числа были меньше $\,-\frac53\,$,
вместе со всеми вещественными числами больше $\,-\frac53\,$.
Символ «объединения», $\,\cup\,$, используется для «составления наборов вместе».
Таким образом,
$\,\cssId{s86}{\text{dom}(f)}
\cssId{s87}{= (-\infty,-\frac53)}
\cssId{s88}{\чашка}
\cssId{s89}{(-\frac53,\infty)}\,$.
Это последнее упражнение по Алгебре I.
(Если вы прошли весь курс,
, поздравляем, определенно нужно!)
Отсюда вы можете перейти к
Геометрии.
или же
Алгебра II.
3.2 Область определения и область значений — College Algebra 2e
Цели обучения
В этом разделе вы:
- Найдите область определения функции, заданной уравнением.
- График кусочно определенных функций.
Фильмы ужасов и триллеры популярны и очень часто очень прибыльны. Однако, когда включены высокобюджетные актеры, места съемок и спецэффекты, студии рассчитывают на еще большее количество зрителей, чтобы добиться успеха. Рассмотрим пять главных триллеров/ужасов начала 2000-х: Я легенда , Ганнибал , Кольцо , Проклятие и Заклятие . На рис. 1 показана сумма в долларах, которую каждый из этих фильмов собрал в прокате на момент выхода, а также продажи билетов на фильмы ужасов в целом по годам. Обратите внимание, что мы можем использовать данные для создания функции суммы, заработанной каждым фильмом, или общих продаж билетов на все фильмы ужасов по годам. При создании различных функций с использованием данных мы можем идентифицировать различные независимые и зависимые переменные, а также анализировать данные и функции для определения домена и диапазона. В этом разделе мы исследуем методы определения области определения и диапазона таких функций.
На рис. 1 показана сумма в долларах, которую каждый из этих фильмов собрал в прокате на момент выхода, а также продажи билетов на фильмы ужасов в целом по годам. Обратите внимание, что мы можем использовать данные для создания функции суммы, заработанной каждым фильмом, или общих продаж билетов на все фильмы ужасов по годам. При создании различных функций с использованием данных мы можем идентифицировать различные независимые и зависимые переменные, а также анализировать данные и функции для определения домена и диапазона. В этом разделе мы исследуем методы определения области определения и диапазона таких функций.
Рисунок 1 На основе данных, собранных www.the-numbers.com. 3
Нахождение области определения функции, определяемой уравнением
В разделе «Функции и обозначения функций» мы познакомились с понятиями домена и диапазона. В этом разделе мы попрактикуемся в определении доменов и диапазонов для конкретных функций. Имейте в виду, что при определении доменов и диапазонов нам необходимо учитывать, что физически возможно или значимо в реальных примерах, таких как продажи билетов и год в приведенном выше примере с фильмом ужасов. Мы также должны рассмотреть, что математически разрешено. Например, мы не можем включать какое-либо входное значение, которое приводит к извлечению четного корня из отрицательного числа, если домен и диапазон состоят из действительных чисел. Или в функции, выраженной в виде формулы, мы не можем включить какое-либо входное значение в область определения, которая привела бы к делению на 0,9.0009
Имейте в виду, что при определении доменов и диапазонов нам необходимо учитывать, что физически возможно или значимо в реальных примерах, таких как продажи билетов и год в приведенном выше примере с фильмом ужасов. Мы также должны рассмотреть, что математически разрешено. Например, мы не можем включать какое-либо входное значение, которое приводит к извлечению четного корня из отрицательного числа, если домен и диапазон состоят из действительных чисел. Или в функции, выраженной в виде формулы, мы не можем включить какое-либо входное значение в область определения, которая привела бы к делению на 0,9.0009
Мы можем представить домен как «область хранения», содержащую «сырье» для «функциональной машины», а ассортимент — как еще одну «область хранения» продуктов машины. См. рис. 2.
Рис. 2
Мы можем записать домен и диапазон в интервальной нотации, которая использует значения в квадратных скобках для описания набора чисел. В обозначении интервала мы используем квадратную скобку [ когда набор включает конечную точку, и круглую скобку (, чтобы указать, что конечная точка либо не включена, либо интервал неограничен. Например, если у человека есть 100 долларов, чтобы потратить, ему нужно будет выразите интервал, который больше 0 и меньше или равен 100, и запишите (0,100].(0,100). Мы обсудим запись интервала более подробно позже.
Например, если у человека есть 100 долларов, чтобы потратить, ему нужно будет выразите интервал, который больше 0 и меньше или равен 100, и запишите (0,100].(0,100). Мы обсудим запись интервала более подробно позже.
Обратимся к поиску области определения функции, уравнение которой приведено. Часто для нахождения области определения таких функций необходимо запомнить три разные формы. Во-первых, если функция не имеет знаменателя или нечетного корня, подумайте, могут ли области определения состоять из всех действительных чисел. Во-вторых, если в уравнении функции есть знаменатель, исключите значения в области значений, при которых знаменатель равен нулю. В-третьих, если есть четный корень, рассмотрите возможность исключения значений, которые сделали бы подкоренное число отрицательным.
Перед тем, как мы начнем, давайте рассмотрим правила записи интервалов:
- Первым записывается наименьшее число из интервала.
- Наибольшее число в интервале записывается вторым после запятой.

- Скобки ( или ) используются для обозначения того, что значение конечной точки не включено, что называется эксклюзивным.
- Скобки [ или ] используются для указания того, что значение конечной точки включено, что называется включением.
См. рис. 3, где представлена сводка обозначений интервалов.
Рисунок 3
Пример 1
Нахождение области определения функции в виде набора упорядоченных пар
Найдите область определения следующей функции: {(2,10),(3,10),(4,20),(5,30),( 6,40)}{(2,10),(3,10),(4,20),(5,30),(6,40)} .
Решение
Сначала определите входные значения. Входное значение является первой координатой в упорядоченной паре. Ограничений нет, так как упорядоченные пары просто перечислены. Область определения — это множество первых координат упорядоченных пар.
{2,3,4,5,6}{2,3,4,5,6}
Попытайся #1
Найдите область определения функции:
{(−5,4),(0,0),(5,−4),(10,−8),(15,−12)}{(−5 ,4),(0,0),(5,−4),(10,−8),(15,−12)}
Как
Для заданной функции, записанной в виде уравнения, найдите область определения.
- Определите входные значения.
- Определите любые ограничения на ввод и исключите эти значения из домена.
- Запишите домен в форме интервала, если это возможно.
Пример 2
Нахождение области определения функции
Нахождение области определения функции f(x)=x2−1.f(x)=x2−1.
Решение
Входное значение, показанное переменной xx в уравнении, возводится в квадрат, а затем результат уменьшается на единицу. Любое действительное число можно возвести в квадрат, а затем уменьшить на единицу, поэтому ограничений на область определения этой функции нет. Домен — это множество действительных чисел.
В интервальной форме область определения ff равна (−∞,∞).(−∞,∞).
Попытайся #2
Найдите область определения функции: f(x)=5−x+x3.f(x)=5−x+x3.
Как
Дана функция, записанная в виде уравнения, включающего дробь, найти область определения.
- Определите входные значения.
- Определите любые ограничения на ввод. Если в формуле функции есть знаменатель, приравняйте знаменатель к нулю и найдите xx. Если формула функции содержит четный корень, установите подкоренное число больше или равное 0, а затем решите.
- Запишите домен в форме интервала, исключив из домена все ограниченные значения.
Пример 3
Нахождение области определения функции, содержащей знаменатель
Нахождение области определения функции f(x)=x+12−x.f(x)=x+12−x.
Решение
Когда есть знаменатель, мы хотим включить только значения ввода, которые не заставляют знаменатель быть равным нулю. Итак, мы установим знаменатель равным 0 и найдем x.x.
2-x=0-x=-2x=22-x=0-x=-2x=2
Теперь мы исключим 2 из домена. Ответами являются все действительные числа, где x<2x<2 или x>2x>2, как показано на рисунке 4. Мы можем использовать символ, известный как объединение, ∪,∪, чтобы объединить два множества. В интервальных обозначениях запишем решение: (−∞,2)∪(2,∞).(−∞,2)∪(2,∞).
Мы можем использовать символ, известный как объединение, ∪,∪, чтобы объединить два множества. В интервальных обозначениях запишем решение: (−∞,2)∪(2,∞).(−∞,2)∪(2,∞).
Рисунок 4
Попытайся #3
Найдите область определения функции: f(x)=1+4x2x−1.f(x)=1+4x2x−1.
Как
Для заданной функции, записанной в виде уравнения с четным корнем, найти область определения.
- Определите входные значения.
- Поскольку имеется четный корень, исключите все действительные числа, которые приводят к отрицательному числу в подкоренном члене. Установите подкоренную часть больше или равной нулю и найдите x.x.
- Решение(я) являются областью определения функции. Если возможно, запишите ответ в интервальной форме.
Пример 4
Нахождение области определения функции с четным корнем
Нахождение области определения функции f(x)=7−x. f(x)=7−x.
f(x)=7−x.
Решение
Если в формуле есть четный корень, мы исключаем любые действительные числа, которые приводят к отрицательному числу в подкоренном члене.
Установите подкоренное число больше или равное нулю и найдите x.x.
7-x≥0-x≥-7x≤77-x≥0-x≥-7x≤7
Теперь мы исключим из домена любое число больше 7. Все ответы представляют собой действительные числа, меньшие или равные 7,7, или (−∞,7].(−∞,7].
Попытайся #4
Найдите область определения функции f(x)=5+2x.f(x)=5+2x.
вопросы и ответы
Могут ли быть функции, в которых домен и диапазон вообще не пересекаются?
Да. Например, функция f(x)=-1xf(x)=-1x имеет множество всех положительных действительных чисел в качестве области определения, но множество всех отрицательных действительных чисел в качестве диапазона. Как более крайний пример, входы и выходы функции могут быть совершенно разными категориями (например, названия дней недели в качестве входов и числа в качестве выходов, как на графике посещаемости), в таких случаях домен и диапазон не имеют общих элементов.
Как более крайний пример, входы и выходы функции могут быть совершенно разными категориями (например, названия дней недели в качестве входов и числа в качестве выходов, как на графике посещаемости), в таких случаях домен и диапазон не имеют общих элементов.
Использование нотаций для указания домена и диапазона
В предыдущих примерах мы использовали неравенства и списки для описания области определения функций. Мы также можем использовать неравенства или другие операторы, которые могут определять наборы значений или данных, чтобы описать поведение переменной в нотации построителя наборов. Например, {x|10≤x<30}{x|10≤x<30} описывает поведение xx в нотации построителя наборов. Фигурные скобки {}{} читаются как «набор», а вертикальная черта | читается как «такой, что», поэтому мы могли бы прочитать {x|10≤x<30}{x|10≤x<30} как «множество x — такие значения, что 10 меньше или равно x,x, а xx меньше 30».
На рис. 5 сравниваются обозначения неравенства, обозначения построителя множеств и обозначения интервалов.
5 сравниваются обозначения неравенства, обозначения построителя множеств и обозначения интервалов.
Рисунок 5
Чтобы объединить два интервала, используя нотацию неравенства или нотацию построителя множеств, мы используем слово «или». Как мы видели в предыдущих примерах, мы используем символ объединения ∪,∪ для объединения двух несвязанных интервалов. Например, объединение множеств {2,3,5}{2,3,5} и {4,6}{4,6} это набор {2,3,4,5,6}.{2,3,4,5,6}. Это множество всех элементов, принадлежащих одному или другой (или оба) из двух оригинальных комплектов. Для наборов с конечным числом таких элементов элементы не обязательно должны быть перечислены в порядке возрастания числового значения. Если исходные два набора имеют некоторые общие элементы, эти элементы должны быть перечислены только один раз в объединенном наборе. Для наборов действительных чисел на интервалах другим примером объединения является
.{х| |x|≥3}=(−∞,−3]∪[3,∞){x| |x|≥3}=(−∞,−3]∪[3,∞)
Нотация Set-Builder и интервальная нотация
Нотация построителя наборов — это метод определения набора элементов, удовлетворяющих определенному условию. Он принимает форму {x|утверждение о x}{x|утверждение о x}, которое читается как «множество всех xx, таких, что утверждение о xx истинно». Например,
Он принимает форму {x|утверждение о x}{x|утверждение о x}, которое читается как «множество всех xx, таких, что утверждение о xx истинно». Например,
{x|4 Интервальное обозначение — это способ описания наборов, включающих все действительные числа между нижним пределом, который может быть или не быть. включены и верхний предел, который может быть включен или не включен. Значения конечной точки перечислены в скобках или круглых скобках. Квадратная скобка указывает на включение в набор, а скобка указывает на исключение из набора. Например, (4,12](4,12] Имея линейный график, опишите набор значений, используя интервальную запись. Опишите интервалы значений, показанные на рис. 6, используя обозначения неравенства, обозначения построителя множеств и обозначения интервалов. Рисунок
6 Для описания значений x,x, включенных в показанные интервалы, мы бы сказали: «xx — действительное число, большее или равное 1 и меньшее или равное 3, или действительное число, большее 5». Как

Пример
5
Описание наборов на линии действительных чисел
Решение
Неравенство 1≤x≤3orx>51≤x≤3orx>5 Обозначение конструктора наборов {x|1≤x≤3orx>5}{x|1≤x≤3orx>5} Обозначение интервала [1,3]∪(5,∞)[1,3]∪(5,∞)
Помните, что при записи или чтении обозначения интервала использование квадратных скобок означает, что граница включена в набор. Использование круглых скобок означает, что граница не включена в набор.
Использование круглых скобок означает, что граница не включена в набор.
Попытайся #5
Учитывая рисунок 7, укажите графическое множество в
- ⓐ слова
- ⓑ нотация конструктора наборов
- ⓒ обозначение интервала
Рисунок 7
Поиск домена и диапазона по графикам
Еще один способ определить область и диапазон функций — использовать графики. Поскольку домен относится к набору возможных входных значений, домен графика состоит из всех входных значений, показанных на x -ось. Диапазон представляет собой набор возможных выходных значений, которые показаны на оси и . Имейте в виду, что если график выходит за пределы видимой части графика, домен и диапазон могут быть больше, чем видимые значения. См. рис. 8.
Рис. 8
Мы можем заметить, что граф простирается по горизонтали от −5−5 вправо без границ, поэтому область определения равна [−5,∞). [−5,∞). Вертикальный экстент графика — это все значения диапазона 55 и ниже, поэтому диапазон равен (−∞,5].(−∞,5]. Обратите внимание, что домен и диапазон всегда записываются от меньших к большим значениям или слева направо. вправо для домена и от нижней части графика к верхней части графика для диапазона.
[−5,∞). Вертикальный экстент графика — это все значения диапазона 55 и ниже, поэтому диапазон равен (−∞,5].(−∞,5]. Обратите внимание, что домен и диапазон всегда записываются от меньших к большим значениям или слева направо. вправо для домена и от нижней части графика к верхней части графика для диапазона.
Пример 6
Поиск домена и диапазона по графику
Найти домен и диапазон функции ff график которого показан на рисунке 9.
Рисунок 9
Решение
Мы можем заметить, что горизонтальная протяженность графика составляет от –3 до 1, поэтому домен ff равно (−3,1].(−3,1].
Вертикальный размер графика составляет от 0 до –4, поэтому диапазон равен [−4,0].[−4,0). См. рис. 10.
Рис. 10
Пример 7
Нахождение области определения и диапазона по графику добычи нефти
Нахождение области определения и диапазона функции ff, график которой показан на рисунке 11.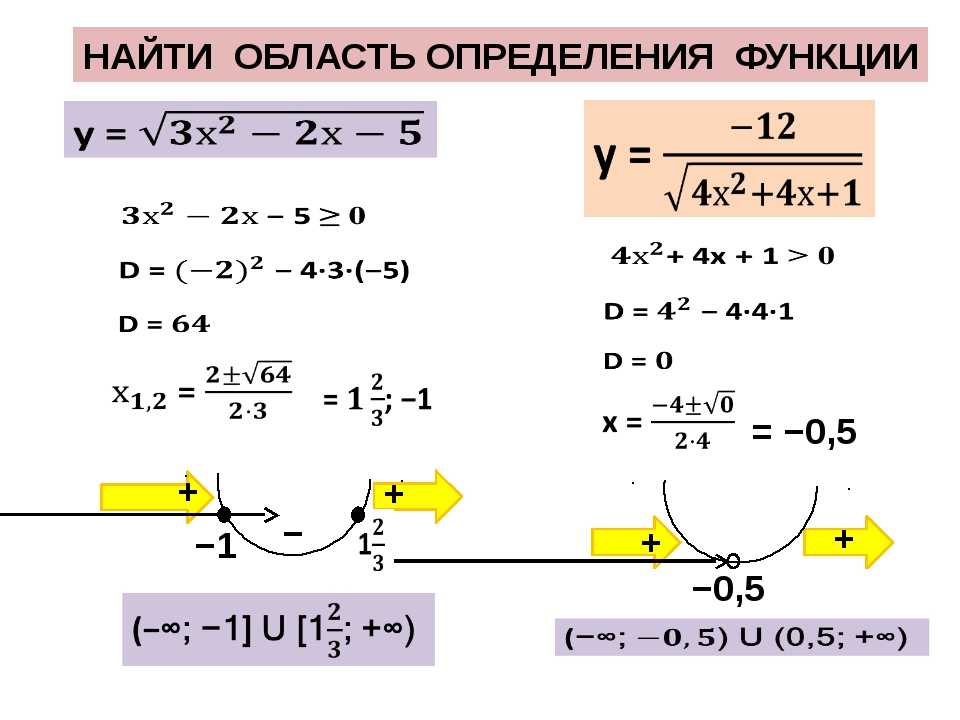
Рисунок 11 (кредит: модификация работы Управления энергетической информации США) 4
Решение
Входное количество по горизонтальной оси — это «годы», которые мы представляем с помощью переменной tt для времени. Выходное количество — «тысячи баррелей нефти в день», которое мы представляем с помощью переменной bb для баррелей. График может продолжаться влево и вправо за пределами того, что просматривается, но на основе видимой части графика мы можем определить домен как 1973≤t≤20081973≤t≤2008, а диапазон составляет примерно 180≤b≤2010,180≤b≤2010.
В интервальных обозначениях домен равен [1973, 2008], а диапазон равен примерно [180, 2010]. Для домена и диапазона мы аппроксимируем наименьшее и наибольшее значения, поскольку они не попадают точно на линии сетки.
Попытайся #6
Учитывая рисунок 12, определите домен и диапазон, используя обозначение интервала.
Рисунок 12
вопросы и ответы
Могут ли домен и диапазон функции совпадать?
Да. Например, область определения и диапазон функции кубического корня — это множество всех действительных чисел.
Поиск доменов и диапазонов функций набора инструментов
Теперь мы вернемся к нашему набору функций набора инструментов, чтобы определить домен и диапазон каждой из них.
Рисунок 13 Для постоянной функции f(x)=c,f(x)=c область определения состоит из всех действительных чисел; ограничений на ввод нет. Единственным выходным значением является константа c,c, поэтому диапазон представляет собой набор {c}{c}, содержащий этот единственный элемент. В записи интервала это записывается как [c,c],[c,c], интервал, который начинается и заканчивается на c.c.
Рисунок
14
Для функции тождества f(x)=x,f(x)=x ограничений на x. x нет. И домен, и диапазон являются набором всех действительных чисел.
x нет. И домен, и диапазон являются набором всех действительных чисел.
Рисунок 15 Для функции абсолютного значения f(x)=|x|,f(x)=|x| ограничений на x.x нет. Однако, поскольку абсолютное значение определяется как расстояние от 0, выходное значение может быть только больше или равно 0.
Рисунок 16 Для квадратичной функции f(x)=x2,f(x)=x2 областью определения являются все действительные числа, поскольку горизонтальная протяженность графика представляет собой всю линию действительных чисел. Поскольку график не содержит отрицательных значений диапазона, диапазон состоит только из неотрицательных действительных чисел.
Рисунок
17
Для кубической функции f(x)=x3,f(x)=x3 областью определения являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. То же самое относится к вертикальному размеру графика, поэтому домен и диапазон включают все действительные числа.
Рисунок 18 Для обратной функции f(x)=1x,f(x)=1x мы не можем делить на 0, поэтому мы должны исключить 0 из области определения. Кроме того, 1, деленная на любое значение, никогда не может равняться 0, поэтому диапазон также не будет включать 0. В нотации построителя множеств мы могли бы также записать {x|x≠0}, {x|x≠0}, множество все действительные числа, отличные от нуля.
Рисунок 19 Для функции обратного квадрата f(x)=1×2,f(x)=1×2 мы не можем делить на 0,0, поэтому мы должны исключить 00 из области определения. Также нет xx, который может дать на выходе 0, поэтому 0 также исключается из диапазона. Обратите внимание, что выход этой функции всегда положителен из-за квадрата в знаменателе, поэтому диапазон включает только положительные числа.
Рисунок
20
Для функции квадратного корня f(x)=x,f(x)=x мы не можем извлечь квадратный корень из отрицательного действительного числа, поэтому домен должен быть 0 или больше. Диапазон также исключает отрицательные числа, потому что квадратный корень из положительного числа xx определяется как положительный, даже несмотря на то, что квадрат отрицательного числа -x-x также дает нам x.x.
Диапазон также исключает отрицательные числа, потому что квадратный корень из положительного числа xx определяется как положительный, даже несмотря на то, что квадрат отрицательного числа -x-x также дает нам x.x.
Рисунок 21 Для функции кубического корня f(x)=x3,f(x)=x3 домен и диапазон включают все действительные числа. Обратите внимание, что нет проблем с извлечением кубического корня или любого корня из нечетного целого числа из отрицательного числа, и результирующий результат будет отрицательным (это нечетная функция).
Как
Имея формулу функции, определите область определения и область значений.
- Исключить из домена любые входные значения, которые приводят к делению на ноль.
- Исключить из домена любые входные значения, которые имеют недействительные (или неопределенные) числовые выходы.
- Используйте допустимые входные значения для определения диапазона выходных значений.

- Посмотрите на график функции и табличные значения, чтобы подтвердить фактическое поведение функции.
Пример 8
Поиск домена и диапазона с помощью функций Toolkit
Найдите домен и диапазон f(x)=2×3-x.f(x)=2×3-x.
Решение
Ограничений по домену нет, так как любое действительное число можно возвести в куб, а затем вычесть из результата.
Домен (−∞,∞)(−∞,∞), а также диапазон (−∞,∞).(−∞,∞).
Пример 9
Нахождение домена и диапазона
Найдите домен и диапазон f(x)=2x+1.f(x)=2x+1.
Решение
Мы не можем вычислить функцию при −1−1, потому что деление на ноль не определено. Область определения равна (−∞,−1)∪(−1,∞).(−∞,−1)∪(−1,∞). Поскольку функция никогда не равна нулю, мы исключаем 0 из диапазона. Диапазон равен (−∞,0)∪(0,∞).(−∞,0)∪(0,∞).
Пример 10
Нахождение домена и диапазона
Найдите домен и диапазон f(x)=2x+4. f(x)=2x+4.
f(x)=2x+4.
Решение
Мы не можем извлечь квадратный корень из отрицательного числа, поэтому значение внутри радикала должно быть неотрицательным.
x+4≥0когда x≥−4x+4≥0когда x≥−4
Область определения f(x)f(x) равна [−4,∞).[−4,∞).
Затем мы находим диапазон. Мы знаем, что f(−4)=0,f(−4)=0, и значение функции увеличивается с увеличением xx без какого-либо верхнего предела. Мы заключаем, что область значений ff равна [0,∞).[0,∞).
Анализ
На рис. 22 представлена функция f.f.
Рисунок 22
Попытайся #7
Найдите домен и диапазон f(x)=−2−x.f(x)=−2−x.
Графики кусочно-определяемых функций
Иногда мы сталкиваемся с функцией, которая требует более одной формулы для получения заданного вывода. Например, в функциях инструментария мы ввели функцию абсолютного значения f(x)=|x|. f(x)=|x|. С доменом всех действительных чисел и диапазоном значений, большим или равным 0, абсолютное значение может быть определено как величина или модуль значения действительного числа независимо от знака. Это расстояние от 0 на числовой прямой. Все эти определения требуют, чтобы выходной сигнал был больше или равен 0,9.0009
f(x)=|x|. С доменом всех действительных чисел и диапазоном значений, большим или равным 0, абсолютное значение может быть определено как величина или модуль значения действительного числа независимо от знака. Это расстояние от 0 на числовой прямой. Все эти определения требуют, чтобы выходной сигнал был больше или равен 0,9.0009
Если мы вводим 0 или положительное значение, вывод совпадает с вводом.
f(x)=xifx≥0f(x)=xifx≥0
Если мы вводим отрицательное значение, вывод будет противоположен вводу.
f(x)=-xifx<0f(x)=-xifx<0
Поскольку для этого требуются два разных процесса или части, функция абсолютного значения является примером кусочной функции. Кусочная функция — это функция, в которой используется более одной формулы для определения выходных данных для разных частей области.
Мы используем кусочные функции для описания ситуаций, в которых правило или отношение изменяются, когда входное значение пересекает определенные «границы». Например, в бизнесе мы часто сталкиваемся с ситуациями, когда цена за единицу определенного товара снижается, когда количество заказанного товара превышает определенное значение. Налоговые скобки — еще один реальный пример кусочных функций. Например, рассмотрим простую налоговую систему, в которой доходы до 10 000 долларов облагаются налогом по ставке 10%, а любой дополнительный доход облагается налогом по ставке 20%. Налог на общий доход SS будет составлять 0,1S0,1S, если S≤10 000 долларов СШАS≤10 000 долларов США, и 1000 долларов США+0,2(S−10 000 долларов США) 1000 долларов США+0,2(S−10 000 долларов США), если S>10 000 долларов США.S>10 000 долларов США.
Налоговые скобки — еще один реальный пример кусочных функций. Например, рассмотрим простую налоговую систему, в которой доходы до 10 000 долларов облагаются налогом по ставке 10%, а любой дополнительный доход облагается налогом по ставке 20%. Налог на общий доход SS будет составлять 0,1S0,1S, если S≤10 000 долларов СШАS≤10 000 долларов США, и 1000 долларов США+0,2(S−10 000 долларов США) 1000 долларов США+0,2(S−10 000 долларов США), если S>10 000 долларов США.S>10 000 долларов США.
Кусочная функция
Кусочная функция — это функция, в которой для определения выходных данных используется более одной формулы. У каждой формулы есть свой домен, а домен функции представляет собой объединение всех этих меньших доменов. Обозначим эту идею следующим образом:
f(x)={формула 1 если xis в домене 1формула 2 если xis в домене 2формула 3 если xis в домене 3f(x)={формула 1 если xis в домене 1формула 2 если xis в домене 1формула 2 если xis в домене domain 2formula 3 если xis в домене 3
В кусочной записи функция абсолютного значения равна
|x|={x if x≥0−x if x<0|x|={x if x≥0-x if x<0
Как
Дана кусочная функция, напишите формулу и определите область определения для каждого интервала.
- Определите интервалы, для которых применяются разные правила.
- Определите формулы, описывающие, как вычислить выход из входа в каждом интервале.
- Используйте фигурные скобки и операторы if для записи функции.
Пример 11
Написание кусочной функции
Музей берет 5 долларов с человека за экскурсию с группой от 1 до 9 человек или фиксированную плату 50 долларов за группу из 10 и более человек. Напишите функцию, связывающую количество людей n,n со стоимостью C.C.
Решение
Потребуются две разные формулы. Для n — значения меньше 10, C=5n.C=5n. Для значений nn, равных 10 или больше, C=50.C=50.
C(n)={5nif0 Функция представлена на рисунке 23. График представляет собой диагональную линию от n=0n=0 до n=10n=10 и константу после нее. Рисунок
23 Компания сотовой связи использует приведенную ниже функцию для определения стоимости C,C в долларах за gg гигабайт передачи данных. C(g)={25if0 Найти стоимость использования 1,5 гигабайта данных и стоимость использования 4 гигабайт данных. Чтобы найти стоимость использования 1,5 гигабайт данных, C(1,5),C(1,5), мы сначала смотрим, к какой части области относятся наши входные данные. Поскольку 1,5 меньше 2, мы используем первую формулу. C(1,5)=25$C(1,5)=25$ Чтобы найти стоимость использования 4 гигабайт данных, C(4),C(4), мы видим, что введенное значение 4 больше 2, поэтому используем вторую формулу. C(4)=25+10(4−2)=45$C(4)=25+10(4−2)=45$ Функция представлена на рисунке 24. Рисунок
24 По заданной кусочной функции нарисуйте график. Нарисуйте график функции. f(x)={x2ifx≤13if1 Каждая функция компонента взята из нашей библиотеки функций инструментария, поэтому мы знаем их формы. На рис. 25 показаны три компонента кусочной функции, построенные в разных системах координат. Рисунок
25
а) f(x)=x2, если x≤1; f(x)=x2, если x≤1; (б) f(x)=3, если 1< x≤2; f(x)=3, если 1< x≤2; (c) f(x)=x, если x>2f(x)=x, если x>2 Теперь, когда мы нарисовали каждую деталь по отдельности, мы объединим их в одной координатной плоскости. См. рис. 26. Рис.
26 Обратите внимание, что график проходит тест вертикальной линии даже при x=1x=1 и x=2x=2, поскольку точки (1,3)(1,3) и (2,2)(2,2 ) не являются частью графика функции, хотя (1,1)(1,1)
и (2,3)(2,3) есть. Нарисуйте следующую кусочную функцию. f(x)={x3ifx<-1-2if-1 Можно ли применить более одной формулы кусочной функции к значению в области? Нет. Каждое значение соответствует одному уравнению в кусочной формуле. 1. Почему домен отличается для разных функций? 2. Как определить область определения функции, определяемой уравнением? 3. Объясните, почему область определения f(x)=x3f(x)=x3 отличается от области определения f(x)=x.f(x)=x. 4. При описании наборов чисел с использованием интервальной записи, когда вы используете круглые скобки и когда вы используете квадратные скобки? 5. Как построить график кусочной функции? В следующих упражнениях найдите область определения каждой функции, используя интервальную запись. 6. f(x)=-2x(x-1)(x-2)f(x)=-2x(x-1)(x-2) 7. f(x)=5−2x2f(x)=5−2×2 8. f(x)=3x−2f(x)=3x−2 9. f(x)=3−6−2xf(x)=3−6−2x 10. f(x)=4−3xf(x)=4−3x 11. f(x)=x2+4f(x)=x2+4 12. f(x)=1−2x3f(x)=1−2×3 13. f(x)=x−13f(x)=x−13 14. f(x)=9x−6f(x)=9x−6 15. f(x)=3x+14x+2f(x)=3x+14x+2 16. f(x)=x+4x−4f(x)=x+4x−4 17. f(x)=x−3×2+9x−22f(x)=x−3×2+9x−22 18. f(x)=1×2−x−6f(x)=1×2−x−6 19. f(x)=2×3-250×2-2x-15f(x)=2×3-250×2-2x-15 20. 5x-35x-3 21. 2х+15-х2х+15-х 22. f(x)=x−4x−6f(x)=x−4x−6 23. f(x)=x−6x−4f(x)=x−6x−4 24. f(x)=xxf(x)=xx 25. f(x)=x2−9xx2−81f(x)=x2−9xx2−81 26. Найдите область определения функции f(x)=2×3−50xf(x)=2×3−50x по: Для следующих упражнений запишите домен и диапазон каждой функции, используя интервальную запись. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. Для следующих упражнений нарисуйте график кусочной функции. Запишите домен в интервальной нотации. 38. f(x)={x+1ifx<−2−2x−3ifx≥−2f(x)={x+1ifx<−2−2x−3ifx≥−2 39. f(x)={2x−1ifx<11+xifx≥1f(x)={2x−1ifx<11+xifx≥1 40. f(x)={x+1ifx<0x−1ifx>0f(x)={x+1ifx<0x−1ifx>0 41. f(x)={3ifx<0xifx≥0f(x)={3ifx<0xifx≥0 42. f(x)={x2 если x<01−x если x>0f(x)={x2 если x<01-x если x>0 43. f(x)={x2x+2ifx<0ifx≥0f(x)={x2x+2ifx<0ifx≥0 44. f(x)={x+1ifx<1x3ifx≥1f(x)={x+1ifx<1x3ifx≥1 45. f(x)={|x|1ifx<2ifx≥2f(x)={|x|1ifx<2ifx≥2 В следующих упражнениях по каждой функции f,f оцените f(−3),f(−2),f(−1),f(−3),f(−2),f(−1), и f(0).f(0). 46. f(x)={x+1ifx<−2−2x−3ifx≥−2f(x)={x+1ifx<−2−2x−3ifx≥−2 47. f(x)={1if x≤-30if x>-3f(x)={1if x≤-30if x>-3 48. f(x)={−2×2+3if x≤−15x−7if x>−1f(x)={−2×2+3if x≤−15x−7if x>−1 В следующих упражнениях для каждой функции f,f оцените f(−1),f(0),f(2),f(−1),f(0),f(2) и f(4 ).f(4). 49. f(x)={7x+3ifx<07x+6ifx≥0f(x)={7x+3ifx<07x+6ifx≥0 50. f(x)={x2−2ifx<24+|x−5|ifx≥2f(x)={x2−2ifx<24+|x−5|ifx≥2 51. f(x)={5xifx<03if0≤x≤3x2ifx>3f(x)={5xifx<03if0≤x≤3x2ifx>3 Для следующих упражнений запишите область определения кусочной функции в интервальной записи. 52. f(x)={x+1ifx<−2−2x−3ifx≥−2f(x)={x+1ifx<−2−2x−3ifx≥−2 53. f(x)={x2−2ifx<1−x2+2ifx>1f(x)={x2−2ifx<1−x2+2ifx>1 54. f(x)={2x−3−3x2ifx<0ifx≥2f(x)={2x−3−3x2ifx<0ifx≥2 55. График y=1x2y=1×2 в окне просмотра [−0,5,−0,1][−0,5,−0,1] и [0,1,0,5].[0,1,0,5]. Определите соответствующий диапазон для смотрового окна. Покажите графики. 56. График y=1xy=1x в окне просмотра [−0,5,−0,1][−0,5,−0,1] и [0,1,0,5].[0,1,0,5]. Определите соответствующий диапазон для смотрового окна. Покажите графики. 57. Предположим, что область значений функции ff равна [−5,8].[−5,8]. Каков диапазон |f(x)|?|f(x)|? 58. Создайте функцию, диапазоном которой являются все неотрицательные действительные числа. 59. Создайте функцию, в которой домен x>2.x>2. 60. Высота снаряда hh зависит от времени его нахождения в воздухе. Высота в футах за tt секунд определяется функцией h(t)=−16t2+96t. 61. Стоимость изготовления xx изделий в долларах определяется функцией C(x)=10x+500.C(x)=10x+500. Задавать вопрос Спросил Изменено
6 лет, 5 месяцев назад Просмотрено
767 раз $\begingroup$ f(x)= $\frac{(\sqrt{x}-\sqrt{x-1} )}{( \sqrt{x}+\sqrt{x-1} )}\;$ первый off $\sqrt{x}$ определено для: $$x > 0 \tag{1}$$ и $\sqrt{x-1}$ определено для: $$x \ge 1 \tag{2}$$ из $(1)$ и $(2)$ мы получаем область определения $f(x)$, которая должна быть $\{x | x\ge 1\}$ Мы нашли области определения элементарных функций, содержащихся в $f(x)$, и пересекли их, чтобы найти область определения $f(x)$. но полагая $x = 0$ получаем $$f(0)= -1$$ почему это решение не содержалось в вышеупомянутом решении? Я всегда нахожу домены составных функций таким образом. Как я могу быть уверен, что некоторые точки, такие как $(0,-1)$ в приведенной выше задаче, все еще не включены в решение? $\endgroup$ 2 $\begingroup$ $f$ — это дробь, а дроби определяются везде, где знаменатель не равен нулю (что так и есть). Числитель определяется, когда $[0,\infty) \cap [1,\infty) = [1,\infty)$, (квадратный корень определяется при $0$), а знаменатель определяется для
$$
\{x : \sqrt{x} + \sqrt{x-1} \neq 0, \, x\geq 0, x\geq 1\} = [1,\infty)
$$
поэтому домен $[1,\infty)$. Таким образом, мы должны видеть, что $f(0)$ не определено. $\endgroup$ 2 $\begingroup$ У нас есть
$$f(x) = \frac{(\sqrt{x}-\sqrt{x-1})}{( \sqrt{x}+\sqrt{x-1})}$$
Домен $f$:
$$D_f = \{ x \in \mathbb{R} : (\sqrt{x}+\sqrt{x-1} \ne 0) \клин (x \ge 0) \клин (x-1 \ge 0 ) \}$$ Анализ
 В этом примере две формулы совпадают в точке встречи, где n=10,n=10, но не все кусочные функции обладают этим свойством.
В этом примере две формулы совпадают в точке встречи, где n=10,n=10, но не все кусочные функции обладают этим свойством. Пример
12
Работа с кусочной функцией
Решение
Анализ
 Мы можем видеть, где функция изменяется от постоянной к смещенной и растянутой идентичности при g=2.g=2. Мы строим графики для различных формул на общем наборе осей, следя за тем, чтобы каждая формула применялась в соответствующей области.
Мы можем видеть, где функция изменяется от постоянной к смещенной и растянутой идентичности при g=2.g=2. Мы строим графики для различных формул на общем наборе осей, следя за тем, чтобы каждая формула применялась в соответствующей области. Как
Пример
13
График кусочной функции
Решение
 Мы можем представить график каждой функции, а затем ограничить график указанной областью. В конечных точках домена мы рисуем открытые кружки, чтобы указать, где конечная точка не включена из-за неравенства меньше или больше; мы рисуем замкнутый круг, где конечная точка включена из-за неравенства «меньше или равно» или «больше или равно».
Мы можем представить график каждой функции, а затем ограничить график указанной областью. В конечных точках домена мы рисуем открытые кружки, чтобы указать, где конечная точка не включена из-за неравенства меньше или больше; мы рисуем замкнутый круг, где конечная точка включена из-за неравенства «меньше или равно» или «больше или равно». Анализ

Попытайся
#8
вопросы и ответы
3.2 Секционные упражнения
Устный

Алгебраический


Графический

Цифровой

Технология

Расширение
Реальные приложения
 h(t)=−16t2+96t.
Какова область определения функции? Что означает домен в контексте проблемы?
h(t)=−16t2+96t.
Какова область определения функции? Что означает домен в контексте проблемы?
Предварительное исчисление алгебры — Как найти область определения этой функции?


Чтобы пояснение было понятнее, рассмотрим в отрицании:
$$\sqrt{x}+\sqrt{x-1} = 0 \Leftrightarrow \sqrt{x-1} = -\sqrt{x}$$
Поскольку $(\forall x \in \mathbb{R}): \sqrt{x} \ge 0 \Rightarrow \sqrt{x-1} = -\sqrt{x}$ неразрешим($\sqrt{x- 1}$ не может быть отрицательным)
Решение $\emptyset$, так как мы учли отрицание, поэтому мы должны снова его инвертировать. Какой результат $\mathbb{R}$ Пусть $D_1$ обозначает первое множество решений, поэтому $D_1 = \mathbb{R}$
Это неравенство уже решено.

 Л. и др. 5-9 кл.)
Л. и др. 5-9 кл.) Л.
Л. Вариант 1
Вариант 1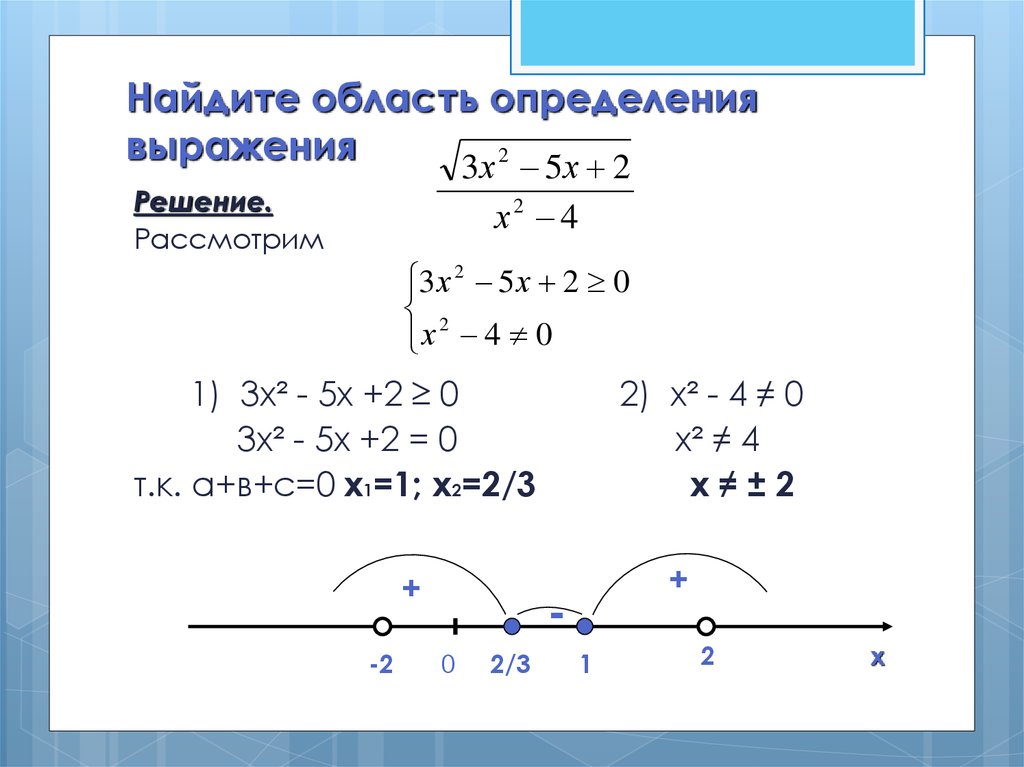 Вариант 1
Вариант 1 Вариант 2
Вариант 2 Вариант 1
Вариант 1 Вариант 1
Вариант 1 Практическая работа
Практическая работа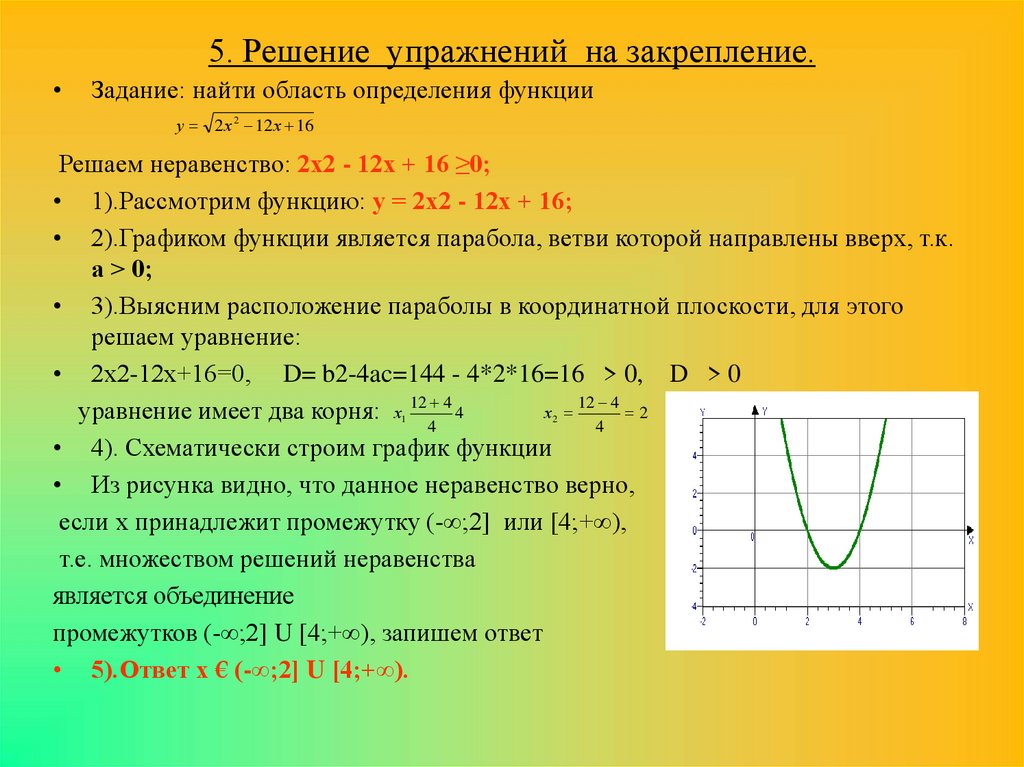 4. Запись вспомогательных алгоритмов на языке Паскаль
4. Запись вспомогательных алгоритмов на языке Паскаль Обработка числовой информации в электронных таблицах
Обработка числовой информации в электронных таблицах Запись формул» (119384)
Запись формул» (119384) 3. Средства анализа и визуализации данных
3. Средства анализа и визуализации данных Коммуникационные технологии
Коммуникационные технологии 2. Всемирная компьютерная сеть Интернет
2. Всемирная компьютерная сеть Интернет Вариант 1
Вариант 1 Вариант 1
Вариант 1