Область определения и множество значений функции: Квадратичная функция, парабола, график, свойства: нули, вершина, ось симметрии, промежутки возрастания, убывания. Тесты

Содержание

Лекция 19. Функция. Область определения и множество значений функции. — Студопедия

Поделись

Функция — одно из важнейших математических понятий.

Определение: Если каждому числу из некоторого множества x поставлено в соответствие единственное число y, то говорят, что на этом множестве задана функция y(x). При этом x называют независимой переменной или аргументом, а y — зависимой переменной или значением функции или простофункцией.

Говорят также, что переменная y является функцией от переменной x.

Обозначив соответствие некоторой буквой, например f, удобно писать: y=f (x), то есть, значение y получается из аргумента x с помощью соответствия f. (Читают: y равно f от x.) Символом f (x) обозначают значение функции, соответствующее значению аргумента, равному x.

Пример 1 Пусть функция задается формулой y=2x²–6. Тогда можно записать, что f(x)=2x²–6. Найдем значения функции для значений х, равных, например, 1; 2,5;–3; т. е. найдем f(1), f(2,5), f(–3):

f(1)=2•1²–6=–4;
f(2,5)=2•2,5²

–6=6,5;
f(–3)=2•(–3)²–6= 12.

Заметим, что в записи вида y=f (x) вместо f употребляют и другие буквы: g, и т. п.

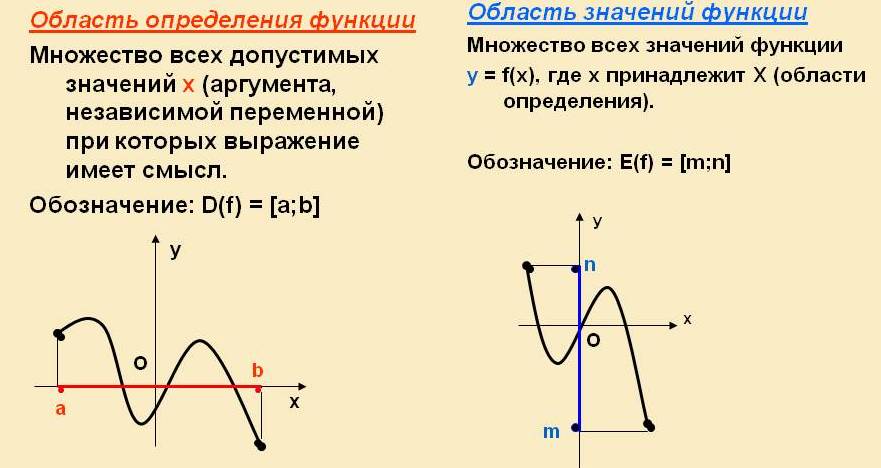
Определение: Область определения функции — это все значения x, при которых существует функция.

Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.

Другими словами, область определения функции, заданной формулой, является все значения аргумента, за исключением тех, которые приводят к действиям, которые мы не можем выполнить. На данный момент мы знаем только два таких действия. Мы не можем делить на нуль и не можем извлечь квадратный корень из отрицательного числа.

Определение: Все значения, которые принимает зависимая переменная образуют область значения функции.

Область определения функции, описывающей реальный процесс, зависит от конкретных условий его протекания. Например, зависимость длины l железного стержня от температуры нагревания t выражается формулой , где l

0 начальная длина стержня, а —коэффициент линейного расширения.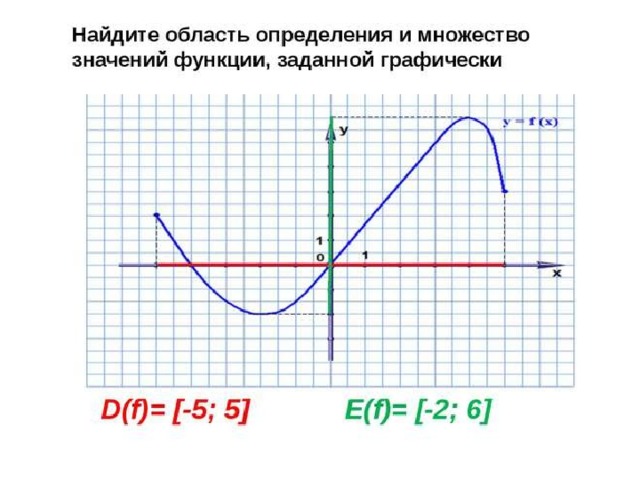

Указанная формула имеет смысл при любых значениях t. Однако, областью определения функцииl=g(t) является промежуток в несколько десятков градусов, для которого справедлив закон линейного расширения.

Пример.

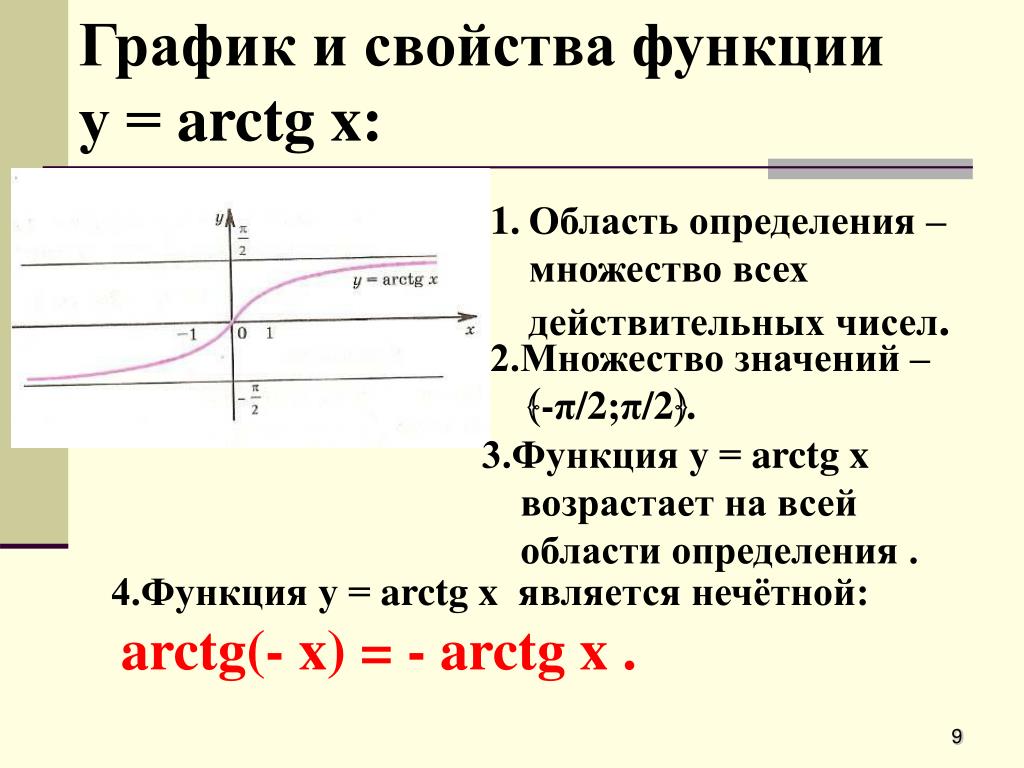
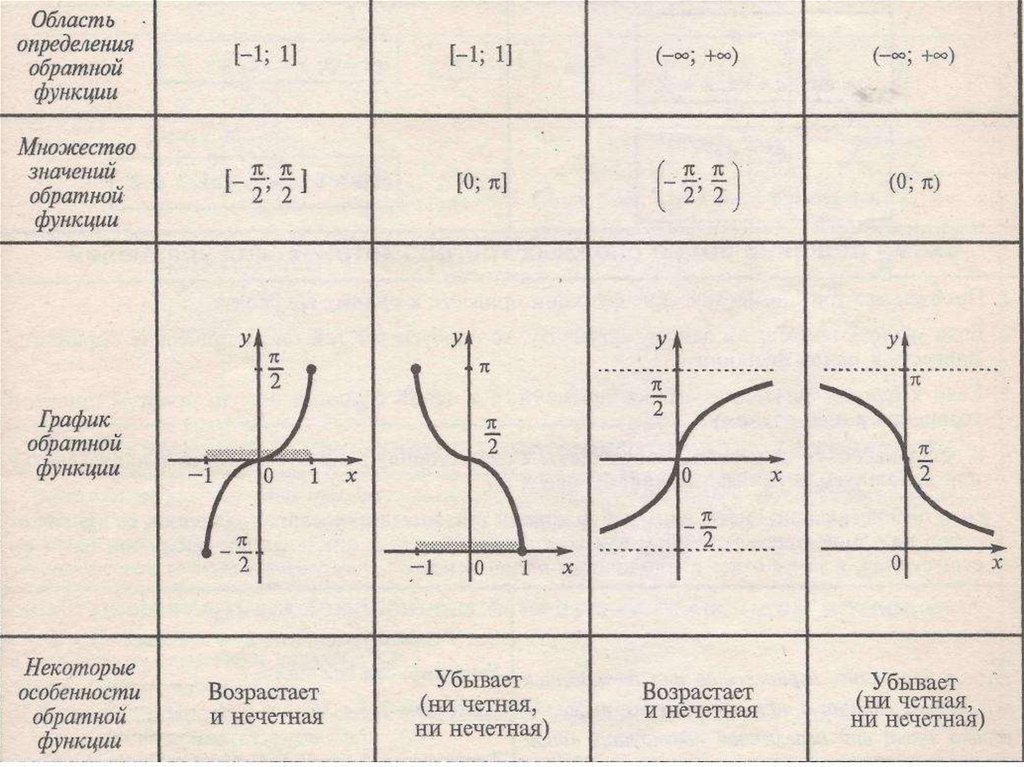
Укажите область значений функции y = arcsinx.

Решение.

Областью определения арксинуса является отрезок [-1; 1]. Найдем наибольшее и наименьшее значение функции на этом отрезке.

Производная положительна для всех x из интервала (-1; 1), то есть, функция арксинуса возрастает на всей области определения. Следовательно, наименьшее значение она принимает при x = -1, а наибольшее при x = 1.

Мы получили область значений функции арксинуса .

Найдите множество значений функции на отрезке [1; 4].

Решение.

Найдем наибольшее и наименьшее значение функции на данном отрезке.

Определим точки экстремума, принадлежащие отрезку [1; 4]:

Вычисляем значения исходной функции на концах отрезка и в точках :

Следовательно, множеством значений функции на отрезке является интервал .

Сейчас покажем, как находить множество значений непрерывной функции y = f(x) на открытых интервалах (a; b), .

Сначала определяем точки экстремума, экстремумы функции, промежутки возрастания и убывания функции на данном интервале. Далее вычисляем односторонние пределы на концах интервала и (или) пределы на бесконечности (то есть, исследуем поведение функции на границах открытого интервала или на бесконечности). Этой информации достаточно, чтобы найти множество значений функции на таких промежутках.

Функция, ее область определения и множество значений. График функции

1. Тема урока: Функция, ее область определения и множество значений. График функции

МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ
Государственное образовательное учреждение
высшего образования Московской области
«Государственный гуманитарно-технологический университет»
Промышленно-экономический колледж
Автор: Савинова Лариса Николаевна,
преподаватель математики

2.

Цель урока:Научиться вычислять частное значение функции, находить ее
область определения и множество значений, строить график
функции.
Содействовать
развитию
математического
мышления
обучающихся.
Побуждать
студентов
к
преодолению
трудностей
в
процессе умственной деятельности.
Развивать культуру устной математической речи, чувство
самоконтроля.
Знания и навыки студентов:
знать
понятие функции, правила нахождения области
определения функции;
уметь
находить частное значение функции, ее область
определения и множество значений, строить графики функций.
При исследовании явлений окружающего мира и в
практической
деятельности
нам
приходится
рассматривать величины различной природы: длину,
площадь, объем, массу, температуру, время и другие. В
зависимости от рассматриваемых условий одни из
величин имеют постоянные числовые значения, у
других эти значения переменные.

Такие величины
соответственно
называются
постоянными
и
переменными.
Математика изучает зависимость между переменными
в процессе их изменения. Например, при изменении
радиуса круга меняется и его площадь, и мы
рассматриваем вопрос об изменении площади круга в
зависимости от изменения его радиуса.
Математическим
выражением
взаимной
связи
реальных величин является идея функциональной
зависимости.
Понятие функции — важнейшее понятие математики

4. 1. Понятие функции

Слово “функция” (от латинского function – исполнение,
осуществление) в математике впервые употреблено
немецким математиком В.Г. Лейбницем.
Пусть даны два непустых множества X и Y. Соответствие
f , которое каждому элементу х Х сопоставляет один и
только один элемент у Y называется функцией и
записывается
у f x , x Х
Говорят еще, что функция f
отображает множество Х
на множество Y.
или
f : X Y.
Например, соответствия f и g, изображенные на
рисунке 1 а и б, являются функциями, а на рисунке 1 в
и г – нет, т.

к. в случае в – не каждому элементу х
соответствует элемент у, а в случае г – не соблюдается
условие однозначности.
Множество Х – область определения функции f – D(f),
множество Y – множество значений функции f – Е( f ).

6. 2. Числовая функция, её частное значение

Если
элементами множеств X и Y
являются
действительные числа, то функцию f
называют
числовой функцией у f x .
Числовой функцией с областью определения D
называется соответствие, при котором каждому числу
х из множества D сопоставляется по некоторому
правилу число у, зависящее от х.
Переменная х называется независимой переменной
или аргументом, а у – зависимой переменной (от х)
или функцией.
Относительно самих величин х и у говорят, что они
находятся в функциональной зависимости и пишут
.
у у x
Частное значение функции у f x при
заданном частном значении аргумента х = а
обозначают
f а или у х а .
2
Пример 1. Найти значение функции f x 2 х 1
при х =3.

f 3 у х 3 2 3 1 17.
2
Решение.
Пример 2. Дано F x 3х 2 .
Найти F 5 , F 0,5 , F a .

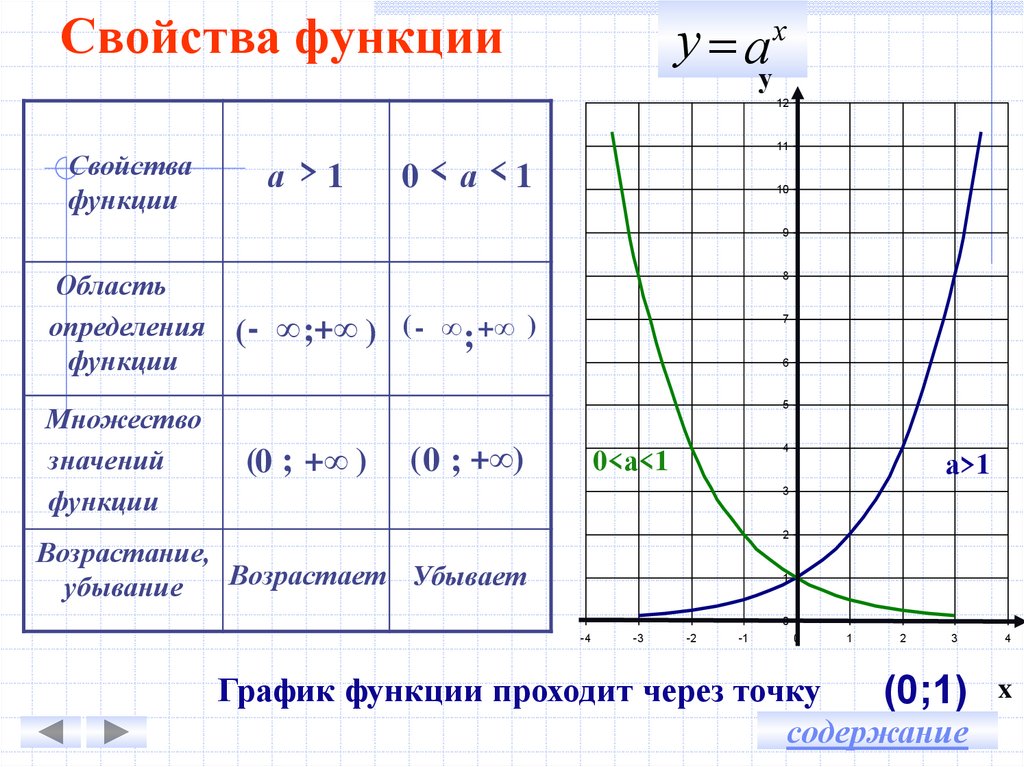
8. 3. Область определения и множество значений функции

Область определения функции – совокупность
всех действительных значений аргумента х, при
которых
функция
определена
и
выражается
действительным числом. Обозначается: D( f )=Х.
Множество чисел
у f x
объединяют в
множество Y и называют множеством значений
функции, т.е. Е f Y .

9. Примеры. Найти область определения функций

1. у х 2 . D y R или D y ; .
Областью определения целой рациональной функции
является множество всех действительных чисел.
2.
у х 3х 10. D y ;
5
2

10. При отыскании области определения дробной функции нужно исключить значения аргумента, при которых знаменатель обращается в нуль

1
3. у .
х
Решение.
Знаменатель обращается в нуль при х 0.
D y ; 0 0; .
Решить самостоятельно :
2
3
1
4.

у
; 5. у
; 6. у
.
1 х
х 4
2х 5
3
7. у 2
.
х 4
Решение.
Знаменатель обращается в нуль при х 2.
D y ; 2 2;2 2; .
2
х 2
8. у
; 9. у 2
.
2
1 х
х 5х 6

12. При отыскании области определения функции, содержащей корень четной степени, нужно исключить значения аргумента, при которых

10. у х 1.
Решение.
х 1 0 х 1.
D y 1; .
Решить самостоятельно :
11. у 2 х 4 ; 12. у х 1.
2

13. При отыскании области определения логарифмической функции нужно исключить значения аргумента, при которых подлогарифмическое

13. у lg x 2 .
Решение.
х 2 0 х 2.
D y 2;
Решить самостоятельно :
14. у lg 2 x 3 ; 15. у log 3 x 9 .
2

14. 4. Способы задания функции

Функция считается заданной , если известна область
определения функции и указано правило, по которому
для каждого значения аргумента можно найти
соответствующее значение функции.
Существуют следующие способы задания функции:
1.

Аналитический – зависимость между аргументом х
и функцией у задается в виде математической
формулы или уравнения. Например, у 2 х3 5 .
х 1
Наиболее совершенный способ в математике,
единственный недостаток – отсутствие наглядности.

15. Например:

Формулой S (r) = πr2 задается функция зависимости площади
круга от радиуса.
Функция ºF (ºC) определяет перевод температуры из градусов
Цельсия в градусы Фаренгейта:
Если деньги положены в банк под p процентов годовых, а сумма,
положенная в банк изначально, равна S0 , то через n лет в банке
будет
– функция от количества лет, на которые
положены средства. Эта формула сложных процентов.
При равномерном движении скорость тела является функцией
времени: s (t) = v · t.
Функция x (t) = A cos (ωt + φ) задает гармонические колебания.
Здесь A – амплитуда колебаний, ω – круговая частота, φ –
начальная фаза.
Функция
называется формулой радиоактивного
распада.

Табличный — значения аргумента и
соответствующие им значения функции записаны
в виде таблицы. Используется на практике для
записи результатов наблюдений и измерений.
Так, значения квадратов, кубов, логарифмов чисел,
тригонометрических функций и т.д. находят с
помощью математических таблиц.
Например, изменение температуры тела больного в
зависимости от времени приведены в таблице:
2.
Температура, °С
36,5
36,8
37,5
38,2
Время суток, час
10
12
14
16

17. 3. Графический — задается график функции.

Графиком функции у f x называется множество
всех точек координатной плоскости М х; f x .
Значения функции у,
соответствующие
значениям аргумента х,
непосредственно
находятся из этого
графика. Преимуществом
графического задания
является его наглядность,
недостатком — неточность.

18. Обратить внимание

Подмножество координатной плоскости является графиком
какой-либо функции, если оно имеет не более одной общей
точки с любой прямой, параллельной оси OY.

Например,
множество, изображенное на рисунке слева не является
графиком функции, так как оно содержит две точки с одной и
той же абсциссой a, но разными ординатами b1 и b2.
Графический способ задания зачастую удобен по сравнению
с аналитическим, так как по графику сразу видно что из себя
представляет функция и можно проанализировать ее
поведение.
4. Словесный способ – состоит в том, что
функциональная зависимость выражается словами.
Пример 1: функция E(x) — целая часть числа x, т.е.
E(x) = [x] — наибольшее из целых чисел, которое не
превышает x. Иными словами, если x = r + q, где r —
целое число и q принадлежит интервалу [0; 1), то [x] = r.
Функция E(x) = [x] постоянна на промежутке [r; r+1) и на
нем [x] = r.
Например, [2,534] = 2,
[47] = 47,
[-0,(23)] = -1.
Очень своеобразно выглядит
график функции у = [х]
Пример 2: функция y = {x} — дробная часть
числа, т.е.
y ={x} = x — [x], где [x] — целая часть числа x.

Или {x} = r + q – r = q
Основными недостатками словесного способа задания
функции являются невозможность вычисления значений
функции при произвольном значении аргумента и
отсутствие наглядности.
Главное преимущество же заключается в возможности
задания тех функций, которые не удается выразить
аналитически.

21. Задание.

1. Указать область определения и область
значений таблично заданной функции:
х
-2
-1
0
1
2
у
9
2
0
2
9
2. Построить график функции
2 при 3 х 0,
у х при 0 х 2
3 при 2 х 4
Вычислить f (-2), f (0,1), f (-3/4), f (3).

22. Задание .

3. Сопоставить каждому графику функции формулу, с
помощью которой эта функция задается

Домен функции: определение, представление и примеры

Функция связывает вход с выходом. Это похоже на машину, которая имеет вход и выход. А выход как-то связан с входом. Есть несколько альтернатив, чтобы думать о функциях, но всегда есть три основных компонента:

Вход
Отношение
Выход

Отношение, в котором каждый вход имеет определенный выход, является математическим определением функции. Функции в математике можно соотнести с реальными операциями принтера. Когда мы вставляем определенное количество бумаги в сочетании с некоторыми командами, мы получаем напечатанные данные на бумаге.

Также читайте о статистике здесь.

Аналогично, для функций мы вводим различные числа и получаем новые числа в результате выполненной операции. Домен и диапазон являются основными символами функции. Домен функции — это входные данные данной функции, с другой стороны, диапазон означает возможные выходные данные, которые мы можем получить.

В этой статье о домене функции мы будем стремиться узнать о значении домена в математике, а также задать вопросы, чтобы понять, как найти домен функции и так далее.

Что такое домен?

Домен в математике можно рассматривать как набор значений, которые входят в функцию; кроме того, диапазон подразумевает все значения, которые выходят.

Функция связывает вход с выходом, т. е. функция связывает каждый элемент множества конкретно с одним элементом другого множества.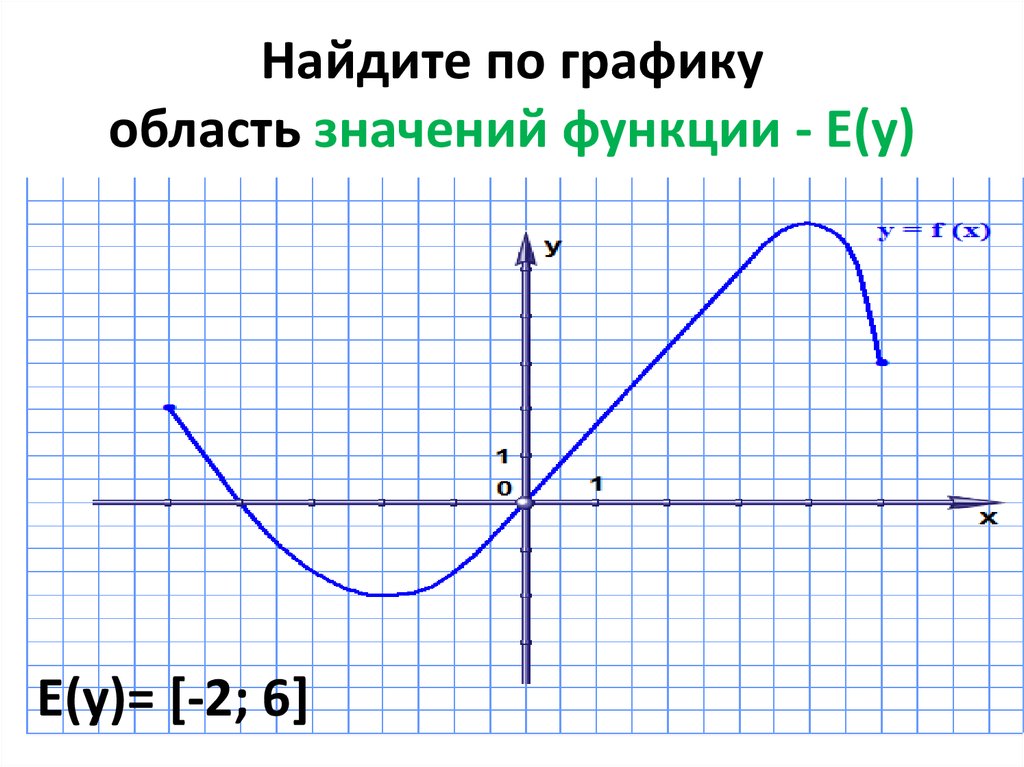 Существуют различные способы представления функций, давайте кратко рассмотрим каждый из них.

Представление функций

Функции должны быть разработаны для отображения значений домена и значений диапазона, а также отношения или связи между ними. Существуют три различные формы представления функций: диаграммы Венна, графические формы и шаблоны реестров. Три шаблона обсуждаются ниже.

Диаграмма Венна

Диаграмма Венна — это мощная форма для описания функции. Диаграммы Венна обычно изображаются двумя кружками со стрелками, объединяющими компоненты в каждом из кружков. Домен показан в одном круге, а значения диапазона помещены в другой. Кроме того, функция указывает стрелки и то, как стрелки связывают различные элементы в двух заданных кругах.

Графическая форма

Функции легко понять, если они представлены в графическом образце с использованием координатных осей. Выражение функции в графической форме помогает нам изучить изменение работы функций, если функция прогрессирует или снижается. Область определения функции представлена по оси x, а диапазон функции отложен по оси y соответственно.

Также читайте о последовательностях и сериях здесь. 9{3}\), функция представляется в виде {(1, 1), (2, 8), (3, 27), (4, 64)}. Здесь первый элемент обозначает домен или значение x, а второй компонент обозначает диапазон или значение f(x) функции.

Зная представление функций, перейдем теперь к более подробному анализу области математики.

Область определения функции

В математике мы можем связать функцию с машиной, которая создает некоторый результат в соответствии с заданным вводом. На примере инструмента для штамповки монет.

Когда мы вставляем монету в инструмент для штамповки монет, в результате получается выдавленный и сплющенный кусок металла. Просмотрев функцию, мы можем соотнести монету и сплющенную часть металла с доменом и диапазоном. В этом примере функция должна быть машиной для чеканки монет.

Точно так же, как устройство для чеканки монет, которое может предложить только один сплющенный кусок металла за раз, функция работает таким же образом, передавая один результат за раз.

Узнайте больше об отношениях и функциях здесь.

Домен и область определения функции

Если f: P → Q является функцией, то множество P называется областью определения функции f, а множество Q обозначается областью определения функции f.

Естественная область определения

Естественная область значений функции обозначает максимальный набор значений, для которых определяется функция, обычно в вещественных числах, но иногда также с целыми или комплексными числами.

Например, основная область определения квадратного корня — это неотрицательные действительные значения, если рассматривать их как функцию действительных чисел. При изучении естественной области множество потенциальных значений функции обычно объявляется ее диапазоном.

Диапазон функции

Диапазон функции — это набор всех ее выходов. Если f: P → Q — функция, то область значений f состоит из тех компонент Q, которые связаны хотя бы с одним элементом P.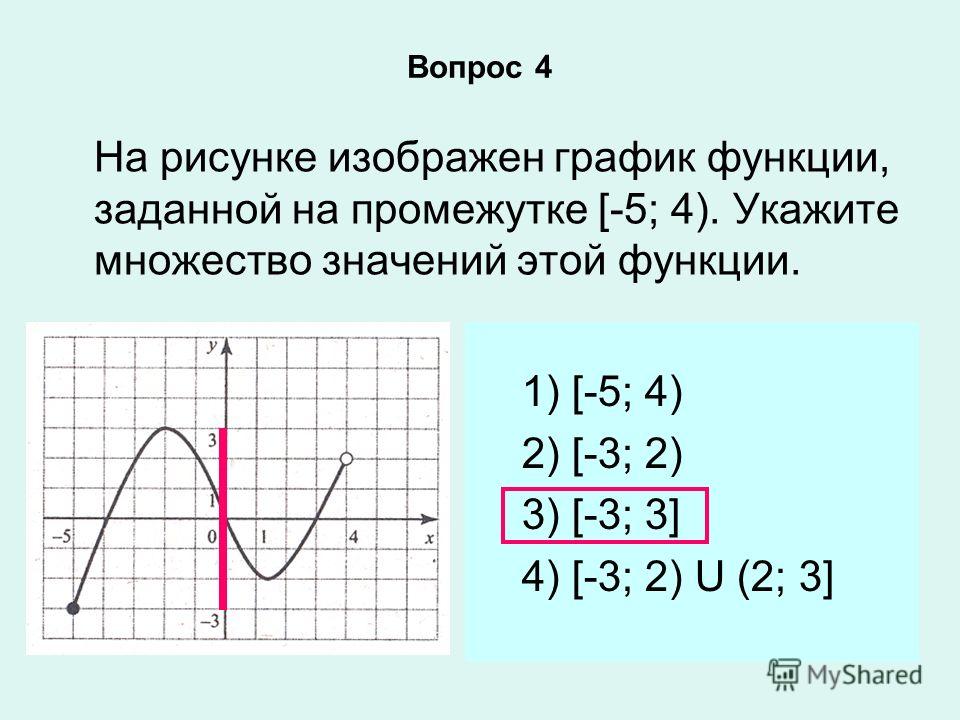 Оно выражается через f(P).

Таким образом, f(P) = {y : y = f(x) для некоторого x ∈ P}

Компоненты области называются прообразами, а компоненты ко-области, которые отображаются, называются картинки. Здесь областью действия функции является множество всех изображений компонентов области.

Как найти домен функции?

Домен, кодовый домен и диапазон — это специальные заголовки для того, что может войти в функцию и что может выйти за ее пределы:

Что может вписаться в функцию, так это определение функциональной области.
То, что может появиться вне функции, называется доменом кода функции.
То, что появляется вне функции, называется диапазоном функции.

Область определения функции можно расположить либо алгебраически, либо графически. Чтобы получить область определения функции алгебраически, нам нужно решить уравнение, чтобы получить значения x. Однако разные типы функций имеют свои средства определения домена.

Пример математики предметной области 1:

Предположим, что X = {2, 3, 4, 5,6}, f: X → Y, где R = {(x,y) : y =3x+1}.

Домен = входные значения данной функции, таким образом, домен = X = {2, 3, 4, 5,6}

Диапазон = выходные значения данной функции = {7, 10, 13, 16, 19 }.

Прочтите эту статью о наборах.

Как найти область определения и область значений уравнения?

Одна вещь, которую следует иметь в виду при определении доменов и диапазонов, заключается в том, что нам необходимо признать, что физически достижимо или значимо в реальных случаях. Мы также обязаны учитывать, что математически допустимо.

Например, мы не можем включить какое-либо входное значение, которое указывает нам брать четный корень числа -ve, если домен и диапазон состоят только из действительных чисел. И наоборот, в функции, выраженной в виде формулы, мы не можем добавить какое-либо входное значение в домен, которое заставит нас делить на ноль. {3}\) будет иметь домен элементов, которые входят в функцию. 9{3}\). Здесь у нас может быть область значений целых чисел, таких как {…,-3,-2,-1,0,1,2,3,…}, для которых диапазоном является множество {…,-27 ,-8,-1,0,1,8,27,…}.

Ознакомьтесь с другими темами по математике здесь.

Возникает вопрос: у каждой ли функции есть домен?

Ответ будет положительным, хотя в более упрощенной математике мы никогда этого не увидим, потому что область определения является чем-то предполагаемым, как и все числа, которые будут работать. Или, если мы рассматриваем целые числа, домен должен быть целым числом и т. д.

Мы можем обратиться к домену и диапазону в интервальной нотации, которая принимает значения в квадратных скобках для определения набора чисел. В записи интервала мы применяем квадратную скобку [], когда набор включает конечную точку, и скобку (), чтобы показать, что конечная точка либо не покрыта, либо данный интервал неограничен.

Решено Пример 4:

Рассмотрим отношение {(2,7),(0,6),(1,5),(3,8),(1,9),(6,10)}

Здесь отношение изображается как набор упорядоченных пар. Домен представляет собой набор координат x, который включает значения {0, 1, 2, 3, 6}, а диапазон подразумевает набор координат y, {7, 6, 5, 8, 9, 10}. Обратите внимание, что элемент домена 1 связан с более чем одним элементом диапазона, (1,5) и (1,9), поэтому это , а не функция.

Решено Пример 5:

Для заданной функции:

Домен содержит множество {A,B,C,E} . Здесь D не входит в домен, так как функция для D не указана.

Диапазоном является множество {3, 2, 5, 6}. 1 не входит в диапазон, так как ни один алфавит в домене не сопоставляется с 1.

Изучите различные концепции линейного графика с помощью этой статьи.

Домен и диапазон из графиков

Другой подход к определению домена и диапазона функций заключается в применении графиков. Для приведенного ниже графика домен указывает на набор вероятных входных значений. Домен графика включает все входные значения, отображаемые на оси X.

С другой стороны, диапазон представляет собой набор возможных выходных значений, представленных на оси Y. Давайте разберемся, как найти домены функций инструментария.

Решено Пример 6:

Давайте рассмотрим пример, чтобы понять, как найти домен и диапазон функции графика:

Для заданной функции графика; домен равен x≥−4, поскольку x не может быть меньше −4. Чтобы выяснить, почему, попробуйте некоторые числа меньше -4, скажем, -7 или -12, и некоторые другие значения, которые больше -4, например, -3 или 6, в вашем калькуляторе, и проверьте ответ.

Единственные, которые будут работать и дадут нам решение, это те, которые больше или эквивалентны -4. Это сделает число под квадратным корнем положительным. 9{Икс}\).

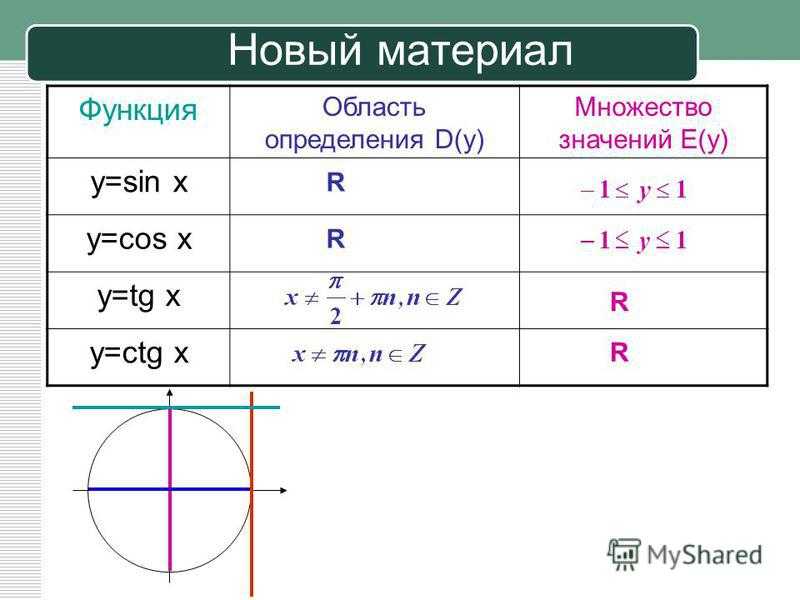
Область тригонометрических функций

Посмотрите на приведенный ниже график функций синуса и косинуса. Мы можем обнаружить, что значение функций колеблется между -1 и 1, и оно определено для всех действительных чисел.

Следовательно, областью применения таких функций является множество R.

Также читайте здесь о многострочных графиках.

Домен функции абсолютного значения

Абсолютная функция говорит y=|ax+b| указывается для всех действительных чисел. Следовательно, область определения функции абсолютного значения включает в себя набор всех действительных чисел.

Рассмотрим пример: |8-x|

|8-х| ≥ 0

8 – x ≥ 0

x ≤ 8.

Для функции абсолютного значения, представленной f(x)=|x|, не существует ограничений на значения x. Однако, поскольку абсолютное значение определяется как расстояние от нуля, результат может быть просто больше или равен нулю.

Область определения функции квадратного корня

Для функции квадратного корня $f(x)=\sqrt{x}$ мы не можем получить квадратный корень из отрицательного действительного числа, поэтому быть нулевым или большим. Если мы включим мнимые числа, все может стать более сложным, однако в большинстве случаев нам требуется учитывать только действительные числа.

Чтобы определить область определения функции квадратного корня, нам нужно решить неравенство x ≥ 0, заменив x подкоренным числом. Давайте возьмем пример того, как вы можете найти домен функции:

Решенный пример 7:

$f(x)=\sqrt{x+6}$.

Здесь задает подкоренное число (т.е. x + 6) равным x в неравенстве.
Это дает нам неравенство x + 6 ≥0.
Это можно решить, вычитая 6 с обеих сторон, что дает вам решение x ≥ −6.
Это означает, что домен содержит все значения x больше или равные -6.
Мы также можем записать это как [−6, ∞). где скобка слева показывает, что −6 является конкретным пределом, а скобки справа показывают, что ∞ таковым не является. Поскольку подкоренное число не может быть значением -ve, нам требуется вычислять только положительные или нулевые значения.

Узнайте больше о пределах и непрерывности здесь.

Область постоянной функции

Для постоянной функции, представленной f(x)=c, домен состоит только из действительных чисел; это означает, что нет никаких ограничений на ввод. Рассмотрим приведенный ниже график для y = 2.

Домен функции идентичности

Для функции идентичности, представленной f(x)=x, снова нет ограничения на значение x. И домен, и диапазон представляют собой совокупность всех действительных чисел. Посмотрите на график ниже.

Также читайте об осях x и y здесь. 9{3}\), домен будет включать все действительные числа, поскольку горизонтальная длина графика — это вся линия действительных чисел.

Область обратной функции

Для обратной функции, представленной $f(x)=\frac{1}{x}$, мы не можем разделить функцию на ноль, поэтому нам нужно исключить ноль из домена.

Домен для такой функции задается как: $(-\infty, 0)\cup (0, \infty)$.

Прочтите эту статью на сайте Locus.

Классификация типов функций

В функциях и типах функций мы познакомились с понятиями домена и диапазона.

В математике область определения функции показывает, для каких значений x функция верна.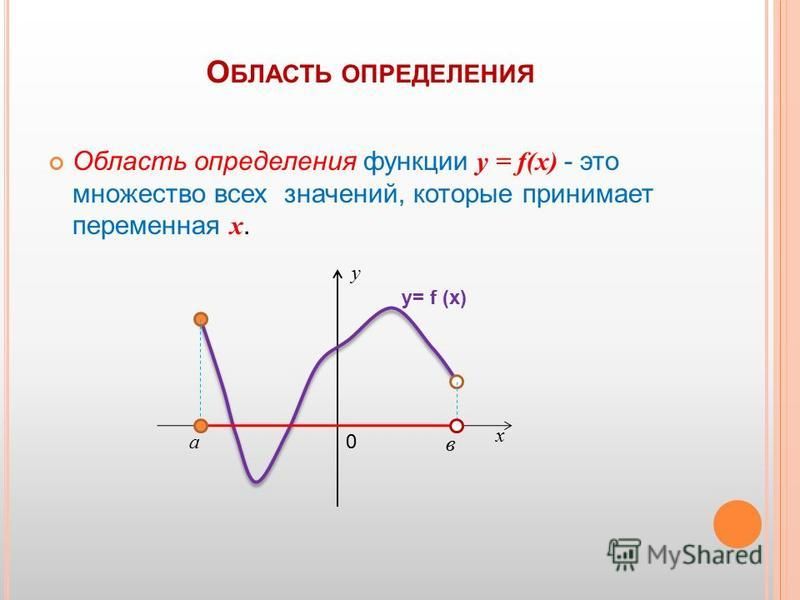 Это указывает на то, что любое значение внутри этого домена будет работать в функции, в то время как любое значение, выходящее за пределы домена, не будет работать в функции.

Чтобы понять значение предметной области в математике, мы должны иметь представление о типах функций для легкого понимания и изучения. Типы функций были классифицированы по разным категориям и показаны в таблице ниже.

Based on Elements

One-One Function
Many-One Function
Onto Function
One-One and Onto Function
Into Function
Constant Function

На основе уравнения

Функция тождества
Линейная функция
Квадратичная функция
Кубическая функция
Полиномиальные функции

На основе диапазона

Функция модуля
Рациональные функции

Составные функции

На основе предметной области

Алгебраические функции
Тригонометрические функции.

Логарифмические функции.

Домен функции: ключевые выводы

Мы можем представить домен как пространство хранения, содержащее исходные вещества для функциональной машины, а диапазон — как еще одно место хранения результатов работы машины.

Часто при нахождении области функций необходимо помнить три различных формы.
Во-первых, если данная функция не имеет знаменателя или четного корня, проверьте, может ли домен включать все действительные числа.
Во-вторых, если в уравнении функции существует знаменатель, исключите значения домена, при которых знаменатель равен нулю.
В-третьих, если в функции есть все четные корни, рассмотрите возможность исключения значений, из-за которых подкоренное число может быть отрицательным.

Прочтите эту статью о линейном неравенстве.

Функция — это отношение, в котором каждый элемент ввода связан ровно с одним компонентом вывода. Функция связывает входы с выходами. Ниже приведены некоторые важные ключевые выводы по этой теме.

Выход : Выход является результатом или ответом функции.
Все выходы вместе называются диапазоном.
Отношение : Отношение — это ассоциация между числами/символами/символами в одном наборе и числами в другом наборе.
Функция управляет элементами из набора, который является доменом, и связывает их с элементами в наборе, который является кодовым доменом.
Зависимая переменная : Зависимой переменной в функции является та, значение которой зависит от одной или нескольких независимых переменных данной функции.
Независимая переменная : Независимая переменная в функции — это та, значение которой не зависит ни от какой другой переменной в функции.
Диаграмма : Диаграмма, иллюстрирующая данные; точнее тот, который объясняет взаимосвязь между двумя или более величинами, измерениями или символами.
Предполагается, что данное отношение является функцией, если каждый из элементов множества A имеет одно и только одно изображение в множестве B.

Если вы читаете Домен функции, вы также можете прочитать о матрицах здесь.

Некоторые функции, например, линейные функции, имеют домены, которые охватывают все возможные значения x .

Другие, такие как уравнения, в которых x попадает в знаменатель, исключают некоторые значения x , чтобы избежать деления на ноль.
Функции квадратного корня имеют более ограниченные области применения, чем некоторые другие функции, поскольку значение внутри квадратного корня должно быть положительным числом, чтобы результат был действительным.

Условные обозначения интервалов, которым следуют при записи домена функции, следующие:

Наименьший член интервала составляется первым.
Член, больший, чем наименьший в интервале, адресуется вторым, за ним следует запятая, и процесс продолжается для остальных чисел.
Круглые скобки ( ) используются для обозначения того, что конечная точка не охвачена, что называется исключительным.
Скобки [ ] используются, чтобы показать, что задействована конечная точка, называемая включительно.

Также читайте о перестановках и комбинациях здесь.

Область определения функции можно упорядочить, поместив входные значения набора упорядоченных пар.

Область определения функции также можно рассчитать, распознав входные значения функции, записанные в формате уравнения.
Значения интервалов, выраженные на числовой прямой, могут быть отображены с использованием записи неравенства, записи построителя множеств и записи интервала.
Для многих функций домен и диапазон можно рассчитать по соответствующим графикам.
Знание функций инструментария может быть использовано для получения предметной области и диапазона соответствующих функций.

Мы надеемся, что приведенная выше статья о домене функции будет полезна для вашего понимания и подготовки к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.

Домен функции Часто задаваемые вопросы

В.1 Что означает домен в математике?

Ответ 1 Домен в математике можно рассматривать как набор значений, которые входят в функцию; кроме того, диапазон подразумевает все значения, которые выходят.

Q.2 Как найти домен и диапазон функции?

Ответ 2 Область определения функции можно упорядочить, поместив входные значения набора упорядоченных пар. Область определения функции также можно рассчитать, распознав входные значения функции, записанные в формате уравнения.

Q.3 Что вы подразумеваете под функцией?

Ответ 3 Функция относится к определенному отношению, которое описывает каждый элемент одного набора только с одним элементом, относящимся к другому набору.

Q.4 Что такое отношение?

Ответ 4 В математике отношение описывает отношения между наборами значений упорядоченных пар. Набор компонентов в первом наборе называется доменом, связанным с набором компонентов в другом наборе, который обозначается как диапазон.

Q.5 Каковы домены и диапазоны функции?

Ответ 5 Если f: P → Q — функция, то множество P называется областью определения функции f. Аналогично. Если f: P → Q — функция, то область значений f состоит из тех компонент Q, которые связаны хотя бы с одним элементом P.

Скачать публикацию в формате PDF

Еще на testbook.com

Атомный номер – знание атомного массового числа, изотопов, изобар и понимание с помощью примеров
Химия в повседневной жизни – использование химии в мыле, моющих средствах, антацидах, лекарствах и т. д.
Электронная конфигурация, правила распространения, стабильность атомов с примерами углеводородов, типы и свойства
Типы функций: изучение значения, классификация, представление и примеры для практики

3.2. Домен и диапазон — математика для специалистов в области общественного здравоохранения и гигиены труда

Одна из наших главных целей в математике — смоделировать реальный мир с помощью математических функций. При этом важно помнить об ограничениях тех моделей, которые мы создаем.

В этой таблице показано соотношение между окружностью и высотой дерева по мере его роста.

Окружность, c	1,7	2,5	5,5	8.2	13,7
Высота, ч	24,5	31	45,2	54,6	92,1

Несмотря на то, что между ними существует тесная взаимосвязь, было бы нелепо говорить о дереве с окружностью -3 фута или высотой 3000 футов. Когда мы определяем ограничения на входы и выходы функции, мы определяем домен и диапазон функции.

Домен : Набор возможных входных значений для функции

Диапазон : Набор возможных выходных значений функции

Используя приведенную выше древовидную таблицу, определите подходящий домен и диапазон.

Мы могли бы объединить предоставленные данные с нашим собственным опытом и соображениями, чтобы аппроксимировать область определения и диапазон функции

h = f ( c ). Для домена возможные значения входной окружности c , нет смысла иметь отрицательные значения, поэтому c > 0. Мы могли бы сделать обоснованное предположение о максимальном разумном значении или посмотреть, что максимальная измеренная окружность составляет около 119 футов. С этой информацией мы бы сказали, что разумный диапазон составляет 0 < 90 225 c 90 226 ≤ 119 футов.

Аналогично для диапазона, нет смысла иметь отрицательную высоту, а максимальная высота дерева может составлять 379 футов, поэтому разумный диапазон 0 < 902:25 ч ≤ 379 футов.

При отправке письма через Почтовую службу США цена зависит от веса письма, как показано в таблице ниже. Определяем домен и диапазон.

Письма
Вес не более	Цена
1 унция	0,44 $
2 унции	0,61 $
3 унции	0,78 $
3,5 унции	0,95 $

Предположим, мы записали Вес как w, а Цена — как p и настроили функцию с именем P , где Цена, p — это функция Веса, w . р = р ( w ).

Поскольку допустимый вес составляет 3,5 унции или меньше, а отрицательный вес не имеет смысла, домен будет 0 < w ≤ 3,5. Технически 0 может быть включен в домен, но логически это будет означать, что мы ничего не рассылаем по почте, так что не помешает его опустить.

Поскольку возможные цены взяты из ограниченного набора значений, мы можем определить диапазон этой функции, только перечислив возможные значения. Диапазон: p = 0,44, 0,61, 0,78 или 0,95 доллара.

В предыдущих примерах мы использовали неравенства для описания области определения и диапазона функций. Это один из способов описания интервалов входных и выходных значений, но не единственный.

Использование неравенств, таких как 0 < c ≤ 163 , 0 < w ≤ 3,5 и 0 < h ≤ 379 подразумевает, что нас интересуют все значения между низкими и высокими значениями, включая высокие значения в эти примеры.

Однако иногда нас интересует конкретный список номеров, например диапазон цен на отправку писем,

p = 0,44 доллара, 0,61 доллара, 0,78 доллара или 0,95 доллара. Эти числа представляют набор конкретных значений: {0,44, 0,61, 0,78, 0,95}

Представление значений в виде набора или предоставление инструкций о том, как строится набор, приводит нас к другому типу нотации для описания домена и диапазона. Предположим, мы хотим описать значения переменной x, равные 10 или больше, но меньше 30. В неравенствах мы должны написать 10 ≤ x < 30 .

При описании доменов и диапазонов мы иногда расширяем это до нотации построителя наборов , которая будет выглядеть следующим образом: { x | 10 ≤ х < 30}. Фигурные скобки {} читаются как «множество», а вертикальная черта | читается как «такой, что», так что в целом мы будем читать { x | 10 ≤ x < 30} как «набор таких значений x, что 10 меньше или равно

x , а x меньше 30».

При описании диапазонов в нотации построителя наборов мы могли бы аналогичным образом написать что-то вроде { f ( x ) | 0 < f ( x ) < 100}, или если бы у вывода была собственная переменная, мы могли бы использовать ее. Таким образом, для нашего примера высоты дерева выше мы могли бы написать для диапазона { ч | 0 < ч ≤ 379}. В нотации построителя наборов, если домен или диапазон не ограничены, мы могли бы написать { t | t — действительное число} или { t | t ∈ ℜ}, читается как «набор таких t-значений, что t является элементом множества действительных чисел.

Более компактной альтернативой нотации построителя наборов является нотация интервала , в которой интервалы значений обозначаются начальным и конечным значениями. Круглые круглые скобки используются для «строго меньше», а квадратные скобки используются для «меньше или равно». Поскольку бесконечность не является числом, мы не можем включить ее в интервал, поэтому мы всегда используем изогнутые скобки с ∞ и -∞. Приведенная ниже таблица поможет вам увидеть, как неравенства соответствуют нотации построителя множеств и нотации интервала:

Неравенство

Установить нотацию Builder

Обозначение интервала

5 < ч ≤ 10	{ ч \| 5 < ч ≤ 10}	(5, 10]
5 ≤ ч < 10	{ ч \| 5 ≤ ч < 10}	[5, 10)
5 < ч ≤ 10	{ ч \| 5 < ч < 10}	(5, 10)
ч < 10	{ ч \| ч < 10}	(-∞, 10)
ч ≥ 10	{ ч \| ч ≥ 10}	[10, ∞)
все действительные числа	{ ч \| ч ∈ ℜ}	(-∞, ∞)

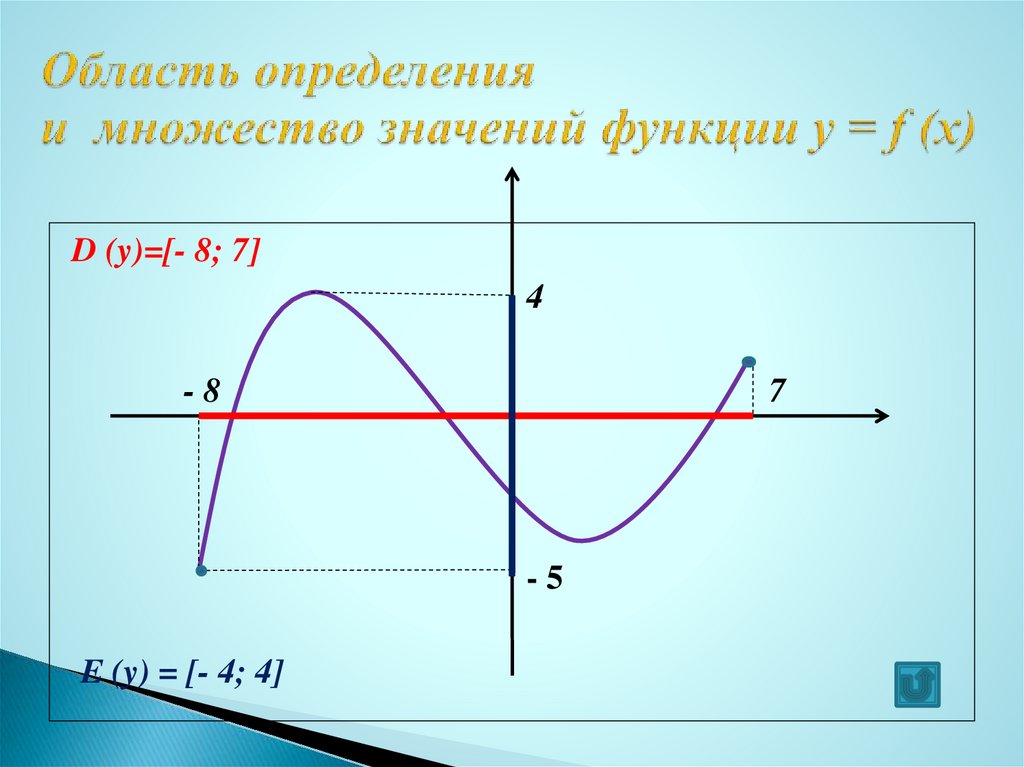Чтобы объединить два интервала вместе, используя неравенства или нотацию построителя множеств, мы можем использовать слово «или». В записи интервалов мы используем символ объединения ∪ для объединения двух несвязанных интервалов вместе.

Опишите интервалы значений, показанные на линейном графике ниже, используя построитель наборов и обозначения интервалов.

Чтобы описать значения x , которые лежат в интервалах, показанных выше, мы бы сказали: « x — это действительное число, большее или равное 1 и меньшее или равное 3, или действительное число, большее чем 5».

В виде неравенства: 1 ≤ x ≤ 3 или x > 5.

В обозначении построителя набора: { x | 1 ≤ x ≤ 3 или x > 5}.

В интервальных обозначениях: [1, 3] ∪ (5, ∞).

Помните при написании или чтении обозначения интервала: использование квадратной скобки [ означает, что начальное значение включено в набор; с помощью круглых скобок ( означает, что начальное значение не включено в набор.

Мы также можем говорить о домене и диапазоне на основе графиков. Поскольку домен относится к набору возможных входных значений, домен графа состоит из всех входных значений, показанных на графике. Помните, что входные значения почти всегда отображаются вдоль горизонтальной оси графика. Точно так же, поскольку диапазон — это набор возможных выходных значений, диапазон графика мы можем видеть из возможных значений вдоль вертикальной оси графика.

Будьте осторожны — если график выходит за пределы окна, в котором мы видим график, домен и диапазон могут быть больше, чем видимые значения.

Определите домен и диапазон графика ниже:

На приведенном выше графике входная величина по горизонтальной оси представляет собой «год», который мы можем записать с помощью переменной y . Результатом является «тысячи баррелей нефти в день», что мы можем записать с помощью переменной b 9.0226 , для бочек. График, вероятно, будет продолжаться влево и вправо за пределы того, что показано, но на основе части графика, которая показана нам, мы можем определить область 1975 ≤ y ≤ 2008, а диапазон составляет приблизительно 180 ≤ б ≤ 2010 .

В интервальных обозначениях доменом будет [1975, 2008], а диапазоном будет около [180, 2010]. Для диапазона мы должны аппроксимировать наименьший и наибольший выходные значения, поскольку они не попадают точно на линии сетки.

Помните, что, как и в предыдущем примере, x и y не всегда являются входными и выходными переменными. Использование описательных переменных — важный инструмент для запоминания контекста проблемы.

Большинство основных формул могут быть оценены на входе. Два общих ограничения:

Квадратный корень из отрицательных значений не является действительным.
Мы не можем делить на ноль.

Найдите домен каждой функции:

а)

б)

Решение

а) Поскольку мы не можем извлечь квадратный корень из отрицательного числа, нам нужно, чтобы внутренняя часть квадратного корня была неотрицательной.

x + 4 ≥ 0, когда x ≥ -4.

Домен f ( x ) равен [-4, ∞).

б) Мы не можем делить на ноль, поэтому нам нужно, чтобы знаменатель был ненулевым.

6 – 3 x = 0, когда x = 2, поэтому мы должны исключить 2 из домена.

Область g ( x ) равна (-∞, 2) ∪ (2, ∞).

Некоторые функции нельзя описать одной формулой.

Кусочная функция : Кусочная функция — это функция, в которой используемая формула зависит от области, в которой находятся входные данные. Мы обозначаем это понятие как:

Музей берет 5 долларов США с человека за экскурсию с группой от 1 до 9 человек.человек или фиксированная плата в размере 50 долларов США за 10 или более человек в группе. Настройте функцию, связывающую количество людей n со стоимостью C .

Для настройки этой функции потребуются две разные формулы. C = 5 n будет работать для значений n меньше 10, а C = 50 будет работать для значений n десять или больше. Обозначив это:

Компания сотовой связи использует приведенную ниже функцию для определения стоимости C в долларах за g гигабайт передачи данных.

Найдите стоимость использования 1,5 гигабайт данных и стоимость использования 4 гигабайт данных.

Чтобы найти стоимость использования 1,5 гигабайт данных, C (1,5), мы сначала смотрим, к какой части домена относятся наши входные данные. Поскольку 1,5 меньше 2, мы используем первую формулу, что дает C (1,5) = 25 долларов США.

Найдем стоимость использования 4 гигабайт данных, C (4), мы видим, что введенное нами значение 4 больше, чем 2, поэтому воспользуемся второй формулой. C (4) = 25 + 10 (4 – 2) = 45 долларов.

Нарисуйте график функции

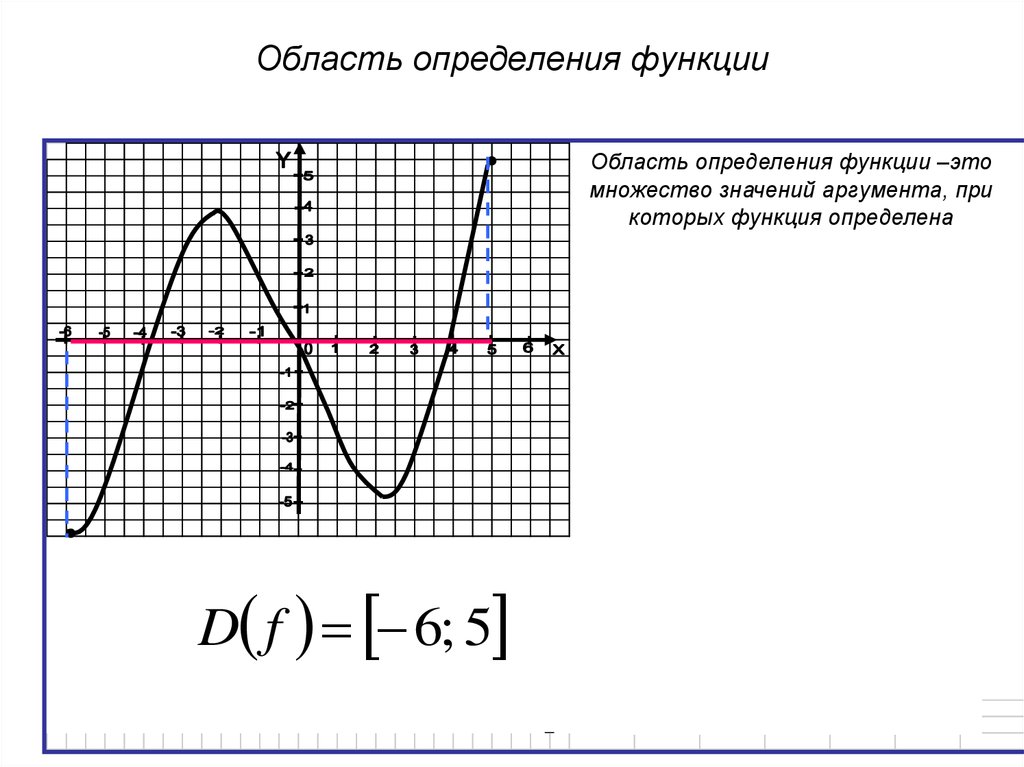Мы можем представить график каждой функции, а затем ограничить график указанной областью. На концах области мы поместили открытые кружки, чтобы указать, где конечная точка не включена из-за строго меньшего неравенства, и замкнутый кружок, где конечная точка включена из-за неравенства меньше или равно -к неравенству. Первая и последняя части являются постоянными функциями, где выход одинаков для всех входов. Среднюю часть мы могли бы распознать как линию и построить график, оценив функцию на паре входов и соединив точки линией.

Теперь, когда у нас есть каждая часть по отдельности, мы объединяем их на одном графике. Когда первая и вторая части встречаются при разрешении x = 1, мы можем представить, как закрытая точка заполняет открытую точку. Поскольку на графике нет разрыва, точку показывать не нужно.

1. Население небольшого города в 1960 году составляло 100 человек. С тех пор население выросло до 1400 человек, зарегистрированных во время переписи 2010 года. Выберите описательные переменные для ввода и вывода и используйте нотацию интервала, чтобы записать домен и диапазон.