Шпаргалка — Основные формулы
Шпаргалка
- формат gif
- размер 100.51 КБ
- добавлен 18 марта 2011 г.
Шпагалка, охватывающая основные формулы старшей школы. Формулы
набраны мелким, хорошо разборчивым шрифтом, в отдельных
табличках.
Данная шпаргалка по математике включает в себя материалы по
следующим темам:
Алгебра.
Формулы сокращенного умножения.
Свойства степеней и корней.
Квадратное уравнение, Теорема Виета.
Координаты вершины параболы.
Арифметическая прогрессия.
Геометрическая прогрессия.
Знаки тригонометрических функций в четвертях тригонометрического
круга.
Формулы привидения.
Таблица значений синуса, косинуса, тангенса и котангенса углов от 0
до 2П.
Тригонометрические тождества.
Тригонометрические формулы двойных углов.
Формулы сложения тригонометрических функций.
Тригонометрические формулы преобразования суммы в произведение.
Тригонометрические формулы преобразования произведения в сумму.
Формулы понижения степени.
Начала анализа.
Таблица производных.
Уравнение касательной.
Свойства интегралов.
Таблица интегралов.
Свойства логарифмов.
Геометрия.
Свойства радиусов правильных многогранников.
Теорема синусов и Теорема косинусов.
Радиусы треугольников.
Формулы площади треугольника.
Формулы объемов призмы, пирамиды, цилиндра, конуса, шара, шарового сегмента.
А также смотрите Основные формулы по физике.
Смотрите также
- формат doc
- размер 21.76 КБ
- добавлен 17 августа 2009 г.
Шпаргалка содержит формулы по математике на следующие темы: Формулы сокращенного умножения.
Свойства степеней. Геометрическая прогрессия. Модуль. Формулы cos и sin. Тригонометрические уравнения. Теоремы сложения. Правила дифференцирования. Уравнение касательной к графику функции. Площадь S фигуры, ограниченной прямыми x=a, x=b. Формула Ньютона-Лебница. Первообразная. Объемы и поверхности тел. Теорема синусов. Теорема косинусов. Неопределенные инт…
pottee
- формат pdf
- размер 57.87 КБ
- добавлен 28 февраля 2011 г.
Сумма и разность углов. Функции двойных, тройных, половинных углов. Формулы универсальной тригонометрической подстановки. Преобразование суммы в произведение. Преобразование произведение в сумму.
Шпаргалка
- формат doc
- размер 59.
41 КБ - добавлен 25 марта 2011 г.
41 КБСодержание: Основные тригонометрические тождества. Формулы суммы и разности. Формулы двойного аргумента. Формулы произведений. Формулы сложения. Формулы половинного аргумента. Формулы понижения степени. Решения тригонометрических уравнений. Выражение формул через тангенс. Таблица значения тригонометрических функций основных углов. Формулы приведения тригонометрических функций.
Шпаргалка- формат doc
- размер 402.5 КБ
- добавлен 13 сентября 2011 г.
Шпаргалка пригодится ученикам 11-ых классов, сдающим ЕГЭ, и ученикам старших классов. Содержит: тригонометрические формулы(тождества), значения тригонометрических функций, графики степенных, логарифмических и др.
функций, таблица производных, алгебраическая и геометрическая прогрессии, свойства степеней, корней, логарифмов, уравнение корней и теорема Виета, уравнение касательной, формулы сокращенного умножения, формулы понижения степени, формулы…
pottee
- размер 130.37 КБ
- добавлен 27 декабря 2009 г.
Шпаргалка пригодится ученикам 11-ых классов, сдающим ЕГЭ, и ученикам старших классов. Содержит: тригонометрические формулы(тождества), значения тригонометрических функций, графики степенных, логарифмических и др. функций, таблица производных, алгебраическая и геометрическая прогрессии, свойства степеней, корней, логарифмов, уравнение корней и теорема Виета, уравнение касательной, формулы сокращенного умножения, формулы понижения степени, формулы.
..
pottee
- формат jar
- размер 118.21 КБ
- добавлен 13 марта 2010 г.
Шпаргалка пригодится всем сдающим ЕГЭ и ученикам старших классов. Содержит: тригонометрические формулы(тождества), значения тригонометрических функций, графики степенных, логарифмических и др. функций, таблица производных, уравнение корней и теорема Виета, формулы сокращенного умножения, нахождения площади прямоугольного и косоугольного треугольников, объема призмы, пирамиды, шара, конуса.rn
pottee
- формат pdf
- размер 51.17 КБ
- добавлен 05 мая 2009 г.
Собраны и размещены все основные и необходимые формулы по школьному курсу математики на одном листе.
Шпаргалка
- формат doc
- размер 477.5 КБ
- добавлен 15 декабря 2010 г.
Шпаргалка по математике. все основные формулы и таблицы. Содержание: Числа, дроби, модуль: Множества. Дроби. Арифметические операции с дробями. Пропорция. Модуль числа. Определение. Свойства модуля. формулы сокращенного умножения. степени и корни: Показательные неравенства. квадратные уравнения: Корни уравнения.
pottee
- формат doc
- размер 13.47 КБ
- добавлен 11 июня 2009 г.
Содержит основные формулы, от сокращённого умножения до тригонометрических формул. Формулы сокращенного умножения и разложения на множители. Формулы сложения. Степени и корни. Формулы двойного аргумента. Формулы половинного аргумента. Стереометрия. Приведенное квадратное Уравнение. Логарифмы. Тригонометрические уравнения. Теорема синусов.
- формат doc
- размер 169 КБ
- добавлен
07 ноября 2011 г.
2011 г. Содержание: Основные тригонометрические формулы. Формулы сложения аргументов. Формулы двойного угла. Формулы понижения степени. Формулы преобразования произведений функций. Формулы преобразования суммы функций. Решение простейших тригонометрических уравнений. Универсальная тригонометрическая подстановка. Вспомогательный аргумент (метод Юниса). и др.
Формулы приведения, тригонометрия, 10 класс. алгебра, урок и презентация
Дата публикации: .
Что будем изучать:
1. Немного повторим.
2. Правила для формул приведения.
3. Таблица преобразований для формул приведения.
4. Примеры.
Повторение тригонометрических функций
Ребята, с формулами привидения вы уже сталкивались, но так их еще не называли. Как думаете: где?
Посмотрите на наши рисунки. Правильно, когда вводили определения тригонометрических функций.
Правило для формул приведения
Давайте введем основное правило: Если под знаком тригонометрической функции содержится число вида π×n/2 + t, где n – любое целое число, то нашу тригонометрическую функцию можно привести к более простому виду, которая будет содержать только аргумент t. Такие формулы и называют формулами привидения.
Вспомним некоторые формулы:
- sin(t + 2π*k) = sin(t)
- cos(t + 2π*k) = cos(t)
- sin(t + π) = -sin(t)
- cos(t + π) = -cos(t)
- sin(t + π/2) = cos(t)
- cos(t + π/2) = -sin(t)
- tg(t + π*k) = tg(x)
- ctg(t + π*k) = ctg(x)
Ребята, формул привидения очень много, давайте составим правило по которому будем определять наши тригонометрические функции при использовании формул привидения:
- Если под знаком тригонометрической функции содержатся числа вида: π + t, π — t, 2π + t и 2π — t, то функция не изменится, то есть, например, синус останется синусом, котангенс останется котангенсом.
- Если под знаком тригонометрической функции содержатся числа вида: π/2 + t, π/2 — t,
3π/2 + t и 3π/2 — t, то функция изменится на родственную, т. е. синус станет косинусом, котангенс станет тангенсом. - Перед получившийся функцией, надо поставить тот знак, который имела бы преобразуемая функция при условии 0
Эти правила применимы и когда аргумент функции задан в градусах!
Так же мы можем составить таблицу преобразований тригонометрических функций:
Примеры применения формул приведения
1.Преобразуем cos(π + t). Наименование функции остается, т.е. получим cos(t). Далее предположим, что π/2
2. Преобразуем sin(π/2 + t). Наименование функции изменяется, т.е. получим cos(t). Далее предположим что 0 sin(t + π/2) = cos(t)
3. Преобразуем tg(π + t). Наименование функции остается, т.е. получим tg(t). Далее предположим, что 0
4. Преобразуем ctg(2700 + t). Наименование функции изменяется, то есть получим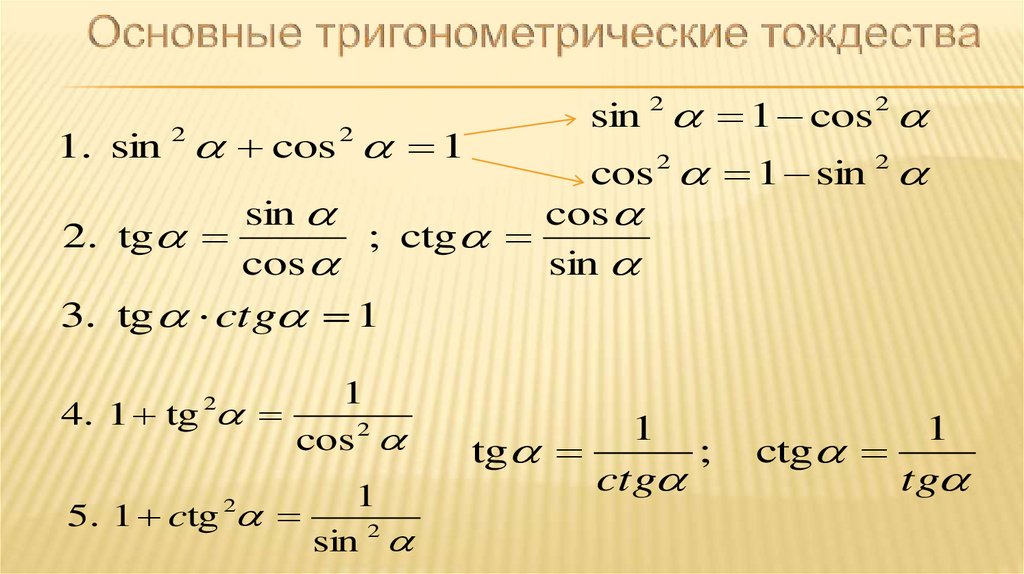 tg(t).
Далее предположим что 0 0, тогда (2700 + t) попадет в четвертую четверть, а там преобразуемая функция котангенс отрицательная, согласно третьему пункту нашего правила следует
поставить минус перед нашей функцией: ctg(2700 + t)=-tg(t).
Задачи с формулами приведения для самостоятельного решения
Ребята, преобразуйте самостоятельно, используя наши правила:
1) tg(π + t),2) tg(2π — t),
3) ctg(π — t),
4) tg(π/2 — t),
5) ctg(3π + t),
6) sin(2π + t),
7) sin(π/2 + 5t),
8) sin(π/2 — t),
9) sin(2π — t),
10) cos(2π — t),
11) cos(3π/2 + 8t),
12) cos(3π/2 — t),
13) cos(π — t).
Основные формулы тригонометрии — Prinsli.com
Введение в основные формулы тригонометрии — Мы знаем, что тригонометрия — это раздел математики, который занимается измерением частей, сторон и углов треугольника. Следовательно, тригонометрия также определяется как изучение отношений между длинами сторон треугольника и углами.
Тригонометрия основана на определенных соотношениях, известных как тригонометрические функции. Эти тригонометрические функции используются в геодезии, навигации, инженерии и т. д.
Тригонометрия и ее формулы имеют множество применений. Например, в географии триангуляция используется для измерения расстояния между ориентирами; в астрономии триангуляция используется для измерения расстояния до ближайших звезд, а также в спутниковых навигационных системах. Формулы тригонометрии могут быть использованы для решения многих различных типов задач. Эти задачи могут включать тригонометрические соотношения (sin, cos, tan, cot, sec, cosec), тождества Пифагора и т. д. тождества углов, тождества полууглов и т. д. приведены здесь. Учащимся 10, 11 и 12 классов будет полезно выучить и запомнить эти математические формулы тригонометрии, чтобы добиться успеха в этой теме.
При изучении тригонометрических формул мы учитываем только прямоугольные треугольники. Прямоугольный треугольник имеет три стороны: Гипотенуза , противолежащая сторона ( Перпендикуляр ) и прилежащая сторона ( Основание ).
Гипотенуза — самая длинная сторона, перпендикуляр — сторона, противоположная углу, а прилежащая сторона — сторона, примыкающая к углу, т. е. сторона, на которую опираются и гипотенуза, и противолежащая сторона.
Обычно гипотенуза обозначается символом H , перпендикуляр обозначен символом P , а основание обозначено символом B .
♦ Формулы в тригонометрии, связанных с кружкой и углами:
1. Площадь круга составляет,
2. Окружность круга —
Где
[приблизительные значения из π и ]
3. 1 радиан = 57,296° = 57°17’44,8″ приблизительно.
4. 1 Прямой угол = 90° = π/2 радиан = 100 г .
5. 2 прямых угла = 180° = π радиан = 200 г .
6. В окружности,
7.
Теорема Пифагора: В любом прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин двух других сторон . То есть
(Гипотенуза) 2 = (Перпендикуляр) 2 + (база) 2
Читать также: Основная концепция тригонометрии: измерение углов
♦ Основные тригонометрические формулы:
Тригонометрическое. Треугольник, когда известны некоторые его стороны и углы, является важнейшей задачей тригонометрии. Для решения этой задачи воспользуемся некоторыми отношениями сторон треугольника к его острому углу. Эти отношения острых углов известны как тригонометрические отношения углов.
Отношение длин двух сторон прямоугольного треугольника называется тригонометрическим отношением.
Когда вещи не могут быть измерены напрямую, тогда тригонометрические отношения используются для нахождения измерения косвенно. Тригонометрические отношения помогают измерить высоту или длину объекта или расстояние между двумя разными объектами.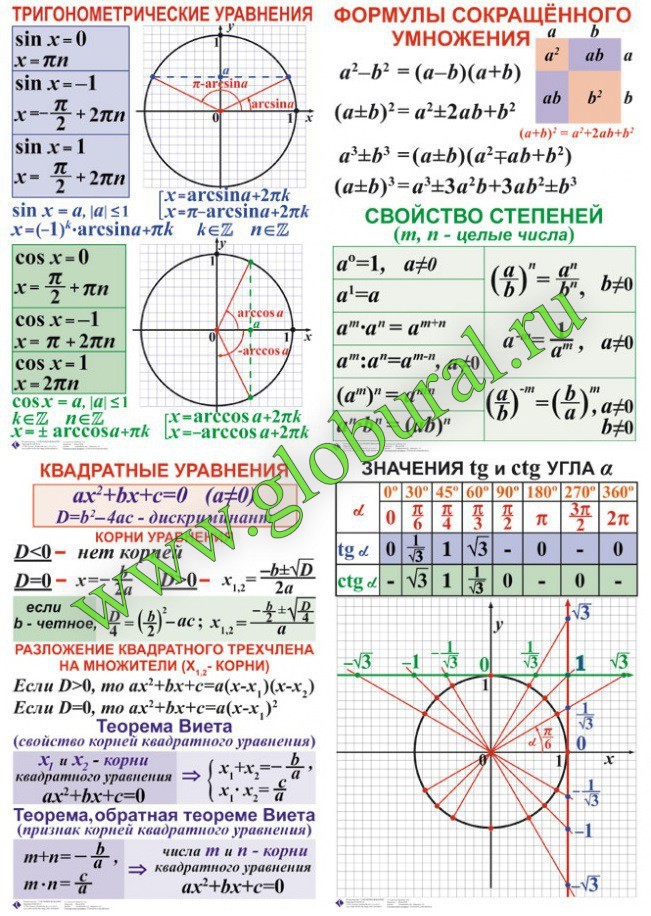
В тригонометрии в основном используются 6 соотношений. Их называют тригонометрическими функциями. Шесть тригонометрических функций: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (cosec или csc).
Право -треугольник Определение: для острого угла θ в правом треугольнике:
1.
2.
3.
4.
5.
6.
♦ Взаимные идентичности:
Взаимные идентичности для тригонометрических функций следующие:
1.
и
1.и 9 0000005
2.
и
3.
и
♦ Отношение идентичности:
.
.
♦ Пифагорейские тождества в тригонометрии:
Пифагорейские тождества в тригонометрии следующие:
1. , то есть 5 90
и
2.
, то есть,
и
3.
, то есть,
и
Важное примечание:
1. Важно отметить, что « sin θ » означает « синус угла θ », а не произведение sin и θ. То же самое верно и для других тригонометрических соотношений.
2. Тригонометрические соотношения, перечисленные выше, определены для острого угла θ.
3. Приведенные выше тригонометрические соотношения зависят только от величины угла θ.
4. Тригонометрические соотношения, перечисленные выше, одинаковы для одного и того же угла.
♦ Тригонометрические коэффициенты для единичного круга:
Тригонометрические коэффициенты для единичного круга, где радиус равен 1, а угол θ определяется следующим образом:
1.
2.
3.
4.
5.
6.
♦ Тригонометрия. Следующая таблица содержит формулы тригонометрии для углов, которые обычно используются при решении задач.
Следовательно, Из этой таблицы тригонометрии очевидно, что
; ;
; ;
; ;
; ;
Также,
♦ Тригонометрические функции углов любой величины и знака:
ровные и нечетные угловые формулы в тригонометрии:
ровные и нечетные угловые формулы в тригонометрии следующие:
.
sec) являются четными функциями, а синус (sin), тангенс (tan), котангенс (cot) и косеканс (cosec или csc) — нечетными.
Тождества кофункций или формулы кофункций тригонометрии:
В тригонометрии тождества кофункций или формулы кофункций описывают отношения между различными тригонометрическими функциями и их дополнительными углами. Шесть Кофункций Идентичности следующие:
Тригонометрические соотношения угла (90 °+θ) с точки зрения θ для всех значений θ:
в тригонометрии, тригонометрические потрочные значения (
.
все значения θ или дополнительные углы:
Мы знаем, что два угла являются дополнительными, если их сумма равна двум прямым углам, то есть 180°. Следовательно, дополнение любого угла θ будет равно 180°-θ. В тригонометрии тригонометрические отношения угла (180°-θ) к отношениям θ для всех значений θ следующие: +θ) относительно значений θ для всех значений θ:
В тригонометрии тригонометрические соотношения угла (180°+θ) относительно соотношений θ для всех значений θ следующие:
Тригонометрические соотношения угла (360 °+θ) с точки зрения θ для всех значений θ:
в тригонометрии, тригонометрические применения для угла (360 ° ° °.
+θ) такие же, как и для θ, для всех значений θ. Эти формулы следующие:
Угловые тождества, трижды формулы углов, формулы произведения на сумму, формулы суммы на произведение и т. д.
Теги: формула тригонометрии, формулы тригонометрии для 10 класса, все формулы тригонометрии, формулы тригонометрии для 11 класса, формула таблицы тригонометрии, формулы тригонометрии для 12 класса, основные формулы тригонометрии, тождества функций Co или формулы функций Co, пифагорейская тригонометрия identity
Тригонометрические формулы Трюки, тождества, тригонометрические соотношения
Содержание
Тригонометрия
Тригонометрическая формула: Тригонометрия является важной частью раздела «Количественные способности», который доставляет учащимся трудные времена с его сложной формулой тригонометрии и вопросами. Тригонометрия — это основной раздел математики, изучающий углы и длины прямоугольного треугольника.
Применение всех формул тригонометрии осуществляется в астрономических исследованиях и других областях науки.
Тригонометрические формулы
Всего существует 6 тригонометрических функций, а именно Sin, Cos, Tan, Sec, Cosec и Cot. Существуют тригонометрические соотношения, которые помогают вывести текущую длину и угол. Все формулы тригонометрии, трюки с формулами тригонометрии и вопросы по тригонометрии вращаются вокруг этих 6 функций. Претенденты могут ознакомиться с деталями тригонометрии, включая формулы, трюки с формулами тригонометрии и вопросы.
Вопросы по теме Тригонометрия задаются на различных конкурсных экзаменах, таких как SSC, Железнодорожный транспорт и т. д. В этом посте мы представляем вам заметки по Формуле Тригонометрии, полезные для экзаменов. Это поможет вам запомнить основные формулы тригонометрии. Вот все формулы тригонометрии для 10 класса и формулы тригонометрии для 11 класса, которые также могут быть полезны при подготовке к 10 и 12 классам.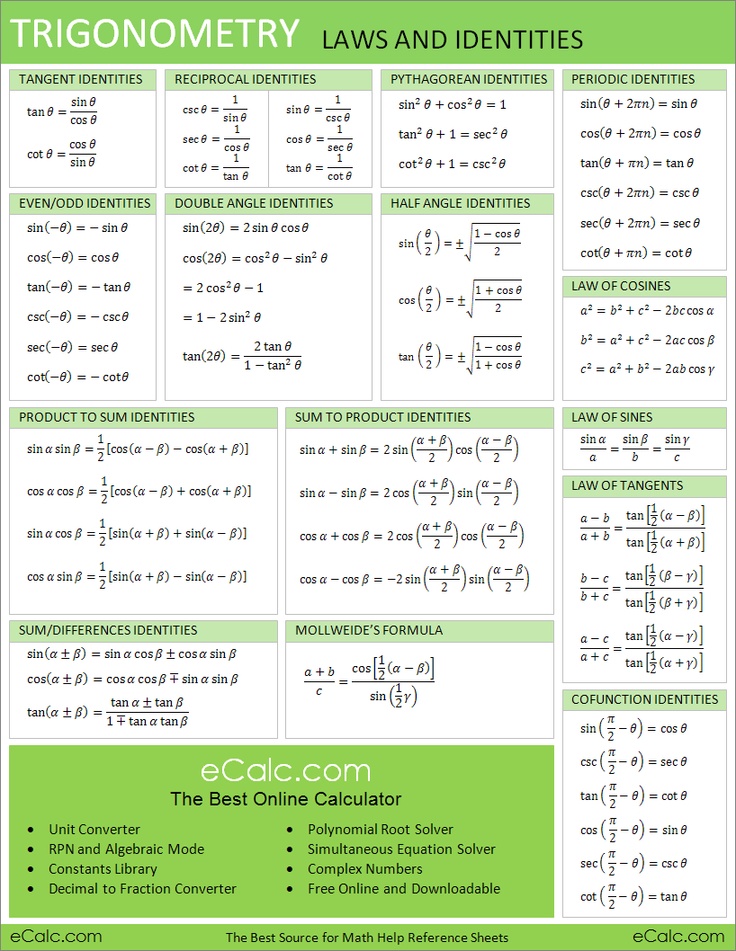
Важные тождества тригонометрических соотношений
Чтобы овладеть основными понятиями тригонометрии, вы должны изучить все важные тригонометрические соотношения и их тождества.
Тригонометрические отношения
Для изучения различных функций тригонометрических отношений мы будем использовать прямоугольный треугольник. Предположим, что ABC — прямоугольный треугольник с углом A = 90°.0475
Различные значения удельного угла тригонометрического отношения
Вы должны изучить следующую таблицу, чтобы решить вопрос, основанный на тригонометрическом соотношении углов 0°, 30°, 45°, 60°
7 Формула тригонометрии: связь между квадратами различных типов тригонометрических отношений0°
Всегда верны результаты:
(i) sin A. sec B = 1 или sin A = cos B
(ii) cos A. cosec B = 1 или sec A = cosec B
(iii) tan A. tan B = 1 или tan A = cot B
(iv) cot A. cot B = 1
(v) sin²A + sin² B = 1
(vi) cos² A + cos² B = 1
Важная тригонометрическая формула для суммы и разности двух углов
(1) sin (A+B) =sinA.