Как найти область определения и область значений кусочно-функционального калькулятора? – Обзоры Вики
Как обновить калькулятор TI-84 Plus?
тогда что такое пример кусочной функции? Кусочная функция — это функция, которая определяется различными формулами или функциями для каждого заданного интервала. Это также в названии: шт. … Как видно из приведенного выше примера, F (X) является кусочной функцией, потому что она однозначно определена для трех интервалов: x > 0, x = 0 и x < 0.
Как найти область и диапазон уравнения?
Чтобы найти домен и диапазон, мы просто решить уравнение y = f(x), чтобы определить значения независимой переменной x и получить домен. Чтобы вычислить диапазон функции, мы просто выражаем x как x = g (y), а затем находим область определения g (y).
com/embed/eWo8tWuaGfU» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″> Как построить график кусочной функции на TI 83 Plus?
- График кусочно-определяемой функции на TI-83+
- Y= (Очистить функции)
- Мода. Выберите точку. Затем график в стандартном окне просмотра. Увеличьте масштаб, чтобы более четко увидеть две функции.
Как построить график ступенчатой функции на TI-84? Решение 34602. Построение графика ступенчатой функции на TI-84 Plus C Silver Edition.
- Нажмите [Y=] для доступа к редактору Y=.
- Нажмите [MATH] и прокрутите вправо, чтобы выбрать меню NUM.
- Нажмите 5:целое(.
- Нажмите [X,T,q,n] [ ) ], чтобы ввести переменную x и завершить команду.
- Нажмите клавишу [GRAPH], чтобы отобразить график.
Как вы делаете y1 на TI-84?
Можно ли сохранять формулы в TI-84 Plus?
Сохранение заметок и формул в графическом калькуляторе TI-84 Plus можно использовать для экономии времени и более надежного запоминания формул.
Его также можно использовать, чтобы получить преимущество на таких экзаменах, как SAT, которые позволяют студентам использовать этот метод.
Как отключить калькулятор Casio от FX? Как сбросить Casio fx-991ES или fx-82ES?
- Включите калькулятор кнопкой ON. На задней панели нет кнопки аппаратного сброса.
- SHIFT 9, чтобы войти в Сброс. …
- 3, чтобы выбрать параметр «Сбросить все».
- = для подтверждения сброса. …
- AC, чтобы вернуться к нормальному расчету, или SHIFT AC, чтобы выключить калькулятор.
Какая последняя ОС для TI 84 Plus? Самая последняя операционная система для TI-84 Plus и TI-84 Plus Silver Edition: 2.55MP. Примечание. Если вы обновляете контроллер TI-Nspire™ с клавиатурой TI-84, см. документ Обновление операционной системы TI-Nspire™.
Как поставить игры на TI 84 Plus?
Как поставить игры на TI-84 Plus CE
- Шаг 1: Материалы для ворот. Все, что вам нужно, перечислено здесь:…
- Шаг 2: Загрузите и установите TI Connect CE.
2, т.е. 27. f(-3) должна быть функцией связанного уравнения.Как построить график кусочной функции на графическом калькуляторе? Вот шаги для построения графика кусочной функции в вашем калькуляторе:
- Нажмите [ALPHA][Y=][ENTER], чтобы вставить шаблон дроби n/d в редактор Y=.
- Введите функциональную часть в числитель и введите соответствующий интервал в знаменатель. …
- Нажмите [GRAPH], чтобы построить график функциональных частей.
Как найти диапазон уравнения?
В целом, шаги для алгебраического нахождения диапазона функции следующие:
- Запишите y = f (x), а затем решите уравнение относительно x, получив что-нибудь в форме x = g (y).
- Найдите область определения g (y), и это будет диапазон f (x). …
- Если вы не можете решить для x, попробуйте построить график функции, чтобы найти диапазон.
Что такое домен в математике? Что такое область определения функции? … Область определения функции набор всех возможных входов для функции.
Например, область определения f (x) = x² — это все действительные числа, а область определения g (x) = 1 / x — все действительные числа, кроме x = 0.Как написать домен в заданной нотации?
Мы можем записать область определения f (x) в обозначениях конструктора множеств как, {x | х ≥ 0}. Если областью определения функции являются все действительные числа (т. Е. Нет ограничений на x), вы можете просто указать область как «все действительные числа» или использовать символ для представления всех действительных чисел.
Методическое пособие «Построение кусочно-заданных функций»
Б-Толкай 2013
ГБОУ СОШ с.Большой-Толкай
Методическое пособие по теме
«Построение кусочно-заданных функций
Составила ученица 9 класса
Кизельбашева Валентина.
Понятие о кусочных функциях. На различных участках числовой прямой функция может быть задана разными формулами. Например: y=f(x), где
f(x)= х2, -3х-2
2х+8, -20
Такие функции назовём кусочными.
Участки числовой прямой, которые различаются формулами задания, назовём составляющими область определения, а их объединение, является областью определения кусочной функции. Точки, которые делят область определения на составляющие, называются граничными точками. Выражения, определяющие кусочную функцию на каждой составляющей области определения, называется входящими функциями.Наличие таких свойств как чётность, нечётность, нули функции, промежутки знакопостоянства, монотонность, ограниченность у кусочных функций устанавливается согласно общепринятым определениям, с учётом особенностей составляющих области определения и входящих функций.
Для того чтобы вычислить значение кусочной функции в заданной точке, необходимо, во-первых, определить, какой составляющей области определения принадлежит эта точка, а, во-вторых, найти значение входящей функции на этой составляющей.
Ответы:
1)Функция убывает на промежутке [-2; +∞).
2)Функция возрастает на промежутках (-∞; -2] и [0; 2].
3)f(x)≥0, если х=0 и |х|≥ 3⅓;
4)у > 0, если х
5)Прямая y=m имеет с графиком две общие точки при m=3 и m=-1;
6)Прямая y=m имеет с графиком одну общую точку при m=-2 и m>1.
Задания для самостоятельной работы:
1)Постройте график функции y=f(x), где
x-1, если х
f(x)=
-1/2x+3, если x ≥ -2.
Укажите промежуток, на котором функция убывает.
2)Постройте график функции у=f(x), где
1/4х2-1, если -2≤ х ≤ 2
f(x)= 2-х, если х > 2
х+2, если х
Укажите промежутки возрастания функции.
3)Постройте график функции у=f(x), где
-х2, если -2≤ х ≤ 2
f(x)= 3х-10, если х > 2
-3x-10, если х
При каких значениях х значения функции у= f(x) неотрицательны?
4)Постройте график функции у= f(x),где
(х+1)2, если х
f(x)=
1-х2, если х ≥0.
При каких значениях х выполняется неравенство у > 0?
5)Постройте график функции у= f(x),где
х2-4х-1, если х ≥ 4
f(x)=
-х2+4х-1, если х
При каких значениях m прямая y=m имеет с графиком этой функции две общие точки?
6)Постройте график функции у= f(x),где
4/х, если х ≤ -2
f(x)= х, если -2
х2-4х+4, если х > 1.
При каких значениях m прямая y=m имеет с графиком этой функции одну общую точку?
Чтобы построить график кусочной функции, нужно:
- Построить в одной системе координат графики входящих функций,
- Провести прямые x=a, x=a, x=a, где a-граничные точки,
- На каждой составляющей области определения (a, a), где i=1…n выбрать тот график, который соответствует входящей функции на этой составляющей.
- Выяснить значение функции в граничных точках.
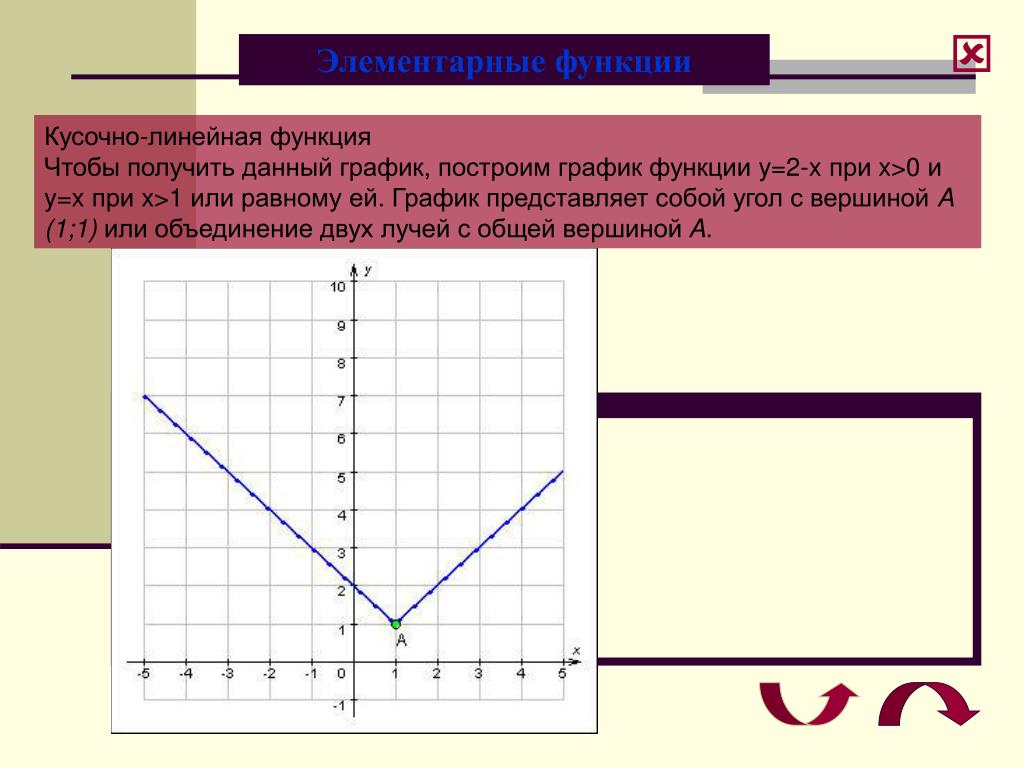
Если каждая входящая кусочной функции является линейной, то будем называть её кусочно-линейной функцией.
f(x)= х2, -3х-2
2х+8, -20
Построение:
- у=х2
- -3х-2
- Выделить часть графика 1.
- У=2х+8
- -20
- Выделить часть графика 2.
Рассмотрим построение графиков кусочных функций.
Постройте график функции y=f(x), где
f(x)= -1/2х+3, если х2
х-4 ,х>2
Укажите промежуток, в котором функция убывает.
Построим в одной системе координат графики функций у=1/2х+3, если х2 и у=х-4 ,х>2
Графиками обеих функций являются прямые. Для построения достаточно двух точек.
у=1/2х+3, х2
х
2
4
у
2
1
у=х-4 ,х>2
х
3
5
у
-1
1
Ответ: Функция убывает на промежутке (-;2]
Постройте график функции y=f(x), где
2-2×2, если 2
f(x)= x-1, если x>1
-x-1, если x
Укажите промежутки возрастания функции.
Первым графиком функции является парабола, ветви направлены вниз. Построим график функции на отрезке [-2;2]
х
-1
0
1
у
0
2
0
Второй график у= х-1 –прямая.
х
-1
1
у
-2
0
Третий график тоже прямая у=-х-1
х
-1
-3
у
0
2
Ответ: Функция возрастает на промежутках[-1;0]
и [1;)
Постройте график функции у=f(x), где
х2-1, если х0
f(x)= (x-1)2 ,если х>0
При каких значениях х выполняется неравенство у0
1)Первым графиком является парабола.
Построим её часть (х0) путем сдвига вниз на 1 графика у= х2.х
0
-1
-2
-3
-4
у
-1
0
3
8
15
Вторым графиком является тоже парабола. Построим её часть (х>0)путем сдвига вдоль оси ох вправо на 1 графика у= х2.
х
1
2
3
4
5
у
0
1
4
9
16
Ответ: при у>0, x1
Постройте график функции у=f(x), где
-х2-4х-3, если x-1
f(x)= x+1, если -11
2/x, если х>1
При каких значениях m прямая у=m имеет с графиком этой функции две общие точки.
Построим в одной системе координат графики функций.
1) Первым графиком функции является часть параболы, ветви направлены
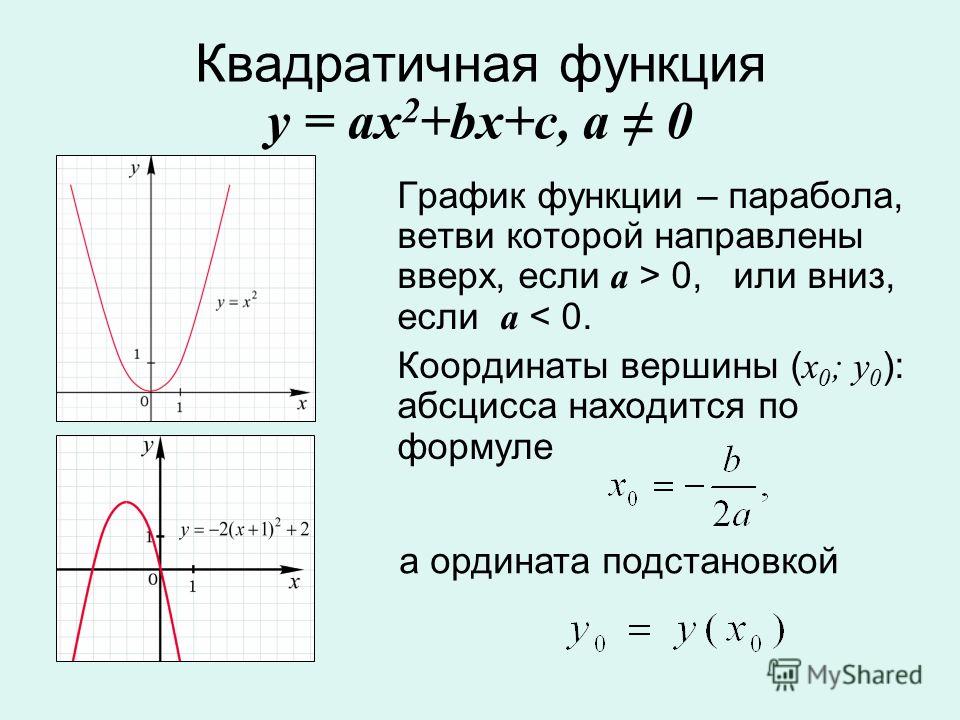
вниз. Найдём вершину параболы по формуле х=-b/2a
х=-(-4)/(-1·2)=-2, то у=-(-2)2-4·(-2)-3=1.Итак, вершина параболы
в точке с координатой (-2;1).
Найдём точки пересечения с осью OX;
у=0. -х2-4х-3=0
х1=-3
х2=-1
Точки пересечения с осью OX: (-3;0) и (-1;0).
Найдём точки пересечения с осью Oу:
х=0
у=-(0)2-4·0-3=3
Точки пересечения с осью OX: (0;3).
Найдём дополнительные точки
х
-2
-3
-4
-5
у
1
0
-3
-8
2) Второй график у= х+1 –прямая.Построим часть прямой
х
0
1
у
1
2
3)Третьим графиком является гипербола.
Построим часть гиперболы при х>1
х
2
4
6
8
у
1
0.5
1/3
0.25
Ответ: прямая у=m имеет с графиком этой функции две общие точкипри m=0 и 1
Постройте график функции у=f(x), где
f(x)= -х2, если |х|1
x2-1если |х| >1
Укажите промежутки возрастания функции.
Раскрывая знак модуля данную систему можно записать в следующем виде:
f(x)= -х2, если -1х1
x2-1если , х >1
x
Графиками данных функций является парабола. Построим первый график.
у=-х2 ,если -1х1
х
-1
0
1
у
0
0.5
0
x2-1если , х >1
x
х
1
2
3
4
-1
-2
-3
-4
у
0
3
8
15
0
3
8
15
Ответ: функция возрастает на промежутках(- ;-1] и [0;1]
Постройте график функции у=f(x), где
х2-4х+4, если x>1
f(x)= x, если -21
4/x, если х-2
При каких значениях m прямая у=m имеет с графиком этой функции одну общую точку?
Построим в одной системе координат графики функций.
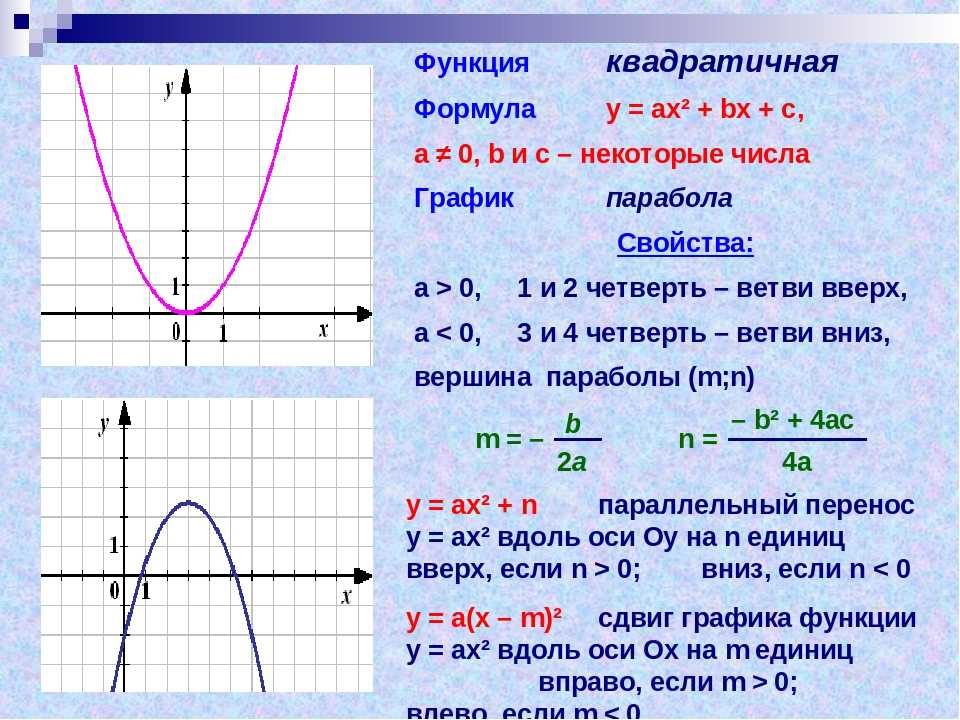
1) Первым графиком функции является часть параболы, ветви направлены
вверх. Найдём вершину параболы по формуле х=-b/2a
х=-(-4)/2·1=2
у=22-4·2+4=0
Итак, вершина параболы
в точке с координатой (2;0).
Найдём точки пересечения с осью OX;
у=0
х2-4х+4=(х-2)2 ; х=0
Точки пересечения с осью OX: (0;2).
Найдём точки пересечения с осью Oу: х=0
у=02-4·0+4=4
Точки пересечения с осью OX: (0;4).
Найдём дополнительные точки
х
1
2
3
4
5
у
1
0
1
4
9
2) Второй график у= х –прямая, проходящая через начало координат.Часть прямой, находящийся в 1 и 3 четверти.
х
-2
-1
0
1
у
-2
-1
0
1
3)Третьим графиком у=4/x, является гипербола, которая находится в 3 четверти.
Построим часть гиперболы при х-2
х
-2
-4
-5
-6
у
-2
-1
-0,8
-2/3
Ответ: прямая у=m имеет с графиком одну общую точку при m=-2 и m>1
Постройте график функции у=.
При каких значениях х выполняется неравенство у3?Область определения данной функции D(у)=(-;0)(0;2) (2;+).
Разложим числитель и знаменатель на множители дроби вынесением общего множителя за скобки. Дальше числитель разложим на множители по формуле
ax2+bx+c=a(x-x1)(x-x2)
Преобразуем дробь: у====-х-1
у=-х-1-линейная функция, графиком является прямая, рисунок 1
рис.1
Для того , чтобы ответить на вопрос
рассмотрим рисунок 2
Рис.2
Ответ: неравенство у3 выполняется при
-4х2.
Найдите все значения к, при которых прямая у=кх пересекает в трёх точках ломанную, заданную условием:
2х+4, если х
у= -2, если-33
2х-8,если х>3
Прямая y= kx пересекает в трех
различных точках эту ломаную, если ее угловой
коэффициент больше углового коэффициента
прямой, проходящей через точку –(3; -2), и
меньше углового коэффициента прямой,
парал.
прямым у=2х+4 ,у=2х-8 .Найдем угловой коэффициент прямой,
проходящей через точку (-3;-2)
-2=-3к, к=2/3
Угловой коэффициент k прямой, парал.
Прямой у=2х+8 , равен 2.
Ответ: прямая имеет с ломанной три общие точки при 2/3
Кусочные функции — функции математического анализа
Это функция, поэтому каждое значение x имеет только одно значение y.
Кусочная функция — это функция, состоящая из частей. Вы заметите, что, хотя может быть несколько разных частей, мы должны быть осторожны, чтобы не иметь несколько выходов (значений y), принадлежащих одному входу (значению x).
Посмотрите на кусочную функцию справа. Предполагая, что каждый блок представляет собой одну единицу, оказывается, что при значении x, равном 2, три разные части функции перекрываются. Но мы знаем, что этого не может быть, иначе это не было бы функцией. Это когда закрытые и открытые точки возвращаются в игру на наших графах предметной области (см. Проект 1, стр. 2). Если точка открыта, то координата исключается, если закрыта, то включается. Вы заметите, что только (2,6) фактически включены в домен.Если бы мы написали уравнение для графика справа, оно выглядело бы так: 6
Это непрерывная функция.
Давайте напишем уравнение для кусочной функции слева, затем пройдемся по тому, как мы будем его изображать, а затем определим домен и диапазон.
Начнем с параболы, так как она самая левая. Парабола является родительской параболой y=x². Но парабола перестает существовать при x=2. Таким образом, парабола будет обозначаться как y=x², x<2.
Линия горизонтальна и находится в точке y=-1, а существа существуют в точке x=2, поэтому она обозначается как y=-1, x < 2.
Наше окончательное уравнение:
f(x) {x², x<2
-1, x > 2
Обратите внимание, что мы используем знак «больше или равно» для области определения горизонтальной линии. «Равно» указывает, что линия y = -1 будет иметь закрытую точку в точке 2. Но y = x² имеет только знак «меньше», который указывает, что круг в точке 2 будет незамкнутым. Это очень важно, поскольку делает функцию функцией.Графики просты, просто работайте в обратном порядке. Если бы мы еще не могли видеть график, мы бы начали с изучения уравнения. Сначала мы нарисуем параболу, а затем прямую. Затем мы стерли бы любую параболу, показанную после x=2. Мы бы поставили открытую точку на x = 2 для параболы и стрелку на другом конце. Линия, которую мы бы стерли после x=2. Мы бы поставили закрытую точку на x=2 и стрелку на другом конце.
Определим область определения кусочной функции. Мы можем видеть, что функция стремится к отрицательной бесконечности, поэтому: (-бесконечность. (Помните, что бесконечность недостижима, поэтому мы используем скобки). Функция также стремится к положительной бесконечности, поэтому наша конечная область значений будет: ( -бесконечность, бесконечность).
Попробуйте найти домен первого графика справа. Нажмите кнопку ниже, чтобы открыть ответ.Отвечать
Это прерывистая функция.
Обратите внимание, что кусочные функции МОГУТ иметь разрыв в графике и все же могут быть функцией. Изучите график слева. Функция не существует при x=0, потому что оба луча имеют открытую точку. Тем не менее, это все еще функция, потому что технически каждый вход x по-прежнему имеет один выход y.
Эта функция просто прерывистая , что означает наличие разрыва. Две приведенные выше кусочные функции являются непрерывными , потому что в функциях нет разрывов. Однако и разрывные, и непрерывные кусочно-функции являются функциями.
Домен для кусочной функции слева будет использовать символ объединения «u» для обозначения того, что домен предназначен для функции, но есть разрыв: (-бесконечность, 0) u (0, бесконечность).
Проект 3 Начало
Кусочно-определенные функции — объяснение, поиск области и часто задаваемые вопросы
Кусочно-определенная функция — это функция, описываемая не одним (одним) уравнением, а двумя или более. Примите во внимание следующее определение функции:
9{2}, 0 \leq x < 1 \end{matrix}\right.\]Упомянутое выше кусочное уравнение является примером уравнения для кусочно заданной функции, в котором утверждается, что определение функции различно на разных участках ее домен.
Для кусочно определенной функции, приведенной выше, областью определения является [−1, 1][−1, 1], но определение функции на [−1, 0][−1, 0] отличается от определения функции на [ 0, 1][0, 1].Как найти область определения кусочной функции
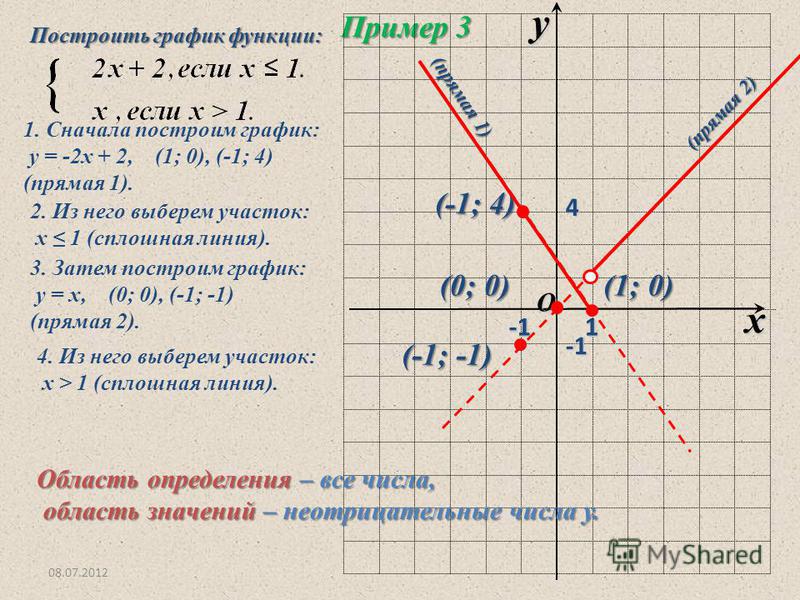
Давайте научимся находить область определения и область значений кусочной функции 9{2} \text{ если x < 0} \\ y = x + 2 \text{ если 0 }\leq x \leq 3 \\ y = 4 \text{ если x }> 3\end{matrix}\right .\]
Очень важно учитывать знаки больше/меньше или равно, потому что две точки в одной и той же области сделают так, что график не будет функцией. Тем не менее:
y = x² — это простая парабола, и вы, вероятно, знаете, что она начинается в начале координат (0, 0) и бесконечно тянется в обоих направлениях. Но наше ограничение — все значения x меньше (<) 0, поэтому мы нарисуем только левую половину графика и оставим незакрашенный кружок в точке (0, 0), так как ограничение меньше 0, и не включает 0,
Наш следующий график представляет собой нормальную линейную функцию, сдвинутую вверх на два, но появляется только от 0 до 3 и включает оба, поэтому мы нарисуем график от 0 до 3 с заштрихованными кругами на 0 и 3.
Окончательная функция — простейшая функция, постоянная функция от y = 4, где есть только горизонтальная линия при значении 4 по оси y, но только после 3 по оси x из-за нашего ограничения.
Посмотрим, как это будет выглядеть без ограничений:
(Изображение будет загружено в ближайшее время)
Теперь давайте найдем область определения и диапазон кусочной функции, добавив ограничения в операторах «если»: от 0 до 3, и константа появляется только после 3, таким образом:
Домен: (−∞, ∞)
Диапазон: (0, ∞)
Наша область значений — это все действительные числа, поскольку наши значения x непрерывны. вдоль оси x, видя, что у нас есть один заштрихованный кружок на линейной функции при x = 0 и один заштрихованный кружок на линейной функции при x = 3. Таким образом, постоянная функция продолжается бесконечно вправо, несмотря на то, что функции визуально останавливаются , график все еще продолжается, следовательно, все действительные числа.
Наш диапазон начинается с 0, но не включает его и продолжается до бесконечности из-за того, что график не опускается ниже y = 0, а самая нижняя точка является квадратичной, не касаясь оси x в начале координат, (0, 0), и тянется бесконечно вверх.
(Изображение будет загружено в ближайшее время)
Решенные примеры
Решение кусочных функций требует построения графиков. Давайте разберемся, как работать с кусочно определенной функцией
Пример:
\[\left\{\begin{matrix} y = x + 2 \text{ если }x < 0 \\ 2 \text{ для }0 \leq x \leq 1 \\ -x + 3 \text{ для }x > 1\end{matrix}\right.\]
Решение:
В этом примере функция является кусочно-линейной, поскольку каждая из трех частей графика представляет собой прямую.
Кусочно-определенные функции также могут содержать разрывы («скачки»).
Функция в приведенном ниже примере состоит из разрывов при x = −2x = −2 и x = 2.Пример:
Нарисуйте график функции, описанной ниже: 9{2} \text{ for }x \leq 2\end{matrix}\right.\]
Обратите внимание, что мы используем маленькие белые кружки на графике, чтобы показать, что конечная точка кривой не включена на графике и сплошные точки для отображения включенных конечных точек.
Пример:
Постройте график функции, определенной ниже.
y = logx для 0
1/(x−2) для x≥1
Решение:
Отрицательные значения x и 0 исключаются из домена, поскольку первая функция, logx, не определены для этих значений. Значение x=2 не включено в домен, так как 2-я функция для этого значения не определена (там она содержит вертикальную асимптоту). Таким образом, область определения этой функции равна {x | 0<х<2}∪{х | х>2}. Это можно проиллюстрировать, используя обозначение интервала как (0,2) ∪ (2, ∞).
2, т.е. 27. f(-3) должна быть функцией связанного уравнения.
Например, область определения f (x) = x² — это все действительные числа, а область определения g (x) = 1 / x — все действительные числа, кроме x = 0.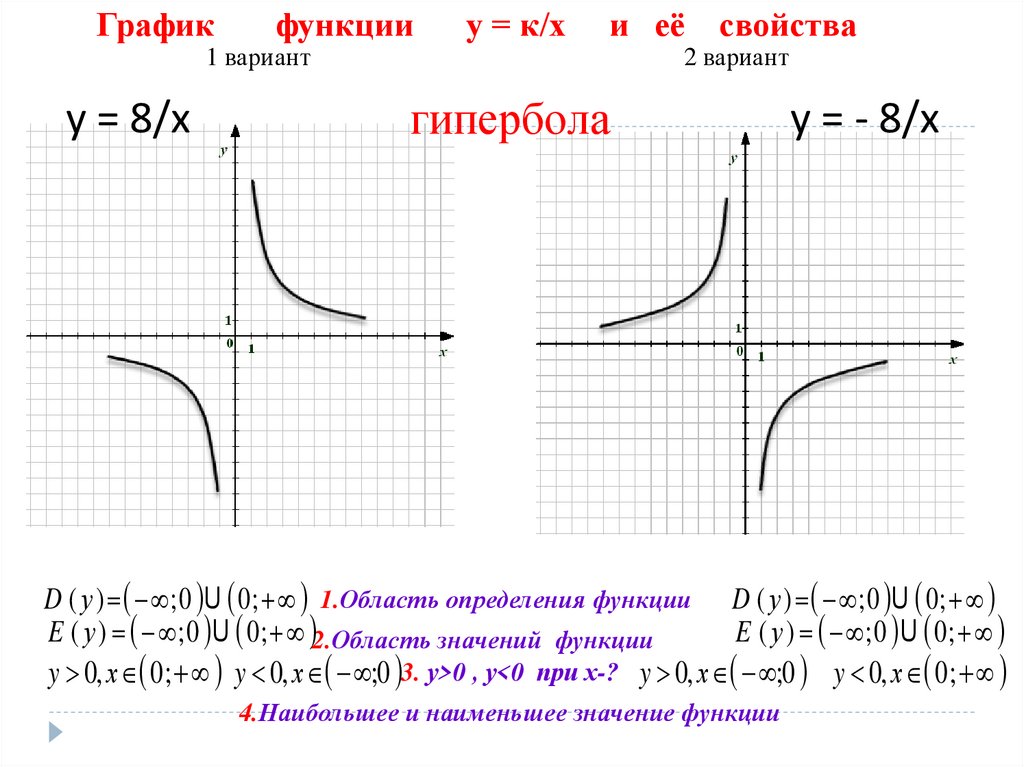
Участки числовой прямой, которые различаются формулами задания, назовём составляющими область определения, а их объединение, является областью определения кусочной функции. Точки, которые делят область определения на составляющие, называются граничными точками. Выражения, определяющие кусочную функцию на каждой составляющей области определения, называется входящими функциями.
Построим её часть (х0) путем сдвига вниз на 1 графика у= х2.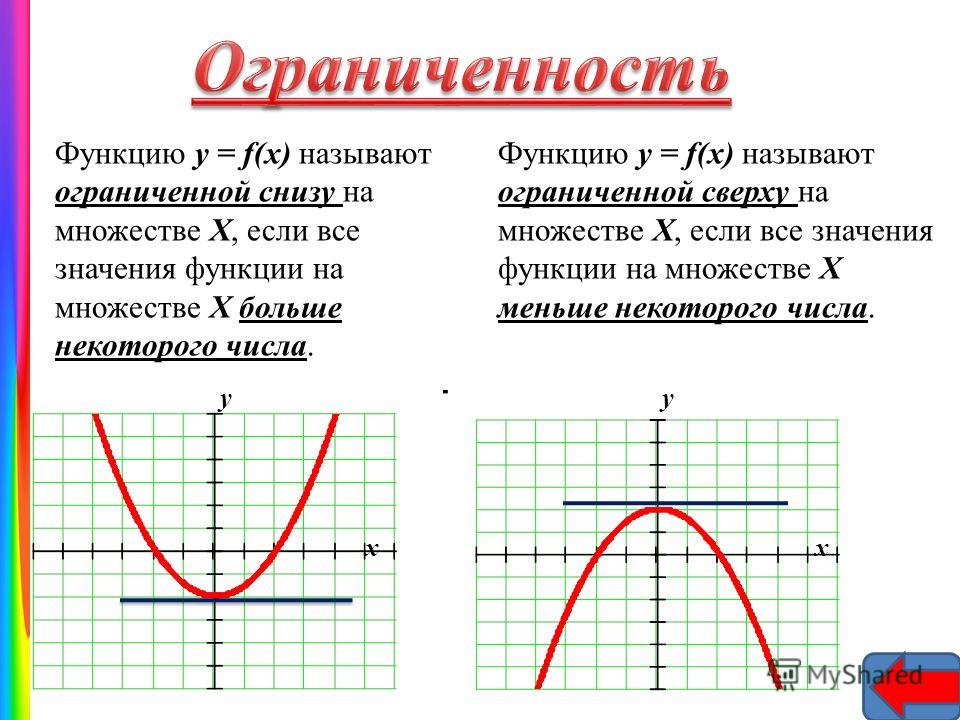
При каких значениях х выполняется неравенство у3?
прямым у=2х+4 ,у=2х-8 .
Проект 1, стр. 2). Если точка открыта, то координата исключается, если закрыта, то включается. Вы заметите, что только (2,6) фактически включены в домен.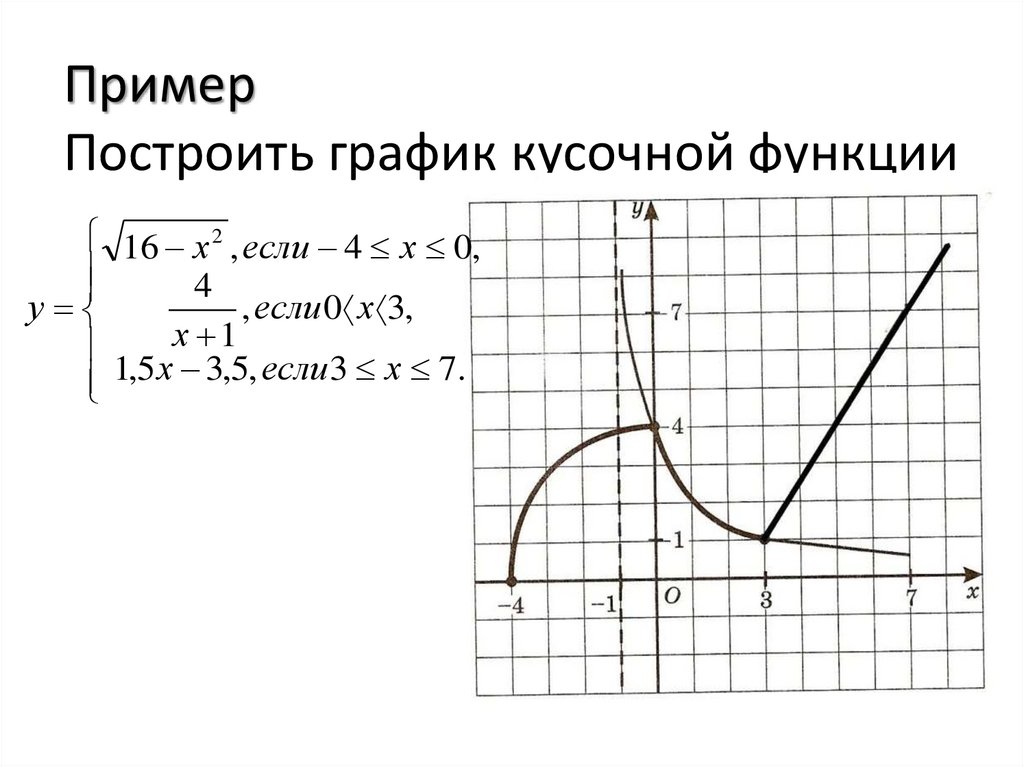
Для кусочно определенной функции, приведенной выше, областью определения является [−1, 1][−1, 1], но определение функции на [−1, 0][−1, 0] отличается от определения функции на [ 0, 1][0, 1].
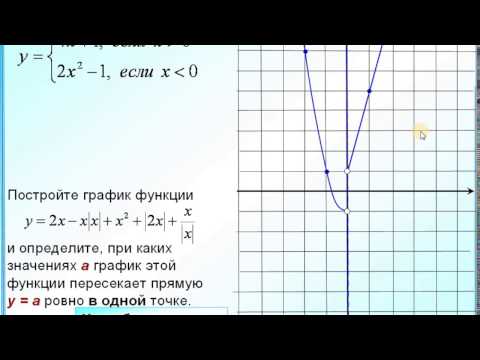
Функция в приведенном ниже примере состоит из разрывов при x = −2x = −2 и x = 2.