Область определения и область значений функции
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Область определения и область значений функции
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЗНАЧЕНИЙ ФУНКЦИИ
Математика есть такая наука,
которая показывает, как из
знаемых количеств находить
другие, нам еще неизвестные.
Д.С. Аничков
Цель урока: научиться находить область определения
функции, заданной формулой.

Задачи урока:
Повторить понятие функции, области определения и
области значений функции;
Повторить нахождение области определения и
области значений функции, заданной графиком;
Систематизировать знания по нахождению области
определения и области значений функций,
изученных ранее.
3. Понятие функции
ПОНЯТИЕ ФУНКЦИИФункция – это такая зависимость переменной У от переменной Х,
при которой каждому значению Х соответствует единственное
значение У.
У
Х
Х
f(x)
у = f(х)
х – независимая переменная, аргумент
у – зависимая переменная, результат,
функция.
У
4. Являются ли изображенные на рисунках линии графиками некоторых функций?
ЯВЛЯЮТСЯ ЛИ ИЗОБРАЖЕННЫЕ НА РИСУНКАХЛИНИИ ГРАФИКАМИ НЕКОТОРЫХ ФУНКЦИЙ?
Не функция
1
Не функция
2
Подсказка
Функция
3
5. Являются ли изображенные на рисунках линии графиками некоторых функций?
ЯВЛЯЮТСЯ ЛИ ИЗОБРАЖЕННЫЕ НА РИСУНКАХЛИНИИ ГРАФИКАМИ НЕКОТОРЫХ ФУНКЦИЙ?
Рис.
 1
1Рис.2
у
0
х
у
0
х
6. Область определения и область значений функции
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЗНАЧЕНИЙ ФУНКЦИИ
Все значения независимой переменной х образуют
область определения функции D(f)
Все значения, которые принимает зависимая переменная у,
образуют область значений функции E(f)
Область значений
функции
E(f)
(х)
у
f
Область определения
функции
х
D(f)
7. Найти Область определения и область значений функции
НАЙТИ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЗНАЧЕНИЙ ФУНКЦИИ
Область определения
функции:
1 х 4
у
3
Область значений
функции:
2
1 у 3
y=f(x)
1
х
-1
0
1
2
3
4
у
1
у = f(x)
х
0 1
Ответ:
Какова
функции?
Каковаобласть
областьопределения
значений функции?
E(f)
D(f)==[-2;4]
[-5;5]
у
у = f(x)
1
-1
0
х
0 1
Вопрос:
Какова
Каковаобласть
областьзначений
определения
функции?
функции?
Ответ:
; 1
;1;1
1;
10.
 найти область определения и область значений функции по ее графикуНАЙТИ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ
найти область определения и область значений функции по ее графикуНАЙТИ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЗНАЧЕНИЙ ФУНКЦИИ ПО ЕЕ ГРАФИКУ
D( у) 0;2 2;
у
Е( у) ; 1 0;
0
-1
2
х
11. Область определения и область значений функции
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЗНАЧЕНИЙ ФУНКЦИИ
№ Аналитическая
модель
1
у кх в
График
функции
у
у
3
к
х
у ах вх с
а 0
2
Область значений
D( y ) ( ; ) Е ( y ) ( ; )
0
2
Область определения
х
у
к 0
0
х
у
к 0
а 0
ув
0
а 0
х
ув
D( y) ( ;0) (0; ) Е ( y) ( ;0) (0; )
D( y ) ( ; )
Е ( y) ув ;
Е ( y) ; ув
12. Область определения и область значений функции
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЗНАЧЕНИЙ ФУНКЦИИ
№ Аналитическая
модель
График
функции
4
у
у х
0
5
у
х
Область значений
D( y ) ( ; )
Е( y) 0;
х
у
0
Область определения
х
D(y) 0;
Е( y) 0;
1) y 3 х 2
2) y 3х 2 2
3) y х 12
х 12 0
3х
4) y
х 23
х 23 0
5) y 2 х 2 3х 4
34
6) y
х 45
1
7) y
2х 1
х 2 3х 4 0
х 45 0
2 х 1 0
14.
 Найдите область определения функции:НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ:
Найдите область определения функции:НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ:Вариант 1
Вариант 2
y х2 2
6
2) y
x 2
y х 2 31
23
2) y
3 х
1)
3)
y
1)
х 4
3)
2
y
х
4 х 12
4)
6 х 23
5) y
x 2 3х
2
y
х
2 х 43
4)
6х 2
5) y
x2 2х
6)
y
х 4
2
7) y х 2 х 43х
8) y х 2 4 х 3
5
6)
y
х 9
2
y х 4 12 х 2 13х
3
х 5
y 2 х
5
х 2
7)
8) y
х2 9
х 3
х 12
5
х 4
15. Проверь себя
ПРОВЕРЬ СЕБЯВариант 1
1)
2)
D(y) ;
D( у) ; 2 2;
Вариант 2
1)
D(y) ;
2)
D( у) ;3 3;
3)
D(y) 4;
3)
D(y) 2;
4)
D(y) ;
4)
D( y) ;
5)
D( у) ; 3 3;0 0;
6)
D(у) ; 3 3;
5)
6)
D( у) ; 2 2;0 0;
D(у) ; 2 2;
8)
;
D( y) 2;
7)
D(y) ;
8)
D(у) 4; 3 3;12 12;
Задание на дом
№8.
 6 (а), 8.11 (б), 8.16 (а, б), 8.22
6 (а), 8.11 (б), 8.16 (а, б), 8.22Историческая справка
Рене Декарт.
(1596-1650),франц.
философ, математик,
физик, филолог. Заложил
основы аналитической
геометрии, дал понятие
переменной величины и
функции, ввел многие
алгебраические
обозначения.
English Русский Правила
Как определить область значения параболы
Содержание
- Тестирование онлайн
- Определение. График
- Преобразование параболы
- Ответ
- Проверено экспертом
Тестирование онлайн
Определение. График
Квадратичной (квадратной) функцией называется функция вида
где a, b, с — числа.
Графиком квадратичной функции является парабола.
Парабола имеет вершину, ось, проведенная через вершину и параллельная оси Оу, делит параболу на две симметричные части. Вершиной параболы называется точка
Если коэффициент а>0, то ветви параболы направлены вверх, если a 2
1) Областью определения функции является множество всех действительных чисел, т. е.
е.
2) Множеством значений функции является промежуток
3) Значение функции y=0 является наименьшим, а наибольшего значения функция не имеет.
4) Функция является четной, график симметричен относительно оси Оу.
6)Парабола имеет с осями координат единственную общую точку (0;0) — начало координат.
7) Значение аргумента x=0 является нулем функции.
8) На промежутке функция убывающая, а на промежутке — возрастающая.
9) Функция принимает положительные значения на множестве , т.е. все точки параболы, кроме начала координат.
Преобразование параболы
Функция y=x 2 — частный случай квадратичной функции.
Квадратичную функцию всегда можно привести у виду , а затем построить параболу с помощью ее геометрических преобразований.
Для построения параболы необходимо:
1) Найти координаты вершины
2) Построить ось симметрии, проанализировать куда направлены ветви параболы
3) Найти точки пересечения параболы с осью Ox (нули), если они есть, решив уравнение
4) Найти точку пересечения с осью Оу, решив уравнение
Зачастую в рамках решения задач нам приходится искать множество значений функции на области определения или отрезке.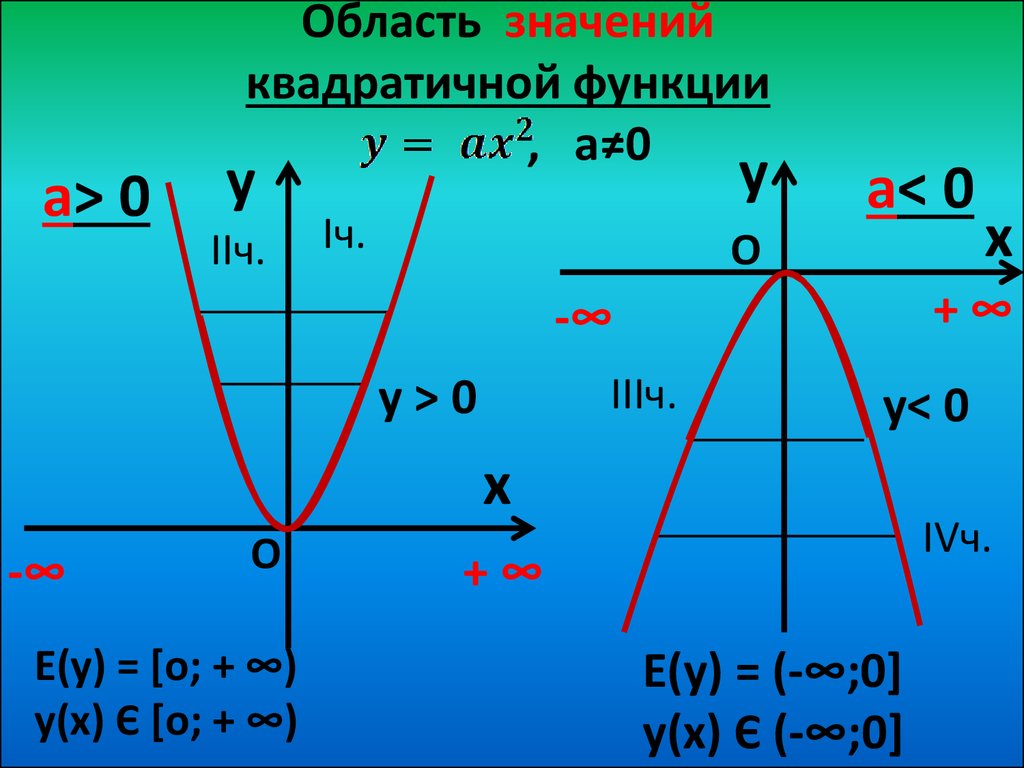 Например, это нужно делать при решении разных типов неравенств, оценках выражений и др.
Например, это нужно делать при решении разных типов неравенств, оценках выражений и др.
В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми ее можно вычислить, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графиками. Прочитав эту статью, вы получите исчерпывающее представление об области значений функции.
Начнем с базовых определений.
Множество значений функции y = f ( x ) на некотором интервале x представляет собой множество всех значений, которые данная функция принимает при переборе всех значений x ∈ X .
Область значений функции y = f ( x ) – это множество всех ее значений, которые она может принять при переборе значений x из области x ∈ ( f ) .
Область значений некоторой функции принято обозначать E ( f ) .
Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.
Важно также различать область значений и область допустимых значений переменной x для выражения в правой части y = f ( x ) . Область допустимых значений x для выражения f ( x ) и будет областью определения данной функции.
Ниже приводится иллюстрация, на которой показаны некоторые примеры. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.
Очевидно, что область значений функции можно получить при проецировании графика функции на ось O y . При этом она может представлять собой как одно число, так и множество чисел, отрезок, интервал, открытый луч, объединение числовых промежутков и др.
Рассмотрим основные способы нахождения области значений функции.
Начнем с определения множества значений непрерывной функции y = f ( x ) на некотором отрезке, обозначенном [ a ; b ] . Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего m a x x ∈ a ; b f ( x ) и наименьшего значения m i n x ∈ a ; b f ( x ) .
Возьмем задачу, в которой нужно определить область значений арксинуса.
Условие: найдите область значений y = a r c sin x .
Решение
В общем случае область определения арксинуса располагается на отрезке [ — 1 ; 1 ] . Нам надо определить наибольшее и наименьшее значение указанной функции на нем.
y ‘ = a r c sin x ‘ = 1 1 — x 2
Мы знаем, что производная функции будет положительной для всех значений x , расположенных в интервале [ — 1 ; 1 ] , то есть на протяжении всей области определения функция арксинуса будет возрастать. Значит, самое маленькое значение она примет при x , равном — 1 , а самое большое – при x , равном 1 .
m i n x ∈ — 1 ; 1 a r c sin x = a r c sin — 1 = — π 2 m a x x ∈ — 1 ; 1 a r c sin x = a r c sin 1 = π 2
Таким образом, область значений функции арксинус будет равна E ( a r c sin x ) = — π 2 ; π 2 .
Ответ: E ( a r c sin x ) = — π 2 ; π 2
Условие: вычислите область значений y = x 4 — 5 x 3 + 6 x 2 на заданном отрезке [ 1 ; 4 ] .
Решение
Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.
Для определения точек экстремума надо произвести следующие вычисления:
y ‘ = x 4 — 5 x 3 + 6 x 2 ‘ = 4 x 3 + 15 x 2 + 12 x = x 4 x 2 — 15 x + 12 y ‘ = 0 ⇔ x ( 4 x 2 — 15 x + 12 ) = 0 x 1 = 0 ∉ 1 ; 4 и л и 4 x 2 — 15 x + 12 = 0 D = — 15 2 — 4 · 4 · 12 = 33 x 2 = 15 — 33 8 ≈ 1 . 16 ∈ 1 ; 4 ; x 3 = 15 + 33 8 ≈ 2 . 59 ∈ 1 ; 4
Теперь найдем значения заданной функции в концах отрезка и точках x 2 = 15 — 33 8 ; x 3 = 15 + 33 8 :
y ( 1 ) = 1 4 — 5 · 1 3 + 6 · 1 2 = 2 y 15 — 33 8 = 15 — 33 8 4 — 5 · 15 — 33 8 3 + 6 · 15 — 33 8 2 = = 117 + 165 33 512 ≈ 2 . 08 y 15 + 33 8 = 15 + 33 8 4 — 5 · 15 + 33 8 3 + 6 · 15 + 33 8 2 = = 117 — 165 33 512 ≈ — 1 . 62 y ( 4 ) = 4 4 — 5 · 4 3 + 6 · 4 2 = 32
62 y ( 4 ) = 4 4 — 5 · 4 3 + 6 · 4 2 = 32
Значит, множество значений функции будет определяться отрезком 117 — 165 33 512 ; 32 .
Ответ: 117 — 165 33 512 ; 32 .
Перейдем к нахождению множества значений непрерывной функции y = f ( x ) в промежутках ( a ; b ) , причем a ; + ∞ , — ∞ ; b , — ∞ ; + ∞ .
Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведении функции в заданных условиях. Для этого у нас есть все необходимые данные.
Условие: вычислите область значений функции y = 1 x 2 — 4 на интервале ( — 2 ; 2 ) .
Решение
Определяем наибольшее и наименьшее значение функции на заданном отрезке
y ‘ = 1 x 2 — 4 ‘ = — 2 x ( x 2 — 4 ) 2 y ‘ = 0 ⇔ — 2 x ( x 2 — 4 ) 2 = 0 ⇔ x = 0 ∈ ( — 2 ; 2 )
У нас получилось максимальное значение, равное 0 , поскольку именно в этой точке происходит перемена знака функции и график переходит к убыванию. См. на иллюстрацию:
См. на иллюстрацию:
То есть y ( 0 ) = 1 0 2 — 4 = — 1 4 будет максимальным значений функции.
Теперь определим поведение функции при таком x, который стремится к — 2 с правой стороны и к + 2 с левой стороны. Иными словами, найдем односторонние пределы:
lim x → — 2 + 0 1 x 2 — 4 = lim x → — 2 + 0 1 ( x — 2 ) ( x + 2 ) = = 1 — 2 + 0 — 2 — 2 + 0 + 2 = — 1 4 · 1 + 0 = — ∞ lim x → 2 + 0 1 x 2 — 4 = lim x → 2 + 0 1 ( x — 2 ) ( x + 2 ) = = 1 2 — 0 — 2 2 — 0 + 2 = 1 4 · 1 — 0 = — ∞
У нас получилось, что значения функции будут возрастать от минус бесконечности до — 1 4 тогда, когда аргумент изменяется в пределах от — 2 до 0 . А когда аргумент меняется от 0 до 2 , значения функции убывают к минус бесконечности. Следовательно, множеством значений заданной функции на нужном нам интервале будет ( — ∞ ; — 1 4 ] .
Ответ: ( — ∞ ; — 1 4 ] .
Условие: укажите множество значений y = t g x на заданном интервале — π 2 ; π 2 .
Решение
Нам известно, что в общем случае производная тангенса в — π 2 ; π 2 будет положительной, то есть функция будет возрастать. Теперь определим, как ведет себя функция в заданных границах:
lim x → π 2 + 0 t g x = t g — π 2 + 0 = — ∞ lim x → π 2 — 0 t g x = t g π 2 — 0 = + ∞
Мы получили рост значений функции от минус бесконечности к плюс бесконечности при изменении аргумента от — π 2 до π 2 ,и можно сказать, что множеством решений данной функции будет множество всех действительных чисел.
Ответ: — ∞ ; + ∞ .
Условие: определите, какова область значений функции натурального логарифма y = ln x .
Решение
Нам известно, что данная функция является определенной при положительных значениях аргумента D ( y ) = 0 ; + ∞ . Производная на заданном интервале будет положительной: y ‘ = ln x ‘ = 1 x . Значит, на нем происходит возрастание функции. Далее нам нужно определить односторонний предел для того случая, когда аргумент стремится к 0 (в правой части), и когда x стремится к бесконечности:
lim x → 0 + 0 ln x = ln ( 0 + 0 ) = — ∞ lim x → ∞ ln x = ln + ∞ = + ∞
Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.
Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.
Ответ: множество всех действительных чисел – область значений функции натурального логарифма.
Условие: определите, какова область значений функции y = 9 x 2 + 1 .
Решение
Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:
y ‘ = 9 x 2 + 1 ‘ = — 18 x ( x 2 + 1 ) 2 y ‘ = 0 ⇔ x = 0 y ‘ ≤ 0 ⇔ x ≥ 0 y ‘ ≥ 0 ⇔ x ≤ 0
В итоге мы определили, что данная функция будет убывать, если x ≥ 0 ; возрастать, если x ≤ 0 ; она имеет точку максимума y ( 0 ) = 9 0 2 + 1 = 9 при переменной, равной 0 .
Посмотрим, как же ведет себя функция на бесконечности:
lim x → — ∞ 9 x 2 + 1 = 9 — ∞ 2 + 1 = 9 · 1 + ∞ = + 0 lim x → + ∞ 9 x 2 + 1 = 9 + ∞ 2 + 1 = 9 · 1 + ∞ = + 0
Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.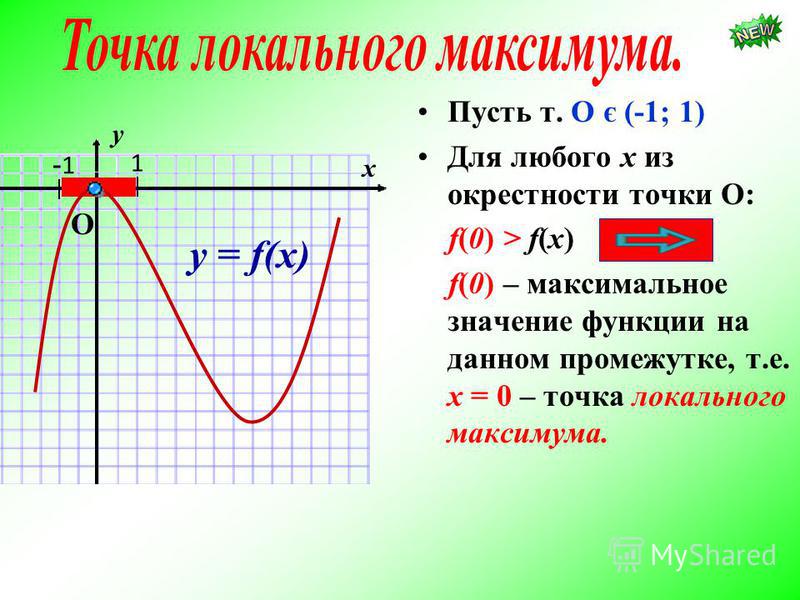
Подведем итоги: когда аргумент изменяется от минус бесконечности до нуля, то значения функции возрастают от 0 до 9 . Когда значения аргумента меняются от 0 до плюс бесконечности, соответствующие значения функции будут убывать от 9 до 0 . Мы отобразили это на рисунке:
На нем видно, что областью значений функции будет интервал E ( y ) = ( 0 ; 9 ]
Ответ: E ( y ) = ( 0 ; 9 ]
Если нам надо определить множество значений функции y = f ( x ) на промежутках [ a ; b ) , ( a ; b ] , [ a ; + ∞ ) , ( — ∞ ; b ] , то нам понадобится провести точно такие же исследования. Эти случаи мы пока не будем разбирать: далее они нам еще встретятся в задачах.
А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.
Условие: определите, какова будет область значений y = x x — 2 .
Решение
Поскольку знаменатель функции не должен быть обращен в 0 , то D ( y ) = — ∞ ; 2 ∪ 2 ; + ∞ .
Начнем с определения множества значений функции на первом отрезке — ∞ ; 2 , который представляет из себя открытый луч. Мы знаем, что функция на нем будет убывать, то есть производная данной функции будет отрицательной.
lim x → 2 — 0 x x — 2 = 2 — 0 2 — 0 — 2 = 2 — 0 = — ∞ lim x → — ∞ x x — 2 = lim x → — ∞ x — 2 + 2 x — 2 = lim x → — ∞ 1 + 2 x — 2 = 1 + 2 — ∞ — 2 = 1 — 0
Тогда в тех случаях, когда аргумент изменяется по направлению к минус бесконечности, значения функции будут асимптотически приближаться к 1 . Если же значения x меняются от минус бесконечности до 2 , то значения будут убывать от 1 до минус бесконечности, т.е. функция на этом отрезке примет значения из интервала — ∞ ; 1 . Единицу мы исключаем из наших рассуждений, поскольку значения функции ее не достигают, а лишь асимптотически приближаются к ней.
Для открытого луча 2 ; + ∞ производим точно такие же действия. Функция на нем также является убывающей:
Функция на нем также является убывающей:
lim x → 2 + 0 x x — 2 = 2 + 0 2 + 0 — 2 = 2 + 0 = + ∞ lim x → + ∞ x x — 2 = lim x → + ∞ x — 2 + 2 x — 2 = lim x → + ∞ 1 + 2 x — 2 = 1 + 2 + ∞ — 2 = 1 + 0
Значения функции на данном отрезке определяются множеством 1 ; + ∞ . Значит, нужная нам область значений функции, заданной в условии, будет объединением множеств — ∞ ; 1 и 1 ; + ∞ .
Ответ: E ( y ) = — ∞ ; 1 ∪ 1 ; + ∞ .
Это можно увидеть на графике:
Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.
Условие: определите область значений синуса y = sin x .
Решение
Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0 ; 2 π и смотрим, каким будет множество значений на нем.
y ‘ = ( sin x ) ‘ = cos x y ‘ = 0 ⇔ cos x = 0 ⇔ x = π 2 + πk , k ∈ Z
В рамках 0 ; 2 π у функции будут точки экстремума π 2 и x = 3 π 2 . Подсчитаем, чему будут равны значения функции в них, а также на границах отрезка, после чего выберем самое большое и самое маленькое значение.
Подсчитаем, чему будут равны значения функции в них, а также на границах отрезка, после чего выберем самое большое и самое маленькое значение.
y ( 0 ) = sin 0 = 0 y π 2 = sin π 2 = 1 y 3 π 2 = sin 3 π 2 = — 1 y ( 2 π ) = sin ( 2 π ) = 0 ⇔ min x ∈ 0 ; 2 π sin x = sin 3 π 2 = — 1 , max x ∈ 0 ; 2 π sin x = sin π 2 = 1
Ответ: E ( sin x ) = — 1 ; 1 .
Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения. Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.
Условие: определите область значения y = 3 a r c cos x 3 + 5 π 7 — 4 .
Решение
Нам известно, что отрезок от 0 до пи есть область значений арккосинуса. Иными словами, E ( a r c cos x ) = 0 ; π или 0 ≤ a r c cos x ≤ π . Мы можем получить функцию a r c cos x 3 + 5 π 7 из арккосинуса, сдвинув и растянув ее вдоль оси O x , но такие преобразования нам ничего не дадут. Значит, 0 ≤ a r c cos x 3 + 5 π 7 ≤ π .
Функция 3 a r c cos x 3 + 5 π 7 может быть получена из арккосинуса a r c cos x 3 + 5 π 7 с помощью растяжения вдоль оси ординат, т.е. 0 ≤ 3 a r c cos x 3 + 5 π 7 ≤ 3 π . Финалом преобразований является сдвиг вдоль оси O y на 4 значения. В итоге получаем двойное неравенство:
0 — 4 ≤ 3 a r c cos x 3 + 5 π 7 — 4 ≤ 3 π — 4 ⇔ — 4 ≤ 3 arccos x 3 + 5 π 7 — 4 ≤ 3 π — 4
Мы получили, что нужная нам область значений будет равна E ( y ) = — 4 ; 3 π — 4 .
Ответ: E ( y ) = — 4 ; 3 π — 4 .
Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.
Условие: вычислите, какова будет область значений функции y = 2 2 x — 1 + 3 .
Решение
Перепишем функцию, заданную в условии, как y = 2 · ( 2 x — 1 ) — 1 2 + 3 . Для степенной функции y = x — 1 2 область значений будет определена на промежутке 0 ; + ∞ , т.е. x — 1 2 > 0 . В таком случае:
2 x — 1 — 1 2 > 0 ⇒ 2 · ( 2 x — 1 ) — 1 2 > 0 ⇒ 2 · ( 2 x — 1 ) — 1 2 + 3 > 3
Значит, E ( y ) = 3 ; + ∞ .
Ответ: E ( y ) = 3 ; + ∞ .
Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.
Условие: дана функция y = 2 sin x 2 — 4 , x ≤ — 3 — 1 , — 3 x ≤ 3 1 x — 3 , x > 3 . Вычислите область ее значений.
Решение
Данная функция является определенной для всех значений x . Проведем ее анализ на непрерывность при значениях аргумента, равных — 3 и 3 :
lim x → — 3 — 0 f ( x ) = lim x → — 3 2 sin x 2 — 4 = 2 sin — 3 2 — 4 = — 2 sin 3 2 — 4 lim x → — 3 + 0 f ( x ) = lim x → — 3 ( 1 ) = — 1 ⇒ lim x → — 3 — 0 f ( x ) ≠ lim x → — 3 + 0 f ( x )
Имеем неустранимый разрыв первого рода при значении аргумента — 3 . При приближении к нему значения функции стремятся к — 2 sin 3 2 — 4 , а при стремлении x к — 3 с правой стороны значения будут стремиться к — 1 .
При приближении к нему значения функции стремятся к — 2 sin 3 2 — 4 , а при стремлении x к — 3 с правой стороны значения будут стремиться к — 1 .
lim x → 3 — 0 f ( x ) = lim x → 3 — 0 ( — 1 ) = 1 lim x → 3 + 0 f ( x ) = lim x → 3 + 0 1 x — 3 = + ∞
Имеем неустранимый разрыв второго рода в точке 3 . Когда функция стремится к нему, ее значения приближаются к — 1 , при стремлении к той же точке справа – к минус бесконечности.
Значит, вся область определения данной функции является разбитой на 3 интервала ( — ∞ ; — 3 ] , ( — 3 ; 3 ] , ( 3 ; + ∞ ) .
На первом из них у нас получилась функция y = 2 sin x 2 — 4 . Поскольку — 1 ≤ sin x ≤ 1 , получаем:
— 1 ≤ sin x 2 1 ⇒ — 2 ≤ 2 sin x 2 ≤ 2 ⇒ — 6 ≤ 2 sin x 2 — 4 ≤ — 2
Значит, на данном промежутке ( — ∞ ; — 3 ] множество значении функции – [ — 6 ; 2 ] .
На полуинтервале ( — 3 ; 3 ] получилась постоянная функция y = — 1 . Следовательно, все множество ее значений в данном случае будет сводится к одному числу — 1 .
На втором промежутке 3 ; + ∞ у нас есть функция y = 1 x — 3 . Она является убывающей, потому что y ‘ = — 1 ( x — 3 ) 2 0 . Она будет убывать от плюс бесконечности до 0 , но самого 0 не достигнет, потому что:
lim x → 3 + 0 1 x — 3 = 1 3 + 0 — 3 = 1 + 0 = + ∞ lim x → + ∞ 1 x — 3 = 1 + ∞ — 3 = 1 + ∞ + 0
Значит, множество значений исходной функции при x > 3 представляет собой множество 0 ; + ∞ . Теперь объединим полученные результаты: E ( y ) = — 6 ; — 2 ∪ — 1 ∪ 0 ; + ∞ .
Ответ: E ( y ) = — 6 ; — 2 ∪ — 1 ∪ 0 ; + ∞ .
Решение показано на графике:
Условие: есть функция y = x 2 — 3 e x . Определите множество ее значений.
Решение
Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:
y ‘ = x 2 — 3 e x ‘ = 2 x e x — e x ( x 2 — 3 ) e 2 x = — x 2 + 2 x + 3 e x = — ( x + 1 ) ( x — 3 ) e x
Мы знаем, что производная обратится в 0 , если x = — 1 и x = 3 . Поместим эти две точки на ось и выясним, какие знаки будет иметь производная на получившихся интервалах.
Поместим эти две точки на ось и выясним, какие знаки будет иметь производная на получившихся интервалах.
Функция будет убывать на ( — ∞ ; — 1 ] ∪ [ 3 ; + ∞ ) и возрастать на [ — 1 ; 3 ] . Точкой минимума будет — 1 , максимума – 3 .
Теперь найдем соответствующие значения функции:
y ( — 1 ) = — 1 2 — 3 e — 1 = — 2 e y ( 3 ) = 3 2 — 3 e 3 = 6 e — 3
Посмотрим на поведение функции на бесконечности:
lim x → — ∞ x 2 — 3 e x = — ∞ 2 — 3 e — ∞ = + ∞ + 0 = + ∞ lim x → + ∞ x 2 — 3 e x = + ∞ 2 — 3 e + ∞ = » open=» + ∞ + ∞ = = lim x → + ∞ x 2 — 3 ‘ e x ‘ = lim x → + ∞ 2 x e x = » open=» + ∞ + ∞ = = lim x → + ∞ 2 x ‘ ( e x ) ‘ = 2 lim x → + ∞ 1 e x = 2 · 1 + ∞ = + 0
Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.
На нем видно, что значения функции будут убывать от плюс бесконечности до — 2 e тогда, когда аргумент меняется от минус бесконечности до — 1 . Если же он изменяется от 3 до плюс бесконечности, то значения будут убывать от 6 e — 3 до 0 , но при этом 0 достигнут не будет.
Таким образом, E ( y ) = [ — 2 e ; + ∞ ) .
Ответ: E ( y ) = [ — 2 e ; + ∞ )
- 5 — 9 классы
- Алгебра
- 8 баллов
как найти область значений функции у параболы
- Попроси больше объяснений
- Следить
- Отметить нарушение
Zonder555 18.04.2013
Ответ
Проверено экспертом
1) Если функция f(x) задана графиком, то нужно найти на графике координату у₀ вершины параболы.
Если ветви параболы направлены вниз, то область значений E(f)=(-∞;y₀].
Если ветви параболы направлены вверх, то область значений E(f)=[y₀;+∞).
2) Если функция задана формулой f(x) = ax²+bx+c, то сначала нужно найти координаты вершины. Сначала координату х : . Затем ее подставить в формулу и найти координату у₀=f(x₀)=ax₀²+bx₀+c.
Если a>0, то область значений функции E(f)=[y₀;+∞).
Если а 0, то область значений функции E(f)=[y₀;+∞).
«>
Название урока и класс: | Функция. Область определения и область значений функции, 9 класс | ||
Цели: | Систематизировать и расширить представления о функциях; выработать умение находить значения функции по заданным значениям аргумента и обратно; выработать умение находить область определения и область значений функции. | ||
Планируемые результаты: | Учащиеся научатся находить область определения и область значений функций, заданных таблицей, графически и с помощью формулы | ||
Этап урока | Время (мин. | Деятельность учителя | Ссылки на карточки Учи.ру |
Организационный момент | 3 | Приветствует детей, проверяет их готовность к уроку. Настраивает на активную работу. | |
Результаты диагностической работы | |||
Откройте тетради, запишите число и «Классная работа». | |||
Актуализация знаний | 4 | На доске изображены графики функций и формулы. | |
Составить соответствие между графиками функций и формулами, которыми заданы функции. | |||
Самоопределение к деятельности | 2 | Посмотрите на доску и назовите ключевое слово главы, которую мы с вами сегодня начнем изучать. | |
Правильно. Это функция. Курс алгебры 9 класса начинается с главы «Квадратичная функция», а тема сегодняшнего урока «Функция. Область определения и область значений функции». | |||
Запишите тему урока в тетрадях. | |||
Введение понятия | 3 | Некоторые факты о функции вы изучали раньше. Чтобы вам было немного проще восстанавливать в памяти ранее изученный материал, я предлагаю ответить на следующие вопросы (Презентация, слайд 2) | |
Какую зависимость называют функцией? | |||
Работа по теме урока | 10 | Презентация (слайды 3 – 14) | |
Физкультминутка | 2 | ||
Закрепление материала | 17 | № 1(в), 9(б,г,е), № 6(б). | |
Выполним упражнения от Учи.ру на интерактивной доске | https://uchi.ru/teachers/groups/10005591/subjects/1/course_programs/9/cards/101056 https://uchi.ru/teachers/groups/10005591/subjects/1/course_programs/9/cards/101061 https://uchi.ru/teachers/groups/10005591/subjects/1/course_programs/9/cards/101062 https://uchi.ru/teachers/groups/10005591/subjects/1/course_programs/9/cards/221912 | ||
Подведение итогов урока | 2 | Назовите основные вопросы, которые рассматривали на уроке. | |
Какое задание было самым сложным для вас? | |||
Домашнее задание | 2 | п. | https://uchi.ru/teachers/groups/10005591/subjects/1/course_programs/9/cards/221914 |
45 | |||
Область определения функции y 3 x 1 3: найти область определения функции у=3(х-1) в минус 3 степени — ЭкоДом: Дом своими руками
Содержание
Как найти область определения функции?
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно углубить знания данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y=x+x-2 или y=5·x2+1·x3, y=xx-5 или y=x-15-3. Рассмотрим теорию и решим несколько примеров с подобными заданиями.
Что значит найти область определения
После того, как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Ограничение области определения
Область определения рассматривается еще в школьной курсе. у действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально определить ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
Определение 1
- при имеющемся знаменателе необходимо производить деление такого типа функции как y=x+2·xx4-1;
- при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа y=x+1 или y=23·x+3x;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y=5·(x+1)-3, y=-1+x113, y=(x3-x+1)2, которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y=lnx2+x4 или y=1+logx-1(x+1) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y=x3+tg2·x+5 или y=ctg(3·x3-1), так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y=arcsin(x+2)+2·x2, y=arccosx-1+x, область определения которых определяется ни интервале от -1 до 1.

При отсутствии хотя бы одного признака, область определения приходится искать другим образом. Рассмотрим пример функции вида y=x4+2·x2-x+12+223·x. Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y=2·x+1. Для вычисления ее значения можем определить x. Из выражения 2·x+1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y=3x-1, а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3x-1знаменатель равняется нулю при х=1, поэтому искомая область определения данной функции примет вид (−∞, 1)∪(1, +∞) и считается числовым множеством.
На рассмотрении примера y=x2-5·x+6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю. Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно, чтобы имело место следующее утверждение:
Когда функция ff считается суммой n функций f1, f2, …, fn, иначе говоря, эта функция задается при помощи формулы y=f1(x)+f2(x)+…+fn(x), тогда ее область определения считается пересечением областей определения функций f1, f2, …, fn. Данное утверждение можно записать как:
D(f)=D(f1)D(f2)…D(fn)
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом для понимания перечисления числовых множеств.
Пример 1
Найти область определения функции вида y=x7+x+5+tgx.
Решение
Заданная функция представляется как сумма четырех: степенной с показателем 7,степенной с показателем 1, постоянной, функции тангенса.
По таблице определения видим, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞), D(f3)=(−∞, +∞), причем область определения тангенса включает в себя все действительные числа, кроме π2+π·k, k∈Z.
Областью определения заданной функции f является пересечение областей определения f1, f2, f3 и f4. То есть для функции существует такое количество действительных чисел, куда не входит π2+π·k, k∈Z.
Ответ: все действительные числа кроме π2+π·k, k∈Z.
Для нахождения области определения произведения функций необходимо применять правило:
Определение 2
Когда функция f считается произведением n функций f1, f2, f3 и fn, тогда существует такая функция f, которую можно задать при помощи формулы y=f1(x)·f2(x)·…·fn(x), тогда ее область определения считается областью определения для всех функций.
Запишется D(f)=D(f1)D(f2)…D(fn)
Пример 2
Найти область определения функции y=3·arctg x·ln x.
Решение
Правая часть формулы рассматривается как f1(x)·f2(x)·f3(x), где за f1является постоянной функцией, f2является арктангенсом, f3– логарифмической функцией с основанием e. По условию имеем, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞) и D(f3)=(0, +∞). Мы получаем, что
D(f)=D(f1)D(f2)D(fn)=(-∞, +∞)(-∞, +∞)D(0, +∞)=(0, +∞)
Ответ: область определения y=3·arctg x·ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y=C·f(x), где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y=C·f(x)– произведение постоянной функции и f. Область определения – это все действительные числа области определения D(f). Отсюда видим, что область определения функции y=C·f(x)является -∞, +∞D(f)=D(f).
Получили, что область определения y=f(x) и y=C·f(x), где C является некоторое действительное число, совпадают. Это видно на примере определения корня y=x считается [0, +∞), потому как область определения функции y=-5·x — [0, +∞).
Области определения y=f(x) и y=−f(x)совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Пример 3
Найти область определения функции y=log3x−3·2x.
Решение
Необходимо рассмотреть как разность двух функций f1 и f2.
f1(x)=log3x и f2(x)=3·2x. Тогда получим, что D(f)=D(f1)D(f2).
Область определения записывается как D(f1)=(0, +∞). Приступим к области определения f2 . в данном случае она совпадает с областью определения показательной, тогда получаем, что D(f2)=(−∞, +∞).
Для нахождения области определения функции y=log3x−3·2x получим, что
D(f)=D(f1)D(f2)=(0, +∞)-∞, +∞
Ответ: (0, +∞).
Необходимо озвучить утверждение о том, что областью определения y=anxn+an-1xn-1+…+a1x+a0 является множество действительных чисел.
Рассмотрим y=anxn+an-1xn-1+…+a1x+a0, где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы (n+1)-ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R.
Пример 4
Найти область определения f1(x)=x5+7×3-2×2+12.
Решение
Примем обозначение f за разность двух функций, тогда получим, что f1(x)=x5+7×3-2×2+12 и f2(x)=3·x-ln 5. Выше было показано, что D(f1)=R. Область определения для f2 является совпадающей со степенной при показателе –ln5, иначе говоря, что D(f2)=(0, +∞).
Получаем, что D(f)=D(f1)D(f2)=-∞, +∞(0, +∞)=(0, +∞).
Ответ: (0, +∞).
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y=f1(f2(x)). Известно, что D(f)является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Известно, что D(f)является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Видно, что область определения сложной функции вида y=f1(f2(x)) находится на пересечении двух множеств таких, где x∈D(f2) и f2(x)∈D(f1). В стандартном обозначении это примет вид
x∈D(f2)f2(x)∈D(f1)
Рассмотрим решение нескольких примеров.
Пример 5
Найти область определения y=ln x2.
Решение
Данную функцию представляем в виде y=f1(f2(x)), где имеем, что f1 является логарифмом с основанием e, а f2 – степенная функция с показателем 2.
Для решения необходимо использовать известные области определения D(f1)=(0, +∞) и D(f2)=(−∞, +∞).
Тогда получим систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-∞, +∞x2∈(0, +∞)⇔⇔x∈(-∞, +∞)x2>0⇔x∈(-∞, +∞)x∈(-∞, 0)∪(0, +∞)⇔⇔x∈(-∞, 0)∪(0, +∞)
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Ответ: (−∞, 0)∪(0, +∞).
Пример 6
Найти область определения функции y=(arcsin x)-12.
Решение
Так как дана сложная функция, необходимо рассматривать ее как y=f1(f2(x)), где f1 является степенной функцией с показателем -12, а f2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D(f1)=(0, +∞) и D(f2)=[−1, 1]. Теперь найдем все множества значений x, где x∈D(f2) и f2(x)∈D(f1). Получаем систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-1, 1arcsin x∈(0, +∞)⇔⇔x∈-1, 1arcsin x>0
Для решения arcsin x>0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [−1, 1], причем обращается в ноль при х=0, значит, что arcsin x>0 из определения x принадлежит промежутку (0, 1].
Преобразуем систему вида
x∈-1, 1arcsin x>0⇔x∈-1, 1x∈(0, 1]⇔x∈(0, 1]
Область определения искомой функции имеет интервал равный (0, 1].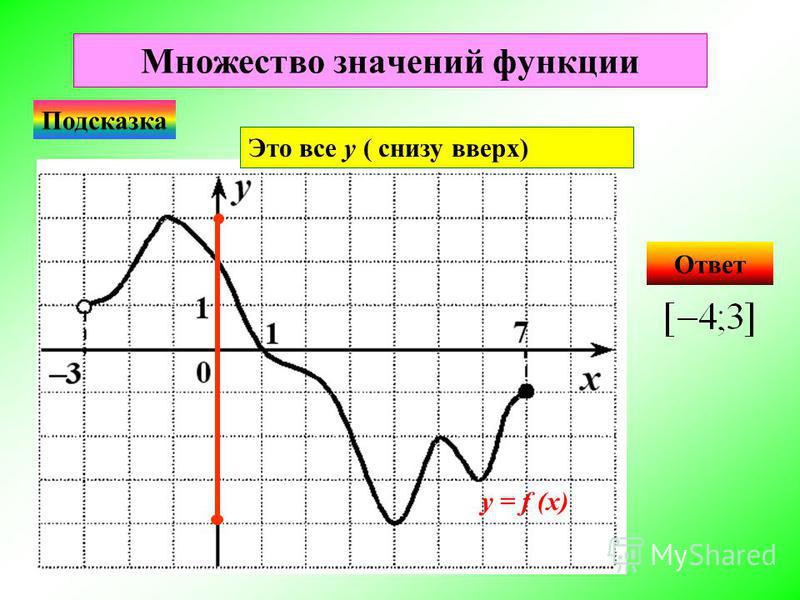
Ответ: (0, 1].
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y=f1(f2(…fn(x)))). Область определения такой функции ищется из x∈D(fn)fn(x)∈D(fn-1)fn-1(fn(x))∈D(fn-2)…f2(f3(…(fn(x)))∈D(f1).
Пример 7
Найти область определения y=sin(lg x4).
Решение
Заданная функция может быть расписана, как y=f1(f2(f3(x))), где имеем f1 – функция синуса, f2 – функция с корнем 4 степени, f3– логарифмическая функция.
Имеем, что по условию D(f1)=(−∞, +∞), D(f2)=[0, +∞), D(f3)=(0, +∞). Тогда областью определения функции – это пересечение множеств таких значений, где x∈D(f3), f3(x)∈D(f2), f2(f3(x))∈D(f1). Получаем, что
x∈D(f3)f3(x)∈D(f2)f2(f3(x))∈D(f1)⇔x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞
Условие lg x4∈-∞, +∞ аналогично условию lg x∈[0, +∞), значит
x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞⇔x∈(0, +∞)lg x∈[0, +∞)lg x∈[0, +∞)⇔⇔x∈(0, +∞)lg x∈[0, +∞)⇔x∈(0, +∞)lg x≥0⇔⇔x∈(0, +∞)lg x≥lg 1⇔x∈(0, +∞)x≥1⇔⇔x∈[1, +∞)
Ответ: [1, +∞).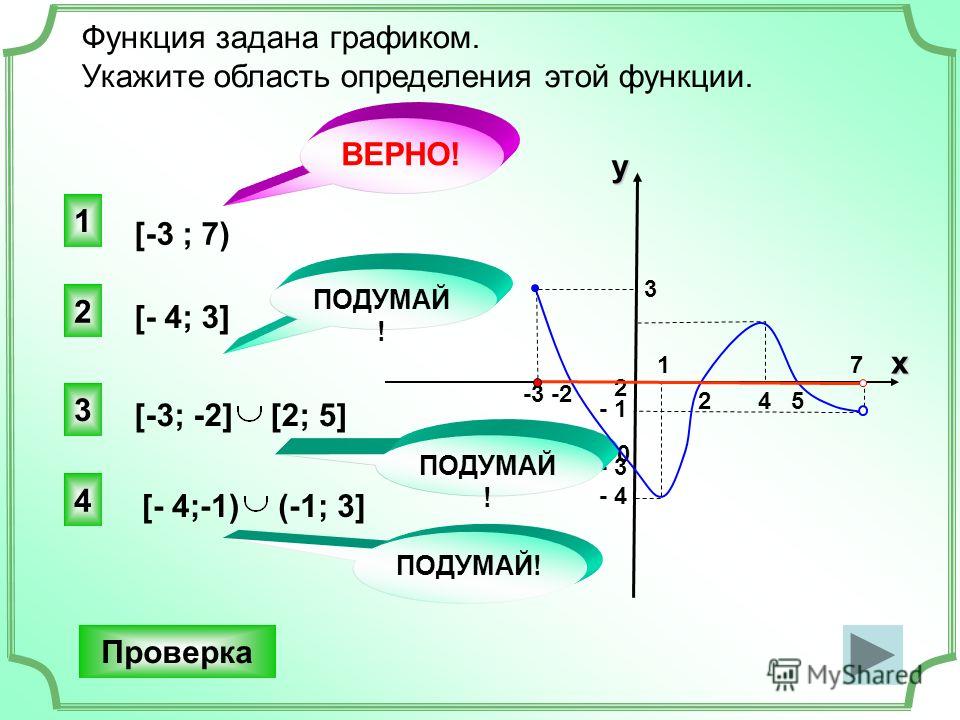
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f1(x)f2(x). Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f2(х) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x∈D(f1)x∈D(f2)f2(x)≠0.
Запишем функцию y=f1(x)f2(x) в виде y=f1(x)·(f2(x))-1. Тогда получим произведение функций вида y=f1(x) с y=(f2(x))-1. Областью определения функции y=f1(x) является множество D(f1), а для сложной y=(f2(x))-1 определим из системы вида x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f2)f2(x)≠0.
Значит, x∈D(f1)x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f1)x∈D(f2)f2(x)≠0.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 8
Найти область определения y=tg(2·x+1)x2-x-6.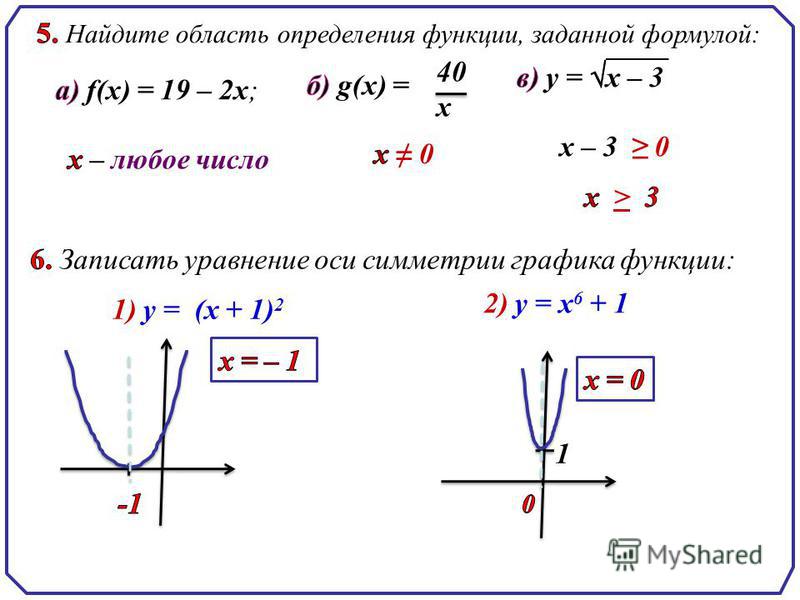
Решение
Заданная функция дробная, поэтому f1 – сложная функция, где y=tg(2·x+1) и f2 – целая рациональная функция, где y=x2−x−6, а область определения считается множеством всех чисел. Можно записать это в виде
x∈D(f1)x∈D(f2)f2(x)≠0
Представление сложной функции y=f3(f4(x)), где f3–это функция тангенс, где в область определения включены все числа, кроме π2+π·k, k∈Z, а f4– это целая рациональная функция y=2·x+1 с областью определения D(f4)=(−∞, +∞). После чего приступаем к нахождению области определения f1:
x∈D(f4)2·x+1∈D(f3)⇔x∈(-∞, +∞)2x+1≠π2+π·k, k∈Z⇔x≠π4-12+π2·k, k∈Z
Еще необходимо рассмотреть нижнюю область определения y=tg(2·x+1)x2-x-6. Тогда получаем, что
x∈D(f1)x∈D(f2)f2(x)≠0⇔x≠π4-12+π2·k, k∈Zx∈-∞, +∞x2-x-6≠0⇔⇔x≠π4-12+π2·k, k∈Zx≠-2x≠3
Ответ: множество действительных чисел, кроме -2, 3 и π4-12+π2·k, k∈Z.
Область определения логарифма с переменной в основании
Определение 3
Определение логарифма существует для положительных оснований не равных 1. Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
А аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y=logaf1(x)logaf2(x), a>0, a≠1. После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y=logaf1(x) и y=logaf2(x) можно определить из получившейся системы вида x∈D(f1)f1(x)>0 и x∈D(f2)f2(x)>0. Иначе эту область можно записать в виде y=logaf1(x)logaf2(x), a>0, a≠1, что означает нахождение y=logf2(x)f1(x) из самой системы вида
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0logaf2(x)≠0=x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
Пример 9
Обозначить область определения функции y=log2·x(x2-6x+5).
Решение
Следует принять обозначения f1(x)=x2−6·x+5 и f2(x)=2·x, отсюда D(f1)=(−∞, +∞) и D(f2)=(−∞, +∞). Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
x∈(-∞, +∞)x2-6x+5>0x∈(-∞, +∞)2·x>02·x≠1⇔x∈(-∞, +∞)x∈(-∞, 1)∪(5, +∞)x∈(-∞, +∞)x>0x≠12⇔⇔x∈0, 12∪12, 1∪(5, +∞)
Отсюда видим, что искомой областью функции y=log2·x(x2-6x+5) считается множнство, удовлетворяющее условию 0, 12∪12, 1∪(5, +∞).
Ответ: 0, 12∪12, 1∪(5, +∞).
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y=(f1(x))f2(x). Ее область определения включает в себя такие значения x, которые удовлетворяют системе x∈D(f1)x∈D(f2)f1(x)>0.
Эта область позволяет переходить от показательно-степенной к сложной вида y=aloga(f1(x))f2(x)=af2(x)·logaf1(x), где где a>0, a≠1.
Пример 10
Найти область определения показательно-степенной функции y=(x2-1)x3-9·x.
Решение
Примем за обозначение f1(x)=x2−1 и f2(x)=x3-9·x.
Функция f1определена на множестве действительных чисел, тогда получаем область определения вида D(f1)=(−∞, +∞). Функция f2является сложной, поэтому ее представление примет вид y=f3(f4(x)), а f3 – квадратным корнем с областью определения D(f3)=[0, +∞), а функция f4 – целой рациональной,D(f4)=(−∞, +∞). Получаем систему вида
x∈D(f4)f4(x)∈D(f3)⇔x∈(-∞, +∞)x3-9·x≥0⇔⇔x∈(-∞, +∞)x∈-3, 0∪[3, +∞)⇔x∈-3, 0∪[3, +∞)
Значит, область определения для функции f2имеет вид D(f2)=[−3, 0]∪[3, +∞). После чего необходимо найти область определения показательно-степенной функции по условию x∈D(f1)x∈D(f2)f1(x)>0.
Получаем систему вида x∈-∞, +∞x∈-3, 0∪[3, +∞)x2-1>0⇔x∈-∞, +∞x∈-3, 0∪[3, +∞)x∈(-∞, -1)∪(1, +∞)⇔⇔x∈-3, -1∪[3, +∞)
Ответ: [−3, −1)∪[3, +∞)
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.Ф
| Функция | Ее область определения |
Сумма, разность, произведение функций f1, f2,…, fn | Пересечение множеств D(f1), D(f2), …, D(fn) |
Сложная функция y=f1(f2(f3(…fn(x))))
В частности, y=f1(f2(x)) | Множество всех x, одновременно удовлетворяющих условиям x∈D(fn),fn(x)∈D(fn-1),fn-1(fn(x))∈D(fn-2),… ,f2(f3(…fn(x)))∈D(f1)
x∈D(f2),f2(x)∈D(f1) |
Расположим функции и их области определения.
| Функция | Ее область определения |
Прямая пропорциональность y=k·x | R |
| Линейная y=k·x+b | R |
Обратная пропорциональность y=kx | -∞, 0∪0, +∞ |
| Квадратичная y=a·x2+b·x+c | R |
| y=anxn+an-1xn-1+…+a1x+a0 | R |
| Целая рациональная | R |
| y=C·f(x), где C — число | D(f) |
Дробная y=f1(x)f2(x)
В частности, если f1(x), f2(x) — многочлены | Множество всех x, которые одновременно удовлетворяют условиям
f2(x)≠0 |
| y=f(x)n, где n — четное | x∈D(f1), f(x)≥0 |
y=logf2(x)f1(x)
В частности, y=logaf1(x)
В частности, y=logf2(x)a | x∈D(f1), f1(x)>0,x∈D(f2), f2(x)>0, f2(x)≠1
x∈D(f1), f1(x)>0
x∈D(f2), f2>0, f2(x)≠1 |
| Показательно-степенная y=(f1(x))f2(x) | x∈D(f1), x∈D(f2), f1(x)>0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения.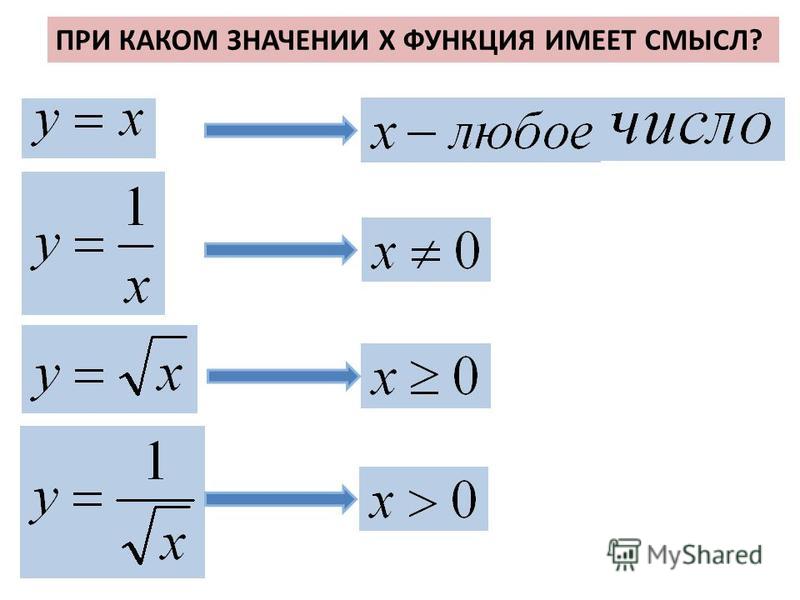 {3} + 2 x\right) — 6\right) = 0$$
{3} + 2 x\right) — 6\right) = 0$$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = — \frac{1}{3} \sqrt[3]{3 \sqrt{705} + 81} — \frac{2}{\sqrt[3]{3 \sqrt{705} + 81}}$$
Зн. экстремумы в точках:
3
/ ________________\ ________________
| 3 / _____ | 3 / _____
| 2 \/ 81 + 3*\/ 705 | 4 2*\/ 81 + 3*\/ 705
-3 + |- ------------------- - -------------------| - ------------------- - ---------------------
________________ | ________________ 3 | ________________ 3
3 / _____ | 3 / _____ | 3 / _____
2 \/ 81 + 3*\/ 705 \ \/ 81 + 3*\/ 705 / \/ 81 + 3*\/ 705
(- ------------------- - -------------------, -------------------------------------------------------------------------------------------------)
________________ 3 2
3 / _____ / ________________\
\/ 81 + 3*\/ 705 | 3 / _____ |
| 2 \/ 81 + 3*\/ 705 |
|- ------------------- - -------------------|
| ________________ 3 |
| 3 / _____ |
\ \/ 81 + 3*\/ 705 / Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумов у функции нет
Максимумы функции в точках:
$$x_{1} = — \frac{1}{3} \sqrt[3]{3 \sqrt{705} + 81} — \frac{2}{\sqrt[3]{3 \sqrt{705} + 81}}$$
Убывает на промежутках
(-oo, -(3*sqrt(705) + 81)**(1/3)/3 - 2/(3*sqrt(705) + 81)**(1/3)]
Возрастает на промежутках
[-(3*sqrt(705) + 81)**(1/3)/3 - 2/(3*sqrt(705) + 81)**(1/3), oo)
Область определения и множество значений
$f(x)=
\begin{cases}
1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>0\\
0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=0\\
-1 \,\,\,\,\,\,\,\,\,\,\,\, x
$f(x)=f_1 \cup f_2 \cup f_3=
\begin{cases}
f_1 = \lbrace (x,y) | x \in \mathbb{R^+} \,\,,\,\, y=1 \rbrace \\
f_2 = \lbrace (0,0) \rbrace \\
f_3 = \lbrace (x,y) | x \in \mathbb{R^-} \,\,,\,\, y=-1 \rbrace
\end{cases}$
функция и обозначается как $\textit{Sgn(x)}$. 2-x}}$
2-x}}$
Определение:
Пол — функция, которая определяет действительное число относительно предыдущего целого. Точнее, $\lfloor x \rfloor$ определяет наибольшее целое не большее $x$.
График функции пол
Определение:
Дробная часть, обозначаемая $\lbrace x \rbrace$ for real $x$, задается формулой
$\lbrace x \rbrace = x — \lfloor x \rfloor$
Очевидно, что
$ 0 \leq \lbrace x \rbrace
Свойства:
1) $ \lfloor x \rfloor = max \lbrace a \in \mathbb{Z} | a \leq x \rbrace$
2) $ \lfloor x \rfloor \leq x \leq \lfloor x \rfloor +1$
3) $x-1 \leq \lfloor x \rfloor \leq x$
4) $\lfloor x-\lfloor x \rfloor \rfloor =0$
5) $\lfloor x+a \rfloor = \lfloor x \rfloor +a \,\,\,\, a \in \mathbb{Z}$
6) $ \lfloor x \rfloor + \lfloor y \rfloor \leq \lfloor x+y \rfloor \leq \lfloor x \rfloor + \lfloor y \rfloor +1$
7) $\lfloor x \rfloor + \lfloor -x \rfloor=$
$\begin{cases}
0 \,\,\,\,\,\, x \in \mathbb{Z} \\
-1 \,\,\,\, x \in \mathbb{R}-\mathbb{Z}
\end{cases}$
8)$\lfloor \lfloor x \rfloor \rfloor=\lfloor x \rfloor$
9) $\lfloor \dfrac{x+m}{n} \rfloor= \lfloor \dfrac{\lfloor x \rfloor+m}{n} \rfloor \,\,\,\, m,n \in \mathbb{Z} \,\,,\,\, n>0 $
10)$\lfloor n \rfloor =\lfloor \dfrac{n}{m} \rfloor + \lfloor \dfrac{n+1}{m} \rfloor \cdots + \lfloor \dfrac{n+m-1}{m} \rfloor \,\,\,\, m,n \in \mathbb{Z} \,\,,\,\, m>0$
11) $\lfloor mx \rfloor = \lfloor x \rfloor + \lfloor x+\dfrac{1}{m} \rfloor + \cdots + \lfloor x+\dfrac{m-1}{m} \rfloor \,\,\,\, m \in \mathbb{Z} \,\,,\,\, m>0$
12) $ \lfloor \dfrac{\lfloor \dfrac{x}{m} \rfloor}{n} \rfloor = \lfloor \dfrac{x}{mn} \rfloor \,\,\,\, m,n \in \mathbb{N}$
Для нахождения области определения и множества значений функции пол стоит использовать приведенные свойства.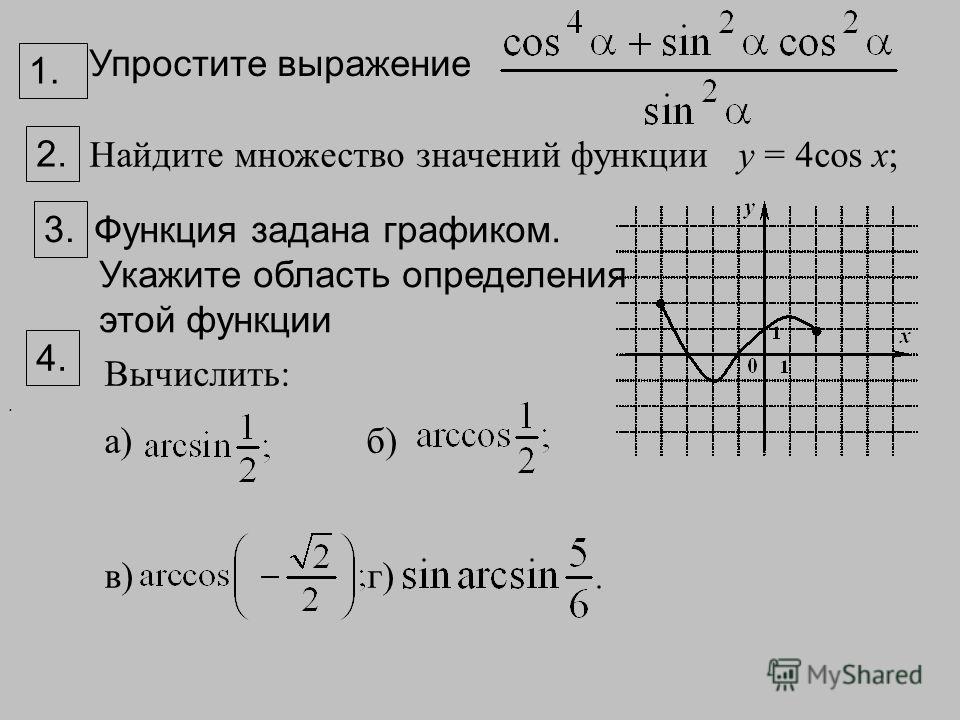
Пример:
Найти область определения и множество значений $f(x)=\dfrac{x-\lfloor x-\lfloor x \rfloor \rfloor}{x+\lfloor x \rfloor+\lfloor -x \rfloor}$.
Решение:
Согласно свойствам
$\lfloor x-\lfloor x \rfloor \rfloor =0$
и
$ \lfloor x \rfloor + \lfloor -x \rfloor =
\begin{cases}
0 \,\,\,\,\,\,\,\,\,\,\, x \in \mathbb{Z} \\ \\
-1 \,\,\,\,\,\,\, x \in \mathbb{R}-\mathbb{Z}
\end{cases}$
So
$y=
\begin{cases}
\dfrac{x}{x}=1 \,\,\,\, x \in \mathbb{Z} — \lbrace 0 \rbrace
\\
\\
\dfrac{x}{x-1} \,\,\,\,\, x \in \mathbb{R}-\mathbb{Z}
\end{cases}$
Следовательно
$D_f=\mathbb{R}-\lbrace 0 \rbrace$
Также для множества значений
$x \in \mathbb{R}-\mathbb{Z}: y=\dfrac{x}{x-1} \rightarrow x =\dfrac{y}{y-1} \in \mathbb{R} — \mathbb{Z} \rightarrow y =\neq 1$
$R_f=\mathbb{R}- \lbrace \dfrac{k}{k-1} | k \in \mathbb{Z}- \lbrace 1 \rbrace \rbrace $
Пример:
Найти область определения и множество значений $f(x)=\dfrac{\lfloor x+1 \rfloor+\lfloor -x \rfloor}{\lfloor 1-x \rfloor+\lfloor x \rfloor}$
Решение:
$f(x)=\dfrac{\lfloor x+1 \rfloor+\lfloor -x \rfloor}{\lfloor 1-x \rfloor+\lfloor x \rfloor}=\dfrac{\lfloor x \rfloor+\lfloor -x \rfloor+1}{\lfloor -x \rfloor+\lfloor x \rfloor+1}=
\begin{cases}
1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x \in \mathbb{Z}
\\
Undefined \,\,\,\,\,\,\,\, x \in \mathbb{R}-\mathbb{Z}
\end{cases}$
Следовательно
$D_f=\mathbb{Z} \,\,\,\,,\,\,\,\, R_f=\lbrace 1 \rbrace$
Графиком $f$ является
Упражнения
Найти область определения и множество значений. {\lfloor x-5 \rfloor+\lfloor 5-x \rfloor} $
{\lfloor x-5 \rfloor+\lfloor 5-x \rfloor} $
Часть 2
Электронная почта:
© 2005 — 2021
Копирование запрещено! В случае копирования администрация сайта обратится в компетентные органы.
Тема 7. Функции — Материалы для подготовки к вступительным экзаменам в СГГА
Тема 7. Функции
1. Понятие функции
Функция y=f(x) – соответствие, при котором каждому числу x из множества D сопоставляется единственное число y из множества E.
x– аргумент функции, y – значение функции; D или D(f) – область определения функции; это совокупность всех значений x, для которых можно вычислить значение функции. E или E(f) – область значений функции; это совокупность всех значений, которые может принимать выражение f(x).
График функции y=f(x) – множество точек (x,y) на координатной плоскости, где x принимает все возможные значения из D(f), а y=f(x).
Четная функция: f(-x)=f(x) для всех ; Нечетная функция: f(-x)=-f(x) для всех ;
График четной функции симметричен относительно оси OY. График нечетной функции симметричен относительно начала координат.
График нечетной функции симметричен относительно начала координат.
Периодическая функция с периодом T>0: f(x+T)=f(x) для всех .
Нули функции – значения x такие, что f(x)=0. Интервалы знакопостоянства – множества значений аргумента, при которых значения функции только положительны или только отрицательны.
На рисунке изображена функция с областью определения [a, e]. Нули функции: x=b, x=c, x=d; интервалы знакопостоянства: y>0 при ; y. Функция возрастает на множестве X, если большему значению аргумента соответствует большее значение функции. То есть для любых , если x12, то f(x1)2). Функция убывает на множестве X, если большему значению аргумента соответствует меньшее значение функции. Т.е. для любых , если x12, то f(x1)>f(x2).
3. Некоторые алгебраические функции
а) линейная . График функции – прямая линия, проходящая через точки (0, b) и .
Функция возрастает при a>0, убывает при a<0.
Частные случаи: y=b – прямая, параллельная оси OX;
y=ax – прямая, проходящая через начало координат.
б) квадратичная . График функции – парабола. Ветви параболы направлены вверх при a>0, вниз при a.
Точки пересечения с осями координат:
с осью OX – (x1, 0) и (x2, 0),
где , D=b2-4ac – корни квадратного трехчлена;
с осью OY – (0, c).
Пример 1. График какой функции является возрастающим:
а) ; б) у = х3 – 27; в) y=2-x?
Решение:
Рассмотрим каждую из функций в отдельности:
а) – степенная функция. Область определения этой функции: . На всей области определения функция монотонна.
Возьмём два значения х1 = 1 и х2 = 4. Им соответствует у1 = – 1, у2 = – 2. Видим, что если х1 < x2 , то у1 > у2.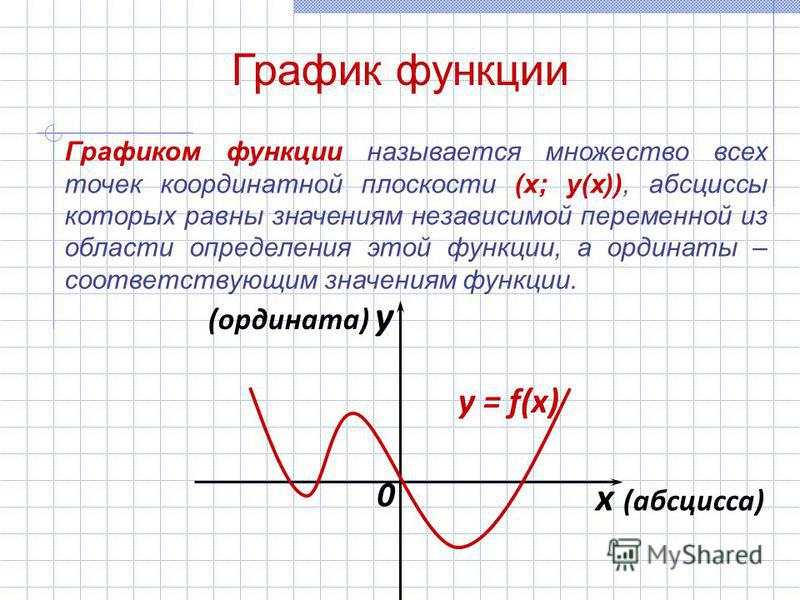 Функция убывающая.
Функция убывающая.
б) у = х3 – 27 – алгебраическая функция. Область определения – множество всех действительных чисел. На всей области определения функция монотонна. Возьмём два значения х1 = 3, х2 = 4. Им соответствует у1 = 0, у2 = 37.
Видим, что если х1 < x2 , то и у1 < у2. Функция возрастающая.
в) y=2-x – показательная функция. Областью определения является множество всех действительных чисел. На всей области определения функция монотонна. Пусть х1 = 0, х2 = 1. Им соответствуют у1 = 1, у2 = 0,5.
Видим, что если х1 < x2 , то у1 > у2. Функция убывающая.
Ответ: б) у = х3 – 27.
Пример 2. Парабола у = 2х2 – (а – 3)х + а + 3 проходит через начало координат. Найдите абсциссу вершины параболы.
Решение:
Найдём значение параметра а. Т.к. парабола проходит через начало системы координат, то координаты точки (0; 0) являются корнями уравнения параболы: 0 = 2 ∙ 02 – (а – 3) ∙ 0 + а + 3; а = – 3.
Уравнение параболы примет вид: у = 2х2 + 6х.
Абсцисса вершины параболы находится по формуле: . Получаем .
Ответ: – 1, 5.
Пример 3. В каких точках график функции f(x) = x2 – 3 пересекает прямую у(х) = х – 1?
Решение:
Ответом на данный вопрос является решение системы
х2 – 3 = х – 1; х2 – х – 2 = 0; х1= – 1, или х2 = 2.
Соответственно, у1 = – 2, у2 = 1.
Ответ: (– 1; – 2), (2; 1).
Пример 4. При каких значениях k прямые – kх + 7у = – 13 и 14у – 3х + 5 = 0 параллельны?
Решение:
Две различные прямые у = k1х + b1 и у = k2х + b2 параллельны, если k1 = k2, но при этом b1 ≠ b2.
В обоих уравнениях выразим у через х.
. Следовательно, . При этом .
Ответ: при k = – 1,5.
Пример 5. Найти точки пересечения прямой у = 5 + х с осями координат.
Решение:
Когда график функции пресекает ось ОХ, значение у = 0.
Получаем уравнение 5 + х = 0, х = – 5.
Когда график функции пересекает ось OY, значение х = 0, т.е. у = 5.
Ответ: (– 5; 0), (0; 5).
Пример 6. Найти нули функции у = (х + 1)∙(х – 2).
Решение:
Решаем уравнение (х + 1)∙(х – 2) = 0.
х + 1 = 0 или х – 2 = 0; х1 = – 1, х2 = 2.
Ответ: (– 1; 0), (2; 0).
Пример 7. Найти область значений функции .
Решение:
Оцениваем последовательно:
. Ответ: .
Пример 8. Найдите сумму целых значений функции у = 3 – 2 sin x.
Решение:
Оценим значение 3 – 2 sin x.
.
Сумма целых чисел: 1 + 2 + 3 + 4 + 5 = 15.
Ответ: 15.
Пример 12. Графиком квадратичной функции является парабола с вершиной в точке А(0; 2), проходящая через точку В(2; – 6). Задайте эту функцию формулой.
Решение:
Уравнение квадратичной функции у = ах2 + bх + с.
1) точка А является вершиной параболы, следовательно .
Уравнение примет вид: у = ах2 + с.
2) точка А принадлежит графику, следовательно её координаты удовлетворяют уравнению, т.е. 2 = а ∙ 0 + с; с = 2.
Уравнение примет вид: у = ах2 + 2.
3) график проходит через точку В. Её координаты также удовлетворяют уравнению: – 6 = а ∙ 22 + 2, – 8 = 4 ∙ а, а = – 2.
Получили уравнение у = – 2х2 + 2.
Ответ: у = – 2х2 + 2.
Пример 13. Найдите g (x) , если f (x) = 2x – 3, g (f (x)) = x. Вычислите g (1).
Вычислите g (1).
Решение:
Так как нужно вычислить g (1), то это значит, что нужно найти x такое, что f (x) = 1.
2x – 3 = 1, х = 2.
Следовательно, g (f (x)) = 2, т.е. g (1) = 2.
Ответ: g (1) = 2.
Пример 14. Написать уравнение прямой, проходящей через точку пересечения кривых y=52x, y=53x-1 и через точку параболы y=(2x-1)2, в которой производная функции, задающей параболу, равна 8.
Решение:
1) найдём точку пересечения кривых:
2) найдём точку параболы, в которой производная равна 8:
3) прямая проходит через две точки (1; 25) и (1,5; 4). Согласно уравнению прямой, проходящей через две точки, имеем:
– 21х + 21 = 0,5у – 12,5; – 42х + 42 = у – 25; у = – 42х + 47.
Ответ: у = – 42х + 47.
Задания для самостоятельного решения
Базовый уровень
1) Вычислите значение функции в точке х0 = 1. 2) Найдите значение функции при х = 4. 3) Для функции вычислите f(-1)-f(1). 4) Найдите g(f(x)), если Вычислите g(f(2)).
2) Найдите значение функции при х = 4. 3) Для функции вычислите f(-1)-f(1). 4) Найдите g(f(x)), если Вычислите g(f(2)).
Укажите длину интервала области определения для функций:
24) .
25) y=log4(5x+6-x2)
26) y=log6(x2+3).
Укажите области значения функций:
27) y=-3sinx.
28) y=0,7cos3x.
29) .
Решите задачи:
30) Сколько натуральных значений может принять функция y=log2(4-x2) на всей области определения?
31) Найдите сумму целых значений функции y=3cosx-5.
32) Укажите функцию, областью значений которой является множество . .
33) Укажите график функции, возрастающей на отрезке [-3; 2].
34) Укажите функцию, которая возрастает на всей области определения.
1) y=-x0,5; 2) y=1-e-x; 3) y=ctg2x; 4) y=|-x|.
35) Найдите нули функции . 36) Найдите нули функции
36) Найдите нули функции
37) Найдите наименьшее значение функции f(x)=32x-1 на промежутке [-3; 1].
38) Вычислите координаты точек пересечения графика функции у = – 2х2 + 4х + 6 с осью OY.
39) Вычислите ординату точки пересечения прямой у = 5 – 2х с осью ОY.
40) Укажите точки пересечения графиков функций у = 2х + 4 и у = – 2х.
41) В каких точках график функции f (x) = 3x2 + 6x пересекает прямую у = 6 – х?
42) Укажите промежутки возрастания функции y=sin3x на интервале . 43) Укажите промежутки убывания функции y=-2cosx на интервале .
Ответы
1) 0; 2) -3/14; 3) – 1; 4) 3; 5) ; 6) ; 7) ;
Как найти область определения функции
После этого экскурса в важную составную матанализа многие согласятся, что найти
область определения функции не очень сложно. Ненамного сложнее, чем Московскую область на карте.
Во-первых, нужно различать виды функций (корень, дробь, синус и др.). Во-вторых,
решать уравнения и неравенства с учетом вида функции (например, на что нельзя делить, какое выражение
не может быть под знаком корня и тому подобное). Согласитесь, не так уж много и не так сложно.
Итак, чтобы находить области определения распространённых функций, порешаем
уравнения и неравенства с одной переменной. А в конце урока обобщим понятие на уровне теории. Пока же —
краткое определение. Область определения функции y=f(x)
— это множество значений X, для которых существуют значения Y.
Будут и задачи для самостоятельного решения, к которым можно
посмотреть ответы.
Приступаем к практике. На рисунке изображён график функции .
Знаменатель дроби не может быть равен нулю, так как на нуль делить нельзя. Поэтому, приравнивая знаменатель
Поэтому, приравнивая знаменатель
нулю, получаем значение, не входящее в область определения функции: 1. То есть, область определения заданной функции —
это все значения «икса» от минус бесконечности до единицы и от единицы до плюс бесконечности. Это хорошо
видно на графике. Приведённый здесь пример функции относится к виду дробей. На уроке разберём решения
всех распространённых видов функций.
Пример 0. Как найти область
определения функции игрек равен квадратному корню из икса минус пять (подкоренное выражение икс минус пять)
()? Нужно всего лишь
решить неравенство
x — 5 ≥ 0,
так как для того, чтобы мы получили действительное значение игрека, подкоренное
выражение должно быть больше или равно нулю. Получаем решение: область определения функции — все значения икса
больше или равно пяти (или икс принадлежит промежутку от пяти включительно до плюс бесконечности).
На чертеже сверху — фрагмент числовой оси. На ней область опредения рассмотренной функции
заштрихована, при этом в «плюсовом» направлении штриховка продолжается бесконечно вместе с самой осью.
Постоянная (константа) определена при любых действительных
значениях x, следовательно, данная функция определена на всём
множестве R действительных чисел. Это можно записать и так:
областью определения данной функции является вся числовая прямая ]- ∞; + ∞[.
Пример 1. Найти область определения функции
y = 2.
Решение. Область определения функции не указана, значит, в силу выше приведённого
определения имеется в виду естественная область определения. Выражение
f(x) = 2 определено при любых действительных
значениях x, следовательно, данная функция определена на всём
множестве R действительных чисел.
Поэтому на чертеже сверху числовая прямая заштрихована на всём протяжении от минус
бесконечности до плюс бесконечности.
В случае, когда функция задана формулой и n — натуральное число:
Пример 2. Найти область определения функции
.
Решение. Как следует из
определения, корень чётной степени имеет смысл, если подкоренное выражение неотрицательно, то есть,
если — 1 ≤ x ≤ 1.
Следовательно, область определения данной функции — [- 1; 1].
Заштрихованная область числовой прямой на чертеже сверху — это область определения
данной функции.
Область определения степенной функции с целым показателем степени
В случае, когда функция задана формулой :
если a — положительное, то областью определения функции является множество
всех действительных чисел, то есть ]- ∞; + ∞[;
если a — отрицательное, то областью определения функции является
множество ]- ∞; 0[ ∪ ]0 ;+ ∞[,
то есть вся числовая прямая за исключением нуля.
На соответствующем чертеже сверху вся числовая прямая заштрихована, а точка,
соответствующая нулю, выколота (она не входит в область определения функции).
Пример 3. Найти область определения функции
.
Решение. Первое слагаемое целой степенью икса, равной 3, а степень икса во втором
слагаемом можно представить в виде единицы — так же целого числа.
Следовательно, область определения данной функции — вся числовая прямая, то есть
]- ∞; + ∞[.
Область определения степенной функции с дробным показателем степени
В случае, когда функция задана формулой :
если
— положительное, то областью определения функции является множество [0; + ∞[;
если
— отрицательное, то областью определения функции является множество ]0; + ∞[.
Пример 4. Найти область определения функции
.
Решение. Оба слагаемых в выражении функции — степенные функции с положительными
дробными показателями степеней. Следовательно, область определения данной функции —
множество [0; + ∞[.
На чертеже сверху заштрихована часть числовой прямой от нуля (включительно) и больше,
причём штриховка продолжается вместе с самой прямой до плюс бесконечности.
Пример 5. Найти область определения функции
.
Решение. Дробный показатель степени данной степенной функции — отрицательный.
Поэтому решим строгое неравенство, когда квадратный трёхчлен в скобках строго больше нуля::
.
Дикриминант получился отрицательный. Следовательно сопряжённое неравенству
квадратное уравнение не имеет корней. А это значит, что квадратный трёхчлен ни при каких значениях
«икса» не равен нулю. Таким образом, область определения данной функции — вся числовая ось, или,
что то же самое — множество R действительных чисел, или,
что то же самое — ]- ∞; + ∞[.
Область определения показательной функции
В случае, когда функция задана формулой ,
областью определения функции является вся числовая прямая, то есть
]- ∞; + ∞[.
Область определения логарифмической функции
Логарифмическая функция
определена при условии, если её аргумент положителен, то есть, областью её определения является множество
]0; + ∞[.
Найти область определения функции самостоятельно, а затем посмотреть решение
Область определения функции y = cos(x) —
так же множество R действительных чисел.
Область определения функции y = tg(x) —
множество R действительных чисел, кроме чисел
.
Область определения функции y = ctg(x) —
множество R действительных чисел, кроме чисел
.
Пример 8. Найти область определения функции
.
Решение. Внешняя функция — десятичный логарифм и на область её определения
распространяются условия области определения логарифмической функции вообще. То есть, её аргумент
должен быть положительным. Аргумент здесь — синус «икса». Поворачивая воображаемый циркуль по
окружности, видим, что условие sin x > 0
нарушается при «иксе» равным нулю, «пи», два, умноженном на «пи» и вообще равным произведению числа «пи»
и любого чётного или нечётного целого числа.
Таким образом, область определения данной функции задаётся выражением
,
где k — целое число.
Область определения обратных тригонометрических функций
Область определения функции y = arcsin(x) —
множество [-1; 1].
Область определения функции y = arccos(x) —
так же множество [-1; 1].
Область определения функции y = arctg(x) —
множество R действительных чисел.
Область определения функции y = arcctg(x) —
так же множество R действительных чисел.
Пример 9. Найти область определения функции
.
Решение. Решим неравенство:
Таким образом, получаем область определения данной функции — отрезок
[- 4; 4].
Пример 10. Найти область определения функции
.
Решение. Решим два неравенства:
Решение первого неравенства:
Решение второго неравенства:
Таким образом, получаем область определения данной функции — отрезок
[0; 1].
Если функция задана дробным выражением, в котором переменная находится в знаменателе
дроби, то областью определения функции является множество R действительных чисел,
кроме таких x, при которых знаменатель дроби обращается в нуль.
Пример 11. Найти область определения функции
.
Решение. Решая равенство нулю знаменателя дроби, находим область определения данной функции — множество
]- ∞; — 2[ ∪ ]- 2 ;+ ∞[.
Пример 12. Найти область определения функции
.
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции —
]- ∞; — 1[ ∪ ]- 1 ; 1[ ∪ ]1 ;+ ∞[.
Пример 13. Найти область определения функции
.
Решение. Область определения первого слагаемого — данной функции — множество
R действительных чисел, второго слагаемого — все
действительные числа, кроме -2 и 2 (получили, решая равенство нулю знаменателя, как в предыдущем примере). В этом случае область определения функции должна удовлетворять
условиями определения обоих слагаемых. Следовательно, область определения данной функции — все
Следовательно, область определения данной функции — все
x, кроме -2 и 2.
Пример 14. Найти область определения функции
.
Решение. Решим уравнение:
Уравнение не имеет действительных корней. Но функция определена только на действительных
числах. Таким образом, получаем область определения данной функции — вся числовая прямая или, что
то же самое — множество R действительных чисел или,
что то же самое — ]- ∞; + ∞[.
То есть, какое бы число мы не подставляли вместо «икса», знаменатель никогда не
будет равен нулю.
Пример 15. Найти область определения функции
.
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции —
]- ∞; — 1[ ∪ ]- 1 ; 0[ ∪ ]0 ; 1[ ∪ ]1 ;+ ∞[.
Пример 16. Найти область определения функции
Найти область определения функции
.
Решение. Кроме того, что знаменатель не может быть равным нулю, ещё и выражение под
корнем не может быть отрицательным. Сначала решим уравнение:
График квадратичной функции под корнем представляет собой параболу, ветви которой
направлены вверх. Как следует из решения квадратного уравнения, парабола пересекает ось Ox в точках
1 и 2. Между этими точками линия параболы находится ниже оси Ox, следовательно значения
квадратичной функции между этими точками отрицательное. Таким образом, исходная функция не определена
на отрезке [1; 2].
Найти область определения функции самостоятельно, а затем посмотреть решение
Если функция задана формулой вида y = kx + b,
то область определения функции — множество
R действительных чисел.
А теперь обобщим решения рассмотренных примеров. Каждой точке графика функции соответствуют:
Каждой точке графика функции соответствуют:
- определённое значение «икса» — аргумента функции;
- определённое значение «игрека» — самой функции.
Верны следующие факты.
- От аргумента — «икса» — вычисляется «игрек» — значения функции.
- Область определения функции — это множества всех значений «икса», для которых существует, то есть может
быть вычислен «игрек» — значение функции. 2$ и $y=0$.1. Найти кооординаты центра масс (полагая распределение масс равномерным)
а) симметричного параболического сегмента с основанием $a$ и высоты $h$;
б) дуги окружности радиуса $R$, стягивающей центральный угол $\alpha $.
2. Найти момент инерции (полагая распределение масс равномерным)
а) полукруга радиуса $R$ относительно его диаметра;
б) конуса с радиусом основания $R$, высоты $H$, относительно его оси;
в) шара радиуса $R$ относительно его диаметра.
Как найти область определения функции???
При решении многих задач приходится искать область определения функции.
 Особенно это нужно знать при построении графика и исследовании функции. Именно поэтому я решил рассмотреть основные варианты, которые могут быть при нахождении области определения функции. Их не так много, наверняка, многие это знают и сами, но думаю, напомнить не будет лишним.
Особенно это нужно знать при построении графика и исследовании функции. Именно поэтому я решил рассмотреть основные варианты, которые могут быть при нахождении области определения функции. Их не так много, наверняка, многие это знают и сами, но думаю, напомнить не будет лишним.И так, область определения функции – это множество всех тех значений переменной х, при каких функция f(x) имеет смысл. То есть значения переменной х, при которых функция от этой переменной существует, а могут быть и такие, при каких она не существует, нам нужны, только те, при которых – существует.
Рассмотрим конкретные варианты, в каких случаях функция может существовать не при всех значениях переменной:
- Во-первых, когда есть дробь, в этом случае знаменатель дроби, недолжен быть равным нулю, потому, что такая дробь не может существовать. То есть, если ваша функция — дробь и в знаменателе есть переменная (потому, что если там только число, то оно никогда не станет нулём) то вам надо всё то выражение, что в знаменателе прировнять к нулю.
 И решив полученное уравнение, вы найдёте те значения переменной x, которые необходимо исключить с области определения.
И решив полученное уравнение, вы найдёте те значения переменной x, которые необходимо исключить с области определения. - Во-вторых, когда есть корень чётной степени, думаю, вы знаете, что в поле вещественных чисел, корень чётной степени может быть только с положительного числа. То есть если в вас есть функция с корнем чётной степени, то что бы найти те числа, которые не будут попадать в область определения, вам надо решить неравенство, где выражение, что под корнем будет меньше нуля.
- В-третьих, когда есть логарифм. Здесь понятно, что область определения логарифма все числа, которые больше ноля. То есть что бы найти те значения переменной, которые надо исключить с области определения, вам надо составить и решить неравенство, где выражение, которое будет под логарифмом должно быть меньше нуля.
- В-четвёртых, не надо забыть о таких обратных тригонометрических функциях, как арксинус и арккосинус, которые определены, только на промежутке [-1;1].
 Соответственно вам надо следить, что бы выражение, которое будет под этими функциями, также попадало в этот промежуток и исключить все значения переменной, которые туда не попадают.
Соответственно вам надо следить, что бы выражение, которое будет под этими функциями, также попадало в этот промежуток и исключить все значения переменной, которые туда не попадают. - И в-пятых, в одном примере может быть несколько этих случаев. Надо разбирать всё, до мельчайших подробностей. Например, в знаменателе дроби, может быть корень из арксинуса :), поэтому вам надо отобрать, только те значения переменной, при которых существует арксинус, при чём значение этого арксинуса должно не должно быть равное нулю (так как оно в знаменателе) и также не должно быть отрицательным (так как есть корень).
Я постарался собрать самые основные случаи, когда область определения функции – это не все вещественные числа. Конечно, примеры могут быть на много сложнее, потому что даже эти четыре варианты можно так скомбинировать, что на то что бы разобраться, что там и от чего зависит, пойдёт не мало времени. И ещё, я даже не все перечислил.
Материалы по теме:
Поделиться с друзьями:
Загрузка…
Домен и Диапазон | Precalculus I
ЦЕЛИ ОБУЧЕНИЯ
К концу этого урока вы сможете:
- Найдите область определения функции, определяемой уравнением.

- График кусочно-определенных функций.
Если вы настроены на фильм ужасов, вы можете посмотреть один из пяти самых популярных фильмов ужасов всех времен — Я — легенда , Ганнибал , Кольцо , Обида , и Заклятие .На диаграмме 1 показана сумма в долларах, которую получил каждый из этих фильмов на момент выхода, а также продажи билетов на фильмы ужасов в целом по годам. Обратите внимание, что мы можем использовать эти данные для создания функции суммы заработка каждого фильма или общей суммы продаж билетов на все фильмы ужасов по годам. Создавая различные функции с использованием данных, мы можем идентифицировать различные независимые и зависимые переменные, а также можем анализировать данные и функции для определения области , и диапазона.В этом разделе мы исследуем методы определения области и диапазона таких функций.

Найдите область определения функции, заданной уравнением
В разделе «Функции и обозначение функций» мы познакомились с концепциями домена и диапазона . В этом разделе мы попрактикуемся в определении доменов и диапазонов для конкретных функций. Имейте в виду, что при определении доменов и диапазонов мы должны учитывать, что физически возможно или значимо в реальных примерах, таких как продажи билетов и год в примере из фильма ужасов выше.Мы также должны учитывать то, что математически разрешено. Например, мы не можем включать какое-либо входное значение, которое приводит к извлечению четного корня из отрицательного числа, если домен и диапазон состоят из действительных чисел. Или в функции, выраженной в виде формулы, мы не можем включать в домен какое-либо входное значение, которое привело бы к делению на 0.
Рисунок 2
Мы можем визуализировать домен как «зону хранения», которая содержит «сырье» для «функциональной машины», а ассортимент — как еще одну «зону хранения» для продукции машины.

Мы можем записать домен и диапазон в нотации интервала , которая использует значения в скобках для описания набора чисел. В обозначении интервала мы используем квадратную скобку [, когда набор включает конечную точку и круглую скобку (чтобы указать, что конечная точка либо не включена, либо интервал неограничен. Например, если у человека есть 100 долларов, чтобы потратить, он или она необходимо указать интервал, который больше 0, но меньше или равен 100, и написать [latex] \ left (0, \ text {} 100 \ right] [/ latex].Мы обсудим обозначения интервалов более подробно позже.
Обратимся к поиску области определения функции, уравнение которой дано. Часто, чтобы найти область таких функций, нужно запомнить три разные формы. Во-первых, если у функции нет знаменателя или четного корня, подумайте, может ли домен состоять только из действительных чисел. Во-вторых, если в уравнении функции есть знаменатель, исключите значения в области, которые заставляют знаменатель быть равным нулю.
 В-третьих, если есть четный корень, подумайте об исключении значений, которые сделали бы подкоренное выражение отрицательным.
В-третьих, если есть четный корень, подумайте об исключении значений, которые сделали бы подкоренное выражение отрицательным.Прежде чем мы начнем, давайте рассмотрим соглашения об обозначении интервалов:
- Первым записывается наименьший член интервала.
- Наибольший член в интервале записывается вторым после запятой.
- Круглые скобки (или) используются для обозначения того, что конечная точка не включена, что называется исключительной.
- Скобки, [или] используются для обозначения того, что конечная точка включена, называемая включающей.
В таблице ниже приведены краткие сведения об обозначениях интервалов.
Пример 1: Нахождение домена функции как набора упорядоченных пар
Найдите домен следующей функции: [latex] \ left \ {\ left (2, \ text {} 10 \ right), \ left (3, \ text {} 10 \ right), \ left (4, \ текст {} 20 \ right), \ left (5, \ text {} 30 \ right), \ left (6, \ text {} 40 \ right) \ right \} [/ latex].

Решение
Сначала определите входные значения. Входное значение — это первая координата в упорядоченной паре . Нет никаких ограничений, так как упорядоченные пары просто перечислены.Домен — это набор первых координат упорядоченных пар.
[латекс] \ влево \ {2,3,4,5,6 \ вправо \} [/ латекс]
Попробуй 1
Найдите домен функции:
[латекс] \ влево \ {\ влево (-5,4 \ вправо), \ влево (0,0 \ вправо), \ влево (5, -4 \ вправо), \ влево (10, -8 \ вправо) , \ влево (15, -12 \ вправо) \ вправо \} [/ латекс]
Решение
Практическое руководство. Для заданной функции, записанной в форме уравнения, найдите область определения.
- Определите входные значения.
- Определите любые ограничения на ввод и исключите эти значения из домена.{2} -1 [/ латекс].
Решение
Входное значение, показанное переменной [latex] x [/ latex] в уравнении, возводится в квадрат, а затем результат уменьшается на единицу.
 {3} [/ latex].
{3} [/ latex].Решение
Практическое руководство. Для функции, записанной в форме уравнения, которое включает дробь, найдите область определения.
- Определите входные значения.
- Укажите любые ограничения на ввод. Если в формуле функции есть знаменатель, установите знаменатель равным нулю и решите относительно [латекс] x [/ латекс]. Если формула функции содержит четный корень, установите подкоренное выражение больше или равным 0, а затем решите.
- Запишите домен в форме интервала, убедившись, что исключены любые запрещенные значения из домена.
Пример 3: Нахождение области определения функции, содержащей знаменатель (рациональная функция)
Найдите область определения функции [latex] f \ left (x \ right) = \ frac {x + 1} {2-x} [/ latex].
Решение
Когда есть знаменатель, мы хотим включить только значения входных данных, которые не заставляют знаменатель быть нулевым. Итак, мы установим знаменатель равным 0 и решим для [latex] x [/ latex].

[латекс] \ begin {case} 2-x = 0 \ hfill \\ -x = -2 \ hfill \\ x = 2 \ hfill \ end {case} [/ latex]
Теперь мы исключим 2 из домена.Все ответы — действительные числа, где [латекс] x 2 [/ latex]. Мы можем использовать символ, известный как объединение, [latex] \ cup [/ latex], чтобы объединить два набора. В обозначении интервалов запишем решение: [latex] \ left (\ mathrm {- \ infty}, 2 \ right) \ cup \ left (2, \ infty \ right) [/ latex].
Рисунок 3
В интервальной форме домен [latex] f [/ latex] равен [latex] \ left (- \ infty, 2 \ right) \ cup \ left (2, \ infty \ right) [/ latex].
Попробуй 3
Найдите область определения функции: [latex] f \ left (x \ right) = \ frac {1 + 4x} {2x — 1} [/ latex].
Решение
Как сделать: для заданной функции, записанной в форме уравнения, включающего четный корень, найдите домен.

- Определите входные значения.
- Поскольку существует четный корень, исключите все действительные числа, которые дают отрицательное число в подкоренном выражении. Установите подкоренное выражение больше или равное нулю и решите для [latex] x [/ latex].
- Решение (я) — это область определения функции. Если возможно, запишите ответ в интервальной форме.
Пример 4: Нахождение домена функции с четным корнем
Найдите домен функции [latex] f \ left (x \ right) = \ sqrt {7-x} [/ latex].
Решение
Если в формуле есть четный корень, мы исключаем все действительные числа, которые приводят к отрицательному числу в подкоренном выражении.
Установите подкоренное выражение больше или равное нулю и решите для [latex] x [/ latex].
[латекс] \ begin {case} 7-x \ ge 0 \ hfill \\ -x \ ge -7 \ hfill \\ x \ le 7 \ hfill \ end {case} [/ latex]
Теперь мы исключим из домена любое число больше 7.
 Все ответы — действительные числа, меньшие или равные [latex] 7 [/ latex] или [latex] \ left (- \ infty, 7 \ right] [/ latex].
Все ответы — действительные числа, меньшие или равные [latex] 7 [/ latex] или [latex] \ left (- \ infty, 7 \ right] [/ latex].Попробуй 4
Найдите область определения функции [латекс] f \ left (x \ right) = \ sqrt {5 + 2x} [/ latex].
Решение
Вопросы и ответы
Могут ли быть функции, у которых домен и диапазон вообще не пересекаются?
Да. Например, функция [latex] f \ left (x \ right) = — \ frac {1} {\ sqrt {x}} [/ latex] имеет набор всех положительных вещественных чисел в качестве области своей области, но набор всех отрицательные действительные числа в качестве диапазона.В качестве более крайнего примера входные и выходные данные функции могут быть совершенно разными категориями (например, названия дней недели в качестве входных данных и числа в качестве выходных данных, как на диаграмме посещаемости), в таких случаях домен и диапазон не имеют общих элементов.

В предыдущих примерах мы использовали неравенства и списки для описания области функций. Мы также можем использовать неравенства или другие утверждения, которые могут определять наборы значений или данных, чтобы описать поведение переменной в нотации построителя множеств.Например, [latex] \ left \ {x | 10 \ le x x , таких что 10 меньше чем или равно [latex] x [/ latex], а [latex] x [/ latex] меньше 30 ».
В таблице ниже сравниваются обозначения неравенства, обозначения построителя множеств и обозначения интервалов.
Чтобы объединить два интервала с использованием нотации неравенства или нотации для построения множеств, мы используем слово «или». Как мы видели в предыдущих примерах, мы используем символ объединения, [latex] \ cup [/ latex], чтобы объединить два несвязанных интервала. Например, объединение наборов [latex] \ left \ {2,3,5 \ right \} [/ latex] и [latex] \ left \ {4,6 \ right \} [/ latex] есть множество [латекс] \ left \ {2,3,4,5,6 \ right \} [/ латекс].
 Это набор всех элементов, которые принадлежат одному или другому (или обоим) из двух исходных наборов.Для наборов с конечным числом таких элементов, элементы не должны быть перечислены в порядке возрастания числового значения. Если исходные два набора имеют некоторые общие элементы, эти элементы должны быть указаны в объединенном наборе только один раз. Для наборов действительных чисел на интервалах другой пример объединения —
Это набор всех элементов, которые принадлежат одному или другому (или обоим) из двух исходных наборов.Для наборов с конечным числом таких элементов, элементы не должны быть перечислены в порядке возрастания числового значения. Если исходные два набора имеют некоторые общие элементы, эти элементы должны быть указаны в объединенном наборе только один раз. Для наборов действительных чисел на интервалах другой пример объединения —.
[латекс] \ left \ {x | \ text {} | x | \ ge 3 \ right \} = \ left (- \ infty, -3 \ right] \ чашка \ left [3, \ infty \ right) [ / латекс]
В этом видео рассказывается, как использовать обозначение интервалов для описания набора.
В этом видео рассказывается, как использовать нотацию Set-Builder для описания набора.
com/embed/rPcGeaDRnyc?feature=oembed» frameborder=»0″ allow=»autoplay; encrypted-media» allowfullscreen=»»>Общее примечание: обозначение построителя множеств и обозначение интервалов
Нотация конструктора наборов — это метод определения набора элементов, удовлетворяющих определенному условию. Он принимает форму [латекс] \ left \ {x | \ text {утверждение о} x \ right \} [/ latex], которое читается как «множество всех [латексных] x [/ латексных] таких, что утверждение про [латекс] х [/ латекс] верно.Например,
Решение
Каждая из функций компонента взята из нашей библиотеки функций набора инструментов, поэтому мы знаем их форму. Мы можем представить себе построение графика каждой функции, а затем ограничение графика указанной областью. На конечных точках домена мы рисуем пустые кружки, чтобы указать, где конечная точка не включена из-за неравенства «меньше или больше»; мы рисуем замкнутый круг, где конечная точка включена из-за неравенства «меньше или равно» или «больше или равно».
 {3} \ text {if} {x} & lt {-1} \\ {-2} \ text {if} {-1} & lt {x} & lt {4} \\ \ sqrt {x} \ text {если } {x} & gt {4} \ end {case} [/ latex]
{3} \ text {if} {x} & lt {-1} \\ {-2} \ text {if} {-1} & lt {x} & lt {4} \\ \ sqrt {x} \ text {если } {x} & gt {4} \ end {case} [/ latex]Вопросы и ответы
Можно ли применить более одной формулы из кусочной функции к значению в домене?
Нет. Каждое значение соответствует одному уравнению в кусочной формуле.
Ключевые понятия
- Область функции включает в себя все реальные входные значения, которые не заставят нас попытаться выполнить неопределенную математическую операцию, такую как деление на ноль или извлечение квадратного корня из отрицательного числа.
- Область функции может быть определена путем перечисления входных значений набора упорядоченных пар.
- Область функции также может быть определена путем идентификации входных значений функции, записанной в виде уравнения.
- Значения интервалов, представленные в числовой строке, можно описать с помощью обозначений неравенства, обозначений построителя множеств и обозначений интервалов.

- Для многих функций домен и диапазон можно определить по графику.
- Понимание функций инструментария может быть использовано для поиска предметной области и диапазона связанных функций.
- Кусочная функция описывается более чем одной формулой.
- Кусочная функция может быть построена на графике с использованием каждой алгебраической формулы в назначенной ей подобласти.
- Почему домен различается для разных функций?
- Как определить область определения функции, заданной уравнением?
- Объясните, почему домен [latex] f \ left (x \ right) = \ sqrt [3] {x} [/ latex] отличается от домена [latex] f \ left (x \ right) = \ sqrt [] {x} [/ латекс]. {3} -50x} [/ латекс] по:
а. используя алгебру.
г. построение графика функции в подкоренном выражении и определение интервалов на оси x , для которых подкоренное выражение неотрицательно.Для следующих упражнений запишите домен и диапазон каждой функции, используя интервальную нотацию.

27.
Домен: ________ Диапазон: ________
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
Для следующих упражнений нарисуйте график кусочной функции. Запишите домен в интервальной записи.
38. [латекс] f (x) = \ begin {cases} {x} + {1} & \ text {if} & {x}
39.[латекс] f \ left (x \ right) = \ begin {case} {2x — 1} & \ text {if} & {x}
40. {2} & \ text {if} & {x} {0} \ end {case} [/ latex]
43.{3} & \ text {if} & x \ ge 1 \ end {case} [/ latex]
45. [латекс] f \ left (x \ right) = \ begin {cases} | x | & \ text {if} & {x} Для следующих упражнений, учитывая каждую функцию [latex] f [/ latex], оцените [latex] f \ left (-3 \ right), f \ left (-2 \ right), f \ left (-1 \ right) [/ latex] и [latex] f \ left (0 \ right) [/ latex].
46. [латекс] f \ left (x \ right) = \ begin {cases} {x + 1} & \ text {if} & {x}
47.
 {2} + {3} & \ text {if} & {x} \ le {-1} \\ {5x} — {7} & \ text {if} & {x}> {-1} \ end { case} [/ latex]
{2} + {3} & \ text {if} & {x} \ le {-1} \\ {5x} — {7} & \ text {if} & {x}> {-1} \ end { case} [/ latex]
Для следующих упражнений, учитывая каждую функцию [latex] f [/ latex], оцените [latex] f \ left (-1 \ right), f \ left (0 \ right), f \ left (2 \ справа) [/ латекс] и [латекс] f \ влево (4 \ справа) [/ латекс]. {2} {-2} & \ text {if} & {x}51.{2}} [/ latex] в окне просмотра [латекс] \ left [-0,5, -0,1 \ right] [/ latex] и [latex] \ left [0,1,0,5 \ right] [/ latex]. Определите соответствующий диапазон для смотрового окна. Покажи графики.
56. График [latex] y = \ frac {1} {x} [/ latex] в окне просмотра [latex] \ left [-0,5, -0,1 \ right] [/ latex] и [latex] \ left [ 0,1, \ text {} 0,5 \ right] [/ latex]. Определите соответствующий диапазон для смотрового окна. Покажи графики.
57. Предположим, что диапазон функции [latex] f [/ latex] равен [latex] \ left [-5, \ text {} 8 \ right] [/ latex].Какой диапазон [латекс] | f \ left (x \ right) |? [/ Latex]
58.
 Создайте функцию, в которой весь диапазон представляет собой неотрицательные действительные числа.
Создайте функцию, в которой весь диапазон представляет собой неотрицательные действительные числа.59 .Создайте функцию, в которой домен [latex] x> 2 [/ latex].
60. Стоимость изготовления изделий из [латекса] x [/ латекса] в долларах определяется функцией [латекс] C \ left (x \ right) = 10x + 500 [/ latex].
A. Фиксированная стоимость определяется, когда произведено ноль единиц продукции. Найдите фиксированную стоимость для этого товара.
B. Сколько стоит изготовление 25 предметов?
С.{2} + 96т [/ латекс]. Какова область применения функции? Что означает домен в контексте проблемы?Глоссарий
- обозначение интервалов
- — способ описания набора, который включает в себя все числа от нижнего предела до верхнего предела; нижнее и верхнее значения указаны в скобках или скобках, квадратная скобка указывает на включение в набор, а скобка указывает на исключение
- кусочная функция
- функция, в которой для определения вывода используется более одной формулы
- обозначение конструктора набора
- метод описания набора правилом, которому подчиняются все его члены; он принимает форму [латекс] \ left \ {x | \ text {утверждение о} x \ right \} [/ latex]
Нахождение обратной функции
Находка
Обратная функция (стр.
3 из 7)Разделы: Определение
/ Инвертирование графика, обратная функция — это функция ?,
Нахождение обратного, доказательство обратногоОбычный метод
поиск обратного — это один из вариантов метода, который я собираюсь использовать ниже.Какой бы метод вы ни использовали, убедитесь, что вы выполняете точно такие же шаги в
один и тот же порядок каждый раз, поэтому вы запомните эти шаги, когда получите
к тесту.- Найти обратное
из и
= 3 x 2.
Вот как процесс
работ:Если вам нужно найти
домен и диапазон,
посмотрите на исходную функцию и ее график. Домен оригинала
функция — это набор всех допустимых значений x ;
в этом случае функция была простым полиномом, поэтому область определения
«все реальные числа». Диапазон исходной функции — весь
и -значения
вы передадите график; в этом случае прямая линия продолжается
всегда в любом направлении, поэтому диапазон также представляет собой «все действительные числа». Чтобы найти домен и диапазон обратного, просто поменяйте местами домен и
Чтобы найти домен и диапазон обратного, просто поменяйте местами домен и
диапазон от исходной функции.Обычно считается
приемлемо для построения приведенного выше графика, проведите по нему горизонтальную линию,
дважды пересекает график, а затем произнесите что-то вроде «Обратный
этой функции не является функцией из-за горизонтальной линии
Контрольная работа».Но некоторые учителя все равно хотят изучать алгебру. Быть уверенным
чтобы уточнить у учителя, какой ответ будет приемлемым
— и сделайте это перед тестом ! Авторские права
Элизабет Стапель 2000-2011 Все права защищеныКак это будет выглядеть
когда я пытаюсь найти обратное алгебраически? Вертикаль
Line Test говорит
что у меня не может быть двух и
с общим значением x .То есть каждый x
должен иметь УНИКАЛЬНЫЙ соответствующий
y
значение. Но посмотрите, что происходит, когда я пытаюсь найти « x
= «:Ну я решил для « x
знак равно
но я не получил УНИКАЛЬНЫЙ « x
знак равноВместо этого я показал, что любое заданное значение x
фактически будет соответствовать двум различным значениям y ,
один от «плюса» от квадратного корня, а другой от
«минус».
Каждый раз, когда вы придумываете
знак «», вы можете быть уверены, что обратное не
функция.Эта функция будет
иметь обратное, что
тоже функция. Практически каждый раз, когда они задают вам проблему, где
они постарались ограничить домен, вы должны позаботиться
с алгеброй и нарисуйте красивую картинку, потому что обратное, вероятно,
— это функция, но, вероятно, потребуются дополнительные усилия, чтобы показать это.В данном случае, поскольку размер домена x
0 и
диапазон (из графика) равен 1
y ,
то обратный будет иметь область 1
x и
диапазон y
0. Вот
как выглядит алгебра:(« x
>
1 «ограничение
исходит из того, что x
находится внутри квадратного корня.)Так
инверсия: y
= sqrt ( x 1), x > 1,
и эта инверсия также является функцией.
Вот график:
1
| 2 | 3 | 4 |
5 | 6 | 7
| Вернуться к указателю Далее
>>Цитируйте эту статью
как:Стапель, Елизавета.«Нахождение обратной функции». Purplemath .
Доступно по номеру
https://www.purplemath.com/modules/invrsfcn3.htm .
Дата обращения [Дата] [Месяц] 2016 г.предварительное вычисление алгебры — Найдите область определения и диапазон рациональной функции $ f (x) = \ frac {3x-1} {x + 2} $ и ее обратной
Поскольку $ f $ — рациональная функция, она определена для всех действительных чисел, кроме тех случаев, когда знаменатель равен нулю, поэтому область определения $ f $ равна $ \ mathbb {R} \ setminus \ {- 2 \} $.
 Теперь диапазон $ f $ — это все действительные числа $ y $, такие, что существует некоторый вход $ x $, где $ f (x) = y $. Итак, чтобы найти все такие $ y $, мы можем просто взять $ f (x) $ равным некоторому произвольному выходу $ y $ и изменить рациональное выражение ($ \ star $) так, чтобы найти, для какого $ y $ существует такой $ x $:
Теперь диапазон $ f $ — это все действительные числа $ y $, такие, что существует некоторый вход $ x $, где $ f (x) = y $. Итак, чтобы найти все такие $ y $, мы можем просто взять $ f (x) $ равным некоторому произвольному выходу $ y $ и изменить рациональное выражение ($ \ star $) так, чтобы найти, для какого $ y $ существует такой $ x $:
$$
\ tag {$ \ star \ star $}
\ begin {align}
f (x) & = y
\\ [1em] \ подразумевает \ qquad
\ frac {3x-1} {x + 2} & = y
\\ [1em] \ подразумевает \ qquad
x & = \ frac {2y + 1} {- y + 3}
\ end {align}
$$
Мы видим, что такой $ x $ существует для всех выходов, кроме $ y = 3 $, где знаменатель рационального выражения для $ x $ равен нулю.{-1} $.Область и диапазон рациональных функций
В
домен
изфункция
ж
Икс
— это набор всех значений, для которых определена функция, а
диапазон
функции — это набор всех значений, которыеж
берет.

Рациональная функция — это функция вида
ж
Икс
знак равно
п
Икс
q
Икс
, где
п
Икс
а также
q
Икс
являются многочленами и
q
Икс
≠
0
.
Область определения рациональной функции состоит из всех действительных чисел
Икс
кроме тех, для которых знаменатель
0
. Чтобы найти эти
Икс
значения, которые нужно исключить из области определения рациональной функции, приравнять знаменатель к нулю и решить для
Икс
.
Например, домен
родительская функция
ж
Икс
знак равно
1
Икс
это набор всех действительных чисел, кроме
Икс
знак равно
0
.Или область определения функции
ж
Икс
знак равно
1
Икс
—
4
это набор всех действительных чисел, кроме
Икс
знак равно
4
.

Теперь рассмотрим функцию
ж
Икс
знак равно
Икс
+
1
Икс
—
2
Икс
—
2
. По упрощению, когда
Икс
≠
2
он становится линейной функцией
ж
Икс
знак равно
Икс
+
1
.Но исходная функция не определена в
Икс
знак равно
2
. Это оставляет график с дырой, когда
Икс
знак равно
2
.
Один из способов найти диапазон рациональной функции — найти область определения обратной функции.
Другой способ — нарисовать график и определить диапазон.
Снова рассмотрим родительскую функцию
ж
Икс
знак равно
1
Икс
.Мы знаем, что функция не определена, когда
Икс
знак равно
0
.
В виде
Икс
→
0
по обе стороны от нуля,
ж
Икс
→
∞
.
 Аналогично, как
Аналогично, какИкс
→
±
∞
,
ж
Икс
→
0
.
График приближается
Икс
-ось как
Икс
стремится к положительной или отрицательной бесконечности, но никогда не касается
Икс
-ось.То есть функция может принимать все реальные значения, кроме
0
.
Итак, диапазон функции — это набор действительных чисел, кроме
0
.
Пример 1:Найдите домен и диапазон функции
y
знак равно
1
Икс
+
3
—
5
.
Чтобы найти исключенное значение в области определения функции, приравняйте знаменатель к нулю и решите относительно
Икс
.
Икс
+
3
знак равно
0
⇒
Икс
знак равно
—
3
Итак, область определения функции — это набор действительных чисел, кроме
—
3
.

Диапазон функции такой же, как и у обратной функции. Итак, чтобы найти диапазон, определите обратную функцию.
Поменять местами
Икс
а также
y
.
Икс
знак равно
1
y
+
3
—
5
Решение для
y
ты получаешь,
Икс
+
5
знак равно
1
y
+
3
⇒
y
+
3
знак равно
1
Икс
+
5
⇒
y
знак равно
1
Икс
+
5
—
3
Итак, обратная функция
ж
—
1
Икс
знак равно
1
Икс
+
5
—
3
.
Исключенное значение в области определения обратной функции можно определить, приравняв знаменатель к нулю и решив для
Икс
.
Икс
+
5
знак равно
0
⇒
Икс
знак равно
—
5
Итак, область определения обратной функции — это набор действительных чисел, кроме
—
5
.
 То есть диапазон данной функции — это набор действительных чисел, кроме
То есть диапазон данной функции — это набор действительных чисел, кроме—
5
.
Следовательно, область определения данной функции равна
{
Икс
∈
ℝ
|
Икс
≠
—
3
}
и диапазон
{
y
∈
ℝ
|
y
≠
—
5
}
.
Пример 2:Найдите домен и диапазон функции
y
знак равно
Икс
2
—
3
Икс
—
4
Икс
+
1
.
Используйте графический калькулятор, чтобы построить график функции.
Когда вы множите числитель и отменяете ненулевые общие множители, функция сводится к линейной функции, как показано.
y
знак равно
Икс
+
1
Икс
—
4
Икс
+
1
знак равно
Икс
+
1
Икс
—
4
Икс
+
1
знак равно
Икс
—
4
Итак, график линейный с дырой в
Икс
знак равно
—
1
.

Используйте график, чтобы определить домен и диапазон.
Функция не определена для
Икс
знак равно
—
1
. Итак, домен
{
Икс
∈
ℝ
|
Икс
≠
—
1
}
или же
—
∞
,
—
1
∪
—
1
,
∞
.
Диапазон функции:
{
y
∈
ℝ
|
y
≠
k
где
y
—
1
знак равно
k
}
.
Для
Икс
≠
—
1
, функция упрощается до
y
знак равно
Икс
—
4
.Функция не определена в
Икс
знак равно
—
1
или функция не принимает значение
—
1
—
4
знак равно
—
5
. Это,
k
знак равно
—
5
.

Следовательно, диапазон функции равен
{
y
∈
ℝ
|
y
≠
—
5
}
или же
—
∞
,
—
5
∪
—
5
,
∞
.
Асимптоты рациональной функции:
An
асимптота
это линия, к которой график функции приближается, но никогда не касается. В родительской функции
ж
Икс
знак равно
1
Икс
, как
Икс
— а также
y
-оси — это асимптоты. График родительской функции будет приближаться к асимптотам, но никогда не касается их.
Чтобы найти вертикальную асимптоту рациональной функции, приравняйте знаменатель к нулю и решите относительно
Икс
.
Если степень многочлена в числителе меньше степени знаменателя, то горизонтальная асимптота — это
Икс
-ось или
y
знак равно
0
.

Функция
ж
Икс
знак равно
а
Икс
,
а
≠
0
имеет тот же домен, диапазон и асимптоты, что и
ж
Икс
знак равно
1
Икс
.
Теперь график функции
ж
Икс
знак равно
а
Икс
—
б
+
c
,
а
≠
0
гипербола, симметричная относительно точки
б
,
c
.Вертикальная асимптота функции равна
Икс
знак равно
б
а горизонтальная асимптота равна
y
знак равно
c
.
В более общем виде функция
ж
Икс
знак равно
а
Икс
+
б
c
Икс
+
d
имеет вертикальную асимптоту при
Икс
знак равно
—
d
c
и горизонтальная асимптота при
y
знак равно
а
c
.
 В более общем смысле, если и числитель, и знаменатель имеют одинаковую степень, то горизонтальная асимптота будет иметь вид
В более общем смысле, если и числитель, и знаменатель имеют одинаковую степень, то горизонтальная асимптота будет иметь видy
знак равно
k
где
k
— отношение старшего коэффициента числителя к знаменателю.
Если степень знаменателя на единицу меньше степени числителя, то функция имеет наклонную асимптоту.
Пример 3:Найдите вертикальную и горизонтальную асимптоты функции
ж
Икс
знак равно
5
Икс
—
1
.
Чтобы найти вертикальную асимптоту, приравняйте знаменатель к нулю и решите относительно
Икс
.
Икс
—
1
знак равно
0
⇒
Икс
знак равно
1
Итак, вертикальная асимптота равна
Икс
знак равно
1
Поскольку степень многочлена в числителе меньше степени знаменателя, горизонтальная асимптота имеет вид
y
знак равно
0
.

Домен
и диапазон — Бесплатная справка по математике
При работе с функциями часто встречаются два термина: домен и диапазон . Что такое домен ? Что такое серия ? Почему они важны? Как мы можем определить домен и диапазон для данной функции?
Определение домена
Домен : набор всех возможных входных значений (обычно это переменная «x»), которые производят действительный выход из конкретной функции.Это набор всех значений, для которых функция математически определена. Довольно часто домен представляет собой набор всех действительных чисел , поскольку многие математические функции могут принимать любой ввод.
Например, многие упрощенные алгебраические функции имеют области, которые могут показаться… очевидными. Какова область определения функции \ (f (x) = 2x + 1 \)? Какие значения мы можем ввести для входа (x) этой функции? Ну ничего! Ответ — все реальные числа.
 Только когда мы дойдем до определенных типов алгебраических выражений, нам нужно будет ограничить область.
Только когда мы дойдем до определенных типов алгебраических выражений, нам нужно будет ограничить область.Мы также можем продемонстрировать домен визуально. Рассмотрим простое линейное уравнение, подобное приведенному ниже графику, построенному на основе функции \ (y = \ frac {x} {2} +10 \). Какие значения являются допустимыми входными данными? Это не вопрос с подвохом — можно вводить любое действительное число! Домен функции — это все действительные числа, потому что вы ничего не можете подставить для x, что не сработает. Визуально мы видим это как линию, которая продолжается вечно в направлениях x (влево и вправо).
Для других линейных функций (линий) линия может быть очень и очень крутой, но если вы представите себе «уменьшение масштаба» достаточно далеко, в конечном итоге любое значение x появится на графике.С другой стороны, прямая горизонтальная линия была бы самым ярким примером неограниченной области всех действительных чисел.
Какие функции не имеют области , состоящей из всех действительных чисел? Что могло бы помешать нам, изучающим алгебру, вставить какое-либо значение во входные данные функции? Что ж, если домен — это набор всех входов, для которых определена функция, то логически мы ищем пример функции, которая нарушает для определенных входных значений.
 Нам нужна функция, которая для определенных входов не выдает допустимый выход , т.е.е., функция для этого входа не определена. Вот пример:
Нам нужна функция, которая для определенных входов не выдает допустимый выход , т.е.е., функция для этого входа не определена. Вот пример:Эта функция определена для почти любого действительного x. Но каково значение y, когда x = 1? Ну, это \ (\ frac {3} {0} \), то есть undefined . Деление на ноль не определено. Следовательно, 1 не входит в область действия этой функции. Мы не можем использовать 1 в качестве входных данных, потому что это нарушает функцию. Все остальные действительные числа являются допустимыми входными данными, поэтому доменом являются все действительные числа, кроме x = 1. Имеет смысл, правда?
Деление на ноль — одно из самых распространенных мест, на которое обращают внимание при решении для области определения функции.Найдите места, которые могут привести к делению на ноль, и запишите значения x, при которых знаменатель будет равен нулю. Это ваши ценности, которые нужно исключить из домена.
Если деление на ноль — обычное место для поиска ограничений в домене, то знак «квадратный корень», вероятно, является вторым по распространенности.
 Конечно, мы знаем, что это на самом деле называется радикальным символом, но вы, несомненно, называете это знаком квадратного корня. Почему это вызывает проблемы с доменом? Потому что, по крайней мере, в области действительных чисел, мы не можем найти квадратный корень из отрицательного значения.
Конечно, мы знаем, что это на самом деле называется радикальным символом, но вы, несомненно, называете это знаком квадратного корня. Почему это вызывает проблемы с доменом? Потому что, по крайней мере, в области действительных чисел, мы не можем найти квадратный корень из отрицательного значения.Что, если нас попросят найти домен \ (f (x) = \ sqrt {x-2} \). Какие значения исключены из домена? Значение меньше 2 приводит к отрицательному числу внутри квадратного корня, что является проблемой. Следовательно, в домене все действительные числа больше или равны 2.
У каких других функций есть домены, не все из которых являются действительными числами? Некоторые «обратные» функции, такие как обратные триггерные функции, также имеют ограниченную область применения. Поскольку синусоидальная функция может иметь только выходов от -1 до +1, ее обратная функция может принимать только входов от -1 до +1.Область обратного синуса от -1 до +1. Однако, , наиболее распространенный пример ограниченного домена — это, вероятно, проблема деления на ноль .
 Когда вас попросят найти домен функции, начните с простого: сначала найдите любые значения, которые заставляют вас делить на ноль. Помните также, что мы не можем извлечь квадратный корень из отрицательного числа, поэтому следите за ситуациями, когда подкоренное выражение («материал» внутри знака квадратного корня) может привести к отрицательному значению. В этом случае это будет недопустимый ввод, поэтому домен не будет включать такие значения.
Когда вас попросят найти домен функции, начните с простого: сначала найдите любые значения, которые заставляют вас делить на ноль. Помните также, что мы не можем извлечь квадратный корень из отрицательного числа, поэтому следите за ситуациями, когда подкоренное выражение («материал» внутри знака квадратного корня) может привести к отрицательному значению. В этом случае это будет недопустимый ввод, поэтому домен не будет включать такие значения.Определение диапазона
Диапазон : Диапазон — это набор всех возможных выходных значений (обычно это переменная y или иногда выражается как \ (f (x) \)), которые возникают в результате использования определенной функции.
Диапазон простой линейной функции почти всегда будет , все действительные числа . График типичной линии, такой как показанный ниже, будет продолжаться бесконечно в любом направлении y (вверх или вниз). Диапазон негоризонтальной линейной функции — это все действительные числа, независимо от того, насколько пологим может выглядеть наклон.

Есть одно заметное исключение: когда y равно константе (например, \ (y = 4 \) или \ (y = 19 \)). Когда у вас есть функция, в которой y равно константе, ваш график представляет собой действительно горизонтальную линию, как график ниже для \ (y = 3 \). В этом случае диапазон — это только одно-единственное значение. Никакие другие возможные значения не могут быть получены из этой функции!
Многие другие функции имеют ограниченный диапазон. Хотя только несколько типов имеют ограниченные домены, вы часто будете видеть функции с необычными диапазонами.4 \) и т.д …) приведет, например, только к положительному результату. Специальные функции, такие как тригонометрические функции, также, безусловно, будут иметь ограниченные возможности.
Сводка : Область функции — это все возможные входных значений, для которых функция определена, а диапазон — все возможные выходных значений.
Если вы все еще не уверены, вы можете разместить свой вопрос на нашей доске сообщений или прочитать урок другого веб-сайта по домену и диапазону, чтобы получить другую точку зрения.
 Или вы можете использовать калькулятор ниже, чтобы определить домен и диапазон ЛЮБОГО уравнения:
Или вы можете использовать калькулятор ниже, чтобы определить домен и диапазон ЛЮБОГО уравнения:Калькулятор домена и диапазона
Нахождение области определения функции
Хорошо, допустим, у нас нет
график функции, как в последнем разделе …Можем ли мы еще найти домен и
диапазон?Домены: Да (пока алгебра не становится слишком волосатым… а для нас не будет.)
Диапазоны: Не совсем (обычно нужен
Изображение
— если это не что-то действительно базовое
.)Итак, мы будем делать домены на
эти — в любом случае, именно здесь и происходит действие.Просить
домен
функция такая же, как при запросе
«Что все
возможно x
ребята
что я могу воткнуть в эту штуку? »Иногда то, что
вы действительно будете искать это«Есть что-нибудь
Я НЕ МОГУ вставлять? «Проверьте это:
Найдем домен
изВы видите
Икс
ребята, что могло бы вызвать здесь проблемы?А как насчет ? Итак,
Икс
знак равно
3 — плохой парень! Все
в остальном все в порядке.
The
домен — это все вещественные числа, кроме
3.Что бы
обозначение интервала быть?Если есть сомнения, график
это на номерной строке:Сделайте интервал
обозначение двумя частями:ВАШ ЧАСТЬ:
Найдите
домен
Иногда вы не можете найти домен быстрым взглядом.Проверьте это:
Давайте найдем
доменХм … Это не так
так очевидно!НО, мы все еще
ищу то же самое:Плохое
Икс
Значит, знаменатель
равен 0!Как мы его находим?
Легкий!Установить знаменатель
= 0
и решай!В
доменПОПРОБОВАТЬ:
Найдите домен * показать работу !! Как насчет
Вот этот?Квадратные корни — что
мы знаем о квадратных корнях?… Итак, 16
можно вставить.
… Итак, 0
в порядке.… Фу! Но,
3,2
в порядке.… Неа! Не могу!
* Нам нужны только реальные числа!Никаких негативов нет!
The
внутри
радикальный не может быть отрицательным, если мы хотим
только реальные ответы (нет
я
ребята).Итак, внутри
радикал должен быть 0 или положительным
номер.Набор и реши! А теперь давайте найдем
доменИтак, домен это . ПОПРОБОВАТЬ:
Найдите
домен.
* Показать работы !!Вот
грязный:Найдем домен
из
Набор
и решай!Домен . 
ВАШ ЧАСТЬ:
Найдите домен .
* Показать работы!Обратные функции
Обратная функция — наоборот!
Начнем с примера:
Здесь у нас есть функция f (x) = 2x + 3 , записанная в виде блок-схемы:
Обратная функция идет другим путем:
Таким образом, обратное: 2x + 3: (y-3) / 2
Обратное значение обычно отображается путем добавления небольшого «-1» после имени функции, например:
ф -1 (у)
Мы говорим « f инверсия y»
Итак, обратная величина к f (x) = 2x + 3 записывается:
f -1 (y) = (y-3) / 2
(я также использовал y вместо x , чтобы показать, что мы используем другое значение.
 )
)Вернуться туда, где мы начали
Самое замечательное в обратном преобразовании состоит в том, что он должен вернуть нам исходное значение:
.
Когда функция f превращает яблоко в банан,
Затем обратная функция f -1 превращает банан обратно в яблоко
Пример:
Используя приведенные выше формулы, мы можем начать с x = 4:
f (4) = 2 × 4 + 3 = 11
Затем мы можем использовать обратное для 11:
ф -1 (11) = (11-3) / 2 = 4
И мы волшебным образом снова получаем 4 !
Мы можем написать это одной строкой:
f -1 (f (4)) = 4
«f, обратное f 4, равно 4»
Таким образом, применение функции f, а затем ее обратного f -1 возвращает нам исходное значение снова:
f -1 (f (x)) = x
Мы могли бы также расположить функции в другом порядке, и он все еще работает:
f (f -1 (x)) = x
Пример:
Начать с:
ф -1 (11) = (11-3) / 2 = 4
А потом:
f (4) = 2 × 4 + 3 = 11
Итак, мы можем сказать:
f (f -1 (11)) = 11
«f f, обратное 11, равно 11»
Решить с помощью алгебры
Мы можем вычислить обратное, используя алгебру.
 Положите y вместо f (x) и решите относительно x:
Положите y вместо f (x) и решите относительно x: Функция: f (x) = 2x + 3 Поместите y вместо f (x): y = 2x + 3 Вычтем 3 с обеих сторон: г-3 = 2x Разделите обе стороны на 2: (у-3) / 2 = x Стороны поменять местами: x = (у-3) / 2 Решение (вместо «x» подставьте «f -1 (y)»): ф -1 (у) = (у-3) / 2 Этот метод хорошо подходит для более сложных инверсий.

Фаренгейта в Цельсия
Полезный пример — преобразование между градусами Фаренгейта и Цельсия:
Для преобразования Фаренгейта в Цельсия: f (F) = (F — 32) × 5 9
Обратная функция (градусы Цельсия обратно по Фаренгейту): f -1 (C) = (C × 9 5 ) + 32
Для вас: посмотрите, сможете ли вы сделать шаги, чтобы создать инверсию!
Инверсия общих функций
До сих пор это было легко, потому что мы знаем, что обратное к умножению — это деление, а обратное к сложению — вычитание, но как насчет других функций?
Вот список, который вам поможет:
(Примечание: вы можете узнать больше об обратном синусе, косинусе и тангенсе.)
Осторожно!
Вы видели «Осторожно!» столбец выше? Это потому, что некоторые инверсии работают только с определенными значениями .
Пример: квадрат и квадратный корень
Когда мы возводим в квадрат отрицательное число , а затем делаем обратное, происходит следующее:
Квадрат: (- 2) 2 = 4
Обратная величина (квадратный корень): √ (4) = 2
Но мы не вернули исходное значение! Мы получили 2 вместо −2 .
 Наша вина в том, что мы не проявляем осторожности!
Наша вина в том, что мы не проявляем осторожности!Итак, функция квадрата (как она есть) не имеет обратной
Но мы можем это исправить!
Ограничить домен (значения, которые могут входить в функцию).
Пример: (продолжение)
Только убедитесь, что мы не используем отрицательные числа.
Другими словами, ограничьте его до x ≥ 0 , и тогда мы сможем получить обратное.
Итак, мы имеем такую ситуацию:
- x 2 имеет ли не инверсию
- но {x 2 | x ≥ 0} (в котором говорится, что «x возведен в квадрат так, что x больше или равен нулю» с использованием нотации создателя множеств) имеет ли обратное.
Нет обратного?
Давайте посмотрим наглядно, что здесь происходит:
Чтобы иметь возможность иметь инверсию, нам нужно уникальных значения .
Подумайте … если есть два или более x-значений для одного y-значения , как мы узнаем, какое из них выбрать, когда вернемся?
Общие функции Без обратного Представьте, что мы перешли от x 1 к определенному значению y, куда мы вернемся? x 1 или x 2 ?
В этом случае у нас не может быть обратного.

Но если мы можем иметь ровно один x для каждого y, мы можем получить обратное.
Это называется «однозначным соответствием» или биективным, например
Биективная функция Имеет инверсию Функция должна быть «биективной», чтобы иметь инверсию.
Таким образом, биективная функция подчиняется более строгим правилам, чем общая функция, что позволяет нам иметь обратную функцию.
Домен и диапазон
Так что же все эти разговоры о « ограничении домена »?
В простейшей форме домен — это все значения, входящие в функцию (а диапазон , — это все значения, которые выходят).
В его нынешнем виде функция, приведенная выше, не имеет инверсии , а не , потому что некоторые значения y будут иметь более одного значения x.
Но мы могли бы ограничить домен так, чтобы для каждого y был уникальный x …
… и теперь у нас может быть обратное:
Также примечание:
- Функция f (x) переходит из области в диапазон,
- Обратная функция f -1 (y) переходит из диапазона обратно в домен.

Давайте изобразим их оба в терминах x … так что теперь это f -1 (x) , а не f -1 (y) :
f (x) и f -1 (x) похожи на зеркальные изображения
(перевернут по диагонали).
Другими словами:
График f (x) и f -1 (x) симметричны по линии y = x
Пример: квадрат и квадратный корень (продолжение)
Первый , мы ограничиваем Домен до x ≥ 0 :
- {x 2 | x ≥ 0} «x в квадрате, так что x больше или равно нулю»
- {√x | x ≥ 0} «квадратный корень из x такой, что x больше или равен нулю»
И вы видите, что это «зеркальные отражения»
друг друга по диагонали y = x.
Примечание: когда мы ограничиваем область до x ≤ 0 (меньше или равно 0), обратное значение будет f -1 (x) = −√x :
- {x 2 | х ≤ 0}
- {−√x | x ≥ 0}
Которые тоже обратные.

Не всегда разрешимо!
Иногда невозможно найти обратную функцию.
Пример: f (x) = x / 2 + sin (x)
Мы не можем вычислить обратное, потому что мы не можем решить для «x»:
у = х / 2 + грех (х)
г …? = х
Примечания к обозначениям
Несмотря на то, что мы пишем f -1 (x), «-1» — это , а не показатель степени (или степени):
f -1 (x) … отличается от … f (x) -1 Функция, обратная функции f f (x) -1 = 1 / f (x) (Взаимный)
Сводка
- Значение, обратное f (x), равно f -1 (y)
- Мы можем найти обратное, перевернув «блок-схему»
- Или мы можем найти обратное с помощью алгебры:
- Вместо f (x) подставьте «y» и
- Решить относительно x
- Нам может понадобиться ограничить домен , чтобы функция имела инверсию
.

- Во-первых, когда есть дробь, в этом случае знаменатель дроби, недолжен быть равным нулю, потому, что такая дробь не может существовать. То есть, если ваша функция — дробь и в знаменателе есть переменная (потому, что если там только число, то оно никогда не станет нулём) то вам надо всё то выражение, что в знаменателе прировнять к нулю.
Как найти область определения функции — Wiki How To Русский
‘).insertAfter(«#intro»),$(‘
‘).insertBefore(«.youmightalsolike»),$(‘
‘).insertBefore(«#quiz_container»),$(‘
‘).insertBefore(«#newsletter_block_main»),fa(! 0),b=document.getElementsByClassName(«scrolltomarker»),a=0;a
В этой статье:
Основы
Область определения дробных функций
Область определения функции с корнем
Область определения функции с натуральным логарифмом
Поиск области определения с помощью графика
Поиск области определения с помощью множества
Показать еще 3…
Показать меньше…
Дополнительные статьи
Область определения функции — это множество чисел, на котором задается функция. Другими словами, это те значения х, которые можно подставить в данное уравнение. Возможные значения у называются областью значений функции. Если вы хотите найти область определения функции в различных ситуациях, выполните следующие действия.
Возможные значения у называются областью значений функции. Если вы хотите найти область определения функции в различных ситуациях, выполните следующие действия.
Шаги
1
Запомните, что такое область определения. Область определения — это множество значений х, при подставлении которых в уравнение мы получаем область значений у.
2
Научитесь находить область определения различных функций. Тип функции определяет метод нахождения области определения. Вот основные моменты, которые вы должны знать о каждом типе функции, о которых пойдет речь в следующем разделе:
- Полиномиальная функция без корней или переменных в знаменателе. Для этого типа функции областью определения являются все действительные числа.
- Дробная функция с переменной в знаменателе. Чтобы найти область определения данного типа функции, знаменатель приравняйте к нулю и исключите найденные значения х.

- Функция с переменной внутри корня. Чтобы найти область определения данного типа функции, задайте подкоренное выражение больше или равно 0 и найдите значения х.
- Функция с натуральным логарифмом (ln). Задайте выражение под логарифмом > 0 и решите.
- График. Нарисуйте график для нахождения х.
- Множество. Это будет список координат х и у. Область определения — список координат х.
3
Правильно обозначайте область определения. Легко научиться правильному обозначению области определения, но важно, чтобы вы правильно записывали ответ и получали высокую оценку. Вот несколько вещей, которые вы должны знать о написании области определения:
- Один из форматов написания области определения: квадратная скобка, 2 конечных значения области, круглая скобка.
- Например, [-1; 5). Это означает область определения от -1 до 5.
- Используйте квадратные скобки [ и ] , чтобы указать, что значение принадлежит области определения.

- Таким образом, в примере [-1; 5) область включает -1.
- Используйте круглые скобки ( и ) , чтобы указать, что значение не принадлежит области определения.
- Таким образом, в примере [-1; 5) 5 не принадлежит области. Область включает только значения, бесконечно близкие к 5, то есть 4,999(9).
- Используйте знак U для объединения областей, разделенных промежутком.
- Например, [-1; 5 ) U (5; 10]. Это означает, что область проходит от -1 до 10 включительно, но не включает 5. Это может быть у функции, где в знаменателе стоит «х — 5».
- Вы можете использовать несколько U по мере необходимости, если область имеет несколько разрывов/промежутков.
- Используйте знаки «плюс бесконечность» и «минус бесконечность», чтобы выразить, что область бесконечна в любом направлении.
- Со знаком бесконечности всегда используйте ( ), а не [ ].
Реклама
- Один из форматов написания области определения: квадратная скобка, 2 конечных значения области, круглая скобка.
1
Запишите пример.
 Например, вам дана следующая функция:
Например, вам дана следующая функция:- f(x) = 2x/(x2 — 4)
2
Для дробных функций с переменной в знаменателе надо приравнять знаменатель к нулю. При нахождении области определения дробной функции необходимо исключить все значения х, при которых знаменатель равен нулю, потому что нельзя делить на ноль. Запишите знаменатель как уравнение и приравняйте его к 0. Вот как это делается:
- f(x) = 2x/(x2 — 4)
- x2 — 4 = 0
- (x — 2 )(x + 2) = 0
- x ≠ 2; — 2
3
Запишите область определения:
- х = все действительные числа, кроме 2 и -2
Реклама
1
Запишите пример. Дана функция y =√(x-7)
2
Задайте подкоренное выражение больше или равным 0. Вы не можете извлечь квадратный корень из отрицательного числа, хотя вы можете извлечь квадратный корень 0.
 Таким образом, задайте подкоренное выражение больше или равным 0. Заметим, что это относится не только к квадратным корням, но и ко всем корням с четной степенью. Тем не менее, это не относится к корням с нечетной степенью, так как отрицательное число может стоять под корнем нечетной степени.
Таким образом, задайте подкоренное выражение больше или равным 0. Заметим, что это относится не только к квадратным корням, но и ко всем корням с четной степенью. Тем не менее, это не относится к корням с нечетной степенью, так как отрицательное число может стоять под корнем нечетной степени.- х — 7 ≧ 0
3
Выделите переменную. Для этого перенесите 7 в правую часть неравенства:
- x ≧ 7
4
Запишите область определения. Вот она:
- D = [7; +∞)
5
Найдите область определения функции с корнем, когда есть несколько решений. Дано: y = 1/√( ̅x2 -4). Приравняв знаменатель к нулю и решив это уравнение, вы получите х ≠ (2; -2). Вот как вы действуете далее:
- Проверьте область за -2 (например, подставив -3), чтобы удостовериться, что подстановка в знаменатель чисел меньше -2 в результате дает число больше 0.
 И это так:
И это так:- (-3)2 — 4 = 5
- Теперь проверьте область между -2 и +2. Подставьте, например, 0.
- 02 — 4 = -4, так что числа между -2 и 2 не подходят.
- Теперь попробуйте числа больше 2, например 3.
- 32 — 4 = 5, так что числа больше 2 подходят.
- Запишите область определения. Вот как записывается эта область:
- D = (-∞; -2) U (2; +∞)
Реклама
- Проверьте область за -2 (например, подставив -3), чтобы удостовериться, что подстановка в знаменатель чисел меньше -2 в результате дает число больше 0.
1
Запишите пример. Допустим, дана функция:
- f(x) = ln(x — 8)
2
Задайте выражение под логарифмом больше нуля. Натуральный логарифм должен быть положительным числом, поэтому задаем выражение внутри скобок больше нуля.
- x — 8 > 0
3
Решите. Для этого обособьте переменную х, прибавив к обеим частям неравенства 8.

- x — 8 + 8 > 0 + 8
- x > 8
4
Запишите область определения. Область определения этой функции есть любое число больше 8. Вот так:
- D = (8; +∞)
Реклама
1
Посмотрите на график.
2
Проверьте значения х, которые отображены на графике. Это может быть легче сказать, чем сделать, но вот несколько советов:
- Линия. Если на графике вы видите линию, которая уходит в бесконечность, то все значения х верны, и область определения включает все действительные числа.
- Обычная парабола. Если вы видите параболу, которая смотрит вверх или вниз, то область определения — все действительные числа, потому что подходят все числа на оси х.
- Лежачая парабола. Теперь, если у вас есть парабола с вершиной в точке (4; 0), которая простирается бесконечно вправо, то область определения D = [4; +∞)
3
Запишите область определения.
 Запишите область определения в зависимости от типа графика, с которым вы работаете. Если вы не уверены в типе графика и знаете функцию, описывающую его, для проверки подставьте координаты х в функцию.
Запишите область определения в зависимости от типа графика, с которым вы работаете. Если вы не уверены в типе графика и знаете функцию, описывающую его, для проверки подставьте координаты х в функцию.Реклама
1
Запишите множество. Множество — это набор координат х и у. Например, вы работаете со следующими координатами: {(1; 3), (2; 4), (5; 7)}
2
Запишите координаты х. Это 1; 2; 5.
3
Область определения: D = {1; 2; 5}
4
Убедитесь, что множество является функцией. Для этого необходимо, чтобы каждый раз, когда вы подставляете значение х, вы получали одно и то же значение y. Например, подставляя х = 3, вы должны получить у = 6, и так далее. Приведенное в примере множество не является функцией, потому что дано два разных значения у: {(1; 4), (3; 5), (1; 5)}.
Реклама
Об этой статье
На других языках
Как найти область определения функции — Wiki How Русский
Область определения функции — это множество чисел, на котором задается функция. Другими словами, это те значения х, которые можно подставить в данное уравнение. Возможные значения у называются областью значений функции. Если вы хотите найти область определения функции в различных ситуациях, выполните следующие действия.
Другими словами, это те значения х, которые можно подставить в данное уравнение. Возможные значения у называются областью значений функции. Если вы хотите найти область определения функции в различных ситуациях, выполните следующие действия.
Эту страницу просматривали 841 768 раз.
Реклама
Площадь функции | Superprof
В этой статье мы обсудим, как вычислить площадь между функцией и осью x.
Площадь между функцией и осью x
Существует два сценария, в которых мы можем найти площадь между функцией и осью x:
- Когда функция неотрицательна, т.е. положительна
- Когда функция отрицательна
Теперь давайте посмотрим, какие шаги следует выполнить при вычислении площади между функцией и осью x.
Лучшие репетиторы по математике
Поехали
Шаги для расчета площади под кривой
Чтобы вычислить площадь под кривой f(x), необходимо выполнить следующие шаги:
Шаг 1 — Зарисовать площадь
Шаг 2. Найдите границы a и b
Найдите границы a и b
Шаг 3. Запишите определенную интегральную функцию
Шаг 4. Интегрируйте функцию
В следующем разделе мы обсудим, как вычислить площадь, когда функция положительна.
Когда функция положительна
Если функция f(x) положительна на интервале [a, b], то площадь области, ограниченной графиком функции f, ось абсцисс (x — ось) а вертикальные линии x = a и x = b определяются следующим образом:
Теперь давайте решим несколько примеров, в которых будем вычислять площадь под кривой.
Пример 1
Вычислить площадь, ограниченную функцией и осью x.
Решение
Выполните следующие действия, чтобы решить этот пример.
Шаг 1. Нарисуйте график
Нарисуйте график. График функции приведен ниже:
Шаг 2 — Найдите границы
Чтобы найти границы a и b функции, мы должны определить x-пересечения кривой. Хотя из графика выше мы можем четко определить, что пределы интегрирования равны 3 и -3, тем не менее, мы можем проверить это еще раз, приравняв функцию равной нулю, как показано ниже: 9Шаг 3. Используя границы, напишите функцию определенного интеграла
Используя границы, напишите функцию определенного интеграла
Шаг 4. Интегрирование функции
Запишите функцию, используя свойство суммы/разности определенных интегралов, например: функция. Первообразная функции равна . Для простоты расчета примем C = 0,
Основная теорема исчисления гласит:
Подставим 3 и -3 в первообразную функции:
Отсюда
Пример 2
Вычислите площадь области, ограниченной функцией xy = 36, линиями x = 6 и x = 12 и осью x.
Решение
Выполните следующие действия, чтобы вычислить площадь.
Шаг 1. Нарисуйте график
График функции приведен ниже:
Шаг 2. Найдите границы =
Эта проблема.
Шаг 3. Используя границы, напишите функцию определенного интеграла
На этом этапе мы будем использовать границы 6 и 12 и запишем функцию в виде определенного интеграла следующим образом:
Шаг 4 — Интегрирование функции
Теперь, чтобы найти определенный интеграл функции, сначала мы вычислим первообразную функции. Первообразная функции равна . Для простоты вычислений предположим, что C = 0,
Первообразная функции равна . Для простоты вычислений предположим, что C = 0,
Основная теорема исчисления гласит:
Подставьте 6 и 12 в первообразную функции следующим образом: функция отрицательна на отрезке [a, b], то график функции находится ниже горизонтальной оси. Площадь функции можно определить следующим образом:
Теперь давайте решим несколько примеров, в которых нам дана отрицательная функция.
Пример 1
Найдите площадь функции, ограниченной графиком и осью x.
Решение
Выполните следующие действия, чтобы решить этот пример.
Шаг 1. Нарисуйте график
Нарисуйте график. График функции приведен ниже:
Нисходящая парабола показывает, что функция отрицательна.
Шаг 2. Найдите границы
Чтобы найти границы a и b функции, мы должны определить x-пересечения кривой. Хотя из графика выше мы можем четко определить, что пределы интегрирования равны 4 и 0, тем не менее, мы можем проверить это еще раз, приравняв функцию равной нулю, как показано ниже:
или
Шаг 3 — Используя границы, напишите определенную интегральную функцию
. На этом шаге мы будем использовать границы 4 и 0 и запишем функцию в определенной интегральной форме следующим образом:
На этом шаге мы будем использовать границы 4 и 0 и запишем функцию в определенной интегральной форме следующим образом:
Шаг 4. Интегрирование функции
Запишите функцию, используя свойство суммы/разности определенных интегралов следующим образом: первообразная функции. Первообразная функции равна . Для простоты вычислений рассмотрим C = 0.
Основная теорема исчисления гласит:
Подставим 4 и 0 в первообразную функции:
Пример 2
Вычислите площадь, ограниченную кривой y = cos x и осью x между и .
Решение
Выполните следующие действия, чтобы решить этот пример.
Шаг 1. Нарисуйте график
Нарисуйте график. График функции y = cos x приведен ниже:
Шаг 2 — Найдите границы
Границы и уже даны в этой задаче.
Шаг 3 — Используя границы, запишите функцию определенного интеграла
На этом шаге мы будем использовать границы и запишем функцию в виде определенного интеграла следующим образом:
Шаг 4 — Интегрируем функцию
Теперь, чтобы найти определенный интеграл функции, сначала мы вычислим первообразную функции. Первообразная функции равна . Для простоты расчета примем C = 0,
Первообразная функции равна . Для простоты расчета примем C = 0,
Фундаментальная теорема исчисления гласит:
Подставим и в первообразную функции следующим образом:
Площадь под кривой — метод, формула, решенные примеры, часто задаваемые вопросы
Площадь под кривой рассчитывается разными методами, из которых наиболее популярен первообразный метод нахождения площади. Площадь под кривой можно найти, зная уравнение кривой, границы кривой и ось, охватывающую кривую. Как правило, у нас есть формулы для нахождения площадей правильных фигур, таких как квадрат, прямоугольник, четырехугольник, многоугольник, круг, но нет определенной формулы для нахождения площади под кривой. Процесс интегрирования помогает решить уравнение и найти искомую площадь.
Для нахождения площадей неправильных плоских поверхностей очень полезны методы первообразных. Здесь мы научимся находить площадь под кривой относительно оси, находить площадь между кривой и прямой и находить площадь между двумя кривыми.
| 1. | Как найти площадь под кривой? |
| 2. | Различные методы поиска площади под кривой |
| 3. | Формула площади под кривой |
| 4. | Область под кривой — круг |
| 5. | Площадь под кривой — парабола |
| 6. | Область под кривой — эллипс |
| 7. | Область между кривой и трапецеидальной линией |
| 8. | Область между двумя кривыми |
| 9. | Решенные примеры |
| 10. | Практические вопросы |
| 11. | Часто задаваемые вопросы по Area Under The Curve |
Как найти площадь под кривой?
Площадь под кривой можно рассчитать за три простых шага. Во-первых, нам нужно знать уравнение кривой (y = f(x)), пределы, в которых должна быть рассчитана площадь, и ось, охватывающую площадь. Во-вторых, мы должны найти интегрирование (первообразную) кривой. Наконец, нам нужно применить верхний предел и нижний предел к интегральному ответу и взять разницу, чтобы получить площадь под кривой. 9б_а\)
Во-вторых, мы должны найти интегрирование (первообразную) кривой. Наконец, нам нужно применить верхний предел и нижний предел к интегральному ответу и взять разницу, чтобы получить площадь под кривой. 9б_а\)
=\( г(б) — г(а)\)
Различные методы поиска площади под кривой
Площадь под кривой можно вычислить тремя способами. Кроме того, метод, используемый для нахождения площади под кривой, зависит от необходимости и доступных входных данных для нахождения площади под кривой. Здесь мы рассмотрим три метода, чтобы найти площадь под кривой.
9нф(х).\дельта х\). Метод — II: В этом методе также используется процедура, аналогичная описанной выше, для нахождения площади под кривой. Здесь область под кривой разделена на несколько прямоугольников. Далее площади этих прямоугольников складываются, чтобы получить площадь под кривой. Этот метод представляет собой простой способ найти площадь под кривой, но он дает только приблизительное значение площади под кривой. b f(x ).dx\)
b f(x ).dx\)
Формула площади под кривой
Площадь кривой может быть рассчитана относительно различных осей как граница данной кривой. Площадь под кривой можно рассчитать относительно оси x или оси y. Для особых случаев кривая находится ниже осей и частично ниже осей. Для всех этих случаев у нас есть производная формула для нахождения площади под кривой.
Площадь по оси x: 9cf(x).dx\)
Область под кривой — круг
Площадь круга рассчитывается путем вычисления площади части круга в первом квадранте. Здесь уравнение окружности x 2 + y 2 = a 2 заменяется уравнением кривой вида y = √(a 2 — x 2 ). Это уравнение кривой используется для нахождения площади относительно оси x и пределов от 0 до a. 9а_0\)
= 4[((a/2)× 0 + (a 2 /2)Sin -1 1) — 0]
= 4(а 2 /2)(π/2)
= 2π r
Следовательно, площадь круга равна π a 2 квадратных единиц.
Площадь под кривой — Парабола
Парабола имеет ось, которая делит параболу на две симметричные части. Здесь мы берем параболу, симметричную относительно оси x и имеющую уравнение y 92}{3}\) квадратных единиц.
Область под кривой — эллипс
Уравнение эллипса с большой осью 2а и малой осью 2b: y = b/a .√(a 2 — x 2 ). Здесь мы вычисляем площадь, ограниченную эллипсом по первой координате и по оси x, и далее умножаем на 4, чтобы получить площадь эллипса. Граничные пределы, взятые по оси x, составляют от 0 до a. Вычисления площади эллипса следующие. 92}{2}.\frac{\pi}{2}\\&=\pi ab\end{align}\)
Следовательно, площадь эллипса составляет πab кв. единиц.
Область под кривой — между кривой и трапецеидальной линией
Площадь между кривой и линией можно легко рассчитать, взяв разность площадей одной кривой и площади под линией. Здесь граница относительно оси и для кривой, и для линии одинакова. На рисунке ниже показаны кривая \(y_1\) = f(x) и линия \(y_2\) = g(x), и цель состоит в том, чтобы найти площадь между кривой и линией. Здесь мы берем интеграл от разности двух кривых и применяем границы, чтобы найти результирующую площадь. 9b_a [f(x) — g(x)].dx\)
На рисунке ниже показаны кривая \(y_1\) = f(x) и линия \(y_2\) = g(x), и цель состоит в том, чтобы найти площадь между кривой и линией. Здесь мы берем интеграл от разности двух кривых и применяем границы, чтобы найти результирующую площадь. 9b_a [f(x) — g(x)].dx\)
Область под кривой — между двумя кривыми
Площадь между двумя кривыми удобно вычислять, взяв разность площадей одной кривой из площади другой кривой. Здесь граница по оси для обеих кривых одинакова. На приведенном ниже рисунке показаны две кривые \(y_1\) = f(x) и \(y_2\) = g(x), и цель состоит в том, чтобы найти площадь между этими двумя кривыми. Здесь мы берем интеграл от разности двух кривых и применяем границы, чтобы найти результат. 94_0\)
= [((4/2)× 0 + (16/2)Sin-11) — 0]
= (16/2)(π/2)
= 4π
Ответ: Следовательно, площадь области, ограниченной кругом в первом квадранте, составляет 4π квадратных единиц
Пример 2: Найдите площадь под кривой для области, заключенной в эллипс x 2 /36 + y 2 /25 = 1.
Решение:
Данное уравнение эллипса ис.х 2 9{-1}1) — 0]\\&=\frac{20}{6}.\frac{36}{2}.\frac{\pi}{2}\\&=30\pi \end{ align}\)
Ответ: Следовательно, площадь эллипса равна 30π квадратных единиц.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайду
9b y.dx\)
Какие существуют методы нахождения площади под кривой?
Существует три основных метода нахождения площади под кривой. Площадь под кривой рассчитывается путем деления пространства площади на множество маленьких прямоугольников, а затем площади складываются для получения общей площади. Второй метод заключается в разделении области на несколько прямоугольников, а затем области складываются для получения необходимой площади. Третий способ – найти площадь с помощью интегрирования.
Третий способ – найти площадь с помощью интегрирования.
Что означает площадь под кривой?
Площадь под кривой означает площадь, ограниченную кривой, осью и граничными точками. Площадь под кривой представляет собой двумерную площадь, рассчитанную с помощью осей координат и формулы интегрирования.
Что представляет площадь под кривой?
Площадь под кривой представляет собой площадь, заключенную под кривой и осью, которая отмечена ограничивающими точками. Эта площадь под кривой дает площадь неправильной плоской формы в двумерном массиве.
Что такое площадь под кривой на графике скорости во времени?
На графике скорость-время скорость отложена по оси у, а время отложено по оси х. При этом предполагается, что площадь является произведением скорости и времени, и это дает пройденное расстояние. Следовательно, площадь под кривой графика зависимости скорости от времени дает пройденное расстояние.
Как интерпретировать площадь под кривой?
Площадь под кривой — это площадь между кривой и осью координат. Дальнейшие границы накладываются поперек кривой относительно оси, чтобы получить требуемую площадь. Площадь под кривой обычно представляет собой площадь неправильных форм, для которых нет формул площади в геометрии.
Дальнейшие границы накладываются поперек кривой относительно оси, чтобы получить требуемую площадь. Площадь под кривой обычно представляет собой площадь неправильных форм, для которых нет формул площади в геометрии.
Как рассчитать площадь под кривой без интегрирования?
Площадь под кривой можно рассчитать даже без использования интегрирования. Площадь под кривой можно разбить на меньшие прямоугольники, а затем суммирование этих площадей дает площади под кривой. Также другой метод состоит в том, чтобы разбить область под кривой на несколько прямоугольников, а затем мы можем взять соответствующие области, чтобы получить площадь под кривой.
Как приблизительно определить площадь под кривой?
Площадь под кривой можно приблизительно рассчитать, разбив площадь на небольшие части в виде небольших прямоугольников. И площади этих прямоугольников можно вычислить, и их суммирование дает площадь под кривой. Другой способ найти приблизительную площадь под кривой — нарисовать набор из нескольких больших прямоугольников, а затем суммировать их площади. Далее мы можем просто найти точную площадь под кривой с помощью определенных интегралов.
Далее мы можем просто найти точную площадь под кривой с помощью определенных интегралов.
Когда использовать площадь под кривой?
Площадь под кривой полезна для нахождения площади неправильной формы на плоскости. Обычно мы находим формулы для нахождения площади круга, квадрата, прямоугольника, четырехугольника, многоугольника, но у нас нет никаких средств для нахождения площади неправильной формы. Здесь мы используем концепцию определенных интегралов для получения значений площадей.
Когда площадь под кривой имеет отрицательное значение?
Площадь под кривой отрицательна, если кривая находится под осью или в отрицательных квадрантах оси координат. Для этого также вычисляется площадь кривой с использованием нормального метода, и к окончательному ответу применяется модуль. Даже при отрицательном ответе берется только значение площади, без учета отрицательного знака ответа.
Исчисление I — Формулы площади и объема
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 7-6: Формулы площади и объема
В этом разделе мы выведем формулы, используемые для вычисления площади между двумя кривыми и объема тела вращения.
Площадь между двумя кривыми
Начнем с формулы для определения площади между \(y = f\left( x \right)\) и \(y = g\left( x \right)\) на интервал \(\left[ {a,b} \right]\). Будем также считать, что \(f\left( x \right) \ge g\left( x \right)\) на \(\left[ {a,b} \right]\).
Теперь мы будем действовать так же, как и при рассмотрении проблемы площадей в главе об интегралах. Сначала мы разделим интервал на \(n\) равных подынтервалов, каждый длиной 9{{\,b}}{{f\влево(x\вправо) — g\влево(x\вправо)\,dx}}\]
Приведенная выше формула будет работать при условии, что две функции имеют вид \(y = f\left( x \right)\) и \(y = g\left( x \right)\). Однако не все функции имеют такую форму.
Однако не все функции имеют такую форму.
Иногда нам придется работать с функциями в виде между \(x = f\left( y \right)\) и \(x = g\left( y \right)\) на интервале \(\ left[ {c,d} \right]\) (интервал значений \(y\)…). Когда это происходит, вывод идентичен. Сначала мы начнем с предположения, что \(f\left( y \right) \ge g\left( y \right)\) на \(\left[ {c,d} \right]\). Затем мы можем разделить интервал на равные подинтервалы и построить прямоугольники на каждом из этих интервалов. Вот набросок этой ситуации. 9{{\,d}}{{f\влево(y\вправо) — g\влево(y\вправо)\,dy}}\]
Таким образом, независимо от формы, в которой находятся функции, мы используем в основном одну и ту же формулу.
Объемы для тела вращения
Прежде чем вывести формулу для этого, мы, вероятно, должны сначала определить, что такое тело вращения. Чтобы получить тело вращения, мы начинаем с функции \(y = f\left( x \right)\) на интервале \(\left[ {a,b} \right]\).
Затем мы вращаем эту кривую вокруг заданной оси, чтобы получить поверхность тела вращения. Для целей этого вывода давайте повернем кривую вокруг оси \(x\). Это дает следующую трехмерную область. 9{{\,b}}{{A\влево( x \вправо)\,dx}}\end{align*}\]
Для целей этого вывода давайте повернем кривую вокруг оси \(x\). Это дает следующую трехмерную область. 9{{\,b}}{{A\влево( x \вправо)\,dx}}\end{align*}\]
Итак, в этом случае объем будет интегралом от площади поперечного сечения при любых \(x\), \(A\left( x \right)\). Также обратите внимание, что в этом случае площадь поперечного сечения представляет собой круг, и мы могли бы пойти дальше и получить формулу и для этого. Однако приведенная выше формула является более общей и будет работать для любого способа получения поперечного сечения, поэтому мы оставим ее как есть.
В разделах, где мы на самом деле используем эту формулу, мы также увидим, что существуют способы создания поперечного сечения, которые на самом деле дают площадь поперечного сечения, которая является функцией \(y\) вместо \(x\) . В этих случаях формула будет, 9{{\,d}}{{A\влево(y\вправо)\,dy}}\]
Примеры Calculate Field Python — ArcGIS Pro
Ввод значений с помощью клавиатуры — не единственный способ редактирования
значения в таблице. В некоторых случаях может потребоваться выполнить
математический расчет для установки значения поля для одной записи
или даже все записи. Вы можете выполнять
простые, а также расширенные расчеты по всем или выбранным
записи.
Кроме того, вы можете рассчитать площадь, длину, периметр и другие параметры.
геометрические свойства полей в атрибутивных таблицах. Разделы ниже содержат примеры использования калькулятора поля. Расчеты выполняются с использованием Python, SQL и Arcade.
В некоторых случаях может потребоваться выполнить
математический расчет для установки значения поля для одной записи
или даже все записи. Вы можете выполнять
простые, а также расширенные расчеты по всем или выбранным
записи.
Кроме того, вы можете рассчитать площадь, длину, периметр и другие параметры.
геометрические свойства полей в атрибутивных таблицах. Разделы ниже содержат примеры использования калькулятора поля. Расчеты выполняются с использованием Python, SQL и Arcade.
В этом разделе рассматриваются примеры Calculate Field на основе Python. Чтобы узнать больше о выражениях Arcade, см. руководство ArcGIS Arcade. Дополнительные сведения о выражениях SQL см. в разделе Вычисление поля.
- Python применяет отступы как часть синтаксиса. Используйте два или четыре пробела для определения каждого логического уровня. Выровняйте начало и конец блоков операторов и будьте последовательны.
- Поля выражения вычисления Python заключены в восклицательные знаки (!!).

- При именовании переменных обратите внимание, что Python чувствителен к регистру, поэтому значение не совпадает со значением.
- После ввода выписок нажмите кнопку Экспорт, если хотите записать их в файл. Кнопка «Импорт» предлагает вам найти и выбрать существующий файл расчета.
Простые вычисления
С помощью короткого выражения можно выполнить множество вычислений.
Примеры простых строк
Строки поддерживаются рядом строковых функций Python, включая использование заглавных букв, rstrip и замену.
Сделать первый символ строки в поле CITY_NAME прописной.
!CITY_NAME!.capitalize()
Удалите все пробелы в конце строки в поле CITY_NAME.
!CITY_NAME!.rstrip()
Замените все вхождения «California» на «California» в поле STATE_NAME.
!STATE_NAME!.replace("california", "California") Доступ к символам в строковом поле можно получить с помощью индексации и нарезки в Python. При индексировании выбираются символы в позиции индекса; нарезка выбирает группу символов. В следующей таблице предположим, что !fieldname! представляет собой строковое поле со значением «abcde».
При индексировании выбираются символы в позиции индекса; нарезка выбирает группу символов. В следующей таблице предположим, что !fieldname! представляет собой строковое поле со значением «abcde».
| Example | Explanation | Result |
|---|---|---|
!fieldname![0] | The first character | «a» |
! fieldname![-2] | Предпоследний символ | «d» |
!fieldname![1:4] второй, четвертый и четвертый символы | «BCD» |
Python также поддерживает форматирование строк с использованием метода format().
Объедините поля FieldA и FieldB, разделенные двоеточием.
"{}:{}".format(!FieldA!, !FieldB!) - Общие строковые операции Python
Простые математические примеры
Python предоставляет инструменты для обработки чисел. Python также поддерживает ряд числовых и математических функций, включая math, cmath, decimal, random, itertools, functools и оператор.
| Operator | Explanation | Example | Result |
|---|---|---|---|
x + y | x plus y | 1.5 + 2.5 | 4.0 |
x — y | x minus y | 3. | 1.1 |
x * y | x times y | 2.0 * 2.2 | 4.4 |
x / y | x divided by y | 4.0 / 1.25 | 3.2 |
x // y | x, разделенный на Y (дивизион пола) | 4,0 //25 | 3,0 | 3,0 | 83,0 | 83,0 | 989000 2,0 | 3,0 | 9028. 0792 0792x modulo y | 8 % 3 | 2 |
-x | negative expression of x | x = 5 -x | -5 |
+x | x is unchanged | x = 5 +x | 5 |
x ** y | x raised to the power из | 2 ** 3 | 8 |
Умножить
!Ранг! * 2
Вычислить объем сферы по заданному радиусу поля.
4.0 / 3.0 * math.pi * !Радиус! ** 3
Прежняя версия:
В ArcGIS Pro используется Python 3, а в ArcGIS Desktop используется Python 2. Python 2 использует целочисленную математику, а это означает, что деление двух целочисленных значений всегда дает целочисленное значение (3/2 = 1). В Python 3 при делении двух целочисленных значений получается значение с плавающей запятой (3/2 = 1,5).
Встроенные функции Python
Python включает ряд встроенных функций, включая max, min, round и sum.
- Встроенные функции Python
Вычислить максимальное значение для каждой записи из списка полей.
max([!поле1!, !поле2!, !поле3!])
Вычислить сумму для каждой записи из списка полей.
sum([!field1!, !field2!, !field3!])
Использовать блоки кода
Используя выражения Python и параметр Code Block, вы можете делать следующее:
- Используйте любую функцию Python в выражении.

- Доступ к функциям и объектам геообработки.
- Доступ к свойствам геометрии объекта.
- Доступ к новому оператору случайных значений.
- Переклассифицировать значения, используя логику if-then-else. Тип выражения
Блок кода Блок кода выражается с помощью функций Python (def). Свойства геометрии выражаются с помощью объектов геообработки, таких как объекты Point, где это уместно. Arcade
Поддерживает функции Arcade.
SQL
Поддерживает выражения SQL.
SQL-выражения были реализованы для лучшей поддержки вычислений с использованием сервисов объектов и многопользовательских баз геоданных, особенно в отношении производительности.
 Вместо того, чтобы выполнять вычисления по одному объекту или строке за раз, к сервису объектов или базе данных задается один запрос.
Вместо того, чтобы выполнять вычисления по одному объекту или строке за раз, к сервису объектов или базе данных задается один запрос.Предыдущая версия:
В ArcGIS Desktop инструмент Вычислить поле поддерживает типы выражений VB, PYTHON и PYTHON_9.3. Тип выражения VB, который поддерживается в некоторых продуктах, не поддерживается в 64-битных продуктах, включая ArcGIS Pro.
Ключевые слова PYTHON и PYTHON_9.3 по-прежнему поддерживаются в ArcGIS Pro для обратной совместимости, но не указаны в качестве вариантов. Скрипты Python, использующие эти ключевые слова, продолжат работать.
Единственная разница между типом выражения Python 3 и устаревшим PYTHON_9Ключевое слово .3 заключается в том, что Python 3 возвращает значения в полях даты как объекты даты и времени Python.
Тип выражения Python 3 не связан с версией Python, установленной вместе с ArcGIS Pro. Это всего лишь третье ключевое слово, связанное с Python, исторически (после PYTHON и PYTHON_9.
 3).
3).Функции Python определяются с помощью ключевого слова def, за которым следует имя функции и входные аргументы функции. Функцию Python можно написать так, чтобы она принимала любое количество входных аргументов (включая полное отсутствие). Значение возвращается из функции с помощью оператора return. Имя функции выбираете вы (не используйте пробелы или начальные числа).
Если значение не возвращается явным образом из функции с оператором return, функция возвращает None.
Помните, Python использует отступы как часть синтаксиса. Используйте четыре пробела для определения каждого логического уровня. Выровняйте начало и конец блоков операторов и будьте последовательны.
Образцы кода — математические
При использовании приведенных ниже математических примеров предположим, что тип выражения Python 3.
Округлите значение поля до двух знаков после запятой.
Выражение: круглый(!площадь!, 2)
Используйте математический модуль для преобразования метров в футы.
 Преобразование возводится в степень 2 и умножается на площадь.
Преобразование возводится в степень 2 и умножается на площадь.Выражение: Метры в футы((плавать(!shape.area!))) Блок кода: импортировать математику def MetersToFeet (площадь): return math.pow(3.2808, 2) * areaВычисление полей с использованием логики в Python
Логические шаблоны могут быть включены в блок кода с помощью операторов if, else и elif.
Классификация на основе значений полей.
Выражение: Переклассифицировать(!WELL_YIELD!) Блок кода: Def Reclass(WellYield): если (WellYield >= 0 и WellYield <= 10): вернуть 1 elif (WellYield > 10 и WellYield <= 20): вернуть 2 elif (WellYield > 20 и WellYield <= 30): вернуть 3 Элиф (WellYield > 30): вернуться 4Примеры кода — геометрия
В дополнение к следующим примерам кода см. раздел Преобразование геометрических единиц ниже для получения дополнительной информации о преобразовании геометрических единиц.
Вычислить площадь объекта.

Выражение: !форма.область!
Вычислить максимальную координату X объекта.
Выражение: !shape.extent.XMax!
Подсчет количества вершин объекта.
Выражение: MySub(!форма!) Блок кода: Def MySub (подвиг): часть = 0 # Подсчитать количество точек в текущем составном объекте partcount = подвиг.partCount количество точек = 0 # Введите цикл while для каждой части объекта (если он состоит из одной части). # особенность, это произойдет только один раз) в то время как partnum < partcount: часть = feat.getPart(partnum) пнт = часть.следующий() # Вводим цикл while для каждой вершины пока пнт: количество точек += 1 пнт = часть.следующий() # Если pnt равно null, то либо деталь закончена, либо # внутреннее кольцо если не пнт: пнт = часть.следующий() часть += 1 вернуть количество очковДля класса точечных объектов сдвиньте координату x каждой точки на 100.

Выражение: shiftXCoordinate(!ФОРМА!) Блок кода: def shiftXCoordinate (форма): сдвигЗначение = 100 точка = форма.getPart (0) точка.X += сдвигЗначение точка возвратаПреобразование единиц измерения геометрии
Свойства площади и длины поля геометрии могут быть изменены с помощью типов единиц измерения, выраженных знаком @.
Подробнее о поддерживаемых линейных и площадных единицах в геообработке
Если данные хранятся в географической системе координат и заданы линейные единицы (например, футы), вычисление длины преобразуется с использованием геодезического алгоритма.
Предупреждение:
Преобразование площадных единиц данных в географическую систему координат дает сомнительные результаты, поскольку десятичные градусы не совпадают по всему миру.
Вычислить длину объекта в ярдах.
Выражение: !shape.length@ярды!
Расчет площади объекта в акрах.
Выражение: !shape.area@acres!
Геодезическая площадь и длина также могут быть рассчитаны с использованием свойств geodesicArea и geodesicLength с символом @, за которым следует ключевое слово единицы измерения.

Расчет геодезической длины объекта в ярдах.
Выражение: !shape.geodesicLength@ярды!
Расчет геодезической площади объекта в акрах.
Выражение: !shape.geodesicArea@acres!
Примеры кода — даты
Дату и время можно вычислить с помощью модулей datetime и time.
Вычислить текущую дату.
Выражение: time.strftime("%d/%m/%Y")Вычислить текущую дату и время.
Выражение: datetime.datetime.now()
Вычислить дату 31 декабря 2000 г.
Выражение: datetime.datetime(2000, 12, 31)
Подсчет количества дней между текущей датой и значением в поле.
Выражение: (datetime.datetime.now() - !field1!).days
Вычислить дату, добавив 100 дней к значению даты в поле.
Выражение: !поле1! + datetime.timedelta(days=100)
Вычислить строку, представляющую дату, используя метод ctime в модуле datetime. В примере создается строка в формате: «Пн, 22 февраля, 10:15:00 2021».

Выражение: !field1!.ctime()
Вычислить день недели (например, воскресенье) для значения даты в поле.
Выражение: !field1!.strftime('%A')Вычислить форматированную строку из поля даты, используя метод strftime модуля datetime и явную строку формата. В примере будет создана строка в формате: «22.02.2021, 10:15:00».
Выражение: !field1!.strftime("%m/%d/%Y, %H:%M:%S")Примеры кода — строки
Вычисления строк могут быть выполнены с использованием различных шаблонов кодирования Python.
Вернуть три крайних правых символа.
Выражение: !SUB_REGION![-3:]
Заменить любую прописную букву P на строчную p.
Выражение: !STATE_NAME!.replace("P","p")Объединить два поля с разделителем-пробелом.
Выражение: !SUB_REGION! + " " + !STATE_ABBR!
Преобразование в правильный регистр
В следующих примерах показаны различные способы преобразования слов таким образом, чтобы в каждом слове первый символ был заглавным, а остальные буквы — строчными.

Выражение: ' '.join([i.capitalize() for i in !STATE_NAME!.split(' ')])Выражение: !STATE_NAME!.title()
Регулярные выражения
Модуль Python re предоставляет операции сопоставления регулярных выражений, которые можно использовать для выполнения сложных правил сопоставления с образцом и замены строк.
- re — Операции с регулярными выражениями
- Практическое руководство по регулярным выражениям
Замените St или St., начиная новое слово в конце строки, на слово Street.
Выражение: update_street(!АДРЕС!) Блок кода: импортировать повторно def update_street (название_улицы): return re.sub(r"""\b(St|St.)\Z""", 'Улица', street_name)Накопительные и последовательные вычисления
Накопительные и последовательные вычисления могут выполняться с использованием глобальных переменных.
Вычислить последовательный идентификатор или номер на основе интервала.

Выражение: автоматическое приращение() Блок кода: запись=0 определение автоинкремента(): глобальная запись pStart = 1 # настроить начальное значение, если требуется pInterval = 1 # настроить значение интервала, если требуется если (рек == 0): запись = pStart еще: запись = запись + pInterval return recВычислить накопительное значение числового поля.
Выражение: накапливать(!ПолеA!) Блок кода: всего = 0 деф накапливать (приращение): глобальный итог если всего: итог += приращение еще: итог = приращение верни всегоВычислить процентное увеличение числового поля.
Выражение: процентное увеличение (с плавающей запятой (! Поле A!)) Блок кода: последнее значение = 0 определение процента увеличения (новое значение): глобальное последнее значение если последнее значение: процент = ((новое значение - последнее значение) / последнее значение) * 100 еще: процент = 0 последнее значение = новое значение процент возвратаСлучайные значения
Случайные значения можно рассчитать с помощью модуля random.

Используйте пакет numpy site для вычисления случайных значений с плавающей запятой от 0,0 до 1,0.
Выражение: получитьслучайное значение() Блок кода: импортировать numpy определение getRandomValue(): return numpy.random.random()Используйте модуль random для вычисления случайных целых чисел от 0 до 10.
Выражение: случайный.randint(0, 10) Блок кода: import random
Вычислить нулевые значения
В выражении Python нулевые значения можно вычислить с помощью Python None.
Следующий расчет будет работать, только если поле допускает значение NULL.
Используйте Python None для вычисления нулевых значений.
Выражение: Нет
Похожие темы
Отзыв по этой теме?
Средние значения и длины функций
Все ресурсы исчисления 2
9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
Исчисление 2 Помощь » Интегралы » Интегральные приложения » Средние значения и длины функций
Какова длина дуги, если , от ?
Возможные ответы:
Правильный ответ:
Пояснение:
Напишите формулу для длины дуги.

Вычислите производные.
Подставим производные и оценки в интеграл.
Сообщить об ошибке
Каково среднее значение функции
с по ?
Возможные ответы:
Правильный ответ:
Пояснение:
Среднее значение функции p(t) от t=a до t=b находится с помощью интеграла
.
В этом случае мы должны вычислить значение интеграла
.
Замена делает этот интеграл более понятным. Позволять . Затем . Мы также должны переписать пределы интегрирования через u. Когда t = 0, u=1, а когда t = 2, u = 5. Выполнение этих замен приводит к интегралу
Вычисление этого интеграла с учетом того, что
дает
Сообщить об ошибке
Каково среднее значение функции на интервале?
Возможные ответы:
Правильный ответ:
Объяснение:
В общем случае среднее значение функции за интервал равно
Это означает, что среднее значение за интервал равно
.

Поскольку первообразная равна , интеграл равен
.
Сообщить об ошибке
Какова длина кривой на интервале?
Возможные ответы:
Правильный ответ:
Объяснение:
Общая формула для нахождения длины кривой на интервале:
В этом примере длину дуги можно найти, вычислив интеграл
.
Производную можно найти с помощью правила степени, , что приводит к
.
На этом этапе замена будет полезна.
Пусть
.
Мы также можем выразить пределы интегрирования в терминах для упрощения вычислений. Когда и когда .
Выполнение этих замен приводит к
.
Теперь используйте правило степени, которое обычно используется , чтобы вычислить интеграл.
Сообщить об ошибке
Заданный интервал, найти среднее значение следующей функции:
Возможные ответы:
Правильный ответ:
Объяснение:
Когда f интегрируемо на [a,b], среднее значение f(x) на [a,b] определяется как:
Для постановки задачи нам дано f( x) и интервалы [a,b].
 Все, что нужно сделать, это решить интеграл по этому интервалу и разделить результат на разницу между двумя интервалами.
Все, что нужно сделать, это решить интеграл по этому интервалу и разделить результат на разницу между двумя интервалами.Итак:
Чтобы решить этот интеграл, у нас есть два варианта. Мы можем FOIL члены для и решить интеграл полученного полинома, или мы можем использовать простую u-подстановку. В любом случае результат всегда будет одинаковым. Мы попробуем оба способа, чтобы доказать, что это верно:
Метод ФОЛЬГИ:
Это один из вариантов ответа!
Метод U-подстановки:
Затем мы должны скорректировать границы нового интеграла, который будет выражаться в u .
Итак, новый интеграл принимает вид:
Как видите, оба метода дают один и тот же ответ!
Сообщить об ошибке
Каково среднее значение между интервалами и ?
Возможные ответы:
Правильный ответ:
Объяснение:
При запросе среднего значения между интервалами формы и затем интеграл становится
, поэтому в этом случае мы можем переписать нашу задачу о среднем значении как
.

Интеграл оценивается в и , что упрощается до
(обратите внимание, что равно 1).
Однако, поскольку мы ищем среднее значение , мы должны разделить все это на b-a, что в данном случае равно 2, поэтому окончательный ответ – 9.0003
.
Сообщить об ошибке
Каково среднее значение функции на интервале?
Возможные ответы:
Правильный ответ:
Объяснение:
Среднее значение функции за интервал определяется как интеграл от функции, деленный на длину интервала.
Общее правило для этого типа интеграции следующее.
Получаем:
Сообщить об ошибке
Чему равно среднее значение функции
на интервале ?
Возможные ответы:
Правильный ответ:
Объяснение:
Среднее значение функции находится путем взятия интеграла функции по интервалу и деления на длину интервала.

Общее правило для этого типа интеграции следующее.
Итак, имеем:
Сообщить об ошибке
Каково среднее значение функции на интервале ?
Возможные ответы:
Правильный ответ:
Объяснение:
Среднее значение функции находится путем взятия интеграла функции по интервалу и деления на длину интервала.
Общее правило для этого типа интеграции следующее.
Итак, имеем:
Сообщить об ошибке
Каково среднее значение функции на интервале?
Возможные ответы:
Правильный ответ:
Объяснение:
Среднее значение функции находится путем взятия интеграла функции по интервалу и деления на длину интервала.

Общее правило для этого типа интеграции следующее.
Итак, у нас есть:
Сообщить об ошибке
← Предыдущая 1 2 3 4 Следующая →
Уведомление об авторских правах 308 практических тестов Вопрос дня Карточки Обучение по концепции
Среднее значение функции
Определение среднего значения
Одним из основных применений определенных интегралов является нахождение среднего значения функции 9б {е\влево( х \вправо)dx} .\]
Геометрически это означает, что существует прямоугольник, площадь которого точно представляет площадь области под кривой \(y = f\left( x \right).\) Значение \(f\left( c \right) \) представляет высоту прямоугольника, а разница \(\left( {b - a} \right)\) представляет ширину.
Рисунок 1.Среднеквадратичное значение функции
Среднеквадратичное значение \(\left({RMS} \right)\) определяется как квадратный корень из среднего (среднего) значения квадрата функции \({{{\left[ {f\left( x \right)} \right]}^2}}\) на интервале \(\left[ {a,b} \right].


 )
)
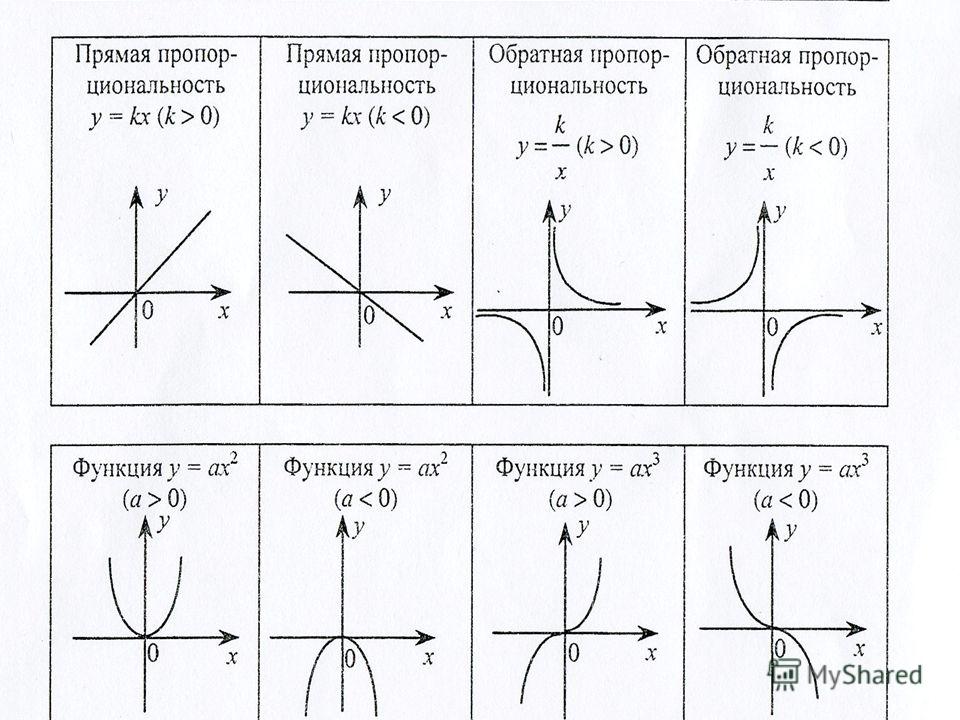
 1, № 1(а), 6(а), № 9(а, в, д), 875(а) на повторение
1, № 1(а), 6(а), № 9(а, в, д), 875(а) на повторение
 Особенно это нужно знать при построении графика и исследовании функции. Именно поэтому я решил рассмотреть основные варианты, которые могут быть при нахождении области определения функции. Их не так много, наверняка, многие это знают и сами, но думаю, напомнить не будет лишним.
Особенно это нужно знать при построении графика и исследовании функции. Именно поэтому я решил рассмотреть основные варианты, которые могут быть при нахождении области определения функции. Их не так много, наверняка, многие это знают и сами, но думаю, напомнить не будет лишним. И решив полученное уравнение, вы найдёте те значения переменной x, которые необходимо исключить с области определения.
И решив полученное уравнение, вы найдёте те значения переменной x, которые необходимо исключить с области определения. Соответственно вам надо следить, что бы выражение, которое будет под этими функциями, также попадало в этот промежуток и исключить все значения переменной, которые туда не попадают.
Соответственно вам надо следить, что бы выражение, которое будет под этими функциями, также попадало в этот промежуток и исключить все значения переменной, которые туда не попадают.


 В-третьих, если есть четный корень, подумайте об исключении значений, которые сделали бы подкоренное выражение отрицательным.
В-третьих, если есть четный корень, подумайте об исключении значений, которые сделали бы подкоренное выражение отрицательным.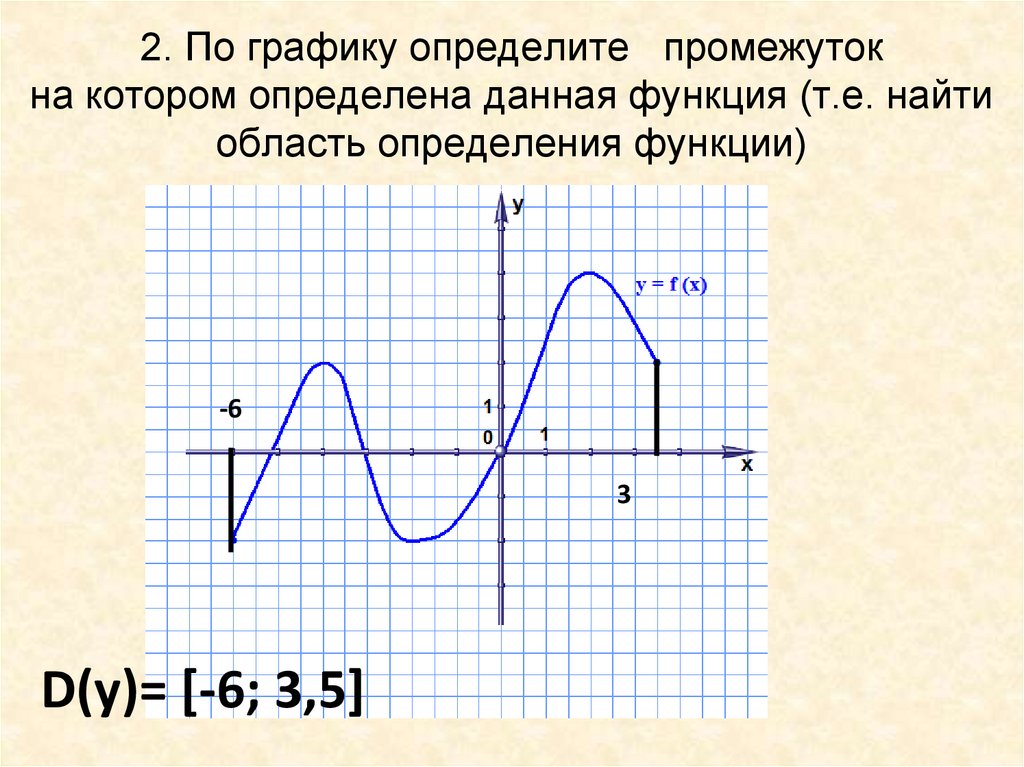
 {3} [/ latex].
{3} [/ latex].
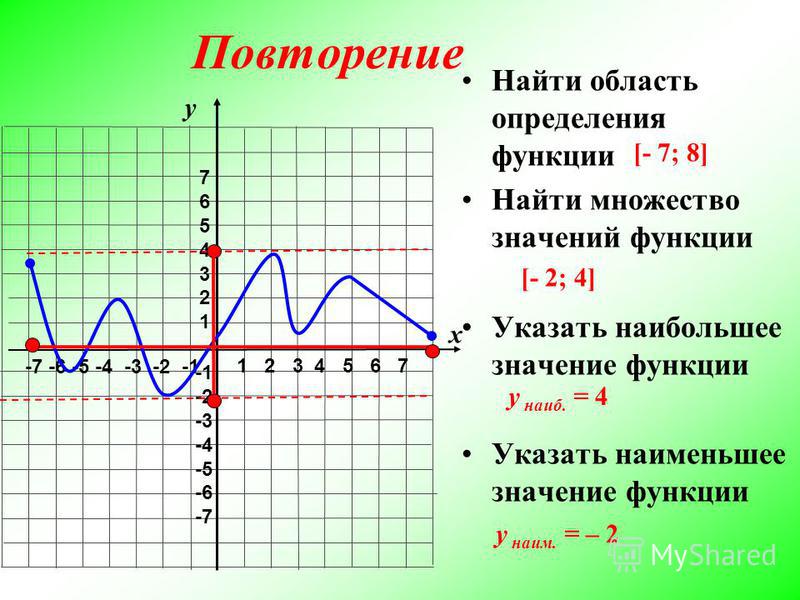
 Все ответы — действительные числа, меньшие или равные [latex] 7 [/ latex] или [latex] \ left (- \ infty, 7 \ right] [/ latex].
Все ответы — действительные числа, меньшие или равные [latex] 7 [/ latex] или [latex] \ left (- \ infty, 7 \ right] [/ latex].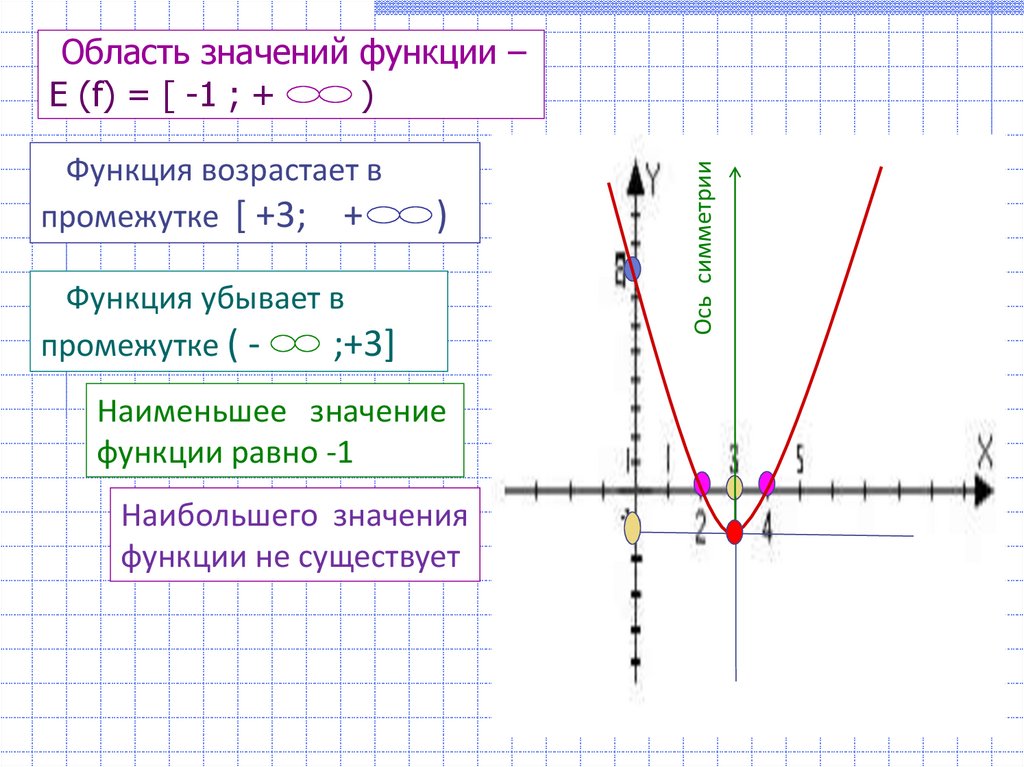
 Это набор всех элементов, которые принадлежат одному или другому (или обоим) из двух исходных наборов.Для наборов с конечным числом таких элементов, элементы не должны быть перечислены в порядке возрастания числового значения. Если исходные два набора имеют некоторые общие элементы, эти элементы должны быть указаны в объединенном наборе только один раз. Для наборов действительных чисел на интервалах другой пример объединения —
Это набор всех элементов, которые принадлежат одному или другому (или обоим) из двух исходных наборов.Для наборов с конечным числом таких элементов, элементы не должны быть перечислены в порядке возрастания числового значения. Если исходные два набора имеют некоторые общие элементы, эти элементы должны быть указаны в объединенном наборе только один раз. Для наборов действительных чисел на интервалах другой пример объединения — {3} \ text {if} {x} & lt {-1} \\ {-2} \ text {if} {-1} & lt {x} & lt {4} \\ \ sqrt {x} \ text {если } {x} & gt {4} \ end {case} [/ latex]
{3} \ text {if} {x} & lt {-1} \\ {-2} \ text {if} {-1} & lt {x} & lt {4} \\ \ sqrt {x} \ text {если } {x} & gt {4} \ end {case} [/ latex]

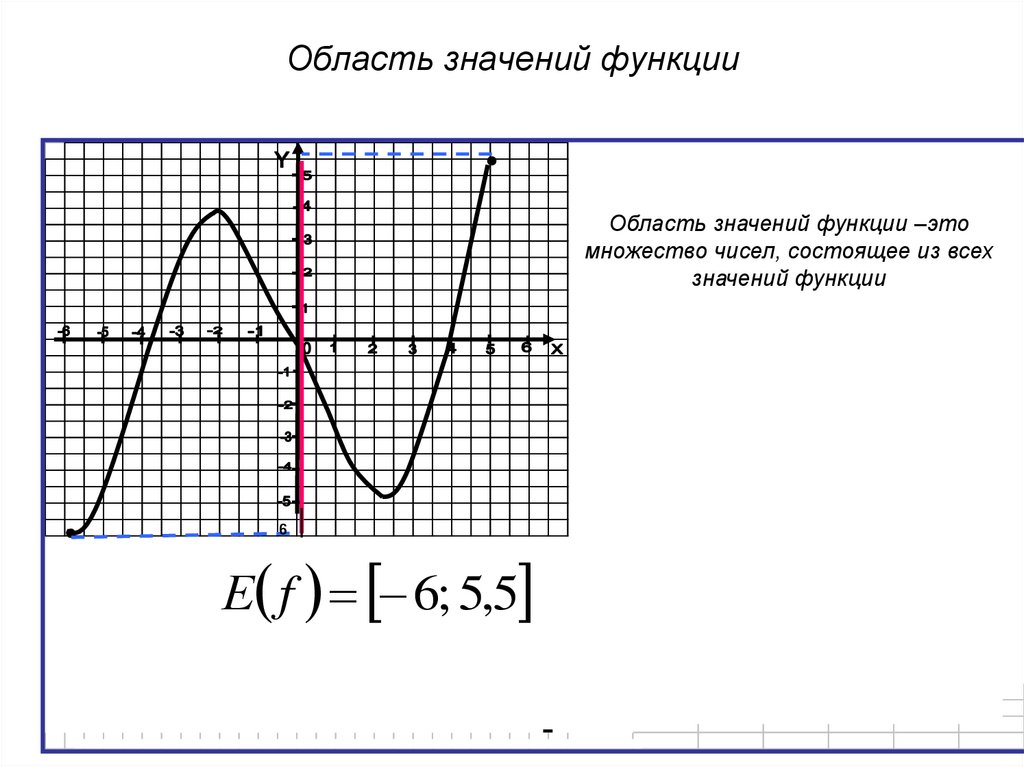 {2} + {3} & \ text {if} & {x} \ le {-1} \\ {5x} — {7} & \ text {if} & {x}> {-1} \ end { case} [/ latex]
{2} + {3} & \ text {if} & {x} \ le {-1} \\ {5x} — {7} & \ text {if} & {x}> {-1} \ end { case} [/ latex]  Создайте функцию, в которой весь диапазон представляет собой неотрицательные действительные числа.
Создайте функцию, в которой весь диапазон представляет собой неотрицательные действительные числа.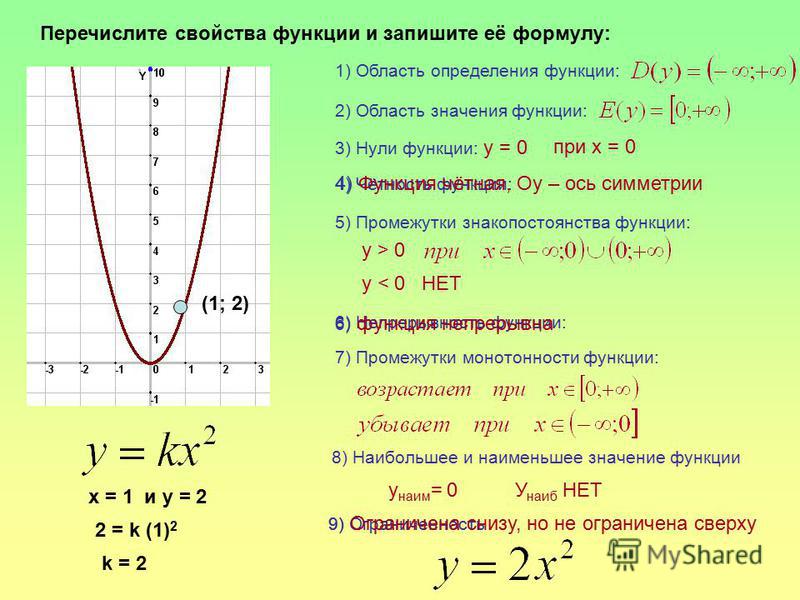
 Чтобы найти домен и диапазон обратного, просто поменяйте местами домен и
Чтобы найти домен и диапазон обратного, просто поменяйте местами домен и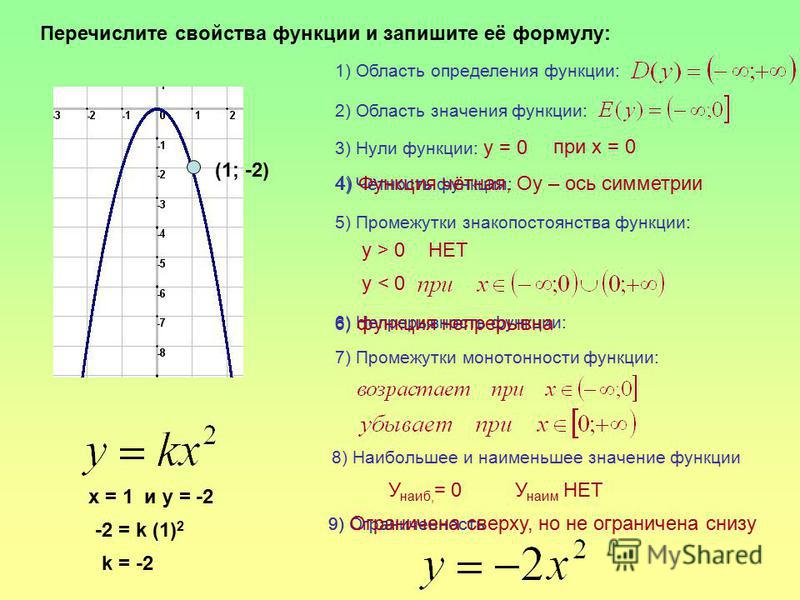

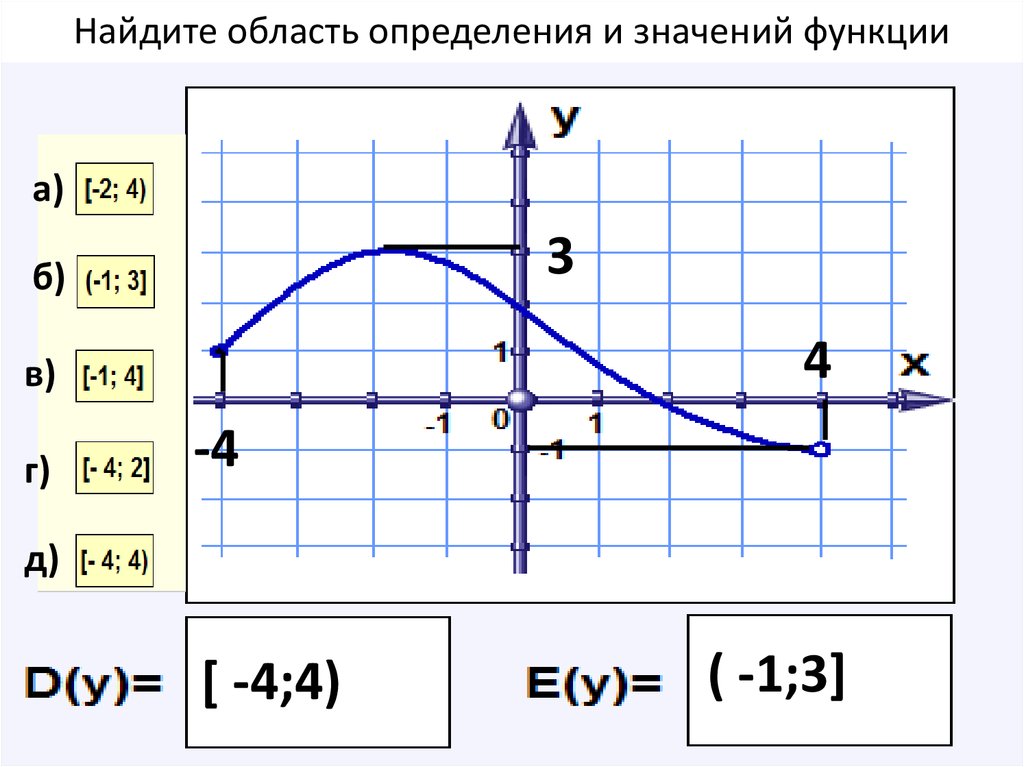 Теперь диапазон $ f $ — это все действительные числа $ y $, такие, что существует некоторый вход $ x $, где $ f (x) = y $. Итак, чтобы найти все такие $ y $, мы можем просто взять $ f (x) $ равным некоторому произвольному выходу $ y $ и изменить рациональное выражение ($ \ star $) так, чтобы найти, для какого $ y $ существует такой $ x $:
Теперь диапазон $ f $ — это все действительные числа $ y $, такие, что существует некоторый вход $ x $, где $ f (x) = y $. Итак, чтобы найти все такие $ y $, мы можем просто взять $ f (x) $ равным некоторому произвольному выходу $ y $ и изменить рациональное выражение ($ \ star $) так, чтобы найти, для какого $ y $ существует такой $ x $:

 Аналогично, как
Аналогично, как