Обозначение область значения функции: виды, свойства, примеры решения задач

alexxlab / / Разное

Mathway | Популярные задачи

1Найти число возможных исходов7 выбор 3
2Найти число возможных исходов8 выбор 3
3Найти число возможных исходов5 выбор 2
4Найти число возможных исходов4 выбор 2
5Найти число возможных исходов8 выбор 4
6Найти число возможных исходов10 выбор 3
7Найти число возможных исходов7 выбор 4
8Найти число возможных исходов6 выбор 3
9Найти число возможных исходов9 выбор 3
10Найти число возможных исходов3 выбор 2
11Найти число возможных исходов6 выбор 4
12Найти число возможных исходов5 выбор 4
13Найти число возможных исходов7 перестановка 3
14Найти число возможных исходов7 выбор 2
15Найти число возможных исходов10 выбор 5
16Найти число возможных исходов10 выбор 6
17Найти число возможных исходов13 выбор 5
18Найти число возможных исходов3 выбор 3
19Найти число возможных исходов4 выбор 1
20Найти число возможных исходов4 выбор 4
21Найти число возможных исходов
5 выбор 1
22Найти число возможных исходов6 перестановка 3
23Найти число возможных исходов8 выбор 5
24Найти число возможных исходов9 перестановка 4
25Найти число возможных исходов13 выбор 3
26Найти число возможных исходов12 выбор 2
27Найти число возможных исходов12 выбор 4
28Найти число возможных исходов 12 выбор 3
29Найти число возможных исходов9 выбор 5
30Найти число возможных исходов9 выбор 2
31Найти число возможных исходов7 выбор 5
32Найти число возможных исходов6 перестановка 6
33Найти число возможных исходов8 перестановка 5
34Найти число возможных исходов8 перестановка 3
35Найти число возможных исходов7 перестановка 5
36Найти число возможных исходов52 выбор 5
37Найти число возможных исходов5 перестановка 3
38Найти число возможных исходов12 выбор 5
39Найти число возможных исходов3 выбор 1
40Найти число возможных исходов11 выбор 5
41Найти число возможных исходов10 выбор 2
42Найти число возможных исходов15 выбор 3
43Найти число возможных исходов52 выбор 4
44Найти число возможных исходов9 выбор 4
45Найти число возможных исходов9 перестановка 3
46Найти число возможных исходов7 перестановка 4
47Найти число возможных исходов7 перестановка 2
48Найти число возможных исходов
11 выбор 4
49Найти число возможных исходов11 выбор 2
50Найти число возможных исходов11 выбор 3
51Найти число возможных исходов10 перестановка 5
52Найти число возможных исходов5 выбор 5
53Найти число возможных исходов6 выбор 1
54Найти число возможных исходов8 перестановка 4
55Найти число возможных исходов 8 выбор 6
56Найти число возможных исходов13 выбор 4
57Вычислитьe
58Найти уравнение, перпендикулярное прямой-7x-5y=7
59Найти число возможных исходов13 выбор 2
60Найти число возможных исходов10 перестановка 2
61Найти число возможных исходов10 перестановка 3
62Найти число возможных исходов10 выбор 7
63Найти число возможных исходов20 выбор 4
64Найти число возможных исходов6 перестановка 4
65Найти число возможных исходов5 перестановка 4
66Найти число возможных исходов6 выбор 5
67Найти число возможных исходов52 выбор 3
68Найти число возможных исходов4 выбор 0
69		Найти число возможных исходов9 перестановка 7
70Найти число возможных исходов6 выбор 2
71Найти число возможных исходов5 перестановка 5
72Найти число возможных исходов5 перестановка 2
73Найти число возможных исходов6 выбор 6
74Найти число возможных исходов7 выбор 6
75Найти число возможных исходов8 перестановка 6
76Найти число возможных исходов7 перестановка 7
77Найти число возможных исходов9 перестановка 5
78Найти число возможных исходов2 перестановка 2
79Найти число возможных исходов10 выбор 8
80Найти число возможных исходов12 выбор 7
81Найти число возможных исходов15 выбор 5
82Найти обратный элемент[[1,0,1],[2,-2,-1],[3,0,0]]
83Определить область значений1/4x-7
84Найти число возможных исходов10 перестановка 7
85Найти число возможных исходов12 выбор 6
86Найти число возможных исходов2 выбор 1
87Найти число возможных исходов30 выбор 3
88Найти число возможных исходов9 выбор 6
89Найти число возможных исходов8 перестановка 2
90Найти число возможных исходов7 выбор 1
91Найти число возможных исходов6 перестановка 2
92Найти число возможных исходов4 перестановка 2
93Найти число возможных исходов4 перестановка 3
94Найти число возможных исходов3 перестановка 3
95Найти число возможных исходов46 выбор 6
96Найти число возможных исходов5 перестановка 1
97Найти число возможных исходов52 выбор 7
98Найти число возможных исходов52 перестановка 5
99Найти число возможных исходов9 выбор 1
100Найти число возможных исходов9 перестановка 6

Область определения и область значения функций

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Область определения
и область значения
функций.
линейная функция
квадратичная функция
Методическая разработка Фоминой Н.М.
МБОУ Лицея №10 г. Химки, Московской обл.

2. Определение функции

• Функцией называют такую зависимость переменной у от
переменной х, при которой каждому значению переменной х
соответствует единственное значение переменной у.
Обозначение функции
y f (x) , где х-независимая переменная (аргумент),
у-зависимая переменная (функция).

3. Область определения

• Все значения независимой переменной образуют область
определения функции.
• Область определения функции _у(х) это все значения
аргумента — Х
• Обозначение области определения — D(у) _

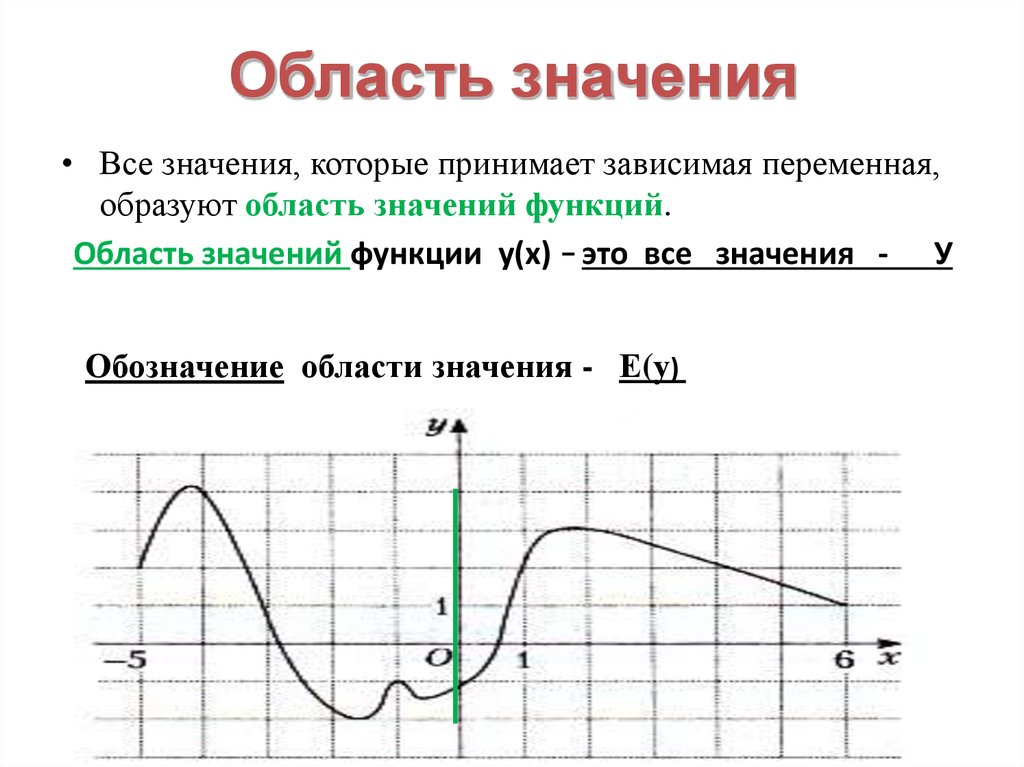
4. Область значения

• Все значения, которые принимает зависимая переменная,
образуют область значений функций.
Область значений функции у(х) это все значения — У
Обозначение области значения — Е(у)

5. График функции

• Графиком функции называют множество всех точек
координатной плоскости, абсциссы которых равны
значениям аргумента, а ординаты – соответствующим
значениям функций.
( х; у ) — координаты точки в плоскости
аргумент
функция
х – абсцисса точки (координата оси ОХ)
у – ордината точки (координата оси ОУ)
у
K>0
Прямая
пропорциональность
y = kx
1. D(y): R
2. E(y): R
х
у
Прямая
пропорциональность
y = kx
1. D(y): R
х
2. E(y): R
K<0
Квадратичная функция
у
D( y ) : R
1
-1
E ( y ) : 0;
-1
у
Квадратичная функция
4
3
2
1
D( y ) : R
-7 -6 -5 -4 -3 -2 -1
E ( y ) : ;0
-1
-2
-3
-4
-5
На рисунке изображен график квадратичной функции
y=f(x) на отрезке [-5; 2]. Найдите f(-8)
ПОДУМАЙ!
1
1
-7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7
ПОДУМАЙ!
2
Не существует
ВЕРНО!
3
5
ПОДУМАЙ!
4
10
7
6
5
4
3
2
1
-2
-3
-4
-5
-6
-7
y=f(x)
y>f(x)
y<f(x)
D( y)
E ( y)
Найдите по графику
область определения функции — D(у)
-5
D(у)= [-5; 4,5]
4

13. Найдите по графику область определения функции

D(у)= [-6; 3,5]

14. Найдите по графику область значений функции — Е(у)

Е(у)= [-2; 5]

15. Найдите по графику область значений функции — Е(у)

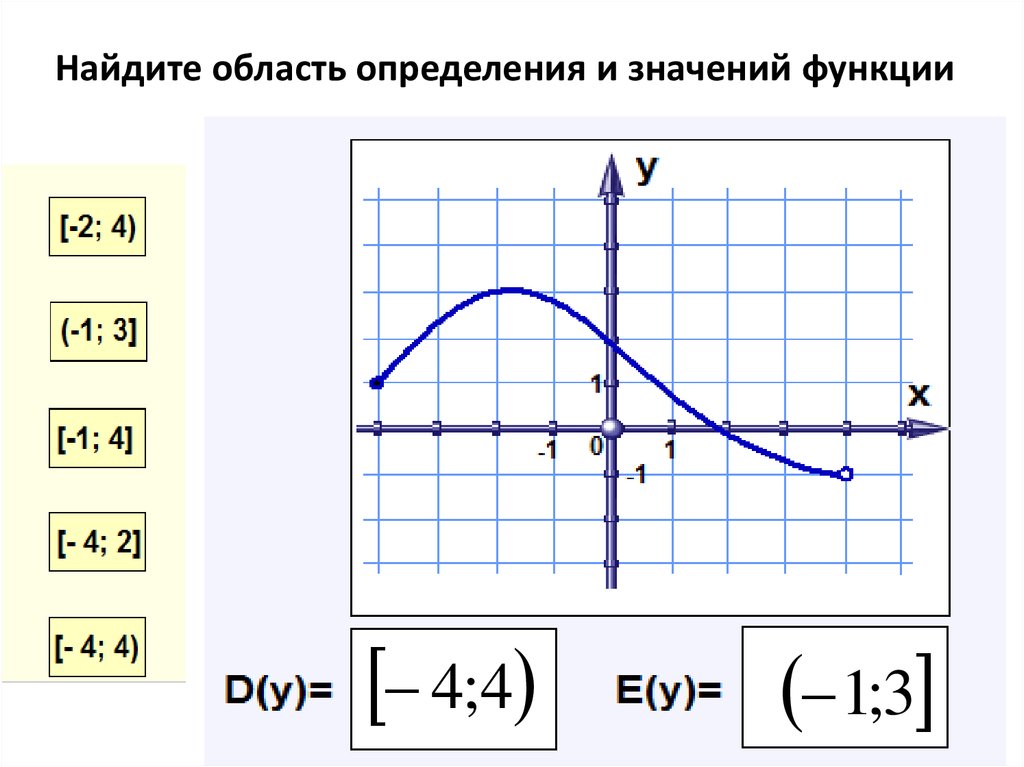
Е(у)= [-2; 6]

16. Найдите область определения и значений функции

4;4
1;3

17. Найдите область определения и значений функции

[ -2;4)
[ -1;4]

18. Найдите область определения и значений функции

[ -4;2]
[ -1;2]
Функция задана графиком на промежутке :
Укажите область значения функции:
A.
B.
C.
D.
E.
2;4
Вопрос 2. Найдите естественную область
определения
выражения
D( y ) : х 1 0
A.
B.
C.
D.

21. Функция

у
Функция
y x
D( y ) : х 0
E ( y ) : 0;
х
Вопрос 12. Какая точка принадлежит графику функции
A.
B.
C.
D.
?
Найдите сумму всех целых значений x,
принадлежащих области определения функции
A.
-19
B.
-6
C.
-21
D.
-13
Областью значений функции, заданной графически,
является:
A.
B.
C.
D.
E.

26. Область определения

,
х≠0
у
D( y ) ( ;0), (0; )
E ( y ) : ( ;0), (0; )
х
Функция задана формулой
При каком значении функции значение аргумента равно 8?
A.
B.
-2,5
C.
6,125
D.
3,5

English     Русский Правила

Обозначение

. Что такое математический символ диапазона?

Задавать вопрос

спросил

Изменено 10 месяцев назад

Просмотрено 99 тысяч раз

$\begingroup$

Бесхитростный вопрос от неофита:

Учитывая цифры: $1,2,3,4,5$

Что такое символ для диапазона чисел?

т. е. наименьшее-наибольшее число в наборе. Например, min max составляет $1-5$.

____ стоит $1-5$. (вставьте математический символ в пустое место).

Если бы такой зверь существовал, меня особенно заинтересовал бы его символ Юникода…

Безуспешно пытался найти несколько онлайн-ресурсов, таких как: http://rapidtables.com/math/symbols/Basic_Math_Symbols.htm. .

  • обозначение

$\endgroup$

3

$\begingroup$

Вы ищете:

  1. Замкнутый интервал : $[a,b]$ представляет множество всех действительных чисел, больших или равных $a$ и меньших или равных $b$.

  2. Целочисленный интервал : $[a\ldotp\ldotp b]$ представляет все целые числа между $a$ и $b$. ($[1\ldotp\ldotp 5] = \{1,2,3,4,5\}$)

$\endgroup$

1

$\begingroup$

Это полезная ссылка на Википедию.

Важно различать, включена ли конкретная конечная точка. Используйте ( или ) для исключения и [ или ] для включения.

Например,

$$(a,b) \;\;\Rightarrow \;\; \{x\in\Bbb R:a

$\endgroup$

2

$\begingroup$

Я хотел бы добавить к ответу Henricus, поскольку он дает ответ для целочисленного диапазона, но не для диапазонов с общим размером шага, что очень часто встречается в программировании.

Выражение

$$\{s k \mid k \in [a..b] \}$$ даст вам диапазон от $sa$ до $sb$ с шагом s.

Итак, если вы хотите написать выражение для чисел $$\{-3,-2,5, -2, -1,5, -1, -0,5, 0, 0,5, 1, 1,5, 2, 2,5, 3\} $$ это можно записать как $$\{\frac{1}{2} k \mid k \in [-6..6] \}.$$

$\endgroup$

2.

3 Использование нотаций для определения домена и диапазона – Math 3080 Подготовка

В предыдущих примерах мы использовали неравенства и списки для описания области определения функций. Мы также можем использовать неравенства или другие операторы, которые могут определять наборы значений или данных, для описания поведения переменной в нотации построителя наборов . Например, [латекс]\{х\верт10\leq xx-значения, где 10 меньше или равно [латекс]х\;[/латекс] и [латекс]\;х[/латекс] меньше 30 ».

На рис. 2-4 сравниваются обозначения неравенства, обозначения построителя множеств и обозначения интервалов.

Рисунок 2-4

Чтобы объединить два интервала, используя нотацию неравенства или нотацию построителя множеств, мы используем слово «или». Как мы видели в предыдущих примерах, мы используем символ объединения [латекс]\чашка[/латекс] для объединения двух несвязанных интервалов. Например, объединение множеств [латекс]\{2,3,5\}[/латекс] и [латекс]\{4,6\}[/латекс] представляет собой множество [латекс]\{2,3 ,4,5,6\}[/латекс]. Это множество всех элементов, принадлежащих одному или другой (или оба) оригинальных двух наборов. Для наборов с конечным числом таких элементов элементы не обязательно должны быть перечислены в порядке возрастания числового значения. Если исходные два набора имеют некоторые общие элементы, эти элементы должны быть перечислены только один раз в объединенном наборе. Для наборов действительных чисел на интервалах другим примером объединения является

.

[латекс]\{{x\vert\vert x\vert\geq3}=(-\infty,-3\rbrack\cup\lbrack3,\infty)\}[/latex]

Обозначение построителя наборов — это метод указания набора элементов, удовлетворяющих определенному условию. Он принимает форму [латекс]\{х\верт\;утверждение\;об\;х\}[/латекс], которое читается как «множество всех [латекс]х[/латекс], таких, что утверждение о [латекс]х[/латекс] верно». Например,

{x|4

Интервальное обозначение — это способ описания наборов, включающих все действительные числа между нижним пределом, который может быть или не быть. включены и верхний предел, который может быть включен или не включен. Значения конечной точки перечислены в скобках или круглых скобках. Квадратная скобка указывает на включение в набор, а скобка указывает на исключение из набора. Например,

[латекс]\влево(4,12\вправо][/латекс]

Для заданного линейного графика опишите набор значений, используя интервальную запись.

  1. Определите интервалы, которые должны быть включены в набор, определяя, где толстая линия накладывается на реальную линию.
  2. В левом конце каждого интервала используйте [ с каждым конечным значением, которое будет включено в набор ([латекс]\пуля[/латекс]) или ( для каждого исключенного конечного значения ([латекс]\цирк[/латекс])
  3. В правом конце каждого интервала используйте ] для каждого конечного значения, которое должно быть включено в набор ([latex]\bullet[/latex]), или ) для каждого исключенного конечного значения ([latex]\circ[/latex]) .
  4. Используйте символ объединения ∪, чтобы объединить все интервалы в один набор.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *