Угол. Обозначение углов / Геометрия / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Угол. Обозначение углов
Угол — геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
На рис. 1 лучи АВ и АС — стороны угла, точка А — вершина угла.
При записи угла в середине пишут букву, обозначающую его вершину. Сам угол на рис. 1 обозначают так: ВАС или САВ (этот угол нельзя обозначить так: АВС или СВА или ВСА или АСВ, т.к. точки В и С не являются вершинами данного угла).
Если углы имеют общую вершину, то их нельзя обозначить одной буквой. Так на рис. 2 углы имеют общую вершину Е, поэтому мы можем использовать для данных углов только следующие обозначения: МЕК или КЕМ, МЕР или РЕМ, РЕК или КЕР. Говорят, что луч ЕР в данном случае делит угол МЕК (или КЕМ) на два угла: МЕР (или РЕМ) и РЕК (или КЕР).
Также иногда углы обозначают цифрами, например, на рис.3 мы имеем 1.
Углы, как и отрезки, можно сравнивать между собой. Чтобы сравнить два угла можно наложить один угол на другой.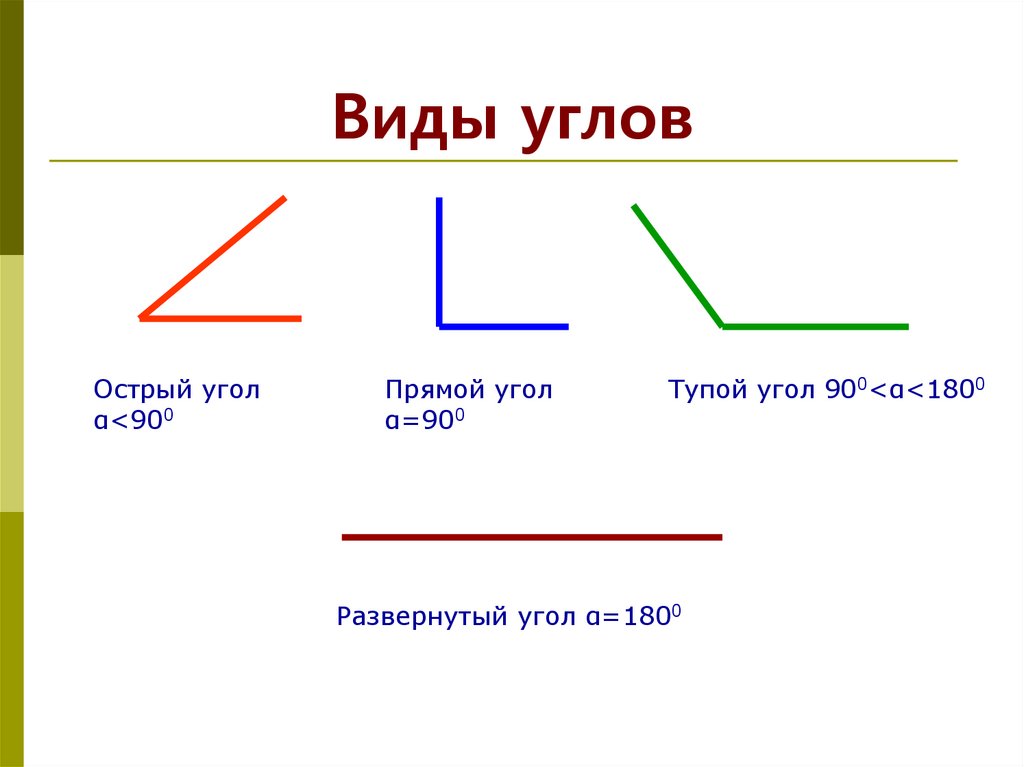
Биссектриса — луч, который делит угол на два равных угла. На рис. 4 углы НОМ и DОМ равны, значит, луч ОМ — биссектриса угла НОD.
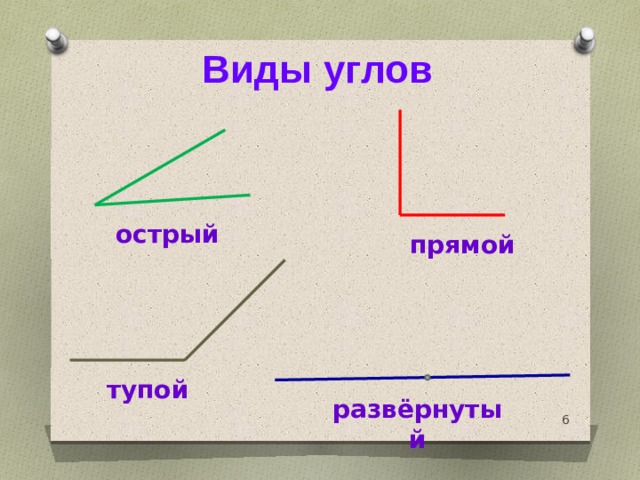
Прямой угол — угол, который можно построить с помощью угольника (рис. 5).
Если начертить два прямых угла с общей вершиной и одной общей стороной, то две другие стороны этих углов составят прямую (рис. 6). Считают, что лучи, составляющие прямую, также образуют угол, который называют
На рис. 6 АОВ и ВОС — прямые, АОС — развернутый.
Развернутый угол равен двум прямым углам, а прямой угол составляет половину развернутого.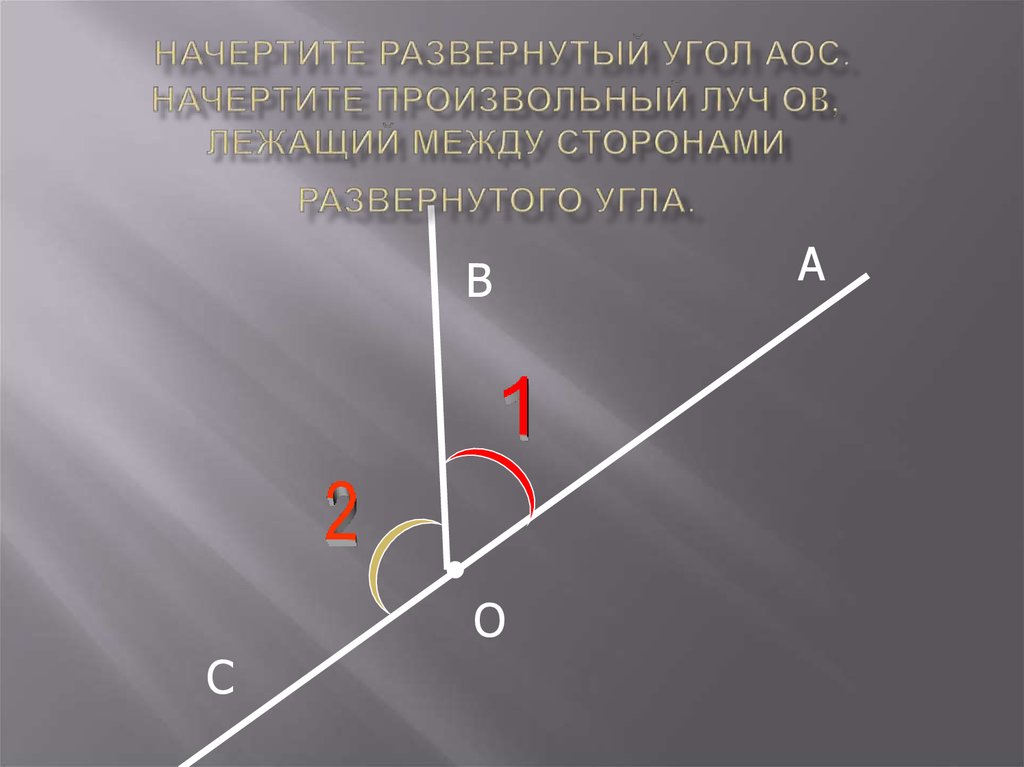
Острый угол — угол, который меньше прямого угла. На рис. 7 МОN — острый.
Тупой угол — угол, который больше прямого угла, но меньше развернутого. На рис. 8 РЕК — тупой.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Прямой и развернутый угол
Чертежный треугольник
Измерение углов.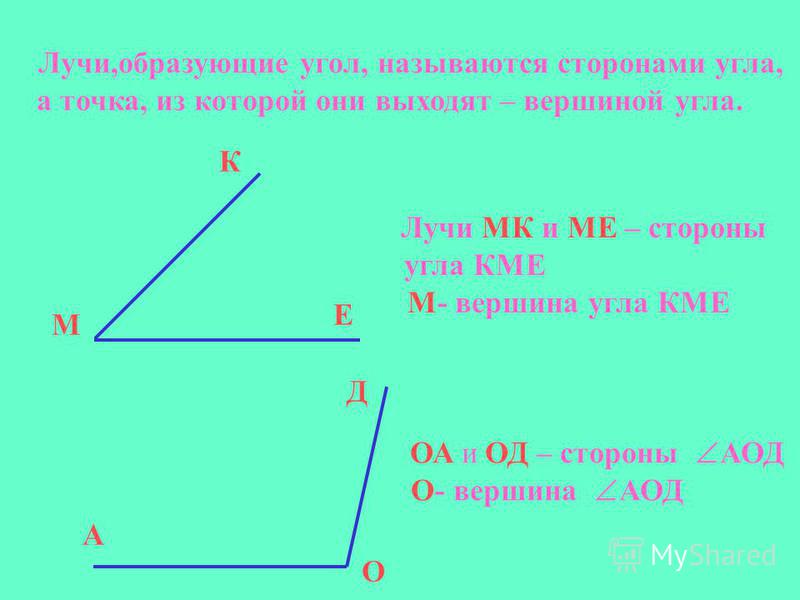 Транспортир. Виды углов
Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 1615, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1641, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1653, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1658, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1776, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1778, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 11, Мерзляк, Полонский, Якир, Учебник
Номер 302, Мерзляк, Полонский, Якир, Учебник
Номер 5, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 219, Мерзляк, Полонский, Якир, Учебник
Номер 391, Мерзляк, Полонский, Якир, Учебник
Номер 686, Мерзляк, Полонский, Якир, Учебник
Номер 714, Мерзляк, Полонский, Якир, Учебник
Номер 1226, Мерзляк, Полонский, Якир, Учебник
Номер 1236, Мерзляк, Полонский, Якир, Учебник
Номер 1237, Мерзляк, Полонский, Якир, Учебник
Номер 1283, Мерзляк, Полонский, Якир, Учебник
Задание 738, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1545, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 759, Мерзляк, Полонский, Якир, Учебник
Задание 81, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Развернутый угол.
 Прямой, тупой, острый и развернутый угол
Прямой, тупой, острый и развернутый уголВ этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом.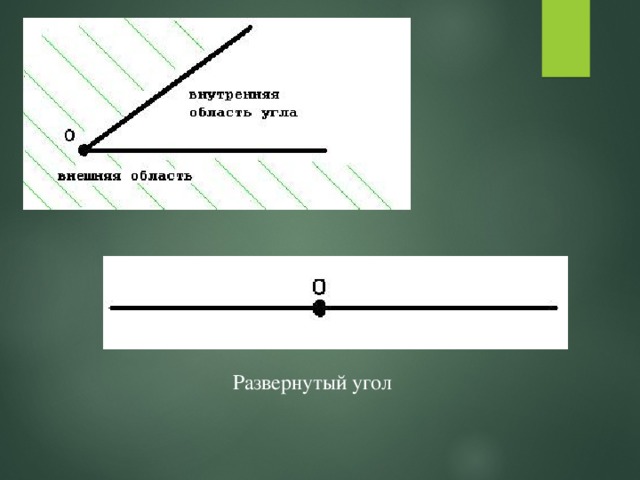 Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.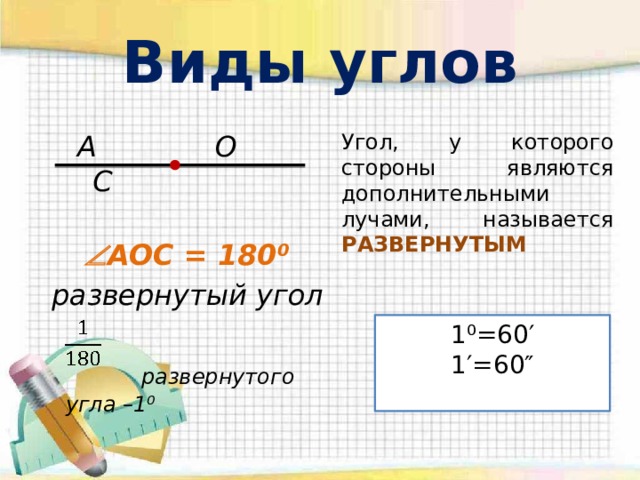
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.

- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла — это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.

- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х. Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
В этой статье мы всесторонне разберем одну из основных геометрических фигур – угол. Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала.
Навигация по странице.
Определение угла.
Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость. Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .
Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости.
Дадим сначала определение луча.
Пусть нам дана некоторая прямая на плоскости.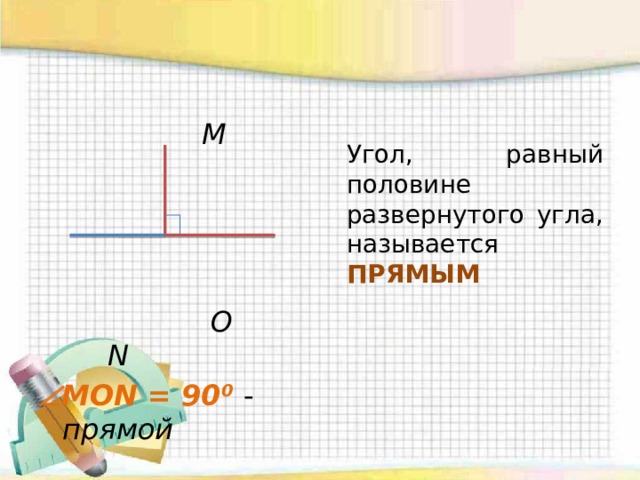 Обозначим ее буквой a
. Пусть O
– некоторая точка прямой a
. Точка O
разделяет прямую a
на две части. Каждая из этих частей вместе с точкой О
называется лучом , а точка О
называется началом луча . Еще можно услышать, что луч называют полупрямой .
Обозначим ее буквой a
. Пусть O
– некоторая точка прямой a
. Точка O
разделяет прямую a
на две части. Каждая из этих частей вместе с точкой О
называется лучом , а точка О
называется началом луча . Еще можно услышать, что луч называют полупрямой .
Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p или луч k ), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА или луч СD ). Покажем изображение и обозначение лучей на чертеже.
Теперь мы можем дать первое определение угла.
Определение.
Угол – это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом. Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .
Возможен случай, когда стороны угла составляют прямую линию.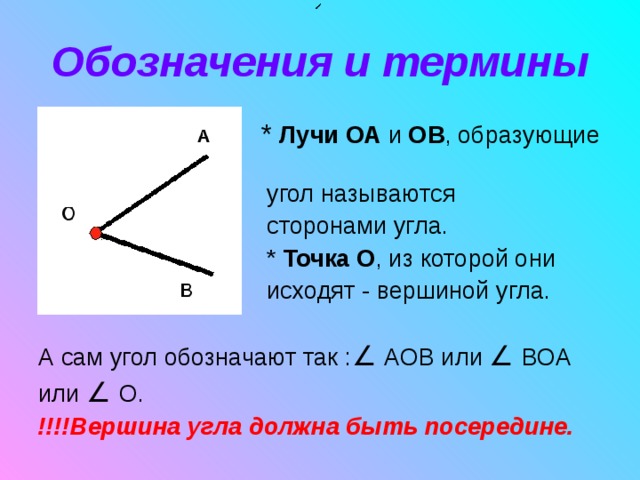 Такой угол имеет свое название.
Такой угол имеет свое название.
Определение.
Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым .
Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла.
Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k
, а другая h
), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA
, а вторая сторона угла OB
), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ). Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла , а другую – внешней областью угла . Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая — внешней.
Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла.
Определение внутренней области угла приводит нас ко второму определению угла.
Определение.
Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.
Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности.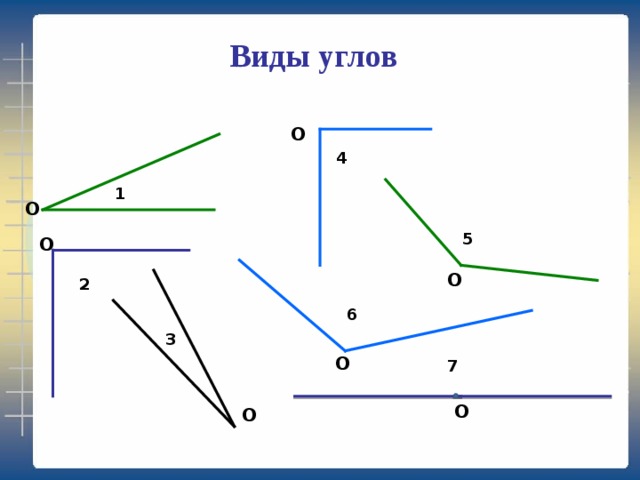 Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Дадим еще определения смежных и вертикальных углов.
Определение.
Смежные углы – это два угла, у которых одна сторона общая, а две другие образуют развернутый угол.
Из определения следует, что смежные углы дополняют друг друга до развернутого угла.
Определение.
Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого.
На рисунке изображены вертикальные углы.
Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.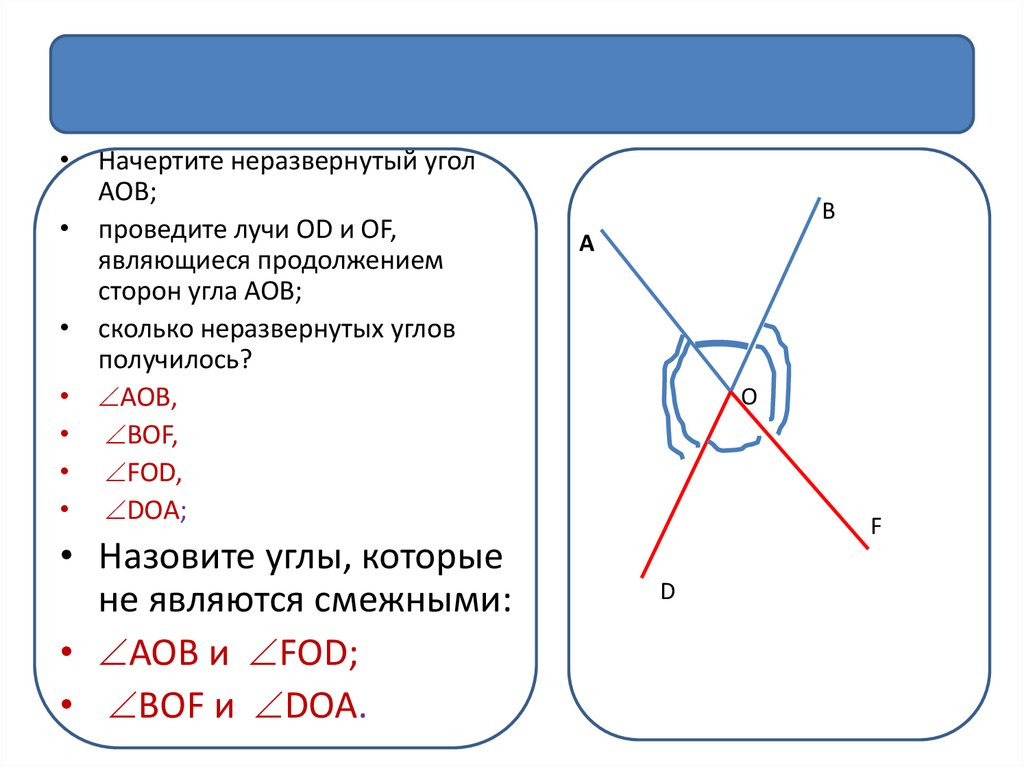
Сравнение углов.
В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае неравных углов разъясним, какой угол считается большим, а какой меньшим.
Напомним, что две геометрические фигуры называются равными, если их можно совместить наложением.
Пусть нам даны два угла. Приведем рассуждения, которые помогут нам получить ответ на вопрос: «Равны эти два угла или нет»?
Очевидно, что мы всегда можем совместить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла. Совместим сторону первого угла с той стороной второго угла, чтобы оставшиеся стороны углов оказались по одну сторону от прямой, на которой лежат совмещенные стороны углов. Тогда, если две другие стороны углов совместятся, то углы называются равными .
Если же две другие стороны углов не совместятся, то углы называются неравными , причем меньшим считается тот угол, который составляет часть другого (большим является тот угол, который полностью содержит другой угол).
Очевидно, что два развернутых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла.
Измерение углов.
Измерение углов основывается на сравнении измеряемого угла с углом, взятым в качестве единицы измерения. Процесс измерения углов выглядит так: начиная от одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют единичными углами, плотно укладывая их один к другому. При этом запоминают количество уложенных углов, которое и дает меру измеряемого угла.
Фактически, в качестве единицы измерения углов может быть принят любой угол. Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия.
Одной из единиц измерения углов является градус .
Определение.
Один градус – это угол, равный одной сто восьмидесятой части развернутого угла.
Градус обозначают символом «», следовательно, один градус обозначается как .
Таким образом, в развернутом угле мы можем уложить 180 углов в один градус. Это будет выглядеть как половинка круглого пирога, разрезанная на 180 равных кусочков. Очень важно: «кусочки пирога» плотно укладываются один к другому (то есть, стороны углов совмещаются), причем сторона первого угла совмещается с одной стороной развернутого угла, а сторона последнего единичного угла совпадет с другой стороной развернутого угла.
При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемом угле до полного покрытия внутренней области измеряемого угла. Как мы уже убедились, в развернутом угле градус укладывается ровно 180 раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30 раз (такой угол составляет шестую часть развернутого угла) и ровно 90 раз (половина развернутого угла).
Для измерения углов, меньших одного градуса (или другой единицы измерения углов) и в случаях, когда угол не удается измерить целым числом градусов (взятых единиц измерения), приходится использовать части градуса (части взятых единиц измерения). Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определение.
Минута – это одна шестидесятая часть градуса.
Определение.
Секунда – это одна шестидесятая часть минуты.
Иными словами, в минуте содержится шестьдесят секунд, а в градусе – шестьдесят минут (3600 секунд). Для обозначения минут используют символ «», а для обозначения секунд – символ «» (не путайте со знаками производной и второй производной). Тогда при введенных определениях и обозначениях имеем , а угол, в котором укладываются 17 градусов 3 минуты и 59 секунд, можно обозначить как .
Определение.
Градусной мерой угла называется положительное число, которое показывает сколько раз градус и его части укладываются в данном угле.
Например, градусная мера развернутого угла равна ста восьмидесяти, а градусная мера угла равна .
Для измерения углов существуют специальные измерительные приборы, наиболее известным из них является транспортир.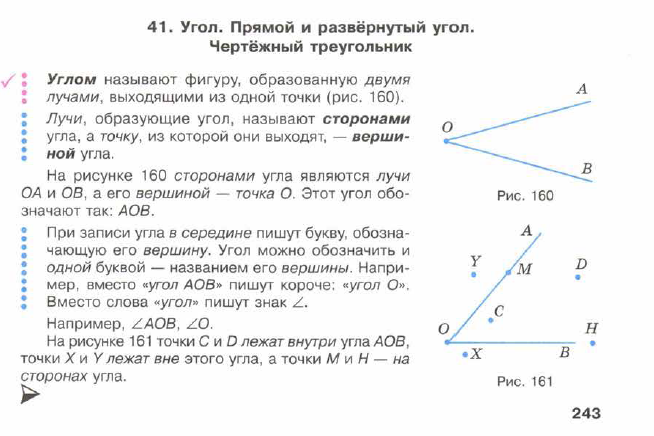
Если известно и обозначение угла (к примеру, ) и его градусная мера (пусть 110 ), то используют краткую запись вида и говорят: «Угол АОВ равен ста десяти градусам».
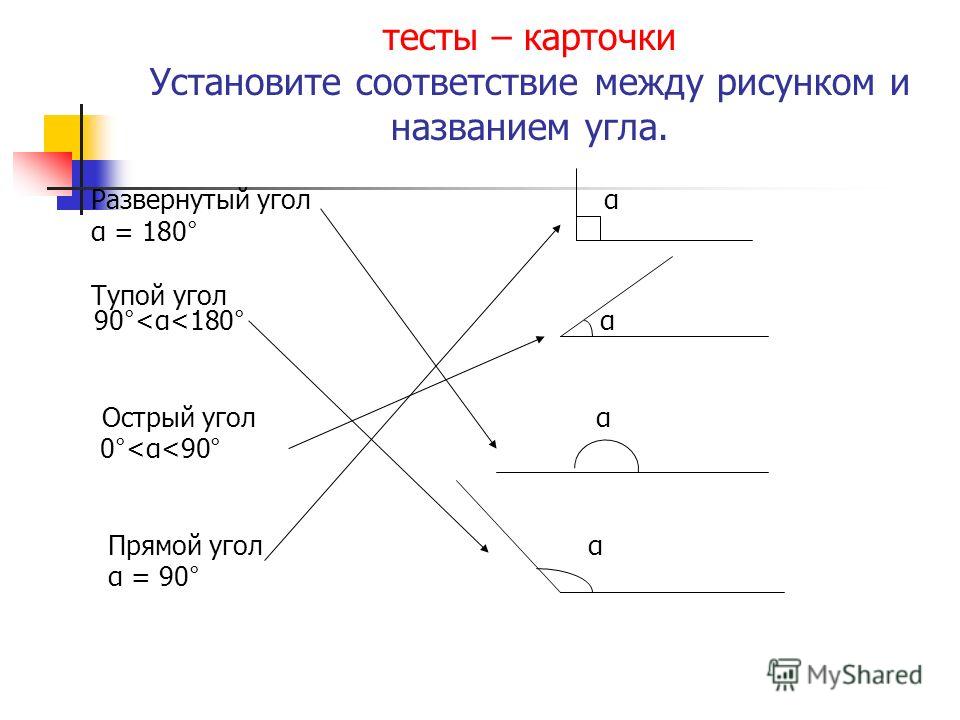
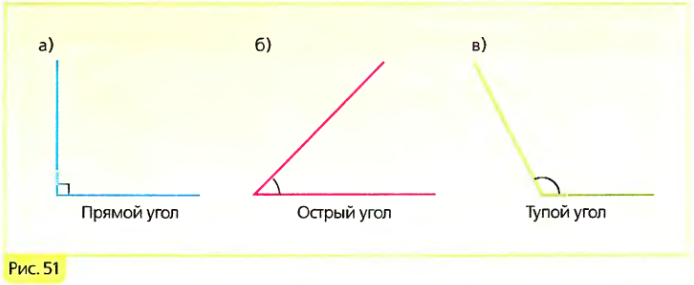
Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180] (в тригонометрии рассматривают углы с произвольной градусной мерой, их называют ). Угол в девяносто градусов имеет специальное название, его называют прямым углом . Угол меньший 90 градусов называется острым углом . Угол больший девяноста градусов называется тупым углом . Итак, мера острого угла в градусах выражается числом из интервала (0, 90) , мера тупого угла – числом из интервала (90, 180) , прямой угол равен девяноста градусам. Приведем иллюстрации острого угла, тупого угла и прямого угла.
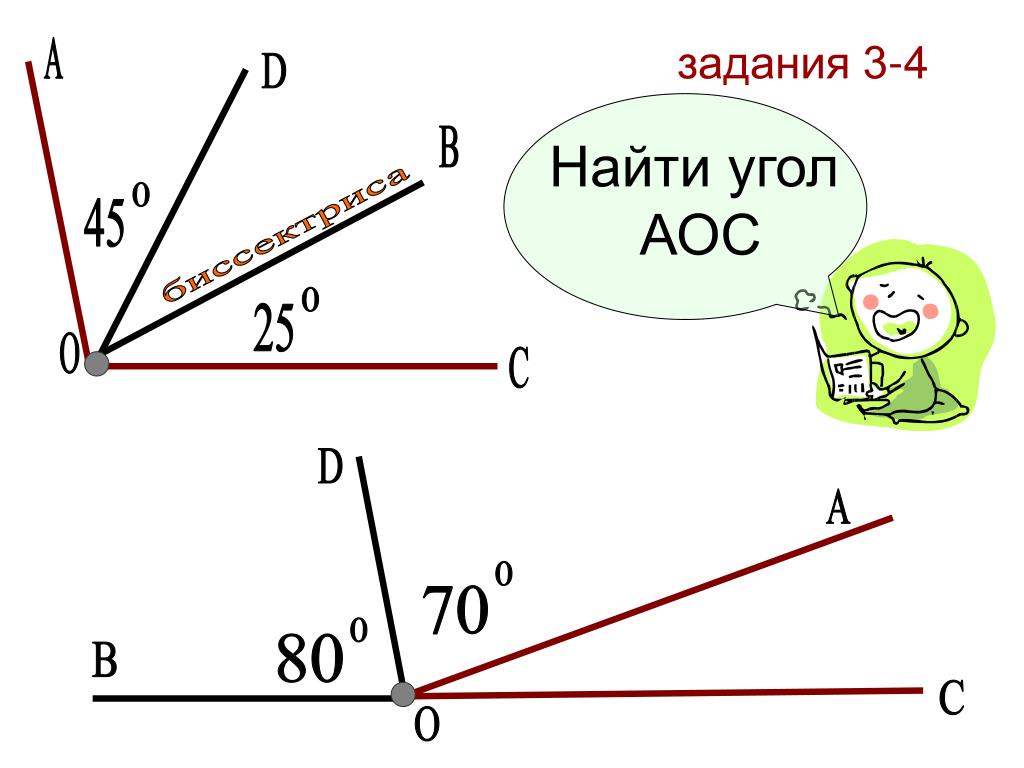
Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, который составляют несколько углов, равна сумме градусных мер составляющих углов.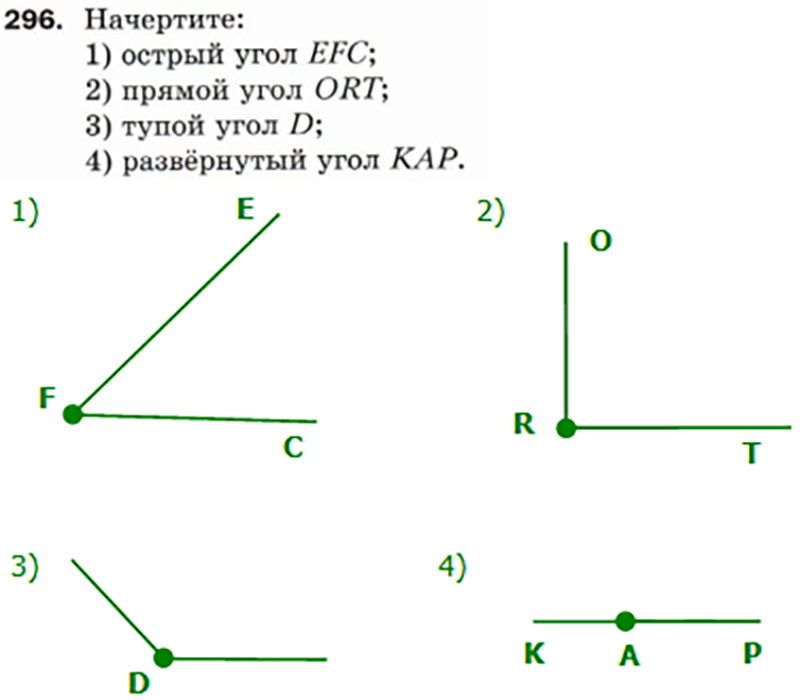 На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
Таким образом, сумма смежных углов равна ста восьмидесяти градусам , так как они составляют развернутый угол.
Из этого утверждения следует, что . Действительно, если углы АОВ и СОD – вертикальные, то углы АОВ и ВОС — смежные и углы СОD и ВОС также смежные, поэтому, справедливы равенства и , откуда следует равенство .
Наряду с градусом удобна единица измерения углов, называемая радианом . Радианная мера широко используется в тригонометрии. Дадим определение радиана.
Определение.
Угол в один радиан – это центральный угол , которому соответствует длина дуги, равная длине радиуса соответствующей окружности.
Дадим графическую иллюстрацию угла в один радиан. На чертеже длина радиуса OA (как и радиуса OB ) равна длине дуги AB , поэтому, по определению угол AOB равен одному радиану.
Для обозначения радианов используют сокращение «рад».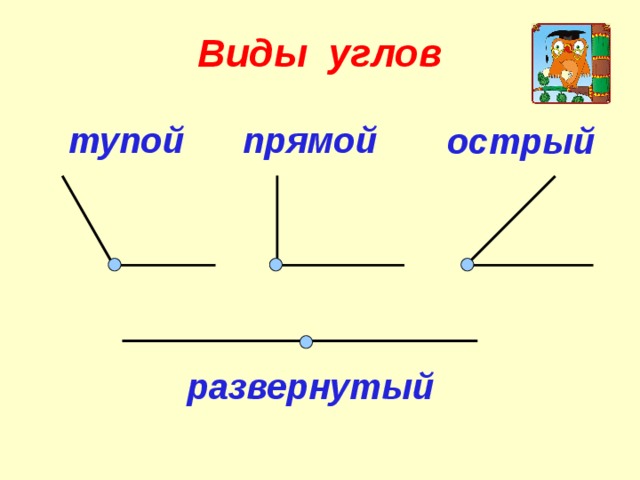 Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Стоит отдельно отметить, что величина угла, выраженная в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом и дугой окружности с центром в вершине данного угла, подобны между собой.
Измерение углов в радианах можно выполнять так же, как и измерение углов в градусах: выяснить, сколько раз угол в один радиан (и его части) укладываются в данном угле. А можно вычислить длину дуги соответствующего центрального угла, после чего разделить ее на длину радиуса.
Для нужд практики полезно знать, как соотносятся между собой градусная и радианная меры, так как довольно часть приходится осуществлять . В указанной статье установлена связь между градусной и радианной мерой угла, и приведены примеры перевода градусов в радианы и обратно.
Обозначение углов на чертеже.
На чертежах для удобства и наглядности углы можно отмечать дугами, которые принято проводить во внутренней области угла от одной стороны угла до другой. Равные углы отмечают одинаковым количеством дуг, неравные углы – различным количеством дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла до другой.
Если на чертеже приходится отмечать много различных углов (обычно больше трех), то при обозначении углов кроме обычных дуг допустимо использование дуг какого-либо специального вида. К примеру, можно изобразить зубчатые дуги, или нечто подобное.
Следует отметить, что не стоит увлекаться с обозначением углов на чертежах и не загромождать рисунки. Рекомендуем обозначать только те углы, которые необходимы в процессе решения или доказательства.
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.

- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Yandex.RTB R-A-339285-1 Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости.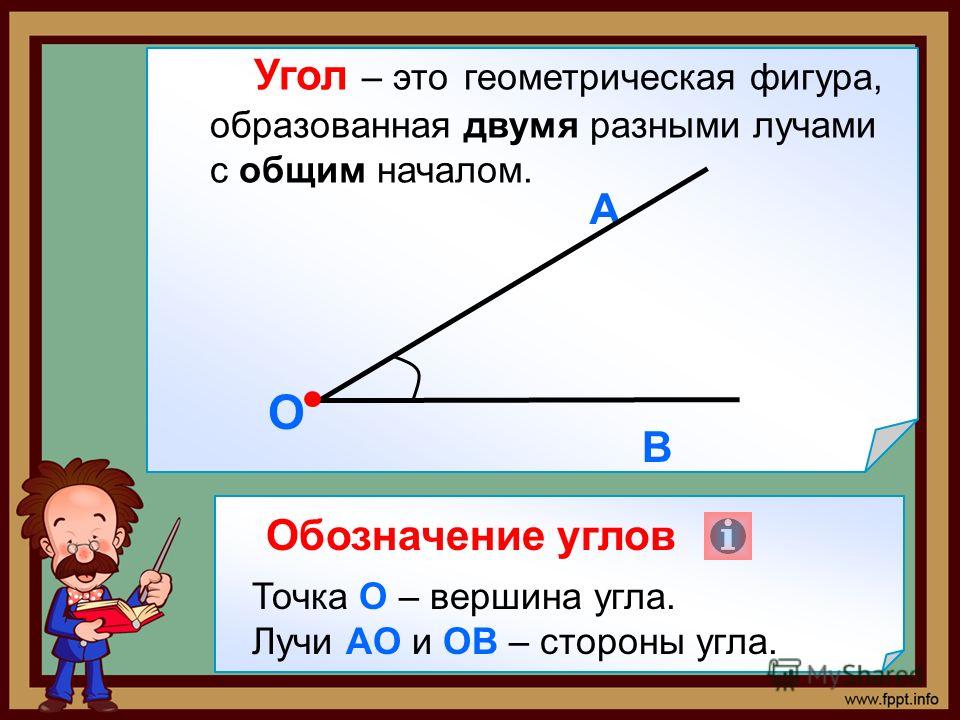 На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым .
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение 6
Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.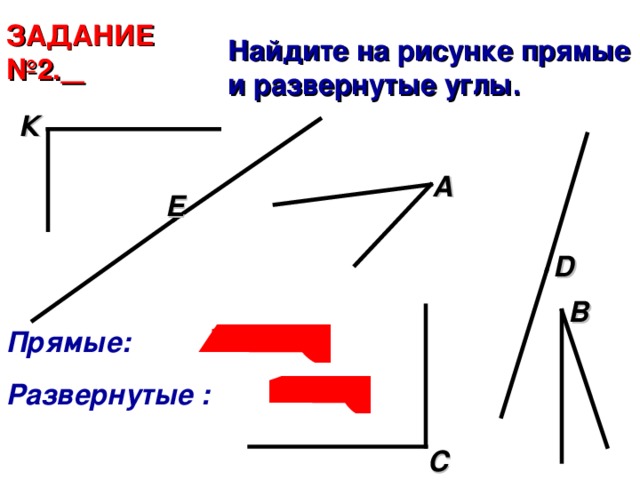
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7
Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус .
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° .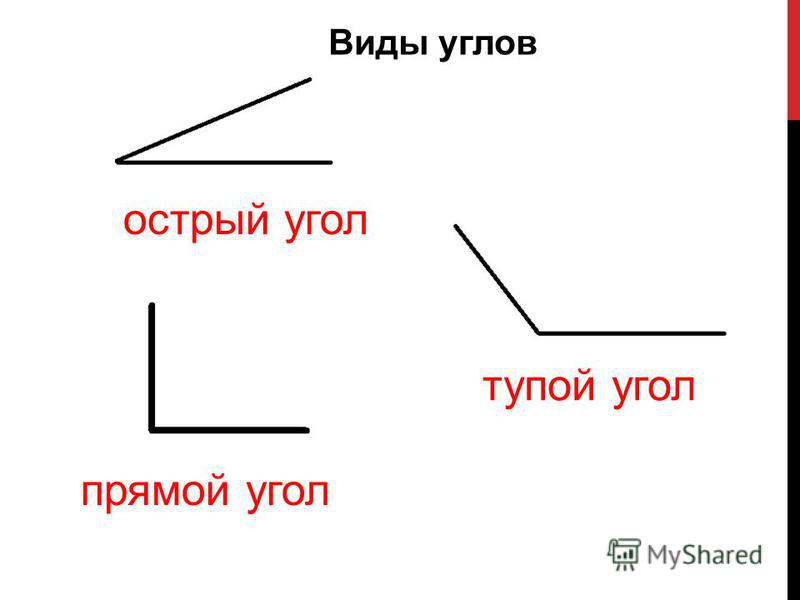 Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты.
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение:
1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» .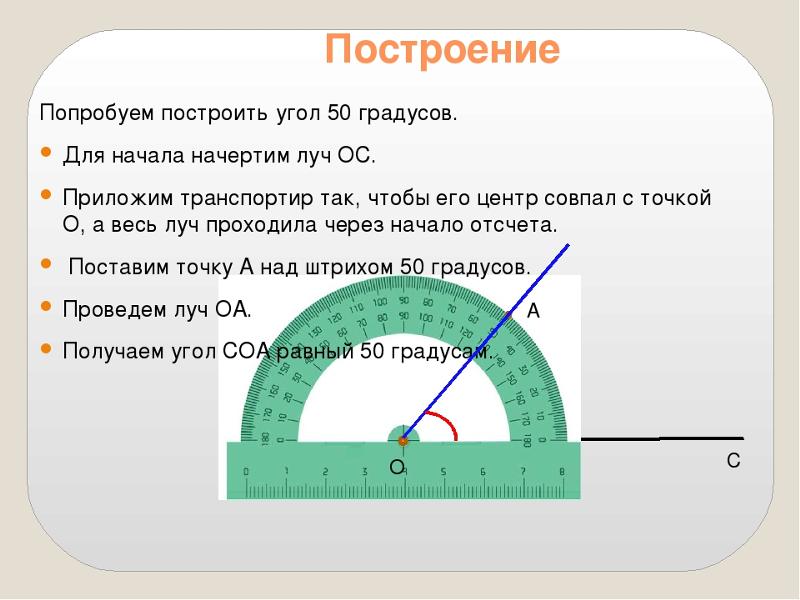
Определение 11
Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший.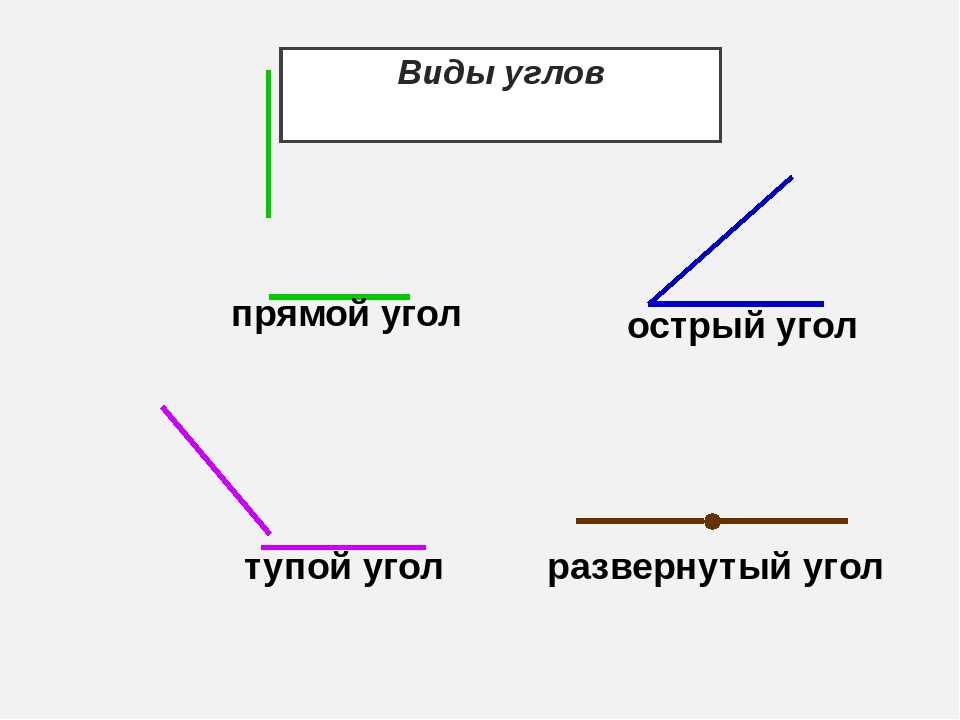 Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников.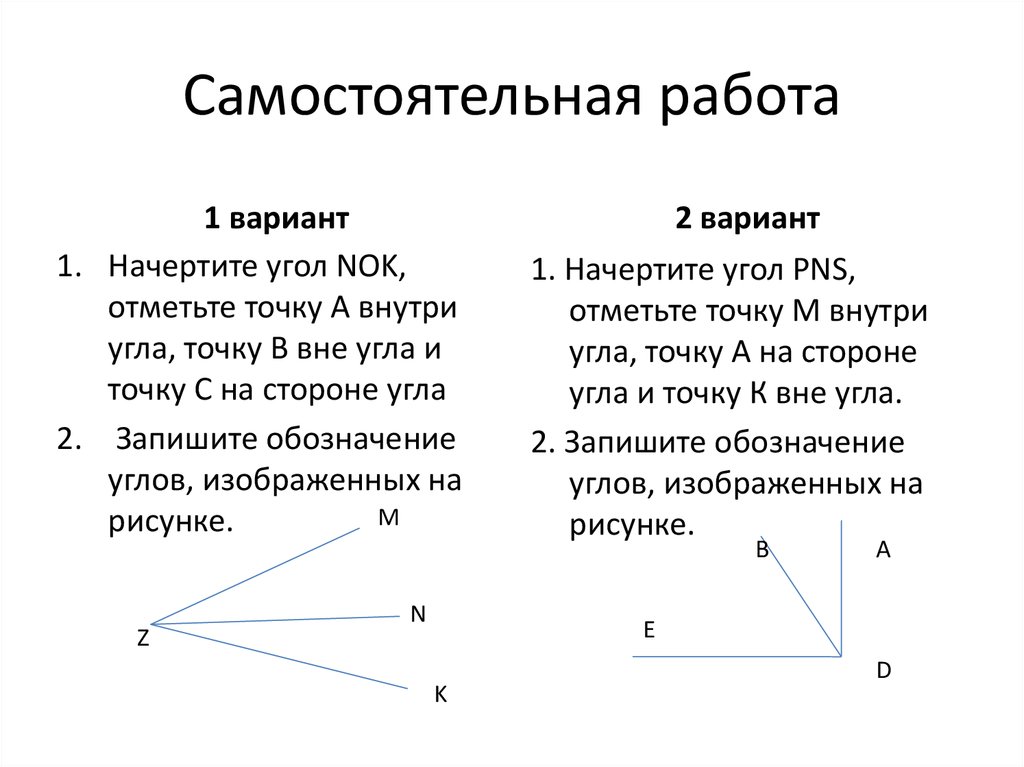 Что же называют радианом.
Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж.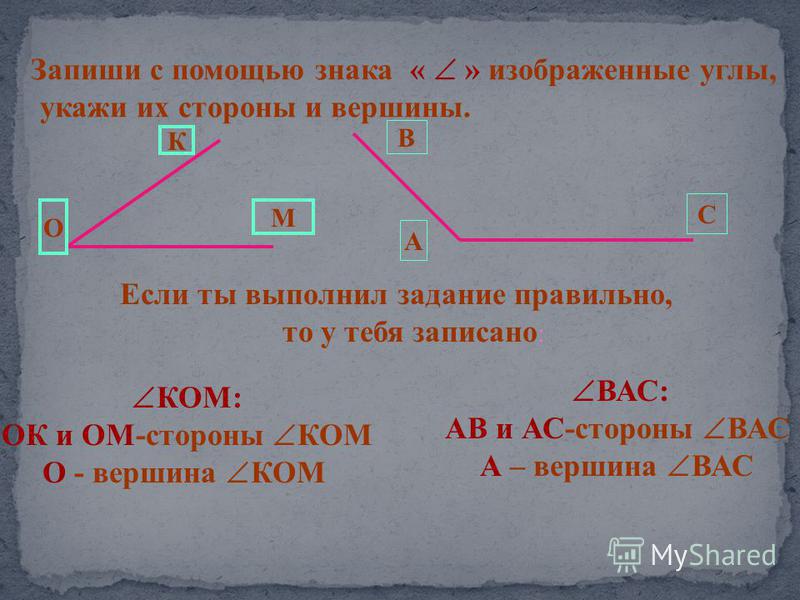 Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Что такое угол?
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160).
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
Например, вместо «угол АОВ» пишут короче: «угол О».
Вместо слова «угол» пишут знак .
Например, AОВ, O.
На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла.
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.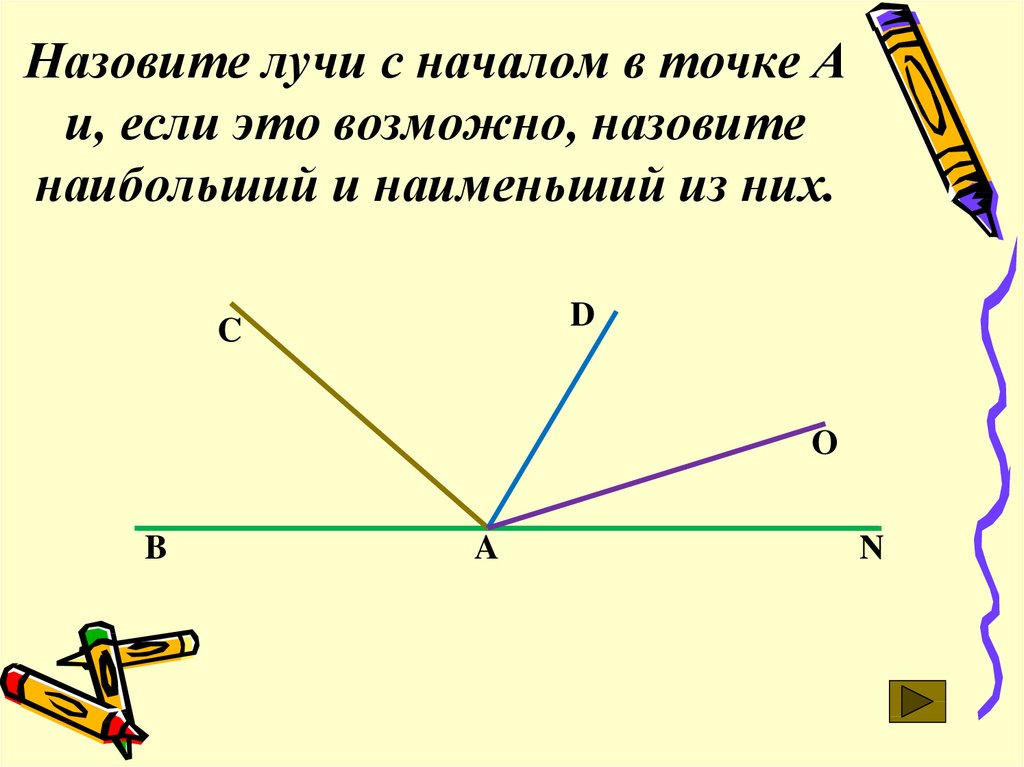
Например, на рисунке 162 ABC = MNK.
Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Пишут: COP
Прямой и развернутый угол
Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164).
Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165).
Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166).
Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.
Прямым углом называют половину развернутого угла.
Чертежный треугольник
Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо:
а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА;
б) провести вдоль второй стороны треугольника луч ОВ.
В результате получим прямой угол АОВ.
Вопросы к теме
1.Что такое угол?
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О.
Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных.
Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла.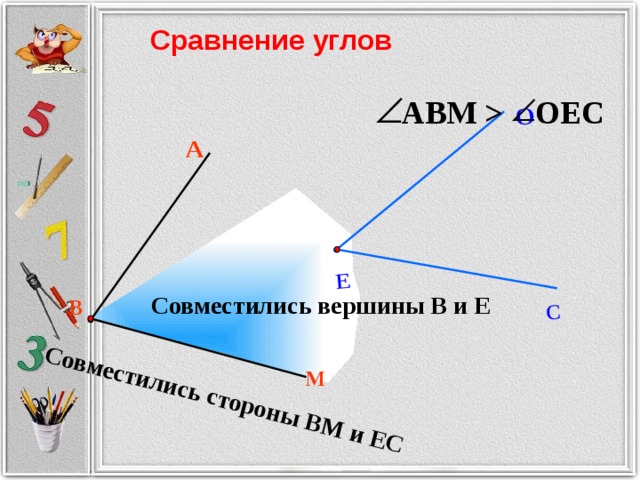
А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым.
Свойства развернутого угла
Развернутый угол обладает такими свойствами:
Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую;
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.
Измерение углов
Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам.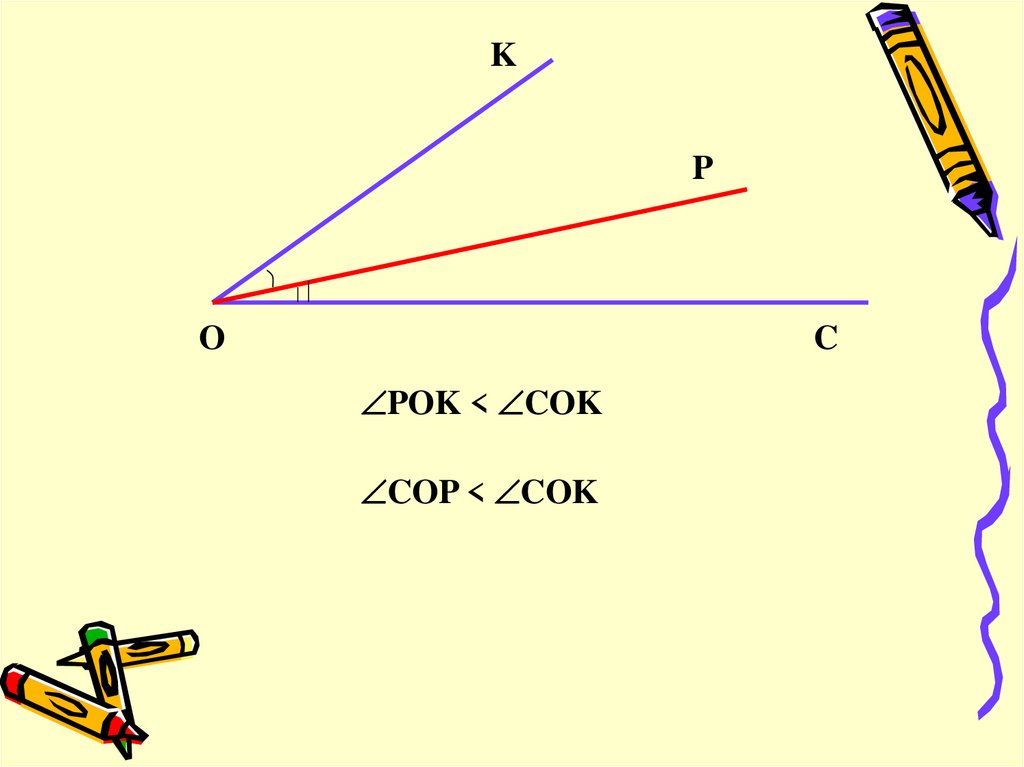
То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид: « ° ».
Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным.
А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. Это и есть развернутый угол.
Практическое задание
1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения.
1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ?
1615.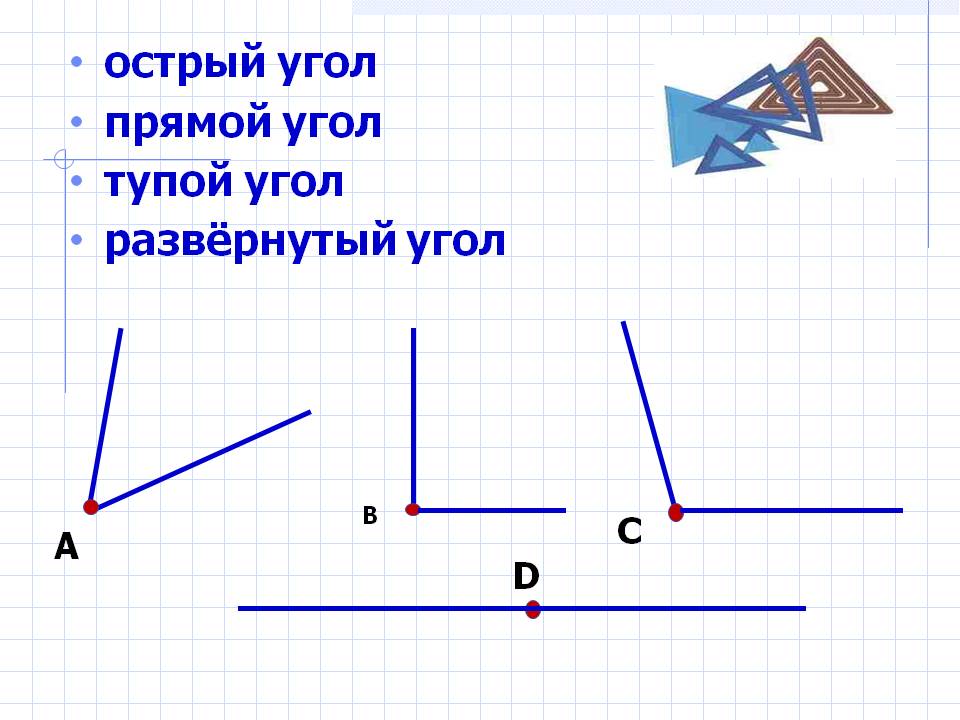 Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.
1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).
1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях.
1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.
1620. Укажите прямые углы в классной комнате.
а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1.
1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600?
1630. Найдите пропущенное число:
а) 2 5 3 б) 2 3 5
13 6 12 1
2 3? 42?
1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?
1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
1635. Найдите с помощью микрокалькулятора:
а) 4,5% от 168; в) 28,3% от 569,8;
б) 147,6% от 2500; г) 0,09% от 456 800.
1636. Решите задачу:
1) Площадь огорода 6,4 а.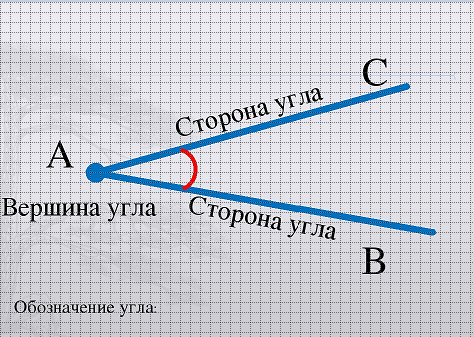 В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось?
1637. Выполните действия:
1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85;
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.
1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК?
1640. Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.
1642. Найдите значение выражения:
а) 14,791: а + 160,961: b, если а = 100, b = 10;
б) 361,62с + 1848: d, если с = 100, d =100.
1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день?
1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?
1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики?
1646. Найдите, сколько составляют:
а) 1% от тонны; в) 5% от 7 т;
б) 1% от литра; г) 6% от 80 км.
1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т?
1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Н.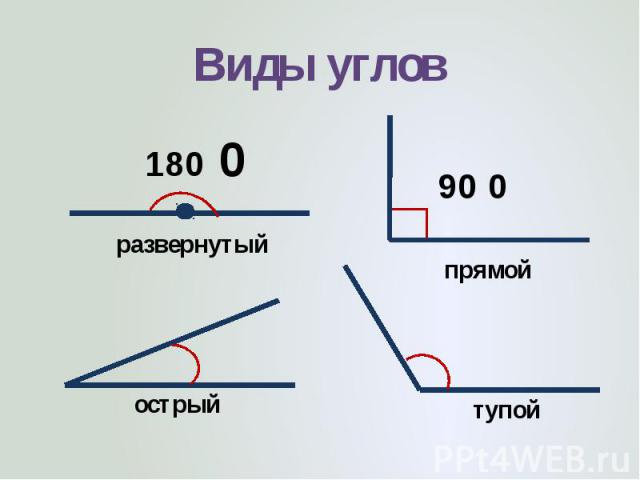 Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам .
В морской терминологии углы обозначаются румбами .
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation . 2010 .
Смотреть что такое «Развернутый угол» в других словарях:
Угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными.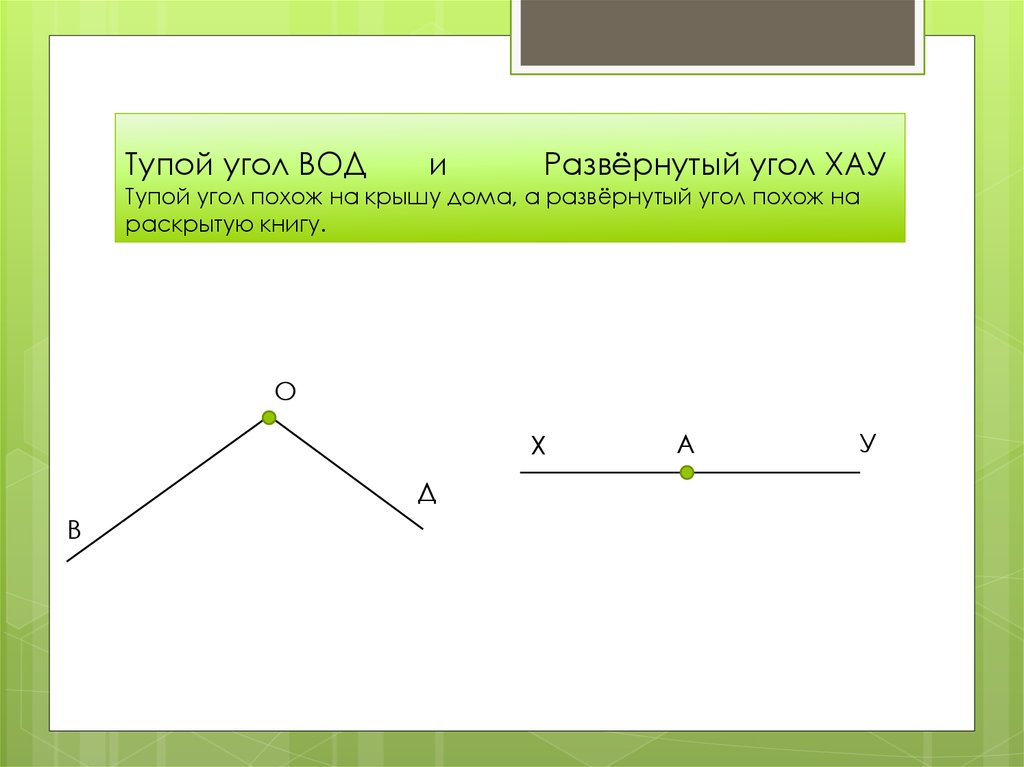 Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
угол — ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… …
Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия
Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь
Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения.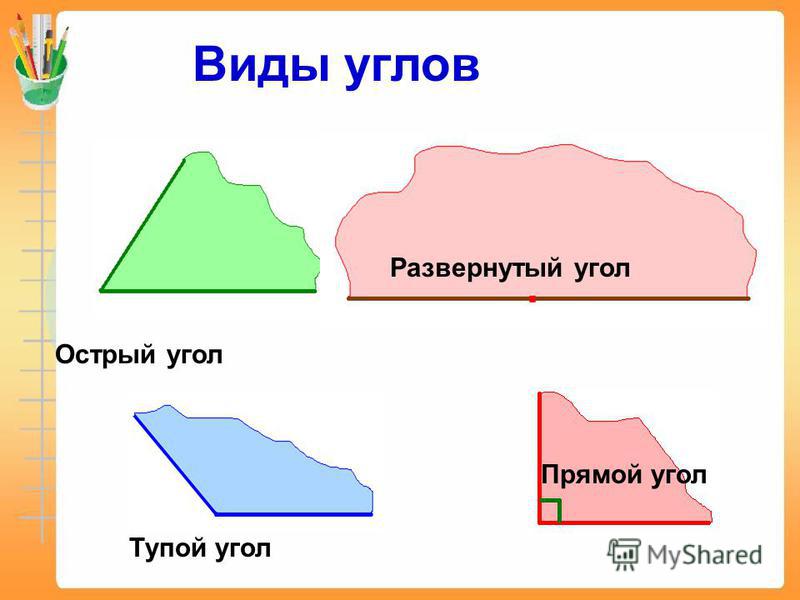 Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия
поперек — ▲ под углом максимум, косой угол поперечный. поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
градус — а, м. 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля.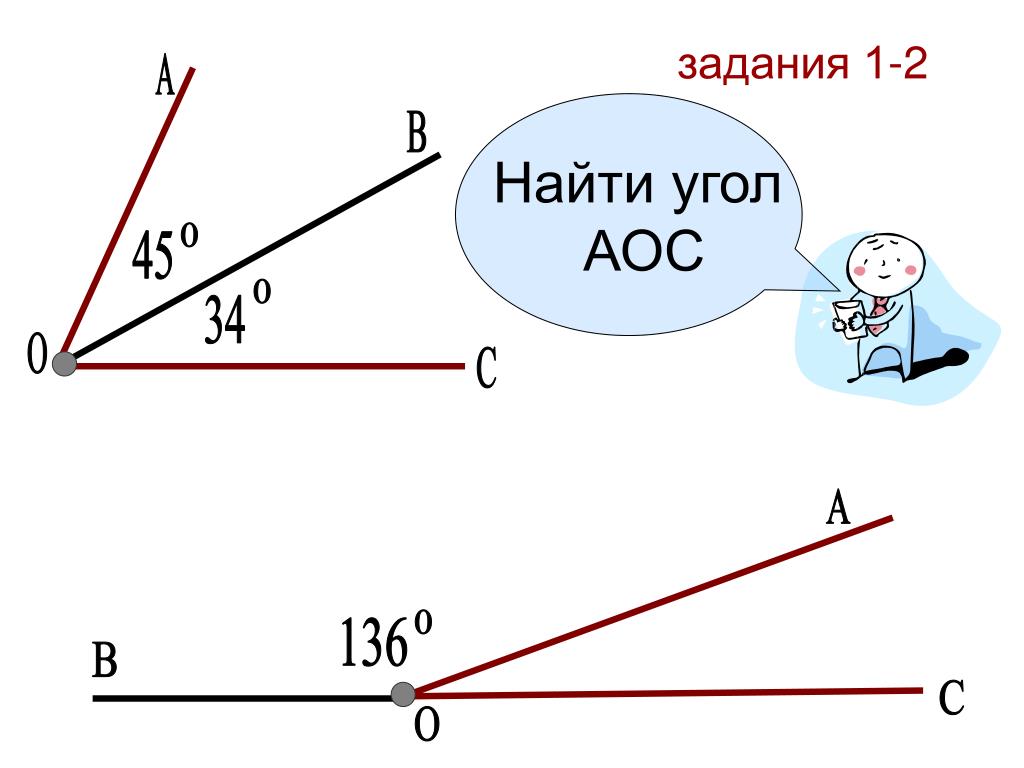 Очень важной с практической точки зрения является проблема о конформном… … Википедия
Очень важной с практической точки зрения является проблема о конформном… … Википедия
Прямой, тупой, острый и развернутый угол. Прямой и развернутый угол Чему равен развернутый угол в градусах
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам .
В морской терминологии углы обозначаются румбами .
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation . 2010 .
Смотреть что такое «Развернутый угол» в других словарях:
Угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
*РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
угол — ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… …
Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У.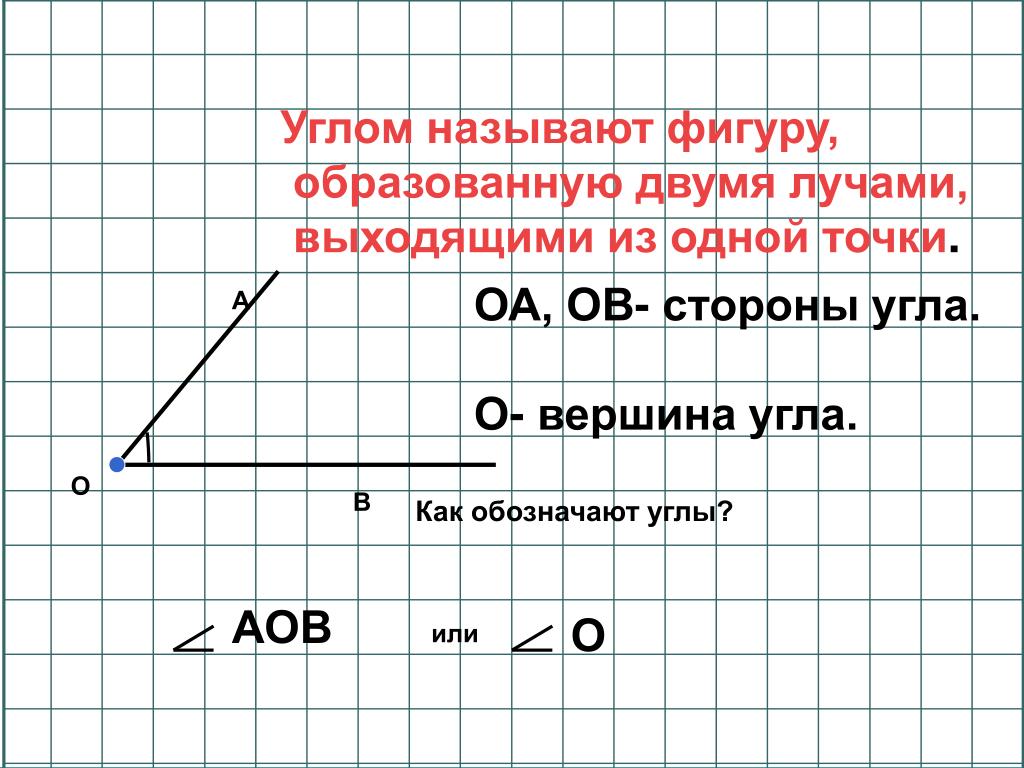 Фигура делит плоскость… … Математическая энциклопедия
Фигура делит плоскость… … Математическая энциклопедия
Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь
Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия
поперек — ▲ под углом максимум, косой угол поперечный. поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
градус — а, м.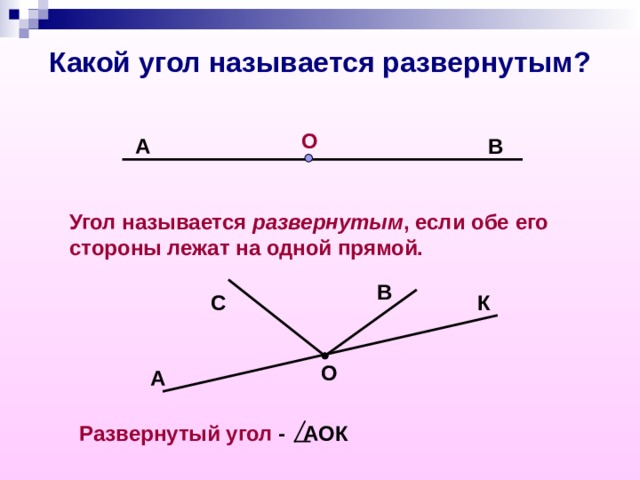 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия
Что такое угол?
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160).
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
Например, вместо «угол АОВ» пишут короче: «угол О».
Вместо слова «угол» пишут знак .
Например, AОВ, O.
На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла.
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
Например, на рисунке 162 ABC = MNK.
Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Пишут: COP
Прямой и развернутый угол
Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164).
Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165).
Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166).
166).
Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.
Прямым углом называют половину развернутого угла.
Чертежный треугольник
Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо:
а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА;
б) провести вдоль второй стороны треугольника луч ОВ.
В результате получим прямой угол АОВ.
Вопросы к теме
1.Что такое угол?
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О.
Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных.
Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла.
А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым.
Свойства развернутого угла
Развернутый угол обладает такими свойствами:
Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую;
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.
Измерение углов
Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам.
То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид: « ° ».
Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным.
А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°.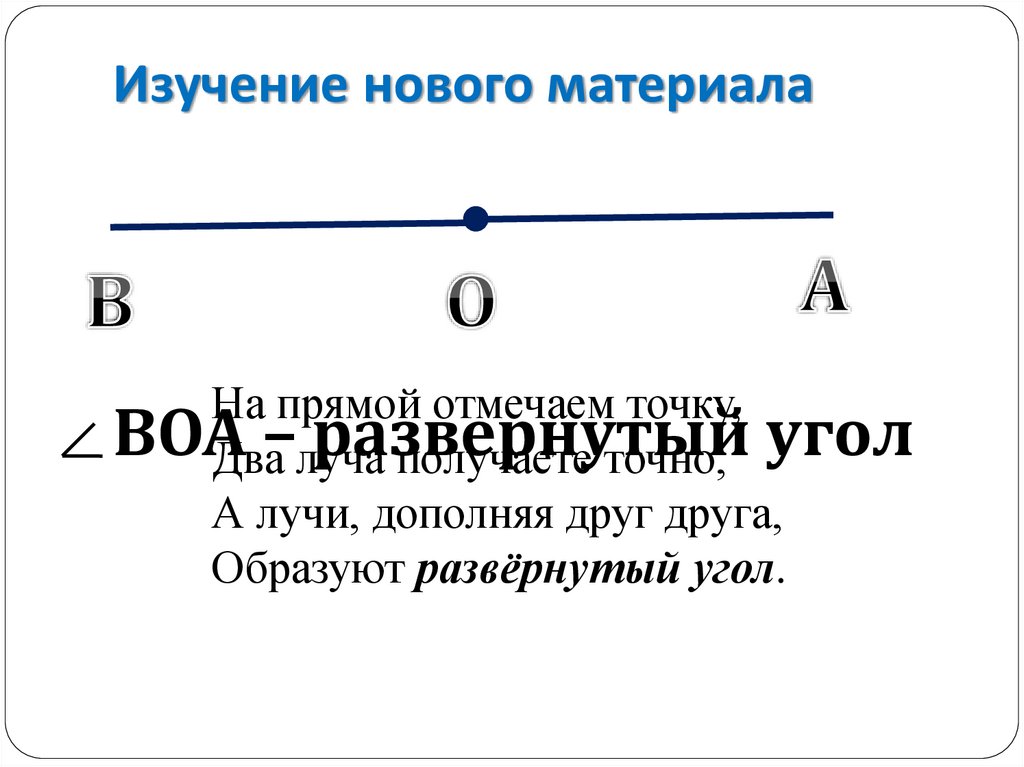 Это и есть развернутый угол.
Это и есть развернутый угол.
Практическое задание
1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения.
1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ?
1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.
1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).
1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях.
1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.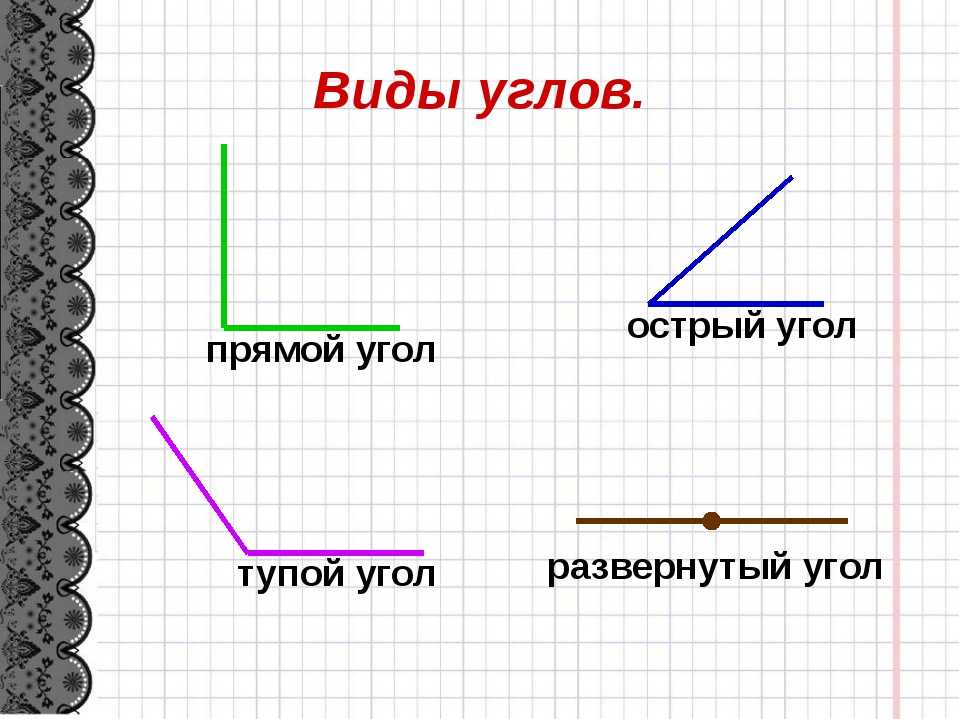
1620. Укажите прямые углы в классной комнате.
а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1.
1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600?
1630. Найдите пропущенное число:
а) 2 5 3 б) 2 3 5
13 6 12 1
2 3? 42?
1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?
1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
1635. Найдите с помощью микрокалькулятора:
а) 4,5% от 168; в) 28,3% от 569,8;
б) 147,6% от 2500; г) 0,09% от 456 800.
1636. Решите задачу:
1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось?
1637. Выполните действия:
1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85;
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.
1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК?
1640. Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.
1642. Найдите значение выражения:
а) 14,791: а + 160,961: b, если а = 100, b = 10;
б) 361,62с + 1848: d, если с = 100, d =100.
1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день?
1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?
1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики?
1646. Найдите, сколько составляют:
а) 1% от тонны; в) 5% от 7 т;
б) 1% от литра; г) 6% от 80 км.
1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т?
1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.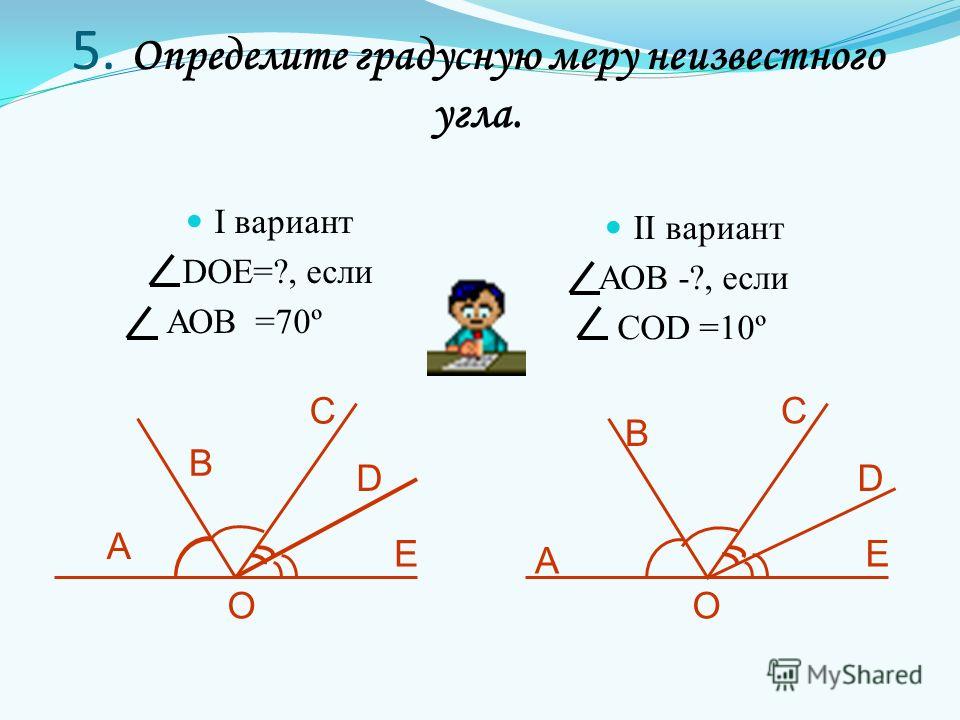
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов.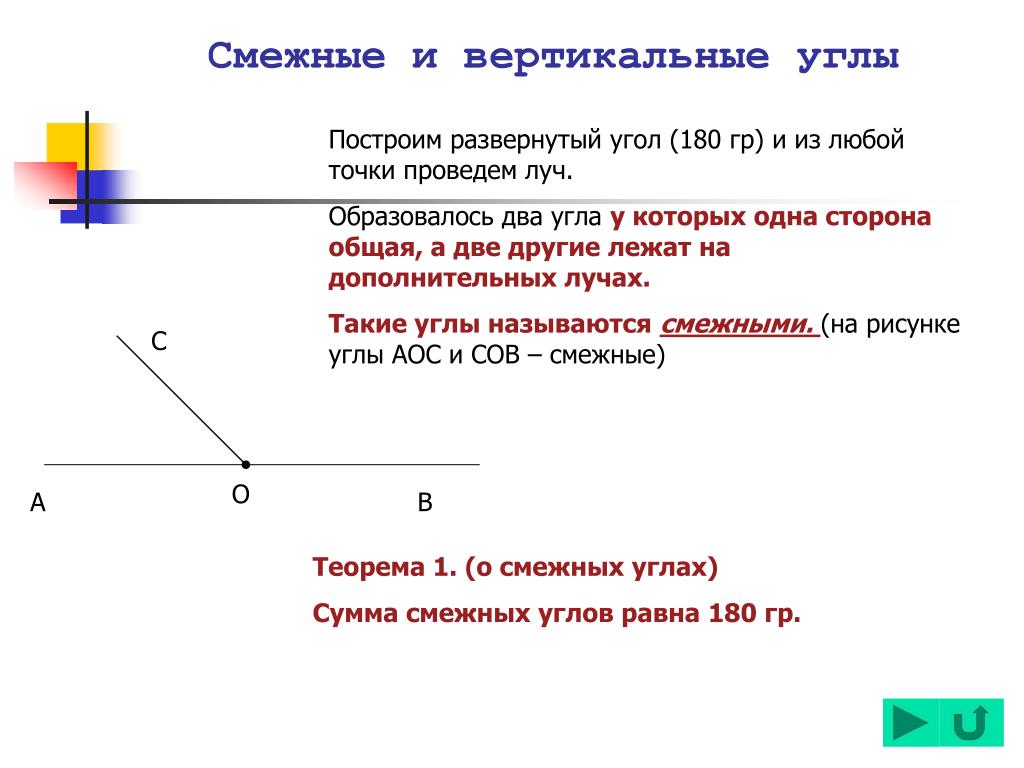 Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.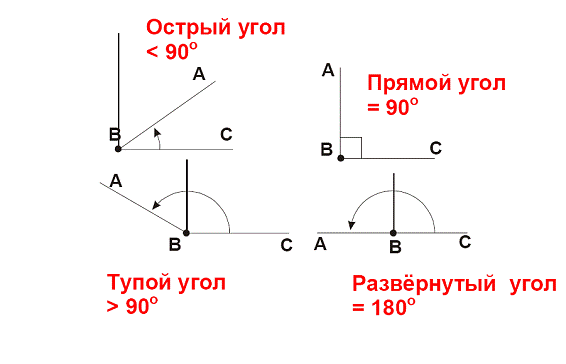 е. их сумма 90 о.
е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
В этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.

- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла — это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.

- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х. Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.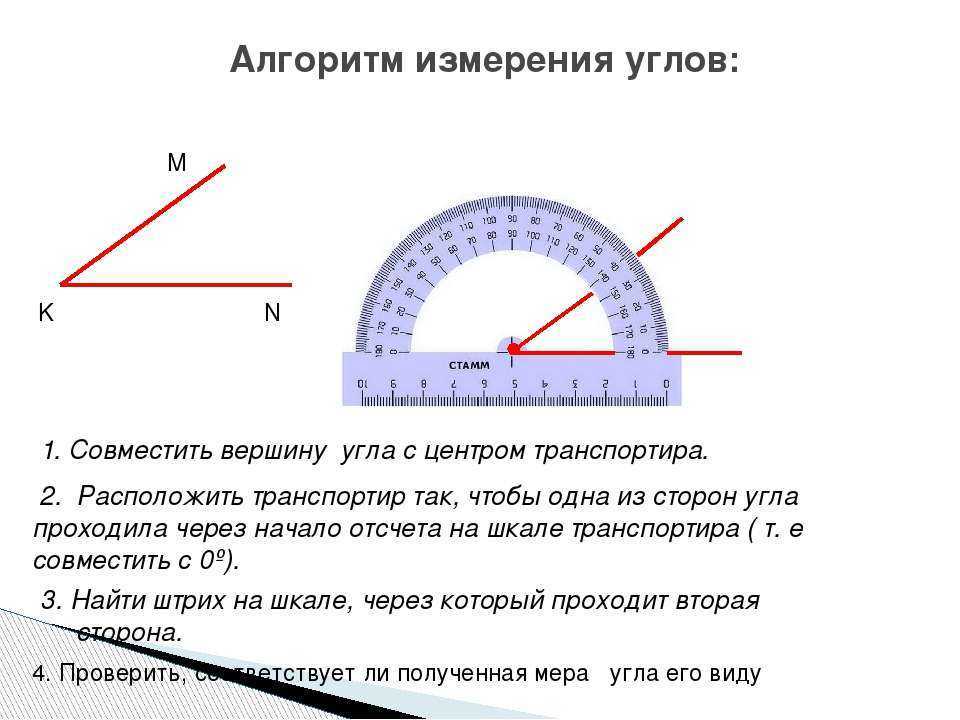
определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Определение 1Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.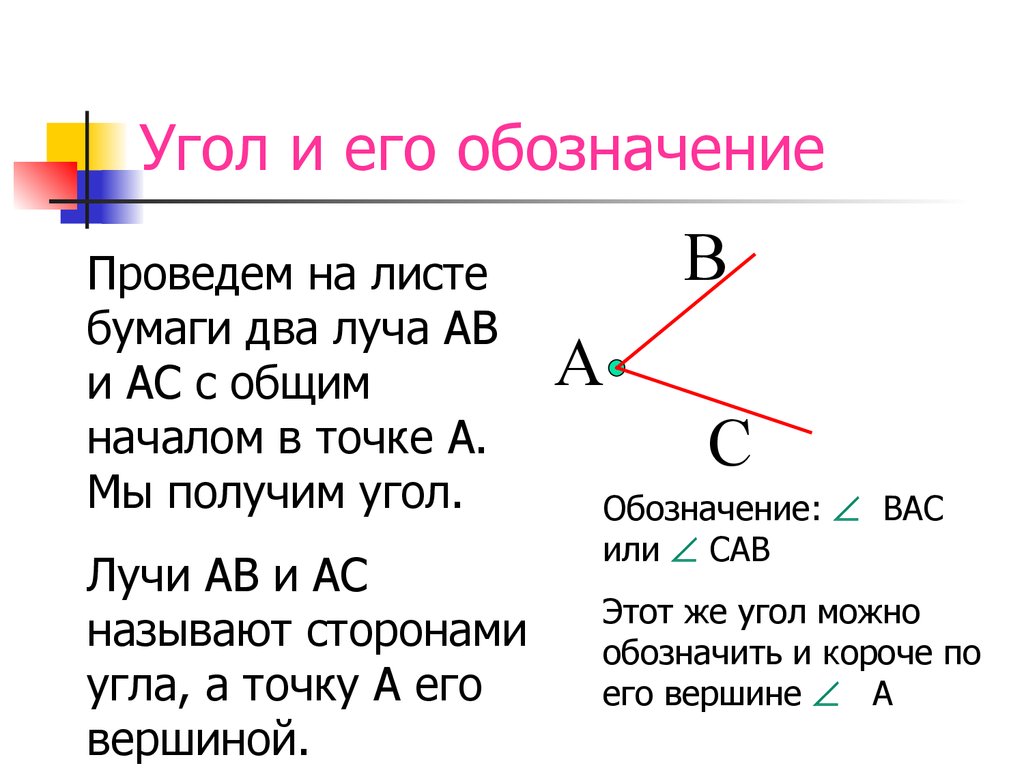
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.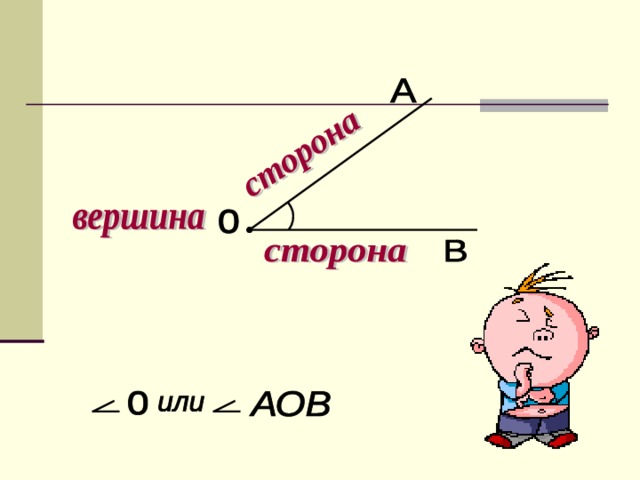
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Определение 6Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Определение 8Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Определение 9Минутой называют одну шестидесятую часть градуса.
Определение 10Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:
1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .
Определение 11Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.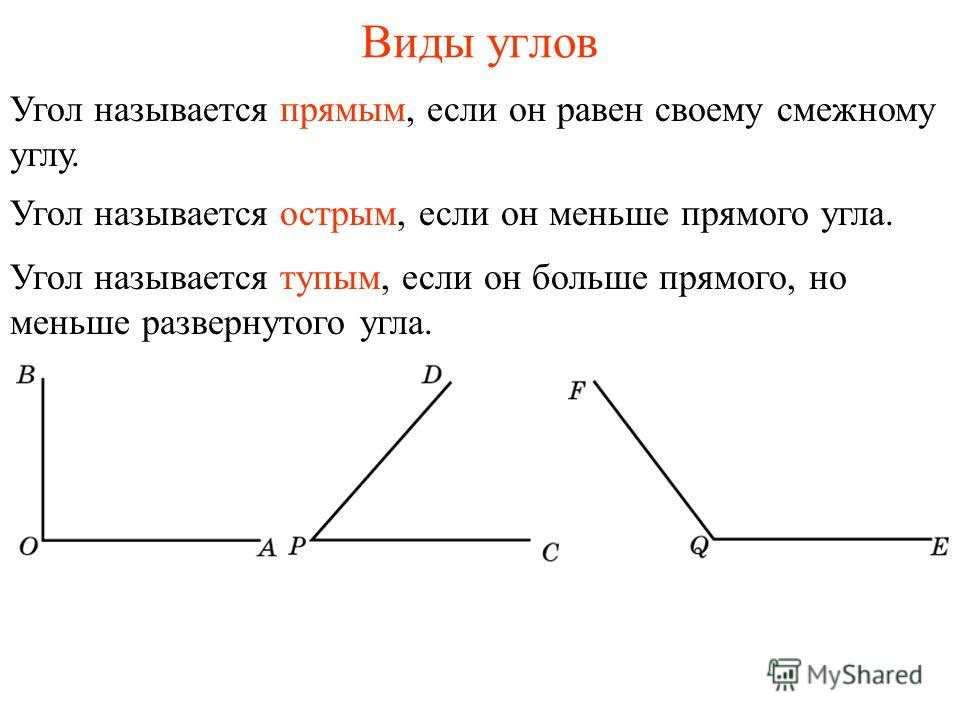
Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.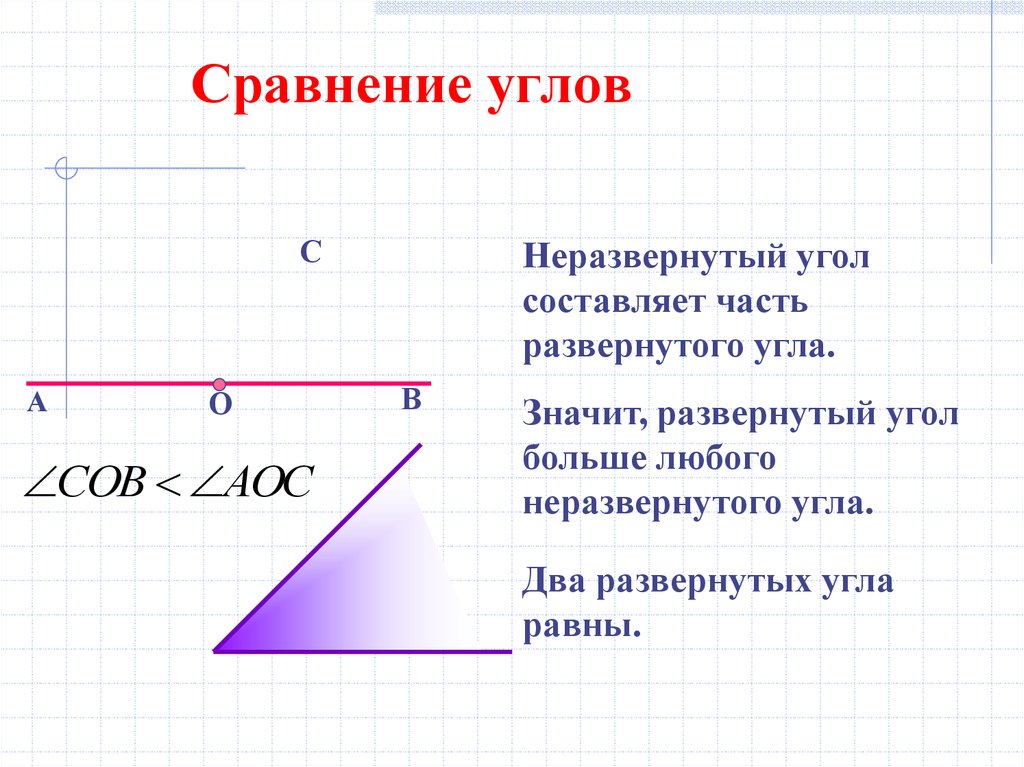
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.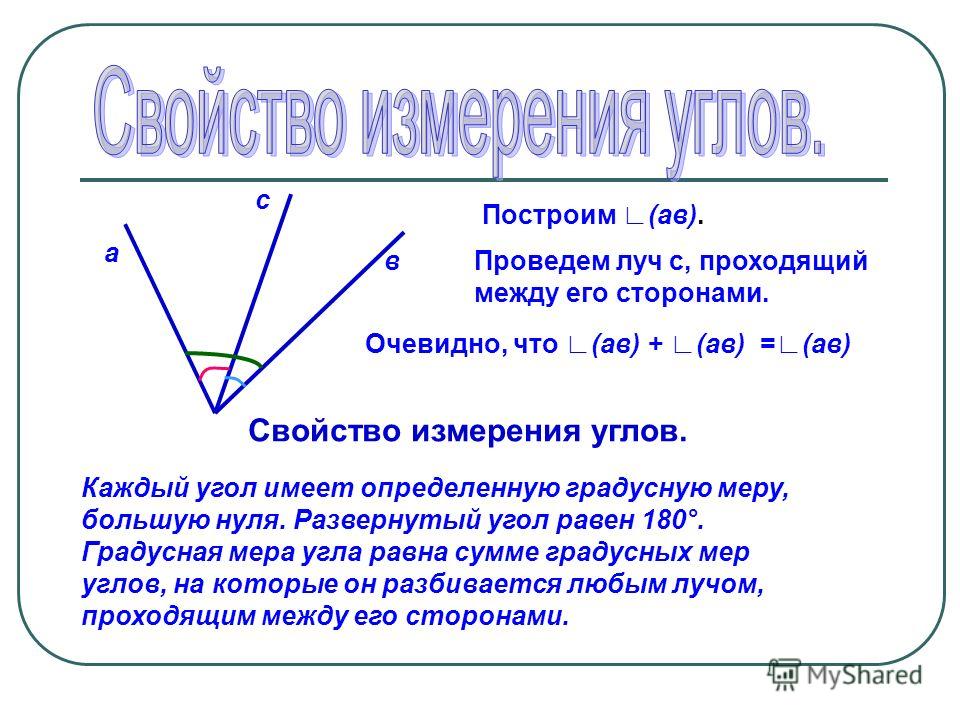
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Решение задач
от 1 дня / от 150 р.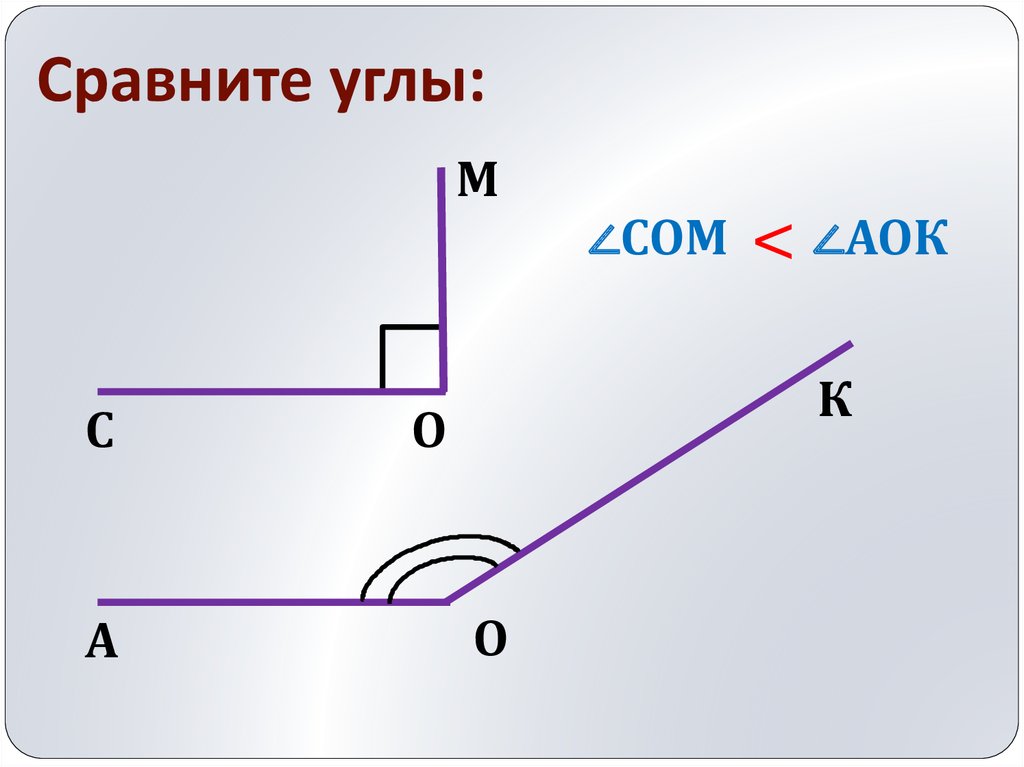 Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Какой угол называют развернутым. Угол называется развернутым, если его стороны лежат на одной прямой
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки.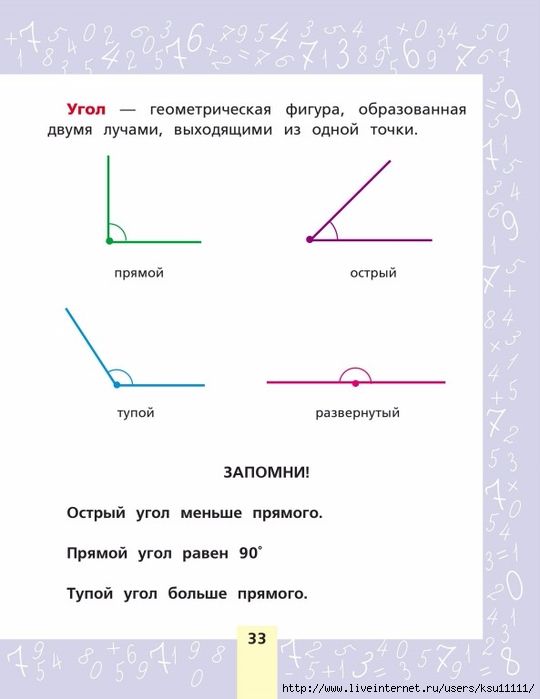 В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.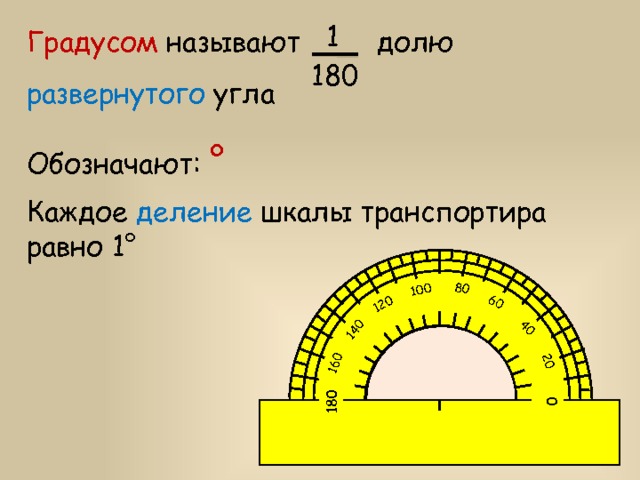
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
«Основные понятия геометрии» — Признак равенства треугольника. Отрезки. Геометрия. Смежные и вертикальные углы. Построение параллельных прямых. Построение треугольника. Выводы. Прямые параллельны. Вершины. Простейшие геометрические фигуры.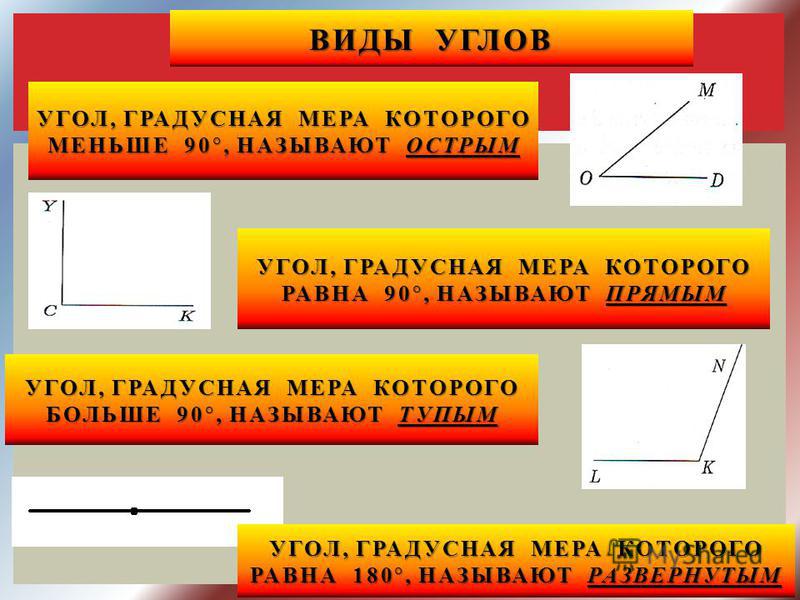 Какая фигура называется треугольником. Равные отрезки имеют равные длины. Угол – это геометрическая фигура, которая состоит из точки и двух лучей.
Какая фигура называется треугольником. Равные отрезки имеют равные длины. Угол – это геометрическая фигура, которая состоит из точки и двух лучей.
«Геометрия в таблицах» — Координаты точки и координаты вектора в пространстве Скалярное произведение векторов в пространстве Движение Цилиндр Конус Сфера и шар Объем прямоугольного параллелепипеда Объем прямой призмы и цилиндра Объем наклонной призмы Объем пирамиды Объем конуса Объем шара и площадь сферы. Таблицы геометрия.
«Геометрия 8 класс» — Каждое утверждение опирается на уже доказанные. У любого здания есть фундамент. Понятие теоремы. Аксиома -утверждение, истинность которых принимается без доказательств. Каждое математическое утверждение, получаемое путем логического доказательства, есть теорема. Так перебирая теоремы, можно добраться до аксиом.
«Геометрия это наука» — Геометрия состоит из двух разделов: планиметрии и стереометрии. Какая геометрическая фигура была отличительным знаком пифагорейцев? Какую форму, по мнению пифагорейцев, имела вся Вселенная? Ответ: 580 – 500 гг. до н. эры. Когда существовала Древняя Греция? Введение. Ответ: «Плоскомерие». Объяснение устройства мира пифагорейцы тесно связывали с геометрией.
до н. эры. Когда существовала Древняя Греция? Введение. Ответ: «Плоскомерие». Объяснение устройства мира пифагорейцы тесно связывали с геометрией.
«Геометрические термины» — Конус. Пирамида. Радиус и центр. Диагональ. Геометрия. Квадрат. Ромб. Куб. Трапеция. Возникновение геометрических терминов. Точка. Линия. Цилиндр. Гипотенуза и катет. Сфера. Призма. Из истории геометрических терминов.
«Что изучает геометрия» — Слово «параллельный» происходит от греческого «параллелос» — идти рядом. История геометрии. Преобразования в основном ограничивались подобием. L=(Р1+Р2)/2 L – длина окружности Р1 — периметр большого квадрата Р2 — периметр малого квадрата. Vпрям. Геометрия в Древней Греции. Муза геометрии, Лувр. Мы узнаем откуда пришла, и какой раньше была геометрия.
Всего в теме 24 презентации
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.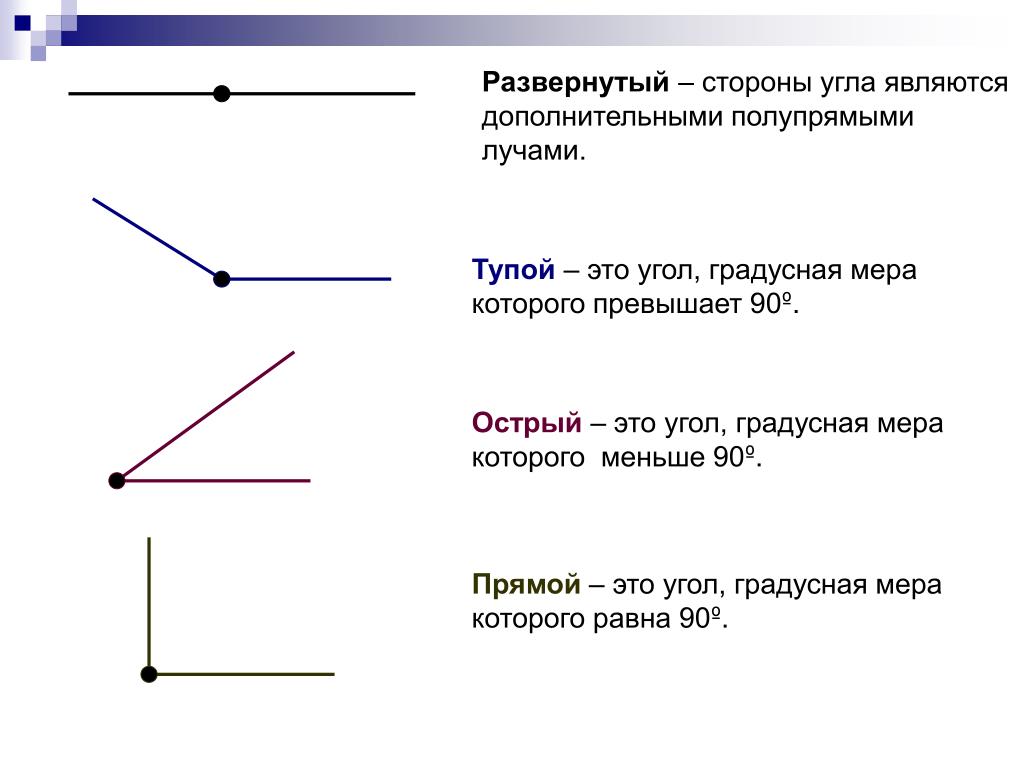
1 оборот = 2π радианам = 360° = 400 градам .
В морской терминологии углы обозначаются румбами .
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation . 2010 .
Смотреть что такое «Развернутый угол» в других словарях:
Угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
угол — ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… …
Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми.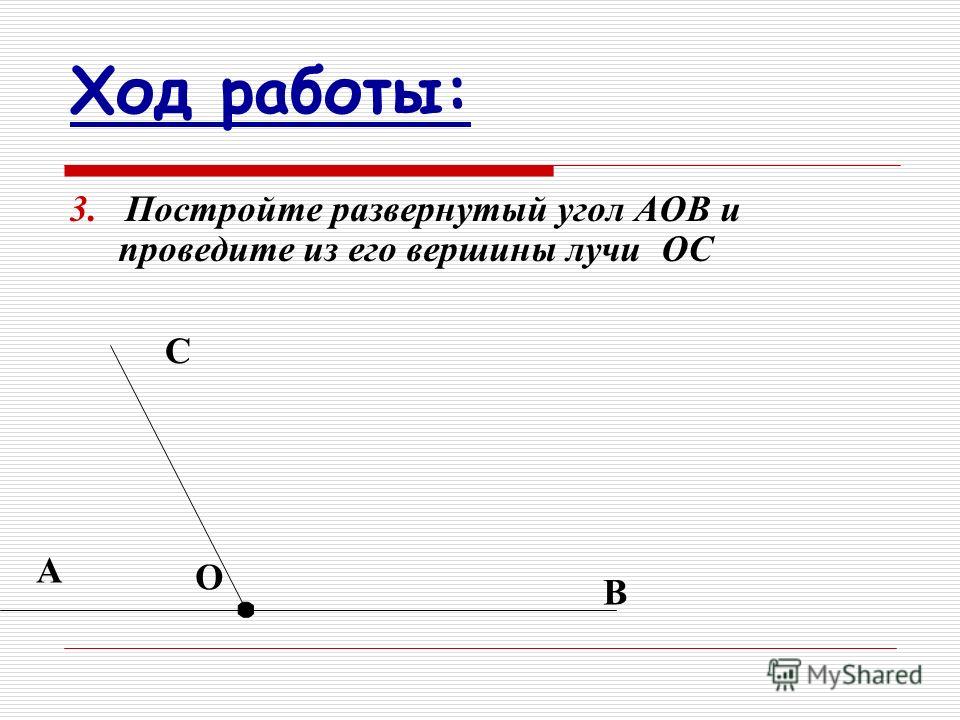 УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия
Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь
Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия
поперек — ▲ под углом максимум, косой угол поперечный.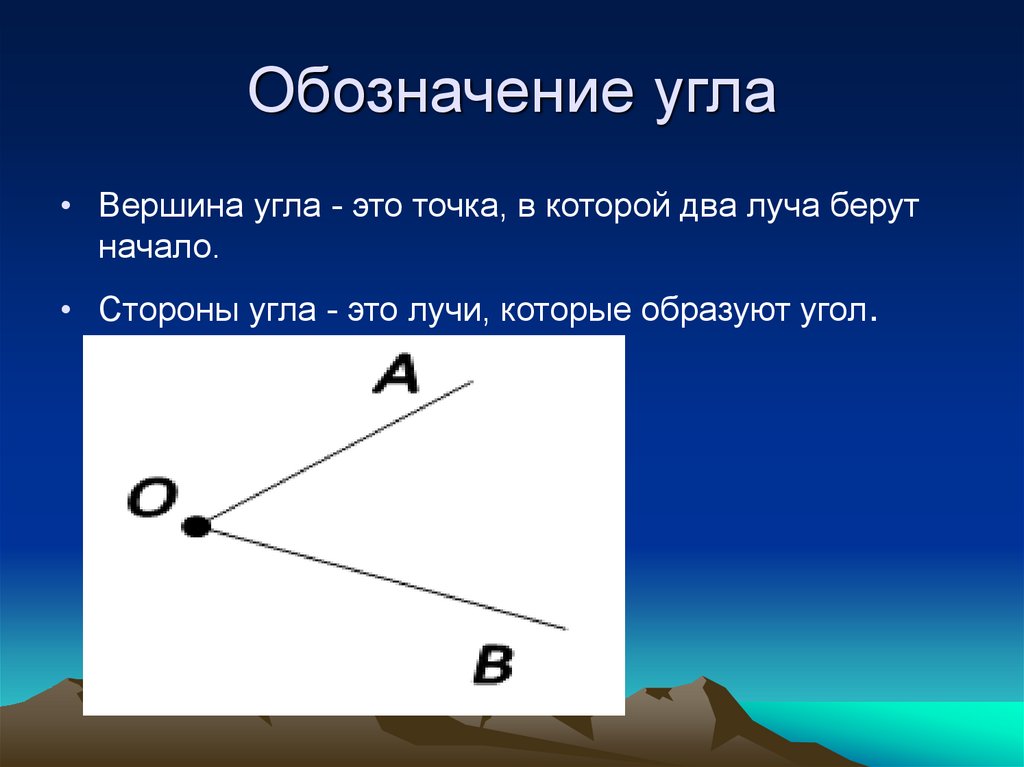 поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
градус — а, м. 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия
Что такое угол?
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160).
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.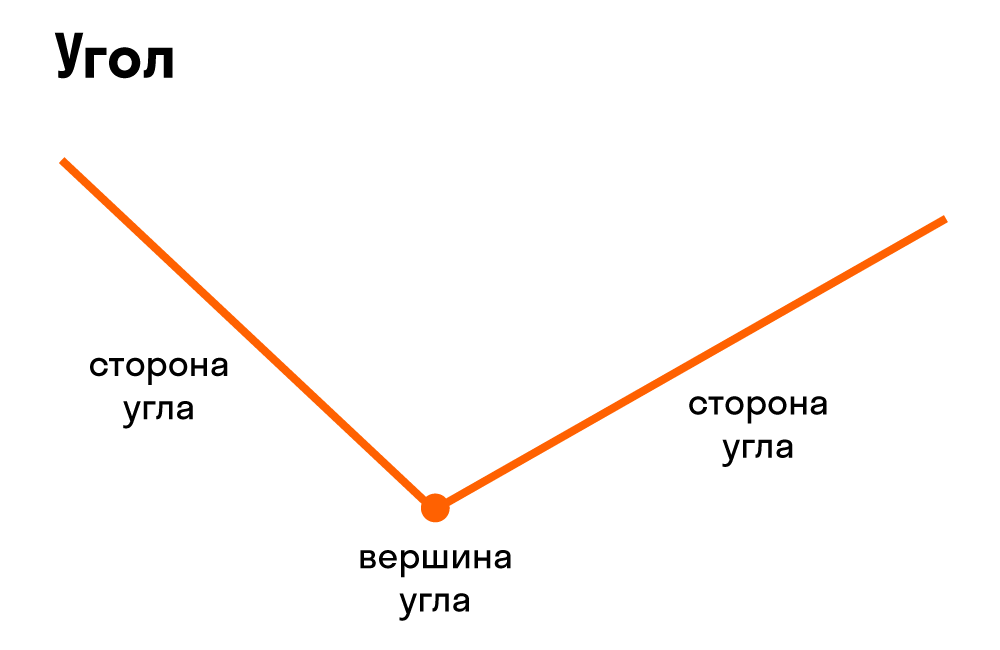
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
Например, вместо «угол АОВ» пишут короче: «угол О».
Вместо слова «угол» пишут знак .
Например, AОВ, O.
На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла.
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
Например, на рисунке 162 ABC = MNK.
Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Пишут: COP
Прямой и развернутый угол
Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164).
164).
Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165).
Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166).
Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.
Прямым углом называют половину развернутого угла.
Чертежный треугольник
Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо:
а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА;
б) провести вдоль второй стороны треугольника луч ОВ.
В результате получим прямой угол АОВ.
Вопросы к теме
1.Что такое угол?
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О.
Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных.
Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла.
А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым.
Свойства развернутого угла
Развернутый угол обладает такими свойствами:
Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую;
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.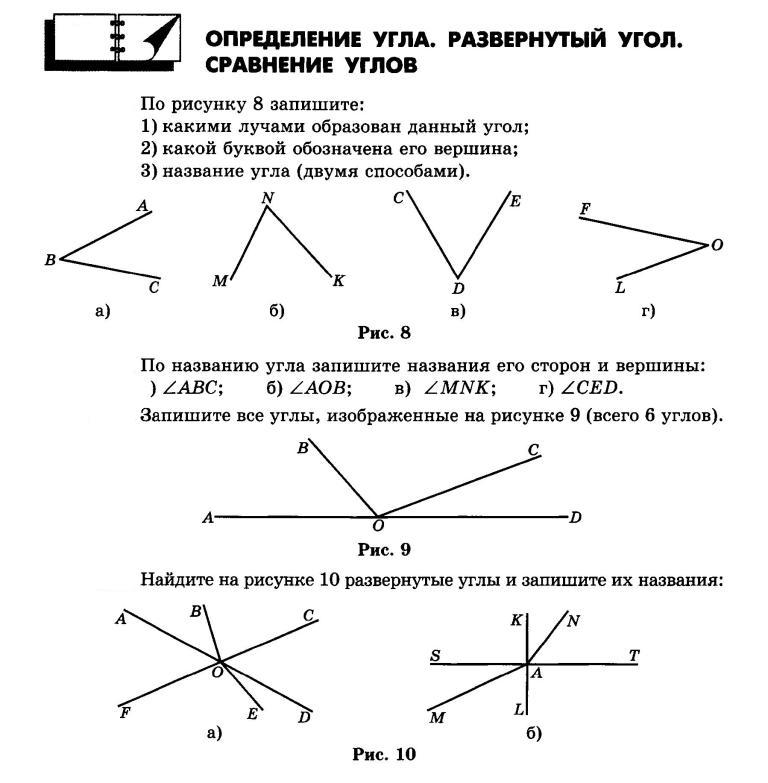
Измерение углов
Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам.
То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид: « ° ».
Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным.
А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. Это и есть развернутый угол.
Это и есть развернутый угол.
Практическое задание
1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения.
1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ?
1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.
1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).
1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях.
1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.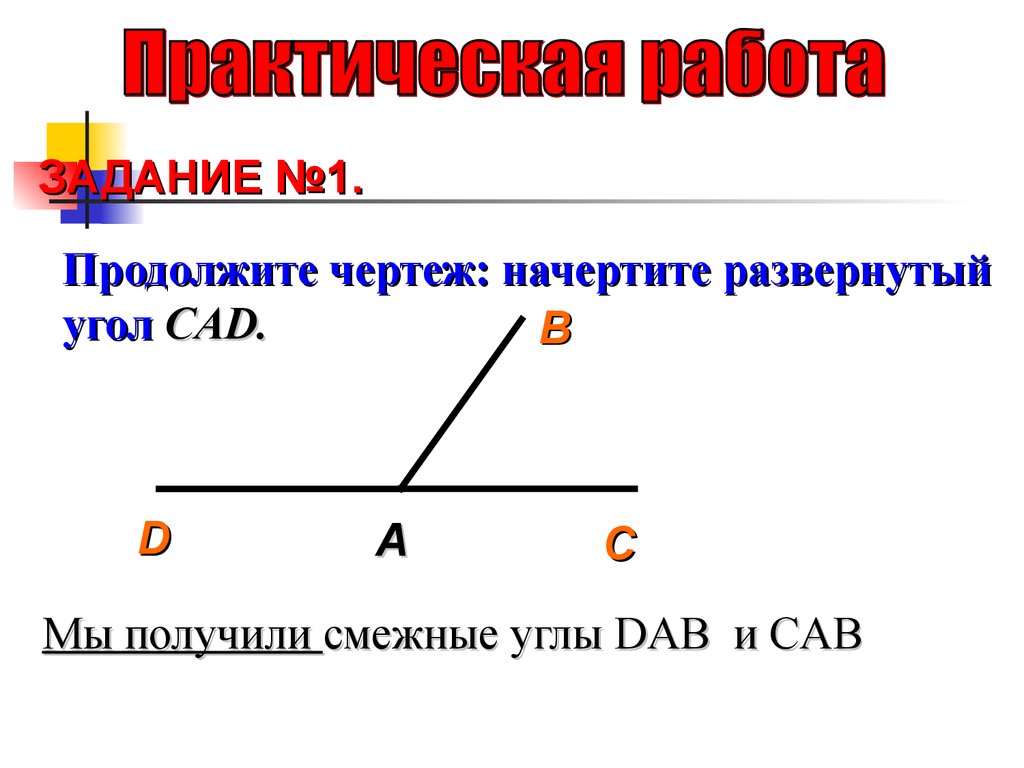
1620. Укажите прямые углы в классной комнате.
а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1.
1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600?
1630. Найдите пропущенное число:
а) 2 5 3 б) 2 3 5
13 6 12 1
2 3? 42?
1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?
1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м.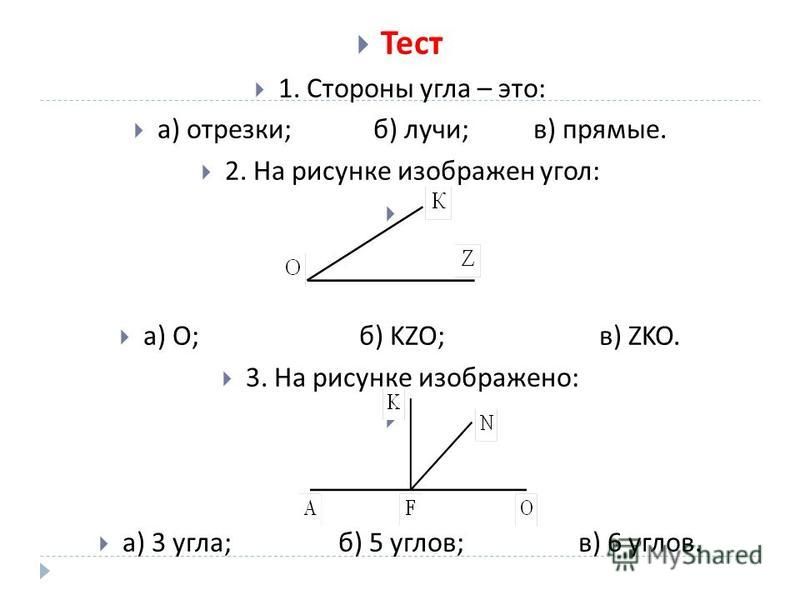 Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
1635. Найдите с помощью микрокалькулятора:
а) 4,5% от 168; в) 28,3% от 569,8;
б) 147,6% от 2500; г) 0,09% от 456 800.
1636. Решите задачу:
1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось?
1637. Выполните действия:
1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85;
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.
1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК?
1640.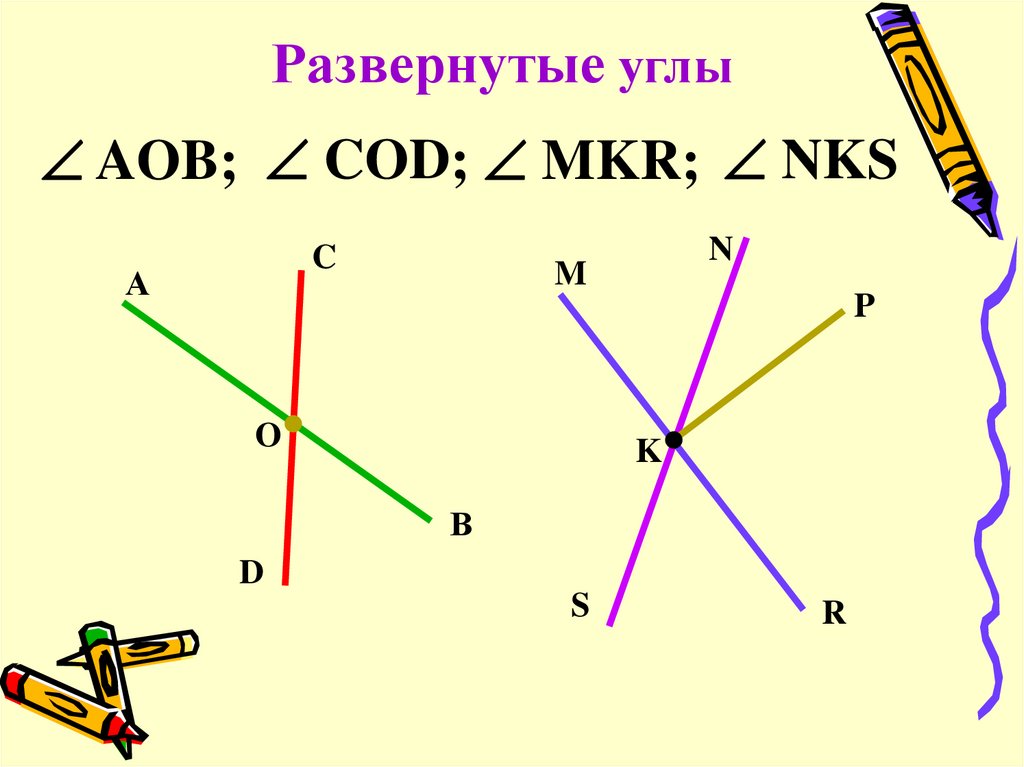 Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.
1642. Найдите значение выражения:
а) 14,791: а + 160,961: b, если а = 100, b = 10;
б) 361,62с + 1848: d, если с = 100, d =100.
1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день?
1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?
1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики?
1646. Найдите, сколько составляют:
а) 1% от тонны; в) 5% от 7 т;
б) 1% от литра; г) 6% от 80 км.
1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т?
1648.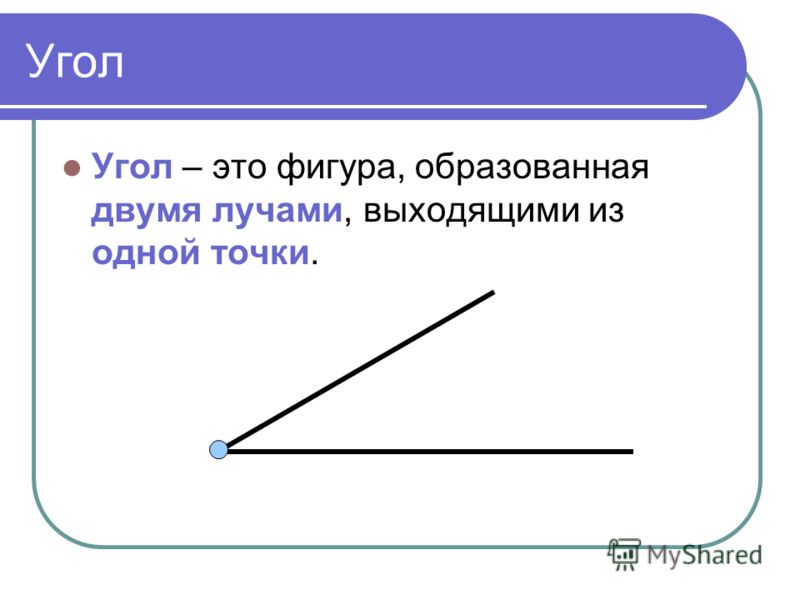 Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.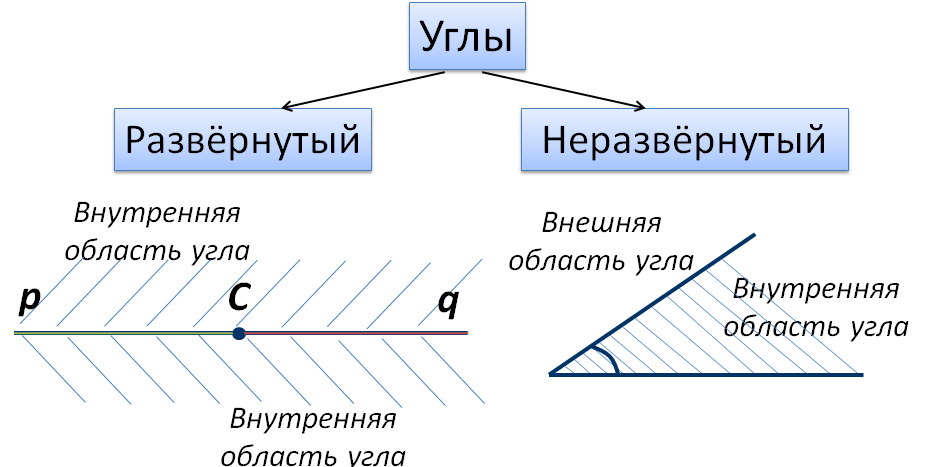
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым .
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение 6
Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7
Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус .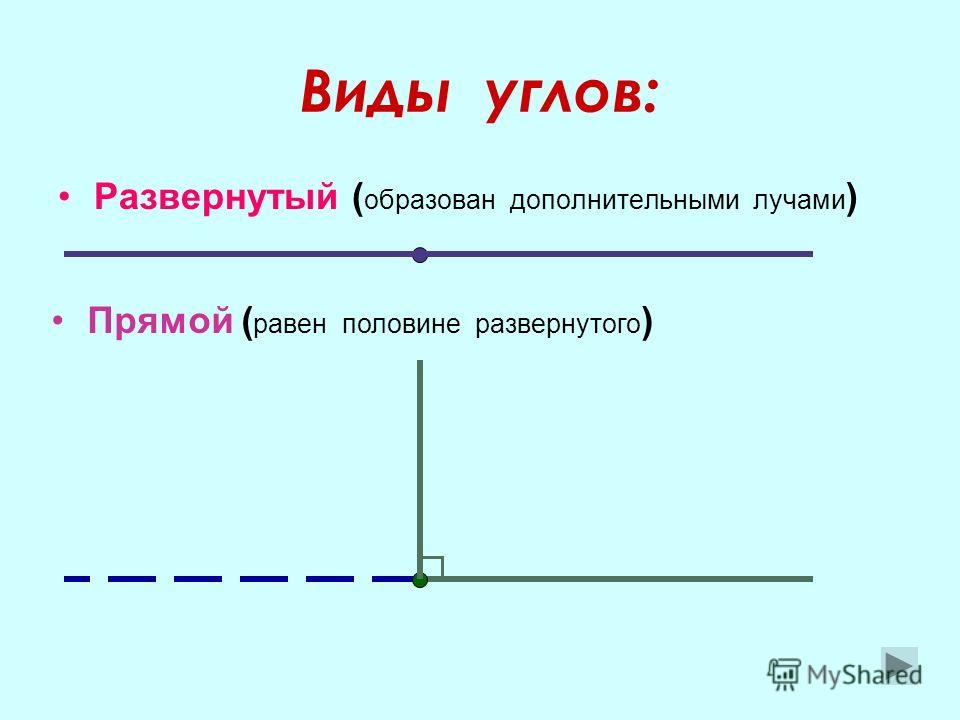
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты.
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение:
1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» .
Определение 11
Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными.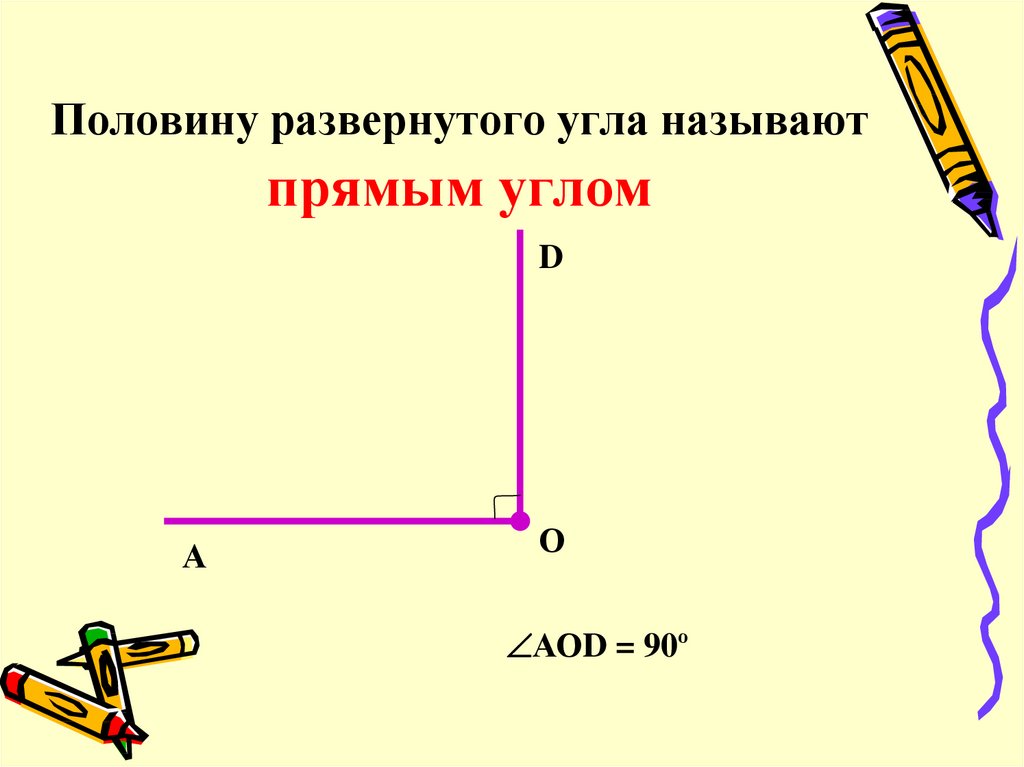 Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла.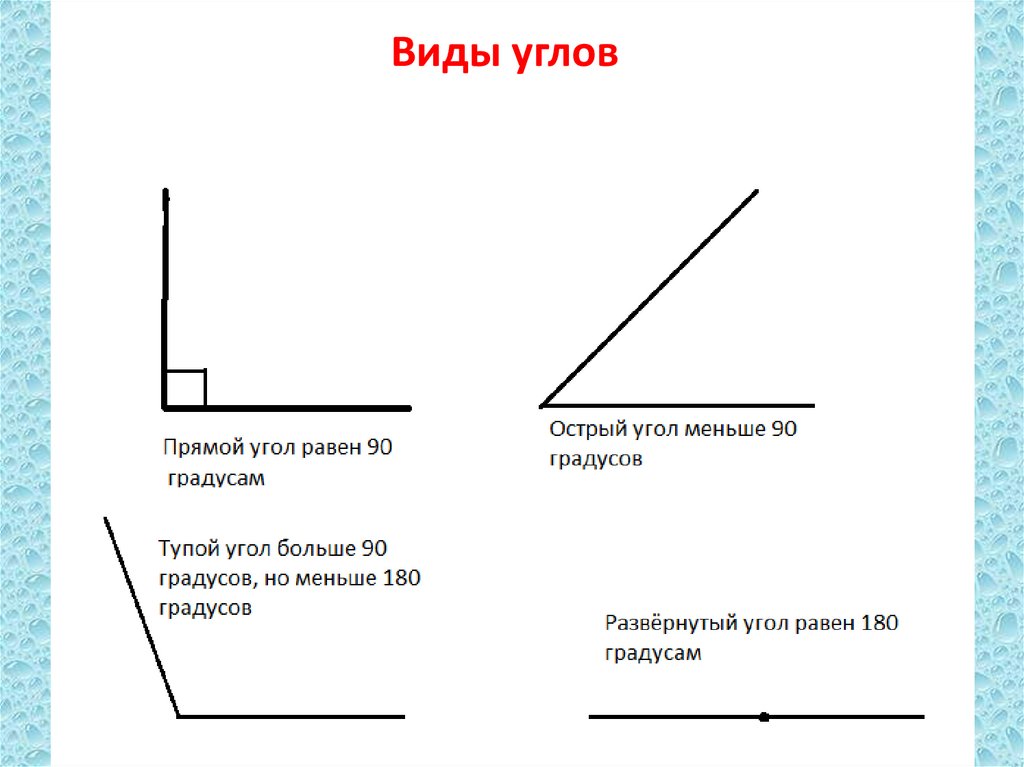 Они считаются подобными.
Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.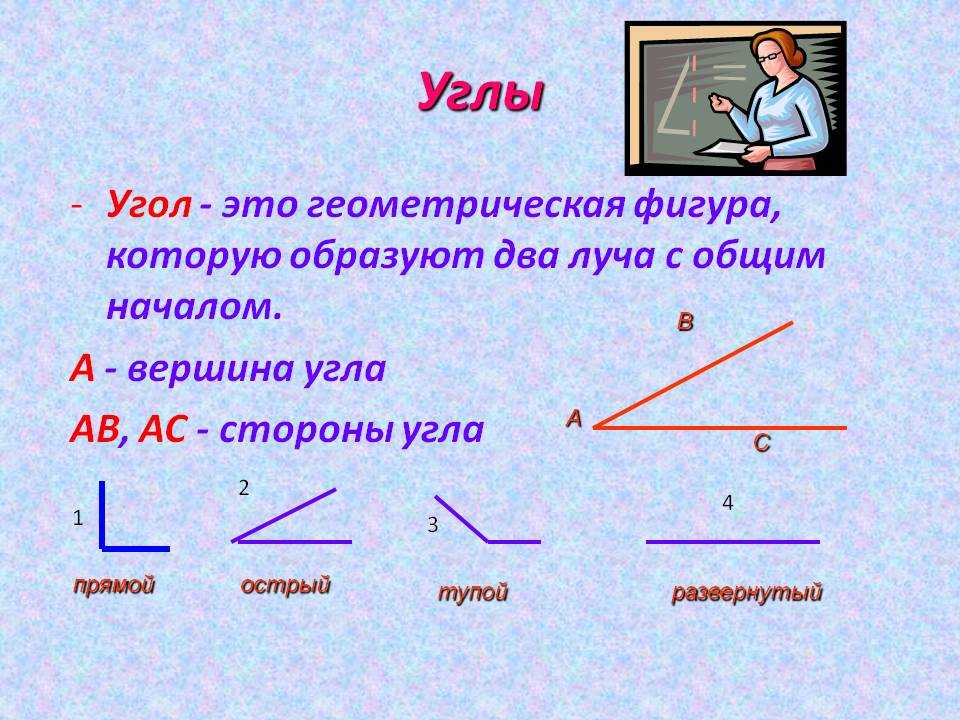
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Прямой, тупой, острый и развернутый угол. Прямой угол. Построение прямого угла Что такое прямой тупой и острый угол
Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.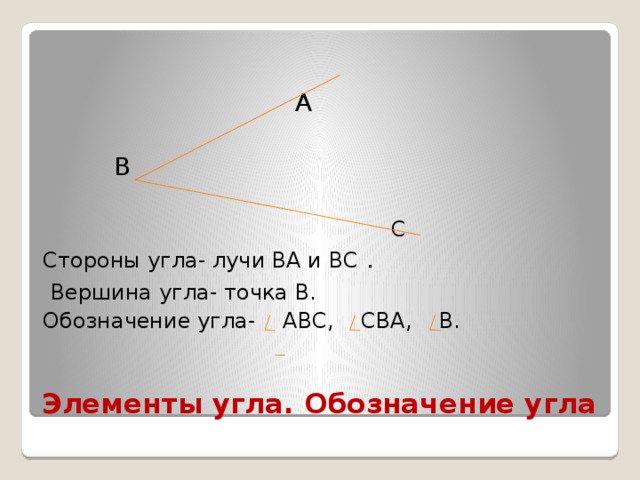
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º.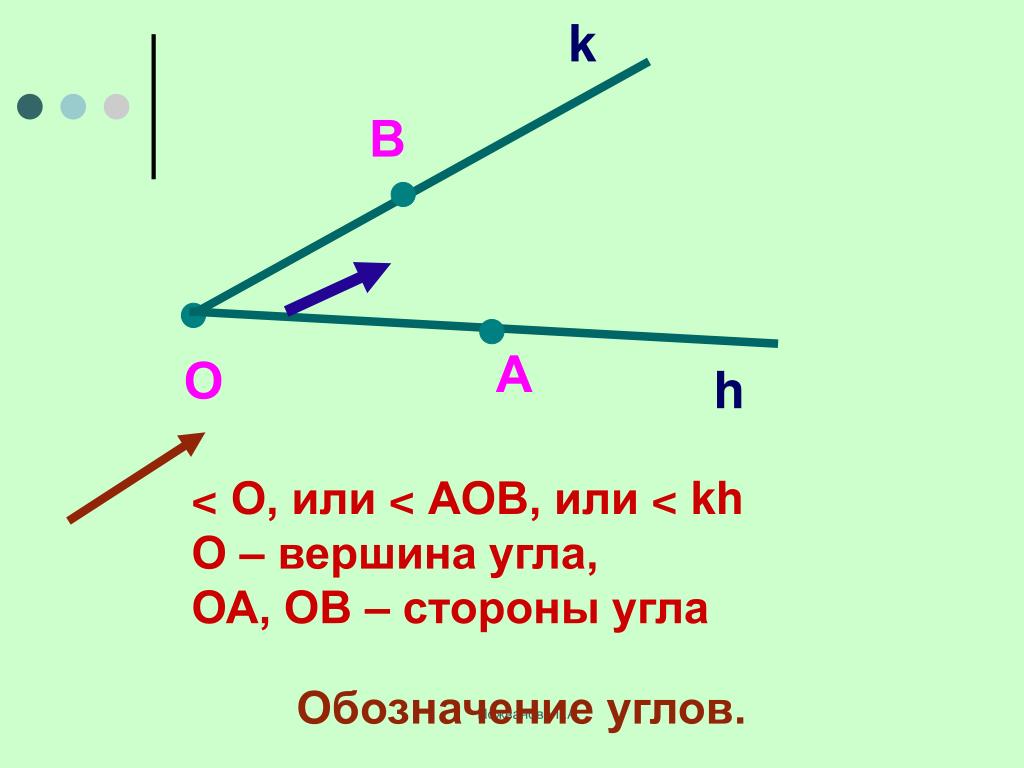 На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине.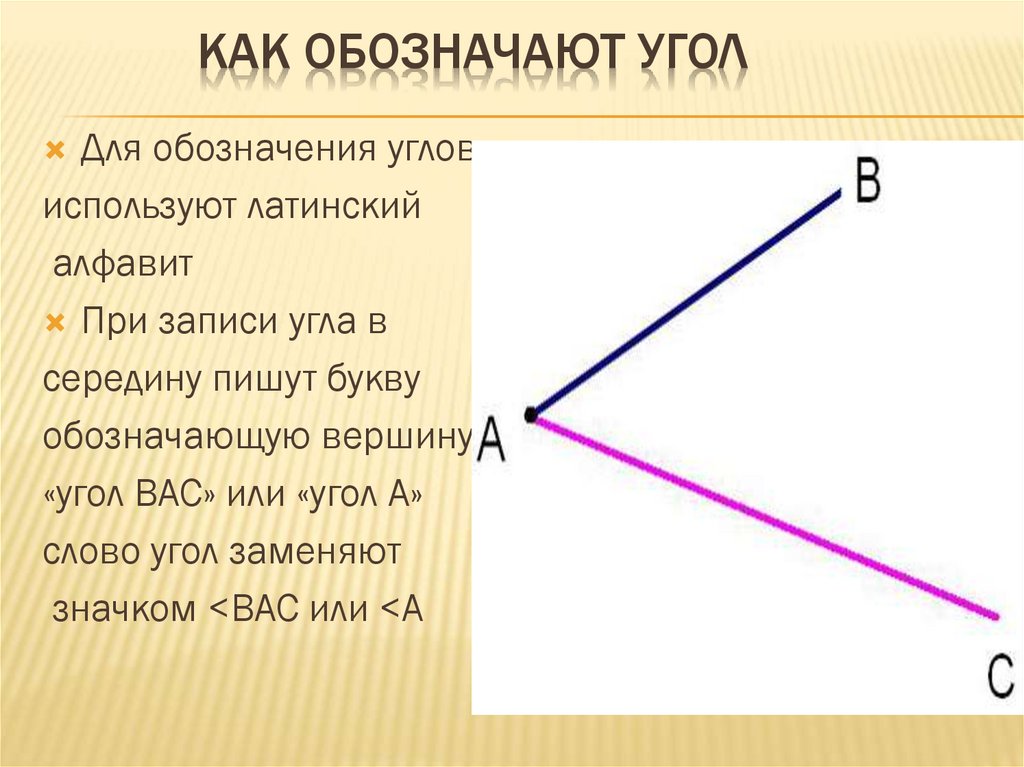 Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым .
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение 6
Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7
Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол.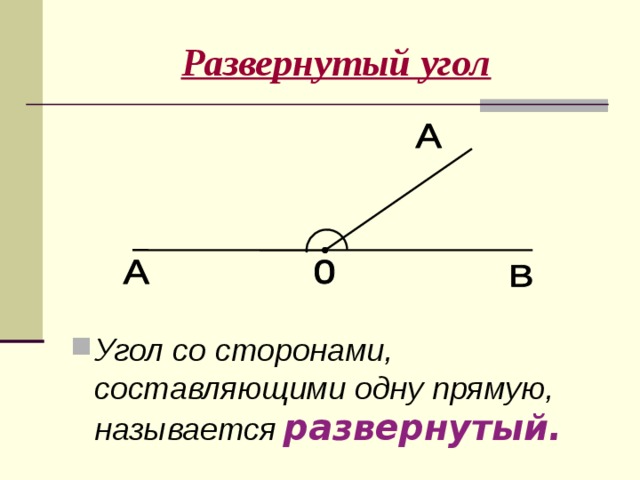 Ниже изображены неравные углы, не совмещенные при наложении.
Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус .
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла.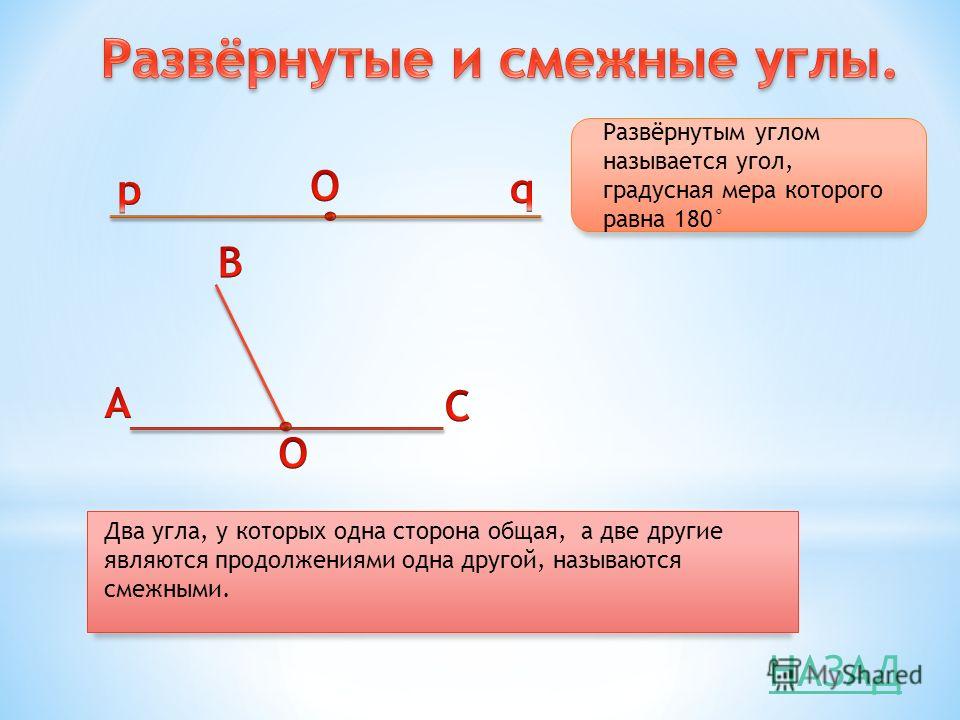 Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты.
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение:
1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» .
Определение 11
Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .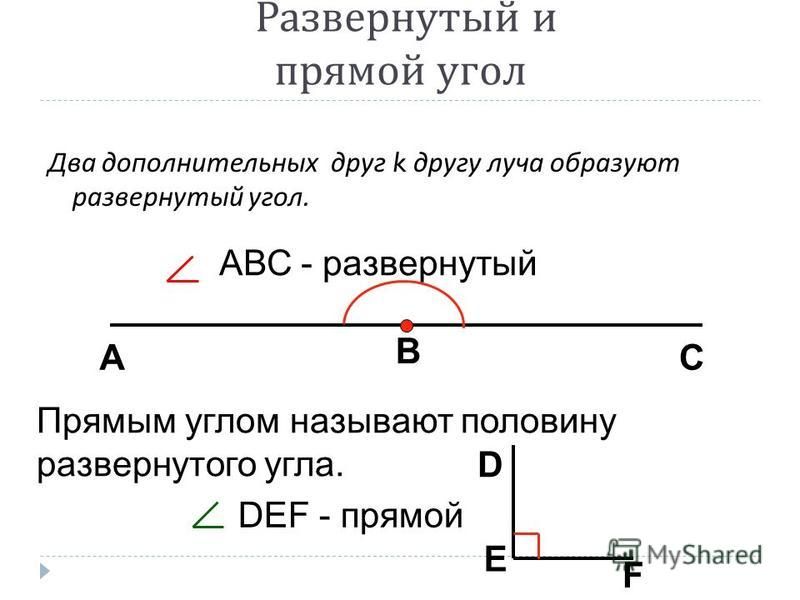
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ.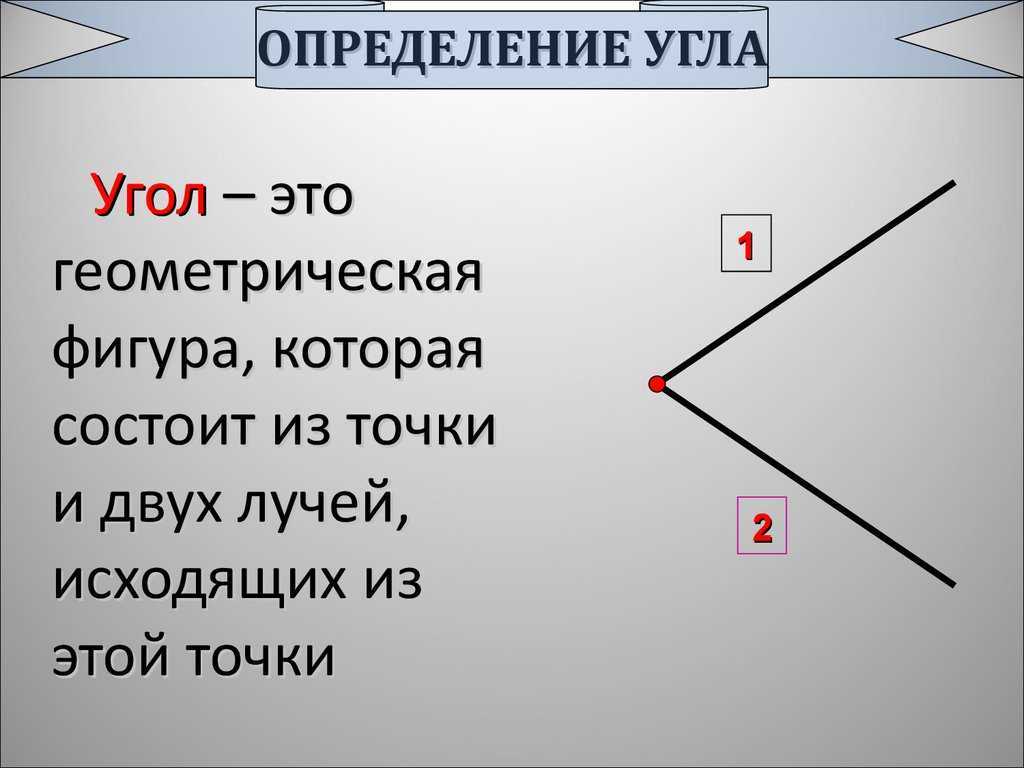 Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.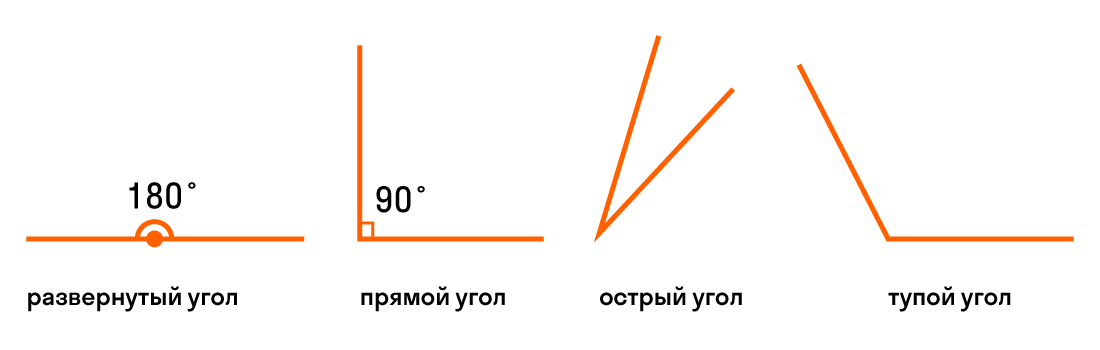
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников.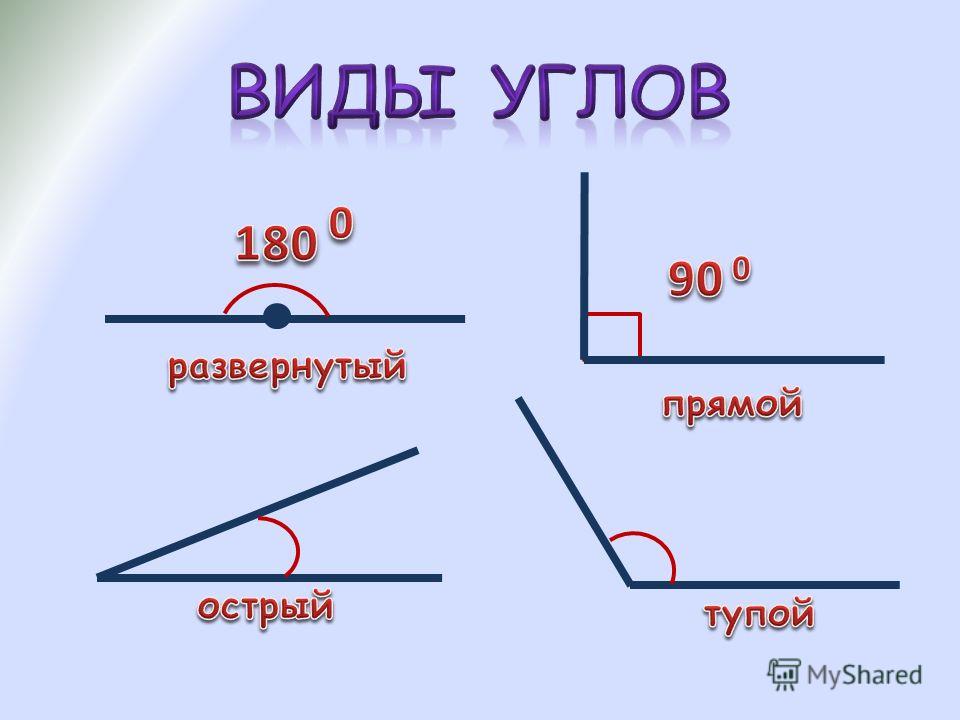 Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
Уголки стальные равнополочные
Размеры и статические параметры уголков стальных равнополочных — британские единицы.

Рекламные ссылки
Свойства стальных уголков равнополочных в имперских единицах указаны ниже.
- Steel Angles — Equal Legs — Metric Units
| Size (in x in) | Dimensions | Static Parameters | |||
|---|---|---|---|---|---|
| Depth — H — (IN) | Толщина — S — (в) | Зона секции (в 2 ) | 118 (в 2 ) 1118 ( 2 ) 1118 ( 2 )) ft) Moment of Inertia — I x — (in 4 ) | ||
| 12 x 12 | 12 | 1 3/8 | 30.9 | 105 | 410.0 |
| 12 | 1 1/4 | 28.3 | 96.4 | 377. 5 5 | |
| 12 | 1 1/8 | 25.6 | 87.2 | 344.1 | |
| 12 | 1 | 22.9 | 77.8 | 310.4 | |
| 10 x 10 | 10 | 1 3/8 | 25.6 | 87.1 | 232.1 |
| 10 | 1 1/4 | 23.5 | 79.9 | 215.1 | |
| 10 | 1 1/8 | 21.2 | 72.3 | 196.2 | |
| 10 | 1 | 19.0 | 64.7 | 177.3 | |
| 10 | 7/8 | 16.7 | 56.9 | 157.6 | |
| 10 | 3/4 | 14.4 | 49.1 | 137.2 | |
| 8 x 8 | 8 | 1 1/8 | 16.7 | 56.9 | 98.0 |
| 8 | 1 | 15. 0 0 | 51.0 | 89.0 | |
| 8 | 7/ 8 | 13.2 | 45.0 | 79.6 | |
| 8 | 3/4 | 11.4 | 38.9 | 69.7 | |
| 8 | 5/8 | 9.6 | 32.7 | 59.4 | |
| 8 | 9/16 | 8.7 | 29.6 | 54.1 | |
| 8 | 1/2 | 7.8 | 26.4 | 48.6 | |
| 6 x 6 | 6 | 1 | 11.0 | 37.4 | 35.5 |
| 6 | 7/8 | 9.7 | 33.1 | 31.9 | |
| 6 | 3/4 | 8.4 | 28.7 | 28.2 | |
| 6 | 5/8 | 7.1 | 24.2 | 24.2 | |
| 6 | 9/16 | 6. 4 4 | 21.9 | 22.1 | |
| 6 | 1/2 | 5.8 | 19.6 | 19.9 | |
| 6 | 7/16 | 5.1 | 17.2 | 17.7 | |
| 6 | 3/8 | 4.4 | 14.9 | 15.4 | |
| 6 | 5/16 | 3.7 | 12.4 | 13.0 | |
| 5 x 5 | 5 | 7/8 | 8.0 | 27.2 | 17.8 |
| 5 | 3/4 | 6.9 | 23.6 | 15.7 | |
| 5 | 5/8 | 5.9 | 20.0 | 13.6 | |
| 5 | 1/2 | 4.8 | 16.2 | 11.3 | |
| 5 | 7/16 | 4.2 | 14.3 | 10.0 | |
| 5 | 3/8 | 3. 6 6 | 12.3 | 8.74 | |
| 5 | 5/16 | 3.0 | 10.3 | 7.42 | |
| 4 x 4 | 4 | 3/4 | 5.4 | 18.5 | 7.67 |
| 4 | 5/8 | 4.6 | 15.7 | 6.66 | |
| 4 | 1/2 | 3.8 | 12.8 | 5.56 | |
| 4 | 7/16 | 3.3 | 11.3 | 4.97 | |
| 4 | 3/8 | 2.9 | 9.8 | 4.36 | |
| 4 | 5. 2 | 1/2 | 3.3 | 11.1 | 3.64 |
| 3 1/2 | 7/16 | 2.9 | 9.8 | 3.26 | |
| 3 1/2 | 3/8 | 2,5 | 8,5 | 2.87 | |
| 3 1/2 | 5/16 | 2. 1 1 | 7.2 | 2.45 | |
| 3 1/2 | 1/4 | 1.7 | 5.8 | 2.01 | |
| 3 x 3 | 3 | 1/2 | 2.75 | 9.4 | 2.22 |
| 3 | 7/16 | 2.43 | 8.3 | 1.99 | |
| 3 | 3/8 | 2.11 | 7.2 | 1.76 | |
| 3 | 5/16 | 1.78 | 6.1 | 1.51 | |
| 3 | 1/4 | 1.44 | 4.9 | 1.24 | |
| 3 | 3/16 | 1.09 | 3.7 | 0.96 | |
| 2 1/2 x 2 1/2 | 2 1/2 | 1/2 | 2.25 | 7.7 | 1.23 |
| 2 1/2 | 3/8 | 1.73 | 5.9 | 0.98 | |
| 2 1/2 | 5/16 | 1. 46 46 | 5.0 | 0.85 | |
| 2 1/2 | 1/4 | 1.19 | 4.1 | 0.70 | |
| 2 1/2 | 3/16 | 0.90 | 3.1 | 0.55 | |
| 2 x 2 | 2 | 3/8 | 1.36 | 4.7 | 0.48 |
| 2 | 5/16 | 1.15 | 3.9 | 0.42 | |
| 2 | 1/4 | 0.94 | 3.2 | 0.35 | |
| 2 | 3/16 | 0.72 | 2.4 | 0.27 | |
| 2 | 1/8 | 0.48 | 1.7 | 0.19 | |
- 1 in = 25.4 mm
- 1 cm 4 = 10 -8 m = 10 4 mm
- 1 in 4 = 4.16×10 5 mm 4 = 41,6 см 4
- 1 см 3 = 10 -6 M 3 = 10 3 MM 3
 x 1/4 — указывает угол 2 дюйма глубокий и широкий — и 1/4 дюйма толщиной .
x 1/4 — указывает угол 2 дюйма глубокий и широкий — и 1/4 дюйма толщиной .Рекламные ссылки
Связанные темы
Связанные документы
Engineering ToolBox — Расширение SketchUp — 3D-моделирование онлайн!
Добавляйте стандартные и настраиваемые параметрические компоненты, такие как балки с полками, пиломатериалы, трубопроводы, лестницы и т. д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, интересными и бесплатными приложениями SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!
Перевести
О Engineering ToolBox!
Мы не собираем информацию от наших пользователей. В нашем архиве сохраняются только электронные письма и ответы. Файлы cookie используются только в браузере для улучшения взаимодействия с пользователем.
Некоторые из наших калькуляторов и приложений позволяют сохранять данные приложения на локальном компьютере. Эти приложения будут — из-за ограничений браузера — отправлять данные между вашим браузером и нашим сервером. Мы не сохраняем эти данные.
Эти приложения будут — из-за ограничений браузера — отправлять данные между вашим браузером и нашим сервером. Мы не сохраняем эти данные.
Google использует файлы cookie для показа нашей рекламы и обработки статистики посетителей. Пожалуйста, прочитайте Конфиденциальность и условия Google для получения дополнительной информации о том, как вы можете контролировать показ рекламы и собираемую информацию.
AddThis использует файлы cookie для обработки ссылок на социальные сети. Пожалуйста, прочитайте AddThis Privacy для получения дополнительной информации.
Реклама в ToolBox
Если вы хотите продвигать свои товары или услуги в Engineering ToolBox — используйте Google Adwords. Вы можете настроить таргетинг на Engineering ToolBox с помощью управляемых мест размещения AdWords.
Citation
Эту страницу можно цитировать как
- Engineering ToolBox, (2008). Стальные уголки — равнополочные . [онлайн] Доступно по адресу: https://www.
 engineeringtoolbox.com/steel-angles-d_1322.html [дата доступа, мес. год].
engineeringtoolbox.com/steel-angles-d_1322.html [дата доступа, мес. год].
Изменить дату доступа.
. .
закрыть
Таблица размеров уголков из конструкционной стали Таблица A36
AISC Таблица размеров уголков из конструкционной стали Таблица A36
Конструкционные материалы Меню
Размеры конструкционной угловой стали AISC A36. В таблице ниже приведены размеры и размеры формы, вес на фут и площадь поперечного сечения для конструкционного стального уголка на АИСК .
Размер ноги 1
x | Вес (фунт/фут) | Площадь (в 2 ) |
. | .375 | .11 |
0,625 х 0,625 х 0,125 | .481 | .141 |
0,750 х 0,750 х 0,125 | .588 | .173 |
0,875 х 0,875 х 0,125 | .694 | ..204 |
1,00 х 1,00 х 0,125 | . | .235 |
1,00 х 1,00 х 0,188 | 1,162 | .342 |
1,00 х 1,00 х 0,250 | 1,492 | .438 |
1,125 х 1,125 х 0,125 | 1,013 | .298 |
1,125 х 1,125 х 0,188 | 1,482 | . |
| 1,25 х 1,25 х .250 | 1,917 | .563 |
| 1,50 х 1,50 х 0,125 | 1,226 | .360 |
1,50 х 1,50 х 0,188 | 1,802 | .53 |
1,50 х 1,50 х .250 | 2,342 | . |
1,50 х 1,50 х .375 | 3.352 | .985 |
1,750 х 1,750 х 0,125 | 1.439 | .423 |
1,750 х 1,750 х 0,188 | 2.122 | .623 |
1,750 х 1,750 х .250 | 2,768 | . |
| 2,00 х 2,00 х 0,125 | 1,671 | .491 |
2,00 х 2,00 х 0,188 | 2,462 | .723 |
2,00 х 2,00 х .250 | 3.213 | .944 |
2,00 х 2,00 х .313 | 3,95 | 1. |
2,00 х 2,00 х .375 | 4.649 | 1,366 |
| 2,50 х 250 .188 | 3.102 | .911 |
2,50 х 2,50 х .250 | 4.064 | 1.194 |
| 2,50 х 2,50 х 0,313 | 5.015 | 1,474 |
2,50 х 2,50
х . | 5.925 | 1.741 |
2,50 х 2,50 х .500 | 7,68 | 2,257 |
3,00 х 3,00 х 0,188 | 3,699 | 1,087 |
| 3,00 х 3,00 х .250 | 4.872 | 1.432 |
| 3,00 х 3,00 х 0,313 | 6. 038 038 | 1,774 |
| 3,00 х 3,00 х 0,375 | 7.159 | 2.104 |
| 3,00 х 3,00 х 0,500 | 9.339 | 2,744 |
| 3,50 х 3,50 х .250 | 5,754 | 1,691 |
| 3,50 х 3,50 х 0,313 | 7.134 | 2,096 |
| 3,50 х 3,50 х 0,375 | 8. 466 466 | 2,488 |
| 3,50 х 3,50 х 0,500 | 11.072 | 3,253 |
| 4,00 х 4,00 х .250 | 6.605 | 1,941 |
| 4,00 х 4,00 х 0,313 | 8.200 | 2.409 |
| 4,00 х 4,00 х 0,375 | 9,743 | 2,863 |
| 4,00 х 4,00 х 0,500 | 12. 774 774 | 3,753 |
| 4,00 х 4,00 х 0,625 | 15,698 | 4,613 |
| 4,00 х 4,00 х 0,750 | 18.516 | 5.441 |
| 5,00 х 5,00 х 0,313 | 10.296 | 3,025 |
| 5,00 х 5,00 х 0,375 | 12.261 | 3,603 |
5,00 х 5,00
х . 500 500 | 16.142 | 4,743 |
| 5,00 х 5,00 х 0,625 | 19.918 | 5.853 |
| 5,00 х 5,00 х 0,750 | 23.587 | 6,931 |
| 6.00 х 6.00 х 0,313 | 12.426 | 3,651 |
| 6.00 х 6.00 х 0,375 | 14.813 | 4.353 |
6. 00 х 6.00
х 0,500 00 х 6.00
х 0,500 | 19.546 | 5,743 |
| 6.00 х 6.00 х 0,625 | 24.172 | 7.103 |
| 6.00 х 6.00 х 0,750 | 28,692 | 8.431 |
| 6.00 х 6.00 х 1.000 | 37.412 | 10,993 |
| 8.00 х 8.00 х 0,500 | 26.454 | 7,773 |
8. 00 х 8.00
х 0,625 00 х 8.00
х 0,625 | 32.782 | 9,633 |
| 8.00 х 8.00 х 0,750 | 39.004 | 11.461 |
| 8.00 х 8.00 х 1.000 | 51.128 | 15.023 |
Связанные ресурсы:
- Средство просмотра свойств форм AISC Ultimate Structural Shapes
- AISC, угол равный ASTM Нога ( алюминий )
- AISC, канал ASTM, Стандарт (алюминий)
AISC, швеллер ASTM (сталь)
- AISC, широкий фланец ASTM №1 (сталь)
- AISC, широкий фланец ASTM № 2 (сталь)
- AISC, Фланец ASTM S (сталь)
- AISC, угол ASTM (сталь) №1
- AISC, угол ASTM (сталь) #2
- AISC, угол ASTM неравный Нога (алюминий)
- AISC, двутавровые балки ASTM (Алюминий)
- AISC, угол ASTM Неравная нога ( сталь )
- МАСК, Структурные тройники ASTM, вырезанные из фланца W
Размеры УГЛОВЫХ стальных балок соответствуют европейским стандартам NEN-EN 10025-1 и NEN-EN 10025-2
| | ||
| УГОЛОК В x Ш x Г | вес кг/м | площадь поверхности м2/м |
| 16 х 16 х 3 | 0,704 | 0,061 |
| 20 х 20 х 3 | 0,902 | 0,077 |
| 20 х 20 х 4 | 1,16 | 0,077 |
| 25 х 25 х 3 | 1,14 | 0,097 |
| 25 х 25 х 4 | 1,49 | 0,097 |
| 25 х 25 х 5 | 1,81 | 0,097 |
| 30 х 30 х 3 | 1,39 | 0,116 |
| 30 х 30 х 4 | 1,81 | 0,116 |
| 30 х 30 х 5 | 2,22 | 0,116 |
| 35 х 35 х 3 | 1,63 | 0,136 |
| 35 х 35 х 4 | 2,13 | 0,136 |
| 35 х 35 х 5 | 2,62 | 0,136 |
| 35 х 35 х 6 | 3,09 | 0,136 |
| 40 х 40 х 3 | 1,88 | 0,155 |
| 40 х 40 х 4 | 2,46 | 0,155 |
| 40 х 40 х 5 | 3,03 | 0,155 |
| 40 х 40 х 6 | 3,58 | 0,155 |
| 45 х 45 х 5 | 3,44 | 0,174 |
| 45 х 45 х 6 | 4,07 | 0,174 |
| 50 х 50 х 4 | 3. 11 11 | 0,194 |
| 50 х 50 х 5 | 3,84 | 0,194 |
| 50 х 50 х 6 | 4,55 | 0,194 |
| 50 х 50 х 7 | 5,25 | 0,194 |
| 50 х 50 х 8 | 5,93 | 0,194 |
| 50 х 50 х 9 | 6,60 | 0,194 |
| 55 х 55 х 6 | 5,05 | 0,213 |
| 55 х 55 х 8 | 6,58 | 0,213 |
| 60 х 60 х 6 | 5,53 | 0,233 |
| 60 х 60 х 7 | 6,38 | 0,233 |
| 60 х 60 х 8 | 7,22 | 0,233 |
| 60 х 60 х 10 | 8,85 | 0,233 |
| 65 х 65 х 6 | 6,02 | 0,252 |
| 65 х 65 х 7 | 6,96 | 0,252 |
| 65 х 65 х 8 | 7,88 | 0,252 |
| 65 х 65 х 9 | 8,80 | 0,252 |
| 70 х 70 х 7 | 7,52 | 0,272 |
| 70 х 70 х 8 | 8,56 | 0,272 |
| 70 х 70 х 9 | 9,50 | 0,272 |
| 70 х 70 х 10 | 10,5 | 0,272 |
| УГОЛОК В x Ш x Г | вес кг/м | площадь поверхности м2/м |
| | ||
| УГОЛОК В x Ш x Г | вес кг/м | площадь поверхности м2/м |
| 75 х 75 х 6 | 6,98 | 0,290 |
| 75 х 75 х 7 | 8,09 | 0,291 |
| 75 х 75 х 8 | 9,17 | 0,291 |
| 75 х 75 х 10 | 11,3 | 0,291 |
| 75 х 75 х 12 | 13,3 | 0,291 |
| 80 х 80 х 8 | 9,81 | 0,311 |
| 80 х 80 х 10 | 12,1 | 0,311 |
| 80 х 80 х 12 | 14,3 | 0,311 |
| 90 х 90 х 8 | 11,1 | 0,351 |
| 90 х 90 х 9 | 12,4 | 0,351 |
| 90 х 90 х 10 | 13,7 | 0,351 |
| 90 х 90 х 12 | 16,2 | 0,351 |
| 100 х 100 х 8 | 12,4 | 0,390 |
| 100 х 100 х 10 | 15,3 | 0,390 |
| 100 х 100 х 12 | 18,2 | 0,390 |
| 100 х 100 х 14 | 21,0 | 0,390 |
| 100 х 100 х 15 | 22,3 | 0,390 |
| 110 х 110 х 10 | 16,9 | 0,430 |
| 110 х 110 х 12 | 20,1 | 0,430 |
| 110 х 110 х 14 | 23,2 | 0,430 |
| 120 х 120 х 10 | 18,5 | 0,469 |
| 120 х 120 х 11 | 20,3 | 0,469 |
| 120 х 120 х 12 | 22,0 | 0,469 |
| 120 х 120 х 15 | 27,1 | 0,469 |
| 130 х 130 х 12 | 24,0 | 0,508 |
| 130 х 130 х 14 | 27,8 | 0,508 |
| 140 х 140 х 13 | 28,0 | 0,547 |
| 140 х 140 х 15 | 32,0 | 0,547 |
| 150 х 150 х 12 | 27,9 | 0,586 |
| 150 х 150 х 14 | 32,2 | 0,586 |
| 150 х 150 х 15 | 34,4 | 0,586 |
| 150 х 150 х 18 | 40,8 | 0,586 |
| 160 х 160 х 15 | 36,8 | 0,625 |
| 180 х 180 х 16 | 44,3 | 0,705 |
| 180 х 180 х 18 | 49,5 | 0,705 |
| 200 х 200 х 16 | 49,4 | 0,785 |
| 200 х 200 х 18 | 55,3 | 0,785 |
| 200 х 200 х 20 | 61,1 | 0,785 |
| 200 х 200 х 24 | 72,5 | 0,785 |
| УГОЛОК В x Ш x Г | вес кг/м | площадь поверхности м2/м |
Размеры указаны в миллиметрах, если не указано иное.
Свойства поперечного сечения угла (L) | Calcresource
Соглашение
-Геометрия
-Момент инерции
-Основные оси
-Момент инерции и изгиба
-Полярный момент инерции L -сечения
-Эластичный раздел Modulus
-пластический модуль сечения
— вокруг оси x
— вокруг оси y
— Радиус инерции
— Формулы сечения уголка (L)
— Связанные страницы
Геометрия
Площадь A и периметр P поперечного сечения угла можно найти по следующим формулам:
\ begin{split} & A & = (h+b-t)t \\ & P & = 2b + 2h \end{split}
Расстояние центра тяжести от левого края сечения x_c и от нижнего края y_c , можно найти, используя первые моменты площади двух катетов: 92\right) \right) \end{split}
У нас есть специальная статья о центроиде сложных областей и о том, как его вычислить. Если вам нужна дополнительная информация, вы можете найти ее здесь.
Момент инерции
Момент инерции углового поперечного сечения можно найти, если всю площадь разделить на три меньшие, A, B, C, как показано на рисунке ниже. Конечную область можно рассматривать как аддитивную комбинацию A+B+C. Тем не менее, более простой расчет может быть достигнут комбинацией (A+C)+(B+C)-C. Кроме того, расчет лучше проводить вокруг нецентроидальных осей x0,y0 с последующим применением теоремы о параллельных осях. 92 \\ & I_{xy} & = I_{x0y0} — A x_c y_c \end{split}
Конечную область можно рассматривать как аддитивную комбинацию A+B+C. Тем не менее, более простой расчет может быть достигнут комбинацией (A+C)+(B+C)-C. Кроме того, расчет лучше проводить вокруг нецентроидальных осей x0,y0 с последующим применением теоремы о параллельных осях. 92 \\ & I_{xy} & = I_{x0y0} — A x_c y_c \end{split}
где x_c расстояние от центра тяжести до оси y0 и x_c расстояние от центра тяжести до оси x0. Выражения для этих расстояний приведены в предыдущем разделе.
Имейте в виду, что оси x, y не являются естественными, L-образное сечение предпочло бы изгибаться, если его не ограничивать. Это будут главные оси, наклоненные относительно геометрических осей x, y, как описано в следующем разделе.
Главные оси
Главные оси — те, для которых произведение инерции I xy поперечного сечения становится равным нулю. Обычно главные оси обозначаются буквами I и II и перпендикулярны друг другу. Моменты инерции, заданные вокруг главных осей, называются главными моментами инерции и являются максимальным и минимальным. В частности, момент инерции вокруг главной оси I максимален, а момент инерции вокруг главной оси II минимален по сравнению с любой другой осью поперечного сечения. Для симметричных сечений главные оси совпадают с осями симметрии. Однако в L-образном сечении нет оси симметрии (за исключением особого случая угла с равными сторонами), и в результате главные оси не видны только при осмотре. Их необходимо вычислить и, в частности, определить их наклон относительно какой-либо удобной геометрической оси (например, x, y). 92} \\ & \tan 2\theta & = -\frac{2I_{xy}}{I_x-I_y} \end{split}
В частности, момент инерции вокруг главной оси I максимален, а момент инерции вокруг главной оси II минимален по сравнению с любой другой осью поперечного сечения. Для симметричных сечений главные оси совпадают с осями симметрии. Однако в L-образном сечении нет оси симметрии (за исключением особого случая угла с равными сторонами), и в результате главные оси не видны только при осмотре. Их необходимо вычислить и, в частности, определить их наклон относительно какой-либо удобной геометрической оси (например, x, y). 92} \\ & \tan 2\theta & = -\frac{2I_{xy}}{I_x-I_y} \end{split}
По определению I_I считается главным главным моментом (максимальным) и I_{ II} второстепенный главный момент (минимальный). Отсюда следует, что: I_I>I_{II}.
Момент инерции и изгиб
Момент инерции (второй момент или площадь) используется в теории балок для описания жесткости балки при изгибе. Изгибающий момент M, приложенный к поперечному сечению, связан с его моментом инерции следующим уравнением:0005
M = E\times I \times \kappa
, где E — модуль Юнга, свойство материала, а \kappa — кривизна балки из-за приложенной нагрузки. Следовательно, из предыдущего уравнения видно, что когда к поперечному сечению балки приложен определенный изгибающий момент M, развиваемая кривизна обратно пропорциональна моменту инерции I.
Следовательно, из предыдущего уравнения видно, что когда к поперечному сечению балки приложен определенный изгибающий момент M, развиваемая кривизна обратно пропорциональна моменту инерции I.
Полярный момент инерции L-образного сечения
Полярный момент инерции описывает жесткость поперечного сечения по отношению к крутящему моменту, так же как описанные выше плоские моменты инерции относятся к изгибному изгибу. Расчет полярного момента инерции I_z вокруг оси z-z (перпендикулярной сечению) можно выполнить с помощью теоремы о перпендикулярных осях: 94 .
РЕКЛАМА
Модуль упругости сечения
Модуль упругости сечения S_x любого поперечного сечения вокруг центральной оси x-x описывает реакцию сечения на упругий изгиб. Он определяется как:
S_x = \frac{I_x}{Y}
где I_x, момент инерции сечения вокруг оси x-x и Y, расстояние от центра тяжести данного сечения волокна (параллельного ось). Для углового сечения из-за его несимметричности S_x отличается для верхнего волокна (на конце вертикального участка) или нижнего волокна (в основании горизонтального участка). Обычно при нахождении модуля упругости учитывается более удаленное волокно (от центра тяжести). Это происходит на кончике вертикальной ноги (для изгиба вокруг х-х). Используя, возможно, большее значение Y, мы получаем меньшее значение S_x, что приводит к более высоким расчетам напряжения, как будет показано вскоре после этого. Обычно это предпочтительнее для дизайна раздела. Следовательно:
Обычно при нахождении модуля упругости учитывается более удаленное волокно (от центра тяжести). Это происходит на кончике вертикальной ноги (для изгиба вокруг х-х). Используя, возможно, большее значение Y, мы получаем меньшее значение S_x, что приводит к более высоким расчетам напряжения, как будет показано вскоре после этого. Обычно это предпочтительнее для дизайна раздела. Следовательно:
S_{x,\textit{min}} = \frac{I_x}{h-y_c}
S_{x,\textit{max}} = \frac{I_x}{y_c}
, где «min Обозначения ” или “max” основаны на предположении, что y_c \lt h-y_c , что справедливо для любого углового сечения.
Аналогично, для модуля упругого сечения S_y относительно оси y-y минимальный модуль упругого сечения находится с помощью:
S_{y,\textit{min}} = \frac{I_y}{b-x_c}
, где обозначение «min» основано на допущении, что x_c \lt b-x_c , что опять же справедливо для любого углового сечения.
Если к оси x-x приложен изгибающий момент M_x, сечение будет реагировать нормальными напряжениями, линейно изменяющимися с расстоянием от нейтральной оси (которая в упругом режиме совпадает с центроидальной осью x-x). Над нейтральной осью напряжения по определению равны нулю. Абсолютное максимальное напряжение будет возникать на самом удаленном волокне, величина которого определяется формулой: аналогично поперечному сечению А для осевой нагрузки. Для последнего нормальным напряжением является F/A. 93 .
Над нейтральной осью напряжения по определению равны нулю. Абсолютное максимальное напряжение будет возникать на самом удаленном волокне, величина которого определяется формулой: аналогично поперечному сечению А для осевой нагрузки. Для последнего нормальным напряжением является F/A. 93 .
РЕКЛАМА
Модуль пластического сечения
Модуль пластического сечения аналогичен упругому, но определяется в предположении полной пластической текучести поперечного сечения за счет изгибного изгиба. В этом случае все сечение разделено на две части, одну на растяжение и одну на сжатие, каждая из которых находится в однородном поле напряжений. Для материалов с равными напряжениями текучести при растяжении и сжатии это приводит к разделению сечения на две равные области, A_t, при растяжении и A_c, при сжатии, разделенные нейтральной осью. Эта ось называется пластическая нейтральная ось и для несимметричных сечений не совпадает с упругой нейтральной осью (которая снова является центроидальной). Модуль пластического сечения задается общей формулой:
Модуль пластического сечения задается общей формулой:
Z = A_c Y_c + A_t Y_t
, где Y_c — расстояние от центра тяжести области сжатия A_c до нейтральной пластической оси, а Y_t — соответствующее расстояние от центра тяжести зоны растяжения. площадь А_т.
Вокруг оси x
В случае углового поперечного сечения нейтральная пластическая ось для изгиба x-x может быть найдена одним из следующих двух уравнений:
\left \{ \begin{array}{ll} (h-y_{pna})t = \frac{A}{2} & \text{ , if } y_{pna} \ge t \\ y_{ pna} b = \frac{A}{2} & \text{ , if } y_{pna} \lt t \\ \end{array} \right.
, который становится:
y_{pna} =\left \{ \begin{array}{ll} h- \frac{A}{2t} & \text{ , если: } t \le {A\over2 b } \\ \frac{A}{2b} & \text{ , если: } t \gt {A\over2 b} \\ \end{array} \right.
где y_\textit{pna}, расстояние пластической нейтральной оси от нижнего конца сечения. Первое уравнение справедливо, когда пластическая нейтральная ось проходит через вертикальную ветвь, а второе — когда она проходит через горизонтальную ветвь. Как правило, нельзя заранее знать, какое уравнение является релевантным. 92 \over4b} \quad , t \gt {A\over2 b}
Как правило, нельзя заранее знать, какое уравнение является релевантным. 92 \over4b} \quad , t \gt {A\over2 b}
где h_1=h-t.
Вокруг оси y
Аналогичным образом можно найти модуль пластического сечения вокруг оси y. Если сориентировать Г-образное сечение так, чтобы вертикальная ветвь стала горизонтальной, то получившаяся фигура по форме подобна первоначально ориентированной. Таким образом, полученные уравнения должны иметь тот же вид, что и для оси абсцисс. Нам нужно только поменять местами h на b и наоборот. Таким образом, точное положение пластической нейтральной оси определяется следующей формулой:
x_{pna} =\left \{ \begin{array}{ll} b- \frac{A}{2t} & \text{ , если: } t \le {A\over2 h} \\ \frac {A}{2h} & \text{ , если: } t \gt {A\over2 h} \\ \end{массив} \right.
где x_\textit{pna}, расстояние пластической нейтральной оси от левого конца сечения. Первое уравнение справедливо, когда пластическая нейтральная ось проходит через горизонтальную ветвь, а вторая — когда она проходит через вертикальную ветвь (см. рисунок ниже).
рисунок ниже).
Для первого случая, когда ось ординат пересекает горизонтальную ветвь, модуль пластичности находится по формуле: 92 \over4h} \quad , t \gt {A\over2 h}
, где b_1=b-t.
Радиус вращения
Радиус вращения R g поперечного сечения относительно оси определяется по формуле: I момент инерции поперечного сечения вокруг той же оси и A его площадь. Размеры радиуса вращения [Длина]. Он описывает, насколько далеко от центра тяжести распределена область. Малый радиус указывает на более компактное сечение. Круг — это форма с минимальным радиусом вращения по сравнению с любым другим сечением той же площади A.
Формулы углового (L) сечения
В следующей таблице перечислены основные формулы для механических свойств углового (L) поперечного сечения.
Угол (L) Секция Формулы | |||
|---|---|---|---|
| Количество | Formula | ||
| Область: | A = B-T) | . 2\right) 92 \over4h} & \quad , t \gt {A\over2 h} \end{массив}\right. 2\right) 92 \over4h} & \quad , t \gt {A\over2 h} \end{массив}\right. | |
Пластиковая нейтральная ось: (расстояния снизу или слева) | y_{pna} =\left \{ \begin{array}{ll} h- \frac{A}{2t} & \text{ , если: } t \le {A\over2 b} \\ \frac{A}{2b} & \text{ , если: } t \gt {A\over2 b} \\ \end{массив } \Правильно. x_{pna} =\left \{ \begin{array}{ll} b- \frac{A}{2t} & \text{ , если: } t \le {A\over2 h} \\ \frac {A}{2h} & \text{ , если: } t \gt {A\over2 h} \\ \end{массив} \right. 92 \right) \end{split} | ||
Связанные страницы
Понравилась эта страница? Поделись с друзьями!
Уголок стальной — Ryerson
Пожалуйста, войдите или продолжите как гость
Почтовый индекс*
Главная//Список акций//Уголок стальной
Ryerson предлагает A36, A529Уголки из углеродистой стали -50 и A572-50, горячекатаные или оцинкованные, уголки L или размер прутка, для использования во многих конструкциях. Изготовленные из свариваемых и формуемых материалов, стальные уголки могут использоваться не только в строительстве, но и в качестве раскосов и уголков в опорных рамах машин, оборудования, транспортных средств и прицепов.
Изготовленные из свариваемых и формуемых материалов, стальные уголки могут использоваться не только в строительстве, но и в качестве раскосов и уголков в опорных рамах машин, оборудования, транспортных средств и прицепов.
Готовы сделать заказ? Перейти к каталогу
Свяжитесь с нами|Перейти к ресурсам
Выберите марку:
A36 — размер стержня A36 — размер стержня, оцинкованный A36- L (конструкции) ASTM A588Соответствует стандарту ASTM A36. Длина склада: 20, 40 и 60 футов.
Свяжитесь с представителем Ryerson для получения дополнительной информации
Узкие результаты:
Фланец в дюймах: — Выберите один —L3L3 1/2L4L5L6L7L8L9Stem в дюймах: — Выберите один —22 1/233 1/24568| Выберите для предложения | Фланец в дюймах | Шток в дюймах | Толстый стержень. в дюймах в дюймах | Вес на фут. в фунтах |
|---|---|---|---|---|
| Л3 | 2 | 3/16 | 3,070 | |
| Л3 | 2 | in Inches»> 1/4 | 4.100 | |
| Л3 | 2 | 16/5 | 5.000 | |
| Л3 | 2 | in Inches»> 3/8 | 5.900 | |
| Л3 | 2 | 1/2 | 7.700 | |
| Л3 | 2 1/2 | in Inches»> 3/16 | 3,350 | |
| Л3 | 2 1/2 | 1/4 | 4.500 | |
| Л3 | 2 1/2 | in Inches»> 16/5 | 5.600 | |
| Л3 | 2 1/2 | 3/8 | 6.600 | |
| Л3 | 2 1/2 | in Inches»> 1/2 | 8.500 | |
| Л3 | 3 | 3/16 | 3,710 | |
| Л3 | 3 | in Inches»> 1/4 | 4.900 | |
| Л3 | 3 | 16/5 | 6.100 | |
| Л3 | 3 | in Inches»> 3/8 | 7.200 | |
| Л3 | 3 | 1/2 | 9.400 | |
| L3 1/2 | 2 1/2 | in Inches»> 1/4 | 4.900 | |
| L3 1/2 | 2 1/2 | 16/5 | 6.100 | |
| L3 1/2 | 2 1/2 | in Inches»> 3/8 | 7.200 | |
| L3 1/2 | 2 1/2 | 1/2 | 9.400 | |
| L3 1/2 | 3 | in Inches»> 1/4 | 5.400 | |
| L3 1/2 | 3 | 16/5 | 6.600 | |
| L3 1/2 | 3 | in Inches»> 3/8 | 7.900 | |
| L3 1/2 | 3 | 1/2 | 10.200 | |
| L3 1/2 | 3 1/2 | in Inches»> 1/4 | 5.800 | |
| L3 1/2 | 16/5 | 7.200 | ||
| L3 1/2 | in Inches»> 3/8 | 8.500 | ||
| L3 1/2 | 1/2 | 11.100 | ||
| Л4 | 3 | in Inches»> 1/4 | 5.800 | |
| Л4 | 3 | 16/5 | 7.200 | |
| Л4 | 3 | in Inches»> 3/8 | 8.500 | |
| Л4 | 3 | 1/2 | 11.100 | |
| Л4 | 3 1/2 | in Inches»> 1/4 | 6.200 | |
| Л4 | 3 1/2 | 16/5 | 7.700 | |
| Л4 | 3 1/2 | in Inches»> 3/8 | 9.100 | |
| Л4 | 3 1/2 | 1/2 | 11.900 | |
| Л4 | 4 | in Inches»> 1/4 | 6.600 | |
| Л4 | 4 | 16/5 | 8.200 | |
| Л4 | 4 | in Inches»> 3/8 | 9.800 | |
| Л4 | 4 | 1/2 | 12.800 | |
| Л4 | 4 | in Inches»> 5/8 | 15.700 | |
| Л4 | 4 | 3/4 | 18.500 | |
| Л5 | 3 | in Inches»> 1/4 | 6.600 | |
| Л5 | 3 | 16/5 | 8.200 | |
| Л5 | 3 | in Inches»> 3/8 | 9.800 | |
| Л5 | 3 | 1/2 | 12.800 | |
| Л5 | 3 1/2 | in Inches»> 1/4 | 7.000 | |
| Л5 | 3 1/2 | 16/5 | 8.700 | |
| Л5 | 3 1/2 | in Inches»> 3/8 | 10.400 | |
| Л5 | 3 1/2 | 1/2 | 13.600 | |
| Л5 | 3 1/2 | in Inches»> 5/8 | 16.800 | |
| Л5 | 3 1/2 | 3/4 | 19.800 | |
| Л5 | 5 | in Inches»> 16.05. | 10.300 | |
| Л5 | 5 | 3/8 | 12.300 | |
| Л5 | 5 | in Inches»> 1/2 | 16.200 | |
| Л5 | 5 | 5/8 | 20.000 | |
| Л5 | 5 | in Inches»> 3/4 | 23.600 | |
| Л6 | 3 1/2 | 1/4 | 7.900 | |
| Л6 | 3 1/2 | in Inches»> 16.05. | 9.800 | |
| Л6 | 3 1/2 | 3/8 | 11.700 | |
| Л6 | 3 1/2 | in Inches»> 1/2 | 15.300 | |
| Л6 | 4 | 16/5 | 10.300 | |
| Л6 | 4 | in Inches»> 3/8 | 12.300 | |
| Л6 | 4 | 1/2 | 16.200 | |
| Л6 | 4 | in Inches»> 5/8 | 20.000 | |
| Л6 | 4 | 3/4 | 23.600 | |
| Л6 | 6 | in Inches»> 16/5 | 12.400 | |
| Л6 | 6 | 3/8 | 14.900 | |
| Л6 | 6 | in Inches»> 1/2 | 19.600 | |
| Л6 | 6 | 5/8 | 24.200 | |
| Л6 | 6 | in Inches»> 3/4 | 28.700 | |
| Л6 | 6 | 1 | 37.400 | |
| Л7 | 4 | in Inches»> 3/8 | 13.600 | |
| Л7 | 4 | 1/2 | 17.900 | |
| Л7 | 4 | in Inches»> 3/4 | 26.200 | |
| Л8 | 4 | 1/2 | 19.600 | |
| Л8 | 4 | in Inches»> 3/4 | 28.700 | |
| Л8 | 6 | 1/2 | 23.000 | |
| Л8 | 6 | in Inches»> 3/4 | 33.800 | |
| Л8 | 6 | 1 | 44.200 | |
| Л8 | 8 | in Inches»> 1/2 | 26.400 | |
| Л8 | 8 | 5/8 | 32.700 | |
| Л8 | 8 | in Inches»> 3/4 | 38.900 | |
| Л8 | 8 | 1 | 51.000 | |
| Л9 | 4 | in Inches»> 1/2 | 21.300А |
Купить карбоновый уголок
- Артикул
- Ресурс
- Общий справочник
- Твердость по Бринеллю
- Окружность кругов
- Таблица цветовых кодов
- Метрическая система
- Весовые формулы
- Руководства по выбору
- Конструкционные профили из углеродистой стали — PDF
- Допуски
- Конструкционные профили из углеродистой стали
Толщина: 7, 36,0000” x 120,0000” x 0,1874”, 2361,1 фунта/лист
Добавить примечания|Удалить
Единица измерения
фунтов
Имя *
Фамилия *
Электронная почта *
Почтовый индекс *
Компания
Центрировать штрих-код для поиска товаров.
Количество:
Единица измерения:
Цена, Единица измерения:
Справочный номер клиента:
Уровень линии заказа:
Заголовок Заказ на поставку:
Номер заказа на покупку в заголовке включен в ваш штрих-код и может иметь приоритет перед предыдущими заказами на покупку в вашей корзине
Информация Speedy Metals для структурных форм HR (углы и каналы HR) Уголки и каналы)
| Анализ | Механические свойства | Приложения | Обрабатываемость_и_Свариваемость | Термообработка | Допуски | Предметы Speedy Metals |
Профиль классифицируется как «Профиль размера стержня», если его наибольший размер (исключая длину) составляет менее 3 дюймов. Это «Структурная форма»), когда хотя бы один из ее размеров (исключая длину) составляет 3 дюйма или больше. Эти формы соответствуют ASTM A36 в отношении изготовления и механических допусков. Угол HR измеряется размером его ножек снаружи и их толщиной. Угол ЧСС может быть равным или неравным (т.е. 2 x 2 x 1/4″ ч. угла / 3 x 2 x 1/4″ ч. угла). В обозначении каналов HR буква или буквы предшествуют размеру и весу на фут, то есть: C3 x 4,1 # — это обозначение AISI для канала шириной 3 дюйма в основании и весом 4,1 фунта на фут стандартного конструкционного канала. «C «профили — швеллеры, изготовленные в соответствии с размерными нормами, принятыми в 1896 Ассоциации американских производителей стали для каналов American Standard. Существенной частью этих стандартов является то, что внутренние поверхности фланцев каналов американского стандарта имеют уклон приблизительно 16-2/3%. Формы «MC» — это каналы, которые нельзя классифицировать как формы «C».
Угол ЧСС может быть равным или неравным (т.е. 2 x 2 x 1/4″ ч. угла / 3 x 2 x 1/4″ ч. угла). В обозначении каналов HR буква или буквы предшествуют размеру и весу на фут, то есть: C3 x 4,1 # — это обозначение AISI для канала шириной 3 дюйма в основании и весом 4,1 фунта на фут стандартного конструкционного канала. «C «профили — швеллеры, изготовленные в соответствии с размерными нормами, принятыми в 1896 Ассоциации американских производителей стали для каналов American Standard. Существенной частью этих стандартов является то, что внутренние поверхности фланцев каналов американского стандарта имеют уклон приблизительно 16-2/3%. Формы «MC» — это каналы, которые нельзя классифицировать как формы «C».
АНАЛИЗ
HR Уголки и швеллеры соответствуют ASTM A36
МЕХАНИЧЕСКИЕ СВОЙСТВА
При условии вычета из указанного выше процентного удлинения для толщин менее 5/16″ и более 3/4″.
Выше приведено общее руководство по свойствам, которое можно считать репрезентативным для структурных форм HR, соответствующих стандарту ASTM A36.
ПРИМЕНЕНИЕ
Используется для общих строительных целей, для использования в клепаных, болтовых или сварных конструкциях зданий, мостов, машин и т. д. Используется для стрел, рельсов, раскосов, рам, кронштейнов, поперечин, вкладышей, грузовых прицепов , кузова грузовиков, стеллажи и т. д.
ОБРАБАТЫВАЕМОСТЬ И СВАРОЧНОСТЬ
ASTM A36 имеет рейтинг обрабатываемости 72%, основанный на 1212 при 100%. Средняя подача поверхностного резания 120 футов/мин.
ASTM A36 легко сваривается всеми сварочными процессами, а полученные сварные швы и соединения имеют чрезвычайно высокое качество.
ТЕРМООБРАБОТКА
ASTM A36, как правило, не подвергается термообработке, но обычно снимается напряжение перед шлифованием или механической обработкой или после сварки и перед механической обработкой. Однако ASTM A-36 можно науглероживать для повышения твердости поверхности.
Снятие напряжения 1100–1250°F. Типичное время выдержки для снятия стресса — один час на дюйм толщины.
Науглероживание 1650°-1700°F.
ДОПУСКИ
| Раздел | Номинальный размер (дюймы) | Длина ноги (дюймы) | Толщина вне квадрата на дюйм ноги (дюйм) | Отклонения от толщины для указанной толщины, больше и меньше | |||
| Более | До | 3/16 и до | Более 3/16 до 3/8, включая | Свыше 3/8 | |||
| УГОЛКИ¹ (Г-образные) | 1 и ниже | 1/32 | 1/32 | 3/128² | 0,008 | 0,010 | — |
| От 1 до 2, включая | 3/64 | 3/64 | 3/128² | 0,010 | 0,010 | 0,012 | |
| От 2 до 3, кроме | 1/16 | 1/16 | 3/128² | 0,012 | 0,015 | 0,015 | |
| от 3 до 4, включая | 1/8 | 3/32 | 3/128² | — | — | — | |
| От 4 до 6, включая | 1/8 | 1/8 | 3/128² | — | — | — | |
| Более 6 | 3/16 | 1/8 | 3/128² | — | — | — | |
¹ При неравных углах сторон более длинная сторона определяет класс
² 2/128 дюйма/дюйм. = 1-1/2 градуса
= 1-1/2 градуса
Другие допуски, например: прямолинейность, скручивание и т. д., согласно спецификациям ASTM A36, ASTM A6 / A 6M.
| Раздел | Номинальный размер (дюймы) | Глубина (дюйм) | Ширина фланца (дюймы) | T + T’† Фланцы вне квадрата макс. дюйм‡ | Толщина паутины Больше и меньше указанной толщины | |||
| Более | Под | Больше | До | 3/16 и до | Более 16 марта | |||
| Канал C и MC | 1-1/2 и ниже | 1/32 | 1/32 | 1/32 | 1/32 | 1/32 | 0,010 | 0,015 |
| От 1-1/2 до 3, кроме | 1/16 | 1/16 | 1/16 | 1/16 | 1/32 | 0,015 | 0,020 | |
| от 3 до 7, включая | 3/32 | 1/16 | 1/16 | 1/16 | 1/32 | — | — | |
| От 7 до 14 лет, включая | 1/8 | 3/32 | 1/8 | 5/32 | 1/32 | — | — | |
| Старше 14 лет | 3/16 | 1/8 | 1/8 | 3/16 | 1/32 | — | — | |
† T + T’ применяется, когда фланцы канала сгибаются внутрь или наружу.