Обратная функция угла: Функция угла, 9 (девять) букв

Обратные тригонометрические функции. Графики обратных тригонометрических функций.

• Альфашкола
• Статьи
• Обратные тригонометрические функции

Обратные тригонометрические функции принято называть с помощью префикса  \(arc\)   (\(arc\) с английского дуга) , например, \(arcsin (x)\), \(arccos(x)\), \(arctan(x)\) и т. д.  При измерении в радианах угол радиан будет соответствовать дуге, длина которой равна \(R\), где \(R\)-радиус окружности. Таким образом, в единичной окружности «дуга, косинус которой равен x», совпадает с «углом, косинус которого равен \(x\)», поскольку длина дуги окружности в радиусах совпадает с измерением угла в радианах. Обозначения \(sin-1 (x)\),  \(cos−1(x)\),  \(tan−1(x)\) и др.  было введено Джоном Гершелем в \(1813\) году.   

 

• Функция \(y=arccos(x)\) обратная для функции \(y=cos(x)\) на отрезке \(y ∈ [ 0 , π] \), где \(x ∈ [ − 1 , 1 ]\). 

​

• Функция \(y=arcsin(x)\) обратная для функции \(y=sin(x)\) на отрезке \(y ∈[ − π / 2 , π / 2 ] \), где \(x ∈ [ − 1 , 1 ] \).

• Функция  \(y=arctg(x)\) обратная для функции \(y=tg(x)\) на отрезке от \([\frac{-\pi}{2}]\) до \([\frac{\pi}{2}]\), где \(y ∈ ( − π / 2 , π / 2 ) \).

• Функция  \(y=arcctg(x)\) обратная для функции \(y=ctg(x)\) на отрезке от \([\frac{-\pi}{2}]\) до \([\frac{\pi}{2}]\), где \(y ∈ ( − π / 2 , π / 2 ) \).

​

 

 

 

 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Оксана Николаевна Хаустова

Репетитор по математике

Стаж (лет)

Образование:

Саратовский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Камо Аркадьевич Филипосян

Репетитор по математике

Стаж (лет)

Образование:

Самаркандский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Ирина Ивановна Ерыгина

Репетитор по математике

Стаж (лет)

Образование:

Армавирский государственный педагогический институт

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Репетитор по алгебре
• Подготовка к ЕГЭ по математике (профильный уровень)
• Подготовка к олимпиадам по физике
• Подготовка к ЕГЭ по английскому языку
• Английский язык для начинающих
• Репетитор для подготовки к ВПР по русскому языку
• Репетитор для подготовки к ЕГЭ по обществознанию
• Репетитор по обществознанию для подготовки к ОГЭ
• Подготовка к ЕГЭ по информатике
• Программирование Pascal

Похожие статьи

• Задачи на движение: по течению и против
• Как заинтересовать детей учить математику?
• Синус, косинус острого угла треугольника
• Модуль числа (Часть 2)
• НИУ ВШЭ: Факультет Психологии
• Финансовый Университет при Правительстве РФ: Управление Персоналом
• Топ-5 тем по геометрии, в которых чаще всего совершают ошибки
• Задачи с прикладным содержанием (вариант 2)

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Обратные тригонометрические функции.

Кратко 

Оглашаю весь список: арксинус, арккосинус, арктангенс, арккотангенс. Они предназначены для того, чтобы по известному синусу, косинусу, тангенсу или арктангенсу угла, определить сам угол. Например, если , то . Если , то . Если , то  и .

Но здесь есть одна проблемка: дело в том, что значению  (например) соответствует бесконечно много углов, а обратная функция (как и любая функция) должна быть определена однозначно. И эта проблемка решена так,… объясню на конкретном примере, а то у меня тут правило кошмарное получилось, которое я сразу удалил :).

Синус принимает все свои возможные значения (от –1 до 1) на отрезке , и во избежание разночтений арксинус возвращает углы только из этого отрезка:

Так, если , то обратная функция все равно вернёт угол  и уже к этому результату нужно «прикрутить» нужное количество радиан , чтобы получить . Таким образом, функция  определена на отрезке  
и, очевидно,  нечётна, то есть,  из-под арксинуса тоже можно вынести минус:

Аналогично, косинус принимает все свои возможные значения (от 1 до –1) на отрезке , и поэтому арккосинус возвращает углы только из этого промежутка:

Функция  определена на том же промежутке , однако не является чётной или нечётной.

С арктангенсом и арккотангенсом всё проще. График  представляет собой ветку тангенса, которая «лежит на боку»:

Данная функция определена на всей числовой прямой  и возвращает углы из интервала . Арктангенс нечётен: . График функции ограничен горизонтальными асимптотами  и  (красный пунктир).

График арккотангенса  ограничен асимптотами  и :

Арккотангенс тоже определён на всей числовой прямой , но возвращает углы из интервала .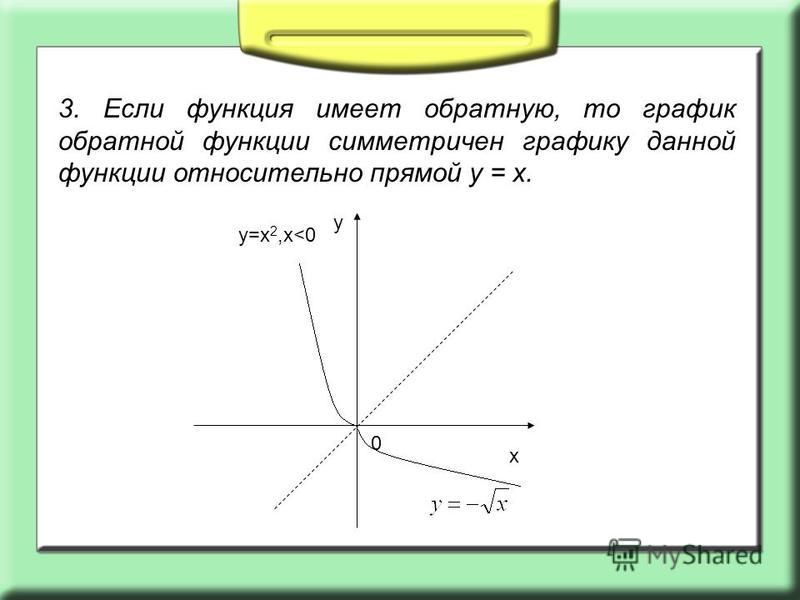 Данная функция не является чётной или нечётной.

Внимание! Функцию  часто машинально «принимают» за арктангенс,
и чтобы не

«обознаться», внимательно всматривайтесь, какая функция вам дана!

Следует отметить, что две взаимно обратные функции взаимоуничтожают друг друга. Вспомним экспоненту и натуральный логарифм:  и наоборот,  (основное логарифмическое тождество).

С тригонометрическими функциями и «арками» то же самое, в частности:
 и  (для допустимых значений «икс») и аналогично для трёх других пар.

Кроме того, у «арков» существуют свои формулы и взаимосвязи, но они не столь актуальны в массовой практике. Кстати, здесь к месту такой совет:

Если ваша задача «зашла в тупик»,
то есть смысл заглянуть в математический справочник или учебник

Потому что различных фактов, правил и формул просто тьма, и это особенно характерно для геометрии и тригонометрии.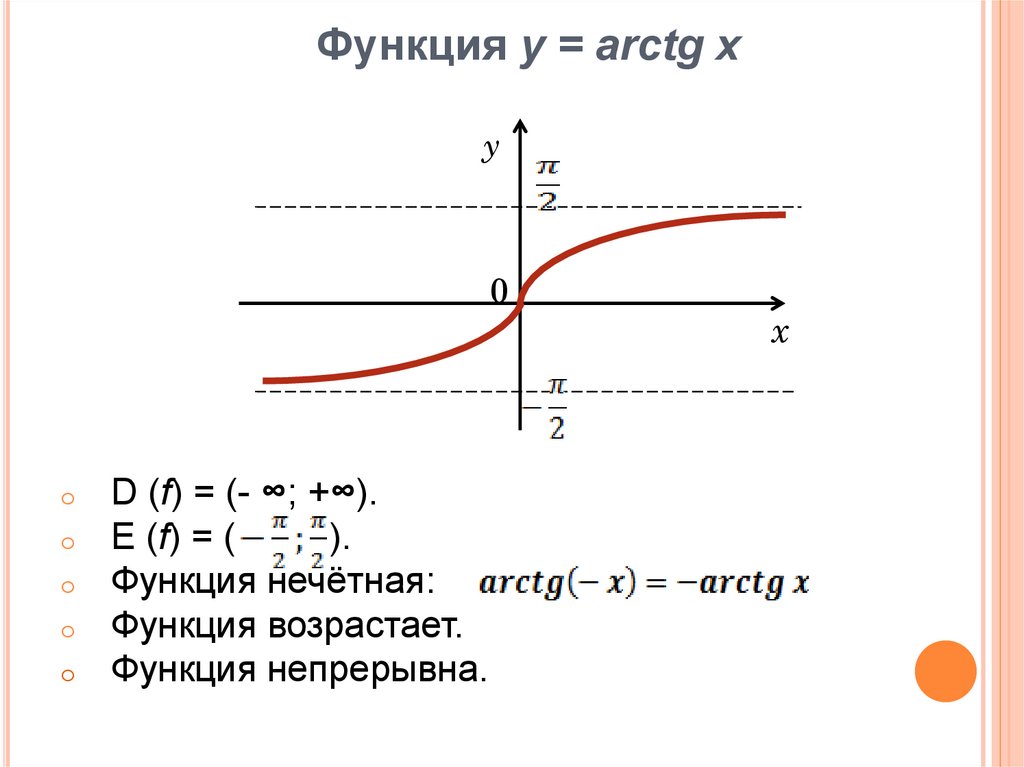

Тех же тригонометрических формул – многие и многие десятки.

5.7. Простейшие тригонометрические уравнения

5.5. Распространённые тригонометрические формулы

| Оглавление |



Функции обратной тригонометрии — Открытый справочник по математике

Функции обратной тригонометрии — Открытый справочник по математике

Открытый справочник по математике

Главная Контакт О Тематический указатель

Для каждого тригонометрическая функция например, у греха есть обратная функция, которая работает в обратном направлении. Эти обратные функции имеют то же имя, но с «дугой» впереди. Таким образом, обратным греху является арксинус и т. д. Когда мы видим «арксинус А», мы понимаем его как «угол, чей грех равен А».

sin30 = 0,5	Означает: синус 30 градусов равен 0,5
arcsin0.5 = 30	Означает: угол, у которого sin равен 0,5, равен 30 градусам.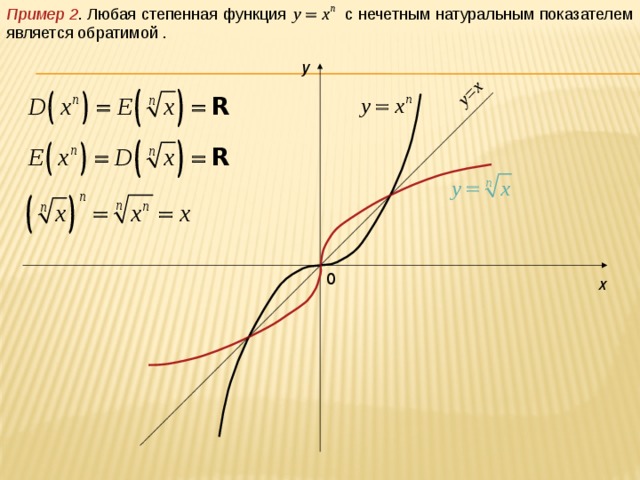

Используйте его, когда вы знаете синус угла и хотите знать фактический угол. Мы пишем обратную функцию так же, как и обычную функцию с «дугой» впереди.

Функция	Обратная функция
грех	дуги
потому что	арккос
желтовато-коричневый	арктический

Обратные значения sec,cot,csc записываются аналогичным образом, но используются редко.

На калькуляторе

Вы всегда будете использовать калькулятор, чтобы найти значения триггерных функций и их инверсий. Например, на калькуляторе обратные кнопки могут быть отмечены arcsin, asin или sin ^-1 .

( Будь осторожен : Последняя форма — грех ^-1 — может ввести в заблуждение, поскольку возведение чего-либо в отрицательную степень подразумевает обратную функцию, то есть , а не , то же самое, что и обратная функция).

Решение прямоугольного треугольника

В прямоугольный треугольник, когда вы знаете любые две стороны, вы можете использовать обратные триггерные функции, чтобы найти все углы. На рисунке ниже нам даны три стороны. Найдем углы А,В,С

• Использование arcsin

  Мы знаем, что синус угла противоположен гипотенузе. Итак, на приведенном выше рисунке Поскольку грех C известен, мы используем обратную функцию греха, чтобы найти угол.
  Так как sinC = 0,6, то Мы бы сказали: «С — это угол, грех которого равен 0,6». С помощью калькулятора находим, что Значит, угол С равен 36,86°.

• Использование arccos

  Мы знаем, что косинус угла прилегает к гипотенузе, поэтому так Калькулятор говорит нам, что это тоже 36,86°.

• Использование арктана

  Используя ту же идею, мы знаем, что функция тангенса угла противоположна прилежащему, поэтому так Калькулятор говорит нам, что это 36,86°.

Таким образом, все три дают одинаковый результат, как и должны. Используйте любую функцию, которая вам нравится, в зависимости от того, с какой стороны вам дано начать.

Примечания

1. Если вам даны любые две стороны прямоугольного треугольника, вы также можете использовать Теорема Пифагора, чтобы найти третью.
2. Вы также можете применить эти методы к другому углу A. Например, sinA равно 8 больше 10,
   , поэтому A = arcsin(0,8)
3. Если у вас есть один угол, другой всегда можно найти, потому что сумма внутренних углов треугольника всегда равна 180°. Вы нашли один, а другой 90°

Большие и отрицательные углы

Напомним, что мы можем подать заявку функции триггера на любой угол, включая большие и отрицательные углы. Но когда мы рассмотрим обратную функцию, мы сталкиваемся с проблемой.

Что, если бы нас попросили найти арксинус, скажем, 0,5? Другими словами, у какого угла синус равен 0,5?

Если мы посмотрим на кривую выше, то увидим четыре угла, синус которых равен 0,5 (красные точки). На самом деле, поскольку график бесконечно продолжается в обоих направлениях, существует бесконечное количество углов, синус которых равен 0,5.
(см. График функции синуса).

Как решить эту проблему?

Чтобы решить эту проблему, диапазон обратной триггерной функции ограничены таким образом, чтобы обратные функции были взаимно однозначными, то есть для каждого входного значения был только один результат. Диапазон может быть разным для каждой функции, но, например, диапазон арксинуса условно ограничен значением -9.от 0 до +90° или же Итак, если вас попросили указать арксинус, скажем, 0,5, «правильный» результат будет равен 30° (sin30 = 0,5). Но помните, что существует бесконечное количество углов, у которых sin равен 0,5.

Другие темы по тригонометрии

Уголки

• Определение угла, свойства углов
• Стандартное положение на углу
• Начальная сторона угла
• Конечная сторона уголка
• Четырехугольники
• Котерминальные углы
• Опорный угол

Тригонометрические функции

• Знакомство с шестью триггерными функциями
• Функции больших и отрицательных углов
• Инверсные триггерные функции
• SOH CAH TOA Память


• Синусоидальная функция (sin) в прямоугольных треугольниках
• Функция обратного синуса (арксинус)
• График функции синуса
• Синусоидальные волны


• Функция косинуса (cos) в прямоугольных треугольниках
• Функция арккосинуса (arccos)
• График функции косинуса


• Касательная функция (тангенс) в прямоугольных треугольниках
• Функция арктангенса (арктангенс)
• График функции касательной


• Функция котангенса cot (в прямоугольных треугольниках)
• Функция секанса сек (в прямоугольных треугольниках)
• Функция косеканса csc (в прямоугольных треугольниках)

Решение задач по тригонометрии

• Общий подход
• Определение наклонного расстояния вдоль склона или пандуса
• Определение угла уклона или пандуса

Исчисление

• Производные тригонометрических функций

(C) 2011 Copyright Math Open Reference.
Все права защищены

Объяснение урока: Обратные тригонометрические функции

В этом объяснении мы научимся вычислять точные значения тригонометрических обратных функций и оценивать композиции тригонометрических функций. и обратные тригонометрические функции при стандартных углах в радианах.

Начнем с напоминания некоторых основных определений и обозначений, относящихся к обратным функциям вообще. Затем мы попадем в особенности вычисления обратных тригонометрических функций.

Определение: обратимая функция и связанные понятия

Функция  𝑓∶𝑋→𝑌 отображает вход 𝑥, принадлежащий домен  𝑋 на выход 𝑦=𝑓(𝑥), принадлежащий диапазону 𝑌.

Область  𝑋 функции 𝑓 представляет собой множество всех возможных входов 𝑥 такое, что 𝑓(𝑥) определено.

Диапазон числа 𝑓(𝑋) — это набор всех результатов, которые мы можем получить, применяя 𝑓 к элементам 𝑋.

Функция является обратимой , если она является функцией один к одному и на ; то есть каждый вход имеет один уникальный вывод и каждый элемент диапазона 𝑌 можно записать в виде 𝑓(𝑥) для некоторое 𝑥 в домене 𝑋.

Пусть 𝑓∶𝑋→𝑌 — обратимая функция. , обратное числа 𝑓, является функция 𝑓∶𝑌→𝑋 со свойством 𝑓(𝑥)=𝑦⟺𝑓(𝑦)=𝑥.

Проще говоря, обратная функция «обращает» исходную функцию. Заметим, что функция 𝑓 должно быть обратимым, чтобы иметь обратную функцию 𝑓. Если функция 𝑦=𝑓(𝑥) обратима, то вход 𝑥 будет отображаться в уникальный выход 𝑦 и 𝑓 сопоставит 𝑦 обратно с исходным 𝑥. Это относится к каждому элементу 𝑥 в домене 𝑋 и каждый элемент 𝑦 в диапазоне 𝑌.

В результате домен и диапазон обратной функции существенно меняются местами по сравнению с исходной функцией. Диапазон 𝑓 равен домену 𝑓, а диапазон 𝑓 равен домен 𝑓. Если домен 𝑓 не равен диапазону 𝑓, мы может иметь возможность ограничить исходный домен, чтобы обеспечить их соответствие.

Напомним определение сложной функции. Даны две функции 𝑔(𝑥) и 𝑓(𝑥), мы вычисляем составную функцию 𝑔(𝑓(𝑥)) по формуле замена каждого экземпляра 𝑥 в 𝑔(𝑥) на 𝑓(𝑥). Если две функции являются обратными, их композиции будут иметь очень предсказуемые результаты в соответствии со следующим правилом. как мы будем продемонстрировать в этом объяснителе, эти результаты справедливы и для тригонометрических функций, и для их обратных функций.

Правило композиции обратных функций

Пусть 𝑓∶𝑋→𝑌 и 𝑔∶𝑌→𝑋 — обратные функции. Затем, применяя 𝑓 к любому 𝑥 в 𝑋, за которым следует 𝑔, возвращает нам 𝑥. Точно так же, если мы применим 𝑔 к любому 𝑦 в 𝑌, за которым следует 𝑓, мы возвращаемся 𝑦. То есть, 𝑔(𝑓(𝑥))=𝑔(𝑦)=𝑥 а также 𝑓(𝑔(𝑦))=𝑓(𝑥)=𝑦.

Теперь, когда мы рассмотрели основные идеи об обратных функциях, мы рассмотрим специальные названия для обратных функций. тригонометрические функции.

Ключевые термины: арксинус, арккосинус и арктангенс

Обратная функция синуса называется арксинус .

Функция, обратная косинусу, называется арккосинус .

Функция, обратная тангенсу, называется арктангенс .

Напомним, что тригонометрические функции не являются взаимно однозначными. Это означает, что синус, косинус и тангенс необратимы, если только мы не ограничить свои домены, чтобы гарантировать, что каждое значение 𝑘 возвращает ровно одно значение 𝜃. С соответствующим ограничения на 𝜃, мы определяем три обратные тригонометрические функции следующим образом.

Определение: Область определения и область значений обратных тригонометрических функций

Для −𝜋2≤𝜃≤𝜋2 и −1≤𝑘≤1 имеем 𝜃=(𝑘)arcsin тогда и только тогда, когда 𝑘=(𝜃)sin.

Для 0≤𝜃≤𝜋 и −1≤𝑘≤1 имеем 𝜃=(𝑘)arccos тогда и только тогда, когда 𝑘=(𝜃)cos.

Для −𝜋2𝜃𝜋2 и 𝑘∈ℝ имеем 𝜃=(𝑘)arctan тогда и только тогда, когда 𝑘=(𝜃)tan.

Теперь вспомним, что когда угол 𝜃 в стандартном положении проходит через координатную точку (𝑥,𝑦), мы можем вычислить все шесть тригонометрических функций, используя 𝑥, 𝑦, и 𝑟=√𝑥+𝑦 согласно следующим определениям.

Определение: Тригонометрические функции в терминах (𝑥, 𝑦)

sinwherecoswheretanwhere𝜃=𝑦𝑟,𝑟≠0𝜃=𝑥𝑟,𝑟≠0𝜃=𝑦𝑥,𝑥≠0

По возможности удобно использовать координатные точки из единичной окружности, где 𝑟=1. Стандарт углы в радианах, найденные на единичной окружности, кратны 𝜋6 и 𝜋4 между 0 и 2𝜋. Мы можем конвертировать между степени и радианах, как это необходимо, используя тот факт, что 180=𝜋∘радиан.

Теперь, когда мы рассмотрели, как вычислять стандартные тригонометрические функции вокруг единичного круга, мы оценим нашу первую обратная тригонометрическая функция. Это потребует мышления «наоборот» от заданного стандартного тригонометрического значения. 𝑘 для определения соответствующего угла 𝜃, где значение 𝑘 находится на единичный круг. Одна из задач будет заключаться в том, чтобы помнить о недавно обнаруженных ограничениях домена и диапазона для обратного тригонометрические функции.

Пример 1.

Вычисление обратных тригонометрических функций в радианах

Вычислите выражение arcsin√32.

Ответ

Начнем с того, что вспомним, что арксинус является обратной тригонометрической функцией синуса. Особенно, arcsin(𝑘) дает нам угол 𝜃 в стандартном положении, для которого грех(𝜃)=𝑘. Диапазон функции 𝜃=(𝑘)arcsin равно −𝜋2≤𝜃≤𝜋2 в радианы. Это означает, что наш угол 𝜃 должен лежать где-то в пределах первого или четвертого квадранта на единичной окружности. По знакомой диаграмме CAST мы знаем, что только косинус положителен в четвертой четверти. Поскольку мы хотим вычислить инверсию синуса при положительном значении, √32, мы можем быть уверены, что 𝜃 находится в первом квадранте.

Теперь вспомним определения тригонометрических функций, выраженных через 𝑥- и 𝑦-координаты из единичного круга: sincostan, где𝜃=𝑦,𝜃=𝑥,𝜃=𝑦𝑥,𝑥≠0.

Чтобы вычислить arcsin√32, нам нужно найти стандартный угол, для которого синус угла равен √32.

Так как sin𝜃=𝑦, мы ищем угол, который пересекает единичную окружность в 𝑦-координата √32. Мы уже знаем, что он должен быть в первом квадранте, поэтому смотрим туда. Находим точку 12,√32, в 𝜃=𝜋3 радиана.

Поскольку sin𝜋3=√32, где −𝜋2≤𝜋3≤𝜋2, заключаем, что arcsinрадиан√32=𝜋3.

В некоторых вопросах нас могут попросить вычислить сумму или разность обратных тригонометрических функций. Мы рассмотрим Пример этого типа следующий.

Пример 2. Оценка разности обратных тригонометрических функций в радианах

Вычислите выражение arctanarcsin(1)−(−1).

Ответ

Во-первых, напомним, что арктангенс обратен тангенсу, а арксинус обратен синусу. Чтобы подойти к этой проблеме, мы оценит arctan(1) и arcsin(-1) отдельно, затем примет их отличие. Мы продолжим использовать радианы, но мы всегда можем изменить угловые меры на градусов по желанию.

Начнем с того, что вспомним, что arctan(𝑘) дает нам угол 𝜃 в стандартном позиция тогда и только тогда, когда tan(𝜃)=𝑘. Область значений функции 𝜃=(𝑘)arctan равна −𝜋2𝜃𝜋2.

Нам нужно найти стандартный угол, для которого тангенс угла равен 1.

В терминах 𝑥- и 𝑦-координат единичной окружности мы определяем тангенс как загар𝜃=𝑦𝑥. Итак, ищем угол, который пересекает единичную окружность в точке (𝑥,𝑦), где 𝑦𝑥=1.

Умножив каждую часть приведенного выше уравнения на 𝑥, мы получим (𝑥)𝑦𝑥=(𝑥)1.

Затем мы упрощаем, что приводит к уравнению 𝑦=𝑥.

Значит, мы ищем точку, где 𝑥- и 𝑦-координаты равны.

Это происходит только в двух точках на единичной окружности, 45∘ и 225∘, как показано ниже. В радианы, эти угловые меры равны 𝜋4 и 5𝜋4.

Поскольку диапазон 𝜃=(𝑘)arctan равен −𝜋2𝜃𝜋2, мы заключаем, что arctan(1) не может быть 5𝜋4. Таким образом, arctan(1)=𝜋4, потому что этот угол находится в правильном диапазоне, а 𝑥- и 𝑦-координаты равны.

Далее нам нужно вычислить arcsin(−1). Другими словами, нам нужно найти стандартный угол для синус угла которого равен −1.

Поскольку sin𝜃=𝑦 на единичной окружности, мы ищем угол, который пересекает единичную окружность в точке 𝑦-координата −1. Единственное место, где у нас есть эта 𝑦-координата на единичная окружность находится в квадрантном угле 3𝜋2.

Из единичного круга видно, что sin3𝜋2=−1; однако арксинус имеет диапазон −𝜋2≤𝜃≤𝜋2, поэтому нам нужно найти котерминальный угол с 3𝜋2 в этом интервале. Чтобы найти котерминальный угол в радианах, мы добавляем или вычитаем кратные 2𝜋. Поскольку 3𝜋2 выше диапазона арксинуса, мы должны вычесть 2𝜋. Таким образом, приведя оба слагаемых к общему знаменателю, равному 2, получим 3𝜋2−2𝜋=3𝜋2−4𝜋2=−𝜋2.

Следовательно, arcsin(−1)=−𝜋2.

Наконец, мы вычисляем arctanarcsin(1)−(−1), подставляя полученные значения выше: arctanarcsin(1)−(−1)=𝜋4−−𝜋2.

Вычитание отрицательного эквивалентно добавлению положительного. Следовательно, используя общий знаменатель 4, мы имеем 𝜋4−−𝜋2=𝜋4+𝜋2=𝜋4+2𝜋4=3𝜋4.

В заключение мы показали, что arctanarcsin(1)−(−1)=3𝜋4.

Теперь рассмотрим, как вычислить композицию стандартных и обратных тригонометрических функций.

Пример 3. Вычисление сложной тригонометрической и обратной тригонометрической функций

Найдите точное значение sinarccos((0)) без использования калькулятора.

Ответ

Чтобы ответить на этот вопрос, мы должны сначала признать, что данная функция синуса содержит арккосинус, который является арккосинусом функция. Мы называем это составной функцией. Напомним, что означает композиция двух функций. Даны две функции 𝑔(𝑥) и 𝑓(𝑥), мы вычисляем составную функцию 𝑔(𝑓(𝑥)) путем замены каждого экземпляра 𝑥 в 𝑔(𝑥) на 𝑓(𝑥). Другой способ думать об этом состоит в том, что мы сначала подставляем самые внутренние значения, а затем работать наружу.

В этом случае пусть 𝑔(𝑥)=(𝑥)sin и 𝑓(𝑥)=(𝑥)arccos; мы должны оценить 𝑔(𝑓(𝑥)) при 𝑥=0. Начнем с вычисления самой внутренней функции 𝑓(𝑥) при 𝑥=0. Это означает, что нам нужно найти стандартный угол, для которого косинус равен 0.

Напомним, что в терминах координат единичной окружности cos(𝜃)=𝑥. Согласно определение арккосинуса, 𝜃=(𝑘)arccos тогда и только тогда, когда 𝑘=(𝜃)cos, где 0≤𝜃≤𝜋. В пределах этого диапазона на единичной окружности мы видим, что 𝑥=0 при 𝜃=𝜋2. Следовательно, cos𝜋2=0 и 𝑓(0)=(0)=𝜋2arccos.

Чтобы оценить 𝑔(𝑓(0)), мы подставляем значение 𝑓(0): 𝑔(𝑓(0))=𝑔𝜋2.

Поскольку 𝑔(𝑥)=(𝑥)sin, то 𝑔𝜋2=𝜋2.sin

Напомним определение синуса через координаты единичной окружности: грех𝜃=𝑦.

Поэтому мы используем 𝑦-координату точки (0,1) для оценки грех𝜋2: грех𝜋2=1.

В заключение мы показали, что sinarccos((0))=1.

Давайте попробуем другой пример с композицией функций. Мы снова будем использовать арккосинус, но на этот раз это внешняя функция композиции.

Пример 4. Вычисление составной тригонометрической и обратной тригонометрической функций

Найдите точное значение arccossin√2−𝜋6 без использования калькулятора.

Ответ

Чтобы оценить это выражение, мы должны сначала признать его как композицию функций арккосинуса (обратного косинуса) и синус. Напомним, что означает композиция двух функций. Даны две функции 𝑔(𝑥) и 𝑓(𝑥), мы вычисляем составную функцию 𝑔(𝑓(𝑥)) по формуле замена каждого экземпляра 𝑥 в 𝑔(𝑥) на 𝑓(𝑥).

В этом случае пусть 𝑔(𝑥)=(𝑥)arccos и 𝑓(𝑥)=√2(𝑥)sin. Чтобы вычислить составную функцию 𝑔(𝑓(𝑥)) при 𝑥=−𝜋6, нам сначала нужно оценить 𝑓−𝜋6=√2−𝜋6sin.

Напомним, что синус определяется как sin𝜃=𝑦 на единичной окружности. Итак, мы ищем 𝑦-координата точки пересечения угла −𝜋6 с единичной окружностью. единичный круг не отображает отрицательные угловые меры, поэтому мы должны добавить 2𝜋 радианы, чтобы найти наименьший положительный угол котерминал с −𝜋6. Мы используем общий знаменатель 6, чтобы найти котерминальный угол: −𝜋6+2𝜋=−𝜋6+12𝜋6=11𝜋6.

Мы видим, что 11𝜋6 находится в четвертом квадранте единичной окружности. В 11𝜋6, находим 𝑦-координату −12. Следовательно, sinsin11𝜋6=−𝜋6=−12.

Теперь мы оцениваем 𝑓(𝑥) как 𝑥=−𝜋6. Учитывая 𝑓(𝑥)=√2(𝑥)sin и sin−𝜋6=−12, имеем 𝑓−𝜋6=√2−12=−√22.

Следовательно, 𝑔𝑓−𝜋6=𝑔−√22.

Так как 𝑔(𝑥)=(𝑥)arccos, то 𝑔−√22=−√22.arccos

Наконец, чтобы вычислить arccos−√22, мы обращаемся к единичному кругу. Мы помним, что арккосинус является обратным косинусу, и этот арккосинус−√22 дает нам угол 𝜃 в стандартном положении, для которого cos(𝜃)=−√22. Определение косинуса, выраженное через координаты единичной окружности, таково: cos𝜃=𝑥. Этот означает, что мы ищем стандартный угол с 𝑥-координатой −√22.

Давайте посмотрим, что еще мы знаем об угле, который хотим найти. Напомним, что область значений функции арккосинуса равна 0≤𝜃≤𝜋. Таким образом, наш угол 𝜃 находится где-то в пределах первого или второго квадрант на единичной окружности. Согласно диаграмме CAST мы знаем, что все тригонометрические функции положительны в первый квадрант. Мы хотим вычислить обратный косинус при отрицательном значении, -√22. Так, мы можем быть уверены, что 𝜃 находится во втором квадранте.

Во втором квадранте мы находим 𝑥-координату −√22 при 𝜃=3𝜋4. Это означает, что arccos−√22=3𝜋4.

В заключение мы показали, что arccossin√2−𝜋6=3𝜋4.

В нашем последнем примере мы исследуем взаимосвязь между косинусом и его обратным значением для различных угловых величин вокруг единицы измерения. круг.

Пример 5. Переписывание уравнения с использованием тригонометрического обратного уравнения

Пусть arccos(𝑥)=𝜃, где 0𝑥1 и 𝜃 в радианах. Найдите первые два положительных значения 𝛼 в терминах 𝜃 такое, что cos(𝛼)=𝑥.

Ответ

Для начала вспомним значение арккосинуса. Арккосинус является обратной величиной косинуса. Если arccos(𝑥)=𝜃, тогда также должно быть верно, что cos(𝜃)=𝑥.

По определению, arccos(𝑥)=𝜃 имеет диапазон 0≤𝜃≤𝜋. Этот указывает, что 𝜃 находится в первом или втором квадранте. Однако нам говорят, что 0𝑥1, и согласно диаграмме CAST только первый или четвертый квадрант имеет положительные значения косинуса. Поэтому 𝜃 находится в первом квадранте; поэтому первое положительное значение 𝛼 равно 𝜃.

Чтобы найти следующее положительное значение 𝛼, нам нужно найти угол, который пересекает единичную окружность в точке то же 𝑥-значение, что и 𝜃. Как показано на диаграмме ниже, 𝑥-координаты в первом квадранте соответствуют 𝑥-координатам в четвертом квадранте.

Чтобы найти следующий положительный угол, где косинус имеет такое же значение, мы вычитаем 𝜃 из 2𝜋. Это означает, что coscos(2𝜋−𝜃)=(𝜃).

Например, как cos𝜋6, так и cos11𝜋6 равны √32, потому что coscos2𝜋−𝜋6=11𝜋6. Аналогично, как cos𝜋3, так и cos5𝜋3 равны 12, потому что cos2𝜋−𝜋3=5𝜋3.

В заключение мы показали, что искомые первые два положительных значения 𝛼 равны 𝜃 и 2𝜋−𝜃.

Давайте закончим повторением некоторых важных моментов объяснения.

Ключевые моменты

• Обратные тригонометрические функции арксинус, арккосинус и арктангенс определяются в терминах стандартной тригонометрической функции следующим образом:
  • Функция, обратная синусу, называется арксинусом .
    • Для −𝜋2≤𝜃≤𝜋2 и −1≤𝑘≤1, 𝜃=(𝑘)⇔𝑘=(𝜃)арксинсин.
  • Обратная функция косинуса называется арккосинус .
    • Для 0≤𝜃≤𝜋 и −1≤𝑘≤1, 𝜃=(𝑘)⇔𝑘=(𝜃)arccoscos.
  • Обратная функция тангенса называется арктангенс .
    • Для −𝜋2𝜃𝜋2 и 𝑘∈ℝ, 𝜃=(𝑘)⇔𝑘=(𝜃)арктантан.
• Единичная окружность — это окружность радиусом 1, центр которой лежит в начале координат плоскости.

  No related posts.