Обратная матрица онлайн калькулятор
Данный калькулятор позволит вам легко найти обратную матрицу при помощи матрицы алгебраических дополнений, а так же получить подробное решение. Калькулятор вычисляет обратную матрицу для матриц размерности от 2 × 2 до 9 × 9. При помощи данного калькулятора вы сможете быстро научиться находить обратную матрицу, благодаря подробно составленному алгоритму решения
Матрица размерности m × n – это таблица чисел у которой m строк и n столбцов.
Элементы матрицы обозначаются как aij, где i – номер строки, j – номер столбца.
Матрица A-1 называется обратной к матрице A, если A ⋅ A-1 = A-1 ⋅ A = E, где E — единичная матрица.
Для нахождения обратной матрицы необходимо, чтобы матрица A была квадратной и не равнялась нулю.
Чтобы записать дробь, воспользуйтесь знаком “ / ” например 3/5 или -3/5
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькуляторы (Теория чисел) |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер сложения |
| Тренажёр вычитания |
| Тренажёр умножения |
| Тренажёр деления |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Примеры нахождения обратной матрицы
Найти обратную матрицу для матрицы A размерности 2 × 2| A-1 = |
|
Решение
Найдем обратную матрицу для матрицы A при помощи матрицы алгебраических дополнений.
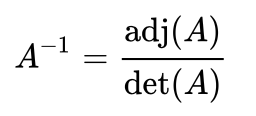 adj(A) — присоединенная матрица составленная из алгебраических дополнений
adj(A) — присоединенная матрица составленная из алгебраических дополненийdet(A) — определитель матрицы A
1. Найдем определитель для матрицы A
det A = 14
(Если вы хотите получить детальное решение нахождения определителя, то
воспользуйтесь калькулятором для нахождения определителя матрицы)
2. Найдем присоединенную матрицу adj(A) составленную из алгебраических дополнений. Для этого каждый элемент исходной матрицы aij заменим на его алгебраическое дополнение Aij
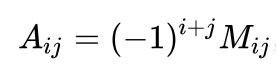 Mij — дополнительный минор, полученный из исходной матрицы A путем вычеркивания i-й строки и j-го
столбца
Mij — дополнительный минор, полученный из исходной матрицы A путем вычеркивания i-й строки и j-го
столбцаИсходная матрицы A состоит из 4 элементов, следовательно нам необходимо найти 4 дополнительных миноров Mij M11 = = = 7
M12 =
= = 4M21 =
= = 0M22 =
= = 2 Теперь запишем значение всех элементов присоединенной матрицы adj(A)A11 = (-1)1 + 1 ⋅ M11 = (-1)2 ⋅ 7 = 7
A12 = (-1)1 + 2 ⋅ M12 = (-1)3
⋅ 4 = -4
A21 = (-1)2 + 1 ⋅ M21 = (-1)3 ⋅ 0 = 0
A22 = (-1)2 + 2 ⋅ M22 = (-1)
4 ⋅ 2 = 2
3. Транспонируем присоединенную матрицу adj(A)4. Разделим все элементы матрицы adj(A)T на определитель исходной матрицы A
| A-1 = |
|
| A-1 = |
|
| A-1 = |
|
| A-1 = |
|
Решение
Найдем обратную матрицу для матрицы A при помощи матрицы алгебраических дополнений.
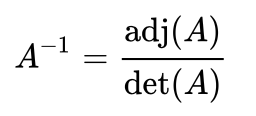 adj(A) — присоединенная матрица составленная из алгебраических дополнений
adj(A) — присоединенная матрица составленная из алгебраических дополненийdet(A) — определитель матрицы A
1. Найдем определитель для матрицы A
det A = -7396
(Если вы хотите получить детальное решение нахождения определителя, то
воспользуйтесь калькулятором для нахождения определителя матрицы)
2. Найдем присоединенную матрицу adj(A) составленную из алгебраических дополнений. Для этого каждый элемент исходной матрицы aij заменим на его алгебраическое дополнение Aij
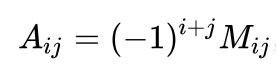 Mij — дополнительный минор, полученный из исходной матрицы A путем вычеркивания i-й строки и j-го
столбца
Mij — дополнительный минор, полученный из исходной матрицы A путем вычеркивания i-й строки и j-го
столбцаИсходная матрицы A состоит из 9 элементов, следовательно нам необходимо найти 9 дополнительных миноров Mij M11 = = = -1128
M12 =
= = -876M13 =
= = -470M21 =
= = -752M22 =
= = -584M23 =
= = 303M31 =
= = 12M32 =
= = 88M33 =
= = 5 Теперь запишем значение всех элементов присоединенной матрицы adj(A)A11 = (-1)1 + 1
⋅
M11 = (-1)2 ⋅ (-1128) = -1128
A12 = (-1)1 + 2 ⋅ M12 = (-1)3 ⋅ (-876) = 876
A13
=
(-1)1 + 3 ⋅ M13 = (-1)4 ⋅ (-470) = -470
A21 = (-1)2 + 1 ⋅ M21 = (-1)3 ⋅ (-752)
= 752
A22 = (-1)2 + 2 ⋅ M22 = (-1)4 ⋅ (-584) = -584
A23 = (-1)2 + 3 ⋅ M23 =
(-1)5 ⋅ 303 = -303
A31 = (-1)3 + 1 ⋅ M31 = (-1)4 ⋅ 12 = 12
A32 = (-1)3 + 2 ⋅
M32 = (-1)5 ⋅ 88 = -88
A33 = (-1)3 + 3 ⋅ M33 = (-1)6 ⋅ 5 = 5
| adj(A) = |
| = |
|
3. Транспонируем присоединенную матрицу adj(A)
| adj(A)T = |
|
| A-1 = |
|
| A-1 = |
|
| A-1 = |
|
Обратная матрица онлайн
Для любой невырожденной квадратной матрицы (т.е. такой определитель которой отличен от нуля), существует обратная матрица, такая, что её произведение на исходную матрицу равно единичной:
A∙A−1 = A−1∙A = E
Наш калькулятор поддерживает два различных способа вычисления обратной матрицы: по методу Гаусса-Жордана и при помощи построения алгебраических дополнений к исходной матрице.
Для нахождения обратной матрицы по методу Гаусса-Жордана, к исходной матрице справа дописывают единичную матрицу:
( A | E )
Затем, с помощью элементарных преобразований приводят исходную матрицу к единичной, выполняя теже самые операции и над единичной матрицей, записанной справа. В результате таких действий исходная матрица приводится к единичной, а единичная к обратной:
( A | E) → ( E | A−1 )
Метод довольно простой, удобный и не очень трудоемкий.
Для нахождения обратной матрицы при помощи метода алгебраических дополнений используют следующую формулу:

где
| A |
— определитель матрицы
A,
Ai j
— алгебраическое дополнение элемента
ai j
матрицы
A.
По определению:
Ai j = (-1) i+j Mi j
где Mi j — минор элемента ai j матрицы A.
По определению — минор элемента ai j матрицы A — это определитель, полученный путем вычеркивания i строки, j столбца матрицы A.
Таким образом, метод алгебраических дополнений для вычисления обратной матрицы порядка n является достаточно трудоемким, поскольку помимо определителя исходной матрицы, нужно вычислить n2 определителей n-1 порядка.
a‘,» = { | «,» maxLength=8 class=mvect>;»,» maxLength=8 class=mvect>}»,»‘,’ | ‘,» maxLength=8 class=mvect1> x«,» + «,» = «,» maxLength=8 class=mvect1> | «,»>B =«,’
|
Обратная матрица, онлайн калькулятор
Наш онлайн калькулятор позволяет найти обратную матрицу всего в пару кликов. Для нахождения обратной матрицы выберите ее размер, введите значения всех элементов матрицы и нажмите кнопку «Вычислить», калькулятор выдаст детальное решение и ответ! Каждый этап будет детально расписан, это поможет вам понять, как был получен ответ и, при необходимости, проверить свое решение.
Заполните элементы матрицы Решили сегодня: раз, всего раз| Понравился сайт? Расскажи друзьям! | |||
Как найти обратную матрицу онлайн
Для того, чтобы найти обратную матрицу онлайн, вам потребуется указать размер самой матрицы. Для этого кликните на иконки «+» или «-» до тех пор, пока значение количества столбцов и строк вас не устроит. Далее введите в поля требуемые элементы. Ниже находится кнопка «Вычислить» — нажав её, вы получите на экране ответ с подробным решением.
В линейной алгебре довольно часто приходится сталкиваться с процессом вычисления обратной матрицы. Она существует только для невыраженных матриц и для квадратных матриц при условии отличного от нуля детерминанта. В принципе, рассчитать её не представляет особой сложности, особенно если вы имеете дело с небольшой матрицей. Но если нужны более сложные расчёты или тщательная перепроверка своего решения, лучше воспользуйтесь данным онлайн калькулятором. С его помощью вы оперативно и с высокой точностью решите обратную матрицу.
С помощью данного онлайн калькулятора вы сможете значительно облегчить себе задачу в плане расчётов. Кроме того, он помогает закрепить материал, полученный в теории – это своеобразный тренажёр для мозга. Не стоит рассматривать его, как замену вычислениям вручную, он может дать вам гораздо больше, облегчив понимание самого алгоритма. К тому же, лишняя перепроверка себя никогда не помешает.
Обратная матрица онлайн
www.matcabi.net позволяет найти обратную матрицу онлайн. Сайт производит вычисление обратной матрицы онлайн. За неколько секунд сервер выдаст точное решение. Обратной матрицей будет являться такая матрица, умножение исходной матрицы на которую дает единичную матрицу, при условии, что определитель начальной матрицы не равен нулю, иначе обратной матрицы для нее не существует. В задачах, когда вычисляем обратную матрицу онлайн, необходимо, чтобы определитель матрицы был отличным от нуля, иначе www.matcabi.net выдаст соответствующее сообщение о невозможности вычислить обратную матрицу онлайн. Такую матрицу еще называют вырожденной. Найти обратную матрицу в режиме онлайн можно только для квадратной матрицы. Операция нахождения обратной матрицы онлайн сводится к вычислению определителя матрицы, затем составляется промежуточная матрица по известному правилу, и в завершении операции — умножения найденного ранее определителя на транспонированную промежуточную матрицу. Точного результата от определения обратной матрицы онлайн можно добиться, изучив теорию по этому курсу. Данная операция занимает особое место в теории матриц и линейной алгебры, позволяет решать системы линейных уравнений, так называемым, матричным методом. Задача по нахождению обратной матрицы онлайн встречается уже в начале изучения высшей математики и присутствует почти в каждой математической дисциплине как базовое понятие алгебры, являясь математическим инструментом в прикладных задачах. www.matcabi.net находит обратную матрицу заданной размерности в режиме онлайн мгновенно. Вычисление обратной матрицы онлайн при заданной её размерности — это нахождение матрицы той же размерности в числовом ее значении, а также в символьном, найденного по правилу вычисления обратной матрицы. Нахождение обратной матрицы онлайн широко распространено в теории матриц. Результат нахождения обратной матрицы онлайн используется при решении линейной системы уравнений матричным методом. Если определитель матрицы будет равен нулю, то обратной матрицы, для которой найден нулевой определитель, не существует. Для того, чтобы вычислить обратную матрицу или найти сразу для нескольких матриц соответствующие им обратные, необходимо затратить не мало времени и усилий, в то время как наш сервер в считанные секунды найдет обратную матрицу онлайн. При этом ответ по нахождению обратной матрицы будет правильным и с достаточной точностью, даже если числа при нахождении обратной матрицы онлайн будут иррациональными. На сайте www.matcabi.net допускаются символьные записи в элементах матриц, то есть обратная матрица онлайн может быть представлена в общем символьном виде при вычислении обратной матрицы онлайн. Полезно проверить ответ, полученный при решении задачи по нахождению обратной матрицы онлайн, используя сайт www.matcabi.net. При совершении операции вычисления обратной матрицы онлайн необходимо быть внимательным и предельно сосредоточенным при решении данной задачи. В свою очередь наш сайт поможет Вам проверить своё решение на тему обратная матрица онлайн. Если у Вас нет времени на долгие проверки решенных задач, то www.matcabi.net безусловно будет являться удобным инструментом для проверки при нахождении и вычислении обратной матрицы онлайн.
Онлайн калькулятор: Обратная матрица по модулю
Продолжаем серию калькуляторов про матрицы, предыдущие калькуляторы: Определитель (детерминант) матрицы, Транспонирование матрицы, Умножение матриц, Обратная матрица.
Калькулятор ниже находит обратную матрицу с помощью союзной матрицы, но выполняет все вычисления в кольце вычетов по модулю натурального числа m. Немного теории, как водится, под калькулятором.

Обратная матрица по модулю
6 24 1 13 16 10 20 17 15Исходная матрица
Обратная матрица
save Сохранить extension Виджет
Итак, обратная матрица — такая матрица, при умножении на которую исходная матрица A даёт в результате единичную матрицу E
В данном калькуляторе используется способ нахождения обратной матрицы через союзную матрицу по формуле
Союзная матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы.
Алгебраическое дополнение элемента матрицы A это число
где — определитель матрицы, получающейся из исходной матрицы A путем вычёркивания i -й строки и j -го столбца (дополнительный минор).
Отличие данного калькулятора от калькулятора Обратная матрица в том, что результаты всех вычислений приводятся к остатку от деления на m, а операция деления на детерминант заменяется на операцию умножения на обратный к значению детерминанта в кольце по модулю элемент, см. Обратный элемент в кольце по модулю.
Калькулятор обратной матрицы nxn
Как найти обратную матрицу?
Существует множество различных методов для нахождения обратной матрицы заданной матрицы. Некоторые из них: обратная матрице методом исключения Гаусса-Жордана и инверсия матрицы с использованием миноров, кофакторов и адъюгата. Мы представим вторую. Минор элемента любой матрицы $ n \ times n $ является определителем матрицы $ (n-1) \ times (n-1) $. Если мы удалим строку и столбец, содержащие элемент, то получим соответствующий минор.{3 + 3} \ left | \ BEGIN {массив} {} куб.см а & б \\ d & e \\ \ {Конец массива} \ Право | \\ \ {Конец массива} \право)\\ \ newline = \осталось( \ BEGIN {массив} {} ссс + \ Влево | \ BEGIN {массив} {} куб.см е & е \\ Здравствуй \\ \ {Конец массива} \ Право | & — \ left | \ BEGIN {массив} {} куб.см д & е \\ г & я \\ \ {Конец массива} \ right | & + \ left | \ BEGIN {массив} {} куб.см d & e \\ г & ч \\ \ {Конец массива} \ Право | \\ \ — \ влево | \ BEGIN {массив} {} куб.см До нашей эры \\ Здравствуй \\ \ {Конец массива} \ right | & + \ left | \ BEGIN {массив} {} куб.см а & с \\ г & я \\ \ {Конец массива} \ Право | & — \ left | \ BEGIN {массив} {} куб.см а & б \\ г & ч \\ \ {Конец массива} \ Право | \\ \ + \ Влево | \ BEGIN {массив} {} куб.см До нашей эры \\ е & е \\ \ {Конец массива} \ Право | & — \ left | \ BEGIN {массив} {} куб.см а & с \\ д & е \\ \ {Конец массива} \ Право | & + \ Влево | \ BEGIN {массив} {} куб.см а & б \\ d & e \\ \ {Конец массива} \ Право | \\ \ {Конец массива} \ right) \ end {align} $$
Адъюгат квадратной матрицы является транспонированием ее матрицы кофакторов.Транспонирование матрицы — это новая матрица, строки которой являются столбцами исходной. Так,$$ adj (A) = \ left ( \ BEGIN {массив} {} ссс + \ Влево | \ BEGIN {массив} {} куб.см е & е \\ Здравствуй \\ \ {Конец массива} \ Право | & — \ left | \ BEGIN {массив} {} куб.см До нашей эры \\ Здравствуй \\ \ {Конец массива} \ Право | & + \ влево | \ BEGIN {массив} {} куб.см До нашей эры \\ е & е \\ \ {Конец массива} \ Право | \\ \ — \ влево | \ BEGIN {массив} {} куб.см д & е \\ г & я \\ \ {Конец массива} \ right | & + \ left | \ BEGIN {массив} {} куб.см а & с \\ г & я \\ \ {Конец массива} \ Право | & — \ left | \ BEGIN {массив} {} куб.см а & с \\ д & е \\ \ {Конец массива} \ Право | \\ \ + \ Влево | \ BEGIN {массив} {} куб.см d & e \\ г & ч \\ \ {Конец массива} \ Право | & — \ left | \ BEGIN {массив} {} куб.см а & б \\ г & ч \\ \ {Конец массива} \ Право | & + \ влево | \ BEGIN {массив} {} куб.см а & б \\ d & e \\ \ {Конец массива} \ Право | \\ \ {Конец массива} \ справа) $$
Для любой квадратной матрицы $ A $ размера nxn, если $ det (A) \ ne0 $, то обратная матрица определяется по формуле $$ A ^ {- 1} = \ гидроразрыва {1} {Det (A)} прил (A) $$ Чтобы найти обратную матрицу заданной матрицы $ A $, нам нужно проверить, обратима ли матрица $ A $.- Если $ det (A) \ ne0 $, матрица $ A $ обратима;
- Если $ det (A) = 0 $, матрица $ A $ необратима или сингулярна.
- Найти определитель матрицы $ A $, $ det (A) $;
- Найти миноры матрицы $ A $;
- Найдите матрицу сомножителей,
- Найдите адъюгат;
- Обратная матрица матрицы $ A $ — это скалярное умножение сопряженного элемента на $ \ frac 1 {det (A)} $.{3 + 3} \ left |
\ BEGIN {массив} {} куб.см
10 и 20 \\
4 и 5 \\
\ {Конец массива}
\ Право | \\
\ {Конец массива}
\право)\\ \ newline =
\осталось(
\ BEGIN {массив} {} ссс
7 и -8 и 2
\\
-70 и 30 и 10
\\
70 & -20 & -30 \\
\ {Конец массива}
\ right) \ end {align} $$ Если мы транспонируем матрицу кофакторов, мы получим
$$ \ осталось ( \ BEGIN {массив} {} ссс 7 и -70 и 70 \\ -8 и 30 и -20 \\ 2 и 10 и -30 \\ \ {Конец массива} \ справа) $$
Наконец, обратная матрица $ A ^ {- 1} $ к матрице $ A $ равна$$ A ^ {- 1} = \ frac 1 {-70} \ left ( \ BEGIN {массив} {} ссс 7 и -70 и 70 \\ -8 и 30 и -20 \\ 2 и 10 и -30 \\ \ {Конец массива} \ Справа) = \ влево ( \ BEGIN {массив} {} ссс — \ frac 1 {10} & 1 & 1 \\ \ frac4 {35} & — \ frac37 & \ frac27 \\ — \ frac {1} {35} & — \ frac17 & \ frac37 \\ \ {Конец массива} \ справа) $$
Работа с обратной матрицей nxn с шагами показывает полное пошаговое вычисление для нахождения определителя матрицы $ A $ 4×4, 3×3 или 2×2 с использованием формулы обратной матрицы.Для любых других матриц просто укажите действительные числа в качестве элементов матрицы и нажмите кнопку GENERATE WORK. Ученики начальной школы и люди, изучающие математику, используют этот калькулятор обратной матрицы nxn для создания работы, проверки результатов обратной матрицы, полученной вручную, или эффективного выполнения домашних заданий. Ученики начальной школы также могут использовать этот калькулятор для решения системы линейных уравнений. ,Метод обратной матрицы — Бесплатная справка по математике
Решение системы линейных уравнений: (урок 5 из 5)
Метод обратной матрицы
Предположим, вам дано уравнение с одной переменной, например, $ 4x = 10 $. затем вы найдете значение $ x $, которое решает это уравнение, умножив уравнение, обратное 4: $ \ color {blue} {\ frac14} \ cdot 4x = \ color {blue} {\ frac14} \ cdot 10 $, так что решение будет $ x = 2.5 $.
Иногда мы можем сделать что-то очень похожее, чтобы решить системы линейных уравнения; в этом случае мы будем использовать обратную матрицу коэффициентов. Но сначала мы должны проверить, что эта инверсия существует! Условия существования обратной матрицы коэффициентов такие же, как и для использования Правило Крамера, то есть
1. В системе должно быть одинаковое количество уравнения как переменные, то есть матрица коэффициентов системы должна быть квадрат.
2. Определитель матрица коэффициентов должна быть отличной от нуля. Причина, конечно же, в том, что обратное матрицы существует именно тогда, когда ее определитель отличен от нуля.
3. Чтобы использовать этот метод, следуйте шаги, продемонстрированные на следующей системе:
$$ \ Начать {выравниваются} -x + 3y + z & = 1 \\ 2х + 5у & = 3 \\ 3x + y — 2z & = -2 \ {Конец выровнен} $$Шаг 1: Перепишите систему, используя умножение матриц:
$$ \ left ({\ begin {array} {* {20} {c}} — 1 \\ 2 \\ 3 \ Конец {массив} \ BEGIN {массив} {* {20} {с}} 3 \\ 5 \\ 1 \ Конец {массив} \ BEGIN {массив} {* {20} {с}} 1 \\ 0 \\ — 2 \ end {array}} \ right) \ left ({\ begin {array} {* {20} {c}} Икс\\ у \\ Z \ end {array}} \ right) = \ left ({\ begin {array} {* {20} {c}} 1 \\ 3 \\ — 2 \ end {array}} \ right) $$и записав матрицу коэффициентов как A, мы имеем
$$ A \ left ({\ begin {array} {* {20} {c}} Икс\\ у \\ Z \ end {array}} \ right) = \ left ({\ begin {array} {* {20} {c}} 1 \\ 3 \\ — 2 \ end {array}} \ right) $$Шаг 2: Найдите обратную матрицу коэффициентов A.{- 1}} \ left ({\ begin {array} {* {20} {c}} 1 \\ 3 \\ {- 2} \ end {array}} \ right) = \ left ({\ begin {array} {* {20} {c}} {- \ frac {{10}} {9}} \\ {\ Гидроразрыва {4} {9}} \\ {- \ frac {{13}} {9}} \ Конец {массив} \ BEGIN {массив} {* {20} {с}} {\ Гидроразрыва {7} {9}} \\ {- \ frac {1} {9}} \\ {\ Гидроразрыва {{10}} {9}} \ Конец {массив} \ BEGIN {массив} {* {20} {с}} {- \ frac {5} {9}} \\ {\ Гидроразрыва {2} {9}} \\ {- \ frac {{11}} {9}} \ end {array}} \ right) \ left ({\ begin {array} {* {20} {c}} 1 \\ 3 \\ {- 2} \ end {array}} \ right) = \ left ({\ begin {array} {* {20} {c}} {21} \\ {- 3} \\ {39} \ end {array}} \ right) $$
, поэтому решение —
$$ \ left ({\ begin {array} {* {20} {c}} Икс\\ у \\ Z \ end {array}} \ right) = \ left ({\ begin {array} {* {20} {c}} {21} \\ {- 3} \\ {39} \ end {array}} \ right) $$ ,Онлайн-калькулятор: Калькулятор обратной матрицы
Калькулятор ниже вычисляет обратную матрицу с помощью алгоритма Гаусса-Жордана. Некоторые теории и формулы можно найти под калькулятором.

Инверсия матрицы
Точность вычисленияЦифры после десятичной точки: 2
сохранить Сохранить расширение Виджет
Матрица, обратная квадратной матрице A, иногда называемая обратной матрицей, представляет собой такую матрицу, что
Для ручного расчета вы можете использовать матрицу сопряжения для вычисления обратной матрицы следующим образом:
Матрица адъюгата — это транспонированная матрица кофакторов A.
Кофактор A определяется как
, где является второстепенным.Вы можете относительно легко использовать этот метод для небольших матриц, 2×2, 3×3 или, может быть, 4×4. Для матриц большего размера проще использовать алгоритм Гаусса-Жордана, реализованный с помощью калькулятора.
.-1 = I, где I — единичная матрица.Результаты
Инверсия матрицы — dCode
Тег (-ы): Matrix
Поделиться

dCode и вы
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !Калькулятор для вычисления функции вычисления квадратной матрицы NxN
Матричный модульный обратный калькулятор
Инструмент для инвертирования матрицы.{-1} = \ frac {1} {\ det (M)} \ begin {bmatrix} 4 & -2 \\ -3 & 1 \\ \ end {bmatrix} = — \ frac {1} {2} \ begin {bmatrix} 4 & -2 \\ -3 & 1 \\ \ end {bmatrix} $$
Для того чтобы матрица была обратимой, важно, чтобы определитель инвертируемой матрицы не был равен нулю.
Как доказать обратимость матрицы?
Матрица обратима, если ее определитель отличен от нуля (отличен от 0).
Необратимая матрица называется сингулярной .{-1} = I $.
Как вычислить модульную обратную матрицу?
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Инверсия матрицы». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate), написанные на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.)) никакие данные, скрипты или доступ к API не будут бесплатными, то же самое для инверсной загрузки матрицы для автономного использования на ПК, планшете, iPhone или Android!
Нужна помощь?
Пожалуйста, заходите в наше сообщество в Discord для получения помощи!
Вопросы / комментарии
Сводка
Инструменты аналогичные
Поддержка
Форум / Справка

Рекламные объявления
Ключевые слова
инверсия, матрица, квадрат, тождество, инверсия, обратимая, сингулярное
Ссылки
Источник: https: // www.dcode.fr/matrix-inverse
© 2020 dCode — Лучший «инструментарий» для решения любых игр / загадок / геокешинга / CTF. ,



