Умножение матрицы на число — Онлайн калькулятор
- Справочник
- Онлайн-калькуляторы
- Тесты с ответами
Умножение матрицы на число онлайн-калькулятором дает матрицу той же размерности, что исходная. Каждый элемент полученной матрицы – это результат произведения соответствующего элемента исходной матрицы на заданное число.
Использование калькулятора на нашем сервисе происходит на бесплатной основе. Вы сможете быстро получить верный ответ на задачу. Формула, автоматизирующая процесс, позволяет совершать вычисления бесконечное количество раз. Калькулятором часто пользуются студенты, учащиеся старшей школы, преподаватели, инженеры.
Чтобы умножить матрицу на число онлайн:
- выберите количество строк и столбцов в матрице;
- введите значения матрицы в пустые поля;
- в необходимое поле введите число, на которое необходимо умножить матрицу;
- для получения решения используйте кнопку «Рассчитать».

Умножение матрицы на число с помощью онлайн-калькулятора
Чтобы умножить матрицу на число, нужно каждый элемент этой матрицы умножить на заданное число. Как это сделать с помощью онлайн-калькулятора:
- Необходимо задать матрицу. Для этого выберите необходимое число строк и столбцов (размерность матрицы), а затем задайте значения:
- В самом нижнем поле укажите число, на которое хотите умножить матрицу, а затем нажмите «Рассчитать». Для произвольной матрицы размерностью 3х2 это будет выглядеть так:
- После нажатия кнопки «рассчитать» ознакомьтесь с решением:
Материалы, которые помогут вам лучше разобраться в теме:
- Матрицы (раздел)
- Умножение матриц: примеры, алгоритм действий, свойства произведения
- Определитель матрицы: алгоритм и примеры вычисления определителя матрицы
- Равенство матриц: как доказать и проверить?
- Действия над матрицами.
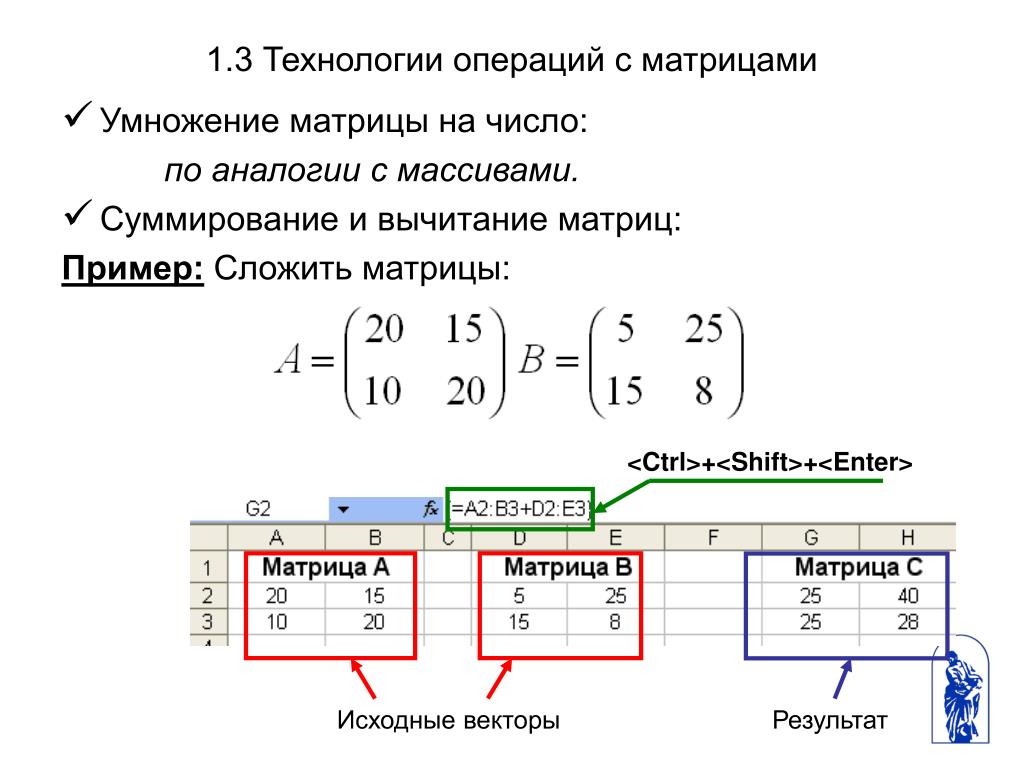
 Сложение и вычитание
Сложение и вычитание - Нахождение ранга матрицы
Ответ:
Решение
Ответ:
Похожие калькуляторы:
- Найти определитель матрицы
- Найти обратную матрицу
- Возведение матрицы в степень
- Умножение матриц
- Транспонирование матрицы
- Сложение и вычитание матриц
- Ранг матрицы
Умножение матрицы на число онлайн
Результатом умножения матрицы A на число k является матрица
bi,j=k*ai,j
Не всегда учащимся требуется только конечный ответ. Мы предоставили возможность проследить за полным алгоритмом вычислений. На сайте доступно умножение матрицы на число онлайн-калькулятором с подробным решением. Так вы сможете свериться с результатом, полученным самостоятельно.
Мы предоставили возможность проследить за полным алгоритмом вычислений. На сайте доступно умножение матрицы на число онлайн-калькулятором с подробным решением. Так вы сможете свериться с результатом, полученным самостоятельно.
Если необходима помощь в профессиональной подготовке контрольных работ и других учебных материалов, обратитесь к консультанту для оформления выгодного заказа.
Понравился калькулятор? Поделись с друзьями!
Разделы калькуляторов
- Решение матриц
- Точка, прямая, плоскость
- Конвертеры
- Объем фигур
- Калькуляторы площади фигур
- Решение уравнений
- Операции над векторами
- Периметр фигур
Поможем с любой работой
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Решение задач
- Отчеты по практике
Все наши услуги
Узнай бесплатно стоимость работыНе получается написать работу самому?
Доверь это кандидату наук!
вектор умножить на матрицу онлайн
вектор умножить на матрицу онлайнВы искали вектор умножить на матрицу онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить произведение матриц, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вектор умножить на матрицу онлайн».
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить произведение матриц, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вектор умножить на матрицу онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вектор умножить на матрицу онлайн,вычислить произведение матриц,вычислить произведение матриц онлайн с решением,дробь умножить на матрицу онлайн,как дробь умножить на матрицу,как умножить матрицу на матрицу 3х3,как умножить обратную матрицу на матрицу,калькулятор матриц онлайн с решением умножение,калькулятор матриц онлайн умножение матриц,калькулятор матриц перемножение,калькулятор матриц произведение,калькулятор матриц умножение,калькулятор матриц умножение матриц онлайн,калькулятор матрицы онлайн умножение,калькулятор матрицы умножение,калькулятор матрицы умножение онлайн,калькулятор онлайн матрицы умножение,калькулятор онлайн умножение матрицы,калькулятор перемножения матриц,калькулятор произведение матриц,калькулятор произведения матриц,калькулятор произведения матриц онлайн,калькулятор умножение матриц,калькулятор умножение матрицу на матрицу,калькулятор умножение матрицы,калькулятор умножение матрицы на матрицу,калькулятор умножение матрицы на матрицу онлайн,калькулятор умножение матрицы онлайн,калькулятор умножения матриц,калькулятор умножения матриц онлайн,матрица на матрицу умножение,матрица на матрицу умножение онлайн,матрица онлайн умножение,матрица умножение на матрицу онлайн,матрица умножение онлайн,матрица умножить на матрицу,матрицу умножить на вектор онлайн,матрицу умножить на матрицу онлайн,матрицу умножить на обратную матрицу,матрицы калькулятор умножение,матрицы найти произведение,матрицы онлайн калькулятор умножение,матрицы перемножение,матрицы умножение калькулятор,матрицы умножение онлайн,матрицы умножение онлайн калькулятор,матрицы умножения,матрицы умножить,множення матриць,найдите произведение матриц,найти произведение матриц,найти произведение матриц калькулятор онлайн,найти произведение матриц онлайн,найти произведение матриц онлайн калькулятор,найти произведение матриц онлайн с решением,найти произведение матрицы,найти произведения матриц,обратную матрицу умножить на матрицу,онлайн калькулятор матриц умножение матриц,онлайн калькулятор матриц умножения,онлайн калькулятор матрицы умножение,онлайн калькулятор найти произведение матриц,онлайн калькулятор перемножение матриц,онлайн калькулятор произведение матриц,онлайн калькулятор произведения матриц,онлайн калькулятор умножение матриц,онлайн калькулятор умножение матриц с подробным решением,онлайн калькулятор умножение матриц с решением,онлайн калькулятор умножение матриц с решением онлайн,онлайн калькулятор умножение матрицы,онлайн калькулятор умножение матрицы на матрицу,онлайн калькулятор умножения матриц,онлайн матрица умножение,онлайн перемножение матриц,онлайн умножение двух матриц,онлайн умножение матриц на матрицу,онлайн умножение матрица,онлайн умножение матрицы,онлайн умножение матрицы на матрицу,онлайн умножение трех матриц,онлайн умножения матриц,онлайн умножить матрицу на матрицу,перемножение матриц,перемножение матриц 3 на 3,перемножение матриц калькулятор,перемножение матриц онлайн,перемножение матриц онлайн калькулятор,перемножение матрицы,перемножить матрицы,перемножить матрицы онлайн,произведение матриц онлайн,произведение матриц онлайн калькулятор,произведения матриц калькулятор,произведения матриц калькулятор онлайн,произведения матриц онлайн калькулятор,решение матриц умножение матриц,умножение двух матриц онлайн,умножение матриц,умножение матриц 2 на 2,умножение матриц калькулятор,умножение матриц калькулятор онлайн,умножение матриц на матрицу онлайн,умножение матриц онлайн,умножение матриц онлайн калькулятор,умножение матриц онлайн калькулятор с подробным решением,умножение матриц онлайн калькулятор с решением,умножение матриц онлайн с решением,умножение матриц с,умножение матриц трех онлайн,умножение матрица,умножение матрица на матрица,умножение матрица на матрица онлайн,умножение матрица на матрицу онлайн,умножение матрица онлайн,умножение матрицу на матрицу калькулятор,умножение матрицы 3х3 на матрицу 3х3,умножение матрицы калькулятор,умножение матрицы калькулятор онлайн,умножение матрицы на вектор онлайн,умножение матрицы на матрицу 3х3,умножение матрицы на матрицу калькулятор,умножение матрицы на матрицу калькулятор онлайн,умножение матрицы на матрицу онлайн,умножение матрицы на матрицу онлайн калькулятор,умножение матрицы на матрицу онлайн с решением,умножение матрицы на матрицы калькулятор,умножение матрицы онлайн,умножение матрицы онлайн калькулятор,умножение обратной матрицы на матрицу,умножение онлайн матрица,умножение трех матриц,умножение число на матриц онлайн,умножения матриц онлайн,умножения матриц онлайн калькулятор,умножения матрицу на матрицу,умножения матрицы,умножить вектор на матрицу онлайн,умножить дробь на матрицу онлайн,умножить матрицу а на матрицу в,умножить матрицу на вектор онлайн,умножить матрицу на дробь онлайн,умножить матрицу на матрицу,умножить матрицу на матрицу онлайн,умножить матрицу на матрицу онлайн с решением,умножить матрицы,умножить матрицы онлайн,умножить матрицы онлайн с решением.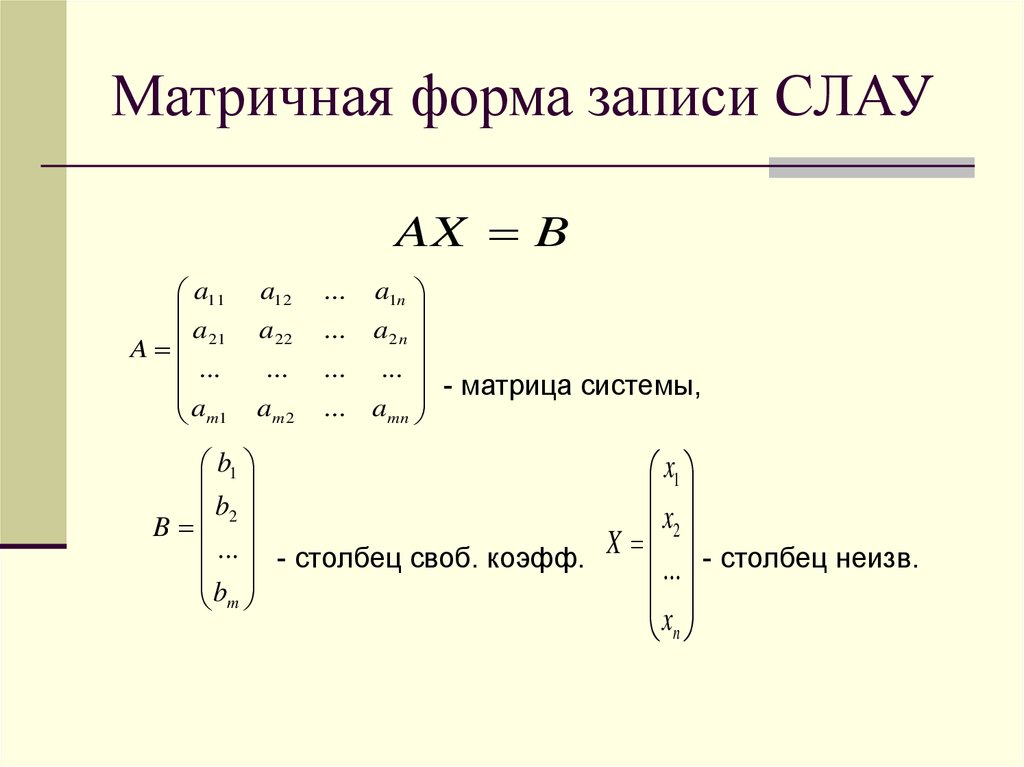
Решить задачу вектор умножить на матрицу онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Произведение двух матриц: формула, решения, свойства
- Произведение матриц: определение, формула, способ нахождения
- Примеры нахождения произведения матриц различной размерности
- Возведение матрицы в степень
- Свойства произведения матриц
- Калькулятор произведения матриц онлайн
Будут и задачи для самостоятельного решения, к которым можно
посмотреть ответы.
Определение. Произведением двух матриц А и В называется матрица С, элемент которой, находящийся на пересечении i-й строки и j-го столбца, равен сумме произведений элементов i-й строки матрицы А на соответствующие (по порядку) элементы j-го столбца матрицы В.
Из этого определения следует формула элемента матрицы C:
Произведение матрицы А на матрицу В обозначается АВ.
Пример 1. Найти произведение двух матриц А и B, если
,
.
Решение. Удобно нахождение произведения двух матриц А и В записывать так, как на рис.2:
На схеме серые стрелки показывают, элементы какой строки матрицы А на элементы
какого столбца матрицы В нужно перемножить для получения элементов матрицы С , а линиями цвета
элемента матрицы C соединены соответствующие элементы матриц A и B, произведения
которых складываются для получения элемента матрицы C.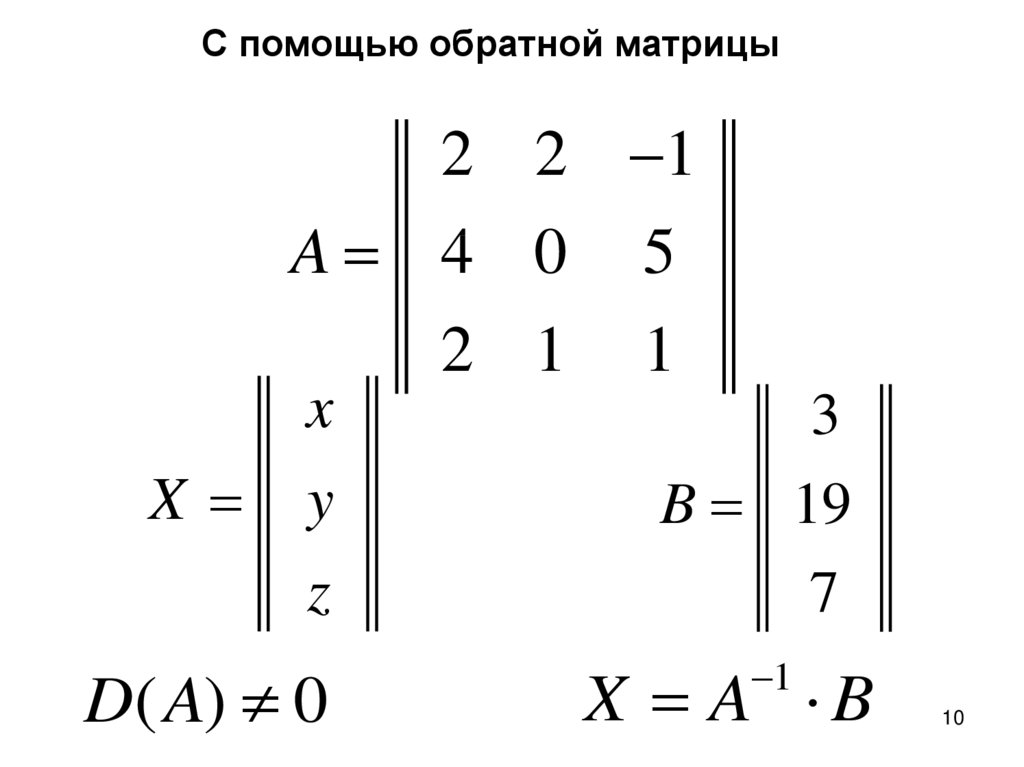
В результате получаем элементы произведения матриц:
Теперь у нас есть всё, чтобы записать произведение двух матриц:
.
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Произведение двух матриц АВ имеет смысл только в том случае, когда число столбцов матрицы А совпадает с числом строк матрицы В .
Эту важную особенность будет легче запомнить, если почаще пользоваться следующими памятками:
Имеет место ещё одна важная особенность произведения матриц относительно числа строк и столбцов:
В произведении матриц АВ число строк равно числу строк матрицы А , а число столбцов равно числу столбцов матрицы В .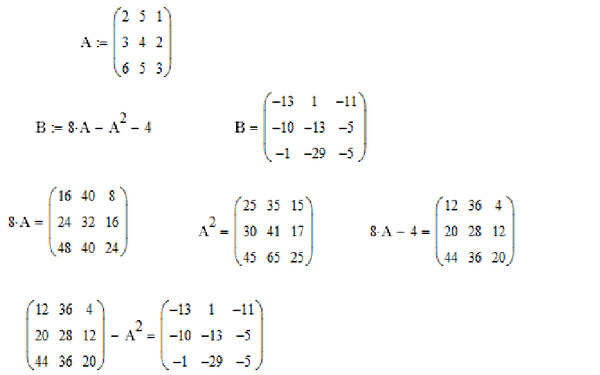
Пример 2. Найти число строк и столбцов матрицы C, которая является произведением двух матриц A и B следующих размерностей:
а) 2 Х 10 и 10 Х 5;
б) 10 Х 2 и 2 Х 5;
в) 4 Х 4 и 4 Х 10.
Решение:
а) 2 Х 5;
б) 10 Х 5;
в) 4 Х 10.
Пример 3. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A — 2, число столбцов в матрице B — 2. Следовательно, размерность матрицы C = AB — 2 X 2.
Вычисляем элементы матрицы C = AB.
Найденное произведение матриц: .
Пример 4. Найти произведение матриц и .
Правильное решение и ответ.
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Матрицы
Пример 5. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A — 2, число столбцов в матрице B — 1. Следовательно, размерность матрицы C = AB — 2 X 1.
Вычисляем элементы матрицы C = AB.
Произведение матриц запишется в виде матрицы-столбца: .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Пример 6. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A — 3, число столбцов в матрице B — 3.
Следовательно, размерность матрицы C = AB — 3 X 3.
Число строк в матрице A — 3, число столбцов в матрице B — 3.
Следовательно, размерность матрицы C = AB — 3 X 3.
Вычисляем элементы матрицы C = AB.
Найденное произведение матриц: .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Пример 7. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A — 1, число столбцов в матрице B — 1. Следовательно, размерность матрицы C = AB — 1 X 1.
Вычисляем элемент матрицы C = AB.
Произведение матриц является матрицей из одного элемента: .
Проверить решение этой и других подобных задач можно на калькуляторе произведения
матриц онлайн.
Программная реализация произведения двух матриц на С++ разобрана в соответствующей статье в блоке «Компьютеры и программирование».
Возведение матрицы в степень определяется как умножение матрицы на ту же самую матрицу. Так как произведение матриц существует только тогда, когда число столбцов первой матрицы совпадает с числом строк второй матрицы, то возводить в степень можно только квадратные матрицы. n-ая степень матрицы путём умножения матрицы на саму себя n раз:
Пример 8. Дана матрица . Найти A² и A³.
Решение:
Найти произведение матриц самостоятельно, а затем посмотреть решение
Пример 9. Дана матрица
Найти произведение данной матрицы и транспонированной матрицы ,
произведение транспонированной матрицы и
данной матрицы.
Правильное решение и ответ.
Свойство 1. Произведение любой матрицы А на единичную матрицу Е соответствующего порядка как справа, так и слева, совпадает с матрицей А , т.е. АЕ = ЕА = А .
Иными словами, роль единичной матрицы при умножении матриц такая же, как и единицы при умножении чисел.
Пример 10. Убедиться в справедливости свойства 1, найдя произведения матрицы
на единичную матрицу справа и слева.
Решение. Так как матрица А содержит три столбца, то требуется найти произведение АЕ , где
—
единичная матрица третьего порядка. Найдём элементы произведения С = АЕ :
Получается, что АЕ = А .
Теперь найдём произведение ЕА , где Е – единичная матрица второго порядка, так как матрица А содержит две строки. Найдём элементы произведения С = ЕА :
Доказано: ЕА = А .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Свойство 2. Произведение матрицы А на нуль-матрицу является нуль-матрицей. Это свойство очевидно, так как все элементы нуль-матрицы равны нулю.
Свойство 3. Произведение матриц некоммутативно:
.
Для этого достаточно показать, что равенство АВ = ВА не выполняется для каких-либо двух матриц.
Пример 11. Найти произведения матриц АВ и ВА, если
,
,
и убедиться в том, что эти произведения не равны друг другу:
.
Решение. Находим:
И действительно, найденные произведения не равны:
.
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Свойство 4. Произведение матриц ассоциативно: (АВ)С = А(ВС) .
Свойство 5. Для произведения матриц выполняется дистрибутивный закон: (А + В) С = АС + ВС , С (А + В) = СА + СВ .
Свойство 6. Определитель произведения двух квадратных матриц равен произведению их определителей: если С = АВ , то
.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Матрицы
Поделиться с друзьями
Начало темы «Матрицы»
Понятие матрицы
Продолжение темы «Матрицы»
Обратная матрица
Умножение матрицы на число
Сложение матриц
Найти ранг матрицы: способы и примеры
Решение матричных уравнений
Другие темы линейной алгебры
Определители
Системы линейных уравнений
| A 1,1 = (-1) 1+1 |
|
∆ 1,1 = (-1 4-5 (-2)) = 6
| A 1,2 = (-1) 1+2 |
|
∆ 1,2 = -(2 4-(-2 (-2))) = -4
| A 1,3 = (-1) 1+3 |
|
∆ 1,3 = (2 5-(-2 (-1))) = 8
| A 2,1 = (-1) 2+1 |
|
∆ 2,1 = -(2 4-5 3) = 7
| A 2,2 = (-1) 2+2 |
|
∆ 2,2 = (-1 4-(-2 3)) = 2
| A 2,3 = (-1) 2+3 |
|
∆ 2,3 = -(-1 5-(-2 2)) = 1
| A 3,1 = (-1) 3+1 |
|
∆ 3,1 = (2 (-2)-(-1 3)) = -1
| A 3,2 = (-1) 3+2 |
|
∆ 3,2 = -(-1 (-2)-2 3) = 4
| A 3,3 = (-1) 3+3 |
|
∆ 3,3 = (-1 (-1)-2 2) = -3
Тогда обратную матрицу можно записать как:
| A -1 = 1 / 10 |
|
| A -1 = |
|
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.
- Находим определитель данной квадратной матрицы A .
- Находим алгебраические дополнения ко всем элементам матрицы A .
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы A .
Как видим, операция транспонирования может применяться как в начале, над исходной матрицей, так и в конце, над полученными алгебраическими дополнениями.
Особый случай : Обратной, по отношению к единичной матрице E , является единичная матрица E .
Похожие на обратные по многим свойствам.
Энциклопедичный YouTube
1 / 5
✪ Как находить обратную матрицу — bezbotvy
✪ Обратная матрица (2 способа нахождения)
✪ Обратная матрица #1
✪ 2015-01-28. Обратная матрица 3×3
✪ 2015-01-27. Обратная матрица 2х2
Субтитры
Свойства обратной матрицы
- det
A
−
1
=
1
det
A
{\displaystyle \det A^{-1}={\frac {1}{\det A}}}
, где
det
{\displaystyle \ \det }
обозначает определитель .
 {-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
{-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
Способы нахождения обратной матрицы
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Точные (прямые) методы
Метод Гаусса-Жордана
Возьмём две матрицы: саму A и единичную E . Приведём матрицу A к единичной матрице методом Гаусса-Жордана применяя преобразования по строкам (можно также применять преобразования и по столбцам, но не в перемешку). После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A −1 .
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λ i {\displaystyle \Lambda _{i}} (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
Λ
1
⋅
⋯
⋅
Λ
n
⋅
A
=
Λ
A
=
E
⇒
Λ
=
A
−
1
{\displaystyle \Lambda _{1}\cdot \dots \cdot \Lambda _{n}\cdot A=\Lambda A=E\Rightarrow \Lambda =A^{-1}}
. {-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}
{-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}
где adj (A) {\displaystyle {\mbox{adj}}(A)} — присоединенная матрица ;
Сложность алгоритма зависит от сложности алгоритма расчета определителя O det и равна O(n²)·O det .
Использование LU/LUP-разложения
Матричное уравнение
A
X
=
I
n
{\displaystyle AX=I_{n}}
для обратной матрицы
X
{\displaystyle X}
можно рассматривать как совокупность
n
{\displaystyle n}
систем вида
A
x
=
b
{\displaystyle Ax=b}
. Обозначим
i
{\displaystyle i}
-ый столбец матрицы
X
{\displaystyle X}
через
X
i
{\displaystyle X_{i}}
; тогда
A
X
i
=
e
i
{\displaystyle AX_{i}=e_{i}}
,
i
=
1
,
…
,
n
{\displaystyle i=1,\ldots ,n}
,поскольку
i
{\displaystyle i}
-м столбцом матрицы
I
n
{\displaystyle I_{n}}
является единичный вектор
e
i
{\displaystyle e_{i}}
. другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³) . {-1}={\frac {1}{\det(\mathbf {A})}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}={\frac {1}{ad-bc}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}.}
{-1}={\frac {1}{\det(\mathbf {A})}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}={\frac {1}{ad-bc}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}.}
Обращение матрицы 2х2 возможно только при условии, что a d − b c = det A ≠ 0 {\displaystyle ad-bc=\det A\neq 0} .
Обратная матрица — презентация онлайн
Похожие презентации:
Матрицы и определители
Обратная матрица
Определитель и его свойства. Обратная матрица
Матрицы, определители. Обратная матрица. Ранг матрицы. Системы линейных уравнений элементы векторной алгебры
Матрицы и определители
Линейная алгебра. Невырожденные матрицы. Обратная матрица. Матричные уравнения
Определители матриц. Обратная матрица, ранг матрицы
Линейная алгебра. Матрицы
Линейная алгебра. Матрицы и действия над ними
Матрицы и определители
1. ОБРАТНАЯ МАТРИЦА
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ –записываем в конспекте
тему, цель занятия, далее
записываем ЗАДАНИЕ
2.
 НАУЧИТЬСЯ СТРОИТЬ ОБРАТНУЮ МАТРИЦУ ДЛЯ ДАННОЙ МАТРИЦЫЦЕЛЬ ЗАНЯТИЯ:
НАУЧИТЬСЯ СТРОИТЬ ОБРАТНУЮ МАТРИЦУ ДЛЯ ДАННОЙ МАТРИЦЫЦЕЛЬ ЗАНЯТИЯ:НАУЧИТЬСЯ СТРОИТЬ
ОБРАТНУЮ МАТРИЦУ
ДЛЯ ДАННОЙ МАТРИЦЫ
3. Задание. Для данной матрицы найти обратную матрицу.
4. СОЗДАТЬ МАТРИЦУ:
ДАННУЮ МАТРИЦУ ВЫ УЖЕ ЗАПИСАЛИ – ЭТО ВАША МАТРИЦА № 3 –ВЫ ЕЕ ПРОСТО ПЕРЕПИСЫВАЕТЕ СЮДА – САВЧЕНКО И САМОЙЛОВ ПОМНЯТ,
ЧТО ОНИ РАБОТАЮТ СО ВТОРЫМ ВАРИАНТОМ МАТРИЦЫ.
ПОМНИТЕ, ЧТО ЗАПИСЬ МАТРИЦЫ ОТ ЗАПИСИ ЕЁ ОПРЕДЕЛИТЕЛЯ
ОТЛИЧАЕТСЯ СКОБКАМИ:: МАТРИЦА – КРУГЛЫЕ, ОПРЕДЕЛИТЕЛЬ –
ВЕРТИКАЛЬНЫЕ.
А ДАЛЕЕ НАЧИНАЕТСЯ САМА РАБОТА –
— ПО ШАГАМ –
— ДЕЛАЕМ ВСЕ ОЧЕНЬ ПОДРОБНО –
И ХОТЯ НА ДАННЫЙ МОМЕНТ ОТЧЕТ ВЫ МНЕ СНОВА БУДЕТЕ ПРИСЫЛАТЬ В
ГУГЛ ФОРМЕ –
— ЭТУ РАБОТУ Я БУДУ ПРОВЕРЯТЬ И ПРИ ПРОВЕРКЕ КОНСПЕКТА ДЛЯ
ДОПУСКА К ДИФЗАЧЕТУ.
В КАЖДОМ ШАГЕ ЕСТЬ ПОЯСНИТЕЛЬНАЯ ТЕОРЕТИЧЕСКАЯ ЧАСТЬ СНАЧАЛА ВЫ ЗАПИСЫВАЕТЕ ЕЕ, ДАЛЕЕ ИЗУЧАЕТЕ НА СЛАЙДЕ
РАЗОБРАННЫЙ ПРИМЕР — ЭТО МОЙ ПРИМЕР С МОЕЙ МАТРИЦЕЙ — ЕГО
ПЕРЕПИСЫВАТЬ НЕ НАДО — И ВЫПОЛНЯЕТЕ ШАГ ДЛЯ СВОЕЙ МАТРИЦЫ.

УСПЕХОВ И УДАЧИ!!!!
6. Шаг 1. Найдем определитель данной матрицы, пользуясь правилом Сарруса:
(+)(главная диагональ)
a11
a12
a13
a21
a22
a23
a31
a32
a33
(-)
(побочная диагональ)
7. ФАКТИЧЕСКИ ЭТОТ ШАГ ВАМИ УЖЕ ВЫПОЛНЕН
ШАГ ВАМИ УЖЕВЫПОЛНЕН
• ВАМ НАДО ПЕРЕПИСАТЬ СЮДА СВОЙ
ОПРЕДЕЛИТЕЛЬ № 3 СО ВСЕМ ПОДРОБНЫМ
ВЫЧИСЛЕНИЕМ И РЕЗУЛЬТАТОМ.
• А ДАЛЕЕ ВЫ ЗАПИСЫВАЕТЕ ВЫВОД – Т.К.
СОГЛАСНО ТЕОРЕМЕ ОБ ОБРАТНОЙ МАТРИЦЕ,
ОНА СУЩЕСТВУЕТ ТОЛЬКО ТОГДА, КОГДА
ОПРЕДЕЛИТЕЛЬ ДАННОЙ МАТРИЦЫ НЕ РАВЕН
НУЛЮ. ( СМОТРИТЕ СЛЕДУЮЩИЙ СЛАЙД)
9. Шаг 2. Транспонируем матрицу:
• В ЭТОМ ШАГЕУБЕДИТЕЛЬНО ПРОШУ
ЗАПИСАТЬ ТОЛЬКО
ТРАНСПОНИРОВАННУЮ
МАТРИЦУ
10. СЛЕДУЮЩИЙ ШАГ – САМЫЙ ОБЪЕМНЫЙ И САМЫЙ СЛОЖНЫЙ, Т.К. ИМЕННО В НЕМ ДОПУСКАЮТСЯ ОШИБКИ, СВЯЗАННЫЕ С ПОТЕРЕЙ КОВАРНОГО ЗНАКА
«МИНУС»СЛЕДУЮЩИЕ СЛАЙДЫ – ЭТО МОЯ ПОПЫТКА ОБЪЯСНИТЬ ВАМ,
КАК РАБОТАЕТ ПОНЯТИЕ «АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕ» И КАК
ОНО СВЯЗАНО С ПОНЯТИЕМ «МИНОР».

ЖЕЛАТЕЛЬНО ПОСМОТРЕТЬ ЭТИ ПОЯСНЕНИЕ В РЕЖИМЕ
ПРЕЗЕНТАЦИИ – Т.К. ИНОГДА ДЕЙСТВИЯ БУДУТ ПРОИСХОДИТЬ
ПОСЛЕДОВАТЕЛЬНО ПРИ НАЖАТИИ КНОПКИ «МЫШКИ».
ПОСЛЕДНИЙ СЛАЙД «ВАЖНО! ЗНАК!» — ОБРАЗЕЦ ДЛЯ
ПОДРАЖАНИЯ ПРИ ОФОРМЛЕНИИ РЕШЕНИЯ.
ЗАКАНЧИВАЕТСЯ ЭТОТ ШАГ ЗАПИСЬЮ МАТРИЦЫ.
ЕСЛИ У ВАС ВОЗНИКАЮТ ВОПРОСЫ ИЛИ СОМНЕНИЯ В
ВЫПОЛНЕНИИ ЭТОГО ШАГА – ФОТО В ЛИЧНОМ СООБЩЕНИИ –
ОБЯЗАТЕЛЬНО ПОСМОТРЮ И ПОМОГУ И, НАДЕЮСЬ, ВЫ
ПОДЕЛИТЕСЬ ЭТИМ ЗНАНИЕМ С ОСТАЛЬНЫМИ.
ОЧЧЕНЬ БОЛЬШОЙ УДАЧИ И ОГРОМНЫХ УСПЕХОВ!!!
.
12. Определение определителя квадратной матрицы n-го порядка
Миноромэлемента
a i jматрицы А
ij
n-го порядка
называется определитель матрицы
(n-1)–го
порядка, полученной из матрицы А
вычеркиванием строки i и столбца j.
а11
А а21
а
31
M 23
а12
а22
а32
a11 a12
a31 a32
а13
а23
а33
1 1 1
А = 2 1 1
1 1 2
а 21 и а33
1 1 1
М 21 : 2 1 1
1 1 2
М 21
1 1
1
2
1 1 1
М 33 : 2 1 1
1 1 2
М 33
1 1
2
1
17.
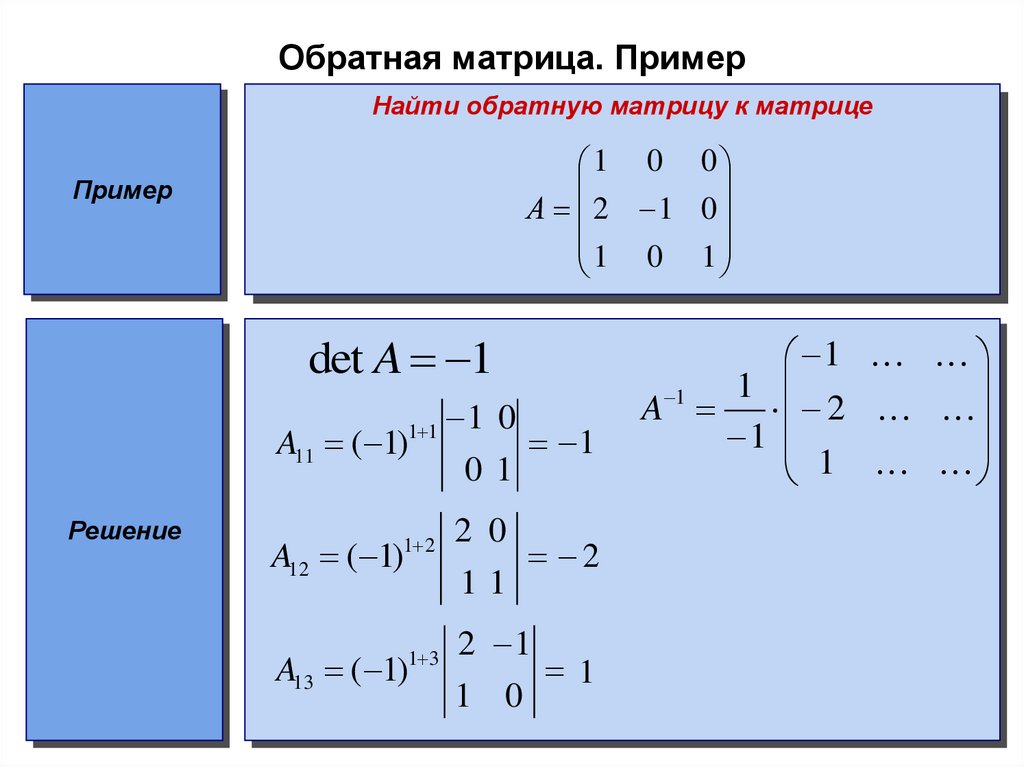 МИНОР — ОПРЕДЕЛИТЕЛЬМИНОР ОПРЕДЕЛИТЕЛЬ
МИНОР — ОПРЕДЕЛИТЕЛЬМИНОР ОПРЕДЕЛИТЕЛЬВЫЧЕРКИВАНИЕ СТРОКИ И СТОЛБЦА
.
• Алгебраическим дополнением Аij
элемента а ij матрицы n-го порядка
называется его
минор, взятый со знаком
1
т.е., имеет место равенство:
i j
Aij 1 M ij
i j
М 21
1 1
1
2
Aij 1 M ij
A21 1 M 21
2 1
i j
М 33
1 1
Aij 1 M ij
i j
2 1
A33 1
3 3
M 33
A21 1 M 21 M 21
2 1
A33 1
3 3
M 33 M 33
23. ВАЖНО: ЗНАК!!
Сумма индексов –Сумма индексов –
число нечетное
число четное
А21 1 М 21 М 21 А33 1 М 33 М 33
3 3
2 1
A12 1
1 2
6 3
0 6
A11 1
1 1
1 3
9 6
6 6 0 3 36 36 1 6 3 9 6 27 21
25. В ШАГЕ 4. ИСПОЛЬЗУЕМ ПРЕДЫДУЩИЕ ЗНАНИЯ
• СНАЧАЛА УМНОЖАЕМ МАТРИЦУ НА ЧИСЛО –ЧИСЛО В ЗНАМЕНАТЕЛЬ ИЩЕМ В ШАГЕ 1.
• ПОТОМ ВСПОМИНАЕМ – ЧТОБЫ УМНОЖИТЬ
ДРОБЬ НА ЧИСЛО – НАДО НА ЭТО ЧИСЛО
УМНОЖИТЬ ЧИСЛИТЕЛЬ ДРОБИ
• А ДАЛЕЕ — ПРИ ВОЗМОЖНОСТИ – СОКРАЩАЕМ
ДРОБИ – ДЛЯ ЭТОГО В ЧИСЛИТИЛЕ И
ЗНАМЕНАТЕЛЕ ИЩЕМ ОБЩИЙ МНОЖИТЕЛЬ –
ПОМНИМ – ДРОБЕЙ ДЕСЯТИЧНЫХ В ЧИСЛИТЕЛЕ И
ЗНАМЕНАТЕЛЕ ИЛИ В ОТВЕТЕ БЫТЬ НЕ ДОЛЖНО
• ОКОНЧАТЕЛЬНЫЙ РЕЗУЛЬТАТ ПОДЧЕРКИВАЕМ.

26. Шаг 4. Составляем обратную матрицу, используя формулу:
27. Получаем матрицу вида:
28. ПЕРЕХОДИМ К ПРОВЕРКЕ — АПОФЕОЗ
• МОЖНО ВЫПОЛНЯТЬ ДЕЙСТВИЕ СОКОНЧАТЕЛЬНО ПОЛУЧЕННОЙ ОБРАТНОЙ
МАТРИЦЕЙ, НО ЭТО ПРИВЕДЕТ К РАБОТЕ С
ДРОБЯМИ – ЧЕГО ХОТЕЛОСЬ БЫ ИЗБЕЖАТЬ
• ПОЭТОМУ СМОТРИМ ПОДСКАЗКУ НА СЛАЙДЕ
( НА БУКВУ «М» ВНИМАНИЕ НЕ ОБРАЩАЙТЕ) – И,
ГЛАВНОЕ, ВИДИМ СКОБКИ – КОТОРЫЕ – ЭТО ВЫ
ЗНАЕТЕ ДАВНО – МЕНЯЮТ ПОРЯДОК ДЕЙСТВИЙ.
• ВЫПОЛНЯЯ УМНОЖЕНИЕ МАТРИЦ – ПОМНИТЕ О
ТОМ, ЧТО МАТРИЦА – ЕДИНЫЙ ОРГАНИЗМ – И
ЕСЛИ ВЫ ИЩИТЕ ЭЛЕМЕНТЫ ПЕРВОЙ СТРОКИ, ТО
ОНИ ВСЕ ДОЛЖНЫ БЫТЬ ЗАПИСАНЫ НА ПЕРВОЙ
СТРОКЕ – И Т.Д. И Т.П.
29. Шаг 5. Проверка найденной матрицы с помощью равенства, выражающего определение обратной матрицы:
30. Используем матрицу вида:
31. Записываем произведение:
32. ЗАВЕРШИВ РАБОТУ:::
• ШЛЕТЕ ОТЧЕТ В ГУГЛ ФОРМУ ПО ССЫЛКЕ,КОТОРУЮ ПРИКРЕПЛЮ К ЗАДАНИЮ.
• НАСТОЯТЕЛЬНО РЕКОМЕНДУЮ::: СНАЧАЛА
СДЕЛАТЬ РАБОТУ НА ЧЕРНОВИКЕ, ОТПРАВИТЬ
ОТЧЕТ, ПОЛУЧИТЬ МОЮ ОЦЕНКУ, И ТОЛЬКО
ПОТОМ ПЕРЕПИСАТЬ РЕШЕНИЕ В КОНСПЕКТ.

• И ЕЩЁ РАЗ НАПОМИНАЮ: Я ОТКРЫТА ДЛЯ
ОБЩЕНИЯ – ОТВЕЧУ НА ВСЕ ВАШИ ВОПРОСЫ –
ФОТО ЛИЧНЫМ СООБЩЕНИЕМ!!!
• УСПЕХОВ И УДАЧИ!!!
English Русский Правила
| A -1 = |
|
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.
- Находим определитель данной квадратной матрицы A .
- Находим алгебраические дополнения ко всем элементам матрицы A .
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы A .
Как видим, операция транспонирования может применяться как в начале, над исходной матрицей, так и в конце, над полученными алгебраическими дополнениями.
Особый случай : Обратной, по отношению к единичной матрице E , является единичная матрица E .
Калькулятор обратной матрицы / Решатель с шагами
Запишите элементы матрицы, и калькулятор найдет ее обратную, применяя к ней различные методы с показанными пошаговыми вычислениями.
РЕКЛАМА
Выберите размер матрицы :
2345
Метод :
Гаусс-Жордан метод исключения Адъюгат
РЕКЛАМА
РЕКЛАМА
Содержание
| 1 | Что такое дощатый фут в пиломатериалах (BF)? |
| 2 | Бортовой фут Формула: |
| 3 | Подставка под доски Единицы: |
| 4 | Важно Толщина: |
| 5 | Как рассчитать доски? |
| 6 | Что вы подразумеваете под термином «Измерение поверхности»? |
| 7 | Что подразумевается под номинальным размером? |
| 8 | Как определить линейное измерение? |
Получите виджет!
Добавьте этот калькулятор на свой сайт, чтобы пользователи могли выполнять простые расчеты.
Получить код
Обратная связь
Насколько легко было пользоваться нашим калькулятором? Сталкивались ли вы с какой-либо проблемой, сообщите нам!
ОБРАТНАЯ СВЯЗЬ
Бесплатный онлайн-калькулятор обратной матрицы вычисляет обратную матрицу квадратной матрицы 2×2, 3×3 или более высокого порядка. 9{-1} = \frac{Adj\left(A\right)}{\begin{vmatrix}A\end{vmatrix} \\} $$
Где:
$$ Adj \left(A\ справа) = \begin{bmatrix}d & -b\\ -c & a \\\end{bmatrix} $$
Для
$$ A = \begin{bmatrix}a & b\\ c & d \\\end{bmatrix} $$
$$ det A = \begin{vmatrix}a & b \\c & d\end{vmatrix} \\ = ad – bc $$
Для обратной матрицы должно выполняться следующее условие
- Матрица должна быть квадратной матрицей.
- Определитель матрицы |A|≠ 0
Мы можем проверить с помощью калькулятора обратной матрицы, удовлетворяет ли матрица вышеуказанным условиям или нет. {t}$$
{t}$$
Чтобы определить обратную матрицу 3×3, мы должны иметь дело с понятием миноров и кофакторов.
Минор:
Минор определяется для каждого элемента матрицы. Минор конкретного элемента — это определитель, полученный после исключения строки и столбца, содержащих этот элемент.
Кофактор:
Кофактор элемента определяется путем умножения минора на сумму показателей строки и столбца конкретного элемента. 9{t}$$
Весь расчет обратной матрицы 3×3 можно быстро выполнить с помощью калькулятора обратной матрицы.
Определитель:
Определитель матрицы — это единственное уникальное представление матрицы. Определитель матрицы равен сумме произведений элементов и его сомножителей для определенной строки и столбца матрицы. Определитель матрицы можно найти с помощью калькулятора определителя.
Сингулярная матрица:
Известно, что max, значение определителя которого равно нулю, является сингулярной матрицей. Для сингулярной матрицы A, |A| = 0, мы не можем найти обратную сингулярную матрицу; это условие применяется, если мы находим обратную матрицу 3 × 3 или любую другую квадратную матрицу.
Несингулярная матрица:
Матрица, определитель которой не равен нулю, называется невырожденной матрицей. Для невырожденной матрицы |A| ≠ 0, и ее также называют обратимой матрицей, поскольку ее обратную можно вычислить.
Метод Гаусса Жордана:
Мы можем реализовать метод Гаусса Жордана с помощью следующих операций:
$$ \begin{bmatrix} a&b&c \\ d&e&f \\g&h& i \end{bmatrix}\\ $$
сделать матрицу единичной матрицей, применяя операции со строками.
$$ \left[\begin{array}{ccc|ccc}a&b&c&1&0&0\\ d&e&f&0&1&0\\g & h& i&0&0&1 \end{array}\right]\\ $$
Нам нужно реализовать операцию строки, чтобы найти обратную матрицы.
Нам нужно преобразовать нашу матрицу в единичную матрицу
Затем нам нужно реализовать операцию со строками.
Результатом будет наша обратная матрица методом исключения Гаусса Жордана.
Калькулятор обратной матрицы быстро находит обратную матрицу методом исключения Гаусса Жордана.
Пример:
Вычисление и решение обратной матрицы 3×3 методом Гаусса-Жордана Исключение:
$$ \begin{bmatrix}1&1&9 \\ 2&5&1\\1&2&7\end{bmatrix}\\ $$
Теперь найдем определитель:
Мы собираемся сделать матрицу единичной, применяя операции со строками.
$$ \left[\begin{array}{ccc|ccc}1&1&9&1&0&0\\ 2&5&1&0&1&0\\1&2&7&0&0&1\end{array}\right]\\ $$
Наша окончательная обратная матрица методом исключения Гаусса Жордана:
$$ Обратная матрица= \begin{bmatrix}3&1&-4 \\ -1,182&-0,182&1,545 \\ -0,091&-0,091&0,273 \\\end{bmatrix} $$
Калькулятор обратной матрицы может найти обратную матрицу 3×3 за считанные секунды.
Работа калькулятора обратной матрицы:
Вычисление обратной матрицы легко найти при использовании калькулятора обратной матрицы. Это можно сделать за считанные минуты самым простым и эффективным способом.
Ввод:
- Выберите размер матрицы из раскрывающегося меню
- Введите значения и нажмите кнопку «Создать матрицу»
- Выберите метод решения обратной матрицы
- Нажмите кнопку расчета
Результат:
Обратимая матрица легко преобразуется в обратную матрицу с помощью калькулятора обратимых матриц.
- Отображаются значения входной матрицы
- Отображаются все шаги вычислений
Часто задаваемые вопросы:
Что такое обратимая матрица?
Матрица, обратная матрице, должна быть невырожденной и квадратной по своей природе.
Можем ли мы найти обратную всем матрицам?
Мы не можем найти обратную сторону всех матриц, только обратимая обратная матрица может быть определена с помощью калькулятора обратной матрицы.
Могу ли я получить исходную матрицу после ее инвертирования?
Вам нужно только предпринять следующие шаги, чтобы получить исходную матрицу с помощью обратной матрицы калькулятора:
- Введите инвертированную матрицу.
- Нажмите кнопку расчета, чтобы получить обратную матрицу.
- Это дает вам исходную матрицу.
Можно ли инвертировать сингулярную матрицу?
Нет, вы не можете инвертировать сингулярную матрицу, потому что при вычислении обратной матрицы определитель становится равным нулю. Вы можете использовать калькулятор обратной матрицы, чтобы определить, является ли матрица единственной или нет.
Вывод:
Нам нужно найти обратную матрицу, чтобы найти решение линейной методом обращения матриц. Обратная матрица 3×3 и обратная матрица 4×4 — это длительная процедура, и нам нужна специальная обратная матрица.
Ссылки:
Из источника Википедии: Обратимая матрица, Свойства, Другие свойства
Из источника embibe.com: Обратная матрица, Значение, Формула, Решенные примеры скоро Эти математические инструменты уже в пути
Функции построения графиков
Рисовать графики математических функций.
Рисование формулы LaTeX
Создание изображения из выражения LaTeX.
Найти n-ю цифру
Вычислить n-ю цифру числа Эйлера.
Найти n-ю цифру золотого сечения
Вычислить n-ю цифру золотого сечения.
Найти n-ю цифру числа пи
Вычислить n-ю цифру числа пи.
Вычислить сумму e цифр
Найти сумму e цифр.
Вычислить сумму цифр золотого сечения
Найти сумму цифр золотого сечения.
Вычислить сумму пи цифр
Найти сумму пи цифр.
Генерировать цифры Чамперноуна
Генерировать цифры константы Чамперноуна.
Найти n-ю цифру Чамперноуна
Вычислить n-ю цифру константы Чамперноуна.
Декодирование последовательности «посмотри и скажи»
Выполните обратную операцию над последовательностью «посмотри и скажи».
Создание P-адических расширений
Вычисление p-адических расширений произвольных чисел.
Создать последовательность панцифровых чисел
Создать список панцифровых чисел.
Создать последовательность номеров Стэнли
Создать список номеров Стэнли.
Создать последовательность номеров звонков
Создать список номеров звонков.
Генерация последовательности номеров Кармайкла
Создание списка номеров Чармичел.
Создать последовательность каталонских номеров
Создать список каталонских номеров.
Создать последовательность треугольных чисел
Создать список треугольных чисел.
Создать составную числовую последовательность
Создать список составных чисел.
Создать последовательность секущих чисел
Создать список секущих чисел.
Создать последовательность чисел Голомба
Создать список чисел Голомба-Сильвермана.
Создать последовательность чисел Эйлера Тотиент
Создать список фи-чисел Эйлера.
Создать последовательность номеров жонглеров
Создать список номеров жонглеров.
Создать последовательность счастливых номеров
Создать список счастливых номеров.
Создать последовательность номеров Моцкина
Создать список номеров Моцкина.
Создать последовательность номеров Padovan
Создать список номеров Padovan.
Создать последовательность псевдосовершенных чисел
Создать список полусовершенных чисел.
Создать последовательность номеров Ulam
Создать список номеров Ulam.
Создать последовательность странных чисел
Создать список странных чисел.
Создать суперсовершенную числовую последовательность
Создать список суперсовершенных чисел.
Продолжить числовую последовательность
Найти закономерность в числовой последовательности и расширить ее.
Разбить число
Найти все разбиения данного целого числа.
Создать последовательность номеров разделов
Создать список номеров функций разделов.
Создание арифметической прогрессии
Создание арифметической последовательности чисел.
Создание геометрической прогрессии
Создание геометрической последовательности чисел.
Создать полиномиальную прогрессию
Создать полиномиальную последовательность чисел.
Создать последовательность натуральных чисел
Создать список натуральных чисел.
Создание степеней двойки
Создание списка чисел степеней двойки.
Создание степеней десяти
Создание списка чисел в степени десятка.
Создание плотной матрицы
Создание матрицы с очень небольшим количеством нулевых элементов.
Создание разреженной матрицы
Создать матрицу с очень небольшим количеством ненулевых элементов.
Умножение матрицы на скаляр
Умножение всех элементов матрицы на число.
Проверить, является ли матрица единственной.
Определить, является ли матрица вырожденной.
Найти матрицу кофакторов
Для заданной матрицы найти ее матрицу кофакторов.
Найдите вспомогательную матрицу
По заданной матрице найдите ее дополнение.
LU Factor a Matrix
Разложить матрицу на LU-факторы.
Найти собственные значения матрицы
Найти собственные значения матрицы.
Украсьте матрицу
Украсьте матрицу, аккуратно выровняв все ее столбцы.
Переформатировать матрицу
Преобразовать матрицу из одного формата в другой формат.
Рисование архимедовой спирали
Создание архимедовой спирали.
Рисование спирали Эйлера
Создание кривой спирали Корню (полиномиальной спирали).
Нарисуйте спираль Фибоначчи
Создать спиральную кривую Фибоначчи.
Рисование спирали Теодора
Создание спирали квадратного корня.
Нарисуйте спираль Ферма
Создайте кривую в виде параболической спирали.
Рисование прямоугольников Фибоначчи
Создание рисунка прямоугольников Фибоначчи.
Нарисуйте головку семени Фибоначчи
Создайте головку цветка Фибоначчи.
Нарисовать фрактал Падована
Создать фрактал равнобуквенных треугольников Падована.
Нарисуйте аполлонову прокладку
Создать фрактал аполлоновой прокладки.
Нарисовать фрактал Мандельброта
Создать фрактал Мандельброта.
Нарисовать фрактал Юлии
Создать фрактал Джулии.
Нарисовать фрактал Рози
Создать фрактал Рози.
Нарисовать кривую фрактала Бланманже
Создать фрактал Бланманже.
Рисование функции Вейерштрасса
Создание фрактала Вейерштрасса.
Нарисуйте кривую Минковского с вопросительным знаком
Генерация фрактала Минковского в виде вопросительного знака.
Нарисуйте функцию Тома
Создайте функцию Тома (также известную как функция попкорна или капли дождя).
Нарисовать функцию Дирихле
Нарисовать функцию Дирихле.
Нарисуйте рог Гавриила
Нарисуйте геометрическую фигуру с бесконечной площадью поверхности и конечным объемом.
Преобразование слов в числа
Преобразование чисел из английского текста в реальные цифры.
Преобразование чисел в слова
Преобразование чисел в письменный текст на английском языке.
Преобразование десятичной записи в экспоненциальную запись
Преобразование чисел, записанных в десятичной форме, в экспоненциальную форму.
Преобразование научной записи в десятичную.
Преобразование чисел, записанных в научной форме, в десятичную форму.
Округление чисел вверх
Применение операции ceil к числам.
Округление чисел в меньшую сторону
Применить операцию пола к числам.
Анализ чисел
Подсчитайте, сколько раз встречается каждое число.
Преобразование числа в виде суммы
Создайте сумму, которая в сумме равна заданному числу.
Создать таблицу умножения
Нарисовать таблицу умножения n×m.
Нарисовать круговую диаграмму
Нарисовать круговую диаграмму и показать относительные размеры данных.
Визуализация процентов
Нарисуйте диаграмму, показывающую проценты.
Подбрось монетку
Подбрось монетку и выпадет орел или решка.
Бросьте кубик
Бросьте кубик и получите число на его стороне.
Найти обратную матрицу с помощью программы «Пошаговое решение математических задач»
Введите матрицу и нажмите кнопку «Обратить».
Помощь
| Матрица 5,3,7 2,4,9 3,6,4 |
В этом разделе мультипликативные тождественные элементы и мультипликативные обратные вводятся и используются для решения матричных уравнений. Это приводит к другому метод решения систем уравнений.
МАТРИЦЫ ИДЕНТИЧНОСТИ Свойство идентичности действительных чисел говорит, что
a * I = a и I * a = a для любого действительного числа a. Если должно быть
мультипликативный
единичная матрица I такая, что:
Если должно быть
мультипликативный
единичная матрица I такая, что:
AI = A и IA = A,
для любой матрицы A, то A и I должны быть квадратными матрицами одинакового размера. В противном случае было бы невозможно найти оба продукта. Например, пусть А матрица 2 X 2 и пусть
представляют собой единичную матрицу 2 X 2. Чтобы найти I, используйте тот факт, что IA = A, или
Умножение двух матриц в левой части этого уравнения и установка элементов матрицы произведения, равных соответствующим элементам A, дает следующая система уравнений с переменными x11, x12, x21, x22
Обратите внимание, что на самом деле это две системы уравнений с двумя переменными. Используйте один из методы предыдущей главы, чтобы найти решение этой системы: x11 = 1, x12 = x21 = 0 и X22 = 1. Из решения системы 2 X 2 единичная матрица равна
Проверить, что при данном определении I оба Al = A и IA = A.
Пример 1
Найденная выше единичная матрица 2 X 2 предлагает следующее обобщение:
вниз по диагонали и 0 в другом месте. n x n тождественная матрица дана
по л где:
n x n тождественная матрица дана
по л где:
Здесь aij = 1, когда i = j (диагональные элементы) и aaj = 0 в противном случае.
Пример 2. СОСТАВЛЕНИЕ И ПРОВЕРКА МАТРИЦЫ ИДЕНТИЧНОСТИ 3 X 3
Пусть K =
Дана единичная матрица I 3 X 3 и показано, что KI = K.
Мультипликативная обратная матрица может быть найдена с помощью преобразования строки матрицы, приведенные в предыдущем уроке и повторенные здесь для удобство.
ПРЕОБРАЗОВАНИЕ СТРОК МАТРИЦЫ
Преобразование строк матрицы:
перестановка любых двух строк матрицы местами;
умножение элементов любой строки матрицы на одинаковые ненулевой скаляр k; и 9(-1) = 1, или
Матричным умножением,
Приравнивание соответствующих элементов дает систему уравнений
Поскольку уравнения (1) и (3) включают только x и z, а уравнения (2) и (4) включают только y и w, эти четыре уравнения приводят к двум системам уравнений:2x + 4z = 1
x-z=0и
2y + 4w = 0
y-w=1.
Запись двух систем в виде расширенных матриц дает
Каждая из этих систем может быть решена методом Гаусса-Жордана. Однако, поскольку элементы слева от вертикальной черты идентичны, две системы могут объединить в одну расширенную матрицу
и одновременно решить следующим образом. Поменяйте местами две строки, чтобы получить 1 в верхний левый угол.Умножьте первую строку на -2 и прибавьте результаты ко второй строке, чтобы получить
Теперь, чтобы получить I во второй строке во втором столбце, умножьте второе ряд на 1/6. 9(-1) — это просто обозначение обратной матрицы A.
Обратное, умножение, сложение, вычитание, определитель, сопряженное
Матрица
См. также: Исключение Гаусса-Жордана, Одновременные линейные уравнения Геометрическое линейное преобразование
Матрица представляет собой прямоугольный массив чисел.
Размер матрицы это ее размерность, а именно количество строк и столбцов матрицы.

Для операций с матрицами используйте два калькулятора ниже.
- Матричный калькулятор умножения, сложения и вычитания
- Обратная матрица, детерминант и сопряженный калькулятор
Чтобы найти обратную матрицу, вы также можете использовать метод исключения Гаусса-Жордана.
Прочтите объяснение матричных операций ниже.
Калькулятор умножения, сложения и вычитания матриц
- Введите размерность матриц. (Строки × Столбцы).
- Для умножения количество столбцов первой матрицы должно быть равно количеству строк второй матрицы, т. е. (a × b)(b × c).
- Для сложения и вычитания размеры двух матриц должны быть одинаковыми.
- Максимальный размер матрицы для этой системы 9 × 9.
РядКол
умножитьсложитьвычесть
РядКол
Сообщайте обо всех ошибках на [email protected]Калькулятор обратной матрицы, определителя и сопряженной матрицы
- Чтобы матрица была обратимой, она должна быть квадратной.

- Введите размерность матрицы. (Строки × Столбцы).
- Максимальный размер матрицы для этой системы 9 × 9.
- Результат будет округлен до 3 знаков после запятой.
РядКол
Пожалуйста, сообщайте обо всех ошибках на [email protected]Операции с матрицами
Сложение и вычитание матриц
Если матрицы A и B имеют одинаковый размер,
- сумма A+B представляет собой матрицу, полученную путем сложения элементов B с соответствующими элементами A.
- разность A−B — это матрица, полученная вычитанием элементов B из соответствующих элементов A.
Если A=a11a12…a1na21a22…a2n⋮⋮⋱⋮am1am2…amn а также B=b11b12…a1nb21b22…a2n⋮⋮⋱⋮bm1bm2…bmn
A+B=a11+b11a12+b12…a1n+b1na21+b21a22+b22…a2n+b2n⋮⋮⋱⋮am1+bm1am2+bm2…amn+bmn
A−B=a11−b11a12−b12…a1n−b1na21−b21a22−b22…a2n−b2n⋮⋮⋱⋮am1-bm1am2-bm2…amn-bmn
Матрицы разных размеров нельзя складывать или вычитать.

Пример:
Если А=120-3 а также В=31-12
A+B=120-3+31-12=43-1-1
A−B=120-3−31-12=-211-5
Умножение матриц
Матрица размера m×n, элемент которой из строки i и столбца j представляет собой сумму произведений соответствующих элементов из строки i матрицы A и столбца j матрицы B.
Элемент ABij в строке i и столбце j таблицы AB определяется как
ABij = ai1b1j+ai2b2j+…+airbrj
Матрицы A и B можно перемножать только в том случае, если количество столбцов матрицы A совпадает с количеством строк матрицы B.
Пример:
А=1210-32 а также Б=3101-12300-211
AB=1210-323101-12300-211=13723-10-72
- Элемент в строке 1 и столбце 1 таблицы AB получается суммированием произведения соответствующих элементов строки 1 таблицы A и столбец 1 таблицы B, т. е.
AB11 = 13+2−1+10=1 - Элемент в строке 1 и столбце 2 таблицы AB получается путем суммирования произведений соответствующих элементов строки 1 таблицы A и столбца 2 таблицы B, т.
 е.
е.
AB12 = 11+22+1−2=3 - Элемент в строке 2 и столбце 1 таблицы AB получается суммированием произведений соответствующих элементов строки 2 таблицы A и столбца 1 таблицы B, т. е.
AB21 = 03+−3−1+20=3 - И так далее
Обратная матрица
Обратная квадратная матрица A – это матрица A−1 такая, что АА-1=I
Пример:
Если А=-325-4, тогда A−1=-2-1-2,5-1,5
, потому что AA−1=-325-4-2-1-2,5-1,5=1001
Один из способов получить обратную квадратную матрицу A — использовать следующую формулу:
A−1 = adj ⁡ Детектор ⁡ A
Если определитель матрицы равен 0, матрица не имеет обратной и называется сингулярной матрицей .
Другой способ найти обратную матрицу состоит в том, чтобы добавить единичную матрицу в правую часть матрицы, а затем использовать метод исключения Гаусса-Жордана, чтобы привести матрицу к ее уменьшенной ступенчатой форме строк.

Запутались и есть вопросы? У нас есть ответы. С Chegg Study вы можете получить пошаговые решения ваших вопросов от эксперта в этой области.
Джимми Си
См. также: Исключение Гаусса-Жордана, Одновременные линейные уравнения, Геометрическое линейное преобразование
Поиск обратной матрицы
обратный любого квадрата матрица; а также мы демонстрируем метод шаг за шагом с примерами.
Предпосылки : Этот материал предполагает знакомство с элементарные матричные операции и ступенчатые преобразования.
Как найти обратную матрицу
n x nПусть A будет матрицей n x n . Чтобы найти обратную матрице A , мы выполняем следующие шаги:
- Используя элементарные операторы, преобразовать матрицу A в ее Эшелонная форма уменьшенного ряда, A ссылка .
- Осмотрите A rref , чтобы определить,
матрица A имеет обратную.

- Если A rref равно единичная матрица, тогда матрица A равна полный ранг; а матрица A имеет обратную.
- Если последняя строка A rref все нули, то матрица А не является полный ранг; и матрица A не имеет обратной.
- Если A — полный ранг, тогда обратная матрица A равно произведению элементарных операторов который произвел A rref , как показано ниже.
А -1 = Е р Е р-1 . . . E 2 E 1
, где
A -1 = обратно матрицы A
R = Количество элементов. трансформировать А по A rref
E i = i оператор элементарной строки используется для преобразования A в A rrefОбратите внимание, что порядок умножения элементарных операторов строк важно, потому что Е и Е и не обязательно равно E j E i .

Реклама
Пример нахождения обратного
Воспользуемся описанным выше методом, чтобы найти обратную матрицу A , показанный ниже.
A = 1 2 2 2 2 2 2 2 1 Первым шагом является преобразование матрицы A в ее уменьшенная форма эшелона ряда, А rref , используя ряд элементарные операторы строк Е и . Мы показываем трансформацию шаги ниже для каждого оператора элементарной строки.
- Умножьте строку 1 числа A на -2 и прибавьте
результат в строке 2 A . Этого можно добиться путем предварительного умножения на на
оператор элементарной строки E 1 , который производит A 1 .

E 1 = 1 0 0 -2 1 0 0 0 1 A 1 = E 1 A = 1 2 2 0 -2 -2 2 2 1 - Multiply row 1 A 1 на -2 и добавить
результат в строке 3 A 1 .

E 2 = 1 0 0 0 1 0 -2 0 1 A 2 = E 2 A 1 = 1 2 2 0 -2 -2 0 -2 -3 - Multiply row 3 of A 2 by -1 and add
ряд 2 A 2 до
ряд 3 из A 2 .

E 3 = 1 0 1 0 1 0 0029 0 0 1 0 0 1 -1 A 3 = E 3 A 2 = 1 2 2 0 -2 -2 0 0 1 - Добавить ряд 3 109 2 из
8 ряд 1 из
A 3 .
E 4 = 1 1 0 0 1 0 0 0 1 A 4 = E 4 A 3 = 1 0 0 0 -2 -2 0 0 1 - Умножить строку 2 из A 4 на -0,5.
E 5 = 1 0 0 0 -0.  5
50 0 0 1 А 5 = E 5 A 4 = 1 0 0 0 1 1 0 0 1 - Умножить строку 3 из A —
5 на
9 и добавьте результат во вторую строку A 5 .
E 6 = 1 0 0 0 1 -1 0 0 1 A rref = E 6 A 5 = 1 0 0 0 1 0 0 0 1 Примечание: Если операции и/или обозначения, показанные выше, неясны, просмотрите элементарные матричные операции и ступенчатые преобразования.

Последняя матрица на шаге 6 приведенной выше таблицы: A rref , уменьшенная форма эшелона ряда для матрица А . Начиная с A rref равен единичной матрице, мы знаем, что A есть полный ранг. И поскольку A — это полный ранг, мы знаем, что A имеет обратную.
Если A меньше полного ранга, A rref будет иметь все нули в последней строке; а также У не было бы обратный.
Находим обратную матрицу А путем вычисления произведения элементарных операторов который произвел A rref , как показано ниже.
А -1 = E 6 E 5 E 4 E 3 E 2 E 1
A -1 = -1 1 0 1 -1.  5
51 0 1 -1 In this example, we used a 3 x 3 matrix to show how найти обратную матрицу. Тот же процесс будет работать с квадратной матрицей любого размера.
Проверьте свое понимание
Задача
Найдите обратную матрицу A , показанную ниже.
Решение
Первым шагом является преобразование матрицы A в ее эшелонированная форма уменьшенного ряда, A rref , с использованием элементарные операторы строк E i выполнить элементарные операции со строками, как показано ниже.
- Умножьте строку 1 числа A на -2 и прибавьте результат в строке 2 A .
А 1 = E 1 A = - Multiply row 2 of A 1 by 0.
 5..
5..
E 2 = 1 0 0 0.5 A rref = E 2 A 1 = 90 Последняя таблица в приведенной выше таблице преобразована А номер , ступенчатая форма сокращенного ряда для матрица А . Поскольку приведенная эшелонная форма строки равна единичная матрица, мы знаем, что A есть полный ранг. И поскольку A — это полный ранг, мы знаем, что A имеет обратную. Находим обратное, вычисляя произведение элементарных операторов что произвело A rref , как показано ниже.

А -1 = E 2 E 1 = 1 0 0 0.5 E 2 E 1 A -1 = 1 0 -1 0.5 Note : In a previous lesson, we described а «ярлык» для найти обратную матрицу 2х2.
Последний урок Следующий урок
вычислить обратное, транспонировать и многое другое!
Вам нужен матричный калькулятор ? У нас есть широкий их выбор, так что вы можете решать различные операции, такие как вычисление обратной матрицы, обратное или умножение матриц.

Операции с матрицами
Выберите нужный калькулятор матриц ниже:
- Калькулятор транспонированных матриц
- Вычислить обратную матрицу 2×2
- Вычислить обратную матрицу 3×3
- Калькулятор обратной матрицы 4×4
- Умножение матриц 2×2
- Умножение матриц 3×3
Вам нужен какой-нибудь другой матричный калькулятор? Спросите нас, и мы сделаем это. Напоминаем также, что если вы хотите вычислить определитель, по ссылке, которую мы только что оставили, вы можете решить их онлайн.
Кроме того, в каждом из матричных калькуляторов, которые мы оставили вам для решения операций, вы найдете , как это сделать с формулой и решенными примерами , чтобы вы понимали, как это делается в каждом конкретном случае. Конечно, если у вас есть какие-либо вопросы, вы можете задать их нам, и мы будем рады вам помочь.
Типы матриц
Существует множество типов матриц Поэтому ниже мы суммируем наиболее важные из них.
Матрица строк
Матрица строк — это матрица , состоящая из одной строки , как следует из названия. Примером матрицы-строки может быть следующий:
Матрица-столбецВ случае матрицы-столбца, как следует из названия, у нас есть один столбец. Пример такого типа матрицы:
Прямоугольная матрицаМы говорим, что матрица прямоугольная, когда количество строк и столбцов различно , то есть его размер mxn. Например, ниже вы можете увидеть прямоугольную матрицу 3×2:
Квадратная матрица
Да количество строк и столбцов одинаковое тогда это квадратная матрица. То есть его размерность nxn, как в следующем примере:
В квадратных матрицах есть несколько типов, таких как верхняя треугольная, нижняя треугольная, диагональная, скалярная, единичная, ортогональная и другие. Здесь вы можете увидеть все типы квадратных матриц.
Транспонированная матрица
Транспонированная матрица (A t ) матрицы A — это та, в которой мы заменили строки на столбцы . Для лучшего понимания ниже вы можете увидеть формулу матрицы транспонирования.
Если вы хотите узнать больше о том, как он рассчитывается, о его свойствах или увидеть практические примеры, не стесняйтесь посетить наш калькулятор транспонирования матриц.
Нулевая матрицаНулевая матрица характеризуется все его элементы равны 0 .
По своей характеристике нулевая матрица обладает следующими свойствами:
- Она симметрична и антисимметрична
- Уникально
- Нильпотент
Типы квадратных матриц
Поскольку существует большое разнообразие квадратных матриц, мы хотели посвятить специальный раздел, чтобы немного рассказать о каждой из них, чтобы вы могли научиться их правильно идентифицировать.

Как мы уже говорили, квадратная матрица — это матрица с одинаковым количеством строк и столбцов. Теперь посмотрим, какие бывают виды:
Верхняя треугольная матрицаВерхняя треугольная матрица — это та, у которой элементов ниже главной диагонали равны нулю .
Нижняя треугольная матрицаВ нижней треугольной матрице происходит прямо противоположное предыдущему типу матрицы, т. е. в этом случае все элементы выше главной диагонали равны нулю .
Диагональная матрицаДиагональная матрица та, что имеет только элементы на главной диагонали . Остальные будут равны нулю.
Среди его свойств стоит отметить, что диагональная матрица является квадратной и симметричной а.
Скалярная матрицаСкалярная матрица подобна диагональной матрице, но отличается от диагональной тем, что все элементов главной диагонали равны .
Матрица или единица измерения
Да все элементы главной диагонали равны 1 мы стоим перед единичной матрицей.
Единичная матрица очень важна, потому что действует как нейтральный элемент в умножении матриц , то есть, если мы умножим любую матрицу на единичную матрицу, исходная матрица не изменится.
Обычная матрицаМы говорим, что это обычная матрица, когда мы можем вычислить ее обратную . Если вы не знаете, как это сделать, вот пара ссылок, которые покажут вам, как вычислить обратную матрицу ранга 2×2 или 3×3:
- Вычислить обратную матрицу 2×2
- Вычислить обратную матрицу 3×3
Если, с другой стороны, матрица не имеет обратной, то является сингулярной матрицей. Для этого его определитель должен быть равен нулю.
Идемпотентная матрицаМатрица является идемпотентной, если при возведении в квадрат остается исходная матрица .
 Это математически выражается следующим образом:
Это математически выражается следующим образом:A 2 = A
Вот некоторые из них примеров идемпотентных матриц , в которых может быть продемонстрировано предыдущее свойство: , умножив его само на себя, мы получим единичную матрицу . То есть:
A 2 = I
Ниже приведена пара решенных упражнений на инволютивные матрицы 9.0008, в котором можно увидеть, как выполняется приведенное выше выражение:
Среди свойств эвольвентной матрицы мы имеем:
- Это квадратные матрицы
- Они обратны сами себе
Симметричная матрица – это матрица, которой равна ее транспонированной матрице , т.е.0157
У нас также есть тип матрицы, который называется антисимметричным и что эквивалентен своей транспонированной матрице, но со знаком минус перед: свойства антисимметричной матрицы имеем:
- Это квадратная матрица
- Элементы главной диагонали равны нулю.

Чтобы закончить с типами матриц, мы рассмотрим ортогональную матрицу. Он так называется, потому что , если мы умножим его на его транспонирование, мы получим единичную матрицу :
A — A t = I
Например:
Наши матричные калькуляторы
несколько матричных калькуляторов, работа которых очень проста.
Вам нужно только выбрать матричный калькулятор для операции, которую вы хотите выполнить, и вы увидите, что есть сетка диапазона nxm.
В каждую ячейку вам нужно будет вписать элементы матрицы, над которой вы хотите работать, так что, когда вы это сделаете, вам нужно будет только нажать кнопку расчета, чтобы получить результат.
Вы хотите рассчитать определители онлайн или узнать, каковы его свойства? Ниже у вас есть вся информация, которую вы ищете, чтобы решить определители матрицы.

Вычислить определители онлайн
Вам нужно вычислить определитель матрицы ? Здесь вы найдете коллекцию онлайн-калькуляторов для решения различных типов определителей в зависимости от их размера:
- Определитель 2×2
- Определитель 3×3
- Определитель 4×4
Во всех случаях мы покажем вам, как решить определитель либо с помощью его математического метода, либо с помощью Excel.
Свойства определителей
удобно знать свойства определителей , чтобы решать их правильно и не делать ошибок при решении упражнений, в которых они задействованы.
- Определитель A равен определителю его транспонирования
Если вы вычислите определитель матрицы A, а затем сделаете то же самое для определителя ее транспонированной матрицы, вы увидите, что они стоят одинаково. Следовательно, у вас есть это равенство:
|A t |= |A|
- Определитель матрицы равен 0, если:
|А| может быть равно нулю, если выполняются некоторые из следующих условий:
- Имеет две абсолютно одинаковые строки или столбца
- Все элементы строки или одного из ее столбцов пусты, то есть равны нулю.

- Элементы строки или столбца являются линейной комбинацией других элементов. Например, может быть так, что сложение элементов строки 1 и строки 2 дает числа строки 3, поэтому в этом случае определитель будет равен нулю. Ярким примером этого критерия является тот, который можно увидеть в следующем примере:
Если вы посмотрите на определитель выше, сумма строк 1 и строк 2 дает строку 3, поэтому они представляют собой линейную комбинацию, и их результат равен нулю.
- Треугольный определитель равен произведению элементов его главной диагонали.
Треугольный определитель — это тот, который заполнен нулями выше или ниже главной диагонали. Это позволяет нам рассчитать его стоимость, просто перемножив элементы, расположенные на главной диагонали.
- При перестановке между ними двух строк или двух столбцов значение определителя меняет знак.

Как видно из следующего примера, если мы переместим две строки или два столбца определителя относительно друг друга, его конечное значение останется тем же, но мы должны изменить знак .
- Если преобразовать строку или столбец в линейную комбинацию других, значение определителя не изменится.
Единственным условием для выполнения этого свойства является наличие следующего умножение элементов одной строки или столбца определителя на число действительное.
В следующем примере вы можете увидеть, как если мы преобразуем столбец 3 в линейную комбинацию столбцов 1 и 2, в результате мы получим то же значение. Однако ранее столбец один был умножен на два.
- При умножении определителя на действительное число мы должны умножать только одну из его строк или столбцов.
То есть, если мы умножим определитель на 2, мы умножим на это число только одну из его строк или один из его столбцов.

- Если элементы строки или столбца образованы двумя слагаемыми, то этот определитель можно разложить на два.
При этом важно отметить, что остальные строки или столбцы определителя, имеющие только одно слагаемое, останутся неизменными в каждом из полученных определителей.
В этом примере теория, изложенная в этом пункте, видна гораздо яснее:
- |А — Б| = |А| — |Б|
Чтобы закончить свойства определителей, если у нас есть определитель произведения можно приравнять к произведению определителей .
Умножение матриц 2×2 может быть утомительной, трудоемкой и подверженной ошибкам задачей. Поэтому мы подготовили для вас калькулятор, способный решить эту операцию мгновенно, и для этого вам просто нужно заполнить значения матрицы 2×2, которую вы хотите умножить.
С помощью этого инструмента вы также сможете вычислить el cuadrado de una matriz 2×2 .
 При этом значения элементов должны совпадать друг с другом. Когда у вас все будет готово, нажмите кнопку расчета, и вы узнаете, как матрица была умножена шаг за шагом, и окончательный результат.
При этом значения элементов должны совпадать друг с другом. Когда у вас все будет готово, нажмите кнопку расчета, и вы узнаете, как матрица была умножена шаг за шагом, и окончательный результат.Подробнее
Онлайн-калькулятор транспонированных матриц — это инструмент, который позволяет автоматически менять строки на столбцы матрицы. Просто выберите размер матрицы из доступных размеров и нажмите кнопку «Рассчитать», чтобы получить транспонирование этой матрицы.
Если вы хотите узнать все о транспонированной матрице Читайте дальше, и мы расскажем вам все об этом типе матриц, используемых в мире математики, физики и других дисциплин.
Подробнее
Вам нужен калькулятор la matriz inversa 2×2 онлайн , чтобы сэкономить время? Воспользуйтесь нашим калькулятором, и вы сможете получить обратную матрицу автоматически за считанные секунды, шаг за шагом.
Для этого необходимо записать каждый из элементов, составляющих matriz inversa 2×2 y pulsar el botón de calcular cuando lo hayas hecho.
 Tras eso, conocerás el resultado y los pasos previos que conlleva a este cálculo como son el determinante 2×2 y la matriz adjunta.
Tras eso, conocerás el resultado y los pasos previos que conlleva a este cálculo como son el determinante 2×2 y la matriz adjunta.Подробнее
Расчет обратной матрицы 3×3 онлайн шаг за шагом с помощью нашего калькулятора, который позволит вам мгновенно найти обратную матрицу.
Sólo tienes Que rellenar correctamente todos los valores Que componen la matriz 3×3 y pulsar sobre el botón de calcular para obtener el resultado paso a paso cómo se ha calculado su matriz inversa a partir de la fórmula que veremos más adelante. cómo se calcula la inversa de una matriz 3×3 .
Подробнее
Вы хотите рассчитать обратную матрицу онлайн ? Тогда вы находитесь в правильном месте.
Ниже вы найдете калькулятор, который позволит вам сэкономить много времени, когда дело доходит до исчисления обратного матриза 4×4 pero además, te enseñamos cómo se hace el cálculo manualmente a través del determinante 4×4 y la matriz transpuesta де ла адъюнта.

Подробнее
Используйте наш калькулятор для умножения матриц 3×3 онлайн и сэкономьте время на этой операции, которая, хотя и проста в выполнении, может сыграть с нами злую шутку, если мы сделаем это быстро.
Если хотите, вы также можете использовать калькулятор, чтобы сделать умножений матриц 3×1 или 3×2 . Вам нужно только оставить данные в соответствующем столбце пустыми и все.
Подробнее
Если вы хотите calcular el determinante de una matriz 2×2 онлайн , то вы находитесь в нужном месте. Здесь вы найдете калькулятор, который позволит вам узнать значение определителя, но мы также покажем вам, как рассчитать его вручную, в Excel или с помощью научного калькулятора.
Вы выбираете как sacar el determinante de una matriz 2×2 .
Подробнее
Расчет определителя матрицы 3×3 онлайн возможен с помощью нашего калькулятора. Просто заполните элементы, из которых состоит определитель, и нажмите на кнопку расчета, чтобы увидеть результат, включая пошаговый метод решения прикрепленных определителей.


 Сложение и вычитание
Сложение и вычитание Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы
Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы Поэтому наш сервис по нахождению обратной матрицы онлайн значительно облегчит вам задачу и станет незаменимым инструментом для решения математических задач. Даже если вы находите обратную матрицу самостоятельно, мы рекомендуем проверить ваше решение на нашем сервере. Ввведите вашу исходную матрицу у нас на Вычисление обратной матрицы онлайн и сверьте ваш ответ. Наша система никогда не ошибается и находит обратную матрицу заданной размерности в режиме онлайн мгновенно! На сайте сайт допускаются символьные записи в элементах матриц , в этом случае обратная матрица онлайн будет представлена в общем символьном виде.
Поэтому наш сервис по нахождению обратной матрицы онлайн значительно облегчит вам задачу и станет незаменимым инструментом для решения математических задач. Даже если вы находите обратную матрицу самостоятельно, мы рекомендуем проверить ваше решение на нашем сервере. Ввведите вашу исходную матрицу у нас на Вычисление обратной матрицы онлайн и сверьте ваш ответ. Наша система никогда не ошибается и находит обратную матрицу заданной размерности в режиме онлайн мгновенно! На сайте сайт допускаются символьные записи в элементах матриц , в этом случае обратная матрица онлайн будет представлена в общем символьном виде.


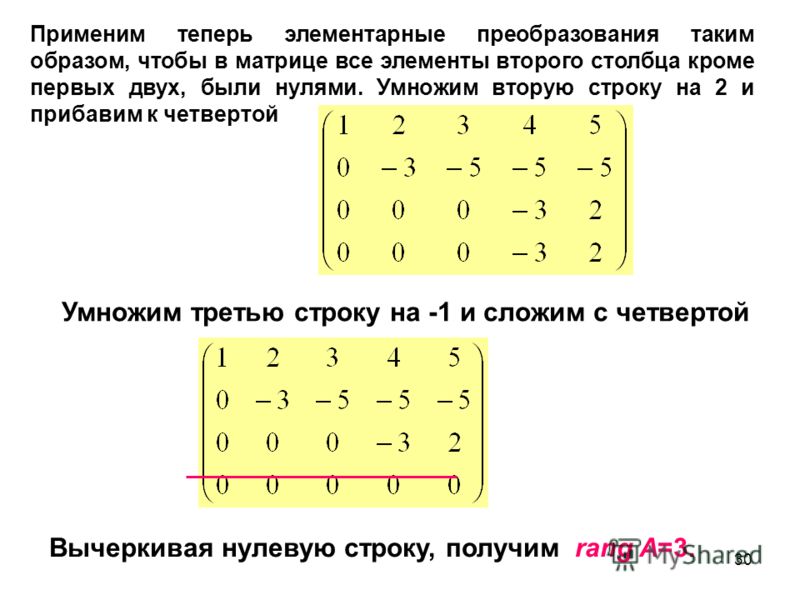
 Следующий шаг — составление матрицы из получившихся дополнений:
Следующий шаг — составление матрицы из получившихся дополнений:
 Результаты вычислений оформляются в отчете формата Word
и в формате Excel
(т.е. имеется возможность проверить решение). см. пример оформления .
Результаты вычислений оформляются в отчете формата Word
и в формате Excel
(т.е. имеется возможность проверить решение). см. пример оформления . {-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
{-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

 Если матричное умножение осуществимо, то в итоге тоже получится матрица. М-да, хорошо мой преподаватель по алгебре не видит, как я объясняю замкнутость алгебраической структуры относительно её элементов =)
Если матричное умножение осуществимо, то в итоге тоже получится матрица. М-да, хорошо мой преподаватель по алгебре не видит, как я объясняю замкнутость алгебраической структуры относительно её элементов =) В рассматриваемом задании часто возникает иллюзия, что речь идёт о каких-то перестановках матриц. Их здесь нет. Снова напоминаю, что в общем случае ПЕРЕСТАВЛЯТЬ МАТРИЦЫ НЕЛЬЗЯ . Так, во втором пункте на втором шаге выполняем умножение , но ни в коем случае не . С обычными числами такой бы номер прошёл, а с матрицами – нет.
В рассматриваемом задании часто возникает иллюзия, что речь идёт о каких-то перестановках матриц. Их здесь нет. Снова напоминаю, что в общем случае ПЕРЕСТАВЛЯТЬ МАТРИЦЫ НЕЛЬЗЯ . Так, во втором пункте на втором шаге выполняем умножение , но ни в коем случае не . С обычными числами такой бы номер прошёл, а с матрицами – нет. Чтобы возвести квадратную матрицу в куб, нужно вычислить произведение:
Чтобы возвести квадратную матрицу в куб, нужно вычислить произведение:
 При расчётах справедлив знакомый алгебраический приоритет: сначала учитываются скобки , затем выполняется возведение в степень / извлечение корней , потом умножение / деление и в последнюю очередь – сложение /вычитание .
При расчётах справедлив знакомый алгебраический приоритет: сначала учитываются скобки , затем выполняется возведение в степень / извлечение корней , потом умножение / деление и в последнюю очередь – сложение /вычитание . Скобки, как и в числовых выражениях, меняют порядок действий: – тут сначала выполняется умножение , потом полученная матрица транспонируется и умножается на 2.
Скобки, как и в числовых выражениях, меняют порядок действий: – тут сначала выполняется умножение , потом полученная матрица транспонируется и умножается на 2.
 Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.
Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта. T+7E$.
T+7E$. T+7E=2\cdot \left(\begin{array} {ccc}
-7 & 13 & -3 \\
-31 & -5 & 7 \\
23 & 31 & 7
\end{array} \right)-3\cdot \left(\begin{array} {ccc}
-5 & 10 & 3 \\
-20 & 12 & -15 \\
13 & 9 & 8
\end{array} \right)+7\cdot \left(\begin{array} {ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array} \right)
$$
T+7E=2\cdot \left(\begin{array} {ccc}
-7 & 13 & -3 \\
-31 & -5 & 7 \\
23 & 31 & 7
\end{array} \right)-3\cdot \left(\begin{array} {ccc}
-5 & 10 & 3 \\
-20 & 12 & -15 \\
13 & 9 & 8
\end{array} \right)+7\cdot \left(\begin{array} {ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array} \right)
$$ 2+3A-9E=2A\cdot A+3A-9E=2 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)\cdot \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} (-3)\cdot(-3)+1\cdot 5 & (-3)\cdot 1+1\cdot 0 \\ 5\cdot(-3)+0\cdot 5 & 5\cdot 1+0\cdot 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} 14 & -3 \\ -15 & 5 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)
=\left(\begin{array} {cc} 28 & -6 \\ -30 & 10 \end{array} \right)+\left(\begin{array} {cc} -9 & 3 \\ 15 & 0 \end{array} \right)-\left(\begin{array} {cc} 9 & 0 \\ 0 & 9 \end{array} \right)=\left(\begin{array} {cc} 10 & -3 \\ -15 & 1 \end{array} \right).
2+3A-9E=2A\cdot A+3A-9E=2 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)\cdot \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} (-3)\cdot(-3)+1\cdot 5 & (-3)\cdot 1+1\cdot 0 \\ 5\cdot(-3)+0\cdot 5 & 5\cdot 1+0\cdot 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} 14 & -3 \\ -15 & 5 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)
=\left(\begin{array} {cc} 28 & -6 \\ -30 & 10 \end{array} \right)+\left(\begin{array} {cc} -9 & 3 \\ 15 & 0 \end{array} \right)-\left(\begin{array} {cc} 9 & 0 \\ 0 & 9 \end{array} \right)=\left(\begin{array} {cc} 10 & -3 \\ -15 & 1 \end{array} \right). $$
$$ Первым делом укажите размер матрицы, нажав на иконки «+» или «-» слева от неё. Затем в поле матрицы введите числа. Также нужно указать степень, в которую возводится матрица. А далее вам остаётся лишь кликнуть на кнопку: «Вычислить» в нижней части поля. Полученный результат будет достоверным и точным, если вы внимательно и правильно ввели все значения. Вместе с ним вам будет предоставлена детальная расшифровка решения.
Первым делом укажите размер матрицы, нажав на иконки «+» или «-» слева от неё. Затем в поле матрицы введите числа. Также нужно указать степень, в которую возводится матрица. А далее вам остаётся лишь кликнуть на кнопку: «Вычислить» в нижней части поля. Полученный результат будет достоверным и точным, если вы внимательно и правильно ввели все значения. Вместе с ним вам будет предоставлена детальная расшифровка решения. см. пример оформления .
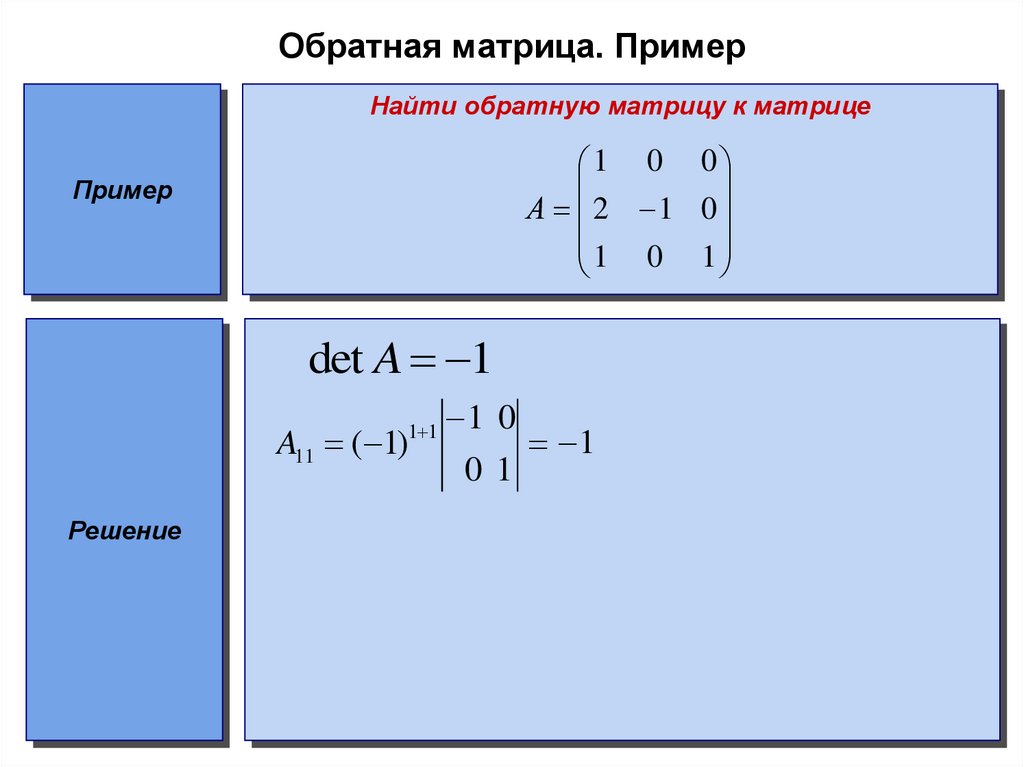
см. пример оформления . Если он не равен нулю, продолжаем решение, иначе — обратной матрицы не существует.
Если он не равен нулю, продолжаем решение, иначе — обратной матрицы не существует.



 е.
е. 




 5
5
 5
5 5..
5..





 Это математически выражается следующим образом:
Это математически выражается следующим образом:




 При этом значения элементов должны совпадать друг с другом. Когда у вас все будет готово, нажмите кнопку расчета, и вы узнаете, как матрица была умножена шаг за шагом, и окончательный результат.
При этом значения элементов должны совпадать друг с другом. Когда у вас все будет готово, нажмите кнопку расчета, и вы узнаете, как матрица была умножена шаг за шагом, и окончательный результат. Tras eso, conocerás el resultado y los pasos previos que conlleva a este cálculo como son el determinante 2×2 y la matriz adjunta.
Tras eso, conocerás el resultado y los pasos previos que conlleva a este cálculo como son el determinante 2×2 y la matriz adjunta.
