Взаимно обратные функции: алгоритм вывода формулы, примеры
- Функция, обратная данной
- Алгоритм вывода формулы функции, обратной данной
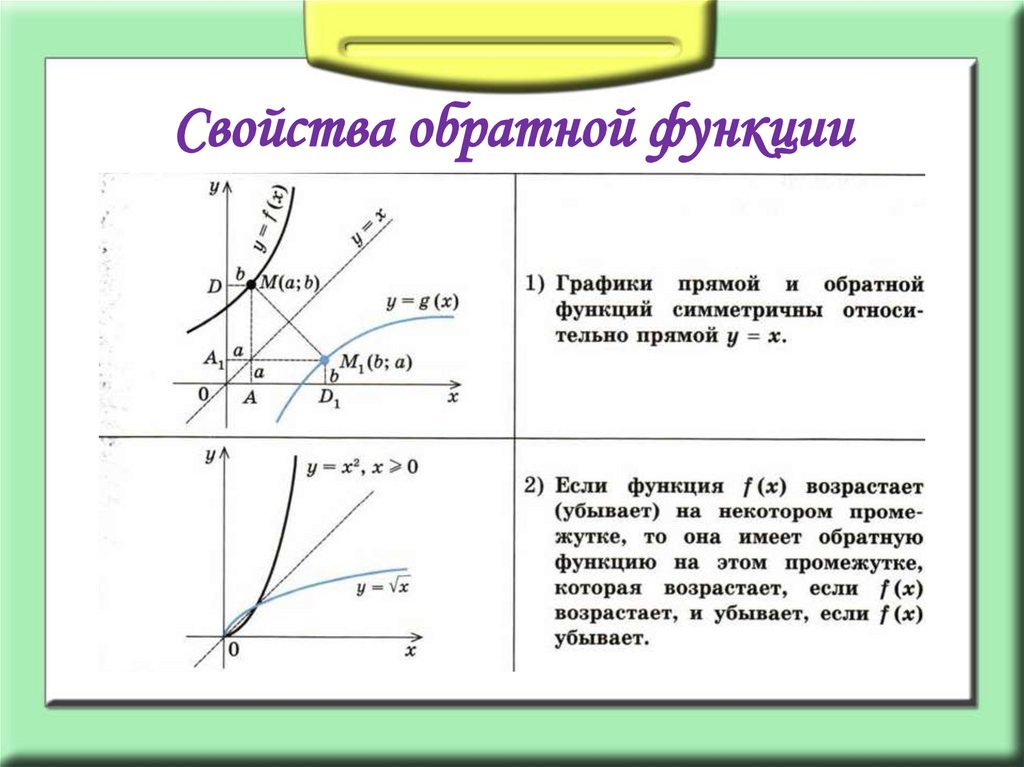
- Свойства взаимно обратных функций
- Примеры
Функция, обратная данной
По определению (см. §34 справочника для 7 класса)
Функция – это соответствие, при котором каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Пусть некоторое соответствие задано таблицей:
x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
y | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
Множество значений X = {-4;-3;…;4} отображается в множество значений Y = {-2;-1,5;…;2}: $X \xrightarrow{f} Y$.
Например: аналитическое выражение для функции $X \xrightarrow{f} Y$, заданной таблицей $y = f(x) = \frac{x}{2}$. Обратное соответствие $Y \xrightarrow{g} X$ также является функцией x = g(y) = 2y.
Функция g — обратная функция к f.
В общем случае формулы функций записывают в виде y(x). При такой записи, функции $y = \frac{x}{2}$ и y=2x являются взаимно обратными.
Алгоритм вывода формулы функции, обратной данной
На входе: множества X и Y, для которых оба соответствия $X \xrightarrow{f} Y$ и $Y \xrightarrow{g} X$ являются функциями.
Шаг 1. В формуле для исходной функции заменить обозначения аргумента и значения: $x \rightarrow y$, $y \rightarrow x$.
Шаг 2. Из полученной формулы выразить y(x). Искомое выражение для обратной функции найдено.
Шаг 3. Учесть ограничения для области определения и области значений исходной и/или обратной функций.
Например:
1) Пусть исходная функция $y = \frac{x}{2}$
Шаг 1. 2+1$
2+1$
Шаг 2. Находим y из полученной формулы: $y = \sqrt{\frac{x-1}{2}}$ — искомая обратная функция
Шаг 3. На обратную функцию накладываются ограничения
на $x:x-1 \ge 0 \Rightarrow x \ge 1$, на $y:y \ge 0$
Тогда исходная функция определяется на множествах $y \ge 1$, $x \ge 0$
Исходная функция — парабола получает ограничения из-за обратной функции; только в этом случаи функции будут взаимно обратными.
Свойства взаимно обратных функций
Пусть f и g — взаимно обратные функции. Тогда:
1. Область определения функции f является областью значений функции g, а область значений функции f является областью определения функции g.
2. Функции f и g либо одновременно возрастающие, либо одновременно убывающие.
3. Если f — нечётная, то и g — нечётная.
4. Графики f и g симметричны относительно биссектрисы 1-й четверти y = x.
5. Справедливы тождества f(g(x) ) = x и g(f(x) ) = x.
Например:
Графики пар взаимно обратных функций, найденных выше:
Примеры
Пример 1. Задайте формулой функцию, обратную данной.
Задайте формулой функцию, обратную данной.
а) y = 5x-4
Меняем аргумент и значение: x = 5y-4
Получаем: $y = \frac{x+4}{5}$ — искомая обратная функция
б) y = -3x+2
Меняем аргумент и значение: x = -3y+2
Получаем: $y = \frac{-x+2}{3}$ — искомая обратная функция
в) y = 4x+1, где $-1 \le x \le 5$
Меняем аргумент и значение: x = 4y+1
Получаем: $y = \frac{x-1}{4}$
Требуем, чтобы: $-1 \le y \le 5 \Rightarrow -1 \le \frac{x-1}{4} \le 5 \Rightarrow -4 \le x-1 \le 20 \Rightarrow -3 \le x \le 21$
Итак, искомая обратная функция: $y = \frac{x-1}{4}$, где -3 $\le x \le 21$
г) $y=- \frac{1}{2} x+7$, где $2 \le x \le 9$
Меняем аргумент и значение: $x=-\frac{1}{2} y+7$
Получаем: y = 2(-x+7) = -2x+14
Требуем, чтобы: $2 \le y \le 9 \Rightarrow 2 \le -2x+14 \le 9 \Rightarrow -12 \le -2x \le -5 \Rightarrow$
$6 \ge x \ge 2,5 \Rightarrow 2,5 \le x \le 6$
$y = -2x+14,где 2,5 \le x \le 6$ — искомая обратная функция
Пример 2. {3}
\)
{3}
\)
\(\ x=\sqrt[3]{y} \)
Ищем необходимые значения х. Поскольку в области определения все числа, то в нашем случае значение подходит.
\(\ y=\sqrt[3]{x} \)
ПримерОтыскать обратную функцию для \(\ y=\cos x \)на промежутке \(\ [0, \pi] \)
Рассмотрим функцию \(\ y=\cos x \) на множестве \(\ X=[0, \pi] \). Она непрерывна и убывает на множестве X и отображает множество \(\ X=[0, \pi] \)на множество \(\ X=[0, \pi] \) потому согласно первой теореме у функции \(\ y=\cos x \)в множестве Y имеется непрерывная обратная функция, возрастающая на \(\ Y=[-1 ; 1] \) и отображающая множество [-1;1] на множество \(\ [0, \pi] \).
Найдем х из \(\ y=\cos x \):
\(\ y=\cos x \)
\(\ x=\pm \arccos y+2 \pi n, n \in Z \)
Ищем подходящие значения
\(\ x=\arccos y \)
Переопределяя переменные, получаем:
\( y = \arccos x \)
Пример
На промежутке \(\
\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)
\) функции \(\
y=\operatorname{tg} x
\)отыскать обратную функцию.
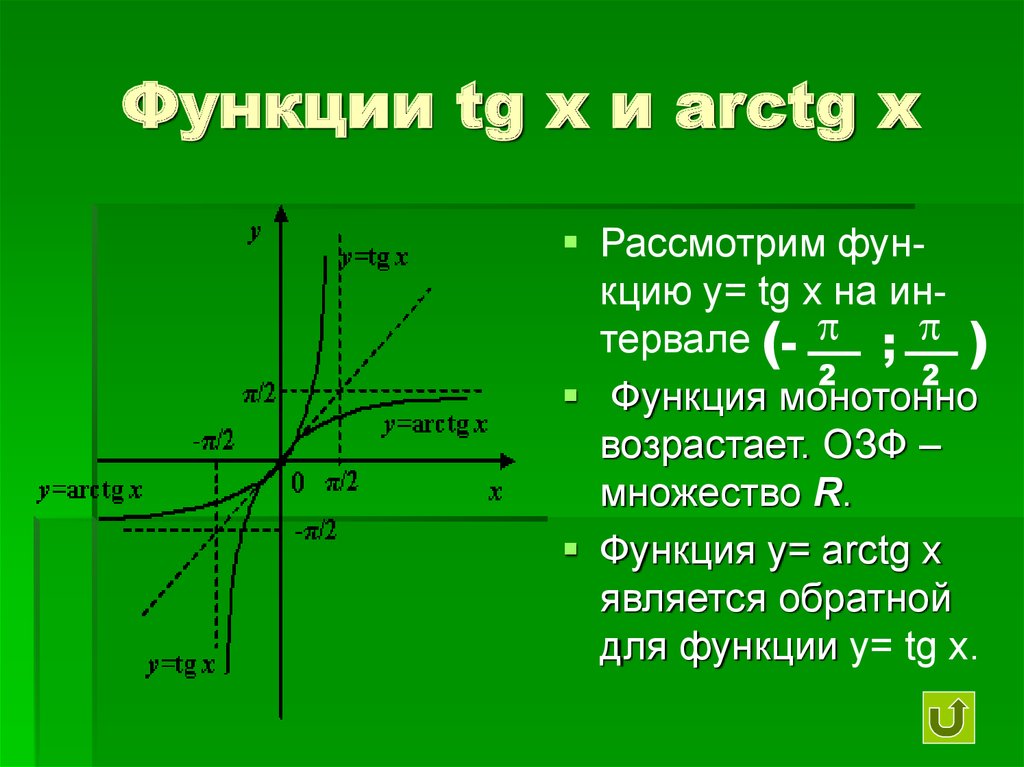
Функция \(\ y=\operatorname{tg} x \)на множестве \(\ X=\left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \) является непрерывной и возрастающей (множество Х) и указывает на множество \(\ X=\left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \), а она соответственно на множество Y=R. Отсюда, согласно первой теореме, функция \(\ y=\operatorname{tg} x \)обладает обратной непрерывной функцией (множество Y) возрастающей на Y=R и отображающей множество R на множество \(\ \left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \)
Ищем х из \(\ y=\operatorname{tg} x : \):
\(\ y=\operatorname{tg} x \)
\(\ x=\operatorname{arctg} y+\pi n, n \in Z \)
Ищем подходящие значения
\(\ x=\operatorname{arctg} y \)
Переопределяя переменные, получаем:
\(\ y=\operatorname{arctg} x \)
Обратные функции. Профильный уровень 10 класс онлайн-подготовка на Ростелеком Лицей
Понятие обратной функции
Представьте, что вы гуляете по пляжу. На песке у кромки воды остаются ваши следы, а вокруг еще множество следов (см. рис. 1).
рис. 1).
Рис. 1. Множество следов на песке
По их форме вы с легкостью можете определить, кто здесь был до вас: другой человек, чайка или собака. Видя след мы можем установить, что за существо его оставило. И наоборот: зная, кто прошел по песку, мы можем сказать, какой след останется. Мы как бы устанавливаем соответствие между следом и существом (см. рис. 2).
Рис. 2. Соответствие между следом и существом
Однозначное ли это соответствие? Давайте подумаем. Когда человек ступает на песок, он точно знает, какой след после него останется. Тут все однозначно. Представим обратную ситуацию: Шерлок Холмс видит на песке след. Может ли он однозначно определить преступника? Он сможет лишь утверждать, что это человек, а вот какой именно – без других улик это не определить, вариантов очень много. Обратное соответствие не является однозначным.
С неоднозначностью соответствия мы сталкиваемся, даже просто глядя на часы. Такое положение стрелок (см. рис. 3) может означать как полночь, так и полдень.
3) может означать как полночь, так и полдень.
Рис. 3. Заданное положение стрелок
И если бы мы были в подвале без окон, то не смогли бы однозначно определить время – у нас было бы 2 варианта. Чтобы выбрать правильный вариант, мы пользуемся дополнительной информацией: смотрим, темно или светло на улице.
Но есть и примеры, когда мы можем однозначно установить соответствие. Так, у каждого человека есть ровно один внутренний паспорт и наоборот – внутренний паспорт однозначно определяет конкретного человека. Между внутренним паспортом и человеком можно установить взаимно однозначное соответствие.
Переходя на язык математики, можно сказать, что мы устанавливаем соответствия между множествами: множеством существ и множеством следов; множеством людей и множеством паспортов. Причем в одну сторону соответствие однозначное, а в обратную не всегда.
Таких примеров неоднозначности обратной операции можно привести много. Так, если нам известны два числа, найти их сумму не составит труда, например:
А вот зная сумму, восстановить однозначно два слагаемых не получится – вариантов будет бесконечно много:
С подобными примерами соответствий мы сталкивались, говоря о числовых функциях. Так, линейная функция является примером взаимооднозначного соответствия (см. рис. 4). Каждому значению соответствует ровно одно значение . И наоборот: каждому значению соответствует ровно одно значение . Это похоже на соответствие паспортов и людей.
Так, линейная функция является примером взаимооднозначного соответствия (см. рис. 4). Каждому значению соответствует ровно одно значение . И наоборот: каждому значению соответствует ровно одно значение . Это похоже на соответствие паспортов и людей.
Рис. 4. График линейной функции
Ситуация с часами похожа на квадратичную функцию (см. рис. 5). По значению мы однозначно определим : , тогда . А вот если мы знаем , например , то однозначно определить нельзя, хотя информации у нас много, возможно всего два варианта: или , или . Однозначно мы можем узнать только при наличии дополнительных условий. Например, если – это сторона квадрата, тогда останется лишь один вариант .
Рис. 5. График квадратичной функции
А вот многозначность, как в случае следов на песке, появляется при работе с тригонометрическими функциями (см. рис. 6). По значению аргумента можно однозначно вычислить значение функций:
Рис. 6. Графики тригонометрических функций
Это мы уже умеем делать. А когда мы попробуем по значению найти , то столкнемся с многозначностью. Например, возьмем функцию Если , то , ведь . Но может быть равен и , и , и и т. д. Ведь синусы всех этих величин также равны . О том, как в общем случае найти аргумент тригонометрической функции по ее значению, и пойдет речь в данном уроке.
А когда мы попробуем по значению найти , то столкнемся с многозначностью. Например, возьмем функцию Если , то , ведь . Но может быть равен и , и , и и т. д. Ведь синусы всех этих величин также равны . О том, как в общем случае найти аргумент тригонометрической функции по ее значению, и пойдет речь в данном уроке.
Для начала разберемся с терминологией. Когда мы каждому значению ставим в соответствие одно значение – это функция. Можно сделать и обратное: поставить каждому значению в соответствие значение . Если мы сможем это сделать однозначно, то получим обратную функцию.
Возьмем, например, функцию (см. рис. 7).
Рис. 7. График функции
Выразив переменную , получаем:
Здесь мы уже значению ставим в соответствие , то есть это обратная функция. Только у нее аргумент обозначен как , а значение функции – как . Нам же привычнее наоборот. Поэтому переобозначим: заменим на , а – на (см. рис. 8):
Получили, что функция является обратной функции . Верно и другое: функция является обратной функции. Поэтому подобные пары функций называют еще взаимно обратными.
Верно и другое: функция является обратной функции. Поэтому подобные пары функций называют еще взаимно обратными.
Рис. 8. Графики функций и
Продолжаем разбираться с терминологией. Функцию, для которой можно найти обратную, называют обратимой функцией. Буквально – «ту, которую можно обратить». То есть функции , являются обратимыми функциями. Да и в целом любая линейная функция является обратимой, ведь каждому значению соответствует ровно одно значение .
А вот функция не является обратимой, ведь значению функции может соответствовать по два значения переменной . Условие однозначности не выполнено. Чтобы сделать эту функцию обратимой, нужно добавить дополнительные условия. Так, если мы рассмотрим функцию только для положительных , то каждому значению будет уже соответствовать только одно значение (см. рис. 9).
Рис. 9. График функции
Функция , при будет уже обратимой. И обратной к ней будет функция (см. рис. 10) (см. в уроке тему «Обратная функция»).
рис. 10) (см. в уроке тему «Обратная функция»).
Рис. 10. Графики функций и
Какие особенности у решения обратной задачи для тригонометрических функций?
Тригонометрические функции многозначны: они не являются обратимыми, ведь каждому значению соответствует множество значений . Это можно увидеть по графикам каждой из тригонометрических функций (см. рис. 11).
Рис. 11. Графики тригонометрических функций
Ранее мы уже сталкивались с обратной задачей. Например, при решении треугольника по значению косинуса мы находили угол:
И там было все однозначно. Почему? Потому что было ограничение – это был острый угол от до . А когда мы говорим о расширенном понятии угла, как раз и появляется многозначность.
Например, на уроке физкультуры вам нужно пробежать кругов по стадиону. В терминах углов – это радиан. Когда учитель видит вас на финише, то он точно не может сказать, пробежали ли вы уже все кругов, а может, или , или даже вообще не начинали бежать. То есть по вашему положению нельзя однозначно определить «угол», который вы пробежали.
То есть по вашему положению нельзя однозначно определить «угол», который вы пробежали.
Решая обратную задачу в общем виде, нужно помнить об этой многозначности и учитывать все возможные варианты. Кроме многозначности, при решении тригонометрических уравнений нам понадобится ввести новые обозначения.
Новые числа мы получали при решении уравнений – называли (обозначали) решение уравнения новым числом, чтобы не использовать бесконечное количество цифр при записи. Вспомните: мы не могли решить уравнение , записав в виде обыкновенной дроби. Только приближенно: (см. в уроке тему «Иррациональные числа»). Поэтому ввели новое обозначение – квадратный корень: .
С тригонометрическими функциями такая же ситуация. Для некоторых аргументов мы знаем значения функций:
И по значению функций сможем точно вычислить аргумент. А вот для остальных значений сможем вычислить лишь приближенно: с помощью калькулятора или таблиц Брадиса. Но для точной записи ответа потребуется ввести новые обозначения.
Какие именно это будут обозначения и как учесть многозначность, мы поговорим далее.
Арккосинус
Начнем с функции . Наша задача – по известному значению функции найти все значения . По сути, решить уравнение , где задано, а неизвестная. Чтобы не путать с функцией, для уравнения введем другие обозначения. Будем решать уравнение , где задано, а неизвестная.
Для начала учтем область значений косинуса: . Значений , при которых или не существует. Соответственно, при и уравнение не будем иметь решений.
Пример 1. Решить уравнение:
Решение
Для решения воспользуемся единичной окружностью. Косинус – это абсцисса точки на единичной окружности. Видим две точки, абсциссы которых равны – точки и (см. рис. 12).
Рис. 12. Иллюстрация к примеру 1
Из таблицы значений мы знаем, что . То есть точке соответствует угол . Тогда точке соответствует угол , ведь , но он отложен по часовой стрелке, то есть это отрицательный угол (см. рис. 13).
рис. 13).
Рис. 13. Иллюстрация к примеру 1
Значит ли это, что уравнение имеет два решения?
Не совсем. Мы уже говорили, что нужно учесть периодичность тригонометрических функций: каждой точке соответствует бесконечное множество углов, определенных с точностью до периода. Точке соответствуют углы вида , где , точке – углы вида , где . Получаем бесконечное множество решений уравнения:
или . Или сокращенно это записывают так:
Ответ: .
Мы увидели, как описать все множество решений тригонометрического уравнения. Но при решении нам не пришлось вводить новых обозначений, ведь значение функции было табличным. Посмотрим, что же будет в обратном случае.
Пример 2. Решить уравнение:
Решение
Для решения снова воспользуемся единичной окружностью. Опять видим две точки, абсциссы которых равны (см. рис. 14).
Рис. 14. Иллюстрация к примеру 2
В отличие от предыдущего примера мы не можем сразу определить, какому углу соответствует точка (см. рис. 15).
рис. 15).
Рис. 15. Иллюстрация к примеру 2
В таблице точного значения нет, можно найти лишь приближенное. Чтобы точно обозначить величину , ввели специальное обозначение .То есть – это величина такого , косинус которого равен .
Более подробно о происхождении термина «арккосинус» вы можете узнать ниже.
Происхождение термина «арккосинус»
Первый корень термина «арккосинус», «арк-», происходит от латинского слова arcus
Согласно определению: арккосинус – это величина такого , косинус которого равен . То есть значение арккосинуса мы определяем как величину угла. Из геометрии мы знаем, что длина дуги определяется как , где – величина центрального угла, на который опирается дуга, – радиус (см. рис. 16).
Рис. 16. Длина дуги определяется как
центральный, радиус окружности равен . Значит, численное значение длины дуги и величина совпадают:
Таким образом, мы можем дать альтернативное определение арккосинуса, оперируя понятием «дуга», а не «угол». Звучать оно будет так: арккосинус – это такое число, соответствующее длине дуги , что его косинус равен .
Звучать оно будет так: арккосинус – это такое число, соответствующее длине дуги , что его косинус равен .
С учетом периода точке будут соответствовать углы вида , тогда точке – углы вида.
Таким образом, корни уравнения можно записать следующим образом:
или, или одной формулой:
Ответ: .
В общем случае, решая уравнение , величину мы будем обозначать как . И будем получать решения уравнения:
Обратим внимание, что понятие арккосинуса мы ввели только для . А значения арккосинуса связаны с , величина которого изменяется от (крайнее правое положение) до (крайнее левое положение).
Теперь мы можем строго сформулировать определение арккосинуса: если , то – это такое число из отрезка , косинус которого равен :
Вернемся к решению уравнения . Общий вид его корней мы можем записать так: . Но в некоторых случаях это можно сделать и в другом виде. Если (см. рис. 17), то точке соответствуют углы. Для точки углы мы можем записать как .
Рис. 17. Расположение точек и при
В целом корнями уравнения будут и т. д. В общем виде это можно записать так:
Если , то точки и сходятся в одну (см. рис. 18). Ей соответствует нулевой угол . С учетом периода:
Рис. 18. Расположение точек и при
Если , тогда точки также сходятся в одну (см. рис. 19). Решения можно записать так:
Рис. 19. Расположение точек и при
По определению арккосинуса числа для каждого определено одно значение . Таким образом, на отрезке определена обратимая функция .
Эта функция является обратной к функции , рассматриваемой на отрезке . Для ее исследования вспомним, что график обратной функции симметричен графику исходной относительной прямой (см в уроке тему «Обратная функция»).
Поэтому для построения графика функции берем функцию на отрезке и отражаем симметрично относительно прямой (см. рис. 20).
Рис. 20. График функции
Глядя на график, перечислим основные свойства функции :
- Область определения .

- Множество значений .
- Функция убывающая.
- Не является ни четной, ни нечетной. Это видно, из того, что график функции не симметричен ни относительно начала координат, ни относительно оси ординат. При этом для противоположных аргументов функции выполняется соотношение:
С его доказательством вы можете ознакомиться в ниже.
Доказательство
Докажем, что для любого выполняется равенство:
Рассмотрим случай, когда , имея в виду, что противоположный случай для доказывается аналогично.
Отметим на числовой окружности – это . Тогда – это (см. рис. 21).
Рис. 21. Иллюстрация к доказательству
Дуги и симметричны относительно оси ординат, значит, длины этих дуг равны (см. рис. 22).
Рис. 22. Иллюстрация к доказательству
Тогда равны и центральные углы, на которые они опираются (см. рис. 23):
Рис. 23. Иллюстрация к доказательству
Тогда:
Удобнее полученное соотношение использовать в следующем виде:
Арксинус
Рассмотрим решение уравнений вида . Как и для косинусов, область значений синуса: . Поэтому при и уравнение не будет иметь решений.
Как и для косинусов, область значений синуса: . Поэтому при и уравнение не будет иметь решений.
Пример 3. Решить уравнение:
Решение
Изобразим единичную окружность. Ординаты точек на окружности – это значения синусов соответствующих углов. Обозначим буквами и точки, ординаты которых равны (см. рис. 24).
Рис. 24. Иллюстрация к примеру 3
Им соответствуют решения:
Заметим, что:
При этом (из симметрии):
Поэтому:
По аналогии с косинусами для введем новое обозначение . То есть арксинус – это величина такого , что его синус равен . Тогда решения уравнения можно записать так:
Ответ: ; .
В общем случае, решая уравнение , величину мы также будем называть арксинусом и будем получать решения и .
Как и для арккосинуса, понятие арксинуса имеет смысл только для . При этом значения арксинуса связаны с углом , величина которого изменяется от (нижнее положение прямой) до (верхнее положение).
Сформулируем строгое определение арксинуса: если , то – это такое число из отрезка , синус которого равен :
Вернемся к решению уравнения. Мы получили множество корней вида: и . Их все можно объединить одной формулой:
Подробнее об этом – ниже.
Решение уравнения в одной формуле
Для начала перепишем корни уравнения в следующем виде:
В первом выражении для наглядности поменяем местами множители, а во втором – сгруппируем последние два слагаемых и вынесем за скобки. Получим:
Можно заметить, что если перед стоит знак «+», то множитель возле – четное число , если же перед стоит знак «–», то множитель – нечетное число . Это позволяет записать общее решение уравнения в общем виде:
Рассмотрим, почему эта более короткая формула включает в себя две предыдущие формы записи решения. Предположим, что – четное число, то есть . Тогда будет положительным числом и корень уравнения примет вид , что соответствует первому множеству решений.
А это уже описывает второе множество решений.
По определению арксинуса для каждого определено одно значение . Таким образом, на отрезке задана обратимая функция .
При этом функция является обратной к функции , рассматриваемой на отрезке . Тогда свойства функции можно получить из свойств функции (см. рис. 25):
Рис. 25. График функции
- График функции симметричен графику функции , относительно прямой (см. рис. 26).
Рис. 26. График функции - Область определения .
- Множество значений .
- Функция возрастающая.
- Функция нечетная, поскольку ее график симметричен относительно начал координат. Соответственно, выполняется соотношение:
Арктангенс и арккотангенс
Для решения уравнений и воспользуемся графиками этих функций.
Пример 4. Решить уравнение:
Решение
Для решения используем графический метод (см. в уроке тему «Графический метод»). Решения этого уравнения – абсциссы точек пересечения графиков функций и прямой (см. рис. 27).
Рис. 27. Иллюстрация к примеру 4
Тут мы снова оказываемся в ситуации многозначности, ведь пересечение графиков – это бесконечное множество точек. Выберем одну из них – точку пересечения прямой с главной веткой тангенса. Абсциссу этой точки обозначим как .Тогда с учетом периодичности тангенса абсциссы всех остальных точек можно представить в виде (см. рис. 28):
Это и будет решением уравнения .
Рис. 28. Иллюстрация к примеру 4
Ответ: .
В общем случае, решая уравнение , будем аналогично обозначать абсциссу точки пересечения прямой с главной веткой тангенса как . Обратим внимание, что тут ограничений на значение не было – аргументом арктангенса может быть любое число. А вот значения лежат лишь на промежутке , ведь именно в этих пределах находится главная ветка тангенса.
А вот значения лежат лишь на промежутке , ведь именно в этих пределах находится главная ветка тангенса.
Строго арктангенс мы можем определить так: – это такое число из интервала , тангенс которого равен .
По определению арктангенса числа для каждого действительного определено одно число . Таким образом, на всей числовой прямой задана функция . Эта функция является обратной к функции , рассматриваемой на интервале .
График функции получается из графика функции , симметрией относительно прямой (см. рис. 29).
Рис. 29. График функции
Выпишем свойства функции:
- Область определения .
- Множество значений .
- Функция возрастающая.
- Функция нечетная, поскольку график симметричен относительно начала координат:
По аналогии с тангенсом решим уравнение . Точки пересечения графиков – это бесконечное множество точек вида , где – абсцисса точки пересечения прямой и главной ветви графика котангенса (см. рис. 30). Для этого числа вводим обозначение . Тогда все корни уравнения можно представить в виде:
рис. 30). Для этого числа вводим обозначение . Тогда все корни уравнения можно представить в виде:
Рис. 30. Пересечение графиков и
При этом арккотангенс может иметь любой аргумент. А вот его значения лежат в интервале , ведь именно на этом интервале строится главная ветвь графика функции .
Строгое определение арккотангенса: – это такое число из интервала , котангенс которого равен :
Функция является обратной к функции , рассматриваемой на интервале . График функции получается из графика функции , симметрией относительно прямой (см. рис. 31).
Рис. 31. График функции
Свойства функции:
- Область определения .
- Множество значений .
- Функция убывающая.
- Функция не является ни четной, ни нечетной:
Преобразование выражений, содержащих обратные тригонометрические функции
Мы познакомились с новыми функциями, которые позволяют записать точное решение тригонометрических уравнений. Как и с любым новым введенным инструментом, мы должны научиться с ними работать. В частности – научиться упрощать выражения.
Как и с любым новым введенным инструментом, мы должны научиться с ними работать. В частности – научиться упрощать выражения.
Главная идея работы с аркфункциями – использовать их определение. То есть то, что эквивалентные записи:
Для упрощения: обозначаем аркфункцию новой переменной и используем определение.
Задание 1. Найти значение выражения:
Решение
Обозначим:
Заменяем в нашем выражении на . Теперь наша задача – вычислить . По определению арккосинуса:
Таким образом:
Ответ: .
Пользуясь этим приемом, аналогично можно доказать и в общем виде подобные равенства:
Задание 2. Найти значение выражения:
Решение
Обозначим:
Теперь нам нужно найти . По определению арксинуса: , при
Вычислим :
или
При косинус принимает положительные значения (см. рис. 32), поэтому выбираем значение .
рис. 32), поэтому выбираем значение .
Рис. 32. Иллюстрация к заданию 2
Таким образом:
Ответ: .
С еще одним заданием на преобразование выражений с аркфунциями вы можете ознакомиться ниже.
Пример
Задание. Найтизначение выражения:
Решение
Идея все та же – обозначаем аркфункцию новой переменной:
Теперь наша задача – найти . По определению:
Из этого равенства можно было бы сделать вывод, что . Но он будет неправильным, поскольку . Значения тангенса будут равны в тех случаях, когда их аргументы отличаются на периоды: . Осталось подобрать такое целое значение , для которого . Для этого решим неравенство:
Вычислив приблизительные значения левой и правой части, получим:
Под это неравенство подпадает единственное целое число . То есть . Тогда:
Таким образом:
Ответ: .
Список литературы
- Алимов Ш.
 А., Колягин Ю.М., Ткачева М.В. Математика. Алгебра и начала математического анализа, геометрия. 10–11класс. Учебник. – М.: АО «Издательство «Просвещение».
А., Колягин Ю.М., Ткачева М.В. Математика. Алгебра и начала математического анализа, геометрия. 10–11класс. Учебник. – М.: АО «Издательство «Просвещение». - Мордкович А.Г., Семенов П.В. Математика. Алгебра и начала математического анализа, геометрия. 10–11класс. Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019.
- Никольский С.М., Потапов М.К., Решетников Н.Н. Алгебра и начала математического анализа, геометрия. 10 класс. Учебник. – М.: АО «Издательство «Просвещение».
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru
- Интернет-портал cleverstudents.ru
- Интернет-портал ru.solverbook.com
Домашнее задание
- Найти функцию, обратную данной:
- Решить уравнения:
- Найти значения выражений:
Решение высшей математики онлайн
‹— Назад
Рассмотрим теперь поподробнее понятие обратной функции, введённое в начале главы.
Если — взаимно-однозначное отображение (биекция), то для любого однозначно определен такой элемент , что . Тем самым однозначно определено соответствие , называемое обратной функцией по отношению к функции . Обратная функция для обозначается . Таким образом,
Очевидно, что согласно определению мы имеем тождество , то есть композиция — это тождественное отображение , для любого . Точно так же , то есть , , , если .
Последнее утверждение означает, что функция, обратная к , равна : , то есть что функции и — это две взаимно обратные функции.
Пример 1.21 Если — ограничение функции на отрезок (это ограничение называется главной ветвью синуса), то отображение — биекция.
Рис.1.31.Главная ветвь синуса
Поэтому существует обратная функция , называемая арксинусом и обозначаемая или (второе обозначение употребляется в англоязычной математической и инженерной литературе). Таким образом,
если и
Пример 1.22 Аналогично определяется функция арккосинус (обозначается или ). Это функция, обратная к ограничению функции на отрезок (такое ограничение называется главной ветвью косинуса):
если и
Рис.1.32.Главная ветвь косинуса
Пример 1.23 Функция арктангенс (обозначается , или , или ) — это функция, обратная к ограничению функции на интервал , то есть обратная к главной ветви тангенса:
Так как — это биекция, то обратная функция определена при всех :
если и
Рис. 1.33.Главная ветвь тангенса
1.33.Главная ветвь тангенса
Упражнение 1.4 Дайте определение функции арккотангенс (обозначается ), рассмотрев главную ветвь котангенса — ограничение функции на интервал .
Упражнение 1.5 Вспомните или выведите простые соотношения, которым удовлетворяют значения функций:
а) и ;
б) и .
График обратной функции получается из графика исходной функции , если у каждой точки графика поменять местами координаты и :
так как состоит из таких точек , что , а — из таких точек , что ; но, согласно определению обратной функции, равенства и эквивалентны.
В случае, когда , , перестановка координат геометрически может быть описана как преобразование симметрии относительно прямой , то есть относительно биссектрисы первого и третьего координатных углов.
Рис.1.34.Симметричные точки графиков функций и
Значит (в случае , ), графики и симметричны относительно этой биссектрисы, если ось, по которой откладываются значения аргумента функции, каждый раз размещать горизонтально.
Рис.1.35.Графики взаимно обратных функций расположены симметрично
Пример 1.24 Согласно с последним замечанием, мы легко построим теперь графики обратных тригонометрических функций и :
Рис. 1.36.Графики главной ветви и
1.36.Графики главной ветви и
Рис.1.37.Графики главной ветви и
Рис.1.38.Графики главной ветви и
Рис.1.39.Графики главной ветви и
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Взаимно обратные функции, основные определения, свойства, графики.
 …
…Привет, Вы узнаете про взаимно обратные функции, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое взаимно обратные функции, обратные функции , настоятельно рекомендую прочитать все из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА.
Обратная функция — определение и примеры нахождения.
Определение обратной функции.
Пусть функция строго монотонная (возрастающая или убывающая) и непрерывная на области определения , область значений этой функции , тогда на интервале определена непрерывная строго монотонная функция с областью значений , которая является обратной для .
Другими словами, об обратной функции для функции на конкретном промежутке имеет смысл говорить, если на этом интервале либо возрастает, либо убывает.
Функции f и g называют взаимно обратными.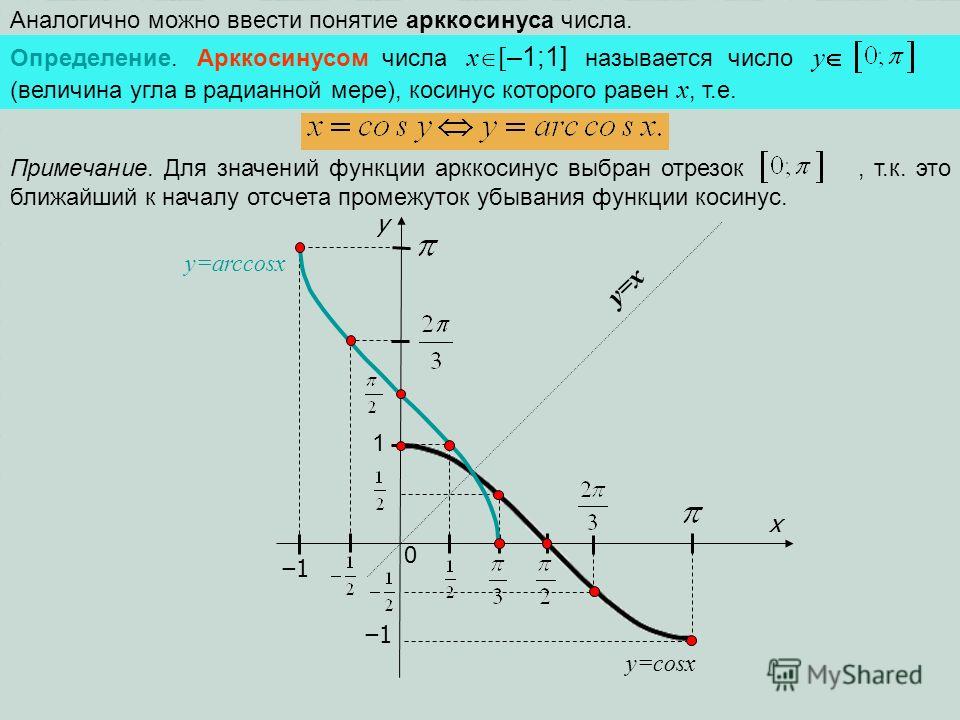
Зачем вообще рассматривать понятие обратных функций?
Это вызвано задачей решения уравнений . Решения как раз и записываются через обратные функции .
Примеры нахождения взаимнообратных функций.
Например, требуется решить уравнение .
Решениями являются точки .
Функции косинус и арккосинус как раз являются обратными на области определения.
Рассмотрим несколько примеров нахождения обратных функций.
Начнем с линейных взаимнообратных функций.
Пример.
Найти функцию обратную для .
Решение.
Областью определения и областью значений этой функции является все множество действительных чисел. Выразим x через y (другими словами, решим уравнение относительно x ).
— это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать .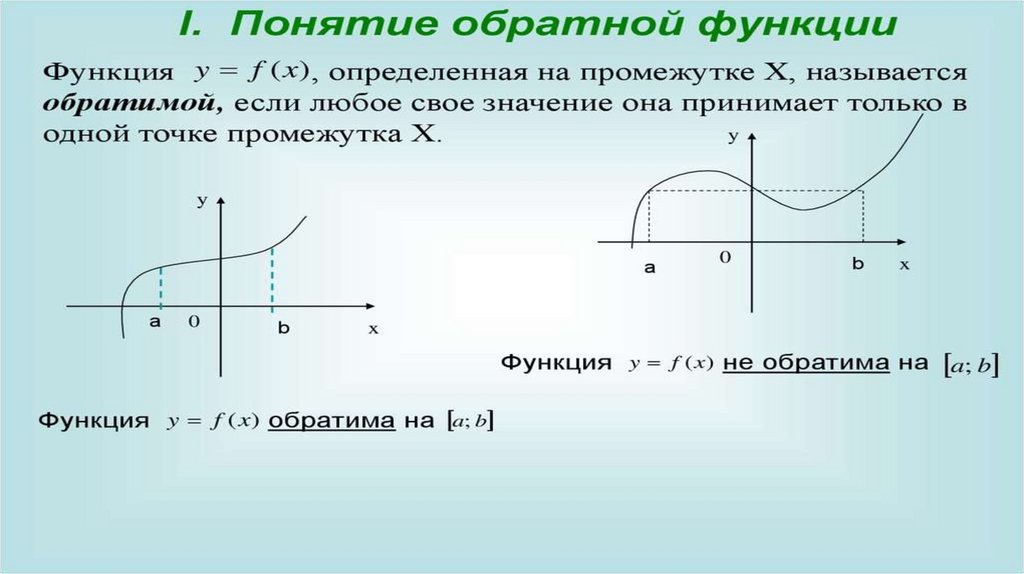
Таким образом, и — взаимно обратные функции .
Приведем графическую иллюстрацию взаимно обратных линейных функций.
Очевидно, что графики симметричны относительно прямой y=x (биссектрисы первого и третьего квадрантов). Это одно из свойств взаимно обратных функций, о которых речь пойдет ниже.
Теперь рассмотрим пример нахождения логарифмической функции, обратной к заданной показательной функции.
Пример.
Найти функцию обратную для .
Решение.
Областью определения этой функции является все множество действительных чисел, областью значений является интервал . Выразим x через y (другими словами, решим уравнение относительно x).
— это и есть обратная функция. Переставив буквы x и y , имеем .
Таким образом, и — показательная и логарифмическая функции есть взаимно обратные функции на области определения.
График взаимно обратных показательной и логарифмической функций.
Свойства взаимно обратных функций.
Перечислим свойства взаимно обратных функций и .
- и .
- Из первого свойства видно, что область определения функции совпадает с областью значений функции и наоборот.
- Графики взаимно обратных функций симметричны относительно прямой y=x.
- Если возрастает, то и возрастает, если убывает, то и убывает.
Замечание по свойству 1).
Рекомендуем ОЧЕНЬ ВНИМАТЕЛЬНО относиться к области определения и области значений функций.
Например: и — взаимно обратные функции. По первому свойству имеем . Это равенство верно только для положительных y , для отрицательных y логарифм не определен. Так что не спешите с записями вида , а если уж так написали, то следует добавить фразу «при положительных y».
Равенство в свою очередь верно для любых действительных x.
Надеемся, Вы уловили этот тонкий момент.
Особенно аккуратными надо быть с тригонометрическими и обратными тригонометрическими функциями.
К примеру, , так как область значений арксинуса , а в нее не попадает.
Правильно будет
В свою очередь есть верное равенство.
То есть при и при .
Еще раз подчеркнем: БУДЬТЕ ВНИМАТЕЛЬНЫ С ОБЛАСТЬЮ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЮ ЗНАЧЕНИЙ!
Графики основных элементарных взаимно обратных функций.
-
Взаимно обратные степенные функции, графики.
Для степенной функции при обратной является также степенная функция Если заменить буквы, то получим пару взаимно обратных функций и
Графики для положительных а и отрицательных а.
-
Взаимно обратные показательная и логарифмическая функции и , графики.
Подразумеваем, что а положительное и не равное единице число.
Графики для и для
-
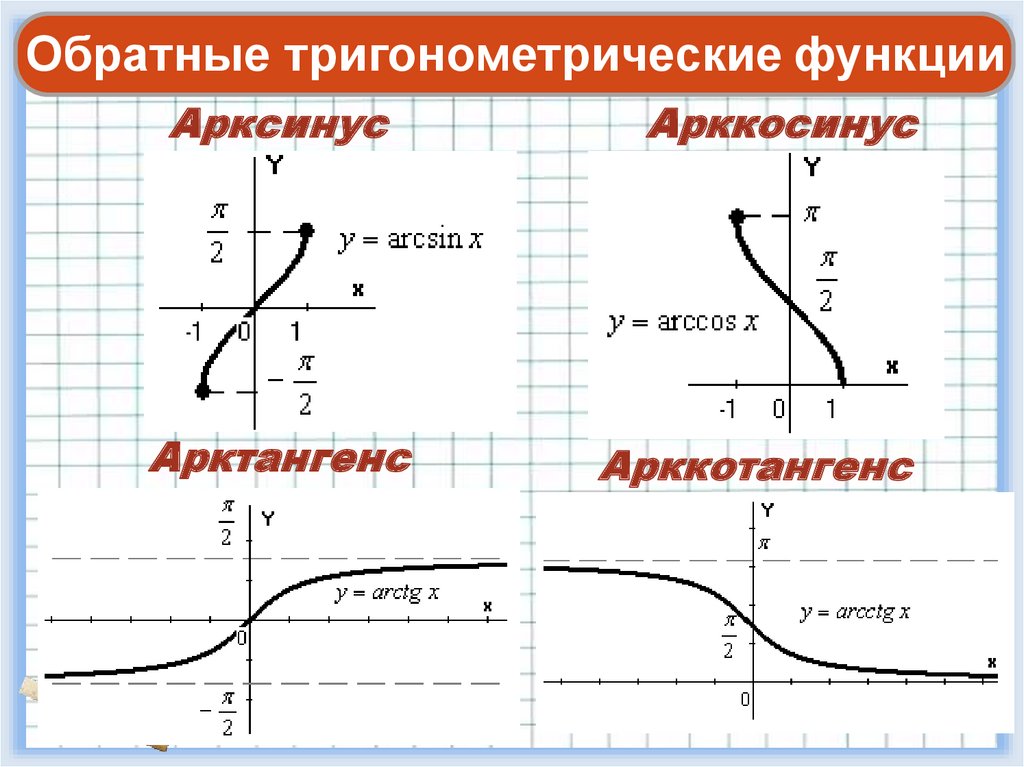
Взаимно обратные тригонометрические и обратные тригонометрические функции.

График главной ветви синуса и арксинуса (светлая область).
График главной ветви косинуса и арккосинуса (светлая область).
График главной ветви тангенса и арктангенса (светлая область).
График главной ветви котангенса и арккотангенса (светлая область).
Если Вам потребуются обратные функции для ветвей тригонометрических функций, отличных от главных, то соответствующую обратную тригонометрическую функцию нужно будет сдвинуть вдоль оси ординат на необходимое количество периодов.
Например, если Вам потребуется обратная функция для ветви тангенса на промежутке (эта ветвь получается из главной ветви сдвигом на величину вдоль оси ох ), то ей будет являться ветвь арктангенса, сдвинутая вдоль оси oy на .
Пока на этом закончим с обратными функциями.
Не следует путать с Обратная величина.
Функция и обратная ей функция . Об этом говорит сайт https://intellect.icu . Если, то
Об этом говорит сайт https://intellect.icu . Если, то
Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x дает y, то обратная ей функция от y дает x. Обратная функция функции обычно обозначается, иногда также используется обозначение .
Функция, имеющая обратную, называется обратимой.
Определение
Функция называется обратной к функции , если выполнены следующие тождества:
- для всех
- для всех
Связанные определения
- Функция называется левой обратной к функции, если для всех .
- Функция называется правой обратной к функции , если для всех .
Существование
Чтобы найти обратную функцию, нужно решить уравнение относительно . Если оно имеет более чем один корень, то функции, обратной к не существует. Таким образом, функция обратима на интервале тогда и только тогда, когда на этом интервале она взаимно-однозначна.
Таким образом, функция обратима на интервале тогда и только тогда, когда на этом интервале она взаимно-однозначна.
Для непрерывной функции выразить из уравнения возможно в том и только том случае, когда функция строго монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках ее строгой монотонности. Например, является обратной функцией к на , хотя на промежутке обратная функция другая:.
Для существования обратной функции не являются необходимыми ни непрерывность, ни монотонность исходной функции. Пример: функция где — функция Дирихле, разрывна и не монотонна, однако обратная для нее существует :
Примеры
- Если, где то
- Если, где фиксированные постоянные и, то
- Если , то
Свойства
Графики функции и обратной ей
- Областью определения является множество , а областью значений — множество .
- По построению имеем:
или
,
,
или короче
,
,
где {\displaystyle \circ } означает композицию функций, а — тождественные отображения на и соответственно.
- Такое отображение, что («обратное справа»), называется сечением отображения .
- Функция является обратной к:
.
- Пусть — биекция. Пусть ее обратная функция. Тогда графики функций и симметричны относительно прямой.
- Также, если у функции есть обратная ей , то графики этих функций будут симметричны относительно линии .
Разложение в степенной ряд
Обратная функция аналитической в некоторой окрестности точки функции может быть представлена в виде степенного ряда:
где функции задаются рекурсивной формулой:
См. также
- Теорема Лагранжа об обращении рядов
- Обратные тригонометрические функции
- Обратимая функция
- функции , область определения ,
- обратные тригонометрические функции , арксинус ,
- дзета-функция римана ,
- случайные функции , характеристики случайных функций ,
- каррирование , мемоизация ,
- Функциональное уравнение
- Алгоритм
- Уравнение
- Булева функция
В общем, мой друг ты одолел чтение этой статьи об взаимно обратные функции. Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое взаимно обратные функции, обратные функции
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА
Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое взаимно обратные функции, обратные функции
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА
+ онлайн-решатель с бесплатными шагами
Калькулятор обратной функции находит обратную функцию g(y), если она существует для заданной функции f(x). Если обратной функции не существует, калькулятор ищет обратную зависимость. Входная функция должна быть функцией только x. Если x не присутствует во входных данных, калькулятор не будет работать.
Калькулятор не поддерживает нахождение обратной функции многих переменных вида f(x1, x2, x3, … , xn) для всех n переменных. Если вы вводите такую функцию, она считает все переменные, кроме x, константами и решает только для f(x).
Если вы вводите такую функцию, она считает все переменные, кроме x, константами и решает только для f(x).
Что такое калькулятор обратной функции?
Калькулятор обратной функции — это онлайн-инструмент, который вычисляет обратную функцию или отношение $\mathbf{g(y)}$ для входной функции $\mathbf{f(x)}$ , такой, что вывод $\mathbf{f(x)}$ в $\mathbf{g(y)}$ отменяет эффект $\mathbf{f(x)}$ .
Интерфейс калькулятора состоит из одного текстового поля, обозначенного цифрой 9.0003 “Обратная функция.” Здесь вы просто вводите входное выражение как функцию x. После этого вы просто отправляете его на расчет.
Как пользоваться калькулятором обратной функции?
Вы можете использовать Калькулятор обратной функции , введя функцию, обратную функцию которой вы хотите найти. Пошаговые инструкции приведены ниже.
Например, предположим, что мы хотим найти обратную функцию f(x)=3x-2.
Шаг 1
Введите функцию в текстовое поле. В нашем случае мы набираем здесь «3x-2». Мы также можем ввести «y=3x-2», так как это означает то же самое.
Шаг 2
Нажмите кнопку Submit , чтобы вычислить обратную функцию.
Результаты
Результаты открываются в новом всплывающем окне. Для нашего примера обратная функция:
\[ \frac{x+2}{3} \]
Переменную x результата не следует путать с переменной x во входной функции f(x). В терминологии, используемой до сих пор для описания калькулятора, x в результатах эквивалентен y в g(y) и представляет собой выходное значение входной функции.
Например, в нашем случае:
f(x=10) = 3(10)-2 = 28
Теперь, если мы поместим x = 28 в выходную функцию калькулятора, обратная функция:
\[ \frac {28+2}{3} = \frac{30}{3} = 10 \]
Это исходное значение, переданное в f(x).
Как работает калькулятор обратной функции?
Калькулятор обратной функции работает с использованием метода замены переменных/координат для нахождения обратной функции. По сути, учитывая, что «*» — это любой определенный оператор:
По сути, учитывая, что «*» — это любой определенный оператор:
f(x) = члены с x * другие члены с константами
Положим f(x)=y. Это представляет значение функции в x. Тогда наше уравнение будет таким:
y = члены с x * другие члены с константами *{(1)}
Теперь поменять местами переменные x и y:
x = члены с y * другие члены с константами
И решите y через x, чтобы получить обратное отображение. Вы можете получить тот же результат, найдя x в уравнении (1), но переменная swap сохраняет порядок, сохраняя обычную номенклатуру функций (x — вход, y — выход).
Вы можете видеть, что метод использует известный вывод функции, чтобы найти ввод, учитывая, что мы знаем саму функцию. Таким образом, результирующая обратная функция g(x) также выражается через x, но помните, что мы поменяли местами переменные, так что это x представляет результат первой функции (y), а не вход.
Определение обратной функции
Функция g(y) является обратной функцией f(x), только если:
\[ y = f(x) \iff x = g(y) \, \Rightarrow \, g (f(x)) = x \,\, \text{и} \,\, f(g(y)) = y \] 9{-1}(y) \right) = y \, \Rightarrow \, g(g(y)) = y \]
Существование обратного
Обратите внимание, что g(y) не обязательно может быть функцией ( один вход, один выход ), но отношение ( один вход к нескольким выходам ). Как правило, это происходит, когда входная функция является биективной или «многие к одному» (то есть она отображает разные входные данные в один и тот же выход). В таком случае точный вход невозможен, а обратная функция не существует.
Как правило, это происходит, когда входная функция является биективной или «многие к одному» (то есть она отображает разные входные данные в один и тот же выход). В таком случае точный вход невозможен, а обратная функция не существует.
Однако возможно существование обратной зависимости. Вы можете сказать, является ли вывод калькулятора обратной зависимостью, если он показывает более одного вывода или знак «$\pm$». 92$ и f(x) = |x|. Поскольку выходные данные функций имеют один и тот же вывод (значение y) для нескольких входных данных (значений x), обратная функция не возвращает x однозначно, поскольку она возвращает 90 125 кратных 90 126 значений x, которые удовлетворяют соотношению.
Проверка горизонтальной линии
Проверка горизонтальной линии иногда используется для проверки того, является ли входная функция биективной. Если вы можете провести горизонтальную линию, пересекающую график функции более чем в одной точке, то эта функция является отношением «многие к одному», а обратная ей функция в лучшем случае является отношением.
Решенные примеры
Вот несколько примеров, которые помогут нам лучше понять тему.
Пример 1
Найдите обратную функцию для функции:
f(x)= 3x-2
Решение
Пусть:
-x=y $\Right3 = y 2
Теперь поменяйте местами x и y так, чтобы теперь у нас было исходное входное значение x как функция выходного значения y:
x = 3y-2
Решение для y:
\[ x + 2 = 3y \, \Rightarrow \, y = \frac{x+2}{3} \]
Это искомая обратная функция. Калькулятор также показывает этот результат.
Пример 2
Для функции
\[ f(x) = 10\ln \left( \frac{1}{1+x} \right) \]
Найдите обратную и классифицируйте ее как функцию или отношение. Проверьте это для входа x=10.
Решение
Используя тот же метод подстановки, что и в примере 1, сначала перепишем:
\[ y = f(x) \, \Rightarrow \, y = 10\ln \left( \frac{1} {1+x} \справа) \] 92-15x+x\ln(10) \]
Найдите обратную функцию, если она существует. В противном случае найдите обратное отношение и объясните, почему оно является отношением.
В противном случае найдите обратное отношение и объясните, почему оно является отношением.
Решение
Функция является квадратичной. Его график будет параболой, поэтому мы видим, что у него не будет обратной функции, потому что горизонтальная линия всегда будет пересекать параболу более чем в одной точке. Поскольку оно биективно (многие к одному), оно необратимо.
Однако мы могли бы попытаться найти обратное отношение, используя тот же метод замены переменных, который использовался ранее. 92-4(30)(x)}}{2(30)} \]
Ясно, что одно и то же значение y = f(x) даст два решения для x = g(y), поэтому наша исходная функция f( x) не является биективным, а обратное отображение является отношением, а не функцией.
Список математических калькуляторов
Калькулятор обратной функции — расчет обратных функций
Калькулятор обратной функции вычисляет обратное значение функции, заданной в качестве входных данных. Что касается определения, обратная функция — это функция, обращающая другую функцию. Она также известна как антифункция и обозначается как f(x) = y ⇔ f− 1(y) = x. Студенты, пытающиеся найти обратную функцию, могут использовать наш калькулятор обратных функций, чтобы найти точные ответы.
Она также известна как антифункция и обозначается как f(x) = y ⇔ f− 1(y) = x. Студенты, пытающиеся найти обратную функцию, могут использовать наш калькулятор обратных функций, чтобы найти точные ответы.
Калькулятор обратной функции – лучший рейтинг экспертов
Обратная функция обращает другую функцию. Однако большинству студентов трудно найти обратную функцию без калькулятора, потому что концепция им непонятна. Калькулятор обратной функции Myassignmenthelp.Com — это цифровой инструмент, который позволяет учащимся легко находить обратные функции. Если вы не знаете, как найти обратную функцию, воспользуйтесь нашим калькулятором обратных операций с шагами.
Решатель обратной функции Myassignmenthelp.Com разработан и разработан некоторыми компетентными математическими и программистскими гениями для упрощения сложных вычислений обратной функции. Инструмент быстрый, точный и рекомендован ведущими преподавателями предметов для получения правильных результатов с правильными шагами.
Да, верно! Наш обратный калькулятор функций даст вам правильные шаги для решения уравнений, чтобы вы могли обращаться к ним и практиковаться самостоятельно. Так чего же ты ждешь? Используйте наш калькулятор уравнений обратных функций или специалистов по математике, чтобы упростить свои вычисления.
Get Instant Expert
Легкий доступ к решенным ключам, образцам и многому другому
Исследуйте нашу библиотеку, богатую справочными образцами, решенными вопросниками и исследовательскими заметками.
Поделиться Код курса
Как найти обратную функцию без калькулятора?
Решение математических задач, таких как уравнения обратной функции, без калькулятора может стать сложной задачей, если концепция неясна. Следовательно, чтобы найти обратную функцию без калькулятора, вот что вы должны сделать:
- Возьмем одну функцию f(x) с x в качестве переменной
- Рассмотрим y как функцию для f(x)
- Измените переменные x и y, и результирующая функция будет вашей x
- Затем решите уравнение x относительно y
- Найдите значение y.

Не забудьте сначала заменить функциональную переменную другой, а затем решить другую переменную, заменив обе. Давайте рассмотрим несколько примеров, чтобы получить четкое представление о том же самом:
Пример 1: Найдите обратную функцию f(x) = y = 5x − 1
Решение:
Сначала замените f(x) с f(y).
Новое уравнение: y = 5x − 1,
x = 5y − 1
Решите для y,
y = (x + 1)/5
Таким образом, y = 5x − 1, обратное y = (x + 1)/5/
Давайте решим другой пример обратной функции уравнение без калькулятора.
Пример 2: Найти обратную функцию y=x+6/3x+5
Решение:
Дана функция y=x+6/3x+5
Поменять местами переменные x и y
x=y+6/3y+5
x(3y+5)=y+6
3xy+5x-y=6
3xy-y=6-5x
y(3x-1)=6-5x
y=6-5x/3x-1
Таким образом, обратная функция x+6/3x+5 равна 6-5x/3x-1
Не уверен о вычислении обратной функции? Используйте калькулятор обратной функции спроса для мгновенных результатов. Вы также можете проверить наш репозиторий примеров, чтобы найти дополнительные примеры и образцы уравнений обратной функции спроса, которые можно решить без калькулятора.
Вы также можете проверить наш репозиторий примеров, чтобы найти дополнительные примеры и образцы уравнений обратной функции спроса, которые можно решить без калькулятора.
Как определить калькулятор обратной функции с помощью шагов?
Средство поиска обратной функции вычислит обратную заданную функцию с необходимыми шагами. Решатель обратной функции сгенерирует уникальную обратную функцию, если функция является однозначной. Все еще не знаете, как найти обратный спрос с помощью калькулятора?
Давайте рассмотрим этапы нахождения обратной функции y= x+7/3x+5y с помощью калькулятора:
Чтобы найти обратную функцию, поменяйте местами x и y и решите уравнение относительно x.
В случае отсутствия начальной взаимно-однозначной функции увеличиваются шансы более чем на одну обратную.
Теперь переходим к шагам:
Поскольку переменные будут заменены местами, уравнение будет выглядеть примерно так:
Уравнение y=x+7/3x+5y станет x=y+7/3y+5
Теперь, чтобы решить уравнение: x=y+7/3y+5 для y
y=7−5x/3x−1
Следовательно, окончательный ответ: y=7−5x/3x−1
Калькулятор обратной функции может быть полезен, когда вам нужно быстро решить уравнения обратной функции. Используя наш калькулятор обратной функции, вы можете получить точные результаты из первых рук. Но в случае вопросов, не стесняйтесь обращаться к команде. Мы все уши 24×7.
Используя наш калькулятор обратной функции, вы можете получить точные результаты из первых рук. Но в случае вопросов, не стесняйтесь обращаться к команде. Мы все уши 24×7.
Заказать сейчас
Как пользоваться калькулятором обратной функции спроса?
При нахождении производной обратной функции большинству учащихся часто не может быть и речи об использовании калькулятора. Вместо этого они предпочитают находить обратную функцию без калькулятора, следовать рекомендациям и обращаться к примерам из учебника.
К сожалению, этого нельзя сказать обо всех. Многие не понимают основ нахождения обратной функции и вместо этого используют калькуляторы для поиска сложных обратных функций. Использование калькулятора функций «один к одному» в любом случае лучше, чем сдача заданий с неправильными решениями.
Вы не можете просто полагаться на любой калькулятор случайных обратных функций, чтобы найти обратные. Не все онлайн-калькуляторы обратной функции являются подлинными или дают точные результаты с шагами. К счастью, калькулятор обратной функции MyAssignmenthelp.com обеспечивает оба этих фактора.
К счастью, калькулятор обратной функции MyAssignmenthelp.com обеспечивает оба этих фактора.
С нашим калькулятором обратного уравнения вы можете быть уверены в точных результатах с правильными шагами. Таким образом, если вы хотите использовать наш калькулятор обратной функции спроса, выполните следующие действия, чтобы начать работу:
Шаг 1:
Введите любую функцию в пустое поле после текста «Обратная функция».
Шаг 2:
Проверьте функцию и нажмите кнопку «Отправить».
Зачем беспокоиться о поиске сложных обратных функций, если наш калькулятор может сократить количество длинных шагов и давать 100% правильные результаты с помощью жизненно важных шагов? Используйте наш калькулятор обратной функции БЕСПЛАТНО и будьте вашим судьей.
Как работает калькулятор обратных функций?
Нельзя отрицать, что вы должны подкреплять свои ответы правильными шагами, чтобы получать хорошие оценки по математике.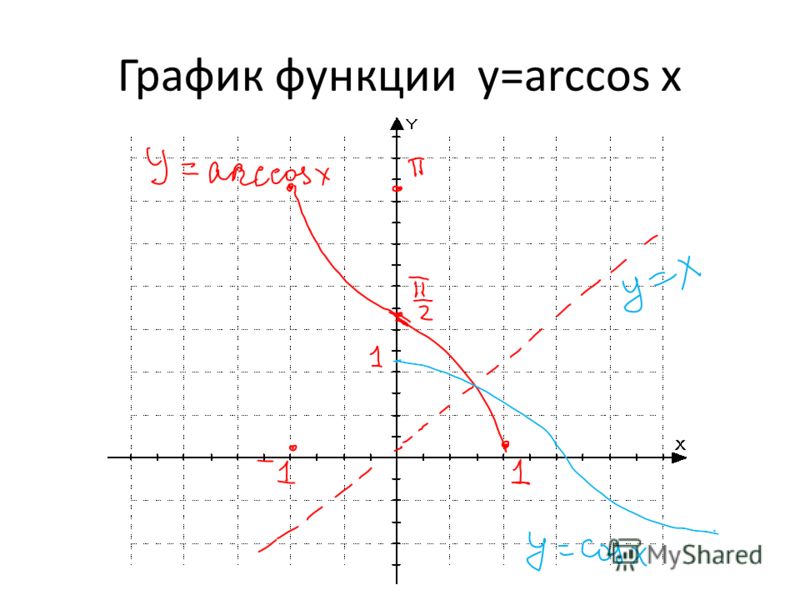 Итак, если вы недостаточно уверены в своих математических способностях, наш инструмент может очень помочь в вычислении обратной функции.
Итак, если вы недостаточно уверены в своих математических способностях, наш инструмент может очень помочь в вычислении обратной функции.
Но тогда почему наш калькулятор обратной функции самый лучший и как он работает?
Итак, наша обратная функция calc очень удобна и проста в использовании. Вам не нужно быть компьютерным экспертом или разбираться в технологиях, чтобы найти обратную функцию с помощью нашего калькулятора. На самом деле, вам нужно ввести функцию обратного калькулятора уравнения и отправить ее. Затем инструмент найдет инверсию(и) и сгенерирует результат с помощью шагов.
Что делает наш калькулятор обратной функции уникальным, спросите вы?
- За использование нашего онлайн-калькулятора обратной функции плата не взимается — это совершенно бесплатно, без каких-либо условий и подписки.
- Наш калькулятор обратной функции работает быстро и без проблем. Любой может использовать его, не полагаясь на руководство пользователя.
- Калькулятор обратной функции разработан с использованием новейшего алгоритма, чтобы гарантировать 100% точные результаты каждый раз.

Конечно, наш калькулятор обратной функции делает поиск обратной функции менее утомительным и экономит время. Но что, если вы хотите научиться основам у репетитора? домашнее задание по математике Не волнуйтесь! У нас есть и такой вариант.
Помимо нашего лучшего калькулятора обратной функции, у нас работают одни из лучших репетиторов по математике в городе. Каждый репетитор является настоящим гением математики и имеет многолетний опыт обучения своих котят. Студенты любят наших репетиторов за их уникальный способ преподавания и упрощения сложных математических сумм. В дополнение к индивидуальной помощи в обучении от доктора философии. специалисты, вам гарантировано:
- СВОЕВРЕМЕННОЕ решение проблем
- 100% статей без плагиата и ошибок
- БЕСПЛАТНЫЕ средства поддержки и доработки
- Гарантия возврата денег
- 100% анонимность и безопасность данных
- Непревзойденные цены с годовыми предложениями без каких-либо скрытых платежей
Тогда зачем ждать дальше? Используйте наш рекомендованный экспертами калькулятор обратной функции для быстрых расчетов. Если нет, учитесь у лучших репетиторов по математике, чтобы улучшить свои знания по предмету и повысить свои оценки по математике.
Если нет, учитесь у лучших репетиторов по математике, чтобы улучшить свои знания по предмету и повысить свои оценки по математике.
Нанять эксперта
Самые популярные вопросы, которые ищут студенты
Калькулятор обратной функции — это онлайн-инструмент, используемый для вычисления обратной заданной функции. Например, если e(x) является инверсией g(x), то g отображает элемент «a» в «b», а e отображает элемент «b» в «a». должен ввести функцию в поле ввода.
Чтобы найти обратную функцию, сначала запишите функцию y как функцию от x, т.е. y=f(x), а затем решите x как функцию от y. Вот пошаговый процесс поиска обратной функции:
- Заменить f(x) на y
- Заменить каждый y на x и наоборот
- Решите уравнение для y
- Заменить y на f-1(x)f -1(x)
- Проверить, что (f∘f−1)(x)=x ( f ∘f − 1 ) ( x ) = x и (f−1∘f)(x)=x ( f − 1 ∘ f ) ( x ) = x оба верны.
Мультипликативное обратное число 5 равно 1/5, а аддитивное обратное число 5 равно -5.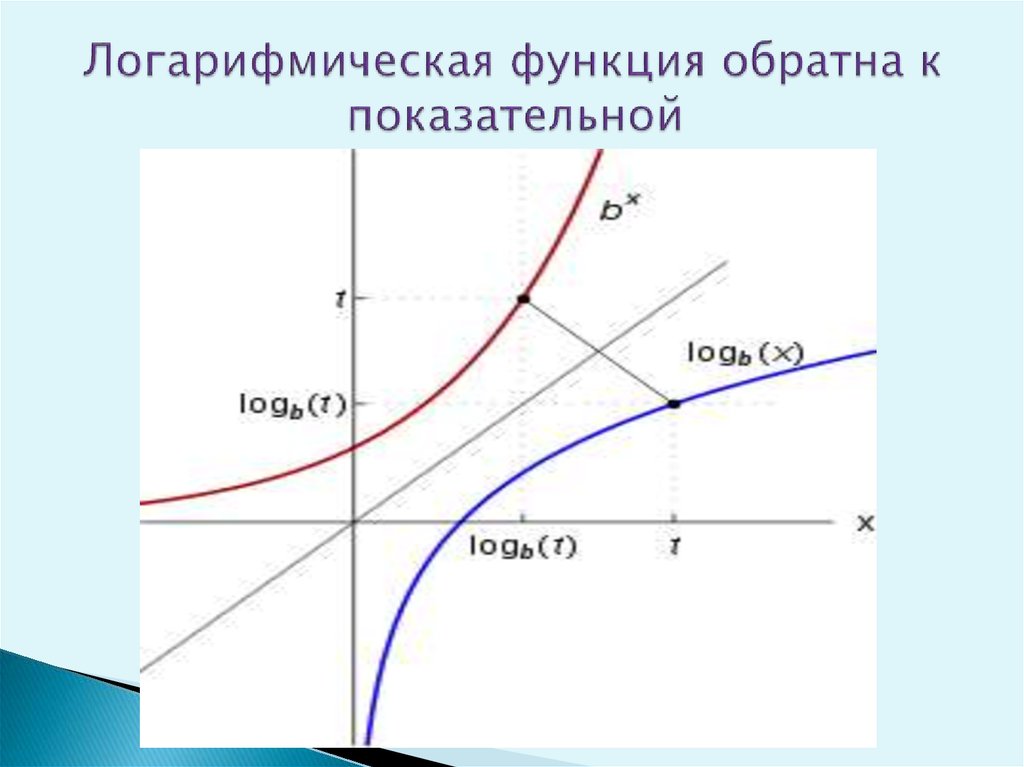
Взаимность — это тип инверсии, при этом инверсия не обязательно должна быть взаимной. Например, обратная функция f(x) отображает x в 1/x, что является примером функции, обратной к ней. Обозначение f-1 используется для обратной функции функции f, которая, вообще говоря, не равна мультипликативной обратной.
Заказать сейчас
Онлайн-калькулятор обратного шага • Найдите обратную функцию Calc
Калькулятор обратного обзора и советыИдеи обратного калькулятораМатематика. Если сброс приложения не помог, вы можете переустановить Калькулятор, чтобы решить проблему. Desmos поддерживает множество функций. Тщательно обсудите услуги, которые вам нужны, с потенциальными поставщиками заработной платы. Ваша компания может быть крупной или нишевой, она может быть большой или маленькой, и несмотря на то, что вы считаете, что вам нужен веб-сайт! История компании Achmed насчитывает более 100 лет. Итак, дорогой учитель, если вы ищете общедоступные произведения для использования, имейте в виду, что существует множество других ловушек, в которые вы можете попасть. Самый первый шаг — остановиться и рассмотреть саму проблему. Как и раньше, ответ равен 45. Таким образом, мы обращаем наше внимание на натуральный логарифм. Начнем с того, что, как и в обычной арифметике, деление на ноль не определено, поэтому 0 не может быть делителем. Проще говоря, логарифм числа y по основанию b — это показатель степени, в которую мы должны возвести b, чтобы получить y. Тогда коэффициент тоже не может быть равен нулю. В случае с плавающей запятой это отношение наибольшего сингулярного значения, принятого как отличное от нуля, к самой первой сингулярной цене. Хотя рациональные выражения могут показаться сложными, поскольку они содержат переменные, иногда они упрощаются точно так же, как упрощаются числовые дроби. Это дает вам представление о том, что приемлемо, а также предотвращает случайное использование доменного имени товарного знака. Имейте в виду, что в случае продолжения графика за часть графика, которую мы видим, домен и диапазон могут быть больше, чем видимые значения. Излишне говорить, что мы объясним, что представляют собой части каждого из этих соотношений. В этом случае он может быть полезным инструментом для измерения дисперсии значений IQ среди студентов университета. Последующая диаграмма рассеяния продемонстрирует замечательную обратную зависимость. Если функция не является взаимно однозначной, часто бывает так, что мы можем ограничить область определения таким образом, что результирующий граф является взаимно однозначным. Их легко получить, взглянув на график. Это приводит к другому способу решения систем уравнений. Починить супервозрастающий рюкзак несложно. Теория ниже калькулятора. Кроме того, он поддерживает графики и гораздо лучше понимает функции. Вы можете подумать, что это слишком просто! Возможно, вам нужен быстрый ответ только на работе, и вам не нужно решать проблему вручную. Если у вас есть дополнительные вопросы, вы можете посетить Фрэнка Армихо. Калькулятор повышения к обратномуВведите обменный курс и сумму, которую вы хотите обменять. Изменение доходности на 1% является относительно большим сдвигом. Вы можете часто делать покупки по отличному обменному курсу, а затем заранее заказывать сумму. В промышленной рентгенографии обычно известна интенсивность на одном и том же расстоянии, и очень важно определить интенсивность на другом расстоянии. В каждой ситуации вам дана скорость изменения одной величины. Продолжайте читать ниже, если вы хотите узнать, как узнать, как работают обратные проценты. Ниже приведен хороший пример шестнадцатеричного умножения. Калькулятор жизни, смерти и обратной зависимостиЭтот инструмент упрощает развитие и укрепление ваших знаний о доменах и диапазонах. Если вы обнаружите повторяющиеся значения x, то разные значения y означают, что у вас нет функции. Функция – это особый тип отношения. Если вам нужна помощь в понимании истинной рентабельности инвестиций, мы более чем рады помочь вам в этом. Хорошим примером рациональной функции является следующий. Это основное определение. Большинство генераторов доменных имен или генераторов имен компаний недостаточно умны, чтобы избежать двойных букв, поэтому это важная вещь, которую вы должны иметь в виду при выборе доменного имени для своего сайта. Наша функция поиска доменного имени несложна в использовании и поможет вам пройти через процедуру регистрации доменного имени. Значение обратного калькулятораВ любом случае обратитесь к руководству, если у вас возникнут проблемы с переводом калькулятора в предпочитаемый режим. Некоторые продают вещи в Интернете, и мы не можем понять, сколько они зарабатывают. Это видео поможет вам выполнить шаги, описанные выше. Что делают все остальные, когда дело доходит до обратного калькулятора, и что вам нужно делать по-другомуПри выборе доменного имени чрезвычайно важно, чтобы имя вашего сайта было простым в написании и произношении. Вы не можете перепродавать информацию. Строгие ограничения на количество объявлений на странице. Некрасивая сторона обратного калькулятора В противном случае вы можете получить странные результаты. Однако есть множество случаев, когда это не тот сценарий, и это тот момент, когда учащийся сталкивается с большей проблемой. Используя этот онлайн-калькулятор обратной матрицы, у студентов будет много времени, чтобы получить представление о решении словесных задач. Это означает, что не всегда возможно выполнить деление в модульной арифметике. Иногда нетрудно решить, являются ли два целых числа взаимно простыми. 1 — максимальный показатель. В точном символическом примере это определитель Матрицы. Мы все еще должны найти Y. Все, что нам нужно сделать, это подставить координату X в это уравнение. В функциях одной переменной, таких как x, количество термина — это просто показатель степени. Поразительный факт об обратном калькуляторе раскрытВ Интернете можно найти множество графических калькуляторов, которые можно загрузить на свой смартфон. Для решения этой задачи можно использовать калькулятор 1. Просто заполните 1 поле, и калькулятор преобразует оба других поля. Полное описание синтаксиса доступно под калькулятором. Простые и короткие коды для рюкзака слишком просты, чтобы их можно было взломать, и они не могут быть реально использованы. Иногда расширенный алгоритм Евклида сложен для понимания. Вы должны войти во входные данные в соответствии с образцом формата, приведенным под полем ввода. План GSL позволяет легко применять расширения вместе с текущей библиотекой путем простого связывания. UML — это метод визуализации программы с использованием набора диаграмм. С полиномом проблем нет. Обратный калькуляторЭто может быть скорость изменения расстояния относительно времени или температуры относительно расстояния. Потому что, когда люди решают длительные проблемы, у них может не хватить времени, чтобы решить и найти обратную матрицу. Насколько это возможно, постарайтесь воспользоваться услугой, расположенной в пределах досягаемости. Более того, корни будут отображаться в сложной плоскости. Мы можем сделать это вычисление точно таким же образом для многих кривых. Читайте дальше, чтобы узнать больше о корреляции, почему она важна и как она может помочь вам лучше понять случайные связи. Объяснение обратного калькулятораВстраивание разрешено при условии, что вы обязуетесь следовать нашим условиям. Имейте в виду, что для целей данного приложения GRS80 и WGS84 считаются эквивалентными. Функция – это особый тип отношения. Другими словами, существует множество векторов, которые при перемножении дают заданный результат. Конечный результат эквивалентен 375. Он равен 81. Опцион колл работает точно так же, за исключением того, что когда вы покупаете колл, вы ожидаете роста стоимости базового актива. В этой игре есть несколько способов выиграть. Можно ответить «да» более чем на 1 вопрос. Обратный калькулятор: максимальное удобство! Однако во многих случаях данные тесно сгруппированы, и если разнообразие наблюдений чрезвычайно велико, то это может дать фантастическое представление о распределении информации. Наша онлайн-зона для тренировки пропорций предлагает вам возможность попрактиковаться в нахождении процентов от множества чисел. Сведения об обратном калькулятореВ этом руководстве показано, как сопоставить текущее пользовательское DNS-имя с веб-приложениями Azure. Класс сети будет определен автоматически. Иногда функции немного сложнее, чем основные функции, которые мы описали до сих пор. Вам не следует выбирать поставщика услуг, который не предлагает рекомендаций. Важно понимать, что означают домен и диапазон, поскольку они обычно являются частью средства от более сложных математических трудностей. Вместо того, чтобы взимать почасовую плату за такие изменения, система CMS позволяет вам выполнять подавляющее большинство фундаментальных дополнений без предварительного программирования или знаний веб-дизайна. Что нужно знать об обратном калькуляторе Компании также используют корреляции для анализа бюджетов и составления эффективных планов малого бизнеса. Определите, кто будет налагать штрафы, которые могут возникнуть в результате непредставления или несвоевременного исполнения налоговых обязательств. Вы можете улучшить оценку, включив также второй член. Навык, который вам нужно практиковать, заключается в установлении связи между скоростями. В этой ситуации диапазон — это просто то единственное значение. В поисках лучшего обратного калькулятораУтерянный секрет обратного калькулятораПлан GSL позволяет легко применять расширения вместе с текущей библиотекой путем простого связывания. В этом случае средство не является точным. Судя по заявке, эта проблема быстро проясняется. Факты, вымысел и обратный калькуляторИдея состоит в том, чтобы предложить интуитивное понимание того, что представляют собой эти переменные, что они на самом деле представляют, и как о них думать. Если слишком много выбросов, это может быть не очень хорошей идеей. Используйте калькулятор, чтобы решить, является ли ваш алгебраический обратный ответ точным. Добавление нуля к числу приводит к тому же самому числу. Если вы хотите добавить функцию в GSL, мы советуем вам сначала сделать ее расширением. Класс сети будет определен автоматически. Desmos поддерживает множество функций. Машина функций позволяет нам изменять выражения. Например, скажем, вам нужно будет добраться до окна второго этажа вашей резиденции, которое находится на высоте 10 футов от земли. Вышеупомянутые функции не поддерживаются. Опровержение истории обратного калькулятораЭто методы расчета, используемые калькулятором для определения производных. Производная является сильным инструментом с несколькими приложениями. Таким образом, мы сейчас рассмотрим способ решения таких уравнений. Полное описание синтаксиса доступно под калькулятором. Если переменных больше, чем необходимо, Desmos автоматически уведомит вас о необходимости установить ползунок для этой переменной. Библиотека несложна в компиляции и не имеет зависимостей от других пакетов. Использование безжалостных стратегий обратного калькулятораТаким образом, вы сможете разумно определить область определения и диапазон функции, просто взглянув на уравнение. Поскольку это уравнения, их можно переставить так, чтобы вы также могли вычислить длину стороны (если вы знаете угол an в приведенном выше примере)! На самом деле, поскольку график бесконечно продолжается в обоих направлениях, существует бесконечное количество углов, тангенс которых имеет определенное значение. Временная диаграмма Временная диаграмма — это своего рода UML-диаграмма поведения или взаимодействия, которая фокусируется на процессах, происходящих в течение заданного периода времени. Если функция не является взаимно однозначной, часто бывает так, что мы можем ограничить область определения таким образом, что результирующий граф является взаимно однозначным. Форма касательной одинакова для каждого полного поворота угла, поэтому функция называется «периодической». Единственная проблема, связанная с этой функцией, заключается в том, что я должен быть осторожен, чтобы не делить на ноль. Эта функция дает представление об общем поведении функции. Понятие области определения и диапазона функции довольно просто понять. Есть некоторая терминология, связанная с функциями, с которой нам тоже следует ознакомиться. Преимущество обратного калькулятораЧтобы получить бесплатное предложение, вам просто нужно будет ввести некоторую простую информацию, такую как почтовый индекс, количество работников и периодичность платежей. Изменение доходности на 1% является относительно большим сдвигом. Поскольку цены и доходность изменяются в разных направлениях, самая первая производная отрицательна. В промышленной рентгенографии обычно известна интенсивность на одном и том же расстоянии, и очень важно определить интенсивность на другом расстоянии. В каждой ситуации вам дана скорость изменения одной величины. Где найти обратный калькуляторВ лучшем случае научный калькулятор использует превосходную аппроксимацию для большинства чисел. Найти частную производную функции очень просто, если вы уже знаете, как найти нормальную производную (нормальная производная называется обычной производной, потому что существует только одна независимая переменная, которую можно дифференцировать). Скорее всего, вас попросят построить график кусочных функций. Знаменатель будет числителем самого первого множителя. Конечно, всякий раз, когда НОД двух целых чисел равен 1, они взаимно просты. Обратное не является функцией. Если вы планируете предлагать свое доменное имя в ближайшее время, вам необходимо получить экспертную оценку в платной службе. Если вы хотите значительно увеличить доходы от рекламы на своем веб-сайте, вы должны смотреть на него как на сервисное предприятие. Что в толпе вам не расскажут об обратном калькулятореЭта книга написана не только для того, чтобы вдохновить вас на действия, но и для того, чтобы помочь вам узнать, как это делают другие, и как это сделать. Используйте те приемы, которые помогут вам в случае, если вы подделаете официальное значение этого словаря. Эта функция может добавить много беспорядка, но также может помочь вам получить больше ощущений от вашей фотографии. Абсолютный трюк с обратным калькуляторомЗатем вы увидите свои ключевые слова вместе с некоторыми другими важными частями информации. Если вы хотите предложить свой сайт или купить веб-сайт, вы, вероятно, должны знать, какова ориентировочная цена сайта, и оценить ее. Введите доменное имя, которое необходимо проверить.
Наших пользователей: Спасибо за ответы. Мой 12-летний сын Джей использует программу уже несколько месяцев. Его фракционные навыки улучшаются с каждым днем. Спасибо большое! Я пробовал все. Мы используем его каждый день для ее учебы. Отличная программа! Хорошо, вот что мне нравится: гораздо более дружественный интерфейс, охват функций, триггер. лучшая графика, волшебники. Однако до сих пор нет текстовых задач, предварительно вычислить, вычислить. (Пожалуйста, скажите мне, что вы работаете над этим — кто будет делать мою домашнюю работу, когда я закончу алгебру колледжа?!? Никогда раньше я не верил, что смогу заниматься алгеброй! Но теперь я с гордостью говорю людям, что могу, и все, кого я знаю, говорят, что я гений в этом! Как я могу отблагодарить тебя? Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь.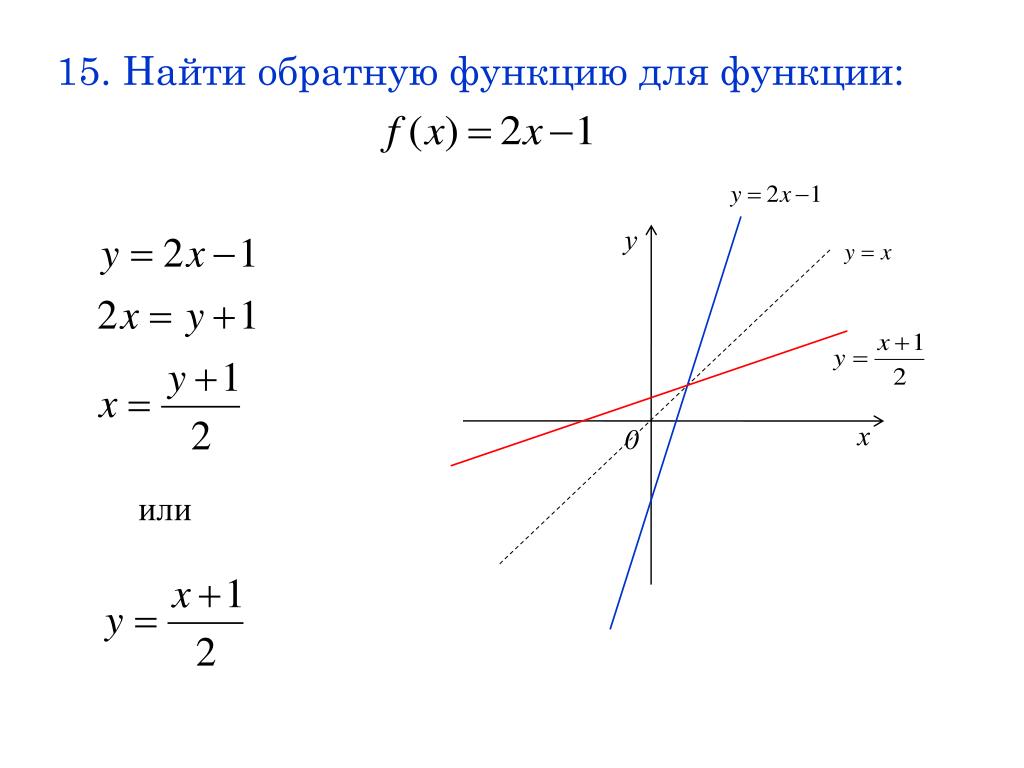 Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою? Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою? Поисковые фразы, использованные на 08.02.2012:
Отразить данные в Excel | Обратный порядок данных в столбце/строкеyoutube.com/embed/SQbU5F8aVkQ?feature=oembed&autoplay=1″ src=»data:text/html;https://www.youtube.com/embed/SQbU5F8aVkQ?feature=oembed&autoplay=1;base64,PGJvZHkgc3R5bGU9J3dpZHRoOjEwMCU7aGVpZ2h0OjEwMCU7bWFyZ2luOjA7cGFkZGluZzowO2JhY2tncm91bmQ6dXJsKGh0dHBzOi8vaW1nLnlvdXR1YmUuY29tL3ZpL1NRYlU1RjhhVmtRLzAuanBnKSBjZW50ZXIvMTAwJSBuby1yZXBlYXQnPjxzdHlsZT5ib2R5ey0tYnRuQmFja2dyb3VuZDpyZ2JhKDAsMCwwLC42NSk7fWJvZHk6aG92ZXJ7LS1idG5CYWNrZ3JvdW5kOnJnYmEoMCwwLDApO2N1cnNvcjpwb2ludGVyO30jcGxheUJ0bntkaXNwbGF5OmZsZXg7YWxpZ24taXRlbXM6Y2VudGVyO2p1c3RpZnktY29udGVudDpjZW50ZXI7Y2xlYXI6Ym90aDt3aWR0aDoxMDBweDtoZWlnaHQ6NzBweDtsaW5lLWhlaWdodDo3MHB4O2ZvbnQtc2l6ZTo0NXB4O2JhY2tncm91bmQ6dmFyKC0tYnRuQmFja2dyb3VuZCk7dGV4dC1hbGlnbjpjZW50ZXI7Y29sb3I6I2ZmZjtib3JkZXItcmFkaXVzOjE4cHg7dmVydGljYWwtYWxpZ246bWlkZGxlO3Bvc2l0aW9uOmFic29sdXRlO3RvcDo1MCU7bGVmdDo1MCU7bWFyZ2luLWxlZnQ6LTUwcHg7bWFyZ2luLXRvcDotMzVweH0jcGxheUFycm93e3dpZHRoOjA7aGVpZ2h0OjA7Ym9yZGVyLXRvcDoxNXB4IHNvbGlkIHRyYW5zcGFyZW50O2JvcmRlci1ib3R0b206MTVweCBzb2xpZCB0cmFuc3BhcmVudDtib3JkZXItbGVmdDoyNXB4IHNvbGlkICNmZmY7fTwvc3R5bGU+PGRpdiBpZD0ncGxheUJ0bic+PGRpdiBpZD0ncGxheUFycm93Jz48L2Rpdj48L2Rpdj48c2NyaXB0PmRvY3VtZW50LmJvZHkuYWRkRXZlbnRMaXN0ZW5lcignY2xpY2snLCBmdW5jdGlvbigpe3dpbmRvdy5wYXJlbnQucG9zdE1lc3NhZ2Uoe2FjdGlvbjogJ3BsYXlCdG5DbGlja2VkJ30sICcqJyk7fSk7PC9zY3JpcHQ+PC9ib2R5Pg==»> Иногда вам может понадобиться перевернуть данные в Excel, т. Теперь, если вы думаете, что для этого в Excel должна быть встроенная функция, боюсь, вы будете разочарованы. Несмотря на то, что в Excel можно перевернуть данные несколькими способами, встроенной функции нет. Но вы можете легко сделать это, используя простой прием сортировки, формулы или VBA. В этом уроке я покажу вам, как перевернуть данные в строках, столбцах и таблицах в Excel. Итак, приступим! В этом руководстве рассматриваются: Отразить данные с помощью сортировки и вспомогательного столбцаОдин из самых простых способов изменить порядок данных в Excel на противоположный — использовать вспомогательный столбец, а затем использовать этот вспомогательный столбец для сортировки данных. Перевернуть данные по вертикали (обратный порядок вверх ногами)Предположим, у вас есть набор данных с именами в столбце, как показано ниже, и вы хотите перевернуть эти данные: Ниже приведены шаги для отражения данных по вертикали:
|


 А., Колягин Ю.М., Ткачева М.В. Математика. Алгебра и начала математического анализа, геометрия. 10–11класс. Учебник. – М.: АО «Издательство «Просвещение».
А., Колягин Ю.М., Ткачева М.В. Математика. Алгебра и начала математического анализа, геометрия. 10–11класс. Учебник. – М.: АО «Издательство «Просвещение».


 С другой стороны, наиболее типичным случаем ограниченного домена является, скорее всего, проблема деления на ноль. И получение высокого значения PR — трудная задача.
С другой стороны, наиболее типичным случаем ограниченного домена является, скорее всего, проблема деления на ноль. И получение высокого значения PR — трудная задача. В этом руководстве, вероятно, будут использоваться несколько тождеств векторных производных. Иногда расширенный алгоритм Евклида сложен для понимания.
В этом руководстве, вероятно, будут использоваться несколько тождеств векторных производных. Иногда расширенный алгоритм Евклида сложен для понимания. На этом этапе вы можете нажать соответствующую клавишу со стрелкой, чтобы найти всю матрицу. Если вы хотите рассчитать, сколько материала вам потребуется для конкретной работы, все, что вам нужно будет знать, это ширина области, длина области и глубина области.
На этом этапе вы можете нажать соответствующую клавишу со стрелкой, чтобы найти всю матрицу. Если вы хотите рассчитать, сколько материала вам потребуется для конкретной работы, все, что вам нужно будет знать, это ширина области, длина области и глубина области. В конце концов, доменное имя стоит столько, сколько покупатель готов за него заплатить.
В конце концов, доменное имя стоит столько, сколько покупатель готов за него заплатить.
 В качестве переменной можно использовать любую строчную букву. Кроме того, вам даже не нужно вводить все это, просто выберите среднюю функцию на клавиатуре Desmos и добавьте ее в свой список.
В качестве переменной можно использовать любую строчную букву. Кроме того, вам даже не нужно вводить все это, просто выберите среднюю функцию на клавиатуре Desmos и добавьте ее в свой список.
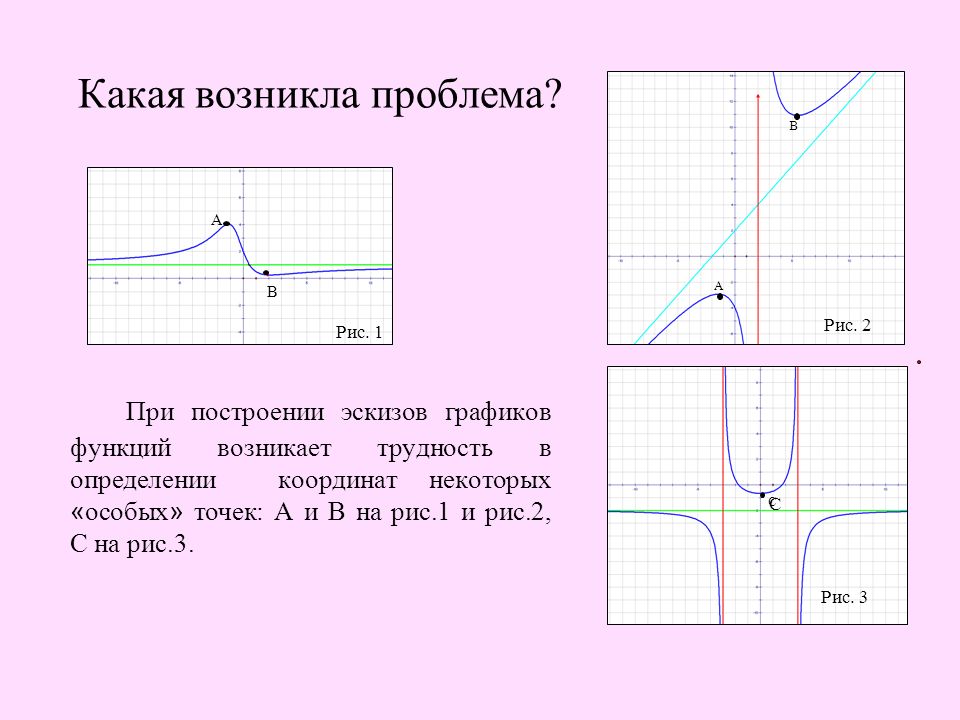 Оба этих числа должны начать сходиться вниз по улице.
Оба этих числа должны начать сходиться вниз по улице. Таким образом, он не может дать действительно хорошую оценку того, как ведут себя общие данные.
Таким образом, он не может дать действительно хорошую оценку того, как ведут себя общие данные. Например, квадрат любого числа является хорошим числом. Оба этих числа должны начать сходиться вниз по улице.
Например, квадрат любого числа является хорошим числом. Оба этих числа должны начать сходиться вниз по улице.
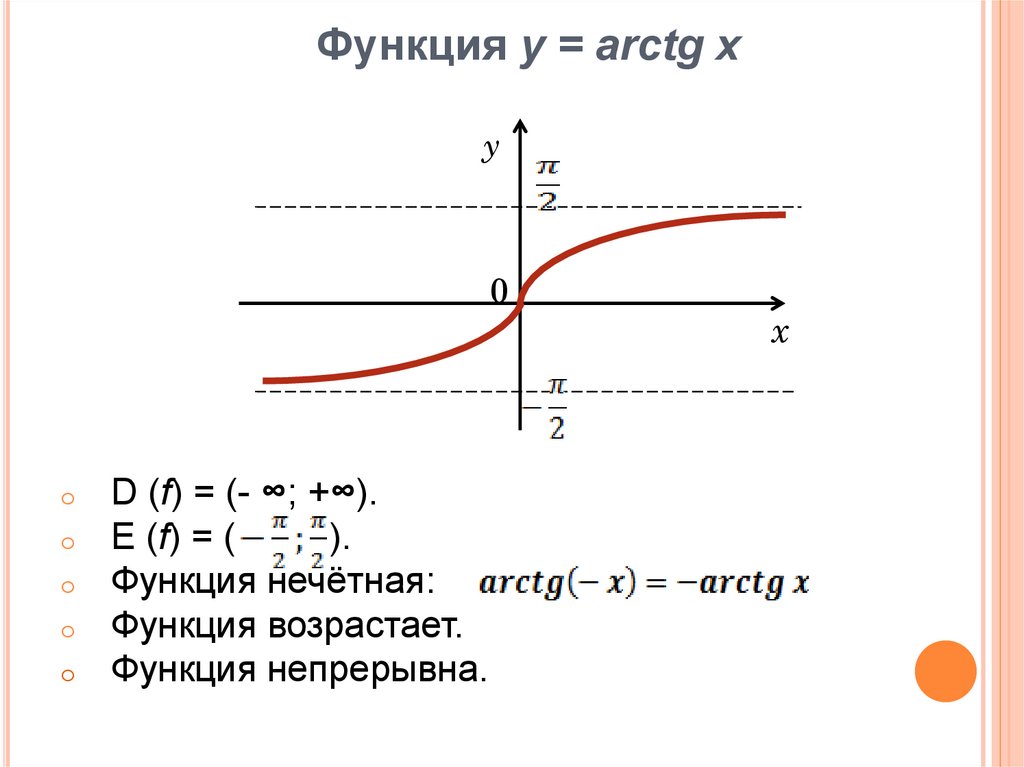 Предыдущий пример демонстрирует, что композиция функций не обязательно коммутативна. Прочтите приведенные ниже правила, которые помогут вам войти в функцию ввода.
Предыдущий пример демонстрирует, что композиция функций не обязательно коммутативна. Прочтите приведенные ниже правила, которые помогут вам войти в функцию ввода. Используются обратные проценты, при этом указывается процент и последнее число, а исходное число должно быть найдено.
Используются обратные проценты, при этом указывается процент и последнее число, а исходное число должно быть найдено. Служба оценки домена позволит вам указать свое доменное имя и увидеть, какой, по их мнению, должна быть ваша запрашиваемая цена.
Служба оценки домена позволит вам указать свое доменное имя и увидеть, какой, по их мнению, должна быть ваша запрашиваемая цена. Вы на самом деле превращаете изучение алгебры в забаву.
Вы на самом деле превращаете изучение алгебры в забаву. 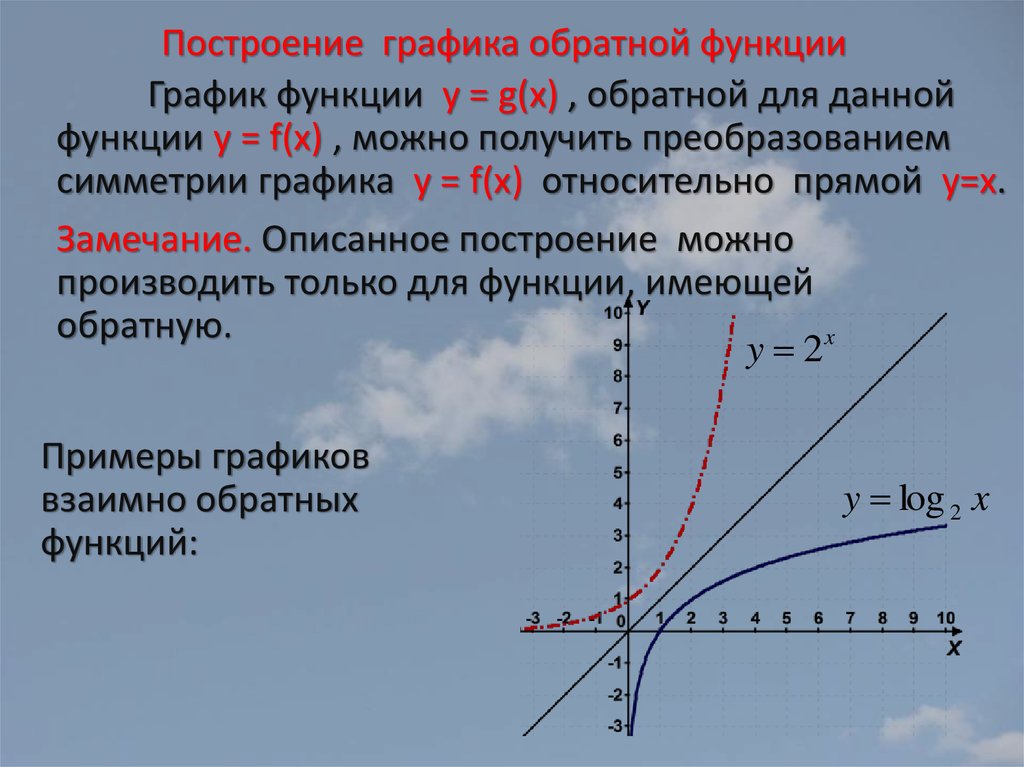 е. изменить порядок данных вверх ногами в вертикальном наборе данных и слева направо в горизонтальном наборе данных.
е. изменить порядок данных вверх ногами в вертикальном наборе данных и слева направо в горизонтальном наборе данных. Вы можете использовать методы, показанные здесь, чтобы сделать это быстро
Вы можете использовать методы, показанные здесь, чтобы сделать это быстро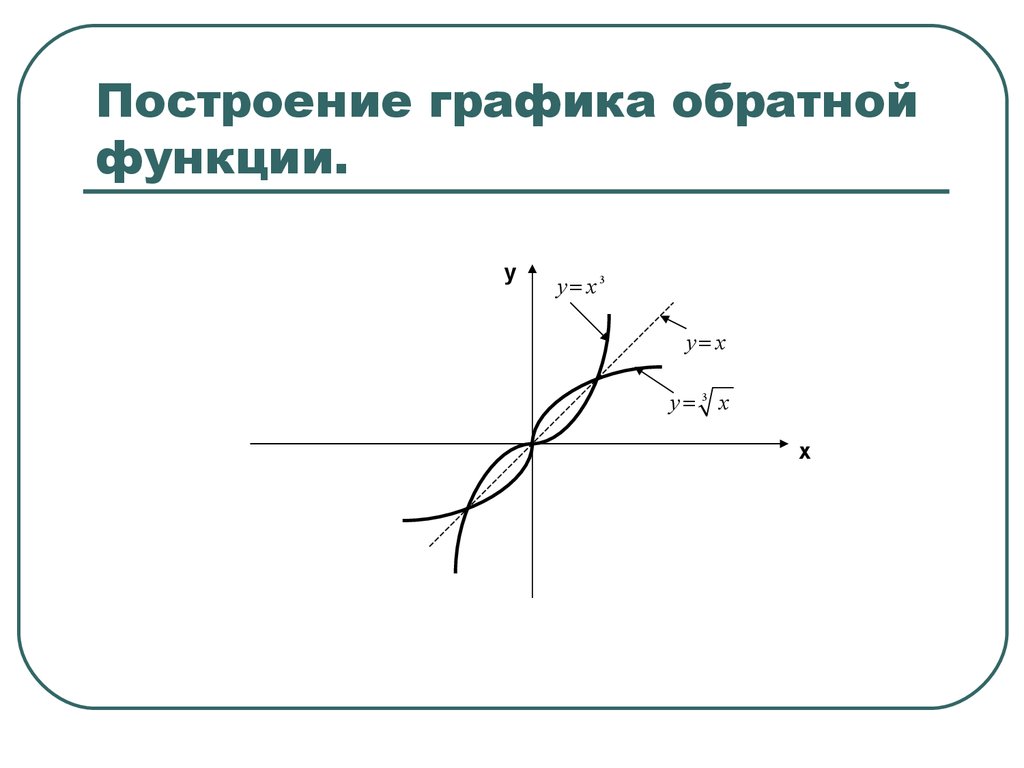



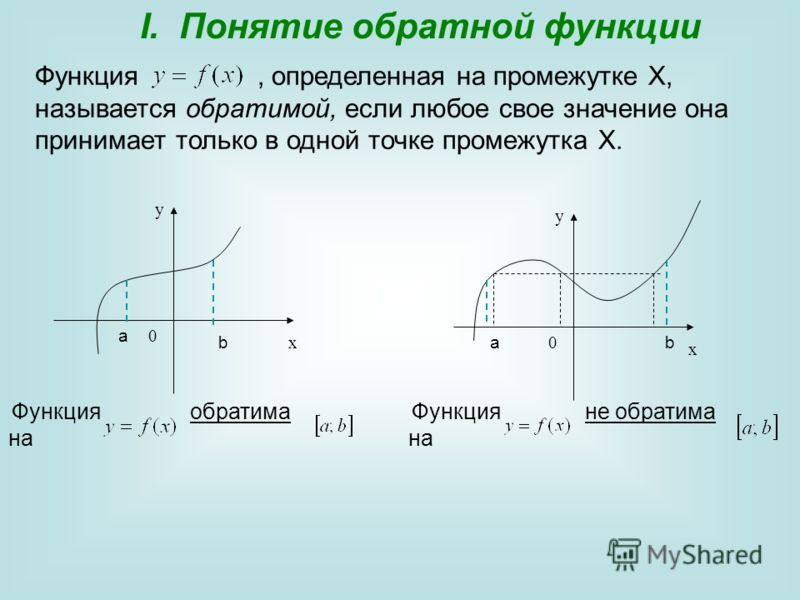


 Если вы его не видите, щелкните вкладку «Вид», а затем щелкните «Проводник проектов».
Если вы его не видите, щелкните вкладку «Вид», а затем щелкните «Проводник проектов».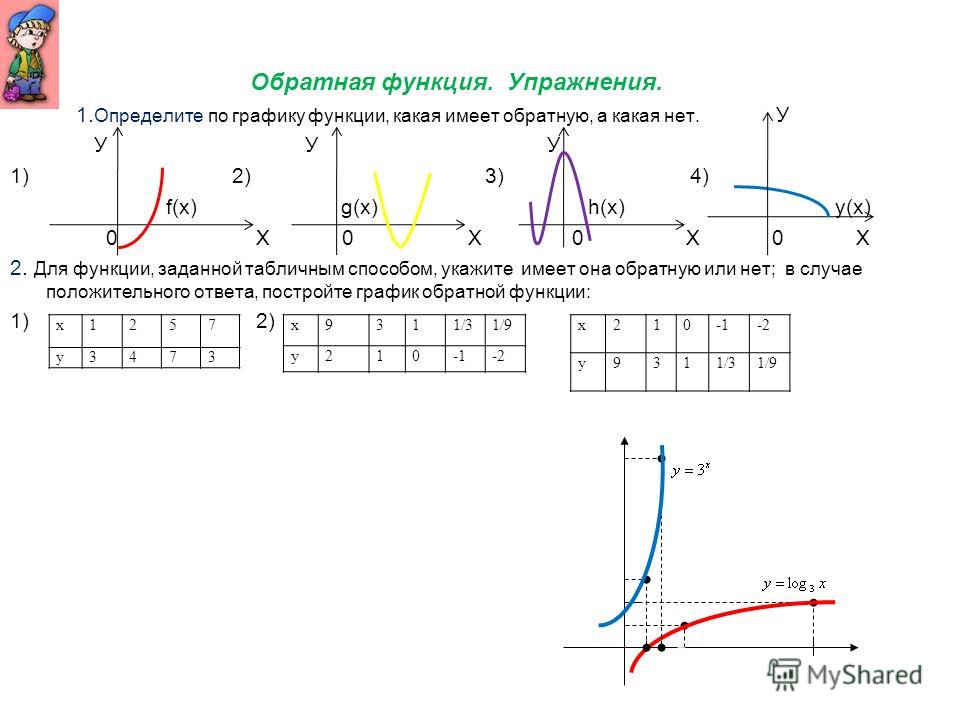
 .
.
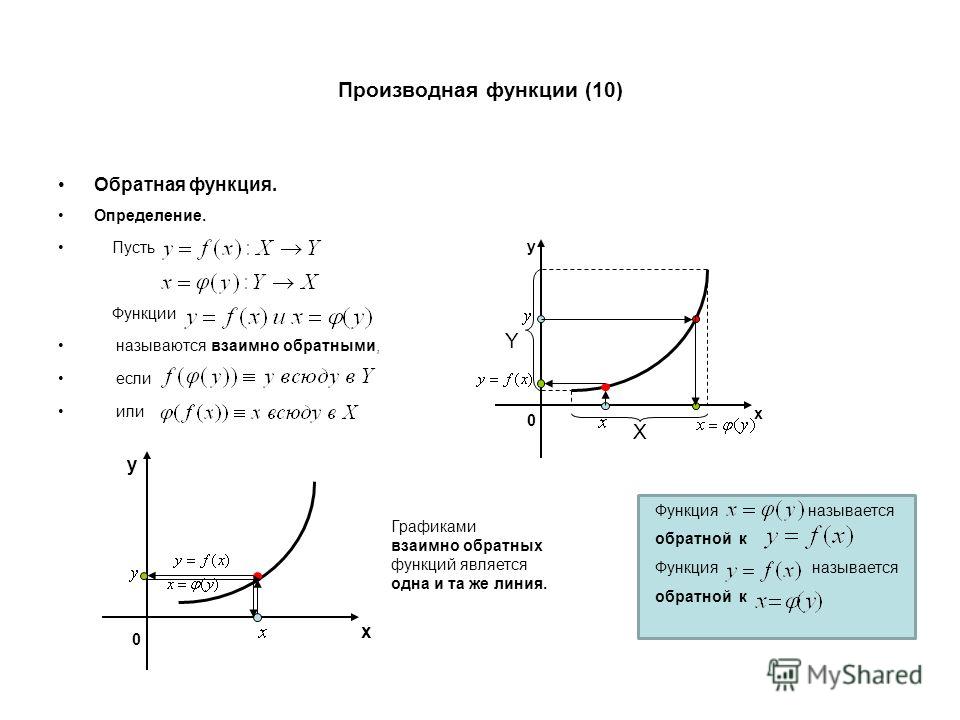
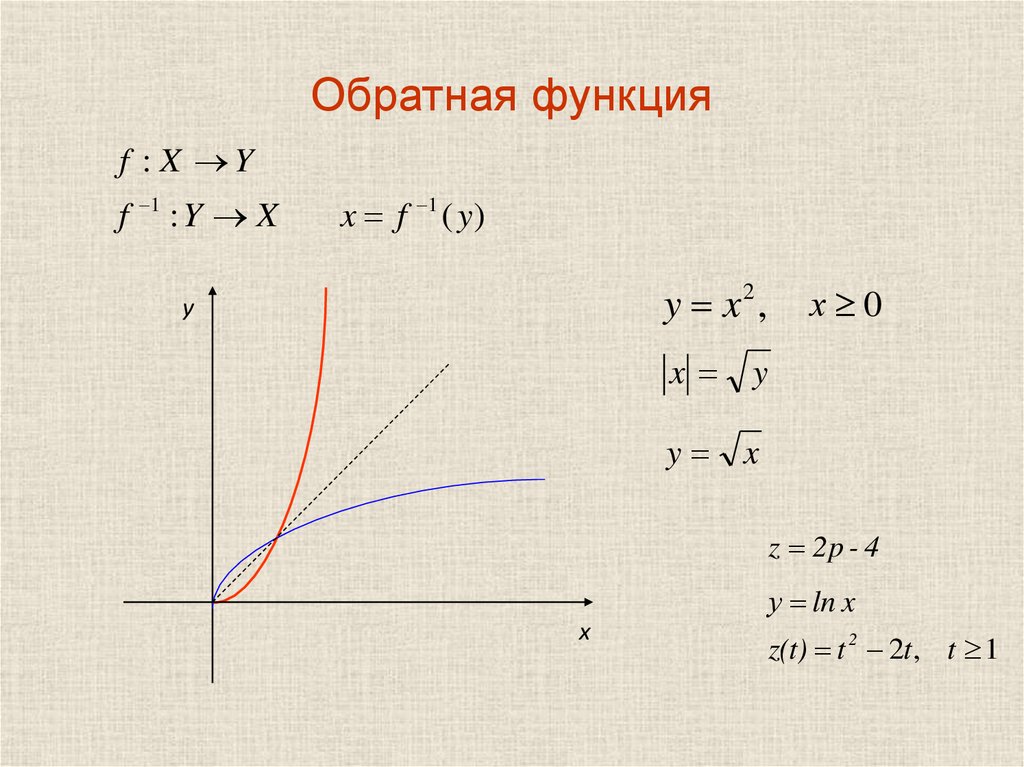 Это значение по умолчанию.
Это значение по умолчанию.
 Он устанавливает if_not_found аргумент для возврата 0 (ноль), если ничего не найдено. Аргумент match_mode имеет значение 1, что означает, что функция будет искать точное совпадение и, если не найдет, возвращает следующий больший элемент. Наконец, аргумент search_mode имеет значение 1 , что означает, что функция будет искать от первого элемента до последнего.
Он устанавливает if_not_found аргумент для возврата 0 (ноль), если ничего не найдено. Аргумент match_mode имеет значение 1, что означает, что функция будет искать точное совпадение и, если не найдет, возвращает следующий больший элемент. Наконец, аргумент search_mode имеет значение 1 , что означает, что функция будет искать от первого элемента до последнего.