Ограничения логарифма. Логарифм правила действия с логарифмами
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Что такое логарифм?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Что такое логарифм? Как решать логарифмы? Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно — уравнения с логарифмами.
Это абсолютно не так. Абсолютно! Не верите? Хорошо. Сейчас, за какие-то 10 — 20 минут вы:
1. Поймете, что такое логарифм .
2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.
3. Научитесь вычислять простые логарифмы.
Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень…
Чувствую, сомневаетесь вы… Ну ладно, засекайте время! Поехали!
Для начала решите в уме вот такое уравнение:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
И логарифм тесно взаимосвязаны. И по сути, является математической записью определения логарифма . Разберем подробно, что такое логарифм, откуда он произошел.
Рассмотрим алгебраическое действие — вычисление показателя х по заданным определенным значениям степени b и основанию а . Это задание в принципе заключается в решении уравнения a x = b , где а и b — некоторые заданные величины, x — неизвестная величина. Обратим внимание, что у данной задачи решения существуют не всегда.
Когда, к примеру, в уравнении a x = b число а положительно, а число b отрицательно , то у такого уравнения корней нет. Но если только а и b положительны и а ≠ 1, то оно непременно имеет исключительно один единственный корень . Достаточно известный факт, что график показательной функции у = а х непременно пересекается с прямой у = b и притом исключительно в одной точке. Абсцисса точки пересечения и будут корнем уравнения .
Достаточно известный факт, что график показательной функции у = а х непременно пересекается с прямой у = b и притом исключительно в одной точке. Абсцисса точки пересечения и будут корнем уравнения .
Для обозначения
Логарифм числа b по основанию а это показатель степени , в которую нужно возвести число а , чтобы получить число b причем a > 0, a ≠ 1, b > 0.
Исходя из определения, получаем основное логарифмическое тождество :
Примеры :
Следствием основного логарифмического тождества является нижеследующее правило .
Из равенства двух вещественных логарифмов получаем равенство логарифмируемых выражений.
Действительно, когда log a b = log a с, то , откуда, b = c .
Рассмотрим, почему для логарифмического тождества
взяты ограничения a > 0, a ≠ 1, b > 0 .Первое условие a ≠ 1 .
Общеизвестно, что единица в любой степени будет единица, и равенство x = log a b может существовать лишь при b = 1 , но при этом log 1 1 будет любым действительным числом . Для недопущения этой неоднозначности и принимается a ≠ 1 .
Обоснуем необходимость условия a > 0 .
При a = 0 по определению логарифма может существовать только при b = 0 . И следовательно тогда log 0 0 может быть любым отличным от нуля действительным числом , так как нуль в любой отличной от нуля степени есть нуль. Не допустить эту неоднозначность дает условие a ≠ 0 . А при a нам бы пришлось отказаться от разбора рациональных и иррациональных значений логарифма , поскольку степень с рациональным и иррациональным показателем определена лишь для положительных оснований.
И заключительное условие b > 0 является следствием из неравенства a > 0 , так как x = log a b, а значение степени с положительным основанием a всегда положительно.
Сегодня мы поговорим о формулах логарифмов и дадим показательные примеры решения .
Сами по себе подразумевают шаблоны решения согласно основным свойствам логарифмов. Прежде применять формулы логарифмов для решения напомним для вас, сначала все свойства:
Теперь на основе этих формул(свойств), покажем примеры решения логарифмов .
Примеры решения логарифмов на основании формул.
Логарифм положительного числа b по основанию a (обозначается log a b) — это показатель степени, в которую надо возвести a, чтобы получить b, при этом b > 0, a > 0, а 1.
Согласно определения log a b = x, что равносильно a x = b, поэтому log a a x = x.
Логарифмы , примеры:
log 2 8 = 3, т. к. 2 3 = 8
к. 2 3 = 8
log 7 49 = 2, т.к. 7 2 = 49
log 5 1/5 = -1, т.к. 5 -1 = 1/5
Десятичный логарифм — это обычный логарифм, в основании которого находится 10. Обозначается как lg.
log 10 100 = 2, т.к. 10 2 = 100
Натуральный логарифм — также обычный логарифм логарифм, но уже с основанием е (е = 2,71828… — иррациональное число). Обозначается как ln.
Формулы или свойства логарифмов желательно запомнить, потому что они понадобятся нам в дальнейшем при решении логарифмов, логарифмических уравнений и неравенств. Давайте еще раз отработаем каждую формулу на примерах.
- Основное логарифмическое тождество
a log a b = b8 2log 8 3 = (8 2log 8 3) 2 = 3 2 = 9
- Логарифм произведения равен сумме логарифмов
log a (bc) = log a b + log a clog 3 8,1 + log 3 10 = log 3 (8,1*10) = log 3 81 = 4
- Логарифм частного равен разности логарифмов
log a (b/c) = log a b — log a c9 log 5 50 /9 log 5 2 = 9 log 5 50- log 5 2 = 9 log 5 25 = 9 2 = 81
- Свойства степени логарифмируемого числа и основания логарифма
Показатель степени логарифмируемого числа log a b m = mlog a b
Показатель степени основания логарифма log a n b =1/n*log a b
log a n b m = m/n*log a b,
если m = n, получим log a n b n = log a b
log 4 9 = log 2 2 3 2 = log 2 3
- Переход к новому основанию
log a b = log c b/log c a,если c = b, получим log b b = 1
тогда log a b = 1/log b a
log 0,8 3*log 3 1,25 = log 0,8 3*log 0,8 1,25/log 0,8 3 = log 0,8 1,25 = log 4/5 5/4 = -1
Как видите, формулы логарифмов не так сложны как кажутся.
Если у вас остались вопросы по решению, пишите их в комментариях к статье.
Заметка: решили получить образование другого класса обучение за рубежом как вариант развития событий.
Начнем со свойства логарифма единицы . Его формулировка такова: логарифм единицы равен нулю, то есть, log a 1=0 для любого a>0 , a≠1 . Доказательство не вызывает сложностей: так как a 0 =1 для любого a , удовлетворяющего указанным выше условиям a>0 и a≠1 , то доказываемое равенство log a 1=0 сразу следует из определения логарифма.
Приведем примеры применения рассмотренного свойства: log 3 1=0 , lg1=0 и .
Переходим к следующему свойству: логарифм числа, равного основанию, равен единице

Примерами использования этого свойства логарифмов являются равенства log 5 5=1 , log 5,6 5,6 и lne=1 .
К примеру, log 2 2 7 =7 , lg10 -4 =-4 и .
Логарифм произведения двух положительных чисел x и y равен произведению логарифмов этих чисел: log a (x·y)=log a x+log a y , a>0 , a≠1 . Докажем свойство логарифма произведения. В силу свойств степени a log a x+log a y =a log a x ·a log a y , а так как по основному логарифмическому тождеству a log a x =x и a log a y =y , то a log a x ·a log a y =x·y . Таким образом, a log a x+log a y =x·y , откуда по определению логарифма вытекает доказываемое равенство.
Покажем примеры использования свойства логарифма произведения: log 5 (2·3)=log 5 2+log 5 3 и .
Свойство логарифма произведения можно обобщить на произведение конечного числа n
положительных чисел x 1 , x 2 , …, x n
как log a (x 1 ·x 2 ·…·x n)=
log a x 1 +log a x 2 +…+log a x n . Данное равенство без проблем доказывается .
Например, натуральных логарифм произведения можно заменить суммой трех натуральных логарифмов чисел 4 , e , и .
Логарифм частного двух положительных чисел x и y равен разности логарифмов этих чисел. Свойству логарифма частного соответствует формула вида , где a>0 , a≠1 , x и y – некоторые положительные числа. Справедливость этой формулы доказывается как и формула логарифма произведения: так как , то по определению логарифма .
Приведем пример использования этого свойства логарифма: .
Переходим к свойству логарифма степени . Логарифм степени равен произведению показателя степени на логарифм модуля основания этой степени. Запишем это свойство логарифма степени в виде формулы: log a b p =p·log a |b| , где a>0 , a≠1 , b и p такие числа, что степень b p имеет смысл и b p >0 .
Сначала докажем это свойство для положительных b
. Основное логарифмическое тождество позволяет нам представить число b
как a log a b
, тогда b p =(a log a b) p
, а полученное выражение в силу свойство степени равно a p·log a b
. Так мы приходим к равенству b p =a p·log a b
, из которого по определению логарифма заключаем, что log a b p =p·log a b
.
Так мы приходим к равенству b p =a p·log a b
, из которого по определению логарифма заключаем, что log a b p =p·log a b
.
Осталось доказать это свойство для отрицательных b . Здесь замечаем, что выражение log a b p при отрицательных b имеет смысл лишь при четных показателях степени p (так как значение степени b p должно быть больше нуля, в противном случае логарифм не будет иметь смысла), а в этом случае b p =|b| p . Тогда b p =|b| p =(a log a |b|) p =a p·log a |b| , откуда log a b p =p·log a |b| .
Например, и ln(-3) 4 =4·ln|-3|=4·ln3 .
Из предыдущего свойства вытекает свойство логарифма из корня : логарифм корня n -ой степени равен произведению дроби 1/n на логарифм подкоренного выражения, то есть, , где a>0 , a≠1 , n – натуральное число, большее единицы, b>0 .
Доказательство базируется на равенстве (смотрите ), которое справедливо для любых положительных b , и свойстве логарифма степени: .
Вот пример использования этого свойства: .
Теперь докажем формулу перехода к новому основанию логарифма вида . Для этого достаточно доказать справедливость равенства log c b=log a b·log c a . Основное логарифмическое тождество позволяет нам число b представить как a log a b , тогда log c b=log c a log a b . Осталось воспользоваться свойством логарифма степени: log c a log a b =log a b·log c a . Так доказано равенство log c b=log a b·log c a , а значит, доказана и формула перехода к новому основанию логарифма .
Покажем пару примеров применения этого свойства логарифмов: и .
Формула перехода к новому основанию позволяет переходить к работе с логарифмами, имеющими «удобное» основание. Например, с ее помощью можно перейти к натуральным или десятичным логарифмам, чтобы можно было вычислить значение логарифма по таблице логарифмов . Формула перехода к новому основанию логарифма также позволяет в некоторых случаях находить значение данного логарифма, когда известны значения некоторых логарифмов с другими основаниями.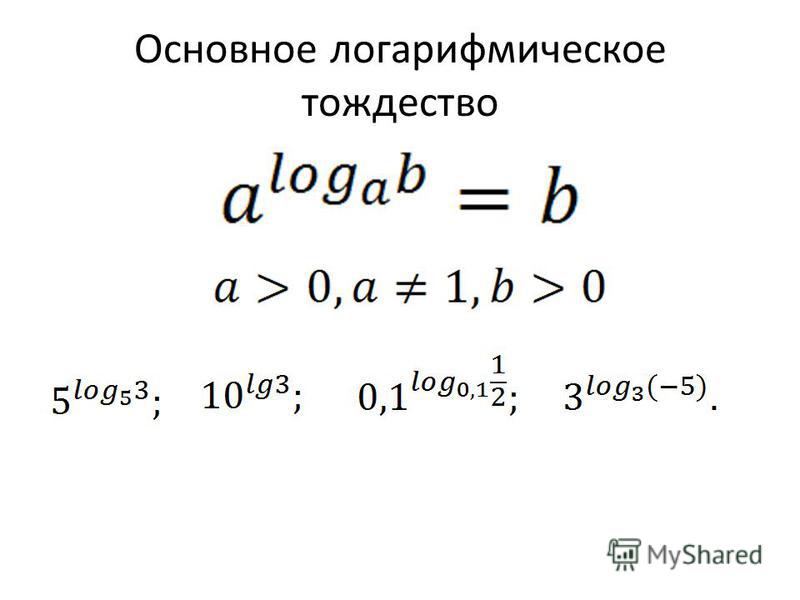
Часто используется частный случай формулы перехода к новому основанию логарифма при c=b вида . Отсюда видно, что log a b и log b a – . К примеру, .
Также часто используется формула , которая удобна при нахождении значений логарифмов. Для подтверждения своих слов покажем, как с ее помощью вычисляется значение логарифма вида . Имеем . Для доказательства формулы достаточно воспользоваться формулой перехода к новому основанию логарифма a : .
Осталось доказать свойства сравнения логарифмов.
Докажем, что для любых положительных чисел b 1 и b 2 , b 1 log a b 2 , а при a>1 – неравенство log a b 1
Наконец, осталось доказать последнее из перечисленных свойств логарифмов. Ограничимся доказательством его первой части, то есть, докажем, что если a 1 >1 , a 2 >1 и a 1 1 справедливо log a 1 b>log a 2 b . Остальные утверждения этого свойства логарифмов доказываются по аналогичному принципу.
Воспользуемся методом от противного. Предположим, что при a 1 >1
, a 2 >1
и a 1 1
справедливо log a 1 b≤log a 2 b
. По свойствам логарифмов эти неравенства можно переписать как и соответственно, а из них следует, что log b a 1 ≤log b a 2
и log b a 1 ≥log b a 2
соответственно. Тогда по свойствам степеней с одинаковыми основаниями должны выполняться равенства b log b a 1 ≥b log b a 2
и b log b a 1 ≥b log b a 2
, то есть, a 1 ≥a 2
. Так мы пришли к противоречию условию a 1
Предположим, что при a 1 >1
, a 2 >1
и a 1 1
справедливо log a 1 b≤log a 2 b
. По свойствам логарифмов эти неравенства можно переписать как и соответственно, а из них следует, что log b a 1 ≤log b a 2
и log b a 1 ≥log b a 2
соответственно. Тогда по свойствам степеней с одинаковыми основаниями должны выполняться равенства b log b a 1 ≥b log b a 2
и b log b a 1 ≥b log b a 2
, то есть, a 1 ≥a 2
. Так мы пришли к противоречию условию a 1
Список литературы.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
- Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).
Оценка для логарифма (можно ли придумать?) : Анализ-I
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| never-sleep |
| ||
27/11/11 |
| ||
| |||
| provincialka |
| |||
18/01/13 |
| |||
| ||||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| never-sleep |
| ||
27/11/11 |
| ||
| |||
| provincialka |
| |||
18/01/13 |
| |||
| ||||
| never-sleep |
| ||
27/11/11 |
| ||
| |||
| provincialka |
| |||
18/01/13 |
| |||
| ||||
| Евгений Машеров |
| |||
11/03/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 8 ] |
Модераторы: Модераторы Математики, Супермодераторы
ПРЕДЕЛЫ ЛОГАРИТМИЧЕСКОЙ ФУНКЦИИ
Логарифмическая функция является обратной экспоненциальной функцией. Логарифмическая функция определяется следующим образом:
Логарифмическая функция определяется следующим образом:
y=logax тогда и только тогда, когда x=ay ; для всех x>0, a>0 и a≠1
Обозначим логарифмическую функцию как
f(x)=logax , где a — основание логарифма.
Есть две наиболее часто используемые базы. Они имеют основание 10 и основание e.
Когда мы используем основание 10, функция известна как десятичная логарифмическая функция и представляется как f(x)=log10x
Когда мы используем основание e, функция известна как функция натурального логарифма и представляется как f(x)=logex
График логарифмической функции выглядит следующим образом:
Методы нахождения предела логарифмическая функция обсуждается ниже.
ПРЕДЕЛЫ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ-
При вычислении предела логарифмической функции используются два основных свойства. Результаты этих двух свойств можно напрямую использовать в качестве формул для нахождения предела. Два свойства:
Два свойства:
x→0loge(1+x)x=1
x→0logb(1+x)x=1logeb
Мы также можем вычислить предел логарифмической функции, используя правило Госпиталя. Обсудим это правило подробнее.
Правило Ло Хоспиталя :
В соответствии с этим правилом для дифференцируемых функций f и g на открытом интервале I, за исключением, возможно, точки c, содержащейся в I, если
x→cf(x)=x→cg(x )=0 или ∞ или -∞ и g'(x)≠0 для всех x в I с x≠c и x→cf'(x)g'(x) существует, то
x→cf(x)g(x)=x→cf'(x)g'(x)
Дифференцирование числителя и знаменателя обычно упрощает и преобразует его в форму, которую можно оценить непосредственно.
ВАЖНЫЕ ПРИМЕРЫ
Вычислить x→elogex-2 / x-2e
Чтобы оценить этот предел, нам нужно применить правило L’Hospital.
Используя правило Л’Госпиталя, мы получаем
НЕКОТОРЫЕ ВАЖНЫЕ ПРЕДЕЛЫ ЛОГАРИТМИЧЕСКИХ ФУНКЦИЙ:
При работе над нахождением пределов логарифмических функций рекомендуется помнить о некоторых важных пределах. Это ускорит и упростит расчеты. Ниже приведены некоторые важные ограничения.
АЛГЕБРА ПРЕДЕЛОВ-
При решении сложных задач на нахождение пределов очень важно понимать алгебру пределов. Таким образом, проблема разбивается на более простые пределы, что облегчает ее решение. Обсудим несколько теорем о пределах и функциях, которые помогают решить проблемы пределов.
Частный случай – если g является постоянной функцией, такой что g(x)=λ, для некоторого действительного числа λ, то
x→a[λ f(x)]= λ x→af(x)
ЗАКЛЮЧЕНИЕ
Обратные экспоненциальные функции также известны как логарифмические функции. Нахождение предела логарифмических функций может стать сложной задачей без необходимых знаний и понимания. Мы обсудили два метода нахождения предела. Выбор метода решения проблемы зависит от сложности проблемы. Большинство проблем эффективно решаются с помощью правила Ло Хоспиталя. Но некоторые вопросы требуют базового метода для их решения. Мы также обсудили алгебру пределов. Понимание этой концепции является обязательным для всех, потому что она разбивает сложные проблемы на более простые.
Мы обсудили два метода нахождения предела. Выбор метода решения проблемы зависит от сложности проблемы. Большинство проблем эффективно решаются с помощью правила Ло Хоспиталя. Но некоторые вопросы требуют базового метода для их решения. Мы также обсудили алгебру пределов. Понимание этой концепции является обязательным для всех, потому что она разбивает сложные проблемы на более простые.
Пределы логарифмических функций
Home Алгебра II Логарифмы и экспоненциальные функции Темы Логарифмические функции Пределы логарифмических функций
Темы
- Введение
- Темы
- Связывание экспонент и логарифмов
- Обратные функции
- Правила для обратных функций
- Основные
- Натуральный Log
- Экспоненциальные функции
- Линейный и экспонентный рост
- Экспоненциальные рост и распад
- Exponivential Equational Equational Equationals
- Functions ExponiTs Exponisters Exponisters Exponisters Exponisters 27
- Повторение обратных операций
- Изменение основания
- Пределы логарифмических функций
- Свойства экспонент и логарифмов
- В реальном мире
- Примеры
- Упражнения
- Задачи Math Shack
- Условия
- Лучшее из Интернета
- Викторины
- Раздаточный материал
- Содержание
- НАЗАД
- СЛЕДУЮЩИЙ
Как и экспоненциальные функции, логарифмические функции имеют свои пределы. Помните, чего не могут экспоненциальные функции: они не могут выводить отрицательное число вместо 9.0166 ф ( х ). Функция, на которую мы обратили внимание, когда думали об экспоненциальных функциях, была f ( x ) = 4 x .
Помните, чего не могут экспоненциальные функции: они не могут выводить отрицательное число вместо 9.0166 ф ( х ). Функция, на которую мы обратили внимание, когда думали об экспоненциальных функциях, была f ( x ) = 4 x .
Поднимем зеркало, взяв логарифм по основанию 4, чтобы получить обратную функцию: f ( x ) = log 4 x .
Если бы мы попытались сделать x отрицательными или равными нулю в этой логарифмической функции, в известной вселенной нет y -значения, которое позволило бы нам это сделать, поэтому логарифмическая функция не определена в x — значения нуля или меньше. Другими словами, его домен равен x > 0.
Вот как выглядит график f ( x ) = log 4 x :
x : экспоненциальная функция никогда не может быть нулевой или отрицательной, обратная (логарифмическая) функция никогда не может иметь отрицательное значение на входе , равное нулю.
Пример задачи
Когда будет f ( x ) = log 5 x быть больше г ( x ) = log 20 x ? Игнорировать отрицательные значения x .
Результатом этих журналов является показатель степени , необходимый выше 5 или 20, чтобы равняться x.
Когда x больше 1, log 5 x будет больше, потому что для 5 требуется больший показатель степени , чем для 20, чтобы равняться любому x в этой области. Пятерка — это маленькая креветка, которой, по сути, нужна поддержка. Например:
За х = 2 получаем 5 0,43 или 20 0,23 .
За х = 5 получаем 5 1 или 20 0,54 .
Однако, когда x меньше 1, log 20 x будет больше, чем log 5 x , потому что для уменьшения этого 20 до размера по сравнению с 5 необходим отрицательный показатель, близкий к нулю.

 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. 04.2013, 13:04
04.2013, 13:04  04.2013, 13:10
04.2013, 13:10 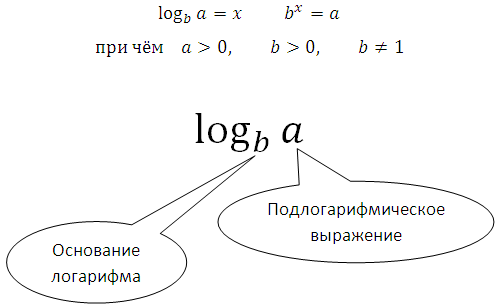 Частичными суммами и оценивайте.
Частичными суммами и оценивайте. Если нужно точнее, несколько членов сохраните без изменения, а в последующих дроби замените на первую из них (самую большую).
Если нужно точнее, несколько членов сохраните без изменения, а в последующих дроби замените на первую из них (самую большую). 04.2013, 13:31
04.2013, 13:31 
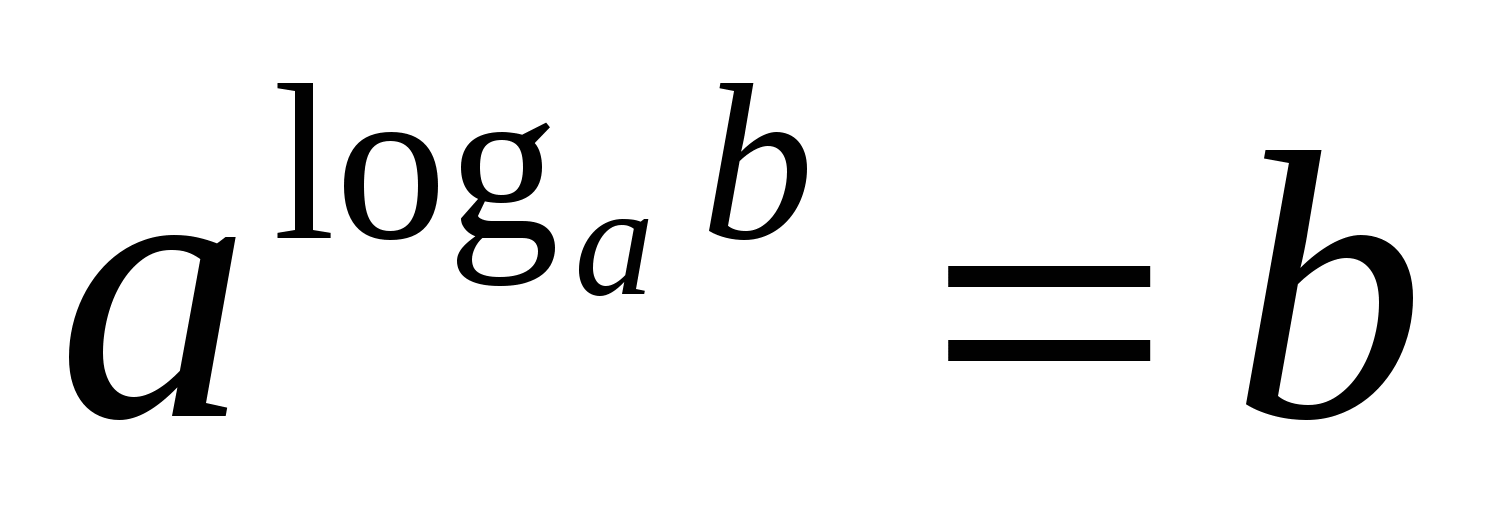 04.2013, 14:37
04.2013, 14:37  04.2013, 14:43
04.2013, 14:43