Калькулятор Перевода Диаметра В Окружность
Инструкции: Используйте этот калькулятор для вычисления окружности круга с заданным диаметром, показывая все шаги. Пожалуйста, введите диаметр d в поле ниже.
Подробнее об этом калькуляторе перевода диаметра в окружность
Данный калькулятор позволит вам рассчитать
Окружность круга
непосредственно из его диаметра, показывая все этапы процесса. Все, что вам нужно предоставить, — это правильное числовое выражение для диаметра. Это может быть число или дробь, или даже составное числовое выражение, при условии, что оно больше 0.
Как только вы укажете действительный диаметр d, вам просто нужно нажать кнопку «Рассчитать», и все этапы процесса будут показаны и представлены вам.
Кроме того, вас может заинтересовать обратный процесс, который заключается в том, как вычислите диаметр из окружности из круга.
Формула расчета отношения диаметра к окружности
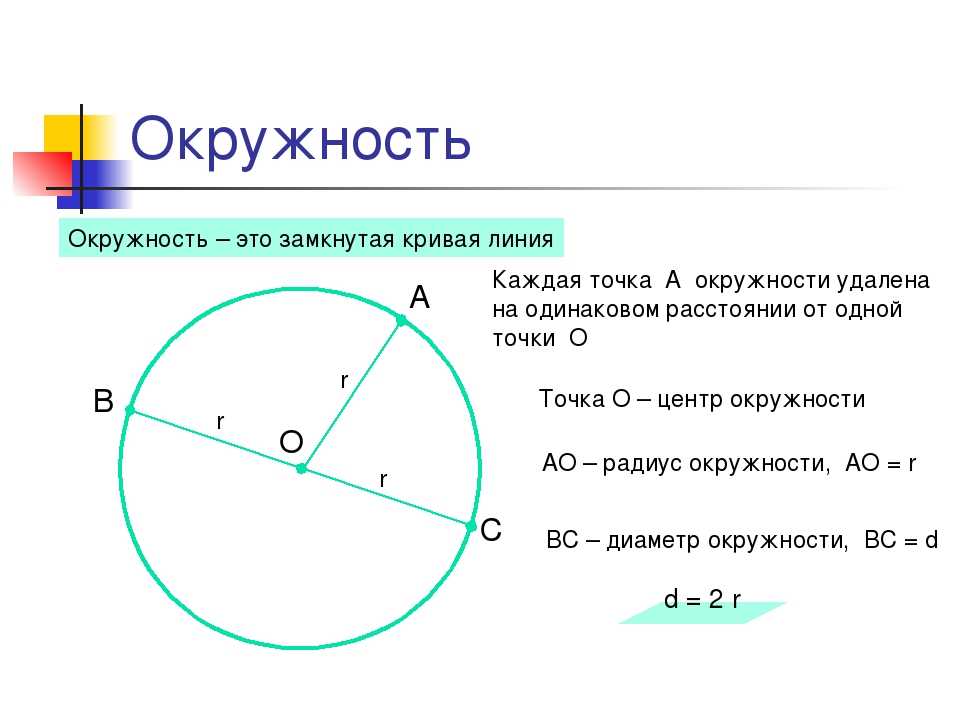
Наиболее типичная ситуация — получить окружность круга, начиная с радиуса, но в формуле есть сокращение, которое позволяет перейти непосредственно от диаметра к окружности, как показано в формуле ниже:
\[ C = \pi d \]
Может ли это стать еще проще? Вы просто умножаете диаметр d на \(\pi\).
Как перейти от диаметра к окружности?
- Шаг 1: Определите диаметр d и его потенциальную единицу длины. Это значение должно быть положительным, иначе вы не сможете продолжить
- Шаг 3: После вычисления C = π d, вы оставляете ответ в терминах π, или оцениваете численно.
В наиболее типичном случае результат измерения окружности будет зависеть от π, поэтому вам может понадобиться
оценить выражение
чтобы получить числовое значение.
Калькулятор соотношения диаметра и радиуса
Возможно, вы из тех, кто не любит диаметры и предпочитает работать с радиусом, в таком случае вы помните, что d = 2r, и тогда вы можете вычислить радиус из диаметра, как показано ниже:
\[\displaystyle r = \frac{d}{2} \]
Если говорить простым языком, то радиус равен половине диаметра
Какова окружность диаметра 12 дюймов?
Это пример, который можно использовать для понимания формулы. Итак, диаметр непосредственно представлен как d = 12 дюймов, и он поставляется с единицей длины.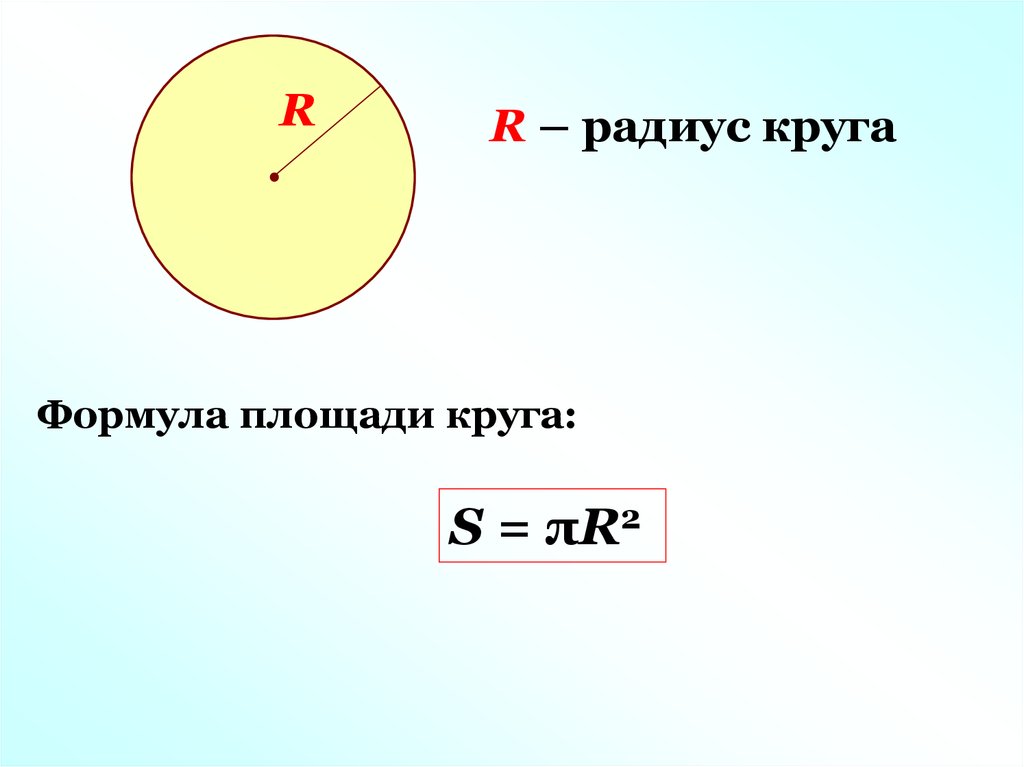
Из приведенной выше формулы следует, что окружность равна C = π d = 12 π дюймов. Теперь, если мы захотим перевести это в числовое значение, то получим, что C = 37,699112 дюйма.
Почему я должен использовать диаметр для вычисления окружности?
Хорошее замечание. Использование диаметра — это одна из известных нам форм нахождения окружности круга, поэтому мы включили ее сюда для полноты картины.
Большинство людей просто вычисляют радиус по диаметру, а для окружности используют общую формулу.
Пример: вычисление окружности из диаметра
Вычислите окружность круга, если его диаметр равен \(\frac{3}{4}\)
Отвечать:
Нам нужно найти окружность \(C\) круга, а из предоставленной информации мы знаем, что диаметр круга равен \(d = \frac{3}{4}\).
Теперь формула для окружности \(C = 2\pi r\), но так как диаметр равен удвоенному периметру, то получается \(d = 2r\), и, следовательно, формула окружности становится:
\[C = d \pi \]
Поэтому все, что нам нужно сделать, это подставить в приведенную выше формулу известное значение известного диаметра \(d = \frac{3}{4}\). Получается следующее:
\[ \begin{array}{ccl}\displaystyle C & = & \displaystyle d \pi \\\\ \\\\ & = & \pi \cdot \frac{3}{4} \\\\ \\\\ & = & \displaystyle \frac{3}{4}\pi{} \end{array} \]
На этом расчеты завершены.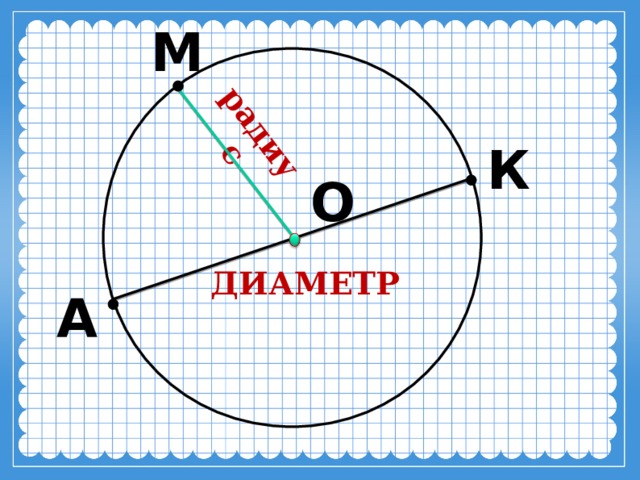
Пример: диаметр к окружности
Теперь, если предположить, что диаметр равен 3, то какова окружность?
Отвечать: Нам нужно найти окружность \(C\) круга, и теперь мы знаем, что \(d = 3 \).
\[C = d \pi \]
Поэтому мы просто подставляем значение \(d = 3\) в следующую формулу:
Следовательно, в данном случае окружность круга равна \(\displaystyle C = 3 \pi{}\).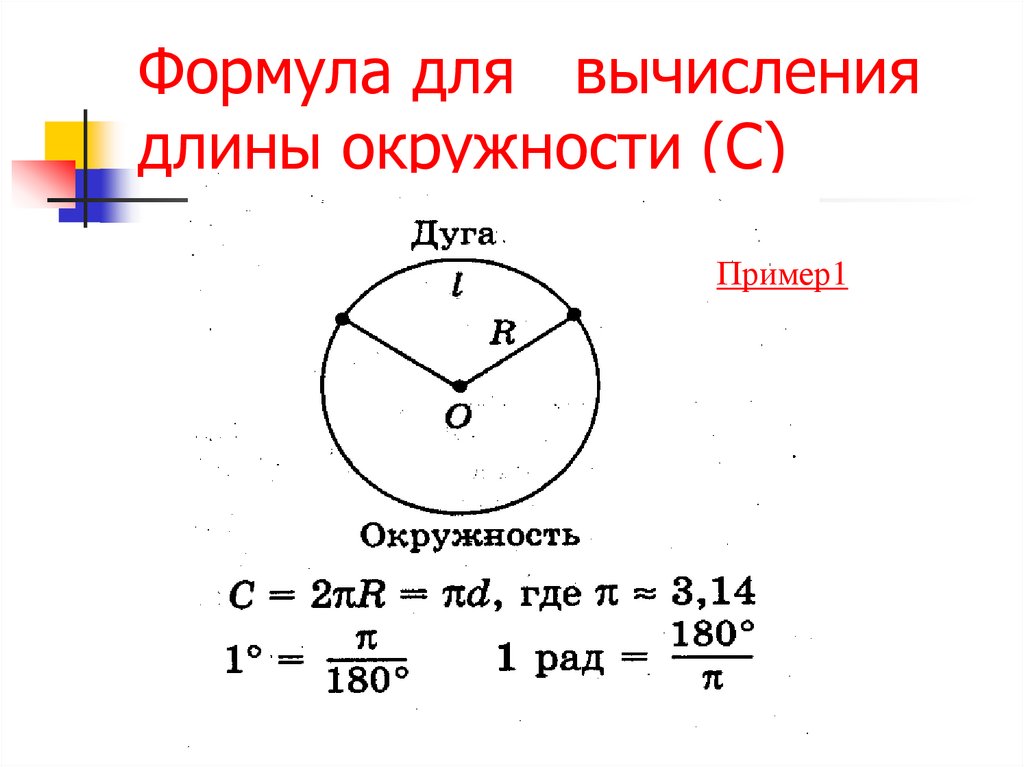
Пример: отношение диаметра к окружности
Какова будет окружность круга, если его диаметр d = -3?
Отвечать: В этом случае окружность не будет четко определенной, потому что диаметр ДОЛЖЕН быть положительным числом. Другими словами, вы не можете построить круг с отрицательным диаметром.
Другие калькуляторы окружностей
Круги встречаются в математике ВЕЗДЕ. Нет такой области математики, в которой окружности не были бы важны. Они дают понятия, знакомые каждому из нас, такие как
площадь круга
и
Окружность круга
.
Идеи площади и окружности кажутся сейчас очень знакомыми, но потребовалось немало времени, чтобы они были поняты так, что стали привычными для нас.
Одним из интересных элементов является то, что площади и окружности не зависят от уравнение окружности только на радиусе. Другими словами, центр не имеет значения для вычисления площади и периметра.
Как объяснить длину окружности? – Обзоры Вики
Окружность круга определяется как линейное расстояние вокруг него. Другими словами, если круг открывается, образуя прямую линию, то длина этой линии будет длиной окружности круга.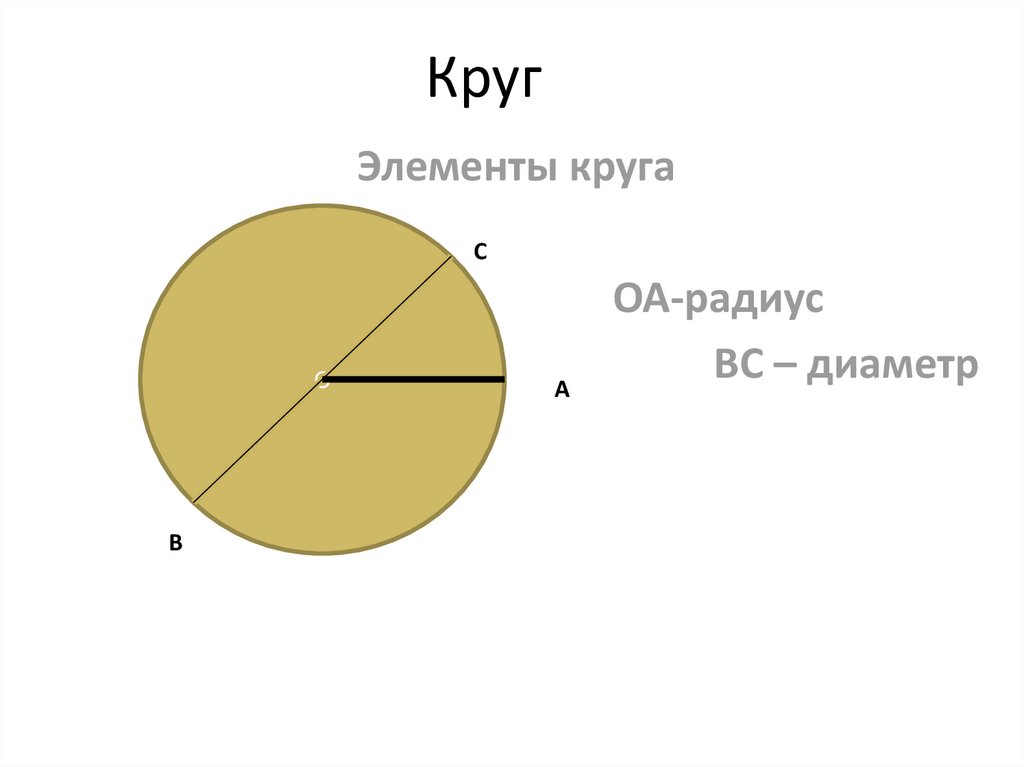 .
.
Следовательно, окружность и периметр круга одинаковы? Золото по периметру Длина окружности. … Длина контура прямоугольной формы называется его периметром, а длина контура круга называется его окружностью.
Почему длина окружности 2 pi r? Поскольку диаметр в два раза больше радиуса, длина окружности равна произведению числа пи и 2r, то есть 2 (пи) * r.
Кроме того, почему длина окружности равна 2πr? Отсюда следует, что отношение окружность: радиус, что равносильно высказыванию отношения окружность: диаметр, постоянно для любой окружности. Если эта константа равна некоторому числу π, то длина окружности = π × диаметр или длина окружности = 2π. × радиус. Значит доказано.
Что такое 3.14 в круге? Кратко, pi— которое пишется как греческая буква p или π — это отношение длины окружности любого круга к диаметру этого круга. Независимо от размера круга это отношение всегда будет равно пи. В десятичной форме значение пи составляет примерно 3.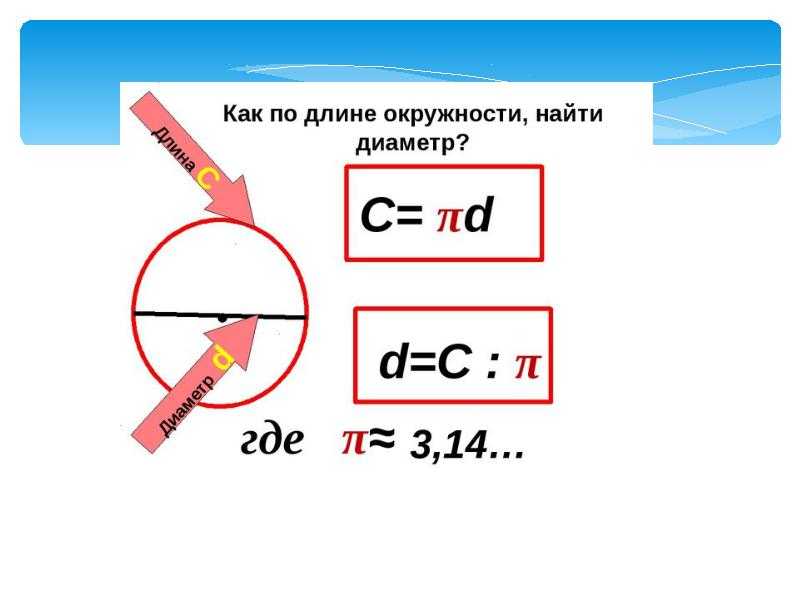 14.
14.
Окружность только для кругов?
Окружность является частным случаем периметра. Оба описывают общую длину границы двухмерной фигуры, но окружность конкретно относится к периметру изогнутой фигуры или дуги. Поэтому применяется только к круги, овалы, эллипсы, дуги и т.д.
Есть ли у окружности периметр? Ответ: периметр круг пи × d. Здесь d — диаметр окружности. Следовательно, периметр круга равен половине периметра круга, равного ½ пи × d.
Окружность равна диаметру? Окружность – это один полный «круг» вокруг круга, а диаметр — это длина отрезка, который делит круг пополам.
Как вы решаете r в C 2pir?
Также радиус равен половине окружности? Расстояние вокруг прямоугольника или квадрата, как вы помните, называется периметром. С другой стороны, расстояние вокруг окружности называется окружностью (с). Половина диаметра, или расстояние от средней точки до границы круга, называется радиусом круга (r).
Половина диаметра, или расстояние от средней точки до границы круга, называется радиусом круга (r).
Кто изобрел пи?
Пи, в математике, отношение длины окружности к ее диаметру. Символ π был изобретен Британский математик Уильям Джонс в 1706 году для представления отношения, а позже популяризировал швейцарский математик Леонард Эйлер.
Является ли pi d таким же, как 2 pi r? 2*pi*r и pi*d — одно и то же.. Общепринято, что мы пишем первое вместо второго. Кроме того, при выводе (с использованием дифференциальных уравнений) длина окружности получается как 2*pi*r.
Всегда ли длина окружности 360 градусов?
На самом деле длина окружности зависит исключительно от радиуса окружности: длина окружности равна 2Πr, где r обозначает длину радиуса. … Таким образом, длина окружности длина дуги 360 градусов этого круга.
Почему длина окружности пи D?
Формула
В математике у нас есть формула, связывающая эти две части круга. Эта формула называется формулой окружности, и она С = фут*д где C обозначает длину окружности, а d обозначает диаметр. А пи это пи или 3.14.
А пи это пи или 3.14.
Почему число 3.14 называется числом пи? Только в 18 веке — примерно через два тысячелетия после того, как Архимед впервые вычислил значение числа 3.14 — имя «пи» впервые было использовано для обозначения числа. … «Он использовал его потому что греческая буква Пи соответствует букве «П»… А число «пи» находится по периметру круга ».
Для чего используется пи? В базовой математике пи используется для найти площадь и длину окружности. Пи используется для нахождения площади путем умножения квадрата радиуса на число Пи.
Как найти периметр?
Чтобы найти периметр прямоугольника, сложите длины четырех сторон прямоугольника. Если у вас есть только ширина и высота, вы можете легко найти все четыре стороны (каждая из двух сторон равна высоте, а две другие стороны равны ширине). Умножьте высоту и ширину на два и сложите результаты.
Окружность равна длине? В качестве существительных разница между длиной и длина окружности
заключается в том, что длина — это измерение расстояния по самому длинному измерению объекта, а окружность — это (геометрическая) линия, которая ограничивает круг или другую двумерную фигуру.
Какова длина окружности 2?
Окружность и площади
| Размер в дюймах | Окружность в дюймах | Площадь в квадратных дюймах |
|---|---|---|
| 1 1/4 | 3.927 | 1.227 |
| 1 1/2 | 4.712 | 1.767 |
| 1 3/4 | 5.498 | 2.405 |
| 2 | 6.283 | 3.142 |
Как найти периметр круга?
Узнай, что у периметра круга есть особое название — «окружность». Символ — заглавная C. Он рассчитывается по формуле Пи х диаметр, или 3.14 xd = C. Его также можно рассчитать по формуле Pi x (2 x радиус) = C или 3.14 x (2 xr) = C.
Диаметр равен половине окружности? Длина окружности равна π⋅d, где d — диаметр окружности. π=3.14159… что равно ~3, поэтому длина окружности примерно в 3 раза больше диаметра.
π=3.14159… что равно ~3, поэтому длина окружности примерно в 3 раза больше диаметра.
Как диаметр связан с окружностью?
Мы узнали, что окружность — это расстояние по окружности, а диаметр — это расстояние по окружности, проходящей через центр. … Чтобы найти длину окружности по диаметру, ты умножаешь диаметр на пи. Чтобы найти диаметр по окружности, нужно длину окружности разделить на число Пи.
Сколько десятичных знаков числа Пи нам действительно нужно? — Новости образования
День Пи по пути НАСА
Получите билет, чтобы исследовать JPL этим летом
Новости образования| 24 октября 2022 г.
Автор NASA/JPL Edu
В то время как мировые рекордсмены, возможно, запомнили более 70 000 цифр числа пи, инженер Лаборатории реактивного движения объясняет, почему на самом деле вам нужна лишь крошечная часть этого числа для большинства вычислений — даже в НАСА.
Обновление: 24 октября 2022 г. .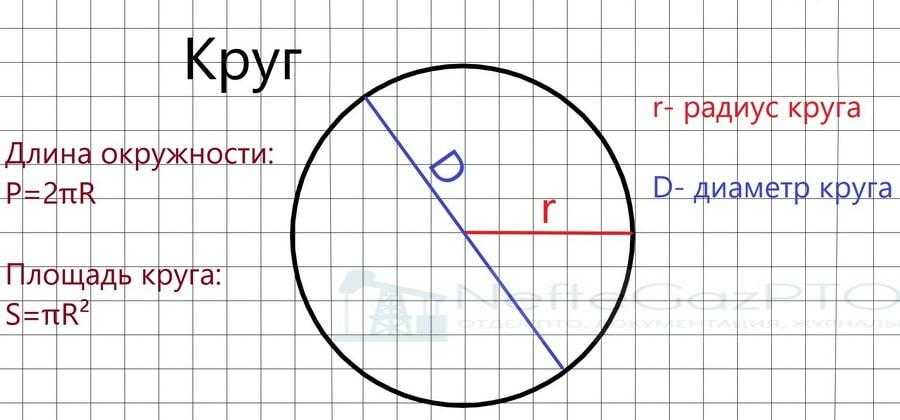 Эта статья, первоначально написанная в 2016 г., была обновлена, чтобы отразить последние значения для космического корабля НАСА «Вояджер-1», который продолжает продвигаться все дальше в межзвездное пространство. Автор, Марк Рэйман, тоже прошел путь от главного инженера миссии НАСА «Рассвет», которая успешно завершилась в 2018 году, до главного инженера по операциям миссии и науке в Лаборатории реактивного движения НАСА.
Эта статья, первоначально написанная в 2016 г., была обновлена, чтобы отразить последние значения для космического корабля НАСА «Вояджер-1», который продолжает продвигаться все дальше в межзвездное пространство. Автор, Марк Рэйман, тоже прошел путь от главного инженера миссии НАСА «Рассвет», которая успешно завершилась в 2018 году, до главного инженера по операциям миссии и науке в Лаборатории реактивного движения НАСА.
На этом рисунке показано более 500 десятичных знаков бесконечного числа пи. Изображение предоставлено: NASA/JPL-Caltech | + Развернуть изображение
Мы получили этот вопрос от фаната на Facebook, который интересовался, сколько знаков после запятой бесконечной математической константы пи (π) ученые и инженеры НАСА-Лаборатории реактивного движения используют при расчетах:
«Использует ли JPL только 3,14 для своего пи расчеты? Или вы используете больше десятичных знаков, например [360 или даже больше]?»
Вот ответ главного инженера JPL по операциям и науке Марка Рэймана:
Спасибо за вопрос! Я не первый раз слышу подобный вопрос.
На самом деле, она была сформулирована много лет назад шестиклассником, энтузиастом науки и космоса, которому позже посчастливилось получить докторскую степень по физике и заняться исследованием космоса. Его звали Марк Рэйман.
Для начала позвольте мне прямо ответить на ваш вопрос. Для вычислений JPL с высочайшей точностью, предназначенных для межпланетной навигации, мы используем 3,141592653589793. Давайте посмотрим на это немного подробнее, чтобы понять, почему мы не используем больше десятичных разрядов. Я думаю, мы даже можем видеть, что нет никаких физически реалистичных расчетов, которые когда-либо выполняли ученые, для которых необходимо включать почти столько десятичных знаков, о которых вы спрашивали. Рассмотрим следующие примеры:
- Самый удаленный от Земли космический корабль — «Вояджер-1». На момент написания этой статьи он находился на расстоянии около 14,7 миллиардов миль (23,6 миллиардов километров). Давайте будем великодушны и назовем это 15 миллиардами миль (24 миллиарда километров).
Теперь предположим, что у нас есть круг с радиусом именно такого размера, 30 миллиардов миль (48 миллиардов километров) в диаметре, и мы хотим вычислить длину окружности, которая равна пи, умноженному на радиус, умноженный на 2. Используя число пи, округленное до 15-го знака после запятой, как я сказал выше, получается чуть больше 94 миллиарда миль (более 150 миллиардов километров). Здесь нам не нужно беспокоиться о том, что именно представляет собой значение (вы можете умножить его, если хотите), а скорее о том, какая ошибка в значении возникает из-за того, что не используется больше цифр числа пи. Другими словами, обрезав число пи до 15-го знака после запятой, мы рассчитали бы длину окружности этого круга, которая немного отличается. Оказывается, наша расчетная длина окружности диаметром 30 миллиардов миль (48 миллиардов километров) будет ошибочной менее чем на полдюйма (около одного сантиметра). Подумай об этом. У нас круг больше 94 миллиарда миль (более 150 миллиардов километров) вокруг, и наши расчеты этого расстояния будут ошибочными не более чем на ширину вашего мизинца.
Проверьте свои математические способности с помощью этой задачи из программы NASA Pi Day Challenge. Можно ли использовать число пи, чтобы определить, какая часть сигнала от «Вояджера-1» достигает Земли? Изображение предоставлено: NASA/JPL-Caltech | + Развернуть изображение | › Просмотреть страницу урока
- Мы можем сделать это ближе к дому, взглянув на нашу планету Земля. Это больше 7,900 миль (12 700 километров) в диаметре на экваторе. Окружность составляет примерно 24 900 миль (40 100 километров). Вот как далеко вы бы проехали, если бы совершили кругосветное путешествие — и не беспокоились бы о холмах, долинах и препятствиях, таких как здания, океанские волны и т. д. Насколько далеко был бы ваш одометр, если бы вы использовали ограниченную версию пи выше? Несоответствие будет размером с молекулу. Конечно, есть много разных типов молекул, поэтому они охватывают широкий диапазон размеров, но я надеюсь, что это дало вам представление. Другой способ увидеть это состоит в том, что ваша ошибка из-за того, что вы не используете больше цифр числа пи, будет более чем в 30 000 раз тоньше волоса!
- Давайте перейдем к самому большому размеру: известной вселенной.
Радиус Вселенной составляет около 46 миллиардов световых лет. Теперь позвольте мне задать (и ответить!) другой вопрос: сколько цифр пи нам потребуется, чтобы вычислить длину окружности радиусом 46 миллиардов световых лет с точностью, равной диаметру атома водорода, простейшего атом? Получается, что 37 знаков после запятой (38 цифр, включая цифру 3 слева от запятой) было бы вполне достаточно. Подумайте о том, насколько фантастически огромна Вселенная. Это, безусловно, далеко за пределами того, что вы можете увидеть своими глазами даже в самую темную, самую прекрасную ночь сверкающих звезд. Это еще далеко за пределы экстраординарного видения космического телескопа Джеймса Уэбба. И необъятность Вселенной действительно далеко, далеко, далеко за пределами того, что мы можем себе даже представить. Теперь подумайте о том, насколько невероятно мал один атом. Разве не удивительно, что нам вообще не нужно использовать много цифр числа пи, чтобы охватить весь этот невероятный диапазон?
Если бы вы держали одну песчинку на расстоянии вытянутой руки, вы могли бы охватить всю площадь космоса, занимаемую этим изображением, которое было получено космическим телескопом Джеймса Уэбба и содержит тысячи галактик.
Возраст самой старой из известных галактик, обнаруженных на изображении, составляет 13,1 миллиарда лет. Изображение предоставлено: НАСА, ЕКА, CSA, STScI | + Развернуть изображение | › Подробнее об изображении | Текстовое описание (PDF)
Пи — интригующее число с интересными математическими свойствами. Забавно думать о его поистине бесконечной последовательности цифр, и может быть удивительно, как часто он появляется в уравнениях, которые используют ученые и инженеры. Но нет никаких вопросов — прозаических или эзотерических — в благородных усилиях человечества по исследованию или постижению чудес космоса, от невообразимо мельчайших до невообразимо огромных масштабов, для которых потребовалось бы очень много таких цифр.
Узнайте больше от Марка в его вдохновляющем выступлении на TEDx «Если это не невозможно, то не стоит и пытаться» и в его журнале «Рассвет», где он часто писал новости о необычной внеземной экспедиции миссии «Рассвет» на протопланету Веста. и карликовая планета Церера.
Узнать больше
Ресурсы для преподавателей
Статьи
Мультимедиа и загрузки
Книги на испанском языке
ТЕГИ: Pi, Pi Day, Dawn, Voyager, Engineering, Science, Mathematics
ОБ АВТОРЕ
NASA/JPL Edu
NASA/JPL Edu поддерживает образование в области естественных наук, технологий, инженерии и математики (STEM), предоставляя мероприятия, ресурсы и материалы NASA и JPL для педагоги и учащиеся классов K-12, а также стажировки и исследования STEM возможности для студентов и преподавателей высших учебных заведений.
- Отправить свое имя на Марс
- Как ученые сделали первое изображение черной дыры
- Итак, вы хотите стать космонавтом?
- Как пройти стажировку в JPL
- Сколько десятичных знаков числа Пи нам действительно нужно?
- Наука, стоящая за первой попыткой НАСА изменить направление движения астероида
Зарегистрируйтесь сегодня и получайте самые свежие оповещения по электронной почте, доставленные прямо на ваш почтовый ящик.

 На самом деле, она была сформулирована много лет назад шестиклассником, энтузиастом науки и космоса, которому позже посчастливилось получить докторскую степень по физике и заняться исследованием космоса. Его звали Марк Рэйман.
На самом деле, она была сформулирована много лет назад шестиклассником, энтузиастом науки и космоса, которому позже посчастливилось получить докторскую степень по физике и заняться исследованием космоса. Его звали Марк Рэйман.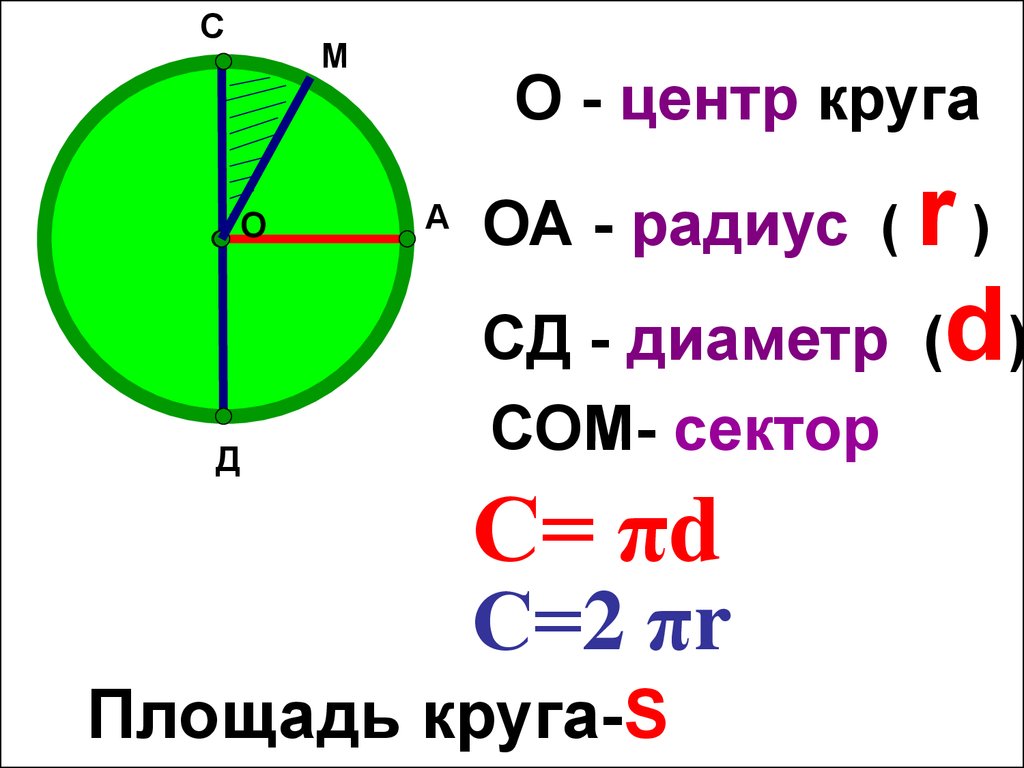 Теперь предположим, что у нас есть круг с радиусом именно такого размера, 30 миллиардов миль (48 миллиардов километров) в диаметре, и мы хотим вычислить длину окружности, которая равна пи, умноженному на радиус, умноженный на 2. Используя число пи, округленное до 15-го знака после запятой, как я сказал выше, получается чуть больше 94 миллиарда миль (более 150 миллиардов километров). Здесь нам не нужно беспокоиться о том, что именно представляет собой значение (вы можете умножить его, если хотите), а скорее о том, какая ошибка в значении возникает из-за того, что не используется больше цифр числа пи. Другими словами, обрезав число пи до 15-го знака после запятой, мы рассчитали бы длину окружности этого круга, которая немного отличается. Оказывается, наша расчетная длина окружности диаметром 30 миллиардов миль (48 миллиардов километров) будет ошибочной менее чем на полдюйма (около одного сантиметра). Подумай об этом. У нас круг больше 94 миллиарда миль (более 150 миллиардов километров) вокруг, и наши расчеты этого расстояния будут ошибочными не более чем на ширину вашего мизинца.
Теперь предположим, что у нас есть круг с радиусом именно такого размера, 30 миллиардов миль (48 миллиардов километров) в диаметре, и мы хотим вычислить длину окружности, которая равна пи, умноженному на радиус, умноженный на 2. Используя число пи, округленное до 15-го знака после запятой, как я сказал выше, получается чуть больше 94 миллиарда миль (более 150 миллиардов километров). Здесь нам не нужно беспокоиться о том, что именно представляет собой значение (вы можете умножить его, если хотите), а скорее о том, какая ошибка в значении возникает из-за того, что не используется больше цифр числа пи. Другими словами, обрезав число пи до 15-го знака после запятой, мы рассчитали бы длину окружности этого круга, которая немного отличается. Оказывается, наша расчетная длина окружности диаметром 30 миллиардов миль (48 миллиардов километров) будет ошибочной менее чем на полдюйма (около одного сантиметра). Подумай об этом. У нас круг больше 94 миллиарда миль (более 150 миллиардов километров) вокруг, и наши расчеты этого расстояния будут ошибочными не более чем на ширину вашего мизинца.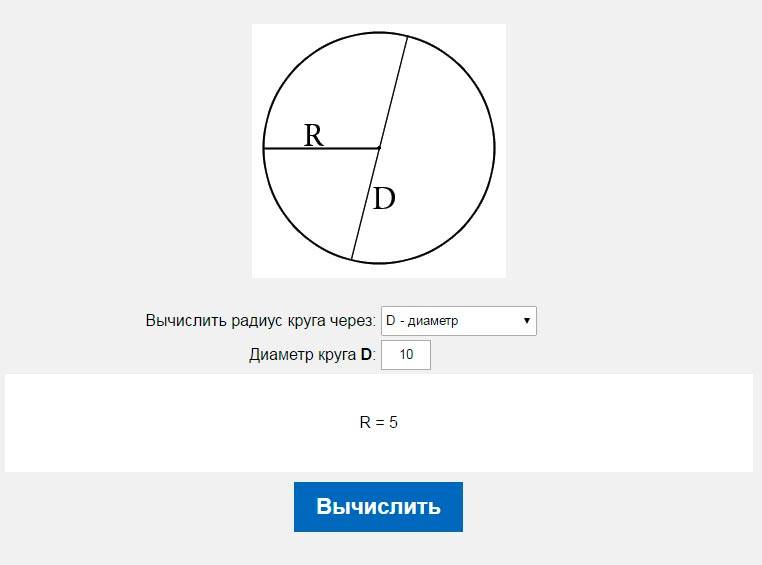
 Радиус Вселенной составляет около 46 миллиардов световых лет. Теперь позвольте мне задать (и ответить!) другой вопрос: сколько цифр пи нам потребуется, чтобы вычислить длину окружности радиусом 46 миллиардов световых лет с точностью, равной диаметру атома водорода, простейшего атом? Получается, что 37 знаков после запятой (38 цифр, включая цифру 3 слева от запятой) было бы вполне достаточно. Подумайте о том, насколько фантастически огромна Вселенная. Это, безусловно, далеко за пределами того, что вы можете увидеть своими глазами даже в самую темную, самую прекрасную ночь сверкающих звезд. Это еще далеко за пределы экстраординарного видения космического телескопа Джеймса Уэбба. И необъятность Вселенной действительно далеко, далеко, далеко за пределами того, что мы можем себе даже представить. Теперь подумайте о том, насколько невероятно мал один атом. Разве не удивительно, что нам вообще не нужно использовать много цифр числа пи, чтобы охватить весь этот невероятный диапазон?
Радиус Вселенной составляет около 46 миллиардов световых лет. Теперь позвольте мне задать (и ответить!) другой вопрос: сколько цифр пи нам потребуется, чтобы вычислить длину окружности радиусом 46 миллиардов световых лет с точностью, равной диаметру атома водорода, простейшего атом? Получается, что 37 знаков после запятой (38 цифр, включая цифру 3 слева от запятой) было бы вполне достаточно. Подумайте о том, насколько фантастически огромна Вселенная. Это, безусловно, далеко за пределами того, что вы можете увидеть своими глазами даже в самую темную, самую прекрасную ночь сверкающих звезд. Это еще далеко за пределы экстраординарного видения космического телескопа Джеймса Уэбба. И необъятность Вселенной действительно далеко, далеко, далеко за пределами того, что мы можем себе даже представить. Теперь подумайте о том, насколько невероятно мал один атом. Разве не удивительно, что нам вообще не нужно использовать много цифр числа пи, чтобы охватить весь этот невероятный диапазон? Возраст самой старой из известных галактик, обнаруженных на изображении, составляет 13,1 миллиарда лет. Изображение предоставлено: НАСА, ЕКА, CSA, STScI | + Развернуть изображение | › Подробнее об изображении | Текстовое описание (PDF)
Возраст самой старой из известных галактик, обнаруженных на изображении, составляет 13,1 миллиарда лет. Изображение предоставлено: НАСА, ЕКА, CSA, STScI | + Развернуть изображение | › Подробнее об изображении | Текстовое описание (PDF)