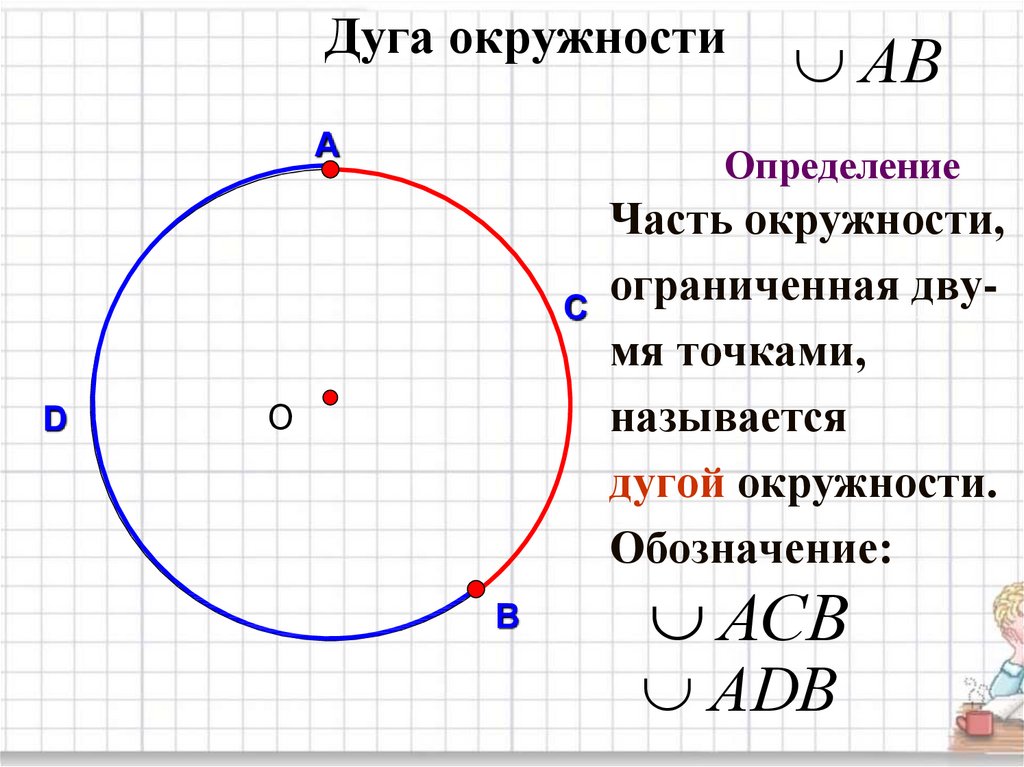
Окружность. Основные теоремы
\[{\Large{\text{Центральные и вписанные углы}}}\]
Определения
Центральный угол – это угол, вершина которого лежит в центре окружности.
Вписанный угол – это угол, вершина которого лежит на окружности.
Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.
Теорема
Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.
Доказательство
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка \(B\) – вершина вписанного угла \(ABC\) и \(BC\) – диаметр окружности:
Треугольник \(AOB\) – равнобедренный, \(AO = OB\), \(\angle AOC\) – внешний, тогда \(\angle AOC = \angle OAB + \angle ABO = 2\angle ABC\), откуда \(\angle ABC = 0,5\cdot\angle AOC = 0,5\cdot\buildrel\smile\over{AC}\).
Теперь рассмотрим произвольный вписанный угол \(ABC\). Проведём диаметр окружности \(BD\) из вершины вписанного угла. Возможны два случая:
1) диаметр разрезал угол на два угла \(\angle ABD, \angle CBD\)(для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1.
2) диаметр не разрезал угол на два угла, тогда у нас появляется ещё два новых вписанных угла \(\angle ABD, \angle CBD\), у которых сторона содержит диаметр, следовательно, для них теорема верна, тогда верна и для исходного угла (который равен разности этих двух углов, значит, равен полуразности дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 2.
Следствия
1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
2. Вписанный угол, опирающийся на полуокружность, прямой.
3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
\[{\Large{\text{Касательная к окружности}}}\]
Определения
Существует три типа взаимного расположения прямой и окружности:
1) прямая \(a\) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние \(d\) от центра окружности до прямой меньше радиуса \(R\) окружности (рис. 3).
2) прямая \(b\) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка \(B\) – точкой касания. В этом случае \(d=R\) (рис. 4).
3) прямая \(c\) не имеет общих точек с окружностью (рис. 5).
Теорема
1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.
Следствие
Отрезки касательных, проведенных из одной точки к окружности, равны.
Доказательство
Проведем к окружности из точки \(K\) две касательные \(KA\) и \(KB\):
Значит, \(OA\perp KA, OB\perp KB\) как радиусы. Прямоугольные треугольники \(\triangle KAO\) и \(\triangle KBO\) равны по катету и гипотенузе, следовательно, \(KA=KB\).
Следствие
Центр окружности \(O\) лежит на биссектрисе угла \(AKB\), образованного двумя касательными, проведенными из одной точки \(K\).
\[{\Large{\text{Теоремы, связанные с углами}}}\]
Теорема об угле между секущими
Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.
Доказательство
Пусть \(M\) – точка, из которой проведены две секущие как показано на рисунке:
Покажем, что \(\angle DMB = \dfrac{1}{2}(\buildrel\smile\over{BD} —
\buildrel\smile\over{CA})\). \circ — \alpha =
\frac12\cdot\buildrel\smile\over{AB}\).
\circ — \alpha =
\frac12\cdot\buildrel\smile\over{AB}\).
Теорема о дугах, стягиваемых равными хордами
Равные хорды стягивают равные дуги, меньшие полуокружности.
И наоборот: равные дуги стягиваются равными хордами.
Доказательство
1) Пусть \(AB=CD\). Докажем, что меньшие полуокружности дуги \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\).
\(\triangle AOB=\triangle COD\) по трем сторонам, следовательно, \(\angle AOB=\angle COD\). Но т.к. \(\angle AOB, \angle COD\) — центральные углы, опирающиеся на дуги \(\buildrel\smile\over{AB}, \buildrel\smile\over{CD}\) соответственно, то \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\).
2) Если \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\), то \(\triangle AOB=\triangle COD\) по двум сторонам \(AO=BO=CO=DO\) и углу между ними \(\angle AOB=\angle COD\). Следовательно, и \(AB=CD\).
Теорема
Если радиус делит хорду пополам, то он ей перпендикулярен.
Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.
Доказательство
1) Пусть \(AN=NB\). Докажем, что \(OQ\perp AB\).
Рассмотрим \(\triangle AOB\): он равнобедренный, т.к. \(OA=OB\) – радиусы окружности. Т.к. \(ON\) – медиана, проведенная к основанию, то она также является и высотой, следовательно, \(ON\perp AB\).
2) Пусть \(OQ\perp AB\). Докажем, что \(AN=NB\).
Аналогично \(\triangle AOB\) – равнобедренный, \(ON\) – высота, следовательно, \(ON\) – медиана. Следовательно, \(AN=NB\).
\[{\Large{\text{Теоремы, связанные с длинами отрезков}}}\]
Теорема о произведении отрезков хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Доказательство
Пусть хорды \(AB\) и \(CD\) пересекаются в точке \(E\).
Рассмотрим треугольники \(ADE\) и \(CBE\). 2\).
2\).
Следствие
Произведение секущей, проведённой из точки \(O\), на её внешнюю часть не зависит от выбора секущей, проведённой из точки \(O\):
Что такое единичная окружность в тригонометрии: определение, связь, понятие
ОпределениеЕдиничная окружность — это окружность с радиусом, равным единице, и центром в начале прямоугольной декартовой системы координат.
Уравнения для задания единичной окружности: x2+y2=1
Понятие единичной окружности непосредственно связано с тригонометрией. Угол поворота можно рассматривать, как движение по окружности. При этом величина угла поворота не зависит от радиуса окружности, что делает использование единичной окружности при математических описаниях очень удобным.
Через координаты точек на единичной окружности дается определение основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Обосновываются их свойства и выводятся основные формулы тригонометрии.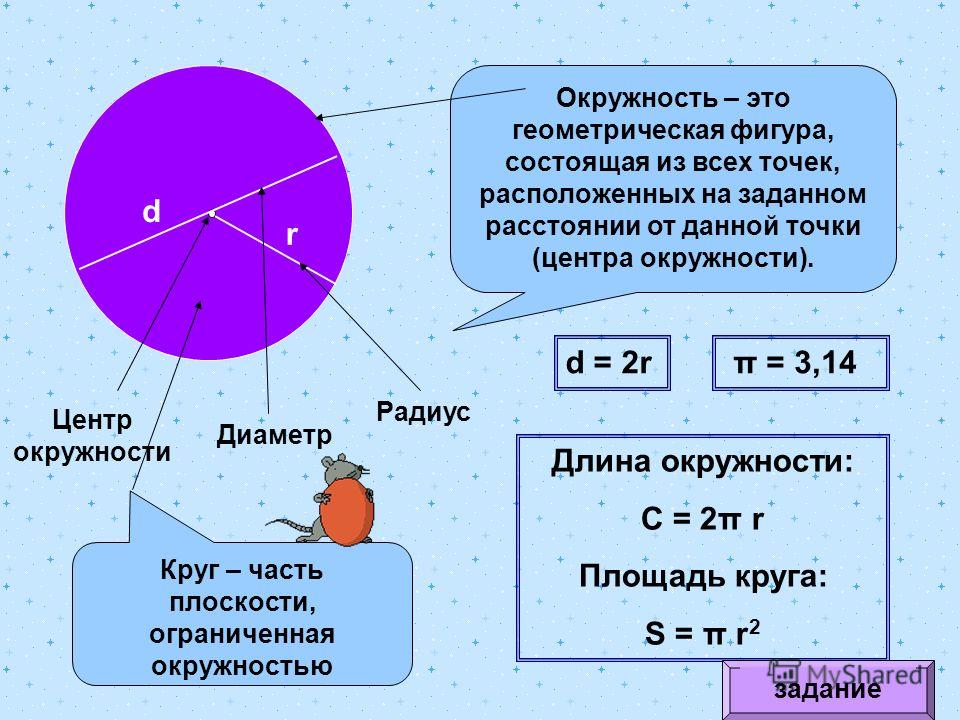
С использованием уравнения единичной окружности и определения синуса и косинуса может быть записано основное тригонометрическое тождество: sin2x+cos2x=1.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Навигация по статьям
Предыдущая статья
Тригонометрия
Следующая статья
Основные тригонометрические формулы
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Градусы и радианы
- Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
- Нахождение значений синуса, косинуса, тангенса и котангенса
- Основные тригонометрические тождества
- Все темы по математике
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Узнать подробнее
ПЛАСТИНЧАТЫЙ ТЕПЛООБМЕННИК В Компас А Бумага теплообменник кожухотрубчатый
Вид работы:
Чертёж
Выполнена:
27 июня 2022 г.

Стоимость:
2 400 руб
Заказать такую же работу
Математические модели инфодемии
Заказать такую же работу
Нужно рассчитать теплообменник
Вид работы:
Контрольная работа
Выполнена:
28 апреля 2022 г.

Стоимость:
3 600 руб
Заказать такую же работу
Задания прикреплены
Вид работы:
Контрольная работа
Выполнена:
21 января 2022 г.

Стоимость:
1 400 руб
Заказать такую же работу
Особенности исторической застройки Красноярска от появления острога до конца века
Вид работы:
Реферат
Выполнена:
27 декабря 2021 г.

Стоимость:
1 000 руб
Заказать такую же работу
по Строительным материалам
Вид работы:
Решение задач
Выполнена:
30 ноября 2021 г.

Стоимость:
1 100 руб
Заказать такую же работу
Смотреть все работы по чертежам в компас
Что такое центр окружности определение. Что такое окружность как геометрическая фигура: основные свойства и характеристики
Разбираемся в том что такое окружность и круг. Формула площади круга и длины окружности.
Мы каждый день встречаем множество предметов, по форме которые образовывают круг или напротив окружность.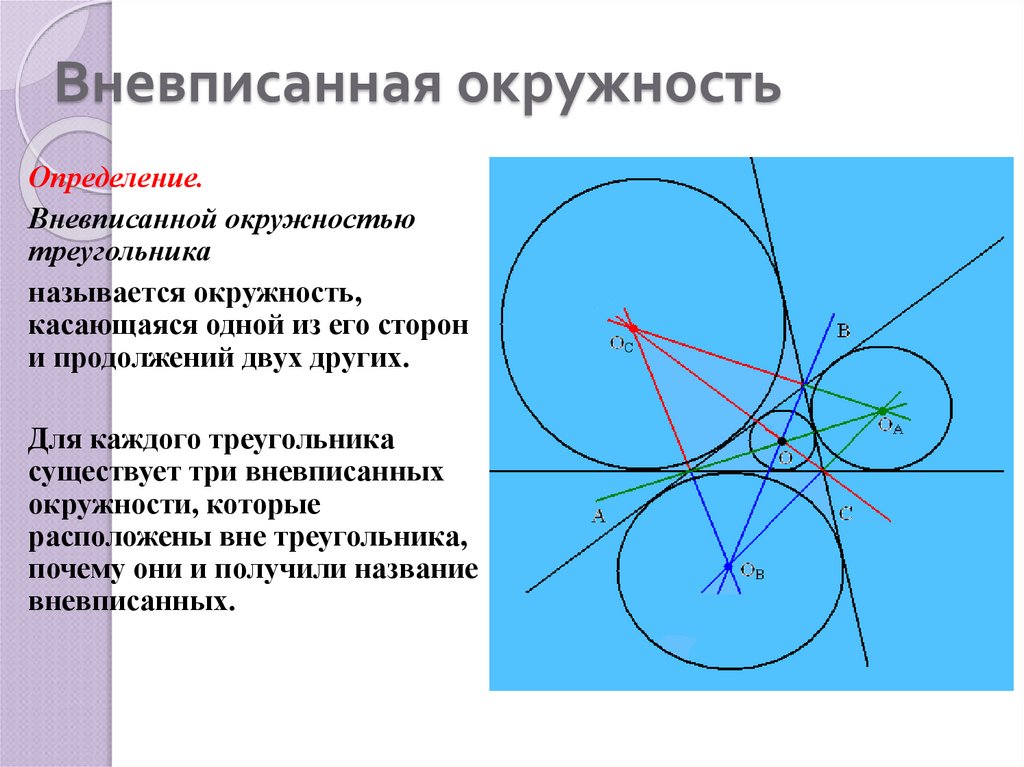 Иногда возникает вопрос, что такое окружность и чем она отличается от круга. Конечно же, мы все проходили уроки геометрии, но иногда не помешает освежить знания весьма простыми объяснениями.
Иногда возникает вопрос, что такое окружность и чем она отличается от круга. Конечно же, мы все проходили уроки геометрии, но иногда не помешает освежить знания весьма простыми объяснениями.
Что такое длина окружности и площадь круга: определение
Итак, окружность является замкнутой кривой линией, которая ограничивает или же напротив, образует круг. Обязательное условие окружности — у нее есть центр и все точки равноудалены от него. Проще говоря, окружность это гимнастический обруч (или как его часто называют хула-хуп) на плоской поверхности.
Длина окружности это общая длина той самой кривой, которая образует окружность. Как известно вне зависимости от размеров окружности соотношение ее диаметра и длины равно числу π = 3,141592653589793238462643.
Из этого следует, что π=L/D, где L — длина окружности, а D — диаметр окружности.
Если Вам известен диаметр, то длину можно найти по простой формуле: L= π* D
В случае если известен радиус: L=2 πR
Мы разобрались, что такое окружность и можем перейти к определению круга.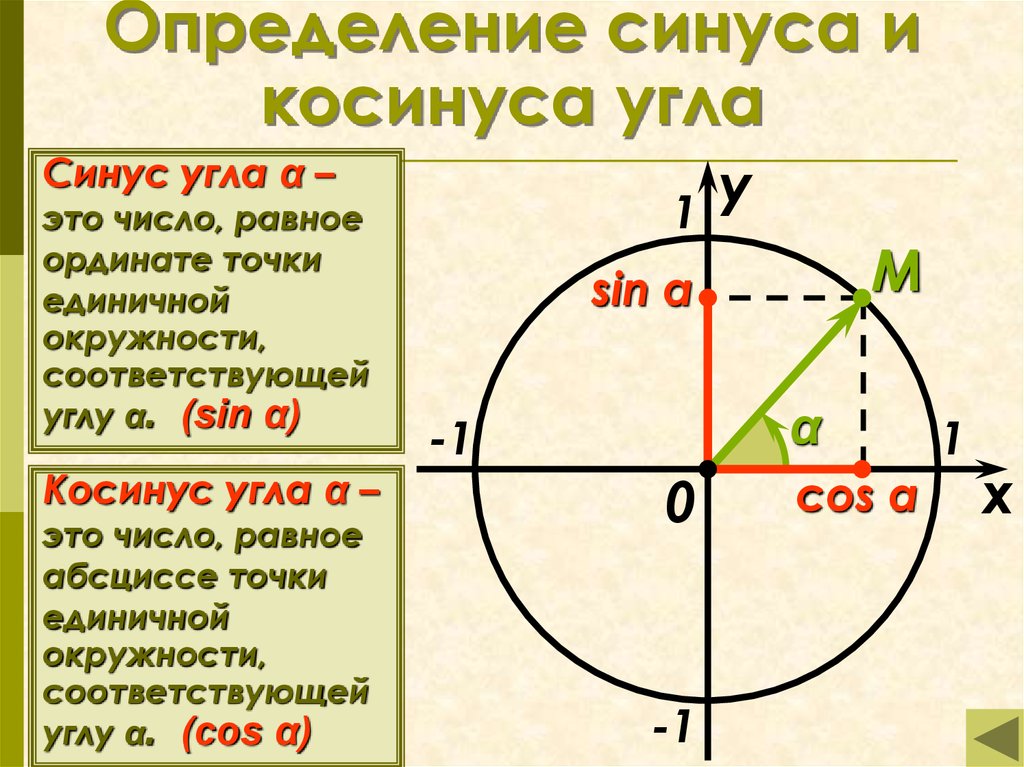
Круг — это геометрическая фигура, которая окружена окружностью. Или же, круг это фигура, рубеж которой состоит из большого количества точек равноудаленных от центра фигуры. Вся площадь, которая находится внутри окружности, включая ее центр, называется кругом.
Стоит заметить, что у окружности и круга, который находится в ней значения радиуса и диаметра одинаковые. А диаметр в свою очередь в два раза больше чем радиус.
Круг имеет площадь на плоскости, которую можно узнать при помощи простой формулы:
Где S — площадь круга, а R — радиус данного круга.
Чем круг отличается от окружности: объяснение
Основное отличие между кругом и окружностью — это то, что круг — геометрическая фигура, а окружность — замкнутая кривая. Также обратите внимание на отличия между окружностью и кругом:
- Окружность это замкнутая линия, а круг — площадь внутри этой окружности;
- Окружность это кривая линия на плоскости, а круг — пространство, сомкнутое в кольцо окружностью;
- Сходство между окружностью и кругом: радиус и диаметр;
- У круга и окружности единый центр;
- В случае если заштриховывается пространство внутри окружности, оно превращается в круг;
- У окружности есть длина, но ее нет у круга, и наоборот, у круга есть площадь, которой нет у окружности.

Круг и окружность: примеры, фото
Для наглядности предлагаем рассмотреть фото, на котором слева изображен круг, а справа окружность.
Формула длины окружности и площади круга: сравнение
Формула длины окружности L=2 πR
Формула площади круга S= πR²
Обратите внимание, что в обеих формулах присутствует радиус и число π. Данные формулы рекомендуется выучить наизусть, так как они простейшие и обязательно пригодятся в повседневной жизни и на работе.
Площадь круга по длине окружности: формула
S=π(L/2π)=L²/4π, где S — площадь круга, L — длина окружности.
Видео: Что такое круг, окружность и радиус
И круг — геометрические фигуры, взаимосвязанные между собой. есть граничная ломаная линия (кривая) круга ,
Определение. Окружность — замкнутая кривая, каждая точка которой равноудалена от точки, называемой центром окружности.
Для построения окружности выбирается произвольная точка О, принятая за центр окружности, и с помощью циркуля проводится замкнутая линия.
Если точку О центра окружности соединить с произвольными точками на окружности, то все полученные отрезки будут между собой равны, и называются такие отрезки радиусами, сокращенно обозначаются латинской маленькой или большой буквой «эр» (r или R ). Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, называется диаметром. Диаметр состоит из двух радиусов , лежащих на одной прямой. Диаметр обозначается латинской маленькой или большой буквой «дэ» (d или D ).
Правило. Диаметр окружности равен двум ее радиусам .
d = 2r
D = 2R
Длина окружности вычисляется по формуле и зависит от радиуса (диаметра) окружности. В формуле присутствует число ¶, которое показывает во сколько раз длина окружности больше, чем ее диаметр. Число ¶ имеет бесконечное число знаков после запятой. Для вычислений принято ¶ = 3,14.
Длина окружности обозначается латинской большой буквой «цэ» (C ). Длина окружности пропорциональна ее диаметру. Формулы для расчета длины окружности по ее радиусу и диаметру:
C = ¶d
C = 2¶r
- Примеры
- Дано: d = 100 см.
- Длина окружности: C = 3,14 * 100 см = 314 см
- Дано: d = 25 мм.
- Длина окружности: С = 2 * 3,14 * 25 = 157 мм
Секущая окружности и дуга окружности
Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.
Дуги окружности делятся секущей на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.
Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.
Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше — большей дуги окружности, а отрезок секущей, называемый хордой , уменьшается по мере удаления секущей от центра окружности.
Определение. Кругом называется часть плоскости, лежащая внутри окружности.
Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.
Так как круг — это часть плоскости, то одним из его параметров является площадь.
Правило. Площадь круга (S ) равна произведению квадрата радиуса (r 2 ) на число ¶.
- Примеры
- Дано: r = 100 см
- Площадь круга:
- S = 3,14 * 100 см * 100 см = 31 400 см 2 ≈ 3м 2
- Дано: d = 50 мм
- Площадь круга:
- S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм 2 ≈ 20 см 2
Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами . Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности .
Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности .
Окружность — геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Данная точка (O) называется центром окружности .
Радиус окружности — это отрезок, соединяющий центр с какой-либо точкой окружности. Все радиусы имеют одну и ту же длину (по определению).
Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром . Центр окружности является серединой любого диаметра.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности . Дуга называется полуокружностью , если отрезок, соединяющий её концы, является диаметром.
Длина единичной полуокружности обозначается через π .
Сумма градусных мер двух дуг окружности с общими концами равна 360º .
Часть плоскости, ограниченная окружностью, называется кругом .
Круговой сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Дуга, которая ограничивает сектор, называется дугой сектора .
Две окружности, имеющие общий центр, называются концентрическими .
Две окружности, пересекающиеся под прямым углом, называются ортогональными .
Взаимное расположение прямой и окружности
- Если расстояние от центра окружности до прямой меньше радиуса окружности (d), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.
- Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку. Такая прямая называется касательной к окружности , а их общая точка называется точкой касания прямой и окружности .
- Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .
Центральные и вписанные углы
Центральный угол — это угол с вершиной в центре окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Вписанный угол измеряется половиной дуги, на которую он опирается.
- Следствие 1.
Вписанные углы, опирающиеся на одну и ту же дугу, равны. - Следствие 2.
Вписанный угол, опирающийся на полуокружность — прямой.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Основные формулы
- Длина окружности:
C = 2∙π∙R
- Длина дуги окружности:
R = С/(2∙π) = D/2
- Диаметр:
D = C/π = 2∙R
- Длина дуги окружности:
l = (π∙R) / 180∙α ,
где α — градусная мера длины дуги окружности)
- Площадь круга:
S = π∙R 2
- Площадь кругового сектора:
S = ((π∙R 2) / 360)∙α
Уравнение окружности
- В прямоугольной системе координат уравнение окружности радиуса r с центром в точке C (x о;y о) имеет вид:
(x — x о) 2 + (y — y о) 2 = r 2
- Уравнение окружности радиуса r с центром в начале координат имеет вид:
x 2 + y 2 = r 2
Чтобы в общих чертах представить себе, что такое окружность, взгляните на кольцо или обруч. Можно также взять круглый стакан и чашку, поставить вверх дном на лист бумаги и обвести карандашом. При многократном увеличении полученная линия станет толстой и не совсем ровной, и края ее будут размытыми. Окружность как геометрическая фигура не имеет такой характеристики, как толщина.
Можно также взять круглый стакан и чашку, поставить вверх дном на лист бумаги и обвести карандашом. При многократном увеличении полученная линия станет толстой и не совсем ровной, и края ее будут размытыми. Окружность как геометрическая фигура не имеет такой характеристики, как толщина.
Окружность: определение и основные средства описания
Окружность — это замкнутая кривая, состоящая из множества точек, расположенных в одной плоскости и равноудаленных от центра окружности. При этом центр находится в той же плоскости. Как правило, он обозначается буквой О.
Расстояние от любой из точек окружности до центра называется радиусом и обозначается буквой R.
Если соединить две любые точки окружности, то полученный отрезок будет называться хордой. Хорда, проходящая через центр окружности, — это диаметр, обозначаемый буквой D. Диаметр делит окружность на две равные дуги и по длине вдвое превышает размер радиуса. Таким образом, D = 2R, или R = D/2.
Свойства хорд
- Если через две любые точки окружности провести хорду, а затем перпендикулярно последней — радиус или диаметр, то этот отрезок разобьет и хорду, и дугу, отсеченную ею, на две равные части.
 Верно и обратное утверждение: если радиус (диаметр) делит хорду пополам, то он перпендикулярен ей.
Верно и обратное утверждение: если радиус (диаметр) делит хорду пополам, то он перпендикулярен ей. - Если в пределах одной и той же окружности провести две параллельные хорды, то дуги, отсеченные ними, а также заключенные между ними, будут равны.
- Проведем две хорды PR и QS, пересекающиеся в пределах окружности в точке T. Произведение отрезков одной хорды всегда будет равно произведению отрезков другой хорды, то есть PT х TR = QT х TS.
Длина окружности: общее понятие и основные формулы
Одной из базовых характеристик данной геометрической фигуры является длина окружности. Формула выводится с использованием таких величин, как радиус, диаметр и константа «π», отражающая постоянство отношения длины окружности к ее диаметру.
Таким образом, L = πD, или L = 2πR, где L — это длина окружности, D — диаметр, R — радиус.
Формула длины окружности может рассматриваться как исходная при нахождении радиуса или диаметра по заданной длине окружности: D = L/π, R = L/2π.
Что такое окружность: основные постулаты
- не иметь общих точек;
- иметь одну общую точку, при этом прямая называется касательной: если провести радиус через центр и точку касания, то он будет перпендикулярен касательной;
- иметь две общие точки, при этом прямая называется секущей.
2. Через три произвольные точки, лежащие в одной плоскости, можно провести не более одной окружности.
3. Две окружности могут соприкасаться только в одной точке, которая расположена на отрезке, соединяющем центры этих окружностей.
4. При любых поворотах относительно центра окружность переходит сама в себя.
5. Что такое окружность с точки зрения симметрии?
- одинаковая кривизна линии в любой из точек;
- относительно точки О;
- зеркальная симметрия относительно диаметра.
6. Если построить два произвольных вписанных угла, опирающихся на одну и ту же дугу окружности, они будут равны. Угол, опирающийся на дугу, равную половине то есть отсеченную хордой-диаметром, всегда равен 90°.
7. Если сравнивать замкнутые кривые линии одинаковой длины, то получится, что окружность отграничивает участок плоскости наибольшей площади.
Окружность, вписанная в треугольник и описанная около него
Представление о том, что такое окружность, будет неполным без описания особенностей взаимосвязи этой с треугольниками.
- При построении окружности, вписанной в треугольник, ее центр всегда будет совпадать с точкой пересечения треугольника.
- Центр окружности, описанной около треугольника, располагается на пересечении срединных перпендикуляров к каждой из сторон треугольника.
- Если описать окружность около то ее центр будет находиться на середине гипотенузы, то есть последняя будет являться диаметром.
- Центры вписанной и описанной окружностей будут находиться в одной точке, если базой для построения является
Основные утверждения об окружности и четырехугольниках
- Вокруг выпуклого четырехугольника можно описать окружность лишь тогда, когда сумма его противоположных внутренних углов равняется 180°.

- Построить вписанную в выпуклый четырехугольник окружность можно, если одинакова сумма длин его противоположных сторон.
- Описать окружность вокруг параллелограмма можно, если его углы прямые.
- Вписать в параллелограмм окружность можно в том случае, если все его стороны равны, то есть он является ромбом.
- Построить окружность через углы трапеции можно, только если она равнобедренная. При этом центр описанной окружности будет располагаться на пересечении четырехугольника и срединного перпендикуляра, проведенного к боковой стороне.
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности. {\circ}}
{\circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей .
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {\circ}
{\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr ,
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p} ,
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника . {\circ}
{\circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
Что такое окружность? : Геометрия
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».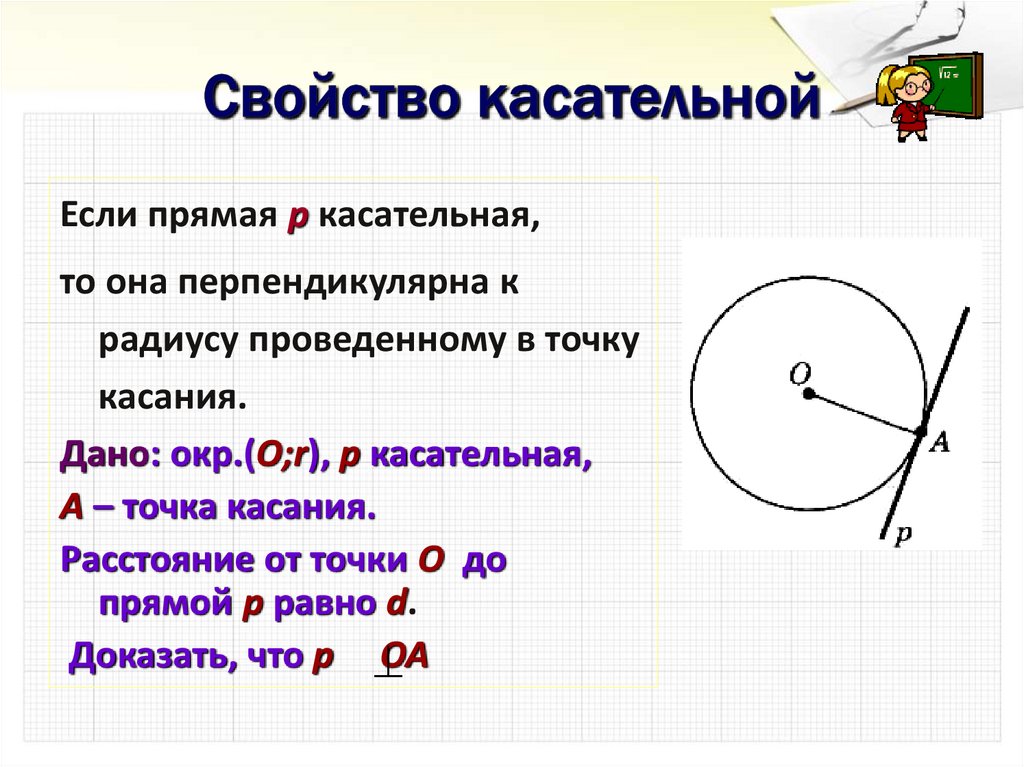
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| AlgolHater |
| ||
17/02/08 |
| ||
| |||
| enko |
| ||
19/08/07 |
| ||
| |||
| Профессор Снэйп |
| |||
18/12/07 |
| |||
| ||||
| Бабай |
| ||
29/12/05 |
| ||
| |||
| незваный гость |
| |||
17/10/05 |
| |||
| ||||
| Бабай |
| ||
29/12/05 |
| ||
| |||
| Gordmit |
| |||
19/06/05 |
| |||
| ||||
| AlgolHater |
| ||
17/02/08 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 8 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Определение по окружности.
 Что такое окружность как геометрическая фигура: основные свойства и характеристики
Что такое окружность как геометрическая фигура: основные свойства и характеристикиОкружность — геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Данная точка (O) называется центром окружности .
Радиус окружности — это отрезок, соединяющий центр с какой-либо точкой окружности. Все радиусы имеют одну и ту же длину (по определению).
Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром . Центр окружности является серединой любого диаметра.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности . Дуга называется полуокружностью , если отрезок, соединяющий её концы, является диаметром.
Длина единичной полуокружности обозначается через π .
Сумма градусных мер двух дуг окружности с общими концами равна 360º .
Часть плоскости, ограниченная окружностью, называется кругом .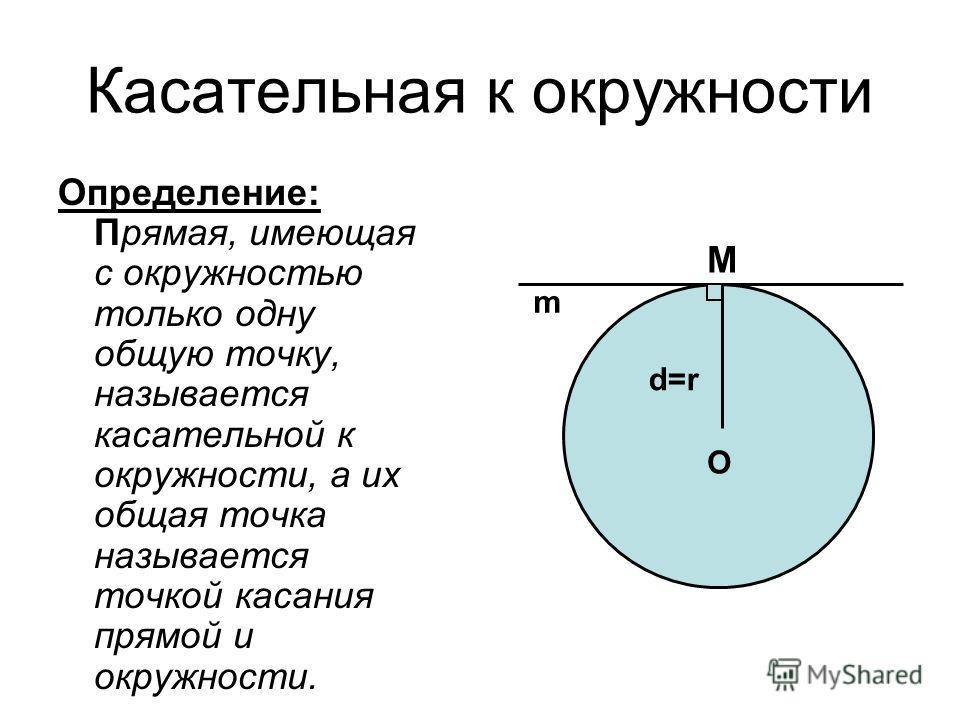
Круговой сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Дуга, которая ограничивает сектор, называется дугой сектора .
Две окружности, имеющие общий центр, называются концентрическими .
Две окружности, пересекающиеся под прямым углом, называются ортогональными .
Взаимное расположение прямой и окружности
- Если расстояние от центра окружности до прямой меньше радиуса окружности (d), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.
- Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку. Такая прямая называется касательной к окружности , а их общая точка называется точкой касания прямой и окружности .
- Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .

Центральные и вписанные углы
Центральный угол — это угол с вершиной в центре окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Вписанный угол измеряется половиной дуги, на которую он опирается.
- Следствие 1.
Вписанные углы, опирающиеся на одну и ту же дугу, равны. - Следствие 2.
Вписанный угол, опирающийся на полуокружность — прямой.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Основные формулы
- Длина окружности:
C = 2∙π∙R
- Длина дуги окружности:
R = С/(2∙π) = D/2
- Диаметр:
D = C/π = 2∙R
- Длина дуги окружности:
l = (π∙R) / 180∙α ,
где α — градусная мера длины дуги окружности)
- Площадь круга:
S = π∙R 2
- Площадь кругового сектора:
S = ((π∙R 2) / 360)∙α
Уравнение окружности
- В прямоугольной системе координат уравнение окружности радиуса r с центром в точке C (x о;y о) имеет вид:
(x — x о) 2 + (y — y о) 2 = r 2
- Уравнение окружности радиуса r с центром в начале координат имеет вид:
x 2 + y 2 = r 2
Сначала разберемся в отличии между кругом и окружностью.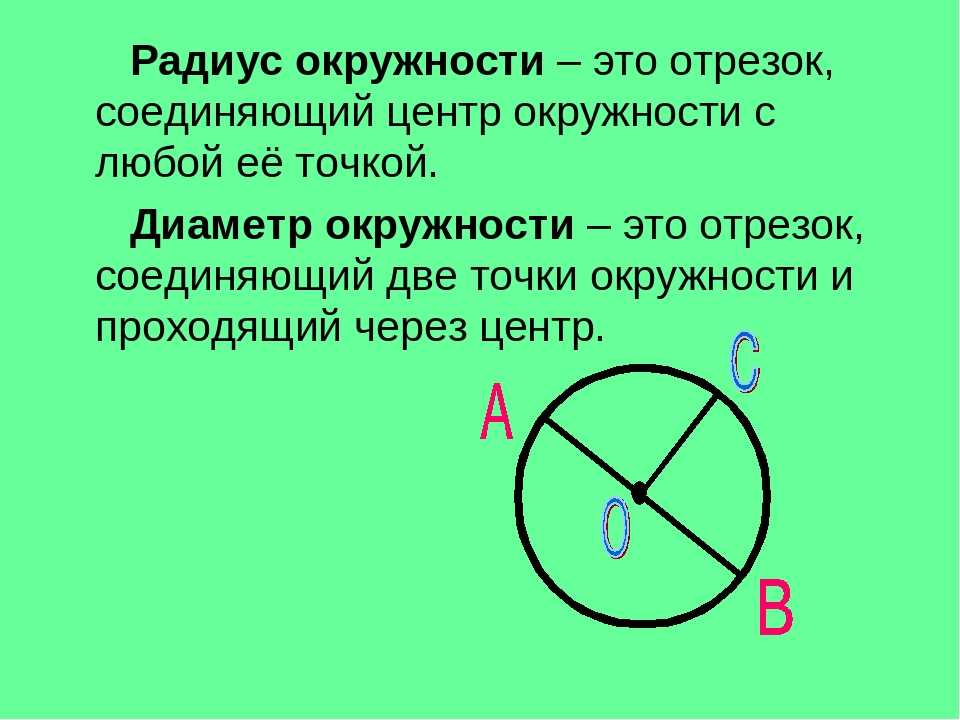 {\circ}}
{\circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей .
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть.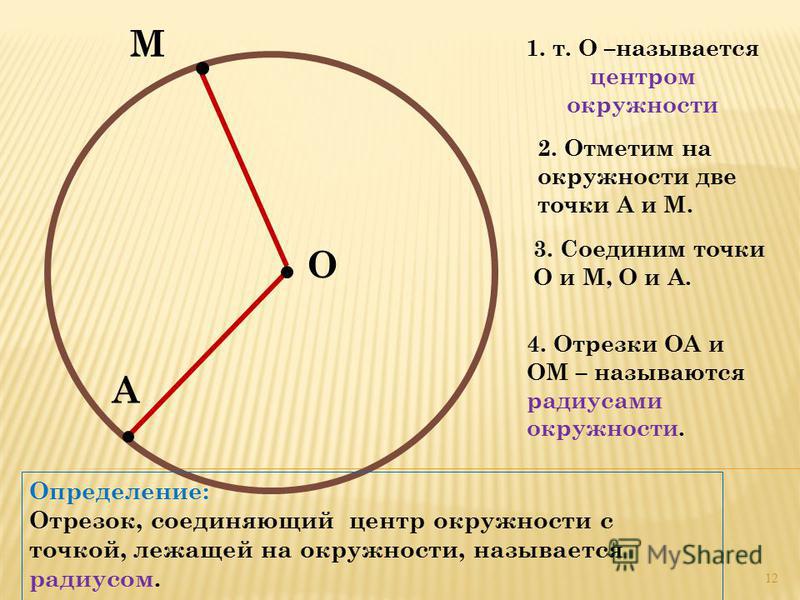 {\circ}
{\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr ,
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p} ,
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника .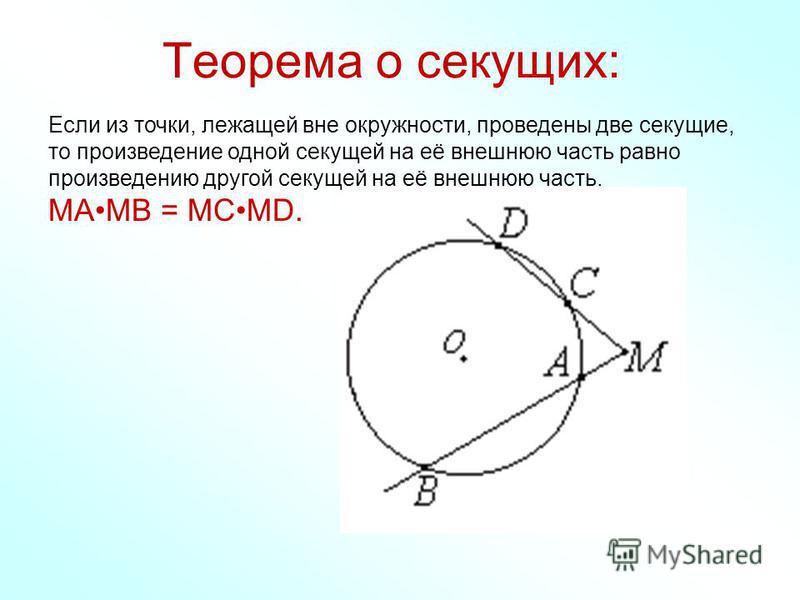 {\circ}
{\circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
Разбираемся в том что такое окружность и круг. Формула площади круга и длины окружности.
Мы каждый день встречаем множество предметов, по форме которые образовывают круг или напротив окружность. Иногда возникает вопрос, что такое окружность и чем она отличается от круга. Конечно же, мы все проходили уроки геометрии, но иногда не помешает освежить знания весьма простыми объяснениями.
Конечно же, мы все проходили уроки геометрии, но иногда не помешает освежить знания весьма простыми объяснениями.
Что такое длина окружности и площадь круга: определение
Итак, окружность является замкнутой кривой линией, которая ограничивает или же напротив, образует круг. Обязательное условие окружности — у нее есть центр и все точки равноудалены от него. Проще говоря, окружность это гимнастический обруч (или как его часто называют хула-хуп) на плоской поверхности.
Длина окружности это общая длина той самой кривой, которая образует окружность. Как известно вне зависимости от размеров окружности соотношение ее диаметра и длины равно числу π = 3,141592653589793238462643.
Из этого следует, что π=L/D, где L — длина окружности, а D — диаметр окружности.
Если Вам известен диаметр, то длину можно найти по простой формуле: L= π* D
В случае если известен радиус: L=2 πR
Мы разобрались, что такое окружность и можем перейти к определению круга.
Круг — это геометрическая фигура, которая окружена окружностью.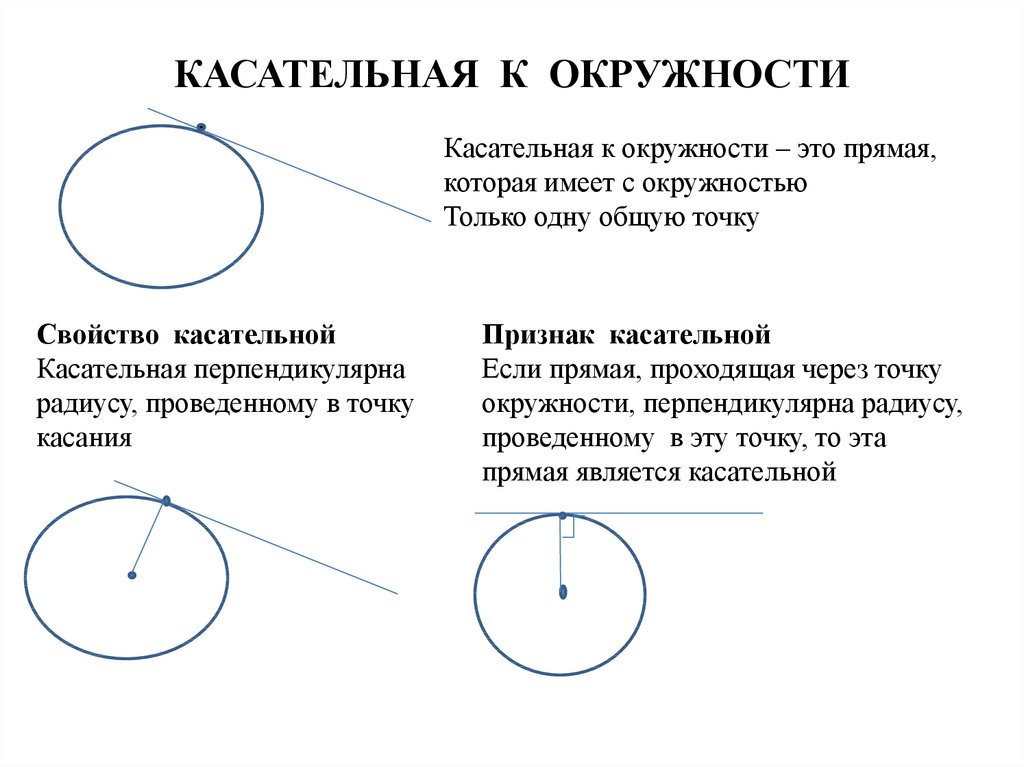 Или же, круг это фигура, рубеж которой состоит из большого количества точек равноудаленных от центра фигуры. Вся площадь, которая находится внутри окружности, включая ее центр, называется кругом.
Или же, круг это фигура, рубеж которой состоит из большого количества точек равноудаленных от центра фигуры. Вся площадь, которая находится внутри окружности, включая ее центр, называется кругом.
Стоит заметить, что у окружности и круга, который находится в ней значения радиуса и диаметра одинаковые. А диаметр в свою очередь в два раза больше чем радиус.
Круг имеет площадь на плоскости, которую можно узнать при помощи простой формулы:
Где S — площадь круга, а R — радиус данного круга.
Чем круг отличается от окружности: объяснение
Основное отличие между кругом и окружностью — это то, что круг — геометрическая фигура, а окружность — замкнутая кривая. Также обратите внимание на отличия между окружностью и кругом:
- Окружность это замкнутая линия, а круг — площадь внутри этой окружности;
- Окружность это кривая линия на плоскости, а круг — пространство, сомкнутое в кольцо окружностью;
- Сходство между окружностью и кругом: радиус и диаметр;
- У круга и окружности единый центр;
- В случае если заштриховывается пространство внутри окружности, оно превращается в круг;
- У окружности есть длина, но ее нет у круга, и наоборот, у круга есть площадь, которой нет у окружности.

Круг и окружность: примеры, фото
Для наглядности предлагаем рассмотреть фото, на котором слева изображен круг, а справа окружность.
Формула длины окружности и площади круга: сравнение
Формула длины окружности L=2 πR
Формула площади круга S= πR²
Обратите внимание, что в обеих формулах присутствует радиус и число π. Данные формулы рекомендуется выучить наизусть, так как они простейшие и обязательно пригодятся в повседневной жизни и на работе.
Площадь круга по длине окружности: формула
S=π(L/2π)=L²/4π, где S — площадь круга, L — длина окружности.
Видео: Что такое круг, окружность и радиус
Чтобы в общих чертах представить себе, что такое окружность, взгляните на кольцо или обруч. Можно также взять круглый стакан и чашку, поставить вверх дном на лист бумаги и обвести карандашом. При многократном увеличении полученная линия станет толстой и не совсем ровной, и края ее будут размытыми. Окружность как геометрическая фигура не имеет такой характеристики, как толщина.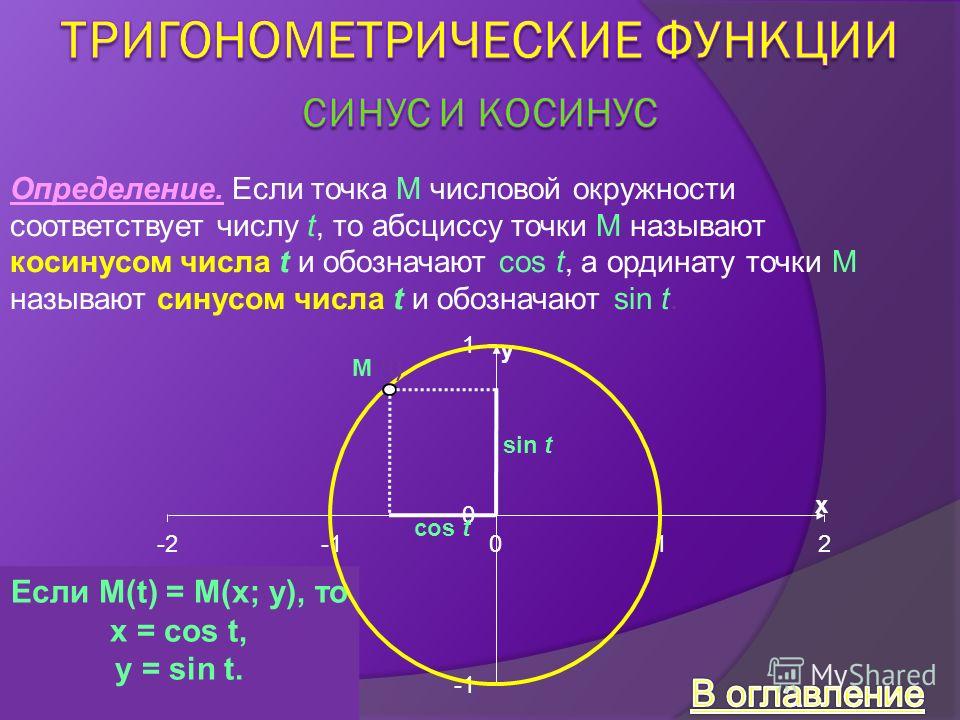
Окружность: определение и основные средства описания
Окружность — это замкнутая кривая, состоящая из множества точек, расположенных в одной плоскости и равноудаленных от центра окружности. При этом центр находится в той же плоскости. Как правило, он обозначается буквой О.
Расстояние от любой из точек окружности до центра называется радиусом и обозначается буквой R.
Если соединить две любые точки окружности, то полученный отрезок будет называться хордой. Хорда, проходящая через центр окружности, — это диаметр, обозначаемый буквой D. Диаметр делит окружность на две равные дуги и по длине вдвое превышает размер радиуса. Таким образом, D = 2R, или R = D/2.
Свойства хорд
- Если через две любые точки окружности провести хорду, а затем перпендикулярно последней — радиус или диаметр, то этот отрезок разобьет и хорду, и дугу, отсеченную ею, на две равные части. Верно и обратное утверждение: если радиус (диаметр) делит хорду пополам, то он перпендикулярен ей.

- Если в пределах одной и той же окружности провести две параллельные хорды, то дуги, отсеченные ними, а также заключенные между ними, будут равны.
- Проведем две хорды PR и QS, пересекающиеся в пределах окружности в точке T. Произведение отрезков одной хорды всегда будет равно произведению отрезков другой хорды, то есть PT х TR = QT х TS.
Длина окружности: общее понятие и основные формулы
Одной из базовых характеристик данной геометрической фигуры является длина окружности. Формула выводится с использованием таких величин, как радиус, диаметр и константа «π», отражающая постоянство отношения длины окружности к ее диаметру.
Таким образом, L = πD, или L = 2πR, где L — это длина окружности, D — диаметр, R — радиус.
Формула длины окружности может рассматриваться как исходная при нахождении радиуса или диаметра по заданной длине окружности: D = L/π, R = L/2π.
Что такое окружность: основные постулаты
- не иметь общих точек;
- иметь одну общую точку, при этом прямая называется касательной: если провести радиус через центр и точку касания, то он будет перпендикулярен касательной;
- иметь две общие точки, при этом прямая называется секущей.

2. Через три произвольные точки, лежащие в одной плоскости, можно провести не более одной окружности.
3. Две окружности могут соприкасаться только в одной точке, которая расположена на отрезке, соединяющем центры этих окружностей.
4. При любых поворотах относительно центра окружность переходит сама в себя.
5. Что такое окружность с точки зрения симметрии?
- одинаковая кривизна линии в любой из точек;
- относительно точки О;
- зеркальная симметрия относительно диаметра.
6. Если построить два произвольных вписанных угла, опирающихся на одну и ту же дугу окружности, они будут равны. Угол, опирающийся на дугу, равную половине то есть отсеченную хордой-диаметром, всегда равен 90°.
7. Если сравнивать замкнутые кривые линии одинаковой длины, то получится, что окружность отграничивает участок плоскости наибольшей площади.
Окружность, вписанная в треугольник и описанная около него
Представление о том, что такое окружность, будет неполным без описания особенностей взаимосвязи этой с треугольниками.
- При построении окружности, вписанной в треугольник, ее центр всегда будет совпадать с точкой пересечения треугольника.
- Центр окружности, описанной около треугольника, располагается на пересечении срединных перпендикуляров к каждой из сторон треугольника.
- Если описать окружность около то ее центр будет находиться на середине гипотенузы, то есть последняя будет являться диаметром.
- Центры вписанной и описанной окружностей будут находиться в одной точке, если базой для построения является
Основные утверждения об окружности и четырехугольниках
- Вокруг выпуклого четырехугольника можно описать окружность лишь тогда, когда сумма его противоположных внутренних углов равняется 180°.
- Построить вписанную в выпуклый четырехугольник окружность можно, если одинакова сумма длин его противоположных сторон.
- Описать окружность вокруг параллелограмма можно, если его углы прямые.
- Вписать в параллелограмм окружность можно в том случае, если все его стороны равны, то есть он является ромбом.

- Построить окружность через углы трапеции можно, только если она равнобедренная. При этом центр описанной окружности будет располагаться на пересечении четырехугольника и срединного перпендикуляра, проведенного к боковой стороне.
Окружность и её элементы. Знакомство с понятиями. 2-й класс
УМК: «Начальная школа XXI века».
Цели урока:
- Образовательная: создать условия для формирования представления об окружности и круге, как о геометрических фигурах и познакомить с их элементами, развивать практическое умение – пользоваться циркулем.
- Развивающая: создать условия для развития творческой деятельности, речи и мыслительных операций: обобщение, анализ, сравнение.
- Воспитательные: создать условия для воспитания трудолюбия, самостоятельности, активности, способности к познанию.
Оборудование: геометрические фигуры (квадрат, куб, шар, круг), модель круга (на каждого ученика), учебник для 2 класса В. Н. Рудницкой «Математика» 1 часть, рабочая тетрадь, циркуль, линейка, картинка с изображением Карандаша (человечка), альбомные листы с изображением окружностей, карточки.
Н. Рудницкой «Математика» 1 часть, рабочая тетрадь, циркуль, линейка, картинка с изображением Карандаша (человечка), альбомные листы с изображением окружностей, карточки.
Ход урока
I. Организация классаII. Актуализация знаний«Долгожданный дан звонок,
Начинается урок.
Тут затеи и задачи,
Игры, шутки, всё для вас!
Пожелаю всем удачи —
За работу, в добрый час!»
Игра. На столе разложены различные геометрические фигуры (накрыты платком).
— Найдите на ощупь: квадрат, куб, шар, круг.
— Чем отличаются? (учитель держит в руках и показывает шар и круг).
III. Сообщение темы урока— Сегодня на уроке, мы с вами отправимся в удивительную страну геометрию, где познакомимся с новой геометрической фигурой и её элементами.
IV. Работа по теме урока1. Знакомство с понятием «окружность».
— Найдите на столе у каждого из вас круг. Возьмите его в руки. Обведите пальчиком границу круга так же как я.
— Может быть, кто-нибудь из вас знает, как называется граница круга? (выслушав ответы детей, учитель вывешивает карточку на доску).
— Прочитайте слово: по слогам, с ударением. Закройте глаза, представьте это слово и ещё раз проговорите его по слогам.
— Какие буквы в этом слове похожи на окружность? («О»). А что вы можете рассказать об этих буквах? (Это безударные гласные, которые нужно запомнить.)
— А теперь возьмите круг, положите его на страницу тетради и обведите шаблон по его границе.
— Уберите шаблон. Посмотрите, у вас получилась окружность. Но для того, что бы построить окружность, не обязательно каждый раз пользоваться шаблоном.
2. Построение окружности с помощью циркуля.
а) — Для построения окружности существует специальный инструмент.
— Послушайте загадку:
«Сговорились две ноги
Делать дуги и круги».Это …… (циркуль).
Учитель вывешивает карточку на доску и показывает инструмент.
— Обратите внимание на гласную, которая пишется после буквы «Ц». Кто может объяснить?
— Какое слово спряталось в слове «циркуль»? («цирк»).
— Слово «цирк» в переводе с латинского языка означает «круг».
— Как вы думаете, почему значение слова связано с кругом? Вспомните, как выглядит арена. (Она круглая, как-будто её построили с помощью циркуля).
б) — У циркуля есть 2 ножки: одна — с остриём, другая — с грифелем.
С циркулем нужно работать очень осторожно. Назовите правила пользования циркулем (нельзя подносить к лицу и глазам, нельзя передавать циркуль соседу иглой вперёд, нельзя им играть, циркуль должен находиться в специальном футляре).
— А теперь посмотрите, как работают с этим инструментом (показ учителя): «Разведу ножки на небольшое расстояние: ножку с остриём ставлю на бумагу, а ножка с грифелем касается бумаги. Аккуратно поворачиваем циркуль вокруг своей оси, при этом сохраняя расстояние между ножками, и получаем окружность. Если расстояние изменится — окружность не получится».
Аккуратно поворачиваем циркуль вокруг своей оси, при этом сохраняя расстояние между ножками, и получаем окружность. Если расстояние изменится — окружность не получится».
в) — Начертите окружность в тетрадях так же как я. (самостоятельная работа детей, помощь учителя), но сначала повторим порядок работы.
г) Обобщение:
— Что вы начертили? (окружность). Как вы думаете, почему её так назвали?
— Окружность — линия, которая идёт по границе круга.
— Посмотрите на свои фигуры. Чем круг отличается от окружности? (показать).
— Круг — это окружность вместе с внутренней областью, ограниченной этой окружностью; его можно погладить. Погладьте. Окружность — это только граница круга (проведите пальчиком по линии), внутри пустая. Круг и окружность как брат и сестра. Они всегда вместе! Нарисовали окружность — возник круг, вырезали круг — ножницы обозначили окружность.
Физминутка.
— А теперь отдохнём, встаньте!- Начертите окружность:
- левой рукой в воздухе;
- правой ногой на полу;
- на спине у соседа;
- носом на потолке.

— Садитесь! Продолжаем работать дальше!
3. Работа по учебнику.
— Откройте учебник на странице 88, найдите №6.
Рассмотрите: как изображаются на плоскости круг и окружность. Сравните. В чём сходство и различие?
— А какие предметы в учебнике на странице 87 в №1 являются окружностью? (Обруч, огненное кольцо, оправа от очков). Назовите предметы, которые имеют форму круга. (Стекло от очков, леденец, солнышко). Приведите свои примеры.
— Ребята, к нам на урок пришёл гость — весёлый Карандаш и принёс с собой замечательную песенку про круг и окружность (вывешивается картинка с изображением Карандаша).
— Послушайте её (учитель поёт):
4. Элементы окружности«У круга есть одна подруга
Знакома всем её наружность.
Она идёт по краю круга
И называется ….. » (окружность).
— Дома вы можете сочинить свою песенку про круг и окружность.
— А сейчас Карандашик просит вас помочь ему выполнить некоторые задания:
а) — Как и любая фигура, окружность тоже имеет свой центр.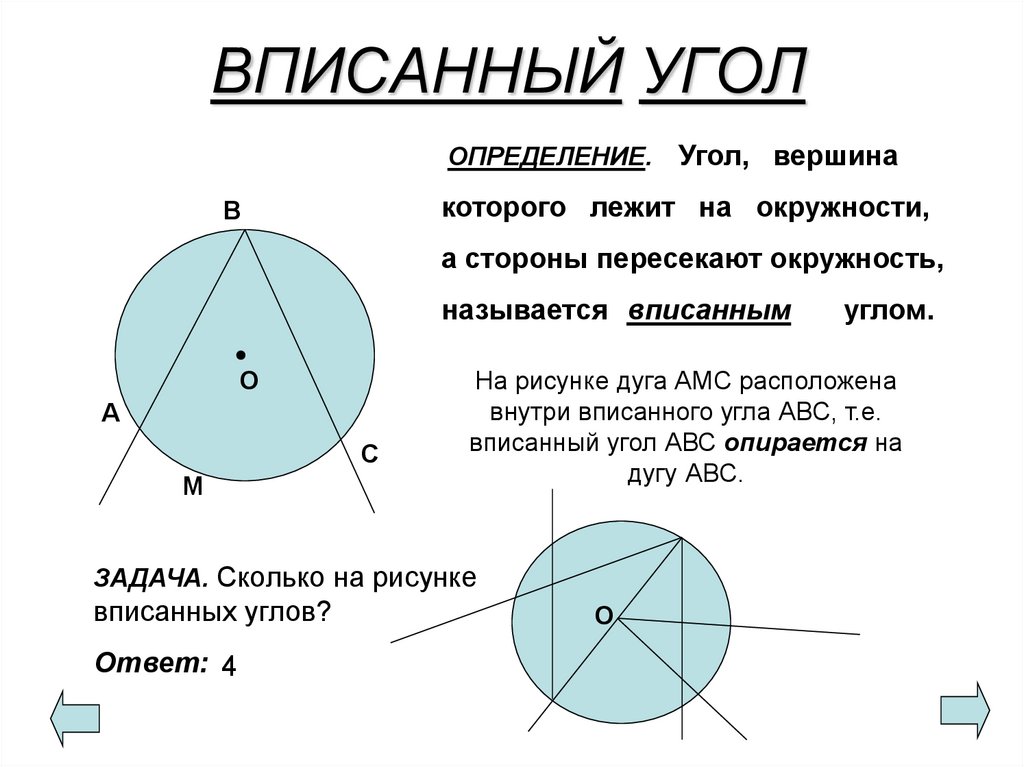 Помогите найти её Карандашу.
Помогите найти её Карандашу.
— Как вы думаете, где она будет находиться? (Найдите у себя прокол от острой ножки циркуля — это и есть центр окружности).
— Отметьте его точкой и обозначьте латинской буквой «O».
б) — На странице 87 учебника, на чертеже найдите центр окружности.
— А какой ещё элемент окружности вы видите на чертеже? Прочитайте!
— Карандашик просит вас помочь ему построить радиус окружности.
— Как же это сделать?
в) — Отметим на окружности точку в любом месте. Я здесь, а вы можете поставить точку в другом месте (показать), но обязательно на окружности и обозначим её латинской буквой «А». (Учитель и дети работают одновременно).
— Соедините точку «А» с центром окружности (по линейке, цветным карандашом).
— Какая получилась фигура? (отрезок ОА).
— Отрезок ОА и есть радиус.
— Радиус — это расстояние от центра окружности до любой точки, лежащей на окружности.
— А можно ещё провести радиус? Кто сможет, попробуйте? (2 ученика у доски).
— Как можно узнать длину радиуса? (с помощью линейки и циркуля).
— Как вы думаете, радиусы, которые мы построили будут одинаковыми или разными? Докажите! (измерьте с помощью линейки или циркуля).
г) — А ведь знаете, в математике есть ещё одно определение окружности.
— Представьте себе, что вы бы отметили множество точек, которые находятся на одинаковом расстоянии от центра, и когда их соединили между собой, то, что получилось тогда? (окружность).
— Вот вы и сами дали второе определение окружности: окружность — это множество точек, которые находятся на одинаковом расстоянии от центра окружности.
5. Рефлексия— А теперь подведём итог урока, то есть выясним: какие же открытия вы совершили сегодня для себя на уроке? (высказываются дети).
— Ребята, а полученные знания вам в жизни пригодятся? Где?
— Итак, что такое окружность? (2 определения: Окружность — это граница круга, замкнутая кривая линия. Окружность — это множество точек, находящихся на одинаковом расстоянии от центра окружности).
— Как называется этот элемент окружности? (учитель показывает на центр окружности)
— Как называется расстояние от центра окружности до любой точки, лежащей на окружности? (радиус)
6. Творческое задание– Вы сегодня отлично поработали на уроке, узнали много нового. Молодцы!
А теперь Карандашик предлагает вам немного отдохнуть и выполнить творческое задание.
а) – Посмотрите, что изображено у каждого из вас на альбомном листе? (окружность)
— Проявив свою фантазию, дорисуйте окружности так, чтобы получились разные предметы. А для этого вам пригодятся знания, полученные на уроках «Окружающего мира» и «Технологии».
— А может быть, кто-нибудь из вас захочет использовать в своей работе не окружность, а круг.
— Что же тогда нужно сделать? Как превратить окружность в круг? (закрасить).
— Итак, приступаем к работе. А интересные работы вы продемонстрируете нашему Карандашику в конце урока. (Включить музыку).
б) Просмотр интересных работ детей и учителя (эмблема олимпийского флага – на основе окружности и дорожный знак «Движение пешеходов запрещено» — на основе круга).
- Дома потренироваться в построении окружности с помощью циркуля и нахождении её элементов: центра и радиуса (всем учащимся обязательно).
- Сочинить песенку или стихотворение про круг и окружность (по желанию учащихся).
Окружность Определение и значение | Dictionary.com
- Верхние определения
- Синонимы
- Викторина
- Связанный контент
- Примеры
- British
- Scientific
- Cultural
Это показывает уровень класса, основанный на сложности слова.
[ ser-kuhm-fer-uhns ]
/ sərˈkʌm fər əns /
Сохранить это слово!
См. синонимы к слову окружность на Thesaurus.com
синонимы к слову окружность на Thesaurus.com
Показывает уровень обучения в зависимости от сложности слова.
сущ.
внешняя граница, особенно круглой области; периметр: длина окружности.
длина такой границы: окружность в одну милю.
область внутри ограничивающей линии: обширная окружность его разума.
ДРУГИЕ СЛОВА ДЛЯ окружности
1 периферия, контур.
См. синонимы к слову окружность на Thesaurus.com
ТЕСТ
Сыграем ли мы «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?
Следует ли вам пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!
Вопрос 1 из 6
Какая форма используется для указания обязательства или обязанности кого-либо?
Начало окружности
1350–1400; Среднеанглийское <позднелатинское окружность, эквивалентное окружности- + fer- (основа от ferre для переноски) + -entia-ence
СЛОВА, КОТОРЫЕ МОГУТ СПУТАТЬСЯ С окружностью
окружность , диаметр, радиус, касательнаяСлова рядом с окружностью
обрезание, обрезание, обрезание, околостолбцовый, обрезание, окружность, окружность, окружность волокнистого хряща, окружность пластинки, окружность, циркумфикс
Dictionary. com Unabridged
Основано на словаре Random House Unabridged Dictionary, © Random House, Inc., 2022
com Unabridged
Основано на словаре Random House Unabridged Dictionary, © Random House, Inc., 2022
Слова, относящиеся к окружности
обхват, амбит, граница, граница, границы, контур, компас, границы, оконечность, бахрома, пределы, губа, край, контур , периферия, ободок, грань
Как использовать окружность в предложении
Эта шапка будет расти вместе с вашими детьми, подходит для размера окружности от 7 до 12 дюймов.
Лучшие зимние шапки: удобные шапки, которые согреют вас|Carsen Joenk|20 января 2021 г.|Popular-Science
Вместо этого, помимо измерения окружности талии, ваш лечащий врач отметит клинические маркеры, указывающие на висцеральные ожирение, говорит Джей.
Некоторые тренеры рекламируют ВИИТ как лучший способ сжечь жир на животе. Вот что говорит наука.|Пэм Мур|15 декабря 2020 г.|Washington Post
Прицельная дальность — это расстояние, на котором вы можете надежно поместить выстрел в пределах круга, который соответствует размеру жизненно важных органов животного — примерно окружности бумажной тарелки для оленя или лося.

Руководство по охоте для начинающих|Ян Форман|30 октября 2020 г.|Outside Online
Каждый ремешок поставляется с двумя разными длинами для более длинной стороны, чтобы соответствовать запястьям с окружностью от 5 до 8 дюймов.
Аксессуары для умных часов, которые можно подарить вашим высокотехнологичным друзьям и родным|Команда PopSci Commerce|1 октября 2020 г.|Popular-Science
Для пейзажных снимков установите камеру в экранный режим, чтобы вас не ослеплял видоискатель, и снимайте прямо на солнце и вокруг него.
11 замечательных микроприключений, которые вы можете совершить прямо сейчас|Редакция|1 октября 2020 г.|Внешний Интернет
Остальное, что выходит за пределы окружности мяса, быстро тает на поверхности плоской поверхности.
Настоящий чизбургерный рай|Джейн и Майкл Стерн|22 июня 2014 г.|DAILY BEAST
Пи официально определяется как отношение длины окружности к ее диаметру.

17 фактов, чтобы разгадать тайну числа Пи|Эбби Хэглейдж|14 марта 2013 г.|DAILY BEAST
Трасса составляет около полутора миль в окружности, а «прямая» – около пяти фарлонгов в длину.
Бирмингемский словарь Шоуэлла | Томас Т. Харман и Уолтер Шоуэлл
Их ветви описывают круг более восьмидесяти футов в окружности, но они больше не приносят плодов.
Кругосветное путешествие женщины|Ида Пфайффер
Высота скалы достигает двухсот пятидесяти футов, а ее окружность составляет около мили.
Британские автомагистрали и переулки от автомобиля|Томас Д. Мерфи
Его окружность не очень велика, но почти одинакова на всем протяжении, что придает ему вид башни.
Кругосветное путешествие женщины|Ида Пфайффер
По окружности ствола расположены зубья шестерни, и эти зубья входят в зацепление с соответствующими зубьями на оси центра.
The Wonder Book of Knowledge|Various
British Dictionary definitions for circumference
circumference
/ (səˈkʌmfərəns) /
noun
the boundary of a specific area or geometric figure, esp of a circle
длина замкнутой геометрической кривой, особенно окружности. Длина окружности равна диаметру, умноженному на π
Длина окружности равна диаметру, умноженному на π
Производные формы окружности
окружность (səˌkʌmfəˈrɛnʃəl), прилагательное окружность, наречиеПроисхождение слова для окружности
C14: от старофранцузского circonference, от латинского окружность — носить, от окружности + ferre — медведь
Английский словарь Коллинза — полное и полное цифровое издание 2012 г. © William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Научные определения окружности
окружность
[ sər-kŭm′fər-əns ]
0020 Граничная линия круга.Граничная линия фигуры, области или объекта.
Длина такой границы. Длина окружности вычисляется путем умножения диаметра на число Пи.
Научный словарь American Heritage® Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Культурные определения окружности
окружность
[ (suhr-kum-fuhr-uhns) ]
Мера расстояния по окружности.
Новый словарь культурной грамотности, третье издание Авторское право © 2005 г., издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены. Определение
в кембриджском словаре английского языка
Примеры окружности
Окружность
Исследователи обнаружили, что бедро окружность и рост были тесно связаны с жировыми отложениями.
Из ВРЕМЕНИ
Работа по внутренним линиям похожа на работу по радиусам внутри круга; работа по внешним линиям похожа на работу по окружности круга .
От внешней политики
Однако многие из этих деревьев снабжены металлическими идентификационными бирками и дендрометрами — металлическими полосами, используемыми для измерения окружности деревьев .
Из NPR
Уравнение для окружности круга 2pr.
Из NPR
В настоящее время его длина составляет 41,42 фута в окружность , 8,06 фута в диаметре и 10,83 фута в высоту и содержит более 8 000 000 футов шпагата.
Из Атлантики
Теоретически, если вы пройдете все окружностей вселенной, вы окажетесь именно там, где начали.
От Business Insider
Затем эта газовая смесь взрывается, при этом взрыв вращается по окружности со сверхзвуковой скоростью.
От Арс Техника
Как отношение между 90 213 окружностью 90 214 и диаметром круга, число Пи печально известно своей непознаваемостью.
От Хаффингтон Пост
Окружность шеи 9По его словам, 0214 может дать более точное представление о составе жира в организме.
От CNN
Окружность его туловища составляет 18 футов.
С NJ.com
Окружность , размер большого пальца его отца, свидетельствовала о тяжелом остром недоедании.
Из Лос-Анджелес Таймс
Это более 5 миль в поперечнике, для окружность 17 миль.
Из проводного
Итак, вот расчет — имейте в виду, что длина окружности составляла 30 локтей, а диаметр — 10.
От Хаффингтон Пост
Обратите внимание, что отношение между окружностью и диаметром равно 3.
От Гизмодо
Альтернативным способом было бы построить примерно круглые балки, чтобы сформировать окружность купола.
Из National Geographic
Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Перевод окружности
на китайский (традиционный)
圓周, 周長, 周線…
Подробнее
на китайском (упрощенном)
圆周, 周长, 周线…
Подробнее
на испанском языке
circunferencia, circunferencia [женский род]…
Узнать больше
на португальском
circunferência, circunferência [женский род]…
Увидеть больше
на других языкахна японском языке
на турецком
на французском
в каталонском языке
на арабском языке
в чешском
на датском
на индонезийском
в Thai
In Vietnamese
в Thai
In Vietnamese
в Thai
In Vietnamese
. 0021
0021
на малайском
на немецком
на норвежском
на корейском
на украинском
на итальянском
на русском
円周…
Узнать больше
daire çevresi, çember, çevresel uzunluk…
Подробнее
circonférence [женский], circonférence… Увидеть больше
окружность…
Узнать больше
مُحيط الدائرة…
Узнать больше
обвод…
Подробнее
омкредс…
Подробнее
keliling, lingkaran…
Увидеть больше
เส้นรอบวง…
Узнать больше
чу ви…
Узнать больше
obwód…
Увидеть больше
лилитан…
Узнать больше
der Umfang…
Увидеть больше
омкреты [мужского рода], омкреты, периферийные…
Узнать больше
원주…
Узнать больше
коло…
Подробнее
circonferenza…
Подробнее
окружность…
Увидеть больше
Нужен переводчик?
Получите быстрый бесплатный перевод!
Как произносится окружность ?
Обзор
обрезанный
обрезание
обрезание
круговорот
окружность
круговой
циркумфлекс
многословие
многословный
Проверьте свой словарный запас с помощью наших веселых викторин по картинкам
- {{randomImageQuizHook.
 copyright1}}
copyright1}} - {{randomImageQuizHook.copyright2}}
Авторы изображений
Попробуйте пройти викторину сейчас
Слово дня
оптимистичный
надежда или вера в то, что в будущем произойдут хорошие вещи
Об этом
Блог
Нестандартное мышление: говорим о творчестве.
Подробнее
Новые слова
тихий уход
Другие новые слова
Окружность — Формула, Примеры | Окружность круга
Окружность круга — это периметр круга. Это общая длина границы круга. Длина окружности есть произведение постоянной π на диаметр окружности. Человеку, идущему по круглому парку или окаймленному круглому столу, требуется эта метрика окружности круга. Длина окружности является линейной величиной, и ее единицы измерения такие же, как единицы длины.
Длина окружности есть произведение постоянной π на диаметр окружности. Человеку, идущему по круглому парку или окаймленному круглому столу, требуется эта метрика окружности круга. Длина окружности является линейной величиной, и ее единицы измерения такие же, как единицы длины.
Окружность — это круглая замкнутая фигура , все ее граничные точки равноудалены от фиксированной точки, называемой центром. Двумя важными показателями круга являются площадь круга и длина окружности. Здесь мы будем стремиться к пониманию формулы и вычислению длины окружности.
| 1. | Что такое длина окружности? |
| 2. | Длина окружности Формула |
| 3. | Как найти длину окружности? |
| 4. | Окружность к диаметру |
| 5. | Часто задаваемые вопросы Длина окружности? |
Что такое длина окружности?
Окружность окружности – это ее граница или длина полной дуги окружности. Давайте разберемся с этой концепцией на примере. Рассмотрим круговой парк, показанный ниже.
Давайте разберемся с этой концепцией на примере. Рассмотрим круговой парк, показанный ниже.
Если мальчик начинает бежать из точки «А» и достигает той же точки, пройдя один полный круг по парку, он преодолевает расстояние. Это расстояние или граница называется окружностью парка, который имеет форму круга. Окружность — это длина границы.
Окружность круга Определение
Окружность круга относится к размеру его границы. Если мы откроем круг и измерим границу точно так же, как измеряем прямую линию, мы получим длину окружности в единицах длины, таких как сантиметры, метры или километры.
Теперь давайте узнаем об элементах, из которых состоит окружность. Это три самых важных элемента круга.
- Центр: Центром окружности называется точка, находящаяся на фиксированном расстоянии от любой другой точки окружности.
- Диаметр: Диаметр — это расстояние по окружности через центр, это линия, которая пересекает окружность с обоих концов и должна проходить через центр.

- Радиус: Радиус круга — это расстояние от центра круга до любой точки на окружности круга.
Длина окружности Формула
Формула длины окружности выражается с использованием радиуса окружности r и значения числа пи. Это выражается как: Длина окружности по формуле = 2πr. При использовании этой формулы окружности, если у нас нет значения радиуса, мы можем найти его, используя диаметр. То есть, если диаметр известен, его можно разделить на 2, чтобы получить значение радиуса, потому что диаметр круга = 2 × радиус. Другой способ рассчитать длину окружности — использовать формулу: длина окружности = π × диаметр. Если нам нужно вычислить радиус или диаметр, когда дана длина окружности, мы используем формулу: Радиус = Длина окружности/2π
Как найти длину окружности?
Хотя длина окружности равна длине ее границы, ее нельзя вычислить с помощью линейки (шкалы), как это обычно делают для других многоугольников. Это потому, что круг — это изогнутая фигура. Следовательно, чтобы вычислить длину окружности, мы применяем формулу, которая использует радиус или диаметр круга и значение Пи (π).
Это потому, что круг — это изогнутая фигура. Следовательно, чтобы вычислить длину окружности, мы применяем формулу, которая использует радиус или диаметр круга и значение Пи (π).
Пи — это специальная математическая константа, значение которой приблизительно равно 3,14159 или π = 22/7. Значение π = 22/7 используется в различных формулах. Это отношение длины окружности к диаметру, где C = πD. Рассмотрим практическую иллюстрацию, чтобы понять, как вычислить длину окружности с помощью формулы длины окружности.
Пример: Если радиус окружности равен 25 единицам, найдите длину окружности. (Возьмем π = 3,14)
Решение: Дано, радиус = 25 единиц
Напишем формулу окружности, а затем подставим в нее значение r (радиуса).
Формула длины окружности = 2πr
С = 2 × π × 25
С = 2 × 3,14 × 25 = 157 единиц
Следовательно, длина окружности равна 157 единицам.
Окружность к диаметру
Отношение длины окружности к диаметру круга используется для определения стандартного определения числа Пи (π). Если вы знаете диаметр ‘d’ круга, то вы можете легко найти длину окружности C, используя соотношение: C = πd. Итак, если окружность C поставить в отношении к диаметру d, мы получим ответ π.
Важные примечания относительно длины окружности
- π(Pi) — математическая константа, представляющая собой отношение длины окружности к ее диаметру. Оно приближается к π = 22/7 или 3,14 .
- Если радиус круга увеличивается дальше и касается границы круга, он становится диаметром круга. Следовательно, Диаметр = 2 × Радиус
- Окружность — это расстояние по окружности или длина окружности.
- Мы можем найти длину окружности, используя радиус или диаметр.
- Формула длины окружности = π× Диаметр; Окружность = 2πr.
☛ Статьи по теме
- Окружность Земли
- Окружность кругов Рабочие листы
- Калькулятор отношения диаметра к окружности
- Калькулятор окружности
Длина окружности Примеры
Пример 1: Если радиус круга равен 28 см, найдите длину окружности.

Решение:
Дано, Радиус круга = 28 см. Чтобы найти длину окружности, воспользуемся формулой длины окружности: 2πr = 2×22/7×28 = 176 см.
Следовательно, длина окружности равна 176 см.Пример 2: Окружность колеса 440 см. Найдите его радиус и диаметр.
Решение:
Учитывая, Окружность колеса = 440 см
Формула длины окружности = 2πr
Подставим известные значения, чтобы сначала найти радиус.
440 = 2πr
440 = 2 × (22/7) × г
радиус = 70 см
Диаметр = 2 × радиус
Диаметр = 2 × 70
Следовательно, радиус равен 70 см, а диаметр 140 см.Пример 3: Периметр прямоугольного провода равен 264 м. Та же проволока сгибается в форме круга. Найдите радиус окружности, образованной по формуле длины окружности.
Решение:
Мы знаем, что периметр прямоугольника = Общая длина используемой проволоки = Длина окружности образовавшегося круга.

Следовательно, длина окружности образовавшегося круга = 264 м
Формула длины окружности = 2πr
Длина окружности = 264Подставим известные значения, чтобы найти радиус.
264 = 2πr
264 = 2 × (22/7) × г
Следовательно, радиус окружности равен 42 м.
перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Забронировать бесплатный пробный урок
Практические вопросы по окружности круга
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об окружности окружности
Что такое длина окружности в геометрии?
Окружность окружности является мерой границы или длины полной дуги окружности. Длина окружности равна произведению π (пи) на диаметр окружности. Длина окружности — это линейная величина, имеющая одинаковые единицы длины.
Длина окружности — это линейная величина, имеющая одинаковые единицы длины.
Как найти длину окружности?
Длина окружности рассчитывается с помощью формулы длины окружности, для которой требуется значение радиуса окружности и значение π (пи). Окружность круга = 2πr, где «r» — радиус круга, а π (пи) — специальная математическая константа со значением, приблизительно равным 3,14159 или π = 22/7.
Как найти диаметр по длине окружности?
Если нам нужно рассчитать диаметр, когда дана длина окружности, мы используем формулу: Длина окружности = π × диаметр или Диаметр = длина окружности/π
Как найти длину окружности по площади?
Длину окружности можно рассчитать, если известна площадь круга. По формуле площади круга можно вычислить радиус. Зная радиус, можно вычислить длину окружности. Площадь круга = πr 2 , \(радиус = \sqrt{\frac{A}{\pi}}\), и C = 2πr = 2\(\pi\sqrt{\frac{A}{\pi }}\).
Какова единица длины окружности?
Окружность круга представляет собой одномерную линейную величину, а единица длины окружности выражается в метрах, дюймах, сантиметрах, футах и т. д. Длина окружности связана с другими линейными величинами, такими как радиус и диаметр окружности.
д. Длина окружности связана с другими линейными величинами, такими как радиус и диаметр окружности.
Что такое периметр круга?
Периметр круга равен длине окружности. Это общая длина внешней границы круга. Периметр или длина окружности — это произведение константы «пи» и диаметра окружности. Он выражается в линейных единицах, таких как м, дюйм, см, фут.
Каково число Пи?
Пи — постоянная величина, используемая для измерения площади и длины окружности круга или других круглых фигур. Символом числа пи является π, а его числовое значение равно 22/7 или 3,14. Кроме того, эти числовые значения используются в зависимости от контекста уравнения.
В чем разница между диаметром и длиной окружности?
Диаметр окружности — это самая длинная хорда, проходящая через центр окружности. Длина окружности – это длина внешней границы окружности. И диаметр, и длина окружности являются длинами и выражаются в линейных единицах. Длина окружности равна произведению диаметра на константу π (пи).
Как найти длину окружности по диаметру?
Длину окружности можно рассчитать, если диаметр известен, поскольку соотношение между длиной окружности и диаметром окружности выражается как Длина окружности = π × Диаметр или диаметр = Длина окружности/π.
Скачать БЕСПЛАТНЫЕ учебные материалы
Circles Worksheet
ОКРУЖНОСТЬ Синонимы: 21 Синонимов и антонимов к ОКРУЖНОСТЬ
См. определение окружность на Dictionary.com
- 3 существительное0214 edge, perimeter
synonyms for circumference
- girth
- ambit
- border
- boundary
- bounds
- circuit
- compass
- confines
- extremity
- fringe
- limits
- край
- край
- контур
- периферия
- край
- край
антонимы к слову окружность
НАИБОЛЕЕ ВАЖНЫЕ
- центр
- внутри
- интерьер
- середина
Тезаурус 21-го века Roget, третье издание Copyright © 2013 by the Philip Lief Group.
ПОПРОБУЙТЕ ИСПОЛЬЗОВАТЬ окружность
Посмотрите, как выглядит ваше предложение с разными синонимами.
Символы: 0/140
ВИКТОРИНА
Расслабьтесь в шезлонге и примите участие в викторине «Слово дня»!
НАЧАТЬ ВИКТОРИНУКак использовать окружность в предложении
Эта шапка будет расти вместе с вашими детьми, подходит для размера окружности от 7 до 12 дюймов.
ЛУЧШИЕ ЗИМНИЕ ШАПКИ: УДОБНЫЕ ШАПКИ, КОТОРЫЕ СОХРАНЯЮТ ВАМ ТЕПЛОКАРСЕН ДЖОЕНК 20 ЯНВАРЯ 2021 г.POPULAR-SCIENCE
Вместо этого, помимо измерения окружности талии, ваш лечащий врач отметит клинические маркеры, указывающие на висцеральное ожирение, говорит Джей.
НЕКОТОРЫЕ ТРЕНЕРЫ РЕКОМЕНДУЮТ ТРЕНИРОВКИ КАК ЛУЧШИЙ СПОСОБ СЖИГАТЬ ЖИР НА ЖИВОТЕ. ВОТ ЧТО ГОВОРИТ НАУКА. ПЭМ МУРЕД 15 ДЕКАБРЯ 2020 г.0021
Прицельная дальность — это расстояние, на котором вы можете надежно поместить выстрел в пределах круга, который соответствует размеру жизненно важных органов животного — примерно окружности бумажной тарелки для оленя или лося.
РУКОВОДСТВО ПО ОХОТНИЧЕСТВУ ДЛЯ НАЧИНАЮЩИХ 30 ОКТЯБРЯ 2020 Г. ВНЕШНИЙ ОНЛАЙН
Каждый ремешок имеет две длины: более длинная сторона подходит для запястий с окружностью от 5 до 8 дюймов.
АКСЕССУАРЫ ДЛЯ СМАРТ-ЧАСОВ, ЧТОБЫ ПОДАРИТЬ ДРУЗЬЯМ И БЛИЗКИМ КОМАНДУ POPSCI COMMERCE 1 ОКТЯБРЯ 2020 г.POPULAR-SCIENCE
Для пейзажной съемки установите камеру в экранный режим, чтобы вас не ослеплял видоискатель, и снимайте прямо на солнце и вокруг него.
11 БОЛЬШИХ МИКРОПРИКЛЮЧЕНИЙ, КОТОРЫЕ ВЫ МОЖЕТЕ СОВЕРШИТЬ СЕЙЧАСРЕДАКТОРЫ 1 ОКТЯБРЯ 2020 Г. ВНЕ ОНЛАЙН
Трасса составляет около полутора миль в окружности, а «прямая» — около пяти фарлонгов в длину.
СЛОВАРЬ ШОУЭЛА БИРМИНГЕМТОМАСА Т. ХАРМАНА И УОЛТЕРА ШОУЭЛЛА
Их ветви описывают круг более восьмидесяти футов в окружности, но они больше не приносят плодов.
ЖЕНСКОЕ ПУТЕШЕСТВИЕ ВОКРУГ СВЕТА
Скала возвышается на двести пятьдесят футов, а ее окружность составляет около мили.
БРИТАНСКИЕ ШОССЕ И ДОРОГИ ОТ МОТОРА КАРТОМАС Д. МЕРФИ
Его окружность не очень велика, но почти одинакова на всем протяжении, что придает ему вид башни.
ЖЕНСКОЕ ПУТЕШЕСТВИЕ ВОКРУГ СВЕТА PFEIFFER
По окружности ствола расположены зубья шестерни, и эти зубья входят в зацепление с соответствующими зубьями на оправке центра.
Wonder Book of Knowledgevarious
Слова, связанные с окружностью
- Связанный
- Граница
- Груницы
- Кон.
- предел
- линия
- выступ
- край
- периметр
- периферия
- обод
- selvage
- skirt
- trim
- trimming
- verge
- abuttals
- ambits
- barriers
- beginnings
- borderlands
- borderlines
- borders
- brinks
- circumferences
- circumscriptions
- compasses
- границы
- края
- концы
- окружение
- границы
- extremities
- frames
- fringes
- frontiers
- hems
- horizons
- limits
- line of demarcations
- lines
- marches
- margins
- marks
- meres
- metes
- outlines
- outposts
- столбы
- периметры
- периферии
- границы
- прогоны
- радиусы
- rims
- sides
- skirts
- terminals
- terminations
- termini
- verges
- abuttals
- ambit
- barrier
- beginning
- border
- borderland
- borderline
- bounds
- brink
- окружность
- окружность
- компас
- границы
- край
- конец
- environs
- extent
- extremity
- frame
- fringe
- frontier
- hem
- horizon
- limits
- line
- line of demarcation
- march
- margin
- mark
- mere
- mete
- контур
- аванпост
- бледный
- периметр
- периферия
- участок
- огород
- radius
- rim
- side
- skirt
- terminal
- termination
- terminus
- verge
- border
- brink
- circumference
- fringe
- hem
- lip
- margin
- perimeter
- периферия
- обод
- юбка
- край
- амфитеатр
- венчик
- band
- belt
- bowl
- bracelet
- circlet
- circuit
- circumference
- circus
- cirque
- coil
- colure
- compass
- cordon
- corona
- crown
- cycle
- disc
- диск
- эклиптика
- корпус
- экватор
- полный оборот
- глобус
- гало
- hoop
- horizon
- lap
- meridian
- orbit
- parallel of latitude
- perimeter
- periphery
- record
- revolution
- ring
- ringlet
- round
- sphere
- stadium
- tire
- поворот
- колесо
- венок
- зодиак
- окружность
- площадь
- границы
- Circle
- Circleling
- Циркуляция
- Округа
- Округа
- .
 линия
линия - орбита
- прогулка
- периметр
- периферия
- дальность
- region
- round
- route
- tour
- tract
- turn
- turning
- twirl
- way
- wheel
- whirl
- wind
- winding
- zone
Roget’s 21st Century Thesaurus, Третье издание Copyright © 2013, Philip Lief Group.
Окружность – определение и значение
- Определение
- Связать
- Список
- Обсудить
- См.
- Услышать
- и Любовь
Определения
из Словаря английского языка American Heritage®, 5-е издание.
- сущ. Линия границы круга.
- сущ. Граница области или объекта.
- сущ. Длина такой линии.

- существительное Поле или область вокруг чего-либо.
из словаря века.
- сущ. Линия, ограничивающая круг; в более широком смысле, ограничивающая линия любой правильной плоской криволинейной фигуры; периферия: как окружность круга или эллипса. Окружность сферы равна окружности большого круга сферы.
- сущ. Следовательно, любая ограничивающая линия: например, окружность города.
- сущ. Пространство, заключенное в круг; что-нибудь круглое по форме.
- сущ. Ходить; многословие.
- Для включения в круглое или сферическое пространство.
из версии GNU Collaborative International Dictionary of English.
- сущ. Линия, огибающая или охватывающая круглую фигуру; периферия.

- сущ. Круг; что-нибудь круглое.
- сущ. Внешняя поверхность сферы или любого круглого тела.
- переходный глагол устарело Включить в круглое пространство; связать.
- сущ. геометрия Линия, ограничивающая круг или другую двумерную фигуру
- существительное геометрия Длина такой линии
- сущ. устаревшее Поверхность круглого или сферического объекта
- глагол устаревший, переходный Включать в круглое пространство; связать.
из WordNet 3.0 Copyright 2006 Принстонского университета. Все права защищены.
- сущ.
 линия границы, охватывающая территорию или объект
линия границы, охватывающая территорию или объект - сущ. длина замкнутой кривой окружности
- существительное размер чего-либо, определяемый расстоянием вокруг него
Этимологии
из Словаря английского языка American Heritage®, 4-е издание
[среднеанглийский, из старофранцузского circonference , от латинского окружность , от окружность , окружность- , причастие настоящего времени окружность , носить с собой: окружность- , окружность- + ферре носить, ; см. bher- в индоевропейских корнях.]
Из латыни окружность , окружность вокруг ; Ферре переноска
Поддержка
Помогите поддержать Wordnik (и сделайте эту страницу свободной от рекламы), приняв слово окружность.
Примеры
Из этого рассуждения непосредственно следует, что для наших сферических существ длина окружности окружности сначала увеличивается с радиусом до тех пор, пока не будет достигнута «окружность вселенной», и что с этого момента она постепенно уменьшается до нуля при еще более возрастающих значениях. радиуса.
Глава 31. Возможность «конечной» и в то же время «неограниченной» Вселенной
Это означает, что окружность составляет около 1000 метров, поэтому v равно 1000 метров в минуту, что дает симулированную гравитацию примерно в 1/6 от земной — такую же, как на Луне (хотя люди внутри движутся так, как если бы гравитация была земной). -обычный).
01.08.08: Стартовая площадка, день 2
Из него получаются трубочки с 44 петлями по окружности или прямые детали шириной до 44 петель, и требуется пряжа среднего веса — как раз для трубчатого шарфа, но немного узковата для вязания шапок.

Архив 2009-01-01
Из него получаются трубочки с 44 петлями по окружности или прямые детали шириной до 44 петель, и требуется пряжа среднего веса — как раз для трубчатого шарфа, но немного узковата для вязания шапок.
Ура новым игрушкам!
К сожалению, это означает, что мои джинсы довольно неудобно носить, потому что ремень 9Окружность 1569 теперь как минимум на две дырки меньше пояса джинсов.
Чизбургер Готический » Бургер Лайт 5 марта
Лорд-Хау представляет собой кольцо земли примерно в сто пятьдесят миль по окружности , шириной в несколько сотен ярдов в самом широком месте и местами возвышающееся на десять футов над уровнем моря.
МАУКИ
Пол Родригес был мексиканским носильщиком, у которого в верхней и боковой части головы был рог 14 см в обхватом и разделен на три вала, которые он скрыл под колпаком.
Человеческие рога
Атолл Хикуэру лежал низко над водой, круг толченого кораллового песка шириной в сто ярдов, двадцатью милями по окружности и от трех до пяти футов над уровнем прилива.

ДОМ МАПУИ
Парк Окружность г. составляет примерно 40 километров (км), простираясь от моста в Ургупе, а затем ведя на север на 6 км по реке Дамса.
Национальный парк Гёреме и скальные памятники Капподокии, Турция
- Большой адронный коллайдер
составляет 27 км по окружности и ускоряет протоны до 99,99999% скорости света (возможно, я не получил правильное число девяток, извините, если это испортит ваши расчеты, если вы пытаетесь это дома) .
Боинг Боинг
Окружность талии как показатель жизненно важных функций в клинической практике: Консенсус рабочей группы IAS и ICCR по висцеральному ожирению риск смерти, это измерение обычно не проводится в клинической практике. В этом Консенсусе предлагается, чтобы измерения окружности талии предоставили практикующим врачам важную возможность улучшить лечение и здоровье пациентов. Мы утверждаем, что одного только ИМТ недостаточно для правильной оценки или управления кардиометаболическим риском, связанным с повышенным ожирением у взрослых, и предоставляем тщательный обзор доказательств, который позволит практикующим врачам и профессиональным сообществам регулярно включать окружность талии в оценку и ведение пациентов.
 с избыточным весом или ожирением. Мы рекомендуем, чтобы уменьшение окружности талии было критически важной целью лечения для снижения неблагоприятных рисков для здоровья как мужчин, так и женщин. Кроме того, мы описываем доказательства того, что клинически значимое уменьшение окружности талии может быть достигнуто с помощью рутинных упражнений средней интенсивности и/или диетических вмешательств. Мы выявляем пробелы в знаниях, включая уточнение пороговых значений окружности талии для данной категории ИМТ, чтобы оптимизировать стратификацию риска ожирения по возрасту, полу и этнической принадлежности. Мы рекомендуем, чтобы медицинские работники были обучены правильно выполнять это простое измерение и рассматривать его как важный «признак жизнедеятельности» в клинической практике.
с избыточным весом или ожирением. Мы рекомендуем, чтобы уменьшение окружности талии было критически важной целью лечения для снижения неблагоприятных рисков для здоровья как мужчин, так и женщин. Кроме того, мы описываем доказательства того, что клинически значимое уменьшение окружности талии может быть достигнуто с помощью рутинных упражнений средней интенсивности и/или диетических вмешательств. Мы выявляем пробелы в знаниях, включая уточнение пороговых значений окружности талии для данной категории ИМТ, чтобы оптимизировать стратификацию риска ожирения по возрасту, полу и этнической принадлежности. Мы рекомендуем, чтобы медицинские работники были обучены правильно выполнять это простое измерение и рассматривать его как важный «признак жизнедеятельности» в клинической практике.Введение
Распространенность избыточной массы тела и ожирения среди взрослых, определяемая с помощью ИМТ, увеличилась во всем мире с 1980-х годов, и ни в одной стране не было продемонстрировано успешного снижения за 33 года зарегистрированных данных 1 . Ожирение является серьезной проблемой общественного здравоохранения во всем мире 2 , и использование одних только измерений ИМТ оказалось недостаточным для помощи клиницистам в оценке и управлении рисками для здоровья, связанными с ожирением, у их пациентов. Например, хотя у многих людей с избыточным весом или ожирением в течение жизни разовьются кардиометаболические осложнения, такие как сахарный диабет 2 типа (СД2) и сердечно-сосудистые заболевания (ССЗ), значительное меньшинство останется свободным от этих хронических заболеваний. описывается как метаболически здоровое ожирение (MHO).
Ожирение является серьезной проблемой общественного здравоохранения во всем мире 2 , и использование одних только измерений ИМТ оказалось недостаточным для помощи клиницистам в оценке и управлении рисками для здоровья, связанными с ожирением, у их пациентов. Например, хотя у многих людей с избыточным весом или ожирением в течение жизни разовьются кардиометаболические осложнения, такие как сахарный диабет 2 типа (СД2) и сердечно-сосудистые заболевания (ССЗ), значительное меньшинство останется свободным от этих хронических заболеваний. описывается как метаболически здоровое ожирение (MHO).
Распространенность MHO среди взрослых сильно различается между исследованиями из-за различий в возрасте, этнической принадлежности и факторов окружающей среды, а также отсутствия универсального определения метаболического здоровья и универсальной системы классификации ожирения 3 . Кроме того, исследования с длительным периодом наблюдения в целом показали, что MHO часто является временным или переходным состоянием для большинства людей с ожирением. Например, в исследовании с 20-летним наблюдением примерно половина взрослых с MHO (определяемой в этом исследовании как имеющая менее двух кардиометаболических параметров, выходящих за пределы здоровых диапазонов) стали метаболически нездоровыми к концу исследования. Кроме того, участники исследования с MHO имели повышенный риск сердечно-сосудистых событий после длительного наблюдения 4 . Точно так же исследование, в котором рассматривался весь спектр возможных определений MHO, показало, что риск сердечно-сосудистых событий, связанных с фенотипом MHO, увеличивался при более длительном периоде наблюдения. Кроме того, аналогичные оценки риска сердечно-сосудистых заболеваний наблюдались, когда MHO определялся критериями, отличными от отсутствия метаболического синдрома 5 . Несмотря на то, что ограничения ИМТ как индекса ожирения были известны на протяжении десятилетий, несколько руководств по ожирению во всем мире по-прежнему твердо рекомендуют, чтобы ИМТ сам по себе был мерой, характеризующей заболеваемость, связанную с ожирением, и риск смерти 9.
Например, в исследовании с 20-летним наблюдением примерно половина взрослых с MHO (определяемой в этом исследовании как имеющая менее двух кардиометаболических параметров, выходящих за пределы здоровых диапазонов) стали метаболически нездоровыми к концу исследования. Кроме того, участники исследования с MHO имели повышенный риск сердечно-сосудистых событий после длительного наблюдения 4 . Точно так же исследование, в котором рассматривался весь спектр возможных определений MHO, показало, что риск сердечно-сосудистых событий, связанных с фенотипом MHO, увеличивался при более длительном периоде наблюдения. Кроме того, аналогичные оценки риска сердечно-сосудистых заболеваний наблюдались, когда MHO определялся критериями, отличными от отсутствия метаболического синдрома 5 . Несмотря на то, что ограничения ИМТ как индекса ожирения были известны на протяжении десятилетий, несколько руководств по ожирению во всем мире по-прежнему твердо рекомендуют, чтобы ИМТ сам по себе был мерой, характеризующей заболеваемость, связанную с ожирением, и риск смерти 9. 0779 6,7,8,9 .
0779 6,7,8,9 .
Неспособность ИМТ полностью отразить кардиометаболический риск частично связана с тем фактом, что ИМТ сам по себе является недостаточным биомаркером абдоминального ожирения. Окружность талии — это простой метод оценки абдоминального ожирения, который легко стандартизировать и применять в клинической практике. Окружность талии тесно связана со смертностью от всех причин 10,11 и смертностью от сердечно-сосудистых заболеваний 12,13 с поправкой на ИМТ или без нее 10,14 . Однако в полной мере связь окружности талии с заболеваемостью и смертностью реализуется только после поправки на ИМТ 9.0779 10,15,16 . Таким образом, окружность талии позволяет дополнительно уточнить неблагоприятный риск для здоровья, характеризуемый ИМТ, и это измерение должно быть включено при стратификации риска для здоровья, связанного с ожирением. Действительно, сопротивление рутинному включению измерения окружности талии в клиническую практику не только игнорирует доказательства его полезности, но и не позволяет использовать возможности для консультирования пациентов относительно фенотипа ожирения с более высоким риском. Кроме того, измерение как ИМТ, так и окружности талии предоставит уникальные возможности для отслеживания полезности лечения и эффективности вмешательств, предназначенных для лечения ожирения и связанных с ним нарушений обмена веществ.
Кроме того, измерение как ИМТ, так и окружности талии предоставит уникальные возможности для отслеживания полезности лечения и эффективности вмешательств, предназначенных для лечения ожирения и связанных с ним нарушений обмена веществ.
В 2017 году Рабочая группа по висцеральному ожирению Международного общества атеросклероза (IAS) и Международного председателя по кардиометаболическим рискам (ICCR) собралась в Праге, Чешская Республика, для обсуждения важности абдоминального ожирения как фактора риска преждевременного атеросклероза и сердечно-сосудистых заболеваний в взрослые (дополнительная информация). Группа согласилась работать над разработкой согласованных документов, которые отражали бы позицию двух организаций. В этом Консенсусе мы обобщаем доказательства того, что одного ИМТ недостаточно для правильной оценки, оценки или управления кардиометаболическим риском, связанным с повышенным ожирением, и рекомендуем использовать окружность талии в качестве рутинного измерения в клинической практике наряду с ИМТ для классификации ожирения.
Методология
Настоящее Заявление о консенсусе разработано для обеспечения консенсуса IAS и Рабочей группы ICCR (дополнительная информация) об окружности талии как антропометрическом показателе, улучшающем ведение пациентов. Заявление о консенсусе было разработано следующим образом. Первая встреча лицом к лицу состоялась 24 апреля 2017 года для рассмотрения высококачественных доказательств, доступных и известных экспертам в данной области. После обсуждения и обсуждения экспертами контекста и качества доказательств была назначена группа исполнительных авторов (Р.Р., И.Дж.Н., Дж.-П.Д., Дж.С. и Ю.М.), которой было поручено написать первый вариант. Впоследствии проект был разослан всем авторам для критического пересмотра интеллектуального содержания, имеющего отношение к опыту каждого автора. Высококачественная опубликованная литература, которая стала доступна после первой личной встречи (до июня 2019 г.).) был определен всеми авторами и рассмотрен исполнительной группой для включения в рукопись. Первый автор координировал окончательную подготовку и подачу Заявления о консенсусе после того, как группа достигла консенсуса и утвердила его содержание.
Первый автор координировал окончательную подготовку и подачу Заявления о консенсусе после того, как группа достигла консенсуса и утвердила его содержание.
Историческая перспектива
Важность распределения жира в организме как фактора риска ряда заболеваний (например, сердечно-сосудистых заболеваний, гипертонии, инсульта и СД2) и смертности признавалась на протяжении нескольких десятилетий. В 1956 году Жан Ваг первым показал важность распределения жира в связи с различными заболеваниями, описав то, что он назвал «андроидным» и «гиноидным» типами ожирения 9.0779 17 . Эти классификации были позже интерпретированы Ahmed Kissebah и его коллегами как накопление жира в верхней и нижней части тела, что отражается высоким или низким соотношением окружности талии и бедер (WHR), соответственно 18 . Фенотипы накопления жира в верхней и нижней частях тела были основаны на морфологии тела, оцененной с помощью внешних антропометрических показателей, таких как кожные складки и окружности.
Популярность WHR возросла, когда эпидемиологи в США и Швеции показали, что WHR отдельно или в сочетании с ИМТ был связан с повышенным риском смерти, сердечно-сосудистых заболеваний и СД2 19,20,21,22 , данные, которые впоследствии были подтверждены во многих исследованиях. Однако более поздние данные показали, что, по сравнению с WHR, только окружность талии была более тесно связана с абсолютным количеством внутрибрюшного или висцерального жира, жирового депо, которое представляет наибольший риск для здоровья 23,24 . Кроме того, когда такое отношение, как WHR, используется для отслеживания изменений в региональных жировых отложениях, полезность отношения ограничена, когда значения как числителя, так и знаменателя изменяются в ответ на лечение. Следовательно, комбинация WHR и ИМТ для оценки риска ожирения была заменена едиными пороговыми значениями только для окружности талии 9.0779 25 . NIH был первым, кто использовал пороговые значения окружности талии (≥88 см у женщин и ≥102 см у мужчин), предложенные Michael Lean и его коллегами, в сочетании с классификацией общего ожирения по ИМТ 25 . Хотя использование этих конкретных значений окружности талии для выявления белых взрослых с абдоминальным ожирением остается краеугольным камнем руководящих принципов по ожирению во всем мире, мы представляем доказательства, чтобы оспорить поддерживающее обоснование и предоставить доказательства в поддержку альтернативных значений окружности талии, которые следует использовать вместе с ИМТ.
Хотя использование этих конкретных значений окружности талии для выявления белых взрослых с абдоминальным ожирением остается краеугольным камнем руководящих принципов по ожирению во всем мире, мы представляем доказательства, чтобы оспорить поддерживающее обоснование и предоставить доказательства в поддержку альтернативных значений окружности талии, которые следует использовать вместе с ИМТ.
В качестве альтернативы измерениям окружности талии, WHR или соотношению окружностей талии и бедер Маргарет Эшвелл и другие предложили соотношение талии и высоты в качестве меры абдоминального ожирения 26,27 . По сравнению с предыдущими измерениями соотношение талии и роста показывает аналогичную, а иногда и несколько более сильную связь с риском сердечно-сосудистых заболеваний или СД2 28,29 . Объяснение того, почему добавление роста увеличивает прогнозирование риска заболевания, может заключаться в том, что низкий рост связан с повышенным риском сердечно-сосудистых заболеваний 9. 0779 30 . У растущих детей и подростков соотношение роста и талии может быть более полезным для классификации абдоминального ожирения, чем только окружность талии. Однако у взрослых людей отношение талии к высоте менее полезно, поскольку рост обычно фиксирован, и значение может быть изменено только путем изменения окружности талии. Более того, рост лишь незначительно связан с окружностью талии 31 . Для оценки эффективности изменений образа жизни у взрослых можно было бы предпочесть окружность талии как простой инструмент. Другие альтернативы окружности талии включают индекс конусности 9.0779 32 и индекс абдоминального ожирения 33 , но они, в лучшем случае, являются лишь немного лучшими предикторами риска заболевания, чем одна только окружность талии.
0779 30 . У растущих детей и подростков соотношение роста и талии может быть более полезным для классификации абдоминального ожирения, чем только окружность талии. Однако у взрослых людей отношение талии к высоте менее полезно, поскольку рост обычно фиксирован, и значение может быть изменено только путем изменения окружности талии. Более того, рост лишь незначительно связан с окружностью талии 31 . Для оценки эффективности изменений образа жизни у взрослых можно было бы предпочесть окружность талии как простой инструмент. Другие альтернативы окружности талии включают индекс конусности 9.0779 32 и индекс абдоминального ожирения 33 , но они, в лучшем случае, являются лишь немного лучшими предикторами риска заболевания, чем одна только окружность талии.
Распространенность абдоминального ожирения
Несмотря на сильную связь между окружностью талии и ИМТ на популяционном уровне, новые данные свидетельствуют о том, что в разных популяциях окружность талии может увеличиваться сверх того, что ожидается в соответствии с ИМТ. Другими словами, фенотип ожирения может со временем измениться на тот, который отражает увеличение абдоминального ожирения 9.0779 34 . Например, Ян Янссен и его коллеги изучили изменения окружности талии для заданного ИМТ за 30-летний период в канадской выборке 35 . Примечательно, что для заданного ИМТ канадцы имели большую окружность талии в 2007 году по сравнению с 1981 годом. В частности, исследователи наблюдали, что окружность талии была больше на 1,1 см у мужчин и на 4,9 см у женщин при ИМТ 25 кг/м 2 . в период с 1981 по 2007 год. Аналогичным образом Сандра Альбрехт и ее коллеги исследовали вековые изменения окружности талии в США (19).88–2007), Англии (1992–2008), Китае (1993–2011) и Мексике (1999–2012) 36 и сообщили о статистически значимом увеличении значений окружности талии по сравнению с ИМТ во всех изученных странах и в большинстве подгрупп.
Другими словами, фенотип ожирения может со временем измениться на тот, который отражает увеличение абдоминального ожирения 9.0779 34 . Например, Ян Янссен и его коллеги изучили изменения окружности талии для заданного ИМТ за 30-летний период в канадской выборке 35 . Примечательно, что для заданного ИМТ канадцы имели большую окружность талии в 2007 году по сравнению с 1981 годом. В частности, исследователи наблюдали, что окружность талии была больше на 1,1 см у мужчин и на 4,9 см у женщин при ИМТ 25 кг/м 2 . в период с 1981 по 2007 год. Аналогичным образом Сандра Альбрехт и ее коллеги исследовали вековые изменения окружности талии в США (19).88–2007), Англии (1992–2008), Китае (1993–2011) и Мексике (1999–2012) 36 и сообщили о статистически значимом увеличении значений окружности талии по сравнению с ИМТ во всех изученных странах и в большинстве подгрупп.
Эти наблюдения согласуются с наблюдениями Томми Виссера и его коллег, которые провели обширный обзор и пришли к выводу, что большинство данных свидетельствует о тенденции, при которой относительное увеличение окружности талии было больше, чем относительное увеличение ИМТ 37 . Это наблюдение, по-видимому, не зависит от возраста, пола и этнической принадлежности, поскольку в нескольких группах не удалось продемонстрировать общую тенденцию к увеличению окружности талии за пределы ожидаемого ИМТ (рис. 1). Неспособность ИМТ обнаружить такое увеличение абдоминального ожирения подтверждает ограниченность одного ИМТ для определения фенотипа ожирения, который несет наибольший риск для здоровья.
Это наблюдение, по-видимому, не зависит от возраста, пола и этнической принадлежности, поскольку в нескольких группах не удалось продемонстрировать общую тенденцию к увеличению окружности талии за пределы ожидаемого ИМТ (рис. 1). Неспособность ИМТ обнаружить такое увеличение абдоминального ожирения подтверждает ограниченность одного ИМТ для определения фенотипа ожирения, который несет наибольший риск для здоровья.
Изменения распространенности абдоминального ожирения (измеряется с помощью окружности талии) и общего ожирения (измеряется с помощью ИМТ), измеренные в различных исследованиях за период времени, указанный на оси x . Общее ожирение определяли как ИМТ ≥30 кг/м 2 . Абдоминальное ожирение определяли как окружность талии ≥88 см и ≥102 см у женщин и мужчин соответственно. Однако Си и соавт. определяли общее ожирение как ИМТ ≥28 кг/м 2 и абдоминальное ожирение как окружность талии ≥80 см и ≥85 см для китайских женщин и мужчин, соответственно 113 . Кроме того, Барзин и соавт. определили общее ожирение как ИМТ ≥30 кг/м 2 и абдоминальное ожирение как окружность талии ≥91 см и ≥89 см для иранских женщин и мужчин, соответственно 114 . Приведенные годы (например, 1999–2011 гг.) указывают на годы, в которые были собраны данные. Ф, женщина; М, муж. Данные взяты из ссылок 37 113 114 115 116 117 118 119 120 121 .
Кроме того, Барзин и соавт. определили общее ожирение как ИМТ ≥30 кг/м 2 и абдоминальное ожирение как окружность талии ≥91 см и ≥89 см для иранских женщин и мужчин, соответственно 114 . Приведенные годы (например, 1999–2011 гг.) указывают на годы, в которые были собраны данные. Ф, женщина; М, муж. Данные взяты из ссылок 37 113 114 115 116 117 118 119 120 121 .
Изображение в натуральную величину
Выводы и рекомендации — распространенность абдоминального ожирения
Хотя распространенность ожирения, измеряемая по ИМТ, в некоторых странах, возможно, стабилизировалась, распространенность абдоминального ожирения, измеряемая по окружности талии, в целом увеличивается.
Отсутствие включения окружности талии в глобальный эпиднадзор за ожирением может неадекватно характеризовать риск для здоровья, связанный с глобальной распространенностью ожирения, поскольку представляется, что распространенность абдоминального ожирения увеличивается.

Текущие тенденции распространенности ожирения, основанные только на ИМТ, следует интерпретировать с осторожностью. Мы рекомендуем уделить серьезное внимание включению окружности талии в исследования по наблюдению за ожирением.
Выявление фенотипа ожирения высокого риска
Окружность талии, ИМТ и показатели здоровья — категориальный анализ
Неудивительно, что окружность талии и ИМТ сами по себе положительно связаны с заболеваемостью 15 и смертностью 13 независимо от возраста, пола и этнической принадлежности, учитывая сильную связь между этими антропометрическими переменными в когортах. Однако также хорошо известно, что для любого заданного ИМТ вариации окружности талии значительны, и в любой данной категории ИМТ взрослые с более высокими значениями окружности талии подвергаются повышенному неблагоприятному риску для здоровья по сравнению с людьми с более низкой окружностью талии. 38,39,40 . Это наблюдение хорошо иллюстрируется Джеймсом Серханом и его коллегами, которые объединили данные 11 проспективных когортных исследований с участием 650 386 белых взрослых из США, Австралии и Швеции в возрасте 20–83 лет 11 . В этом исследовании авторы отметили, что окружность талии была положительно связана со смертностью в каждой исследованной категории ИМТ, от 20 кг/м 2 до 50 кг/м 2 . Этот вывод согласуется с выводами Эллен де Холландер и ее коллег, которые провели метаанализ с участием более 58 000 преимущественно белых пожилых людей со всего мира и сообщили, что смертность с поправкой на возраст и курение была значительно выше у людей с повышенным окружность талии в пределах нормального веса, избыточного веса и ожирения согласно ИМТ 41 . Способность окружности талии увеличивать неблагоприятный риск для здоровья, наблюдаемый в данной категории ИМТ, обеспечивает основу для современной системы классификации, используемой для характеристики риска для здоровья, связанного с ожирением 8,42 .
38,39,40 . Это наблюдение хорошо иллюстрируется Джеймсом Серханом и его коллегами, которые объединили данные 11 проспективных когортных исследований с участием 650 386 белых взрослых из США, Австралии и Швеции в возрасте 20–83 лет 11 . В этом исследовании авторы отметили, что окружность талии была положительно связана со смертностью в каждой исследованной категории ИМТ, от 20 кг/м 2 до 50 кг/м 2 . Этот вывод согласуется с выводами Эллен де Холландер и ее коллег, которые провели метаанализ с участием более 58 000 преимущественно белых пожилых людей со всего мира и сообщили, что смертность с поправкой на возраст и курение была значительно выше у людей с повышенным окружность талии в пределах нормального веса, избыточного веса и ожирения согласно ИМТ 41 . Способность окружности талии увеличивать неблагоприятный риск для здоровья, наблюдаемый в данной категории ИМТ, обеспечивает основу для современной системы классификации, используемой для характеристики риска для здоровья, связанного с ожирением 8,42 .
Окружность талии, ИМТ и последствия для здоровья — непрерывный анализ
Несмотря на наблюдение, что связь между окружностью талии и неблагоприятным риском для здоровья варьируется в зависимости от категории ИМТ 11 , современные системы классификации риска ожирения рекомендуют использовать одни и те же пороговые значения окружности талии для все категории ИМТ 42 . Мы предполагаем, что важная информация об ИМТ и окружности талии теряется, когда они преобразуются из непрерывных в широкие категориальные переменные, и что эта потеря информации влияет на то, как ИМТ и окружность талии предсказывают заболеваемость и смертность. В частности, когда ИМТ и окружность талии рассматриваются как категориальные переменные в одной и той же модели прогнозирования риска, они обе положительно связаны с заболеваемостью и смертностью 38 . Однако, когда ИМТ и окружность талии рассматриваются как непрерывные переменные в одной и той же модели прогнозирования риска, прогнозирование риска по окружности талии улучшается, тогда как связь между ИМТ и неблагоприятным риском для здоровья ослабевает 10,43 . Полная сила связи между окружностью талии и заболеваемостью и/или смертностью не полностью осознается до корректировки ИМТ 11,12,41 .
Полная сила связи между окружностью талии и заболеваемостью и/или смертностью не полностью осознается до корректировки ИМТ 11,12,41 .
Доказательства в поддержку корректировки окружности талии для ИМТ получены от Janne Bigaard и его коллег, которые сообщают, что существует тесная связь между окружностью талии и смертностью от всех причин после корректировки для ИМТ 43 . Например, окружность талии на 10% больше соответствовала 1,48 (95% ДИ 1,36–1,61) раза выше смертности во всем диапазоне окружности талии как у мужчин, так и у женщин после поправки на ИМТ. Это наблюдение было подтверждено Тобиасом Пишоном и его коллегами, которые заметили, что самый высокий квинтиль окружности талии (≥102,7 см у мужчин и ≥89,0 см у женщин) был связан с повышенным риском смерти от всех причин на 1,33 (95% ДИ 1,24). –1,44) до корректировки ИМТ, с повышенным риском смерти 2,05 (95% ДИ 1,80–2,33) после корректировки ИМТ 10 .
В соответствии с наблюдениями, основанными на бессимптомных взрослых, Таис Коутиньо и его коллеги сообщают об аналогичных наблюдениях для когорты из 14 284 взрослых с ССЗ, за которыми наблюдали в течение 2,3 года (5 696 смертей). Когорта была разделена на терцили как по окружности талии, так и по ИМТ. По сравнению с самым низким терцилем окружности талии, для самого высокого терциля окружности талии после поправки на возраст, пол, курение, сахарный диабет, гипертонию и ИМТ (ОР 1,29) наблюдалась значительная связь с риском смерти., 95% ДИ 1,20–1,39). Напротив, после поправки на возраст, пол, курение, сахарный диабет, артериальную гипертензию и окружность талии увеличение терцилей ИМТ было обратно связано с риском смерти (ОР 0,64, 95% ДИ 0,59–0,69) 44 .
Когорта была разделена на терцили как по окружности талии, так и по ИМТ. По сравнению с самым низким терцилем окружности талии, для самого высокого терциля окружности талии после поправки на возраст, пол, курение, сахарный диабет, гипертонию и ИМТ (ОР 1,29) наблюдалась значительная связь с риском смерти., 95% ДИ 1,20–1,39). Напротив, после поправки на возраст, пол, курение, сахарный диабет, артериальную гипертензию и окружность талии увеличение терцилей ИМТ было обратно связано с риском смерти (ОР 0,64, 95% ДИ 0,59–0,69) 44 .
Результаты этого систематического обзора 44 частично подтверждены Diewertje Sluik и его коллегами, которые изучили взаимосвязь между окружностью талии, ИМТ и выживаемостью у 5435 человек с СД2 в течение 4,6 лет наблюдения (межквартильный диапазон 2,0–9)..8 лет) 45 . В этом проспективном когортном исследовании когорта была разделена на квинтили как по ИМТ, так и по окружности талии. После поправки на продолжительность СД2, лечение инсулином, распространенный инфаркт миокарда, инсульт, рак, статус курения, продолжительность курения, уровень образования, физическую активность, потребление алкоголя и ИМТ, ОР риска смерти, связанный с наивысшим терцилем, составил 2,11 (95%). ДИ 1,23–3,61) по сравнению с самым низким квинтилем окружности талии. Напротив, по сравнению с самым низким квинтилем ИМТ (с поправкой на те же переменные, с заменой ИМТ окружностью талии) ОР риска смерти для самого высокого квинтиля ИМТ составил 0,33 (9).5% ДИ 0,19–0,60). Таким образом, когда связь между окружностью талии и ИМТ с заболеваемостью и смертностью рассматривается в непрерывных моделях, для данной окружности талии чем выше ИМТ, тем ниже неблагоприятный риск для здоровья.
ДИ 1,23–3,61) по сравнению с самым низким квинтилем окружности талии. Напротив, по сравнению с самым низким квинтилем ИМТ (с поправкой на те же переменные, с заменой ИМТ окружностью талии) ОР риска смерти для самого высокого квинтиля ИМТ составил 0,33 (9).5% ДИ 0,19–0,60). Таким образом, когда связь между окружностью талии и ИМТ с заболеваемостью и смертностью рассматривается в непрерывных моделях, для данной окружности талии чем выше ИМТ, тем ниже неблагоприятный риск для здоровья.
Почему связь между окружностью талии и неблагоприятным риском для здоровья увеличивается после поправки на ИМТ, не установлено. Возможно, оздоровительный эффект более высокого ИМТ при данном обхвате талии объясняется повышенным накоплением подкожно-жировой клетчатки в нижней части тела 46 . Например, в исследовании более 2000 пожилых участников исследования «Здоровье, старение и состав тела» Марике Снайдер и ее коллеги были одними из первых, кто сообщил, что масса жировой ткани бедра отрицательно связана с непереносимостью глюкозы и дислипидемией после учета абдоминального жира. тканевая масса 47 . Это наблюдение было подтверждено Софи Иствуд и ее коллегами, которые сообщили, что у взрослых жителей Южной Азии защитное действие общей подкожной жировой ткани на СД2 и HbA 9Уровни 1829 1c появляются только после учета накопления висцеральной жировой ткани (VAT) 48 .
тканевая масса 47 . Это наблюдение было подтверждено Софи Иствуд и ее коллегами, которые сообщили, что у взрослых жителей Южной Азии защитное действие общей подкожной жировой ткани на СД2 и HbA 9Уровни 1829 1c появляются только после учета накопления висцеральной жировой ткани (VAT) 48 .
Причинный механизм, объясняющий ослабление заболеваемости и смертности, связанный с повышенным ожирением нижней части тела при данном уровне абдоминального ожирения, не установлен. Мы предполагаем, что повышенная способность накапливать избыточное потребление энергии в ягодично-бедренных подкожных адипоцитах может защищать от избыточного отложения липидов в НДС и эктопических депо, таких как печень, сердце и скелетные мышцы (рис. 2). Таким образом, для данной окружности талии больший ИМТ может представлять собой фенотип с повышением уровня подкожной жировой ткани в нижней части тела. В качестве альтернативы, у взрослых с повышенным ИМТ для данной окружности талии может быть снижена сумма НДС. Избыточное накопление липидов в НДС и эктопических депо связано с повышенным кардиометаболическим риском 47,48,49 . При этом НДС является установленным маркером заболеваемости 50,51 и смертности 24,52 . Эти результаты обеспечивают правдоподобный механизм, с помощью которого более низкие значения ИМТ или окружности бедер при заданной окружности талии могут увеличить неблагоприятный риск для здоровья.
Избыточное накопление липидов в НДС и эктопических депо связано с повышенным кардиометаболическим риском 47,48,49 . При этом НДС является установленным маркером заболеваемости 50,51 и смертности 24,52 . Эти результаты обеспечивают правдоподобный механизм, с помощью которого более низкие значения ИМТ или окружности бедер при заданной окружности талии могут увеличить неблагоприятный риск для здоровья.
Способность подкожной жировой ткани (ПЖТ) увеличиваться за счет гиперплазии (образования новых жировых клеток) позволяет безопасно накапливать избыточную энергию из рациона в правильно расширяющемся подкожном «метаболическом приемнике». Когда этот процесс становится насыщенным или в ситуациях, когда жировая ткань имеет ограниченную способность к увеличению, происходит выброс избыточной энергии, которая должна храниться в висцеральной жировой ткани, а также в обычно худых органах, таких как скелетные мышцы, печень. , поджелудочная железа и сердце, процесс, описанный как эктопическое отложение жира. Висцеральное ожирение связано с гиперлиполитическим состоянием, устойчивым к действию инсулина, наряду с измененной секрецией адипокинов, включая воспалительные цитокины, тогда как набор метаболических дисфункций специфически связан с увеличением скелетных мышц, печени, поджелудочной железы, эпикарда, перикарда и интрамиокарда. толстый. СЖК, свободная жирная кислота.
, поджелудочная железа и сердце, процесс, описанный как эктопическое отложение жира. Висцеральное ожирение связано с гиперлиполитическим состоянием, устойчивым к действию инсулина, наряду с измененной секрецией адипокинов, включая воспалительные цитокины, тогда как набор метаболических дисфункций специфически связан с увеличением скелетных мышц, печени, поджелудочной железы, эпикарда, перикарда и интрамиокарда. толстый. СЖК, свободная жирная кислота.
Полноразмерное изображение
Это мнение подкрепляется Дженнифер Кук и ее коллегами, которые сообщили, что ИМТ является независимым и положительным коррелятом НДС у взрослых до поправки на окружность талии; однако ИМТ отрицательно связан с массой НДС после поправки на окружность талии 53 . В этом исследовании также сообщалось, что после поправки на окружность талии ИМТ был положительно связан с массой подкожной жировой ткани нижней части тела и массой скелетных мышц. Эти наблюдения подтверждают предполагаемый механизм, описанный выше, и, следовательно, отрицательную связь, обычно наблюдаемую между ИМТ и заболеваемостью и смертностью после поправки на окружность талии, можно объяснить уменьшением отложения подкожной жировой ткани и мышечной массы в нижней части тела, повышенным накоплением висцеральное ожирение или и то, и другое.
Таким образом, комбинация ИМТ и окружности талии может идентифицировать фенотип ожирения с самым высоким риском гораздо лучше, чем каждый из показателей по отдельности. Хотя рекомендации по лечению ожирения, разработанные несколькими профессиональными обществами, признают важность измерения окружности талии, в контексте стратификации риска будущей сердечно-метаболической заболеваемости и смертности эти рекомендации ограничивают рекомендацию измерять окружность талии только взрослыми, определяемыми по ИМТ как имеющие избыточный вес или ожирение. На основании наблюдений, описанных в этом разделе, окружность талии может быть столь же важной, если не более информативной, у лиц с более низким ИМТ, у которых повышенная окружность талии с большей вероятностью указывает на висцеральное ожирение и повышенный кардиометаболический риск. Это наблюдение особенно верно для пожилых людей 54 .
Выводы и рекомендации — выявление фенотипа ожирения высокого риска
В категориальном анализе окружность талии связана с результатами для здоровья во всех категориях ИМТ, независимо от пола и возраста.

Когда ИМТ и окружность талии рассматриваются как непрерывные переменные в одной и той же модели прогнозирования риска, окружность талии остается положительным предиктором риска смерти, но ИМТ не связан или отрицательно связан с этим риском.
Сила связи между окружностью талии и заболеваемостью и/или смертностью не полностью осознается до тех пор, пока не будет сделана поправка на ИМТ.
Улучшенная способность окружности талии прогнозировать последствия для здоровья по сравнению с ИМТ может быть, по крайней мере, частично объяснена способностью окружности талии идентифицировать взрослых с увеличенной массой НДС.
Мы рекомендуем, чтобы измерения окружности талии и ИМТ стали стандартной частью клинических визитов (то есть общепринятым «жизненным показателем»).

Важность в клинических условиях
Для практикующих врачей решение о включении новой меры в клиническую практику в значительной степени обусловлено двумя важными, но очень разными вопросами. Первый фокусируется на том, улучшают ли мера или биомаркер прогнозирование риска конкретного заболевания в конкретной популяции. Например, улучшает ли добавление нового фактора риска прогностическую эффективность установленного алгоритма прогнозирования риска, такого как объединенные когортные уравнения (PCE) или Framingham Risk Score (FRS) у взрослых с риском сердечно-сосудистых заболеваний? Второй вопрос касается того, приведет ли улучшение нового маркера риска к соответствующему снижению риска, например, сердечно-сосудистых событий. Во многих ситуациях, даже если биомаркер не способствует прогнозированию риска, он все же может служить отличной мишенью для снижения риска. Здесь мы рассматриваем важность окружности талии в клинических условиях, отвечая на эти два вопроса.
Прогнозирование риска
Оценка полезности любого биомаркера, такого как окружность талии, для прогнозирования риска требует глубокого понимания эпидемиологического контекста, в котором оценивается оценка риска. Кроме того, необходимо выполнить несколько статистических контрольных показателей, чтобы биомаркер улучшил прогнозирование риска по сравнению с традиционными мерами. Эти критерии особенно важны для окружности талии, поскольку существуют установленные половые и этнические различия в пороговых уровнях окружности талии 55,56 . В 2009 г. Американская кардиологическая ассоциация опубликовала научное заявление о необходимых критериях оценки новых маркеров риска сердечно-сосудистых заболеваний 57 , за которым последовали рекомендации по оценке сердечно-сосудистого риска у бессимптомных взрослых в 2010 г. (ссылка 58 ). Новые биомаркеры должны как минимум иметь независимую статистическую связь с риском для здоровья после учета установленных маркеров риска в контексте многофакторной эпидемиологической модели. Однако одной этой характеристики недостаточно, так как многие новые биомаркеры соответствуют этому минимальному стандарту, но не улучшают прогнозирование риска значимо по сравнению с традиционными маркерами. Поэтому были разработаны более строгие контрольные показатели для оценки полезности биомаркеров, которые включают калибровку, дискриминацию 58 и чистое улучшение реклассификации 59 . Поэтому для критической оценки окружности талии как нового биомаркера для использования в алгоритмах прогнозирования риска необходимо применять эти строгие критерии.
Однако одной этой характеристики недостаточно, так как многие новые биомаркеры соответствуют этому минимальному стандарту, но не улучшают прогнозирование риска значимо по сравнению с традиционными маркерами. Поэтому были разработаны более строгие контрольные показатели для оценки полезности биомаркеров, которые включают калибровку, дискриминацию 58 и чистое улучшение реклассификации 59 . Поэтому для критической оценки окружности талии как нового биомаркера для использования в алгоритмах прогнозирования риска необходимо применять эти строгие критерии.
Многочисленные исследования демонстрируют статистическую связь между окружностью талии и смертностью и заболеваемостью в эпидемиологических когортах. Например, систематический обзор и мета-регрессионный анализ 18 исследований, включающих >680 000 участников из Европы с периодом наблюдения до 24 лет, показали, что окружность талии была связана с увеличением смертности от всех причин выше значений 9.5 см для мужчин и 80 см для женщин 60 . Примечательно, что увеличение окружности талии выше этих пороговых значений было связано с повышенным относительным риском смерти от всех причин даже среди лиц с нормальным ИМТ (20,0–24,9 кг/м 2 ) 60 . В США проспективное наблюдение в течение 9 лет за 14 699 чернокожими, белыми и представителями смешанной этнической принадлежности в исследовании «Риск атеросклероза в сообществах» показало, что окружность талии была связана с повышенным риском ишемической болезни сердца (553 события; RR 1,37, 9).5% ДИ 1,21–1,56), но не со смертью от всех причин 61 .
Примечательно, что увеличение окружности талии выше этих пороговых значений было связано с повышенным относительным риском смерти от всех причин даже среди лиц с нормальным ИМТ (20,0–24,9 кг/м 2 ) 60 . В США проспективное наблюдение в течение 9 лет за 14 699 чернокожими, белыми и представителями смешанной этнической принадлежности в исследовании «Риск атеросклероза в сообществах» показало, что окружность талии была связана с повышенным риском ишемической болезни сердца (553 события; RR 1,37, 9).5% ДИ 1,21–1,56), но не со смертью от всех причин 61 .
Несмотря на наличие надежной статистической связи со смертностью от всех причин независимо от ИМТ, нет убедительных доказательств того, что добавление окружности талии к стандартным моделям риска сердечно-сосудистых заболеваний (таким как FRS 62 или PCE 63 ) улучшает прогнозирование риска использование более строгих статистических критериев. Например, исследование, оценивающее полезность PCE для определенных ВОЗ классов ожирения 42 в пяти больших эпидемиологических когортах, состоящих примерно из 25 000 человек, оценили, будет ли улучшена дискриминация риска PCE за счет включения специфических для ожирения показателей ИМТ и окружности талии 64 . Исследователи обнаружили, что, хотя каждый показатель был индивидуально связан (ИМТ: ОР 1,04, 95% ДИ 1,02–1,07; окружность талии: ОР 1,11, 95% ДИ 1,09–1,13 на 1 SD увеличение) с повышенным риском атеросклеротических сердечно-сосудистых заболеваний, значительного улучшения не наблюдалось. произошло в c-статистике при добавлении либо ИМТ, либо окружности талии к другим переменным PCE 64 . Аналогичным образом, объединенный анализ четырех французских популяционных исследований, включающих более 20 000 участников, оценивал полезность дополнительных факторов риска при добавлении к FRS для 10-летнего прогноза риска ишемической болезни сердца 65 . Исследователи обнаружили, что ИМТ ( P = 0,03), но не окружность талии ( P = 0,42) оставался связанным с риском ишемической болезни сердца при добавлении к FRS, но добавление любого фактора не улучшало различение модели 65 .
Исследователи обнаружили, что, хотя каждый показатель был индивидуально связан (ИМТ: ОР 1,04, 95% ДИ 1,02–1,07; окружность талии: ОР 1,11, 95% ДИ 1,09–1,13 на 1 SD увеличение) с повышенным риском атеросклеротических сердечно-сосудистых заболеваний, значительного улучшения не наблюдалось. произошло в c-статистике при добавлении либо ИМТ, либо окружности талии к другим переменным PCE 64 . Аналогичным образом, объединенный анализ четырех французских популяционных исследований, включающих более 20 000 участников, оценивал полезность дополнительных факторов риска при добавлении к FRS для 10-летнего прогноза риска ишемической болезни сердца 65 . Исследователи обнаружили, что ИМТ ( P = 0,03), но не окружность талии ( P = 0,42) оставался связанным с риском ишемической болезни сердца при добавлении к FRS, но добавление любого фактора не улучшало различение модели 65 .
Только на основании этих наблюдений можно сделать вывод, что измерение окружности талии в клинических условиях не поддерживается, поскольку прогнозирование риска не улучшается. Однако Нэнси Кук и другие продемонстрировали, насколько сложно добавление любого биомаркера существенно улучшить прогностическую эффективность 59,66,67,68 . Действительно, Майкл Пенчина и его коллеги подсчитали, что немодифицируемые факторы риска, такие как возраст, пол и этническая принадлежность, охватывают 63–80% прогностической эффективности моделей сердечно-сосудистого риска, и что добавление систолического артериального давления, уровней не-ЛПВП в плазме холестерина, сахарного диабета или курение в модели с другими факторами риска увеличивает прогностическую эффективность, измеренную с-статистикой, всего на 0,004–0,013 (ссылка 9).0779 69 ). Кроме того, любое добавочное значение окружности талии к алгоритмам прогнозирования риска может быть подавлено более непосредственными, нижестоящими причинными факторами риска, такими как повышенное кровяное давление и аномальные концентрации глюкозы в плазме. Другими словами, окружность талии может не улучшать прогностические показатели, поскольку, независимо от ИМТ, окружность талии является основным фактором изменений последующих кардиометаболических факторов риска.
Однако Нэнси Кук и другие продемонстрировали, насколько сложно добавление любого биомаркера существенно улучшить прогностическую эффективность 59,66,67,68 . Действительно, Майкл Пенчина и его коллеги подсчитали, что немодифицируемые факторы риска, такие как возраст, пол и этническая принадлежность, охватывают 63–80% прогностической эффективности моделей сердечно-сосудистого риска, и что добавление систолического артериального давления, уровней не-ЛПВП в плазме холестерина, сахарного диабета или курение в модели с другими факторами риска увеличивает прогностическую эффективность, измеренную с-статистикой, всего на 0,004–0,013 (ссылка 9).0779 69 ). Кроме того, любое добавочное значение окружности талии к алгоритмам прогнозирования риска может быть подавлено более непосредственными, нижестоящими причинными факторами риска, такими как повышенное кровяное давление и аномальные концентрации глюкозы в плазме. Другими словами, окружность талии может не улучшать прогностические показатели, поскольку, независимо от ИМТ, окружность талии является основным фактором изменений последующих кардиометаболических факторов риска. Подробное обсуждение достоинств различных подходов (например, c-статистики, чистого индекса реклассификации и индекса дискриминации) для определения полезности новых биомаркеров для улучшения прогнозирования риска выходит за рамки этой статьи, и читателю предлагается ознакомиться с недавними исследованиями. критика, чтобы получить представление об этом важном вопросе 66,69 .
Подробное обсуждение достоинств различных подходов (например, c-статистики, чистого индекса реклассификации и индекса дискриминации) для определения полезности новых биомаркеров для улучшения прогнозирования риска выходит за рамки этой статьи, и читателю предлагается ознакомиться с недавними исследованиями. критика, чтобы получить представление об этом важном вопросе 66,69 .
Снижение риска
Вопрос о том, улучшает ли добавление измерения окружности талии прогностическую эффективность установленных алгоритмов оценки риска, является клинически значимым вопросом, на который еще предстоит ответить; однако влияние таргетной окружности талии на заболеваемость и смертность является совершенно другим вопросом, имеющим равную или большую клиническую значимость. В литературе существует несколько примеров, когда маркер риска может улучшить прогнозирование риска, но клиническая модификация маркера не влияет на снижение риска. Например, низкий уровень холестерина ЛПВП является центральным фактором риска, связанным с риском ишемической болезни сердца в алгоритмах множественного прогнозирования риска, однако повышение уровня холестерина ЛПВП в плазме фармакологически не улучшает исходы ССЗ 70 . И наоборот, фактор риска может существенно не улучшить статистическое прогнозирование риска, но может быть важной поддающейся изменению целью для снижения риска. Действительно, мы утверждаем, что при любом значении ИМТ окружность талии является основным фактором ухудшения маркеров или факторов кардиометаболического риска и, следовательно, уменьшение окружности талии является важным шагом на пути к снижению риска кардиометаболических заболеваний.
И наоборот, фактор риска может существенно не улучшить статистическое прогнозирование риска, но может быть важной поддающейся изменению целью для снижения риска. Действительно, мы утверждаем, что при любом значении ИМТ окружность талии является основным фактором ухудшения маркеров или факторов кардиометаболического риска и, следовательно, уменьшение окружности талии является важным шагом на пути к снижению риска кардиометаболических заболеваний.
Как мы описали ранее, окружность талии хорошо зарекомендовала себя как независимый предиктор заболеваемости и смертности, и полная сила окружности талии реализуется после учета ИМТ. Мы предполагаем, что связь между окружностью талии и тяжелыми клиническими конечными точками в значительной степени объясняется связью между изменениями окружности талии и соответствующими кардиометаболическими факторами риска. Например, данные рандомизированных контролируемых исследований (РКИ) неизменно показывают, что, независимо от пола и возраста, уменьшение окружности талии, вызванное образом жизни, связано с улучшением кардиометаболических факторов риска с соответствующей потерей веса или без нее 71,72,73,74,75,76 . Эти наблюдения остаются неизменными независимо от того, вызвано ли уменьшение окружности талии ограничением энергии (то есть ограничением калорийности) 73,75,77 или увеличением расхода энергии (то есть физическими упражнениями) 71,73,74, 75 . Ранее мы утверждали, что связующим звеном между изменением окружности талии и кардиометаболическим риском является висцеральное ожирение, которое является сильным маркером кардиометаболического риска 24 . В совокупности эти наблюдения подчеркивают критическую роль уменьшения окружности талии за счет изменения образа жизни в последующем снижении заболеваемости и смертности (рис. 3).
Эти наблюдения остаются неизменными независимо от того, вызвано ли уменьшение окружности талии ограничением энергии (то есть ограничением калорийности) 73,75,77 или увеличением расхода энергии (то есть физическими упражнениями) 71,73,74, 75 . Ранее мы утверждали, что связующим звеном между изменением окружности талии и кардиометаболическим риском является висцеральное ожирение, которое является сильным маркером кардиометаболического риска 24 . В совокупности эти наблюдения подчеркивают критическую роль уменьшения окружности талии за счет изменения образа жизни в последующем снижении заболеваемости и смертности (рис. 3).
Иллюстрация важной роли уменьшения окружности талии в увязке улучшения образа жизни с последующим снижением риска заболеваемости и смертности. Преимущества, связанные с уменьшением окружности талии, могут наблюдаться с изменением ИМТ или без него.
Преимущества, связанные с уменьшением окружности талии, могут наблюдаться с изменением ИМТ или без него.
Полноразмерное изображение
Таким образом, вопрос о том, влияет ли окружность талии на прогностическую эффективность моделей сердечно-сосудистого риска, еще предстоит выяснить. Тем не менее, в настоящее время четко установлено, что окружность талии является ключевым фактором изменения уровней кардиометаболических факторов риска и маркеров. Следовательно, уменьшение окружности талии является важным шагом в снижении кардиометаболического риска, поскольку оно предлагает прагматичную и простую цель для управления рисками для пациентов.
Выводы и рекомендации — окружность талии и прогнозирование рисков
Комбинация ИМТ и окружности талии лучше определяет фенотип ожирения с высоким риском, чем любой из показателей по отдельности.
Мы рекомендуем измерять окружность талии в клинической практике, поскольку она является ключевым фактором риска; например, у многих пациентов изменены факторы риска сердечно-сосудистых заболеваний из-за абдоминального ожирения.

Окружность талии является критическим фактором, который можно использовать для измерения снижения риска сердечно-сосудистых заболеваний после принятия здорового образа жизни.
Высокочувствительный жизненно важный показатель
Данные нескольких обзоров и метаанализов подтверждают, что, независимо от возраста и пола, снижение потребления энергии с помощью диеты или увеличение расхода энергии с помощью физических упражнений связано со значительным уменьшением окружности талии. 78,79,80,81,82,83,84,85,86,87 . Для исследований, в которых отрицательный энергетический баланс вызывается только диетой, данные РКИ показывают, что окружность талии уменьшается независимо от состава диеты и продолжительности лечения 88 . Неясно, существует ли зависимость «доза-реакция» между отрицательным энергетическим балансом, вызванным диетой, и окружностью талии.
Хотя интуитивно можно предположить, что увеличение количества упражнений будет положительно связано с соответствующим уменьшением окружности талии, на сегодняшний день это мнение не подтверждается данными РКИ 71,74,89,90,91 . Например, Роберт Росс и его коллеги провели крупное РКИ, в котором участники ( n = 300) были распределены либо в контрольную группу, либо в группу вмешательства с различными уровнями упражнений: низкий, определяемый как 180 ккал за тренировку для женщин и 300 ккал за тренировку для женщин. сеанс для мужчин; и высокий, определяемый как 360 ккал за сеанс для женщин и 600 ккал за сеанс для мужчин 74 . Удвоение расхода энергии, вызванное упражнениями, не привело к разнице в уменьшении окружности талии между группами упражнений. Тем не менее, все группы вмешательства значительно уменьшили окружность талии (~ 5 см) по сравнению с контрольной группой (9).1475 P < 0,001) 74 . Эти результаты согласуются с выводами Кристофера Слентца и его коллег, которые не сообщили об отсутствии различий в окружности талии или снижении НДС между низким уровнем (14 ккал/кг массы тела в неделю, n = 46) и высоким уровнем (23 ккал/кг массы тела в неделю). /кг массы тела в неделю, n = 42) группы упражнений 90,91 . Кроме того, Тимоти Черч и его коллеги провели РКИ, в ходе которого участникам были назначены различные уровни физических упражнений (низкие, 4 ккал/кг массы тела в неделю, н = 155; умеренная, 8 ккал/кг массы тела в неделю, n = 104; или высокая, 12 ккал/кг массы тела в неделю, n = 103), которая соответствовала интенсивности (50% пикового потребления кислорода (VO 2 пик)) 71 . Значительное уменьшение окружности талии наблюдалось во всех группах упражнений по сравнению с контрольной группой без упражнений, без различий между различными предписанными уровнями 71 .
/кг массы тела в неделю, n = 42) группы упражнений 90,91 . Кроме того, Тимоти Черч и его коллеги провели РКИ, в ходе которого участникам были назначены различные уровни физических упражнений (низкие, 4 ккал/кг массы тела в неделю, н = 155; умеренная, 8 ккал/кг массы тела в неделю, n = 104; или высокая, 12 ккал/кг массы тела в неделю, n = 103), которая соответствовала интенсивности (50% пикового потребления кислорода (VO 2 пик)) 71 . Значительное уменьшение окружности талии наблюдалось во всех группах упражнений по сравнению с контрольной группой без упражнений, без различий между различными предписанными уровнями 71 .
В нескольких РКИ изучалось влияние интенсивности упражнений на окружность талии 74,90,91,92 . Небольшое исследование, проведенное Брайаном Ирвингом и его коллегами, показало, что группа упражнений высокой интенсивности (выше лактатного порога 3 дня в неделю и ниже лактатного порога 2 дня в неделю) ( n = 9) значительно уменьшила окружность талии по сравнению с группа низкой интенсивности (ниже лактатного порога 5 дней в неделю) ( n = 11) 92 . Однако существенных различий в снижении НДС с помощью однослойной КТ между группами высокой и низкой интенсивности не наблюдалось. Большое РКИ, проведенное Сленцем и его коллегами, показало, что увеличение интенсивности упражнений от умеренной (40–55% VO 9 до1829 2 пик, n = 40) до интенсивной (65–80% VO 2 пик, n = 42) интенсивность не была связана с различиями в уменьшении окружности талии 90,91 . Однако исследователи не фиксировали уровень упражнений между группами интенсивности, что могло бы объяснить их наблюдения. Росс и его коллеги контролировали расход энергии между умеренной интенсивностью (50% VO 2 пик, n = 76) и высокой интенсивностью (75% VO 2 пик, n = 76) группы упражнений 74 . Их наблюдения согласуются с наблюдениями Сленца и его коллег, согласно которым различия в интенсивности упражнений не влияли на уменьшение окружности талии. Эти результаты согласуются с метаанализом, проведенным в 2017 году, в котором не наблюдалось различий в уменьшении окружности талии между высокоинтенсивными интервальными тренировками и упражнениями средней интенсивности 93 .
Однако существенных различий в снижении НДС с помощью однослойной КТ между группами высокой и низкой интенсивности не наблюдалось. Большое РКИ, проведенное Сленцем и его коллегами, показало, что увеличение интенсивности упражнений от умеренной (40–55% VO 9 до1829 2 пик, n = 40) до интенсивной (65–80% VO 2 пик, n = 42) интенсивность не была связана с различиями в уменьшении окружности талии 90,91 . Однако исследователи не фиксировали уровень упражнений между группами интенсивности, что могло бы объяснить их наблюдения. Росс и его коллеги контролировали расход энергии между умеренной интенсивностью (50% VO 2 пик, n = 76) и высокой интенсивностью (75% VO 2 пик, n = 76) группы упражнений 74 . Их наблюдения согласуются с наблюдениями Сленца и его коллег, согласно которым различия в интенсивности упражнений не влияли на уменьшение окружности талии. Эти результаты согласуются с метаанализом, проведенным в 2017 году, в котором не наблюдалось различий в уменьшении окружности талии между высокоинтенсивными интервальными тренировками и упражнениями средней интенсивности 93 . Таким образом, имеющиеся данные свидетельствуют о том, что увеличение интенсивности упражнений не связано с дальнейшим уменьшением окружности талии.
Таким образом, имеющиеся данные свидетельствуют о том, что увеличение интенсивности упражнений не связано с дальнейшим уменьшением окружности талии.
Масса НДС обычно не измеряется в клинических условиях, поэтому интересно, связано ли уменьшение окружности талии с соответствующим снижением НДС. Хотя данные систематических обзоров и метаанализов демонстрируют связь между уменьшением окружности талии и НДС 79,82,84,85,94 , общая дисперсия является скромной (~40%) 75,95,96 . Следует отметить, что, насколько нам известно, каждое исследование, в котором сообщалось об уменьшении окружности талии, также сообщало о соответствующем снижении НДС. Таким образом, хотя разумно предположить, что уменьшение окружности талии связано с уменьшением массы НДС, точная оценка индивидуального уменьшения НДС по окружности талии невозможна. Тем не менее, соответствующее снижение НДС с окружностью талии дозозависимым образом подчеркивает важность рутинного измерения окружности талии в клинической практике. Особый интерес для практиков представляет то, что в нескольких обзорах наблюдалось значительное снижение НДС в ответ на физические упражнения без потери веса 9.0779 80,85 .
Особый интерес для практиков представляет то, что в нескольких обзорах наблюдалось значительное снижение НДС в ответ на физические упражнения без потери веса 9.0779 80,85 .
Выводы и рекомендации — изменения окружности талии в ответ на лечение
Упражнения и/или диета в соответствии с рекомендациями руководства связаны со значительным уменьшением окружности талии, независимо от возраста, пола или этнической принадлежности.
Имеющиеся данные РКИ свидетельствуют о том, что упражнения связаны со значительным уменьшением окружности талии, независимо от количества или интенсивности упражнений.
Уменьшение окружности талии, вызванное физическими упражнениями или диетой, наблюдается с потерей веса или без нее.
Мы рекомендуем практикующим врачам регулярно измерять окружность талии, так как это дает им простой антропометрический показатель для определения эффективности стратегий, основанных на образе жизни, направленных на снижение абдоминального ожирения.

Измерение окружности талии
Появление окружности талии в качестве надежного независимого маркера заболеваемости и смертности поразительно, учитывая отсутствие единого мнения относительно оптимального протокола измерения окружности талии. Более того, протоколы окружности талии, рекомендованные ведущими органами здравоохранения, не имеют научного обоснования. В 2008 году группа экспертов провела систематический обзор 120 исследований, чтобы определить, влияет ли протокол измерения на взаимосвязь между окружностью талии, заболеваемостью и смертностью, и обнаружила аналогичные закономерности связи между результатами и всеми протоколами измерения окружности талии в зависимости от размера выборки, пола, возраст и национальность 97 . После тщательного изучения различных протоколов, описанных в литературе, комиссия рекомендовала использовать протокол измерения окружности талии, описанный в рекомендациях ВОЗ 98 (средняя точка между нижней границей грудной клетки и гребнем подвздошной кости) и в рекомендациях NIH 99. (верхняя граница гребня подвздошной кости), вероятно, являются более надежными и выполнимыми измерениями как для практикующего врача, так и для широкой публики. Этот вывод был сделан, поскольку оба протокола измерения окружности талии используют костные ориентиры для определения правильного места измерения окружности талии.
(верхняя граница гребня подвздошной кости), вероятно, являются более надежными и выполнимыми измерениями как для практикующего врача, так и для широкой публики. Этот вывод был сделан, поскольку оба протокола измерения окружности талии используют костные ориентиры для определения правильного места измерения окружности талии.
Группа экспертов признала, что могут существовать различия в измерениях абсолютной окружности талии из-за различий в протоколах между методами ВОЗ и NIH. Однако в нескольких исследованиях сравнивались меры в местах, рекомендованных ВОЗ и NIH. Jack Wang и его коллеги не сообщили об отсутствии различий между протоколами гребня подвздошной кости и средней точки у мужчин и об абсолютной разнице в 1,8 см у женщин 100 . Эти наблюдения были подтверждены Кейтлин Мейсон и Питером Кацмарзиком, которые сообщили об отсутствии различий между протоколами гребня подвздошной кости (NIH) и средней точки (ВОЗ) для мужчин и абсолютной разнице в ~ 2 см для женщин 101 . Что еще более важно, Мейсон и Кацмарзик сообщили, что оценки распространенности абдоминального ожирения (здесь определяется как окружность талии> 88 см для женщин и> 102 см для мужчин), выявленные с использованием протоколов гребня подвздошной кости и средней точки, составили около 32% для обоих протоколов у мужчин и 47% и 41% для протоколов гребня подвздошной кости и средней точки, соответственно, у женщин 101 . Следовательно, хотя принятие стандартного подхода к измерению окружности талии повысило бы полезность измерений окружности талии для стратификации риска, связанного с ожирением, оценки распространенности абдоминального ожирения в преимущественно белом населении с использованием протоколов гребня подвздошной кости или средней точки, по-видимому, не имеют существенного значения. другой.
Что еще более важно, Мейсон и Кацмарзик сообщили, что оценки распространенности абдоминального ожирения (здесь определяется как окружность талии> 88 см для женщин и> 102 см для мужчин), выявленные с использованием протоколов гребня подвздошной кости и средней точки, составили около 32% для обоих протоколов у мужчин и 47% и 41% для протоколов гребня подвздошной кости и средней точки, соответственно, у женщин 101 . Следовательно, хотя принятие стандартного подхода к измерению окружности талии повысило бы полезность измерений окружности талии для стратификации риска, связанного с ожирением, оценки распространенности абдоминального ожирения в преимущественно белом населении с использованием протоколов гребня подвздошной кости или средней точки, по-видимому, не имеют существенного значения. другой.
Следует отметить, что наблюдение о том, что протоколы NIH и ВОЗ существенно не отличаются, не согласуется с выводами, сделанными Yumi Matsushita и его коллегами, которые отобрали 940 взрослых японцев и сообщили, что средняя разница между протоколами гребня подвздошной кости и средней точки для мужчин составила ~2 см, тогда как у женщин разница составляла ~9 см (refs 102,103 ). Тем не менее, измерения окружности талии, оцененные в двух местах, имели одинаковую способность скрининга метаболического синдрома, как это определено Национальной образовательной программой по холестерину, в когорте из 1140 взрослых японцев 102 .
Тем не менее, измерения окружности талии, оцененные в двух местах, имели одинаковую способность скрининга метаболического синдрома, как это определено Национальной образовательной программой по холестерину, в когорте из 1140 взрослых японцев 102 .
В нескольких исследованиях оценивалась взаимосвязь между окружностью талии, измеренной самостоятельно и техническим специалистом 104,105,106,107,108 . Инструкции по самостоятельному измерению окружности талии часто предоставляются в точечной форме посредством простых опросов 108 . Наблюдается хорошее совпадение между окружностью талии, измеренной самостоятельно, и окружностью талии, измеренной техническим специалистом, с сильными коэффициентами корреляции в диапазоне от 0,8 до 0,9 как для мужчин, так и для женщин. Тем не менее, как мужчины, так и женщины, как правило, недооценивают окружность своей талии по сравнению со значениями, измеренными техническим специалистом, с разницей в пределах от 1 до 3 см. Кроме того, высокий ИМТ и большая исходная окружность талии связаны с большей степенью занижения данных 9.0779 105 107 . В целом эти наблюдения обнадеживают и предполагают, что самостоятельные измерения окружности талии могут быть получены простым способом и хорошо согласуются со значениями, измеренными техническим специалистом.
Кроме того, высокий ИМТ и большая исходная окружность талии связаны с большей степенью занижения данных 9.0779 105 107 . В целом эти наблюдения обнадеживают и предполагают, что самостоятельные измерения окружности талии могут быть получены простым способом и хорошо согласуются со значениями, измеренными техническим специалистом.
Видеоинструкции с подробными иллюстрациями пошаговых процедур как технического, так и самостоятельного измерения окружности талии можно найти в свободном доступе на сайте myhealthywaist (http://www.myhealthywaist.org/evaluating-cmr/ клинические инструменты/обхват-талии-измерение-руководства/index.html).
Выводы и рекомендации — измерение окружности талии
В настоящее время не существует единого мнения об оптимальном протоколе измерения окружности талии, и для любого из протоколов измерения окружности талии, рекомендованных ведущими органами здравоохранения, представлено мало научного обоснования.

Протокол измерения окружности талии не оказывает существенного влияния на взаимосвязь между окружностью талии, смертностью от всех причин и смертностью от ССЗ, ССЗ и СД2.
Абсолютные различия в окружности талии, полученные по двум наиболее часто используемым протоколам, по гребню подвздошной кости (NIH) и по средней точке между последним ребром и гребнем подвздошной кости (WHO), как правило, невелики для взрослых мужчин, но гораздо больше для женщин.
Классификация абдоминального ожирения может различаться в зависимости от протокола измерения окружности талии.
Мы рекомендуем измерять окружность талии на уровне гребня подвздошной кости или посередине между последним ребром и гребнем подвздошной кости.
 Протокол, выбранный для измерения окружности талии, следует использовать последовательно.
Протокол, выбранный для измерения окружности талии, следует использовать последовательно.Самостоятельные измерения окружности талии можно получить простым способом, и они хорошо согласуются со значениями, измеренными техническим специалистом.
Пороговые значения для оценки риска
Текущие рекомендации по выявлению ожирения указывают на то, что неблагоприятный риск для здоровья увеличивается при переходе от категорий нормального веса к категориям ИМТ с ожирением. Более того, в каждой категории ИМТ люди с высокими значениями окружности талии подвергаются повышенному риску неблагоприятных последствий для здоровья по сравнению с людьми с нормальными значениями окружности талии 109 . Например, единый порог окружности талии для белых взрослых (мужчины >102 см; женщины >88 см) в настоящее время используется для обозначения высокой окружности талии, независимо от категории ИМТ. Следует отметить, что эти специфические для пола пороги были первоначально разработаны с использованием данных поперечного сечения взрослых белых, среди которых окружность талии 102 см у мужчин и 88 см у женщин соответствовала ИМТ 30,0 кг/м 9 .0779 2 , что является порогом ИМТ для ожирения 109 . Таким образом, эти пороговые значения окружности талии были разработаны для использования вместо ИМТ в качестве альтернативного способа выявления ожирения и, следовательно, не были разработаны на основе взаимосвязи между окружностью талии и неблагоприятным риском для здоровья.
Следует отметить, что эти специфические для пола пороги были первоначально разработаны с использованием данных поперечного сечения взрослых белых, среди которых окружность талии 102 см у мужчин и 88 см у женщин соответствовала ИМТ 30,0 кг/м 9 .0779 2 , что является порогом ИМТ для ожирения 109 . Таким образом, эти пороговые значения окружности талии были разработаны для использования вместо ИМТ в качестве альтернативного способа выявления ожирения и, следовательно, не были разработаны на основе взаимосвязи между окружностью талии и неблагоприятным риском для здоровья.
Чтобы устранить это ограничение, Кристофер Ардерн и его коллеги разработали и перекрестно подтвердили пороговые значения окружности талии в рамках категорий ИМТ в отношении предполагаемого риска сердечно-сосудистых заболеваний в будущем (с использованием FRS) 110 . Полезность полученных значений сравнивалась с пороговыми значениями окружности талии (для женщин > 88 см; для мужчин > 102 см), рекомендованными ведущими органами здравоохранения. Результаты их исследования показали, что текущие рекомендации, использующие единый порог окружности талии для всех категорий ИМТ, недостаточны для выявления лиц с повышенным риском для здоровья. У обоих полов использование пороговых значений окружности талии для конкретных категорий ИМТ улучшило выявление лиц с высоким риском будущих коронарных событий, что побудило авторов предложить значения окружности талии для конкретных категорий ИМТ (таблица 1). В 2009, Harpreet Bajaj и его коллеги сравнили прогностическую эффективность значений окружности талии Ардерна (таблица 1) с традиционными значениями окружности талии (мужчины> 102 см; женщины> 88 см) для смертности от всех причин в большой когорте из 5453 преимущественно белых взрослых. с высоким кардиометаболическим риском 111 . Как для мужчин, так и для женщин значения окружности талии по Ардерну значительно улучшили прогноз смертности по сравнению с традиционными значениями. Эти наблюдения являются многообещающими и подтверждают, по крайней мере, для белых взрослых, клиническую полезность пороговых значений окружности талии для конкретных категорий ИМТ, приведенных в таблице 1.
Результаты их исследования показали, что текущие рекомендации, использующие единый порог окружности талии для всех категорий ИМТ, недостаточны для выявления лиц с повышенным риском для здоровья. У обоих полов использование пороговых значений окружности талии для конкретных категорий ИМТ улучшило выявление лиц с высоким риском будущих коронарных событий, что побудило авторов предложить значения окружности талии для конкретных категорий ИМТ (таблица 1). В 2009, Harpreet Bajaj и его коллеги сравнили прогностическую эффективность значений окружности талии Ардерна (таблица 1) с традиционными значениями окружности талии (мужчины> 102 см; женщины> 88 см) для смертности от всех причин в большой когорте из 5453 преимущественно белых взрослых. с высоким кардиометаболическим риском 111 . Как для мужчин, так и для женщин значения окружности талии по Ардерну значительно улучшили прогноз смертности по сравнению с традиционными значениями. Эти наблюдения являются многообещающими и подтверждают, по крайней мере, для белых взрослых, клиническую полезность пороговых значений окружности талии для конкретных категорий ИМТ, приведенных в таблице 1.
Полноразмерная таблица
Следует отметить, что пороговые значения окружности талии для афроамериканцев и белых мужчин и женщин были разработаны для афроамериканцев и белых мужчин и женщин 112 . Как и в предыдущем исследовании, пороговые значения оптимальной окружности талии увеличились по категориям ИМТ в обеих этнических группах и были выше у мужчин, чем у женщин. Однако не было выявлено различий в окружности талии между этническими группами каждого пола .112 .
Pischon и его коллеги исследовали связь между ИМТ, окружностью талии и риском смерти среди 359 387 взрослых из девяти стран в когорте Европейского проспективного исследования рака и питания 10 . В этом исследовании авторы подтвердили, что при заданном ИМТ у мужчин и женщин риск смерти увеличивался на 17% у мужчин и на 13% у женщин на каждые 5 см увеличения окружности талии. Хотя значения окружности талии, которые оптимизировали прогнозирование риска смерти для любого заданного значения ИМТ, не сообщались, полученные данные подтверждают мнение о том, что пороговые значения окружности талии увеличиваются по категориям ИМТ и что комбинация окружности талии и ИМТ обеспечивает более точное прогнозирование риска для здоровья. чем любое антропометрическое измерение в отдельности.
чем любое антропометрическое измерение в отдельности.
Были разработаны значения окружности талии для этнической принадлежности, оптимизированные для выявления взрослых с повышенным риском сердечно-сосудистых заболеваний (таблица 2). За некоторыми исключениями, значения, представленные в таблице 2, были получены с использованием данных поперечного сечения и не учитывались в связи с ИМТ. Диапазон значений окружности талии высокого риска как для взрослых мужчин (80–98 см), так и для женщин (80–96 см) значительно варьируется в зависимости от этнической принадлежности, что подтверждает необходимость определения значений окружности талии для этнической принадлежности. Проспективные исследования с использованием репрезентативных групп населения необходимы для точного установления пороговых значений окружности талии для конкретных этнических групп и категорий ИМТ, которые отличают взрослых с повышенным риском для здоровья.
Таблица 2 Пороговые значения для этнической принадлежностиПолноразмерная таблица
Как отмечалось выше, значения окружности талии для этнической принадлежности в Таблице 2 были оптимизированы для выявления взрослых с повышенным риском сердечно-сосудистых заболеваний. Значения окружности талии в Японии, однако, были оптимизированы для идентификации мужчин и женщин со значениями НДС >100 см 3 на уровне пупка 112 , измеренными с помощью КТ. Основанием для использования НДС в качестве результата было то, что было обнаружено, что кардиометаболический риск существенно возрастает при этом уровне НДС для взрослых японских мужчин и женщин 9.0779 56 . Соответственно, японские пороговые значения окружности талии были установлены на уровне 85 см у мужчин и 90 см у женщин, что соответствовало порогу НДС в 100 см 3 (ref. 112 ).
Значения окружности талии в Японии, однако, были оптимизированы для идентификации мужчин и женщин со значениями НДС >100 см 3 на уровне пупка 112 , измеренными с помощью КТ. Основанием для использования НДС в качестве результата было то, что было обнаружено, что кардиометаболический риск существенно возрастает при этом уровне НДС для взрослых японских мужчин и женщин 9.0779 56 . Соответственно, японские пороговые значения окружности талии были установлены на уровне 85 см у мужчин и 90 см у женщин, что соответствовало порогу НДС в 100 см 3 (ref. 112 ).
Выводы и рекомендации — значения окружности талии для оценки риска для здоровья
Исходя из имеющихся данных, мы подвергаем сомнению обоснование текущих рекомендаций, рекомендующих использовать единый порог окружности талии для белых взрослых (мужчины> 102 см; женщины> 88 см) для обозначения высокой окружности талии, независимо от категории ИМТ.

Мы рекомендуем провести проспективные исследования с использованием репрезентативных групп населения, чтобы удовлетворить потребность в пороговых значениях окружности талии для конкретных категорий ИМТ для разных этнических групп (например, те, которые предложены в таблице 1 для белых взрослых). Однако эта рекомендация не умаляет важности измерения окружности талии для отслеживания изменений с течением времени и, следовательно, полезности стратегий, направленных на снижение абдоминального ожирения и связанного с ним риска для здоровья.
Выводы
Основная рекомендация настоящего Консенсуса заключается в том, что в клинической практике следует регулярно измерять окружность талии, поскольку это может предоставить дополнительную информацию для руководства ведением пациентов. Действительно, десятилетия исследований предоставили недвусмысленные доказательства того, что окружность талии предоставляет как независимую, так и дополнительную информацию к ИМТ для прогнозирования заболеваемости и смертности. На основании этих наблюдений отказ от измерения окружности талии в рутинной клинической практике не обеспечивает оптимального подхода к стратификации пациентов в соответствии с риском. Измерение окружности талии в клинических условиях важно и возможно. Самостоятельное измерение окружности талии легко получить и хорошо согласуется с окружностью талии, измеренной техническим специалистом. Многочисленные эпидемиологические исследования и РКИ в настоящее время продемонстрировали, что уменьшение окружности талии может быть достигнуто с помощью рутинных упражнений средней интенсивности и/или изменения диеты.
На основании этих наблюдений отказ от измерения окружности талии в рутинной клинической практике не обеспечивает оптимального подхода к стратификации пациентов в соответствии с риском. Измерение окружности талии в клинических условиях важно и возможно. Самостоятельное измерение окружности талии легко получить и хорошо согласуется с окружностью талии, измеренной техническим специалистом. Многочисленные эпидемиологические исследования и РКИ в настоящее время продемонстрировали, что уменьшение окружности талии может быть достигнуто с помощью рутинных упражнений средней интенсивности и/или изменения диеты.
Пробелы в наших знаниях все еще остаются, и уточнение пороговых значений окружности талии для данной категории ИМТ для разных возрастов, пола и этнической принадлежности потребует дальнейшего изучения. Чтобы удовлетворить эту потребность, мы рекомендуем проводить проспективные исследования в соответствующих популяциях. Несмотря на эти пробелы в наших знаниях, представленные здесь убедительные данные свидетельствуют о том, что измерение окружности талии улучшает ведение пациентов и что его исключение из рутинной клинической практики для большинства пациентов более недопустимо. Соответственно, включение измерения окружности талии в рутинную практику дает практикующим врачам важную возможность улучшить уход за пациентами и их здоровье. Медицинские работники должны быть обучены правильному выполнению этого простого измерения и должны рассматривать его как важный жизненно важный показатель для оценки и идентификации, как важную цель лечения в клинической практике.
Соответственно, включение измерения окружности талии в рутинную практику дает практикующим врачам важную возможность улучшить уход за пациентами и их здоровье. Медицинские работники должны быть обучены правильному выполнению этого простого измерения и должны рассматривать его как важный жизненно важный показатель для оценки и идентификации, как важную цель лечения в клинической практике.
Ссылки
Ng, M. et al. Глобальная, региональная и национальная распространенность избыточного веса и ожирения среди детей и взрослых в 1980–2013 гг.: систематический анализ для исследования глобального бремени болезней, 2013 г. Lancet 384 , 766–781 (2014).
ПабМед ПабМед Центральный Google ученый
Афшин А., Форузанфар М. Х., Рейтсма М. Б. и Сур П. Влияние избыточного веса и ожирения на здоровье в 195 стран за 25 лет.
 Н. англ. Дж. Мед. 377 , 13–27 (2017).
Н. англ. Дж. Мед. 377 , 13–27 (2017).ПабМед Google ученый
Phillips, C.M. Метаболически здоровое ожирение на протяжении всей жизни: эпидемиология, детерминанты и последствия. Энн. Н. Я. акад. науч. 1391 , 85–100 (2017).
ПабМед Google ученый
Белл, Дж. А. и др. Естественное течение здорового ожирения старше 20 лет. г. Дж. Ам. Сб. Кардиол. 65 , 101–102 (2015).
ПабМед Google ученый
Экель, Н., Мейдтнер, К., Калле-Ульманн, Т., Стефан, Н. и Шульце, М. Б. Метаболически здоровое ожирение и сердечно-сосудистые события: систематический обзор и метаанализ. евро. Дж. Прев. Кардиол. 23 , 956–966 (2016).
ПабМед Google ученый
«>Garvey, W. T. et al. Американская ассоциация клинических эндокринологов и Американский колледж эндокринологов, комплексные клинические рекомендации по оказанию медицинской помощи пациентам с ожирением. Эндокр. Практика. 22 (Приложение 3), 1–203 (2016).
ПабМед Google ученый
Jensen, M.D. et al. Руководство AHA/ACC/TOS 2013 г. по лечению избыточного веса и ожирения у взрослых: отчет рабочей группы Американского колледжа кардиологов/Американской кардиологической ассоциации по практическим рекомендациям и Обществу по борьбе с ожирением.
 Тираж 129 , S102–S138 (2014).
Тираж 129 , S102–S138 (2014).ПабМед Google ученый
Цигос, К. и др. Ведение ожирения у взрослых: Европейские рекомендации по клинической практике. Обес. Факты 1 , 106–116 (2008).
ПабМед ПабМед Центральный Google ученый
Pischon, T., Boeing, H., Hoffmann, K. & Bergmann, M. Общее и абдоминальное ожирение и риск смерти в Европе. Н. англ. Дж. Мед. 359 , 2105–2120 (2008 г.).
КАС пабмед Google ученый
Черхан, Дж. Р. и др. Объединенный анализ окружности талии и смертности у 650 000 взрослых. Майо Клин. проц. 89 , 335–345 (2014).
ПабМед ПабМед Центральный Google ученый
«>Song, X. et al. Сравнение различных показателей суррогатного ожирения как предикторов смертности от сердечно-сосудистых заболеваний в четырех европейских популяциях. евро. Дж. Клин. Нутр. 67 , 1298–1302 (2013).
КАС пабмед Google ученый
Seidell, JC. Окружность талии и соотношение талии и бедер в связи со смертностью от всех причин, раком и апноэ во сне. евро. Дж. Клин. Нутр. 64 , 35–41 (2010).
КАС пабмед Google ученый
«>Jacobs, E. J. et al. Окружность талии и смертность от всех причин в большой когорте в США. Арх. Стажер Мед. 170 , 1293–1301 (2010).
ПабМед Google ученый
Vague, J. Степень мужской дифференциации ожирения: фактор, определяющий предрасположенность к диабету, атеросклерозу, подагре и мочекаменной болезни. утра. Дж. Клин. Нутр. 4 , 20–34 (1956).
КАС пабмед Google ученый
Kissebah, A.H. et al. Связь распределения жира в организме с метаболическими осложнениями ожирения.
 Дж. Клин. Эндокринол. Метаб. 54 , 254–260 (1982).
Дж. Клин. Эндокринол. Метаб. 54 , 254–260 (1982).КАС пабмед Google ученый
Кроткевски М., Бьорнторп П., Сьостром Л. и Смит У. Влияние ожирения на обмен веществ у мужчин и женщин: важность регионального распределения жировой ткани. Дж. Клин. Инвестировать. 72 , 1150–1162 (1983).
КАС пабмед ПабМед Центральный Google ученый
Hartz, A.J., Rupley, D.C. Jr., Kalkhoff, R.D. & Rimm, A.A. Связь ожирения с диабетом: влияние уровня ожирения и распределения жира в организме. Пред. Мед. 12 , 351–357 (1983).
КАС пабмед Google ученый
Ларссон Б. и др. Распределение абдоминальной жировой ткани, ожирение и риск сердечно-сосудистых заболеваний и смерти: 13-летнее наблюдение за участниками исследования мужчин 1913 года рождения.
 Br. Мед. J. (Clin. Res. Ed.) 288 , 1401–1404 (1984).
Br. Мед. J. (Clin. Res. Ed.) 288 , 1401–1404 (1984).Google ученый
Ohlson, L. O. et al. Влияние распределения жира в организме на заболеваемость сахарным диабетом: 13,5-летнее наблюдение за участниками исследования мужчин 19 лет рождения13. Диабет 34 , 1055–1058 (1985).
КАС пабмед Google ученый
Снайдер, М. Б., ван Дам, Р. М., Виссер, М. и Зайделл, Дж. К. Какие аспекты жировых отложений особенно опасны и как мы их измеряем? Междунар. Дж. Эпидемиол. 35 , 83–92 (2006).
КАС пабмед Google ученый
Neeland, I. J. et al. Висцеральный и эктопический жир, атеросклероз и кардиометаболические заболевания: заявление с изложением позиции. Ланцет Диабет Эндокринол. 7 , 715–725 (2019).

ПабМед Google ученый
Lean, M.E., Han, T.S. & Morrison, C.E. Окружность талии как показатель, указывающий на необходимость контроля веса. BMJ 311 , 158–161 (1995).
КАС пабмед ПабМед Центральный Google ученый
Hsieh, S.D. & Yoshinaga, H. Отношение талии к росту как простой и полезный предиктор факторов риска ишемической болезни сердца у женщин. Интерн. Мед. 34 , 1147–1152 (1995).
КАС пабмед Google ученый
Ashwell, M., Lejeune, S. & McPherson, K. Отношение окружности талии к росту может быть лучшим индикатором необходимости контроля веса. BMJ 312 , 377 (1996).
КАС пабмед ПабМед Центральный Google ученый
«>Эшвелл, М., Ганн, П. и Гибсон, С. Соотношение талии и роста является лучшим скрининговым инструментом, чем окружность талии и ИМТ для взрослых кардиометаболических факторов риска: систематический обзор и метаанализ. Обес. 13 , 275–286 (2012).
КАС пабмед Google ученый
Пааянен, Т. А., Оксала, Н. К., Куукасярви, П. и Кархунен, П. Дж. Низкий рост связан с ишемической болезнью сердца: систематический обзор литературы и метаанализ. евро. Heart J. 31 , 1802–1809 (2010).

ПабМед Google ученый
Хан, Т. С. и др. Влияние роста и возраста на окружность талии как показатель ожирения у взрослых. Междунар. Дж. Обес. Относ. Метаб. Беспорядок. 21 , 83–89 (1997).
КАС пабмед Google ученый
Вальдес Р., Зайделл Дж. К., Ан Ю. И. и Вайс К. М. Новый индекс абдоминального ожирения как показатель риска сердечно-сосудистых заболеваний. Межпопуляционное исследование. Междунар. Дж. Обес. Относ. Метаб. Беспорядок. 17 , 77–82 (1993).
КАС пабмед Google ученый
Amankwah, N. et al. Индекс абдоминального ожирения в качестве альтернативного измерения центрального ожирения при физикальном обследовании. Открыто. Нутр. J. 12 , 21–29 (2018).
Google ученый
«>Янссен И., Шилдс М., Крейг С.Л. и Тремблей М.С. Изменения фенотипа ожирения у канадских детей и взрослых, 1981–2007–2009 гг. Ожирение 20 , 916–919 (2012).
ПабМед Google ученый
Альбрехт, С. С., Гордон-Ларсен, П., Стерн, Д. и Попкин, Б. М. Растет ли окружность талии на индекс массы тела по-разному в Соединенных Штатах, Англии, Китае и Мексике? евро. Дж. Клин. Нутр. 69 , 1306–1312 (2015).
КАС пабмед ПабМед Центральный Google ученый
Висшер, Т. Л., Хайтманн, Б. Л., Риссанен, А., Лахти-Коски, М. и Лисснер, Л.
 Прорыв в эпидемии ожирения? Объясняется предвзятостью или неправильной интерпретацией данных? Междунар. Дж. Обес. 39 , 189–198 (2015).
Прорыв в эпидемии ожирения? Объясняется предвзятостью или неправильной интерпретацией данных? Междунар. Дж. Обес. 39 , 189–198 (2015).КАС Google ученый
Rexrode, K.M. et al. Абдоминальное ожирение и ишемическая болезнь сердца у женщин. JAMA 280 , 1843–1848 (1998).
КАС пабмед Google ученый
Despres, J. P. Избыток висцеральной жировой ткани/эктопический жир недостающее звено в парадоксе ожирения? Дж. Ам. Сб. Кардиол. 57 , 1887–1889 (2011).
ПабМед Google ученый
Zhang, X. et al. Абдоминальное ожирение и смертность китайских женщин. Арх. Стажер Мед. 167 , 886–892 (2007).
ПабМед Google ученый
«>Всемирная организация здравоохранения. Ожирение: предотвращение глобальной эпидемии и борьба с ней: отчет о консультации ВОЗ (Серия технических отчетов Всемирной организации здравоохранения, 894) (ВОЗ, 2000 г.).
Bigaard, J. et al. Окружность талии, ИМТ, курение и смертность среди мужчин и женщин среднего возраста. Обес. Рез. 11 , 895–903 (2003).
ПабМед Google ученый
Коутиньо, Т. и др. Центральное ожирение и выживаемость у пациентов с ишемической болезнью сердца: систематический обзор литературы и совместный анализ данных отдельных субъектов.
 Дж. Ам. Сб. Кардиол. 57 , 1877–1886 (2011).
Дж. Ам. Сб. Кардиол. 57 , 1877–1886 (2011).ПабМед Google ученый
Слуик, Д. и др. Взаимосвязь между общим и абдоминальным ожирением и смертностью у лиц с сахарным диабетом. утра. Дж. Эпидемиол. 174 , 22–34 (2011).
ПабМед Google ученый
Despres, J.P. & Lemieux, I. Абдоминальное ожирение и метаболический синдром. Природа 444 , 881–887 (2006).
КАС пабмед Google ученый
Snijder, M.B. et al. Низкий уровень подкожного жира на бедрах является фактором риска неблагоприятного уровня глюкозы и липидов, независимо от большого количества абдоминального жира. Азбука здоровья. Диабетология 48 , 301–308 (2005).
КАС пабмед Google ученый
«>Льюис, Г. Ф., Карпентье, А., Адели, К. и Джакка, А. Нарушение накопления и мобилизации жира в патогенезе резистентности к инсулину и диабета 2 типа. Эндокр. 23 , 201–229 (2002).
КАС пабмед Google ученый
Despres, J.P. et al. Инсулинорезистентный дислипидемический синдром: вклад висцерального ожирения и терапевтические последствия. Междунар. Дж. Обес. Относ. Метаб. Беспорядок. 19 (Прил. 1), S76–S86 (1995).
ПабМед Google ученый
Nguyen-Duy, T.B., Nichaman, M.
 Z., Church, T.S., Blair, S.N. & Ross, R. Висцеральный жир и печеночный жир являются независимыми предикторами метаболических факторов риска у мужчин. утра. Дж. Физиол. Эндокринол. Метаб. 284 , E1065–E1071 (2003 г.).
Z., Church, T.S., Blair, S.N. & Ross, R. Висцеральный жир и печеночный жир являются независимыми предикторами метаболических факторов риска у мужчин. утра. Дж. Физиол. Эндокринол. Метаб. 284 , E1065–E1071 (2003 г.).КАС пабмед Google ученый
Кук, Дж. Л. и др. Висцеральный жир является независимым предиктором смертности от всех причин у мужчин. Ожирение 14 , 336–341 (2006).
ПабМед Google ученый
Кук, Дж. Л., Янишевски, П. М. и Росс, Р. Индекс массы тела и окружность бедер и бедер отрицательно связаны с висцеральной жировой тканью после контроля окружности талии. утра. Дж. Клин. Нутр. 85 , 1540–1544 (2007).
КАС пабмед Google ученый
Янссен И., Кацмарзик П. Т. и Росс Р.
 Индекс массы тела обратно пропорционален смертности пожилых людей после поправки на окружность талии. Дж. Ам. Гериатр. соц. 53 , 2112–2118 (2005).
Индекс массы тела обратно пропорционален смертности пожилых людей после поправки на окружность талии. Дж. Ам. Гериатр. соц. 53 , 2112–2118 (2005).ПабМед Google ученый
Альберти К.Г., Зиммет П. и Шоу Дж. Метаболический синдром: новое всемирное определение. Ланцет 366 , 1059–1062 (2005).
ПабМед Google ученый
Зиммет П., Мальяно Д., Мацузава Ю., Альберти Г. и Шоу Дж. Метаболический синдром: глобальная проблема общественного здравоохранения и новое определение. Дж. Атеросклера. тромб. 12 , 295–300 (2005).
КАС пабмед Google ученый
Hlatky, M.A. et al. Критерии оценки новых маркеров сердечно-сосудистого риска: научное заявление Американской кардиологической ассоциации. Тираж 119 , 2408–2416 (2009).

ПабМед ПабМед Центральный Google ученый
Гренландия, П. и др. Руководство ACCF/AHA 2010 г. по оценке сердечно-сосудистого риска у бессимптомных взрослых: краткое изложение: отчет целевой группы Фонда Американского колледжа кардиологов/Американской кардиологической ассоциации по практическим рекомендациям. Тираж 122 , 2748–2764 (2010).
ПабМед Google ученый
Пенчина, М.Дж., Д.Агостино, Р.Б., Пенчина, К.М., Янссенс, А.С. и Гренландия, П. Интерпретация возрастающей ценности маркеров, добавленных в модели прогнозирования риска. утра. Дж. Эпидемиол. 176 , 473–481 (2012).
ПабМед ПабМед Центральный Google ученый
Кармиенке, С. и др. Параметры общего и абдоминального ожирения и их сочетание по отношению к смертности: систематический обзор и мета-регрессионный анализ.
 евро. Дж. Клин. Нутр. 67 , 573–585 (2013).
евро. Дж. Клин. Нутр. 67 , 573–585 (2013).КАС пабмед Google ученый
Hong, Y. et al. Метаболический синдром, его основные кластеры, ишемическая болезнь сердца и смертность от всех причин: результаты проспективного анализа риска атеросклероза в популяционном исследовании. Дж. Междунар. Мед. 262 , 113–122 (2007).
КАС пабмед Google ученый
Wilson, P.W. et al. Прогнозирование ишемической болезни сердца с использованием категорий факторов риска. Тираж 97 , 1837–1847 (1998).
КАС пабмед Google ученый
Goff, D.C. Jr., Lloyd-Jones, DM, Bennett, G. & Coady, S. Руководство ACC/AHA 2013 г. по оценке сердечно-сосудистого риска: отчет Американского колледжа кардиологов/Американской кардиологической ассоциации силу на практических рекомендациях.
 Тираж 129 , S49–S73 (2014).
Тираж 129 , S49–S73 (2014).ПабМед Google ученый
Khera, R. et al. Точность объединенного когортного уравнения для оценки событий риска атеросклеротических сердечно-сосудистых заболеваний по классам ожирения: объединенная оценка пяти продольных когортных исследований. Дж. Ам. Сб. Кардиол . https://doi.org/10.1016/S0735-1097(18)32279-4 (2018 г.).
Артикул пабмед ПабМед Центральный Google ученый
Empana, J.P. et al. Прогнозирование риска ИБС во Франции: объединенный анализ исследований D.E.S.I.R., трех городов, PRIME и SU.VI.MAX. евро. Дж. Кардиовасц. Пред. Реабилит. 18 , 175–185 (2011).
КАС пабмед Google ученый
Кук, Н. Р. Методы оценки новых биомаркеров: новая парадигма.
 Междунар. Дж. Клин. Практика. 64 , 1723–1727 (2010).
Междунар. Дж. Клин. Практика. 64 , 1723–1727 (2010).КАС пабмед ПабМед Центральный Google ученый
Кук, Н. Р. Использование и неправильное использование кривой рабочих характеристик приемника при прогнозировании рисков. Тираж 115 , 928–935 (2007).
ПабМед Google ученый
Пенчина, М. Дж., Д. Агостино, Р. Б., старший Д. Агостино, Р. Б. младший, и Васан, Р. С. Оценка дополнительной прогностической способности нового маркера: от площади под кривой ROC до реклассификации и далее. г. Стат. Мед. 27 , 157–172 (2008).
ПабМед Google ученый
Pencina, M.J. et al. Количественная оценка основных факторов риска ишемической болезни сердца. Тираж 139 , 1603–1611 (2018).

Центральный пабмед Google ученый
Lincoff, A.M. et al. Эвацетрапиб и сердечно-сосудистые исходы при сосудистых заболеваниях высокого риска. г. Н. англ. Дж. Мед. 376 , 1933–1942 (2017).
ПабМед Google ученый
Черч, Т. С., Эрнест, С. П., Скиннер, Дж. С. и Блэр, С. Н. Влияние различных доз физической активности на кардиореспираторную выносливость у малоподвижных женщин, женщин с избыточным весом или ожирением в постменопаузе с повышенным кровяным давлением: рандомизированное контролируемое исследование. JAMA 297 , 2081–2091 (2007 г.).
КАС пабмед Google ученый
О’Донован Г. и др. Изменения кардиореспираторной выносливости и факторов риска ишемической болезни сердца после 24 недель упражнений средней или высокой интенсивности с равными энергозатратами.
 J. Appl. Физиол. 98 , 1619–1625 (2005).
J. Appl. Физиол. 98 , 1619–1625 (2005).ПабМед Google ученый
Росс, Р. и др. Снижение ожирения и связанных с ним сопутствующих заболеваний после снижения веса, вызванного диетой или физическими упражнениями, у мужчин: рандомизированное контролируемое исследование. г. н.э. Стажер Мед. 133 , 92–103 (2000).
КАС пабмед Google ученый
Росс Р., Хадсон Р., Стотц П. Дж. и Лам М. Влияние количества и интенсивности упражнений на абдоминальное ожирение и толерантность к глюкозе у взрослых с ожирением: рандомизированное исследование. Энн. Стажер Мед. 162 , 325–334 (2015).
ПабМед Google ученый
Росс, Р. и др. Вызванное физическими упражнениями снижение ожирения и резистентности к инсулину у женщин: рандомизированное контролируемое исследование.
 Обес. Рез. 12 , 789–798 (2004).
Обес. Рез. 12 , 789–798 (2004).ПабМед Google ученый
Шорт, К. Р. и др. Влияние аэробных упражнений на возрастные изменения чувствительности к инсулину и окислительной способности мышц. Диабет 52 , 1888–1896 (2003).
КАС пабмед Google ученый
Weiss, E. P. et al. Улучшение толерантности к глюкозе и действие инсулина, вызванное увеличением расхода энергии или снижением потребления энергии: рандомизированное контролируемое исследование. утра. Дж. Клин. Нутр. 84 , 1033–1042 (2006).
КАС пабмед ПабМед Центральный Google ученый
Частон, Т. Б. и Диксон, Дж. Б. Факторы, связанные с процентным изменением висцерального жира по сравнению с подкожным абдоминальным жиром во время похудения: результаты систематического обзора.
 Междунар. Дж. Обес. 32 , 619–628 (2008).
Междунар. Дж. Обес. 32 , 619–628 (2008).КАС Google ученый
Хаммонд, Б. П., Бреннан, А. М. и Росс, Р. в Состав тела: здоровье и работоспособность в упражнениях и спорте (под редакцией Лукаски, Х.К.) 109–128 (CRC Press, Taylor and Francis Group, 2017) .
Кей С.Дж. и Фиатарон Сингх М.А. Влияние физической активности на абдоминальный жир: систематический обзор литературы. Обес. 7 , 183–200 (2006).
КАС пабмед Google ученый
Merlotti, C., Ceriani, V., Morabito, A. & Pontiroli, A.E. Потеря подкожного жира больше, чем потеря висцерального жира с помощью диеты и упражнений, препаратов, способствующих снижению веса, и бариатрической хирургии: критический обзор и метаданные -анализ. Междунар. Дж. Обес. 41 , 672–682 (2017).

КАС Google ученый
Окавара К., Танака С., Миячи М., Исикава-Таката К. и Табата И. Зависимость доза-реакция между аэробными упражнениями и уменьшением висцерального жира: систематический обзор клинических испытаний. Междунар. Дж. Обес. 31 , 1786–1797 (2007).
КАС Google ученый
O’Neill, T., Shalev-Goldman, E. & Ross, R. в Лечебная физкультура у взрослых с ожирением (изд. Hansen, D.) 43-72 (Nova Science Publishers, 2013) .
Сабаг А. и др. Упражнения и эктопический жир при диабете 2 типа: систематический обзор и метаанализ. Диабет Метаб. 43 , 195–210 (2017).
КАС пабмед Google ученый
Verheggen, R. J. et al. Систематический обзор и метаанализ эффектов физических упражнений по сравнению с гипокалорийной диетой: различные эффекты на массу тела и висцеральную жировую ткань.
 Обес. Откр. 17 , 664–690 (2016).
Обес. Откр. 17 , 664–690 (2016).КАС пабмед Google ученый
Сантос, Ф.Л., Эстевес, С.С., да Кошта Перейра, А., Янси, У.С. младший и Нуньес, Дж.П. Систематический обзор и метаанализ клинических испытаний влияния низкоуглеводной диеты на сердечно-сосудистые факторы риска. Обес. 13 , 1048–1066 (2012).
КАС пабмед Google ученый
Гепнер Ю. и др. Влияние различных вмешательств на образ жизни на мобилизацию запасов жира: рандомизированное контролируемое исследование ЦЕНТРАЛЬНОЙ магнитно-резонансной томографии. Тираж 137 , 1143–1157 (2018).
ПабМед Google ученый
Sacks, F. M. et al. Сравнение диет для похудения с различным составом жиров, белков и углеводов. Н. англ. Дж.
 Мед. 360 , 859–873 (2009).
Мед. 360 , 859–873 (2009).КАС пабмед ПабМед Центральный Google ученый
Keating, S.E. et al. Влияние тренировочной дозы аэробных упражнений на жир в печени и висцеральное ожирение. Дж. Гепатол. 63 , 174–182 (2015).
ПабМед Google ученый
Slentz, C.A. et al. Влияние количества упражнений на массу тела, состав тела и показатели центрального ожирения. STRRIDE: рандомизированное контролируемое исследование. г. арх. Стажер Мед. 164 , 31–39 (2004).
ПабМед Google ученый
Slentz, C.A. et al. Отсутствие активности, физические упражнения и висцеральный жир. STRRIDE: рандомизированное контролируемое исследование интенсивности и количества упражнений. J. Appl. Физиол. 99 , 1613–1618 (2005).

ПабМед Google ученый
Ирвинг, Б.А. и др. Влияние интенсивности тренировок на абдоминальный висцеральный жир и состав тела. Мед. науч. Спортивное упражнение. 40 , 1863–1872 (2008 г.).
ПабМед ПабМед Центральный Google ученый
Wewege, M., van den Berg, R., Ward, R.E. & Keech, A. Влияние высокоинтенсивных интервальных тренировок по сравнению с непрерывными тренировками средней интенсивности на состав тела у взрослых с избыточным весом и ожирением: систематический анализ обзор и метаанализ. Обес. 18 , 635–646 (2017).
КАС пабмед Google ученый
Vissers, D. et al. Влияние физических упражнений на висцеральную жировую ткань у взрослых с избыточным весом: систематический обзор и метаанализ.
 PLoS One 8 , e56415 (2013 г.).
PLoS One 8 , e56415 (2013 г.).КАС пабмед ПабМед Центральный Google ученый
Янишевски П. М. и Росс Р. Физическая активность в лечении ожирения: помимо снижения массы тела. Заяв. Физиол. Нутр. Метаб. 32 , 512–522 (2007).
ПабМед Google ученый
Кук Дж. Л., Ли С., Хеймсфилд С. Б. и Росс Р. Окружность талии и распределение жировой ткани на животе: влияние возраста и пола. утра. Дж. Клин. Нутр. 81 , 1330–1334 (2005).
КАС пабмед Google ученый
Росс, Р. и др. Зависит ли взаимосвязь между окружностью талии, заболеваемостью и смертностью от протокола измерения окружности талии? Обес. 9 , 312–325 (2008).
КАС пабмед Google ученый
«>Образовательная инициатива NHLBI по борьбе с ожирением. Практическое руководство по выявлению, оценке и лечению избыточного веса и ожирения у взрослых (NIH, 2000).
Wang, J. et al. Сравнение окружностей талии, измеренных в 4 местах. утра. Дж. Клин. Нутр. 77 , 379–384 (2003).
ПабМед Google ученый
Mason, C. & Katzmarzyk, P.T. Изменчивость измерений окружности талии в зависимости от места анатомического измерения. Ожирение 17 , 1789–1795 (2009).
ПабМед Google ученый
Мацусита Ю., Томита К., Йокояма Т. и Мизоуэ Т. Оптимальное место измерения окружности талии для оценки метаболического синдрома.
 Diabetes Care 32 , e70 (2009).
Diabetes Care 32 , e70 (2009).ПабМед Google ученый
Мацусита Ю., Томита К., Йокояма Т. и Мизоуэ Т. Взаимосвязь между окружностью талии в четырех местах и метаболическими факторами риска. Ожирение 18 , 2374–2378 (2010).
ПабМед Google ученый
Пендергаст, К. и др. Влияние разницы в окружности талии на стоимость медицинского обслуживания среди субъектов с избыточным весом и ожирением: когорта PROCEED. Value Health 13 , 402–410 (2010 г.).
ПабМед Google ученый
Spencer, E. A., Roddam, A. W. & Key, T. J. Точность измерений талии и бедер по самооценке в 4492 участника EPIC-Oxford. Нутр общественного здравоохранения. 7 , 723–727 (2004).
ПабМед Google ученый
«>Bigaard, J., Spanggaard, I., Thomsen, B.L., Overvad, K. & Tjonneland, A. Окружность талии, измеренная самостоятельно и техническим специалистом, различается у мужчин и женщин среднего возраста. Дж. Нутр. 135 , 2263–2270 (2005).
КАС пабмед Google ученый
Wolf, A. M. et al. ПРОДОЛЖЕНИЕ: предполагаемая когорта ожирения экономической оценки и детерминанты: исходное состояние здоровья и использование здравоохранения в выборке США. Диабет Ожирение. Метаб. 10 , 1248–1260 (2008).
КАС пабмед Google ученый
«>Ардерн, С. И., Янссен, И., Росс, Р. и Кацмарзик, П. Т. Разработка пороговых значений окружности талии, связанных со здоровьем, в рамках категорий ИМТ. Обес. Рез. 12 , 1094–1103 (2004).
ПабМед Google ученый
Баджадж, Х. С., Бреннан, Д. М., Хугверф, Б. Дж., Доши, К. Б. и Кашьяп, С. Р. Клиническая полезность окружности талии для прогнозирования смертности от всех причин в профилактической кардиологической клинике: исследование базы данных PreCIS. Ожирение 17 , 1615–1620 (2009).
ПабМед Google ученый
«>Си, Б. и др. Многовековые тенденции распространенности общего и абдоминального ожирения среди взрослых китайцев, 1993–2009 гг. Обес. 13 , 287–296 (2012).
КАС пабмед Google ученый
Барзин М. и др. Тенденции роста ожирения и абдоминального ожирения за 10 лет наблюдения среди взрослых жителей Тегерана: Тегеранское исследование липидов и глюкозы (TLGS). Нутр общественного здравоохранения. 18 , 2981–2989 (2015).
ПабМед Google ученый
«>Liese, A.D., Doring, A., Hense, H.W. & Keil, U. Пятилетние изменения окружности талии, индекса массы тела и ожирения в Аугсбурге, Германия. евро. Дж. Нутр. 40 , 282–288 (2001).
КАС пабмед Google ученый
Czernichow, S. et al. Тенденции распространенности ожирения среди работающих взрослых в центрально-западной Франции: популяционное исследование, 1995–2005 гг. Пред. Мед. 48 , 262–266 (2009).
ПабМед Google ученый
Ford, E. S., Maynard, L.
 M. & Li, C. Тенденции средней окружности талии и абдоминального ожирения среди взрослых в США, 19 лет99–2012. JAMA 312 , 1151–1153 (2014).
M. & Li, C. Тенденции средней окружности талии и абдоминального ожирения среди взрослых в США, 19 лет99–2012. JAMA 312 , 1151–1153 (2014).ПабМед ПабМед Центральный Google ученый
Огден, К.Л., Кэрролл, М.Д., Кит, Б.К. и Флегал, К.М. Распространенность детского и взрослого ожирения в США, 2011–2012 гг. JAMA 311 , 806–814 (2014).
КАС пабмед ПабМед Центральный Google ученый
Gearon, E., Tanamas, S.K., Stevenson, C., Loh, V.H.Y. & Peeters, A. Изменения окружности талии независимо от веса: значение для мониторинга ожирения на уровне населения. Пред. Мед. 111 , 378–383 (2018).
ПабМед Google ученый
Окосун И.С. и др. Абдоминальное ожирение у взрослых в США: распространенность и тенденции, 1960–2000 гг.
 Пред. Мед. 39 , 197–206 (2004).
Пред. Мед. 39 , 197–206 (2004).ПабМед Google ученый
Экзаменационный комитет по критериям «ожирения» в Японии и Японское общество изучения ожирения. Новые критерии «болезни ожирения» в Японии. Обр. J. 66 , 987–992 (2002).
Google ученый
Аль-Одат, А.З., Ахмад, М.Н. и Хаддад, Ф.Х. Ссылки на антропометрические показатели центрального ожирения и метаболического синдрома у иорданских мужчин и женщин. Диабет Метаб. Синдр. 6 , 15–21 (2012).
ПабМед Google ученый
Уайлдман, Р. П., Гу, Д., Рейнольдс, К., Дуан, X. и Хе, Дж. Соответствующие предельные значения индекса массы тела и окружности талии для классификации избыточного веса и центрального ожирения среди взрослых китайцев. утра.
 Дж. Клин. Нутр. 80 , 1129–1136 (2004).
Дж. Клин. Нутр. 80 , 1129–1136 (2004).КАС пабмед Google ученый
Юн, Ю. С. и О, С. В. Оптимальные пороговые значения окружности талии для диагностики абдоминального ожирения у взрослых корейцев. Эндокринол. Метаб. 29 , 418–426 (2014).
Google ученый
Bouguerra, R. et al. Пороговые значения окружности талии для выявления абдоминального ожирения среди взрослого населения Туниса. Диабет Ожирение. Метаб. 9 , 859–868 (2007).
КАС пабмед Google ученый
Делавари А., Форузанфар М. Х., Алихани С., Шарифиан А. и Келишади Р. Первое общенациональное исследование распространенности метаболического синдрома и оптимальных пороговых значений окружности талии на Ближнем Востоке: национальное обследование факторов риска неинфекционных заболеваний Ирана.
 Diabetes Care 32 , 1092–1097 (2009).
Diabetes Care 32 , 1092–1097 (2009).ПабМед ПабМед Центральный Google ученый
Мисра, А. и др. Точки отсечения окружности талии и уровни действий для азиатских индейцев для выявления абдоминального ожирения. Междунар. Дж. Обес. 30 , 106–111 (2006).
КАС Google ученый
Brauer, P. et al. Рекомендации по предотвращению увеличения веса и использованию поведенческих и фармакологических вмешательств для лечения избыточного веса и ожирения у взрослых в учреждениях первичной медико-санитарной помощи. CMAJ 187 , 184–195 (2015).
ПабМед ПабМед Центральный Google ученый
Zhang, C., Rexrode, K.M., van Dam, R.M., Li, T.Y. & Hu, F.B. Абдоминальное ожирение и риск смертности от всех причин, сердечно-сосудистых заболеваний и рака: шестнадцать лет наблюдения за женщинами в США . Тираж 117 , 1658–1667 (2008 г.).
ПабМед Google ученый
Snijder, M.B. et al. Ассоциации окружности бедер и бедер независимо от окружности талии с заболеваемостью диабетом 2 типа: исследование Хорна. утра. Дж. Клин. Нутр. 77 , 1192–1197 (2003).
КАС пабмед Google ученый
Browning, L.M., Hsieh, S.D. & Ashwell, M. Систематический обзор отношения талии к росту как скринингового инструмента для прогнозирования сердечно-сосудистых заболеваний и диабета: 0,5 может быть подходящим глобальным граничным значением. Нутр. Рез. 23 , 247–269 (2010).
ПабМед Google ученый
Walls, H.L. et al. Тенденции ИМТ взрослых городских жителей Австралии, 1980–2000 гг. Общественный. Нутр Здоровья. 13 , 631–638 (2010).
ПабМед Google ученый
de Hollander, E.L. et al. Связь между окружностью талии и риском смертности с учетом индекса массы тела у людей в возрасте от 65 до 74 лет: метаанализ 29 когорт с участием более 58 000 пожилых людей. Междунар. Дж. Эпидемиол. 41 , 805–817 (2012).
ПабМед ПабМед Центральный Google ученый
Иствуд, С. В. и др. Жир на бедрах и мышцы вносят свой вклад в избыточный кардиометаболический риск у выходцев из Южной Азии, независимо от висцеральной жировой ткани. Ожирение 22 , 2071–2079 (2014).
ПабМед Google ученый
Всемирная организация здравоохранения. Физический статус: использование и интерпретация антропометрии: отчет Комитета экспертов ВОЗ (ВОЗ, 1995).
Робертс, К.А., Уайлдер, Л.Б., Джексон, Р.Т., Мой, Т.Ф. и Беккер, Д.М. Точность самостоятельного измерения окружности талии и бедер у мужчин и женщин. Дж. Ам. Диета. доц. 97 , 534–536 (1997).
КАС пабмед Google ученый
Janssen, I., Katzmarzyk, P. T. & Ross, R. Индекс массы тела, окружность талии и риск для здоровья: доказательства в поддержку текущих рекомендаций Национального института здравоохранения. Арх. Стажер Мед. 162 , 2074–2079 (2002).
ПабМед Google ученый
Staiano, A.E., Bouchard, C. & Katzmarzyk, P.T. Пороговые значения окружности талии для определения повышенного кардиометаболического риска у белых и афроамериканцев. Обес. Факты 6 , 317–324 (2013).
ПабМед ПабМед Центральный Google ученый
Лахти-Коски М., Харальд К., Маннисто С., Лаатикайнен Т. и Йоусилахти П. Пятнадцатилетние изменения индекса массы тела и окружности талии у взрослых финнов. евро. Дж. Кардиовасц. Пред. Реабилит. 14 , 398–404 (2007).
ПабМед Google ученый
Скачать ссылки
Благодарности
Авторы признательны за финансовую поддержку IAS и ICCR, независимой академической организации, базирующейся в Университете Лаваля, Квебек, Канада, которые отвечали за координацию подготовки нашего отчета. Ни IAS, ни ICCR не предоставили финансирования или гонораров членам группы авторов для подготовки этой статьи. Научный руководитель ICCR (J.-PD) финансируется за счет гранта Фонда (ссылочный номер финансирования FDN-167278) Канадского института исследований в области здравоохранения.
Информация об авторе
Авторы и организации
Школа кинезиологии и медицинских исследований, Медицинский факультет, кафедра эндокринологии и метаболизма, Королевский университет, Кингстон, Онтарио, Канада
Robert Ross
Кафедра сердечно-сосудистой медицины и общественной медицины, Высшая школа медицины Осакского университета, Осака, Япония
Shizuya Yamashita
Факультет медицинских наук Университета Бен-Гуриона в Негеве, Беэр-Шева, Израиль
Iris Shai
Департамент медицинских наук и Институт медицинских исследований EMGO, Университет VU Амстердам, Амстердам, Нидерланды
Jaap Seidell
Кафедра фармакологических и биомолекулярных наук, Universita’ degli Studi di Milano, Милан, Италия
Paolo Magni
Научный институт исследований, госпитализации и здравоохранения (IRCCS) MultiMedica, Сесто-Сан-Джованни, Италия
Paolo Magni
Липидная клиника Кардиологический институт (InCor), Университет Сан-Паулу, Больница медицинской школы, Сан-Паулу , Бразилия
Рауль Д.
 Сантос
СантосГоспиталь Израэлита Альберта Эйнштейна, Сан-Паулу, Бразилия
Рауль Д. Сантос
Кафедра кинезиологии, медицинский факультет, Университет Лаваля, Квебек 9, Канада0021
Бенуа Арсено и Жан-Пьер Депре
Отделение клинического питания и обмена веществ, Клиника Лас Кондес, Сантьяго, Чили
Ада Куэвас
Отделение питания и эпидемии, Harvart Temidology. Школа общественного здравоохранения Чана, Бостон, Массачусетс, США
Frank B. Hu
Факультет диетологии, Университет Суррея, Гилфорд, Великобритания
Брюс А. Гриффин
Факультет медицины – DIMED, Университет Падуи, Падуя, Италия
Alberto Zambon
Школа медицинских наук, Университет Нового Южного Уэльса, Австралия, Сидней, Новый Южный Уэльс, Австралия
Филип Бартер
Fondation Cœur Etères, Lille, France
Jean-Charles Fruch Fruch Fruch
120 2Jean-Charles Fruch Fruch
120 2.

Отделение эндокринологии, метаболизма и диабета и отделение кардиологии, Медицинский факультет Колорадского университета Аншутца, Аврора, Колорадо, США
Robert H. Eckel
Department of Endocrinology and Metabolism, Sumitomo Hospital, Osaka, Japan
Yuji Matsuzawa
Department of Medicine, Faculty of Medicine, Université Laval, Québec, QC, Canada
Jean-Pierre Després
80 Департамент внутренних болезней , Отделение кардиологии, Юго-западный медицинский центр Техасского университета, Даллас, Техас, США
Ян Дж. Ниланд и Бенуа Арсено
Authors
- Robert Ross
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Ian J. Neeland
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Shizuya Yamashita
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Iris Shai
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Jaap Seidell
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- Paolo Magni
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Raul D.
 Santos
SantosПросмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Benoit Arsenault
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Ada Cuevas
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Frank B. Hu
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Bruce A. Griffin
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Альберто Замбон
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Philip Barter
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Jean-Charles Fruchart
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Robert H.
 Eckel
EckelПосмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Yuji Matsuzawa
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Jean-Pierre Després
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Contributions
R.R., I.J.N. и Ж.-П.Д. Подобрал данные для статьи. Р.Р., И.Дж.Н., С.Ю., И.С., Дж.С., Ф.Б.Х., Ю.М. и Ж.-П.Д. внес существенный вклад в обсуждение содержания. Р.Р., И.Дж.Н. и Ж.-П.Д. написал статью. Р.Р., И.Дж.Н., И.С., Дж.С., П.М., Р.Д.С., Б.А., А.С., Ф.Б.Х., Б.А.Г., А.З., П.Б., Дж.-К.Ф., Р.Х.Е., Ю.М. и Ж.-П.Д. рассмотрел и / или отредактировал рукопись перед отправкой.
Автор, ответственный за переписку
Переписка с Роберт Росс.
Декларации этики
Конкурирующие интересы
I. J.N. сообщает о получении вознаграждения за консультации и работу в консультативном совете от Boehringer Ingelheim/Lilly Alliance и AMRA Medical, а также исследовательского гранта от Novo Nordisk. Ф.Б.Х. сообщает о получении гонорара от Metagenics и Standard Process и исследовательского гранта от Калифорнийской комиссии по орехам. Р.Д.С. сообщает о получении консультаций и спикеров от Amgen, Astra Zeneca, Akcea, Biolab, Esperion, Kowa, Merck, MSD, Novo Nordisk, Sanofi Regeneron, Akcea, Kowa и Esperion. С.Ю. сообщает о грантах и личных вознаграждениях от Kowa Company, Ltd., Otsuka Pharmaceutical Co., Ltd., Shionogi & Co., Ltd., Bayer Yakuhin, Ltd., MSD K.K., Takeda Pharmaceutical Company, Ltd., Sanwa Kagaku Kenkyusho Co., Ltd., Astellas Pharma Inc., Daiichi-Sankyo Company, Ltd., Astra Zeneka K.K. и Какен Фармасьютикал Ко., Лтд.; гранты от Kyowa Medex Co., Ltd., Nippon Boehringer Ingelheim Co., Ltd., Национального института биомедицинских инноваций, Hayashibara Co., Ltd., Teijin Pharma Limited, Kissei and Mochida Pharmaceutical Company, Ltd.
J.N. сообщает о получении вознаграждения за консультации и работу в консультативном совете от Boehringer Ingelheim/Lilly Alliance и AMRA Medical, а также исследовательского гранта от Novo Nordisk. Ф.Б.Х. сообщает о получении гонорара от Metagenics и Standard Process и исследовательского гранта от Калифорнийской комиссии по орехам. Р.Д.С. сообщает о получении консультаций и спикеров от Amgen, Astra Zeneca, Akcea, Biolab, Esperion, Kowa, Merck, MSD, Novo Nordisk, Sanofi Regeneron, Akcea, Kowa и Esperion. С.Ю. сообщает о грантах и личных вознаграждениях от Kowa Company, Ltd., Otsuka Pharmaceutical Co., Ltd., Shionogi & Co., Ltd., Bayer Yakuhin, Ltd., MSD K.K., Takeda Pharmaceutical Company, Ltd., Sanwa Kagaku Kenkyusho Co., Ltd., Astellas Pharma Inc., Daiichi-Sankyo Company, Ltd., Astra Zeneka K.K. и Какен Фармасьютикал Ко., Лтд.; гранты от Kyowa Medex Co., Ltd., Nippon Boehringer Ingelheim Co., Ltd., Национального института биомедицинских инноваций, Hayashibara Co., Ltd., Teijin Pharma Limited, Kissei and Mochida Pharmaceutical Company, Ltd. ; и персональные сборы от Ono Pharmaceutical Company, Ltd., Skylight Biotec, Inc., Pfizer, Astellas Amgen, Sanofi и Aegerion. С.Ю. также имеет патенты, выданные Fujirebio и Kyowa Medex Co., Ltd. R.H.E. сообщает о своей роли научного консультанта PROMINENT (Kowa Company Ltd.) и членстве в консультативных комитетах Novo Nordisk и Sanofi/Regeneron. Остальные авторы заявляют об отсутствии конкурирующих интересов.
; и персональные сборы от Ono Pharmaceutical Company, Ltd., Skylight Biotec, Inc., Pfizer, Astellas Amgen, Sanofi и Aegerion. С.Ю. также имеет патенты, выданные Fujirebio и Kyowa Medex Co., Ltd. R.H.E. сообщает о своей роли научного консультанта PROMINENT (Kowa Company Ltd.) и членстве в консультативных комитетах Novo Nordisk и Sanofi/Regeneron. Остальные авторы заявляют об отсутствии конкурирующих интересов.
Дополнительная информация
Информация о рецензировании
Nature Reviews Endocrinology благодарит Р. Келишади и других анонимных рецензентов за их вклад в рецензирование этой работы.
Примечание издателя
Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Ссылки по теме
Рекомендации по измерению окружности талии: http://www.myhealthywaist.org/evaluating-cmr/clinical-tools/waist-circumference-measurement-guidelines/index. html
html
Дополнительная информация
Дополнительная информация
Глоссарий
- Калибровка
Способность правильно предсказать долю участников в данной группе, которые испытают событие.
- Дискриминация
Вероятность того, что диагностический тест или инструмент прогнозирования риска различают более высокий и более низкий риск.
- Чистое улучшение реклассификации
Относительное увеличение предсказанных вероятностей для людей, которые участвуют в событиях, и уменьшение для людей, которые этого не делают.
- С-статистика
Мера согласия для бинарных результатов в модели логистической регрессии.
- ВО 2 пик
Наивысшее значение VO 2 (т.
 е. потребление кислорода), полученное во время добавочного или другого высокоинтенсивного нагрузочного теста.
е. потребление кислорода), полученное во время добавочного или другого высокоинтенсивного нагрузочного теста.- Лактатный порог
Интенсивность упражнений, при которой концентрация лактата и/или молочной кислоты в крови начинает экспоненциально возрастать.
- Подвздошный гребень
Верхняя граница крыла подвздошной кости.
Права и разрешения
Открытый доступ Эта работа находится под лицензией Creative Commons Attribution 4.0 International License. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на статью, если иное не указано в кредитной строке; если материал не включен в лицензию Creative Commons, пользователям необходимо будет получить разрешение от держателя лицензии на воспроизведение материала. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.




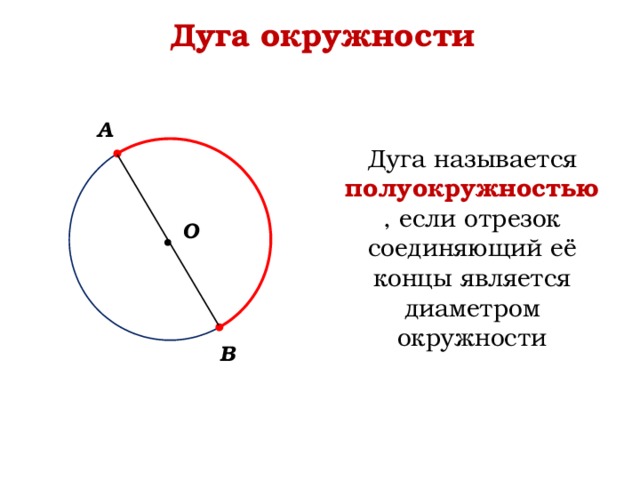

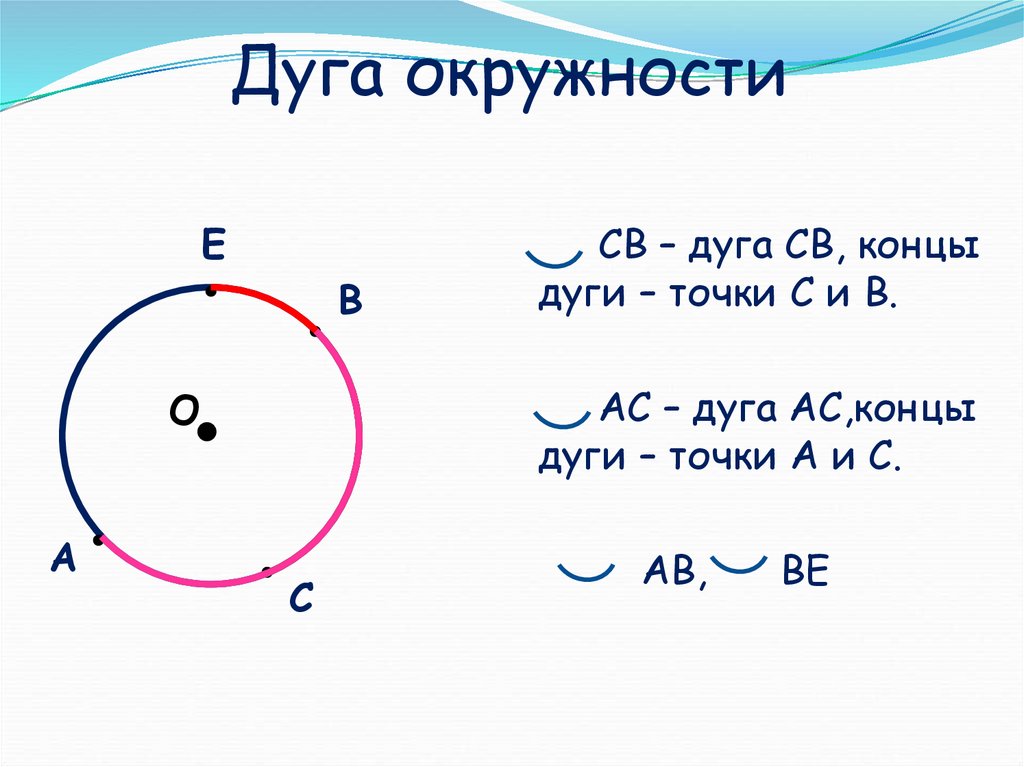
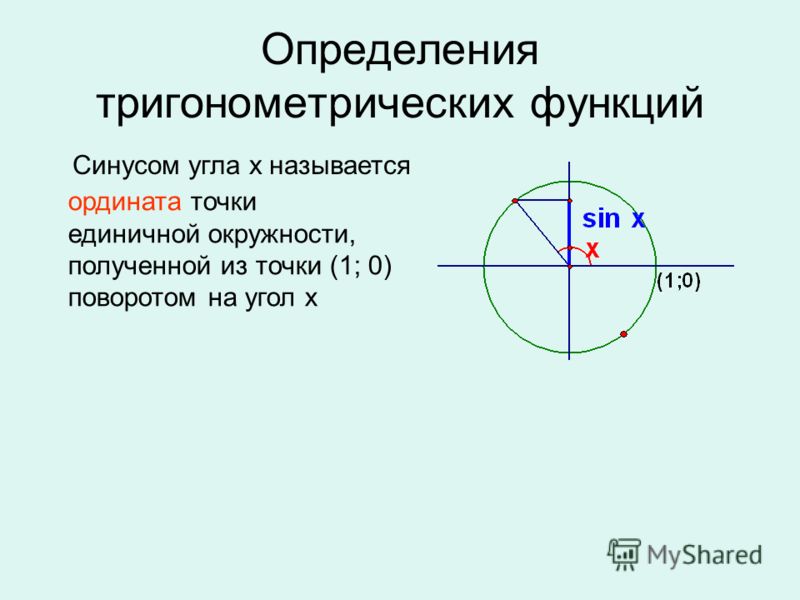 Верно и обратное утверждение: если радиус (диаметр) делит хорду пополам, то он перпендикулярен ей.
Верно и обратное утверждение: если радиус (диаметр) делит хорду пополам, то он перпендикулярен ей.

 А вы?
А вы? А вы?
А вы?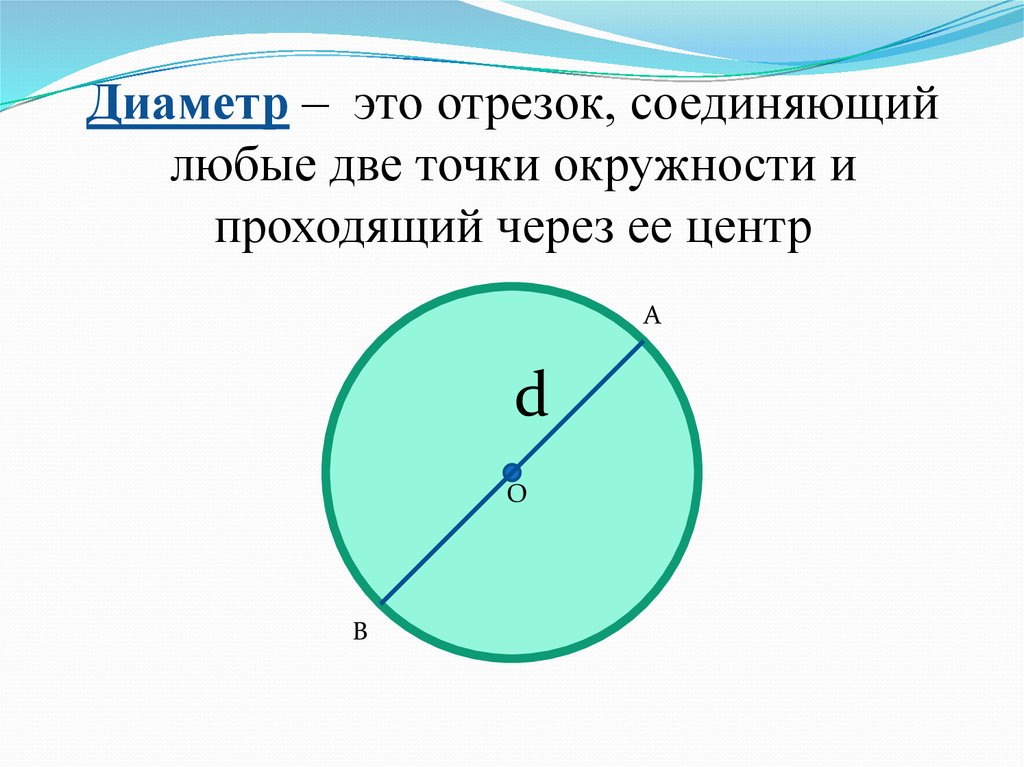
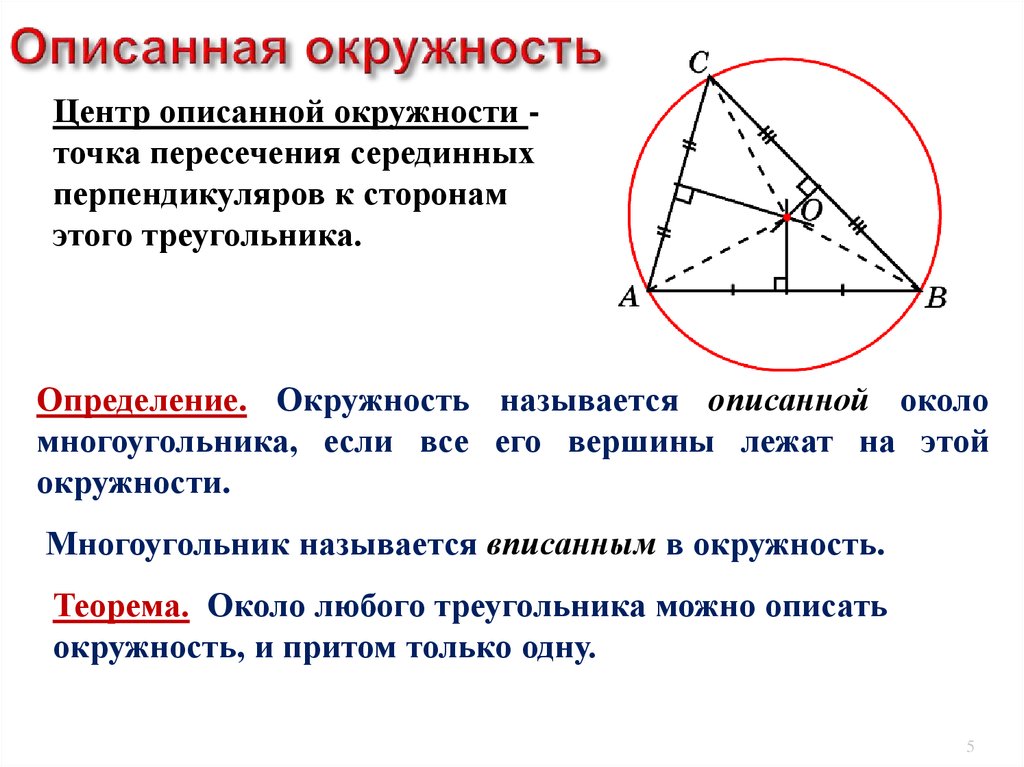 Мы можем не оговаривать, что радиус положительный, но радости с этого мало.
Мы можем не оговаривать, что радиус положительный, но радости с этого мало.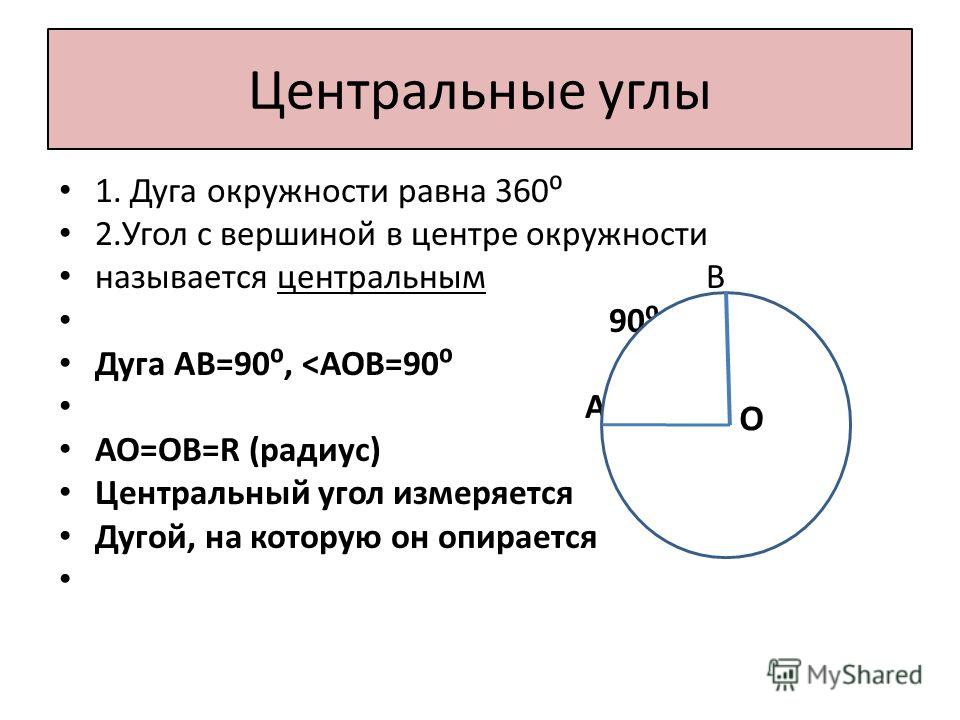 2. Вся плоскость — это объединение непересекающихся окружностей — орбит точек плоскости, включая орбиту начала отсчёта -окружность нулевого радиуса. Так вот, если точку не принимать за окружность, то смысла в этом действии было бы мало. Ну хотя эта ситуация, конечно, довольно специфическая.
2. Вся плоскость — это объединение непересекающихся окружностей — орбит точек плоскости, включая орбиту начала отсчёта -окружность нулевого радиуса. Так вот, если точку не принимать за окружность, то смысла в этом действии было бы мало. Ну хотя эта ситуация, конечно, довольно специфическая.  С одной стороны, точка — это окружность нулевого радиуса, а с другой стороны окружность — это множество точек
С одной стороны, точка — это окружность нулевого радиуса, а с другой стороны окружность — это множество точек

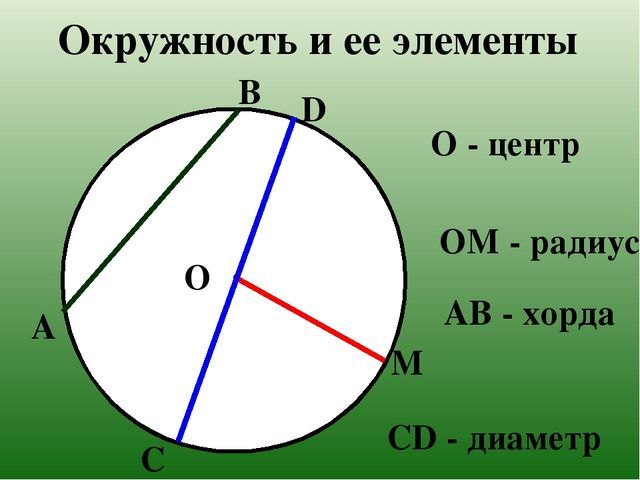


 Это …… (циркуль).
Это …… (циркуль).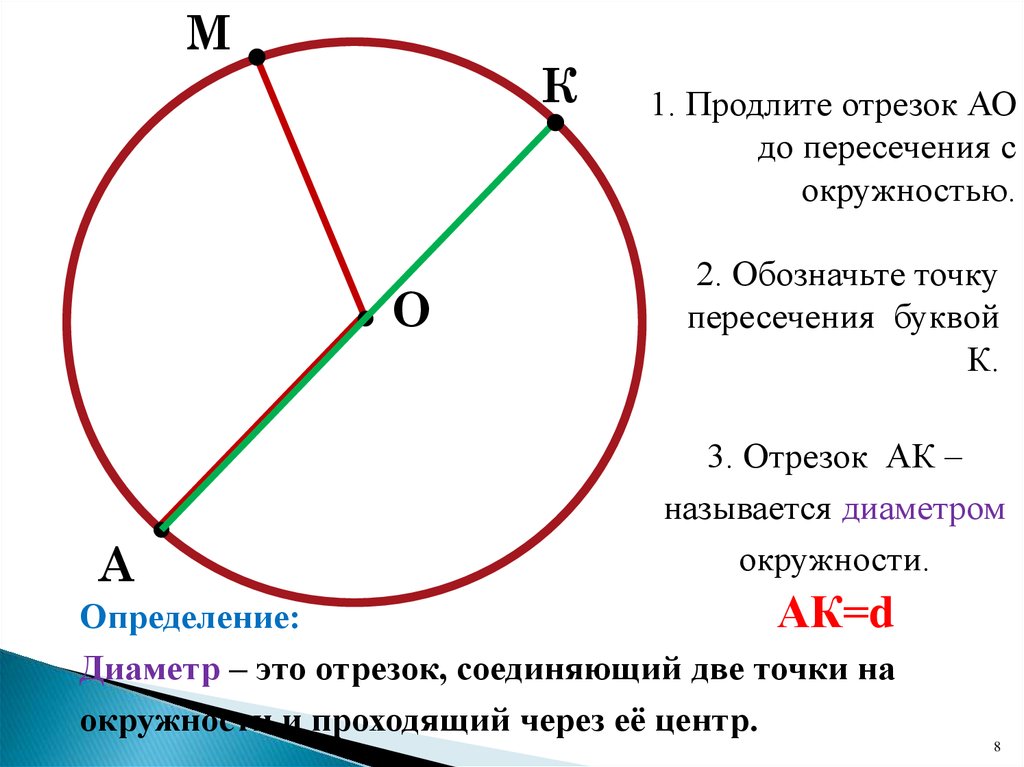
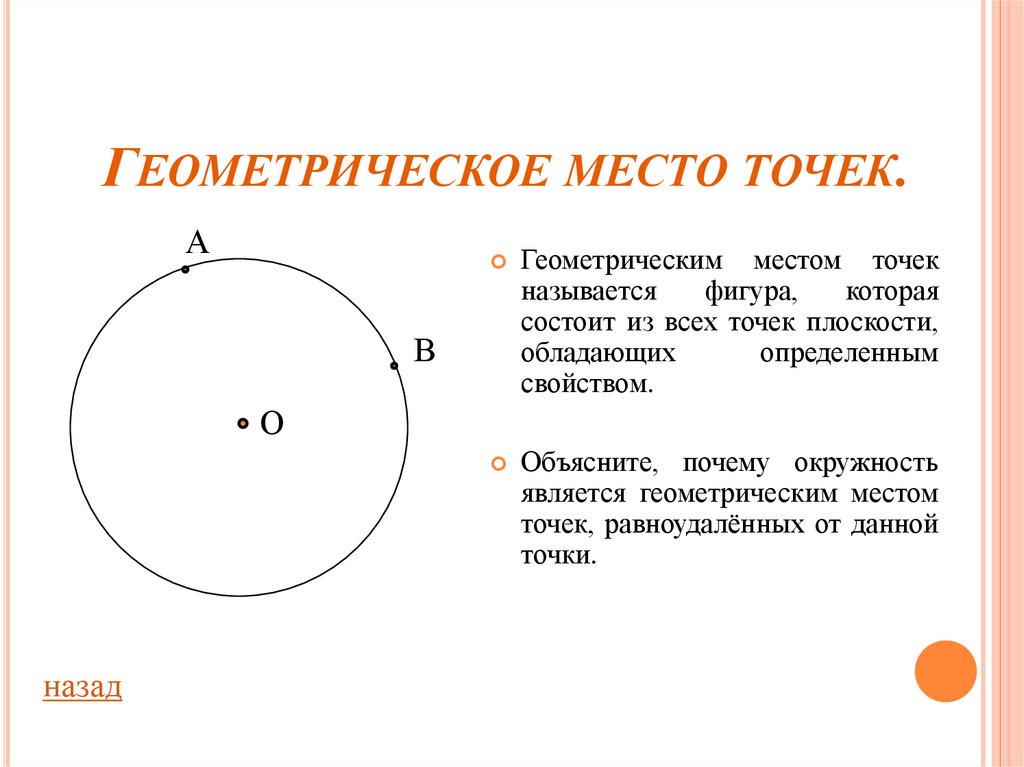
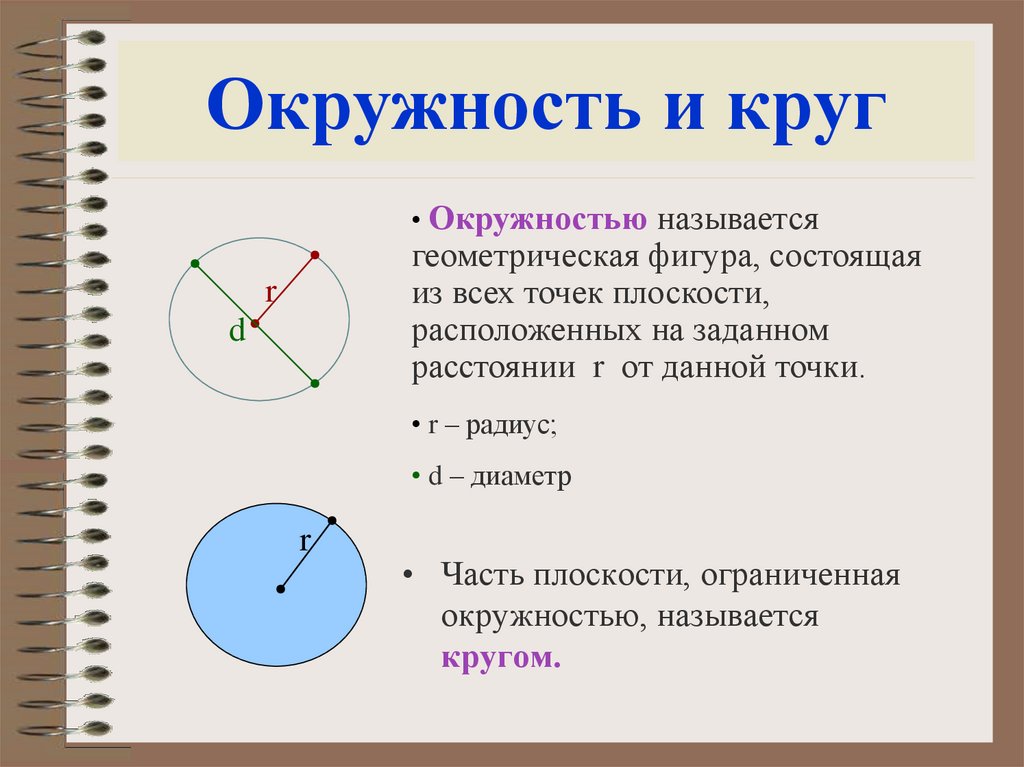
 copyright1}}
copyright1}}