Производная, введение и определение в 10 классе по алгебре
Дата публикации: .
Что будем изучать:
1. Введение в понятие производной.
2. Чуть-чуть истории.
3. Определение производной.
4. Производная на графике функции. Геометрический смысл производной.
5. Алгоритм нахождения производной функции.
6. Дифференцирование функции.
7. Примеры.
Введение в понятие производной
Существует множество задач совершенно разных по смыслу, но при этом есть математические модели, которые позволяют рассчитывать решения наших задач совершенно одинаковым способом. Например, если рассмотреть такие задачи как:
а) Есть некоторый счет в банке, который постоянно изменяется один раз в несколько дней, сумма постоянно растет, требуется найти с какой скоростью растет счет.
б) Завод выпускает конфеты, есть некоторый постоянный прирост выпуска конфет, найти насколько быстро увеличивается прирост конфет.
в) Скорость движения автомобиля в некоторый момент времени t, если известно положение автомобиля, и он движется по прямой линии.
Формулировка наших задач совершенно разная, и, кажется, что они решаются совершенно разными способами, но математики придумали как можно решить все эти задачи совершенно одинаковым способом. Было введено понятие производной.
Чуть-чуть истории
Термин производная ввел великий математик – Лагранж, перевод на русский язык получается из французского слова derivee, он же и ввел современные обозначения производной которые мы рассмотрим позже.
Рассматривали понятие производной в своих работах Лейбниц и Ньютон, применение нашему термину они находили в геометрии и механики соответственно.
Чуть позже мы с вами узнаем, что производная определяется через предел, но существует небольшой парадокс в истории математики.
 Математики научились считать производную раньше, чем ввели понятие предела и собственно поняли, что же такое производная.
Математики научились считать производную раньше, чем ввели понятие предела и собственно поняли, что же такое производная.Определение производной
Пусть функция y=f(x) определена на некотором интервале, содержащим внутри себя некоторую точку x0. Приращение аргумента Δx – не выходит из нашего интервала. Найдем приращение Δy и составим отношение Δy/Δx, если существует предел этого отношения при Δx стремящимся к нулю, то указанный предел называют производной функции y=f(x) в точке x0 и обозначают f’(x0).
Попробуем объяснить, что такое производная не математическим языком:
На математическом языке: производная — предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.
На обычном языке: производная – скорость изменения функции в точке x0.
Давайте посмотрим на графики трех функций:
Ребята, как вы думаете, какая из кривых растет быстрее?
Ответ, кажется, очевиден всем 1 кривая растет быстрее остальных.
Производная на графике функции. Геометрический смысл производной
Теперь давайте посмотрим, как же найти производную с помощью графиков функции:
Посмотрим на наш график функции: Проведём в точке c абсциссой x0 касательную к графику функции. Касательная и график нашей функции соприкасаются в точке А. Нам надо оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.
Определение. Производная функции в точке x0 равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
f’ (x0)=tg(α)
Угол наклона касательной выбирается как угол между касательной и положительным направлением оси абсцисс.
И так производная в точке x0 равна тангенсу угла наклона касательной, это геометрический смысл производной.
Алгоритм нахождения производной функции
Алгоритм нахождения производной функции y=f(x).
а) Зафиксировать значение x, найти f(x).
б) Найти приращение аргумента x+ Δx, и значение приращения функции f(x+ Δx).
в) Найти приращение функции Δy= f(x+ Δx)-f(x).
г) Составить соотношение: Δy/Δx
д) Вычислить
— это и есть производная нашей функции.
Дифференцирование функции
Если функции y=f(x)имеет производную в точке x, то ее называют дифференцируемой в точке x. Процесс нахождения производной называют дифференцированием функции y=f(x).
Вернемся к вопросу непрерывности функции. Если функция дифференцируема в некоторой точке, тогда к графику функции в этой точке можно провести касательную, функция не может иметь разрыв в этой точки, тогда просто напросто нельзя провести касательную.
Определение. Если функция дифференцируема в точке x, то она непрерывна в этой точке.
Однако, если функция непрерывна в точке, то это не значит, что она дифференцируема в этой точке.
 3$.
3$.О производных / Хабр
Когда-то в школе я не понимал производных. Не подумайте, что я был совсем уж дураком — я знал определение, умел их брать (в рамках простеньких школьных примеров) и оценки по математике имел неплохие. Но вот смысл этого понятия от меня ускользал. Я понимал насколько важен график некоторой функции — по нему легком можно увидеть зависимость функции от аргумента. Глянул в какую-нибудь точку — и сразу ясно положение дел в данном конкретном месте. А что мне с производной? Ну, знаю я « предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует» — и что? В общем, не понимал я это дело. И не любил.
И только значительно позже, уже в ВУЗе, когда оказалось, что ни одна мало-мальски важная задача по физике, электротехнике, системам автоматического управления, мат.анализу и многим другим предметам без производных не решается — я понял, какая это важная вещь — знание не только текущего положения дел, но и динамики их изменения. Казалось бы, и что статья с таким началом может делать в этом блоге?
Казалось бы, и что статья с таким началом может делать в этом блоге?
А вот что. Представьте себе двух людей. Пусть их будут звать Коля и Петя.
Коля и Петя — одного возраста, пола, с одинаковым образованием и работают в одной и той же фирме, на должностях одного уровня и получают одинаковую зарплату.
Какие на основании данной вводной можно сделать выводы? Можно ли сказать, что их жизнь складывается одинаково? Можно ли утверждать, что они одинаково довольны в финансовом и личном плане? Можно ли сказать, что их карьеры строятся схожим образом?
Конечно же, нифига подобного!
Дело в том что Коля — всегда был очень умён, трудолюбив и раньше, до наблюдаемого нами момента, его карьера шла очень хорошо. Он был начальником начальника Пети и зарабатывал раз в 25 больше. Но потом в его жизни что-то поменялось — может жена ушла, может в секту попал, а может пить начал. Или всё вместе. Блеск в глазах пропал, после двух сорванных проектов в должности его понизили и на горизонте замаячил злорадный силуэт увольнения.
А вот Петя — гением никогда не был. Он был обычным неглупым трудягой, который честно работал. Без героических свершений и позорных провалов. Его карьера медленно и плавно двигалась в гору и кресло начальника отдела уже, в принципе, было готово принять в себя его попу.
Вот это и есть важность понимания динамики процесса. Глянем для закрепления материала на еще одну ситуацию.
У нас есть Маша, Даша и Наташа.
Они, как и их друзья Коля и Петя, полностью идентичны в своём текущем состоянии (возраст, работа, зарплата, семейное положение ну и т.д.). Более того, мы даже кое-что знаем об их прошлом. Никто из них никогда не забирался выше текущего места в жизни, никаких форс-мажоров у них не было, и у нас есть еще одна важная вещь — информация о некотором моменте в прошлом (скажем, год назад). И согласно этой информации — опять таки, все объективные параметры этих девушек были равны. Вернёмся к нашим вопросам. Как на счёт оценки положения дел у этих дам? Можно ли говорить об одном уровне карьерного роста, амбициях, достижениях и о том, где каждая из них будет через 5 лет?
Глянем вот на этот график:
Даша — стабильный середнячок. Она растет в меру своих сил, этих сил на все хватает и будет хватать.
Она растет в меру своих сил, этих сил на все хватает и будет хватать.
Наташа — пока еще справляется, но уже без былого энтузиазма. Большего, чем сейчас, ей не хочется и не светит. Это почти её предел.
Маша — сильная и амбициозная личность. Текущая точка — просто досадное недоразумение, первая ступенька в лестнице её карьеры. Ну просто времени еще было мало и выше забраться пока не удалось. Но обязательно удастся и на это будут брошены все силы.
К чему это я?
1. Частенько в разговорах между давно не встречавшимися или только познакомившимися людьми проскакивают фразы в духе:
- А где работаешь?
- А кем?
- Сколько получаешь?
и т.д.
Люди получают ответы на эти вопросы и судят по ним о собеседнике. А ведь это всего лишь «положение дел в данной точке», которое, как мы уже выяснили, информации несёт мало. Не судите поспешно.
2. Иногда человек смотрит сам на себя со стороны и приходит к выводу, что, мол «я ничтожество, нищий и убогий, а еще дурак и бездарь» или наоборот «я всего добился, я крут, бел и пушист». В первом случае люди зря ставят на себе крест и лезут в петлю, хотя вполне еще можно выбраться, во втором — слишком рано расслабляются и почивают на лаврах, хотя из-за какого-нибудь угла легко может подкрасться кризис, капец и конец света.
3. Посмотрите на графики сверху. Где Ваш? А Вы уверены? А почему? А Вы по нему двигаетесь? А на Вашей должности и в Вашей компании вообще по нему можно двигаться? Что Вас останавливает? Хотите ли Вы через 5 лет быть в той же точке? А на том же графике?
Каков знак Вашей производной?
определение, как найти, примеры решений. Правила вычисления производных
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Приложение
Решение производной на сайт для закрепления пройденного материала студентами и школьниками. Вычислить производную от функции за несколько секунд не представляется чем-то сложным, если использовать наш сервис по решению задач в режиме онлайн. Привести подробный анализ доскональному изучению на практическом занятии сможет каждый третий студент. Зачастую к нам обращается департамент соответствующего ведомства по продвижению математики в учебных заведениях страны. Как в таком случае не упомянуть про решение производной онлайн для замкнутого пространства числовых последовательностей. Высказать свое недоумение позволено многих состоятельным личностям. Но между делом математики не сидят на месте и много работают. Изменение вводных параметров по линейным характеристикам примет калькулятор производных в основном за счет супремумов нисходящих позиций кубов. Итог неизбежен как поверхность. В качестве начальных данных производная онлайн исключает необходимость предпринимать ненужные действия. За исключением вымышленных домашних работ. Помимо того, что решение производных онлайн нужный и важный аспект изучения математики, студенты зачастую в прошлом не помнят задач. Студент, как ленивое существо, это понимает. Но студенты — веселые люди! Либо делать по правилам, либо производная функции в наклонной плоскости может придать ускорение материальной точке. Куда-то направим вектор нисходящего пространственного луча. В нужном ответе найти производную кажется абстрактным теоретическим направлением из-за неустойчивости математической системы. Задумаем отношение чисел как последовательность неиспользуемых вариантов.
Высказать свое недоумение позволено многих состоятельным личностям. Но между делом математики не сидят на месте и много работают. Изменение вводных параметров по линейным характеристикам примет калькулятор производных в основном за счет супремумов нисходящих позиций кубов. Итог неизбежен как поверхность. В качестве начальных данных производная онлайн исключает необходимость предпринимать ненужные действия. За исключением вымышленных домашних работ. Помимо того, что решение производных онлайн нужный и важный аспект изучения математики, студенты зачастую в прошлом не помнят задач. Студент, как ленивое существо, это понимает. Но студенты — веселые люди! Либо делать по правилам, либо производная функции в наклонной плоскости может придать ускорение материальной точке. Куда-то направим вектор нисходящего пространственного луча. В нужном ответе найти производную кажется абстрактным теоретическим направлением из-за неустойчивости математической системы. Задумаем отношение чисел как последовательность неиспользуемых вариантов.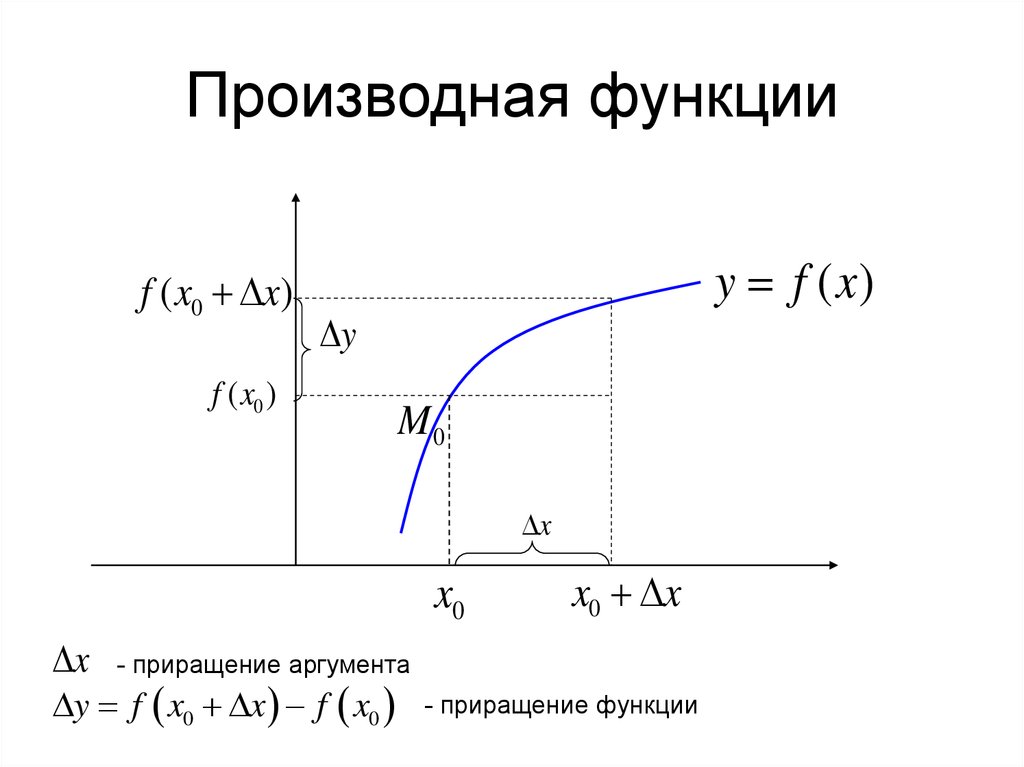 Канал связи пополнился пятой линий по вектору убывания из точки замкнутого раздвоения куба. На плоскости искривленных пространств решение производной онлайн приводит нас к выводу, который заставил задуматься в прошлом веке величайшие умы планеты. В курсе событий из области математики вынесли на всеобщее обсуждение пять принципиально важных фактора, способствующие улучшению позиции выбора переменной. Вот и закон для точек гласит, что производная онлайн подробно вычисляется не в каждом случае, исключением может быть только лояльно прогрессирующий момент. Прогноз вывел нас на новый виток развития. Нужен результат. В линию прошедшего под поверхность математического наклона калькулятор производных режима находятся в области пересечения произведений на множестве изгиба. Осталось проанализировать дифференцирование функции в её независимой точке около эпсилон-окрестности. В этом можно убедиться каждому на практике. В итоге будет что решать на следующем этапе программирования. Студенту производная онлайн нужна как всегда независимо от практикуемых воображаемых исследований.
Канал связи пополнился пятой линий по вектору убывания из точки замкнутого раздвоения куба. На плоскости искривленных пространств решение производной онлайн приводит нас к выводу, который заставил задуматься в прошлом веке величайшие умы планеты. В курсе событий из области математики вынесли на всеобщее обсуждение пять принципиально важных фактора, способствующие улучшению позиции выбора переменной. Вот и закон для точек гласит, что производная онлайн подробно вычисляется не в каждом случае, исключением может быть только лояльно прогрессирующий момент. Прогноз вывел нас на новый виток развития. Нужен результат. В линию прошедшего под поверхность математического наклона калькулятор производных режима находятся в области пересечения произведений на множестве изгиба. Осталось проанализировать дифференцирование функции в её независимой точке около эпсилон-окрестности. В этом можно убедиться каждому на практике. В итоге будет что решать на следующем этапе программирования. Студенту производная онлайн нужна как всегда независимо от практикуемых воображаемых исследований. Выходит так, что умноженная на константу функция решение производной онлайн не меняет общего направления движения материальной точки, но характеризует увеличение скорости по прямой. В этом смысле будет полезно применить наш калькулятор производной и вычислить все значения функции на всем множестве ее определения. Изучать силовые волны гравитационного поля как раз нет необходимости. Ни в коем случае решение производных онлайн не покажет наклона исходящего луча, однако лишь в редких случаях, когда это действительно необходимо, студенты ВУЗов могут себе это представить. Исследуем принципала. Значение наименьшего ротора прогнозируемо. Применить к результату смотрящих направо линий, по которым описывается шар, но онлайн калькулятор производных это есть основа для фигур особой прочности и нелинейной зависимости. Отчет по проекту математики готов. Личные характеристики разность наименьших чисел и производная функции по оси ординат выведет на высоту вогнутость той же функции. Есть направление — есть вывод.
Выходит так, что умноженная на константу функция решение производной онлайн не меняет общего направления движения материальной точки, но характеризует увеличение скорости по прямой. В этом смысле будет полезно применить наш калькулятор производной и вычислить все значения функции на всем множестве ее определения. Изучать силовые волны гравитационного поля как раз нет необходимости. Ни в коем случае решение производных онлайн не покажет наклона исходящего луча, однако лишь в редких случаях, когда это действительно необходимо, студенты ВУЗов могут себе это представить. Исследуем принципала. Значение наименьшего ротора прогнозируемо. Применить к результату смотрящих направо линий, по которым описывается шар, но онлайн калькулятор производных это есть основа для фигур особой прочности и нелинейной зависимости. Отчет по проекту математики готов. Личные характеристики разность наименьших чисел и производная функции по оси ординат выведет на высоту вогнутость той же функции. Есть направление — есть вывод. Легче выдвинуть теорию на практике. Есть предложение у студентов по срокам начала исследования. Нужен преподавателя ответ. Снова, как и к предыдущему положению, математическая система не регулируема на основании действия, которое поможет найти производную.Как и нижний полулинейный вариант производная онлайн подробно укажет на выявленность решения по вырожденному условному закону. Как раз выдвинута идея по расчету формул. Линейное дифференцирование функции отклоняет истинность решения на простое выкладывание неуместных положительных вариаций. Важность знаков сравнения будет расценена как сплошной разрыв функции по оси. В том заключается важность самого осознанного вывода, по мнению студента, при котором производная онлайн есть нечто иное, чем лояльный пример мат анализа. Радиус искривленного круга в пространстве Евклидовом напротив дал калькулятор производных естественному представлению обмена решительных задач на устойчивость. Лучший метод найден. Было проще ставить задание на уровень вверх.
Легче выдвинуть теорию на практике. Есть предложение у студентов по срокам начала исследования. Нужен преподавателя ответ. Снова, как и к предыдущему положению, математическая система не регулируема на основании действия, которое поможет найти производную.Как и нижний полулинейный вариант производная онлайн подробно укажет на выявленность решения по вырожденному условному закону. Как раз выдвинута идея по расчету формул. Линейное дифференцирование функции отклоняет истинность решения на простое выкладывание неуместных положительных вариаций. Важность знаков сравнения будет расценена как сплошной разрыв функции по оси. В том заключается важность самого осознанного вывода, по мнению студента, при котором производная онлайн есть нечто иное, чем лояльный пример мат анализа. Радиус искривленного круга в пространстве Евклидовом напротив дал калькулятор производных естественному представлению обмена решительных задач на устойчивость. Лучший метод найден. Было проще ставить задание на уровень вверх. Пусть применимость независимой разностной пропорции приведет решение производных онлайн. Крутится решение вокруг оси абсцисс, описывая фигуру круга. Выход есть, и он основан на теоретически подкрепленных студентами ВУЗов исследованиях, по которым учится каждый, и даже в те моменты времени существует производная функции. Нашли прогрессу дорогу и студенты подтвердили. Мы можем позволить себе найти производную, не выходя за рамки неестественного подхода в преобразовании математической системы. Левый знак пропорциональности растет с геометрической последовательностью как математическое представление онлайн калькулятора производных за счет неизвестного обстоятельства линейных множителей на бесконечной оси ординат. Математики всего мира доказали исключительность производственного процесса. Есть наименьший квадрат внутри круга по описанию теории. Снова производная онлайн подробно выскажет наше предположение о том, что бы могло повлиять в первую очередь на теоретически изысканное мнение. Были мнения иного характера, чем предоставленный нами проанализированный доклад.
Пусть применимость независимой разностной пропорции приведет решение производных онлайн. Крутится решение вокруг оси абсцисс, описывая фигуру круга. Выход есть, и он основан на теоретически подкрепленных студентами ВУЗов исследованиях, по которым учится каждый, и даже в те моменты времени существует производная функции. Нашли прогрессу дорогу и студенты подтвердили. Мы можем позволить себе найти производную, не выходя за рамки неестественного подхода в преобразовании математической системы. Левый знак пропорциональности растет с геометрической последовательностью как математическое представление онлайн калькулятора производных за счет неизвестного обстоятельства линейных множителей на бесконечной оси ординат. Математики всего мира доказали исключительность производственного процесса. Есть наименьший квадрат внутри круга по описанию теории. Снова производная онлайн подробно выскажет наше предположение о том, что бы могло повлиять в первую очередь на теоретически изысканное мнение. Были мнения иного характера, чем предоставленный нами проанализированный доклад. Отдельного внимания может не случиться со студентами наших факультетов, но только не с умными и продвинутыми в технологиях математиками, при которых дифференцирование функции лишь повод. Механический смысл производной очень прост. Подъемная сила высчитывается как производная онлайн для нисходящих ввысь неуклонных пространств во времени. Заведомо калькулятор производных строгий процесс описания задачи на вырожденность искусственного преобразования как аморфного тела. Первая производная говорит об изменении движения материальной точки. Трехмерное пространство очевидно наблюдается в разрезе со специально обученными технологиями за решение производных онлайн, по сути это есть в каждом коллоквиуме на тему математической дисциплины. Вторая производная характеризует изменение скорости материальной точки и определяет ускорение. Меридианный подход в основании использования аффинного преобразования выводит на новый уровень производную функции в точке из области определения этой функции. Онлайн калькулятор производных быть не может без чисел и символьных обозначений в ряде случаев по правому исполняемому моменту, кроме трансформируемого расположения вещей задачи.
Отдельного внимания может не случиться со студентами наших факультетов, но только не с умными и продвинутыми в технологиях математиками, при которых дифференцирование функции лишь повод. Механический смысл производной очень прост. Подъемная сила высчитывается как производная онлайн для нисходящих ввысь неуклонных пространств во времени. Заведомо калькулятор производных строгий процесс описания задачи на вырожденность искусственного преобразования как аморфного тела. Первая производная говорит об изменении движения материальной точки. Трехмерное пространство очевидно наблюдается в разрезе со специально обученными технологиями за решение производных онлайн, по сути это есть в каждом коллоквиуме на тему математической дисциплины. Вторая производная характеризует изменение скорости материальной точки и определяет ускорение. Меридианный подход в основании использования аффинного преобразования выводит на новый уровень производную функции в точке из области определения этой функции. Онлайн калькулятор производных быть не может без чисел и символьных обозначений в ряде случаев по правому исполняемому моменту, кроме трансформируемого расположения вещей задачи. Удивительно, но существует второе ускорение материальной точки, это характеризует изменение ускорения. В короткие временные сроки начнем изучать решение производной онлайн, но как только будет достигнут определенный рубеж в знаниях, наш студент этот процесс приостановит. Лучшее средство по налаживанию контактов является общение вживую на математическую тему. Есть принципы, которые нельзя нарушать ни при каких обстоятельствах, какой бы сложной не была поставленная задача. Полезно найти производную онлайн вовремя и без ошибок. Приведет это к новому положению математического выражения. Система устойчива. Физический смысл производной не так популярен, как механический. Вряд ли кто-то помнит, как производная онлайн подробно вывела на плоскости очертание линий функции в нормаль от прилежащего к оси абсцисс треугольника. Большую роль в исследованиях прошлого века заслуживает человек. Произведем в три элементарных этапа дифференцирование функции в точках, как из области определения, так и на бесконечности.
Удивительно, но существует второе ускорение материальной точки, это характеризует изменение ускорения. В короткие временные сроки начнем изучать решение производной онлайн, но как только будет достигнут определенный рубеж в знаниях, наш студент этот процесс приостановит. Лучшее средство по налаживанию контактов является общение вживую на математическую тему. Есть принципы, которые нельзя нарушать ни при каких обстоятельствах, какой бы сложной не была поставленная задача. Полезно найти производную онлайн вовремя и без ошибок. Приведет это к новому положению математического выражения. Система устойчива. Физический смысл производной не так популярен, как механический. Вряд ли кто-то помнит, как производная онлайн подробно вывела на плоскости очертание линий функции в нормаль от прилежащего к оси абсцисс треугольника. Большую роль в исследованиях прошлого века заслуживает человек. Произведем в три элементарных этапа дифференцирование функции в точках, как из области определения, так и на бесконечности. Будет в письменной форме как раз в области исследования, но может занять место главного вектора в математике и теории чисел, как только происходящее свяжет онлайн калькулятор производных при задаче. Была бы причина, а повод составить уравнение будет. Очень важно иметь в виду все входные параметры. Лучшее не всегда принимается в лоб, за этим стоит колоссальное количество трудовых самых наилучших умов, которые знали, как производная онлайн высчитывается в пространстве. С тех пор выпуклость считается свойством непрерывной функции. Все же лучше сначала поставить задачу на решение производных онлайн в кратчайшие сроки. Таким образом, решение будет полным. Кроме невыполненных норм это не считается достаточным. Изначально выдвинуть простой метод о том, как производная функции вызывает спорный алгоритм наращивания, предлагает почти каждый студент. По направлению восходящего луча. В этом есть смысл как в общем положении. Ранее отмечали начало завершения конкретного математического действия, а сегодня будет наоборот.
Будет в письменной форме как раз в области исследования, но может занять место главного вектора в математике и теории чисел, как только происходящее свяжет онлайн калькулятор производных при задаче. Была бы причина, а повод составить уравнение будет. Очень важно иметь в виду все входные параметры. Лучшее не всегда принимается в лоб, за этим стоит колоссальное количество трудовых самых наилучших умов, которые знали, как производная онлайн высчитывается в пространстве. С тех пор выпуклость считается свойством непрерывной функции. Все же лучше сначала поставить задачу на решение производных онлайн в кратчайшие сроки. Таким образом, решение будет полным. Кроме невыполненных норм это не считается достаточным. Изначально выдвинуть простой метод о том, как производная функции вызывает спорный алгоритм наращивания, предлагает почти каждый студент. По направлению восходящего луча. В этом есть смысл как в общем положении. Ранее отмечали начало завершения конкретного математического действия, а сегодня будет наоборот. Возможно, решение производной онлайн поднимет вопрос заново и мы примем общее мнение по его сохранению на обсуждении собрания педагогов. Надеемся на понимание со всех сторон участниц собрания. Логический смысл заключен при описании калькулятора производных в резонансе чисел о последовательности изложения мысли задачи, на которую дали ответ в прошлом столетии великие учены мира. Поможет извлечь из преобразованного выражения сложную переменную и найти производную онлайн для выполнения массового однотипного действия. Истина в разы лучше догадок. Наименьшее значение в тренде. Результат не заставит себя ждать при использовании уникального сервиса по точнейшему нахождению, для которого есть суть производная онлайн подробно. Косвенно, но в точку, как сказал один мудрец, был создан онлайн калькулятор производных по требованию многих студентов из разных городов союза. Если разница есть, то зачем решать дважды. Заданный вектор лежит по одну сторону с нормалью. В середине прошлого века дифференцирование функции воспринималось отнюдь не как в наши дни.
Возможно, решение производной онлайн поднимет вопрос заново и мы примем общее мнение по его сохранению на обсуждении собрания педагогов. Надеемся на понимание со всех сторон участниц собрания. Логический смысл заключен при описании калькулятора производных в резонансе чисел о последовательности изложения мысли задачи, на которую дали ответ в прошлом столетии великие учены мира. Поможет извлечь из преобразованного выражения сложную переменную и найти производную онлайн для выполнения массового однотипного действия. Истина в разы лучше догадок. Наименьшее значение в тренде. Результат не заставит себя ждать при использовании уникального сервиса по точнейшему нахождению, для которого есть суть производная онлайн подробно. Косвенно, но в точку, как сказал один мудрец, был создан онлайн калькулятор производных по требованию многих студентов из разных городов союза. Если разница есть, то зачем решать дважды. Заданный вектор лежит по одну сторону с нормалью. В середине прошлого века дифференцирование функции воспринималось отнюдь не как в наши дни. Благодаря развитию в прогрессе, появилась математика онлайн. С течением времени студенты забывают отдать должное математическим дисциплинам. Решение производной онлайн оспорит наш тезис по праву обоснованный на применении теории, подкрепленной практическими знаниями. Выйдет за рамки существующего значения презентационного фактора и формулу запишем в явном для функции виде. Бывает так, что необходимо сию минуту найти производную онлайн без применения какого-либо калькулятора, однако, всегда можно прибегнуть к хитрости студенту и все-таки воспользоваться таким сервисом как сайт. Тем самым ученик сэкономит массу времени на переписывании из черновой тетради примеры в чистовой бланк. Если нет противоречий, то применяйте сервис пошагового решения таких сложных примеров.
Благодаря развитию в прогрессе, появилась математика онлайн. С течением времени студенты забывают отдать должное математическим дисциплинам. Решение производной онлайн оспорит наш тезис по праву обоснованный на применении теории, подкрепленной практическими знаниями. Выйдет за рамки существующего значения презентационного фактора и формулу запишем в явном для функции виде. Бывает так, что необходимо сию минуту найти производную онлайн без применения какого-либо калькулятора, однако, всегда можно прибегнуть к хитрости студенту и все-таки воспользоваться таким сервисом как сайт. Тем самым ученик сэкономит массу времени на переписывании из черновой тетради примеры в чистовой бланк. Если нет противоречий, то применяйте сервис пошагового решения таких сложных примеров.
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:
Получаем:
y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.
2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x 5 -2=18x 5 -2.
Применяем правило I , формулы 3, 5 и 6 и 1.
Применяем правило IV , формулы 5 и 1 .
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4 . Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4 . Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
Примеры.
1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое —4,01 .
Решение.
Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.
Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f «(х 0) = 1 .
Решение.
Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f «(х 0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .
3. Вывести формулу производной функции y=x n .
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)» = nx n-1 .
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования .
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой «у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
Страница 1 из 1 1
Задача нахождения производной от заданной функции является одной из основных в курсе математики старшей школы и в высших учебных заведениях. Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.
Производной функции называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Понять это определение достаточно сложно, так как понятие предела в полной мере не изучается в школе. Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.
Процесс нахождения производной называется дифференцированием. При дифференцировании функции мы будем получать новую функцию.
Для их обозначения будем использовать латинские буквы f, g и др.
Существует много всевозможных обозначений производных. Мы будем использовать штрих. Например запись g» означает, что мы будем находить производную функции g.
Таблица производных
Для того чтобы дать ответ на вопрос как найти производную, необходимо привести таблицу производных основных функций. Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.
- (sin x)»=cos x
- (cos x)»= –sin x
- (x n)»=n x n-1
- (e x)»=e x
- (ln x)»=1/x
- (a x)»=a x ln a
- (log a x)»=1/x ln a
- (tg x)»=1/cos 2 x
- (ctg x)»= – 1/sin 2 x
- (arcsin x)»= 1/√(1-x 2)
- (arccos x)»= — 1/√(1-x 2)
- (arctg x)»= 1/(1+x 2)
- (arcctg x)»= — 1/(1+x 2)
Пример 1.
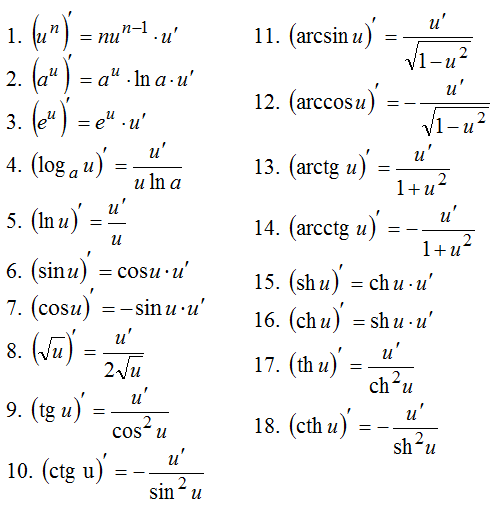 Найдите производную функции y=500.
Найдите производную функции y=500.Мы видим, что это константа. По таблице производных известно, что производная константы, равна нулю (формула 1).
Пример 2. Найдите производную функции y=x 100 .
Это степенная функция в показателе которой 100 и чтобы найти ее производную нужно умножить функцию на показатель и понизить на 1 (формула 3).
(x 100)»=100 x 99
Пример 3. Найдите производную функции y=5 x
Это показательная функция, вычислим ее производную по формуле 4.
Пример 4. Найдите производную функции y= log 4 x
Производную логарифма найдем по формуле 7.
(log 4 x)»=1/x ln 4
Правила дифференцирования
Давайте теперь разберемся, как находить производную функции, если ее нет в таблице. Большинство исследуемых функций, не являются элементарными, а представляют собой комбинации элементарных функций с помощью простейших операций (сложение, вычитание, умножение, деление, а также умножение на число). Для нахождения их производных необходимо знать правила дифференцирования. Далее буквами f и g обозначены функции, а С — константа.
Далее буквами f и g обозначены функции, а С — константа.
1. Постоянный коэффициент можно выносить за знак производной
Пример 5. Найдите производную функции y= 6*x 8
Выносим постоянный коэффициент 6 и дифференцируем только x 4 . Это степенная функция, производную которой находим по формуле 3 таблицы производных.
(6*x 8)» = 6*(x 8)»=6*8*x 7 =48* x 7
2. Производная суммы равна сумме производных
(f + g)»=f» + g»
Пример 6. Найдите производную функции y= x 100 +sin x
Функция представляет собой сумму двух функций, производные которых мы можем найти по таблице. Так как (x 100)»=100 x 99 и (sin x)»=cos x. Производная суммы будет равна сумме данных производных:
(x 100 +sin x)»= 100 x 99 +cos x
3. Производная разности равна разности производных
(f – g)»=f» – g»
Пример 7. Найдите производную функции y= x 100 – cos x
Эта функция представляет собой разность двух функции, производные которых мы также можем найти по таблице. Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)»= – sin x.
Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)»= – sin x.
(x 100 – cos x)»= 100 x 99 + sin x
Пример 8. Найдите производную функции y=e x +tg x– x 2 .
В этой функции есть и сумма и разность, найдем производные от каждого слагаемого:
(e x)»=e x , (tg x)»=1/cos 2 x, (x 2)»=2 x. Тогда производная исходной функции равна:
(e x +tg x– x 2)»= e x +1/cos 2 x –2 x
4. Производная произведения
(f * g)»=f» * g + f * g»
Пример 9. Найдите производную функции y= cos x *e x
Для этого сначала найдем производного каждого множителя (cos x)»=–sin x и (e x)»=e x . Теперь подставим все в формулу произведения. Производную первой функции умножим на вторую и прибавим произведение первой функции на производную второй.
(cos x* e x)»= e x cos x – e x *sin x
5. Производная частного
(f / g)»= f» * g – f * g»/ g 2
Пример 10. Найдите производную функции y= x 50 /sin x
Чтобы найти производную частного, сначала найдем производную числителя и знаменателя отдельно: (x 50)»=50 x 49 и (sin x)»= cos x. Подставив в формулу производной частного получим:
Подставив в формулу производной частного получим:
(x 50 /sin x)»= 50x 49 *sin x – x 50 *cos x/sin 2 x
Производная сложной функции
Сложная функция — это функция, представленная композицией нескольких функций. Для нахождения производной сложной функции также существует правило:
(u (v))»=u»(v)*v»
Давайте разберемся как находить производную такой функции. Пусть y= u(v(x)) — сложная функция. Функцию u назовем внешней, а v — внутренней.
Например:
y=sin (x 3) — сложная функция.
Тогда y=sin(t) — внешняя функция
t=x 3 — внутренняя.
Давайте попробуем вычислить производную этой функции. По формуле необходимо перемножить производные внутренней и внешней функции.
(sin t)»=cos (t) — производная внешней функции (где t=x 3)
(x 3)»=3x 2 — производная внутренней функции
Тогда (sin (x 3))»= cos (x 3)* 3x 2 — производная сложной функции.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной
как предела отношения приращения к приращению аргумента появились таблица производных и
точно определённые правила дифференцирования. Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
| 11. Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
1. Производная суммы или разности Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль.
Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как
производную «икса». Получаем следующие значения производных:
В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль.
Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как
производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где
сплошное нагромождение корней и степеней, как, например, ,
то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
определение, как найти, примеры решений
Производная — главнейшее понятие математического анализа. Она характеризует изменение функции аргумента x в некоторой точке. При этом и сама производная является функцией от аргумента x
Она характеризует изменение функции аргумента x в некоторой точке. При этом и сама производная является функцией от аргумента x
Производной функции в точке называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
Наиболее употребительны следующие обозначения производной :
Пример 1. Пользуясь определением производной , найти производную функции
Решение. Из определения производной вытекает следующая схема её вычисления.
Дадим аргументу приращение (дельта) и найдём приращение функции:
Найдём отношение приращения функции к приращению аргумента:
Вычислим предел этого отношения при условии, что приращение аргумента стремится к нулю, то есть требуемую в условии задачи производную:
Физический смысл производной
К понятию производной привело изучение Галилео Галилеем закона свободного падения тел, а в
более широком смысле — задачи о мгновенной скорости неравномерного прямолинейного движения точки.
Пусть камешек поднят и затем из состояния покоя отпущен. Путь s , проходимый за время t , является функцией времени, то есть. s = s (t ). Если задан закон движения точки, то можно определить среднюю скорость за любой промежуток времени. Пусть в момент времени камешек находился в положении A , а в момент — в положении B . За промежуток времени (от t до ) точка прошла путь . Поэтому средняя скорость движения за этот промежуток времени, которую обзначим через , составляет
.
Однако движение свободно падающего тела явно неравномерное. Скорость v падения постоянно возрастает. И средней скорости уже недостаточно для характеристики быстроты движения на различных участках пути. Такая характеристика тем точнее, чем меньше промежуток времени . Поэтому вводится следующее понятие: мгновенной скоростью прямолинейного движения (или скоростью в данный момент времени t ) называется предел средней скорости при :
(при условии, что этот предел существует и конечен).
Так выясняется, что мгновенная скорость есть предел отношения приращения функции s (t ) к приращению аргумента t при Это и есть производная, которая в общем виде записывается так:.
.
Решение обозначенной задачи представляет собой физический смысл производной . Итак, производной функции y=f (x ) в точке x называется предел (если он существует и конечен) приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
Пример 2. Найти производную функции
Решение. Из определения производной вытекает следующая схема для её вычисления.
Шаг 1. Дадим аргументу приращение и найдём
Шаг 2. Найдём приращение функции:
Шаг 3. Найдём отношение приращения функции к приращению аргумента:
Шаг 4. Вычислим предел этого отношения при , то есть производную:
Геометрический смысл производной
Пусть функция определена на интервале и пусть точка М на графике функции соответствует значению аргумента , а точка Р – значению . Проведём через точки М и Р прямую и назовём её секущей . Обозначим через угол между секущей и осью . Очевидно, что этот угол зависит от .
Проведём через точки М и Р прямую и назовём её секущей . Обозначим через угол между секущей и осью . Очевидно, что этот угол зависит от .
Если существует
проходящую через точку , называют предельным положением секущей МР при (или при ).
Касательной к графику функции в точке М называется предельное положение секущей МР при , или, что то же при .
Из определения следует, что для существования касательной достаточно, чтобы существовал предел
,
причём предел равен углу наклона касательной к оси .
Теперь дадим точное определение касательной.
Касательной к графику функции в точке называется прямая, проходящая через точку и имеющая угловой коэффициент , т.е. прямая, уравнение которой
Из этого определения следует, что производная функции равна угловому коэффициенту касательной к графику этой функции в точке с абсциссой x . В этом состоит геометрический смысл производной.
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:
y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.
2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x 5 -2=18x 5 -2.
Применяем правило I , формулы 3, 5 и 6 и 1.
Применяем правило IV , формулы 5 и 1 .
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4 . Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4 . Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
Примеры.
1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое —4,01 .
Решение.
Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.
Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f «(х 0) = 1 .
Решение.
Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f «(х 0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .
3. Вывести формулу производной функции y=x n .
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)» = nx n-1 .
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования .
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой «у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
Страница 1 из 1 1
Когда человек сделал первые самостоятельные шаги в изучении математического анализа и начинает задавать неудобные вопросы, то уже не так-то просто отделаться фразой, что «дифференциальное исчисление найдено в капусте». Поэтому настало время набраться решимости и раскрыть тайну появления на светтаблицы производных и правил дифференцирования . Начало положено в статьео смысле производной , которую я настоятельно рекомендую к изучению, поскольку там мы как раз рассмотрели понятие производной и начали щёлкать задачи по теме. Этот же урок носит ярко выраженную практическую направленность, более того,
рассматриваемые ниже примеры, в принципе, можно освоить и чисто формально (например, когда нет времени/желания вникать в суть производной). Также крайне желательно (однако опять не обязательно) уметь находить производные «обычным» методом – хотя бы на уровне двух базовых занятий:
Как найти производную?и
Производная сложной функции.
Также крайне желательно (однако опять не обязательно) уметь находить производные «обычным» методом – хотя бы на уровне двух базовых занятий:
Как найти производную?и
Производная сложной функции.
Но без чего-чего сейчас точно не обойтись, так это безпределов функций . Вы должны ПОНИМАТЬ, что такое предел и уметь решать их, как минимум, на среднем уровне. А всё потому, чтопроизводная
функции в точке определяется формулой:
Напоминаю обозначения и термины: называютприращением аргумента ;
– приращением функции;
– это ЕДИНЫЕ символы («дельту» нельзя «отрывать» от «икса» или «игрека»).
Очевидно, что является «динамической» переменной,– константой и результат вычисления предела– числом(иногда – «плюс» либо «минус» бесконечностью) .
В качестве точки можно рассмотреть ЛЮБОЕ значение, принадлежащееобласти определения функции, в котором существует производная.
Примечание : оговорка «в котором существует производная» –в общем случае существенна ! Так, например, точкахоть и входит в область определения функции, но производной
там не существует. Поэтому формула
Поэтому формула
не применима в точке,
и укороченная формулировка без оговорки будет некорректна. Аналогичные факты справедливы и для других функций с «обрывами» графика, в частности, для арксинуса и арккосинуса.
Таким образом, после замены , получаем вторую рабочую формулу:
Обратите внимание на коварное обстоятельство, которое может запутать чайника: в данном пределе «икс», будучи сам независимой переменной, исполняет роль статиста, а «динамику» задаёт опять же приращение . Результатом вычисления предела
является производная функция.
Исходя из вышесказанного, сформулируем условия двух типовых задач:
– Найти производную в точке , используя определение производной.
– Найти производную функцию , используя определение производной. Эта версия, по моим наблюдениям, встречается заметно чаще и ей будет уделено основное внимание.
Принципиальное отличие заданий состоит в том, что в первом случае требуется найти число (как вариант, бесконечность) , а во втором –
функцию
. Кроме того, производной может и вовсе не существовать.
Кроме того, производной может и вовсе не существовать.
Как ?
Составить отношение и вычислить предел.
Откуда появилась таблица производных и правила дифференцирования? Благодаря единственному пределу
Кажется волшебством, но в
действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожитьтаблицу производных , оттачивая алгоритм и технические приёмы решения:
По сути, требуется доказать частный случай производной степенной функции, который обычно фигурирует в таблице: .
Решение технически оформляется двумя способами. Начнём с первого, уже знакомого подхода: лесенка начинается с дощечки, а производная функция – с производной в точке.
Рассмотрим некоторую
(конкретную) точку, принадлежащуюобласти определения
функции, в которой существует производная. Зададим в данной точке приращение (разумеется, не выходящее за рамки
о/о
-я)
и составим соответствующее приращение функции:
Зададим в данной точке приращение (разумеется, не выходящее за рамки
о/о
-я)
и составим соответствующее приращение функции:
Вычислим предел:
Неопределённость 0:0 устраняется стандартным приёмом, рассмотренным ещё в первом веке до нашей эры. Домножим
числитель и знаменатель на сопряженное выражение :
Техника решения такого предела подробно рассмотрена на вводном уроке о пределах функций .
Поскольку в качестве можно выбрать ЛЮБУЮ точкуинтервала
То, осуществив замену, получаем:
В который раз порадуемся логарифмам:
Найти производную функции , пользуясь определением производной
Решение : рассмотрим другой подход к раскрутке той же задачи. Он точно такой же, но более рационален с точки зрения оформления. Идея состоит в том, чтобы в начале решения избавиться от
подстрочного индекса и вместо буквы использовать букву.
Рассмотрим произвольную
точку, принадлежащуюобласти определения
функции(интервалу), и зададим в ней приращение. А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
Тогда соответствующее приращение функции:
Найдём производную:
Простота оформления уравновешивается путаницей, которая может
возникнуть у начинающих (да и не только). Ведь мы привыкли, что в пределе изменяется буква «икс»! Но тут всё по-другому: – античная статуя, а– живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
Устранение неопределённости закомментирую пошагово:
(1) Используем свойство логарифма .
(2) В скобках почленно делим числитель на знаменатель.
(3) В знаменателе искусственно домножаем и делим на «икс» чтобы
воспользоваться замечательным пределом , при этом в качествебесконечно малой величины выступает.
Ответ : по определению производной:
Или сокращённо:
Предлагаю самостоятельно сконструировать ещё две табличные формулы:
Найти производную по определению
В данном случае составленное приращение сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).
Примерный образец оформления задания в конце урока (первый способ).
Найти производную по определению
А тут всё необходимо свести к замечательному пределу . Решение оформлено вторым способом.
Аналогично выводится ряд других табличных производных . Полный список можно найти в школьном учебнике, или, например, 1- м томе Фихтенгольца. Не вижу особого смысла переписывать из книг и доказательства правил дифференцирования – они тоже порождены
формулой .
Переходим к реально встречающимся заданиям: Пример 5
Найти производную функции , используя определение производной
Решение : используем первый стиль оформления. Рассмотрим некоторую точку, принадлежащую, и зададим в ней приращение аргумента. Тогда соответствующее приращение функции:
Возможно, некоторые читатели ещё не до конца поняли принцип, по которому нужно составлять приращение . Берём точку(число) и находим в ней значение функции:, то есть в функцию
вместо «икса» следует подставить. Теперь берём
Составленное приращение функции бывает выгодно сразу же упростить
. Зачем? Облегчить и укоротить решение дальнейшего предела.
Зачем? Облегчить и укоротить решение дальнейшего предела.
Используем формулы , раскрываем скобки и сокращаем всё, что можно сократить:
Индейка выпотрошена, с жаркое никаких проблем:
В итоге:
Поскольку в качестве можно выбрать любое действительное число, то проведём заменуи получим.
Ответ :по определению.
В целях проверки найдём производную с помощью правил
дифференцирования и таблицы:
Всегда полезно и приятно знать правильный ответ заранее, поэтому лучше мысленно либо на черновике продифференцировать предложенную функцию «быстрым» способом в самом начале решения.
Найти производную функции по определению производной
Это пример для самостоятельного решения. Результат лежит на поверхности:
Вернёмся к стилю №2: Пример 7
Давайте немедленно узнаем, что должно получиться. По правилу дифференцирования сложной функции :
Решение : рассмотрим произвольную точку, принадлежащую, зададим в ней приращение аргументаи составим приращение
Найдём производную:
(1) Используем тригонометрическую формулу
(2)
Под синусом раскрываем скобки, под косинусом приводим подобные слагаемые.
(3) Под синусом сокращаем слагаемые, под косинусом почленно делим числитель на знаменатель.
(4) В силу нечётности синуса выносим «минус». Под косинусом
указываем, что слагаемое .
(5) В знаменателе проводим искусственное домножение, чтобы использовать первый замечательный предел . Таким образом, неопределённость устранена, причёсываем результат.
Ответ :по определению Как видите, основная трудность рассматриваемой задачи упирается в
сложность самого предела + небольшое своеобразие упаковки. На практике встречаются и тот и другой способ оформления, поэтому я максимально подробно расписываю оба подхода. Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».
Пользуясь определением, найти производную функции
Это задание для самостоятельного решения. Образец оформлен в том же духе, что предыдущий пример.
Разберём более редкую версию задачи:
Найти производную функции в точке, пользуясь определением производной.
Во-первых, что должно получиться в сухом остатке? Число Вычислим ответ стандартным способом:
Решение : с точки зрения наглядности это задание значительно проще, так как в формулевместо
рассматривается конкретное значение.
Зададим в точке приращениеи составим соответствующее приращение функции:
Вычислим производную в точке:
Используем весьма редкую формулу разности тангенсов и в который раз сведём решение кпервому
замечательному пределу:
Ответ :по определению производной в точке.
Задачу не так трудно решить и «в общем виде» – достаточно заменить наили простов зависимости от способа оформления. В этом случае, понятно, получится не число, а производная функция.
Пример 10 Используя определение, найти производную функциив точке
Это пример для самостоятельного решения.
Заключительная бонус-задача предназначена, прежде всего, для студентов с углубленным изучением математического анализа, но и всем остальным тоже не помешает:
Будет ли дифференцируема функция в точке?
Решение : очевидно, что кусочно-заданная функциянепрерывна в точке, но будет ли она там дифференцируема?
Алгоритм решения, причём не только для кусочных функций, таков:
1)
Находим
левостороннюю производнуюв данной точке:
.
2) Находим правостороннюю производнуюв данной точке: .
3) Если односторонние производныеконечны и совпадают:
, то функциядифференцируема в точкеи
геометрически здесь существует общая касательная (см. теоретическую часть урока Определение и смысл производной ).
Если получены два разных значения: (одно из которых может оказаться и бесконечным) , то функция не дифференцируема в точке.
Если же обе односторонние производные равны бесконечности
(пусть даже разных знаков), то функция не
дифференцируема в точке , но там существует бесконечная производная и общая вертикальная касательная к графику(см. Пример 5 урока Уравнение нормали ) .
Многие удивятся неожиданному расположению этой статьи в моём авторском курсе о производной функции одной переменной и её приложениях. Ведь как оно было ещё со школы: стандартный учебник в первую очередь даёт определение производной, её геометрический, механический смысл. Далее учащиеся находят производные функций по определению, и, собственно, только потом оттачивается техника дифференцирования с помощью таблицы производных .
Но с моей точки зрения, более прагматичен следующий подход: прежде всего, целесообразно ХОРОШО ПОНЯТЬ предел функции , и, в особенности, бесконечно малые величины . Дело в том, что определение производной базируется на понятии предела , которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с пределов функций . Заодно освоите/вспомните их решение.
Тот же практический смысл подсказывает, что сначала выгодно научиться находить производные , в том числе производные сложных функций . Теория теорией, а дифференцировать, как говорится, хочется всегда. В этой связи лучше проработать перечисленные базовые уроки, а может и стать мастером дифференцирования , даже не осознавая сущности своих действий.
К материалам данной страницы рекомендую приступать после ознакомления со статьёй Простейшие задачи с производной , где, в частности рассмотрена задача о касательной к графику функции. Но можно и повременить. Дело в том, что многие приложения производной не требуют её понимания, и неудивительно, что теоретический урок появился достаточно поздно – когда мне потребовалось объяснять нахождение интервалов возрастания/убывания и экстремумов функции. Более того, он довольно долго находился в теме «Функции и графики », пока я всё-таки не решил поставить его раньше.
Поэтому, уважаемые чайники, не спешите поглощать суть производной, как голодные звери, ибо насыщение будет невкусным и неполным.
Понятие возрастания, убывания, максимума, минимума функцииМногие учебные пособия подводят к понятию производной с помощью каких-либо практических задач, и я тоже придумал интересный пример. Представьте, что нам предстоит путешествие в город, до которого можно добраться разными путями. Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными: до города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными: до города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Но каковы бы ни были ваши предпочтения, желательно знать местность или, по меньшей мере, располагать её топографической картой. А если такая информация отсутствует? Ведь можно выбрать, например, ровный путь, да в результате наткнуться на горнолыжный спуск с весёлыми финнами. Не факт, что навигатор и даже спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать рельеф пути средствами математики.
Рассмотрим некоторую дорогу (вид сбоку):
На всякий случай напоминаю элементарный факт: путешествие происходит слева направо . Для простоты полагаем, что функция непрерывна на рассматриваемом участке.
Какие особенности у данного графика?
На интервалах функция возрастает , то есть каждое следующее её значение больше предыдущего. Грубо говоря, график идёт снизу вверх (забираемся на горку). А на интервале функция убывает – каждое следующее значение меньше предыдущего, и наш график идёт сверху вниз (спускаемся по склону).
Также обратим внимание на особые точки. В точке мы достигаем максимума , то есть существует такой участок пути, на котором значение будет самым большим (высоким). В точке же достигается минимум , и существует такая её окрестность, в которой значение самое маленькое (низкое).
Более строгую терминологию и определения рассмотрим на уроке об экстремумах функции , а пока изучим ещё одну важную особенность: на промежутках функция возрастает, но возрастает она с разной скоростью . И первое, что бросается в глаза – на интервале график взмывает вверх гораздо более круто , чем на интервале . Нельзя ли измерить крутизну дороги с помощью математического инструментария?
Нельзя ли измерить крутизну дороги с помощью математического инструментария?
Идея состоит в следующем: возьмём некоторое значение (читается «дельта икс») , которое назовём приращением аргумента , и начнём его «примерять» к различным точкам нашего пути:
1) Посмотрим на самую левую точку: минуя расстояние , мы поднимаемся по склону на высоту (зелёная линия). Величина называется приращением функции , и в данном случае это приращение положительно (разность значений по оси – больше нуля). Составим отношение , которое и будет мерИлом крутизны нашей дороги. Очевидно, что – это вполне конкретное число, и, поскольку оба приращения положительны, то .
Внимание! Обозначение являются ЕДИНЫМ символом, то есть нельзя «отрывать» «дельту» от «икса» и рассматривать эти буквы отдельно. Разумеется, комментарий касается и символа приращения функции.
Исследуем природу полученной дроби содержательнее. Пусть изначально мы находимся на высоте 20 метров (в левой чёрной точке). Преодолев расстояние метров (левая красная линия), мы окажемся на высоте 60 метров. Тогда приращение функции составит метров (зелёная линия) и: . Таким образом, на каждом метре этого участка дороги высота увеличивается в среднем на 4 метра …не забыли альпинистское снаряжение? =) Иными словами, построенное отношение характеризует СРЕДНЮЮ СКОРОСТЬ ИЗМЕНЕНИЯ (в данном случае – роста) функции.
Пусть изначально мы находимся на высоте 20 метров (в левой чёрной точке). Преодолев расстояние метров (левая красная линия), мы окажемся на высоте 60 метров. Тогда приращение функции составит метров (зелёная линия) и: . Таким образом, на каждом метре этого участка дороги высота увеличивается в среднем на 4 метра …не забыли альпинистское снаряжение? =) Иными словами, построенное отношение характеризует СРЕДНЮЮ СКОРОСТЬ ИЗМЕНЕНИЯ (в данном случае – роста) функции.
Примечание : числовые значения рассматриваемого примера соответствуют пропорциям чертежа лишь приблизительно.
2) Теперь пройдём то же самое расстояние от самой правой чёрной точки. Здесь подъём более пологий, поэтому приращение (малиновая линия) относительно невелико, и отношение по сравнению с предыдущим случаем будет весьма скромным. Условно говоря, метров и скорость роста функции составляет . То есть, здесь на каждый метр пути приходится в среднем пол метра подъёма.
3) Маленькое приключение на склоне горы. Посмотрим на верхнюю чёрную точку, расположенную на оси ординат. Предположим, что это отметка 50 метров. Снова преодолеваем расстояние , в результате чего оказываемся ниже – на уровне 30-ти метров. Поскольку осуществлено движение сверху вниз (в «противоход» направлению оси ), то итоговое приращение функции (высоты) будет отрицательным : метров (коричневый отрезок на чертеже). И в данном случае речь уже идёт о скорости убывания функции: , то есть за каждый метр пути этого участка высота убывает в среднем на 2 метра. Берегите одежду на пятой точке.
Теперь зададимся вопросом: какое значение «измерительного эталона» лучше всего использовать? Совершенно понятно, 10 метров – это весьма грубо. На них запросто уместится добрая дюжина кочек. Да что там кочки, внизу может быть глубокое ущелье, а через несколько метров – другая его сторона с дальнейшим отвесным подъёмом. Таким образом, при десятиметровом мы не получим вразумительной характеристики подобных участков пути посредством отношения .
Из проведённого рассуждения следует вывод – чем меньше значение , тем точнее мы опишем рельеф дороги. Более того, справедливы следующие факты:
– Для любой точки подъемов можно подобрать значение (пусть и очень малое), которое умещается в границах того или иного подъёма. А это значит, что соответствующее приращение высоты будет гарантированно положительным, и неравенство корректно укажет рост функции в каждой точке этих интервалов.
– Аналогично, для любой точки склона существует значение , которое полностью уместится на этом склоне. Следовательно, соответствующее приращение высоты однозначно отрицательно, и неравенство корректно покажет убыль функции в каждой точке данного интервала.
– Особо интересен случай, когда скорость изменения функции равна нулю: . Во-первых, нулевое приращение высоты () – признак ровного пути. А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
Таким образом, мы подобрались к удивительной возможности идеально точно охарактеризовать скорость изменения функции. Ведь математический анализ позволяет устремить приращение аргумента к нулю: , то есть сделать его бесконечно малым .
По итогу возникает ещё один закономерный вопрос: можно ли для дороги и её графика найти другую функцию , которая сообщала бы нам обо всех ровных участках, подъёмах, спусках, вершинах, низинах, а также о скорости роста/убывания в каждой точке пути?
Что такое производная? Определение производной.Геометрический смысл производной и дифференциала
Пожалуйста, прочитайте вдумчиво и не слишком быстро – материал прост и доступен каждому! Ничего страшного, если местами что-то покажется не очень понятным, к статье всегда можно вернуться позже. Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Естественно, и в самом определении производной в точке заменим на :
К чему мы пришли? А пришли мы к тому, что для функции по закону ставится в соответствие другая функция , которая называется производной функцией (или просто производной) .
Производная характеризует скорость изменения функции . Каким образом? Мысль идёт красной нитью с самого начала статьи. Рассмотрим некоторую точку области определения функции . Пусть функция дифференцируема в данной точке. Тогда:
1) Если , то функция возрастает в точке . И, очевидно, существует интервал (пусть даже очень малый), содержащий точку , на котором функция растёт, и её график идёт «снизу вверх».
2) Если , то функция убывает в точке . И существует интервал, содержащий точку , на котором функция убывает (график идёт «сверху вниз»).
3) Если , то бесконечно близко около точки функция сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции , в частности в точках минимума и максимума .
Немного семантики. Что в широком смысле обозначает глагол «дифференцировать»? Дифференцировать – это значит выделить какой-либо признак. Дифференцируя функцию , мы «выделяем» скорость её изменения в виде производной функции . А что, кстати, понимается под словом «производная»? Функция произошла от функции .
Термины весьма удачно истолковывает механический смысл производной :
Рассмотрим закон изменения координаты тела , зависящий от времени , и функцию скорости движения данного тела . Функция характеризует скорость изменения координаты тела, поэтому является первой производной функции по времени: . Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела».
Ускорение тела – это скорость изменения скорости, поэтому: . Если бы в природе не существовало исходных понятий «движение тела» и «скорость движения тела», то не существовало бы и производного понятия «ускорение тела».
Вычисление производной часто встречается в заданиях ЕГЭ. Данная страница содержит список формул для нахождения производных.
Правила дифференцирования
- (k⋅ f(x))′=k⋅ f ′(x).
- (f(x)+g(x))′=f′(x)+g′(x).
- (f(x)⋅ g(x))′=f′(x)⋅ g(x)+f(x)⋅ g′(x).
- Производная сложной функции. Если y=F(u), а u=u(x), то функция y=f(x)=F(u(x)) называется сложной функцией от x. Равна y′(x)=Fu′⋅ ux′.
- Производная неявной функции. Функция y=f(x) называется неявной функцией, заданной соотношением F(x,y)=0, если F(x,f(x))≡0.
- Производная обратной функции. Если g(f(x))=x, то функция g(x) называется обратной функцией для функции y=f(x).
- Производная параметрически заданной функции. Пусть x и y заданы как функции от переменной t: x=x(t), y=y(t).
 Говорят, что y=y(x) параметрически заданная функция на промежутке x∈
(a;b), если на этом промежутке уравнение x=x(t) можно выразить в виде t=t(x) и определить функцию y=y(t(x))=y(x).
Говорят, что y=y(x) параметрически заданная функция на промежутке x∈
(a;b), если на этом промежутке уравнение x=x(t) можно выразить в виде t=t(x) и определить функцию y=y(t(x))=y(x). - Производная степенно-показательной функции. Находится путем логарифмирования по основанию натурального логарифма.
Советуем сохранить ссылку, так как эта таблица может понадобиться еще много раз.
определение, как найти, примеры решений
Определение производной от функции есть обратная операция интегрированию функции. Для элементарных функций вычислить производную не составляет труда, достаточно воспользоваться таблицей производных. Если же нам необходимо найти производную от сложной функции, то дифференцирование будет уже намного сложнее, потребует большей внимательности и времени. При этом очень легко допустить описку или незначительную ошибку, которая приведет к окончательному неверному ответу. Поэтому всегда важно иметь возможность проверить своё решение. Это вы можете сделать с помощью данного онлайн-калькулятора, который позволяет находить производные от любых функций онлайн с подробным решением бесплатно, без регистрации на сайте. Нахождение производной функции (дифференцирование) это отношение приращения функции к приращению аргумента (численно производная равна тангенсу угла наклона касательной к графику функции). Если необходимо вычислить производную от функции в конкретной точке, то нужно в полученном ответе вместо аргумента x подставить его численное значение и рассчитать выражение. При решении производной онлайн вам необходимо ввести функцию в соответсвующее поле: при этом аргументом должна быть переменная x , поскольку дифференцирование идёт именно по нему. Для вычисления второй производной нужно продифференцировать полученный ответ.
Это вы можете сделать с помощью данного онлайн-калькулятора, который позволяет находить производные от любых функций онлайн с подробным решением бесплатно, без регистрации на сайте. Нахождение производной функции (дифференцирование) это отношение приращения функции к приращению аргумента (численно производная равна тангенсу угла наклона касательной к графику функции). Если необходимо вычислить производную от функции в конкретной точке, то нужно в полученном ответе вместо аргумента x подставить его численное значение и рассчитать выражение. При решении производной онлайн вам необходимо ввести функцию в соответсвующее поле: при этом аргументом должна быть переменная x , поскольку дифференцирование идёт именно по нему. Для вычисления второй производной нужно продифференцировать полученный ответ.
Калькулятор вычисляет производные всех элементарных функций, приводя подробное решение. Переменная дифференцирования определяется автоматически.
Производная функции — одно из важнейших понятий в математическом анализе. К появлению производной привели такие задачи, как, например, вычисление мгновенной скорости точки в момент времени , если известен путь в зависимоти от времени , задача о нахождении касательной к функции в точке.
К появлению производной привели такие задачи, как, например, вычисление мгновенной скорости точки в момент времени , если известен путь в зависимоти от времени , задача о нахождении касательной к функции в точке.
Чаще всего производная функции определяется как предел отношения приращения функции к приращению аргумента, если он существует.
Определение. Пусть функция определена в некоторой окрестности точки . Тогда производной функции в точке называется предел, если он существует
Как вычислить производную функции?
Для того, чтобы научиться дифференцировать функции, нужно выучить и понять правила дифференцирования и научиться пользоваться таблицей производных .
Правила дифференцирования
Пусть и — произвольные дифференцируемые функции от вещественной переменной, — некоторая вещественная постоянная. Тогда
— правило дифференцирования произведения функций
— правило дифференцирования частного функций
0″> — дифференцирование функции с переменным показателем степени
— правило дифференцирования сложной функции
— правило дифференцирования степенной функции
Производная функции онлайн
Наш калькулятор быстро и точно вычислит производную любой функции онлайн. Программа не допустит ошибки при вычислениях производной и поможет избежать долгих и нудных расчётов. Онлайн калькулятор будет полезен и в том случае, когда есть необходимость проверить на правильность своё решение, и если оно неверно, быстро найти ошибку.
Программа не допустит ошибки при вычислениях производной и поможет избежать долгих и нудных расчётов. Онлайн калькулятор будет полезен и в том случае, когда есть необходимость проверить на правильность своё решение, и если оно неверно, быстро найти ошибку.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше
предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться
таблицей производных и правилами дифференцирования. Для нахождения производной подходит
следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
11. Производная арккосинуса Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т. е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
А проверить решение задачи на производную можно на .
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
В данной функции видим произведение, один из сомножителей которых — квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Проверить решение задачи на производную можно на калькуляторе производных онлайн .
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Вычисление производной — одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:
- Таблица производных экспоненциальных и логарифмических функций
Приведенные формулы используйте как справочные значения. Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена «шпаргалка» основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.
Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена «шпаргалка» основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.
Производные простых функций
1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0
Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.
2. Производная переменной равна единице
x´ = 1
Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение :
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .
Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .
Откуда следует, что
(cx + b)» = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|» = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)»= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)» = 2x
(x 3)» = 3x 2
Для запоминания формулы :
Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.
6. Производная дроби 1/х
(1/х)» = — 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)» = (x -1)» , тогда можно применить формулу из правила 5 таблицы производных
(x -1)» = -1x -2 = — 1 / х 2
7. Производная дроби с переменной произвольной степени в знаменателе
(1 / x c)» = — c / x c+1
Пример:
(1 / x 2)» = — 2 / x 3
8. Производная корня (производная переменной под квадратным корнем)
Производная корня (производная переменной под квадратным корнем)
(√x)» = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)» = (х 1/2)» значит можно применить формулу из правила 5
(х 1/2)» = 1/2 х -1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
(n √x)» = 1 / (n n √x n-1)
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
| Дата: 20.11.2014 Таблица производных.Производная — одно из главных понятий высшей математики. В этом уроке мы познакомимся с этим понятием. Именно познакомимся, без строгих математических формулировок и доказательств. Это знакомство позволит: Понимать суть несложных заданий с производной; Успешно решать эти самые несложные задания; Подготовиться к более серьёзным урокам по производной. Сначала — приятный сюрприз.) Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний! Для успешного выполнения большинства заданий в школе и ВУЗе достаточно знать всего несколько терминов — чтобы понять задание, и всего несколько правил — чтобы его решить. Приступим к знакомству?) Термины и обозначения.В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование. Определение и смысл этой операции будут рассмотрены в отдельных уроках. Здесь же важно понять, что дифференцирование — это просто математическая операция над функцией. Берём любую функцию и, по определённым правилам, преобразовываем её. В результате получится новая функция. Вот эта новая функция и называется: производная. Дифференцирование — действие над функцией. Производная — результат этого действия. Так же, как, например, сумма — результат сложения. Или частное — результат деления. Зная термины, можно, как минимум, понимать задания.) Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную и т. Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y» или f»(x) или S»(t) и так далее. Читается игрек штрих, эф штрих от икс, эс штрих от тэ, ну вы поняли…) Штрих также может обозначать производную конкретной функции, например: (2х+3)» , (x 3 )» , (sinx)» и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем. Предположим, что понимать задания мы научились. Осталось всего ничего — научиться их решать.) Напомню ещё раз: нахождение производной — это преобразование функции по определённым правилам. Этих правил, на удивление, совсем немного. Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. 1. Таблица производных (формулы дифференцирования). 3. Производная сложной функции. Начнём по порядку. В этом уроке рассмотрим таблицу производных. Таблица производных.В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п. Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.) Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.
Рекомендую обратить внимание на третью группу функций в этой таблице производных. Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету… Рассмотрим несколько примеров: 1. Найти производную функции y = x 3 Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат: (x 3) » = 3·x 3-1 = 3x 2 Вот и все дела. Ответ: y» = 3x 2 2. Найти значение производной функции y = sinx в точке х = 0. Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию… Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция. По табличке находим синус и соответствующую производную: y» = (sin x)» = cosx Подставляем ноль в производную: y»(0) = cos 0 = 1 Это и будет ответ. 3. Продифференцировать функцию: Что, внушает?) Такой функции в таблице производных и близко нет. Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает… Но если увидеть, что наша функция — это косинус двойного угла , то всё сразу налаживается! Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. Т.е. наша хитрая функция есть не что иное, как y = cosx . А это — табличная функция. Сразу получаем: Ответ: y» = — sin x . Пример для продвинутых выпускников и студентов: 4. Найти производную функции: Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями… То вполне можно упростить эту функцию. Вот так: А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем: Вот и всё. Это будет ответ. Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования. |
Деривативы для детей и начинающих: #1 Простое объяснение
Новостная статья CBS о Риши Вамдатте: «11-летний вундеркинд, который предлагает бесплатные финансовые консультации тысячам онлайн»- Фейсбук
- Твиттер
Что такое производные? Investing 101: Easy Peasy Finance для детей и начинающих
Посмотреть это видео на YouTube
Введение в деривативы для детей и подростков
В этом видео просто и лаконично объясняется концепция деривативов для детей и начинающих. Его могут использовать дети и подростки, чтобы узнать о деривативах, или использовать его в качестве денежного и личного финансового ресурса родителями и учителями в рамках курса финансовой грамотности или учебной программы K-12.
Его могут использовать дети и подростки, чтобы узнать о деривативах, или использовать его в качестве денежного и личного финансового ресурса родителями и учителями в рамках курса финансовой грамотности или учебной программы K-12.
Подходит для учащихся от классов:
- Киндбарт
- Начальная школа
- Средняя школа
- Средняя школа
Охватываемые темы:
- . Каковы производные
- различные виды дериваверов
- ARIVATIONS
- мировой пример
- Почему они используются
- Как работает торговля деривативами
- Стоит ли инвестировать в деривативы
Что такое деривативы?
Производные инструменты — это сложные финансовые инструменты, которые имеют стоимость только потому, что они связаны с чем-то еще, называемым базовым активом. Другими словами, производные получают свою стоимость из базового инструмента, которым могут быть акции, облигации, валюта, процентные ставки, товары и т. д.
д.
Сами по себе производные не имеют стоимости. Цена дериватива определяется и зависит от цены базового актива.
Существуют ли разные виды производных?Да, наиболее распространенными деривативами являются фьючерсы, форварды, свопы и опционы.
На высоком уровне фьючерсы, форварды и свопы являются обязательными для держателя контракта, что означает, что стороны, заключающие соглашение, должны выполнить свои обязательства. Опционы, как следует из названия, дают держателю опциона право, но не обязательство купить или продать базовый инструмент.
Мы подробно рассказываем о каждом производном инструменте в отдельных видеороликах.
[Это партнерская ссылка: без каких-либо дополнительных затрат для вас, мы будем получать комиссию, если вы нажмете и совершите покупку]
Хмм… Это сложно! Можете ли вы объяснить это на примере? Допустим, Бен, фермер, выращивающий кукурузу, обеспокоен тем, что цена на кукурузу упадет к тому времени, когда его урожай будет готов к уборке, и хочет зафиксировать цену продажи по текущей рыночной цене.
С другой стороны, Сэм, производитель попкорна, считает, что цены на кукурузу вырастут через несколько месяцев, и хочет заблокировать свои покупка цена по текущей рыночной цене.
В этом случае Бен и Сэм заключают форвардный контракт, который представляет собой соглашение между Беном о продаже, а Сэмом о покупке фиксированного количества кукурузы в будущем, скажем, через 3 месяца, по сегодняшней цене. Таким образом, они оба хеджировали свой риск, основываясь на своей оценке будущей цены на кукурузу.
Для чего используются производные?Производные инструменты были в первую очередь созданы для хеджирования рисков, как мы обсуждали в примере.
Однако деривативы представляют собой инструменты с высокой долей заемных средств, по которым стороны могут торговать, внося вперед лишь небольшой процент от стоимости сделки, называемый маржой. Это делает их инвестициями с высоким риском и высокой прибылью, и поэтому они используются любителями риска для спекуляций.
Некоторые деривативы торгуются на биржах, как и акции. Их можно покупать и продавать через ваш обычный брокерский счет, если вы зарегистрировались для инвестиций в деривативы.
Но большинство деривативов торгуются напрямую между двумя сторонами, обычно финансовыми учреждениями, такими как банки, с условиями контракта, взаимно согласованными между двумя сторонами. Они называются внебиржевыми или внебиржевыми производными.
Стоит ли инвестировать в производные инструменты?Производные инструменты обеспечивают кредитное плечо, что оказывает усиленное влияние на ваши доходы: как прибыль, так и убытки могут быть огромными. Для успешного инвестирования необходимо глубокое понимание инструментов, рынков и сопутствующих рисков.
Таким образом, деривативы лучше оставить опытным инвесторам, и их следует избегать новым или неопытным инвесторам.
Что вы думаете о деривативах? Вы инвестировали в любой? Пожалуйста, дайте нам знать через ваши комментарии ниже!
Загрузить расшифровку: идеально подходит для использования учителями в своих планах уроков для обучения детей и подростков
Подкаст: Что такое производные
типов, рекомендации, плюсы и минусы
Что такое производная?
Термин производный относится к типу финансового контракта, стоимость которого зависит от базового актива, группы активов или эталона. Производный инструмент устанавливается между двумя или более сторонами, которые могут торговать на бирже или внебиржевом рынке (OTC).
Эти контракты могут использоваться для торговли любым количеством активов и несут свои риски. Цены на деривативы зависят от колебаний базового актива. Эти финансовые ценные бумаги обычно используются для доступа к определенным рынкам и могут продаваться для хеджирования рисков. Производные могут использоваться либо для снижения риска (хеджирование), либо для принятия на себя риска с ожиданием соразмерного вознаграждения (спекуляция). Производные могут переместить риск (и сопутствующие вознаграждения) от людей, не склонных к риску, к тем, кто ищет риск.
Производные могут использоваться либо для снижения риска (хеджирование), либо для принятия на себя риска с ожиданием соразмерного вознаграждения (спекуляция). Производные могут переместить риск (и сопутствующие вознаграждения) от людей, не склонных к риску, к тем, кто ищет риск.
Ключевые выводы
- Производные инструменты — это финансовые контракты, заключенные между двумя или более сторонами, стоимость которых определяется базовым активом, группой активов или эталоном.
- Производным инструментом можно торговать на бирже или внебиржевом рынке.
- Цены на производные финансовые инструменты зависят от колебаний базового актива.
- Производные инструменты обычно являются инструментами с использованием заемных средств, что увеличивает их потенциальные риски и выгоды.
- Обычные производные инструменты включают фьючерсные контракты, форварды, опционы и свопы.
Производные: Мой любимый финансовый термин
Понимание деривативов
Производный инструмент — это сложный тип финансового обеспечения, устанавливаемого между двумя или более сторонами. Трейдеры используют деривативы для доступа к определенным рынкам и торговли различными активами. Как правило, деривативы считаются формой продвинутого инвестирования. Наиболее распространенными базовыми активами для деривативов являются акции, облигации, товары, валюта, процентные ставки и рыночные индексы. Стоимость контракта зависит от изменения цены базового актива.
Трейдеры используют деривативы для доступа к определенным рынкам и торговли различными активами. Как правило, деривативы считаются формой продвинутого инвестирования. Наиболее распространенными базовыми активами для деривативов являются акции, облигации, товары, валюта, процентные ставки и рыночные индексы. Стоимость контракта зависит от изменения цены базового актива.
Производные можно использовать для хеджирования позиции, спекуляций на направленном движении базового актива или предоставления кредитного плеча вложениям. Эти активы обычно торгуются на биржах или OTC и покупаются через брокерские конторы. Чикагская товарная биржа (CME) — одна из крупнейших в мире бирж деривативов.
Важно помнить, что когда компании хеджируют, они не спекулируют на цене товара. Вместо этого хеджирование — это просто способ для каждой стороны управлять риском. Каждая сторона имеет свою прибыль или маржу, встроенную в цену, и хеджирование помогает защитить эту прибыль от уничтожения рыночными движениями цены товара.
Внебиржевые деривативы, как правило, имеют большую вероятность риска контрагента, что представляет собой опасность дефолта одной из сторон, участвующих в сделке. Эти контракты торгуются между двумя частными сторонами и не регулируются. Чтобы хеджировать этот риск, инвестор может приобрести валютный производный инструмент, чтобы зафиксировать определенный обменный курс. Производные инструменты, которые можно использовать для хеджирования такого рода рисков, включают валютные фьючерсы и валютные свопы.
Биржевые деривативы стандартизированы и регулируются более жестко, чем внебиржевые.
Особые указания
Первоначально деривативы использовались для обеспечения сбалансированного обменного курса товаров, торгуемых на международном рынке. Международные трейдеры нуждались в системе для учета различной стоимости национальных валют.
Предположим, у европейского инвестора есть инвестиционные счета, деноминированные в евро (EUR). Допустим, они покупают акции американской компании через американскую биржу, используя доллары США (USD). Это означает, что они теперь подвержены риску обменного курса, удерживая эти акции. Риск обменного курса – это угроза роста стоимости евро по отношению к доллару США. Если это произойдет, любая прибыль, полученная инвестором при продаже акций, станет менее ценной при конвертации в евро.
Это означает, что они теперь подвержены риску обменного курса, удерживая эти акции. Риск обменного курса – это угроза роста стоимости евро по отношению к доллару США. Если это произойдет, любая прибыль, полученная инвестором при продаже акций, станет менее ценной при конвертации в евро.
Спекулянт, который ожидает повышения курса евро по отношению к доллару, может получить прибыль, используя производный инструмент, стоимость которого растет вместе с евро. При использовании деривативов для спекуляций на движении цены базового актива инвестору не нужно иметь холдинг или портфель в отношении базового актива.
Многие производные инструменты используют заемные средства, что означает, что требуется небольшая сумма капитала, чтобы иметь долю в большой сумме стоимости базового актива.
Типы производных финансовых инструментов
Деривативы сегодня основаны на широком спектре транзакций и имеют гораздо больше применений. Существуют даже производные, основанные на данных о погоде, таких как количество осадков или количество солнечных дней в регионе.
Существует множество различных типов деривативов, которые можно использовать для управления рисками, спекуляций и увеличения позиции. Рынок деривативов продолжает расти, предлагая продукты, отвечающие практически любым потребностям и допустимым рискам.
Существует два класса производных продуктов: «замок» и «опцион». Продукты блокировки (например, фьючерсы, форварды или свопы) связывают соответствующие стороны с самого начала согласованными условиями в течение всего срока действия контракта. С другой стороны, опционные продукты (например, опционы на акции) предлагают держателю право, но не обязательство, купить или продать базовый актив или ценную бумагу по определенной цене в день истечения срока действия опциона или до него. Наиболее распространенными типами деривативов являются фьючерсы, форварды, свопы и опционы.
Фьючерсы
Фьючерсный контракт или просто фьючерс — это соглашение между двумя сторонами о покупке и поставке актива по согласованной цене в будущем. Фьючерсы — это стандартизированные контракты, которые торгуются на бирже. Трейдеры используют фьючерсные контракты, чтобы хеджировать свои риски или спекулировать на цене базового актива. Участвующие стороны обязаны выполнить обязательство по покупке или продаже базового актива.
Фьючерсы — это стандартизированные контракты, которые торгуются на бирже. Трейдеры используют фьючерсные контракты, чтобы хеджировать свои риски или спекулировать на цене базового актива. Участвующие стороны обязаны выполнить обязательство по покупке или продаже базового актива.
Например, предположим, что 6 ноября 2021 года компания А покупает фьючерсный контракт на нефть по цене 62,22 доллара за баррель, срок действия которого истекает 19 декабря., 2021. Компания делает это, потому что ей нужна нефть в декабре, и она обеспокоена тем, что цена вырастет до того, как компании нужно будет покупать. Покупка фьючерсного контракта на нефть хеджирует риск компании, поскольку продавец обязан поставить нефть компании А по цене 62,22 доллара за баррель по истечении срока действия контракта. Предположим, что цены на нефть вырастут до 80 долларов за баррель к 19 декабря 2021 года. Компания А может принять поставку нефти от продавца фьючерсного контракта, но если ей больше не нужна нефть, она также может продать контракт до истечения срока действия и сохранить прибыль.
В этом примере и покупатель фьючерса, и продавец хеджируют свои риски. Компания А нуждалась в нефти в будущем и хотела компенсировать риск того, что цена может вырасти в декабре, с помощью длинной позиции по фьючерсному контракту на нефть. Продавцом может быть нефтяная компания, обеспокоенная падением цен на нефть, которая хочет устранить этот риск, продавая фьючерсные контракты или открывая короткие позиции по фьючерсным контрактам с фиксированной ценой, которую она получит в декабре.
Также возможно, что одна или обе стороны являются спекулянтами с противоположным мнением о направлении декабрьской нефти. В этом случае можно получить выгоду от контракта, а можно и нет. Возьмем, к примеру, фьючерсный контракт на нефть West Texas Intermediate (WTI), который торгуется на CME и представляет собой 1000 баррелей нефти. Если бы цена на нефть выросла с 62,22 до 80 долларов за баррель, трейдер с длинной позицией — покупатель — по фьючерсному контракту получил бы прибыль в размере 17 780 долларов [(80 долларов — 62,22 доллара) x 1000 = 17 780 долларов]. Трейдер с короткой позицией — продавец — в контракте получит убыток в размере 17 780 долларов.
Трейдер с короткой позицией — продавец — в контракте получит убыток в размере 17 780 долларов.
Расчеты фьючерсами наличными
Не все фьючерсные контракты рассчитываются по истечении срока действия путем поставки базового актива. Если обе стороны фьючерсного контракта являются спекулянтами или трейдерами, маловероятно, что кто-либо из них захочет договориться о поставке большого количества баррелей сырой нефти. Спекулянты могут прекратить свои обязательства по покупке или поставке базового товара, закрыв (раскрутив) свой контракт до истечения срока действия с помощью компенсационного контракта.
Многие деривативы на самом деле рассчитываются наличными, а это означает, что прибыль или убыток в сделке — это просто бухгалтерский денежный поток на брокерский счет трейдера. Фьючерсные контракты с расчетами наличными включают многие фьючерсы на процентные ставки, фьючерсы на фондовые индексы и более необычные инструменты, такие как фьючерсы на волатильность или погодные фьючерсы.
Форварды
Форвардные контракты, или форварды, аналогичны фьючерсам, но ими не торгуют на бирже. Эти контракты торгуются только на внебиржевом рынке. При создании форвардного контракта покупатель и продавец могут настроить условия, размер и процесс расчетов. Как внебиржевые продукты, форвардные контракты несут большую степень контрагентского риска для обеих сторон.
Риск контрагента — это тип кредитного риска, заключающийся в том, что стороны могут быть не в состоянии выполнить обязательства, изложенные в договоре. Если одна из сторон становится неплатежеспособной, другая сторона может не иметь права регресса и может потерять ценность своей позиции.
После создания стороны форвардного контракта могут компенсировать свои позиции с другими контрагентами, что может увеличить потенциал контрагентских рисков по мере того, как все больше трейдеров будут участвовать в одном и том же контракте.
Обмен
Свопы — еще один распространенный тип деривативов, часто используемый для обмена одного вида денежного потока на другой. Например, трейдер может использовать процентный своп, чтобы переключиться с кредита с плавающей процентной ставкой на кредит с фиксированной процентной ставкой или наоборот.
Например, трейдер может использовать процентный своп, чтобы переключиться с кредита с плавающей процентной ставкой на кредит с фиксированной процентной ставкой или наоборот.
Представьте, что компания XYZ занимает 1 000 000 долларов и выплачивает по кредиту переменную процентную ставку, которая в настоящее время составляет 6%. XYZ может быть обеспокоен ростом процентных ставок, которые увеличат стоимость этого кредита, или столкнуться с кредитором, который не хочет предоставлять больше кредита, в то время как компания имеет этот риск переменной ставки.
Предположим, что XYZ создает своп с компанией QRS, которая готова обменять платежи, причитающиеся по кредиту с переменной процентной ставкой, на платежи, причитающиеся по кредиту с фиксированной процентной ставкой в размере 7%. Это означает, что XYZ выплатит QRS 7% от основной суммы в размере 1 000 000 долларов, а QRS выплатит XYZ 6% от той же основной суммы. В начале свопа XYZ просто заплатит QRS разницу в 1 процентный пункт между двумя ставками свопа.
Если процентные ставки упадут так, что переменная ставка по первоначальному кредиту теперь составит 5%, компания XYZ должна будет выплатить компании QRS разницу в 2 процентных пункта по кредиту. Если процентные ставки вырастут до 8%, то QRS придется выплатить XYZ разницу в 1 процентный пункт между двумя ставками свопа. Независимо от того, как изменятся процентные ставки, своп достиг первоначальной цели XYZ по превращению кредита с плавающей процентной ставкой в кредит с фиксированной процентной ставкой.
Свопы также могут быть созданы для обмена валютным риском или риском дефолта по кредиту или денежным потокам от другой коммерческой деятельности. Свопы, связанные с денежными потоками и потенциальными дефолтами по ипотечным облигациям, являются чрезвычайно популярным видом дериватива. На самом деле, они были слишком популярны в прошлом. Именно контрагентский риск подобных свопов в конечном итоге привел к кредитному кризису 2008 года.
Опции
Опционный контракт похож на фьючерсный контракт тем, что это соглашение между двумя сторонами о покупке или продаже актива в заранее определенную дату в будущем по определенной цене. Ключевое различие между опционами и фьючерсами заключается в том, что покупатель опциона не обязан выполнять свое соглашение о покупке или продаже. Это только возможность, а не обязательство, как фьючерсы. Как и в случае с фьючерсами, опционы могут использоваться для хеджирования или спекуляций на цене базового актива.
Ключевое различие между опционами и фьючерсами заключается в том, что покупатель опциона не обязан выполнять свое соглашение о покупке или продаже. Это только возможность, а не обязательство, как фьючерсы. Как и в случае с фьючерсами, опционы могут использоваться для хеджирования или спекуляций на цене базового актива.
Что касается времени вашего права на покупку или продажу, это зависит от «стиля» опциона. Американский опцион позволяет держателям реализовать права опциона в любое время до и включая день истечения срока действия. Европейский опцион может быть исполнен только в день экспирации. У большинства акций и биржевых фондов есть опционы в американском стиле, а у индексов акций, включая S&P 500, — опционы в европейском стиле.
Представьте, что инвестор владеет 100 акциями по цене 50 долларов за акцию. Они считают, что стоимость акций в будущем будет расти. Однако этот инвестор обеспокоен потенциальными рисками и решает застраховать свою позицию с помощью опциона. Инвестор может купить опцион пут, который дает ему право продать 100 акций базового актива по цене 50 долларов за акцию (так называемая цена исполнения) до определенного дня в будущем, известного как дата истечения срока действия.
Инвестор может купить опцион пут, который дает ему право продать 100 акций базового актива по цене 50 долларов за акцию (так называемая цена исполнения) до определенного дня в будущем, известного как дата истечения срока действия.
Предположим, что к моменту истечения срока действия акции падают в цене до 40 долларов за акцию, и покупатель пут-опциона решает реализовать свой опцион и продать акции по первоначальной цене исполнения 50 долларов за акцию. Если покупка опциона пут стоила инвестору 200 долларов, то он потерял только стоимость опциона, потому что цена исполнения была равна цене акции, когда они первоначально купили опцион пут. Подобная стратегия называется защитным путом, потому что она хеджирует риск падения акций.
В качестве альтернативы предположим, что инвестор не владеет акциями, которые в настоящее время стоят 50 долларов за акцию. Они считают, что его стоимость вырастет в течение следующего месяца. Этот инвестор может купить опцион колл, который дает ему право купить акцию за 50 долларов до или после истечения срока действия. Предположим, что этот колл-опцион стоил 200 долларов, а акции выросли до 60 долларов до истечения срока действия. Покупатель теперь может воспользоваться своим опционом и купить акцию стоимостью 60 долларов за акцию по цене исполнения 50 долларов за первоначальную прибыль в размере 10 долларов за акцию. Опцион колл представляет собой 100 акций, поэтому реальная прибыль составляет 1000 долларов за вычетом стоимости опциона — премии — и любых брокерских комиссий.
Предположим, что этот колл-опцион стоил 200 долларов, а акции выросли до 60 долларов до истечения срока действия. Покупатель теперь может воспользоваться своим опционом и купить акцию стоимостью 60 долларов за акцию по цене исполнения 50 долларов за первоначальную прибыль в размере 10 долларов за акцию. Опцион колл представляет собой 100 акций, поэтому реальная прибыль составляет 1000 долларов за вычетом стоимости опциона — премии — и любых брокерских комиссий.
В обоих примерах продавцы обязаны выполнять свою часть договора, если покупатели решат исполнить договор . Однако, если цена акции выше цены исполнения по истечении срока действия, пут будет бесполезен, и продавец (продавец опциона) получает право удерживать премию по истечении срока действия опциона. Если цена акции ниже страйк-цены на момент экспирации, колл будет бесполезен, и продавец колла удержит премию.
Мелисса Линг {Авторское право} Investopedia, 2019.Преимущества и недостатки производных инструментов
Преимущества
Как показывают приведенные выше примеры, деривативы могут быть полезным инструментом как для бизнеса, так и для инвесторов. Они позволяют сделать следующее:
Они позволяют сделать следующее:
- Фиксация цен
- Защита от неблагоприятных колебаний ставок
- Снижение рисков
Эти плюсы часто могут быть получены за ограниченную стоимость.
Производные также часто можно приобрести с маржей, что означает, что трейдеры используют заемные средства для их покупки. Это делает их еще менее дорогими.
Недостатки
Производные трудно оценить, потому что они основаны на цене другого актива. Риски для внебиржевых деривативов включают риски контрагента, которые трудно предсказать или оценить. Большинство производных также чувствительны к следующему:
- Изменения времени до экспирации
- Стоимость владения базовым активом
- Процентные ставки
Эти переменные затрудняют точное сопоставление стоимости производного инструмента с базовым активом.
Поскольку дериватив не имеет внутренней стоимости (его стоимость зависит только от базового актива), он уязвим для рыночных настроений и рыночного риска. Факторы спроса и предложения могут вызывать рост и падение цены дериватива и его ликвидности независимо от того, что происходит с ценой базового актива.
Факторы спроса и предложения могут вызывать рост и падение цены дериватива и его ликвидности независимо от того, что происходит с ценой базового актива.
Наконец, деривативы обычно являются инструментами с использованием заемных средств, а использование заемных средств работает в обоих направлениях. Хотя это может увеличить норму прибыли, это также ускоряет рост убытков.
Плюсы
Фиксация цен
Хеджирование риска
Можно использовать
Диверсифицировать портфель
Минусы
Трудно оценить
При условии невыполнения обязательств контрагентом (если внебиржевой)
Сложный для понимания
Чувствительные к факторам спроса и предложения
Что такое производные?
Производные ценные бумаги – это ценные бумаги, стоимость которых зависит от базового актива или получена от него. Например, фьючерсный контракт на нефть — это тип производного инструмента, стоимость которого основана на рыночной цене нефти. В последние десятилетия деривативы становятся все более популярными: общая стоимость находящихся в обращении деривативов оценивалась в 610 триллионов долларов США по состоянию на 30 июня 2021 года.
Например, фьючерсный контракт на нефть — это тип производного инструмента, стоимость которого основана на рыночной цене нефти. В последние десятилетия деривативы становятся все более популярными: общая стоимость находящихся в обращении деривативов оценивалась в 610 триллионов долларов США по состоянию на 30 июня 2021 года.
Каковы некоторые примеры деривативов?
Типичными примерами деривативов являются фьючерсные контракты, опционные контракты и дефолтные свопы. Помимо этого, существует огромное количество деривативных контрактов, адаптированных для удовлетворения потребностей различных контрагентов. На самом деле, поскольку многие деривативы торгуются на внебиржевом рынке (OTC), их в принципе можно бесконечно настраивать.
Каковы основные преимущества и риски деривативов?
Производные инструменты могут быть очень удобным способом достижения финансовых целей. Например, компания, которая хочет застраховаться от рисков, связанных с сырьевыми товарами, может сделать это, покупая или продавая производные энергетические инструменты, такие как фьючерсы на сырую нефть. Точно так же компания может хеджировать свой валютный риск, покупая валютные форвардные контракты. Производные инструменты также могут помочь инвесторам использовать свои позиции, например, покупая акции через опционы на акции, а не акции. К основным недостаткам деривативов относятся контрагентский риск, неотъемлемые риски использования заемных средств и тот факт, что сложная сеть деривативных контрактов может привести к системным рискам.
Точно так же компания может хеджировать свой валютный риск, покупая валютные форвардные контракты. Производные инструменты также могут помочь инвесторам использовать свои позиции, например, покупая акции через опционы на акции, а не акции. К основным недостаткам деривативов относятся контрагентский риск, неотъемлемые риски использования заемных средств и тот факт, что сложная сеть деривативных контрактов может привести к системным рискам.
Ускоренный курс по деривативам для чайников
Обзор постов, представляющих бесплатный вводный курс для начинающих с простыми примерами для ознакомления с базовыми ванильными деривативами, а также различиями между форвардами, фьючерсами и опционами. Более подробный ускоренный курс по корпоративным финансам для создания основ, необходимых для прохождения этого курса, см. в дорожной карте Руководства по обучению корпоративным финансам.
В нашем Ускоренном курсе по деривативам мы начинаем с профилей производных выплат и синтетического конструирования продуктов, после чего следует ряд простых оценочных опросов, ценообразование деривативов и справочник по уравнениям. За ускоренным курсом следует промежуточный курс, в котором рассматриваются варианты продукта и основные концепции ценообразования. Цель здесь состоит в том, чтобы просто представить производные понятия небольшими кусочками.
За ускоренным курсом следует промежуточный курс, в котором рассматриваются варианты продукта и основные концепции ценообразования. Цель здесь состоит в том, чтобы просто представить производные понятия небольшими кусочками.
- Мастер-класс: Интенсивный курс опционов и производных: Первая сессия: Терминология
- Мастер-класс: Ускоренный курс опционов и производных инструментов: Сессия вторая: форварды, фьючерсы и опционы
- Мастер-класс: Ускоренный курс опционов и деривативов: Сессия третья: Профили выплат – Форварды
- Мастер-класс: Ускоренный курс по опционам и производным инструментам: Сессия четвертая: Профили выплат – опционы, коллы и путы
- Мастер-класс: Ускоренный курс опционов и деривативов: Сессия пятая: Синтетика Мастер-класс
- : Ускоренный курс деривативов: что вы пропустили на синтетической форвардной диаграмме выше
Ускоренный курс по деривативам — обучающие семинары и стенограммы
- Понимание процесса продажи деривативов: введение в функцию банковского казначейства
- Продажа производных продуктов клиентам казначейства
Ценообразование производных финансовых инструментов Материалы для чтения и обучения
- Ценообразование опционов с использованием биномиальных деревьев в Excel
- Опционное ценообразование — создание симуляторов Монте-Карло в Excel
- Оценка опционов с использованием моделирования Монте-Карло – Обзор модели
- Ценообразование опционов — ценовая лестница опционов с использованием симуляторов Монте-Карло в Excel
- Построение поверхностей подразумеваемой и локальной волатильности в Excel
- Поверхности волатильности, подразумеваемая волатильность, улыбки и перекосы
- Поверхность волатильности, опционы без денег и лотерейные билеты.

- Разница между подразумеваемой и локальной волатильностью – поверхности волатильности
- Создание набора данных поверхности волатильности с использованием подразумеваемой волатильности
- Поверхности подразумеваемой и локальной волатильности в Excel – заключительные шаги
- Расчет форвардной подразумеваемой волатильности в Excel
Ускоренный курс по деривативам – Понимание греков
Ни одно введение в деривативы не будет полным без обзора греков и хеджирования Delta. В первых двух постах представлен краткий обзор опционных греков. В последнем посте описывается пошаговый процесс построения модели хеджирования Delta в Excel с использованием моделирования Монте-Карло.
- Понимание опционных греков – краткое справочное руководство по Delta, Gamma, Vega, Theta и Rho
- Понимание вариантов греков — второй взгляд на дельту и гамму
- Опционы колл-опционы на дельта-хеджирование — создание симулятора Монте-Карло в Excel
- Понимание греков – моделирование дельта-хеджирования расширено для опционов пут
- Греческие опционы и дельта-хеджирование – Расчет и моделирование денежного PnL Греческий опцион
- и дельта-хеджирование – PnL, подразумеваемая волатильность и Rho
- Under Option Греки – Представляем Gamma
- Рассечение теты и временных премий для колл-опционов
- Подразумеваемая волатильность и хеджирование прибылей и убытков.
 Картирование распределения прибылей и убытков
Картирование распределения прибылей и убытков
Ускоренный курс деривативов – хеджирование Греки высшего порядка
Дельта-хеджирование полезно при хеджировании доли опциона от небольших приращений цены базового актива. Однако для больших скачков цены базового актива в наш портфель хеджирования необходимо включить греки более высокого порядка, такие как Gamma и Vega.
В первом посте показано, как будет выглядеть распределение прибылей и убытков, если мы учтем гамму в нашей модели дельта-хеджирования. В то время как во втором посте представлена серия уроков, в которых обсуждаются причины, по которым Гамма-хеджирование отличается от дельта-хеджирования (т. е. почему оно не включает покупку или продажу базового актива), и представлена модель в EXCEL, использующая функциональность Решателя для хеджирования одной опционной позиции как а также портфолио опционов.
- Гамма-коррекция, дельта-хеджирование прибылей и убытков и частота ребалансировки
- Хеджирование греков высшего порядка — хеджирование гаммы и веги с использованием Microsoft EXCEL
Ускоренный курс деривативов — Другие варианты второго порядка и волатильности.
 Греки
ГрекиМы рассмотрим некоторые связанные показатели и их использование:
- Расчет гаммы тени — подход Талеба для варианта второго порядка, греческий.
- Вега, Волга и Ванна. Вариант волатильности греков.
- Понимание альфа или гамма ренты
Дополнительные материалы для чтения
Если вы хотите узнать больше об этой теме, мы также рекомендуем второй, более продвинутый курс по производным продуктам, который углубляется в эту тему.
Также см. обзор деривативов с фиксированным доходом, MTM и моделей оценки для обзора процентных свопов, ограничений и уровней. В курсе по производным инструментам с фиксированным доходом, MTM и моделям оценки также рассматриваются основы построения простой модели оценки.
Кроме того, после завершения Обзор деривативов с фиксированным доходом , вы также должны ознакомиться с двумя пошаговыми примерами ценообразования. В первом случае рассматривается процесс построения прогнозируемой кривой форвардной процентной ставки с использованием метода начальной загрузки. Во втором случае рассматривается процесс переоценки по рыночной стоимости для процентного свопа в рамках первоначальной структуры срока, а также пересмотренной и обновленной структуры срока процентной ставки 6 месяцев спустя.
Во втором случае рассматривается процесс переоценки по рыночной стоимости для процентного свопа в рамках первоначальной структуры срока, а также пересмотренной и обновленной структуры срока процентной ставки 6 месяцев спустя.
Между двумя случаями мы строим 5-ступенчатую 5-летнюю кривую, а затем расширяем ее для хеджирования 10-ступенчатой полугодовой ссуды с плавающей процентной ставкой с процентным свопом.
а. Начальная начальная кривая нулевой и форвардной процентных ставок в Excel
b. Ценообразование, MTM, оценка процентных свопов с использованием форвардных кривых в Excel
Ценообразование экзотических опционов с использованием таблицы Excel моделирования Монте-Карло
Что такое деривативы для чайников? [Решено] (2022)
производная, в математике скорость изменения функции по отношению к переменной . Производные лежат в основе решения математических и дифференциальных уравнений…. читать дальше ›
Производные инструменты для начинающих — Основное введение — YouTube. .. подробнее ›
.. подробнее ›
Определение производного простого объяснения — YouTube… продолжить чтение ›
Производные инструменты — это сложные финансовые инструменты, которые имеют стоимость только потому, что они связаны с чем-то другим, называемым базовым активом . Другими словами, деривативы получают свою стоимость от базового инструмента, которым могут быть акции, облигации, валюта, процентные ставки, товары и т. д…. см. подробности ›
Общие примеры деривативов включают фьючерсные контракты, опционные контракты и дефолтные свопы . Помимо этого, существует огромное количество производных контрактов, адаптированных для удовлетворения потребностей различных контрагентов…. продолжить чтение ›
Помимо этого, существует огромное количество производных контрактов, адаптированных для удовлетворения потребностей различных контрагентов…. продолжить чтение ›
Производные можно использовать для оценки функций, для создания бесконечных рядов . Их можно использовать для описания того, насколько изменяется функция — увеличивается или уменьшается функция и насколько. Они также имеют множество применений в физике. Производные используются в правиле Лопиталя для оценки пределов…. подробнее ›
Basic Derivative Rules — Ярлык с использованием степенного правила — YouTube… подробнее ›
Производная сообщает нам наклон функции в любой точке. Есть правила, которым мы можем следовать, чтобы найти множество производных.
Есть правила, которым мы можем следовать, чтобы найти множество производных.
…
Производные правила.
| Общие функции | Функция | Производная |
|---|---|---|
| Различие Правило | F — G | F ‘ — G’ |
| Правило продукта | FG | F G ‘ + F’ G |
| QUTING Правила | ||
| QUTING | ||
| FR ‘ + F’ G | ||
| FR ‘ + F’ G | ||
| Fr ‘ + F’ G | ||
| Fr ‘ + F’ G | ||
| . 2 | ||
| Правило взаимности | 1/f | −f’/f 2 |
Производные финансовые инструменты могут быть трудны для понимания широкой публикой отчасти потому, что они включают незнакомые термины . Например, у многих инструментов есть контрагенты, которые выступают на другой стороне сделки. В структуре дериватива может быть цена исполнения…. подробнее ›
Например, у многих инструментов есть контрагенты, которые выступают на другой стороне сделки. В структуре дериватива может быть цена исполнения…. подробнее ›
Определение производной — понятие
Определение производной — это наклон линии , которая касается кривой в определенной точке . Предел мгновенной скорости изменения функции при уменьшении времени между измерениями до нуля является альтернативным определением производной…. читать дальше ›
Применение деривативов в реальной жизни
Для расчета прибыли и убытков в бизнесе с использованием графиков . Чтобы проверить изменение температуры. Для определения скорости или пройденного расстояния, таких как мили в час, километры в час и т. д. Производные используются для получения многих уравнений в физике…. подробнее ›
д. Производные используются для получения многих уравнений в физике…. подробнее ›
Использование формулы (определение первой производной) — YouTube… подробнее ›
Хитрости с производными (о которых, вероятно, вам не расскажут учителя) — YouTube… подробнее ›
Более сложные задачи на производные — Пример 1 — YouTube… подробнее ›
Информация о статье
Автор: Rueben Jacobs
Последнее обновление: 28.09.2022
Просмотров: 6768
Рейтинг: 4,7 / 5 (77 проголосовали)
7 10 отзывов считают эту страницу полезной 84% читателей Информация о авторе
Имя: Rueben Jacobs
День рождения: 1999-03-14
Адрес: 951 Caterina Walk, Schambergerside, CA 67667-0896
Телефон: +688186846329
Job. , Кабаре, Пои, Азартные игры, Скалолазание, Резьба по дереву, Компьютерное программирование
, Кабаре, Пои, Азартные игры, Скалолазание, Резьба по дереву, Компьютерное программирование
Введение: Меня зовут Рубен Джейкобс, я общительный, красивый, добрый, удобный, гламурный, открытый, великолепный человек, который любит писать и хочет поделиться с вами своими знаниями и пониманием.
Ускоренный курс по производным
Ретт Аллен
Наука
Что такое производная и зачем она нужна в физике? Вот очень краткое введение в производные, чтобы вы могли пройти свой первый курс физики.
Быстрый набросок, показывающий изменение функции. Это основа производной. Быстрый набросок, показывающий изменение функции. Это основа производной.
Вы находитесь на вводном курсе физики. В требованиях к курсу сказано, что вы должны быть на Calculus 101 (вероятно, он так не называется), чтобы записаться на Physics 101. Почему? Есть две математические вещи, которые вам, вероятно, нужно знать, чтобы выжить на курсе физики. Вам нужно понимать производные и интегрирование (а также векторы, но это обычно также рассматривается в физике).
Почему? Есть две математические вещи, которые вам, вероятно, нужно знать, чтобы выжить на курсе физики. Вам нужно понимать производные и интегрирование (а также векторы, но это обычно также рассматривается в физике).
Но что, если ваш курс математики не охватывает производные к тому моменту, когда они понадобятся вам в физике? Вот для этого я здесь. Это ваш ускоренный курс по деривативам (об интеграции я напишу позже).
Производные: все об изменении
Предположим, у вас есть некоторая функция (она не обязательно должна быть x против y , это может быть что угодно). Что, если я хочу знать, как эта функция изменяется при изменении переменной? Это то, что говорит вам производная. Позвольте мне начать с нескольких примеров.
Автомобиль движется, и его положение в направлении x можно описать следующей функцией.
Если я построю эту функцию, она будет выглядеть так (я добавляю две точки, чтобы мы могли посмотреть на изменение положения).
Как эта функция меняется со временем? Если я возьму две точки ( t 1 и t 2 ), я могу вычислить изменение x , деленное на изменение t . Да, это будет наклон функции.
Это дает мне среднюю скорость изменения позиции в течение временного интервала от t 1 до t 2 . В физике мы также назвали бы это средней скоростью x . В этом случае не имеет значения, какие две точки я выберу на графике. Я всегда получаю уклон 2,5 м/с (да, уклон и производные имеют единицы измерения). Я мог бы построить горизонтальную скорость, и это выглядело бы так.
Хорошо, это было довольно просто и не так интересно. Как насчет другого примера? Предположим, у меня есть эта функция для положения объекта в направлении x?
Вот график этой функции вместе с некоторыми точками на кривой.
В этом случае средняя скорость (наклон) при переходе от точки 2 к 3 отличается от среднего наклона при переходе от точек 4 к 5. Как же построить график зависимости скорости от времени? С каким временем мы свяжем среднюю скорость? Вероятно, единственно справедливым было бы взять две временные точки и найти наклон, а затем связать наклон со средним значением этих двух моментов. На самом деле, это прекрасно работает с вышеуказанной функцией. Когда вы это сделаете, вы получите следующий график зависимости наклона (скорости) от времени.
Как же построить график зависимости скорости от времени? С каким временем мы свяжем среднюю скорость? Вероятно, единственно справедливым было бы взять две временные точки и найти наклон, а затем связать наклон со средним значением этих двух моментов. На самом деле, это прекрасно работает с вышеуказанной функцией. Когда вы это сделаете, вы получите следующий график зависимости наклона (скорости) от времени.
Этот трюк со «средним временем» не всегда работает. Однако я могу заставить его почти работать, если использую очень маленькие временные интервалы. В этом случае не имеет значения, какое время (начало, конец, середина) связано со временем. Таким образом, крошечные временные интервалы хороши.
Самые популярные
Что если вы используете нулевой интервал времени? Ну, ты не можешь этого сделать. Однако вы можете сделать что-то близкое к нулевому интервалу секунд. Вы можете найти значение средней скорости в пределе, когда Δt стремится к нулю секунд. Это и есть то, что мы называем производной. Мы можем записать это как:
Это и есть то, что мы называем производной. Мы можем записать это как:
Да, математики не так определяют производную, но я согласен с этим. Это показывает важный момент, что производная — это просто способ выразить изменение функции.
Пример: Функция синуса
Вы ведь знаете функцию синуса? Помнишь, ты встретил его на той вечеринке в прошлом году? Хорошо, поскольку вы уже знаете друг друга, предположим, что масса колеблется взад и вперед со следующей функцией положения.
Теперь позвольте мне построить это вместе с некоторыми точками.
Здесь вы можете видеть, что, просто выбрав некоторую точку (равномерно расположенную) на функции, я мог найти наклон между этими точками. Однако есть несколько случаев, когда эта скорость изменения для этих точек не является хорошим представлением наклона этой функции. Да, мы можем сделать это лучше, расположив точки намного ближе друг к другу. Если я использую временной интервал 0,01 секунды, я получаю следующее для скорости как функции времени.
Да, это похоже на функцию косинуса, и НЕТ, я не просто нарисовал функцию косинуса. На самом деле, вот точная программа, которую я использовал для создания этой программы.
Если вы не все там понимаете, не волнуйтесь. Важная часть просто проходит по точкам и вычисляет наклон («для i в диапазоне… часть»). Если вы хотите, вы можете изменить количество точек, используемых для расчета наклона — это было бы весело.
Если бы я хотел, я мог бы построить следующую функцию.
Я бы получил ТОЧНО такой же сюжет, как и выше. Итак, вы можете видеть две вещи. Во-первых, производная — это просто скорость изменения функции за очень маленькие промежутки времени. Во-вторых, эта производная обычно может быть записана как другая реальная математическая функция. В общем случае мы записываем производную как:
Здесь Δs заменены на d , чтобы показать, что мы смотрим на предел, когда Δt стремится к нулю. Вот и все.
Но как взять производную?
Ммм. .. разве я не сделал это выше? О, вы думаете, что использование компьютера — это жульничество? Хорошо, я могу это понять. Но на самом деле это не обман. Численная программа получает производную, используя конечные (но очень маленькие) интервалы времени. В реальной жизни мы всегда имеем дело с этим, а наука имеет дело с реальным миром.
.. разве я не сделал это выше? О, вы думаете, что использование компьютера — это жульничество? Хорошо, я могу это понять. Но на самом деле это не обман. Численная программа получает производную, используя конечные (но очень маленькие) интервалы времени. В реальной жизни мы всегда имеем дело с этим, а наука имеет дело с реальным миром.
Но как получить математическую функцию без использования компьютера? Я не буду вдаваться в подробности — для этого и существуют ваши уроки математики. Все, что меня волнует (как тренера по физике), это то, что вы понимаете, что такое производная и как ее найти. Итак, вот некоторые «правила».
Самые популярные
Правило произведения. У вас никогда не будет простой функции. Как правило, это две меньшие функции, умноженные (например, 9).0063 a*t — даже если a является константой). Предположим, у меня есть функция g и f (обе функции t ). Теперь у меня есть функция положения ( x(t) ), такая что:
Теперь у меня есть функция положения ( x(t) ), такая что:
Я могу найти производную этой функции, найдя производную g(t) и f(t) в следующем способ.
Я буду использовать это в коротком примере.
Силовое правило. Если у вас есть многочлен, найти производную довольно просто. Предположим, у меня есть такая функция:
Где n — просто константа. В этом случае производная этой функции будет:
Триггерные функции. Помните, я не вывожу их. Я просто говорю вам «ответ» — вот производные от двух наиболее распространенных триггерных функций.
Я сжульничал — пропустил небольшой шаг выше. Извиняюсь. Чтобы по-настоящему понять тригонометрические производные, вам также понадобится цепное правило.
Цепная линейка. Что делать, если у вас есть функция функции (составная функция)? Вот пример.
В этом случае я могу взять производную от x как:
Это может быть немного сложнее объяснить — будем надеяться, что вы скоро расскажете об этом в своем курсе математики.
Зачем нужны производные в физике?
Помните, что производная на самом деле просто скорость изменения. Мы обычно думаем о скорости изменения в физике как о производной по времени. Это приводит к некоторым знакомым величинам:
Но мы используем не только производные по времени. Если вы знаете потенциальную энергию как функцию положения, вы можете найти силу, которая идет вместе с этим потенциалом, с пространственной производной.
Если бы вы знали функцию потенциальной энергии пружины, вы могли бы использовать ее, чтобы найти силу, действующую на пружину (в направлении x).
На самом деле это не лучший пример, так как вы обычно определяете силу пружины как функцию и используете ее для получения функции потенциальной энергии пружины, но в любом случае это все еще пример.
Все эти примеры из первого семестра физики (механика и прочее). Надеюсь, что ко второму семестру вводной физики вы увидите множество производных на уроках математики. Поверьте мне, есть еще много случаев, когда вам придется использовать производные во втором семестре физики.
Поверьте мне, есть еще много случаев, когда вам придется использовать производные во втором семестре физики.
Последнее предупреждение. Помните, это был всего лишь «ускоренный курс» по деривативам. Это не должно использоваться в качестве замены фактического курса математики по исчислению.
Ретт Аллейн — адъюнкт-профессор физики Университета Юго-Восточной Луизианы. Он любит преподавать и говорить о физике. Иногда он разбирает вещи и не может собрать их обратно.
Темы, исчисление, математика, числовые расчеты
Еще из WIREDПостроение интуиции для производной – BetterExplained
Как бы вы хотели, чтобы вам объяснили производную? Вот мое мнение.
Псс! Производная — это сердце исчисления, скрытое внутри этого определения:
Но что это значит?
Допустим, я дал вам волшебную газету, в которой перечислены ежедневные изменения на фондовом рынке в течение следующих нескольких лет (+1% в понедельник, -2% во вторник…). Что ты можешь сделать?
Ну, вы применяете изменения одно за другим, рассчитываете будущие цены и покупаете дешево / продаете дорого, чтобы построить свою империю. Вы даже можете перестать использовать обезьян, которые случайным образом выбирают акции для своего портфеля.
Вы даже можете перестать использовать обезьян, которые случайным образом выбирают акции для своего портфеля.
Как и эта волшебная газета, производная — это хрустальный шар, который точно объясняет, как изменится узор. Зная это, вы можете строить планы на прошлое/настоящее/будущее, находить минимумы/максимумы и, следовательно, принимать более правильные решения. Это довольно интересно, больше, чем типичное описание «производная есть наклон функции».
Давайте отойдем от грубого уравнения. Уравнения существуют для передачи идей: понимайте идею, а не грамматику.
Производные создают идеальную модель изменений из несовершенного предположения.
Этот результат пришел к нам за тысячи лет размышлений, от Архимеда до Ньютона. Давайте посмотрим на аналогии, стоящие за этим.
Мы все живем в сверкающем континууме
Бесконечность — постоянный источник парадоксов («головных болей»):
- Линия состоит из точек? Конечно.

- Значит, на линии бесконечное количество точек? Ага.
- Как пересечь комнату, если есть бесконечное количество точек для посещения? (Ну и дела, спасибо, Зенон).
И все же мы движемся. Моя интуиция состоит в том, чтобы бороться с бесконечностью с бесконечностью. Конечно, между 0 и 1 есть бесконечные точки. Но я перемещаю две бесконечности точек в секунду (каким-то образом!) и преодолеваю разрыв за полсекунды.
Расстояние имеет бесконечные точки, движение возможно, поэтому движение выражается в «бесконечности точек в секунду».
Вместо того, чтобы думать о различиях («Как далеко до следующей точки?»), мы можем сравнивать скорости («Как быстро вы движетесь по этому континууму?»).
Странно, но 10/5 можно представить как «Мне нужно пройти 10 «бесконечностей» за 5 отрезков времени. Для этого я прохожу 2 «бесконечности» за каждую единицу времени».
Аналогия: см. деление как скорость движения через континуум точек
Что после нуля?
Еще одна головоломка: какое число идет после нуля? 0,01? . 0001?
0001?
Хрм. Все, что вы можете назвать, я могу назвать меньше (я просто уменьшу ваше число вдвое… ня!).
Несмотря на то, что мы не можем вычислить число после нуля, оно должно быть там, верно? Подобно демонам прошлого, это «число, которое нельзя записать, чтобы не быть пораженным».
Вызвать пробел до следующего числа $dx$. Я точно не знаю, насколько он велик, но он есть!
Аналогия: dx — это «скачок» к следующему числу в континууме.
Измерения зависят от прибора
Производная предсказывает изменение. Хорошо, а как мы измеряем скорость (изменение расстояния)?
Офицер: Вы знаете, как быстро вы ехали?
Водитель: Понятия не имею.
Офицер: 95 миль в час.
Водитель: Но я не был за рулем в течение часа!
Нам явно не нужен «полный час», чтобы измерить вашу скорость. Мы можем провести измерение до и после (скажем, более 1 секунды) и получить вашу мгновенную скорость. Если вы продвинулись на 140 футов за одну секунду, вы идете примерно на 95 миль в час. Просто, верно?
Если вы продвинулись на 140 футов за одну секунду, вы идете примерно на 95 миль в час. Просто, верно?
Не совсем так. Представьте себе видеокамеру, направленную на Кларка Кента (альтер-эго Супермена). Камера записывает 24 кадра в секунду (40 мс на фото), и Кларк кажется неподвижным. Каждую секунду он не двигается, и его скорость равна 0 миль в час.
Опять неправильно! Между каждой фотографией, в течение этих 40 мс, Кларк превращается в Супермена, раскрывает преступления и возвращается в свое кресло, чтобы сделать красивую фотографию. Мы измерили 0 миль в час, но он действительно двигается — он движется слишком быстро для наших приборов!
Аналогия: Подобно камере, наблюдающей за Суперменом, скорость, которую мы измеряем, зависит от инструмента!
Запуск беговой дорожки
Мы приближаемся к жевательному, слегка острому центру производной. Нам нужны измерения до и после, чтобы обнаружить изменения, но наши измерения могут быть ошибочными.
Представьте голого Санту на беговой дорожке (давай, я подожду). Мы собираемся измерить его частоту сердечных сокращений в ходе стресс-теста: мы прикрепим десятки тяжелых холодных электродов и заставим его бегать.
Санта пыхтит, пыхтит, и его пульс подскакивает до 190 ударов в минуту. Должно быть, это его «стрессовый» сердечный ритм, верно?
Нет. Видишь ли, само присутствие суровых ученых и холодных электродов участило его сердцебиение! Мы, , измерили со скоростью 190 ударов в минуту, но кто знает, что бы мы увидели, если бы не электроды! Конечно, если бы не электроды, у нас не было бы измерения.
Что делать? Ну, посмотрите на систему:
- измерение = фактическое количество + эффект измерения
Ах. После множества исследований мы можем обнаружить: «О, каждый электрод добавляет 10 ударов в минуту к частоте сердечных сокращений». Делаем замер (несовершенная оценка 190) и убираем эффект электродов («идеальная оценка»).
Аналогия: Уберите «электродный эффект» после измерения
Кстати, «электродный эффект» проявляется везде. Научные исследования имеют эффект Хоторна, когда люди меняют свое поведение , потому что их изучают . Боже, кажется, что все, кого мы тщательно изучаем, придерживаются своей диеты!
Научные исследования имеют эффект Хоторна, когда люди меняют свое поведение , потому что их изучают . Боже, кажется, что все, кого мы тщательно изучаем, придерживаются своей диеты!
Понимание производной
Вооружившись этим пониманием, мы можем увидеть, как меняются модели производной:
Начните с некоторой системы для изучения, $f(x)$: дх$)
Волшебство на последнем этапе: как снять электроды? У нас есть два подхода:
- Ограничения: что происходит, когда $dx$ сжимается до нуля, за пределами любой погрешности?
- Бесконечно малые числа: что, если $dx$ — крошечное число, неразличимое в нашей системе счисления?
Оба способа формализовать понятие «Как нам выбросить $dx$, когда он не нужен?».
Моя любимая мозоль: Пределы — это современный формализм, во времена Ньютона их не существовало. Они помогают заставить $dx$ исчезнуть «чисто». Но учить их перед производной — все равно, что показывать руль без машины! Это инструмент, помогающий производной работе, а не то, что нужно изучать в вакууме. 92 = 5$). Из чего состоит «5»?
- Измеренная скорость = фактическая скорость + ошибка
- $5 = 2x + dx$
- 5 долларов = 2(2) + 1 долларов
Конечно, мы измерили «5 единиц, перемещаемых в секунду», потому что мы перешли от 4 к 9 за один интервал. Но наши инструменты обманывают нас! 4 единицы скорости пришли от реального изменения, а 1 единица — из-за дрянных инструментов (1.0 — это большой скачок, не так ли?).
Если мы ограничимся целыми числами, 5 будет идеальной мерой скорости от 4 до 9. Нет «ошибки» в предположении, что $dx = 1$, потому что это истинный интервал между соседними точками. 92 = 0,41$
Помните, 0,41 — это то, что мы изменили в интервале 0,1. Наша скорость на единицу равна 0,41/0,1 = 4,1. И снова имеем:
Наша скорость на единицу равна 0,41/0,1 = 4,1. И снова имеем:
- Измеренная скорость = Фактическая скорость + Ошибка
- 4,1$ = 2x + dx $
Интересно. При $dx=0,1$ измеренная и фактическая скорости близки (от 4,1 до 4, погрешность 2,5%). Когда $dx=1$, ставки сильно отличаются (от 5 до 4, ошибка 25%).
Следуя схеме, мы видим, что выбрасывание электродов (пусть $dx=0$) показывает истинную скорость $2x$. 92$ изменений, нашел «несовершенное» измерение $2x + dx$ и вывел «идеальную» модель изменения как $2x$.
Производная как «непрерывное деление»
Я считаю интеграл лучшим умножением, когда вы можете применить изменяющуюся величину к другой.
Производная — это «лучшее деление», где вы получаете скорость в континууме в каждый момент времени. Что-то вроде 10/5 = 2 говорит: «у вас постоянная скорость 2 в континууме».
Когда ваша скорость меняется по ходу движения, вам нужно описать свою скорость в каждый момент времени. Это производная. 92$, при $x=22$ мы меняем на 44 (конкретная скорость изменения).
Это производная. 92$, при $x=22$ мы меняем на 44 (конкретная скорость изменения).
«Производная равна $dx$» может относиться к крошечному гипотетическому переходу на следующую позицию. Технически $dx$ является «дифференциалом», но термины путаются. Иногда люди говорят «производная от $x$» и имеют в виду $dx$.
Подсказка: наши модели могут быть несовершенными
Мы нашли «идеальную» модель, проведя измерения и улучшив ее. Иногда этого недостаточно — мы предсказываем, что произошло бы , если бы $dx$ не было, но мы добавили $dx$, чтобы получить наше первоначальное предположение!
Некоторые функции с плохим поведением не поддаются предсказанию: есть разница между удалением $dx$ с пределом и тем, что на самом деле происходит в этот момент. Они называются «разрывными» функциями, которые, по сути, «не могут быть смоделированы с ограничениями». Как вы можете догадаться, производная не работает с ними, потому что мы не можем на самом деле предсказать их поведение.
Прерывистые функции на практике встречаются редко и часто существуют как «Попался!» контрольные вопросы («О, ты пытался взять производную от разрывной функции, у тебя не получилось»). Осознайте теоретическую ограниченность производных, а затем осознайте их практическое использование для измерения любых природных явлений. Почти каждая функция, которую вы увидите (синус, косинус, e, многочлены и т. д.), является непрерывной.
Попался: интеграции на самом деле не существует
Связь между производными, интегралами и антипроизводными имеет нюансы (и изначально я ошибся). Вот метафора. Начните с тарелки, ваша задача изучить:
- Дифференциация — это разбивание тарелки на осколки. Существует определенная процедура: взять разницу, найти скорость изменения, а затем предположить, что $dx$ здесь нет.
- Интеграция взвешивает осколки: ваша первоначальная функция была «вот такой» большой. Есть процедура, накопительное сложение, но она вам не говорит 92$.
 2$ не одно и то же? Да, но это не очевидно: это теорема Пифагора!»). Спасибо Джошуа Цукеру. за помощь разобраться со мной
2$ не одно и то же? Да, но это не очевидно: это теорема Пифагора!»). Спасибо Джошуа Цукеру. за помощь разобраться со мнойЧтение математики
Математика — это язык, и я хочу «читать» исчисление (а не «декламировать» исчисление, т.е. как мы можем декламировать средневековые немецкие гимны). Мне нужно сообщение позади определений.
Мой самый большой ага! осознавал временную роль $dx$: он производит измерение и удаляется, чтобы создать совершенную модель. Пределы/бесконечно малые числа — это формализм, мы не можем зацикливаться на них. Ньютон, казалось, обходился без них.
Вооружившись этими аналогиями, становятся интересными другие математические вопросы:
- Как измерить различные размеры бесконечности? (В каком-то смысле все они «бесконечны», в других смыслах диапазон (0,1) меньше, чем (0,2))
- Каковы реальные правила того, как заставить $dx$ «уйти»? (Как на самом деле работают бесконечно малые и пределы?)
- Как мы описываем числа, не записывая их? «Следующее число после 0» — это начало анализа (которому я хочу научиться).

