|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Троичное конструктное кодирование булевых выражений
Брусенцов Н. П., Владимирова Ю. С.
П., Владимирова Ю. С.
Булева алгебра – первооснова, или начало, всякой науки, исследующей взаимосвязи, будь то логика, математика, информатика или, скажем, структурная лингвистика. Ввиду же фундаментальности наук этого рода не будет преувеличением усмотреть в ней и начало науки вообще – способности рассуждать, умозаключать, доказывать.
Компьютерная информатика также «произрастает» из булевой алгебры, что наиболее очевидно. Однако дальнейшее развитие способности компьютера, становление «искусственного интеллекта», оставляет желать лучшего. Впрочем, при нынешнем засилии формализма и естественный человеческий интеллект оказывается под угрозой – поневоле превращаемся в роботов.
Пора бы придать компьютерной информатике здравый диалектический характер.
В этой статье речь пойдет об усовершенствованной конструктной реализации булевой алгебры в диалоговой системе структурированного программирования ДССП [1-3].
Конструктами в ДССП называются нестандартные, определяемые (конструируемые) пользователем типы данных, введением которых достигается высокоуровневая специализация этой системы в заданном классе приложений.
Конструкты типа «булево выражение» предоставляют возможность оперирования переменными, принимающими в качестве значений n-арные выражения булевой алгебры, и функционально полный набор базисных операций, позволяющих в сочетании с штатными средствами конструирования программ в ДССП эффективно реализовать логико-алгебраические процедуры [5].
Функционально конструкт определяется форматом принимаемых переменными значений и набором интерпретирующих эти значения базисных операций. Формат характеризуется структурой, информационной емкостью и способами доступа. Например, формат «вектор битов» с параметром n – длина вектора предоставляет доступ к отдельным битам по их номерам, а также к вектору в целом.
Принцип отображения булевых выражений конструктами в простейших случаях заключается во взаимно однозначном сопоставлении входящих в выражение букв-переменных (следуя Аристотелю, будем называть их терминами) последовательно пронумерованным компонентам-битам в формате конструкта. Другими словами, каждая переменная представлена в формате конструкта собственным битом. Значение же, принимаемое битом, указывает статус его переменной в отображаемом выражении. Например, элементарная конъюнкция
Заметим, что всевозможные 2nn-арные элементарные конъюнкции пронумерованы значениями отображающего n-битного вектора, интерпретируемыми как двоичные натуральные числа. В приведенном примере номера последовательно убывают от 1111 для xyzu до 0000 для x‘y‘z‘u‘.
В приведенном примере номера последовательно убывают от 1111 для xyzu до 0000 для x‘y‘z‘u‘.
Эта нумерация использована в конструкте, отображающем булевы выражения в совершенной дизъюнктивной нормальной форме (СДНФ). Его формат – 2n-компонентный вектор битов, пронумерованных n-битными числами от 11…1 до 00…0, и таким образом однозначно сопоставленных n-арным элементарным конъюнкциям. Биты, соответствующие входящим в отображаемое СДНФ-выражение конъюнкциям, принимают значение 1, а все прочие – значение 0. Например, при n = 2 отображающий вектор состоит из 4-х битов, пронумерованных числами 11, 10, 01, 00, которым соответствуют элементарные конъюнкции xy, xy‘, x‘y, x‘y‘, так что выражение xy v x‘y отобразится в 1010, а выражение xy‘ v x‘y v x‘y‘ отобразится в 0111.
Конструкт описанного типа, названный двоичной ДК-шкалой, позволяет эффективно компьютеризовать алгебру n-арных СДНФ-выражений. Очевидно, что операции конъюнкции и дизъюнкции над такими выражениями сводятся к побитным конъюнкциям и дизъюнкциям ДК-шкал, а операция отрицания-дополнения СДНФ-выражения – к побитной инверсии его ДК-шкалы. Существенное достоинство ДК-шкалы – ее экономность: произвольная n-арная булева функция кодируется 2
Очевидно, что операции конъюнкции и дизъюнкции над такими выражениями сводятся к побитным конъюнкциям и дизъюнкциям ДК-шкал, а операция отрицания-дополнения СДНФ-выражения – к побитной инверсии его ДК-шкалы. Существенное достоинство ДК-шкалы – ее экономность: произвольная n-арная булева функция кодируется 2
Выражения в совершенной конъюнктивной нормальной форме (СКНФ-выражения) аналогично отображаются n-арной двоичной КД-шкалой. Вернее, 2n-битный вектор допускает ДК-интерпретацию и КД-интерпретацию: ДК – это дизъюнкция элементарных конъюнкций (СДНФ), а КД – конъюнкция элементарных дизъюнкций (СКНФ).
Наряду с ДК- и КД-шкалами не лишены смысла и менее экономные конструкты на основе формата цепь элементарных конъюнкций либо дизъюнкций. Цепь – это совокупность n-арных векторов, допускающая добавление, удаление, а также перестановку отдельных ее членов. В отличие от шкалы, где членам СНФ-выражения сопоставлены позиции битов-компонент отображающего вектора, так что номера позиций кодируют соответствующие члены, в цепи коды членов СНФ-выражения содержатся непосредственно и могут располагаться в любой последовательности, в частности, упорядочиваться по тому или иному критерию, что способствует дальнейшему развитию конструктной алгебры.
Шкалы и цепи, основанные на отображении элементарных конъюнкций и дизъюнкций векторами битов (двоичные конструкты), позволяют компьютеризовать алгебру совершенных нормальных форм, СДНФ- и СКНФ-выражений. В системе с двоичными конструктами эффективно реализуются процедуры синтеза и преобразования СНФ-выражений, такие как тождественное преобразование выражения в двойственную форму, инвертирование, получение дополнения, получение дуала (выражения, двойственного данному), получение единого выражения из нескольких заданных по предписанным взаимосвязям, выявление и доказательство отношений, в которых состоят сопоставляемые выражения, решение булевых уравнений [5, 6].
Компьютеризация булевой алгебры в полном объеме достигнута применением конструктов, в основу которых положен вектор трехзначных элементов (тритов). Конструкты этого рода естественно называть троичными. О том, что в троичном коде успешно преодолевается несовершенство двоичного кодирования, убедительно свидетельствует троичный симметричный код чисел, в котором три значения трита интерпретируются как 1, 0, -1 т. е. к двоичным 1 и 0 добавлена отрицательная единица. Не имеющих удовлетворительного решения в двоичном коде проблем представления чисел со знаком и округления чисел в симметричном троичном коде просто нет.
е. к двоичным 1 и 0 добавлена отрицательная единица. Не имеющих удовлетворительного решения в двоичном коде проблем представления чисел со знаком и округления чисел в симметричном троичном коде просто нет.
Точно так же компенсируется неполноценность отображения вектором битов элементарных конъюнкции и дизъюнкции, оказывающаяся причиной того, что двоичные конструкты отображают булевы выражения только в совершенных нормальных формах. Используемые в них для представления элементарных конъюнкций и дизъюнкций n-битные векторы способны кодировать только индивидные конъюнкции и предполные дизъюнкции, но не могут отобразить элементарную конъюнкцию или дизъюнкцию, в которой некоторые термины умалчиваются («элиминированы» по Булю-Порецкому), т. е. в которой статус терминов трехзначен: неинвертированное вхождение, вхождение под знаком инверсии, невхождение.
Сопоставив этим состояниям значения трита 1, -1, 0, которые далее ради удобства будем обозначать +, -, 0, получаем отображение n-тритным вектором не только индивидных конъюнкций и предполных дизъюнкций, но и элементарных n-арных конъюнкций и дизъюнкций произвольного вида.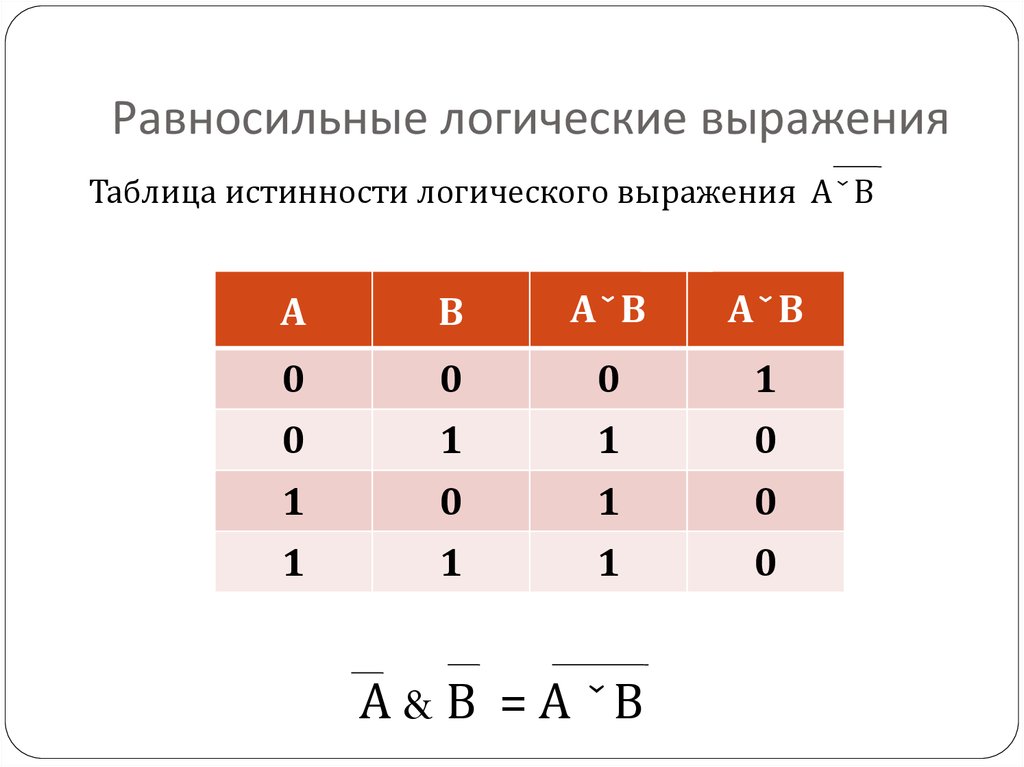 Так, конъюнкциям xyz‘u, xz‘u, yz‘, z‘ будут соответствовать значения 4-тритного конструкта-вектора К-типа: ++-+, +0-+, 0+-0, 00-0, а дизъюнкциям x‘ v y‘ v z v u‘, x‘ v z v u‘, y‘ v z, z – значения 4-тритного конструкта-вектора Д-типа: —+-, -0+-, 0-+0, 00+0.
Так, конъюнкциям xyz‘u, xz‘u, yz‘, z‘ будут соответствовать значения 4-тритного конструкта-вектора К-типа: ++-+, +0-+, 0+-0, 00-0, а дизъюнкциям x‘ v y‘ v z v u‘, x‘ v z v u‘, y‘ v z, z – значения 4-тритного конструкта-вектора Д-типа: —+-, -0+-, 0-+0, 00+0.
Построенные на n-тритных векторах ДК- и КД-цепи при должным образом пересмотренных наборах интерпретирующих базисных процедур способны отображать теперь не только СНФ-выражения, но и произвольное булево выражение в нормальной форме с фиксированным порядком размещения терминов в элементарных конъюнкциях и дизъюнкциях. Например, выражение xy v x‘y, отобразимое 2-арной двоичной ДК-цепью 11 01, троичной 2-арной цепью отобразимо как в СДНФ ++ -+, так и в минимальной ДНФ 0+, а выражение xy‘ v x‘y v x‘y‘ (двоичная ДК-цепь 10 01 00) троичной ДК-цепью отображается в четырех вариантах: +- -+ —, +- -0, 0- -+, -0 0-, -0 0-, т.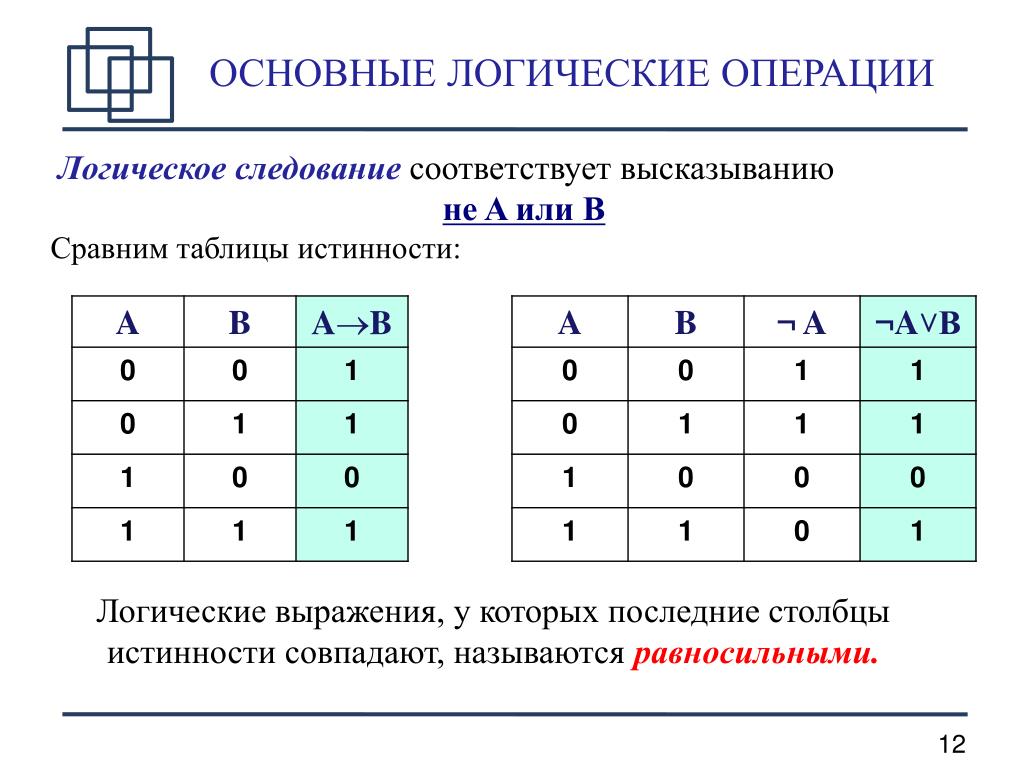 е. в СДНФ, в двух тупиковых и в минимальной ДНФ.
е. в СДНФ, в двух тупиковых и в минимальной ДНФ.
Угадывается «алгебраическая полнота» троичного отображения, и в булевой алгебре она действительно имеет место: посредством троичных конструктов удается перепоручить компьютеру практически все, что может делать в булевой алгебре человек и даже то, чего еще не может (например, минимизации произвольного булева выражения [7]).
Описанное усовершенствование компьютерной реализации булевой алгебры представляет собой один из результатов конструктного подхода к информатике. Результат фундаментальный, поскольку касается основы и вместе с тем открывает пути совершенствования последующих ступеней – алгебраизации силлогистики, модальной и диалектической логики [8], упорядочения теории вероятностей и нечетких множеств [9, 10].
Литература
- Брусенцов Н. П., Златкус Т. В., Руднев И. А. ДССП-диалоговая система структурированного программирования // Программное оснащение микрокомпьютеров. – М.: Изд-во Моск. ун-та, 1982. С. 11-40.

- Брусенцов Н. П. Микрокомпьютеры. – М.: «Наука», 1985. С. 141-170.
- Развиваемый адаптивный язык РАЯ диалоговой системы программирования ДССП / Н. П. Брусенцов, В. Б. Захаров, И. А. Руднев, С. А. Сидоров, Н. А. Чанышев. – М.: Изд-во Моск. ун-та, 1987. 80 с.
- Концептуальная характеристика РИИИС-процессора / Н. П. Брусенцов, С. П. Маслов, Х. Рамиль Альварес, С. А. Сидоров // Интегрированная система обучения, конструирования программ и разработки дидактических материалов. – М.: Изд-во ф-та ВМиК МГУ, 1996 г. С. 16-43.
- Владимирова Ю. С. Конструктная реализация булевой алгебры // Интегрированная система обучения, конструирования программ и разработки дидактических материалов. – М.: Изд-во ф-та ВМиК МГУ, 1996 г. С. 44-69.
- Брусенцов Н. П., Владимирова Ю. С. Решение булевых уравнений // Методы математического моделирования. – М.: Диалог-МГУ, 1998. С. 59-68. Solution of Boolean Equations. // Computational mathematics and modeling, Vol. 9 , № 4, 1998, pp. 287-295.

- Брусенцов Н. П., Владимирова Ю. С. Троичный минимизатор булевых выражений // Программные системы и инструменты. Тематический сборник № 2. – М.: Факультет ВМиК МГУ, 2001. С. 205-207.
- Брусенцов Н. П. Трехзначная диалектическая логика // Программные системы и инструменты. Тематический сборник № 2. – М.: Факультет ВМиК МГУ, 2001. С. 36-44.
- Брусенцов Н. П., Деркач А. Ю. Логическая модель теории вероятностей и нечетких множеств Заде // Цифровая обработка информации и управление в чрезвычайных ситуациях. Материалы Второй международной конференции (28-30 ноября 2000 г., Минск.) – Минск: Институт технической кибернетики НАН Беларуси, 2000. Том 1, с. 41-44.
- Брусенцов Н. П., Деркач А. Ю. Трехзначная логика, нечеткие множества и теория вероятностей // Программные системы и инструменты. Тематический сборник № 2. – М.: Факультет ВМиК МГУ, 2001. С. 88-91.
Заметки о трехзначной логике
Доложено на Ломоносовских чтениях 2002 г. на факультете ВМиК МГУ.
Опубликовано в: Программные системы и инструменты: Тематический сборник № 3 // Под ред. Л. Н. Королева.- М. Издательский отдел ВМиК МГУ, 2002, с. 6-10.
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 3 из 5Следующая ⇒
2.1Булево выражение
Для логических схем, представляющих собой соединение нескольких логических элементов, в левой части таблицы истинности перечисляются все возможныекомбинации входных сигналов, а в правой части – соответствующие значения на выходе логической схемы. Очевидно, что левые части таблицы будут одинаковыми для всех функций двух переменных, для всех функций трёх переменных и т. д.Традиционно комбинации сигналов в нихрасполагают в порядке возрастания соответствующих двоичных кодов. На рисунке 3.7 приведен пример логической схемы и таблица истинности, полностью описывающая ее работу.
Рисунок 3.
Вероятность ошибки уменьшается, если не решать задачу «в лоб», а проанализировать её работу с точки зрения уже известных нам правил логического сложения, умножения и инверсии. Очевидно, что в рассматриваемой схеме осуществляется логическое сложение нескольких логических произведений. Можно записать логическое выражение, соответствующее данной схеме:
. (3.1) Булево выражение в виде суммы произведений называется дизъюнктивно нормальной формой (ДНФ). Булево выражение в виде произведения сумм называется конъюнктивной нормальной формой (КНФ). По правилу логического сложения выражение (3.1) имеет на выходе логическую 1 ( f =1) только в том случае, если равно 1 хотя бы одно из четырех произведений, входящих в сумму. По правилу логического умножения каждое произведение будет равно 1 только в том случае, когда все входящие в произведение переменные равны 1. * Произведение будет равно 1 только тогда, когда будет выполняться условие: и , и . При этом от значений остальных входных переменных – и – значение данного произведения не зависит. Поэтому логические 1 будут в строках, соответствующих полным произведениям , в которых , а переменные и перечисляются во всех четырех возможных комбинациях: =0101, 0111, 1101 и 1111. * Произведение будет равно 1 только тогда, когда будет выполняться условие: и (т. е. ), и , и . От значения не вошедшей в данное произведение переменной произведение не зависит. Поэтому логические 1 будут в строках таблицы истинности, соответствующих полным произведениям , в которых и одновременно , а переменная перечисляется во всех двух возможных комбинациях: =0011 и 0111. * Произведение будет равно 1 только тогда, когда будет выполняться условие: и (т. * Произведение будет равно 1 только тогда, когда будет выполняться условие: и (т. е. ), (т. е. ), и и . Поэтому логическая 1, соответствующая данному полному произведению всех переменных, будет только в той строке таблицы истинности, где =0011. Анализ всех этих возможностей показывает, что они могут совпадать для нескольких произведений. Например, комбинация входных переменных 0011 встречается в произведениях и . А сочетание 0111 встречается даже в трех произведениях: и в , и в , и в . Это говорит о том, что для данного логического выражения есть возможности минимизации.
2.2 Основные законы и правила алгебры логики
Основные тождества булевой алгебры, используемые для преобразования формул функций, получили название законов и правил. После определения операций алгебры эти тождества являются следствиями этих определений и могут быть доказаны. Основными законами и правилами булевой алгебры являются: Законы коммутативности (переместительные) для дизъюнкции и конъюнкции . Законы ассоциативности (сочетательные) для дизъюнкции и конъюнкции . Первый и второй законы дистрибутивности (распределительные) . Законы идемпотентности (повторения) для дизъюнкции и конъюнкции . Законы отрицания (инверсии) . Законы двойственности или «правило де Моргана» . Правило свертки . Правила поглощения . Правила полного склеивания . Правило неполного склеивания . Правило Порецкого . Правила операций с константами
Доказательство большинства законов и правил алгебры логики очевидны. Например,
⇐ Предыдущая12345Следующая ⇒ Читайте также: Техника нижней прямой подачи мяча Комплекс физических упражнений для развития мышц плечевого пояса Стандарт Порядок надевания противочумного костюма Общеразвивающие упражнения без предметов |
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Логические выражения и операторы. Урок 6 курса «Python. Введение в программирование»
Логические выражения и логический тип данных
Часто в реальной жизни мы соглашаемся с каким-либо утверждением или отрицаем его. Например, если вам скажут, что сумма чисел 3 и 5 больше 7, вы согласитесь, скажете: «Да, это правда». Если же кто-то будет утверждать, что сумма трех и пяти меньше семи, то вы расцените такое утверждение как ложное.
Подобные фразы предполагают только два возможных ответа – либо «да», когда выражение оценивается как правда, истина, либо «нет», когда утверждение оценивается как ошибочное, ложное. В программировании и математике если результатом вычисления выражения может быть лишь истина или ложь, то такое выражение называется логическим.
Например, выражение 4 > 5 является логическим, так как его результатом является либо правда, либо ложь. Выражение 4 + 5 не является логическим, так как результатом его выполнения является число.
На позапрошлом уроке мы познакомились с тремя типами данных – целыми и вещественными числами, а также строками. Сегодня введем четвертый – логический тип данных (тип bool). Его также называют булевым. У этого типа всего два возможных значения: True (правда) и False (ложь).
>>> a = True >>> type(a) <class 'bool'> >>> b = False >>> type(b) <class 'bool'>
Здесь переменной a было присвоено значение True, после чего с помощью встроенной в Python функции type() проверен ее тип. Интерпретатор сообщил, что это переменная класса bool. Понятия «класс» и «тип данных» в данном случае одно и то же. Переменная b также связана с булевым значением.
Переменная b также связана с булевым значением.
В программировании False обычно приравнивают к нулю, а True – к единице. Чтобы в этом убедиться, можно преобразовать булево значение к целочисленному типу:
>>> int(True) 1 >>> int(False) 0
Возможно и обратное. Можно преобразовать какое-либо значение к булевому типу:
>>> bool(3.4)
True
>>> bool(-150)
True
>>> bool(0)
False
>>> bool(' ')
True
>>> bool('')
FalseИ здесь работает правило: всё, что не 0 и не пустота, является правдой.
Логические операторы
Говоря на естественном языке (например, русском) мы обозначаем сравнения словами «равно», «больше», «меньше». В языках программирования используются специальные знаки, подобные тем, которые используются в математике: > (больше), < (меньше), >= (больше или равно), <= (меньше или равно), == (равно), != (не равно).
Не путайте операцию присваивания значения переменной, обозначаемую в языке Python одиночным знаком «равно», и операцию сравнения (два знака «равно»). Присваивание и сравнение – разные операции.
>>> a = 10 >>> b = 5 >>> a + b > 14 True >>> a < 14 - b False >>> a <= b + 5 True >>> a != b True >>> a == b False >>> c = a == b >>> a, b, c (10, 5, False)
В данном примере выражение c = a == b состоит из двух подвыражений. Сначала происходит сравнение (==) переменных a и b. После этого результат логической операции присваивается переменной c. Выражение a, b, c просто выводит значения переменных на экран.
Сложные логические выражения
Логические выражения типа kByte >= 1023 являются простыми, так как в них выполняется только одна логическая операция. Однако, на практике нередко возникает необходимость в более сложных выражениях. Может понадобиться получить ответа «Да» или «Нет» в зависимости от результата выполнения двух простых выражений. Например, «на улице идет снег или дождь», «переменная news больше 12 и меньше 20″.
Может понадобиться получить ответа «Да» или «Нет» в зависимости от результата выполнения двух простых выражений. Например, «на улице идет снег или дождь», «переменная news больше 12 и меньше 20″.
В таких случаях используются специальные операторы, объединяющие два и более простых логических выражения. Широко используются два оператора – так называемые логические И (and) и ИЛИ (or).
Чтобы получить True при использовании оператора and, необходимо, чтобы результаты обоих простых выражений, которые связывает данный оператор, были истинными. Если хотя бы в одном случае результатом будет False, то и все сложное выражение будет ложным.
Чтобы получить True при использовании оператора or, необходимо, чтобы результат хотя бы одного простого выражения, входящего в состав сложного, был истинным. В случае оператора or сложное выражение становится ложным лишь тогда, когда ложны оба составляющие его простые выражения.
Допустим, переменной x было присвоено значение 8 (x = 8), переменной y присвоили 13 (y = 13). Логическое выражение y < 15 and x > 8 будет выполняться следующим образом. Сначала выполнится выражение y < 15. Его результатом будет True. Затем выполнится выражение x > 8. Его результатом будет False. Далее выражение сведется к True and False, что вернет False.
>>> x = 8 >>> y = 13 >>> y < 15 and x > 8 False
Если бы мы записали выражение так: x > 8 and y < 15, то оно также вернуло бы False. Однако сравнение y < 15 не выполнялось бы интерпретатором, так как его незачем выполнять. Ведь первое простое логическое выражение (x > 8) уже вернуло ложь, которая, в случае оператора and, превращает все выражение в ложь.
В случае с оператором or второе простое выражение проверяется, если первое вернуло ложь, и не проверяется, если уже первое вернуло истину. Так как для истинности всего выражения достаточно единственного True, неважно по какую сторону от or оно стоит.
>>> y < 15 or x > 8 True
В языке Python есть еще унарный логический оператор not, то есть отрицание. Он превращает правду в ложь, а ложь в правду. Унарный он потому, что применяется к одному выражению, стоящему после него, а не справа и слева от него как в случае бинарных and и or.
>>> not y < 15 False
Здесь у < 15 возвращает True. Отрицая это, мы получаем False.
>>> a = 5 >>> b = 0 >>> not a False >>> not b True
Число 5 трактуется как истина, отрицание истины дает ложь. Ноль приравнивается к
Ноль приравнивается к False. Отрицание False дает True.
Практическая работа
Присвойте двум переменным любые числовые значения.
Используя переменные из п. 1, с помощью оператора
andсоставьте два сложных логических выражения, одно из которых дает истину, другое – ложь.Аналогично выполните п. 2, но уже с оператором
or.Попробуйте использовать в логических выражениях переменные строкового типа. Объясните результат.
Напишите программу, которая запрашивала бы у пользователя два числа и выводила бы
TrueилиFalseв зависимости от того, больше первое число второго или нет.
Примеры решения и дополнительные уроки в android-приложении и pdf-версии курса
Таблица истинности онлайн
Назначение сервиса.
Построение СКНФ
Построение СДНФ
Построение полинома Жегалкина
Построение карты Вейча-Карно
Минимизация булевой функции методом Квайна
Например, логическое выражение abc+ab~c+a~bc необходимо ввести так: a*b*c+a*b=c+a=b*c
Для ввода данных в виде логической схемы используйте этот сервис.
Для булевой функции, заданной вектором значений (например, 00111011) используйте ввод данных через таблицу.
Правила ввода логической функции
- Вместо символа
v(дизъюнкция, ИЛИ) используйте знак +. y).
y).
- Максимальное количество переменных равно 10.
Для создания любого логического устройства необходимо определить зависимость каждой из выходных переменных от действующих входных переменных такая зависимость называется переключательной функцией или функцией алгебры логики.
Функция алгебры логики называется полностью определённой если заданы все 2n её значения, где n – число выходных переменных.
Если определены не все значения, функция называется частично определённой.
Устройство называется логическим, если его состояние описывается с помощью функции алгебры логики.
Для представления функции алгебры логики используется следующие способы:
- словесное описание – это форма, которая используется на начальном этапе проектирования имеет условное представление.

- описание функции алгебры логики в виде таблицы истинности.
- описание функции алгебры логики в виде алгебраического выражения: используется две алгебраические формы ФАЛ:
а) ДНФ – дизъюнктивная нормальная форма – это логическая сумма элементарных логических произведений. ДНФ получается из таблицы истинности по следующему алгоритму или правилу:
1) в таблице выбираются те строки переменных для которых функция на выходе =1.
2) для каждой строки переменных записывается логическое произведение; причём переменные =0 записываются с инверсией.
3) полученное произведение логически суммируется.
Fднф= X1*Х2*Х3 ∨ Х1x2Х3 ∨ Х1Х2x3 ∨ Х1Х2Х3
ДНФ называется совершенной, если все переменные имеют одинаковый ранг или порядок, т.е. в каждое произведение обязательно должны включаться все переменные в прямом или инверсном виде.
б) КНФ – конъюнктивная нормальна форма – это логическое произведение элементарных логических сумм.
КНФ может быть получена из таблицы истинности по следующему алгоритму:
1) выбираем наборы переменных для которых функция на выходе =0
2) для каждого набора переменных записываем элементарную логическую сумму, причём переменные =1 записываются с инверсией.
3) логически перемножаются полученные суммы.
Fскнф=(X1 V X2 V X3) ∧ (X1 V X2 V X3) ∧ (X1 V X2 V X3) ∧ (X1 V X2 V X3)
КНФ называется совершенной, если все переменные имеют одинаковый ранг.
По алгебраической форме можно построить схему логического устройства, используя логические элементы.
Рисунок1- Схема логического устройства
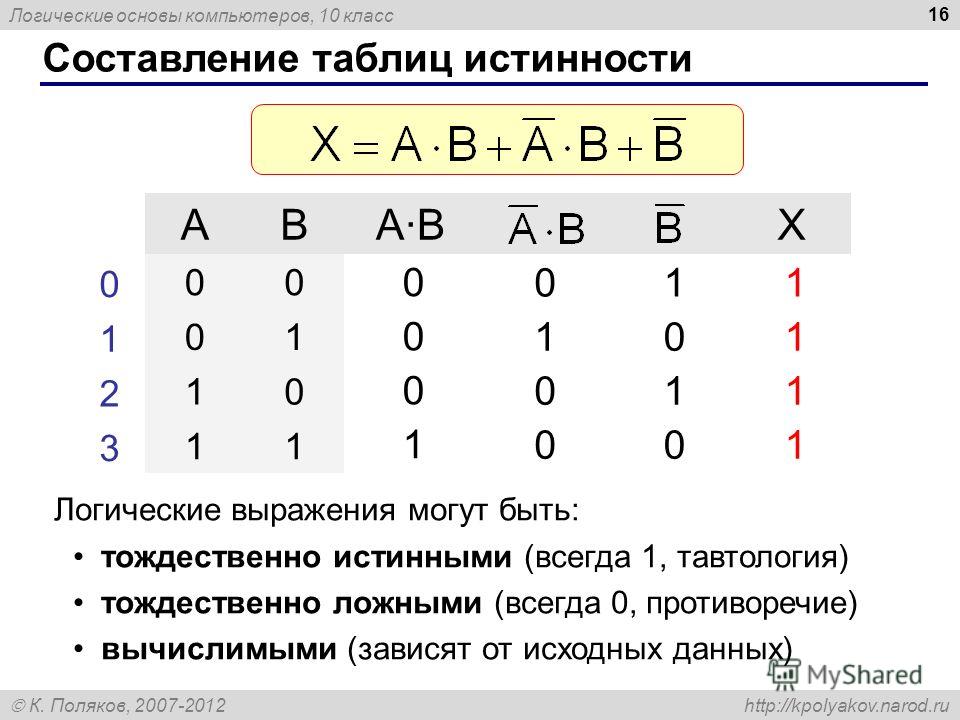
Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2N строк, так как существует 2N различных комбинаций возможных значений аргументов.
Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2N строк, так как существует 2N различных комбинаций возможных значений аргументов.
Операция НЕ — логическое отрицание (инверсия)
Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее:- если исходное выражение истинно, то результат его отрицания будет ложным;
- если исходное выражение ложно, то результат его отрицания будет истинным.
не А, Ā, not A, ¬А, !A
Результат операции отрицания НЕ определяется следующей таблицей истинности:
| A | не А |
| 0 | 1 |
| 1 | 0 |
Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот.

Операция ИЛИ — логическое сложение (дизъюнкция, объединение)
Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами. Результатом операции ИЛИ является выражение, которое будет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений.Применяемые обозначения: А или В, А V В, A or B, A||B.
Результат операции ИЛИ определяется следующей таблицей истинности:
| A | B | А или B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложен тогда, когда аргументы А и В — ложны.
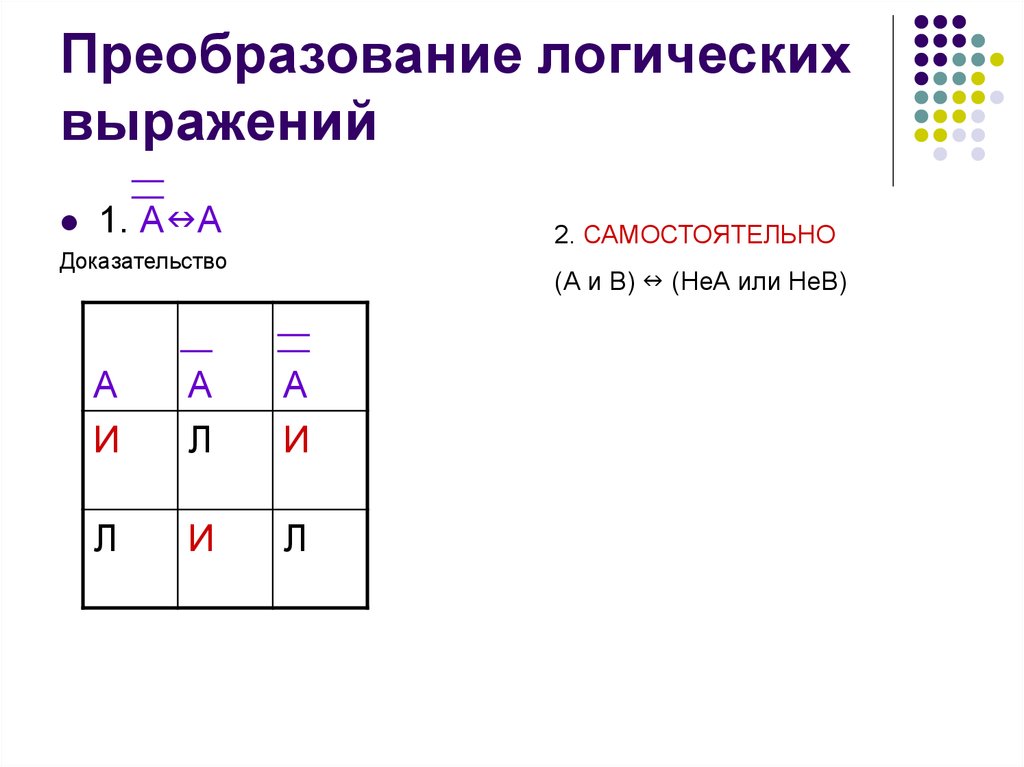
Операция И — логическое умножение (конъюнкция)
Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.Применяемые обозначения: А и В, А Λ В, A & B, A and B.
Результат операции И определяется следующей таблицей истинности:
| A | B | А и B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.

Операция «ЕСЛИ-ТО» — логическое следование (импликация)
Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.Применяемые обозначения:
если А, то В; А влечет В; if A then В; А→ В.
Таблица истинности:
| A | B | А → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.
Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)
Применяемое обозначение: А ↔ В, А ~ В.
Таблица истинности:
| A | B | А↔B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.
Операция «Сложение по модулю 2» (XOR,
исключающее или, строгая дизъюнкция) Применяемое обозначение: А XOR В, А ⊕ В.
Таблица истинности:
| A | B | А⊕B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.
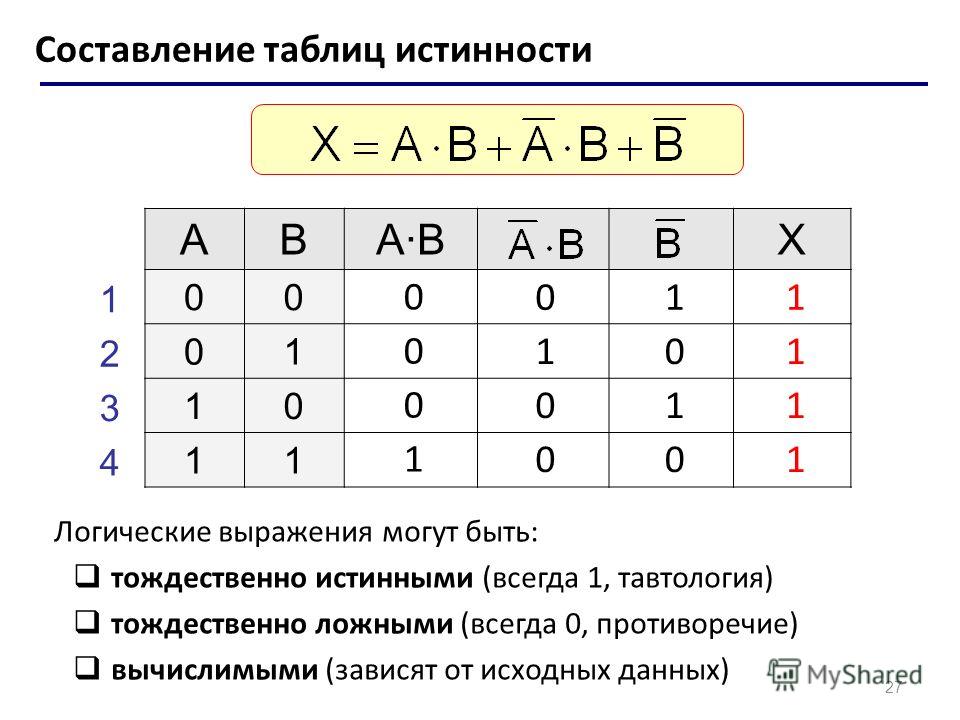
Приоритет логических операций
- Действия в скобках
- Инверсия
- Конъюнкция ( & )
- Дизъюнкция ( V ), Исключающее ИЛИ (XOR), сумма по модулю 2
- Импликация ( → )
- Эквивалентность ( ↔ )
Совершенная дизъюнктивная нормальная форма
Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами:- Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x1,x2,…xn).
- Все логические слагаемые формулы различны.
- Ни одно логическое слагаемое не содержит переменную и её отрицание.
- Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.
СДНФ можно получить или с помощью таблиц истинности или с помощью равносильных преобразований.

Для каждой функции СДНФ и СКНФ определены единственным образом с точностью до перестановки.
Совершенная конъюнктивная нормальная форма
Совершенная конъюнктивная нормальная форма формулы (СКНФ) это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам:- Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x1,x2,…xn).
- Все элементарные дизъюнкции различны.
- Каждая элементарная дизъюнкция содержит переменную один раз.
- Ни одна элементарная дизъюнкция не содержит переменную и её отрицание.
1.1. Логические выражения и логические операции
Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным. Примеры высказываний:
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3. Следующие предложения высказываниями не являются:
Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают. С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно. Примеры высказываний:
Каждое из этих высказываний характеризует свойства или состояние конкретного объекта (в пермом предложении — погоды, во втором — окружающего мира). Каждое из этих высказываний несет значение «истина» или «ложь». В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только 0 или 1. Простые высказывания назвали логическими переменными, а сложные — логическими функциями. Значения логической функции также только 0 или 1. Для простоты записи высказывания обозначаются латинскими буквами А, В, С. Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным. В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита. Существуют разные варианты обозначения истинности и ложности логических переменных:
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями. С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением). Логическое выражение — это символическая запись высказывания, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками). Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение. Введем перечисленные логические операции. Конъюнкция — логическое умножение (от латинского conjunctio — союз, связь):
Конъюнкция — это логическая операция, ставящая в соответствие каждым двум простым (или исходным) высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Если хотя бы одно из составляющих высказываний ложно, то и полученное из них с помощью союза «И»сложное высказывание также считается ложным. В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Итак, если два высказывания соединены союзом «И», то полученное сложное высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.
Дизъюнкция — логическое сложение (от латинского disjunctio — разобщение, различие):
Дизъюнкция — это логическая операция, которая каждым двум простым (или исходным) высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно. В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
Итак, если два высказывания соединены союзом «ИЛИ», то полученное сложное высказывание истинно когда истинно хотя бы одно из составляющих высказываний. Рассмотренные выше операции были двуместными (бинарными), т.е. выполнялись над двумя операндами (высказываниями). В алгебре логики определена и широко используется и одноместная (унарная) операция отрицание. Инверсия — отрицание (от латинского disjunctio — разобщение, различие):
Отрицание — логическая операция, которая с помощью связки «не» каждому исходному высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается. В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.
Итак, если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным.
Логическое следование (импликация): Высказывание, составленное из двух высказываний при помощи связки «если .
A => B «Из А следует В» Итак, новое высказывание, полученное с помощью импликации, является ложным тогда и только тогда, когда условие (посылка А) — истинно, а следствие (заключение В) — ложно и истинно во всех остальных случаях. Пример. Дано сложное высказывание: «Если выглянет солнце, то станет тепло». Требуется записать его в виде логической формулы. Обозначим через А простое высказывание «выглянет солнце», а через В — «станет тепло». Тогда логической формулой этого сложного высказывания будет импликация: A -> B.
Эквивалентность (логическое тождество): Высказывание, составленное из двух высказываний при помощи связки «тогда и только тогда, когда», называется эквивалентностью (эквивалентность — логическое тождество, равнозначность, взаимная обусловленность. )
A <=> B «А равносильно В» Итак, новое высказывание, полученное с использованием эквивалентности, является истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
В алгебре логики логические связки и соответствующие им логические операции имеют специальные названия и обозначаются следующим образом:
Примеры записи сложных высказываний с помощью обозначения логических связок:
|
Что такое булевская логика и как она используется в программировании
Булева логика является ключевой концепцией любого языка программирования, независимо от того, создаете ли вы видеоигру на C++, разрабатываете следующее лучшее приложение на Swift, выполняете поиск в реляционных базах данных на SQL, или работа с большими данными в Python. В этой статье мы расскажем, что такое логическая логика, как она работает и как создавать собственные логические выражения.
Что такое булева логика?
Булева логика — это тип алгебры, в котором результаты рассчитываются либо как ИСТИНА, либо как ЛОЖЬ (известные как значения истинности или переменные истинности). Вместо использования арифметических операторов, таких как сложение, вычитание и умножение, логическая логика использует три основных логических оператора: И, ИЛИ и НЕ.
ИСТИНА и ЛОЖЬ: их может быть только два
За булевой логикой стоят два очень простых слова: ИСТИНА и ЛОЖЬ.
Обратите внимание, что логическое значение TRUE или FALSE очень отличается от ввода строк «True» и «False» в ваш код. На самом деле языки программирования помещают эти два логических значения в свой собственный тип объекта, отдельный от целых чисел, строк и чисел с плавающей запятой. Но в то время как числовые или строковые значения в программировании могут быть практически бесконечными, есть только два возможных логических значения: ИСТИНА и ЛОЖЬ.
Как это работает? Булева логика рассматривает сообщаемую связь между вещами и определяет, сохраняется ли эта связь. Например, возьмем уравнение:
2 + 2 = 4
Здесь у нас есть две части, 2 + 2 и 4, и мы сообщаем, что эти две части равны друг другу. Это правильно? Да, так что логический результат этого будет ИСТИНА. В этом примере комбинация двух частей 2 + 2 и 4 вместе с отношением (= равно) называется логическим выражением.
Давайте посмотрим на другое логическое выражение:
10 – 4 = 5
Здесь мы сообщаем, что 4, вычитаемое из 10, равно 5. Верно? Конечно, нет, и именно поэтому это логическое выражение вернет значение FALSE.
Boolean Expression | Result |
2 + 2 = 5 | FALSE |
5 – 1 = 4 | TRUE |
4 * 5 > 10 | TRUE |
40 / 10 < 1 | FALSE |
Building Boolean expressions
Keep in Имейте в виду, что булевская логика работает только тогда, когда выражение может быть ИСТИНА или ЛОЖЬ. Например, выражение 3 + 8 не является логическим выражением, потому что оно не сравнивается и не связано с чем-то другим. Но выражение 3 + 8 = 10 является логическим выражением, потому что теперь мы можем оценить каждую сторону и посмотреть, является ли отношение между ними ИСТИННЫМ или ЛОЖНЫМ (в данном случае ЛОЖНЫМ).
Но выражение 3 + 8 = 10 является логическим выражением, потому что теперь мы можем оценить каждую сторону и посмотреть, является ли отношение между ними ИСТИННЫМ или ЛОЖНЫМ (в данном случае ЛОЖНЫМ).
Мы можем строить логические выражения со всеми видами данных, включая переменные. Например, предположим, что мы присвоили эти значения переменным x и y где-то в нашем коде:
x равно 7
y равно 3
Теперь мы можем построить логические выражения, используя наши переменные:
Логическое выражение | Результат |
x + y < 11 | 4 ЛОЖЬ0003 |
x * y = 21 | TRUE |
x / y > 10 | FALSE |
x + (2 * y) = 13 | TRUE |
Логические выражения также могут определять, идентичны ли две строки. Просто помните, что большинство языков программирования чувствительны к регистру.
Просто помните, что большинство языков программирования чувствительны к регистру.
Boolean Expression | Результат |
«I Love Codecademy» = «I Love Codecademy» | True |
«I True | |
« I Love ». | |
«Я люблю Codecademy» = «Я ЛЮБЛЮ Codecademy» | FALSE |
Существует множество других способов построения булевых выражений, в зависимости от языка программирования. Например, вы можете использовать логическое выражение, чтобы определить, содержится ли число в списке в Python или текстовая строка находится в таблице базы данных SQL.
Булевы операторы
Теперь, когда вы понимаете основы булевых выражений, давайте рассмотрим еще один ключевой аспект булевой логики: булевы операторы. Есть три основных логических оператора: И, ИЛИ и НЕ.
Есть три основных логических оператора: И, ИЛИ и НЕ.
Чтобы лучше понять, как работают логические операторы, давайте на мгновение представим, что мы находимся в магазине мороженого. Скажем, мы собираемся приготовить мороженое из двух шариков с разными вкусами. Но я немного привередлив в еде, поэтому могу не принимать каждую комбинацию пломбира, которую получаю. Мы можем использовать логические выражения и логические операторы, чтобы выяснить, буду ли я есть мороженое или нет.
AND
Логический оператор AND используется для подтверждения истинности двух или более логических выражений.
Например, в моем мороженом я хочу, чтобы первый вкус был шоколадным, а второй — ванильным. Мы могли бы превратить это в логическое выражение с оператором И, которое выглядит примерно так:
Аромат_1 = Шоколад И Аромат_2 = Ваниль
Это означает, что первый аромат должен быть шоколадным, а второй аромат должен быть ванильным. В противном случае я не буду есть мороженое.
Мы могли бы организовать эту ситуацию в таблицу таких возможностей, как это:
Flavor_1 | Flavor_2 | ETH SUNDAE? |
Chocolate | Vanilla | Yes |
Chocolate | Strawberry | No |
Mango | Vanilla | No |
Mango | Strawberry | No |
Tables like this are used in Boolean logic all the time. Их называют таблицами истинности, и мы можем составить одну из них для нашего примера с мороженым. Если что-то соответствует моим придирчивым условиям вкуса мороженого, то это ПРАВДА. Если нет, то это ЛОЖЬ.
Если нет, то это ЛОЖЬ.
Вот как выглядела бы приведенная выше таблица в виде таблицы истинности:
Flavor_1 | Flavor_2 | Result |
TRUE | TRUE | TRUE |
TRUE | ЛОЖЬ | ЛОЖЬ |
ЛОЖЬ | ИСТИНА | 6 3 ЛОЖЬ 60041 |
ЛОЖЬ | ЛОЖЬ | ЛОЖЬ |
ИЛИ
9
Например, если бы я хотел, чтобы первым ароматом была клубника, а вторым ароматом был манго, то логическое выражение было бы таким:
Аромат_1 = Клубника ИЛИ Аромат_2 = Манго
Мы могли бы организовать возможности как:
Аромат_1 | Аромат_2 | Ешьте мороженое? |
Strawberry | Mango | Yes |
Strawberry | Cherry | Yes |
Cherry | Mango | Да |
Vanilla | Raspberry | No |
And the truth table would look like this:
Flavor_1 | Flavor_2 | Результат |
ИСТИНА | ИСТИНА | ИСТИНА | 33UE | 0036 | FALSE | TRUE |
FALSE | TRUE | TRUE |
FALSE | FALSE | FALSE |
Note что оператор ИЛИ возвращает ИСТИНА, если одно из двух логических выражений истинно, а также когда оба выражения истинны. По этой причине этот оператор ИЛИ также известен как включающий оператор ИЛИ. В качестве альтернативы есть также оператор XOR (исключающее или), который возвращает ИСТИНА только тогда, когда одно из двух выражений истинно.
По этой причине этот оператор ИЛИ также известен как включающий оператор ИЛИ. В качестве альтернативы есть также оператор XOR (исключающее или), который возвращает ИСТИНА только тогда, когда одно из двух выражений истинно.
NOT
Логический оператор NOT отличается от AND и OR тем, что принимает только один аргумент. Он проверяет, является ли значение FALSE или нет. Иными словами, он меняет значения TRUE на FALSE, а значения FALSE на TRUE. Например, я ненавижу ромовый изюм и абсолютно не буду есть ничего с ромовым изюмом. Как это может выглядеть в виде таблицы?
Вкус | Ешь мороженое? |
Chocolate | Yes |
Rum Raisin | No |
The truth table looks like this:
Flavor | Результат |
False | True |
True | FALSE | FALSE | 0082 |
You can combine Boolean expressions to express my sundae preference when Rum Raisin is involved like so:
NOT (Flavor_1 = Rum Raisin OR Flavor_2 = Rum Raisin)
Flavor_1 | Flavor_2 | Ешьте мороженое? |
Шоколад | Малина | Да |
Peach | Rum Raisin | No |
Rum Raisin | Mint | No |
Rum Raisin | Rum Raisin | No |
Предложение ИЛИ в круглых скобках вернет TRUE для всего, что содержит ромовый изюм. Применение к нему НЕ изменит значение выражения ИЛИ с ИСТИНА на ЛОЖЬ и наоборот. Подобно операторам в арифметике, логические операторы имеют порядок старшинства: сначала обращаются к элементам в круглых скобках, затем к оператору НЕ, И и, наконец, к ИЛИ. Наша новая таблица истинности выглядит так:
Применение к нему НЕ изменит значение выражения ИЛИ с ИСТИНА на ЛОЖЬ и наоборот. Подобно операторам в арифметике, логические операторы имеют порядок старшинства: сначала обращаются к элементам в круглых скобках, затем к оператору НЕ, И и, наконец, к ИЛИ. Наша новая таблица истинности выглядит так:
Flavor_1 | Flavor_2 | Result |
FALSE | FALSE | TRUE |
FALSE | ИСТИНА | ЛОЖЬ |
ИСТИНА | ЛОЖЬ | ЛОЖЬ3 30041 |
True | True | False |
Применение своей логики Boolean
Итак, что следующее после изучения базовых знаний логика Boolean??
Булева логика имеет решающее значение для создания кода, который помогает вашей программе быстро принимать решения относительно данных и входных данных, поэтому попробуйте применить свои логические знания в онлайн-курсе программирования. И если вы не уверены, какой курс выбрать следующим, взгляните на наши карьерные пути разработчиков. Мы поможем вам сосредоточиться на лучших навыках, необходимых для достижения желаемой должности.
И если вы не уверены, какой курс выбрать следующим, взгляните на наши карьерные пути разработчиков. Мы поможем вам сосредоточиться на лучших навыках, необходимых для достижения желаемой должности.
Курсы и учебные пособия по основам кода | Codecademy
Хотите научиться программировать, но не знаете, с чего начать? Наша область Code Foundations предоставляет обзор основных приложений программирования и учит важным концепциям, которые вы найдете в каждом языке программирования. Этот контент подготовит вас к тому, чтобы наметить курс на более техническое обучение…
Codecademy
{{#сравнить сложность «==» «Новичок»}} Подходит для начинающих {{еще}} {{~#сравнить сложность «==» «Продвинутая»~}}{{/compare}} {{сложность}} {{/сравнивать}} {{урокКоличество}} Уроки
Логические выражения — Visual Basic
Обратная связь Редактировать
Твиттер LinkedIn Фейсбук Эл. адрес
адрес
- Статья
- 3 минуты на чтение
Логическое выражение — это выражение, результатом которого является значение логического типа данных: True или False . Булевы выражения могут принимать несколько форм. Самым простым является прямое сравнение значения логической переменной с литералом Boolean , как показано в следующем примере.
Если новыйКлиент = Истина Тогда
' Вставьте код для выполнения, если newCustomer = True.
Еще
' Вставьте код для выполнения, если newCustomer = False.
Конец, если
Два значения оператора =
Обратите внимание, что оператор присваивания newCustomer = True выглядит так же, как выражение в предыдущем примере, но выполняет другую функцию и используется по-другому. В предыдущем примере выражение
В предыдущем примере выражение newCustomer = True представляет логическое значение, а знак = интерпретируется как оператор сравнения. В автономном операторе знак = интерпретируется как оператор присваивания и присваивает значение справа переменной слева. Следующий пример иллюстрирует это.
Если новыйКлиент = Истина Тогда
новыйКлиент = Ложь
Конец, если
Для получения дополнительной информации см. Сравнение значений и заявления.
Операторы сравнения
Операторы сравнения, такие как = , < , > , <> , <= и >= , производят сравнение выражений в левой части логических выражений оператор к выражению в правой части оператора и оценивая результат как Верно или Ложно . Следующий пример иллюстрирует это.
42 < 81
Поскольку 42 меньше 81, логическое выражение в предыдущем примере оценивается как True . Дополнительные сведения об этом типе выражений см. в разделе Сравнение значений.
Дополнительные сведения об этом типе выражений см. в разделе Сравнение значений.
Операторы сравнения в сочетании с логическими операторами
Выражения сравнения можно комбинировать с использованием логических операторов для получения более сложных логических выражений. В следующем примере демонстрируется использование операторов сравнения в сочетании с логическим оператором.
x > y And x < 1000
В предыдущем примере значение общего выражения зависит от значений выражений с каждой стороны оператора And . Если оба выражения равны True , то общее выражение оценивается как True . Если какое-либо из выражений равно False , то все выражение оценивается как False .
Операторы короткого замыкания
Логические операторы AndAlso и OrElse проявляют поведение, известное как короткое замыкание . Оператор короткого замыкания сначала оценивает левый операнд. Если левый операнд определяет значение всего выражения, то выполнение программы продолжается без вычисления правого выражения. Следующий пример иллюстрирует это.
Если левый операнд определяет значение всего выражения, то выполнение программы продолжается без вычисления правого выражения. Следующий пример иллюстрирует это.
Если 45 < 12 И также testFunction(3) = 81 Тогда
'Добавить код для продолжения выполнения.
Конец, если
В предыдущем примере оператор оценивает левое выражение, 45 < 12 . Поскольку левое выражение оценивается как False , все логическое выражение должно оцениваться как False . Таким образом, выполнение программы пропускает выполнение кода в блоке If без оценки правильного выражения, testFunction(3) . В этом примере не вызывается testFunction() , поскольку левое выражение искажает все выражение.
Аналогично, если левое выражение в логическом выражении с использованием OrElse оценивается как True , выполнение переходит к следующей строке кода без оценки правильного выражения, поскольку левое выражение уже проверило все выражение.
Сравнение с операторами без короткого замыкания
Напротив, обе стороны логического оператора оцениваются, когда используются логические операторы И и Или . Следующий пример иллюстрирует это.
Если 45 < 12 И testFunction(3) = 81 Тогда
'Добавить код для продолжения выполнения.
Конец, если
В предыдущем примере вызывается testFunction() , хотя левое выражение оценивается как False .
Выражения в скобках
Скобки можно использовать для управления порядком вычисления логических выражений. Выражения, заключенные в круглые скобки, вычисляются первыми. Для нескольких уровней вложенности приоритет отдается наиболее глубоко вложенным выражениям. Внутри круглых скобок оценка выполняется в соответствии с правилами приоритета операторов. Дополнительные сведения см. в разделе Приоритет операторов в Visual Basic.
См. также
- Логические и побитовые операторы в Visual Basic
- Сравнение значений
- Заявления
- Операторы сравнения
- Эффективная комбинация операторов
- Приоритет оператора в Visual Basic
- Логический тип данных
Обратная связь
Отправить и просмотреть отзыв для
Этот продукт Эта страница
Просмотреть все отзывы о странице
логических выражений
логических выраженийЛогический тип данных — bool
В C++ тип данных bool используется для представления логических данных. Каждая константа или переменная
Каждая константа или переменная bool содержит один из
два значения: true или false .
true и false — это две константы C++.
true имеет значение 1 .
false имеет значение 0 .
Если проверочное выражение не имеет тип bool ,
оно автоматически приводится к типу bool , когда оно
оценивается.
Ненулевое значение приводится к true , а нулевое значение приводится к false .
Логические выражения
Логическое выражение может быть простым логическим значением или более сложное выражение, включающее один или несколько реляционных и логических операторов. Реляционные операторы принимают два операнда и проверяют связь между ними. их. В следующей таблице показаны реляционные операторы и соответствующие символы C++.| Реляционные операторы | |
|---|---|
| Символ С++ | Описание |
| == | равно |
| != | не равно |
| > | больше |
| < | меньше |
| >= | больше или равно |
| <= | меньше или равно |
номер 1 оценивается какtrue, если значение, хранящееся вnumber1, меньше, чем значение, хранящееся вnumber2, и оценивается какложьиначе.
Когда оператор отношения применяется между переменными типа
char, утверждение с точки зрения того, где два операнда попадают в сопоставление последовательность определенного набора символов. Например,символ1 <символ2оценивается какtrue, если значение, хранящееся вcharacter1, приходит перед символом, хранящимся всимвол2в последовательности сопоставления машины, на которой вычисляется выражение. Вы можете думать о последовательность сопоставления в алфавитном порядке, чтобы помочь вам понять ее. Набор символов ASCII широко используется в качестве последовательности сопоставления.Простое логическое выражение является либо логической переменной, либо логическим константа или выражение, включающее операторы отношения, которое оценивает либо истина или ложь . Эти простые логические выражения могут быть объединены с использованием логических операций , определенных над логическими значениями.
Там три логических оператора: И, ИЛИ и НЕ . Вот таблица показывая, как они используются в C++.
| Логические операторы | |
|---|---|
| Символ С++ | Описание |
| && | и Логический оператор:
|
| || | Логический оператор или :
|
| ! | Логический оператор , а не .
|
Приоритет операторов
Если реляционные операторы и логические операторы объединены в одном
выражение в C++, логический оператор NOT ! имеет наивысший приоритет,
реляционные операторы имеют следующий наивысший приоритет, а логические
операторы И && и ИЛИ || имеют самые низкие. Выражения в скобках
всегда оцениваются первыми .
В следующей таблице приведены приоритеты всех операторов C++. мы видели до сих пор.
Наивысший приоритет | ( ) | | ++х --х | | ! Унарный + Унарный - | | * / % | | + - | | << >> | | < <= > >= | | == != | | && | | || | | = | | х++ х-- | В Самый низкий приоритет
Операторы в одной строке таблицы имеют одинаковый приоритет. Если
выражение содержит несколько операторов с одинаковым приоритетом, большинство
группы операторов слева направо. Некоторые операторы имеют различный приоритет
на основе того, где переменные находятся по отношению к ним, для них x представляет переменную.
Если
выражение содержит несколько операторов с одинаковым приоритетом, большинство
группы операторов слева направо. Некоторые операторы имеют различный приоритет
на основе того, где переменные находятся по отношению к ним, для них x представляет переменную.
© Департамент компьютерных наук Университета Регины.
Правила логических выражений — Документация по базе данных векторов Milvus
Обзор
Выражение-предикат выводит логическое значение. Milvus проводит скалярную фильтрацию путем поиска с помощью предикатов. Выражение предиката при оценке возвращает либо ИСТИНА, либо ЛОЖЬ. См. Справочник по Python SDK API для получения инструкций по использованию предикатных выражений.
Правила грамматики EBNF описывают правила булевых выражений:
Expr = LogicalExpr | НОЛЬ
LogicalExpr = LogicalExpr BinaryLogicalOp LogicalExpr
| UnaryLogicalOp LogicalExpr
| "("ЛогическоеВыражение")"
| Одновыражение;
BinaryLogicalOp = "&&" | "и" | "||" | "или же";
UnaryLogicalOp = "не";
Одновыражение = ТерминВыражение | СравнитьВыражение;
TermExpr = IDENTIFIER "in" ConstantArray;
Константа = ЦЕЛОЕ ЧИСЛО | ПЛАВАТЬ
КонстантаВыражение = Константа
| ConstantExpr BinaryArithOp
| UnaryArithOp КонстантаВыражение;
ConstantArray = "[" ConstantExpr { "," ConstantExpr } "]";
UnaryArithOp = "+" | "-"
BinaryArithOp = "+" | "-" | "*" | "/" | "%" | "**";
CompareExpr = IDENTIFIER CmpOp IDENTIFIER
| ИДЕНТИФИКАТОР CmpOp ConstantExpr
| ИДЕНТИФИКАТОР CmpOp ConstantExpr
| ConstantExpr CmpOpRestricted IDENTIFIER CmpOpRestricted ConstantExpr;
CmpOpRestricted = "<" | "<=";
CmpOp = ">" | ">=" | "<" | "<=" | "=="| знак равно
MatchOp = "нравится" | "КАК";
В следующей таблице приведено описание каждого символа, упомянутого в приведенных выше правилах логических выражений.
| Обозначение | Описание |
|---|---|
| = | Определение. |
| , | Конкатенация. |
| ; | Прекращение. |
| | | Чередование. |
| {...} | Повторение. |
| (...) | Группировка. |
| НОЛЬ | Пусто. Выражение может быть пустой строкой. |
| ЦЕЛОЕ ЧИСЛО | Целые числа, такие как 1, 2, 3. |
| ПЛАВАЮЩИЙ | Числа с плавающей запятой, такие как 1.0, 2.0. |
| КОНСТ | Целые числа или числа с плавающей запятой. |
| ИДЕНТИФИКАТОР | Идентификатор. В Milvus ИДЕНТИФИКАТОР представляет имя поля. |
| Логическая операция | LogicalOp — это логический оператор, поддерживающий объединение более одной реляционной операции в одном сравнении. Возвращаемое значение LogicalOp либо TRUE (1), либо FALSE (0). Существует два типа LogicalOps, включая BinaryLogicalOps и UnaryLogicalOps. Возвращаемое значение LogicalOp либо TRUE (1), либо FALSE (0). Существует два типа LogicalOps, включая BinaryLogicalOps и UnaryLogicalOps. |
| UnaryLogicalOp | UnaryLogicalOp относится к унарному логическому оператору «не». |
| Двоичная логическая операция | Двоичные логические операторы, выполняющие действия над двумя операндами. В сложном выражении с двумя или более операндами порядок вычисления зависит от правил приоритета. |
| Арифметическая операция | ArithmeticOp, а именно арифметический оператор, выполняет математические операции, такие как сложение и вычитание над операндами. |
| UnaryArithOp | UnaryArithOp — это арифметический оператор, выполняющий операцию над одним операндом. Отрицательный UnaryArithOp изменяет положительное выражение на отрицательное или наоборот. |
| Бинарарифоп | BinaryArithOp, а именно бинарный оператор, выполняет операции над двумя операндами. В сложном выражении с двумя или более операндами порядок вычисления зависит от правил приоритета. В сложном выражении с двумя или более операндами порядок вычисления зависит от правил приоритета. |
| CmpOp | CmpOp — это оператор отношения, который выполняет действия над двумя операндами. |
| CmpOpRestricted | CmpOpRestricted ограничено значениями «Меньше чем» и «Равно». |
| КонстантЭкспр | ConstantExpr может быть константой или BinaryArithOp для двух ConstExpr или UnaryArithOp для одного ConstantExpr. Он определяется рекурсивно. |
| Массив констант | ConstantArray заключен в квадратные скобки, а ConstantExpr может повторяться в квадратных скобках. ConstArray должен включать хотя бы один ConstantExpr. |
| ТерминВыражение | TermExpr используется для проверки наличия значения IDENTIFIER в массиве констант. TermExpr представлен "in". |
| СравнитьВыражение | CompareExpr, а именно выражение сравнения, может быть реляционной операцией над двумя IDENTIFIER, или реляционной операцией над одним IDENTIFIER и одним ConstantExpr, или тернарной операцией над двумя ConstantExprs и одним IDENTIFIER. |
| Одновыражение | SingleExpr, а именно одиночное выражение, может быть либо TermExpr, либо CompareExpr. |
| Логическое выражение | LogicalExpr может быть BinaryLogicalOp для двух LogicalExpr, или UnaryLogicalOp для одного LogicalExpr, или LogicalExpr, сгруппированным в круглых скобках, или SingleExpr. LogicalExpr определяется рекурсивно. |
| Выражение | Expr, аббревиатура, означающая выражение, может быть LogicalExpr или NIL. |
| МатчОп | MatchOp, а именно оператор сопоставления, сравнивает строку со строковой константой или константой префикса строки. |
Операторы
Логические операторы:
Логические операторы выполняют сравнение двух выражений.
| Символ | Операция | Пример | Описание |
|---|---|---|---|
| 'и' && | и | выражение1 && выражение2 | Истинно, если оба выражения expr1 и expr2 верны. |
| 'или' || | или | выражение1 || выражение2 | Истинно, если либо expr1, либо expr2 истинны. |
Двоичные арифметические операторы:
Двоичные арифметические операторы содержат два операнда и могут выполнять основные арифметические операции и возвращать соответствующий результат.
| Символ | Операция | Пример | Описание |
|---|---|---|---|
| + | Дополнение | а + б | Добавьте два операнда. |
| - | Вычитание | а-б | Вычесть второй операнд из первого операнда. |
| * | Умножение | а*б | Умножить два операнда. |
| / | Подразделение | а/б | Разделить первый операнд на второй операнд. |
| ** | Мощность | а ** б | Возвести первый операнд в степень второго операнда. |
| % | Модуль | а % б | Разделить первый операнд на второй и получить оставшуюся часть. |
Операторы отношения:
Операторы отношения используют символы для проверки равенства, неравенства или относительного порядка между двумя выражениями.
| Символ | Операция | Пример | Описание |
|---|---|---|---|
| < | Менее | а < б | Истинно, если a меньше b. |
| > | Больше | а > б | Истинно, если a больше b. |
| == | Равно | а == б | Истинно, если a равно b. |
| != | Не равно | а != б | Истинно, если a не равно b. |
| <= | Меньше или равно | а <= б | Истинно, если a меньше или равно b. |
| >= | Больше или равно | а >= б | Истинно, если a больше или равно b. |
Приоритет и ассоциативность операторов
В следующей таблице перечислены приоритеты и ассоциативность операторов. Операторы перечислены сверху вниз в порядке убывания приоритета.
| Приоритет | Оператор | Описание | Ассоциативность |
|---|---|---|---|
| 1 | + - | UnaryArithOp | Слева направо |
| 2 | не | UnaryLogicOp | Справа налево |
| 3 | ** | Двоичный АрифОп | Слева направо |
| 4 | * / % | Двоичный АрифОп | Слева направо |
| 5 | + - | Двоичный АрифОп | Слева направо |
| 6 | < <= > >= | CmpOp | Слева направо |
| 7 | == != | CmpOp | Слева направо |
| 8 | как НРАВИТСЯ | MatchOp | Слева направо |
| 9 | && и | BinaryLogicOp | Слева направо |
| 10 | || или | BinaryLogicOp | Слева направо |
Выражения обычно оцениваются слева направо. Сложные выражения оцениваются по одному. Порядок, в котором вычисляются выражения, определяется приоритетом используемых операторов.
Сложные выражения оцениваются по одному. Порядок, в котором вычисляются выражения, определяется приоритетом используемых операторов.
Если выражение содержит два или более операторов с одинаковым приоритетом, оператор слева вычисляется первым.
Например, 10/2 * 5 будет вычислено как (10/2), а результат умножен на 5.
Когда операция с более низким приоритетом должна быть обработана первой, она должна быть заключена в круглые скобки.
Например, 30 / 2 + 8. Обычно это вычисляется как 30, деленное на 2, а затем к результату добавляется 8. Если вы хотите разделить на 2 + 8, это должно быть записано как 30 / (2 + 8).
Скобки могут быть вложены в выражения. Сначала оцениваются самые внутренние выражения в скобках.
Использование
Примеры использования всех доступных логических выражений в Milvus перечислены ниже ( int64 представляет скалярное поле, содержащее данные типа INT64, float представляет скалярное поле, содержащее данные типа с плавающей запятой, и VARCHAR представляет скалярное поле, содержащее данные типа VARCHAR):
- CmpOp
"int64 > 0"
"0 < int64 < 400"
"500 <= int64 < 1000"
VARCHAR > "str1"
- BinaryLogicalOp и скобки
"(int64 > 0 && int64 < 400) или (int64 > 500 && int64 < 1000)"
- TermExpr и UnaryLogicOp
Milvus поддерживает удаление только сущностей с четко указанными первичными ключами, что может быть достигнуто просто с помощью терм-выражения в .
"int64 не в [1, 2, 3]"
VARCHAR отсутствует в ["str1", "str2"]
- TermExpr, BinaryLogicalOp и CmpOp (в разных полях)
"int64 в [1, 2, 3] и float != 2"
- BinaryLogicalOp и CmpOp
"int64 == 0 || int64 == 1 || int64 == 2"
- CmpOp и UnaryArithOp или BinaryArithOp
"200+300 < int64 <= 500+500"
- MatchOp (совпадение префикса)
VARCHAR как "префикс%"
Что дальше
Теперь, когда вы знаете, как работают наборы битов в Milvus, вы также можете:
- Узнать, как проводить гибридный поиск.
- Узнайте, как использовать строки для фильтрации результатов поиска.
Полезна ли эта страница?
Writing Logical Expressions
Writing Logical ExpressionsWriting Logical Expressions
In this section:
|
A logical expression determines whether a particular condition правда. Существует два вида логических выражений: реляционные и логические. Сущности, которые вы хотите сравнить, определяют тип выражения.
Существует два вида логических выражений: реляционные и логические. Сущности, которые вы хотите сравнить, определяют тип выражения.
Реляционное выражение возвращает ИСТИНА или ЛОЖЬ на основе сравнения двух отдельных значений (либо переменных, либо констант). Логическое выражение возвращает TRUE или FALSE в зависимости от результатов двух или более реляционных выражений.
Вы можете использовать логическое выражение для присвоения значения числовой переменной. Если выражение истинно, переменная получает значение 1. Если выражение ложно, переменная получает значение 0.
К началу страницы |
x
Выражения отношения
Выражение отношения возвращает ИСТИНА или ЛОЖЬ на основе сравнения двух отдельных значений (либо переменных, либо констант). В следующем синтаксисе перечислены операторы, которые можно использовать в реляционном выражении:
В следующем синтаксисе перечислены операторы, которые можно использовать в реляционном выражении:
character_expression char_operator character_constant
numeric_expression numeric_operator numeric_constant
где:
- char_operator
Может быть любым из следующих: EQ, NE, OMITS, CONTAINS.
- numeric_operator
Может быть любым из следующих: EQ, NE, LE, LT, GE, GT.
К началу страницы |
x
Логические выражения
Как:
|
Логические выражения возвращают значение true (1) или false (0) в зависимости от результата двух или более выражений отношения. Логические выражения часто используются в условных выражениях, которые описаны в разделе Написание условных выражений. Вы также можете присвоить результат логического выражения числовой или символьной переменной, которая будет равна 1 (если выражение истинно) или 0 (если ложно). Они строятся с использованием переменных и констант, связанных операторами.
Логические выражения часто используются в условных выражениях, которые описаны в разделе Написание условных выражений. Вы также можете присвоить результат логического выражения числовой или символьной переменной, которая будет равна 1 (если выражение истинно) или 0 (если ложно). Они строятся с использованием переменных и констант, связанных операторами.
К началу страницы |
x
Синтаксис: использование логических выражений
Синтаксис логического выражения:
(реляционное_выражение) {И|ИЛИ} (реляционное_выражение)
НЕ (логическое_выражение) Логические выражения сами по себе могут использоваться в качестве строительных блоков для более сложных выражений. Используйте И или ИЛИ, чтобы соединить выражения и заключить каждое выражение в круглые скобки.
К началу страницы |
x
Оценка логических выражений
Ссылка:
|
Буквенно-цифровые константы со встроенными пробелами, используемые в выражении, должны быть заключены в одинарные кавычки. Пример:
IF NAME EQ 'JOHN DOE'
ИЛИ нельзя использовать между константами в выражении отношения. Например, следующее выражение недопустимо:
IF COUNTRY EQ 'США' ИЛИ 'БРАЗИЛИЯ' ИЛИ 'ГЕРМАНИЯ'
Вместо этого оно должно быть закодировано как последовательность относительных выражений:
IF (COUNTRY EQ 'США') ИЛИ (СТРАНА EQ 'БРАЗИЛИЯ') ИЛИ (СТРАНА EQ 'ГЕРМАНИЯ')
К началу страницы |
x
Справочник: Логические операторы
В следующем списке показаны логические операторы, которые можно использовать в выражении:
Описание | Оператор |
|---|---|
Равенство | Эквалайзер |
Неравенство | СВ |
Менее | LT |
Больше | ГТ |
Меньше или равно | ЛЭ |
Больше или равно | ГЭ |
Содержит указанную строку символов | СОДЕРЖИТ |
Пропускает указанную строку символов | ПРОПУСКАЕТ |
Отрицание | НЕ |
Соединение | И |
Разъединение | ИЛИ |
Логические операторы оцениваются после числовых операторов слева направо в следующем порядке приоритета:
Заказ | Операторы |
|---|---|
1 | EQ NE LE LT GE GT НЕ СОДЕРЖИТ ПРОПУСК |
2 | И |
3 | или |
| Webfocus |
Boolean Elements
, будь то создание уравнений. объединить логические условия.
объединить логические условия.
Обозначение
Булевы (логические) уравнения выражаются аналогично математическим уравнениям. Однако переменные в логических выражениях имеют только два возможных значения: истина или ложь . Для уравнения, использующего логическое выражение, эквивалентные стороны знака равенства, = , будут только истинными или ложными .
В следующем списке показаны основные элементы записи логических выражений.
-
~A: инверсия ( NOT )A, когдаAравноверно,~Aравноложно2
A + B: значениеАИЛИБA · B: значениеAИBA ⊕ B: значение исключающего ИЛИ ( XOR )AсBQ: эквивалентное значение результата (ВЫХОД) логического выражения
Результирующее значение Q из логического выражения выглядит следующим образом:
Q = A + B
Уравнение, показывающее логически эквивалентные выражения (где обе части имеют одинаковое результирующее значение), может выглядеть следующим образом:
~(A + B) = ~A · ~B
Логические операторы
Все Логические выражения являются результатом комбинации условий и операторов. Эти операторы объединяют отдельные условия вместе и вычисляют одно условие
Эти операторы объединяют отдельные условия вместе и вычисляют одно условие true или false . Ниже приведены основные логические операторы. Их использование как в булевой алгебре, так и в коде показано вместе с их таблицей истинности.
Идентичность
Идентичность означает, что значение результата совпадает с самим условием.
Q = A
пусть A = ложь let Q = A
Пример - Мигание пикселей при нажатии
let A = false
навсегда (функция () {
A = input.buttonA.isPressed()
если) {
свет.setAll (0xff0000)
} еще {
свет.очистить()
}
пауза(500)
}) Таблица истинности
| A | А |
|---|---|
| Ф | Ф |
| Т | Т |
НЕ (Отрицание)
Оператор НЕ называется отрицанием или обратным. Он принимает одно логическое значение и делает его противоположным: true переходит в false и false переходит в true .
Q = ~A
пусть A = ложь let Q = !(A)
Пример - Мигание пикселей при ненажатии
пусть А = ложь
навсегда (функция () {
A = input.buttonA.isPressed()
если)) {
свет.setAll (0xff0000)
} еще {
свет.очистить()
}
пауза(500)
}) Таблица истинности
| A | ~А |
|---|---|
| Ф | Т |
| Т | Ф |
ИЛИ (Дизъюнкция)
Оператор ИЛИ дает true , когда одно или несколько условий равны верно .
Q = A + B
пусть A = ложь пусть B = ложь пусть Q = А || B
Пример — Мигание при любом нажатии
пусть A = false
пусть B = ложь
навсегда (функция () {
A = input.buttonA.isPressed()
B = input.buttonB.isPressed()
если (А || В) {
свет.setAll (0xff0000)
} еще {
свет.очистить()
}
пауза(500)
}) Таблица истинности
| A | Б | А + В |
|---|---|---|
| Ф | Ф | Ф |
| Т | Ф | Т |
| Ф | Т | Т |
| Т | Т | Т |
И (соединение)
Оператор И требует, чтобы все условия были истинными , чтобы результат был истинным .
Q = A · B
пусть A = ложь пусть B = ложь пусть Q = A && B
Пример — мигание только при двойном нажатии
пусть A = false
пусть B = ложь
навсегда (функция () {
A = input.buttonA.isPressed()
B = input.buttonB.isPressed()
если (А && В) {
свет.setAll (0xff0000)
} еще {
свет.очистить()
}
пауза(500)
}) Таблица истинности
| A | Б | А · В |
|---|---|---|
| Ф | Ф | Ф |
| Т | Ф | Ф |
| Ф | Т | Ф |
| Т | Т | Т |
Исключающее ИЛИ (исключающее ИЛИ)
Исключающее ИЛИ (исключающее ИЛИ) означает, что выполняется только одно или другое условие. Оба условия не могут быть истинными одновременно. XOR распространен в булевой алгебре, но не имеет оператора в JavaScript.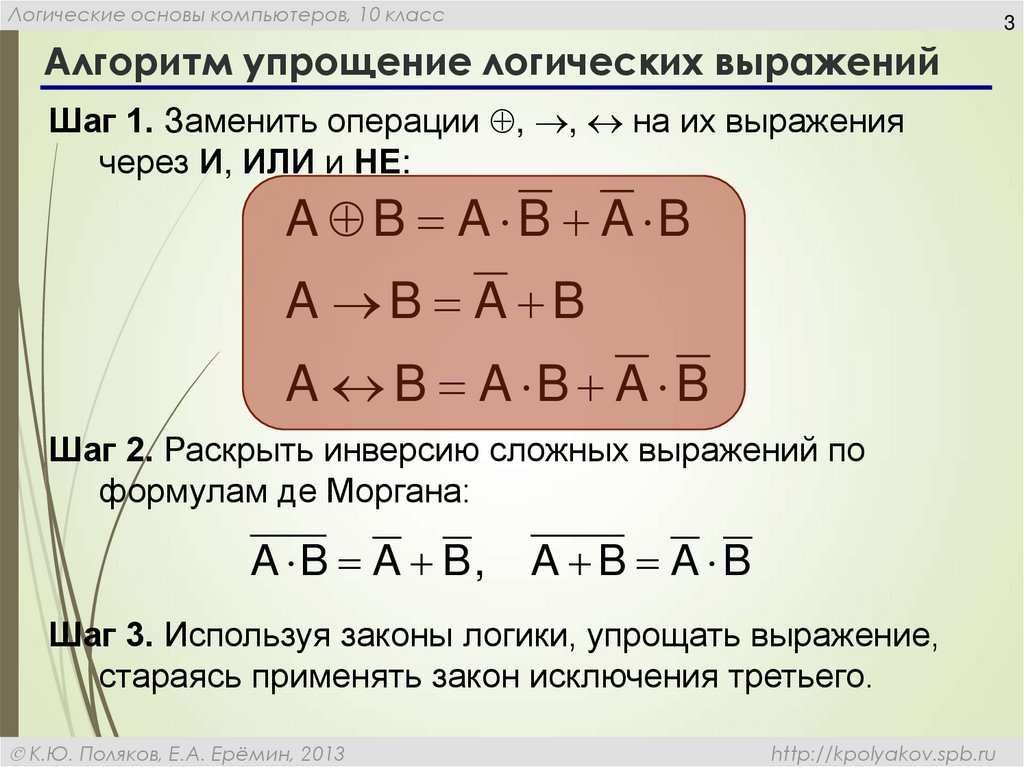




 Все правила по сольфеджио
Все правила по сольфеджио
 7 – Логическая схема и соответствующая ей таблица истинности
7 – Логическая схема и соответствующая ей таблица истинности Рассмотрим все эти возможности отдельно и по порядку.
Рассмотрим все эти возможности отдельно и по порядку. е. ), и , и . От значения не вошедшей в данное произведение переменной произведение не зависит. Поэтому логические 1 будут в строках таблицы истинности, соответствующих полным произведениям , в которых и одновременно , а переменная перечисляется во всех двух возможных комбинациях: =0101 и 0111.
е. ), и , и . От значения не вошедшей в данное произведение переменной произведение не зависит. Поэтому логические 1 будут в строках таблицы истинности, соответствующих полным произведениям , в которых и одновременно , а переменная перечисляется во всех двух возможных комбинациях: =0101 и 0111.

 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.009 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.009 с.) y).
y).


 Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
 Если высказывание истинно, то его значение равно 1, если ложно — 0.
Если высказывание истинно, то его значение равно 1, если ложно — 0.





 е. множеству получившемуся в результате отрицания множества А соответствует множество, дополняющее его до универсального множества.
е. множеству получившемуся в результате отрицания множества А соответствует множество, дополняющее его до универсального множества.  .., то …», называется логическим следованием, импликацией (импликация от латинского implico — тесно связываю).
.., то …», называется логическим следованием, импликацией (импликация от латинского implico — тесно связываю). 

 » (В. Шекспир) А V ¬ A <=> В
» (В. Шекспир) А V ¬ A <=> В
 Там
три логических оператора: И, ИЛИ и НЕ . Вот таблица
показывая, как они используются в C++.
Там
три логических оператора: И, ИЛИ и НЕ . Вот таблица
показывая, как они используются в C++.