Тригонометрический круг ☑️ со всеми значениями, круг синусов и косинусов, линия, ось тангенса на окружности, как пользоваться и находить точки
Общие сведения
Для правильного решения тригонометрических задач следует изучить основные понятия, формулы, а также методы нахождения основных величин. Раздел математики, изучающий функции косинуса, синуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса и арккотангенса, называется тригонометрией. Окружность, которая используется для решения геометрических задач на плоскости, имеет единичный радиус.
Значения функций, которые можно по ней находить, называются тригонометрическими. Однако существует множество способов нахождения их значений, но в некоторых ситуациях при использовании формул приведения решение затянется на продолжительное время, а вычисления будут громоздкими. Чтобы этого избежать, нужно использовать тригонометрический круг со всеми значениями. С его помощью также можно определить, является ли функция четной или нечетной.
Углы и их классификация
Перед тем как понять основное назначение тригонометрических функций, следует обратить внимание на классификацию углов. Она является важной для вычисления тригонометрических выражений.
- Острые.
- Прямые.
- Тупые.
- Развернутые.
- Выпуклые.
- Полные.
К первому типу относятся углы любой размерности градусной единицы измерения, которая не превышает 90 (а<90). Если значение соответствует 90, то он является прямым (а=90). Угол считается тупым, при выполнении следующего условия: 90<a<180. Если градусная размерность угла соответствует 180, то он является развернутым (а = 180). Выпуклым считается угол, когда выполняется такое условие: 180 < a < 360. Следует отметить, что он является смежным с острым углом. В случае, когда значение градусной размерности соответствует 360 градусам, то он является полным (а=360).
Однако углы измеряются не только в градусах, но и в радианах. Для решения тригонометрических задач оптимальным выбором градусной меры является радиан. Для соотношения между двумя единицами измерения применяется простая формула: 180 (град) = ПИ (рад). Из соотношения можно вывести формулу для перевода градусов в радианы: Pрад = (а * ПИ) / 180. Переменная «а» — значение величины градусной меры заданного угла. Обратное соотношение принимает следующий вид: а = (Ррад * 180) / ПИ.
Для быстрого перевода единиц измерения применяют такие инструменты: радианная табличка, программное обеспечение и тригонометрическая окружность. Однако для начала следует обратить внимание на тригонометрические функции, которые присутствуют в задачах физико-математического уклона.
Информация о функциях
Тригонометрических функций всего четыре вида: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существует столько же типов обратных функций: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg). Они получили широкое применение не только в математических задачах, но также используются в физике, электронике, электротехнике и других дисциплинах. Основной их особенностью считается возможность представления какого-либо закона.
Например, зависимость амплитуды напряжения переменного тока от времени описывается следующим законом: u = Um * cos (w*t) (графиком является косинусоида). Гармонические звуковые колебания также подчиняются определенному закону, в котором присутствует тригонометрическая функция. Кроме того, можно находить значения корня тригонометрического уравнения.
Синусом угла называется величина, равная отношению противолежащего катета прямоугольного треугольника к его гипотенузе. Следовательно, косинус — отношение прилежащего катета к гипотенузе. Тангенс — отношение величины противолежащего катета к прилежащему. Котангенс является обратной функцией тангенсу, т. е. отношение прилежащего к противолежащему.
Функции arcsin, arccos, arctg, arcctg применяются в том случае, когда нужно найти значение угла в градусах или радианах. Вычисления выполняются по специальным таблицам Брадиса или с помощью программ. Также можно использовать тригонометрическую окружность.
Тригонометрический круг
Чтобы воспользоваться тригонометрической окружностью для решения задач, нужны такие базовые знания: понятие о синусе, косинусе, тангенсе, котангенсе, системе координат и теореме Пифагора. Для построения единичной окружности используется декартовая система координат с двумя осями. Точка «О» — центр пересечения координатных осей, ОХ — ось абсцисс, ОУ — ординат.
Для решения задач различного типа применяется и теорема Пифагора. Она справедлива только для прямоугольного треугольника (один из углов — прямой). Ее формулировка следующая: квадрат гипотенузы в произвольном прямоугольном треугольнике равен сумме квадратов катетов.
- a + b = 180.
- cos(a) = sin(b).
- cos(b) = sin(a).
- tg(a) = ctg(b).
- tg(b) = ctg(a).
- tg(a) = 1 / ctg(a).
- tg(b) = 1 / ctg(b).
Существуют и другие тригонометрические тождества, но для работы с кругом этого перечня будет достаточно.
Построение «инструмента»
Построить окружность, которая ускорит процесс решения задач, довольно просто. Для этого потребуются бумага, карандаш, резинка и циркуль. Далее необходимо нарисовать любую немаленькую окружность. После этого отметить ее центр карандашом, поставив точку. Пусть она будет называться «О». Через эту точку следует провести две перпендикулярные прямые (угол пересечения равен 90 градусам). Обозначить их следующим образом: «х» (горизонтальная) и «у» (вертикальная).
Окружность является единичной, но не стоит рисовать ее такой, поскольку работать будет неудобно. Этот прием называется масштабированием. Он широко применяется практически во всех сферах человеческой деятельности. Например, инженеры не чертят двигатель космического корабля в натуральную величину, поскольку с таким «рисунком» будет неудобно и невозможно работать. Они используют его макет.Окружность пересекается с осями декартовой системы координат в 4 точках со следующими координатами: (1;0), (0;1), (-1;0) и (0;-1). Области, которые делят декартовую систему координат на 4 части, называются четвертями. Их четыре:
- Первая состоит из положительных координат по х и у.
- Вторая имеет по х отрицательные и положительные по у.
- Третья — только отрицательные значения.
- Четвертая — положительные значения по х и отрицательные по у.
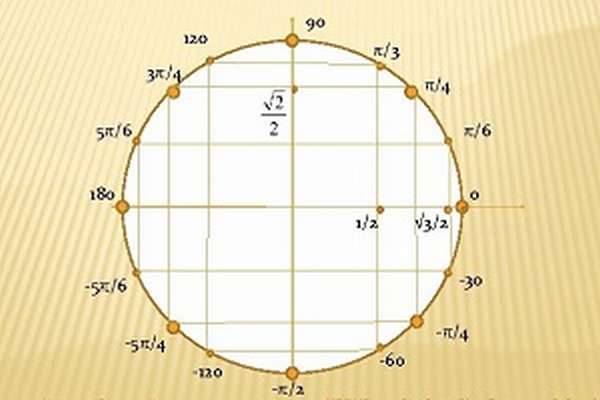
Исходя из этих особенностей, определяется числовой знак функции, позволяющий определить ее четность и нечетность. Кроме того, на ней следует отметить углы следующим образом: 0 и 2ПИ соответствует точке с координатами (1;0), ПИ/2 — (0;1), ПИ — (-1;0) и 3ПИ/2 — (0;-1).
Готовый макет
Для решения задач специалисты рекомендуют иметь рабочий и готовый макеты тригонометрических окружностей. Первый применяется для нахождения значений нестандартных углов (например, синуса 185 градусов). Тригонометрическим кругом (рис. 1) удобно пользоваться в том случае, когда значение угла является стандартным (90, 60 и т. д.).
Рисунок 1. Готовый макет тригонометрического круга синусов и косинусов.
Для нахождения необходимых значений объединяют две фигуры — единичную окружность и прямоугольный треугольник. Гипотенуза последнего равна 1 и соответствует радиусу окружности. Ось ОХ — косинусы, ОУ — синусы. С помощью этого «инструмента» определение синусов и косинусов становится намного проще. Для нахождения значения sin(30) необходимо воспользоваться следующим алгоритмом:
- Отметить угол на окружности и достроить его до прямоугольного треугольника.
- Если катет лежит напротив угла в 30 градусов, то он равен 0,5 от длины гипотенузы.
- sin(30) = 1 * 0,5 = 0,5.
Для нахождения косинуса необходимо использовать основное тригонометрическое тождество, которое связывает sin и cos: (sin(a))^2 + (cos(a))^2 = 1. Из равенства величина cos(30) = sqrt[1 — (sin(30))^2]= sqrt[1 — 0,5^2] = sqrt(3) / 2.
Однако после всех вычислений следует выбрать знак функции. В данном случае угол находится в первой четверти. Следовательно, функция имеет положительный знак. Для нахождения тангенса и котангенса можно воспользоваться следующими формулами: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a). Подставив значения синуса и косинуса, можно определить значение tg: tg(30) = 0,5 / (sqrt(3) / 2) = 1 / sqrt(3) = sqrt(3) / 3. Тогда котангенс можно найти двумя способами:
- Через известный тангенс: ctg(30) = 1 / (1 / sqrt(3)) = sqrt(3).
- Использовать основное отношение: ctg(30) = (sqrt(3) / 2) / (1/2) = sqrt(3).
Вычислить значения синуса и косинуса для угла 60 градусов очень просто. Для этого нужно воспользоваться основными тождествами: sin(60) = сos(30) = sqrt(3) / 2, cos(60) = sin(30) = 1/2, tg(30) = ctg(60) = sqrt(3) / 3, tg(60) = ctg(30) = sqrt(3). Значения для 45 градусов определяются следующим образом:
- Прямоугольный треугольник с углом 45 градусов является равносторонним (катеты равны).
- (sin(45))^2 + (cos(45))^2 = 1.
- 2 * (sin(45))^2 = 1.
- sin(45) + cos(45) = sqrt(2) / 2.
Тангенс и котангенс равен 1. Если угол равен 90, то необходимо внимательно посмотреть на рисунок 1. Следовательно, sin(90) = 1, cos(90) = 0, tg(90) = 1 и ctg(90) не существует. Линия тангенса на окружности не отображается. В этом случае нужно пользоваться основными тригонометрическими тождествами.
Правила использования
Инструмент позволяет легко и быстро находить значения тригонометрических функций любых углов. Если при решении задачи требуется найти sin(270), то нужно выполнить простые действия:
- Пройти против часовой стрелки (положительное направление) 180 градусов, а затем еще 90.
- На оси синусов значение составляет -1 (точка лежит на оси).
Существуют задачи, в которых угол представлен отрицательным значением. Например, нужно определить синус, косинус, тангенс и котангенс угла (-7ПИ/6). В некоторых случаях заданное значение следует перевести в градусы: -7ПИ/6 = -210 (градусам). Если в условии отрицательный угол, то движение следует осуществлять по часовой стрелке от нулевого значения (пройти полкруга, а затем еще 30). Можно сделать вывод о том, что значение -210 соответствует 30. Следовательно, синус вычисляется следующим образом: sin(-210) = -(sin(ПИ + 30)) = — 1/2, cos(-210) = sqrt(3)/2, tg(-210) = sqrt(3)/3 и ctg(-210) = sqrt(3).
Пример случая, когда нет необходимости переводить радианы в градусы, является следующим: нужно вычислить значения тригонометрических функций угла 5ПИ/4. Необходимо расписать значение угла таким образом: 5ПИ/4 = ПИ + ПИ/4. Против часовой стрелки следует пройти половину круга (ПИ), а затем его четвертую часть (ПИ/4). Далее нужно спроецировать координаты точки на ось синусов и косинусов. Это соответствует значению sqrt(2)/2. Тангенс и котангенс заданного угла будут равны 1.
Встречаются задачи, в которых значение угла превышает 360 градусов. Например, требуется найти значения тригонометрических функций угла (-25ПИ/6). Для решения необходимо разложить угол следующим образом: (-25ПИ/6) = — (4ПИ + ПИ/6). Можно не делать обороты, поскольку 4ПИ соответствует двойному обороту и возврату в точку (-ПИ/6). Это объясняется периодом функций синуса и косинуса, который равен 2ПИ. Значения функций sin, сos, tg и ctg равны следующим значениям: — 1/2, sqrt(3)/2, sqrt(3)/3 и sqrt(3) соответственно.
Таким образом, тригонометрический круг позволяет оптимизировать вычисления в дисциплинах с физико-математическим уклоном, в которых используются тригонометрические функции. Не имеет смысла устанавливать дополнительное программное обеспечение, пользоваться таблицами, поскольку это занимает некоторое время. При помощи этого «универсального инструмента» можно найти значение любого угла.
Основные значения тригонометрических функций. Часть 2
Продолжение (начало здесь)
Перевод радиан в градусы и градусы в радианы
На тригонометрическом круге помимо углов в градусы мы наблюдаем радианы.
 Подробнее про радианы:+ показать
Подробнее про радианы:+ показать
 , то очевидно, что в окружности укладывается
, то очевидно, что в окружности укладывается  радиан, то есть
радиан, то есть  радиан.
радиан.
1 рад ≈ 57,295779513° ≈ 57°17′44,806″ ≈ 206265″.
Все знают, что  радиан – это
радиан – это 
Так вот, например,  , а
, а  . Так, мы научились переводить радианы в углы.
. Так, мы научились переводить радианы в углы.
Теперь наоборот, давайте переводить градусы в радианы.
Допустим, нам надо перевести  в радианы. Нам поможет пропорция. Поступаем следующим образом:
в радианы. Нам поможет пропорция. Поступаем следующим образом:
Так как,  радиан, то заполним таблицу:
радиан, то заполним таблицу:

Откуда 
Тренируемся находить значения синуса и косинуса по кругу
Давайте еще уточним следующее.
Ну хорошо, если нас просят вычислить, скажем,  , – здесь обычно путаницы не возникает – все начинают первым делом искать
, – здесь обычно путаницы не возникает – все начинают первым делом искать  на круге.
на круге.
А если просят вычислить, например,  … Многие, вдруг, начинают не понимают где искать этот ноль… Частенько ищут его в начале координат. Почему?
… Многие, вдруг, начинают не понимают где искать этот ноль… Частенько ищут его в начале координат. Почему?
1) Давайте договоримся раз и навсегда! То, что стоит после  или
или  – это аргумент=угол, а углы у нас располагаются на круге, не ищите их на осяx! (Просто отдельные точки попадают и на круг, и на ось…) А сами значения синусов и косинусов – ищем на осях!
– это аргумент=угол, а углы у нас располагаются на круге, не ищите их на осяx! (Просто отдельные точки попадают и на круг, и на ось…) А сами значения синусов и косинусов – ищем на осях!
2) И еще! Если мы от точки «старт» отправляемся против часовой стрелки (основное направление обхода тригонометрического круга), то мы откладываем положительные значения углов, значения углов растут при движении в этом направлении.
Если же мы от точки «старт» отправляемся по часовой стрелке, то мы откладываем отрицательные значения углов.
Пример 1.
Найти значение  .
.
Решение:
Находим на круге  . Проецируем точку на ось синусов (то есть проводим перпендикуляр из точки
. Проецируем точку на ось синусов (то есть проводим перпендикуляр из точки  к оси синусов (оу)).
к оси синусов (оу)).

Приходим в 0. Значит,  .
.
Пример 2.
Найти значение  .
.
Решение:
Находим на круге  (проходим против часовой стрелки
(проходим против часовой стрелки  и еще
и еще  ). Проецируем точку на ось синусов (а она уже лежит на оси синусов).
). Проецируем точку на ось синусов (а она уже лежит на оси синусов).

Попадаем в -1 по оси синусов.
Значит,  .
.
Заметим, за точкой  «скрываются» такие точки, как
«скрываются» такие точки, как  (мы могли бы пойти в точку, помеченную как
(мы могли бы пойти в точку, помеченную как  , по часовой стрелке, а значит появляется знак минус),
, по часовой стрелке, а значит появляется знак минус),  и бесконечно много других.
и бесконечно много других.
Можно привести такую аналогию:
Представим тригонометрический круг как беговую дорожку стадиона.

Вы ведь можете оказаться в точке «Флажок», отправляюсь со старта против часовой стрелки, пробежав, допустим, 300 м. Или пробежав, скажем, 100м по часовой стрелке (считаем длину дорожки 400 м).
А также вы можете оказаться в точке «Флажок» (после «старт»), пробежав, скажем, 700 м, 1100 м, 1500 м и т. д. против часовой стрелки. Вы можете оказаться в точке «Флажок», пробежав 500 м или 900 м и т. д. по часовой стрелке от «старт».
Разверните мысленно беговую дорожку стадиона в числовую прямую. Представьте, где на этой прямой будут, например, значения 300, 700, 1100, 1500 и т.д. Мы увидим точки на числовой прямой, равноотстоящие друг от друга. Свернем обратно в круг. Точки «cлепятся» в одну.
Так и с тригонометрическим кругом. За каждой точкой скрыто бесконечно много других.
Скажем, углы  ,
,  ,
,  ,
,  и т.д. изображаются одной точкой. И значения синуса, косинуса в них, конечно же, совпадают. (Вы заметили, что мы прибавляли/вычитали
и т.д. изображаются одной точкой. И значения синуса, косинуса в них, конечно же, совпадают. (Вы заметили, что мы прибавляли/вычитали  или
или  ? Это период для функции синус и косинус.)
? Это период для функции синус и косинус.)
Пример 3.
Найти значение  .
.
Решение:
Переведем для простоты  в градусы
в градусы
 (позже, когда вы привыкнете к тригонометрическому кругу, вам не потребуется переводить радианы в градусы):
(позже, когда вы привыкнете к тригонометрическому кругу, вам не потребуется переводить радианы в градусы):

Двигаться будем по часовой стрелки от точки  Пройдем полкруга (
Пройдем полкруга ( ) и еще
) и еще 
Понимаем, что значение синуса  совпадает со значением синуса
совпадает со значением синуса  и равняется
и равняется 
 .
.
Заметим, если б мы взяли, например,  или
или  и т.д., то мы получили бы все тоже значение синуса.
и т.д., то мы получили бы все тоже значение синуса.
Пример 4.
Найти значение  .
.
Решение:
 Все же, не будем переводить радианы в градусы, как в предыдущем примере.
Все же, не будем переводить радианы в градусы, как в предыдущем примере.
 .
.
То есть нам надо пройти против часовой стрелки полкруга и еще четверть полкруга и спроецировать полученную точку на ось косинусов (горизонтальная ось).

Пример 5.
Найти значение  .
.
Решение:
Как отложить на тригонометрическом круге  ?
?

 Если мы пройдем
Если мы пройдем  или
или  , да хоть
, да хоть  , мы все равно окажемся в точке, которую мы обозначили как «старт». Поэтому, можно сразу пройти в точку на круге
, мы все равно окажемся в точке, которую мы обозначили как «старт». Поэтому, можно сразу пройти в точку на круге 

Пример 6.
Найти значение  .
.
Решение:

Мы окажемся в точке  (
( приведет нас все равно в точку ноль). Проецируем точку круга
приведет нас все равно в точку ноль). Проецируем точку круга  на ось косинусов (смотри тригонометрический круг), попадаем в
на ось косинусов (смотри тригонометрический круг), попадаем в  . То есть
. То есть  .
.
Тригонометрический круг – у вас в руках
Вы же уже поняли, что главное – запомнить значения тригонометрических функций первой четверти. В остальных четвертях все аналогично, нужно лишь следить за знаками. А «цепочку-лесенку» значений тригонометрических функций, вы, надеюсь уже не забудете. 
Как находить значения тангенса и котангенса основных углов смотрите здесь.
 После чего, познакомившись с основными значениями тангенса и котангенса, вы можете пройти тест по теме «Нахождение значений косинусов, синусов, тангенсов и котангенсов различных углов»
После чего, познакомившись с основными значениями тангенса и котангенса, вы можете пройти тест по теме «Нахождение значений косинусов, синусов, тангенсов и котангенсов различных углов»
Ссылочка на пустой шаблон круга. Тренируйтесь!
Тригонометрический круг. Основные значения тригонометрических функций
Если вы уже знакомы с тригонометрическим кругом, и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, тригонометрический круг:

Мы же здесь будем все подробно разбирать шаг за шагом.
Тригонометрический круг – не роскошь, а необходимость
 Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений.
Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!
Нас выручит тригонометрический круг! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул, чему равен синус, скажем, 300 градусов, или -45.

Никак?.. можно, конечно, подключить формулы приведения… А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!
А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.
Знакомство с тригонометрическим кругом
Давайте по порядку.
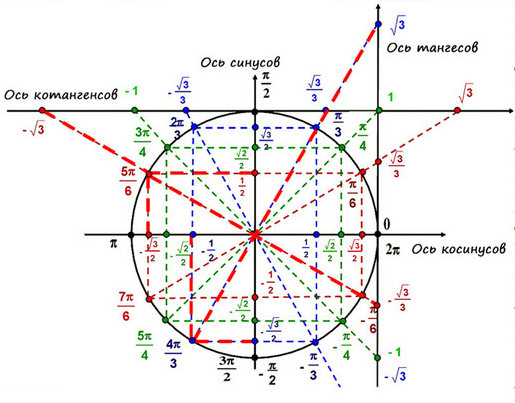
Сначала выпишем вот такой ряд чисел:

А теперь такой:

И, наконец, такой:

Конечно, понятно, что, на самом-то деле, на первом месте стоит  , на втором месте стоит
, на втором месте стоит  , а на последнем –
, а на последнем –  . То есть нас будет больше интересовать цепочка
. То есть нас будет больше интересовать цепочка  .
.
Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».
И зачем оно нам?
Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы  .
.
 Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Это почему же, спросите вы?
Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.

Треугольник АОВ – прямоугольный, в нем  . А мы знаем, что против угла в
. А мы знаем, что против угла в  лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть 1).
лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть 1).
Значит, АВ= (а следовательно, и ОМ=
(а следовательно, и ОМ= ). А по теореме Пифагора
). А по теореме Пифагора 

Надеюсь, уже что-то становится понятно?
Наконец, что такое синус, косинус в прямоугольном треугольнике?


Так вот точка В и будет соответствовать значению  , а точка М – значению
, а точка М – значению 
Аналогично с остальными значениями первой четверти.
Как вы понимаете, привычная нам ось (ox) будет осью косинусов, а ось (oy) – осью синусов. Про тангенс и котангенс позже.
Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг, без которого никуда в тригонометрии.

А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье.
Тригонометрический круг со всеми значениями, числовая окружность синус косинус тангенс котангенс, как пользоваться тригонометрическим кругом
Тригонометрический круг один из основных элементов геометрии для решения уравнений с синусом, косинусом, тангенсом и котангенсом.
Каково определение данного термина, как строить данный круг, как определить четверть в тригонометрии, как узнать углы в построенном тригонометрическом круге — об этом и многом другом расскажем далее.
Тригонометрическая окружность
Тригонометрическим видом числовой окружности в математике является круг, имеющий одинарный радиус с центром в начале координатной плоскости. Как правило, она образована пространством из формул синуса с косинусом, тангенсом и котангенсом на системе координат.
Назначение такой сферы с n-мерным пространством в том, что благодаря ей могут быть описаны тригонометрические функции. Выглядит она просто: круг, внутри которого находится система координат и множественные прямоугольного вида треугольники, образованные из этой окружности по тригонометрическим функциям.
Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике
Прямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты две стороны треугольника, которые прилегают к углу 90°, а третья гипотенуза, она всегда длиннее катетов.
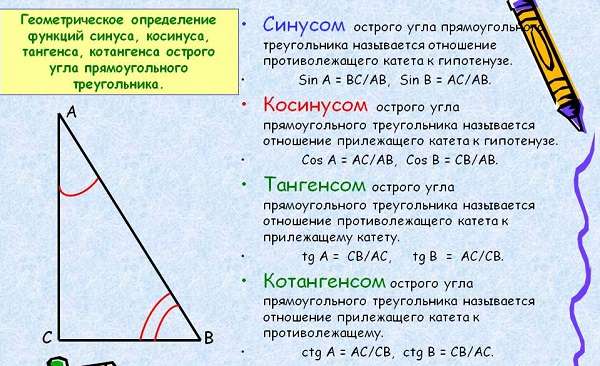
Синусом называется отношение одного из катетов к гипотенузе, косинусом отношение другого катета к ней, а тангенсом отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение.
Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a).
Построение единичной окружности
Построение единичной окружности сводится к ее прорисовке с единичным радиусом в центре системы координат. Затем для построения нужно отсчитать углы и, двигаясь против часовой стрелки, обойти по целому кругу, проставляя соответствующие им линии координаты.
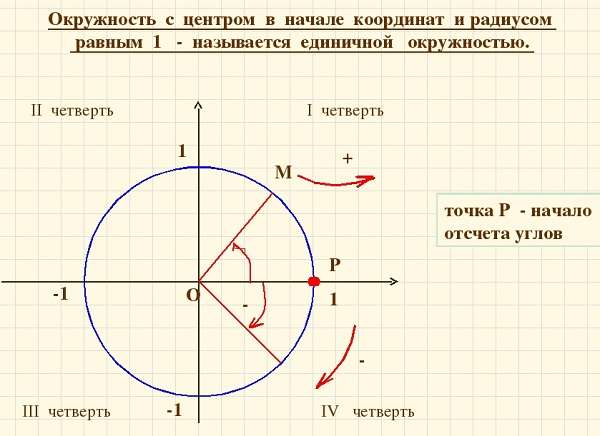
Начинается построение после черчения круга и установки точки в его центре с размещения системы координат ОХ. Точкой О сверху оси координат является синус, а Х косинус. Соответственно они являются абсциссой и ординатой. Затем нужно провести измерения ∠. Они проводятся градусами и радианами.
Сделать перевод этих показателей просто полный круг равен двум пи радиан. Угол от нуля против часовой стрелки идет со знаком +, а ∠ от 0 по часовой стрелке со знаком -. Положительные и отрицательные значения синуса с косинусом повторяются каждый оборот круга.
Углы на тригонометрическом круге
Для того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто.
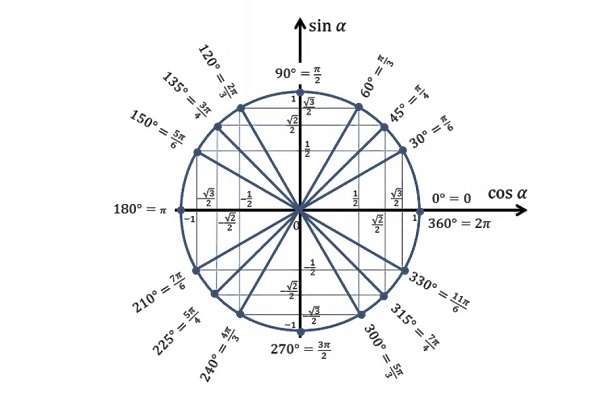
Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три 360°. Как пользоваться этой информацией?
Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними.
Измеряются углы в радианах:
- от 0 до 90° значения углов от 0 до ∏/2,
- от 90 до 180° значения углов от ∏/2 до ∏,
- от 180 до 270° от ∏ до 3*∏/2,
- последняя четверть от 2700 до 3600 — значения от 3*∏/2 до 2*∏.
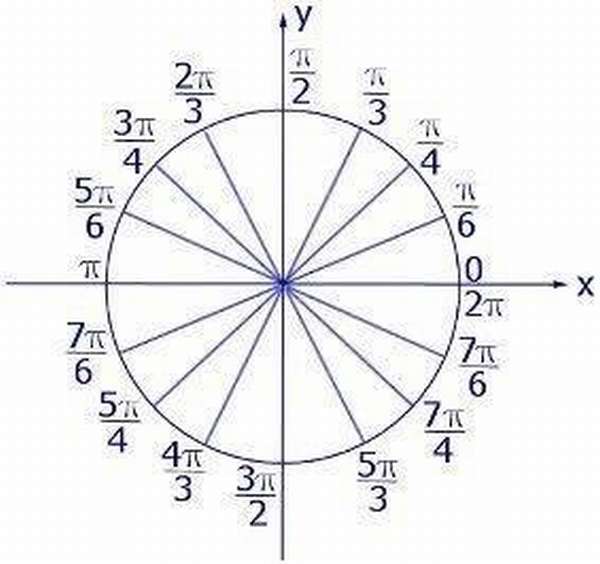
Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке.
Перевод углов из градусов в радианы
Углы возможно измерить в градусах либо радианах. Требуется осознавать связь между обоими значениями. Эта взаимосвязь выражена в тригонометрии с помощью специальной формулы. Благодаря пониманию связи, можно научиться оперативным образом управлять углами и переходить от градусов к радианам обратно.
Для того чтобы точно узнать, чему равен один радиан, можно воспользоваться следующей формулой:
1 рад. = 180 / ∏ = 180 / 3,1416 = 57,2956
В конечном итоге, 1 радиан равен 57°, а в 1 градусе 0,0175 радиан:
1 градус = (∏ /180) рад. = 3,1416 / 180 рад. = 0,0175 рад.

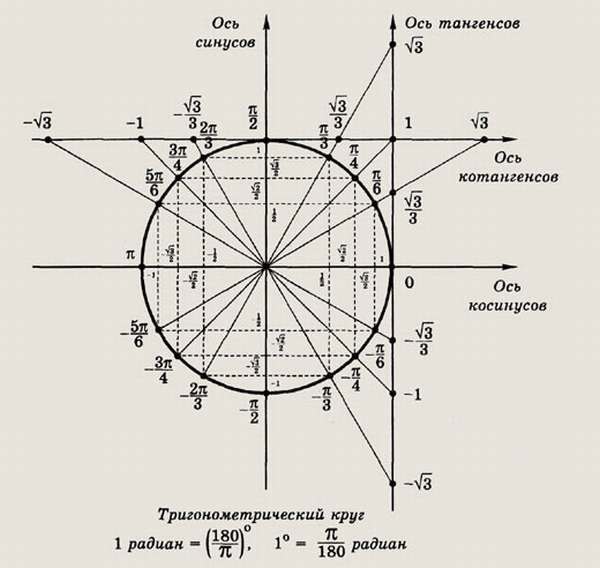
Косинус, синус, тангенс, котангенс на тригонометрической окружности
Косинус с синусом, тангенсом и котангенсом на тригонометрической окружности функции углов альфа от 0 до 360 градусов. Каждая функция обладает положительным или отрицательным значением в зависимости от того, какая величина у угла. Они символизируют отношения к прямоугольным треугольникам, образованным в круге.

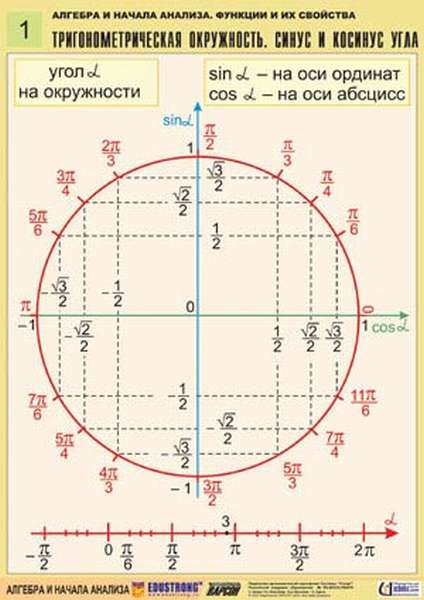

Заключение
В целом, тригонометрическая окружность – единичная окружность, необходимая для решения соответствующих задач и описания функций. Она состоит из многих составляющих, запомнить которые нужно обязательно для правильного решения последующих задач.
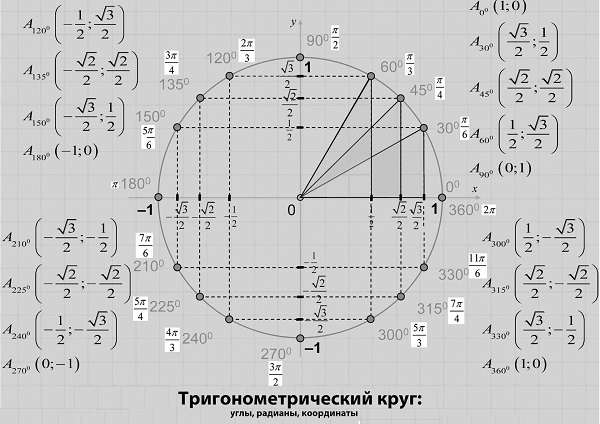
Тригонометрический круг синус и косинус
Тригонометрический круг представляет значения тригонометрических функций синус (sin) и косинус (cos) в виде координат точек единичной окружности при различных значениях угла альфа в градусах и радианах.Поскольку я сам вечно путаюсь при переводе координат точек окружности в синусы и косинусы, для простоты все значения косинусов (cos) для углов от 0 до 360 градусов (от 0 пи до 2 пи) подчеркнуты зеленой черточкой. Даже при распечатке этого рисунка тригонометрического круга на черно-белом принтере все значения косинуса будут подчеркнуты, а значения синуса будут без подчеркивания. Если вам интересно, то можете посмотреть отдельные тригонометрические круги для синуса и косинуса.
Напротив указанных углов на окружности расположены точки, а в круглых скобках указаны координаты этих точек. Первой записана координата Х (косинус)
Давайте проведем обзорную экскурсию по этому уголку математического зоопарка. Прежде всего, нужно отметить, что здесь присутствует декартова система координат — одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая — вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы — cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы — sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы — на диване перед телевизором по горизонтали.
В этой системе координат нарисована окружность радиусом, равным единице. Центр окружности находится в начале системы координат — там, где в центе рисунка пересекаются оси абсцисс (ось Х) и ординат (ось У).
Из центра окружности проведены тоненькие черточки, которые показывают углы 30, 45, 60, 120, 135, 150, 210, 225, 240, 300, 315, 330 градусов. В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.
Линии углов заканчиваются точками на единичной окружности. Возле каждой точки, в круглых скобках, записаны координаты этой точки. Первой записана координата Х, которая соответствует косинусу угла, образовавшего эту точку. Второй записана координата У этой точки, что соответствует значению синуса угла. По картинке довольно легко находить синус и косинус заданного угла и наоборот, по заданному значению синуса или косинуса, можно легко найти значение угла. Главное, не перепутать синус с косинусом.
Обращаю особое внимание на тот факт, что если вы по значению синуса или косинуса ищите угол, обязательно нужно дописывать период угла. Математики очень трепетно относятся к этому аппендициту тригонометрических функций и при его отсутствии могут влепить двойку за, казалось бы, правильный ответ. Что такое период при нахождении угла по значению тригонометрической функции? Это такая штучка, которая придумана математиками специально для того, чтобы запутываться самим и запутывать других. Особенно блондинок. Но об этом мы поговорим как-нибудь в другой раз.
Всё, что собрано в кучку на рисунке тригонометрического круга синуса и косинуса, можно внимательно рассмотреть на отдельных картинках с портретами синуса 0, 30, 45 градусов (ссылки на отдельные странички я буду добавлять по мере увеличения фотогалереи синусов и косинусов).
Найти решение:
Синусы и косинусы круг — здесь картинка во всей своей тригонометрической красе.
Угол 120 градусов в радианах — равен 2/3 пи или 2 пи деленное на 3, на картинке очень красиво нарисовано.
Значения синусов косинусов углов в радианах — на картинке есть такие, надеюсь, именно те углы, которые вы ищете.
Значение косинуса угла в 45 градусов — равно корню из двух деленному на два, можете проверить по рисунку.
Тригонометрическая окружность — я не совсем уверен, что представленная на картинке окружность является тригонометрической, но что-то от тригонометрии в этой окружности определенно есть, например, синусы и косинусы на окружности — вылитая тригонометрия.
Тригонометрический круг рисунок — есть здесь такой. Правда, не самый красивый рисунок, можно нарисовать гораздо красивее и понятнее. Мне минус в репутацию — почему я до сих пор не нарисовал его для блондинок? Представляете ситуацию в картинной галерее будущего: экскурсовод объясняет группе школьников «Перед вами всемирно известное полотно «Тригонометрическая мадонна с единичным отрезком на руках» — картина гениального художника эпохи Раннего Математического Возрождения …» Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!
Круг синусов и косинусов — именно такой круг совершенно случайно оказался здесь на картинке.
Угол 9 градусов сколько это в пи — в пи это 1/20 или пи/20.
Решение: для перевода градусов в пи радиан, нужно имеющиеся у нас градусы разделить на 180 градусов (это 1 пи радиан). У нас получается 9/180 = 1/20
Ответ: 9 градусов = 1/20 пи.
Синус это вверх или в сторону — синус — это вверх, в сторону — это косинус.
Комментарии к этой статье запрещены. Из-за огромного их количества мои ответы на ваши вопросы о тригонометрическом круге уже не публикуются. Вопросы можете задавать в комментариях к другим страницам. Постараюсь решить проблему за счет удаления части комментариев, тем самым освобожу место для новых.
Тригонометрический круг со всеми значениями

Тригонометрический круг — один из основных элементов геометрии для решения уравнений с синусом, косинусом, тангенсом и котангенсом.
Каково определение данного термина, как строить данный круг, как определить четверть в тригонометрии, как узнать углы в построенном тригонометрическом круге — об этом и многом другом расскажем далее.
Тригонометрическая окружность
Тригонометрическим видом числовой окружности в математике является круг, имеющий одинарный радиус с центром в начале координатной плоскости. Как правило, она образована пространством из формул синуса с косинусом, тангенсом и котангенсом на системе координат.

Назначение такой сферы с n-мерным пространством в том, что благодаря ей могут быть описаны тригонометрические функции. Выглядит она просто: круг, внутри которого находится система координат и множественные прямоугольного вида треугольники, образованные из этой окружности по тригонометрическим функциям.
Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике
Прямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты — две стороны треугольника, которые прилегают к углу 90°, а третья — гипотенуза, она всегда длиннее катетов.

Синусом называется отношение одного из катетов к гипотенузе, косинусом — отношение другого катета к ней, а тангенсом — отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение.
Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a).
Построение единичной окружности
Построение единичной окружности сводится к ее прорисовке с единичным радиусом в центре системы координат. Затем для построения нужно отсчитать углы и, двигаясь против часовой стрелки, обойти по целому кругу, проставляя соответствующие им линии координаты.

Начинается построение после черчения круга и установки точки в его центре с размещения системы координат ОХ. Точкой О сверху оси координат является синус, а Х — косинус. Соответственно они являются абсциссой и ординатой. Затем нужно провести измерения ∠. Они проводятся градусами и радианами.
Сделать перевод этих показателей просто — полный круг равен двум пи радиан. Угол от нуля против часовой стрелки идет со знаком +, а ∠ от 0 по часовой стрелке со знаком -. Положительные и отрицательные значения синуса с косинусом повторяются каждый оборот круга.
Углы на тригонометрическом круге
Для того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто.

Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три — 360°. Как пользоваться этой информацией?
Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними.
Измеряются углы в радианах:
- от 0 до 90° — значения углов от 0 до ∏/2;
- от 90 до 180° — значения углов от ∏/2 до ∏;
- от 180 до 270° — от ∏ до 3*∏/2;
- последняя четверть от 2700 до 3600 — значения от 3*∏/2 до 2*∏.

Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке.
Перевод углов из градусов в радианы
Углы возможно измерить в градусах либо радианах. Требуется осознавать связь между обоими значениями. Эта взаимосвязь выражена в тригонометрии с помощью специальной формулы. Благодаря пониманию связи, можно научиться оперативным образом управлять углами и переходить от градусов к радианам обратно.
Для того чтобы точно узнать, чему равен один радиан, можно воспользоваться следующей формулой:
1 рад. = 180 / ∏ = 180 / 3,1416 = 57,2956
В конечном итоге, 1 радиан равен 57°, а в 1 градусе 0,0175 радиан:
1 градус = (∏ /180) рад. = 3,1416 / 180 рад. = 0,0175 рад.

Косинус, синус, тангенс, котангенс на тригонометрической окружности
Косинус с синусом, тангенсом и котангенсом на тригонометрической окружности — функции углов альфа от 0 до 360 градусов. Каждая функция обладает положительным или отрицательным значением в зависимости от того, какая величина у угла. Они символизируют отношения к прямоугольным треугольникам, образованным в круге.




Заключение
В целом, тригонометрическая окружность – единичная окружность, необходимая для решения соответствующих задач и описания функций. Она состоит из многих составляющих, запомнить которые нужно обязательно для правильного решения последующих задач.
Тригонометрические уравнения
 Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений
Градусы и радианы
Знакомство с тригонометрической окружностью
Повороты на тригонометрической окружности
Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».
Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах.
1 радиан = 180/π ≈ 57,3 градусов
Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.
Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!
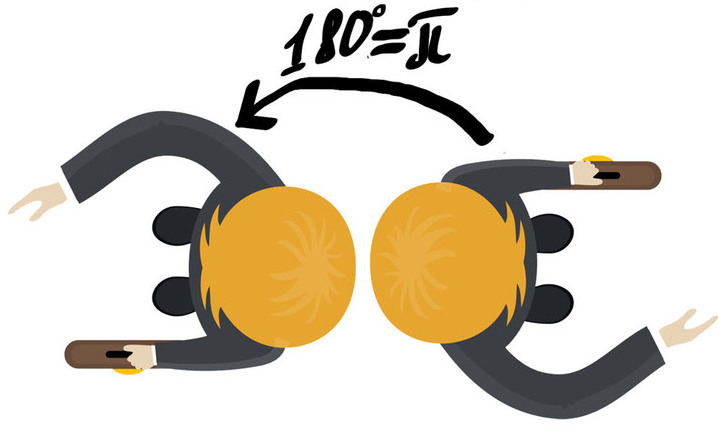
О графиках синуса, косинуса и тангеса поговорим в другой статье.
А сейчас начем с декартовой (прямоугольной) системы координат.
Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.
На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:
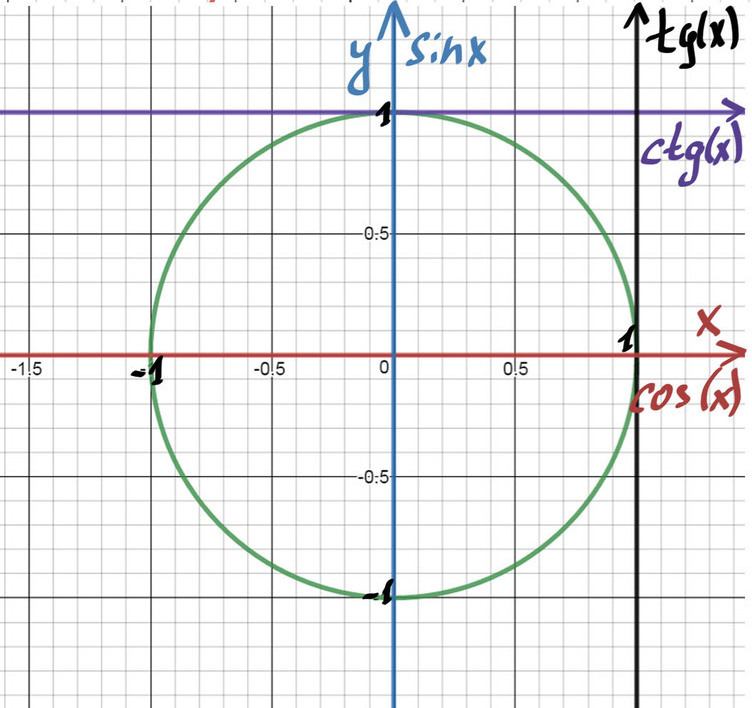
Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.
А теперь отметим основные значения градусов и радиан на окружности.
Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.
Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).
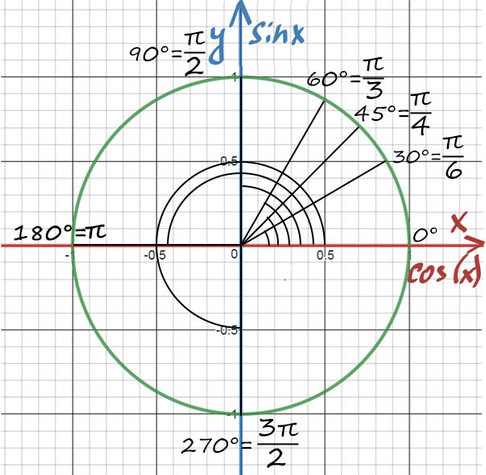
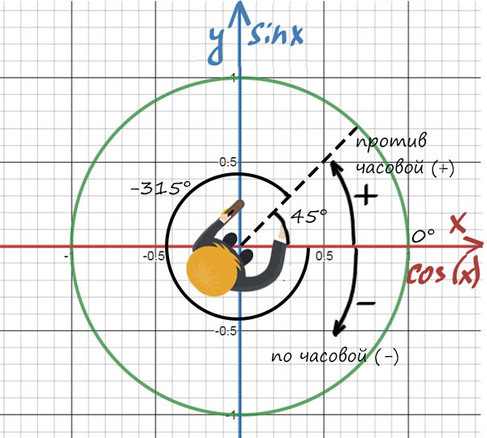
А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):

От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).
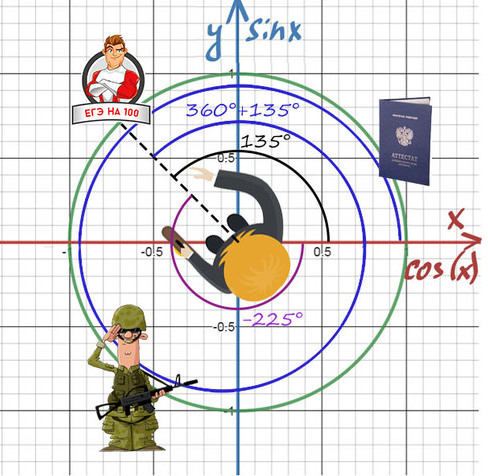
Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).
Главное — направление, куда мы будем смотреть, а не угол!
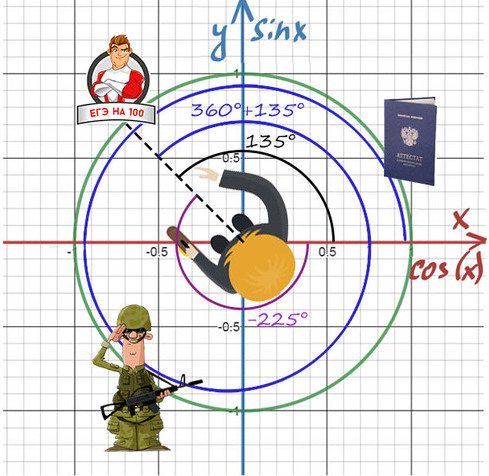
Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!
Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°…
А теперь у тебя есть два пути:
Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:
А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.
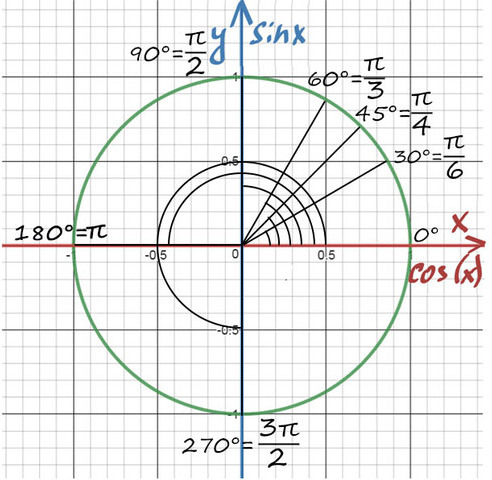
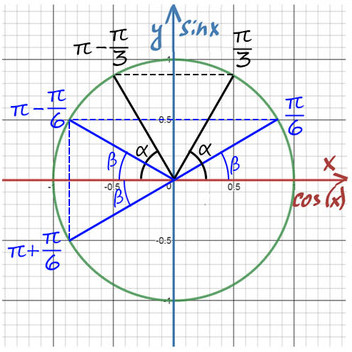
Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.
Сразу попробуем разобрать на примере:
Пример №1. cos(x) = ½
1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.
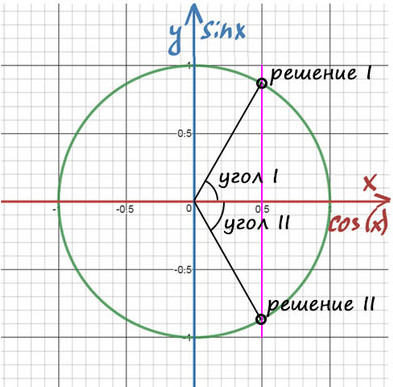
2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.
Дело за малым — найти эти углы.
Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.
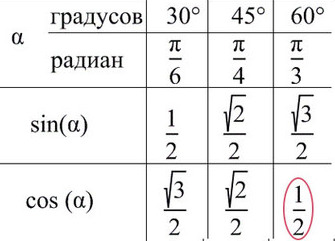
Или запомнить такой прием:
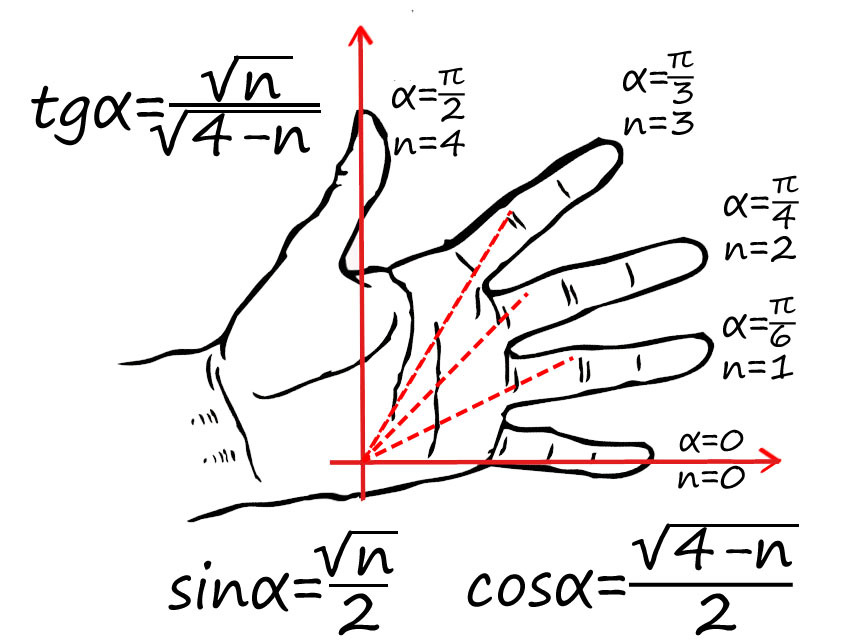
Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).
Например, требуется найти sin(π/2): π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.
cos(π/4) — ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.
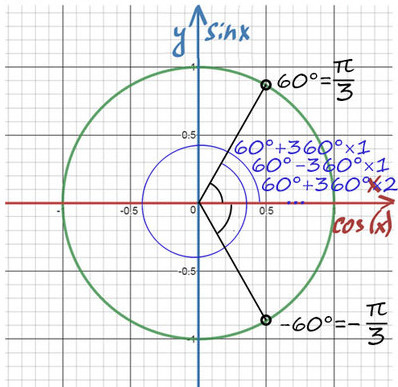
При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).
Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).
И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:
Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на …=-225°=135°=495°=…
То же самое и здесь! Разные углы могут отражать одно и то же направление.
Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.
Таким образом, попасть в первое направление 60° можно: …,60°-360°, 60°, 60°+360°,…
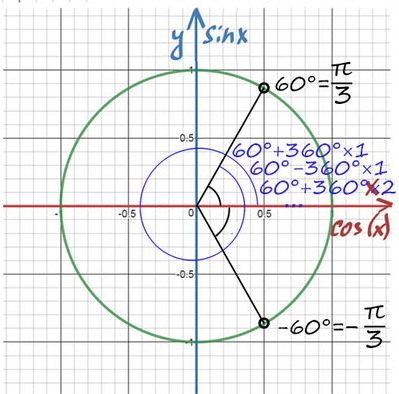
И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)
Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.
Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.
Ответ: x = π/3 + 2πn, x= −π/3 + 2πk, (n, k)∈Ζ.
Пример №2. 2sinx = √2
Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2
1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.
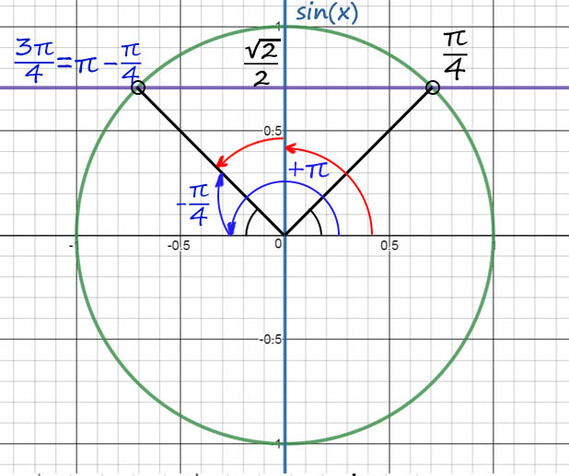
2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.
Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.
И еще не забудем добавить +2πn, n∈Ζ.
Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.
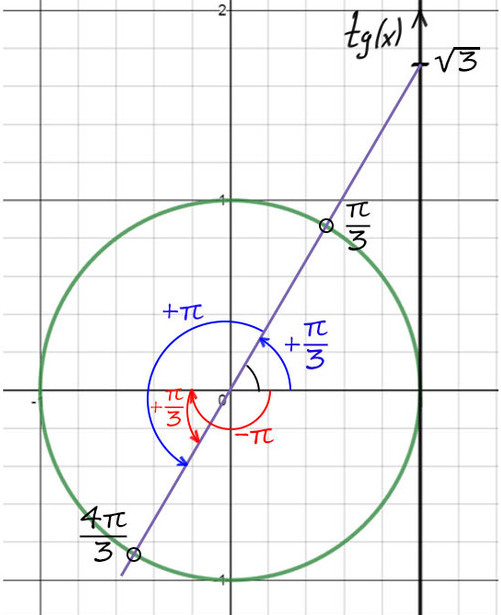
Пример №3. tg(x + π/4) = √3
Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.
tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.
1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.
2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.
По мнемоническому правилу при тангенсе √3 первое значение — это π/3.
3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.
4) Но мы нашли только y, вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.
Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.
Теперь корни на окружности будут здесь:
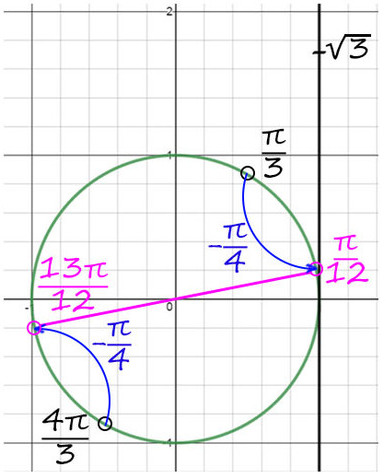
Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.
Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).
Ответ можно записать и так: π/12 + πn, n∈Ζ.
Пример №4: −10ctg(x) = 10
Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.
1) Проведем прямую через эту точку и начало координат.
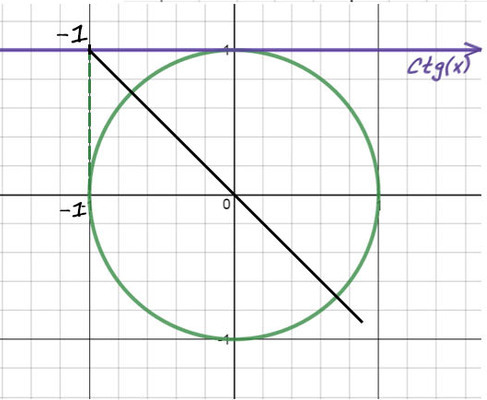
2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).
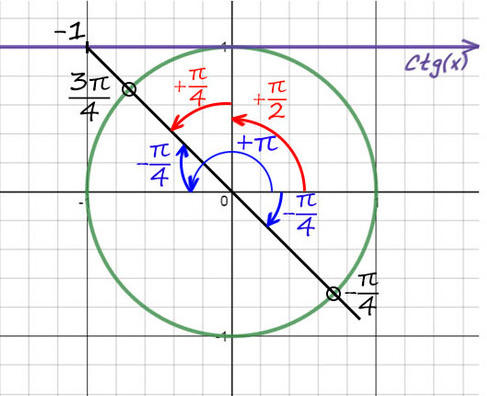
Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π…) так намного меньше шансов запутаться.
Не забываем добавить к каждой точке 2πk.
Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.
Алгоритм решения тригонометрических уравнений (на примере cos(x) = −√3/2):
- Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
- Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
- Точки пересечения с окружностью и будут являться корнями уравнения.
- Значение одной точки (без разницы, как в нее попадете) +2πk.
Будь в курсе новых статеек, видео и легкого математического юмора.
Пи
Нарисуйте круг диаметром (полностью поперек круга) 1
Тогда окружность (полностью по кругу) равна 3,14159265 … число, известное как Pi
Pi (произносится как «пирог») часто пишется с использованием греческого символа π
.Определение π:
Окружность
, разделенная на Диаметр
окружности.
Длина окружности, деленная на диаметр круга, всегда равна π, независимо от того, насколько большой или малый круг!
Чтобы помочь вам вспомнить, что такое π … просто нарисуйте эту диаграмму.
В поисках Пи себя
Нарисуйте круг или используйте что-нибудь круглое, например тарелку.
Измерьте по краю (окружность ):
Получил 82 см
Измерьте поперек круга (диаметр ):
Получил 26 см
Делить:
82 см / 26 см = 3.1538 …
Это довольно близко к π. Может если точнее замерил?
Использование Pi
Мы можем использовать π, чтобы найти окружность, когда мы знаем диаметр
Окружность = π × Диаметр
Пример: вы ходите по кругу диаметром 100 м. Как далеко вы прошли?
Пройденное расстояние = Окружность
= π × 100 м
= 314,159 … м
= 314 м (с точностью до м)
Также мы можем использовать π, чтобы найти диаметр, если нам известна окружность
Диаметр = Окружность / π
Пример: Сэм измерил 94 мм на внешней стороне трубы… каков его диаметр?
Диаметр = Окружность / π
= 94 мм / π
= 29,92 … мм
= 30 мм (с точностью до мм)
Радиус
Радиус составляет половину диаметра, поэтому мы также можем сказать:
Для круга радиусом из 1
Расстояние на полпути вокруг окружности равно π = 3,14159265 …
цифр
π примерно равно:
3.14159265358979323846…
Цифры продолжаются без единого шаблона.
π было вычислено с точностью до пятидесяти триллионов десятичных знаков, но все еще нет , нет шаблона для цифр
Приближение
Быстрое и простое приближение для π — 22/7
22/7 = 3,1428571 …
Но, как видите, 22/7 — это , не совсем верно . На самом деле π не равно отношению любых двух чисел, что делает его иррациональным числом.
Действительно хорошее приближение, лучше, чем 1 часть из 10 миллионов, составляет:
355/113 = 3,1415929 …
(подумайте о «113355», косой чертой посередине «113/355», затем переверните «355/113»)
Резюме:
| 22/7 | = | 3,14 28571 … |
| 355/113 | = | 3,141592 9 … |
| π | = | 3.14159265 … |
Вспоминая цифры
Я обычно помню просто «3.14159», но вы также можете сосчитать буквы:
«Можно мне сегодня большую тару сливочного масла»
3 1 4 1 5 9 2 6 5
До 100 знаков после запятой
Вот π с первыми 100 десятичными знаками:
| 3,14159265358979323846264338327950288 4197169399375105820974944592307816 4062862089986280348253421170679… |
Расчет числа Пи самостоятельно
Есть много специальных методов, используемых для вычисления π, и вот один из них, который вы можете попробовать сами: он называется серия Нилаканта (в честь индийского математика, жившего в 1444–1544 годах).
Это продолжается вечно и имеет такую схему:
3+ 4 2 × 3 × 4 — 4 4 × 5 × 6 + 4 6 × 7 × 8 — 4 8 × 9 × 10 +…
(Обратите внимание на узор + и -, а также на узор чисел под линиями.)
Это дает следующие результаты:
| Срок | Результат (до 12 знаков после запятой) |
|---|---|
| 1 | 3 |
| 2 | 3,166666666667 |
| 3 | 3,133333333333 |
| 4 | 3.145238095238 |
| … | … и т. Д.! … |
Возьмите калькулятор (или используйте электронную таблицу) и посмотрите, сможете ли вы получить лучшие результаты.
День Пи
День числа Пи отмечается 14 марта. Март — 3-й месяц, поэтому он выглядит как 3/14
. ,Алгоритм— Как рассчитать точку на окружности круга?
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Что такое Пи? | Живая наука
Понять число Пи так же просто, как сосчитать до единицы, двух, 3,1415926535…
Хорошо, мы будем здесь на некоторое время, если будем продолжать в том же духе. Вот что важно: Пи (π) — это 16-я буква греческого алфавита, которая используется для обозначения наиболее широко известной математической константы.
По определению, пи — это отношение длины окружности к ее диаметру. Другими словами, пи равно длине окружности, деленной на диаметр (π = c / d). И наоборот, длина окружности равна pi, умноженному на диаметр (c = πd).Независимо от того, насколько большой или маленький круг, число Пи всегда будет одним и тем же. Это число равно примерно 3,14, но это немного сложнее. [10 удивительных фактов о пи]
Значение пи
Пи — иррациональное число, что означает, что это действительное число, которое не может быть выражено простой дробью. Это потому, что математики называют «бесконечной десятичной дробью» — после десятичной точки цифры идут вечно.
Начиная с математики, ученики знакомятся с числом «пи», равным 3.14 или 3.14159. Хотя это иррациональное число, некоторые используют рациональные выражения для оценки пи, например, 22/7 из 333/106. (Эти рациональные выражения имеют точность только до пары десятичных знаков.)
Хотя нет точного значения числа Пи, многие математики и любители математики заинтересованы в вычислении числа Пи с точностью до как можно большего числа цифр. Мировой рекорд Гиннеса по количеству цифр числа Пи принадлежит Раджвиру Мина из Индии, который в 2015 году называл число Пи с точностью до 70000 знаков после запятой (с завязанными глазами).Между тем, некоторые компьютерные программисты вычислили значение числа Пи более чем с 22 триллионами цифр. Подобные расчеты часто проводятся в День числа Пи, псевдопраздник, который отмечается каждый год 14 марта (3/14).
Цифры Пи
Первые 100 цифр Пи:
3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 7067
На первом сайте piday указан миллион цифр.
Жизнь пи
Пи была известна уже почти 4000 лет и была открыта древними вавилонянами.Табличка где-то между 1900-1680 годами до нашей эры. обнаружил, что пи равняется 3,125. Древние египтяне делали аналогичные открытия, о чем свидетельствует папирус Райнда 1650 г. до н. Э. В этом документе египтяне вычислили площадь круга по формуле, которая дает пи примерно 3,1605. Есть даже библейский стих, где кажется, что число пи было приблизительно равным:
И сделал он расплавленное море, в десять локтей от края до края; оно было кругом, и высота его была пять локтей; вокруг него было тридцать локтей. — 3 Царств 7:23 (версия короля Якова)
Первое вычисление числа Пи было выполнено Архимедом Сиракузским (287-212 до н.э.). Один из величайших математиков мира Архимед использовал теорему Пифагора, чтобы найти площади двух многоугольников. Архимед аппроксимировал площадь круга на основе площади правильного многоугольника, вписанного в круг, и площади правильного многоугольника, внутри которого был описан круг. Многоугольники в том виде, в каком их отображал Архимед, давали верхнюю и нижнюю границы площади круга, и он аппроксимировал число пи между 3 1/7 и 3 10/71.
Пи начал обозначаться символом пи (π) в 1706 году британским математиком Уильямом Джонсом. Джонс использовал 3,14159 в качестве вычисления числа пи.
Pi r в квадрате
В основах математики число пи используется для определения площади и длины окружности. Пи используется для определения площади путем умножения квадрата радиуса на пи. Итак, пытаясь найти площадь круга радиусом 3 сантиметра, π3 2 = 28,27 см. Поскольку круги естественным образом встречаются в природе и часто используются в других математических уравнениях, число «Пи» присутствует повсюду и используется постоянно.
Пи даже проник в литературный мир. Пилиш — это диалект английского языка, в котором количество букв в последовательных словах следует за цифрами пи. Вот пример из «Not A Wake» Майка Кейта, первой книги, когда-либо написанной полностью на пилише.
Теперь я падаю, усталый житель пригорода, в жидкости под деревьями, Дрейфую рядом с лесами, тлеющими красными в сумерках над Европой.
Теперь имеет 3 буквы, I имеет 1 букву, осень имеет 4 буквы, имеет 1 букву и т. Д. И т. Д.
Эта статья была обновлена 19 октября 2018 г. старшим писателем Live Science Брэндоном Спектором.
,Python все точки на окружности с заданным радиусом и центром
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
