Тригонометрическая окружность. Радианная мера угла
Тригонометрическая окружность, радианная мера угла. Тригонометрические функции произвольного угла
Синус, косинус произвольного угла
Чтобы понять, что такое тригонометрические функции, обратимся к окружности с единичным радиусом. Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР, который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ. Так как окружность имеет радиус, равный единице, то ОР = R = 1.
Если с точки Р опустить перпендикуляр на ось ОХ, то получим прямоугольный треугольник с гипотенузой, равной единице.
Если радиус-вектор двигается по часовой стрелке, то данное направление называется отрицательным, если же он двигается против движения часовой стрелки — положительным.
Синусом угла данной окружности, образованного радиусом-вектором ОР, является ордината точки Р вектора на окружности.
То есть, для получения значения синуса данного угла альфа необходимо определиться с координатой У на плоскости.
Как данное значение было получено? Так как мы знаем, что синус произвольного угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе, получим, что
А так как R = 1, то sin(α) = y0.
В единичной окружности значение ординаты не может быть меньше -1 и больше 1, значит,
Синус принимает положительное значение в первой и второй четверти единичной окружности, а в третьей и четвертой — отрицательное.
Косинусом угла данной окружности, образованного радиусом-вектором ОР, является абсцисса точки Р вектора на окружности.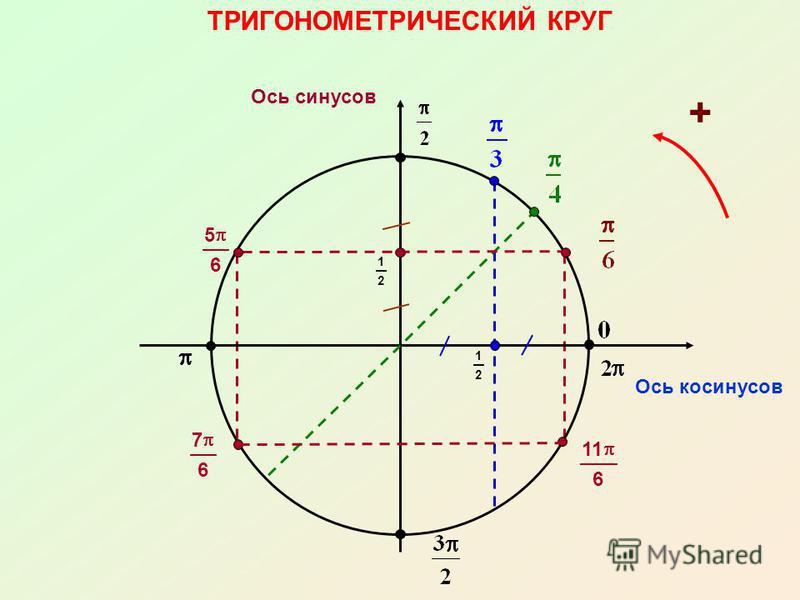
То есть, для получения значения косинуса данного угла альфа необходимо определиться с координатой Х на плоскости.
Косинус произвольного угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе, получим, что
А так как R = 1, то cos(α) = x0.
В единичной окружности значение абсциссы не может быть меньше -1 и больше 1, значит,
Косинус принимает положительное значение в первой и четвертой четверти единичной окружности, а во второй и в третьей — отрицательное.
Тангенсом произвольного угла считается отношение синуса к косинусу.
Если рассматривать прямоугольный треугольник, то это отношение противолежащего катета к прилежащему. Если же речь идет о единичной окружности, то это отношение ординаты к абсциссе.
Судя по данным отношениям, можно понять, что тангенс не может существовать, если значение абсциссы равно нулю, то есть при угле в 90 градусов. Все остальные значения тангенс принимать может.
Тангенс имеет положительное значение в первой и третьей четверти единичной окружности, а во второй и четвертой является отрицательным.
Котангенсом произвольного угла называется отношение косинуса к синусу.
Рассматривая прямоугольный треугольник — отношение прилежащего катета к противолежащему, то есть абсциссы к ординате.
Так как ордината находится в знаменателе дроби, то котангенс не может существовать при угле альфа, равном нулю градусов.
Котангенс принимает те же значения в четвертях единичной окружности, что и тангенс.
Все перечисленные функции являются периодичными.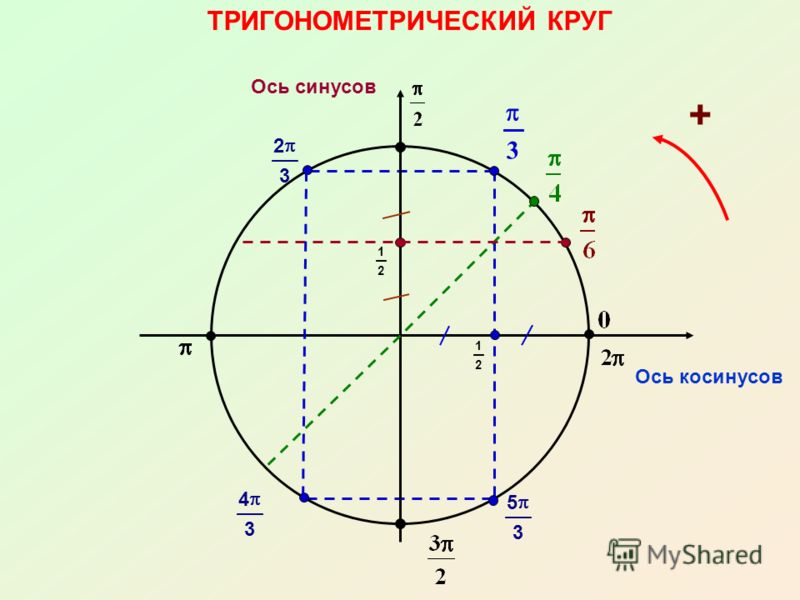
Косинус и синус имеют период 360 градусов, то есть 2Пи, а тангенс и котангенс 180 градусов, то есть Пи.
Радианная мера угла
Радианной мерой произвольного угла в единичной окружности является отношение длины дуги центрального угла к радиусу окружности.
Данное определение применимо к окружностям с произвольной длиной радиуса.
Радианная мера связана с градусной мерой простым соотношением:
При этом для получения величины 1 рад, следует 180 градусов разделить на значение числа π.
Например, давайте получим радианную меру угла в 30 градусов:
2 * π * 30 : 360 = π/6 ≈ 0,52.
Существуют таблицы, которые позволяют без расчетов определить радианную меру основных углов:
Итак, напоминаем, что при рассмотрении тригонометрических функций мы рассматриваем окружность, которая имеет единичный радиус.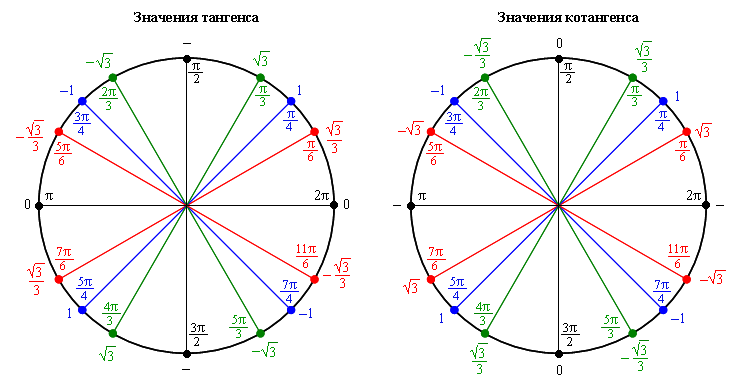
Данное упрощение используется для удобства. Все отношения справедливы для произвольных окружностей, с произвольным радиусом.
Пример. Давайте построим точки на единичной окружности, которые будут соответствовать повороту радиус-вектора на угол
Решение. За начало отсчета принимаем точку Р0. Угол, равный нулю радиан совпадает с данной точкой.
Мы знаем, что граничными считаются углы 0, π/2, π, 3π/2, 2π. Если использовать угол π/2 и разделить первую четверть на 3 равных части, то первое от начала отсчета разделение будет соответствовать углу π/6. На графике данная точка имеет место Рπ/6.
Чтобы получить угол π/4, необходимо прямой угол разделить на две части. Если необходимо отметить угол с отрицательным аргументом, необходимо пойти по часовой стрелке от начальной точки. Например, точка — π/4 будет находиться симметрично относительно оси ОХ в 4 четверти.
Давайте теперь вспомним, каким образом исчисляются углы, выраженные в радианной мере. Чему, например, соответствует в радианах π/4? Чтобы это узнать, следует числовое значение числа π разделить на 4.
3,14 : 4 = 0,78, если углу π/2 соответствует 3,14 : 2 = 1,57. Следовательно, на окружности угол, равный единице будет лежать выше π/4, но ниже π/2. Отрицательное значение угла симметрично положительному относительно оси ОХ.
Таким же образом следует найти и местонахождение угла, равного 2. Так как граничному прямому углу соответствует значение 1,57, то угол, равный двум, будет находиться во второй четверти.
Можно убедиться, что каждому числу соответствует своя ордината и абсцисса на плоскости.
Отсюда можно сделать вывод, что:
Синус некоторого числа — это значение ординаты на плоскости, которая соответствует точке этого числа на единичной окружности.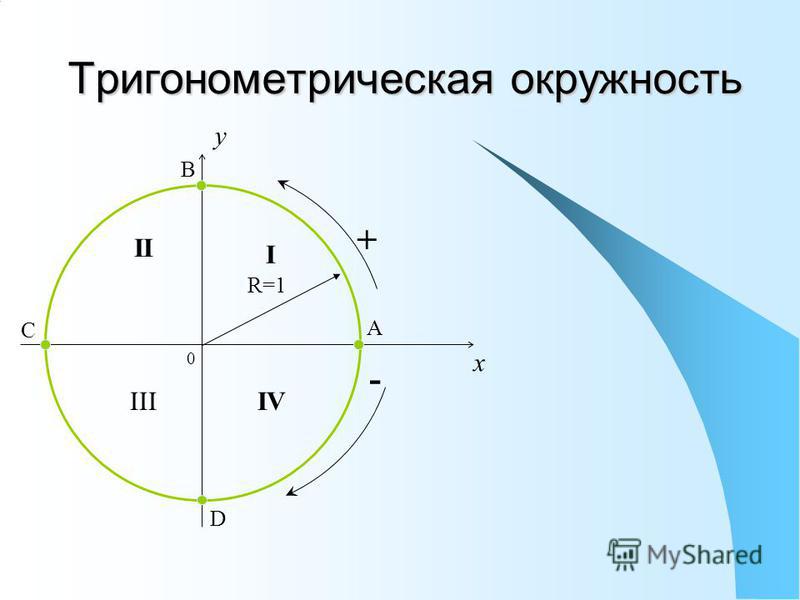
Косинус некоторого числа — это значение абсциссы на плоскости, которая соответствует точке этого числа на единичной окружности.
Тангенс некоторого числа — это значение, полученное в результате отношения синуса к косинусу, иначе говоря, отношение ординаты к абсциссе.
Котангенс некоторого числа — это значение, полученное в результате отношения косинуса к синусу, иначе говоря, отношение абсциссы к ординате.
Синус и косинус имеют период, равный 6,28 (2 ). Тангенс и котангенс имеет период, равный 3,14 ( ).
тригонометрия — Почему мы используем единичный круг для решения для sin и cos
Я только начал изучать тригонометрию.
Существует четкая разница между изучением таких функций, как синус и косинус, в области тригонометрии или аналитической геометрии и изучением функций синуса и косинуса в исчислении (также известном как реальный анализ).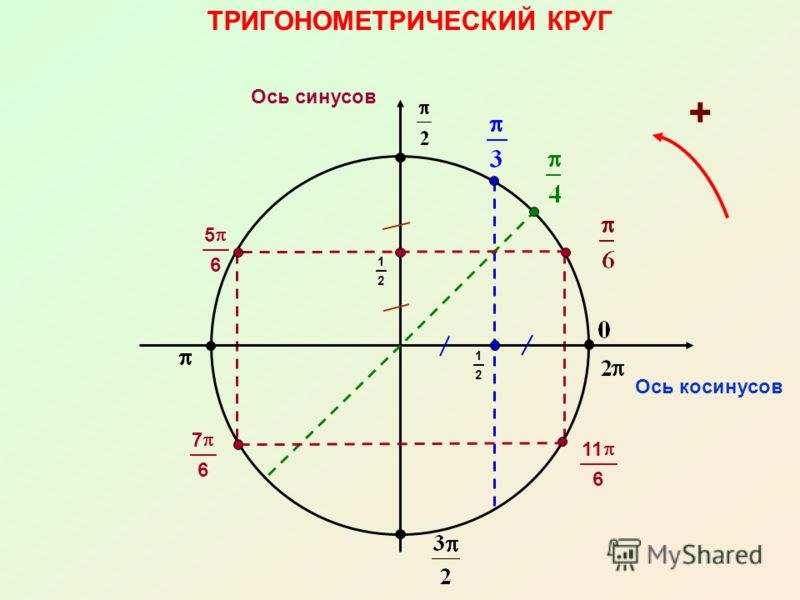
В тригонометрии или аналитической геометрии самое главное, чтобы определения казались осмысленными. Вот почему в области тригонометрии или аналитической геометрии область функций синуса и косинуса составляет углов . Это означает, что вы применяете эти функции в любом произвольном прямоугольном треугольнике, независимо от длины гипотенузы. Затем функции синуса и косинуса измеряют отношение катетов прямоугольного треугольника к гипотенузе прямоугольного треугольника. Такой подход имеет смысл .
В исчислении эти разумные
В качестве дальнейшего изменения вы познакомитесь с несколько причудливым и несколько двусмысленным понятием радиан .
Для студента на переходном этапе вы в конечном итоге начнете с идеи, что радианы измеряют углы, и что $(360)$ градусов равняется $(2\pi)$ радианам. Это ступенька к определению функций синуса и косинуса в исчислении, и она основана на идее, что длина окружности единичного круга равна $(2\pi).$ 9\circ)$ соответствует $(1/8)$ оборота, поэтому его эквивалентно рассматривать как $(\pi/4)$. Это означает, что в исчислении $\sin(\pi/4) = (1/\sqrt{2}).$ Обратите внимание, что я сказал $\sin(\pi/4)$, а не $\sin(\ pi/4)$ радиан .
Причина, по которой вы запутались, заключается в том, что вы застряли в промежутке между аналитической геометрией/тригонометрией, где нет такого понятия, как радиан, а углы измеряются в градусах, и математическим исчислением.
Еще большая путаница. Когда вы впервые знакомитесь с термином радиан естественно рассматривать его как относящийся к углу. Как ни странно, в исчислении радиан относится к безразмерной пропорции между определенной длиной дуги и длиной дуги полного оборота, а именно $(2\pi)$.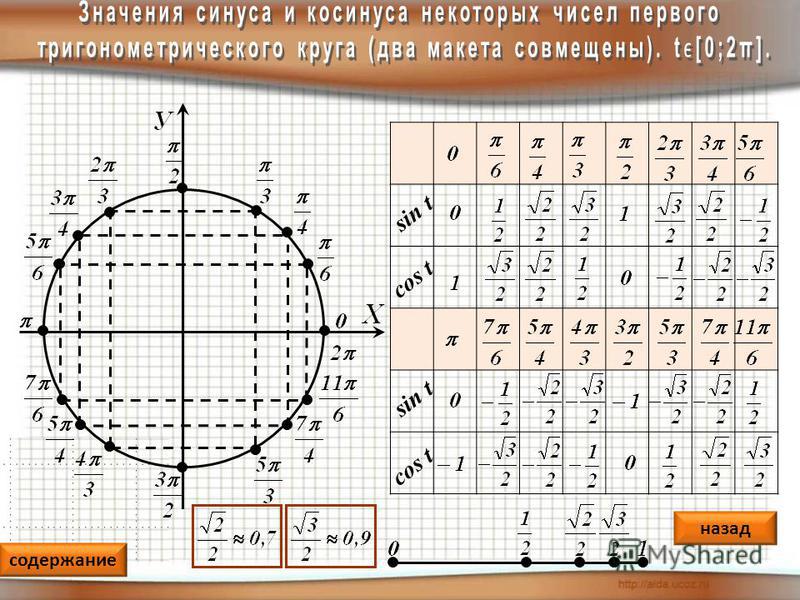
Таким образом, когда изучающий математику использует термин радианы, он имеет в виду , а не , относящийся к углу, а вместо этого имеет в виду
Не может быть, чтобы ты не запутался во всем этом, как и я. Лучший способ прояснить ситуацию в своем уме — объяснить свое замешательство профессору математики в колледже, а не учителю математики в средней школе, и попросить профессора все объяснить.
лаборатория 1ucasvb
79557434791
2311 1394809260 Функции синуса и косинуса для окружности, как.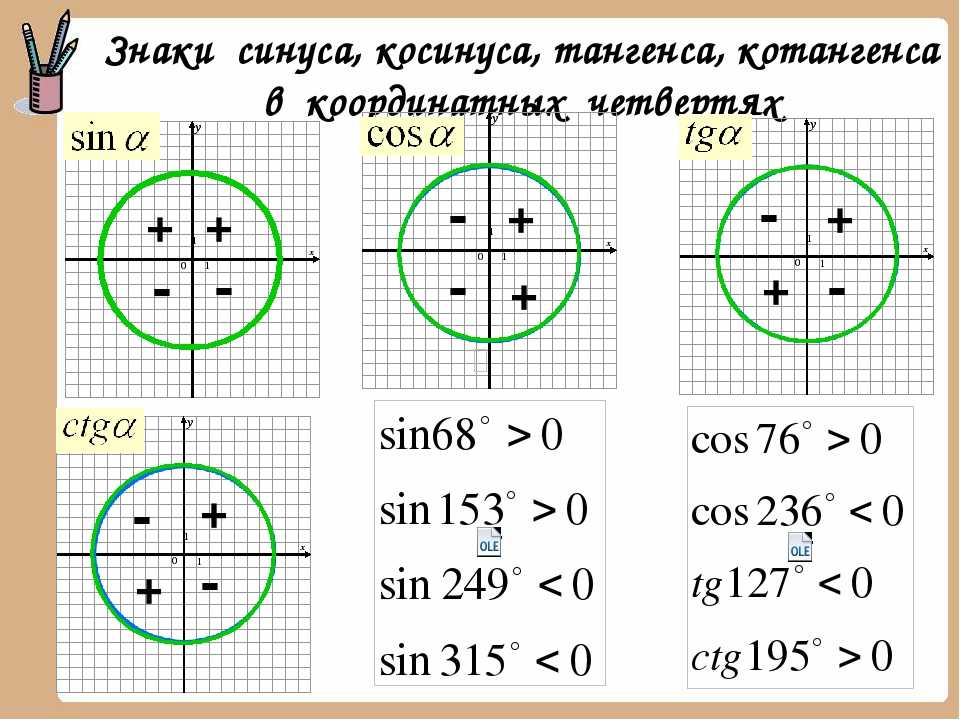
..( Edit : анимация также доступна без водяных знаков, с более высоким разрешением и более низкой частотой кадров на Викискладе.)
С ДНЕМ ПИ! Чтобы отпраздновать это, вот эта долгожданная анимация обычных тригонометрических функций, синуса и косинуса, геометрически заданных в терминах единичного круга.
Я знаю, что эта анимация немного похожа на несколько других моих предыдущих анимаций, но это именно та версия, которую я должен был сделать давным-давно, если не сделать ее в первую очередь.
Вот чем на самом деле являются функции синуса и косинуса, которым вас учили, в терминах единичного круга.
Во-первых, у нас есть единичная окружность (с радиусом = 1) зеленого цвета, расположенная в начале координат внизу справа.
В середине этого круга желтым цветом представлен угол тета (θ), который мы собираемся подставить в наши тригонометрические функции. Этот угол представляет собой величину вращения против часовой стрелки вокруг круга, начиная справа, по оси X, как вы можете видеть.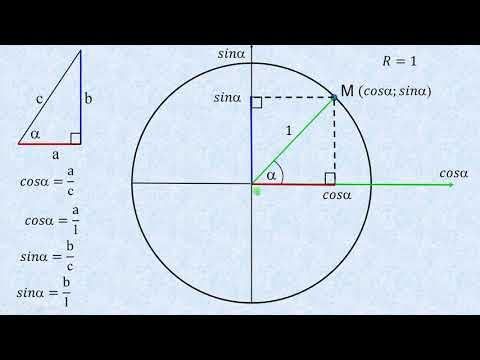
Под этим углом, начиная с исходной точки, мы проводим наружу (слабую) зеленую линию. Эта линия пересекает единичный круг в одной точке — зеленой точке, которую вы видите вращающейся с постоянной скоростью при изменении угла θ, также с постоянной скоростью.
Теперь возьмем вертикальное положение этой точки и спроецируем ее прямо (вдоль слабой красной линии) на график слева от круга. Это дает нам красную точку. Координата Y этой красной точки (такая же, как координата Y зеленой точки) является значением синусоидальной функции, вычисленной для угла θ, то есть:
координата y зеленой точки = sin θ
По мере изменения угла θ мы можем видеть, как красная точка перемещается вверх и вниз, отслеживая красный график. Это график синусоидальной функции. Слабые вертикальные линии, которые проходят слева, отмечают каждый квадрант круга, то есть под каждым углом 90° или π/2 радиана.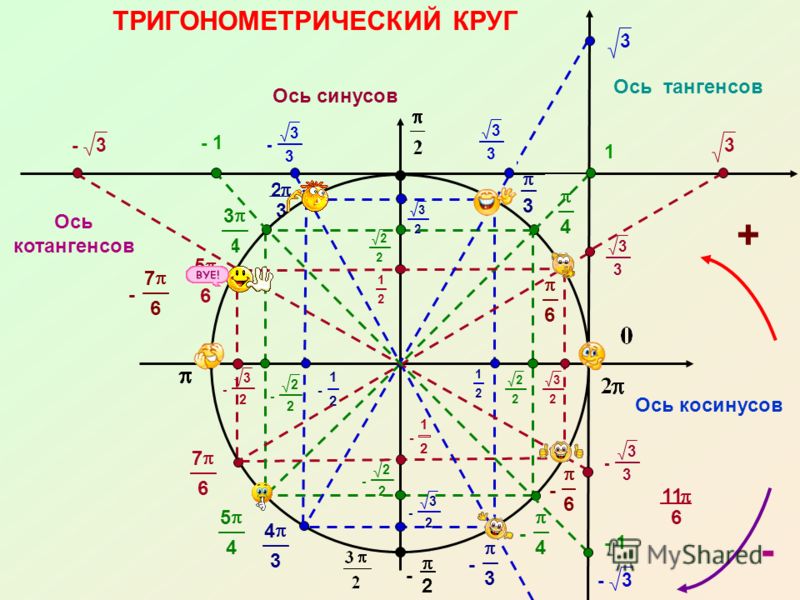
Теперь проделываем то же самое с координатой x зеленой точки. Однако, поскольку координата x наклонена по сравнению с обычным способом, которым мы строим графики (где y = f(x), где y вертикальна, а x горизонтальна), мы должны «наклонить» ее, чтобы повторить описанный выше процесс в том же самом. ориентация. Это было представлено тем «изгибом», который вы видите в правом верхнем углу.
Итак, зеленая точка спроецирована вверх (по бледно-голубой линии), и эта «изогнутая» проекция заканчивается на самом правом краю верхнего графика, в синей точке. Координата y этой синей точки (которая, как вы видите, благодаря нашему «изгибу» совпадает с координатой x зеленой точки) есть значение функции косинуса, вычисленное по углу θ, то есть :
x координата зеленой точки = cos θ
Синяя кривая, описываемая этой точкой при ее движении вверх и вниз при изменении θ, является графиком функции косинуса.
Обратите внимание еще раз, как он ведет себя при пересечении каждого квадранта, отражая тот факт, что cos(0) = 1, cos(π/2) = 0, cos(π) = -1 и cos(3π/2) = 0.
И ну вот. Вот и все. Вот что такое синус и косинус. Просто, да?
Теперь, хотя сама концепция довольно проста, многие люди не понимают, что на самом деле представляют функции синуса и косинуса, потому что визуализация, подобная этой, не представлена им, когда они впервые изучают тригонометрию.
Многие учителя и множество школьных учебников не упоминают ничего из этого подробно, как я пытался сделать здесь, вместо этого бросая ученикам кучу формул. Но геометрическая интуиция, представленная здесь, гораздо проще для понимания, в целом гораздо полезнее и останется с вами на всю жизнь, как только вы ее освоите. Формулы и важные значения синуса и косинуса больше не нужно запоминать, потому что теперь вы должны понимать, какими должны быть эти значения, учитывая лежащую в основе логику вещей. И в этом вся суть математики: придавать вещам смысл, чтобы они были очевидны для всех.