Таблица горнера как пользоваться: Простая физика — EASY-PHYSIC

Содержание

Простая физика — EASY-PHYSIC

Всем доброго времени суток! В этой статье мы научимся делить многочлены по схеме Горнера. Это простой и мощный механизм, которым совершенно необходимо владеть, чтобы решать некоторые рациональные уравнения задания 15 профильного ЕГЭ.

При решении таких уравнений корни заранее неизвестны, да и при разложении многочлена на множители мы также не знаем заранее, на какой бином поделится наш многочлен. Как же узнать, на какой бином разделить многочлен?

Если многочлен имеет целые корни, то они являются делителями свободного члена — правило вытекает из теоремы Безу

Пример 1.

Определим, какие числа являются, например, корнями многочлена . Если этот многочлен имеет целые корни, то они являются делителями числа (-2): это могут быть . Проверим подстановкой — если при подстановке этих чисел в исходный многочлен получим ноль, то данное число — корень:

Кроме 1, ни одно число не подошло, значит, бином поделит этот многочлен нацело (без остатка). Деление теперь можно выполнить как в столбик (уголком), так и по схеме Горнера — сейчас мы до нее дойдем, только еще раз потренируемся в определении корней.

Пример 2.

Определим корни многочлена . Целые делители свободного члена — только 1 и (-1):

Корнем многочлена является 1, поэтому многочлен без остатка поделится на бином .

Пример 3.

Определим корни многочлена . Целые делители свободного члена — . Проверим их:

Корнями многочлена являются как 1, так и (-1), поэтому многочлен без остатка поделится на биномы и — а в итоге на .

Теперь, когда мы научились определять, есть ли у многочлена целые корни, можем перейти собственно к схеме Горнера. Чтобы ею воспользоваться, нужно составить таблицу, в верхней строке которой будут расположены коэффициенты нашего многочлена. Поучимся заполнять эту строку. Определим коэффициенты многочлена и запишем их в таблицу. Этот многочлен пятой степени, поэтому коэффициентов будет 6: при каждой из степеней , включая нулевую (свободный член). Если какой-то степени нет в записи многочлена, то это означает, что коэффициент при ней нулевой:

Получили эдакую зашифрованную запись многочлена.

Еще пример, многочлен , его коэффициенты:

Полдела сделано: верхнюю строку научились заполнять, а нижняя — это уже решение, то есть результат деления в таком же, «зашифрованном», виде. Каков же порядок заполнения нижней строки? Во-первых, у нее будет дополнительная ячейка слева, куда мы впишем корень многочлена, образующий бином, на который мы собираемся делить. Например, если делим на , то корнем многочлена является число 2, если делим на , то в эту ячейку впишем (-9). Пример: хотим разделить на , таблица изначально будет выглядеть так:

Как уже было сказано, ответ будет «зашифрован» в пустых пока ячейках. Наверное, вы догадались, что там окажутся коэффициенты нового, полученного при делении, многочлена. Только внимание! Степень полученного многочлена уменьшится на 1: ведь мы делим на бином, куда входит в первой степени. Например, если сейчас мы начнем заполнять эту табличку, то под двойкой, которая была в делимом коэффициентом при пятой степени, окажется коэффициент при четвертой степени искомого частного, под 4 — коэффициент при кубе частного и т.д.

Так же просто заполнить вторую ячейку нижней строки: в нее просто вписывается число, стоящее в первой строчке:

Рассмотрим дальнейшее заполнение таблицы на конкретном примере: разделим на бином (так как (-1) — это корень данного многочлена). Заполняем таблицу, пока только ту часть, которую умеем:вписываем коэффициенты в верхнюю строку, в дополнительную ячейку слева — корень (-1), в следующую переносим 1 из верхней строки:

Чтобы заполнить следующую ячейку, берем корень, умножаем его на имеющийся коэффициент и прибавляем к полученному числу то, которое стоит над пустой ячейкой:

Чтобы заполнить следующую, все повторяем:

И опять:

И вот так закончится заполнение таблицы:

«Расшифровываем» ответ, при этом помним, что степень понизилась на 1::

Ответ:

Ноль в последней графе — это нулевой остаток от деления — то есть один многочлен поделился на другой «нацело».

Решим еще пример. Разделим на . Составим таблицу:

Начинаем рассчитывать коэффициенты и заполнять таблицу. Первое число из верхней строки переписываем вниз, умножаем на него корень, к результату добавляем число из верхней строки:

Также вычисляем следующий коэффициент:

И далее:

Получили ответ: . Здесь остаток от деления также равен нулю.

Этот способ хорош своей быстротой и простотой. Им можно пользоваться и при делении с остатком: тогда в последней графе таблицы будет стоять не ноль, а этот самый остаток. Недостаток способа — неудобство деления в случае, если корень не целый, а представляет собой дробь.

Попробуем выполнить деление по схеме Горнера, если корень не целый, да еще и остаток есть. Поделим многочлен на бином . Заполняем таблицу:

Расшифруем ответ:

Итак, получилось следующее. При делении получился многочлен и остаток . Запишем это иначе: . Если есть желание проверить — раскройте скобки в этой формуле.

Наконец, об уравнениях высоких степеней. Иногда однократное деление не приводит к окончанию решения, потому что корней несколько и многочлен можно продолжать делить. В этом случае, выполнив деление и получив новый многочлен степенью ниже, снова пытаются найти целые корни среди делителей его свободного члена. При этом подстановка предполагаемых корней в многочлен может занимать даже больше времени, чем заполнение таблицы по Горнеру. Тогда таблицу продолжают вниз, дополняя ее просто новыми строками, а в случае появления остатка (деление не выполнено) эту строчку зачеркивают и пробуют новый корень в следующей строке. Пример:

Решить уравнение: . Делителями свободного члена являются: и так далее. Пробуем сначала подставить 1 и (-1) в сам многочлен — такая подстановка дает нам один корень, это 1. Выполняем деление по схеме Горнера:

Запишем, что получилось: — получили тот же свободный член, и можем снова использовать те же делители, чтобы проверить, не являются ли они корнями. Однако теперь подстановка 1 и (-1) показывает, что эти два числа не являются корнями. Проверяем тогда 2 и (-2) — только не будем подставлять их в многочлен, а сразу попытаемся делить по Горнеру. А таблица у нас уже готова, и в ней все коэффициенты! Поэтому продолжаем ее заполнять, добавляя строки:

Так как остаток ненулевой, то 2 — не корень. Строку вычеркнем и попробуем (-2):

Та же картина, опять получили ненулевой остаток. Далее пробуем 3 и (-3):

Получилось! Теперь имеем: . Делителями нового свободного члена являются . Пробовать не будем: очевидно, что они не могут быть корнями — это выяснилось на предыдущих этапах. Поэтому пробуем .

Получили: . Дальше деление по Горнеру можно и не выполнять: корни с очевидностью можно найти по теореме Виета — это 5 и 6. Тогда . Разложение выполнено, корни уравнения найдены.

Надеюсь, статья вам помогла, до следующих исследований!

EDSAC aka «Very simple machine» / Хабр

Обучаясь в техническом вузе невольно сталкиваешься с такими профильными предметами, как например «низкоуровневое программирование». Первые ассоциации — конечно ассемблер, во вторую очередь — C и C++. Но не тут то было, вашему вниманию представляется ~~актуальнейшая~~ электронная вычислительная машина EDSAC.

Рис. 1. Непосредственно EDSAC

Согласно Википедии, EDSAC (Electronic Delay Storage Automatic Calculator) был создан в 1949 году в Кембриджском университете по заказу Министерства Обороны Великобритании. Разработка EDSAC стала следствием своего рода «гонки вооружений» между Великобританией и США за первенство в разработке высокопроизводительных ЭВМ военного назначения. Первый в мире действующий и практически используемый компьютер с хранимой в памяти программой.

Я был бы не против поработать с этой машиной вживую, но к сожалению в нашей статье будем работать в EDSAC Simulator, найти который вы можете здесь.

Рис. 2. EDSAC Simulator

Программа состоит из двух загрузчиков: Initial Orders 1 (IO1) и Initial Orders (IO2). В свою очередь загрузчики состоят из инструкций. В IO1 инструкции загружаются в ячейки 0-30, программа начинает работу с 31 ячейки.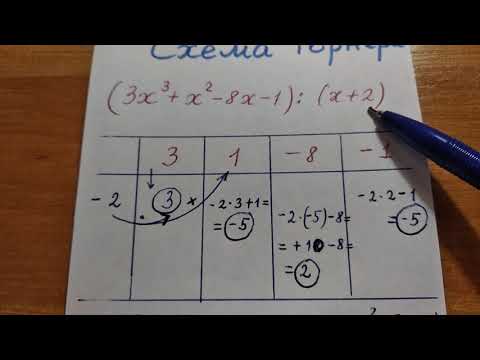 Ячеек памяти всего 1024. «Пустая» программа примет следующий вид:

[31] T 32 S

В квадратных скобках записываются комментарии к коду, в данном случае в комментарии указан адрес начала программы. Теперь к самой инструкции. Первая инструкция программы обязательно должна иметь вид T <N+1> S, где N — адрес последней инструкции программы, S — код длины слова. S обозначает «короткое слово» (17 бит), L — «длинное» слово (35 бит). Так же имеется аккумулятор aka оперативная память размером 71 бит, 35-битный умножающий регистр (2 «коротких» слова). Первое слово в умножающим регистре используется для целых чисел, с помощью второго (правого) слова можно задать дробное число.

Рис. 3. Короткое словоРис. 4. Длинное слово

Старший бит sign отвечает за знак числа. «Короткие» слова разделены на перфоленте одним битом (sandwich digit). В «длинном» слове sandwich digit считается частью слова, прибавляется к ячейке справа. Получается, что «длинное» слово состоит из 2 ячеек (n и n+1; n — обязательно чётное число). Чётная (правая) ячейка составляет 18 бит (само слово + sandwich digit), нечётная (левая) состоит из 17 бит, при этом старший бит отвечает за знак числа.

В инструкции T 32 S буква T обозначает код операции, в данном случае программа запишет значение из аккумулятора в ячейку 32 и обнулит аккумулятор. Возникает вопрос: что за операции и как понять за что отвечают эти самые операции? Ниже представлен список операций для EDSAC.

Инструкция	Комментарий
A n	Добавление числа из ячейки памяти n в аккумулятор
S n	Вычитание числа из ячейки памяти n из аккумулятора
H n	Копирование числа из ячейки памяти n в умножающий регистр
V n	Умножение числа из ячейки памяти n на число в умножающем регистре; добавление результата в аккумулятор
N n	Умножение числа из ячейки памяти n на число в умножающем регистре; вычитание результата из аккумулятора
T n	Перенос числа из аккумулятора в ячейку памяти n с обнулением аккумулятора
U n	Перенос числа из аккумулятора в ячейку памяти n без обнуления аккумулятора
C n	Побитовое «И» числа в ячейке памяти n с числом в умножающем регистре; добавление результата в аккумулятор
R 2^n-2	Сдвиг числа в аккумуляторе на n битов вправо
L 2^n-2	Сдвиг числа в аккумуляторе на n битов влево
E n	Если число в аккумулятор >= 0, то совершается переход в ячейку n, иначе программа просто продолжает работу
G n	Если число в аккумулятор < 0, то совершается переход в ячейку n, иначе программа просто продолжает работу
I n	Считать следующий символ с бумажной ленты и сохранить его как младшие 5 бит в ячейке n.
O n	Вывести символ, представленный старшими 5 битами ячейки памяти n
F n	Прочесть вывод последнего символа для проверки
X	Отсутствие операции
Y	Округлить число в аккумуляторе до 34 бит
Z	Остановить машину; Зазвенит ~~очень странный~~ предупреждающий звонок.

Рис. 5. Бинарные коды символов в EDSAC

EDSAC работает в бинарной системе, поэтому у каждого символа есть бинарное представление. Символ # (π) вызывает режим figure shift (печать цифр), символ * (Erase) вызывает режим letter shift (печать букв и символов). В EDSAC Simulator “θ” представляется символом “@“, «φ” представляется символом “!».

Теперь перейдём к самому интересному — напишем программу. По божьему веленью, по хотенью преподавателя мне выпала нелёгкая доля разработки программы, реализующую расчёт значения многочлена по схеме Горнера с «длинным» результатом, при этом переполнение игнорируется. Если вы вдруг не знаете что такое схема Горнера, то почитать об этом вы можете здесь. Задание звучит совсем просто, но смущает только одно словосочетание — «длинный» результат. Вот тут и начинаются интересности. Под «длинным» результатом очевидно подразумевают представление ответа в виде «длинного» слова, что несколько усложняет нам задачу. С заданием мы разобрались, приступим к разбору самой программы.

Листинг 1. EDSAC order code. Расчёт значения многочлена по схеме Горнера.

[31] T 76 S [инструкция, ссылающаяся на последнюю инструкцию + 1]
[32] A 69 S [загрузка в аккумулятор степени многочлена]
[33] T 1 S [запись степени многочлена в ячейку 1]
[34] A 71 S [загрузка старшего коэффициента в аккумулятор]
[35] T 2 S [запись старшего коэффициента в рабочую ячейку 2]
[36] H 68 S [запись 1 в умножающий регистр]
[37] V 2 S [умножение числа из ячейки 2 на число в умножающем регистре]
[38] R 1 S [сдвиг числа вправо на 2 бита, для коррекции умножения]
[39] T 2 L [запись старшего коэффициента в длинную ячейку]
[40] A 70 S [загрузка в аккумулятор адреса 1-го элемента массива]
[41] L 0 L [сдвиг аккумулятора, для коррекции]
[42] A 54 S [прибавляем код инструкции с нулевым полем адреса]
[43] T 54 S [запись сформированной инструкции, обнуление аккумулятора]
[44 loop] A 1 S [загружаем в аккумулятор счётчик необработанных элементов массива]
[45] S 68 S [вычитание константы = 1]
[46] E 48 S [if (acc >= 0) goto 48 else end]
[47] Z 0 S [точка остановки, завершение программы]
[48] T 1 S [обновляем значение счетчика и обнуляем аккумулятор]
[49] H 67 S [запись X0 в умножающий регистр]
[50] V 2 L [умножение числа из ячейки 2 на число в умножающем регистре]
[51] L 1024 S [сдвиг числа влево на 12 бит, для коррекции умножения]
[52] L 4 S [сдвиг числа влево на 4 бита, для коррекции умножения]
[53] T 2 L [запись результата умножения в длинную ячейку]
[54 r1] A 0 S [загрузка в аккумулятор значения из ячейки 0]
[55] T 4 S [запись в рабочую ячейку 4]
[56] H 68 S [запись 1 в умножающий регистр]
[57] V 4 S [умножение числа из ячейки 4 на число в умножающем регистре]
[58] R 1 S [сдвиг числа вправо на 2 бита, для коррекции умножения]
[59] A 2 L [добавление числа из "длинной" ячейки 2 в аккумулятор]
[60] T 2 L [запись этого значения в "длинную" ячейку 2, обнуление аккумулятора]
[61] A 68 S [загрузка в аккумулятор значение константы = 1]
[62] L 0 L [сдвиг аккумулятора, для коррекции]
[63] A 54 S [прибавляем код инструкции, исполненной на предыдущем шаге]
[64] T 54 S [записываем сформированную инструкцию в память]
[65] XS
[66] E 44 S [повторяем все операции; аккумулятор обнулен]
[67] P 1 L [X0 - фиксированное значение X, по которому мы вычисляем значение многочлена ]
[68 const 1] P 0 L [1]
[69 power] P 2 S [степень многочлена]
[70 addr] P 36 S [адрес 1-го элемента массива]
[71] P 0 L [a4 = 1]
[72] P 30 S [a3 = 60]
[73] P 7 S [a2 = 14]
[74] P 3 L [a1 = 7]
[75] P 2 L [a0 = 5]

Разберём по строчкам. С 31 ячейкой мы уже разобрались — начало программы, ссылка на ячейку с последней инструкцией + 1. Дальше объяснение лучше всего начать с конца. В конце программы с 67 по 75 строчку идёт объявление констант. В 67 строчку мы вводим значение X₀, для которого нам нужно посчитать значение многочлена. В 68 строчке находится константа 1 для работы с счётчиком необработанных чисел массива. В 69 строчке находится степень многочлена. В 70 строчку занесён адрес 1-го элемента массива. В 71 строчке находится значение старшего коэффициента (предполагается, что многочлен хотя бы первой степени). С 72 по 75 строчку (многочлен 4 степени) идёт массив чисел, представляющий собой значения всех коэффициентов многочлена, кроме старшего. Многочлен примет следующий вид:

Далее с 32 по 39 строчку идёт запись констант в ячейки памяти, с которыми мы будем работать в дальнейшем. В 35 строчке идёт запись старшего коэффициента в «короткую» ячейку 2, дальше число из этой короткой ячейки умножается на 1, для того чтобы преобразовать его в «длинное» слово, записываем старший коэффициент в «длинную» ячейку 2, то есть запись в ячейки 2-3, в этих ячейках в итоге у нас и будет записан результат.

С 40 по 43 строчки идёт создание инструкции чтения для передачи следующего коэффициента. Передаётся адрес элемента и в ячейке 54 идёт чтение числа по этому адресу.

С 44 строчки по 59 строчку находится цикл, на каждом этапе цикла число из «длинной» ячейки 2 умножается на X

0 и к полученному числу прибавляется следующий коэффициент, который в свою очередь превращается в «длинное» слово умножением на 1. Как видно по коду, в 1 ячейке находится счётчик необработанных чисел массива, когда расчёт будет окончен, счётчик будет равен нулю и программа в 47 строчке закончит работу.

С 61 по 64 строчку создаётся инструкция чтения следующего коэффициента. К адресу элемента (который там уже записан) прибавляется 1 и в ячейке 54 произойдёт чтение числа по новому адресу. В 65 строчке стоит пустая операция, зачем это нужно? Это нужно для возможного дебагинга программы, вместо X S можно записать Z S и выполнить пошаговый дебагинг (в данном случае в инструкциях упущено число, по умолчанию программа будет считать, что там записан ноль).

66 строчка возвращает нас к началу цикла, возвращать она будет всегда, потому что к этому моменту у нас всегда будет обнулённый аккумулятор.

Рис. 6. Результат выполнения программы

Как видно по рис. 6, программа вывела нам число 0.0000000000000000000000011100111101, где первый ноль отвечает за знак числа, а остальные 34 бита за само число. Переведём полученное число в десятичную систему и получим верный результат — 1853. Проведём теперь эксперимент с отрицательными числами, введём новые коэффициенты:

Теперь нам придётся немного видоизменить программу, а конкретно значение констант.

Листинг 2. Изменение констант

[67] P 5 S [X0 - фиксированное значение X, по которому мы вычисляем значение многочлена ]
[68 const 1] P 0 L [1]
[69 power] P 2 S [степень многочлена]
[70 addr] P 36 S [адрес 1-го элемента массива]
[71] P 55536 S [a4 = -20000]
[72] P 2 S [a3 = 4]
[73] P 9 L [a2 = 19]
[74] P 5 L [a1 = 11]
[75] P 268 S [a0 = 536]

Рис. 7. Результат выполнения программы

В результате работы программы мы получаем 1. 11111110100000101000101011110010010, знаковый бит говорит нам, что число отрицательное. Отрицательные числа в EDSAC представлены в виде дополнительного кода, подробнее об числах в EDSAC можно почитать в статье моего друга и коллеги. Переведём число в прямой код — 0.0000001011111010111010100001101110. Переведём полученное число в десятичную систему и получим верный результат — -199993454.

Делая выводы, можно отметить, что всё что мы сегодня делали — ~~бесконечно устарело~~ было очень интересно и познавательно. Сегодня мы рассмотрели программу только на IO1, в планах есть написать вторую небольшую статью с той же программой на IO2. Это моя первая статья, очень надеюсь, что она Вам понравилась.

P.S. Полезные ссылки здесь и здесь.

Хорнер’Мелход). Используйте метод Хорнера для вычисления многочлена f(c) =26 + 215 34 43 512 61 + at = 1445 и при 0 = -145 в 6-разрядной арифметике с плавающей запятой (FPA6). В cach CaSc результаты ваших расчетов должны быть представлены в стандартной таблице an-1 an-? абн абн-! ab2 0b1 bn1 для метода Таким образом, ваши ответы на задачу должны состоять из таблиц Ao приведенной выше формы, за которыми в каждом случае следует оценка полинома в FPA6.

) заключение по результату

Вопрос

Пошаговый ответ

Horner’$ Melhod) . Используйте метод Хорнера для вычисления многочлена f(c) =26 + 215 34 43 512 61 + при & = 1445 и при 0 = -145 в арифметике с 6-значной плавающей запятой (FPA…

Horner’$ Melhod) . Используйте метод Хорнера для вычисления многочлена f(c) =26 + 215 34 43 512 61 + при & = 1445 и при 0 = -145 в 6-разрядной арифметике с плавающей запятой (FPA6). В cach CaSc результаты ваших расчетов должны быть представлены в стандартной таблице an-1 an-? абн абн-! ab2 0b1 bn_1 для метода_ Таким образом, ваши ответы на задачу должны состоять из таблиц Ao приведенной выше формы, за которыми в каждом случае следует оценка полинома в FPA6.) заключение по результату

Вопрос о лучшем совпадении:

Используйте формулу. (3.10) или алгоритм 3.2 для построения интерполяционных полиномов первой, второй и третьей степени для следующих данных. Аппроксимируйте указанное значение, используя каждый из полиномов. а. f (8.4) если f (8.1) = 16,94410, f (8.3) = 17,56492, f (8.6) = 18,50515, f (8.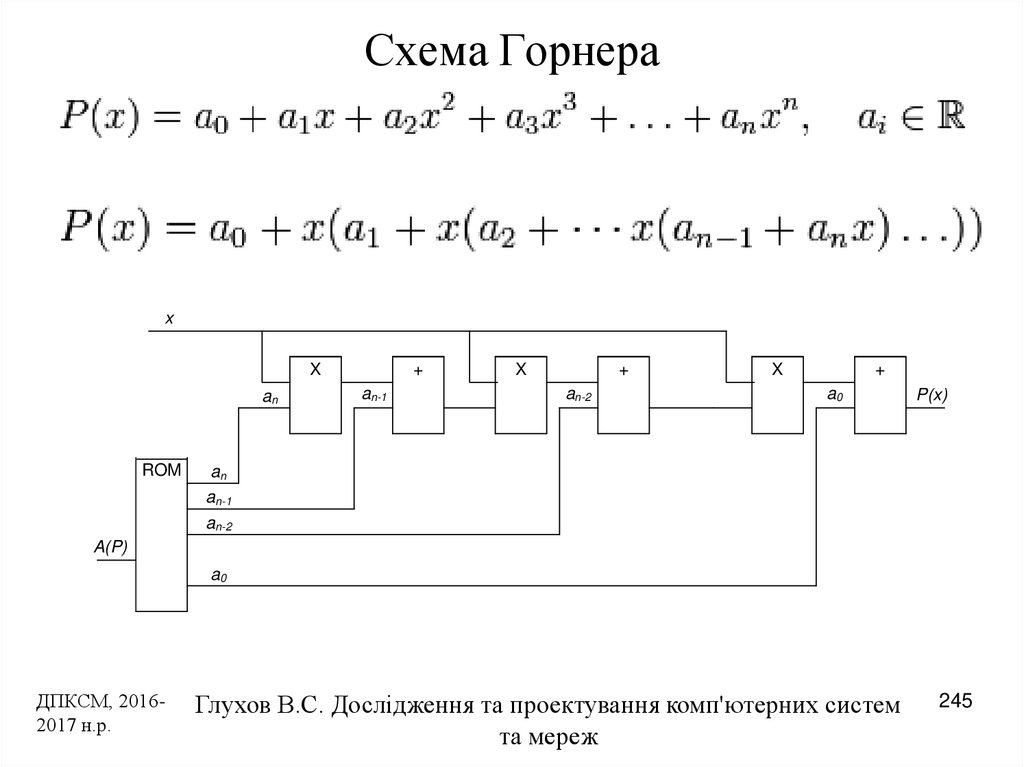 7) = 18,82091 Численный анализ Q3

Поделиться вопросом

Добавить в плейлист

Хммм, кажется, у вас нет плейлистов. Пожалуйста, добавьте свой первый плейлист.

Лабораторная работа №5: Полиномы и метод Ньютона

Лабораторная работа №5: Многочлены и метод Ньютона

Введение
Советы по MATLAB
Метод Хорнера
Метод Хорнера плюс производная
Метод Ньютона-Хорнера
дефляция
Хорнер Факторинг
Множественные полиномиальные корни
Назначение

Это долгий и сложный проект. Мы разрешаем 3 лабораторных дня для этого.

Не будет нет лаборатории , понедельник, 11 октября.

Полиномы так часто встречаются в математических вычислениях, что важно иметь хорошее представление о:

как оценить многочлен;
как вычислить производную многочлена;
как найти один действительный корень многочлена;

Вспомним, что мы уже знаем о MATLAB и многочленах, и обсудим некоторые другие команды MATLAB, которые будут полезны.

MATLAB не позволит нам использовать ноль в качестве индекса вектора. Так что, к сожалению, если мы хотим сохранить коэффициенты многочлена в векторе индекс коэффициента не может соответствовать показатель степени 9(n-2) + … + c(n-1) * x + c(n)

MATLAB имеет встроенную команду, которая, учитывая коэффициенты c полинома, оценит его в точке x

px = многозначный ( c , x )

многозначный ([1, -2, 12], [0, 1, 2, 3, 4])

Команда polyder вычисляет коэффициенты производной многочлен. Таким образом, для оценки производной в точке требуется два шага:

cp = полидер ( c )
pp = многозначный ( cp , x )

Сегодня мы напишем собственные версии этих подпрограмм!

MATLAB может взять набор корней (действительных или мнимых) и построить коэффициенты соответствующего полинома. команда поли(v) . Если я установлю

v = [0, 1, 2, 3];
с = поли [v];

с = [1, -6, 11, -6, 0]

Упражнение

MATLAB также может найти корни, учитывая коэффициенты. (Разве это невозможно?) Попробуйте команды:

с = [1, -6, 11, -6, 0]
v = корни ( с )

Предположим, кто-то просит вас оценить многочлен

92 — 5) * (х — 2) — 4

p(2)

Важная идея здесь заключается в том, что всякий раз, когда мы можем переписать многочлен как

p(x) = q(x) * (x — a) + константа

x=a

p(a)=constant

р(х) = q(х) * (х — а) + р(а)

По сути, это форма синтетического подразделения , в котором мы находимся. всегда делится на линейный множитель вида x-a . Помните синтетическое деление? Это метод, с помощью которого можно упростить полиномиальную дробь, в этом любимый метод частичных дробей из исчисления.

Метод Хорнера : вычисление многочлена с коэффициентами c в точке x делаем следующее:

 
        px = с (1)
        для я = 2: п
          px = px * x + с (я)
        конец

Совет по программированию : чтобы использовать этот метод, нам нужно определить порядок n полинома. Мы могли бы передать это в качестве дополнительного аргумент, но не достаточно ли MATLAB умен, чтобы знать, сколько записей там находятся в векторе коэффициентов? Да, это. Помните, что по умолчанию все в MATLAB «на самом деле» представляет собой двумерный массив. Твой Вектор полиномиальных коэффициентов на самом деле представляет собой матрицу с 1 строкой и н колонки. Чтобы спросить MATLAB, сколько столбцов в элементе данных c есть, пишем:

п = размер (с, 2)

строк

м = размер (с, 1)

Классная дискуссия : С одной стороны, в этом нет ничего страшного. Кто угодно может вычислить многочлен. Но подумайте об этом с точки зрения вычислений. Метод Хорнера использует значительно меньшее количество умножений. Чтобы убедиться в этом, определите количество умножений необходимо оценить 92+8*х+12 используя «естественный» способ вычисления многочлена. Теперь определите количество умножений, используемых в методе Горнера. Если р(х) были многочленом степени 20, сколько умножений было бы вовлеченный?

Упражнение . Работая с приведенным выше планом, напишите M-файл. называется horner.m вида 92+3*х-4 который имеет следующие значения:

 
        Х: -1 0 1 2 3
        Р(Х): -10 -4 -2 2 14

Если мы хотим использовать метод Ньютона, нам понадобится не только многочлен, но и его производная. Мы могли бы сделать это много неправильно способами, но оказывается, есть очень эффективный способ в дополнение к методу Горнера. 2 + 3 * х — 4 который имеет следующие значения:

 
        Х: -1 0 1 2 3
        Р(Х): -10 -4 -2 2 14
        Р'(Х): 10 3 2 7 18

Теперь, если метод Хорнера позволяет легко вычислить значение и производную полинома в любой точке x , тогда мы все готовы использовать Метод Ньютона! Вместо написания двух функций, оценивающих функции и ее производной, мы просто передаем коэффициенты многочлен.

Вот набросок того, как будет выглядеть такой алгоритм:

 
      корень функции = polynew ( c, x )

      ФАТОЛ = ?
      ШАГМАКС = ?

      для шага = 1, STEPMAX

        пкс = ?
        пп = ?

        если ( | пикс |

Я преднамеренно очень небрежен в этом наброске по двум причинам. Вам нужно подумать, как вы заполняете правильные шаги, и я хочу поощрять вас развивать свои идеи программирования, начиная с расплывчатый набросок, подобный этому, а затем заполнение деталей. Получить сначала правильно общую картинку, а уж потом ее заполнять!

Проблема программирования : ваш M-файл для метода Хорнера теперь возвращает сразу два значения, px и pp . Как вы думаете, что это правильный способ вызвать вашу функцию Хорнера и «поймать» оба значения оно хочет вернуться?

Упражнение . Работая с приведенным выше планом, напишите M-файл. называется polynew.m , который принимает коэффициенты многочлена и отправной точкой, и ищет корень. Вам нужно будет вызвать ваш файл метода Хорнера как часть решения. Начать с 92 — 6*х+10

Теперь метод Ньютона дает нам способ найти один корень многочлена. Но дело в том, что многочлен степени n состоит в том, что мы знаем, что он вполне может иметь целых n действительных корней. Предположим, у нас есть нашел один корень многочлена, есть ли способ поискать другой?

Очевидно, есть несколько очень простых способов попробовать это. Мы могли бы например, просто выберите другую начальную точку. Если это все еще сходились к исходному корню, мы могли бы продолжать пробовать множество других начальных точки. Но это неорганизованный способ действовать. Более того, это может быть, что многочлен имеет только один действительный корень с кратностью больше 1. Не было бы никакого способа сказать, что это было так используя этот случайный метод.

Вместо этого мы можем попытаться быть методичными, используя идею, известную как дефляция . Идея дефляции очень проста: если p(x) имеет n корней, и мы знаем один из них, r1 , то искать для других мы могли бы также разделить множитель x-r1 и рассмотрим более простой многочлен p2(x) :

p2(x) = p(x) / (x — r1)

p2(x)

x = r1

p(x)

р1

p2(x)

p3(x)

Предположительно, если наши расчеты достаточно точны, мы могли бы имеют хорошие шансы найти каждый действительный корень исходного многочлена, и мы также учли бы их множественность. То есть, если 3,5 — это корень с кратностью 4, мы бы нашли это значение 4 отдельных раза.

Предполагая, что r1 является корнем p(x) , мы можем использовать разновидность метода Хорнера для определения полиномиального множителя p2(x) , так что

p(x) = p2(x) * (x — r1) + p(r1)

Метод Хорнера для факторинга с остатком : Учитывая коэффициенты c многочлена p(x) определяют количества б :

 
        б(1) = с(1)
        для i = 2:n-1
          b(i) = c(i) + r1 * b(i-1)
        конец
        rem = c(n) + r1 * b(n-1)

p2(x)

rem

p(r1)

. Упражнение . Руководствуясь вышеприведенной схемой, создайте M-файл. horner_factor.m , с формой

функция [ b, rem ] = horner_factor ( c, r1 )

Прежде чем мы перейдем к поиску нескольких корней, давайте удостоверимся, что это хорошая штука не только хорошо выглядит, но и работает! Мы возьмем простой проблему, и посмотрим, сможет ли код вытащить корни, как мы их укажем.

Упражнение :

Определите c4 = poly ([1, 2, 3, 4]) ;
Убедитесь, что polyval ( c4, [1, 2, 3, 4] ) равно нулю.
Выделите корень x = 1 , используя ваш horner_factor . код, сохраняющий полученные полиномиальные коэффициенты как c3 ;
Проверяем значения поливала ( c3, [1, 2, 3, 4] ) ;
Теперь, работая с c3 , находим c2 и c1 , каждый раз отбрасывая еще один корень.

Итак, давайте посмотрим, сможем ли мы набросать метод получения некоторых или всех действительных корней многочлена p(x) . Ну и первый корень r1 легко, потому что мы можем просто использовать метод Ньютона для p(x) . Но тогда мы можем использовать метод Хорнера, чтобы переписать p(x) как

p(x) = p2(x) * (x — r1) + p(r1)

p(r1)

p2(x)

Вот набросок рутины, которая вам нужна.

 корни функции = mulpolynew ( c, x )  Установите  корня  в «пустой» вектор;
 Установите  n  на размер вектора коэффициентов.No related posts.

Таблица горнера как пользоваться: Простая физика — EASY-PHYSIC

Простая физика — EASY-PHYSIC

EDSAC aka «Very simple machine» / Хабр

Вопрос

Horner’$ Melhod) . Используйте метод Хорнера для вычисления многочлена f(c) =26 + 215 34 43 512 61 + при & = 1445 и при 0 = -145 в арифметике с 6-значной плавающей запятой (FPA…

Рекомендуемый AI ответ:

Рекомендация видео с лучшим совпадением:

Вопрос о лучшем совпадении:

Рекомендуемые видео

Поделиться вопросом

Добавить в плейлист

Хммм, кажется, у вас нет плейлистов. Пожалуйста, добавьте свой первый плейлист.

Лабораторная работа №5: Полиномы и метод Ньютона

Добавить комментарий Отменить ответ