ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ • Большая российская энциклопедия
ТРИГОНОМЕТРИ́ЧЕСКИЕ ФУ́НКЦИИ, элементарные функции синус, косинус, тангенс, котангенс, секанс, косеканс. Обозначаются соответственно $\sin x$, $\cos x$, $\text{tg}\, x$, $\text{ctg}\, x$, $\sec x$, $\text{cosec}\, x$. Используются и др. обозначения, напр. $\tan x$, $\cot x$, $\text{cotg}\,x$, $\text{ctn}\,x$.
Пусть $A$ – точка окружности единичного радиуса с центром в начале координат и $α$ – угол между осью абсцисс и вектором $OA$, отсчитываемый от положительного направления оси абсцисс (рис. 1). При этом если отсчёт ведётся против часовой стрелки, то величина угла считается положительной, а если по часовой стрелке – отрицательной. Если ($x_α$,$y_α$) – декартовы прямоугольные координаты точки $A$, то Т. ф. синус и косинус определяются как $$\sin α=y_α,\,\,\cos α=x_α,$$ Остальные Т. ф. определяются равенствами$$\text{tg}\,α=\frac{\sin α}{\cos α},\,\text{ctg}\,α=\frac{\cos α}{\sin α},\\ \text{sec}\,α=\frac{α}{\cos α},\,\,\text{cosec}\,α=\frac{1}{\sin α}.
$$
Угол может измеряться как в (угловых) градусах, так и в радианах и изменяется от $–∞$ до $+∞$. Чаще используется радианное измерение, при этом обозначение радиан опускается и Т. ф. считаются функциями числового аргумента. При радианном измерении считается, что α есть взятая с соответствующим знаком длина дуги единичной окружности, соединяющей точки (1, 0) и $A$, при этом допускается, что эта дуга, прежде чем закончиться в точке $A$, может неск. раз наматываться на окружность. Точку $A$ называют ещё точкой $α$, при этом нужно иметь в виду, что числам $α$ и $α+2kπ$, $k=0,±1,±2,…,$ соответствует одна и та же точка единичной окружности. Иногда точки этой окружности делят на четверти, при этом в I четверти окружности находятся точки, для которых $2kπ < α < 2kπ+π/2$, во II четверти – точки, для которых $2kπ+π/2 < α < 2kπ+π,$ в III четверти – точки, для которых $2kπ+π < α < 2kπ+3π/2$, в IV четверти – точки, для которых $2kπ+3π/2 < α < 2kπ+2π$, $k=0,±1,±2,.
..$.
Для углов, величины которых лежат между 0 и $π/2$, значения Т. ф. можно определять как отношения сторон прямоугольного треугольника. На рис. 2 показан прямоугольный треугольник с катетами $a$, $b$ и гипотенузой $c$. Для угла $α$, противолежащего катету $a$, справедливы равенства $$\sin α=a/c,\,\cos α=b/c,\,\text{tg}\,α=a/b,\\ \text{ctg}\,α=b/a,\,\text{sec}\,α=c/b,\,\text{cosec}\,α=c/a.$$
На рис. 3 показано представление Т. ф. как отрезков, связанных с единичной окружностью:$$\sin α=AB,\,\cos α=OB,\,\text{tg}\,α=CD,\\ \text{ctg}\,α=EF, \text{sec}\,α=OC,\,\text{cosec}\,α=OF$$ (римские цифры I–IV на рис. 3 обозначают четверти единичной окружности). С этими отрезками связано происхождение названий Т. ф. Так, лат. слово «tangens» означает касающийся ($\text{tg}\,α$ изображается отрезком $CD$ касательной к окружности), «secans» – секущая ($\text{sec}\,α$ изображается отрезком $OC$ секущей к окружности.
Назв. «синус» (лат. sinus – пазуха) – перевод араб. слова «джайб», являющегося, по-видимому, искажением санскр. слова «джива» (букв. – тетива лука), которым инд. математики обозначали синус ($\sin α$ изображается отрезком $AB$). Названия «косинус», «котангенс», «косеканс» происходят от сокр. слова «complementi» (дополнение). Напр., «косинус» – от «complementi sinus» (синус дополнения). Это связано с тем, что $\cos α$, $\text{ctg}\,α$, $\text{cosec}\,α$ равны соответственно синусу, тангенсу и секансу аргумента, дополняющего $α$ до $π/2$: $$\cos α=\sin(π/2-α),\,\text{ctg}\,α=\text{tg}\,(π/2-α),\\ \text{cosec}\,α=\sec(π/2-α).$$
Т. ф. секанс и косеканс используются редко, обычно их сразу выражают через синус и косинус по формулам$$\text{sec}\,α=1/\cos α,\,\text{cosec}\,α=1/\sin α,$$поэтому в дальнейшем они не участвуют.
Т. ф. sinα и cosα определены при всех действительных α, множество значений этих функций – отрезок [–1, 1].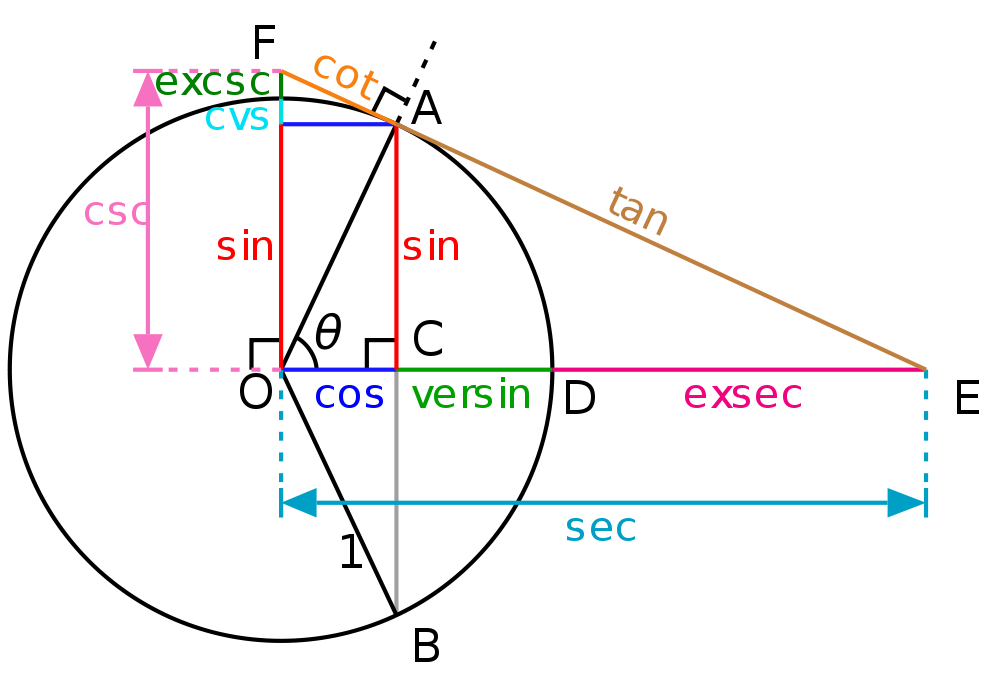
Функция $\text{tg}\,α$ определена при всех действительных α таких, что $α≠π/2+kπ$, $k=0,±1,±2,…$. Функция $\text{ctg}\,α$ определена при всех действительных α таких, что $α≠kπ$, $k=0,±1,±2,…$. Множеством значений функций тангенс и котангенс является множество всех действительных чисел.
Все Т. ф. являются периодич. функциями. Наименьший положительный период функций синус и косинус равен $2π$, т. е. для любого действительного $α$ $$\sin(α+2π)=\sin α,\,\cos(α+2π)=cos α,$$наименьший положительный период функций тангенс и котангенс равен $π$, т. е. для любого $α$ из областей их определения$$\text{tg}(α+π)=\text{tg} α,\,\text{ctg}(α+π)=\text{ctg} α.$$ График функции синус см. в ст. Синусоида, график функции косинус получается сдвигом синусоиды влево на величину $π/2$. График функции тангенс – тангенсоида – приведён на рис. 4, график функции котангенс приведён на рис.
5, он получается зеркальным отражением тангенсоиды относительно оси абсцисс и сдвигом влево на $π/2$. Функция $\sin α$ положительна в I и II четвертях единичной окружности, в др. четвертях она отрицательна. Функция $\cos α$ положительна в I и IV четвертях, в др. четвертях она отрицательна. Функции $\text{tg} α$ и $\text{ctg} α$ положительны в I и III четвертях, в др. четвертях они отрицательны. Функция $\sin α$ возрастает в I и IV четвертях, в др. четвертях она убывает. Функция $\cos α$ возрастает в III и IV четвертях, в др. четвертях она убывает. Функция $\text{tg}\,α$ возрастает во всех интервалах, где она определена. Функция $\text{ctg}\,α$ убывает во всех интервалах, где она определена.
Значения Т. ф. любого аргумента можно выразить через Т. ф. аргумента, лежащего в I четверти. Для этого нужно исходный аргумент представить в виде $2kπ+β$, где $0 ⩽ β < 2π$, а $k$ – целое число, и воспользоваться равенством $f(2kπ+β)=f(β)$, где $f$ – любая из Т.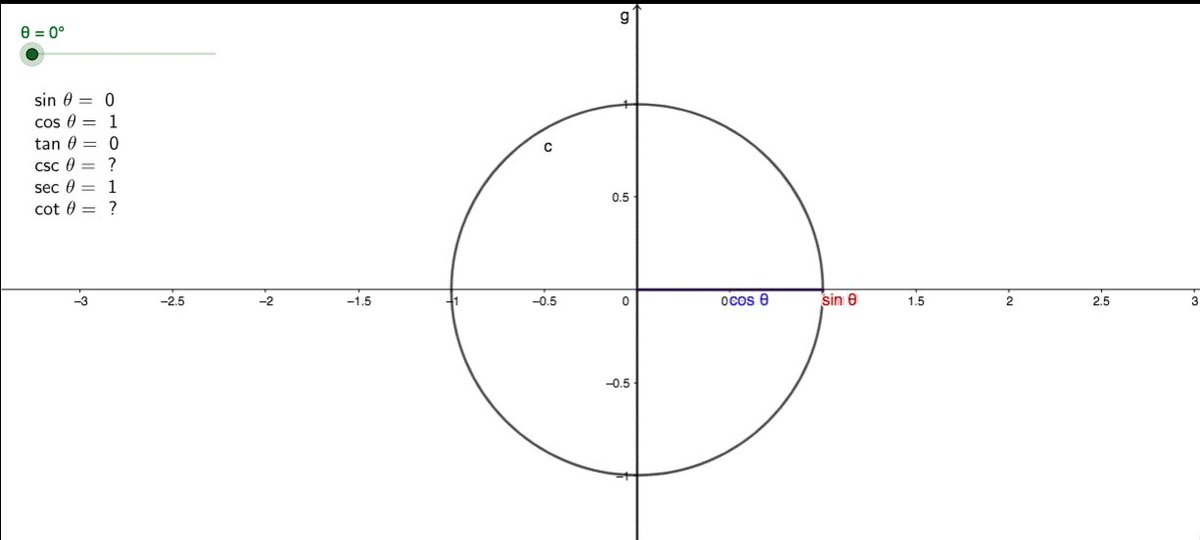
ф. Затем, если $β$ не лежит в I четверти, нужно воспользоваться формулами приведения, которые дают значения Т. ф. аргумента $β$, $π/2 < β < 2π$, через значения Т. ф. аргумента $α$, $0 < α < π/2$. Эти формулы даны в таблице:
| $β$ | $\sin β$ | $\cos β$ | $\text{tg}\,β$ | $\text{ctg}\,β$ |
|---|---|---|---|---|
| $π/2-α$ | $\cos α$ | $\sin α$ | $\text{ctg}\,α$ | $\text{tg}\,α$ |
| $π/2+α$ | $\cos α$ | $-\sin α$ | $-\text{ctg}\,α$ | $-\text{tg}\,α$ |
| $π-α$ | $\sin α$ | $-\cos α$ | $-\text{tg}\,α$ | $\text{ctg}\,α$ |
| $π+α$ | $-\sin α$ | $-\sin α$ | $\text{ctg}\,α$ | $\text{tg}\,α$ |
| $3π/2-α$ | $-\cos α$ | $\sin α$ | $-\text{ctg}\,α$ | $-\text{tg}\,α$ |
| $2π-α$ | $-\sin α$ | $\cos α$ | $-\text{tg}\,α$ | $-\text{ctg}\,α$ |
Для некоторых значений аргумента значения Т.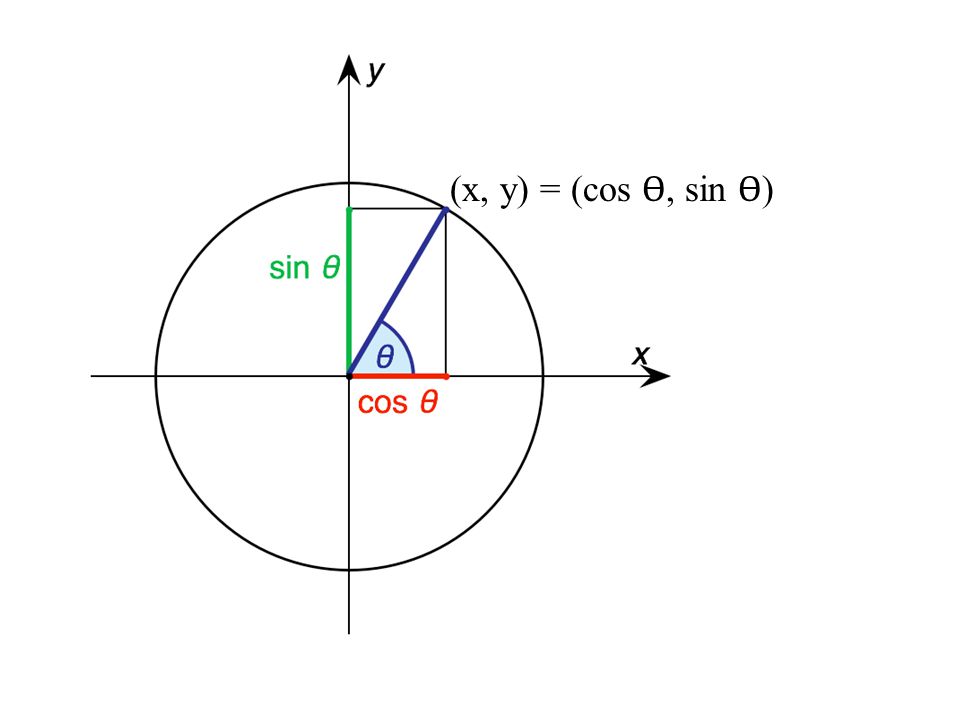
ф. можно найти из геометрич. соображений. Так, $$\sin 0 = \cos \frac{π}{2} = \text{tg}\,0=0,$$ $\text{ctg}\,0$ не существует;$$\sin\frac{π}{6}=\cos\frac{π}{3}=\frac{1}{2};\\ \text{tg}\,\frac{π}{6}=\text{ctg}\,\frac{π}{3}=\frac{\sqrt{3}}{3}\approx0,5774;\\ \sin\frac{π}{4}=\cos\frac{π}{4}=\frac{\sqrt{2}}{2}\approx 0,7071,\\ \text{tg}\, \frac{π}{4}=\text{ctg}\,\frac{π}{4}=1;\\ \sin\frac{π}{3}=\cos\frac{π}{6}=\frac{\sqrt{3}}{2}\approx 0,8660,\\ \text{tg}\,\frac{π}{3}=\cos\frac{π}{6}=\sqrt{3}\approx 1,7322;\\ \sin\frac{π}{2}=\cos 0=1,\,\, \text{ctg}\,\frac{π}{2}=0,$$ $\text{tg}\,\frac{π}{2}$ не существует.
Для любого значения аргумента значения Т. ф. можно находить с помощью их разложения в степенные ряды (см. ниже).
Функции $\sin nα$ и $\cos nα$ при любом натуральном $n$ можно находить с помощью Муавра формулы, выражая их через многочлены от $\sin α$ и $\cos α$.
Наиболее важные соотношения между Т. ф. одного аргумента: $$\sin^2α+\cos^2α=1,\,\,\text{tg}\,α\,\text{ctg}\,α=1;\\ 1+\text{tg}^2\,α=\frac{1}{\cos^2α},\,\,1+\text{ctg}^2α=\frac{1}{\sin^2α}.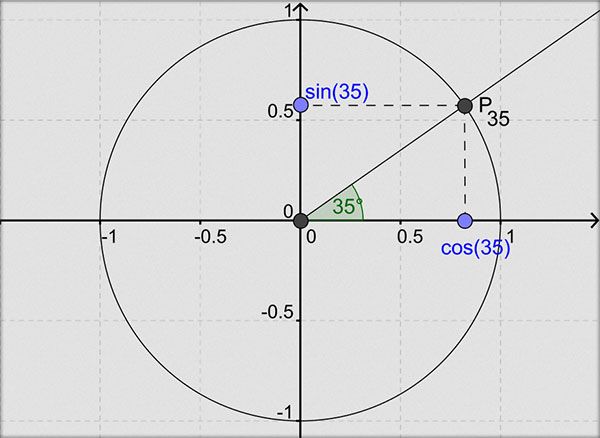
n\arcsin a+kπ,\\ α=±\arccos a+2kπ,\,k=0,±1,±2,…\,.$$ Решения уравнений $\text{tg}\,α=a$, $\text{ctg}\,α=a$ для любого действительного $a$ суть $$α=\text{arctg}\,a+kπ,\,α=\text{arcctg}\,a+kπ,\,k=0,±1,±2,…\,.$$
Т. ф. определяются также для комплексных значений аргумента как аналитич. продолжения Т. ф. действительного аргумента.
Т. ф. появились в связи с исследованиями в астрономии и геометрии. Соотношения отрезков в треугольнике и окружности, являющиеся, по существу, Т. ф., встречаются уже в работах математиков Древней Греции – Евклида, Архимеда, Аполлония Пергского и др. Однако эти соотношения не являются у них самостоят. объектом исследования, так что Т. ф. как таковые ими не изучались. Т. ф. рассматривались как отрезки и в таком виде применялись Аристархом Самосским, Гиппархом, Менелаем и Птолемеем при решении сферич. треугольников. Птолемей составил первую таблицу хорд для острых углов через 30´ с точностью до 10–6.
Это была первая таблица синусов. Формулы преобразования сумм Т. ф. в произведения выводились Региомонтаном и Дж. Непером в связи с изобретением последним логарифмов (1614). Региомонтан дал таблицу синусов через 1´. Разложения Т. ф. в степенные ряды получены И. Ньютоном (1669). В совр. форму теорию Т. ф. привёл Л. Эйлер (18 в.), который предложил и принятую ныне символику.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | sin(60) | ||
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |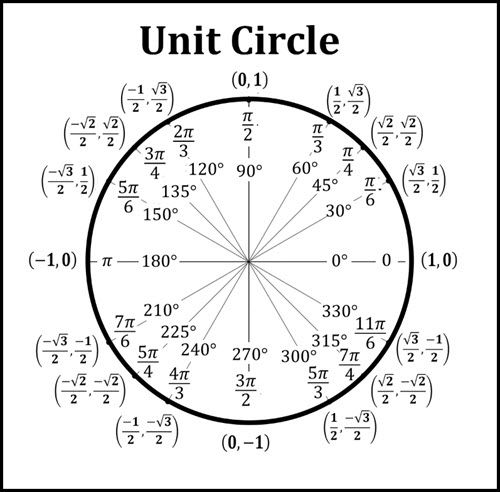
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
python 2.7 — Рисование круга с помощью cos() sin(), без повторяющихся пикселей, без пробелов?
спросил
Изменено 1 год, 10 месяцев назад
Просмотрено 2к раз
Мне интересно нарисовать круг разного радиуса с помощью функций sin() и cos().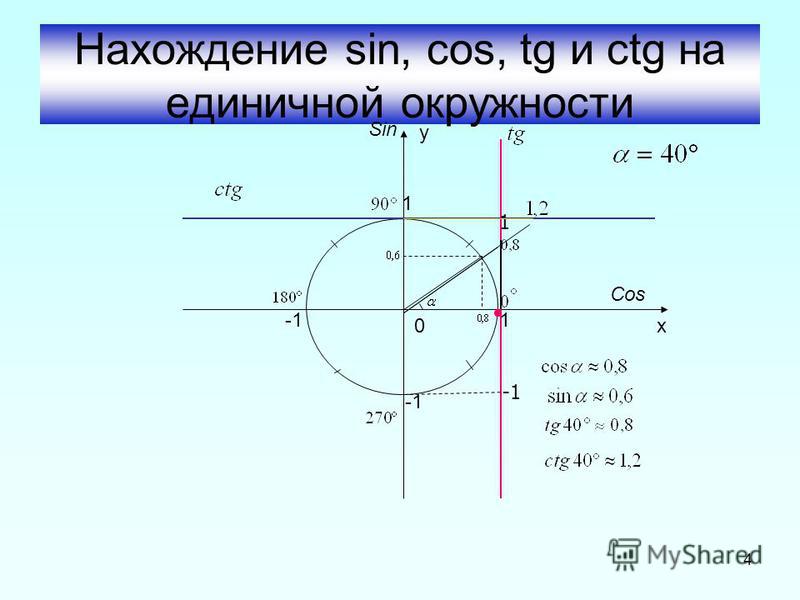
Существует ли золотое правило для увеличения радианов, чтобы не было нескольких графиков в одном и том же месте и не было пробелов в круге, нарисованном на пиксельном дисплее?
х = cos(r) * радиус у = грех (r) * радиус р = р + с
Я предполагаю, что s как-то связан с делением 2 × PI на число, полученное из радиуса?
Я уверен, что это либо очень просто, либо невозможно из-за ограничений вычислений с плавающей запятой.
Спасибо за внимание
Энтони
- питон-2.7
- тригонометрия
1
Длина дуги равна просто s = r * delta_fi , где r — радиус окружности, fi — угол, а delta_fi — изменение угла.
Проекция этой дуги на ось x равна delta_x = s * sin(fi) , а на ось y — delta_y = s * cos(fi)
Вам нужен такой delta_fi , что либо delta_x , либо delta_y равно 1.
Очевидно, задача симметрична, и мы можем решить ее для fi от -45° до 350 delta 45° и для 3 delta 45° до 45° 3. а затем применить то же решение в других квадрантах. Имеем:
r * delta_fi * cos(fi) = 1
Отсюда:
delta_fi = 1/cos(fi)/r
Координаты окружности действительно могут быть полностью определены с помощью тригонометрической функций синуса и косинуса:
x = cos(угол)
y = sin(угол)
Если радиус имеет любое значение, отличное от 1 (которое определяет единичную окружность), основные принципы тригонометрических функций все еще применяются и , поэтому можно вывести следующие уравнения:
x = cos(угол) * радиус
y = sin(угол) * радиус
Чтобы реализовать это в Python (с любезной помощью Numpy), все что необходимо в дополнение к тому, что мы уже определили, это подходящий вектор (или одномерный массив) для угла, который будет оцениваться функцией x и y.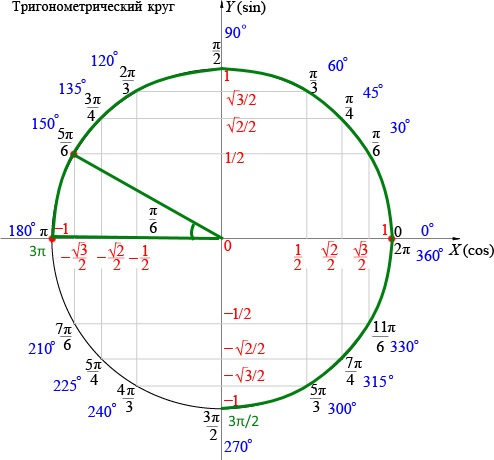
импортировать numpy как np
r = 2 # Произвольное значение радиуса
angle = np.linspace(0, 2*np.pi, 1000) # Вектор, покрывающий все углы от
# от 0 до 2*pi (полный круг в радианах)
# с произвольным количеством
# элементов, в данном примере 1000
х = np.cos(угол)*r
y = np.sin(угол)*r
При построении этого круга не забудьте подогнать размер фигуры под квадрат, иначе круг будет искажен.
импортировать matplotlib.pyplot как plt plt.figure(figsize=(3, 3)) plt.plot(x, y)
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Юнит Круг | Brilliant Math & Science Wiki
Акшай Ядав, Энди Хейс, Ареян Манзур, и
способствовал
Содержимое
- Отношение к прямоугольным треугольникам
- Углы в единичной окружности
- Координаты в единичном круге
- Специальные углы на единичной окружности
Каждая точка на единичной окружности соответствует прямоугольному треугольнику с вершинами в начале координат и точкой на единичной окружности.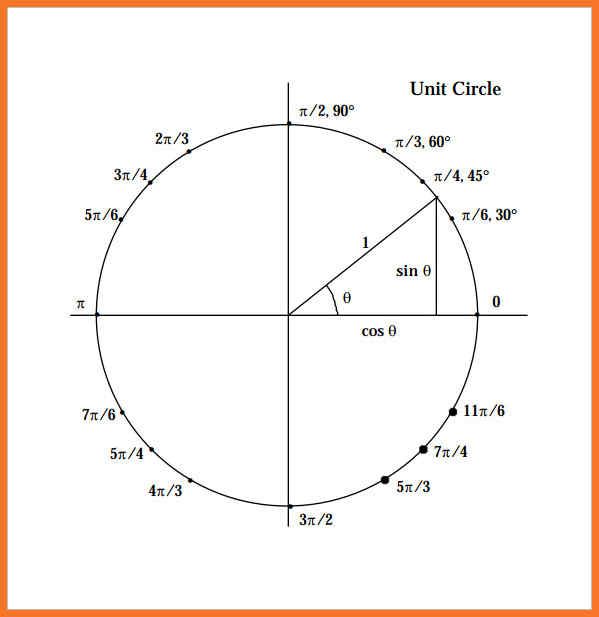
Длины катетов прямоугольного треугольника равны абсолютным значениям координат xxx и yyy соответственно.
Этот прямоугольный треугольник используется для применения тригонометрических соотношений.
sin (θ) = противоположная гипотенуза = bccos (θ) = смежная гипотенуза = актан (θ) = противоположная смежная = ba \begin {массив} {rll} \ sin (\ theta) & = \ frac {\ text {напротив}} {\ text {гипотенуза}} & = \ frac {b} {c} \\ \\ \ cos (\ theta) & = \ frac {\ text {смежный}} {\ text {гипотенуза}} & = \ frac {a} {c} \\ \\ \ tan (\ theta) & = \ frac {\ text {напротив}} {\ text {смежно}} & = \ frac {b} {a} \\ \\ \end{массив}sin(θ)cos(θ)tan(θ)=hypotenuseopposite=hypotenuseadjacent=adjacentopposite=cb=ca=ab 9Угол \circ∘ равен 14\frac{1}{4}41 пути по окружности, что будет равно 2π4=π2.\frac{2\pi}{4}=\frac{\pi} {2}.42π=2π.
Некоторые возможные значения θ\thetaθ перечислены ниже вместе с соответствующими значениями синуса и косинуса.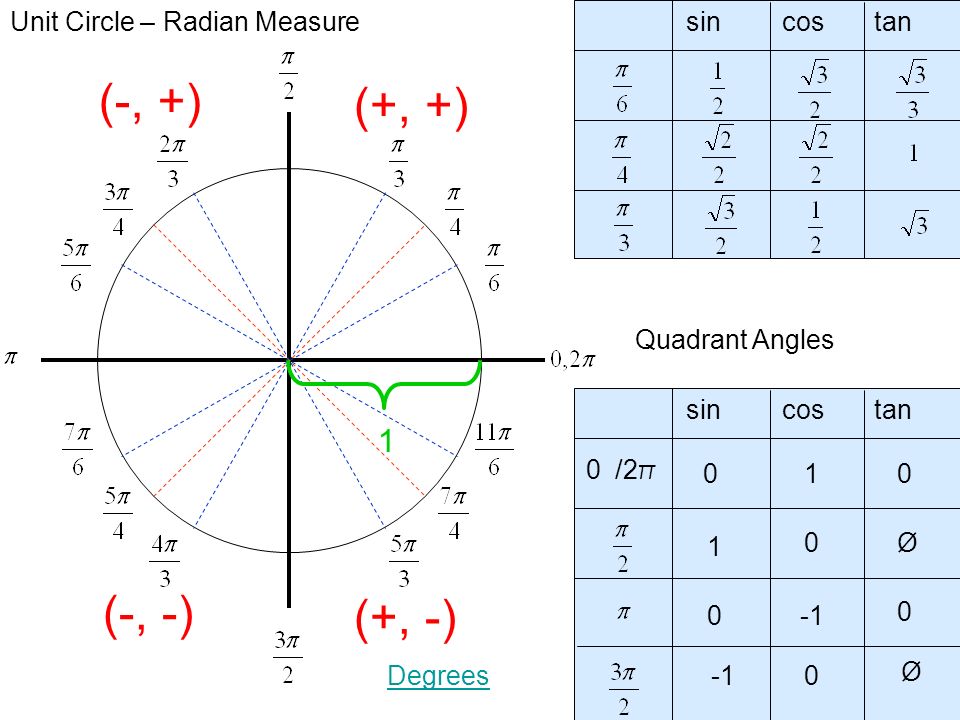
мера угла, θsinθcosθ001π61232π42222π33212π210 \начать{массив} { | с | с | с | } \hline \text{мера угла, } \theta & \sin \theta & \cos \theta\\ \hline 0 и 0 и 1 \\ \hline \dfrac{\pi}{6} & \dfrac{1}{2} & \dfrac{\sqrt{3}}{2} \\ \hline \ dfrac {\ pi} {4} & \ dfrac {\ sqrt {2}} {2} & \ dfrac {\ sqrt {2}} {2} \\ \hline \dfrac{\pi}{3} & \dfrac{\sqrt{3}}{2} & \dfrac{1}{2} \\ \hline \dfrac{\pi}{2} & 1 & 0 \\ \hline \end{массив} мера угла, θ06π4π3π2πsinθ02122231cosθ12322210
Тригонометрия, с которой мы уже знакомы, основана только на прямоугольных треугольниках и острых углах. Однако с помощью Unit Circle мы можем расширить наше понимание тригонометрических функций, а также познакомиться с использованием неострых углов.
Дополнительную информацию о круговой системе измерения углов можно найти на ее вики-странице.
Угол на единичной окружности всегда измеряется от положительной оси ххх с вершиной в начале координат.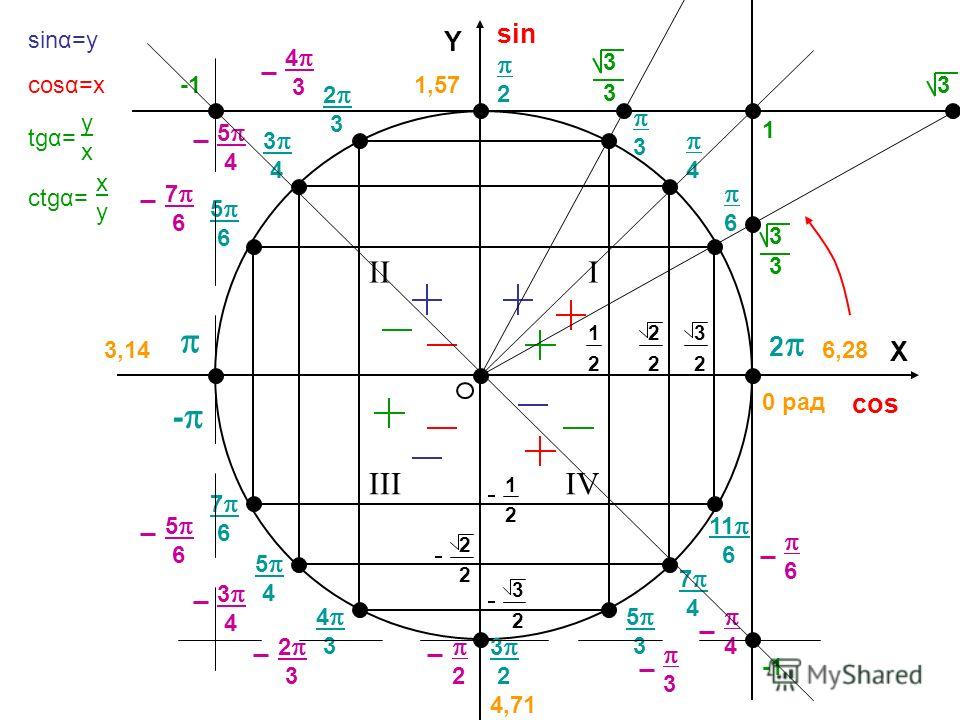
Измеряется до точки на единичной окружности. Луч, начинающийся в начале координат и содержащий точку единичной окружности, называется 9-м.\circ,2πrad=360∘, любые градусы можно перевести в радианы и наоборот.
Пусть ddd будет измерением угла в градусах, а rrr будет измерением того же самого угла в радианах.
r=πd180r = \frac{\pi d}{180}r=180πd
d=180rπd = \frac{180r}{\pi}d=π180r
Прямоугольный треугольник AOBAOBAOB с прямым углом при AAA лежит на декартовой плоскости так, что OA‾\overline{OA}OA лежит на оси xxx , точка OOO лежит в начале координат, а точка BBB лежит в любом месте единичной окружности. Обратите внимание, что OB=1OB=1OB=1 единиц.
Тригонометрические функции синуса и косинуса приведены ниже. При определении этих функций в терминах единичного круга возможны отрицательные длины. Если OA‾\overline{OA}OA расположен вдоль отрицательной оси xxx, то OAOAOA считается отрицательным.
Аналогично, если AB‾\overline{AB}AB простирается ниже оси xxx, то ABABAB считается отрицательным.
sin(θ)=противоположная гипотенуза=ABOB=AB1=ABcos(θ)=прилежащая гипотенуза=OAOB=OA1=OA. \begin{выровнено} \ sin (\ theta) &= \ frac {\ text {напротив}} {\ text {гипотенуза}} = \ frac {AB} {OB} = \ frac {AB} {1} = AB \\ \cos (\theta) &= \frac{\text{смежный}}{\text{гипотенуза}} = \frac{OA}{OB} = \frac{OA}{1} = OA. \end{align}sin(θ)cos(θ)=hypotenuseopposite=OBAB=1AB=AB=hypotenuseadjacent=OBOA=1OA=OA.
По этому соглашению синус угла считается координатой yyy точки на единичной окружности, заданной этим углом. Точно так же косинус угла считается xxx-координатой точки на единичной окружности, заданной этим углом. В общем, чтобы вычислить синус или косинус любого угла θ,\theta,θ, посмотрите на координаты точки на единичной окружности, образованной этим углом.
Основная статья: Специальные углы на единичной окружности
Специальные углы — это углы на единичной окружности, координаты которых известны.