Свойства хорд и дуг окружности
- Диаметр, перпендикулярный хорде, делит эту хорду и дуги, которые она стягивает пополам.
- Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
- Большая из двух хорд расположена ближе к центру окружности.
- У равных дуг равны и хорды.
- Дуги, заключенные между параллельными хордами, равны.
- Произведения длин отрезков, на которые разбита каждая из хорд, равны: \(AE\cdot EB=CE\cdot ED\).
Вопросы
Часть окружности, ограниченная двумя точками, это
Сообщить об ошибке
Обязательные
Математическая грамотность
Грамотность чтения
История Казахстана
Предметы по профилю
Биология
Химия
Английский язык
Французский язык
География
Немецкий язык
Информатика
Основы права
Русская литература
Математика
Физика
Русский язык
Всемирная история
Укажите предмет *
Скопируйте и вставьте вопрос задания *
Опишите подробнее найденную ошибку в задании *
Прикрепите скриншот
Объем файла не должен превышать 1МБ
Казахский
Русский
Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market
2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами
Окружность и круг. Части окружности и круга
Репетиторы ❯ Математика ❯ Окружность и круг. Части окружности и круга
Автор: Владимир Л., онлайн репетитор по математике
●
11.10.2011
●
Раздел: Математика
Многие предметы вокруг нас имеют форму, похожую на геометрические фигуры.
Чтобы разобраться, что такое окружность и чем она отличается от круга, необходимо иметь чёткое представление об этих фигурах. Если поставить круглый стакан на лист бумаги и обвести его карандашом, получится линия, изображающая окружность. Если рассмотреть эту линию под микроскопом, то мы увидим толстую неровную чету. Геометрическая окружность не имеет ширины. Все её точки одинаково удалены от центра. Кольцо, обруч напоминают своей формой окружность.
Окружностью называется фигура, которая состоит из всех точек плоскости, находящихся на данном расстоянии от данной точки. Эта точка называется центром окружности и обычно обозначается О.
Расстояние от точек окружности до её центра называется радиусом окружности и обычно обозначается R. Радиусом также называется любой отрезок, соединяющий точку окружности с её центром.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр, называется диаметром.
Что же такое круг? Круг мы можем вырезать из бумаги.
Арена цирка, дно стакана или тарелка имеют форму круга. Если окружность это «черта» (мы можем ниточкой выложить окружность), то круг это все, что находится внутри окружности.
Кругом называется фигура, которая состоит из всех точек плоскости, находящихся на расстоянии не большем данного, от данной точки. Эта точка называется центром круга, а данное расстояние – радиусом круга. Границей круга является окружность с теми же центром и радиусом.
Окружность и круг состоят из разнообразных частей.
Две точки, взятые на окружности, разобьют эту окружность на две части – две дуги, концами которых будут взятые точки.
Отрезок, соединяющий две точки окружности, называется хордой окружности, и хордой круга, ограниченного этой окружностью.
Хорда, проходящая через центр окружности или круга, называется диаметром окружности или круга. Диаметр делит круг на два полукруга, а окружность – на две полуокружности.
Диаметр делится центром окружности пополам, и поэтому он равен двум радиусам.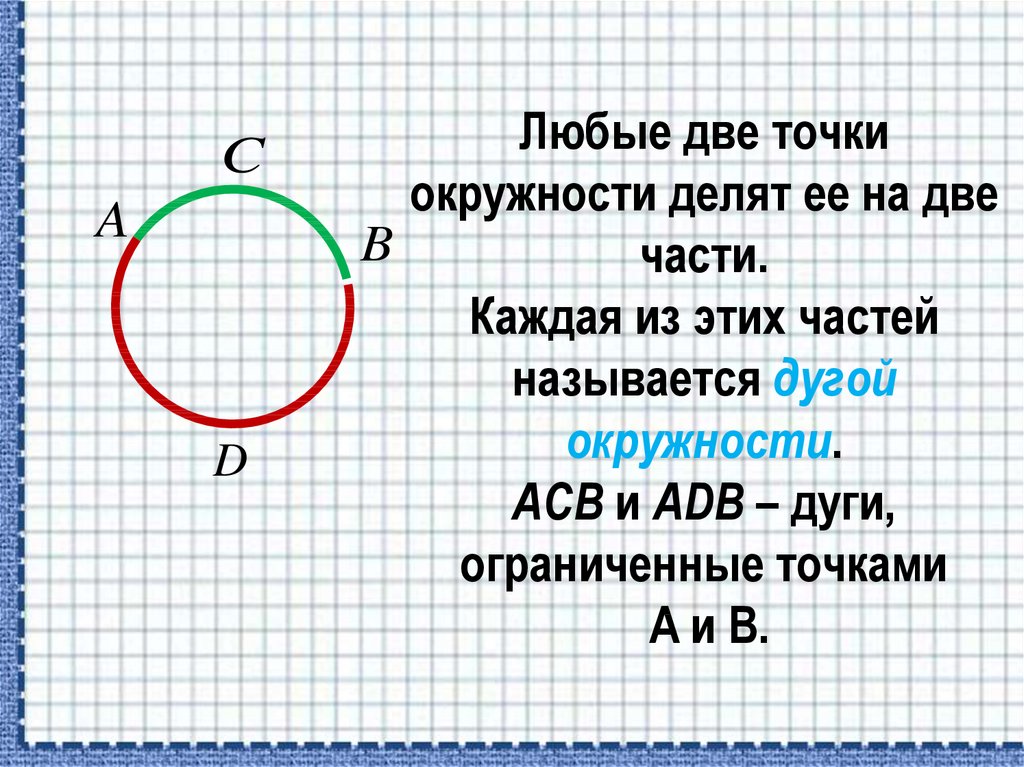
Два радиуса разбивают круг на секторы.
Хорда разбивает круг на сегменты.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
запросов по одному слову.
Что вы называете вложенными кругами, которые не являются концентрическими?спросил
Изменено 4 года, 3 месяца назад
Просмотрено 8к раз
Окружности на изображении не имеют одного центра, поэтому они не концентричны. Есть ли слово для описания кругов, которые перекрываются (полностью или нет) так, что замкнутые круги меньше, чем внешние круги?
- однословные запросы
- математика
На вашем конкретном изображении эти окружности являются касательными окружностями (т. е. все они касаются друг друга). Точнее, они представляют собой окружности, касающиеся внутренних касаний. Согласно Википедии, поскольку все они пересекаются в одной точке, они также известны как «круги поцелуев» (полагаю, неофициально).
Конечно, существует несколько способов рисования кругов, которые «вложены друг в друга, но не концентричны»:
Я бы назвал круги в A вложенными кругами ; и окружности в B и C касательные внутри окружности . Поскольку круги в B касаются в одной точке, их также можно назвать кругами поцелуев . Я бы назвал круги в D вложенными кругами , но, поскольку не все они являются касательными, я бы назвал их , а не касательными кругами
Если вам нужна более формальная терминология, возможно, вам стоит спросить math.se.
1
Я углубляюсь в математику и геометрию, но семейство кругов на изображении называется параболическим карандашом . Такие наборы кругов называются карандаш из кругов . Он также является частью аполлонических кругов .
Параболический пучок (как предельный случай) определяется, когда две образующие окружности касаются друг друга в одной точке. Он состоит из семейства реальных окружностей, касающихся друг друга в одной общей точке. Вырожденная окружность с нулевым радиусом в этой точке также принадлежит карандашу.
Также это могут быть коаксиальные (или коаксиальные) круги.
За исключением двух особых случаев пучка концентрических окружностей и пучка совпадающих прямых, любые две окружности в карандаше имеют одну и ту же радикальную ось, и все окружности в карандаше имеют коллинеарные центры. Любые три или более кругов из одного семейства называются соосными кругами или соосными кругами.
Дополнительная информация:
Карандаш кругов — это другое название определенных семейств кругов, которые имеют определенные характеристики внутри семейства.
Третий тип карандаша — параболический карандаш. Это семейство окружностей , все из которых имеют одну общую точку, и, таким образом, все касаются друг друга либо внутри, либо снаружи. Кроме того, набор окружностей, ортогональный параболическому карандашу, является другим параболическим карандашом.
Источник: http://www.math.washington.edu/~king/coursedir/m445w04/as/ga2/gp2/groupassign2.html
Коаксиальные окружности — это окружности, центры которых коллинеарны и имеют общую радикальную линию. Набор всех коаксиальных окружностей называется пучком коаксиальных окружностей (Коксетер и Грейцер, 1967, стр. 35). Можно комбинировать два типа коаксиальных систем, показанных выше, так что наборы будут ортогональными.
Изображение аполлонических кругов:
0
Эксцентрик : Не расположен по центру или не имеет своей оси или другой части, расположенной по центру.
1
Я только что узнал, что в топологии это известно как гавайская серьга. Всякий раз, когда вы видите «нисходящий» в математике, это обычно означает, что что-то становится меньше или вкладывается во что-то другое. Некоторые распространенные обороты речи включают нисходящая последовательность или нисходящая последовательность наборов . С вашей картинкой я мог бы сказать нисходящий набор кругов некоторым коллегам и быть полностью понятым (это также относится ко всем картинкам в ответе Дж. Р.).
В топологии (раздел математики, изучающий такие формы) мы называем это гавайской серьгой.
Источник: Студентка математики, прошла курс топологии.
2
Без требования уменьшения размера кругов, как показано, перекрывающиеся круги просто пересекаются .
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Части кругов
Круг — это особая фигура, поэтому у него есть части со специальными именами.
Существуют также специальные углы, линии и линейные сегменты, характерные только для кругов. В этой главе мы рассмотрим их все.
- Окружность: Обратите внимание, что окружность это плоская фигура, состоящая из всех точек, равноудаленных от фиксированной точки.
- Центр: Эта фиксированная точка называется центром окружности. Круги называются по названию центра.
- Радиус: Любой сегмент с одной конечной точкой в центре окружности и другой конечной точкой на окружности является радиусом. (Множественное число от радиуса — радиусы.)
- Хорда: Любой отрезок, концы которого лежат на окружности, является хордой.
- Диаметр: Любая хорда, проходящая через центр окружности, является диаметром.
На рис. 1:
Рисунок 1 Специальные точки и отрезки, относящиеся к окружности.
Из определения радиуса и диаметра видно, что все радиусы окружности равны по длине и все диаметры окружности равны по длине.
- Секанс: Любая линия, содержащая аккорд, является секущей.
- Касательная: Любая линия, проходящая в той же плоскости, что и окружность, и пересекающая окружность ровно в одной точке, является касательной.
- Точка касания: Точка, в которой касательная пересекает окружность, является точкой касания.
На рис. 2:
Рисунок 2 Сеанс и касательная к окружности.
- Общие касательные: Прямая, касающаяся двух окружностей в одной плоскости, является общей касательной.
- Внутренняя общая касательная: Общая касательная, пересекающая отрезок, соединяющий центры двух окружностей, является внутренней общей касательной.
