Построение двух графиков онлайн. Калькуляторы для построения графика функции
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.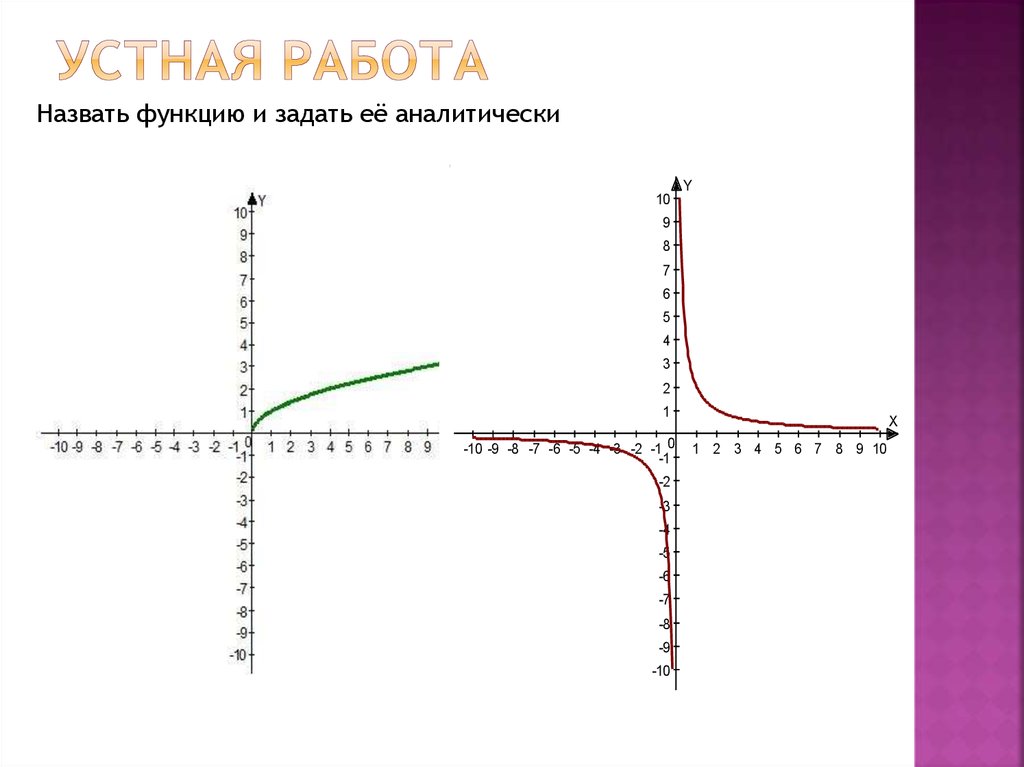
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т.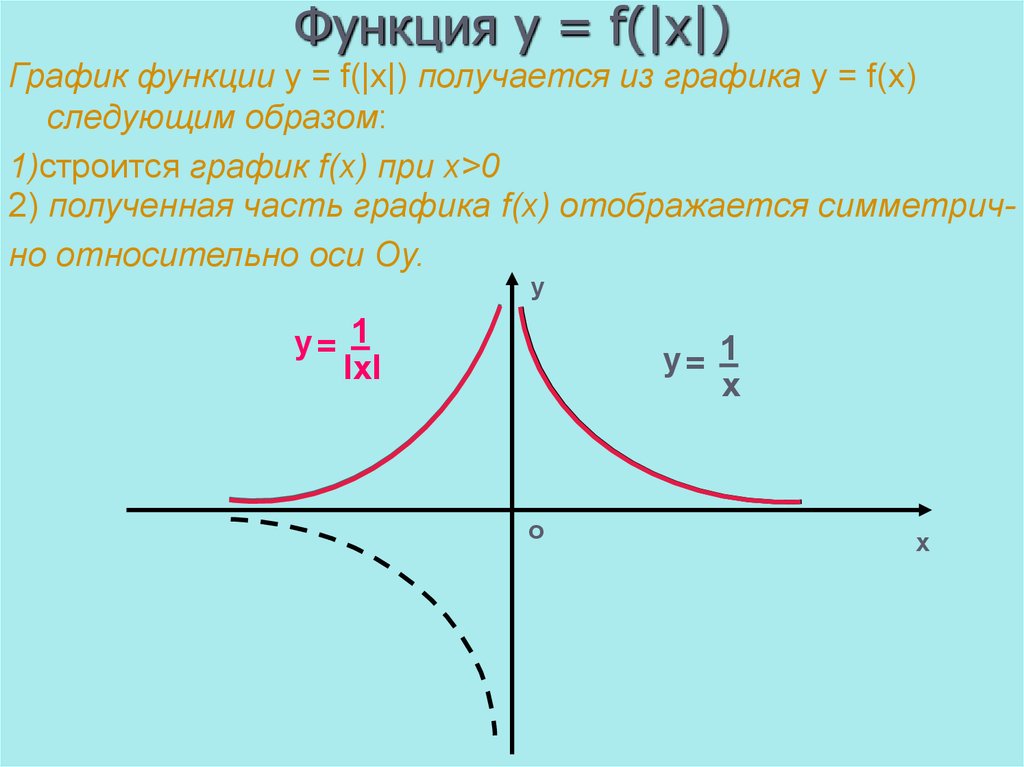 3$.
3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Построение графиков онлайн на миллиметровке.
 Строим график функций онлайн
Строим график функций онлайнК сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus. ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости).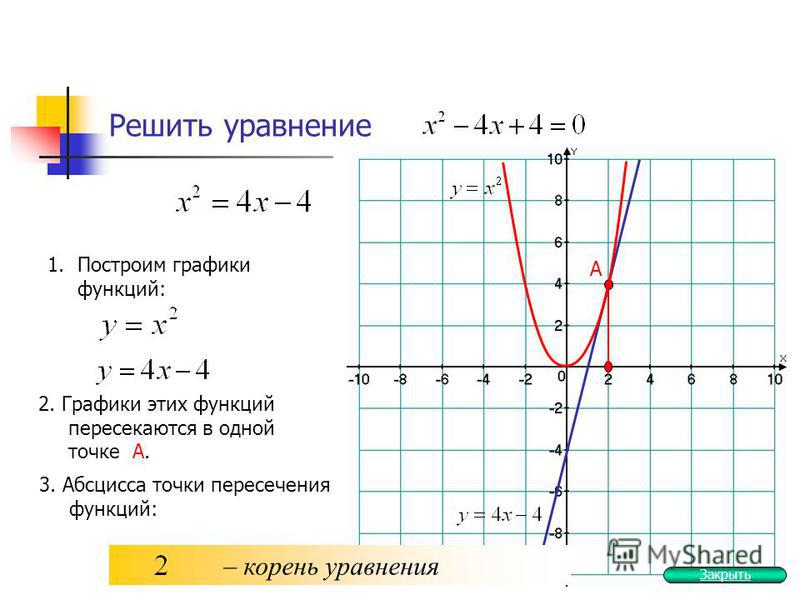 В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 наименьшее значение функция у = х 2 — 2х принимает при х = 1 .
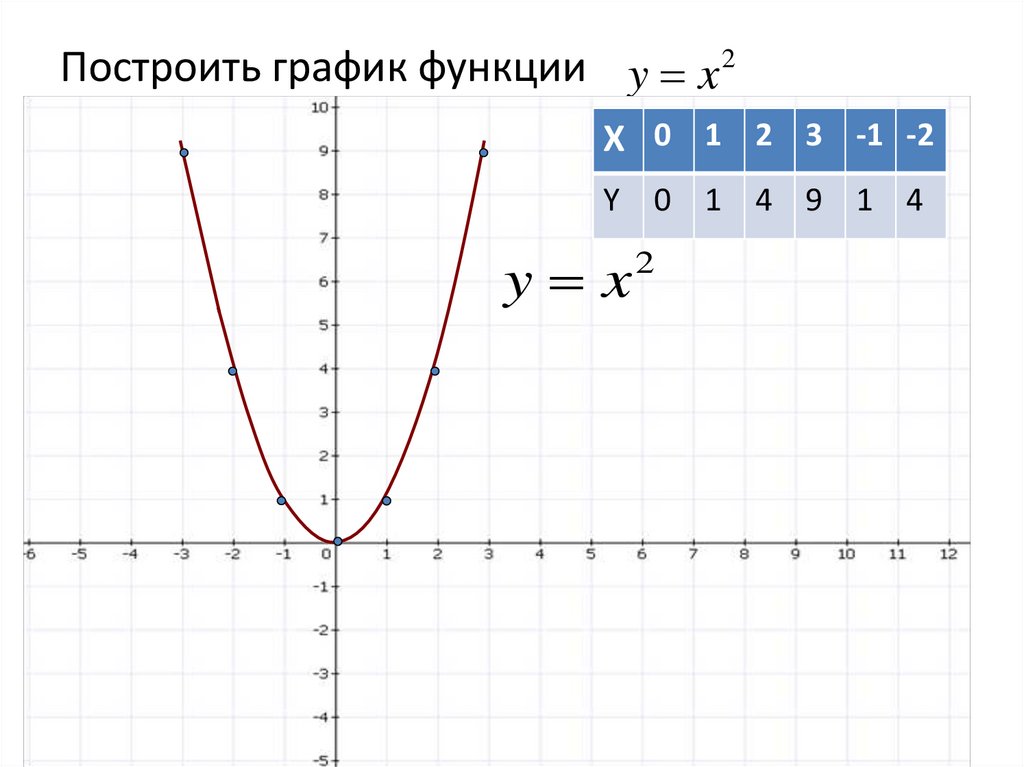
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.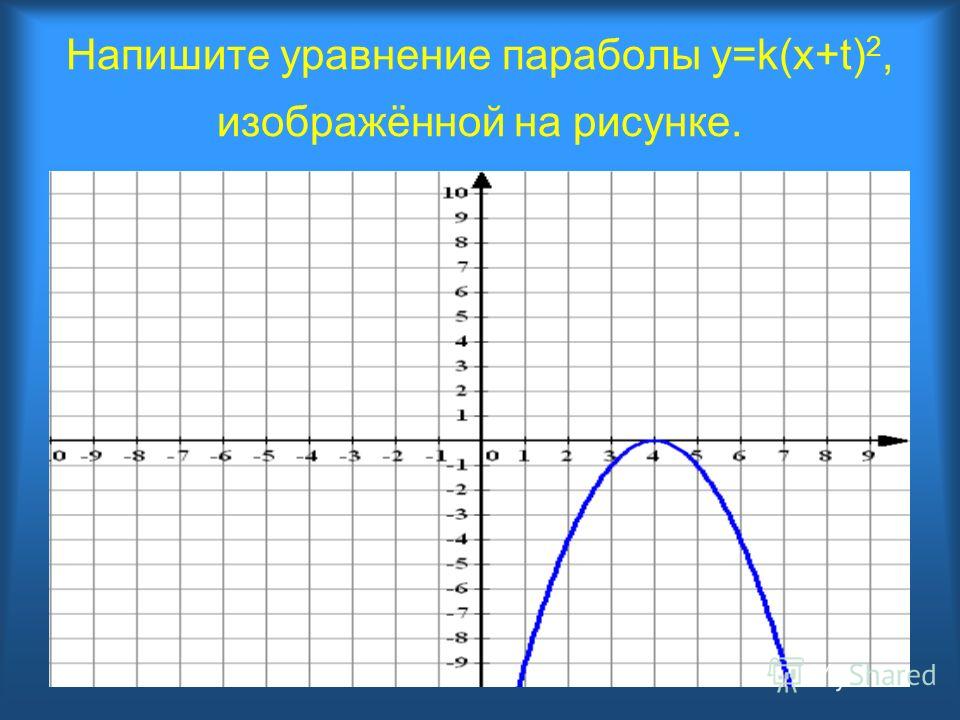
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
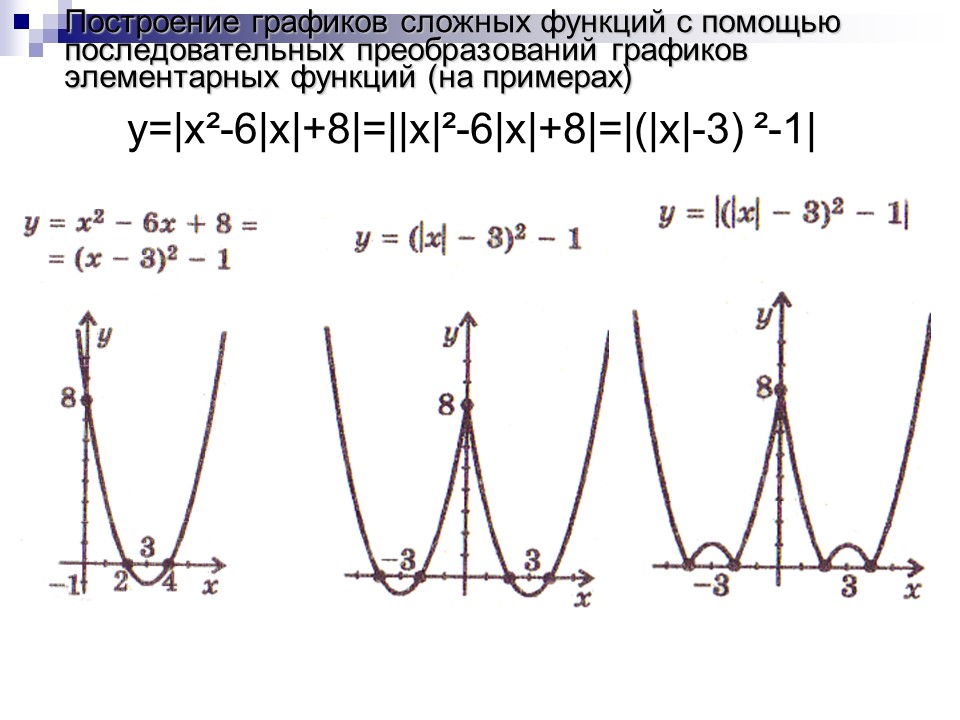
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .
если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.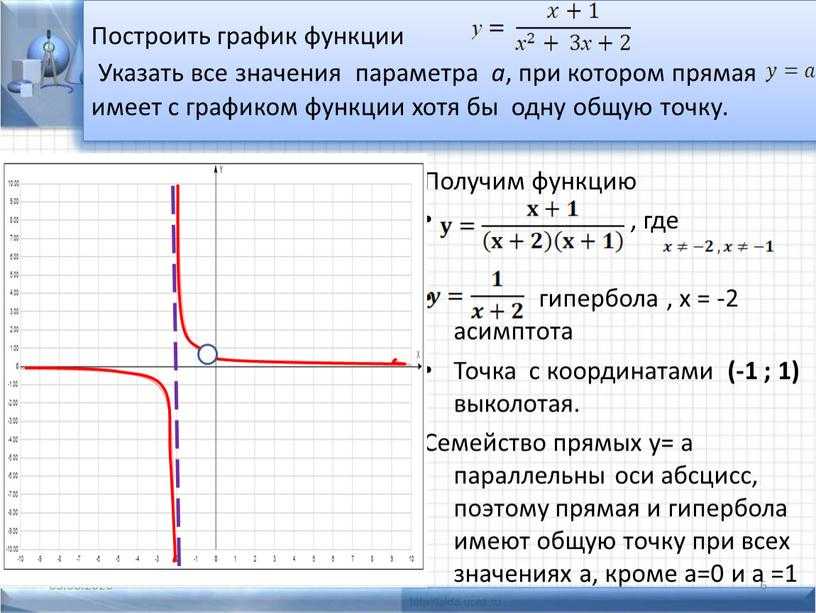
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y.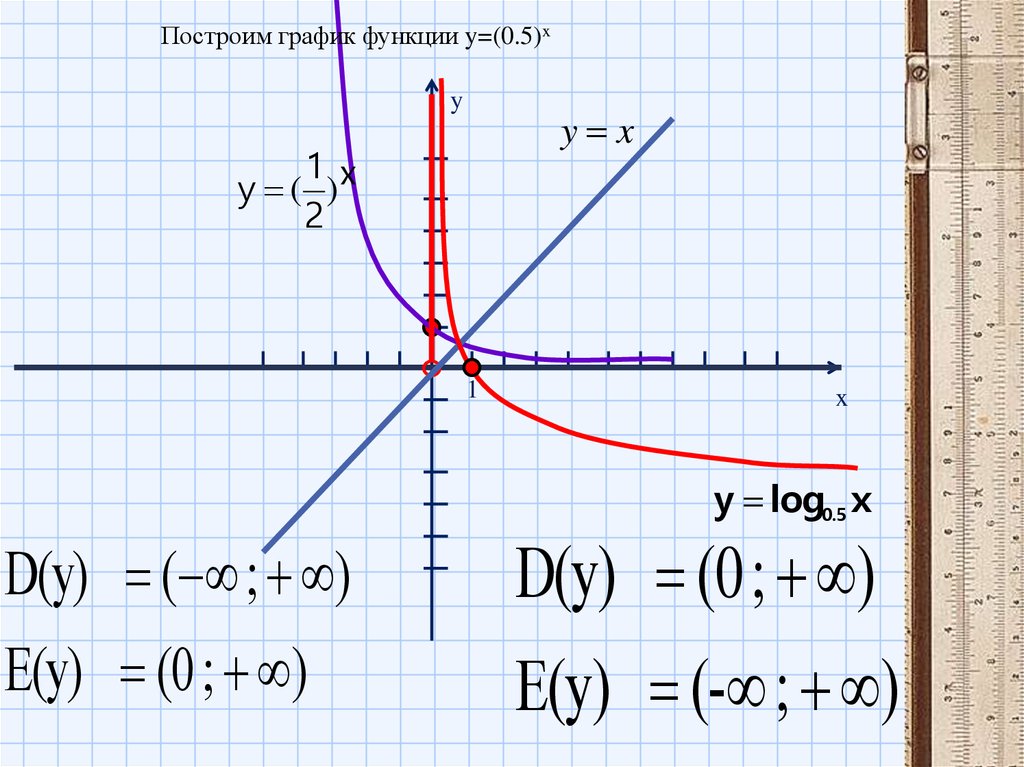 Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
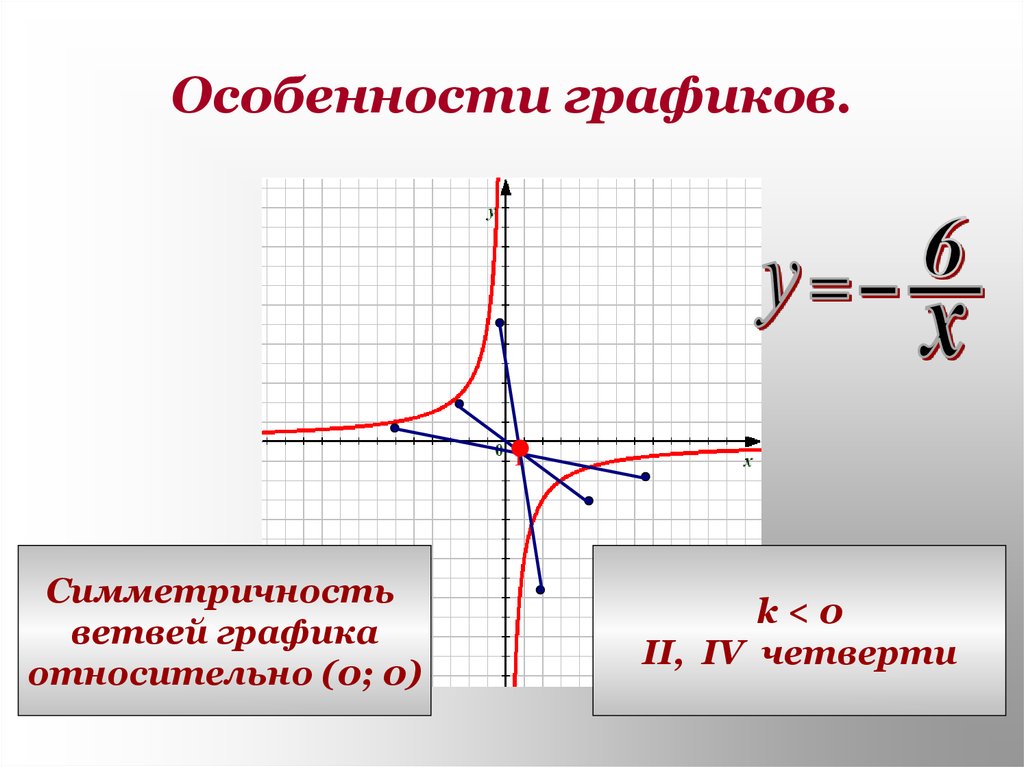
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.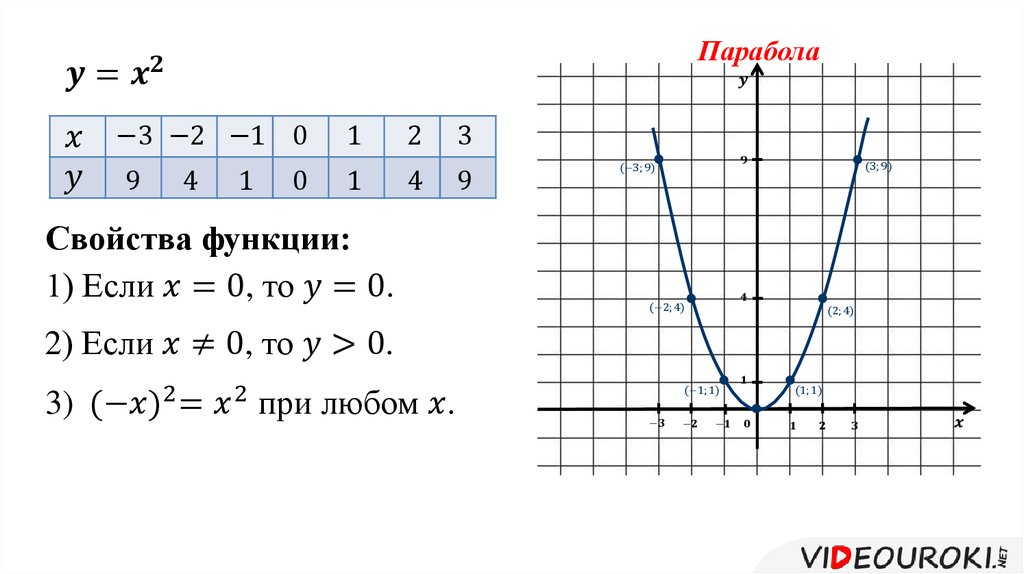
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция.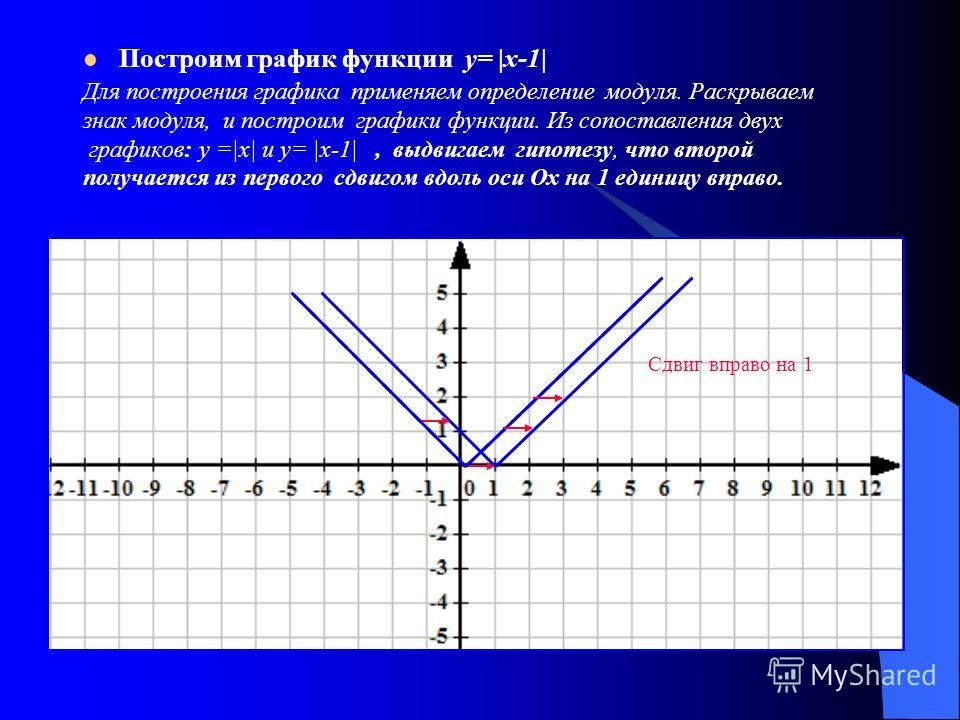 Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком.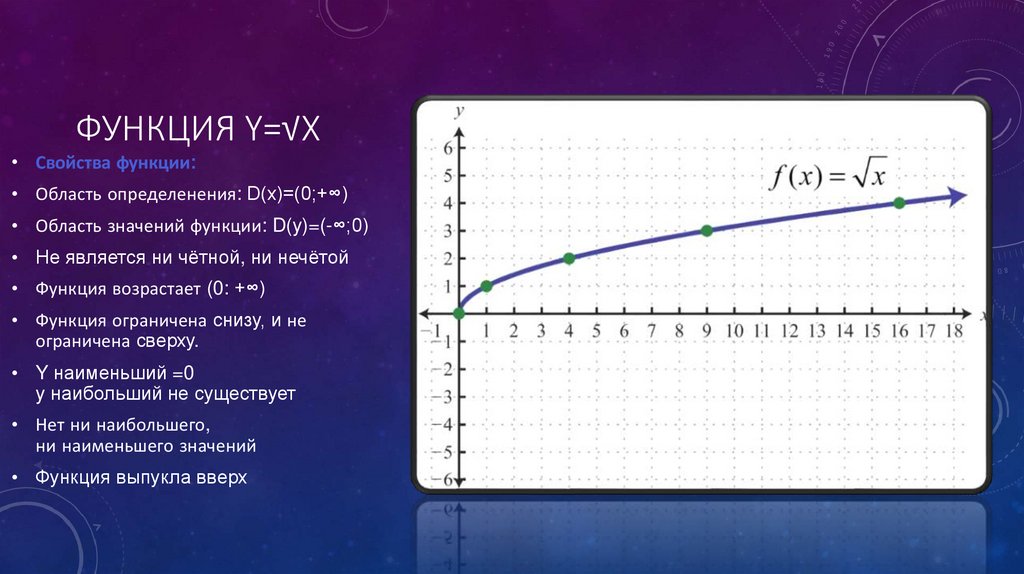 Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Гистограммы Excel и функция ЧАСТОТА • My Online Training Hub
Гистограмма , также известная как частотное распределение, представляет собой диаграмму, иллюстрирующую распределение значений, попадающих в группы.
Так как мой 5-летний сын увлекается своим футболом, мы возьмем в качестве примера забитые голы… хотя в футбольных матчах 5-летнего ребенка нельзя считать забитые голы!
Ниже приведен конечный результат. Я добавил к этой диаграмме кумулятивный процент, чтобы облегчить дальнейшую интерпретацию данных, но сама гистограмма представляет собой столбчатую диаграмму.
Из гистограммы видно, что мы забили 2-3 гола в 11 матчах. А из кумулятивного процента видно, что в 80% матчей забивается от нуля до трех голов.
Мы также можем использовать этот тип диаграммы для построения графика:
- Распределение оценок учащихся
- Производительность продавцов, напр.
 группы могут быть единицами, проданными
группы могут быть единицами, проданными - Распределение заработной платы по численности персонала
- Плюс различные баллы, рейтинги и другие данные, которые вы хотите увидеть частотное распределение.
Как создать диаграмму гистограммы
Первое, что нам нужно сделать, это скомпилировать наши данные в таблицу, которая может быть использована в нашей диаграмме.
Слева у нас есть список голов за последние 25 матчей. Первое, что нам нужно сделать, это указать наши группы или корзины, как их часто называют.
Поскольку наш диапазон данных очень мал (от нуля до 6 целей), наши ячейки будут небольшими: 0–1, 2–3, 4–5 и 6–7. число от 0 до 6, но я хочу показать вам, как использовать ЧАСТОТА функция , так что у нас будут небольшие группы.
Далее нам нужно настроить таблицу, которая будет питать гистограмму следующим образом:
Объяснение таблицы частот
Столбец группы
Это просто группы, которые будут отображаться на горизонтальной оси диаграммы.
Столбец интервалов
Ячейки являются верхними пределами групп и используются формулой ЧАСТОТА. Вы можете видеть, что значение ячейки для группы «2-3» равно 3.
Столбец частоты
Столбец частоты содержит формулу ЧАСТОТА. Функция FREQUENCY на самом деле является формулой массива, что означает, что ее необходимо вводить с помощью CTRL+SHIFT+ENTER.
Синтаксис функции ЧАСТОТА:
=ЧАСТОТА(массив_данных, массив_бинов)
и наша формула:
{=ЧАСТОТА(K5:K29,N5:N8)} Примечание: вводятся фигурные скобки в Excel, когда вы нажимаете CTRL+SHIFT+ENTER для ввода формулы.
Совет: выберите все ячейки, которые будут содержать вашу формулу ЧАСТОТЫ (в нашем случае O5:O8), затем введите формулу, затем нажмите CTRL+SHIFT+ENTER и ваша формула будет автоматически введена во все необходимые ячейки с фигурные скобки.
Примечание: поскольку этот диапазон, содержащий формулу ЧАСТОТА (O5:O8), является массивом, вы можете редактировать только весь массив. Excel выдаст вам ошибку, если вы попытаетесь изменить часть массива самостоятельно.
Excel выдаст вам ошибку, если вы попытаетесь изменить часть массива самостоятельно.
Совокупность % Столбец
Это просто совокупный процент частоты. Чтобы вычислить это, формула в первой ячейке:
=СУММ($O$5:O5)/СУММ($O$5:$O$8)
Совет: Ссылка на первую ячейку в приведенной выше формуле, $ O$5 — это то, что называется абсолютной ссылкой, а вторая, O5, — относительной ссылкой. Это делается для того, чтобы при копировании формулы в оставшиеся ячейки она автоматически обновлялась, чтобы включить в формулу следующую ячейку, и, таким образом, вычисляла совокупный процент.
Введите ниже свой адрес электронной почты, чтобы загрузить образец рабочей тетради.
Отправляя свой адрес электронной почты, вы соглашаетесь с тем, что мы можем отправить вам наш информационный бюллетень Excel по электронной почте.
Теперь, когда у нас есть готовая таблица частот, мы можем построить гистограмму.
Как создать гистограмму
- Выделите таблицу частотных данных (ячейки M4:P8)
- На вкладке «Вставка» ленты выберите «Столбец» > «Двухмерный столбец».
 У вас должно получиться что-то вроде этого.
У вас должно получиться что-то вроде этого.
- Удаление данных корзины с графика. Выберите синие столбцы данных корзины (просто щелкните один из столбцов) и нажмите клавишу удаления, чтобы удалить их.
- Измените совокупный % на линейный график. Выберите столбец Cum %, щелкните правой кнопкой мыши и выберите Изменить тип диаграммы серии.
- Выберите график.
- Переместить совокупный % на дополнительную ось. Выберите на диаграмме строку Cum %, щелкните правой кнопкой мыши и выберите Format Data Series.
- На вкладке «Параметры серии» выберите «Вторичная ось». Теперь это должно выглядеть так:
- Удалите зазор между стержнями. Выберите полосы частот на диаграмме, щелкните правой кнопкой мыши и выберите «Формат ряда данных».
- На вкладке «Параметры серии» уменьшите ширину зазора до 0 %.
- Добавить метки и формат.
 Выберите диаграмму и на вкладке «Макет» на ленте добавьте заголовок диаграммы и метки осей. Нажмите внутри меток, чтобы добавить свой текст.
Выберите диаграмму и на вкладке «Макет» на ленте добавьте заголовок диаграммы и метки осей. Нажмите внутри меток, чтобы добавить свой текст. - Переместите легенду в правый верхний угол диаграммы. Нажмите на легенду и перетащите внешний край окна вверх. Измените размер поля с помощью маркеров, чтобы данные располагались рядом, а не стопкой. Это улучшит его положение в верхней части диаграммы.
- Удалить линии сетки. Нажмите на горизонтальные линии сетки и нажмите клавишу удаления, чтобы удалить их.
- Изменение размера диаграммы. Щелкните внутри области диаграммы, чтобы были видны манипуляторы (см. квадраты и кружки на контуре диаграммы на изображении ниже), и измените ее размер, захватив средний манипулятор с правой стороны и перетащив его вправо. чтобы изменить его размер и заполнить пробел, оставшийся от легенды.
- Добавьте метки данных к линейной диаграмме.
 Выберите строку на диаграмме и на вкладке «Макет» на ленте выберите «Метки данных» > «Выше».
Выберите строку на диаграмме и на вкладке «Макет» на ленте выберите «Метки данных» > «Выше». - Изменение цвета полосы. Выберите полосы частот и на вкладке «Формат» на ленте и выберите новый цвет в разделе «Стили диаграммы».
Теперь ваша диаграмма должна выглядеть так:
Хотя это может показаться большим количеством шагов, как только вы освоитесь с форматированием диаграмм, вы сможете сделать все это примерно за минуту.
Наш курс премиум-класса включает подробные видеоуроки по диаграммам Excel. Нажмите здесь, чтобы записаться на наш курс обучения Excel.
Создание диаграммы
- Создание диаграммы
- Дизайнер диаграммы
- Применение функций на столбцах
- Advanced Summarizing
- Выбор Crabt Type
 д., просто перетащив нужные столбцы на соответствующие полки в области дизайна.
д., просто перетащив нужные столбцы на соответствующие полки в области дизайна.Посмотрите видео ниже, чтобы получить представление о создании диаграмм.
Тип диаграммы можно изменить в любое время, не создавая ее заново. Вы также можете применять соответствующие агрегатные функции к столбцам, чтобы вычислять и суммировать данные так, как вам нужно.
Создание диаграммы
Чтобы открыть страницу Chart Designer , выполните один из следующих способов.
Метод 1:
Чтобы создать диаграмму, выполните следующие действия:
- Откройте рабочую область, в которой вы хотите создать диаграмму.
- Нажмите кнопку Create в левом верхнем углу рабочей области и выберите Chart View .
- В открывшемся диалоговом окне Select Base Table выберите нужную таблицу в рабочей области, на которой вы хотите создать диаграмму, и нажмите ОК .

- Откроется Дизайнер диаграмм , как показано ниже.
Способ 2:
Вы можете создать новую диаграмму, открыв соответствующую таблицу данных, в которой вы хотите создать диаграмму, и выбрав New > New Chart View на панели инструментов.
Способ 3:
Вы также можете создать новую диаграмму с помощью кнопки Reports в строке меню. Быстрая ссылка Создание новых отчетов будет доступен внутри кнопки Reports в строке меню. После нажатия ссылки Создать новые отчеты появится раскрывающийся список со всеми типами представлений.
Нажмите Chart View и выберите нужную базовую таблицу. Вы перейдете на страницу Chart Designer .
Примечание:
- Вы также можете создавать диаграммы на основе таблицы запросов , следуя тем же инструкциям, что и выше.

Chart Designer
С левой стороны находится панель списка столбцов , в которой перечислены все столбцы, доступные в таблице. С правой стороны вы можете увидеть Design Are a с полками для удаления столбцов и Область предварительного просмотра ниже для просмотра созданной диаграммы.
Чтобы создать диаграмму, необходимо перетащить необходимые столбцы, перечисленные на панели списка столбцов , на соответствующие полки. Вы также можете установить флажок рядом с каждым перечисленным столбцом, чтобы автоматически разместить столбцы на соответствующих полках. После удаления столбцов нажмите на опцию Щелкните здесь, чтобы создать график , чтобы создать новый график.
Ниже приводится краткое описание каждой из полок вкладки Graph .
- Ось X : Столбец, опущенный на эту полку, отображается горизонтально по оси X.

- Ось Y : Столбец, опущенный на эту полку, отображается вертикально по оси Y. Вы можете поместить несколько столбцов на эту полку, чтобы создать диаграммы с несколькими осями Y.
Вот пример, иллюстрирующий создание простой гистограммы. Мы создадим диаграмму для отображения Тенденция продаж за все годы с использованием выборочных данных о продажах в магазине. Перетащите столбцы Дата и Продажи на оси X и Y и нажмите кнопку « Щелкните здесь, чтобы создать график» . Вы заметите, что как только кнопка будет нажата, будет создана гистограмма.
- Цвет : Когда столбец перетаскивается на эту полку, диаграмма будет дополнительно классифицирована, показывая каждую точку данных в этом столбце разными цветами (разные ряды данных) на диаграмме.
Продолжая приведенный выше пример, если вы хотите создать диаграмму Продажи по датам по регионам , перетащите столбец Регион на полку Цвет .
 Теперь диаграмма будет дополнительно классифицирована на основе регионов , и каждому региону будет присвоен уникальный цвет, как показано на снимке экрана ниже.
Теперь диаграмма будет дополнительно классифицирована на основе регионов , и каждому региону будет присвоен уникальный цвет, как показано на снимке экрана ниже. - Текст : включает соответствующее значение удаленного столбца в качестве метки данных на диаграмме в соответствии с функцией, примененной к столбцу.
- Включить столбцы во всплывающую подсказку : Включает соответствующие значения отброшенных столбцов во всплывающую подсказку диаграммы в соответствии с функцией, примененной к столбцу.
На следующем снимке экрана показано, как будет выглядеть окончательная диаграмма (в режиме просмотра), когда выбраны параметры Текст и Включить столбцы для всплывающей подсказки .
В режиме Edit Design вы заметите, что при наведении курсора мыши на правый верхний угол области списка столбцов появляется меню.
 Вы можете расширять, сортировать и фильтровать список столбцов, используя параметры, доступные в этом меню. Доступные варианты:
Вы можете расширять, сортировать и фильтровать список столбцов, используя параметры, доступные в этом меню. Доступные варианты: - Развернуть все и свернуть все: «Развернуть все» позволяет развернуть список полей, «Свернуть все » свернуть таблицу.
- Применить сортировку: Вы можете отсортировать столбец по имени или по типу, а также дополнительно отсортировать его по возрастанию или по убыванию.
- Применить фильтры: Этот параметр полезен, когда вам нужно отфильтровать столбцы на основе типа данных.
- Показать Задействованные столбцы: Список столбцов, участвующих в создании отчета.
Применение функций к столбцам
Zoho Analytics позволяет применять агрегатные/категориальные функции, такие как Sum, Count, Average, Min, Max и т. д. , к столбцам данных в группу и суммировать данные в графики.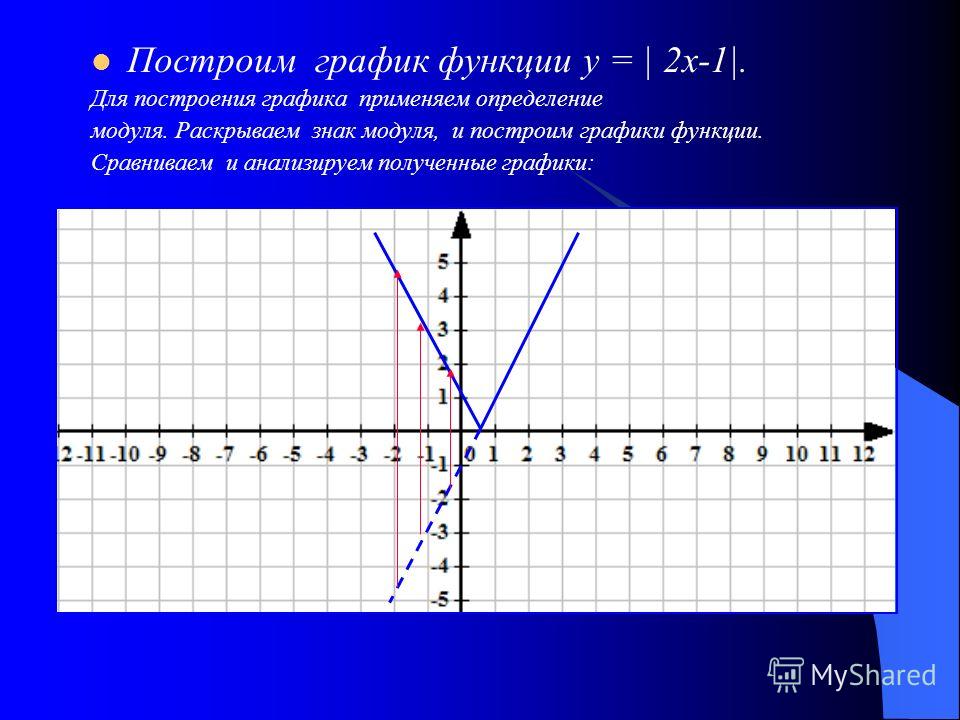 Когда вы применяете функцию к столбцу, будет возвращено одно значение, полученное на основе значений в столбце. Функция по умолчанию для Числовой (включая Валюта ) Тип данных — Сумма , а для Дата тип данных — Год . Если тип данных столбца является строковым (столбец категорий/размеров), а не числовым, то по умолчанию применяется функция Фактические значения .
Когда вы применяете функцию к столбцу, будет возвращено одно значение, полученное на основе значений в столбце. Функция по умолчанию для Числовой (включая Валюта ) Тип данных — Сумма , а для Дата тип данных — Год . Если тип данных столбца является строковым (столбец категорий/размеров), а не числовым, то по умолчанию применяется функция Фактические значения .
Чтобы изменить применяемую по умолчанию функцию, после удаления столбца выберите требуемую функцию (агрегатную/категориальную) из раскрывающегося списка, присутствующего в столбце. В раскрывающемся списке отображаются все применимые функции в зависимости от типа данных столбца, как показано на снимках экрана ниже.
Строковые данные Тип
Тип цифр данных
Дата Данные Данные Тип
Например, если вы хотите построить Средний . функцию из раскрывающегося списка для столбца Продажи (ось Y), Месяц и год функцию для столбца Дата (ось X) и выберите Фактические значения функция для Область (столбец цвета), а затем нажмите кнопку «Нажмите здесь, чтобы создать график» .
функцию из раскрывающегося списка для столбца Продажи (ось Y), Месяц и год функцию для столбца Дата (ось X) и выберите Фактические значения функция для Область (столбец цвета), а затем нажмите кнопку «Нажмите здесь, чтобы создать график» .
В следующих таблицах перечислены все функции вместе с их описанием.
Типы числовых и валютных данных:
| Функция | Описание |
| Возвращает сумму всех значений столбцов4 Сумма | Суммирование будет производиться на уровне каждой категории/группы, показанной в отчете. |
| Максимум [Max] | Возвращает максимальное значение в столбце. |
| Минимум [мин.] | Возвращает минимальное значение в столбце. |
| Среднее [Среднее] | Возвращает среднее значение всех значений в столбце. |
| Стандартное отклонение | Возвращает стандартное отклонение, полученное на основе всех значений в столбце. |
| Медиана | Возвращает среднее значение столбца. |
| Режим | Возвращает значение, которое чаще всего встречается в столбце. |
| Процентиль | Возвращает процентиль столбца. по умолчанию возвращается 50-й процентиль. Вы можете изменить это по мере необходимости. например, 90-й процентиль столбца — это число, под которым находится 90% значений столбца. |
| Дисперсия | Возвращает дисперсию столбца. |
| Количество | Возвращает количество значений в столбце. |
| Число уникальных значений | Возвращает количество уникальных значений в столбце. |
| Измерение | Обрабатывает значения в столбце как измеримое числовое значение. Возвращает каждое уникальное значение, представленное в виде числового значения, для отображения в отчете. Возвращает каждое уникальное значение, представленное в виде числового значения, для отображения в отчете. |
| Измерение | Обрабатывает значения в столбце как текстовое (категориальное/размерное) значение. Возвращает каждое уникальное значение, представленное в виде текстового значения, которое будет отображено в отчете. |
| Диапазон | Группирует весь диапазон числовых значений, присутствующих в столбце, в несколько диапазонов.. например, если ваш диапазон данных составляет от 0 до 1000, он будет сгруппирован как от 0 до 100, от 101 до 250… 901-1000. Вы также можете указать размер пользовательского диапазона для группировки данных, используя ссылку «Добавить новый диапазон». т. е. если вы установите размер диапазона равным 50, то он будет сгруппирован как от 0 до 50, от 51 до 100 …. |
Тип данных даты — фактическое значение Функции:
| Функция | Описание |
| Год | Возвращает все отдельные значения года, присутствующие в столбце. Например, 2003, 2010 Например, 2003, 2010 |
| Квартал и год | Возвращает все отдельные значения квартала и года, присутствующие в столбце. Например, Q1 2010 |
| Месяц и год | Возвращает все различные значения месяца и года, присутствующие в столбце. Например, март 2010 г. |
| Неделя и год | Возвращает все отдельные значения недели года, присутствующие в столбце. Например, W1 2010 |
| Полная дата | Возвращает все отдельные даты, присутствующие в столбце. Например, 01.01.2011 |
| Дата и время | Возвращает все различные пары даты и времени, присутствующие в столбце. Например. 12.01.2010 00:10:07 часов |
Дата Тип данных — сезонное значение Функции:
| Функция | Описание |
| Квартал | Помогает определить сезонные тренды на основе кварталов, представленных в столбце за все годы. Например, Q1, Q2. Например, Q1, Q2. |
| Месяц | Помогает определить сезонные тенденции на основе месяцев за все годы. Например, январь, февраль. |
| Неделя | Помогает определить сезонные тренды на основе недель за все годы. Например, неделя 1, неделя 2. |
| День недели | Помогает определить сезонные тенденции на основе дня недели за все годы. Например, воскресенье, понедельник. |
| День месяца | Помогает определить сезонные тенденции на основе дня месяца по всем датам. Например, от 1 до 31. |
| Час дня | Помогает определить тенденции по часам в течение дня. Например, от 0 до 23 часов. |
Дата Тип данных — функция агрегата:
| Функция | Описание |
| Количество | Возвращает количество значений даты в столбце. |
| Число уникальных дат | Возвращает количество уникальных значений дат в столбце. |
Строка (категорический/размер) Тип данных:
| Функция | Описание |
0474| Будут перечислены все отдельные значения в столбце. | |
| Количество | Количество значений в столбце будет указано. |
| Число уникальных значений | Будет указано количество уникальных значений в столбце. |
Расширенные параметры суммирования
При создании диаграммы Zoho Analytics предоставляет расширенные функции суммирования, помимо основных функций, таких как Сумма, Макс, Мин или Среднее . Это позволяет суммировать значения данных в этом столбце на основе значений в других столбцах. Используя это, вы сможете выполнять некоторые мощные расчеты на диаграмме, такие как промежуточный итог продаж за годы или вычислять разницу в продажах по сравнению с предыдущим годом и т. д.,
д.,
Ниже приведены расширенные варианты суммирования:
| Функция | Описание |
| Нормальный | . По умолчанию этот параметр будет выбран. |
| % от итога | Отображает процент от общего итога всех данных в ряду диаграммы. |
| Итого | Отображает данные в последовательных точках данных диаграммы в виде промежуточного итога на основе выбранного базового поля. |
| Разница с | Отображает данные в каждой точке данных как разницу со значением в предыдущей точке данных на основе выбранного базового поля. |
| % от предыдущего значения | Отображает данные в каждой точке данных в процентах от значения в предыдущей точке данных на основе выбранного базового поля. |
| % разницы от | Отображает данные в каждой точке данных в виде процента отличий от значения в предыдущей точке данных на основе выбранного базового поля. |
| 100% Группа | Отображает процент значения точки данных от общего количества группы на основе выбранного базового поля. Это будет полезно при создании гистограммы со 100% накоплением и диаграммы с областями со 100% накоплением. Когда вы создаете диаграмму продаж по годам с разбивкой по регионам, с помощью этой функции вы можете получить процент продаж в каждом регионе, как показано в примере слева. |
| Скользящее среднее | Отображает рассчитанное скользящее значение каждой точки данных на основе предоставленных вами входных данных. Выбранная суммарная функция будет взята за основу для расчета. С его помощью вы можете выполнить расчет суммы, среднего, минимума и максимума. Это будет полезно для визуализации тренда ваших данных. Пример слева иллюстрирует впечатление от вашего веб-сайта по сравнению со скользящим средним числом показов за последние 30 дней. |
На следующем снимке экрана показан образец диаграммы с применением различных расширенных сводных функций.
Выбор типа диаграммы
После создания диаграммы вы можете легко изменить ее на другой тип диаграммы, просто нажав кнопку, не изменяя отображаемые данные. Например, вы создали линейчатую диаграмму, но затем решили, что хотите, чтобы данные отображались в виде круговой диаграммы. Вы можете сделать это, изменив тип диаграммы с помощью панели инструментов, или вы можете использовать Кнопка Другие графики на панели инструментов.
Панель инструментов предоставляет вам возможность выбора между типами круговой, гистограммы, гистограммы с накоплением, линейной, точечной и табличной диаграммы на верхнем уровне. Если вы не нашли нужный тип диаграммы, нажмите кнопку Other Charts на панели инструментов и выберите тип диаграммы, который вы хотите применить, в появившемся диалоговом окне Chart Options . Вы можете просмотреть краткое описание каждого типа диаграммы в нижней части диалогового окна, щелкнув конкретный тип диаграммы.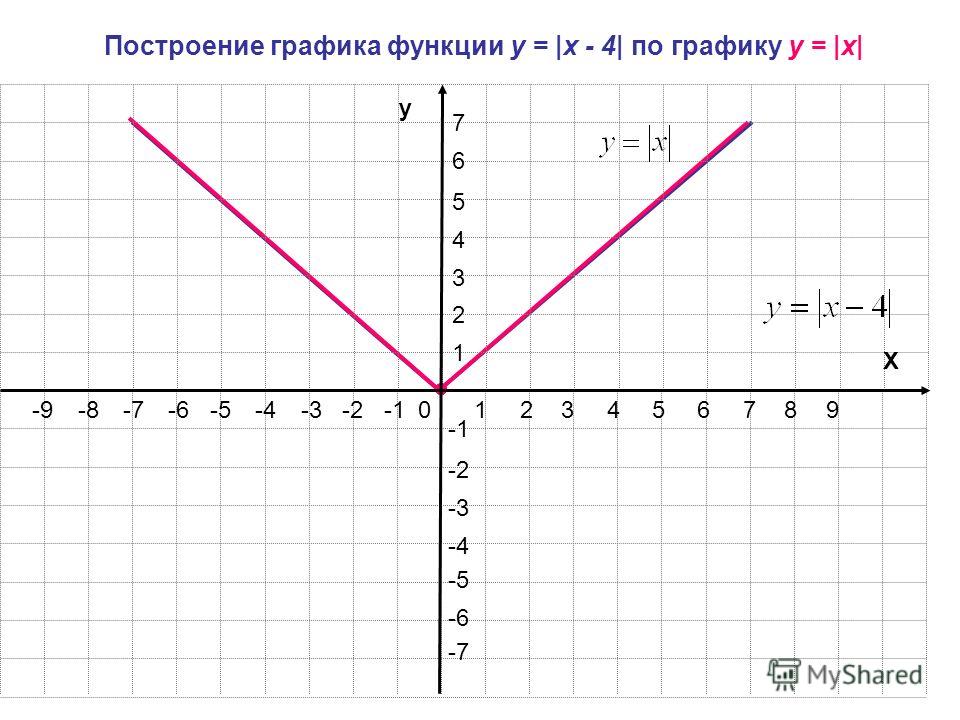

 д.
д.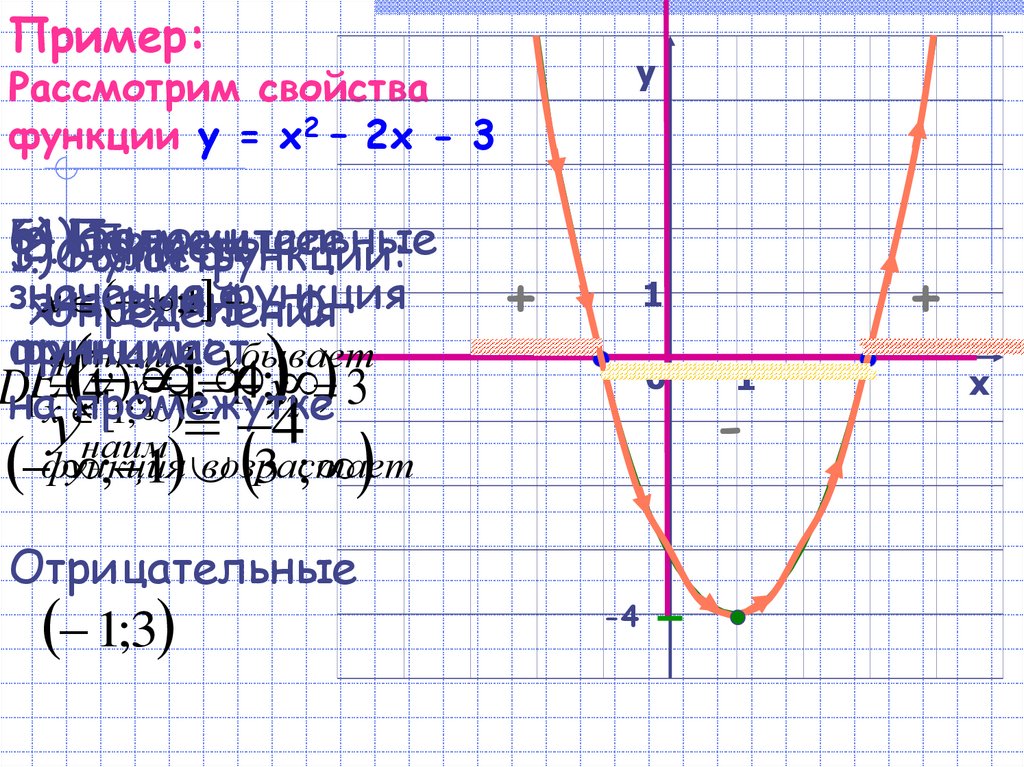 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. группы могут быть единицами, проданными
группы могут быть единицами, проданными У вас должно получиться что-то вроде этого.
У вас должно получиться что-то вроде этого. Выберите диаграмму и на вкладке «Макет» на ленте добавьте заголовок диаграммы и метки осей. Нажмите внутри меток, чтобы добавить свой текст.
Выберите диаграмму и на вкладке «Макет» на ленте добавьте заголовок диаграммы и метки осей. Нажмите внутри меток, чтобы добавить свой текст. Выберите строку на диаграмме и на вкладке «Макет» на ленте выберите «Метки данных» > «Выше».
Выберите строку на диаграмме и на вкладке «Макет» на ленте выберите «Метки данных» > «Выше».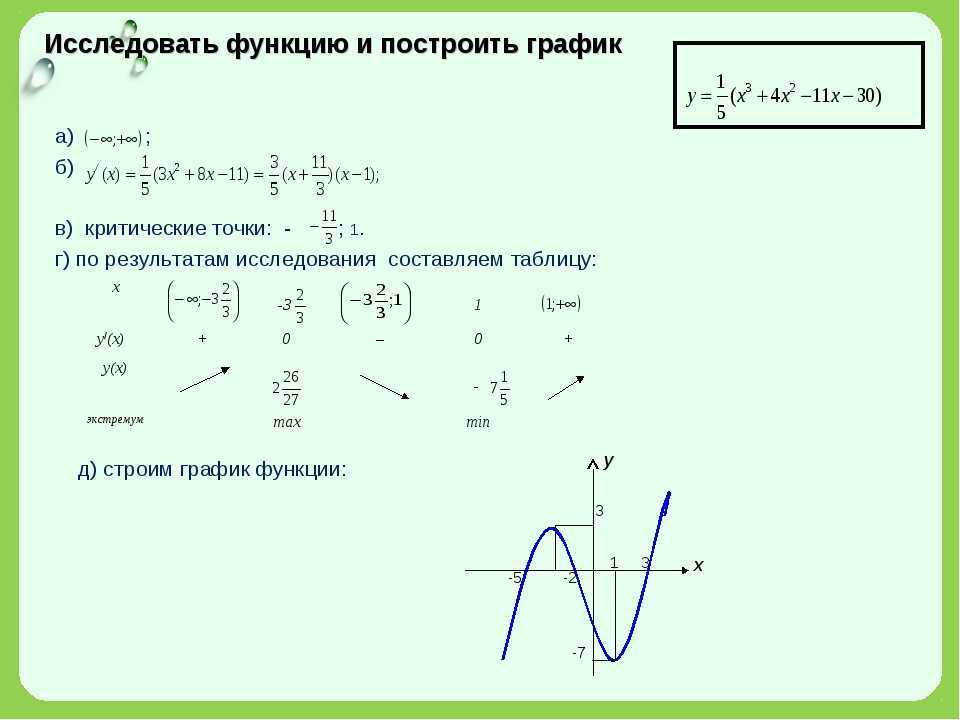

 Теперь диаграмма будет дополнительно классифицирована на основе регионов , и каждому региону будет присвоен уникальный цвет, как показано на снимке экрана ниже.
Теперь диаграмма будет дополнительно классифицирована на основе регионов , и каждому региону будет присвоен уникальный цвет, как показано на снимке экрана ниже.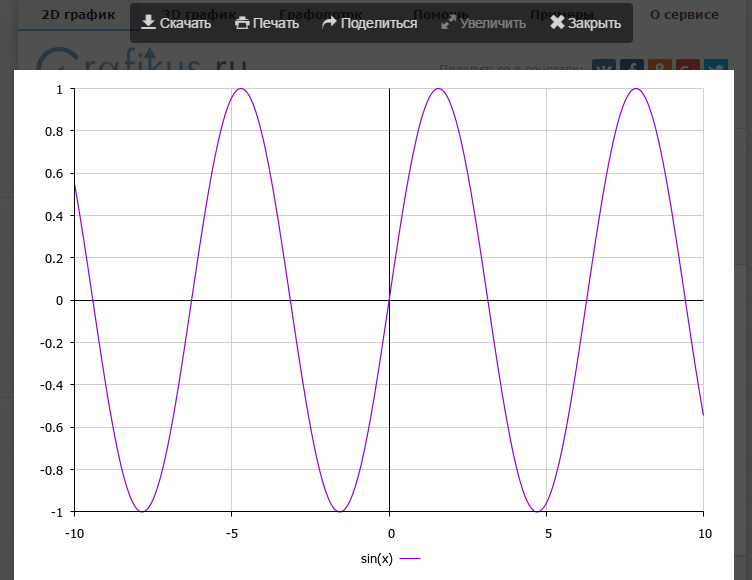 Вы можете расширять, сортировать и фильтровать список столбцов, используя параметры, доступные в этом меню. Доступные варианты:
Вы можете расширять, сортировать и фильтровать список столбцов, используя параметры, доступные в этом меню. Доступные варианты: