Полное исследование функции — шаг за шагом
В статье перечислены основные пункты, по которым принято делать исследование функции. Стать носит теоретический характер, подробно объясняется на «пальцах» что и как нужно исследовать. Поэтому если вас интересуют практические примеры, то смело можно пропускать прочтение данного текста и переходить к примерам, ссылка в конце статьи.
1. Область определения функции D(y).
Область определения D(y) — это множество всех значений аргумента x, на котором задана функция. Другими словами — это промежуток по оси икс, в пределах которого функция f(x) непрерывна и определена.
К примеру, если функция непрерывна, то ответ таков: D(y) = R, где R — это множество всех значений икс, от минус бесконечности до плюс бесконечности. В ином случае, точка разрыва включается в ответ. Пусть функция неопределена в точке х = 1, тогда область определения исключает данную точку: D(y) = (-00; 1),(1;+00).
(-00 и +00 это знак бесконечности).
2. Четность, нечетность, периодичность функции.
Четность или нечетность показывает существует ли симметричность функции относительно начала координат или оси ординат. Чтобы определить четность/нечетность, берем икс со знаком минус, подставляем его в исследуемую функцию f(x) на место обычных иксов и считаем. В случае, если на выходе имеем точно такую же функцию, как исходная, с такими же знаками всех коэффициентов, то говорят, что данная функция четная: Записывается так: y(-x) = y(x). График четной функции симметричен относительно центра координат.
В случае, если на выходе получается исходная функция, но со знаком минус за скобками, то говорят что функция нечетная и записывается это так: y(-x) = -y(x). График нечетной функции, симметричен относительно оси ординат. Существует и третий случай, когда на выходе получается «разношерстная» функция, в которой все знаки перемешались и не помогают никакие манипуляции, чтобы функция стала похожей на исходную или исходную со знаком минус.
Тогда говорят, что данная функция ни четная, ни нечетная и она не обладает никакой симметрией.
Свойство периодичности присуще тригонометрическим функциям, оно показывает существует ли период или другими словами некоторый повторяющийся регулярный интервал аргумента, при котором функция сохраняет свои значения при добавлении к аргументу этого периода на всей области определения.
3. Точки пересечения с осями координат ОХ и ОУ.
При пересечении графика функции f(x) с осью икс (ОХ), координата у = 0. Найденные точка(и) будет иметь координаты М1(х;0). При пересечении графика функции f(x) оси игрек (ОУ), координата х = 0, соответственно точка(и) пересечения будет иметь координаты М2(0;y).
4. Поиск вертикальных, наклонных или горизонтальных асимптот.
Традиционно исследование начинается с поиска вертикальных асимптот.
В случае, если функция f(x) терпит бесконечный разрыв в какой-либо точке х, то прямая, проведенная через эту точку параллельно оси игрек, будет являться вертикальной асимптотой. Чтобы доказать это, необходимо вычислить пределы от исходной функции f(x) при икс стремящемся к минус и плюс бесконечности (если это возможно) или один из этих пределов. В случае, если хоть в одном из них получится ответ бесконечность, это и будет являться доказательством.
Далее идет поиск наклонных или горизонтальных асимптот. Многие иногда путаются в этих понятиях, считая их независимыми, не связанными друг с другом, что конечно же неверно. Наклонная асимптота имеет уравнение y = kx + b, а горизонтальная — это частный случай наклонной, в котором коэффициент при икс равен нулю (k = 0), ее уравнение y = b. Чтобы найти наклонную асимптоту функции необходимо вычислить два предела:
Если коэффициент k = 0, то при поиске коэффициента b будет рассчитываться предел от функции f(x) и при подстановке в формулу y = kx + b мы получим уравнение горизонтальной асимптоты y = b, т.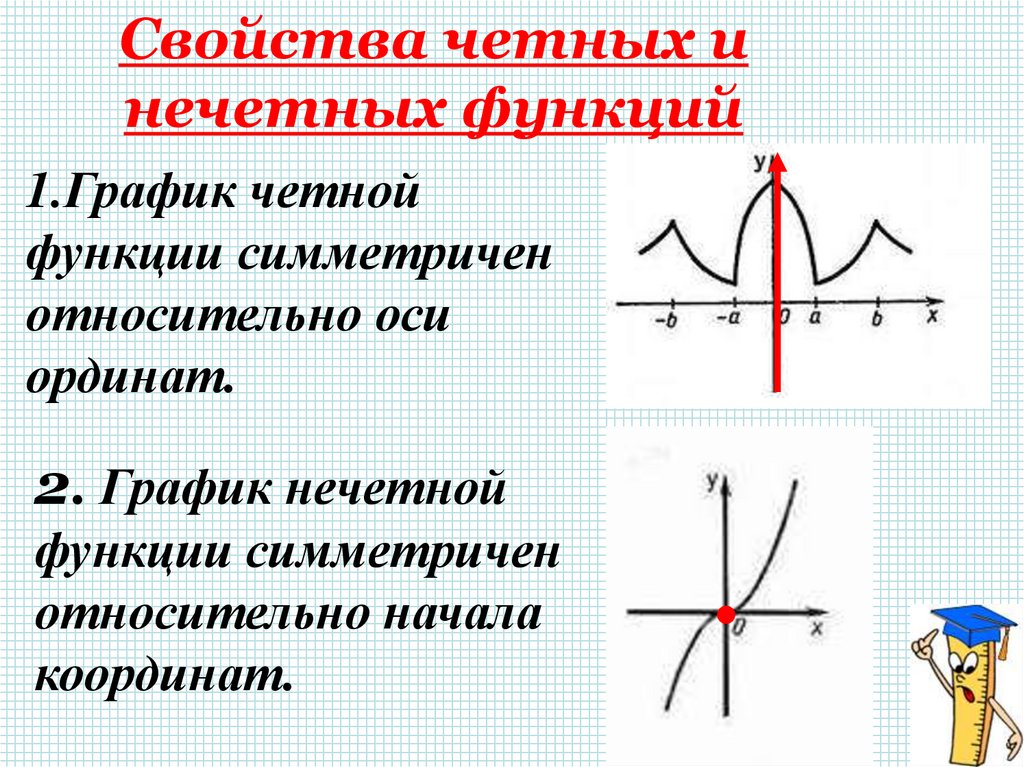
е. прямую, параллельную оси икс. Если коэффициент k будет равен бесконечности, неважно плюс или минус, в таком случае дальнейшие вычисления не осуществляются, а в ответе записываем, что наклонные асимптоты отсутствуют.
5. Промежутки возрастания и убывания (промежутки монотонности), экстремумы функции.
Промежутки монотонности функции f(x) находятся при помощи первой производной. Алгоритм таков: берем первую производную от f(x), приравниваем результат производной к нулю f ‘(x) = 0, находим корень(корни) данного уравнения x1, x2 и т. д. Таким образом мы получаем экстремумы функции. Далее чертим ось икс и отмечаем на ней закрашенными кружочками найденные корни x1, x2…
Нужно помнить, что если функция имеет точки разрыва в области определения, их также необходимо отметить на числовой оси, отмечая пустыми кружочками.
Получаем несколько промежутков, границами которых вперемешку являются точки из корней и точек разрыва, это не страшно, просто нужно будет это учитывать в дальнейшем при оформлении ответа.
Далее начинаем исследовать знаки производной на каждом из полученных промежутков. Берем по одному числу из каждого промежутка, подставляем в производную f ‘(x) и отмечаем знаки (плюс или минус), рисуя их прямо над осью в исследуемом промежутке.
Остается самое интересное! Анализируем результаты, изучая каждую точку :
— закрашенная точка, в которой идет смена знаков с плюса на минус ( смотрим слева и справа от точки )- это точка максимума. Под осью икс рисуем стрелочку вверх, там где плюс и стрелочку вниз, там где минус.
— закрашенная точка, в которой идет смена знаков с минуса на плюс — это точка минимума. Также помечаем стрелочками направления вниз и вверх.
— пустая точка (пустой кружок) — это точка разрыва и ее мы не имеем права записать в минимумы или максимумы, в этой точке функция не определена, не существует.
Итак, с экстремумами «рассчитались» и нам остается найти промежутки возрастания и убывания функции, или другими словами — промежутки монотонности.
Собственно, здесь все предельно просто: промежутки, в которых стрелочка смотрит вверх это промежутки возрастания функции, где стрелочка вниз — промежутки убывания. Важный момент — учитываем точки разрыва ( незакрашенные точки ), когда записываем ответ.
Если в промежутке (a;b) имеется точка разрыва c (точка с пустым кружочком), то ответ записывается с учетом этой точки: (a;c),(c;b).
6. Промежутки выпуклости и вогнутости, точки перегиба функции.
Чтобы найти промежутки, в которых функция выпукла и вогнута, а также точки перегиба, необходимо найти вторую производную. Вторая производная берется от первой: ( f ‘(x) )’ = f ‘ ‘(x). Далее, как и в предыдущем пункте, приравниваем вторую производную к нулю, находим корни уравнения. Рисуем ось икс, отмечаем найденные корни закрашенными точками, точки разрыва отмечаем пустыми кружочками.
Исследуем знаки второй производной на каждом из промежутков.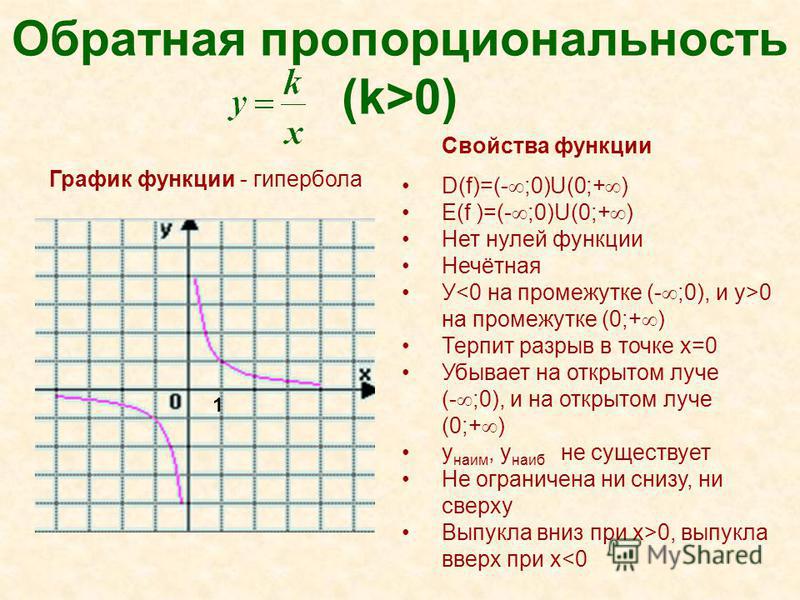
Там где вторая производная положительна рисуем скобку в виде улыбки, здесь функция вогнута. В ином случае, рисуем унылую скобку, здесь функция выпукла. Соответственно, при записи промежутков вогнутости и выпуклости функции не забываем учитывать точки разрыва. Точки перегиба находим там, где вторая производная меняет свой знак с + на — и наоборот, и точка закрашенная.
7. Построение графика.
Учитывая все предыдущие расчеты и найденные величины — точки разрыва, точки пересечения с осями координат, асимптоты, точки экстремумы, точки перегиба, строим график исследуемой функции. Желательно делать все это на листке в клетку, с масштабом побольше, чтобы как можно точнее получился график функции.
Конечно, сухая теория без практики это не дело, а потому предлагаю перейти к примерам исследования функции с помощью производной.
Определение четной и нечетной функции онлайн. Основные свойства функции: четность, нечетность, периодичность, ограниченность
Интернет
Которые в той или иной степени были вам знакомы.
Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.
Определение 1.
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).
Определение 2.
Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
Доказать, что у = х 4 — четная функция.
Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.
Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.
Доказать, что у = х 3 ~ нечетная функция.
Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.
Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.
Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.
Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
2\,1
\end{cases}
\quad\Leftrightarrow\quad \begin{cases} x=0\\
\mathrm{tg}\,(\cos x)=\mathrm{tg}\,1
\end{cases}\quad\Leftrightarrow\quad x=0\]
Следовательно, значение \(a=-\mathrm{tg}\,1\)
нам подходит.
Ответ:
\(a\in \{-\mathrm{tg}\,1;0\}\)
Задание 2 #3923
Уровень задания: Равен ЕГЭ
Найдите все значения параметра \(a\) , при каждом из которых график функции \
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)
\[\begin{aligned} &3\mathrm{tg}\,\left(-\dfrac{ax}5\right)+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right)\quad \Rightarrow\quad -3\mathrm{tg}\,\dfrac{ax}5+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right) \quad \Rightarrow\\ \Rightarrow\quad &\sin \dfrac{8\pi a+3x}4+\sin \dfrac{8\pi a-3x}4=0 \quad \Rightarrow \quad2\sin \dfrac12\left(\dfrac{8\pi a+3x}4+\dfrac{8\pi a-3x}4\right)\cdot \cos \dfrac12 \left(\dfrac{8\pi a+3x}4-\dfrac{8\pi a-3x}4\right)=0 \quad \Rightarrow\quad \sin (2\pi a)\cdot \cos \frac34 x=0 \end{aligned}\]
Последнее уравнение должно быть выполнено для всех \(x\)
из области определения \(f(x)\)
, следовательно, \(\sin(2\pi a)=0 \Rightarrow
a=\dfrac n2, n\in\mathbb{Z}\)
.
1) Пусть \(a>0\) . Тогда график функции \(f(x)\) будет выглядеть следующим образом:
Тогда для того, чтобы уравнение имело 4 решения, нужно, чтобы график \(g(x)=|a+2|\cdot \sqrtx\)
проходил через точку \(A\)
:
Следовательно, \[\dfrac{64}9a=|a+2|\cdot \sqrt8 \quad\Leftrightarrow\quad
\left[\begin{gathered}\begin{aligned} &9(a+2)=32a\\
&9(a+2)=-32a \end{aligned} \end{gathered}\right.
\quad\Leftrightarrow\quad
\left[\begin{gathered}\begin{aligned} &a=\dfrac{18}{23}\\
&a=-\dfrac{18}{41} \end{aligned} \end{gathered}\right.\]
Так как \(a>0\)
, то подходит \(a=\dfrac{18}{23}\)
.
2) Пусть \(a
Нужно, чтобы график \(g(x)\)
прошел через точку \(B\)
: \[\dfrac{64}9a=|a+2|\cdot \sqrt{-8} \quad\Leftrightarrow\quad
\left[\begin{gathered}\begin{aligned} &a=\dfrac{18}{23}\\
&a=-\dfrac{18}{41} \end{aligned} \end{gathered}\right.\]
Так как \(a
3) Случай, когда \(a=0\)
, не подходит, так как тогда \(f(x)=0\)
при всех \(x\)
, \(g(x)=2\sqrtx\)
и уравнение будет иметь только 1 корень.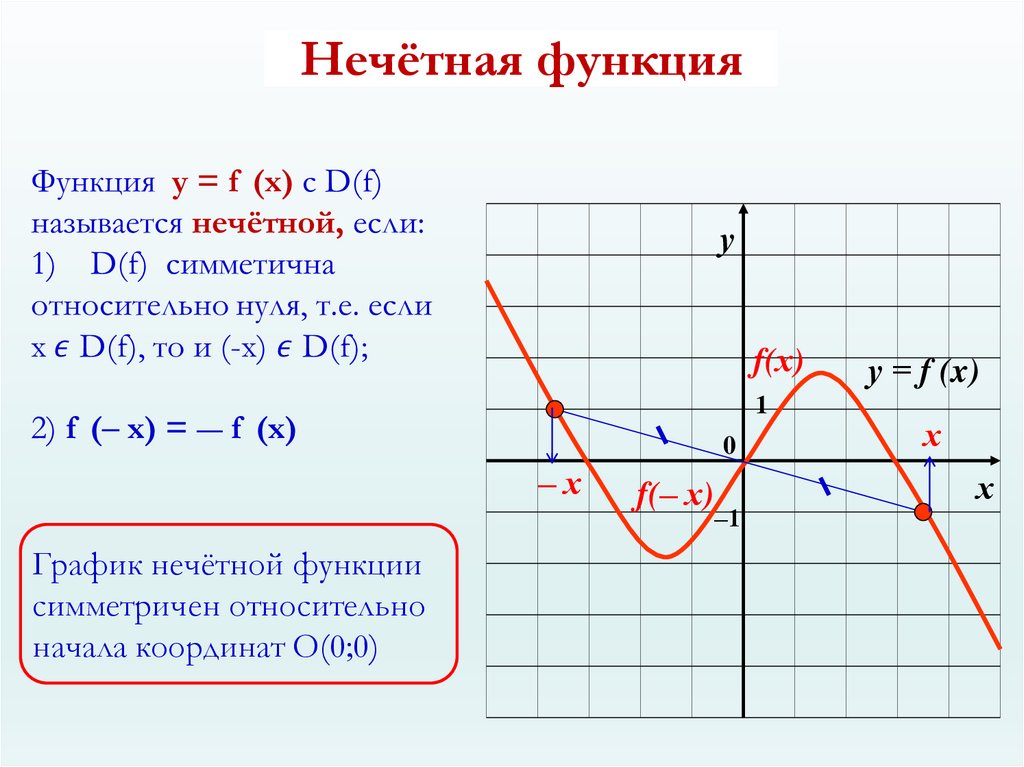
{\log_{\sqrt2} t_1}\)
, то первое уравнение совокупности перепишется в виде \
Как мы уже говорили, любое кубическое уравнение имеет не более трех решений, следовательно, каждое уравнение из совокупности будет иметь не более трех решений. А значит и вся совокупность будет иметь не более шести решений.
Значит, чтобы исходное уравнение имело шесть решений, квадратное уравнение \((*)\)
должно иметь два различных решения, а каждое полученное кубическое уравнение (из совокупности) должно иметь три различных решения (причем ни одно решение одного уравнения не должно совпадать с каким-либо решением второго!)
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \
2) Также нужно, чтобы оба корня были положительными (так как \(t>0\)
).
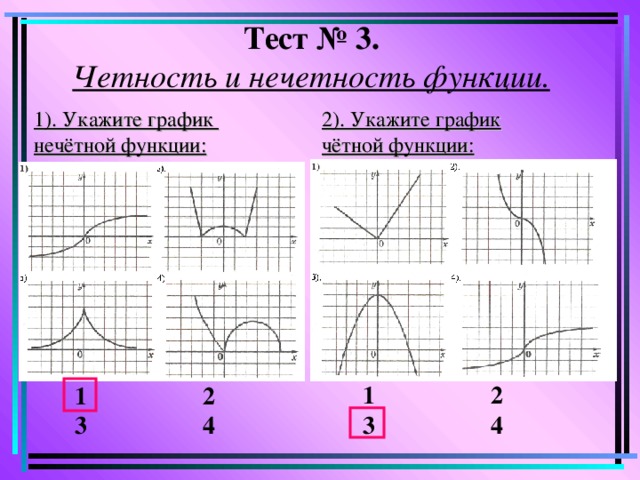2+2}\cdot \ln 2\cdot 2x\)
. Ноль производной: \(x=0\)
. При \(x0\)
, при \(x>0\)
: \(g»
Функция \(f(x)\)
при \(x>0\)
является возрастающей, а при \(x
Действительно, при \(x>0\)
первый модуль раскроется положительно (\(|x|=x\)
), следовательно, вне зависимости от того, как раскроется второй модуль, \(f(x)\)
будет равно \(kx+A\)
, где \(A\)
– выражение от \(a\)
, а \(k\)
равно либо \(13-10=3\)
, либо \(13+10=23\)
. При \(x
Найдем значение \(f\)
в точке минимума: \
Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций \(f\) и \(g\) имели хотя бы одну точку пересечения. Следовательно, нужно: \ Решая данную совокупность систем, получим ответ: \\]
Ответ:
\(a\in \{-2\}\cup\)
Исследование функции.
1) D(y) – Область опрделения: множество всех тех значений переменной х. при которых алгебраические выражения f(x) и g(x) имеют смысл.
Если функция задана формулой,
то область определения состоит из всех
значений независимой переменной, при
которых формула имеет смысл.
2) Свойства функции: четность/нечетность, периодичность:
Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента.
Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (симметричная относительно центра координат).
Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (симметричная относительно оси ординат).
Ни чётная ни нечётная функция (функция общего вида) — функция, не обладающая симметрией. В эту категорию относят функции, не подпадающие под предыдущие 2 категории.
Функции, не принадлежащие ни одной из категорий выше, называются ни чётными ни нечётными (или функциями общего вида).
Нечётные функции
Нечётная степень где — произвольное целое число.
Чётные функции
Чётная
степень где —
произвольное целое
число.
Периоди́ческая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (
3) Нули (корни) функции — точки, где она обращается в ноль.
Нахождение точки пересечения графика с осью Oy . Для этого нужно вычислить значение f (0). Найти также точки пересечения графика с осью Ox , для чего найти корни уравнения f (x ) = 0 (или убедиться в отсутствии корней).
Точки, в которых график пересекает ось , называют нулями функции . Чтобы найти нули функции нужно решить уравнение , то есть найти те значения «икс» , при которых функция обращается в ноль.
4) Промежутки постоянства знаков, знаки в них.
Промежутки, где функция f(x) сохраняет знак.
Интервал
знакопостоянства – это интервал, в
каждой точке которого функция
положительна либо отрицательна.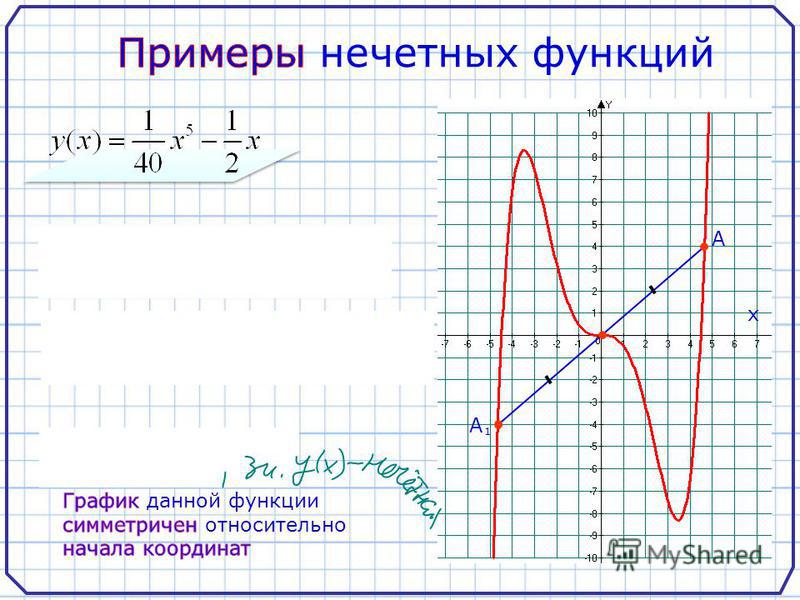
ВЫШЕ оси абсцисс.
НИЖЕ оси .
5) Непрерывность (точки разрыва, характер разрыва, ассимптоты).
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Устранимые точки разрыва
Если предел функции существует , но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:
,
то точка называется точкой устранимого разрыва функции (в комплексном анализе -устранимая особая точка).
Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности , что и обосновывает название точки, как точки устранимого разрыва.
Точки разрыва первого и второго рода
Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов :
если
оба односторонних предела существуют
и конечны, то такую точку называют точкой
разрыва первого рода .
Точки устранимого разрыва являются
точками разрыва первого рода;
если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода .
Аси́мпто́та — прямая , обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви вбесконечность.
Вертикальная
Вертикальная асимптота — прямая предела .
Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
Горизонтальная
Горизонтальная асимптота — прямая вида при условии существования предела
.
Наклонная
Наклонная асимптота — прямая вида при условии существования пределов
Замечание:
функция может иметь не более двух
наклонных (горизонтальных) асимптот.
Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при (или ) не существует.
если в п. 2.), то , и предел находится по формуле горизонтальной асимптоты, .
6) Нахождение промежутков монотонности. Найти интервалы монотонности функции f (x )(то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной f (x ). Для этого находят производную f (x ) и решают неравенство f (x )0. На промежутках, где это неравенство выполнено, функция f (x )возрастает. Там, где выполнено обратное неравенство f (x )0, функция f (x )убывает.
Нахождение
локального экстремума. Найдя
интервалы монотонности, мы можем сразу
определить точки локального экстремума
там, где возрастание сменяется убыванием,
располагаются локальные максимумы, а
там, где убывание сменяется возрастанием
— локальные минимумы.
Вычислить значение
функции в этих точках. Если функция
имеет критические точки, не являющиеся
точками локального экстремума, то
полезно вычислить значение функции и
в этих точках.
Нахождение наибольшего и наименьшего значений функции y = f(x) на отрезке (продолжение)
1. Найти производную функции: f (x ). 2. Найти точки, в которых производная равна нулю: f (x )=0x 1, x 2 ,… 3. Определить принадлежность точек х 1 , х 2 , … отрезку [a ; b ]: пусть x 1a ;b , а x 2a ;b . |
Интегрирование четных и нечетных функций: методы
Функции могут иметь интересные графики — скрытые закономерности, фантастические формы и симметрии . Возьмем, к примеру, график ниже.
График симметричной функции четвертого порядка — StudySmarter Originals
Что-то заметили? Похоже, мы поместили зеркало на ось Y! Давайте теперь посмотрим на другой график:
График симметричного паттерна с использованием функции косинуса — StudySmarter Originals
График с отражением поперек оси x не является функцией, так как он не прошел тест вертикальной линии.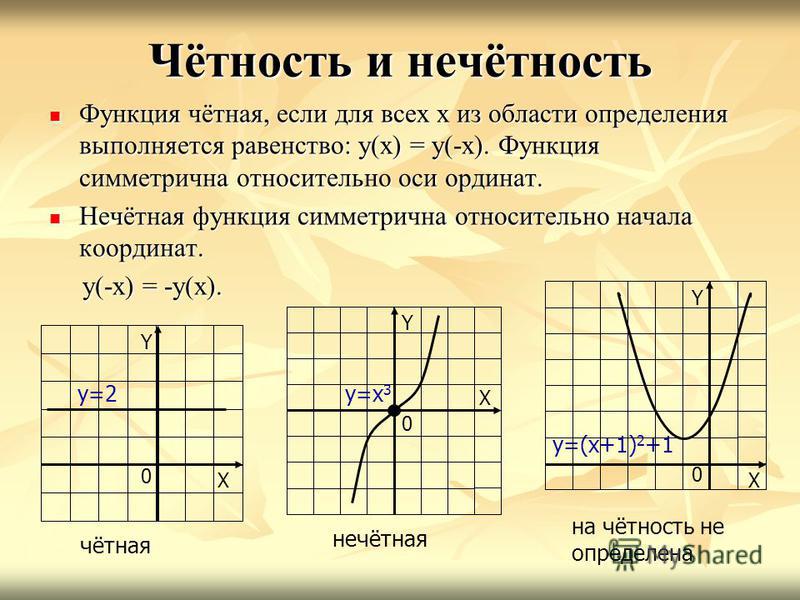
Однако, если мы сдвинем часть под осью x влево, у нас появится вращательная симметрия относительно начала координат!
График косинуса, преобразованный в функцию — StudySmarter Originals
Функции, которые имеют эти типы симметрии, получают уникальные имена. Кроме того, эти симметрии могут быть использованы в нашу пользу при интегрировании этих функций.
Что такое четные и нечетные функции?
Некоторые функции можно разделить на четные функции или нечетные функции . Но что это значит? Давайте рассмотрим каждое определение.
Говорят, что функция является четной функцией, или симметричной функцией, если для всех значений x ее области определения.
Другими словами, четная функция — это функция, выход которой не меняется, если мы меняем знак ее входа. Как насчет нечетных функций?
Говорят, что функция является нечетной функцией, или антисимметричной функцией, если для всех значений x своей области определения.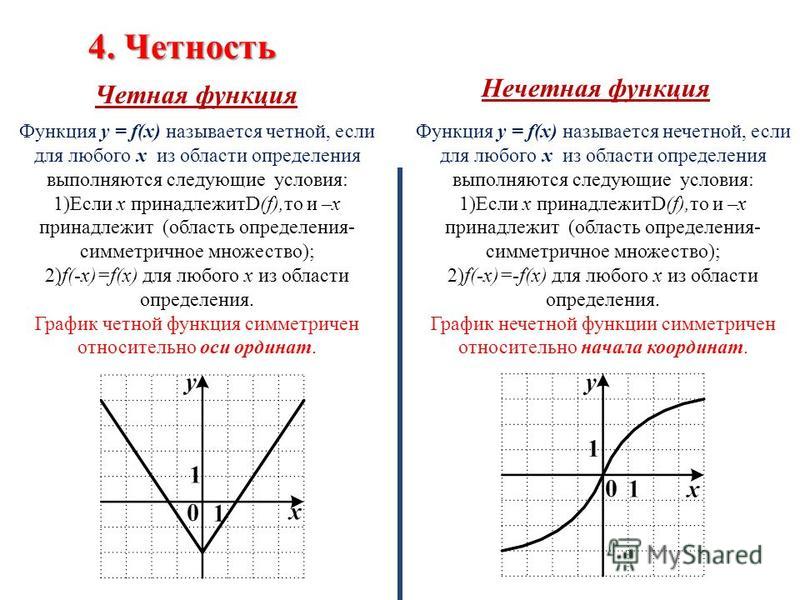
Напротив, если мы изменим знак входа нечетной функции, мы получим противоположный знак ее выхода. Мы можем воспользоваться этой симметрией при нахождении определенных интегралов четных или нечетных функций.
Имейте в виду, что некоторые функции не являются ни четными, ни нечетными!
Определенные интегралы четных функций
Для графиков четных функций каждое значение слева от y-ai отражает значение справа от него. Эта характеристика дает нам формулу для определенных интегралов четных функций.
Позвольте быть функцией, которая является интегрируемой в интервале . Если функция четная, то справедлива следующая формула:
Посмотрим на площадь между четной функцией и положительной осью x.
Площадь между четной функцией и положительной осью x — StudySmarter Originals
Мы можем сравнить ее с площадью между той же функцией и отрицательной осью x.
Площадь между той же четной функцией и отрицательной осью X — StudySmarter Originals
Обратите внимание, что области одинаковы; они просто отражаются по оси Y.
Это наблюдение означает, что мы можем найти площадь всего интервала, умножив любую из этих площадей на 2. Обычно мы используем площадь над положительной осью x, что дает нам формулу для интегрирования четных функций:
Определенные интегралы от нечетные функции
График нечетной функции подобен четной функции, но зеркальные значения отрицательны. Ниже приведена формула интегрирования нечетных функций.
Позвольте быть функцией, которая является интегрируемой в интервале . Если функция нечетная, то справедлива следующая формула:
Рассмотрим определенный интеграл нечетной функции.
Интеграл нечетной функции — StudySmarter Originals
Обратите внимание, что площади снова одинаковы, но теперь они отражаются по обеим осям. В этом случае одна область является отрицательной по отношению к другой. Поэтому, если их сложить, результат будет равен 0. Отсюда получаем формулу для определенных интегралов от нечетных функций:
Доказательство интегралов четных и нечетных функций
Мы можем использовать свойства четных и нечетных функций для доказательства формул интегрирования четных и нечетных функций.
Давайте прыгать в это!
Доказательство интеграла четной функции
Позвольте быть четной функцией. Рассмотрим определенный интеграл .
Мы можем разбить этот интеграл на два интервала, используя свойства интегралов.
Так как это четная функция, мы можем заменить на в первом члене правой части уравнения.
Теперь мы делаем u-подстановку (см. Интегрирование заменой) в том же термине, позволяя . Таким образом, и нижний предел интегрирования становится .
Теперь мы используем знак минус внутри интеграла, чтобы изменить пределы определенного интеграла.
Поскольку все интегралы, участвующие в приведенном выше уравнении, являются определенными интегралами, переменная интегрирования не имеет никакого значения. Следовательно, первый и второй члены правой части уравнения равны.
Эта эквивалентность дает нам формулу интегрирования четных функций.
Доказательство интеграла нечетной функции
Пусть — нечетная функция. Рассмотрим определенный интеграл .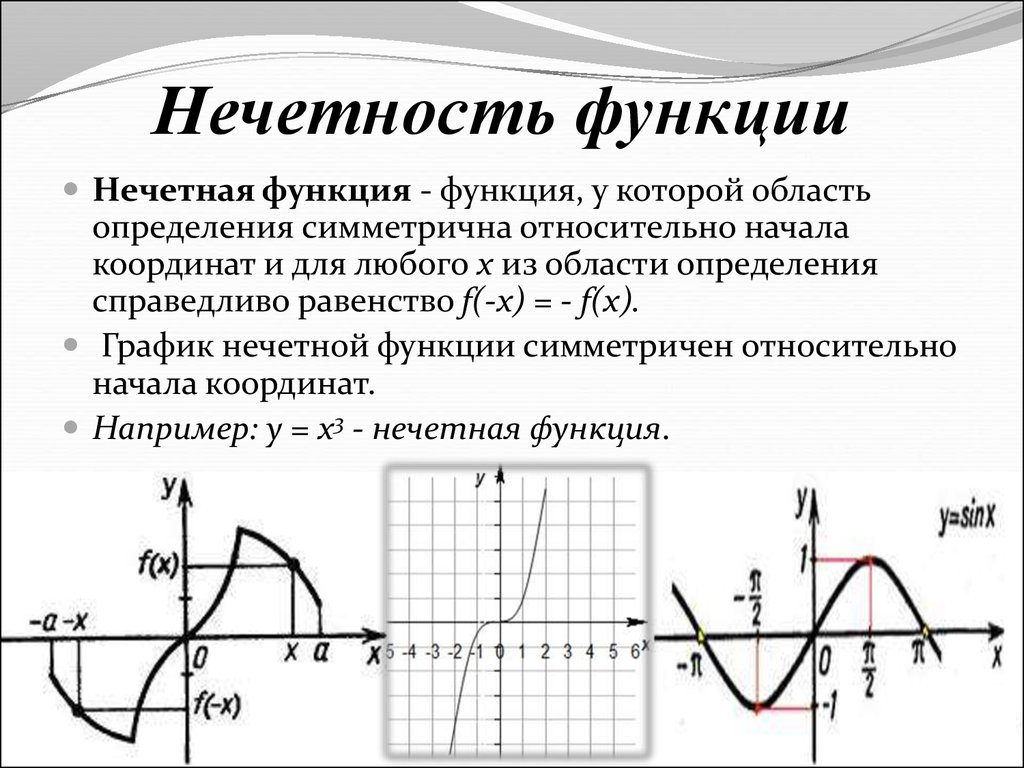
Разделим и этот интеграл.
Поскольку это нечетная функция, мы можем заменить ее на . Эта замена существенно меняет знак функции с положительного на отрицательный и снова на положительный.
Теперь мы можем действовать так же, как и для интеграла от четной функции, выполнив ту же u-подстановку и упрощение.
Два члена в правой части уравнения являются отрицательными по отношению друг к другу. Значит, их сумма равна 0. Это упрощение дает нам формулу интегрирования нечетных функций.
Примеры интегрирования четных и нечетных функций
При использовании формул интегрирования четных и нечетных функций мы должны быть уверены, что наша функция четная или нечетная. Давайте посмотрим, как это делается.
Найти значение определенного интеграла:
Решение:
Начнем с проверки, является ли заданная функция четной или нечетной.
Приравнять к подынтегральной функции определенного интеграла.
Вычисляйте и упрощайте, используя свойства показателей степени.
Мы проверили, что функция четная, потому что . Теперь мы можем использовать формулу интегрирования четных функций.
Интегрировать с помощью основных формул интегрирования.
Оценивайте и упрощайте.
Использование этой формулы заключается в том, что оценка относительно проста. Давайте посмотрим на другой пример.
Найти значение определенного интеграла: .
Решение:
Еще раз начнем с проверки, является ли функция четной или нечетной.
Приравнять к подынтегральной функции определенного интеграла.
Вычисляйте и упрощайте, используя свойства показателей степени.
Вычесть -1.
Мы проверили, что функция нечетная, потому что . Теперь мы можем использовать формулу интегрирования нечетных функций.
Обратите внимание, что нам не нужно было использовать какое-либо другое правило интеграции!
Вот небольшой совет по полиномиальным функциям! Если все показатели полиномиальной функции являются четными числами (или постоянными членами), то функция четная.
Точно так же, если все показатели полиномиальной функции нечетны, то функция нечетна. Используя этот ярлык, вам не нужно вычислять f(-x) , и вы можете быстро узнать, какую формулу использовать!
Интеграция четных и нечетных функций — основные выводы
- Некоторые функции можно разделить на четные функции или нечетные функции.
- Четные функции — это такие функции, что для каждого x в своей области.
- Нечетные функции — это такие функции, что для каждого x в своей области.
- Если четная функция, интегрируемая на интервале, то .
- Если нечетная функция, интегрируемая на интервале, то .
- Четные функции также известны как симметричные функции . Нечетные функции также известны как антисимметричные функции .
Все о нечетной и четной функции
Термины «четный» и «нечетный» используются для описания симметрии функции.
Четная функция симметрична относительно оси Y графика. Нечетная функция симметрична относительно начала координат графика (0,0). Это означает, что поворот нечетной функции на 180 градусов вокруг начала координат даст вам ту же функцию, с которой вы начали. Для их классификации используются соотношения симметрии четных и нечетных функций. Степенная функция f(x) = xn является четной функцией, если n четно, а f(x) является нечетной функцией, если n нечетно, отсюда и названия четных и нечетных функций. Давайте рассмотрим еще несколько четных и нечетных функций и узнаем о них. Функция может быть четной, нечетной или и той, и другой, или она не может быть ни четной, ни нечетной. Мы рассмотрим несколько примеров, чтобы помочь вам понять концепцию.
Четные и нечетные функции
Четная функция. Для всех значений x в области f функция f(x) с действительным знаком называется четной функцией, если выходное значение f(-x) равно то же, что f(x). Следующее уравнение должно выполняться четной функцией: Для всех значений x в D(f) f(-x) = f(x), где D(f) означает область определения функции f.
Иными словами, уравнение f(-x) – f(x) = 0 выполняется для каждого x при заданной четной функции. Рассмотрим следующий пример: f(x) = x².
Для всех значений x f(-x) = (-x)² = x², поскольку квадрат отрицательного числа равен квадрату его положительного значения. Для всех x это означает, что f(-x) равно f(x). В результате функция f(x) = x² является четной функцией.
Примеры четных и нечетных функций
Нечетная функция. Для всех значений x в области f функция f(x) с действительным знаком считается нечетной функцией, если выходное значение f(-x) совпадает с отрицательным значением f(x). Следующее уравнение должно храниться в нечетной функции: Для всех значений x в D(f) f(-x) = -f(x), где D(f) означает область определения функции f. Другими словами, уравнение f (-x) + f (x) = 0 выполняется для каждого x для нечетной функции. Рассмотрим следующий пример: f(x) = x³.
Поскольку куб отрицательного числа совпадает с отрицательным кубом положительного значения числа, f(-x) = (-x)³ = -(x³) для всех значений x.
Для всех x это означает f(-x) = -f(x). В результате f(x) = x³ — нечетная функция.
Свойства четных и нечетных функций
Сумма двух четных функций равна двум четным функциям, тогда как сумма двух нечетных функций равна двум нечетным функциям.
При сравнении двух четных функций разность четная, а при сравнении двух нечетных функций разность нечетная.
Если одна из функций не является нулевой функцией, сумма четной и нечетной функций не является ни четной, ни нечетной.
Произведение двух четных функций также является четной функцией, как и произведение двух нечетных функций.
Нечетное является результатом четной и нечетной функции.
Частное двух четных функций также является четной функцией, как и частное двух нечетных функций.
