Онлайн исследовать функцию на непрерывность и построить график: Точки разрыва функции онлайн

Виды точек разрыва функции

Непрерывность функции: основные понятия и свойства

Определение. Пусть на некотором промежутке определена функция f(x) и x₀ – точка этого промежутка. Если , то f(x) называется непрерывной в точке x₀.
Из определения следует, что о непрерывности можно говорить лишь по отношению к тем точкам, в которых f(x) определена (при определении предела функции такого условия не ставилось). Для непрерывных функций , то есть операции f и lim перестановочны. Соответственно двум определениям предела функции в точке можно дать два определения непрерывности – «на языке последовательностей» и «на языке неравенств» (на языке ε-δ). Предлагается это сделать самостоятельно.
Для практического использования иногда более удобно определение непрерывности на языке приращений.
Величина Δx=x-x₀ называется приращением аргумента, а Δy=f(x)-f(x₀) – приращением функции при переходе из точки x₀ в точку x.
Определение. Пусть f(x) определена в точке x₀. Функция f(x) называется непрерывной в точке x₀, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть Δy→0 при Δx→0.

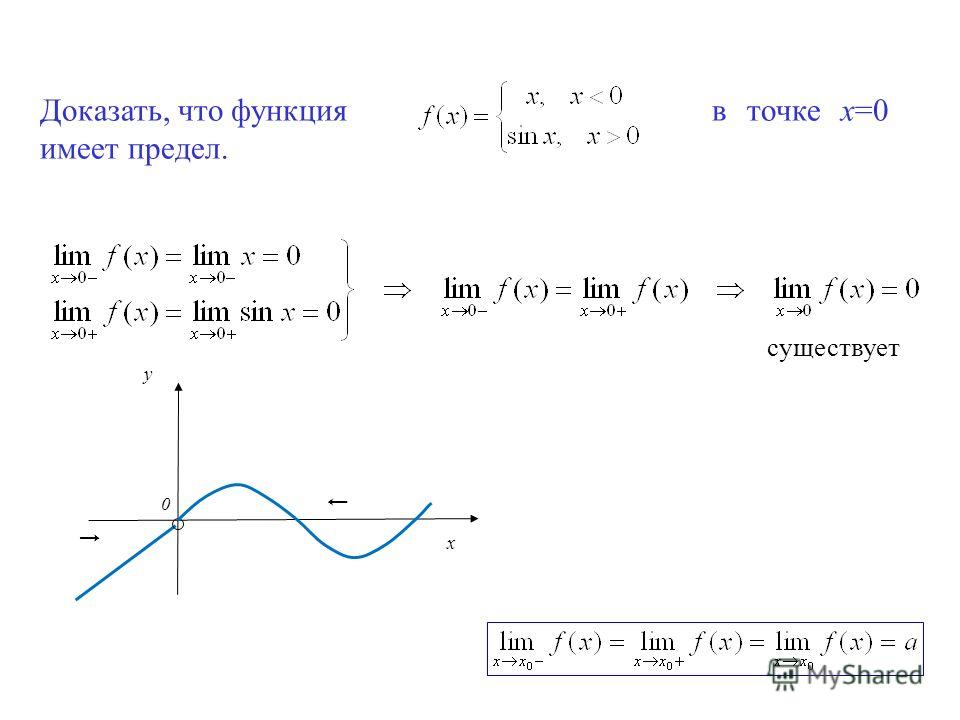
Пример №1. Доказать, что функция y=sinx непрерывна при любом значении x.
Решение. Пусть x₀ – произвольная точка. Придавая ей приращение Δx, получим точку x=x₀+Δx. Тогда Δy=f(x)-f(x₀) = sin(x₀+Δx)-sin(x) = . Получаем .

Определение. Функция y=f(x) называется непрерывной в точке x₀ справа (слева), если

Функция, непрерывная во внутренней точке, будет одновременно непрерывной справа и слева. Справедливо и обратное утверждение: если функция непрерывна в точке слева и справа, то она будет непрерывной в этой точке. Однако функция может быть непрерывной только с одной стороны. Например, для , , f(1)=1, следовательно, эта функция непрерывна только слева (график этой функции см. выше в пункте 5.7.2).
Определение. Функция называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка.
В частности, если промежутком является отрезок [a,b], то на его концах подразумевается односторонняя непрерывность.

Свойства непрерывных функций

1. Все элементарные функции непрерывны в своей области определения.
2. Если f(x) и φ(x), заданные на некотором промежутке, непрерывны в точке x₀ этого промежутка, то в этой точке будут также непрерывны функции
3. Если y=f(x) непрерывна в точке x₀ из X, а z=φ(y) непрерывна в соответствующей точке y₀=f(x₀) из Y, то и сложная функция z=φ(f(x)) будет непрерывной в точке x ₀.

Разрывы функции и их классификация

Признаком непрерывности функции f(x) в точке x₀ служит равенство , которое подразумевает наличие трех условий:
1) f(x) определена в точке x₀;
2) ;
3) .
Если хотя бы одно из этих требований нарушено, то x₀ называют точкой разрыва функции. Другими словами, точкой разрыва называется точка, в которой эта функция не является непрерывной. Из определения точек разрыва следует, что точками разрыва функции являются:
а) точки, принадлежащие области определения функции, в которых f(x) теряет свойство непрерывности,
б) точки, не принадлежащие области определения f(x), которые являются смежными точками двух промежутков области определения функции.
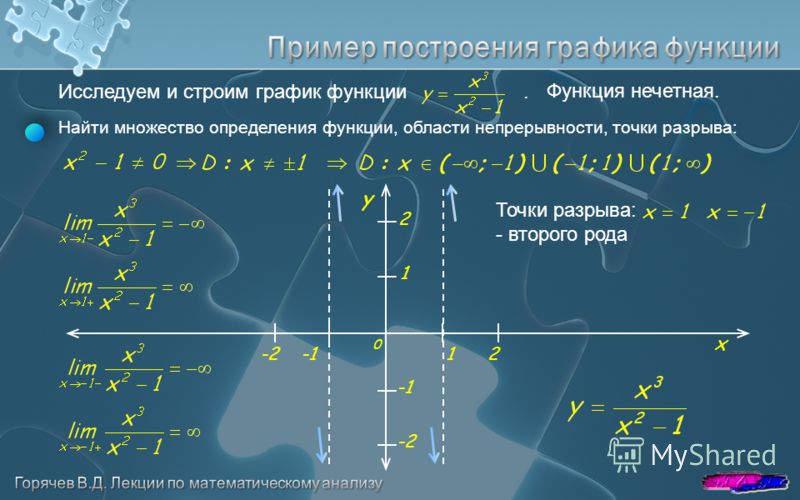
Например, для функции точка x=0 есть точка разрыва, так как функция в этой точке не определена, а функция имеет разрыв в точке x=1, являющейся смежной для двух промежутков (-∞,1) и (1,∞) области определения f(x) и не существует.

Для точек разрыва принята следующая классификация.
1) Если в точке x₀ имеются конечные и , но f(x₀+0)≠f(x₀-0), то x₀ называется точкой разрыва первого рода, при этом называют скачком функции.

Пример 2. Рассмотрим функцию
Разрыв функции возможен только в точке x=2 (в остальных точках она непрерывна как всякий многочлен).
Найдем , . Так как односторонние пределы конечны, но не равны друг другу, то в точке x=2 функция имеет разрыв первого рода. Заметим, что , следовательно функция в этой точке непрерывна справа (рис. 2).
2) Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен ∞ или не существует.

Пример 3. Функция y=2^1/x непрерывна для всех значений x, кроме x=0. Найдем односторонние пределы: , , следовательно x=0 – точка разрыва второго рода (рис. 3).
3) Точка x=x₀ называется точкой устранимого разрыва, если f(x₀+0)=f(x₀-0)≠f(x₀).
Разрыв «устраним» в том смысле, что достаточно изменить (доопределить или переопределить) значение функции в этой точке, положив

, и функция станет непрерывной в точке x₀.
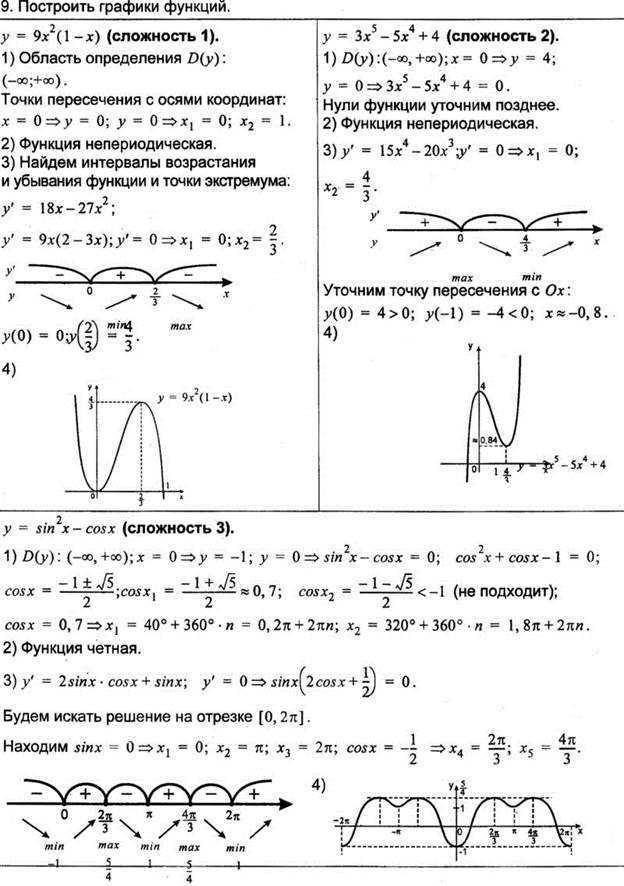
Пример 4. Известно, что , причем этот предел не зависит от способа стремления x к нулю. Но функция в точке x=0 не определена. Если доопределим функцию, положив f(0)=1, то она окажется непрерывной в этой точке (в остальных точках она непрерывна как частное непрерывных функций sinx и x).
Пример 5. Исследовать на непрерывность функцию .
Решение. Функции y=x³ и y=2x определены и непрерывны всюду, в том числе и в указанных промежутках. Исследуем точку стыка промежутков x=0:
, , f(0)=0. Получаем, что:

,

откуда следует, что в точке x=0 функция непрерывна.

Определение. Функция, непрерывная на промежутке за исключением конечного числа точек разрыва первого рода или устранимого разрыва, называется кусочно-непрерывной на этом промежутке.

Примеры разрывных функций

Пример 1. Функция определена и непрерывна на (-∞,+∞) за исключением точки x=2. Определим тип разрыва. Поскольку и , то в точке x=2 разрыв второго рода (рис. 6).
Пример 2. Функция определена и непрерывна при всех x, кроме x=0, где знаменатель равен нулю. Найдем односторонние пределы в точке x=0:

.

Односторонние пределы конечны и различны, следовательно, x=0 – точка разрыва первого рода (рис. 7).
Пример 3. Установить, в каких точках и какого рода разрывы имеет функция
Эта функция определена на [-2,2]. Так как x² и 1/x непрерывны соответственно в промежутках [-2,0] и [0,2], то разрыв может быть только на стыке промежутков, то есть в точке x=0. Поскольку , то x=0 является точкой разрыва второго рода.

Пример 4. Можно ли устранить разрывы функций:
а) в точке x=2;
б) в точке x=2;
в) в точке x=1?
Решение. О примере а) сразу можно сказать, что разрыв f(x) в точке x=2 устранить невозможно, так как в этой точке бесконечные односторонние пределы (см. пример 1).

б) Функция g(x) хотя имеет конечные односторонние пределы в точке x=2
(,),
но они не совпадают, поэтому разрыв также устранить нельзя.
в) Функция φ(x) в точке разрыва x=1 имеет равные односторонние конечные пределы: . Следовательно, разрыв может быть устранен переопределением функции в точке x=1, если положить f(1)=1 вместо f(1)=2.

Пример №5. Показать, что функция Дирихле

разрывна в каждой точке числовой оси.
Решение. Пусть x₀ – любая точка из (-∞,+∞). В любой ее окрестности найдутся как рациональные, так и иррациональные точки. Значит, в любой окрестности x₀ функция будет иметь значения, равные 0 и 1. В таком случае не может существовать предела функции в точке x₀ ни слева, ни справа, значит функция Дирихле в каждой точке числовой оси имеет разрывы второго рода.

Пример 6. Найти точки разрыва функции

и определить их тип.
Решение. Точками, подозрительными на разрыв, являются точки x₁=2, x₂=5, x₃=3.
В точке x₁=2 f(x) имеет разрыв второго рода, так как Точка x₂=5 является точкой непрерывности, так как значение функции в этой точке и в ее окрестности определяется второй строкой, а не первой: .
Исследуем точку x₃=3: , , откуда следует, что x=3 – точка разрыва первого рода.

Для самостоятельного решения.
Исследовать функции на непрерывность и определить тип точек разрыва:
1) ; Ответ: x=-1 – точка устранимого разрыва;
2) ; Ответ: Разрыв второго рода в точке x=8;

3) ; Ответ: Разрыв первого рода при x=1;
4)
Ответ: В точке x₁=-5 устранимый разрыв, в x₂=1 – разрыв второго рода и в точке x₃=0 — разрыв первого рода.
5) Как следует выбрать число A, чтобы функция

была бы непрерывной в точке x=0?
Ответ: A=2.
6) Можно ли подобрать число A так, чтобы функция

была бы непрерывной в точке x=2?
Ответ: нет.

Задана функция y=f(x) и два значения аргумента x₁ и x₂. Требуется: 1) установить, является ли данная функция непрерывной или разрывной из данных значений аргумента; 2) в случае разрыва определить, какого он рода; 3) все рассуждения обосновать.
, x₁ = 1, x₂ = 3
Решение:
а)
Предел конечен и равен числу. Следовательно, в точке x₁

функция непрерывна.

б)

Предел в точке x=3 не существует. Следовательно, в этой точке функция имеет разрыв. Поскольку один из пределов равен бесконечности, то эта точка разрыва второго рода.

в)

Ответ:

Исследование функций и построение графиков

1.

Исследование функций и построение графиков

2. Теоретический материал

3. Содержание

1) Область определения функции
2) Свойства функции (четность, нечетность,
периодичность)
4) Точки пересечения функции с осями
координат
5) Непрерывность функции. Характер точек
разрыва
6) Асимптоты
7) Экстремумы функции. Исследование функции
на монотонность
8) Выпуклость функции. Точки перегиба

4. Область определения функции

Определение. Областью определения
функции называется множество значений
независимой переменной, при которых
функция определена.
Примеры.
y ln( x 1)
y
2
x 3
2
D f ( 1, )
D f R \ 3

5. Четные и нечетные функции

Функция y=f(x)
называется четной,
если
y
y = |x|
x
Функция y=f(x)
называется нечетной,
если
x D f f ( x) f ( x)
x D f f ( x) f ( x)
y
y = f (x)
x

6. Периодичные функции

Определение. Функция y=f(x) называется
периодической, если существует такое
положительное число Т, что если х принадлежит Df ,
то х±Т также принадлежит Df и f(x+T)=f(T).
y
y=cosx
x

7. Точки пересечения с осями координат

При исследовании функции необходимо
найти координаты точек пересечения графика
функции с осями координат.
Абсциссы точек пересечения графика
функции с осью Ох находятся из системы
уравнений у=f(x) и у=0, а ординаты точек
пересечения графика функции с осью Оу
находятся из системы уравнений у=f(x) и х=0.

8. Непрерывность Характер точек разрыва

Функция у=f(x) называется непрерывной в
точке х0, если функция определена в точке х0 и
предел функции в точке х0 равен значению
функции в точке х0.
x0 D f lim f ( x) f ( x0 )
x x0
Функции, непрерывные в каждой точке из
области определения функции, называются
непрерывными функциями.
Примеры непрерывных функций: y=cosx,
y=sinx, y=ex , y=Pn(x) (многочлен степени n).

9. Точки разрыва функции

Определение. Точкой разрыва функции
называется точка из области определения
функции, в которой функция не является
непрерывной.
Пример. Функция
sin x
, если x 0;
f ( x) x
0, если x 0
разрывна в 0, так как
lim
x 0
f ( x) lim
x 0
sin x
1, f (0) 0
x

10. Классификация точек разрыва Точки устранимого разрыва

Если в точке х0 существуют конечные односторонние
пределы функции, равные между собой, но не равные
значению функции в точке х0, то точка х0 называется
точкой устранимого разрыва.
y
lim f ( x) lim f ( x) f ( x )
x x0
x
x x0
0

11. Классификация точек разрыва Точки скачка

Если в точке х0 существуют конечные
односторонние пределы функции, не равные между
собой, то точка х0 называется точкой скачка
(точкой разрыва I рода).
y
lim f ( x) lim f ( x)
x x0
x
x x0

12. Классификация точек разрыва Точки разрыва II рода

Если хотя бы один из односторонних пределов
функции в точке х0 не существует или бесконечен,
то точка называется точкой разрыва II рода.
y
1
, если х 0;
f ( x) х
0, если х 0.
y=1/x
x
lim f ( x) ; lim f ( x)
x 0
x 0

13. Вертикальные асимптоты

Прямая х=х0 называется вертикальной
асимптотой графика функции при х х0, если
lim f ( x)
x x0
x x0
.
lim f ( x) или
y
y = ln(x2-1)
x

14. Наклонные асимптоты

Если существует прямая y=kx+b такая, что
lim ( f ( x) kx b) 0 , то эта прямая называется
x
асимптотой графика функции f при x .
Для того чтобы прямая y=kx+b была асимптотой,
необходимо и достаточно, чтобы выполнялись
следующие условия:
lim
x
f ( x)
k,
x
lim ( f ( x) kx) b .
x

15. Экстремумы функции

Пусть функция f (x) определена и непрерывна на
интервале (а, b). Точка х0 интервала (а, b)
называется точкой строгого максимума (минимума)
функции f (x), если в некоторой проколотой
окрестности точки х0 f (x)< f (x0) ( f (x) > f (x0) ).
Точки минимума и точки максимума функции
называются точками экстремума функции.
Необходимое условие экстремума. Пусть
точка х0 — точка экстремума функции. Тогда либо
производная функции в этой точке равна 0, либо
не существует.

16. Исследование функции на монотонность

Известно, что если f ‘(x)>0 (f ‘(x)>0) в (а, b), то
функция f (x) строго возрастает (строго убывает)
в (а, b).
Рассмотрим функцию f(x) = x + 1|x
1
1
f ( x) x 1 2
x
x
Критические точки функции х=±1. f ‘(x)>0 при х<-1
и при х>1; f ‘(x)<0 при -1<x<0 и при 0<x<1.
x , 1 ; 1,
x , 1 ; 1,
функция возрастает
функция убывает

17. Выпуклость функции

Функция у=f(х), определенная на интервале (а, b),
называется выпуклой вверх (вниз) в интервале (а, b),
если для любых х1и х2 из интервала (а, b) из того, что
х1<х2, следует, что часть графика функции между
точками (х1,f(х1)) и (х2,f(х2)) лежит выше (ниже) хорды,
соединяющей эти точки.
а
x1
x2 b
функция выпукла вверх
a
x1
x2 b
функция выпукла вниз

18.

Выпуклость функции. Точки перегибаТакже говорят, что график функции f (x) имеет
на интервале (a, b) выпуклость, направленную вниз
(вверх), если график этой функции в пределах (a, b)
лежит не ниже (не выше) любой своей касательной.
Если график функции в точке (х0, f(x0))
переходит с одной стороны касательной на
другую, то точка х0 называется точкой перегиба
функции f(x).

19. Достаточные условия выпуклости функции и существования точек перегиба

Достаточное условие строгой выпуклости функции
Если на интервале (а,b) f »(x)>0, то на интервале (а,b)
функция выпукла вниз, и если на интервале f »(x)<0, то
на интервале (а,b) функция выпукла вверх.
Достаточное условие строгой выпуклости
функции
Если в левой и правой полуокрестностях
некоторой точки х0 f »(x) имеет противоположные
знаки, то точка х0 – точка перегиба функции.

20. Практический материал

21. Исследуем функцию и построим её график.

1). Поскольку знаменатель положителен при всех ,
область определения функции — вся ось
2). Функция f(x) — нечётная, поскольку при смене знака x
числитель меняет знак, а знаменатель остаётся без
изменения, откуда f(-x) = — f(x). Следовательно, график
функции симметричен относительно начала
координат.
Периодической функция не является.
3). Поскольку область определения этой элементарной
функции — вся вещественная ось, вертикальных
асимптот график не имеет.
4). Найдём наклонные асимптоты при
. Имеем:
в виде
Таким образом, асимптотой как при
служит прямая
.
, так и при
5). Найдём точки пересечения с осями координат. Имеем:
f(0) = 0, причём x=0 — единственное решение
уравнения f(x) = 0. Значит, график y = f(x) пересекает
сразу и ось Ox, и ось Oy в начале координат.
Очевидно, что f(x)>0 при x>0 и f(x)<0 при x<0.
6) Найдём производную:
Очевидно, что f´(x) ≥ 0 при всех
; единственная
точка, в которой f´(x) = 0 — это x=0. Значит, функция
f(x) возрастает на всей оси Ox, а в стационарной точке
x=0 имеет горизонтальную касательную.
7) Найдём вторую производную:
Знаменатель этой дроби положителен при всех x.
Числитель имеет корни x=0 и x=±√3, при этом f’’(x)>0
на интервалах
и
— на этих интервалах
функция выпукла. На интервалах
и
выполняется обратное неравенство f’’(x)<0, здесь
функция вогнута. Все три точки, в которых f’’(x)=0, то
есть точки — √3, 0, √3, являются точками перегиба.
8). Теперь мы можем построить график с учётом всех
предыдущих пунктов исследования функции. График
имеет такой вид:

27. Исследуем функцию f(x) = (x2 – 2x)ex и построим её график.

1). Ясно, что D(f) = R, поскольку оба сомножителя в
выражении f(x) определены при любом . Область
значений E(f) найдём после того, как отыщем
локальные экстремумы функции.
2). Функция не является ни чётной, ни нечётной; не
является она и периодической.
3). Область определения не имеет граничных точек,
значит, нет и вертикальных асимптот графика.
4) Будем искать наклонные асимптоты в виде y = kx + b.
Коэффициент k найдём по формуле
:
при
имеем
так что при
асимптоты нет, причём функция f(x)
стремится к
при
.
При
имеем:
Теперь найдём значение b по формуле
Имеем:
.
Таким образом, k=0 и b=0, так что при
асимптота
имеет уравнение y=0, то есть совпадает с осью Ox.
5). Точка пересечения с осью Oy равна f(0)=0. Заодно
нашли одну точку пересечения с осью Ox. Чтобы найти
все точки пересечения графика с осью Ox, решаем
уравнение f(x) = (x2 – 2x)ex . Поскольку ex ≠ 0, решаем
уравнение
, откуда получаем два
корня: x=0 и x=2. Так как точек разрыва нет, то имеем
три интервала знакопостоянства функции:
,и
.
Знак функции определяется множителем x2 – 2x,
поскольку ex >0 при всех x. Значит, f(x)>0 при
и при
и f(x)<0 при
.
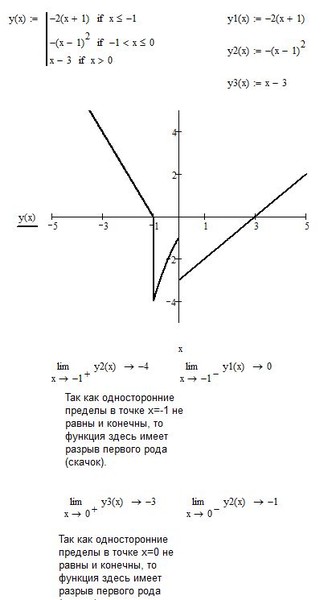
6) Вычислим производную:
Интервалы возрастания задаются неравенством f‘(x)>0,
то есть, с учётом того, что ex >0, неравенством x2 –
2x>0. Решением этого неравенства служит множество
На этих двух интервалах функция
возрастает. Легко видеть, что на интервале
выполняется неравенство f‘(x)<0, следовательно, это
интервал убывания функции. В точке -√2 возрастание
сменяется убыванием, значит, точка -√2 — точка
локального максимума.
Значение функции в этой точке равно
В точке √2 убывание сменяется возрастанием, значит,
точка √2 — точка локального минимума функции.
Значение функции в точке минимума таково:
Теперь мы можем примерно представить, как идёт
график функции:
Эскиз графика
функции f(x)
Становится очевидно, что область значений функции -это
7) По эскизу графика видно, что где-то в местах,
обведённых кружочками, должно смениться
направление выпуклости, то есть должны быть точки
перегиба. Для исследования этого найдём вторую
производную:
Решим неравенство
, эквивалентное неравенству
x2+2x-2>0. Решением этого квадратного неравенства
служит объединение интервалов
и
. На этих интервалах функция
выпукла.
Ясно, что на интервале
функция
будет вогнутой. Тем самым точки
и
— это точки перегиба. Значения
функции в точках перегиба такие:
8). Осталось построить окончательный чертёж:
График функции (x2 – 2x)ex .

Как найти непрерывность на интервале с помощью графических функций

Все ресурсы исчисления 1

10 Диагностические тесты 438 практических тестов Вопрос дня Карточки Learn by Concept

Исчисление 1 Помощь » Функции » Графические функции » Интервалы » Продолжение на интервале » Как найти непрерывность на интервале с помощью графика функций

На каком из следующих интервалов функция непрерывна?

Возможные ответы:

Правильный ответ:

Объяснение:

Функция имеет устранимый разрыв в точке .

Поскольку эта функция не определена в  , не является ли она непрерывной на любом интервале, содержащем .

Обратите внимание, что правильным ответом является открытый интервал, который доходит до , но не включает .

Сообщить об ошибке

Описать функцию 

на интервале  .

Возможные ответы:

Непрерывный; Недифференцируемый

Непрерывный; Дифференцируемый

Непрерывный; Недифференцируемый

Непрерывный; Дифференцируемая

Правильный ответ:

Непрерывная; Недифференцируемый

Объяснение:

Эта функция (показана ниже) определена для каждого значения на интервале с заданными условиями (на самом деле она определена для всех действительных чисел) и, следовательно, непрерывна. Однако в точке (0, 0) есть точка возврата, поэтому функция в этой точке недифференцируема.

Сообщить об ошибке

На каком интервале производная функции:

непрерывна?

Возможные ответы:

Функция не является непрерывной.

Правильный ответ:

Объяснение:

Производная функции, использующей степенное правило

, равна ,

, поэтому она не является непрерывной, когда или имеет отрицательное значение.

Это происходит, когда , поэтому интервал непрерывности будет равен, когда , то есть интервалу .

Сообщить об ошибке

Для каких значений  

?

Возможные ответы:

Правильный ответ:

Объяснение:

Для рациональных выражений точки разрыва часто возникают, когда знаменатель равен нулю (вызывает деление на ноль).

Здесь мы отмечаем, что знаменатель будет равен нулю при положительных и отрицательных 4; однако сначала мы должны убедиться, что ни один из них не является факторизуемым.

При разложении на множители рационального выражения получается следующее:

 

Теперь мы видим, что точка x=4 была устранимым разрывом, и фактически единственный раз, когда эта функция является разрывной, приходится на x=-4.

Напомним: чтобы функция была непрерывной в точке, точка должна существовать, должен существовать предел, и предел должен равняться точке.

Сообщить об ошибке

Оцените следующий предел:

Возможные ответы:

Не существует

Правильный ответ:

Объяснение:

Предел стремления любой асимптотической функции (функции с асимптотой) к бесконечности всегда является ее горизонтальной асимптотой.

Чтобы найти горизонтальную асимптоту рационального выражения, нужно сначала найти следующие условия:

1. Если в числителе находится наибольшая степень x, то горизонтальной асимптоты не существует.
2. Если наибольшая степень x находится в знаменателе, то горизонтальная асимптота равна 0.
3. Если в обоих случаях наивысшая степень, разделите старшие коэффициенты.

В случае этой задачи наибольшая мощность находится в обоих, поэтому мы делим старшие коэффициенты

Следовательно, наш предел равен 2.

Сообщить об ошибке

Уведомление об авторских правах Тесты 438 практических тестов Вопрос дня Карточки Учитесь по концепции 92-bx+3 & \mbox{if } 2\leq x<3 \\ 2x-a+b & \mbox{if } x\geq 3 \end{cases}$$

Jake’s Math Lessons Complete Calculus 1 Package

 

Зачетный балл: Глава 2.4 № 36 в книге Джеймса Стюарта «Исчисление одной переменной: концепции и контексты».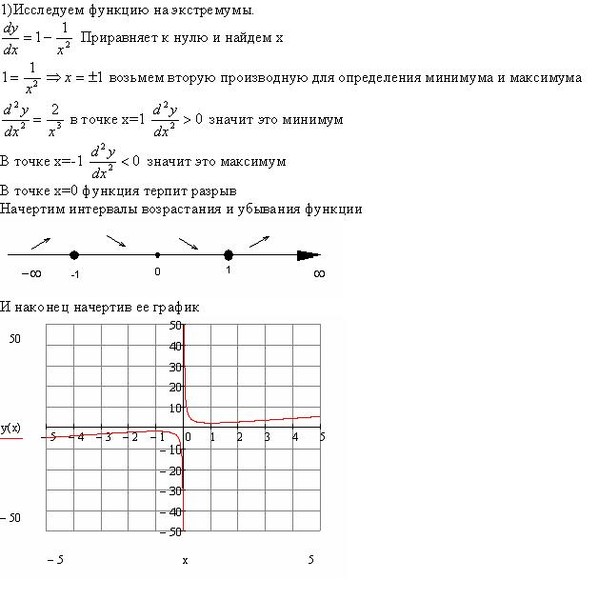

Как найти

a и b , чтобы кусочная функция была везде непрерывной.

Когда мы видим кусочные функции, подобные этой, и наша цель состоит в том, чтобы убедиться, что они непрерывны везде, есть два случая, которые мы хотим рассмотреть отдельно:

1. сделать каждую отдельную часть непрерывной в своей сокращенной области,
2. и выровнять разные части, когда наша функция переключается между ними.

Сначала давайте рассмотрим каждую часть по отдельности в сокращенной области, где

фактически определяется этой функцией.

Часть 1:

когда

При рассмотрении функции для нахождения x значений, где функция не является непрерывной, две очень распространенные вещи, которые нужно искать, это извлечение квадратного корня из отрицательного числа или деление по нулю. Очевидно, нам не нужно беспокоиться о извлечении квадратного корня из отрицательного числа, поскольку у нас нет квадратных корней. Однако у нас есть дробь, и поэтому мы должны рассмотреть, существует ли x , которое заставит нас делить на ноль.

Глядя на знаменатель нашей дроби, мы видим, что мы разделим на ноль, если подставим некоторое число вместо x , что даст

$$x-2=0.$$

Очевидно, это произойдет, когда

. И на самом деле это единственное значение для x , где не непрерывно. Однако помните, что я сказал, что мы хотим увидеть, есть ли какие-либо значения x , которые приводят к тому, что функция не является непрерывной в пределах нашего ограниченного домена для конкретной части функции. Поскольку НЕ в домене , мы можем сказать, что эта часть нашей функции непрерывна во всей своей области и не будет вносить никаких разрывов в f .

Часть 2 :

когда

Глядя на эту часть нашей кусочной функции, ясно, что нам нужно учитывать наши константы a и b.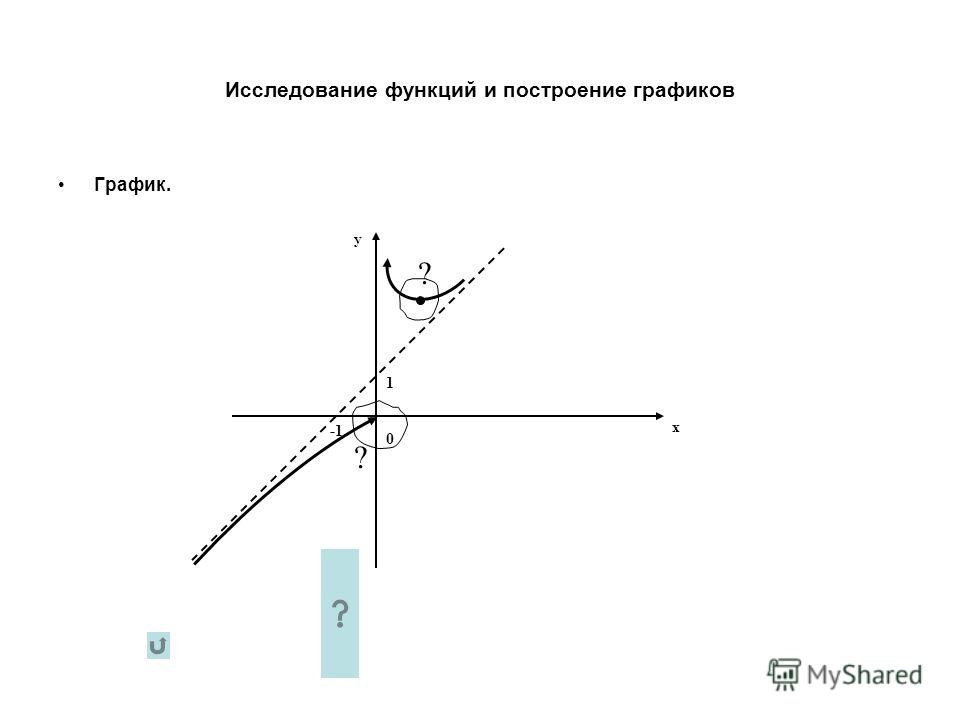   Поскольку наша функция f является функцией x (обозначается как f(x) ), мы можем считать другие буквы в этой части нашей функции ( a и b ) константами. Я обсуждал это более подробно здесь, но в основном это означает, что a и b — это некий заданный номер, они не меняются.

Однако важно понимать, что независимо от того, какие значения мы выберем для a и b , эта часть нашей функции будет просто полиномом. Точнее, это будет квадратичная функция. Независимо от того, что наши a и b в конечном итоге будут иметь терм

, терм x и постоянный терм. Поскольку мы знаем, что эта часть нашей функции будет полиномом независимо от того, каковы наши a и b , мы можем сказать, что эта часть нашей функции будет непрерывной для любых a и b , которые мы выберем.

Это так, потому что многочлены всегда и везде непрерывны. Если бы этот участок нашей функции был непрерывен всюду, то он, несомненно, был бы непрерывен и в нашей ограниченной области

. Поэтому нам не нужно беспокоиться о том, что наши a и b вызовут здесь какие-либо разрывы.

Часть 3 :

когда

На самом деле это будет похоже на часть 2 выше. Глядя на эту функцию, мы можем видеть, что независимо от того, какие значения a и b мы выберем здесь, они оба будут константами, которые объединятся в одну константу, когда мы объединяем одинаковые члены. Как только мы это сделаем, у нас останется x термин и постоянный термин. Следовательно, это тоже многочлен (в этом случае это тоже была бы линейная функция) и в результате была бы всюду непрерывна. Из-за этого он должен быть непрерывным на нашем ограниченном домене

.

Теперь мы показали, что никаких разрывов внутри любой из наших ограниченных областей, составляющих нашу кусочную функцию, мы не получим, а вот на их краях. Мы также должны убедиться, что выбираем a и b , чтобы мы могли переключаться с одной части нашей функции на другую, не прыгая вверх или вниз и не оставляя дыры в нашей функции. Если мы не выберем правильные a и b , мы можем получить разрывы в значениях x , где мы переключаемся с одной функции на другую.

Чтобы предотвратить это, нам нужно убедиться, что наши первые две части f(x) плавно переходят, когда

(это место, где мы переключаемся между этими двумя функциями), и мы должны убедиться, что вторая и третья части нашей функции имеют плавный переход между ними при .

Непрерывность в точке

Помните по определению, что функция f(x) непрерывна в точке

, если $$\lim_{x \to a} f(x) = f(a).$$

Нам нужно применить это правило здесь, чтобы убедиться, что наша функция f непрерывна на

. Следовательно, нам нужно выбрать a и b так, чтобы $$\lim_{x \to 2} f(x) = f(2).$$

Как я объяснил здесь, предел будет существовать только в том случае, если оба его односторонних предела существуют и равны друг другу. Следовательно, вместо того, чтобы найти указанный выше предел, мы на самом деле хотим найти эти два односторонних предела: 9{-}} (x+2) = f(2).$$

— это линейная функция, непрерывная везде, поэтому мы можем просто подключиться, чтобы найти этот предел.

$$4=f(2)$$

Теперь нам нужно вычислить правую часть уравнения. Чтобы найти f(2) , нам просто нужно подставить

в нашу функцию f(x) , которая является нашей исходной кусочной функцией. Первое, что нам нужно сделать, это решить, какая часть определяет нашу функцию, когда . Мы знаем, что когда. Мы можем использовать эту часть, чтобы найти 92-b(2)+3$$

$$4=4a-2b+3$$

$$1=4a-2b$$

Обратите внимание, у нас есть только одно уравнение в этой точке, которое связывает две неизвестные константы, делая невозможно найти одно единственное решение для a и b . 2-b(2)+3$$ 92-b(2)+3$$

$$4a-2b+3=4a-2b+3$$

Обратите внимание, что обе части этого уравнения одинаковы. Из-за этого это уравнение на самом деле будет верным независимо от того, что мы подставим для a и b . На самом деле это совсем не помогает нам в данном случае, но было важно протестировать его и посмотреть, что он нам сказал. Итак, мы знаем, что f будет непрерывным в

до тех пор, пока

$$1=4a-2b.$$

На данный момент мы нашли набор a и b значения, которые делают f непрерывными в

. Но нам нужно найти только один a и один b, которые выполнят это для всех значений x .

Но это ничего не говорит нам о том, будет ли оно также непрерывным в

. Проверка этого может дать нам другую связь между a и b , которую мы можем использовать, чтобы найти единственное уникальное решение для двух констант, которое сделает f 9{+}} 2x-a+b = f(3)$$

Поскольку a и b являются константами,

является линейной функцией и в результате непрерывна везде. 2-bx+3 = 6-a+b$$ 92-b(3)+3 = 6-a+b$$

$$9a-3b+3 = 6-a+b$$

$$10a-4b=3$$

Собираем все вместе

Теперь у нас есть другое соотношение, которое связывает с и b с . Само по себе это не очень полезно, но мы можем взять предыдущее уравнение, которое мы нашли, обеспечив непрерывность f в точке

, и решить следующую систему уравнений:

$$\mbox{(1):         }4a-2b=1$$

$$\mbox{(2):         }10a-4b=3.$$

Теперь, когда у нас есть два уравнения, связывающие эти две неизвестные константы, у нас достаточно информации для их решения. Вам всегда нужно как минимум столько уравнений, сколько у вас есть переменных (или в данном случае неизвестных констант). Есть несколько разных способов решить такую ​​систему уравнений, но я буду использовать подстановку. Сначала мы найдем b в уравнении (1), а затем подставим его в уравнение (2).

$$4a-2b=1$$

$$-2b=-4a+1$$

$$\mbox{(3):         }b=2a-\frac{1}{2}$$

Теперь мы подставим это в уравнение (2) и найдем a .

$$10a-4\Big(2a-\frac{1}{2}\Big)=3$$

$$10a-8a+2=3$$

$$2a+2=3$ $

$$2a=1$$

$$a=\frac{1}{2}$$

Теперь мы можем подставить это обратно в наше уравнение для b , уравнение (3).

$$b=2\Big(\frac{1}{2}\Big)-\frac{1}{2}$$

$$b=1-\frac{1}{2}$$

$$b=\frac{1}{2}$$

Теперь мы показали, что f(x) будет непрерывным в

и при если и . Мы уже показали, что f непрерывно для , и для всех значений a и b . Теперь мы также знаем, что f непрерывно в и если и . Следовательно, мы можем сказать, что f было бы непрерывным везде , если и .

На самом деле, мы можем видеть, что f является непрерывным, подставив значения, которые мы нашли для a и b , и изобразив их на графике с помощью Desmos.

С такой проблемой вы, скорее всего, столкнетесь несколько раз. На самом деле это удобно, когда вы пытаетесь решить задачу подобного типа, которая требует, чтобы вы сделали функцию везде дифференцируемой. Если вы хотите это увидеть, я работал над одним из них, и вы можете увидеть это, щелкнув эту ссылку: Решение. Найдите значения a и b, которые делают функцию дифференцируемой везде.

ЯРЛЫК – Другие примеры

Ознакомьтесь с другими затронутыми мною темами и проблемами, над которыми я работал.

No related posts.