Умножение десятичных дробей — примеры, правила как умножать в 5 классе
Десятичные дроби — хитрый зверек, но только не для нас. В этой статье научимся умножать десятичные дроби, чтобы решать задачки на контрольной в 5 классе и старше легко и быстро.
Записывайтесь на онлайн-фестиваль для родителей SmartFest!
Ждём вас 8 октября в 13:00. Вместе с педагогами, психологами и другими экспертами в образовании и воспитании ответим на главные вопросы мам и пап.
Бесплатный урок по математике
Записаться
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
обыкновенный вид — ½ или a/b,
десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
Вернемся к обыкновенным дробям позже, а сейчас обсудим десятичные дроби. Их знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
0,8
7,42
9,932
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Запишитесь и участвуйте в розыгрыше 8 уроков
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то она равна нулю.
Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д.
Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь в десятичную.
Как решаем:
Знаменатель равен 10 — это один ноль.
Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Ответ:
Пример 2. Перевести в десятичную дробь.
Как решаем:
Знаменатель равен 1000 — это три нуля.
Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
Так как в числителе только две цифры, то на пустующие места пишем нули.
В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Ответ:
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Свойства умножения
С десятичными дробями можно производить те же действия, что и с любыми другими числами: складывать и вычитать, делить и умножать.
| Свойства умножения десятичных дробей |
|---|
|
Умножение десятичных дробей друг на друга можно упростить и просто умножить натуральные числа. Главное — правильно поставить запятую в ответе.
Главное — правильно поставить запятую в ответе.
Если в задаче даны десятичные дроби с разными знаками — используем правило умножения отрицательных чисел. Как быстро запомнить:
| «−−» | минус на минус дает плюс |
| «−+» | минус на плюс дает минус |
| «+−» | плюс на минус дает минус |
| «++» | плюс на плюс дает плюс |
Числа с единицей и нулями (10, 100, 1000 и т. д.) называются разрядными единицами, так как цифра 1 — единственная значимая цифра в числе и от ее местоположения зависит количественное значение числа. Важно запомнить правила для умножения и деления на разрядную единицу:
Чтобы умножить число на разрядную единицу, достаточно к числу справа дописать столько нулей, сколько их содержит разрядная единица.
Чтобы разделить число на разрядную единицу, достаточно от числа справа отбросить столько нулей, сколько их содержит разрядная единица.

Как умножать десятичные дроби в столбик
Чтобы перемножить десятичные дроби нужно сделать три шага:
Записать десятичные дроби в столбик и умножить друг на друга, как обыкновенные числа.
Посчитать количество знаков после запятой у каждой дроби. Сложить их количество.
Полученное количество знаков отсчитать справа налево и поставить запятую.
Пример: умножить 3, 11 на 0,01.
Как решаем:
Запишем дроби в столбик и умножим их, как будто у нас нет никаких запятых:
Получаем: 311 ∗ 001 = 311.
Считаем общее количество цифр после запятой у обеих дробей — в нашем примере их четыре (по две на каждую).
Берем число, которое получилось после умножения и отсчитываем справа налево 4 знака. Но у нас получилось всего три цифры, а не четыре. Значит добавляем перед ними один ноль и вуаля — четыре цифры после запятой готовы
Ответ: 3,11 ∗ 0,01 = 0,0311.
| Примеры умножения десятичных дробей столбиком: |
|---|
Как умножать десятичные дроби на натуральные числа
Умножение десятичных дробей на обычные числа происходит так же, как и умножение между десятичными дробями. Чтобы считать быстрее, умножайте их в столбик по правилам выше. А вот и примерчики!
Пример 1. Умножить десятичную дробь 2,27 на целое число 15.
Как решаем:
умножить столбиком данные числа и отделить два знака запятой.
Ответ: 15 ∗ 2,27 = 34,05.
Пример 2. Умножить 11 на 0,005.
Как решаем:
умножить столбиком данные числа и отделить три знака запятой.
Ответ: 11 ∗ 0,005 = 0,055.
Пример 3. Умножить 0,1557.. на 3.
Как решаем:
Округлить бесконечную дробь:
0,1557..≈ 0,156
0,156 * 3 ≈ 0,468.

Ответ: 0,1557.. ∗ 3 ≈ 0,468.
Как умножать десятичные дроби на 10, 100, 1000
Чтобы умножить десятичную дробь на 10, 100, 1000, нужно просто перенести запятую в дроби вправо на столько знаков, сколько нулей стоит во втором множителе. Лишние нули слева можно отбросить. А если цифр не хватает — дописываем нули.
Примеры:
1,15 ∗ 10 = 11,5;
22,345 ∗ 100 = 2 234,5;
8,99 ∗ 1 000 = 8 990;
0,54678 ∗ 10 000 = 5467,8;
0,07 ∗ 1 000 = 70;
0,00033 ∗ 100 = 0,033.
Как умножать десятичные дроби на 0,1, 0,01, 0,001
Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001, нужно перенести запятую в дроби влево на столько знаков, сколько нулей стоит перед единицей. Ноль целых — тоже считаем. Если цифр не хватает — просто дописываем дополнительный ноль — один или несколько — после запятой.
Примеры:
34,9 ∗ 0,1 = 3,49;
1,8 ∗ 0,1 = 0,18;
145,7 ∗ 0,01 = 1,457;
9655,1 ∗ 0,001 = 9,6551;
11,9 ∗ 0,0001 = 0,00119.

Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить на 0,9.
Как решаем:
Записать 0,9 в виде обыкновенной дроби:
Умножить числа по правилам
Ответ:
Пример 2. Умножить 0,18 на .
Как решаем:
Записать в виде десятичной дроби:
Произвести умножение в столбик или при помощи калькулятора:
Ответ:
Шпаргалки по математике родителей
Все формулы по математике под рукой
Как расставить десятичные дроби в ответах калькулятора? – Обзоры Вики
com/embed/g1h40zOgSHI» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Как получить десятичные ответы на Casio FX 83gt? Нажмите, Shift, Mode, 2, чтобы вернуться к десятичной системе. мода. Вы также можете использовать кнопку S<=>D для переключения дробей и десятичных знаков.
Как перевести калькулятор Casio на десятичные числа?
Как в калькуляторе поставить 4 знака после запятой? Чтобы перейти к четырем десятичным знакам, нажмите кнопку 4, а затем кнопку ENTER.
Что такое 2 десятичных разряда? Округление десятичного числа до двух знаков после запятой равносильно округлению до сотое место, что является вторым знаком справа от десятичной точки. Например, 2.83620364 можно округлить до двух знаков после запятой как 2.84, а 0.7035 можно округлить до двух знаков после запятой как 0.70.
Как мне изменить мой калькулятор Casio с научного представления на десятичный?
Дисплей перейдет в десятичное представление. Модели Casio: Нажмите [SHIFT] [MODE] [6: Fix]. Затем вам будет предложено ввести число от 0 до 9. Введенное вами число фиксирует количество десятичных цифр, которые будут иметь ваши результаты.
Также Как получить десятичные ответы на Casio FX 991ES plus? Если вы введете операцию 14÷9 в Casio fx-991ES PLUS C, вы с такой же вероятностью увидите на экране 14/9. Если вам нужна десятичная дробь, просто нажмите клавишу S⇔D. Вы можете продолжать нажимать клавишу S⇔D, чтобы переключаться между различными форматами ответа.
Как заставить мой Casio FX 991ex показывать десятичные дроби?
Как найти 4 знака после запятой в финансовом калькуляторе?
Чтобы перейти на четыре десятичных знака, нажмите кнопку 4, а затем кнопку ENTER.
Как перевести калькулятор с дробей на точные десятичные числа?
com/embed/phfP5oB2MkU» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Как получить десятичные знаки на Casio FX 115 ES Plus?
Как избавиться от десятичных дробей в калькуляторе Casio?
Объяснение:
- Модели TI: нажмите [SCI / ENG]. На дисплее отображается FLO SCI ENG. Используйте клавишу со стрелкой влево, чтобы выбрать FLO. …
- Модели Casio: нажмите [SHIFT] [MODE] [6: Fix]. Затем вам будет предложено ввести число от 0 до 9.…
- Модели Sharp: нажмите [SET UP] [1: FSE] [0: FIX]. Это заставляет калькулятор использовать фиксированное количество десятичных знаков.

Как округлить десятичные дроби на калькуляторе?
Как называется 5-й знак после запятой? 1 = тысячные. 2 = десятые. 3 = десятитысячные. 4 = миллионные. 5 = сто тысячных (Видео решения | Стенограмма)
Что такое 1 десятичный знак?
Чтобы округлить до десятичного знака: посмотрите на первую цифру после запятой при округлении до одного десятичного знака или на вторую цифру для двух десятичных знаков. нарисуйте вертикальную линию справа от требуемой цифры разряда. посмотрите на следующую цифру. если это 5 или более, увеличьте предыдущую цифру на единицу.
Что такое десятичное число в математике? В алгебре десятичное число может быть определяется как число, целая часть которого и дробная часть разделены десятичной точкой. Точка в десятичном числе называется десятичной точкой. Цифры после запятой показывают значение меньше единицы. … В десятичной форме это 0.1. Сотая означает 1/100.
Точка в десятичном числе называется десятичной точкой. Цифры после запятой показывают значение меньше единицы. … В десятичной форме это 0.1. Сотая означает 1/100.
Решение десятичных уравнений по математике. Образовательный портал Решение столбиком онлайн калькулятор с запятыми
Простые арифметические действия — это основа дальнейшего обучения детей точным наукам. Математика сопровождает людей повсюду на протяжении всей жизни, а потому важно понимать её с самых азов. Вычитание десятичных дробей в столбик вызывает у многих школьников трудности, тогда как с действиями с простыми числами они отлично справляются. На самом деле в этом нет ничего сложного — главное уяснить алгоритм решения.
Как вычитать десятичные дроби в столбик
При записи десятичных дробей нижние и верхние разряды чисел должны соотвествовать друг другу: целые под целыми, десятые под десятыми, сотые под сотыми, тысячные под тысячными
Действия с десятичными дробями производятся так же, как и с натуральными. Основные правила, которые важно знать при решении примеров на вычитание в столбик:
Основные правила, которые важно знать при решении примеров на вычитание в столбик:
- Сначала следует уравнять количество знаков после запятой. Это делается путём добавления нулей. Например, необходимо вычесть из дроби 5,5 число 2,03. Как видно из примера, количество знаков после запятой разное. Чтобы сделать их одинаковым, в дробь 5,5 (пять целых пять десятых) в конце добавляем ноль и получаем 5,50 (пять целых пятьдесят сотых). Это правило следует из правил вычитания простых дробей. Как известно, дроби с разными знаменателями нельзя складывать или вычитать. Прежде их необходимо привести в общему знаменателю. В приведённом примере десятичные дроби можно записать в виде 5 5/10 и 2 3/100. Из целых чисел нужно вычитать целые, из дробных — дробные. В примере знаменатели у дробей разные, наименьший общий знаменатель равен 100. Следовательно, числитель и знаменатель дроби 5/10 следует умножить на 10, в итоге получим 50/100, что в переводе в десятичную дробь будет выглядеть как 5,50.
- Числа записать таким образом, чтобы запятая нижнего находилась в том же месте, что и у верхнего.
 Проще всего записывать числа, начиная с запятой. Поставить две запятые сверху и снизу, а затем уже расписывать знаки по обе стороны. Это правило, кстати, действует на основании того же правила вычитания простых дробей — из целого вычитаются целые, а из дробных — дробные. Запятая в результате должна располагаться точно под двумя верхними.
Проще всего записывать числа, начиная с запятой. Поставить две запятые сверху и снизу, а затем уже расписывать знаки по обе стороны. Это правило, кстати, действует на основании того же правила вычитания простых дробей — из целого вычитаются целые, а из дробных — дробные. Запятая в результате должна располагаться точно под двумя верхними. - Выполнить действие, не обращая внимания на запятую. Вычитают десятичные дроби справа налево, то есть начиная с самой правой цифры после запятой.
- Поставить в ответе запятую под запятой. Так мы сможем правильно отразить результат вычисления.
Вычитать нужно по цифрам разрядов: целые из целых, сотые из сотых и так далее
Вычитание всегда можно проверить сложением.
Карточки для уроков
Чтобы было проще изучить алгоритм действий, можно распечатать для детей специальные карточки-памятки, которые помогут быстрее освоить новый материал.
Фотогалерея: варианты карточек для занятий
Видео: как вычитать десятичные дроби столбиком
Освоив это простое действие, дети смогут в дальнейшем лучше учиться, ведь примеры с десятичными дробями решают не только на математике, но и на физике, химии, астрономии. Главное — понять алгоритм.
Главное — понять алгоритм.
Калькулятор дробей предназначен для быстрого расчета операций с дробями, поможет легко дроби сложить, умножить, поделить или вычесть.
Современные школьники начинают изучение дробей уже в 5 классе, с каждым годом упражнения с ними усложняются. Математические термины и величины, которые мы узнаем в школе, редко могут пригодиться нам во взрослой жизни. Однако дроби, в отличие от логарифмов и степеней, встречаются в повседневности достаточно часто (измерение расстояния, взвешивание товара и т.д.). Наш калькулятор предназначен для быстрого проведения операций с дробями.
Для начала определим, что такое дроби и какие они бывают. Дробями называют отношение одного числа к другому, это число, состоящее из целого количества долей единицы.
Разновидности дробей:
- Обыкновенные
- Десятичные
- Смешанные
Пример обыкновенных дробей:
Верхнее значение является числителем, нижнее знаменателем. Черточка показывает нам, что верхнее число делится на нижнее. Вместо подобного формата написания, когда черточка находится горизонтально, можно писать по-другому. Можно ставить наклонную линию, например:
Черточка показывает нам, что верхнее число делится на нижнее. Вместо подобного формата написания, когда черточка находится горизонтально, можно писать по-другому. Можно ставить наклонную линию, например:
1/2, 3/7, 19/5, 32/8, 10/100, 4/1
Десятичные дроби являются самой популярной разновидностью дробей. Они состоят из целой части и дробной, отделенные запятой.
Пример десятичных дробей:
0,2, или 6,71 или 0,125
Состоят из целого числа и дробной части. Чтобы узнать значение этой дроби, нужно сложить целое число и дробь.
Пример смешанных дробей:
Калькулятор дробей на нашем сайте способен быстро в онлайн-режиме выполнить любые математические операции с дробями:
- Сложение
- Вычитание
- Умножение
- Деление
Для осуществления расчета нужно ввести цифры в поля и выбрать действие. У дробей нужно заполнить числитель и знаменатель, целое число может не писаться (если дробь обыкновенная). Не забудьте нажать на кнопку «равно».
Удобно, что калькулятор сразу предоставляет процесс решения примера с дробями, а не только готовый ответ. Именно благодаря развернутому решению вы можете использовать данный материал при решении школьных задач и для лучшего освоения пройденного материала.
Вам нужно осуществить расчет примера:
После введения показателей в поля формы получаем:
Чтобы сделать самостоятельный расчет, введите данные в форму.
Фарафонова Наталия Игоревна
После прохождения темы «Действия с десятичными дробями» для отработки навыка счета и проверки усвоения материала можно провести индивидуальную работу с учащимися по карточкам. Каждый учащийся должен без ошибок выполнить задания по всем действиям. По каждому действию представлено много вариантов, это дает возможность каждому учащемуся несколько раз решить задание по каждому действию с десятичными дробями и добиться безошибочного результата или выполнить задание с минимальным количеством ошибок. Так как каждый учащийся выполняет индивидуальное задание, учитель имеет возможность, по мере представления ему выполненных заданий, с каждым учеником обсудить их персонально. Если ученик допустил ошибки, то учитель исправляет их, и предлагает сделать задание из другого варианта. Так, до тех пор, пока учащийся не выполнит все задание или его большую часть без ошибок. Карточки лучше делать на цветной бумаге.
Если ученик допустил ошибки, то учитель исправляет их, и предлагает сделать задание из другого варианта. Так, до тех пор, пока учащийся не выполнит все задание или его большую часть без ошибок. Карточки лучше делать на цветной бумаге.
На последнем этапе работы, можно предложить решить пример, содержащий несколько действий.
За каждый безошибочно выполненный вариант, независимо от того, с какой попытки было верно выполнено задание, учащимся можно поставить отличную отметку, можно выставить среднюю оценку, после выполнения всей работы, на усмотрение учителя.
Сложение десятичных дробей.
1 вариант
7,468 + 2,85
9,6 + 0,837
38,64 + 8,4
3,9 + 26,117
2 вариант
19,45 + 34,8
4,9 + 0,716
75,86 + 4,2
5,6 + 44,408
3 вариант
24,38 + 7,9
6,5 + 0,952
48,59 + 1,8
35,906 + 2,8
4 вариант
7,6 + 319,75
888,99 + 4,5
64,15 + 18,9
4,5 + 0,738
5 вариант
7,62 + 8,9
25,38 + 0,09
12,842 + 8,6
412 + 78,83
6 вариант
70,7 + 3,8645
3,65 + 0,89
61,22 + 31. 719
719
12,842 + 8,6
Ответы: 1 вариант: 10,318; 10,437; 47,04; 30,017;
2 вариант: 54,25; 5,616; 80,06; 50,008;
3 вариант: 32,28; 7,452; 50,19; 38,706;
4 вариант: 327,35; 893,49; 83,05; 5,238;
5 вариант: 16,52; 25,47; 21,442; 490,83;
6 вариант: 74,5645; 4,54; 92,939; 21,442;
Вычитание десятичных дробей.
1 вариант
26,38 — 9,69
41,12 — 8,6
5,2 — 3,445
7 — 0,346
2 вариант
47,62 — 8,78
54,06 — 9,1
7,1 — 6,346
3 — 1,551
3 вариант
50,41 — 9,62
72,03 — 6,3
9,2 — 5,453
4 — 2,662
4 вариант
60,01 — 8,364
123,61 — 69,8
8,7 — 4,915
10 — 3,817
5 вариант
6,52 — 3,8
7,41 — 0,758
67,351 — 9,7
22 — 0,618
6 вариант
4,5 — 0,496
61,3 — 20,3268
24,7 — 15,276
50 — 2,38
Ответы: 1 вариант: 16,69; 32,52; 1,755; 6,654;
2 вариант: 38,84; 44,96; 0,754; 1,449;
3 вариант: 40,79; 65,73; 3,747; 1,338;
4 вариант: 51,646; 53,81; 3,785; 6,183;
5 вариант: 2,72; 6,652; 57,651; 21,382;
6 вариант: 4,004; 40,9732; 9,424; 47,62;
Умножение десятичных дробей.
1 вариант
7,4 · 3,5
20,2 · 3,04
0,68 · 0,65
2,5 · 840
2 вариант
2,8 · 9,7
6,05 · 7,08
0,024 · 0,35
560 · 3,4
3 вариант
6,8 · 5,9
6,06 · 8,05
0,65 · 0,014
720 · 4,6
4 вариант
34,7 · 8,4
9,06 · 7,08
0,038 · 0,29
3,6 · 540
5 вариант
62,4 · 2,5
0,038 · 9
1,8 · 0,009
4,125 · 0,16
6 вариант
0,28 · 45
20,6 · 30,5
2,3 · 0,0024
0,0012 · 0,73
7 вариант
68 · 0,15
0,08 · 0,012
1,4 · 1,04
0,32 · 2,125
8 вариант
4,125 · 0,16
0,0012 · 0,73
1,4 · 1,04
720 · 4,6
Ответы: 1 вариант: 25,9; 61,408; 0,442; 2100;
2 вариант: 27,16; 42,834; 0,0084; 1904;
3 вариант: 40,12; 48,783; 0,0091; 3312;
4 вариант: 291,48; 64,1448; 0,01102; 1944;
5 вариант: 156; 0,342; 0,0162; 0,66;
6 вариант: 12,6; 628,3; 0,00552; 0,000876;
7 вариант: 10,2; 0,00096; 1,456; 0,68;
8 вариант: 0,66; 0,000876; 1,456; 3312;
Деление десятичной дроби на натуральное число.
1 вариант
62,5: 25
0,5: 25
9,6: 12
1,08: 8
2 вариант
0,28: 7
0,2: 4
16,9: 13
22,5: 15
3 вариант
0,75: 15
0,7: 35
1,6: 8
0,72: 6
4 вариант
2,4: 6
1,5: 75
0,12: 4
1,69: 13
5 вариант
3,5: 175
1,8: 24
10,125: 9
0,48: 16
6 вариант
0,35: 7
1,2: 3
0,2: 5
7,2: 144
7 вариант
151,2: 63
4,8: 32
0,7: 25
2,3: 40
8 вариант
397,8: 78
5,2: 65
0,9: 750
3,4: 80
9 вариант
478,8: 84
7,3: 4
0,6: 750
5,7: 80
10 вариант
699,2: 92
1,8: 144
0,7: 875
6,3: 24
Ответы: 1 вариант: 2,5; 0,02; 0,8; 0,135;
2 вариант: 0,04; 0,05; 1,3; 1,5;
3 вариант: 0,05; 0,02; 0,2; 0,12;
4 вариант: 0,4; 0,02; 0,03; 0,13;
5 вариант: 0,02; 0,075; 1,125; 0,03;
6 вариант: 0,05; 0,4; 0,04; 0,05;
7 вариант: 2,4; 0,15; 0,28; 0,0575;
8 вариант: 5,1; 0,08; 0,0012; 0,0425;
9 вариант: 5,7; 1,825; 0,0008; 0,07125;
10 вариант: 7,6; 0,0125; 0,0008; 0,2625;
Деление на десятичную дробь.
1 вариант
32: 1,25
54: 12,5
6: 125
2 вариант
50,02: 6,1
34,2: 9,5
67,6: 6,5
3 вариант
2,8036: 0,4
3,1: 0,025
0,0008: 0,16
4 вариант
4: 32
303: 75
687,4: 10
1,59: 100
5 вариант
5: 16
336: 35
412,5: 10
24,3: 100
6 вариант
41,82: 6,8
73,44: 3,6
7,2: 0,045
32,89: 4,6
Ответы: 1 вариант: 25,6; 4,32; 0,048;
2 вариант: 8,2; 3,6; 10,4;
3 вариант: 7,009; 124; 0,005;
4 вариант: 0,125; 4,04; 68,74; 0,0159;
5 вариант: 0,3125; 9,6; 41,25; 0,243;
6 вариант: 6,15; 20,4; 160; 7,15;
Совместные действия с десятичными дробями.
824,72 — 475: (0,071 + 0,929) + 13,8
(7,351 + 12,649) ·105 — 95,48 — 4,52
(3,82 — 1,084 + 12,264)·(4,27 + 1,083 — 3,353) + 83
278 — 16,7 — (15,75 + 24,328 + 39,2)
57,18 ·42 — 74,1: 13 + 21,35: 7
(18,8: 16 + 9,86 ·3) ·40 — 12,73
(2 — 0,25 ·0,8) : (0,16: 0,5 — 0,02)
(3,625 + 0,25 + 2,75) : (28,75 + 92,25 — 15) : 0,0625
Ответы: 1) 363,52; 2) 2000; 3) 113; 4) 182,022; 5) 2398,91; 6) 1217,47; 7) 6; 8) 1.
Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение. Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор.
Особенности
Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .
Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:
Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:
- Цифры.
- Знаки арифметических действий.
- Удаление раннее введенных символов.
Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.
Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:
- умножение;
- деление;
- сложение;
- вычитание.
Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.
Достоинства и недостатки
- Помогает школьнику не просто быстро получить правильный результат математических вычислений, но и понять сам принцип расчета.
- Очень простой, интуитивно понятный интерфейс для каждого пользователя.
- Установить приложение можно даже на самое бюджетное Андроид устройство с операционной системой 2.2 и более поздней версией.
- Калькулятор сохраняет историю проведенных математических вычислений, которую можно в любой момент очистить.
Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит.
Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
В этом уроке мы рассмотрим каждую из этих операций по отдельности.
Содержание урока
Сложение десятичных дробейКак мы знаем, десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей, целые и дробные части складываются по отдельности.
Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик.
Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой» .
Запишем дроби в столбик так, чтобы запятая оказалась под запятой:
Складываем дробные части: 2 + 3 = 5. Записываем пятёрку в дробной части нашего ответа:
Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой» :
Для этого опять же соблюдаем правило «запятая под запятой» :
Получили ответ 8,5. Значит, выражения 3,2 + 5,3 равно 8,5
3,2 + 5,3 = 8,5
На самом деле не всё так просто как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим.
Разряды в десятичных дробяхУ десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.
Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.
Разряды в десятичных дробях хранят в себе нéкоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.
Например, рассмотрим десятичную дробь 0,345
Позиция, где находится тройка, называется разрядом десятых
Позиция, где находится четвёрка, называется разрядом сотых
Позиция, где находится пятёрка, называется разрядом тысячных
Посмотрим на данный рисунок. Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых .
Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых .
Если мы сложим дроби , и то получим изначальную десятичную дробь 0,345
Сначала мы получили ответ , но перевели его в десятичную дробь и получили 0,345 .
При сложении десятичных дробей соблюдаются те же правила что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными.
Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой» . Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.
Пример 1. Найти значение выражения 1,5 + 3,4
В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа:
Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9
Пример 2. Найти значение выражения: 3,51 + 1,22
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»
В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа:
Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа:
Теперь складываем целые части 3+1=4. Записываем четвёрку в целой части нашего ответа:
Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»:
Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73
3,51 + 1,22 = 4,73
Как и в обычных числах, при сложении десятичных дробей может произойти . В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд.
Пример 3. Найти значение выражения 2,65 + 3,27
Записываем в столбик данное выражение:
Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:
Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:
Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа:
Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа:
Получили ответ 5,92. Значит значение выражения 2,65 + 3,27 равно 5,92
2,65 + 3,27 = 5,92
Пример 4. Найти значение выражения 9,5 + 2,8
Записываем в столбик данное выражение
Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:
Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12. Записываем число 12 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 12,3.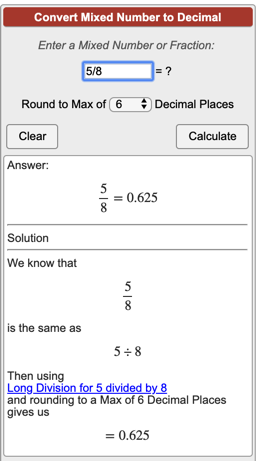 Значит значение выражения 9,5 + 2,8 равно 12,3
Значит значение выражения 9,5 + 2,8 равно 12,3
9,5 + 2,8 = 12,3
При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями.
Пример 5 . Найти значение выражения: 12,725 + 1,7
Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым. В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:
Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа:
Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа:
Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд:
Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа:
Записываем число 14 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425
12,725+ 1,700 = 14,425
Вычитание десятичных дробейПри вычитании десятичных дробей нужно соблюдать те же правила что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:
Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3
2,5 − 2,2 = 0,3
Пример 2. Найти значение выражения 7,353 — 3,1
В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.
Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.
Теперь можно записать в столбик данное выражение и вычислить его:
Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253
7,353 — 3,1 = 4,253
Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.
Пример 3. Найти значение выражения 3,46 − 2,39
Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:
Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:
Записываем ноль в десятой части нашего ответа:
Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07
3,46−2,39=1,07
Пример 4 . Найти значение выражения 3−1,2
В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,23 оказалась под числом 3
Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль:
Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:
Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу.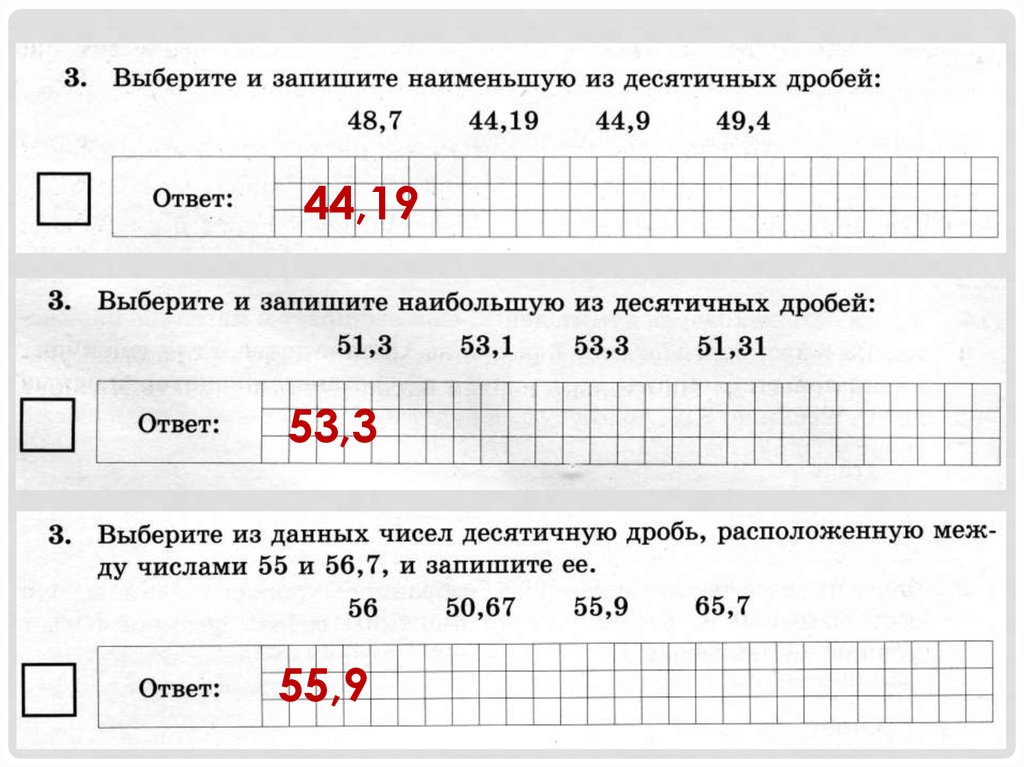 В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:
В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8
Умножение десятичных дробейУмножение десятичных дробей это просто и даже увлекательно. Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.
Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Пример 1. Найти значение выражения 2,5 × 1,5
Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют:
Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.
Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.
Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 3,75. Значит значение выражения 2,5 × 1,5 равно 3,75
2,5 × 1,5 = 3,75
Пример 2. Найти значение выражения 12,85 × 2,7
Перемножим эти десятичные дроби, не обращая внимания на запятые:
Получили 34695. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую:
Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695
12,85 × 2,7 = 34,695
Умножение десятичной дроби на обычное числоИногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число.
Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби. Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Например, умножим 2,54 на 2
Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую:
Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08
2,54 × 2 = 5,08
Умножение десятичных дробей на 10, 100, 1000Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа.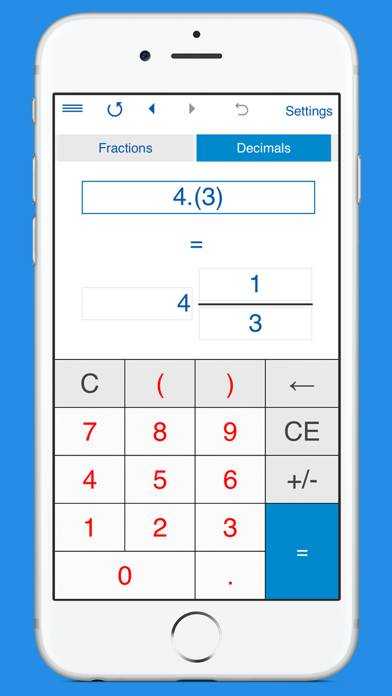 Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.
Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.
Например, умножим 2,88 на 10
Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:
Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.
Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8
2,88 × 10 = 28,8
Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.
2,88 × 10 = 28,8
Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288
2,88 × 100 = 288
Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
2,88 × 1000 = 2880
Умножение десятичных дробей на 0,1 0,01 и 0,001Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.
Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.
Например, умножим 3,25 на 0,1
Умножаем эти дроби, как обычные числа, не обращая внимания на запятые:
Получили 325. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.
Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:
Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325
3,25 × 0,1 = 0,325
Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 3,25 × 0,1 этим способом. Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325
3,25 × 0,1 = 0,325
Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
3,25 × 0,01 = 0,0325
Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325
3,25 × 0,001 = 0,00325
Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000. Типичная ошибка большинства людей.
Типичная ошибка большинства людей.
При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе.
А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе.
Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях.
Деление меньшего числа на большее. Продвинутый уровень.В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь . Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих»
Дробь это ответ к задаче «как разделить одно яблоко на двоих»
Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя.
Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.
При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.
Итак, разделим 1 на 2. Решим этот пример уголком:
Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице» , то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:
Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:
Настал момент, когда единицу можно дробить на две части. Для этого справа от полученной единички дописываем ещё один ноль:
Для этого справа от полученной единички дописываем ещё один ноль:
Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:
Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10
Получили ответ 0,5. Значит дробь равна 0,5
Половину яблока можно записать и с помощью десятичной дроби 0,5. Если сложить эти две половинки (0,5 и 0,5), мы опять получим изначальное одно целое яблоко:
Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см
Пример 2. Найти значение выражения 4: 5
Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:
Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8.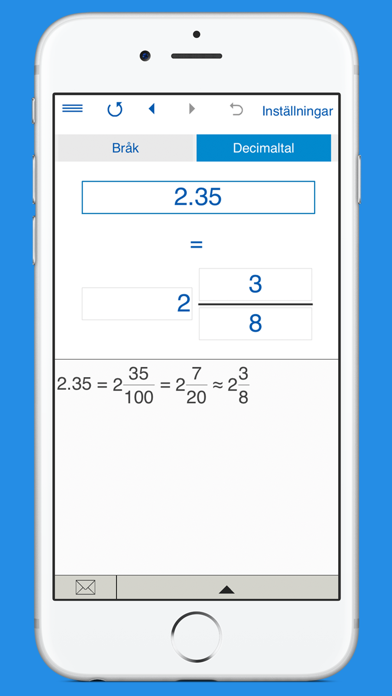 Записываем восьмёрку в частном.
Записываем восьмёрку в частном.
Завершаем пример, умножив 8 на 5, и получив 40:
Получили ответ 0,8. Значит значение выражения 4: 5 равно 0,8
Пример 3. Найти значение выражения 5: 125
Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0
Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:
Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0
Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50
Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:
Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125. Записываем четвёрку в частном:
Завершаем пример, умножив 4 на 125, и получив 500
Получили ответ 0,04. Значит значение выражения 5: 125 равно 0,04
Значит значение выражения 5: 125 равно 0,04
Деление чисел без остатка
Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части:
Допишем ноль к остатку 4
Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном:
40−40=0. Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:
9: 5 = 1,8
Пример 2 . Разделить 84 на 5 без остатка
Сначала разделим 84 на 5 как обычно с остатком:
Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой:
и завершаем пример, проверив есть ли еще остаток:
Деление десятичной дроби на обычное число
Десятичная дробь, как мы знаем состоит из целой и дробной части.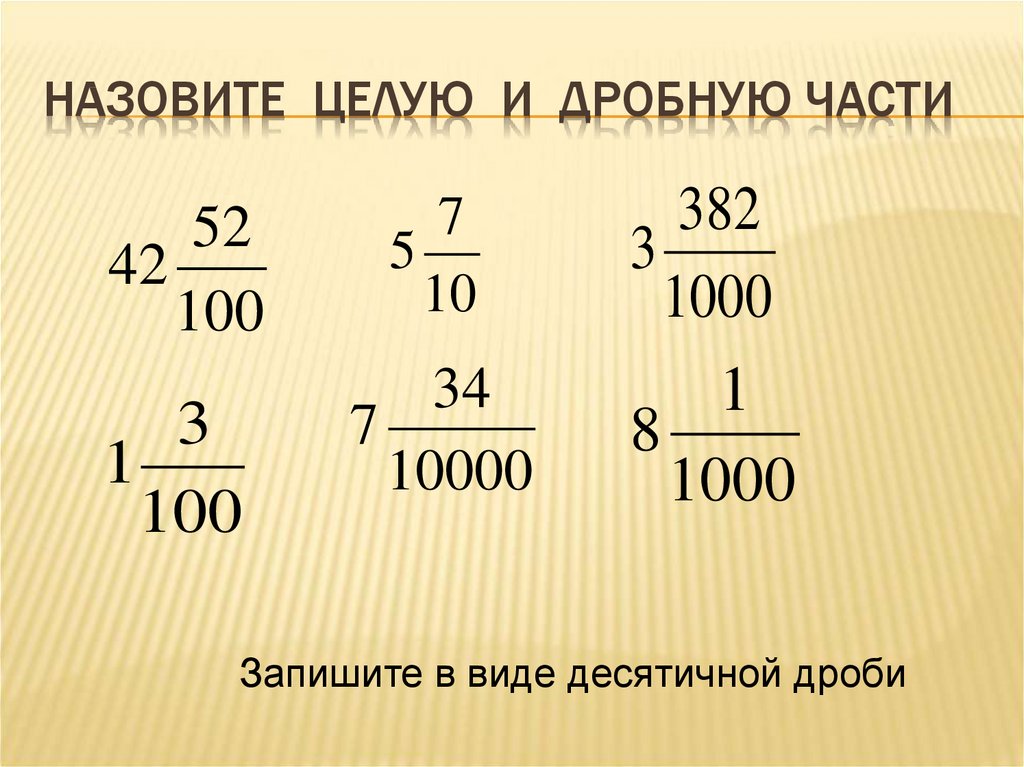 При делении десятичной дроби на обычное число в первую очередь нужно:
При делении десятичной дроби на обычное число в первую очередь нужно:
- разделить целую часть десятичной дроби на это число;
- после того, как целая часть будет разделена, нужно в частном сразу же поставить запятую и продолжить вычисление, как в обычном делении.
Например, разделим 4,8 на 2
Запишем этот пример уголком:
Теперь разделим целую часть на 2. Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:
Теперь умножаем частное на делитель и смотрим есть ли остаток от деления:
4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено. Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
8: 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель:
Получили ответ 2,4. Значение выражения 4,8: 2 равно 2,4
Пример 2. Найти значение выражения 8,43: 3
Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки:
Сразу же ставим запятую после двойки:
Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток:
Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления:
24−24=0. Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:
Получили ответ 2,81. Значит значение выражения 8,43: 3 равно 2,81
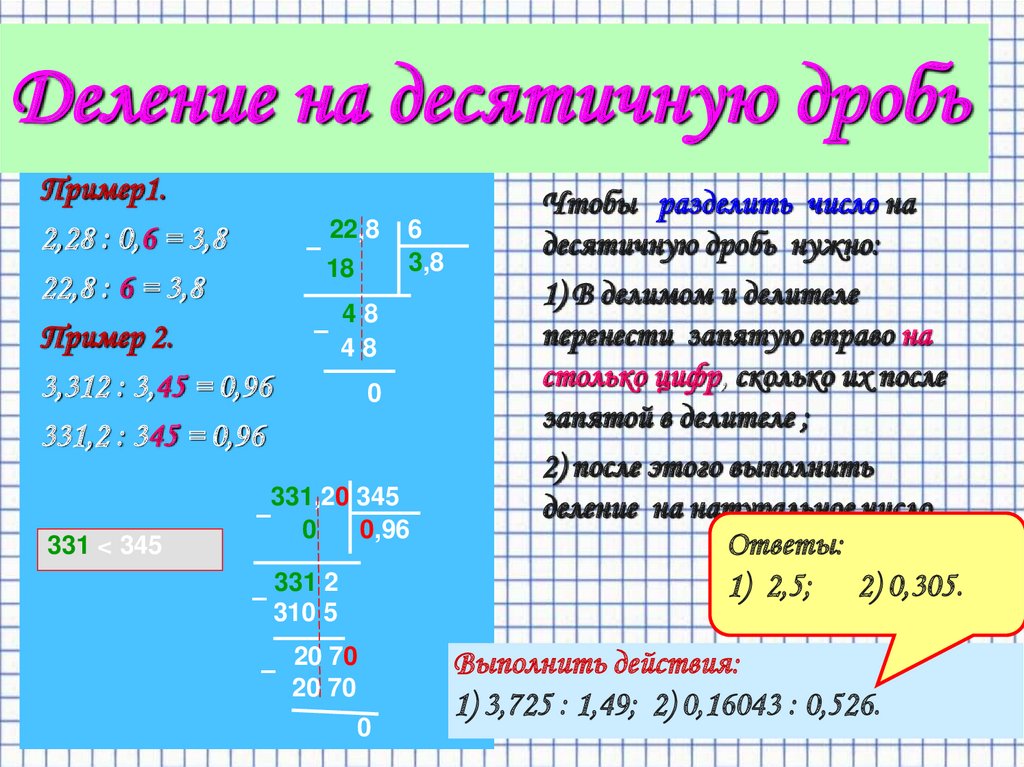
Деление десятичной дроби на десятичную дробь
Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.
Например, разделим 5,95 на 1,7
Запишем уголком данное выражение
Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:
В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:
После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:
Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?
Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9: 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.
Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:
(9 × 2 ) : (3 × 2 ) = 18: 6 = 3
Как видно из примера, частное не поменялось.
Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17.
На самом деле внутри этого процесса происходило умножение на 10. Вот как это выглядело:
5,91 × 10 = 59,1
Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.
Деление десятичной дроби на 10, 100, 1000
Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и . Например, разделим 2,1 на 10. Решим этот пример уголком:
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 2,1: 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21
Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:
2,1: 100 = 0,021
Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:
2,1: 1000 = 0,0021
Деление десятичной дроби на 0,1, 0,01 и 0,001
Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и . В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.
В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.
После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:
Значит значение выражения 6,3: 0,1 равно 63
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 6,3: 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63
Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630
В результате получим 630
Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:
6,3: 0,001 = 6300
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
правило, примеры. Перевод десятичных чисел в дробь и наоборот — онлайн калькулятор Перевод десятичной дроби в смешанное число
Словари. Энциклопедии. История. Литература. Русский язык » История » Перевод десятичной дроби в обыкновенную и наоборот: правило, примеры. Перевод десятичных чисел в дробь и наоборот — онлайн калькулятор Перевод десятичной дроби в смешанное число
Вот, казалось бы, перевод десятичной дроби в обычную — элементарная тема, но многие ученики её не понимают! Поэтому сегодня мы подробно рассмотрим сразу несколько алгоритмов, с помощью которых вы разберётесь с любыми дробями буквально за секунду.
Напомню, что существует как минимум две формы записи одной и той же дроби: обыкновенная и десятичная. Десятичные дроби — это всевозможные конструкции вида 0,75; 1,33; и даже −7,41. А вот примеры обыкновенных дробей, которые выражают те же самые числа:
Сейчас разберёмся: как от десятичной записи перейти к обычной? И самое главное: как сделать это максимально быстро?
Основной алгоритм
На самом деле существует как минимум два алгоритма. И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного.
Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага:
Важное замечание по поводу отрицательных чисел. Если в исходном примере перед десятичной дробью стоит знак «минус», то и на выходе перед обыкновенной дробью тоже должен стоять «минус». Вот ещё несколько примеров:
Примеры перехода от десятичной записи дробей к обычной
Особое внимание хотелось бы обратить на последний пример. {3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
{3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
Наконец, последний пример:
Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.
Что делать с целой частью
На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.
Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:
Затем вспоминаем про «утерянную» единицу и дописываем её спереди:
\[\frac{22}{25}\to 1\frac{22}{25}\]
Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:
Ещё парочка примеров:
\[\begin{align}& 2,15\to 0,15=\frac{15}{100}=\frac{3}{20}\to 2\frac{3}{20}; \\& 13,8\to 0,8=\frac{8}{10}=\frac{4}{5}\to 13\frac{4}{5}. \\\end{align}\]
В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)
В заключение хотел бы рассмотреть ещё один приём, который многим помогает.
Преобразования «на слух»
Давайте задумаемся о том, что вообще такое десятичная дробь. Точнее, как мы её читаем. Например, число 0,64 — мы читаем его как «ноль целых, 64 сотых», правильно? Ну, или просто «64 сотых». Ключевое слово здесь — «сотых», т.е. число 100.
А что насчёт 0,004? Это же «ноль целых, 4 тысячных» или просто «четыре тысячных». Так или иначе, ключевое слово — «тысячных», т.е. 1000.
Ну и что в этом такого? А то, что именно эти числа в итоге «всплывают» в знаменателях на втором этапе алгоритма. Т.е. 0,004 — это «четыре тысячных» или «4 разделить на 1000»:
Попробуйте потренироваться сами — это очень просто. Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому
Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому
А какое-нибудь 1,125 — это «1 целая, 125 тысячных», поэтому
В последнем примере, конечно, кто-то возразит, мол, не всякому ученику очевидно, что 1000 делится на 125. Но здесь нужно помнить, что 1000 = 10 3 , а 10 = 2 ∙ 5, поэтому
\[\begin{align}& 1000=10\cdot 10\cdot 10=2\cdot 5\cdot 2\cdot 5\cdot 2\cdot 5= \\& =2\cdot 2\cdot 2\cdot 5\cdot 5\cdot 5=8\cdot 125\end{align}\]
Таким образом, любая степень десятки раскладывается лишь на множители 2 и 5 — именно эти множители нужно искать и в числителе, чтобы в итоге всё сократилось.
На этом урок окончен. Переходим к более сложной обратной операции — см. «
Алгебра и математика – сложные науки, которые легко не даются даже тем, кто уделяет им достаточно много времени. Проблемы могут возникнуть с любыми задачами. Например, не каждый знает, как десятичную дробь перевести в обыкновенную дробь.
Особенности дроби
Чтобы легко переводить один вид дроби в другой, лучше всего понимать, что это такое. Их можно назвать нецелым числом. Оно состоит из одной или же нескольких частей единицы.
Их можно назвать нецелым числом. Оно состоит из одной или же нескольких частей единицы.
В первую очередь, выделяют обыкновенные или так называемые простые дроби. В отношении любого вида действует правило, что знаменатель не может равняться нулю . Если это так, то это значит, что значение целое, то есть оно не может быть дробью.
Существует несколько видов написания такого числа. Используется горизонтальная линия или наклонная черта, причем второй вариант может выглядеть в печатном виде тремя разными способами. В школьных тетрадях же, как правило, обыкновенные дроби записывают с классической горизонтальной линией.
Помимо простых, выделяют смешанные и составные дроби. Первые отличаются тем, что имеют ещё и целое число, записываемое в начале. У составных числитель и знаменатель как будто тоже является ещё одной дробью.
Как десятичную дробь перевести в обыкновенную дробь?
Десятичную дробь перевести в обычную дробь не так трудно, так как, несмотря на внешние изменения, суть числа останется одинаковой. Ключевая разница в том, что десятичные записываются с использованием запятых , а не черточек. Конечно, это не значит, что дробь ½ будет равняться 1,2.
Ключевая разница в том, что десятичные записываются с использованием запятых , а не черточек. Конечно, это не значит, что дробь ½ будет равняться 1,2.
Десятичная дробь формируется из двух составляющих. Первая располагается до знака и обозначает целое число. Вторая, та, что находится после него, это десятые, сотые и другие числа. Их название зависит от того, насколько они отдалены от запятой.
Иногда превратить одну дробь в другую очень просто, особенно если нецелая часть – это десятые, а не сотые или тысячные. Классический пример –0,5. В первую очередь, его стоит правильно прочитать, то тогда получится ноль целых, пять десятых. Ноль целых никак записать не получится, а вот пять десятых легко превращаются в 5/10. Всё, что остается – провести сокращение путем деления на пять. Результат – ½.
Дробь с целым числом
Необходимо рассмотреть и другие примеры, с повышенной сложностью. Стоит взять 2,25. Как и до этого, для начала, лучше всего правильно обозначить название дроби. В этот раз имеется две целых, двадцать пять сотых. В связи с тем, что после знака находится две цифры, то они являются сотыми.
В этот раз имеется две целых, двадцать пять сотых. В связи с тем, что после знака находится две цифры, то они являются сотыми.
Как десятичную дробь перевести в обыкновенную дробь:
- Нецелая часть записывается в виде 25/100.
- Осталось дописать две целых. Они ставятся в начало, и таким образом получается смешанная дробь.
- 25/100 можно сократить. Для простоты, реально начинать с деления на 5, но неплохо сразу воспользоваться числом 25. В результате сокращения получается ¼.
- Остается лишь подписать две целые к ¼. Результат – 2 ¼.
Наконец, стоит рассмотреть и процесс работы с тысячными. Для разбора возьмем 4,112. Вновь работу нужно начать с верного прочтения. Получится четыре целых, сто двенадцать тысячных. Без труда удастся выделить первую цифру, 4, а затем подставить к ней сто двенадцать тысячных. Они выглядят так – 112/100.
Остается лишь сократить, чтобы придать лучший вид. В этом конкретном примере общим делителем является шесть. Результат – простая дробь 4 14/125.
Результат – простая дробь 4 14/125.
Перевод дробей в проценты
Практически любую дробь реально без особого труда перевести в проценты. Чтобы это сделать, нужно понимать, что процент – это одна сотая . Другими словами, 1% сразу возможно легко записать в дробном виде – 1/100 или 0,01.
В случае же с другими вариантами, придется обратиться к десятичным дробям, то есть тем, что пишутся через запятую. С ними задача решается очень просто. Достаточно умножить десятичную дробь на 100, и получится искомый процент.
- 0,27 * 100% = 27%
Если же необходимо осуществить перевод обыкновенной дроби, то сначала её придется превратить в десятичную.
- Например, 2/5 равняются 0,4.
- 0,4 * 100% = 40%.
Если процесс перевода в проценты всё равно вызывает трудности, то, при желании, можно воспользоваться различными автоматическими сервисами, которых достаточно много в интернете. Вписав в соответствующие поля числитель и знаменатель, удастся легко узнать, какой из этого получится процент.
В целом же, перевод дробей в проценты всегда завязан на умножении на 100. Для того, чтобы легко с этим справляться, необходимо понимать, как перевести обыкновенную дробь в десятичную, но, для начала, стоит разобраться и в обратном процессе.
Видео инструкция
В самом начале нужно все-таки узнать, что такое дробь и каких видов она бывает. А бывает она трех видов. И первый из них это обыкновенная дробь, например ½, 3/7,3/432 и т. д. Эти числа также можно записывать при помощи горизонтальной черточки. И первое, и второе будет одинаково верно. Цифра сверху называется числительным, а снизу знаменателем. Есть даже поговорка, для тех людей, кто постоянно путает эти два названия. Она звучит так: «Зззззапомни! Зззззнаменатель — внизззззу! ». Это поможет не запутаться. Обыкновенная дробь это всего лишь два числа, которые делятся друг на друга. Черточка в них и обозначает знак деления. Ее можно заменить знаком двоеточие. Если стоит вопрос «как дробь перевести в число», то это очень просто. Следует всего лишь числитель поделить на знаменатель. И все. Дробь переведена.
Следует всего лишь числитель поделить на знаменатель. И все. Дробь переведена.
Второй вид дробей называется десятичным. Это ряд цифр с запятой. К примеру, 0,5, 3,5 и т. д. Назвали их десятичными, только потому, что после запетой первая цифра обозначает «десятки», вторая в десять раз больше «сотни» и так далее. А первые цифра до запятой, называются целыми. Например, число 2,4 звучит так, двенадцать целых и двести тридцать четыре тысячных. Такие дроби появляются в основном из-за того, что поделив два числа без остатка не получается. И большинство обыкновенных дробей, во время того как их будут переводить в числа, в конечном итоге имеют вид десятичной дроби. Например, одна вторая ровняется ноль целым пяти десятым.
И заключительный третий вид. Это смешанные числа. Пример этого можно привести такой, как 2½. Звучит так, две целых и одна вторая. В старших классов такой вид дробей уже не используются. Их наверняка необходимо будет приводить или в обыкновенный вид дроби, или в десятичный. Сделать это так же легко. Просто целое число нужно умножить на знаменатель и, полученное обозначение, сложить с числительным. Возьмем наш пример 2½. Два умножается на два, получается четыре. Четыре плюс один, равно пяти. И дробь формой 2½ образуется в 5/2. А пять, поделив на два можно получить десятичную дробь. 2½=5/2=2,5. Уже стало понятно, как переводить дроби в числа. Следует всего лишь разделить числитель на знаменатель. Если числа большие можно воспользоваться калькулятором.
Сделать это так же легко. Просто целое число нужно умножить на знаменатель и, полученное обозначение, сложить с числительным. Возьмем наш пример 2½. Два умножается на два, получается четыре. Четыре плюс один, равно пяти. И дробь формой 2½ образуется в 5/2. А пять, поделив на два можно получить десятичную дробь. 2½=5/2=2,5. Уже стало понятно, как переводить дроби в числа. Следует всего лишь разделить числитель на знаменатель. Если числа большие можно воспользоваться калькулятором.
Если на нем получается не целые числа и после запятой идет очень много цифр, то тогда данное значение можно округлить. Округляется все очень просто. Сначала следует определиться, к какой цифре нужно округлить. Следует рассмотреть пример. Человеку нужно округлить число ноль целых, девять тысяч семьсот пятьдесят шесть десятитысячных или в цифровом значении 0,6. Округление необходимо сделать до сотых. Это означает, что в данный момент до семи сотых. После цифры семь в дроби идет пять. Теперь нужно использовать правила для округления. Цифры больше пяти округляются в большую сторону, а меньшие – в меньшую. В примере у человека — пять, она стоит на пограничье, но считается, что округление происходит в большую сторону. Значит, все цифры после семерки убираем и к ней прибавляем единицу. Получается 0,8.
Цифры больше пяти округляются в большую сторону, а меньшие – в меньшую. В примере у человека — пять, она стоит на пограничье, но считается, что округление происходит в большую сторону. Значит, все цифры после семерки убираем и к ней прибавляем единицу. Получается 0,8.
Также возникают ситуации, когда человеку необходимо быстро перевести обыкновенную дробь в число, а калькулятора рядом нет. Для этого стоит применить деление столбиком. Первым делом следует на листке написать рядом друг с другом числитель и знаменатель. Между ними ставится уголок деления, он похож на букву «Т», только лежащую на боку. Для примера можно взять дробь десять шестых. И так, десять следует поделить на шесть. Сколько шестерок может вместиться в десятке, только одна. Единица записывается под уголком. Десять отнять шесть получится четыре. Сколько шестерок будет в четверке, несколько. Значит, в ответе после единицы ставится запятая, а четверка умножается на десять. В сорока шесть шестерок. В ответе дописывается шестерка, а от сорока отнимается тридцать шесть. Получается опять четыре.
Получается опять четыре.
В данном примере произошло зацикливание, если продолжить делать все точно также получится ответ 1,6(6) Цифру шесть продолжается для бесконечности, но применив правило округления, можно привести получение число к 1,7. Что намного удобней. Из этого можно сделать вывод, что не все обыкновенные дроби можно перевести в десятичные. В некоторых происходит зацикливание. Но зато любую десятичную дробь можно перевести в простую. Здесь поможет элементарное правило, как слышится, так и пишется. Например, число 1,5, слышится, как одна целых двадцать пять сотых. Так и нужно записать, одна целая, двадцать пять поделить на сто. Одна целая это сто, а значит, простая дробь будет сто двадцать пять на сто (125/100) . Все также просто и понятно.
Вот и было разобраны самые основные правила и преобразования, которые связанны с дробями. Все они несложные, но знать их следует. В повседневную жизнь уже давно вошли дроби, особенно десятичные. Это хорошо видно на ценниках в магазинах. Круглые цены уже давно не кто не пишет, а с дробями цена кажется визуально на много дешевле. Также одна из теорий гласит, что человечество отвернулось от римских цифр и приняла в оборот арабские, только потому, что в римских не было дробей. И многие ученые соглашаются с этим предположением. Ведь с дробями можно вести подсчеты более точней. А в наш век космических технологий, точность в расчетах нужна как никогда. Так что изучать дроби в школе по математики жизненно необходимо для понимания многих наук и технических достижений.
Круглые цены уже давно не кто не пишет, а с дробями цена кажется визуально на много дешевле. Также одна из теорий гласит, что человечество отвернулось от римских цифр и приняла в оборот арабские, только потому, что в римских не было дробей. И многие ученые соглашаются с этим предположением. Ведь с дробями можно вести подсчеты более точней. А в наш век космических технологий, точность в расчетах нужна как никогда. Так что изучать дроби в школе по математики жизненно необходимо для понимания многих наук и технических достижений.
Простые дроби не всегда удобны в обращении. В отчет или в ведомость их не вставишь, да и современные компьютерные программы не всегда дружат с такими числами. Перевести простую дробь в (или в десятичную дробь) не составит труда.
Вам понадобится
- листок бумаги, ручка, калькулятор
Инструкция
Перевести дробь в число — значит разделить числитель на знаменатель. Числитель — это верхняя часть дроби, знаменатель — нижняя. Если под рукой есть калькулятор, то нажмите на кнопки, и задача выполнена. В результате у вас получится либо целое число, либо десятичная дробь. Десятичная дробь может получится с длинным остатком после запятой. В этом случае дробь нужно округлить до определенного, нужного вам разряда, используя правила округления (цифры до 5 округляются в меньшую сторону, от 5 включительно и более — в большую сторону).
В результате у вас получится либо целое число, либо десятичная дробь. Десятичная дробь может получится с длинным остатком после запятой. В этом случае дробь нужно округлить до определенного, нужного вам разряда, используя правила округления (цифры до 5 округляются в меньшую сторону, от 5 включительно и более — в большую сторону).
Если калькулятора под рукой не оказалось, но придется делить в столбик. Напишите числитель дроби рядом со знаменателем, между ними уголочек, означающий деление. К примеру, переведите в число дробь 10/6. Для начала 10 разделите на 6. Получится 1. Запишите результат по уголком. Перемножьте 1 на 6, получится 6. Вычтите 6 из 10. Получится остаток 4. Остаток нужно снова разделить на 6. Допишите к 4 цифру 0, и разделите 40 на 6. Получится 6. Запишите 6 в результат, после запятой. Перемножьте 6 на 6. Получится 36. Вычтите 36 из 40. Получится вновь остаток 4. Далее можно не продолжать, поскольку становится очевидным, что результатом будет число 1,66(6). Округлите данную дробь до того разряда, который вам необходим. Например, 1,67. Это и есть окончательный результат.
Например, 1,67. Это и есть окончательный результат.
Калькулятор десятичной дроби
Добро пожаловать в наш калькулятор десятичной дроби — интеллектуальный инструмент, который поможет вам преобразовать любое десятичное число в дробь в мгновение ока . Вы узнаете, как превратить десятичную дробь в дробь или даже как преобразовать повторяющиеся десятичные дроби в дроби. Основная идея этого преобразователя дробей состоит в том, чтобы преобразовать любую десятичную дробь в дробь — отношение двух целых чисел.
Предпочитаете смотреть , а не читать? Узнайте все, что вам нужно в 90 секунд с этим видео мы сделали для вас :
Вы уже знаете, в чем разница между пропорциями и дробями? Перейдите к нашему калькулятору коэффициентов, чтобы узнать!
Почему полезно преобразовывать десятичную дробь в дробь?
В повседневной жизни мы используем числа, как десятичные, так и дробные. Хотя десятичные дроби могут показаться более естественными для письма, есть несколько проблем, которые могут возникнуть рано или поздно.
Хотя десятичные дроби могут показаться более естественными для письма, есть несколько проблем, которые могут возникнуть рано или поздно.
Например, используя рациональные числа, мы иногда вынуждены округлять значения в какой-то момент, в зависимости от того, сколько значащих цифр нам нужно использовать. Пишет то же самое 9Число 0003 в дробной форме дает нам точное значение .
Вычисление дробных показателей более просто с дробями, чем с десятичными. Что такое 4 2,5 ? Ну, это не так очевидно на первый взгляд. А как насчет 4 5 / 2 ? Легче представить это как (√4)⁵ = 2⁵ = 32 . Эта проблема становится еще более проблематичной, когда мы имеем дело с повторяющимися цифрами, поэтому стоит знать, как превратить повторяющуюся десятичную дробь в дробь.
Существуют также более практичные способы использования дробей вместо десятичных. Представьте, что вы на вечеринке и хотите разделить торт или пиццу на равные части. Если есть группа из шести человек, какую часть суммы получит каждый? Это либо около
Если есть группа из шести человек, какую часть суммы получит каждый? Это либо около 0,166 , либо ровно 1 / 6 — на ваш выбор.
С другой стороны, вы также можете решить все наоборот, заменив любую дробь десятичной или даже дробью процентами. Все зависит от контекста.
Как превратить десятичную дробь в дробь?
Наша цель состоит в том, чтобы найти два целых числа , числитель и знаменатель, которые при делении друг на друга составляют начальное значение. Допустим, мы хотим оценить, что такое 0,125 в виде дроби:
Установите начальный числитель таким же, как начальное число (
0,125), и установите знаменатель как1.Переместить десятичную точку в конец числителя
0,125 → 1,25 → 12,5 → 125. Каждый скачок соответствует умножению числителя на 10.Поскольку мы передвинули точку на три цифры, это означает, что мы должны умножить знаменатель на 1000, что равно 10 в степени 3.

Определите наибольший общий делитель чисел
125и1000, который равен 125.Разделите оба значения на 125, числитель равен
1, а знаменатель равен8.В результате этого конвертера дробей мы выяснили, что
0,125в виде дроби равно1 / 8.
Как преобразовать повторяющуюся десятичную дробь в дробь?
Преобразование повторяющейся десятичной дроби в дробь немного сложнее. Давайте посмотрим, как наш калькулятор десятичной дроби справляется с этой задачей. Учтите 0,6252525… , что равно 0,625 с двумя повторяющимися цифрами. Мы также можем записать это как 0,625 или 0,6(25) :
Пусть наше число будет
х, так чтох = 0,6252525….Умножьте его на 100, что равно 10 в степени 2 (количество повторяющихся цифр).

100x = 62,5252525….Вычтите эти два значения:
100x - x = 99x = 62,5252525… - 0,6252525… = 61,9. Как вы можете видеть, используя этот трюк , конечные цифры просто компенсируют !Переместите десятичную точку, пока значение не станет целым числом:
61,9 → 619. Это эквивалентно умножению числа на 10, поэтому990x = 619.Разделим обе части на 990, получим
х = 619 / 990.Оцените наибольший общий делитель чисел 619 и 990, чтобы определить, можно ли упростить дробь. НОД на самом деле равен 1. Это означает, что 619 и 990 являются взаимно простыми числами , так что наша дробь уже имеет простейшую форму.
0,625в виде дроби равно619 / 990.
Как использовать калькулятор десятичной дроби? — Преобразователь дробей на практике
Теперь, когда мы знаем, как преобразовать десятичную дробь в дробь, давайте рассмотрим задачу. Есть ли разница между
Есть ли разница между a = 1,83 и b = 1,833 ? Другими словами, имеет ли значение количество повторяющихся цифр для преобразования дробей, и если да, то каким образом? Начните с a :
- Одна повторяющаяся цифра означает, что нам нужно найти
9a, что равно16,5. - Умножение на 10 дает
90a = 165, так чтоa = 165 / 90. - gcf 165 и 90 равен 15, поэтому мы можем записать дробь в ее простейшей форме,
a = 11 / 6.
Так как насчет того, чтобы превратить другую десятичную дробь в дробь, следуя той же процедуре?
- Две повторяющиеся цифры означают, что нам нужно найти
99b, то есть181,5. - Умножение на 10 дает
990b = 1815, так чтоb = 1815 / 990. - gcf 1815 и 990 равен 165, поэтому мы можем записать дробь в ее простейшей форме,
b = 11 / 6.
Отлично! a и b точно такие же. Вы можете проверить это с помощью этого калькулятора десятичной дроби, если вы еще не уверены! Вы можете записать свою десятичную дробь несколькими различными способами, и это не изменит результат преобразования ее в дробь.
Кроме того, вы можете преобразовать результаты неправильной дроби в смешанное число. Есть два способа сделать это:
Разделите числитель и знаменатель и возьмите целую часть результата. Для дробной части используйте оператор по модулю над числителем со знаменателем в качестве делителя.
… или переписать сначала целую часть и просто преобразовать десятичную часть в дробь. В конце соедините обе части.
Калькулятор преобразования десятичной дроби в форму эквивалентной дроби
Онлайн-калькулятор преобразования десятичной дроби в дробь, который просто преобразует десятичное число в дробь и мгновенно возвращает повторяющуюся десятичную дробь к исходной дробной форме. Читайте дальше, чтобы узнать о десятичной дроби, ее таблице преобразования и о том, как превратить десятичную дробь в дробь в мгновение ока.
Читайте дальше, чтобы узнать о десятичной дроби, ее таблице преобразования и о том, как превратить десятичную дробь в дробь в мгновение ока.
Это термин алгебры, в котором десятичная дробь представляет число, знаменатель или нижнее число которого равно 10. Оно может быть кратным или степенью 10, например, 100, 1000, 10000 и т. д. , Все десятичные дроби можно записывать вместе с десятичной или точкой. Таким образом будет проще выполнять вычисления сложения и умножения, в которых используются дроби.
Пример десятичной дроби:7/10 называется десятичной дробью. Если мы запишем его как 0,7, то это будет известно как десятичное число. Для преобразования десятичных знаков в дроби существует ряд определенных правил, однако для удобства преобразования мы также можем использовать калькулятор десятичных знаков в дроби.
Таблица десятичных дробей: Таблицу десятичных дробей можно использовать для преобразования некоторых часто используемых дробей в эквивалентные им десятичные числа.
В основном десятичные и дробные числа всегда обозначают число, которое не является четным целым числом. Преобразуйте десятичные дроби в дроби, следуя простому набору правил.
- Прежде всего, мы должны составить дробь, используя десятичное число. В начальной дроби мы будем использовать десятичную дробь в качестве числителя, также известного как число, которое находится сверху. Знаменатель будет равен 1. Знаменатель — это число, которое присутствует внизу. Например, в случае 0,65, чтобы изменить десятичную дробь, мы запишем это как 0,65/1 в соответствии с этим правилом. В этом примере 0,65 — числитель, а 1 — знаменатель.
- На втором шаге мы умножим верхние и нижние числа на 10. Это умножение удалит десятичный разряд. Мы будем продолжать умножать эти оба числа на 10 до тех пор, пока числитель или верхнее число не превратится в целое значение или целое число. Мы продолжим приведенный выше пример, чтобы объяснить этот шаг математически:
0,65/1 = (0,65 × 10) / (1 × 10) = 6,5 / 10
6,5 / 10 не является целым или целым числом, поэтому мы еще раз умножим его на 10
6,5 / 10 = (6,5 × 10) / (10 × 10) = 65 / 100
- На третьем шаге мы уменьшим дробь.
 Для этого мы должны найти наибольший общий делитель верхнего и нижнего чисел, а затем разделить оба числа на этот НОД или наибольший общий делитель. В приведенном выше примере GFC равен 5 для обоих чисел, поэтому мы просто разделим их на 5 следующим образом:
Для этого мы должны найти наибольший общий делитель верхнего и нижнего чисел, а затем разделить оба числа на этот НОД или наибольший общий делитель. В приведенном выше примере GFC равен 5 для обоих чисел, поэтому мы просто разделим их на 5 следующим образом:
(65 разделить на 5) / (100 разделить на 5) = 13 / 20
Вот небольшой совет, который вы можете использовать калькулятор десятичных дробей для быстрых и точных расчетов.
Пример:
У нас есть десятичное число 2,625, чтобы преобразовать его в дробь. Как это можно сделать?
- Прежде всего, перепишите заданное десятичное число. Разделите его на 1:
2,625 будут заменены на 2,625 / 1
- Теперь нам нужно умножить оба числа на 1000, так как после запятой 3 цифры. Это устранит десятичную дробь:
2,625 / 1 × 1000 / 1000 = 2625 / 1000
- Теперь на третьем шаге найдите GFC для обоих чисел. В этом примере это будет 125,
- Разделите оба числа на GFC:
2625÷125 / 1000÷125 = 21/8
- 21/8 — неправильная дробь, поэтому упростим ее.

2. 5 / 8
2,625=2. 5 / 8
Преобразование отрицательного десятичного числа в дробь:Иногда мы получаем десятичные значения с отрицательным знаком. В таких случаях в первую очередь мы должны исключить знак минус из настоящего десятичного числа. Теперь нам нужно выполнить преобразование при положительном значении. Как только мы получим ответ, мы снова поставим знак минус. Например, если c = b, то верно, что -b = -c. Калькулятор десятичной дроби также работает с отрицательными десятичными значениями.
Как преобразовать повторяющуюся десятичную дробь в дробь?- Чтобы преобразовать повторяющуюся десятичную дробь в дробь, мы должны составить уравнение, в котором x будет равен десятичному числу.
- Теперь нам нужно подсчитать цифры, которые стоят после запятой, это будет y.
- Для создания второго уравнения обе части первого уравнения будут умножены на 10y.
- Будет выполнено вычитание уравнения 2 из уравнения 1.

- Теперь проведем вычисления для x
- На последнем шаге дробь будет уменьшена. Этот расчет кажется немного сложным, поэтому, чтобы избежать путаницы, лучше воспользоваться помощью калькулятора повторяющихся десятичных и дробных чисел.
Пример:
Как преобразовать повторяющееся десятичное число «2,666» в дробь?
Выполните все описанные выше шаги один за другим.
- Для создания уравнения данное повторяющееся десятичное число будет равно x.
Уравнение номер 1: x=2,666
- На втором этапе мы подсчитаем цифры, которые присутствуют после десятичной дроби. В данном случае это три числа. Следовательно, по правилу y = 3,
- На третьем шаге мы должны создать еще одно уравнение. Для этого обе части уравнения 1 умножим на 1000.
Уравнение номер 2: 1000x=2666,666
- Теперь уравнение 1 будет вычтено из второго уравнения.
1000х = 2666,666 – х = 2,666
999x = 2664
- Теперь произведем вычисления для x.

X = 2664 / 999
- На последнем шаге мы должны уменьшить дробь. Для этого просто найдите GFC.
2664÷333 / 999÷333 = 83
- При упрощении этой неправильной дроби получим:
Ответ: 2. 2 / 3
Точность ответа можно проверить с помощью онлайн-калькулятора десятичных дробей.
О калькуляторе десятичной дроби:Онлайн-калькулятор преобразования десятичной дроби в дробь — это инструмент, который позволяет преобразовать десятичную дробь в дробную и вернуть повторяющуюся десятичную дробь к ее первоначальной и простейшей дробной форме. В частности, этот инструмент специально разработан для преобразования десятичной дроби в эквивалентную ей дробь.
Что ж, проведите пальцем вниз, чтобы узнать, как этот калькулятор десятичных дробей преобразует десятичные числа в простейшую дробную форму!
Как превратить десятичную дробь в дробь с помощью калькулятора десятичной дроби: Не беспокойтесь, этот калькулятор очень прост в использовании, так как имеет удобный интерфейс. предоставить точные результаты в течение нескольких секунд.
предоставить точные результаты в течение нескольких секунд.
Ввод:
- Прежде всего, вы должны ввести десятичное число в специальное поле этого калькулятора
- Далее вы должны ввести повторение десятичной дроби (повторить) в указанное поле, но вам просто нужно ввести повторяющееся значение (где это применимо)
Выходы:
После того, как вы закончите, все, что вам нужно нажать кнопку расчета, этот калькулятор преобразования десятичной дроби в дробь сгенерирует:
- Десятичное число в дробь
- Подробное объяснение (пошаговые) расчетов, соответствующих заданным входам
Помните, что вы не можете преобразовать десятичное число в форму дроби на калькуляторе; калькулятор только может помочь вам сделать это с карандашом и бумагой.
Когда дело доходит до преобразования десятичной дроби в дробь, вы сначала решаете, какой тип дроби вы хотите использовать, это может быть ближайшая шестнадцатая часть дюйма, ближайшая восьмая часть дюйма и т. д. Затем вы должны просто умножьте десятичную дробь на желаемую дробь и округлите ответ до ближайшего целого числа.
Что такое 0,1 как дробь?0,1 выражается дробью как 1/10.
Что такое 0,05 в виде дроби?.05 выражается дробью как 1/20.
Что такое 0,5 как дробь?0,5 выражается дробью как 1/2.
В чем разница между десятичной дробью и дробью? Говорят, что дроби — это простое математическое выражение отношений целых чисел, и даже они не всегда делятся на легко выражаемое десятичное число. В то время как десятичные дроби — это термин, который можно использовать для описания длинных, сложных и потенциально бесконечных чисел, таких как значение числа пи.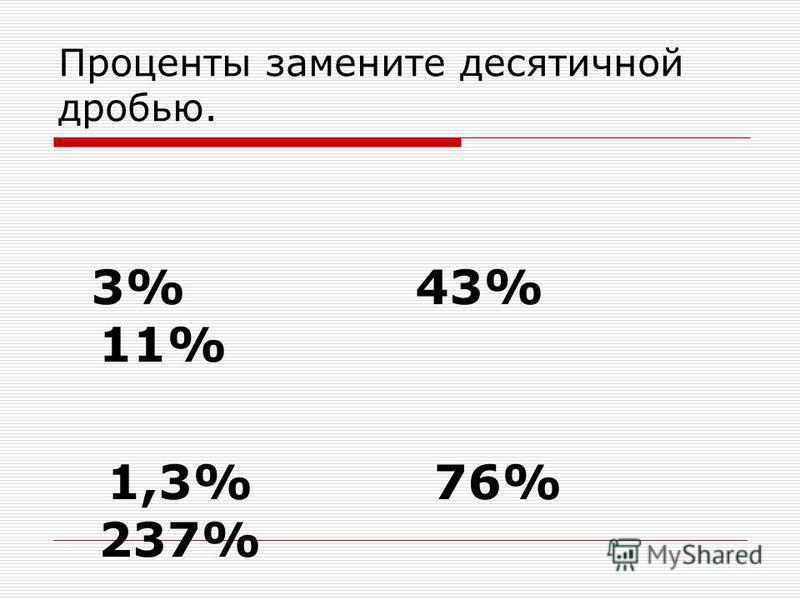
Связь между десятичными дробями, дробями и процентами заключается в том, что все они представляют собой различные числовые выражения, имеющие одинаковое значение.
Как 0,043 превращается в дробь?0,043 выражается в форме дроби как 43/1000, но (если вам нужно) вы можете легко уменьшить эту дробь примерно до 1/25.
Как преобразовать 1666,67 в дробь?Все, что вам нужно переместить запятую на два знака вправо, означает 166667, это числитель, а знаменатель равен 100. Итак, 1666,67 выражается дробью как 166667/100.
Что такое 12,8 как дробь?12,8 выражаются дробью как 64/5.
Что такое 0,06, повторяющееся как дробь?0,6 выражение, повторяющееся в виде дроби, равно 2/33.
Что такое 0,5 Повторение в виде дроби? 0,5 повторение десятичного выражения равно 5/9.
0,15 повторение выражается дробью как 5/33.
Что такое 0,81, повторяющееся как дробь?.81 повторение выражается дробью как 9/11.
Вывод:Этот онлайн-калькулятор преобразования десятичных дробей работает на основе усовершенствованного алгоритма решения уравнения, включающего десятичные числа. Всякий раз, когда вы хотите перепроверить точность своих вычислений, связанных с десятичными дробями, или если требуемое преобразование невозможно выполнить вручную, вы можете использовать этот онлайн-инструмент для получения желаемых результатов.
Ссылки:Из источника Википедии, свободной энциклопедии – Десятичные дроби – Десятичное числовое выражение/система также называется потенциальной системой счисления с основанием десять
Из источника исследования – Повторяющееся десятичное число – Преобразование повторяющихся десятичных дробей в дроби
Из источника mathsisfun — определение десятичной дроби вместе с примером
Калькулятор десятичной дроби — MathCracker.
 com
comИнструкции: Используйте этот калькулятор для преобразования заданного десятичного числа, которое вы предоставляете, в дробь, показывая все шаги. Пожалуйста, введите один десятичное число (например, число типа «3,4673» или число типа «.345279») в форме ниже:
Об этом калькуляторе десятичной дроби
Что такое десятичная дробь? Десятичная дробь относится к способу выражения чисел с использованием числа десять в качестве основания, а также степеней десяти и десятых долей.
Проще говоря, десятичные дроби — это числа, какими вы их знаете, это последовательность цифр (числа от 0 до 9), за которой, возможно, следуют десятые части, представленные через точку «.» и последовательность цифр
Пример цифры: Например, 45,34556 и 0,5678 — это цифры. 2 = 100\). 9к}\]
2 = 100\). 9к}\]
и, возможно, вы захотите уменьшить дробь справа до наименьшего выражения.
Таблица преобразования десятичных дробей в дроби
Существуют классические таблицы, которые дают четкое представление об эквивалентности наиболее часто используемых дробей и их преобразовании в десятичные числа.
Преимущества и недостатки использования диаграммы по сравнению с формулой преобразования десятичных дробей в дроби
- Использование диаграммы прямое: вы просто смотрите на диаграмму и немедленно получаете преобразование десятичной дроби в дробь
- Проблема с диаграммой заключается в том, что там нет точного десятичного числа или дроби, которую вы ищете
- Используя формулу преобразования, вы уверены, что можете преобразовать ЛЮБОЕ число, но вам действительно нужно поработать над вычислением.
Калькуляторы с дробями и процентами
Естественно, как вы, наверное, уже поняли, дроби, десятичные числа и проценты тесно связаны между собой. И часто это просто разные форматы для
представлять ту же информацию в более удобном для данного контекста виде.
И часто это просто разные форматы для
представлять ту же информацию в более удобном для данного контекста виде.
Например, использование калькулятора преобразования процентов в дроби выполняет ту же работу, что и этот калькулятор преобразования десятичных дробей в дроби, с той разницей, что вам нужно будет сначала преобразуйте десятичную дробь в проценты.
Естественно, вы можете столкнуться с обратной ситуацией. Может быть, вы хотите преобразовать дробь в десятичную, что просто общий алгоритм деления арифметики. Обратите внимание, что преобразование дроби в десятичную может привести к конечному десятичному числу или потенциально к повторяющейся десятичной дроби.
Например, дробь \(\displaystyle \frac{3}{5}\) просто соответствует 0,6 (простое конечное десятичное число), но дробь \(\displaystyle \frac{1}{3}\) соответствует повторяющемуся десятичному числу 0,33333…..
Пример: Преобразование десятичного числа в дробь
Вопрос : Вычислите число 3,4563 как дробь.
Решение:
Вы ввели следующее десятичное число \(D = \displaystyle 3.4563\), и цель состоит в том, чтобы преобразовать его в дробь. 9{4} \] \[ = 3,4563 \times 10000= 34563 \]
Итак, разделив обе части на \(10000\), мы получим
\[ 3,4563 = \displaystyle \frac{34563}{10000} \]
, а поскольку найденная дробь уже упрощена, делается вывод, что простейшая дробь, эквивалентная \(3,4563\), равна \(3,4563\).
Таким образом, выражение десятичной дроби в простейшем виде равно \(\displaystyle 3.4563 = \frac{ 34563}{10000}\), что завершает вычисление.
Пример 2
Вопрос Выразите 0,625 в виде дроби.
Решение:
Вы ввели следующее десятичное число \(D = \displaystyle 0.625\), и цель состоит в том, чтобы преобразовать его в дробь.
Шаг 1: Нам нужно умножить \(D = 0,625\) на степень 10, чтобы в результирующем выражении не было десятичных значений справа от ‘. ‘ знак.
‘ знак.
Итак, разделив обе части на \(1000\), мы получим
\[ 0,625 = \displaystyle \frac{625}{1000} \]
Дальнейшее упрощение дроби, полученной в результате предыдущего шага, показало, что: \[\frac{ 625}{ 1000} = \frac{ 125 \times 5}{ 125 \times 8} = \frac{ \cancel{ 125} \times 5}{ \cancel{ 125} \times 8} = \ гидроразрыв{ 5}{ 8}\]
Таким образом, выражение десятичной дроби в простейшем виде равно \(\displaystyle 0.625 = \frac{ 5}{ 8}\), что завершает вычисление.
Пример 3
Вопрос Вычислить 0,8 как дробь
Решение:
Вы ввели следующее десятичное число \(D = \displaystyle 0.8\), и цель состоит в том, чтобы преобразовать его в дробь.
Шаг 1: Нам нужно умножить \(D = 0,8\) на степень 10, чтобы в результирующем выражении не было десятичных значений справа от ‘.’ знак.
Шаг 2: Это просто делается путем подсчета количества цифр справа от точки ‘. ‘. Для предоставленного числа у нас есть \(k = 1\) цифр справа от точки. 9{1} \] \[ = 0,8 \times 10= 8 \]
‘. Для предоставленного числа у нас есть \(k = 1\) цифр справа от точки. 9{1} \] \[ = 0,8 \times 10= 8 \]
Итак, разделив обе части на \(10\), мы получим
\[ 0,8 = \displaystyle \frac{8}{10} \]
Дальнейшее упрощение дроби, полученной в результате предыдущего шага, показало, что: \[\frac{ 8}{ 10} = \frac{ 2 \times 4}{ 2 \times 5} = \frac{ \cancel{ 2} \times 4}{ \cancel{ 2} \times 5} = \ дробь { 4} { 5} \]
Следовательно, выражение десятичной дроби в простейшем виде равно \(\displaystyle 0.8 = \frac{ 4}{ 5}\), что завершает вычисление.
Повторяющийся калькулятор десятичной дроби | Математические калькуляторы
Калькулятор повторяющихся десятичных дробей используется для вычисления того, сколько число, записанное повторяющимися десятичными цифрами, может быть записано дробями. Этот простой на вид онлайн-калькулятор на самом деле вычисляет 6 шагов для выполнения задачи преобразования.
| Неповторяющаяся часть | |
| Повторяющееся число |
| The Number | ||
| Vulgar Fraction | ||
| / | ||
| / | ||
★ ★ ★ ★ ★ [ 32 Голоса ]
Все, что вам нужно знать о калькуляторе повторяющихся десятичных дробей
Любые предположения, сколько времени вам потребуется, чтобы сделать все эти вычисления? Правильно, больше, чем вы думаете.
Итак, двигаясь дальше, каждый расчет, который вы делаете, процессор будет делать намного быстрее, давая вам точные результаты, чем вы способны произвести. Однако, учитывая тот факт, что время имеет решающее значение и есть и другие задачи, которые необходимо выполнить, iCalculator разработал повторяющийся калькулятор десятичной дроби, чтобы помочь вам сэкономить время.
Что такое повторяющееся преобразование десятичной дроби в дробную?
Прежде чем мы начнем с деталей калькулятора десятичной дроби, давайте сначала разберемся в его функции. Как указано в его названии, этот калькулятор вычисляет преобразование повторяющегося десятичного числа в его дробный эквивалент.
Чтобы лучше понять это, предположим, вам нужно найти дробный эквивалент, скажем, 0,333333
Преобразование повторяющихся десятичных чисел в дроби для одной повторяющейся цифры
Итак, дайте ему имя, скажем, x.
Теперь,
- x = 0,333333———-(1)
- 10x = 3,33333——(2)
- Вычесть (1) из (2)
- 9x = 3
- x = 3/9
- x = 1/3
Таким образом, ясно, что 1/3 является дробным эквивалентом 0,333333
Но нет, это относится к одной повторяющейся цифре после запятой. Что, если у вас есть число с двумя повторяющимися десятичными цифрами, например, 0,21212121. В таком случае
Что, если у вас есть число с двумя повторяющимися десятичными цифрами, например, 0,21212121. В таком случае
Преобразование повторяющихся десятичных чисел в дроби для двух повторяющихся цифр
x = 0,21212121—(1)
Теперь мы не можем умножить обе части на 10, потому что это изменит порядок повторяющихся десятичных знаков. . Итак, нам нужно умножить обе части на 100. Итак, теперь у нас есть
100x = 21,212121—(2)
Теперь вычтите (1) из (2), и мы получим
- 99x = 21
- x = 21/99
- x = 7/33
Преобразование повторяющихся десятичных чисел в дроби для трех повторяющихся цифр
Аналогичным образом, если повторяющиеся десятичные цифры находятся в наборе из трех, вам нужно умножить обе стороны на 1000, например, предположим, что
x = 0,738738738738
Помня о приведенном выше правиле,
- 1000x = 738,738738738
- 999x = 738
- x = 738/999
- x = 82/111
Проще говоря, чтобы найти дробный эквивалент повторяющегося десятичного числа, вам нужно обе стороны умножить на 10-й показатель степени, экспоненциальное значение которого равно количество повторяющихся цифр.
Однако, если у вас есть однозначное повторяющееся десятичное число, такое как 738,333333, то как вы будете решать эту проблему? Звучит сложно? Нет, запомните правило. Просто умножьте 738,333333 на 10, и вы получите 7383,33333. Это то же самое путешествие сейчас, верно? Нет. Это даст вам неправильный ответ.
Повторяющееся преобразование десятичной дроби в смешанную дробь
Это потому, что в таком случае число слева от десятичной точки (или число перед десятичной точкой, как вам лучше запомнить) не используется. Затем вы работаете с данной дробью, как обычно.
Таким образом, работая над 0,33333, вы получите долю 1/3. Теперь идет поворот смешанных фракций. 738, которые вы отложили, станут причиной того, что дробь станет смешанной, и у вас будет
x = 738⅓
Для подтверждения просто умножьте 738 на 3, добавьте к нему 1 и разделите сумму на 3, и вы получите 738,33333.
В конце концов, все сводится к тому, насколько быстро вы упрощаете дроби. И помните, не было бы онлайн-калькуляторов или любых других математических калькуляторов, если бы упрощение дробей было таким простым.
И помните, не было бы онлайн-калькуляторов или любых других математических калькуляторов, если бы упрощение дробей было таким простым.
Использование калькулятора десятичной дроби в реальной жизни
От выпечки до банковских операций и химических экспериментов, этот конкретный математический расчет играет важную роль во всех них. Счета, статистика, инженерия, повторяющееся преобразование десятичной дроби в дробь нашли свое применение во всех сферах жизни. Вряд ли найдется какая-нибудь математическая работа, в которой не использовались бы дроби. И всякий раз, когда вы сталкиваетесь с десятичными дробями, велика вероятность, что вам понадобятся дроби для дальнейших вычислений.
Заключение
Волшебный мир математики и десятичных дробей часто приводит вас к точке, где вам нужно выйти в царство дробей. И всякий раз, когда это происходит, вам больше не нужно беспокоиться о выполнении всех этих шагов расчета, математические вычисления вручную остались в прошлом. Калькулятор десятичной дроби от iCalculator сделает это за вас быстро и точно.
Калькулятор десятичной дроби от iCalculator сделает это за вас быстро и точно.
Калькулятор десятичных дробей [Бесплатный онлайн-конвертер]
Калькулятор десятичных дробей поможет вам преобразовать десятичные значения в дроби. Это бесплатный и простой в использовании инструмент. Кроме того, вы найдете таблицу преобразования здесь.
С детства нас очень интересовали числа и уравнения. Вспомните свой урок математики, когда вы были ребенком. Играть с простыми числами было легко и весело, пока не появились числа с очками. Да, это десятичные дроби! Затем мы перешли к преобразованию десятичной дроби в дробную. Это очень интересно для тех, кто любит математику. Но очень обидно, кто не любит математику. Не волнуйся. Наш инструмент поможет вам и сделает вашу работу легкой и быстрой.
Итак, прежде всего, давайте повторим некоторые основы.
Десятичные числа — это такие значения, как 2,56, 31,03, 0,004 и т. д. С другой стороны, дробные значения похожи на 1/4, 1/2, 3/8, 100/990 и так далее.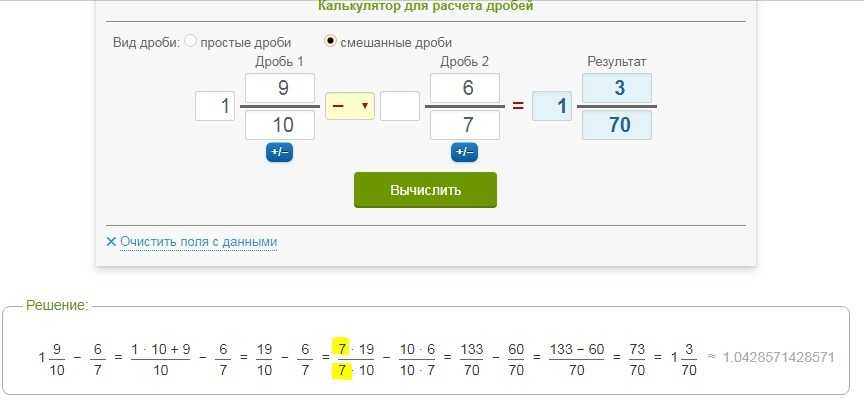
Посмотрите на этот пример, чтобы понять разницу между десятичными дробями и дробями.
Десятичная = 0,5
Дробная = 1/2
Что это значит? Если мы разделим 1 на 2, то получим ответ 0,5. Это самый простой пример для понимания. Но некоторые расчеты могут быть очень сложными. Итак, для этого вы можете использовать этот конвертер. Более того, в этой статье мы обсудим, как преобразовать десятичные дроби в дроби вручную с помощью простой формулы. Итак, следите за обновлениями.
Как преобразовать десятичную дробь в дробь?
Для конвертации важно знать единицы после запятой.
Давайте разберемся на простом примере.
0,123
Здесь 1 соответствует десятым, 2 соответствует сотым и 3 соответствует тысячным.
Пример 1: Узнать дробь 0,35
Последняя цифра 5, то есть сотая. Итак, мы должны умножить и разделить на 100.
(0,35 * 100) / 100 = 35/100 = 7/20
Итак, мы можем сказать, что дробь от 0,35 равна 7/20 .
Возьмем еще несколько примеров.
Пример 2: Чему равна доля 1,5?
Здесь последняя цифра стоит на десятой, поэтому умножаем 1,5 на 10 и делим на 10.
(1,5*10)/10 = 15/10 = 3/2
Итак, получается 3 /2 и это неправильная дробь. Следовательно, мы можем преобразовать его в правильную дробь.
То есть 1 1 ⁄ 2 .
Пример 3: Вычисление доли 4,125
Здесь последняя цифра стоит в тысячном разряде, поэтому мы умножаем и делим 4,125 на 1000.
(4,125 * 1000) / 1000 = 4125/1000 переведя в правильную дробь, получим 4 1 ⁄ 8 .
Пример 4: преобразование 0,625 в дробь
0,625 = 625/1000
gcd(625,1000) = 125
0,625 = (625/125)/(1000/125) = 5/8
Как пользоваться?
- Самое главное, это онлайн-калькулятор. Поэтому вам понадобится смарт-устройство с активным подключением к Интернету.
- Затем откройте Калькулятор десятичных дробей в любом браузере, таком как Chrome, Firefox или Safari.

- Во-первых, вы можете увидеть поля ввода в верхней части веб-страницы для ввода десятичного значения.
- Итак, введите десятичные числа, которые вы хотите преобразовать в дроби.
- После этого нажмите «Рассчитать» , чтобы показать результат.
- В результате вы получите приведенный ниже результат преобразования с полной формулой и расчетом.
Процесс преобразования повторяющихся десятичных значений в дроби
Примеры повторяющихся десятичных чисел: 0,66666666…, 4,7628888888… Основная проблема при вводе этих чисел заключается в том, что последняя цифра повторяется вечно.
Например, вы хотите найти дробь 0,44444… Итак, вы можете ввести 0,4 в поле ввода. Поскольку 4 — это только цифра, которая продолжает повторяться.
Что делать с отрицательными значениями?
В этом случае соблюдается простое правило.
Если x = y, то –x = –y
Итак, чтобы найти дробь от –1,5, просто введите -1,5 в поле ввода. В результате вы получите отрицательный результат дроби. Эта функция делает этот инструмент более уникальным. Потому что вы можете конвертировать как положительные, так и отрицательные значения.
В результате вы получите отрицательный результат дроби. Эта функция делает этот инструмент более уникальным. Потому что вы можете конвертировать как положительные, так и отрицательные значения.
Таблица преобразования
| Десятичная дробь | Дробь |
|---|---|
| 0.00001 | 1/100000 |
| 0.0001 | 1/10000 |
| 0.001 | 1/1000 |
| 0.01 | 1/100 |
| 0.08333333 | 1/12 |
| 0.009 | 1/11 |
| 0.1 | 1/10 |
| 0.11111111 | 1/9 |
| 0.125 | 1/8 |
| 0.14285714 | 1/7 |
| 0.16666667 | 1/6 |
| 0.2 | 1/5 |
| 0.22222222 | 2/9 |
| 0.25 | 1/4 |
0. 28571429 28571429 | 2/7 |
| 0.3 | 3/10 |
| 0.33333333 | 1/3 |
| 0.375 | 3/8 |
| 0.4 | 2/5 |
| 0.42857143 | 3/7 |
| 0.44444444 | 4/9 |
| 0.5 | 1/2 |
| 0.55555555 | 5/9 |
| 0.57142858 | 4/7 |
| 0.6 | 3/5 |
| 0.625 | 5/8 |
| 0.66666667 | 2/3 |
| 0.7 | 7/10 |
| 0.71428571 | 5/7 |
| 0.75 | 3/4 |
| 0.77777778 | 7/9 |
| 0.8 | 4/5 |
| 0.83333333 | 5/6 |
| 0.85714286 | 6/7 |
| 0.875 | 7/8 |
0.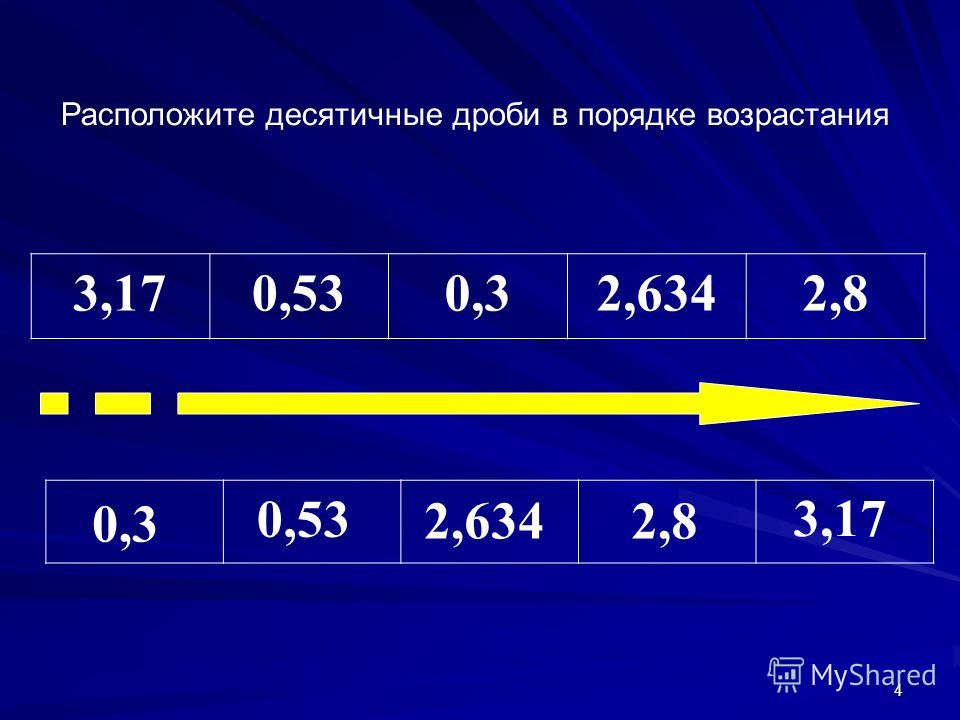 88888889 88888889 | 8/9 |
| 0.9 | 9/10 |
| 1.1 | 11/10 |
| 1.2 | 6/5 |
| 1.25 | 5/4 |
| 1.3 | 13/10 |
| 1.4 | 7/5 |
| 1.5 | 3/2 |
| 1.6 | 8/5 |
| 1.7 | 17/10 |
| 1.75 | 7/4 |
| 1.8 | 9/5 |
| 1.9 | 19/10 |
| 2,5 | 5/2 |
Заключение
Итак, в первую очередь речь шла о калькуляторе десятичной дроби. По сути, это онлайн-калькулятор. Кроме того, мы объяснили процесс преобразования с помощью формулы и простых примеров. Кроме того, этот инструмент сэкономит вам время и силы. Кроме того, он дает очень точные результаты. Потому что он сделан с использованием языка программирования javascript.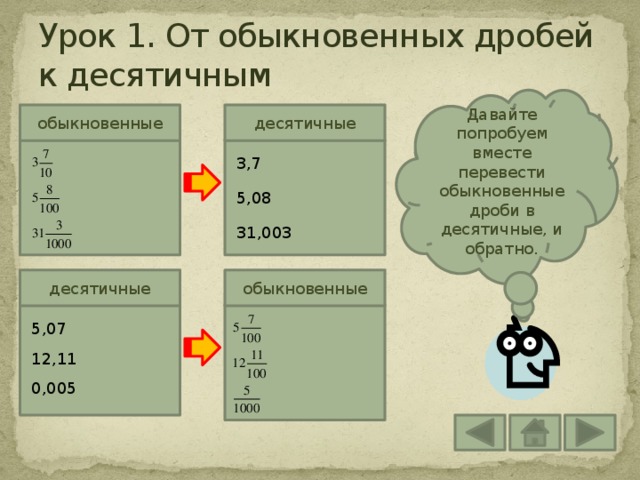 Для каждого преобразования он выполняет алгоритм и выдает правильный результат.
Для каждого преобразования он выполняет алгоритм и выдает правильный результат.
Калькулятор округления десятичных до дробей
Бесплатный и удобный онлайн-калькулятор округления десятичной дроби доступен здесь для округления заданные десятичные дроби до ближайшего половинного значения или 1/4, или 1/8, или 1/16, или т. д., за доли секунды. Все, что вам нужно сделать Выберите способ расчета из выпадающего списка, введите значение, которое нужно округлить, и нажмите непосредственно на кнопку кнопка расчета для получения точного результата с подробными шагами.
сообщите об этом объявлении
Округлить до половины (1/2) Округлить до четверти (1/4) Округлить до 1/8 (1/8) Округлить до 1/16 1/32 округлить до ближайшего 1/64
сообщите об этом объявлении
Связанные калькуляторы:
- Округление до ближайшего 1/2 Калькулятор
- Округление до 1/4 Калькулятор
- Округление до 1/8 Калькулятор
- Округление до ближайшего 1/16 Калькулятор
- Округление до ближайшего 1/32 Калькулятор
- Округление до ближайшего 1/64 Калькулятор
Калькулятор округления десятичных до дробей: Вы ищете такой калькулятор, который
имеет дело с немедленным округлением десятичных дробей до ближайшей дроби? Вот лучший и идеальный инструмент, т. е.
Калькулятор округления десятичной дроби до дроби, который поможет вам округлить заданное десятичное число до ближайшего
дробь за доли секунды. Однако вы также можете найти пошаговое решение для округления десятичной дроби.
до ближайшей дроби в дальнейших модулях.
е.
Калькулятор округления десятичной дроби до дроби, который поможет вам округлить заданное десятичное число до ближайшего
дробь за доли секунды. Однако вы также можете найти пошаговое решение для округления десятичной дроби.
до ближайшей дроби в дальнейших модулях.
Следующие модули помогут вам понять процесс округления чисел до ближайшей дробной части. Просто погрузитесь в дальнейшие разделы и четко изучите предмет.
Подробное решение округления десятичных дробей до ближайшей половины (1/2)
Возьмем в качестве примера десятичное число 25,87 и следуем правилам или указаниям, чтобы округлить число до ближайшую 1/2 и получить точные результаты:
- Сначала определите число, где 25,87 — заданный вход.
- Правило округления числа до ближайшей половины, если дробная часть числа близка до 0,5, затем убираем дробную часть и прибавляем к данному числу 1/2.
- Если дробная часть намного больше 1/2, то увеличьте на 1 до целой части и удалите
дробная часть.

- Если число после запятой намного меньше 1/2, то дробную часть и результатом будет целая часть.
- В этом примере дробная часть больше 0,5, поэтому результат округления до ближайшей половины равен 26.
Как округлить десятичные дроби до четверти (1/4)?
Выполните следующие шаги для округления чисел до ближайшей 1/4 и легко изучите концепцию:
- Прежде всего обратите внимание на дробную часть в заданном десятичном числе.
- Затем округлите номер детали в дробной части до ближайшего кратного одной четверти.
- Запишите полученный результат в дробях от 4.
- Наконец, получите округленное значение до ближайшей четверти.
Округление до одной восьмой (1/8) Пример с шагами
Пример:
Найти 234,45, округленное до ближайшей 1/8?
Решение:
Данное десятичное число для округления до ближайшей 1/8 равно 234,45
Теперь посмотрим на дробную часть, т. е. равно кратному 1/8. Здесь 0,5 в дроби от 8 равно
эквивалентно 4/8.
е. равно кратному 1/8. Здесь 0,5 в дроби от 8 равно
эквивалентно 4/8.
Следовательно, 234,45, округленное до ближайшей 1/8, равно 234 4/8.
Подробные шаги для округления до ближайшей 1/16
Вот простые шаги, которые необходимо выполнить, чтобы округлить десятичную дробь до ближайшей дроби 1/16 и получить результаты быстро и без усилий.
- Обратите внимание на число в дробной части, которое необходимо округлить. Здесь значение, которое нужно округлить, равно 875,23
- . Теперь округлим дробную часть, т. е. 0,23, ближайшую к 0,25.
- Можно представить в дроби 16, что эквивалентно 4/16.
- Наконец, целая часть и дробная часть дают округленное значение 875,23, т.е. 875 4/16.
Как округлить десятичную дробь до 1/32?
Чтобы округлить десятичную дробь до ближайшей 1/32, мы должны проверить и выполнить приведенные ниже шаги, чтобы получить приблизительное значение, ближайшее к 1/32:
- Сначала определите дробную часть числа.

- Теперь округляем до ближайшего кратного 1/32.
- После того, как вы выполните вышеуказанный шаг, полученное число будет дробным от 32.
- Наконец, запишите полученное эквивалентное число в дробной части.
Пошаговое решение для округления десятичной дроби до ближайшего 1/64
- На первом этапе мы должны соблюдать заданное число.
- Затем разделите дробную часть и начните округлять число до ближайшего кратного 1/64.
- Найдите или запишите эквивалентное значение, которое является ближайшей долей 1/64.
- Наконец, округлите десятичную дробь до ближайшей дробной части 1/64.
1. Как округлить десятичную дробь до дроби с помощью калькулятора?
Нажмите на калькулятор округления десятичных до дробей на нашей главной странице. После входа в
страницу калькулятора, выберите расчет и введите десятичную дробь в отведенное поле, затем нажмите «Рассчитать».
кнопку, чтобы получить результаты в более быстром темпе.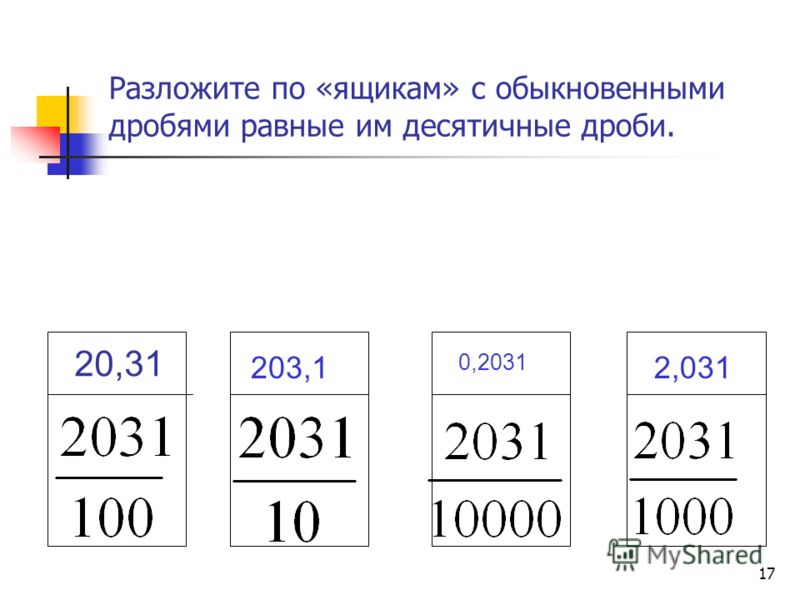





 Проще всего записывать числа, начиная с запятой. Поставить две запятые сверху и снизу, а затем уже расписывать знаки по обе стороны. Это правило, кстати, действует на основании того же правила вычитания простых дробей — из целого вычитаются целые, а из дробных — дробные. Запятая в результате должна располагаться точно под двумя верхними.
Проще всего записывать числа, начиная с запятой. Поставить две запятые сверху и снизу, а затем уже расписывать знаки по обе стороны. Это правило, кстати, действует на основании того же правила вычитания простых дробей — из целого вычитаются целые, а из дробных — дробные. Запятая в результате должна располагаться точно под двумя верхними.


 Для этого мы должны найти наибольший общий делитель верхнего и нижнего чисел, а затем разделить оба числа на этот НОД или наибольший общий делитель. В приведенном выше примере GFC равен 5 для обоих чисел, поэтому мы просто разделим их на 5 следующим образом:
Для этого мы должны найти наибольший общий делитель верхнего и нижнего чисел, а затем разделить оба числа на этот НОД или наибольший общий делитель. В приведенном выше примере GFC равен 5 для обоих чисел, поэтому мы просто разделим их на 5 следующим образом: