Коэффициент ранговой корреляции Спирмена онлайн
Примеры решенийКоэффициент СпирменаКоэффициент Кендалла Коэффициент конкордацииКоэффициент контингенции Группировка данных Показатели вариации Доверительный интервал Различие средних
Назначение сервиса. С помощью данного онлайн-калькулятора производится:
- расчет коэффициента ранговой корреляции Спирмена;
- вычисление доверительного интервала для коэффициента и оценка его значимости;
- Шаг №1
- Шаг №2
- Видеоинструкция
Инструкция. Укажите количество данных (количество строк), нажмите Далее. Полученное решение сохраняется в файле Word (см пример нахождения коэффициента ранговой корреляции Спирмена). Также создается шаблон решения в Excel.
Количество строк
Укажите количество данных (количество строк), нажмите Далее. Полученное решение сохраняется в файле Word (см пример нахождения коэффициента ранговой корреляции Спирмена). Также создается шаблон решения в Excel.
Количество строк
Расчет коэффициента состоит из следующих этапов:
- Ранжирование признаков по возрастанию. Ранг – это порядковый номер. Если встречаются два одинаковых значения, им присваивают одинаковое значение ранга, равное среднему арифметическому рангов этих значений.
- Определение разности рангов каждой пары сопоставляемых значений, d = dx — dy.
- Возведение в квадрат разность di и нахождение общей суммы, ∑d2.

- Вычисление коэффициента корреляции рангов по формуле: где d2 – квадратов разностей между рангами; N – количество признаков, участвовавших в ранжировании.
Свойства коэффициента ранговой корреляции Спирмена
- Нормируемость. Коэффициент корреляции рангов может принимать значения от -1 до +1.
p = 1свидетельствует о возможном наличии прямой связи,p =-1свидетельствует о возможном наличии обратной связи. - Ограниченность. Для оценки данных необходима выборка от 5 до 40 наблюдений по каждой переменной. При большом количестве одинаковых рангов по сопоставляемым переменным коэффициент дает приближенные значения. При совпадении значений вносится поправка на одинаковые ранги. В этом случае формула имеет вид:
где d

- Независимость. Чтобы получить адекватный результат, необязательно наличие нормального закона распределения коррелируемых рядов.
Область применения. Коэффициент корреляции рангов используется для оценки качества связи между двумя совокупностями. Кроме этого, его статистическая значимость применяется при анализе данных на гетероскедастичность.
Пример. По выборке данных наблюдаемых переменных X и Y:
- составить ранговую таблицу;
- найти коэффициент ранговой корреляции Спирмена и проверить его значимость на уровне 2a
- оценить характер зависимости
Решение. Присвоим ранги признаку Y и фактору X.
| X | Y | ранг X, dx | ранг Y, dy |
| 28 | 21 | 1 | 1 |
| 30 | 25 | 2 | 2 |
| 36 | 29 | 4 | 3 |
| 40 | 31 | 5 | 4 |
| 30 | 32 | 3 | 5 |
| 34 | 6 | 6 | |
| 56 | 35 | 8 | 7 |
| 54 | 38 | 7 | 8 |
| 60 | 39 | 10 | 9 |
| 56 | 41 | 9 | 10 |
| 60 | 42 | 11 | 11 |
| 68 | 44 | 12 | 12 |
| 70 | 46 | 13 | 13 |
| 76 | 50 | 14 | 14 |
Матрица рангов.

| ранг X, dx | ранг Y, dy | (dx — dy)2 |
| 1 | 1 | 0 |
| 2 | 2 | 0 |
| 4 | 3 | 1 |
| 5 | 4 | 1 |
| 3 | 4 | |
| 6 | 6 | 0 |
| 8 | 7 | 1 |
| 7 | 8 | 1 |
| 10 | 9 | 1 |
| 9 | 10 | 1 |
| 11 | 11 | 0 |
| 12 | 12 | 0 |
| 13 | 13 | 0 |
| 14 | 14 | 0 |
| 105 | 105 | 10 |
Проверка правильности составления матрицы на основе исчисления контрольной суммы:
Сумма по столбцам матрицы равны между собой и контрольной суммы, значит, матрица составлена правильно.

По формуле вычислим коэффициент ранговой корреляции Спирмена.
Связь между признаком Y и фактором X сильная и прямая
Значимость коэффициента ранговой корреляции Спирмена
Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена при конкурирующей гипотезе Hi. p ≠ 0, надо вычислить критическую точку:
где n — объем выборки; ρ — выборочный коэффициент ранговой корреляции Спирмена: t(α, к) — критическая точка двусторонней критической области, которую находят по таблице критических точек распределения Стьюдента, по уровню значимости α и числу степеней свободы k = n-2.

По таблице Стьюдента находим t(α/2, k) = (0.1/2;12) = 1.782
Поскольку Tkp < ρ, то отклоняем гипотезу о равенстве 0 коэффициента ранговой корреляции Спирмена. Другими словами, коэффициент ранговой корреляции статистически — значим и ранговая корреляционная связь между оценками по двум тестам значимая.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Калькулятор коэффициента корреляции — MathCracker.com
Решатели Статистика
Инструкции:
Вы можете использовать этот пошаговый калькулятор коэффициента корреляции для двух переменных X и Y. Все, что вам нужно сделать, это ввести данные X и Y в формате, разделенном запятыми или пробелами (например: «2, 3, 4, 5 "или" 3 4 5 6 7 ").
Все, что вам нужно сделать, это ввести данные X и Y в формате, разделенном запятыми или пробелами (например: «2, 3, 4, 5 "или" 3 4 5 6 7 ").
Данные X (через запятую)
Данные Y (через запятую)
Имя переменной X (необязательно)
Имя переменной Y (необязательно)
Вычисленный выше коэффициент корреляции соответствует коэффициенту корреляции Пирсона. Требования для его вычисления заключаются в том, чтобы две переменные X и Y измерялись, по крайней мере, на уровне интервала (что означает, что он не работает с номинальными или порядковыми переменными).
Формула для коэффициента корреляции Пирсона:
\[r =\frac{n \sum_{i=1}^n x_i y_i — \left(\sum_{i=1}^n x_i \right) \left(\sum_{i=1}^n y_i \right) }{\sqrt{n \sum_{i=1}^n x_i^2 — \left( \sum_{i=1}^n x_i \right)^2} \sqrt{n \sum_{i=1}^n y_i^2 — \left( \sum_{i=1}^n y_i \right)^2} }\]
или эквивалентно
\[r = \frac{\sum_{i=1}^n x_i y_i — \frac{1}{n}\left(\sum_{i=1}^n x_i \right) \left(\sum_{i=1}^n y_i \right) }{\sqrt{\sum_{i=1}^n x_i^2 — \frac{1}{n}\left( \sum_{i=1}^n x_i \right)^2} \sqrt{\sum_{i=1}^n y_i^2 — \frac{1}{n}\left( \sum_{i=1}^n y_i \right)^2}} = \frac{SS_{XY}}{\sqrt{SS_{XX}\cdot SS_{YY} }}\]
Если у вас есть две или более переменных, вы можете использовать наш
калькулятор корреляционной матрицы
. Кроме того, если данные для переменных \(X\) и \(Y\) не соответствуют параметрическим предположениям для корреляции Пирсона, вам следует использовать это
Калькулятор корреляции Спирмена
вместо.
Кроме того, если данные для переменных \(X\) и \(Y\) не соответствуют параметрическим предположениям для корреляции Пирсона, вам следует использовать это
Калькулятор корреляции Спирмена
вместо.
Могу ли я использовать z-значения для вычисления коэффициента корреляции
Безусловно! Вы повсюду видели z-значения в статистике и, естественно, задаетесь вопросом, можете ли вы
вычислить корреляцию с z-оценками
. Вы определенно можете это сделать, и на самом деле это обычный способ делать это в статистике социальных наук.
Другие калькуляторы, похожие на этот калькулятор корреляции
Также существует понятие коэффициент множественной корреляции , когда у вас есть более одного предиктора, который получается путем вычисления корреляции между наблюдаемыми значениями \(Y\) и прогнозируемыми значениями \(\hat Y\) с помощью регрессии.
Базовый пакет статистики Калькулятор коэффициента корреляции Коэффициент корреляции Коэффициент корреляции Пирсона Статистический решатель
Коэффициент ранговой корреляции Спирмена
Пишу на заказ дипломные, курсовые, магистерские работы по психологии, а также рефераты и эссе; делаю контрольные, отчеты по практике и статистические расчеты.

Я профессиональный психолог и автор работ по психологии с многолетним стажем. Выступаю как индивидуальный предприниматель (ИП): заключаю договор, выдаю чеки об оплате.
Помогаю студентам-психологам более 12 лет (этот сайт существует с 2007). Делаю качественно и быстро. Помогу даже с очень трудными темами.
Вы всегда можете узнать у меня, как идут дела с дипломной; оперативно передать пожелания руководителя; спросить то, что не понятно. Я всегда на связи.
Опишите ситуацию, и я скажу стоимость написания вашей работы.
Главная / Статистические расчеты / Анализ взаимосвязей / Коэффициент корреляции Спирмена
Коэффициент корреляции Спирмена – статистический критерий, который наиболее часто используется при обработке эмпирических данных в курсовых, дипломных и магистерских работах по психологии. Этот критерий относится к типу непараметрических и не требует, чтобы данные были распределены по нормальному закону. Достаточно, если психологические показатели представлены в порядковой шкале, то есть учитывается только тот факт, что один показатель больше или меньше, чем другой.
Достаточно, если психологические показатели представлены в порядковой шкале, то есть учитывается только тот факт, что один показатель больше или меньше, чем другой.
Расчет коэффициента корреляции Спирмена
При проведении эмпирического исследования в дипломной по психологии для расчета коэффициента корреляции Спирмена удобнее пользоваться статистическими программами. Однако, этот критерий нетрудно рассчитать и вручную.
Пример расчета коэффициента корреляции Спирмена
Предположим, в рамках дипломной работы по психологии проводится исследование влияния климата в коллективе на состояние сотрудников. Одна из задач исследования состоит в выявлении взаимосвязи между климатом и эмоциональным истощением сотрудников.
Выдвигаем гипотезу — существует отрицательная взаимосвязь между социально-психологическим климатом в коллективе и степенью истощения сотрудников.
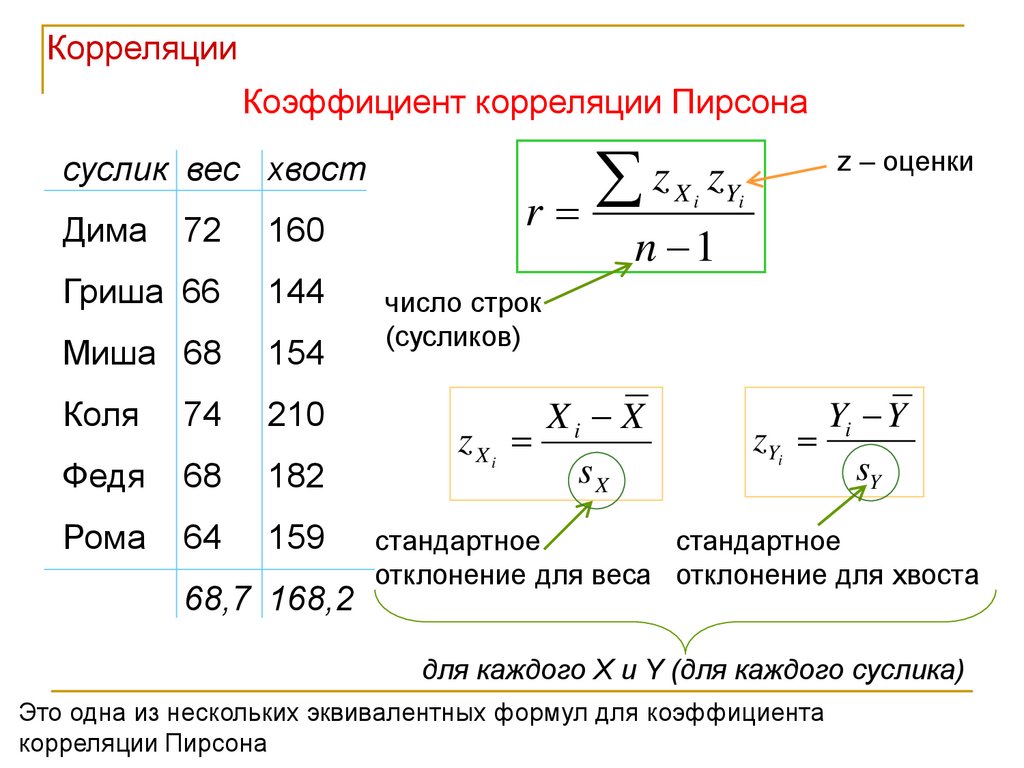
В таблице приводятся данные, отражающие этапы расчета коэффициентов ранговой корреляции Спирмена.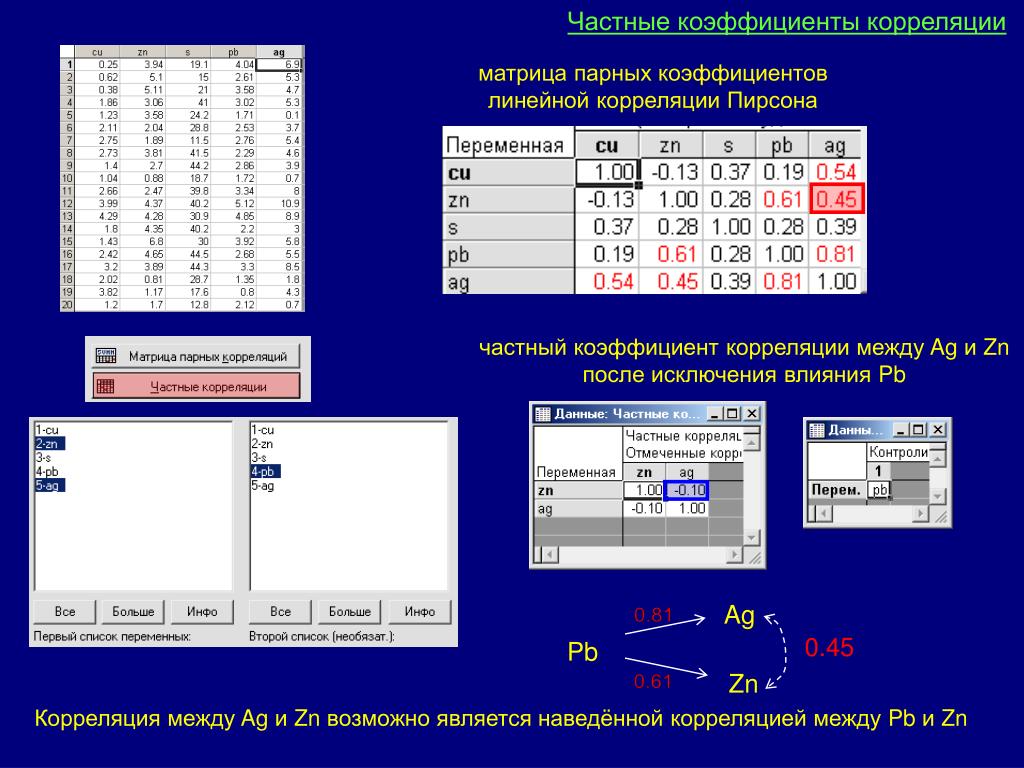 Суть расчета сводится к тому, что от собственно значений переходим к их рангам (ранг отражает положение показателя в общем списке и записывается в виде натурального числа). Далее находятся разности между рангами, эти разности возводятся в квадрат и суммируются.
Суть расчета сводится к тому, что от собственно значений переходим к их рангам (ранг отражает положение показателя в общем списке и записывается в виде натурального числа). Далее находятся разности между рангами, эти разности возводятся в квадрат и суммируются.
№ | Эмоциональное истощение (Х) | Психологический климат (Y) | Ранг Х | Ранг Y | Ранг Х-Ранг Y | (Ранг Х-Ранг Y)2 |
1 | 15 | 0,7 | 6 | 8 | -2 | 4 |
2 | 15 | 0,6 | 6 | 5,5 | 0,5 | 0,25 |
3 | 15 | 0,6 | 6 | 5,5 | 0,5 | 0,25 |
4 | 13 | 0,5 | 1 | 3 | -2 | 4 |
5 | 15 | 0,7 | 6 | 8 | -2 | 4 |
6 | 14 | 0,5 | 2 | 3 | -1 | 1 |
7 | 15 | 0,7 | 6 | 8 | -2 | 4 |
8 | 15 | 0,5 | 6 | 3 | 3 | 9 |
9 | 16 | 1 | 10 | 10 | 0 | 0 |
10 | 15 | 0 | 6 | 1 | 5 | 25 |
Сумма | 0 | 51,5 | ||||
Формула расчёта коэффициента корреляции Спирмена
Сумма(D2)
R= 1 — 6—————-
N(N2-1)
D – разность между рангами
Сложность расчёта корреляций Спирмена вручную связана с необходимостью вводить поправки на одинаковые ранги, что достаточно трудоемко.
Поправка для Х:
Тх=(73-7)/12=336/12=28
Поправка для Y:
Тy=(2(33-3)+(23-2))/12=(48+6)/12=4,5
Сумма(D2)+Тх+ Тy 51,5+28+4,5
Rэмп= 1 — 6———————= 1 – 6—————————=
N(N2-1) 10(10*10 – 1)
84 504
=1- 6 ———— =1 — ———-=1 – 0,50909= 0,4909
990 990
В специальной таблице находим значение критического значения коэффициента ранговой корреляции для выборки из 10 человек и для уровня значимости 0,05:
Rкр (10)=0,64
Rэмп˂ Rкр (0,49˂0,64)
Следовательно, не существует связи между социально-психологическим климатом в коллективе и степенью истощения сотрудников. Для интерпретации данного результаты (а интерпретировать результаты статистических расчётов в дипломах по психологии очень важно) можно сказать следующее. Возможно, в коллективе сотрудников, где проводилось исследование, существуют социально-психологические или организационные факторы, которые опосредуют влияние климата в коллективе на эмоциональное истощение сотрудников. В связи с этим прямая взаимосвязь между этими показателями нивелируется.
Возможно, в коллективе сотрудников, где проводилось исследование, существуют социально-психологические или организационные факторы, которые опосредуют влияние климата в коллективе на эмоциональное истощение сотрудников. В связи с этим прямая взаимосвязь между этими показателями нивелируется.
Анализ результатов расчета коэффициентов ранговой корреляции Спирмена
Если коэффициент ранговой корреляции Спирмена вычисляется с помощью статистической программы, то она сама выделяет статистически значимые корреляции при заданном уровне статистической значимости (0,05 или 0,01).
Если расчёт коэффициента ранговой корреляции Спирмена проводится вручную, то после получения эмпирического значения его нужно сравнить с критическим. Критические значения коэффициентов ранговой корреляции Спирмена приводятся в специальных таблицах для разного объема выборки и уровня статистической значимости.
Далее нужно сравнить эмпирический и критический коэффициенты:
- если значение эмпирического коэффициента ранговой корреляции больше или равно критическому, то делается вывод о существовании статистически значимой корреляционной связи между показателями;
- если значение эмпирического коэффициента ранговой корреляции меньше (как в приведенном выше примере) критического, следовательно, статистически значимой корреляционной связи между показателями нет.

Несмотря на различные алгоритмы расчета корреляций Пирсона и Спирмена логика их анализа и интерпретации одинакова.
Различия коэффициентов корреляций Пирсона и Спирмена
На защите дипломных работ по психологии студента могут спросить о причинах, по которым он выбрал тот или иной тип коэффициента корреляции. То есть, важно понимать, чем принципиально различаются коэффициенты корреляции Пирсона и Спирмена.
Не вдаваясь в математические тонкости, можно сказать следующее:
- Для корреляций Пирсона данные должны быть распределены нормально, или выборка должна быть достаточно большой. Для корреляций Спирмена данные могут быть любыми.
- Корреляции Пирсона дают более точный результат о взаимосвязях показателей, чем корреляции Спирмена. В то же время коэффициент Пирсона более чувствителен к случайным выбросам показателей. Например, у всех испытуемых показатели тревожности находятся в диапазоне от 5 до 15, а у одного – 25 баллов.
 Испытуемый мог отвечать наобум, что привело к такому показателю и при расчёте по Пирсону это существенно исказит результат. В то же время на расчет коэффициента Спирмена такого рода выбросы не оказывают заметного влияния.
Испытуемый мог отвечать наобум, что привело к такому показателю и при расчёте по Пирсону это существенно исказит результат. В то же время на расчет коэффициента Спирмена такого рода выбросы не оказывают заметного влияния.
Таким образом, в курсовых, дипломных и магистерских работах по психологии для анализа взаимосвязей между показателями лучше использовать коэффициенты ранговой корреляции Спирмена.
Надеюсь, эта статья поможет вам написать работу по психологии самостоятельно. Если понадобится помощь, обращайтесь (все виды работ по психологии; статистические расчеты). Заказать
Коэффициент ранговой корреляции Кендалла. Решение задач и контрольных работ по статистике онлайн
Краткая теория
Коэффициент корреляции Кендалла
используется в случае, когда переменные представлены двумя порядковыми шкалами
при условии, что связанные ранги отсутствуют. Вычисление коэффициента Кендалла связано с подсчетом числа совпадений и инверсий.
Этот коэффициент изменяется в пределах и рассчитывается по формуле:
Для расчета все единицы ранжируются по признаку ; по ряду другого признака подсчитывается для каждого ранга число последующих рангов, превышающий данный (их обозначим через ), и число последующих рангов ниже данного (их обозначим через ).
Можно показать, что
и коэффициент ранговой корреляции Кендалла можно записать как
Для того, чтобы при уровне значимости , проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Кендалла при конкурирующей гипотезе , надо вычислить критическую точку:
где – объем выборки; – критическая точка двусторонней критической области, которую находят по таблице функции Лапласа по равенству
Если
– нет
оснований отвергнуть нулевую гипотезу. Ранговая корреляционная связь между
признаками незначимая.
Ранговая корреляционная связь между
признаками незначимая.
Если – нулевую гипотезу отвергают. Между признаками существует значимая ранговая корреляционная связь.
Пример решения задачи
При приеме на работу семи кандидатам на вакантные должности было предложено два теста. Результаты тестирования (в баллах) приведены в таблице:
| Тест | Кандидат | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 31 | 82 | 25 | 26 | 53 | 30 | 29 |
| 2 | 21 | 55 | 8 | 27 | 32 | 42 | 26 |
Вычислить
ранговый коэффициент корреляции Кендалла между
результатами тестирования по двум тестам и на уровне
оценить его значимость.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Вычислим коэффициент Кендалла. Ранги факторного признака располагаются строго в порядке возрастания и параллельно записываются соответствующие им ранги результативного признака . Для каждого ранга из числа следующих за ним рангов подсчитывается количество больших него по величине рангов (заносится в столбец ) и число рангов, меньших по значению (заносится в столбец ).
Расчетная вспомогательная таблица
| 1 | 1 | 6 | 0 |
| 2 | 4 | 3 | 2 |
| 3 | 3 | 3 | 1 |
| 4 | 6 | 1 | 2 |
| 5 | 2 | 2 | 0 |
| 6 | 5 | 1 | 0 |
| 7 | 7 | 0 | 0 |
| Сумма | 16 | 5 |
Искомый коэффициент корреляции Кендалла:
Вычислим критическую точку:
-коэффициент корреляции незначим
Вывод к задаче
Таким
образом взаимосвязь между результатами тестирования по
двум тестам является достаточно слабой.
Корреляционный анализ · Loginom Help
| Описание Обработчик на основании вычисляемых коэффициентов корреляции выявляет взаимосвязь между рядами данных входного набора. Применяется для оценки предполагаемой зависимости факторов. Пример: Проведем корреляционный анализ на основе небольшой таблицы, содержащей данные о количестве продаж четырех видов товаров по датам. Исходная таблица:
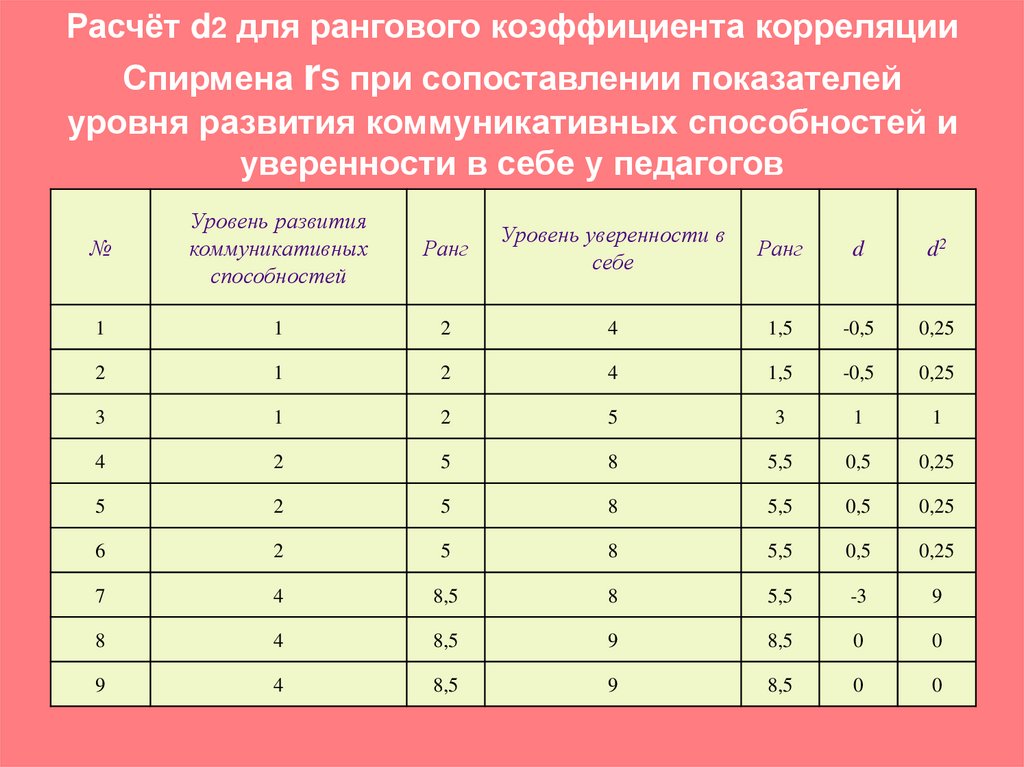
Определим корреляцию товара «Спагетти» с остальными товарами на основе коэффициентов Пирсона (в мастере настройки обработчика поле «Спагетти» отметим в «Наборе 1», а остальные товары — в «Наборе 2»). Выходная таблица:
Как видно из таблицы, ряд продаж для товара «Томатная паста» имеет очень большую положительную корреляцию, а товара «Макароны» — отрицательную.
Включает список флагов, позволяющих выбрать коэффициенты для оценки корреляции:
В таблице необходимо выбрать ряды для анализа взаимосвязи. Для каждого поля из «Набора 1», отмеченного флагом, будут вычислены коэффициенты корреляции с полями, отмеченными флагами в «Наборе 2». |
Расчет парной корреляции и корреляции по Спирмену
|
|
|
|||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Калькулятор коэффициента корреляции — коэффициенты корреляции r Пирсона, r Спирмена и тау Кендалла
Используйте этот калькулятор для оценки коэффициента корреляции любых двух наборов данных. Инструмент может вычислить коэффициент корреляции Pearson r , коэффициент ранговой корреляции Spearman ( r s ), коэффициент ранговой корреляции Kendall ( τ ) и взвешенный коэффициент корреляции Pearson . две случайные величины. Он также вычисляет p-значения , значения z и доверительные интервалы , а также уравнение регрессии наименьших квадратов.
Быстрая навигация:
- Что такое коэффициент корреляции?
- Использование калькулятора коэффициента корреляции
- Коэффициент Пирсона, коэффициент Спирмена и коэффициент Кендалла
- Уравнения коэффициента корреляции
- Формула коэффициента корреляции Пирсона
- Формула ранговой корреляции Спирмена
- Формула тау Кендалла
- Взвешенный коэффициент корреляции
Явление, измеряемое коэффициентом корреляции, представляет собой статистическую корреляцию . Мы говорим, что две случайные величины или двумерные данные коррелированы, если между ними существует какая-то форма количественной связи, какая-то статистическая взаимосвязь. Тривиальным примером может быть построение графика изменения средней дневной температуры и потребления мороженого или интенсивности облачности и осадков в данном регионе. Мы заметим, что две переменные имеют тенденцию изменяться вместе до такой степени, что предполагает некоторую зависимость между ними. Зависимость может быть связана с прямой причинностью, косвенной причинностью или может быть полностью ложной.
Мы заметим, что две переменные имеют тенденцию изменяться вместе до такой степени, что предполагает некоторую зависимость между ними. Зависимость может быть связана с прямой причинностью, косвенной причинностью или может быть полностью ложной.
Коэффициент корреляции , рассчитанный для двух переменных, X и Y, является мерой степени изменения зависимой переменной (Y) при изменении независимой переменной (X). Он количественно определяет как силу, так и направление отношений. Положительный коэффициент корреляции отражает прямую связь между переменными, а отрицательный – обратную (когда X больше, Y меньше и наоборот). Коэффициент, равный нулю, означает полное отсутствие статистической связи (ортогональность), тогда как коэффициент, равный единице (или минус единице), предполагает идеальную корреляцию (X и Y изменяются в унисон).
Таким образом, мы можем различать три основных типа корреляции:
- Нет корреляции — коэффициент ровно 0.

- Положительная корреляция — коэффициент от 0 до 1
- Отрицательная корреляция — коэффициент находится в диапазоне от -1 до 0
Ниже показан пример отрицательной корреляции с соответствующим коэффициентом корреляции Пирсона (R).
Существуют различные типы коэффициентов, количественно определяющие различные типы корреляций с точки зрения того, как переменные соотносятся друг с другом — линейная/нелинейная, функциональная/нефункциональная и т. д. (см. ниже коэффициент Пирсона, Спирмена и Кендалла). Как и любой другой статистический показатель, коэффициент корреляции является всего лишь оценкой и имеет присущую ему неопределенность. Показатель Z, p-значение и доверительные интервалы можно использовать для количественной оценки неопределенности любого коэффициента корреляции. Наш калькулятор коэффициента корреляции поддерживает три самых популярных коэффициента и оценки неопределенности для всех из них.
Использование калькулятора коэффициента корреляции Чтобы использовать этот калькулятор коэффициента корреляции, сначала введите данные, которые вы хотите проанализировать: один столбец для каждой переменной, X и Y. При желании вы можете ввести веса пар в третий столбец, и в этом случае они будут применены к значениям, в результате чего получится взвешенный коэффициент корреляции (применяется только к коэффициенту Пирсона). Столбцы разделяются пробелами, табуляцией или запятыми, поэтому копирование и вставка из Excel или другой электронной таблицы должно работать нормально. Все столбцы должны иметь одинаковое количество значений.
При желании вы можете ввести веса пар в третий столбец, и в этом случае они будут применены к значениям, в результате чего получится взвешенный коэффициент корреляции (применяется только к коэффициенту Пирсона). Столбцы разделяются пробелами, табуляцией или запятыми, поэтому копирование и вставка из Excel или другой электронной таблицы должно работать нормально. Все столбцы должны иметь одинаковое количество значений.
Затем вам нужно выбрать тип коэффициента для расчета. Калькулятор поддерживает следующие коэффициенты:
- Коэффициент корреляции Пирсона (r)
- Коэффициент корреляции Спирмена (r s )
- Коэффициент корреляции Кендалла (τ)
Соответствующий коэффициент будет зависеть от типа ваших данных и типа соответствия, которое, как считается, лежит в основе предполагаемой зависимости. Этот шаг имеет решающее значение для получения правильных выводов о наличии или отсутствии корреляции, а также о ее силе. Если вам нужно руководство по этому поводу, сравнение трех коэффициентов корреляции, которые поддерживает этот калькулятор, можно найти ниже, и оно должно быть очень полезным.
Если вам нужно руководство по этому поводу, сравнение трех коэффициентов корреляции, которые поддерживает этот калькулятор, можно найти ниже, и оно должно быть очень полезным.
Наконец, вы можете изменить доверительный уровень 95% по умолчанию для вычисленных доверительных интервалов. Значения p и доверительные интервалы для коэффициентов Пирсона и Спирмена рассчитываются с использованием преобразования Фишера и выполняются при условии независимости наблюдений. То же предположение относится к оценкам, связанным с коэффициентом ранговой корреляции Кендалла.
Калькулятор корреляции коэффициентов выдаст выбранный коэффициент и размер выборки. Он также выводит z-показатель, p-значение и доверительные интервалы (двусторонние и односторонние границы) для всех значений, кроме взвешенного коэффициента Пирсона. Выходные данные также включают уравнение регрессии по методу наименьших квадратов (линию регрессии) в форме y = m · x + b, где m — наклон, а b — точка пересечения линии регрессии с координатой y.
Выбор правильного коэффициента корреляции имеет важное значение для получения правильных выводов. Нарушение допущений, лежащих в основе статистической модели, приводит к бессмысленным (или вводящим в заблуждение) числам. Выбор неправильного коэффициента также может означать, что вы не сможете получить истинную корреляцию, например. если вы используете коэффициент Пирона, в то время как отношение нелинейно. Как Арндт и др. сформулируйте это так: «Неправильный выбор может скрыть важные результаты из-за низкой мощности или привести к ложным ассоциациям из-за завышенной частоты ошибок I типа». [5] .
Чтобы помочь вам с выбором, ниже приведена таблица с основными характеристиками и допущениями для трех наиболее часто используемых коэффициентов, а также рекомендации о том, когда какой из них использовать.
| Атрибут/Тест | Пирсона r | Спирмена r | Тау Кендалла |
|---|---|---|---|
| Поддерживаемые типы данных | Интервал, соотношение | Порядковый, интервальный, коэффициент | Порядковый, интервальный, коэффициент |
| Предположения об однородности | Гомоскедастичность | Нет | Нет |
| Предположения о зависимости | Линейная зависимость | Монотонная зависимость | Монотонная зависимость |
| Восприимчивость к выбросам (надежность) | Чувствительный | Прочный | Прочный |
| Предположения для вывода (H 0 для p-значений, охват CI) | Пары выборок являются независимыми и одинаково распределенными (IID) и подчиняются двумерному нормальному распределению | Пары образцов независимы и одинаково распределены (IID) | Пары образцов независимы и одинаково распределены (IID) |
| Вывод, если коэффициент равен 0: | X и Y — линейно некоррелированные случайные величины* | X и Y — монотонно некоррелированные случайные величины* | X и Y — монотонно некоррелированные случайные величины* |
| Вывод, если коэффициент равен 1 или -1 | X и Y являются совершенно линейно зависимыми случайными величинами | X и Y совершенно монотонно зависимые случайные величины | X и Y совершенно монотонно зависимые случайные величины |
* Обратите внимание, что отсутствие корреляции не требует независимости, тогда как наличие корреляции означает зависимость.
Поскольку часто ошибочно полагают, что r Пирсона требует, чтобы и X, и Y были нормально распределены , следует повторить, что это не так. Как отмечает Spearman [2] , «… метод «моментов произведения» действителен, независимо от того, следует ли распределение нормальному закону частоты, если« регрессия »линейна». Таким образом, ни один коэффициент не зависит от предположений о распределении для своей достоверности.
Нормальность является предположением только для расчета соответствующих статистических данных, и если они представляют интерес, вы можете использовать наш калькулятор проверки нормальности для проверки отклонений. Имейте в виду, что высокие значения p в тестах на нормальность могут быть связаны только с небольшим размером выборки и недостаточной чувствительностью тестов.
Как видите, сделать правильный выбор не так уж и просто, ведь для этого нужно знать свои данные и понимать потенциальную зависимость. Убедитесь, что вы понимаете последствия выбора одного метода вместо другого.
Калькулятор коэффициента корреляции поддерживает несколько различных коэффициентов. Уравнения, используемые для расчета каждого из них, объясняются здесь более подробно.
Формула коэффициента корреляции ПирсонаФормула для вычисления Пирсона ρ (коэффициент корреляции между продуктом и моментом населения, ро) выглядит следующим образом:0034 — это ковариация переменных X и Y, а σ X (сигма X) — стандартное отклонение совокупности X, а σ Y Y. Математически это определяется как качество наименьших квадратов соответствие исходным данным. Это применимо, когда мы знаем среднее значение генеральной совокупности и стандартные отклонения, что редко бывает на практике. Следовательно, в большинстве случаев применимой формулой является уравнение для коэффициента корреляции выборки Пирсона r.
Формула для Пирсона r равна [1] :
, что по существу такое же, как и для ρ Пирсона, но вместо средних значений генеральной совокупности и стандартных отклонений мы имеем выборочные средние значения и стандартные отклонения. Числитель представляет выборочную ковариацию cov(x,y), а знаменатель представляет собой произведение выборочных стандартных отклонений σ x и σ y . Большой оператор Σ — это известный оператор суммирования. Это уравнение позволяет легко понять, почему 9Корреляцию 0033 можно определить как стандартизированную форму ковариации .
Числитель представляет выборочную ковариацию cov(x,y), а знаменатель представляет собой произведение выборочных стандартных отклонений σ x и σ y . Большой оператор Σ — это известный оператор суммирования. Это уравнение позволяет легко понять, почему 9Корреляцию 0033 можно определить как стандартизированную форму ковариации .
The formula for computing Spearman’s r s (Spearman’s rank correlation coefficient) is as follows [2] :
where rg X and rg Y обозначают ранговые преобразованные значения X и Y. Таким образом, коэффициент корреляции Спирмена r s — это просто коэффициент корреляции Пирсона, вычисленный с использованием ранговых значений вместо необработанных значений двух переменных, поэтому он может выявить нелинейные, а также линейные отношения между X и Y, если Y является монотонная функция X. Другими словами, Спирмен r s оценивает, насколько хорошо произвольная монотонная функция может описать связь между двумя переменными, не налагая никаких предположений на частотное распределение переменных [4] .
Другими словами, Спирмен r s оценивает, насколько хорошо произвольная монотонная функция может описать связь между двумя переменными, не налагая никаких предположений на частотное распределение переменных [4] .
Формула для вычисления коэффициента ранговой корреляции Кендалла τ (тау), часто называемого коэффициентом τ Кендалла или просто τ Кендалла, выглядит следующим образом: Где n — количество пар, а sgn() — стандартная знаковая функция. Коэффициент, рассчитанный с помощью приведенного выше уравнения, известен как (τ A ) и работает только при отсутствии связей в данных. Калькулятор использует слегка модифицированное уравнение (τ B ), который правильно учитывает связи в наборах данных [6] .
Тау Кендалла количественно определяет сходство порядков ранжированных преобразованных данных и может быть интерпретировано как вероятность того, что по мере увеличения X Y будет увеличиваться с перемасштабированием от -1 до 1. Этот коэффициент не был так популярен в недалеком прошлом, в основном из-за его запретительной вычислительная сложность, но простота интерпретации и другие ее желательные качества — высокая мощность с хорошей надежностью в сочетании с интуитивной интерпретацией как вероятность того, что любая пара наблюдений будет иметь одинаковый порядок по обеим переменным, масштабированным от -1 до 1 [5] — сделайте его главным кандидатом на многие исследовательские вопросы.
Этот коэффициент не был так популярен в недалеком прошлом, в основном из-за его запретительной вычислительная сложность, но простота интерпретации и другие ее желательные качества — высокая мощность с хорошей надежностью в сочетании с интуитивной интерпретацией как вероятность того, что любая пара наблюдений будет иметь одинаковый порядок по обеим переменным, масштабированным от -1 до 1 [5] — сделайте его главным кандидатом на многие исследовательские вопросы.
Формула для расчета взвешенного коэффициента корреляции Пирсона выглядит следующим образом:
Уравнение состоит из взвешенной ковариации x и y, деленной на произведение взвешенных стандартных отклонений x и y . Взвешенная ковариация x и y при заданном векторе весов w может быть вычислена как:
, где m x и m y – взвешенные средние значения x и y, вычисленные обычным способом.
Используя те же обозначения, формула для взвешенного стандартного отклонения выглядит следующим образом:
Она вычисляется эквивалентно для y.
Практический примерКоэффициент корреляции имеет широкое применение в различных научных и прикладных дисциплинах, таких как биология, генетика, эпидемиология, психология (психометрия), психиатрия, финансы, торговля акциями, маркетинг, менеджмент и многие другие. В простой линейной регрессии, аппроксимируемой методом наименьших квадратов, коэффициент детерминации равен просто r в квадрате Пирсона (r 2 ).
Известный случай, который мы можем рассмотреть как практическую проблему, — это связь курения с различными заболеваниями и сокращением продолжительности жизни. Наблюдая за тенденциями в отношении здоровья населения, исследователи заметили потенциальную связь между курением и различными заболеваниями, включая многие виды рака, а также смертностью от всех причин. Как выглядит одно из таких соотношений? Допустим, мы возьмем репрезентативную выборку курящих мужчин 50 лет и старше и измерим как количество сигарет, которые они выкуривают в день, так и возраст, в котором они умерли. Количество сигарет — это наша независимая переменная X, тогда как продолжительность жизни в годах — это наша зависимая переменная Y.
Количество сигарет — это наша независимая переменная X, тогда как продолжительность жизни в годах — это наша зависимая переменная Y.
| Metric / Case | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сигарет в день | 25 | 46 | 17 | 26 | 5 | 23 | 24 | 35 | 29 | 4 | 13 | 8 | 6 | 23 | 19 |
| Долговечность | 60 | 53 | 86 | 77 | 78 | 77 | 65 | 72 | 58 | 91 | 66 | 84 | 73 | 78 | 75 |
Подставив числа в калькулятор и выбрав коэффициент корреляции Кендалла, мы можем количественно определить взаимосвязь между курением и долголетием. В этом случае коэффициент равен -0,541, что означает, что существует умеренная обратная связь между X и Y. Чем больше количество сигарет, тем ниже продолжительность жизни — зависимая от дозы зависимость. Полученное значение p, равное 0,0022, показывает, что наблюдение такой отрицательной корреляции было бы крайне маловероятным, если бы вместо этого не было никакой положительной корреляции.
В этом случае коэффициент равен -0,541, что означает, что существует умеренная обратная связь между X и Y. Чем больше количество сигарет, тем ниже продолжительность жизни — зависимая от дозы зависимость. Полученное значение p, равное 0,0022, показывает, что наблюдение такой отрицательной корреляции было бы крайне маловероятным, если бы вместо этого не было никакой положительной корреляции.
[1] Пирсон К. (1896) «Математический вклад в теорию эволюции. III. Регрессия, наследственность и панмиксия», Philosophical Transactions A 373: 253–318
2 ] Спирмен К. (1904) «Доказательство и измерение связи между двумя вещами», American Journal of Psychology 15 (1): 72–101; DOI: 10.2307/1412159[3] Кендалл М. (1938) «Новая мера ранговой корреляции», Биометрика 30(1–2):81–89; DOI:10.1093/biomet/30.1-2.81
[4] Hauke J., Kossowski T. (2011) «Сравнение значений коэффициентов корреляции Пирсона и Спирмена на одних и тех же наборах данных», Quaestiones Geographicae 30(2) :87-93; DOI: 10. 2478/v10117-011-0021-1
2478/v10117-011-0021-1
[5] Arndt et al (1999) «Корреляция и прогнозирование рейтингов психиатрических симптомов — корреляция Спирмена r и тау Кендалла», Journal of Psychiatric Research , 33(2): 97-104; DOI: 10.1016/s0022-3956(98)
[6] Найт В. (1966) «Компьютерный метод расчета тау Кендалла с негруппированными данными», Журнал Американской статистической ассоциации 61 (314): 436–439; DOI:10.2307/2282833
Наши статистические калькуляторы упоминались в научных статьях и статьях, опубликованных в авторитетных научных журналах:
Калькулятор корреляции Спирмена — MathCracker.com
Решатели Статистика
Инструкции: Вы можете использовать этот инструмент Калькулятор корреляции Спирмена для вычисления коэффициента корреляции Спирмена для двух переменных X и Y. Все, что вам нужно сделать, это ввести данные X и Y в формате, разделенном запятыми или пробелами (например: «2, 3, 4). , 5″ или «3 4 5 6 7»).
Все, что вам нужно сделать, это ввести данные X и Y в формате, разделенном запятыми или пробелами (например: «2, 3, 4). , 5″ или «3 4 5 6 7»).
Данные X (разделенные запятыми)
Данные Y (разделенные запятыми)
Имя переменной X (необязательно)
Имя переменной Y (необязательно)
Вычисленный выше коэффициент корреляции соответствует коэффициенту корреляции Спирмена. Требования для его вычисления заключаются в том, что две переменные X и Y измеряются по крайней мере на уровне интервала (что означает, что он не работает с номинальными или порядковыми переменными). 92} }\]
или эквивалентно
\[r_S = \ frac {SS _ {\ тильда X \ тильда Y}} {\ sqrt {SS _ {\ тильда X \ тильда X} \ cdot SS _ {\ тильда Y \ тильда Y} }} \]
Для данных уровня интервала вы должны использовать
Калькулятор коэффициента корреляции Пирсона
вместо. Кроме того, чтобы графически визуализировать данные и лучше понять линейную связь между переменными X и Y, вы можете использовать наш
производитель диаграмм рассеяния
Кроме того, чтобы графически визуализировать данные и лучше понять линейную связь между переменными X и Y, вы можете использовать наш
производитель диаграмм рассеяния
Отчет о ранговой корреляции Спирмена
Как сообщить о корреляции Спирмена? Очень похоже на то, как это сообщается для случая корреляции Пирсона. Обычно вы пишете что-то вроде: «Порядковые переменные X и Y демонстрируют значительную степень линейной связи, \(r_s = 0,894, p < 0,001\)».
Как оценить, является ли корреляция Спирмена значимой?
Наиболее распространенный способ оценить, является ли наблюдаемое значение корреляции Спирмена значимым, — это сравнить его с соответствующим значением. Критические ценности Спирмена
.
Критические ценности Спирмена
.
Базовый пакет статистики Калькулятор коэффициента корреляции Ранговая корреляция Калькулятор ранговой корреляции Корреляция Спирмена Калькулятор корреляции Спирмена Калькулятор корреляции Спирмена Ранговая корреляция Спирмена Решатели статистики
Калькулятор коэффициента корреляции
Калькулятор корреляции и калькулятор ковариации вычисляют корреляцию и проверяют значимость результата.
Информация
Что такое ковариация?
Ковариация проверяет взаимосвязь между двумя переменными.
Диапазон ковариации не ограничен от отрицательной бесконечности до положительной бесконечности. Для независимых переменных ковариация равна нулю .
Положительная ковариация — изменения идут в одном направлении, при увеличении одной переменной обычно увеличивается и вторая переменная, а при уменьшении одной переменной обычно уменьшается и вторая переменная.
Отрицательная ковариация — противоположное направление, при увеличении одной переменной обычно уменьшается вторая переменная, а при уменьшении одной переменной обычно увеличивается вторая переменная.
Как рассчитать ковариацию
Формула ковариации:
Cov(X,Y) = E[(X-E[X])(Y-E[Y])]
Cov(X,Y) = E[XY]-E(X)E[Y]
S XY — the sample covariance between X and Y.
| S XY = | Σ(x i -x̄)(y i -ȳ) |
| n — 1 |
What is correlation ?
Можно сказать, что существует корреляция между двумя переменными или статистическая связь, когда значение одной переменной может хотя бы частично предсказать значение другой переменной.
Корреляция представляет собой стандартизированную ковариацию, диапазон корреляции находится в диапазоне от -1 до 1.
Корреляция игнорирует вопрос о причине и следствии, зависит ли X от Y или Y зависит от X, или обе переменные зависят от третьей переменной Z.
Аналогично к ковариации для независимых переменных корреляция равна нулю .
Положительная корреляция — изменения идут в одном направлении, при увеличении одной переменной обычно увеличивается и вторая переменная, а при уменьшении одной переменной обычно уменьшается и вторая переменная.
Отрицательная корреляция — противоположное направление, при увеличении одной переменной обычно уменьшается вторая переменная, а при уменьшении одной переменной обычно увеличивается вторая переменная.
Идеальная корреляция — Когда вы знаете значение одной переменной, вы можете вычислить точное значение второй переменной. Для совершенной положительной корреляции r = 1, а для совершенной отрицательной корреляции r = -1.
Что такое коэффициент корреляции Пирсона?
Коэффициент корреляции Пирсона — это тип корреляции, который измеряет линейную связь между двумя переменными
Как рассчитать корреляцию Пирсона?
Population Pearson correlation formula
| ρ XY = | E[(X-E[X])(Y-E[Y])] |
| σ X σ Y |
Population Pearson корреляционная формула — с использованием ковариации0763
| R = | σ (x I — x̄) (Y I — ȳ) |
| √ (σ (x I — X̄) 2 999999999999999999999999. — X̄). ȳ) 2 ) |
Sample Pearson correlation formula — using the covariance
| r = | S XY |
| S X S Y |
Assumptions
- Непрерывные переменные — Две переменные являются непрерывными (отношение или интервал).

- Выбросы — Значение выборочной корреляции чувствительно к выбросам. Мы проверяем выбросы на парном уровне, на остатках линейной регрессии,
- Линейность — линейная связь между двумя переменными, корреляция представляет собой размер эффекта линейности. (обычно используемый размер эффекта f 2 получен из R 2 (r и R одинаковы)
- Нормальность — Двумерное нормальное распределение. Вместо проверки двумерной нормальности мы вычисляем линейную регрессию и проверяем нормальность остатков.
- Гомоскедастичность , однородность дисперсии — дисперсия остатков постоянна и не зависит от независимых переменных X i
Тесты
переменные и X и Y имеют двумерное нормальное распределение или размер выборки большой, то вы можете использовать t-критерий.
Когда ρ 0 ≠ 0, выборочное распределение не будет симметричным, поэтому вы не можете использовать t-распределение. В этом случае для преобразования распределения следует использовать преобразование Фишера.
В этом случае для преобразования распределения следует использовать преобразование Фишера.
После использования преобразования выборочное распределение стремится к нормальному распределению.
Что такое ранговый коэффициент корреляции Спирмена?
Коэффициент ранговой корреляции Спирмена — это непараметрическая статистика, которая измеряет монотонную связь между двумя переменными.
Что такое монотонная ассоциация? когда одна переменная увеличивается, обычно увеличивается и вторая переменная, или когда одна переменная увеличивается, обычно вторая переменная уменьшается.
Вы можете использовать ранговую корреляцию Спирмена, когда две переменные не соответствуют предположениям корреляции Пирсона. как в следующих случаях:
- Порядковые дискретные переменные
- Нелинейные данные
- Распределение данных не является двумерным нормальным.
- Данные содержат выбросы
- Данные не соответствуют предположению о гомоскедастичности.
 Дисперсия остатков не постоянна.
Дисперсия остатков не постоянна.
Как рассчитать ранговую корреляцию Спирмена?
Ранжируйте данные отдельно для каждой переменной, а затем вычислите корреляцию Пирсона ранжированных данных.
Наименьшее значение получает 1, второе — 2 и т. д. Даже при обратном ранжировании, когда наибольшее значение равно 1, результатом будет то же значение корреляции.
Связанные данные
Когда данные содержат повторяющиеся значения, каждое значение получает среднее значение рангов. В приведенном ниже примере значение 8 рангов равно 4 и 5, следовательно, оба значения получат средний ранг: (4 + 5)/2 = 4,5 .
Example
Data
| X | Y |
|---|---|
| 7.3 | 7 |
| 8 | 6.6 |
| 5.4 | 5.4 |
| 2.7 | 3.7 |
| 8 | 9.9 |
9. 1 1 |
| X | Y
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|




 Испытуемый мог отвечать наобум, что привело к такому показателю и при расчёте по Пирсону это существенно исказит результат. В то же время на расчет коэффициента Спирмена такого рода выбросы не оказывают заметного влияния.
Испытуемый мог отвечать наобум, что привело к такому показателю и при расчёте по Пирсону это существенно исказит результат. В то же время на расчет коэффициента Спирмена такого рода выбросы не оказывают заметного влияния. 09.17
09.17 Из этого можно сделать вывод, что «Томатная паста» является сопутствующим товаром, а «Макароны» — заместителем товара «Спагетти». Корреляция продаж товара «Кофе» с товаром «Спагетти» является отрицательной, но при этом абсолютное значение корреляции невелико, и, следовательно, можно говорить об отсутствии взаимосвязи между продажами этих товаров.
Из этого можно сделать вывод, что «Томатная паста» является сопутствующим товаром, а «Макароны» — заместителем товара «Спагетти». Корреляция продаж товара «Кофе» с товаром «Спагетти» является отрицательной, но при этом абсолютное значение корреляции невелико, и, следовательно, можно говорить об отсутствии взаимосвязи между продажами этих товаров.
 Следует применять, если необходимо узнать линейную зависимость между двумя процессами или частями процессов, происходящими с некоторым временным лагом.
Следует применять, если необходимо узнать линейную зависимость между двумя процессами или частями процессов, происходящими с некоторым временным лагом. Первые полторы тысяч разложений.
Первые полторы тысяч разложений.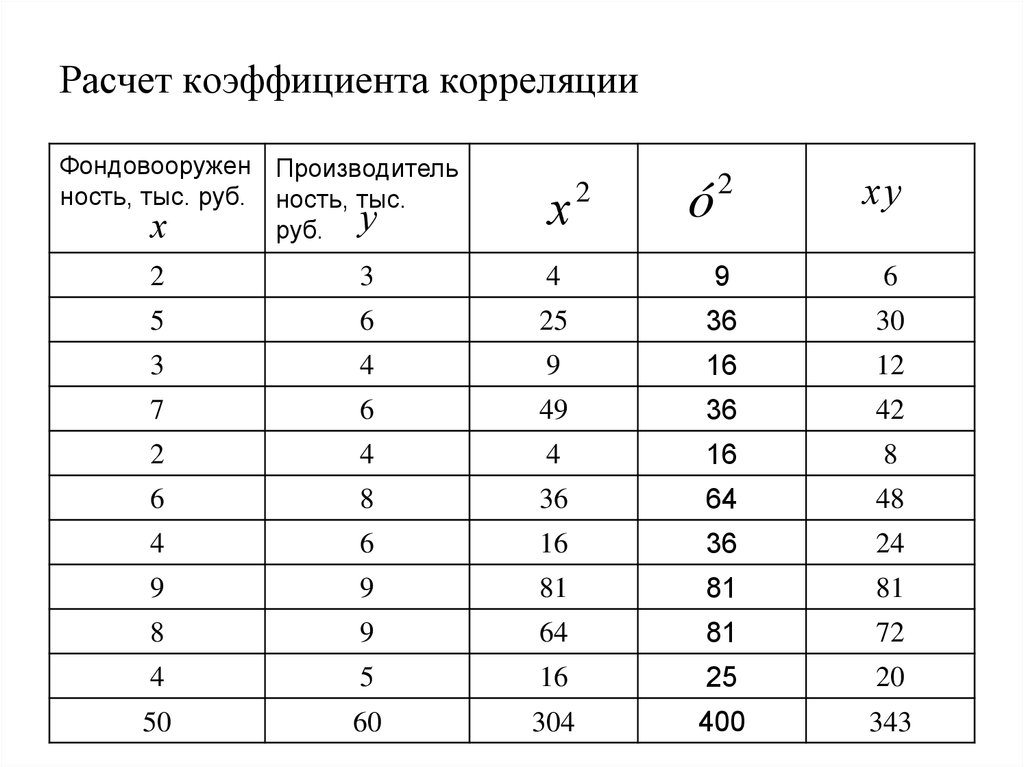 Парная корреляция (Пирсена) характеризует взаимосвязь двух последовательностей xi и yi
Парная корреляция (Пирсена) характеризует взаимосвязь двух последовательностей xi и yi Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн 1.2.1
1.2.1

 net в публикациях используйте:
net в публикациях используйте:  Мы прилагаем разумные усилия для предоставления точной и своевременной информации
и периодически обновлять информацию и программное обеспечение без предварительного уведомления. Мы
не давать никаких гарантий или заявлений
в отношении точности или полноты такой информации (или программного обеспечения), и не предполагает
ответственности или ответственности за ошибки или упущения в содержании этого веб-сайта
сайт или какие-либо программные ошибки в онлайн-приложениях. Вы используете этот веб-сайт НА СВОЙ СОБСТВЕННЫЙ РИСК. Ни при каких обстоятельствах и
ни по какой правовой теории мы не несем ответственности перед вами или любым другим
лицо для любого прямого, косвенного, специального, случайного, образцового или
косвенный ущерб, возникающий в результате вашего доступа к этому веб-сайту или его использования.
Мы прилагаем разумные усилия для предоставления точной и своевременной информации
и периодически обновлять информацию и программное обеспечение без предварительного уведомления. Мы
не давать никаких гарантий или заявлений
в отношении точности или полноты такой информации (или программного обеспечения), и не предполагает
ответственности или ответственности за ошибки или упущения в содержании этого веб-сайта
сайт или какие-либо программные ошибки в онлайн-приложениях. Вы используете этот веб-сайт НА СВОЙ СОБСТВЕННЫЙ РИСК. Ни при каких обстоятельствах и
ни по какой правовой теории мы не несем ответственности перед вами или любым другим
лицо для любого прямого, косвенного, специального, случайного, образцового или
косвенный ущерб, возникающий в результате вашего доступа к этому веб-сайту или его использования. net Дом
net Дом

 Дисперсия остатков не постоянна.
Дисперсия остатков не постоянна.


 Введите значения $X$, разделенные запятыми
Введите значения $X$, разделенные запятыми
 Поскольку значение коэффициента корреляции положительное, существует сильная положительная связь между оценками судьи А и судьями Б.
Поскольку значение коэффициента корреляции положительное, существует сильная положительная связь между оценками судьи А и судьями Б.