|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного… Динамика и детерминанты показателей газоанализа юных спортсменов в восстановительном периоде после лабораторных нагрузок до отказа… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Интересное: Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются… Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов. Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 19Следующая ⇒ Задачей сферической тригонометрии является решение сферического треугольника, то есть вычисление его неизвестных элементов через заданные (известные). Известно, что для нахождения какого-либо угла или стороны треугольника необходимо, чтобы три любых других его элемента были известны (заданы). Рассмотрим (без вывода) четыре основные теоремы сферической тригонометрии, устанавливающие необходимую аналитическую зависимость между элементами сферического треугольника. I. Формула косинуса стороны. Эта формула связывает между собой все три стороны и один из углов сферического треугольника. Для любого сочетания таких четырех элементов установлена зависимость, что … «… косинус стороны сферического треугольника равняется произведению косинусов двух других сторон плюс произведение синусов тех же сторон на косинус угла между ними…».
Рис. 2.2. Сферический треугольник
Применительно к стороне а (рис. 2.2) сферического треугольника АВМ, руководствуясь теоремой косинуса стороны, можем записать: cos a = cos b · cos m + sin b · sin m · cos A Для сторон b и m зависимость между элементами треугольника выразится формулами:
II. Формула синусов связывает между собой противолежащие элементы сферического треугольника → углы и стороны. «… во всяком сферическом треугольнике синусы сторон относятся как синусы противолежащих углов…». Для сферического треугольника АВМ (рис. 2.2) можем записать соотношения:
Формула синусов применяется для вычисления одного из элементов, входящих в записанные равенства, если известны три других элемента. III. Формула котангенсов связывает между собой четыре элемента сферического треугольника, лежащие рядом. «… котангенс крайнего угла, умноженный на синус среднего, равняется произведению котангенса крайней стороны на синус средней без произведения косинусов средних элементов…». Если в сферическом треугольнике АВМ (рис. ctg A · sin B = ctg a · sin m — cos B · cos m Всего для треугольника можно написать шесть таких соотношений, а именно:
Формула котангенсов применяется для вычисления стороны или угла сферического треугольника, если они лежат рядом с тремя заданными элементами. IV. Формула косинуса угла связывает между собой три угла и одну из сторон сферического треугольника. «… косинус угла сферического треугольника равняется произведению синусов двух других углов на косинус стороны между ними без произведения косинусов тех же углов…». Для каждого из углов сферического треугольника АВМ можно написать формулы:
Эти формулы удобны при вычислении угла по двум другим углам и стороне между ними, а также служат для нахождения стороны по трем заданным углам.
Рис. 2.3. Прямоугольный сферический треугольник
Решение прямоугольных треугольников проще, чем косоугольных, так как один из их элементов (угол 90°) всегда известен и для решения треугольника достаточно знать только два элемента. То же самое относится и к четвертным треугольникам, в которых один из элементов (сторона 90°) всегда известен. Если в сферическом треугольнике АВМ (рис. 2.3) заданы угол В = 90°, катет а и угол М, то для вычисления неизвестного угла А можно применить формулу косинуса угла (6.4) → cos A = sin B · sin M · cos a — cos B · cos M. Если теперь заменить все функции угла В = 90° их значениями (sin B = 1, cos B = 0), то получим cos A = sin M · cos a (2.
2.3. Вычисление горизонтных координат светил по таблицам логарифмических функций мореходных таблиц «МТ-75» При вычислении счислимой высоты (hС) и азимута (АС) светила по формулам сферической тригонометрии, как по натуральным значениям тригонометрических функций, так и по логарифмам, наиболее удобными являются формулы:
В формуле знак «~» означает, что при φС и δ одноименных из большей величины вычитается меньшая, а при разноименных → величины φС и δ складываются. Значения , и табулированы так, что при вычислениях не нужно делить аргументы ZC, φС~δ и tM, а значения тригонометрических функций возводить в квадрат, → все эти действия выполнены в таблицах 5 а (5б) «МТ-75» (в «МТ-2000» таких таблиц нет). Производить исследование формулы на знаки тригонометрических функций не требуется, так как оба члена ее правой части всегда положительны. Методику вычисления горизонтных координат светил с помощью «МТ-75» рассмотрим на примере решения конкретной задачи. Задача: Вычислить значения счислимых высоты (hC) и азимута (АС) светила, если: φС = 43°20,6′N; δ = 17°36,7′N; tM = 17°12,4′W. Решение:
⇐ Предыдущая12345678910Следующая ⇒ Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой. |
Все страницы — Юнионпедия
Все страницы — ЮнионпедияНовый! Скачать Юнионпедия на вашем Android™ устройстве!
Установить
Более быстрый доступ, чем браузер!
Все страницы · Предыдущая (Степени свободы (механика)) · Следующий (Счёт по Крепелину)
Из:
| Сферические теоремы косинусов | Сферические функции | Сферические гармоники |
| Сферические координаты | Сферическое движение | Сферическое зеркало |
| Сферихты | Сферикон | Сфермион |
| Сфермионы | Сферосомы | Сферосепаловые |
| Сферофиза | Сферофиза солонцовая | Сферофорус |
| Сфероцилиндрический шлем | Сфероид | Сфероид Маклорена |
| Сферокобальтит | Сферолит | Сферолиты |
| Сферолобиум | Сферомак | Сфероптерис высокий |
| Сферопласт | Сфейр | Сфейр Насрулла Бутрос |
| Сфейр Насраллах-Пьер | Сфейр, Насрулла | Сфейр, Насрулла Бутрос |
| Сфейр, Насраллах-Пьер | Сфекс | Сфекс жёлтокрылый |
| Сфекс желтоватый | Сфекс желтокрылый | Сфексы |
| Сфекодина хвостатая | Сфекомирма Фрея | Сфен |
| Сфенакодон | Сфенакодонты | Сфендони (эсминец) |
| Сфениты | Сфенические числа | Сфеническое число |
| Сфенкел | Сфено | Сфенотома |
| Сфенозух | Сфенозухи | Сфенозухии |
| Сфеноидит | Сфеноклея | Сфеноклея цейлонская |
| Сфеноклеевые | Сфенебея | Сфенек, Эдвиж |
| Сфенел | Сфенел (сын Капанея) | Сфенел (сын Персея) |
| Сфенел Аргосский | Сцяг працы | Сцёке, Ларс |
| Сцайпен | Сциталина | Сциталиновые |
| Сцифифора | Сцифифора гидрофилаксовая | Сцифоидные |
| Сцифоидные медузы | Сцифомедузы | Сциртоидные |
| Сцирпоидес | Сцирпоидес обыкновенный | Сциариды |
| Сциадопитис | Сциадопитис мутовчатый | Сциадопитисовые |
| Сциапод | Сцибор из Сцибожице | Сцибор-Рыльский |
| Сцибор-Рыльский Александр | Сцибор-Рыльский, Александр | Сцибор-Мархоцкий |
| Сцибор-Мархоцкий, Игнаций | Сциборский | Сциборский Николай Орестович |
Сциборский М.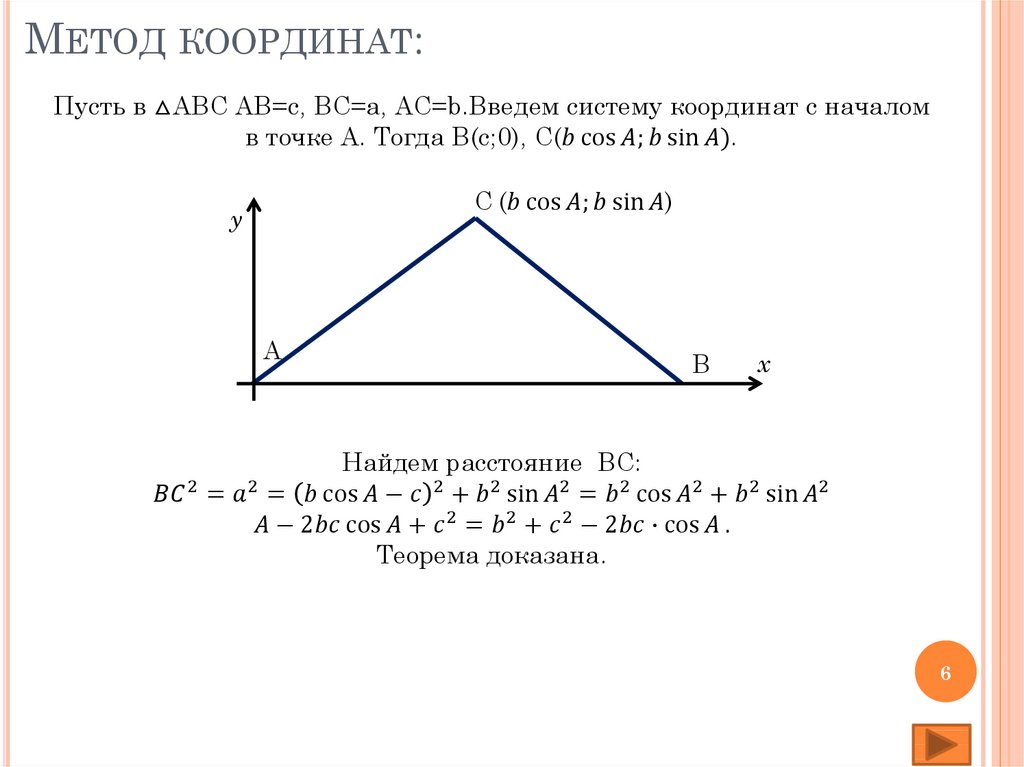 | Сциборский Микола | Сциборский, Николай |
| Сциборский, Николай Орестович | Сциборский, Микола | Сцидмениды |
| Сцилард | Сцилард (лунный кратер) | Сцилард Лео |
| Сцилард, Лео | Сцилакозух | Сцилакозавр |
| Сциллы | Сцилла | Сцилла (значения) |
| Сцилла (мифология) | Сцилла и Харибды | Сцилла и Харибда |
| Сцилла испанская | Сциллард, Лео | Сцилли |
| Сцимитар | Сцимнодалатия Шервуда | Сцимнодалатии |
| Сцинтиграфия | Сцинтиграфия скелета | Сцинтиграфия желудка |
| Сцинтиллятор | Сцинтилляторы | Сцинтилляция |
| Сцинтилляционный счётчик | Сцинтилляционный счетчик | Сцинтилляционный детектор |
| Сцинава | Сцинава (станция) | Сцинава (гмина) |
| Сцинава (значения) | Сциндапсус | Сциндия |
| Сцинк | Сцинк Святого Луки | Сцинк Телфэра |
| Сцинки | Сцинковый геккон | Сцинковый геккон Пржевальского |
| Сцинковые | Сцинковые гекконы | Сцинкообразные |
| Сцинография | Сцио, Ивонн | Сциофит |
| Сциофиты | Сциогелиофиты | Сциоли, Даниэль |
| Сциоподы | Сципио дель Кампо | Сципио дель Кампо, Юзеф |
| Сципио дель Кампо, Михаил | Сципио дель Кампо, Михал | Сципион |
| Сципион Коркул | Сципион Африканский | Сципион Африканский Старший |
| Сципион Африканский младший | Сципион Африканский Младший | Сципион Азиатский |
| Сципион Аммирато | Сципион Сигеле | Сципион Эмилиан |
| Сципион Эмилиан Африканский | Сципион де Дрё-Брезе | Сципион де Дре-Брезе |
| Сципион дель Кампо, Михаил | Сципион дель Ферро | Сципион Брейслак |
| Сципион Боргезе | Сципион Виктор де Шамбона | Сципион Дель Ферро |
| Сципион, Рива-Роччи | Сципионы | Сципионикс |
| Сципионе Рива-Роччи | Сципионе Ребиба | Сципионе Маффеи |
| Сциентист | Сциентизм | Сциентология |
| Сциены | Сцорпроба | Сцеёвице |
| Сцевка | Сцевола | Сцевола (значения) |
| Сцевола Квинт Цервидий | Сцевола Квинт Муций | Сцевола Понтифик |
| Сцевола Авгур | Сцевола Юрисконсульт | Сцевола Гай Муций |
| Сцевола, Квинт Цервидий | Сцевола, Муций | Сцегенный |
| Сцегенный, Пётр | Сцегенный, Петр | Сцелифрон Шестакова |
| Сцелидозавр | Сцелидозавриды | Сцены сексуального характера |
| Сцены сексуального характера (фильм) | Сцены у моря | Сцены у моря (фильм) |
| Сцены в магазине | Сцены в магазине (фильм) | Сцены из супружеской жизни |
| Сцены из супружеской жизни (фильм) | Сцены из Киото и его пригородов | Сцены из жизни святого Зиновия |
| Сцены из жизни Карла Борромея | Сцена | Сцена «Миниатюра» |
| Сцена (сериал) | Сцена (значения) | Сцена (песня) |
| Сцена «Миниатюра» | Сцена с кузнецами | Сцена Палм Дезерт |
| Сцена Палм-Дезерт | Сцена в саду Раундхэй | Сцена в саду Роундхэй |
| Сцена в Гайд-парке | Сцена из домашней жизни русских царей | Сцена на Северо-Западе (Портрет Джона Генри Лефроя) |
| Сцена при дворе Кристиана VII | Сцена-молот | Сцена-Молот |
| Сценарист | Сценаристы | Сценаристка |
| Сценарии | Сценарии (метод) | Сценарии развития Восточной Сибири и российского Дальнего Востока |
| Сценарии командной строки | Сценарий | Сценарий (фильм) |
| Сценарий (в психологии) | Сценарий (значения) | Сценарий (кинематограф) |
| Сценарий (компьютеры) | Сценарий (психология) | Сценарий (программирование) |
| Сценарий фильма | Сценарий использования | Сценарий катастрофы |
| Сценарий командной строки | Сценарный язык | Сценарный язык программирования |
| Сценарный кадр | Сценарное программирование | Сценарное планирование |
| Сценическая речь | Сценическая магия | Сценический украинский танец |
| Сценический танец | Сценический характер | Сценический дебют |
| Сценический дебют (фильм) | Сценический монитор | Сценический образ |
| Сценический псевдоним | Сценические украинские танцы | Сценическое фехтование |
| Сценическое расстройство личности | Сценическое имя | Сценка |
| Сценограф | Сценография | Сцепщик |
| Сцепинский Юрий Евгеньевич | Сцепка | Сцепка (филателия) |
| Сцепка Шарфенберга | Сцеплянки | Сцепление |
| Сцепление (компьютер) | Сцепление (механика) | Сцепление (программирование) |
| Сцепление генов | Сцепленное с полом Наследование | Сцепленное с полом наследование |
| Сцепленное наследование | Сцепленное наследование генов | Сцепленное наследование признаков |
| Сцепные колёса | Сцепные оси | Сцепная масса |
| Сцепная ось | Сцепной вес | Сцепной вес локомотива |
| Сцепное | Сцепное (Липецкая область) | Сцепное устройство |
| Счьотник | Счьотник, Атанасие | Счёт |
| Счёт (финансы) | Счёт текущих операций | Счёт Омера |
| Счёт времени по олимпиадам | Счёт движения капиталов | Счёт депо |
| Счёт на оплату | Счёт на оплату (Россия) | Счёт на пальцах |
3)Элементы сферической тригонометрии
1)Приближенные
вычисления. Соотношение между угловой
и радиальной мерами измерения углов и
длинами дуг.
Соотношение между угловой
и радиальной мерами измерения углов и
длинами дуг.
Приближённые вычисления, вычисления, в которых данные и результат (или по крайней мере только результат) являются числами, лишь приближённо представляющими истинные значения соответствующих величин. П. в. возникают в связи с численным решением задач и обусловлены неточностями, которые присущи формулировке задачи и способам её решения. Общие правила и теорию методов П. в. принято называть численными методами.Обозначение единиц измерения плоского угла:
градус- «°»;минута — «’»;секунда — «»».
Соотношение между угловыми единицами:
1° = 1/360 полного оборота = 2Π/З60 рад = 0,017453 рад;
1’ = 1/60° = Π/108*10-2 рад = 0,000 291 рад;1’’ = 1/60’’ = Π/648*10-3 рад = 0,000 005 рад.
2)Тригонометрические функции малых углов.
Пусть
a будет какой-нибудь острый угол. Возьмём
на одной из его сторон произвольную
точку и опустим из неё перпендикуляр
на другую сторону угла.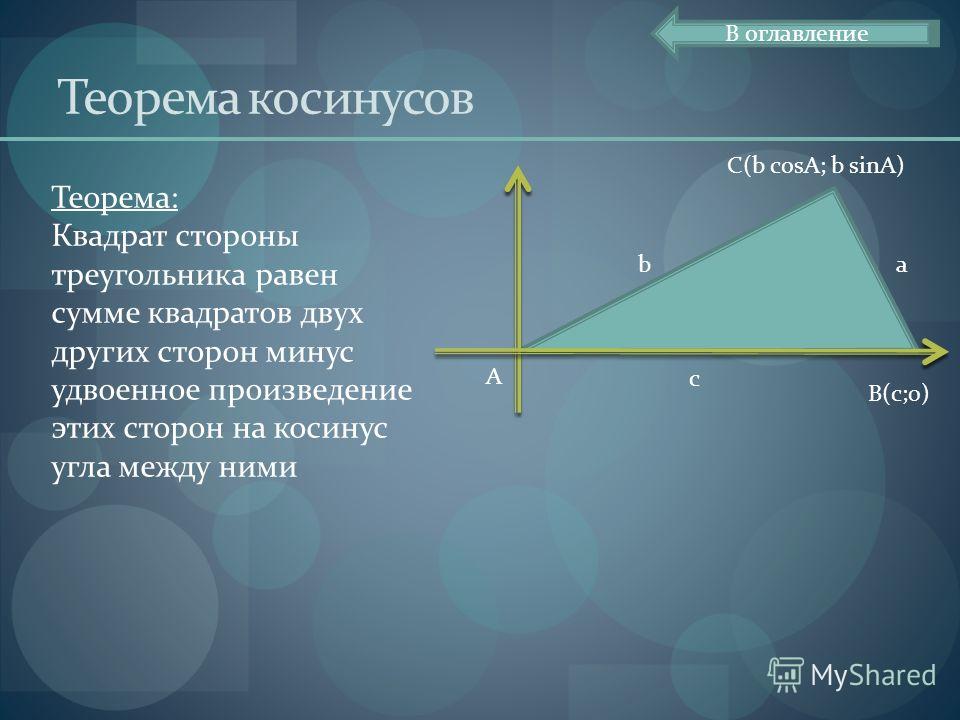 Тогда мы получим
прямоугольный треугольник. Возьмём
отношения сторон этого треугольника
попарно, а именно:1) отношение катета,
противолежащего углу, к гипотенузе,
Тогда мы получим
прямоугольный треугольник. Возьмём
отношения сторон этого треугольника
попарно, а именно:1) отношение катета,
противолежащего углу, к гипотенузе,
2) отношение катета, прилежащего углу, к гипотенузе,
3) отношение катета, противолежащего углу, к катету прилежащему,и обратные им отношения.
Величина каждого из этих отношений не зависит от положения точки на стороне угла.Все указанные отношения называются тригонометрическими функциями. Чаще других отношений берутся следующие четыре:
1)
отношение катета, противолежащего углу
a, к гипотенузе называется синусом угла
a и обозначается sin(a),2) отношение катета,
прилежащего углу a, к гипотенузе называется
косинусом угла a и обозначается соs(a),3)
отношение катета, противолежащего углу
a, к катету прилежащему называется
тангенсом угла a и обозначается tg(a),4)
отношение катета, прилежащего углу a, к
катету противолежащему называется
котангенсом угла a и обозначается
сtg(a).Так как каждый из двух катетов
меньше гипотенузы, то синус и косинус
каждого угла есть число меньшее единицы. Зависимости между тригонометрическими
функциями одного и того же угла. Простейшие
из этих зависимостей следующие четыре:
Зависимости между тригонометрическими
функциями одного и того же угла. Простейшие
из этих зависимостей следующие четыре:
;;;
Сферическая тригонометрия занимается изучением соотношений между сторонами и углами сферических треугольников (например, на поверхности Земли и на небесной сфере).Сферические треугольники. На поверхности шара кратчайшее расстояние между двумя точками измеряется вдоль окружности большого круга, т. е. окружности, плоскость которой проходит через центр шара. Вершины сферического треугольника являются точками пересечения трех лучей, выходящих из центра шара и сферической поверхности. Сторонами a, b, c сферического треугольника называют те углы между лучами, которые меньше 180 (если один из этих углов равен 180, то сферический треугольник вырождается в полуокружность большого круга). Каждой стороне треугольника соответствует дуга большого круга на поверхности шара (см. рисунок).
Углы
A, B, C сферического треугольника,
противолежащие сторонам a, b, c соответственно,
представляют собой, по определению,
меньшие, чем 180, углы между дугами больших
кругов, соответствующими сторонам
треугольника, или углы между плоскостями,
определяемыми данными лучами. Геометрия
на поверхности шара является неевклидовой;
в каждом сферическом треугольнике сумма
сторон заключена между 0 и 360, сумма углов
заключена между 180 и 540. В каждом сферическом
треугольнике против большей стороны
лежит больший угол. Сумма любых двух
сторон больше третьей стороны, сумма
любых двух углов меньше, чем 180 плюс
третий угол.Сферический треугольник
единственным образом определяется (с
точностью до преобразования симметрии):1)
тремя сторонами, 2) тремя углами, 3) двумя
сторонами и заключенным между ними
углом, 4) стороной и двумя прилежащими
к ней углами.
Геометрия
на поверхности шара является неевклидовой;
в каждом сферическом треугольнике сумма
сторон заключена между 0 и 360, сумма углов
заключена между 180 и 540. В каждом сферическом
треугольнике против большей стороны
лежит больший угол. Сумма любых двух
сторон больше третьей стороны, сумма
любых двух углов меньше, чем 180 плюс
третий угол.Сферический треугольник
единственным образом определяется (с
точностью до преобразования симметрии):1)
тремя сторонами, 2) тремя углами, 3) двумя
сторонами и заключенным между ними
углом, 4) стороной и двумя прилежащими
к ней углами.
4)Формула косинуса стороны.
Формула косинуса стороны связывает три стороны и один из углов сферического треугольника. Удобна для нахождения неизвестного угла или стороны, противолежащей этому углу, и читается следующим образом: «в сферическом треугольнике косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов этих сторон на косинус угла между ними»
Формула
косинуса угла связывает три угла и сторону сферического
треугольника, удобна для нахождения
неизвестной стороны или угла,
противолежащего этой стороне, и
читается так: «косинус угла сферического
треугольника равен отрицательному
произведению косинусов двух других
углов плюс произведение синусов этих
углов на косинус стороны между ними». ;
;
С*sinA=a*sinc;
6)Формулы пяти элементов и котангенсов.
Формула котангенсов (4-х рядом лежащих элементов) связывает 4 рядом лежащих элемента, используется для нахождения крайних элементов и читается следующим образом: «произведение котангенса крайнего угла на синус среднего угла равно произведению котангенса крайней стороны на синус средней стороны минус произведение косинусов средних элементов «.
ctg A*sinC=ctg a*sin b-cos b *cos C.
7) Решение прямоугольных сферических треугольников. Правило Модюи-Непера. Дополнительные формулы для решение косоугольных сферических треугольников.
Прямоугольным
называется такой сферический треугольник,
у которого один из углов равен 90°.
Прямоугольные сферические треугольники
более рационально решать по правилам
Модюи-Непера:в прямоугольном сферическом
треугольнике косинус любого среднего
элемента равен произведению котангенсов
крайних смежных с ним элементов;
косинус отдельно лежащего элемента
сферического треугольника равен
произведению синусов двух не смежных
с ним рядом лежащих элементов. Примечание: в обоих правилах принято,
что катеты лежат рядом друг с другом и
что вместо катетов надо брать их
дополнения до 90°, изменяя соответственно
наименования тригонометрических
функций.
Примечание: в обоих правилах принято,
что катеты лежат рядом друг с другом и
что вместо катетов надо брать их
дополнения до 90°, изменяя соответственно
наименования тригонометрических
функций.
8)Фигура и размеры Земли.
Земля представляет
собой неправильной формы шар. Длина его
экваториального радиуса равна 6 378 245 м.
а полярного—6 356 863 м. Как видно,
экваториальный диаметр Земли длиннее
полярного примерно на 42,8 км. Если
изобразить отклонение формы Земли от
шара на глобусе с поперечником в 1 м по
экватору, то его полярная ось будет
короче экваториальной на 3,35 мм. Фигура
Земли имеет форму геоида, что переводится
как «землеподобный». Геоидом называется фигура, ограничивающая
невозмущённую поверхность уровня
мирового океана, мысленно проходит под
материками и островами, таким образом,
что она в каждой своей точке перпендикулярна
отвесной линии и имеющая неправильную
геометрическую форму. Геометрия геоида
очень сложна, поэтому вместо геоида при
решении штурманских задач используют
более простые модели Земли: эллипсоид
вращения,
сферу, карту. Размеры
референц-эллипсоида Красовского: большая
полуось а=6378245 м; в=6356863 м; полярное сжатие
а=(а-в)/а=1/298,3; эксцентриситет
е=0,0818;R=6371110м.
Размеры
референц-эллипсоида Красовского: большая
полуось а=6378245 м; в=6356863 м; полярное сжатие
а=(а-в)/а=1/298,3; эксцентриситет
е=0,0818;R=6371110м.
9)Основные элементы на поверхности небесной сферы и земного сфероида.
Плоскость истинного меридиана наблюдателя пересекается с плоскостью истинного горизонта по линии N — S, которая называется полуденной линией, так как в этой плоскости Солнце бывает точно в полдень.
Вертикальную
плоскость, проходящую через глаз
наблюдателя перпендикулярно плоскости
истинного меридиана наблюдателя,
называют плоскостью первого вертикала
(плоскость 3). Она пересекается с плоскостью
истинного горизонта наблюдателя по
линии Ost—W. Таким образом, пересечение
взаимно перпендикулярных плоскостей
истинного меридиана наблюдателя и
первого вертикала дает четыре главные
линии на плоскости истинного горизонта
наблюдателя, которые указывают на
главные точки горизонта: N, S, Ost и W. Если
наблюдатель станет лицом к северу, то
за спиной у него будет юг, справа—восток,
слева—запад. Линии N—S, Ost—W в любой
точке земной поверхности (кроме полюсов)
занимают вполне определенное положение.
Направления N, S, Ost и W называют главными
направлениями, или главными румбами,
которые делят истинный горизонт на
четыре четверти: NOst— северо-восточную,
SOst — юго-восточную, SW—юго-западную и
NW—северозападную. Каждая четверть
делится на 8 румбов, а весь горизонт—на
32 румба.Основные географические точки,
линии и круги на земном шаре.Земля
непрерывно вращается в направлении с
запада на восток. Диаметр, вокруг которого
происходит это вращение, называется
осью вращения Земли.Земля непрерывно
вращается в направлении с запада на
восток. Диаметр, вокруг которого
происходит это вращение, называется
осью вращения Земли.
Линии N—S, Ost—W в любой
точке земной поверхности (кроме полюсов)
занимают вполне определенное положение.
Направления N, S, Ost и W называют главными
направлениями, или главными румбами,
которые делят истинный горизонт на
четыре четверти: NOst— северо-восточную,
SOst — юго-восточную, SW—юго-западную и
NW—северозападную. Каждая четверть
делится на 8 румбов, а весь горизонт—на
32 румба.Основные географические точки,
линии и круги на земном шаре.Земля
непрерывно вращается в направлении с
запада на восток. Диаметр, вокруг которого
происходит это вращение, называется
осью вращения Земли.Земля непрерывно
вращается в направлении с запада на
восток. Диаметр, вокруг которого
происходит это вращение, называется
осью вращения Земли.
Эта
ось пересекается с поверхностью Земли
в двух точках, которые называются
географическими полюсами: один Северным
(С), а другой Южным (Ю). Северным называется
тот полюс, в котором, если смотреть на
него сверху, вращение Земли направлено
против хода часовой стрелки. Противоположный
полюс называется Южным.
Противоположный
полюс называется Южным.
Через
любую точку на земном шаре можно провести
бесчисленное множество больших и малых
кругов.Большим называется круг,
образованный на земной поверхности
плоскостью сечения, проходящей через
центр Земли. Малым называется круг,
образованный на земной поверхности
плоскостью сечения, не проходящей через
центр Земли. Большой круг, плоскость
которого перпендикулярна оси вращения
Земли, называется экватором. Экватор
делит земной шар на Северное и Южное
полушария. Малый круг, плоскость которого
параллельна плоскости экватора,
называется параллелью. Через каждую
точку на земной поверхности можно
провести только, одну параллель, которая
называется параллелью места. Большой
круг, проходящий через полюсы Земли,
называется географическим, или истинным
меридианом. Через каждую точку на земной
поверхности, кроме полюсов, можно
провести только один меридиан, который
называется меридианом места. Меридиан,
проходящий через Гринвичскую
астрономическую обсерваторию, находящуюся
в Англии вблизи Лондона, принят по
международному соглашению в качестве
начального меридиана.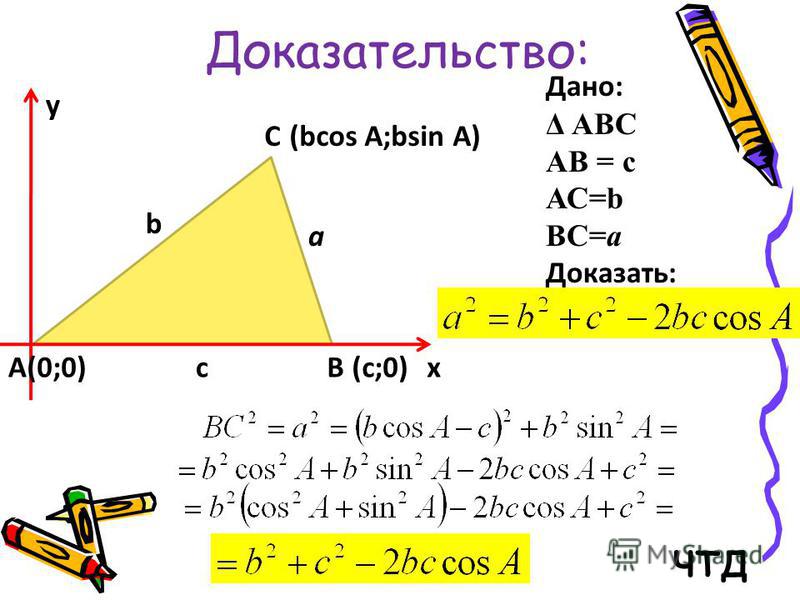 Начальный меридиан
делит земной шар на Восточное и Западное
полушария. Плоскость экватора и плоскость
начального меридиана являются основными
плоскостями, от которых производится
отсчет географических координат.
Начальный меридиан
делит земной шар на Восточное и Западное
полушария. Плоскость экватора и плоскость
начального меридиана являются основными
плоскостями, от которых производится
отсчет географических координат.
Сферические теоремы косинусов wiki | TheReaderWiki
Copyright
The image is from Wikipedia Commons
MinecraftStatus.net | CheckTheIP.com | TheDicts.com | TheReaderWeb | Wikipedia
Сферический треугольник.
Первая и вторая сферические теоремы косинусов устанавливают соотношения между сторонами и противолежащими им углами сферического треугольника.
Теоремы косинусов для сферического треугольника со сторонами a, b, c и углами A, B, C имеют следующий вид:
- cos c = cos a cos b + sin a sin b cos C , {\displaystyle \cos c=\cos a\cos b+\sin a\sin b\cos C,}
- cos
A
=
−
cos
B
cos
C
+
sin
B
sin
C
cos
a
.
 {\displaystyle \cos A=-\cos B\cos C+\sin B\sin C\cos a.}
{\displaystyle \cos A=-\cos B\cos C+\sin B\sin C\cos a.}
Эти две теоремы двойственны по отношению друг к другу, поскольку углы и стороны всякого сферического треугольника дополняются до развёрнутого угла сторонами и углами соответствующего полярного треугольника. Поэтому достаточно доказать одну из них.
Сферический треугольник для определения кратчайшего расстояния между точками на Земле.
Если угол C — прямой, первая теорема косинусов переходит в сферическую теорему Пифагора:
- cos c = cos a cos b . {\displaystyle \cos c=\cos a\cos b.}
Хотя для решения косоугольных сферических треугольников обычно используются более удобные формулы, с помощью теоремы косинусов выводится важная для геодезии формула длины ортодромии — кратчайшего расстояния между точками на земной поверхности с известными координатами (в предположении сферичности Земли). Обозначим географические широты двух данных точек
φ
A
{\displaystyle \varphi _{A}}
и
φ
B
{\displaystyle \varphi _{B}}
, разность долгот —
Δ
λ
A
B
{\displaystyle \Delta \lambda _{AB}}
, кратчайшее расстояние между ними обозначим d, длину дуги в 1 градус — a. Тогда формула длины ортодромии[2]:
Обозначим географические широты двух данных точек
φ
A
{\displaystyle \varphi _{A}}
и
φ
B
{\displaystyle \varphi _{B}}
, разность долгот —
Δ
λ
A
B
{\displaystyle \Delta \lambda _{AB}}
, кратчайшее расстояние между ними обозначим d, длину дуги в 1 градус — a. Тогда формула длины ортодромии[2]:
- cos ( d a ) = sin φ A ⋅ sin φ B + cos φ A ⋅ cos φ B ⋅ cos Δ λ A B {\displaystyle \cos \left({\frac {d}{a}}\right)=\sin \varphi _{A}\cdot \sin \varphi _{B}+\cos \varphi _{A}\cdot \cos \varphi _{B}\cdot \cos \Delta \lambda _{AB}}
Эта формула сразу получается применением теоремы косинусов к стороне AB сферического треугольника PnAB.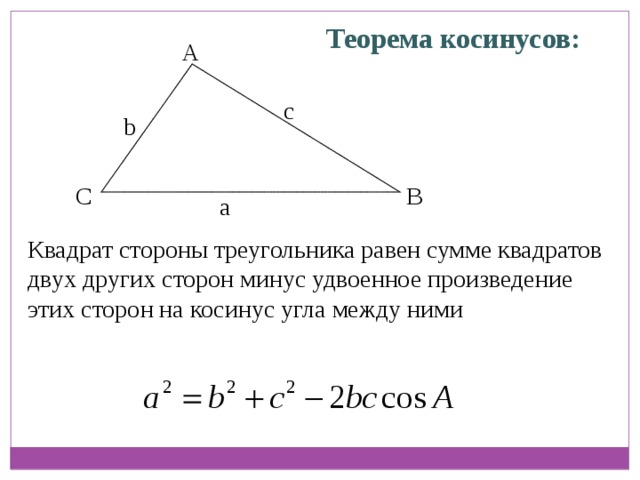 Подобная формула справедлива для любой сферической поверхности и поэтому её можно применять также для определения углового расстояния между звёздами по известным их экваториальным координатам[3].
Подобная формула справедлива для любой сферической поверхности и поэтому её можно применять также для определения углового расстояния между звёздами по известным их экваториальным координатам[3].
Теорема косинусов в её втором виде (соотношение между тремя углами и стороной) может быть применена для вычисления взаимного наклонения двух орбит при известном наклонении каждой орбиты к какой-то другой плоскости. Например, по этой формуле можно вычислить наклонение орбиты Плутона к орбите Нептуна, используя наклонения их орбит к эклиптике и долготы их восходящих узлов.
Математики средневекового Востока использовали утверждение, равносильное сферической теореме косинусов, при решении конкретных астрономических задач. Эти соотношения, используемые при определении высоты Солнца, встречаются в сочинениях Сабита ибн Корры, ал-Махани, ал-Баттани, Ибн Юниса, ал-Бируни.
Первая явная формулировка теоремы дана в XV веке Региомонтаном, который назвал её «теоремой Альбатегния» (по латинизированному имени ал-Баттани).
- Сферическая теорема синусов
- Теорема косинусов
- ↑ Приводится по изданию: Степанов Н. Н. Формулы косинуса стороны // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 24—28. — 154 с.
- ↑ Михайлов В.С., Кудрявцев В.Г., Давыдов В.С. 26.2. Основные формулы ортодромии. Способы её задания // Навигация и лоция. — Киев, 2009. Архивная копия от 25 июля 2012 на Wayback Machine
- ↑ Меёс Ж. 9. Угловое расстояние между объектами // Астрономические формулы для калькуляторов. — Мир, 1988. — С. 44—46. — 168 с. — ISBN 5030009361.
- ↑ Lee Kai Ming. PHYS 2021 — The Physical Universe. — 2010. — С. 6. Архивировано 3 декабря 2008 года.
- Вентцель М. К. Сферическая тригонометрия. 2-е изд., ИГКЛ, 1948, 115с.
- Матвиевская Г. П. Очерки истории тригонометрии: Древняя Греция. Средневековый Восток.
 Позднее Средневековье. — Изд. 2-е. — М.: Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9.
Позднее Средневековье. — Изд. 2-е. — М.: Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9. - Степанов Н. Н. Сферическая тригонометрия. — Л.-М., 1948.
Other Languages
- English
- Esperanto
- Español
- Română
- Svenska
- Українська
- Tiếng Việt
Copyright
- This page is based on the Wikipedia article Сферические теоремы косинусов;
it is used under the Creative Commons Attribution-ShareAlike 3.
 0 Unported License (CC-BY-SA).
You may redistribute it, verbatim or modified, providing that you comply with the terms of the CC-BY-SA.
0 Unported License (CC-BY-SA).
You may redistribute it, verbatim or modified, providing that you comply with the terms of the CC-BY-SA.
Сферический треугольник и его применение
Сферический треугольник и его применение.
Сферический треугольник — геометрическая фигура на поверхности сферы, образованная пересечением трёх больших кругов. Три больших круга на поверхности сферы, не пересекающихся в одной точке, образуют восемь сферических треугольников. Сферический треугольник, все стороны которого меньше половины большого круга, называется эйлеровым.
Сторона
сферического треугольника измеряется
величиной опирающегося на неё центрального
угла. Угол сферического треугольника
измеряется величиной двугранного угла
между плоскостями, в которых лежат стороны
этого угла. Соотношения между элементами
сферических треугольников изучает сферическая
тригонометрия.
Свойства сферического треугольника:
- Помимо трёх признаков равенства плоских треугольников, для сферических треугольников верен ещё один: два сферических треугольника равны, если их соответствующие углы равны.
- Для сторон сферического треугольника выполняются 3 неравенства треугольника: каждая сторона меньше суммы двух других сторон и больше их разности.
- Сумма всех сторон a + b + c всегда меньше 2πR.
- Величина 2πR − (a + b + c) называется сферическим дефектом
- Сумма углов сферического треугольника s = α + β + γ всегда меньше 3π и больше π
- Величина называется сферическим избытком или сферическим эксцессом
- Площадь сферического треугольника определяется по формуле .
- В отличие от плоского треугольника, у сферического треугольника может быть два, и даже три угла по 90° каждый.
Среди всех сферических
многоугольников наибольший интерес
представляет сферический треугольник. Три больших окружности, пересекаясь попарно
в двух точках, образуют на сфере восемь
сферических треугольников. Зная элементы
(стороны и углы) одного из них, можно определить
элементы все остальных, поэтому рассматривают
соотношения между элементами одного
из них, того, у которого все стороны меньше
половины большой окружности. Стороны
треугольника измеряются плоскими углами
трехгранного угла ОАВС, углы треугольника
– двугранными углами того же трехгранного
угла см на рис.
Три больших окружности, пересекаясь попарно
в двух точках, образуют на сфере восемь
сферических треугольников. Зная элементы
(стороны и углы) одного из них, можно определить
элементы все остальных, поэтому рассматривают
соотношения между элементами одного
из них, того, у которого все стороны меньше
половины большой окружности. Стороны
треугольника измеряются плоскими углами
трехгранного угла ОАВС, углы треугольника
– двугранными углами того же трехгранного
угла см на рис.
Свойства сферических
треугольников во многом отличаются от
свойств треугольников на плоскости. Так,
к известным трем случаям равенства прямолинейных
треугольников добавляется еще и четвертый:
два треугольника АВС и А`В`С` равны, если
равны соответственно три угла РА = РА`,
РВ = РВ`, РС = РС`. Таким образом, на сфере
не существует подобных треугольников,
более того, в сферической геометрии нет
самого понятия подобия, т.к. не существует
преобразований, изменяющих все расстояния
в одинаковое (не равное 1) число раз. Эти
особенности связаны с нарушением евклидовой
аксиомы о параллельных прямых и также
присущи геометрии Лобачевского. Треугольники,
имеющие равные элементы и различную ориентацию,
называются симметричными, таковы, например,
треугольники АС`С и ВСС`
Эти
особенности связаны с нарушением евклидовой
аксиомы о параллельных прямых и также
присущи геометрии Лобачевского. Треугольники,
имеющие равные элементы и различную ориентацию,
называются симметричными, таковы, например,
треугольники АС`С и ВСС`
Сумма углов всякого сферического треугольника всегда больше 180°. Разность РА+РВ +РС – p = d (измеряемая в радианах) – величина положительная и называется сферическим избытком данного сферического треугольника. Площадь сферического треугольника: S = R2 d где R – радиус сферы, а d – сферический избыток. Эта формула впервые была опубликована голландцем А.Жираром в 1629 и названа его именем.
Если рассматривать
двуугольник с углом a, то при 226 =
2p/n (n – целое число) сферу можно
разрезать ровно на п копий
такого двуугольника, а площадь сферы
равна 4пR2 = 4p при R = 1, поэтому площадь двуугольника
равна 4p/n = 2a. Эта формула верна и при a =
2pт/п и, следовательно, верна для всех a.
Если продолжить стороны сферического
треугольника АВС и выразить площадь сферы
через площади образующихся при этом двуугольников
с углами А, В, С и его собственную площадь,
то можно прийти к вышеприведенной формуле
Жирара.
Под сферическим
треугольником подразумевается треугольник
на поверхности сферы, составленный из
дуг больших кругов – т. е. таких окружностей,
центром которых является центр сферы.
Углы сферического треугольника – это
углы между касательными к его сторонам,
проведенными в его вершинах. Как и углы
обычного треугольника, они меняются от
0 до 180°. В отличие от плоского треугольника,
у сферического сумма углов не равна 180°,
а больше: в этом нетрудно убедиться, рассмотрев,
например, треугольник, образованный дугами
двух меридианов и экватора на глобусе:
хотя меридианы сходятся в полюсе, оба
они перпендикулярны экватору, а значит,
у этого треугольника два прямых угла!
У сферического треугольника может быть два прямых угла
Уже у индийца
Варахамихиры (V–VI вв.), у арабских математиков
и астрономов начиная с IX в. (Сабит ибн
Корра, ал-Баттани), а у западных математиков
начиная с Региомонтана (XV в.) встречается
в различных формулировках замечательная
теорема о сферических треугольниках. Вот как она может быть сформулирована
в современных обозначениях:
Вот как она может быть сформулирована
в современных обозначениях:
cos a = cos b cos c + sin b sin c cos A. Сферическая теорема косинусов очень важна и для астрономии, и для географии. Эта теорема позволяет по координатам двух городов A и B находить расстояние между ними. Кроме того, математикам стран ислама сферическая теорема косинусов помогала в решении другой практической задачи: в городе с данными координатами находить направление на священный город Мекку (всякий правоверный мусульманин должен пять раз день молится в направлении Мекки). При решении этой задачи, считая город B Меккой, требовалось найти угол A того же треугольника.
Страница из «Собрания правил науки астрономии», XI в., автор неизвестен.
В астрономии сферическая
теорема косинусов позволяет
переходить из одной системы координат
на небесной сфере в другую. Чаще всего
используются три такие системы: у одной
экватором служит небесный экватор, а
полюсами – полюсы мира, вокруг которых
происходит видимое суточное вращение
светил; у другой экватором является эклиптика
– круг, по которому в течение года совершается
видимое движение Солнца на фоне звезд;
у третьей роль экватора выполняет горизонт,
а роль полюсов – зенит и надир. В частности,
благодаря сферической теореме косинусов
можно вычислять высоту Солнца над горизонтом
в разные моменты времени и в разные дни
в году.
В частности,
благодаря сферической теореме косинусов
можно вычислять высоту Солнца над горизонтом
в разные моменты времени и в разные дни
в году.
Паруса в архитектуре — сферический треугольник, обеспечивающий переход от квадратного в плане подкупольного пространства к окружности купола. Па́рус, пандати́в (от фр. pendentif) — часть свода, элемент купольной конструкции, посредством которого осуществляется переход от прямоугольного основания к купольному перекрытию или его барабану. Парус имеет форму сферического треугольника, вершиной опущенной вниз, и заполняет пространство между подпружными арками, соединяющими соседние столпы подкупольного квадрата. Основания сферических треугольников парусов в сумме образуют окружность и распределяют нагрузку купола по периметру арок.
Купол на парусах
Роспись паруса
Джордж Нельсон (George Nelson)
May 23rd, 2010
«Дизайнер
может несколько расслабиться
и развлечься; в результате может
возникнуть шутка, забава. Удивительно,
как часто это бывает очень
значительная забава» Джордж
Нельсон
Удивительно,
как часто это бывает очень
значительная забава» Джордж
Нельсон
Джордж Нельсон – американский дизайнер, архитектор, критик и теоретик дизайна. (1908, Хартфорд, Коннектикут – 1986, Нью-Йорк)
Проектировал осветительную арматуру, часы, мебель, упаковку, занимался выставочным дизайном.
Наиболее известные дизайн проекты Джорджа Нельсона представляют собой виртуозную стилизацию геометрических форм в духе оп-арта или геометрического абстракционизма.
Форму своего знаменитого
черного стула дизайнер строит на
основе сферического треугольника, широко
использовавшегося в
Джордж Нельсон
(George Harold Nelson, 1908—1986 гг.)
гравюра Эшера
Концентрические
сферы. 1935г.Торцовая гравюра 24 на 24 см.
1935г.Торцовая гравюра 24 на 24 см.
Четыре полые концентрические сферы освещены центральным источником света. Каждая сфера состоит из сетки, образованной девятью большими пересекающимися кольцами; они членят сферическую поверхность на 48 подобных сферических треугольников. Ма́уриц Корне́лис Э́шер (нидерл. Maurits Cornelis 17 июня 1898, Леуварден, Нидерланды — 27 марта 1972, Ларен, Нидерланды) — нидерландский художник-график.
Применение сферического треугольника:
- Использование в трехмерной графике сферических треугольников
- В астрономии
- В географии. Теорема сферического треугольника позволяет по координатам двух городов A и B находить расстояние между ними.
- В архитектруе
- В дизайне в виде стула от Джорджа Нельсона
- В гравюре
ЭЛЕМЕНТЫ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ И АСТРОНОМИИ
ЭЛЕМЕНТЫ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ И АСТРОНОМИИ
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Скибо Я. М. 1
М. 1
1МАОУ «Гимназия№1»
Дятел О.И. 1
1МАОУ «Гимназия №1»
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Проблема
В одной из игре «Что? Где? Когда?» был задан вопрос: «Сумма углов какого треугольника равна 181˚37’26’’?». Тогда я очень заинтересовалась этой темой, ведь в школе мы учили, что всегда сумма углов треугольника будет равна 180˚. Конечно, я не учла, что существуют разные геометрии, соответственно и разные правила. Заинтересовавшись вопросом, я узнала что существует такая странная неевклидова геометрия — сферическая. Эта тема меня сразу же увлекла, ведь я решила посвятить будущую профессию изучению космоса, астрономии, а именно здесь сферическая геометрия — неотъемлемая часть. И тем не менее в повседневной жизни и даже на уроках геометрии в школе нам не приходилось с ней сталкиваться, поэтому не все представляют себе, что она изучает и для чего нужна.
И тем не менее в повседневной жизни и даже на уроках геометрии в школе нам не приходилось с ней сталкиваться, поэтому не все представляют себе, что она изучает и для чего нужна.
Актуальность
Сейчас сферическая геометрия нужна не только астрономам, штурманам морских кораблей, самолётов, космических кораблей, которые по звёздам определяют свои координаты, но и строителям шахт, метрополитенов, тоннелей, а также при геодезических съёмках больших территорий поверхности Земли, когда становится необходимым учитывать её шарообразность.
Гипотеза: некоторые свойства сферического треугольника совпадут со свойствами Евклидова треугольника.
Цель: целью настоящего исследования является изучение понятий и фактов сферической геометрии треугольника и сравнение их с обычной евклидовой геометрией треугольника.
Задачи:
Для достижения цели исследования нам необходимо было решить ряд задач:
Изучить основные понятия сферической геометрии треугольника.
Проанализировать и сравнить понятия сферической евклидовой геометрии треугольника
Доказать ряд теорем евклидовой геометрии треугольника (в том числе, теорему синусов и косинусов) для сферического треугольника.
На основе полученных знаний решить задачи по теме сферической геометрии.
Разработать памятку сравнения сферической и неевклидовой геоетрии.
Объект исследования — понятие сферической геометрии.
Предмет исследования — определения и теоремы сферической геометрии треугольника.
Методы исследования — аналогия и сравнительный анализ сферического и евклидового треугольника.
Структура работы обусловлена целью исследования. Работа состоит из двух частей: в первой приводится общая теория о сфере, понятие сферического треугольника, сферические теоремы синусов и косинусов, двойственная теорема косинусов
Во второй части работы я рассмотрела решения задач на применение рассмотренных теорем, а также задачи практического характера.
Практическая значимость
Мне и ученикам, собирающимся поступать на технические специальности, полезно изучение этой темы, т.к. в вузе она активно используется в программе. Я разработаю сравнительную таблицу сферической геометрии и планиметрии для наиболее ясного восприятия.
Основная часть
Основные понятия сферической геометрии.
Вернусь к вопросу: «Сумма углов какого треугольника равна 181˚37’26’’?». Ответ: Бермудского треугольника (рис. 1). Почему? Потому что он расположен на сфере! Наша Земля имеет форму шара, приплюснутого с полюсов. Современная наука дает название такому телу – геоид. Хотя в переводе с греческого «геоид» переводится, как «нечто, похожее на форму Земли», тем не менее, это остается фактом. Геоид с шаром приближается довольно неплохо. Поэтому, для удобства изучения сферической геометрии, форму нашей планеты принимают за шар, сферу. Вторая оговорка, которую стоит иметь ввиду, в случае работы с сравнительно небольшим участком земли (относительно площади всей поверхности Земли), достаточно плоской геометрии из-за незначительной кривизны. Однако, если речь идет о чем-то глобальном, то дело уже становится существенным и тогда удобно рассматривать сферу, как некий аналог плоскости. Другой подход заключается в том, что можно сказать, что у нас есть пространство и в нем находятся сферы, а все, что находится на сфере, находится в самом обычном традиционном евклидовом пространстве, где существуют законы евклидовой стереометрии.
Вторая оговорка, которую стоит иметь ввиду, в случае работы с сравнительно небольшим участком земли (относительно площади всей поверхности Земли), достаточно плоской геометрии из-за незначительной кривизны. Однако, если речь идет о чем-то глобальном, то дело уже становится существенным и тогда удобно рассматривать сферу, как некий аналог плоскости. Другой подход заключается в том, что можно сказать, что у нас есть пространство и в нем находятся сферы, а все, что находится на сфере, находится в самом обычном традиционном евклидовом пространстве, где существуют законы евклидовой стереометрии.
Рис.1
Поэтому мы будем проводить аналогию между этими геометриями (сферической и планиметрией). Например, точки сферы будут сопоставляться, как точки «плоскости».
Возникает вопрос: что же такое прямые и отрезки на сфере? «Прямая» на сфере – это большой круг, окружность, которая проходит через диаметрально противоположные точки, или сечение сферы плоскостью проходящее через ее центр (экватор и меридианы, важно: не стоит путать с тропиками, они не проходят через диаметрально противоположные точки).
Вот основные аксиомы про прямые в сферической геометрии.
Через две точки, не являющимися диаметрально противоположными, проходит только одна прямая.
Любые две прямые пересекаются в 2 – х диаметрально противоположных точках.
Последнее порождает такую удивительную фигуру, как двуугольник. Это фигура, напоминающая «дольку», состоящая из двух углов.
Есть такие базовые вещи из школьной геометрии, как, например, признаки равенства треугольников (1-й, 2-й и 3-й). Так вот они работают и на сфере. А что происходит на плоскости, когда углы треугольников равны друг другу? На плоскости они подобны. А на сфере? Оказывается, в сферической геометрии такие треугольники также будут равны, ведь подобных треугольников здесь не существует.
Еще одной характеристикой треугольника на сфере будет дефект. Дефект – разница между настоящей суммой и эталонной (такой, как если бы она была, будь треугольник на плоскости). Пусть у нас есть треугольник, где сумма углов равна 270 градусов. На плоскости она составляла бы 180 градусов. А вот разность между суммой на сфере и плоскости и называется дефектом. Т.е.
Дефект – разница между настоящей суммой и эталонной (такой, как если бы она была, будь треугольник на плоскости). Пусть у нас есть треугольник, где сумма углов равна 270 градусов. На плоскости она составляла бы 180 градусов. А вот разность между суммой на сфере и плоскости и называется дефектом. Т.е.
ДЕФЕКТ = α + β + µ — 180˚
Снова обратимся к бермудскому треугольнику. Его дефект равен примерно 1,5˚. Треугольник не очень большой, следовательно, дефект тоже маленький.
Теорема: DABC∝k*SABC
Дефект треугольника пропорционален его площади (это работает и на плоскости, просто k=0).
Теперь рассмотрим многоугольник. Пусть m – n-угольник.
Dm = α + β + µ — 180˚(n-2)
Dm = k*Sm
Если m состоит из нескольких n-угольников (допустим m1 и m2)
Sm = Sm1 + Sm2 ⇒Dm = Dm1 + Dm2
S = α/360˚*4πR²
У двуугольника дефект соответственно равен 2α, т. к. в евклидовой геометрии сумма углов равна нулю.
к. в евклидовой геометрии сумма углов равна нулю.
Из практики, на плоскую карту положить сферу без искажений невозможно. Ведь то, что является прямой на плоскости, на сфере – кривая. Почему? Виной этому, например сумма углов треугольника. В пространстве существуют другие поверхности, где внутренняя геометрия – евклидова. В пример приведу конус, цилиндр. В них локальные фигуры похожи на плоскость, чего нельзя сказать о сфере. В частности, когда мы пытаемся ее изобразить, то получается, допустим, что «прямые2 перестают быть прямыми. Обычно также жертвуют тем, что площади будут искажаться. Так Гренландия окажется больше Австралии (!), что, конечно, ложно.
При изучении сферической геометрии и использовании ее в расчетах на Земле и в космосе сразу возникает интересный вопрос: Как посчитать расстояние между двумя точками на сфере? (К этому вопросу я еще вернусь позднее)
Сферическим расстоянием между двумя точками сферы называется длина кратчайшей из дуг большой окружности, проведенной через эти точки (рис. 2).
2).
Рис. 2
В случае когда точки А и В диаметрально противоположны, через них можно провести бесконечно много больших окружностей, но все они будут иметь одинаковую длину.
Также в отличие от обычной геометрии любые две сферические прямые пересекаются в двух диаметрально противоположных точках — на сфере отсутствует само понятие параллельности. Другое существенное отличие прямой на сфере от прямой на плоскости заключается в том, что сферическая прямая замкнута, двигаясь по ней в одну сторону, мы в конце концов вернемся в исходную точку, то есть точка не разбивает сферическую прямую на две части, подобные лучам обычной прямой.
Если две точки А и В принадлежат большой окружности, то длина меньшей из её двух дуг, соединяющих эти точки, принимается за сферическое расстояние между А и В. Самую меньшую дугу естественно считать сферическим отрезком АВ. Диаметрально противоположные точки соединены бесконечным числом сферических отрезков — больших полуокружностей.
Сферическое расстояние АВ выражается через радианную меру а центрального угла АОВ и радиус сферы R: по известной формуле для длины дуги, оно равно Ra. Если принять радиус сферы за единицу длины, то сферическое расстояние окажется равным угловой величине a соответствующей дуги.
Для сферического расстояния выполняются аксиомы расстояния:
|АВ|>0, причем |АВ|=0 в том случае, когда А = В.
Для любых точек А и В |АВ|=|ВА|.
Для любых точек А, В, С |АС|<|АВ|+|ВС|.
Любая точка С сферического отрезка АВ разбивает его на два, и сумма их сферических длин, как и в планиметрии, равна длине всего отрезка, или АОС + СОВ = АОВ. А для любой точки D вне отрезка имеет место «сферическое неравенство треугольника»: сумма сферических расстояний от D до А и от D до В больше АВ, или AOD + DOB — АОВ. Здесь существует полное соответствие между сферической и плоской геометриями.
Здесь существует полное соответствие между сферической и плоской геометриями.
Неравенство треугольника — одно из основополагающих свойств в геометрии на сфере. Именно благодаря ему, точно так же, как и в планиметрии, сферический отрезок короче любой сферической ломаной, а значит, и любой кривой на сфере, соединяющей его концы. Вслед за определением сферического расстояния на сферу переносят и почти все понятия плоской геометрии, потому что из можно выразить через расстояния на плоскости.
Определим теперь углы на сфере. Рассмотрим две сферические прямые а и b (рис. 3). Они разбивают сферу на четыре двуугольника подобно тому, как пересекающиеся прямые на плоскости разбивают её на четыре плоских угла. Каждому из двуугольников отвечает один из двугранных углов, образуемых диаметральными плоскостями, содержащими а и Ь.
Рис. 3
Угол между сферическими прямыми — большими окружностями — определяется как угол между их плоскостями, или, что то же самое, как угол между касательными к этим окружностям в точке их пересечения. Величиной этого двугранного угла и измеряется, по определению, угол при вершине двуугольника. А угол между сферическими прямыми равен меньшему из углов образуемых ими двуугольников.
Величиной этого двугранного угла и измеряется, по определению, угол при вершине двуугольника. А угол между сферическими прямыми равен меньшему из углов образуемых ими двуугольников.
Хочу обратить внимание на соответствие, которое возникает между понятиями в геометрии на сфере и в стереометрии. Точкам сферы сопоставляется лучи, которые проведены в неё из центра О сферы, а любой фигуре на сфере — объединение всех пересекающих её лучей с общим началом в О. Сферической прямой отвечает содержащая её диаметральная плоскость, сферическому отрезку — плоский угол, двуугольнику — двугранный угол, сферической окружности — коническая поверхность, ось которой проходит через полюсы окружности. Равным сферическим фигурам соответствуют равные фигуры из лучей, движениям сферы — движения пространства, переводящие сферу в себя. Геометрические величины также находят себе пары: например, длина сферического отрезка — величина соответствующего плоского угла.
Сферическая система координат.
Представьте: мы находимся в неизвестной местности, не понимаем наше расположение и, конечно, хотим определить его, т.е. наши координаты. Что мы можем сделать? Созерцать звезды!
Во – первых, надо определить направление на север (на компас лучше не ориентироваться, ведь северный географический и северный магнитный полюс – разные вещи), поэтому ищем Полярную звезду. Полярная звезда располагается в ручке ковша Малой Медведицы и находится в направлении севера с небольшим отклонением. Она светит ярче других светил, поэтому более заметна. Отмечу, что так таковой небесной сферы не существует, однако, для удобства наблюдения звезд, необходимо было их проецировать на некоторую дугу, которая и внемлет точки нашего наблюдения. Земля вертится вокруг своей оси, следовательно изображения звезд тоже движутся для земного наблюдателя, а вот Полярная звезда, из – за расположения в северном центре покоится.
Для дальнейшего исследования необходимо ввести понятие сферической системы координат.
Наиболее широко применяются три пространственные системы координат. Первая из них — прямоугольная, или Декартова. Вторая, цилиндрическая, система координат, представляет собой нечто среднее между прямоугольной и полярной системами. Более сложна для восприятия, но просто необходима при решении многих задач, сферическая система координат (рис. 4). Она похожа на цилиндрическую: в ней также имеются плоскость а с полярной осью и дополнительная ось Oz, перпендикулярная плоскости а. Однако положение точки М пространства определяется такими координатами: угол ср, как и в цилиндрической системе, расстоянием R от точки М до полюса О (именно от точки М, а не от её проекции!) и ещё одним углом р — его образуют отрезок ОМ и положительное направление оси Oz. Сферическая система координат наиболее близка к географической, но отличается от неё тем, что на глобусе угол (3 отсчитывается не от вертикальной оси, а от горизонтальной плоскости, в которой лежит экватор. Кроме того, в географической системе добавлены понятия «северная (южная) широта» и «восточная (западная) долгота», чтобы указать направление отсчёта углов. Это позволяет обойтись без отрицательных значений.
Кроме того, в географической системе добавлены понятия «северная (южная) широта» и «восточная (западная) долгота», чтобы указать направление отсчёта углов. Это позволяет обойтись без отрицательных значений.
полярная ось Рис.5
Рис. 4
Почему в астрономии для определения положения светил используются именно сферические системы координат? Ответ прост; из — за того, что расстояния до небесных тел бывают известны редко даже сейчас, а в древности, когда закладывались основы астрономии, — и подавно. А поскольку положение точки в прямоугольной системе координат задаётся тремя линейными величинами, то такая система для большинства астрономических целей непригодна.
Сферические координаты издавно употреблялись в астрономии, формулы, связывающие сферические координаты с прямоугольными, приведены Ж. Лагранжем (1173), названия сферические координаты предложил Р. Бальтцер (1882).
Бальтцер (1882).
Соответствие между аксиоматикой сферической геометрии и планиметрии.
В предыдущем пункте были введены, то есть определены важнейшие понятия сферической геометрии. Снова отмечу, что в планиметрии понятие прямой не определяется — это первичное понятие геометрии плоскости. Несмотря на это, требуется чтобы для прямых выполнялись на плоскости некоторые аксиомы. Так какие же из них будут справедливы в сферической геометрии — для сферических прямых?
Аксиома, гласящая, что каждая прямая есть множество точек, в сферической геометрии выполняется — большие окружности суть множества точек. Однако уже со следующей аксиомой: для любых двух точек А и В существует единственная содержащая эти точки прямая — дело обстоит сложнее. Если точки А и В сферы не являются диаметрально противоположными, то это предложение верно, но для диаметрально противоположных точек А и В существует бесконечно много сферических прямых, содержащих эти точки: пересечение сферы с любой плоскостью, содержащей диаметр АВ, даст такую прямую. Можно сказать, что эта аксиома почти выполняется на сфере. Оговорка почти приводит к следующим следствиям.
Можно сказать, что эта аксиома почти выполняется на сфере. Оговорка почти приводит к следующим следствиям.
1.Любые две различные прямые на сфере пересекаются в диаметрально противоположных точках сферы.
Как следствие: в сферической геометрии нет содержательного понятия параллельности — нет различных параллельных прямых. Разумеется, не выполняется и аксиома параллельных, а следовательно, не имеет смысла говорить и о параллельных переносах.
В планиметрии одна из трех различных точек, принадлежащих одной прямой, лежит между двумя другими (если, скажем, точка В лежит между А и С, то это означает, что |АВ| + |ВС| = |АС|, тогда точка В принадлежит отрезку АС). В сферической геометрии такое понятие «лежать между» определить нельзя: например, если точки А, В и С лежат на большой окружности и разделены дугами градусной меры 120° (см. рис. 6), то ни про одну из них нельзя сказать, что она лежит между двумя другими. Грубо говоря, это объясняется тем, что в планиметрии точка разбивает прямую на два «отдельных» множества — открытых луча, а на сфере это неверно. Таким образом, об аксиомах порядка на сферических прямых говорить не приходится.
Грубо говоря, это объясняется тем, что в планиметрии точка разбивает прямую на два «отдельных» множества — открытых луча, а на сфере это неверно. Таким образом, об аксиомах порядка на сферических прямых говорить не приходится.
Рис. 6
Одна из аксиом планиметрии гласит: всякая прямая разбивает плоскость на две открытые полуплоскости — два непустых множества, таких, что для точек А и В, принадлежащих разным множествам, отрезок АВ пересекает данную прямую, а если А и В принадлежат одному множеству, то АВ не пересекает прямую.
Легко видеть, что утверждение верно и в сферической геометрии: большая окружность разбивает сферу на две открытые полусферы, причем выполнены соответствующие требования.
Проанализировав все планиметрические аксиомы, я выяснила, что некоторые из аксиом выполняются и в сферической геометрии, другие же приходится отбросить.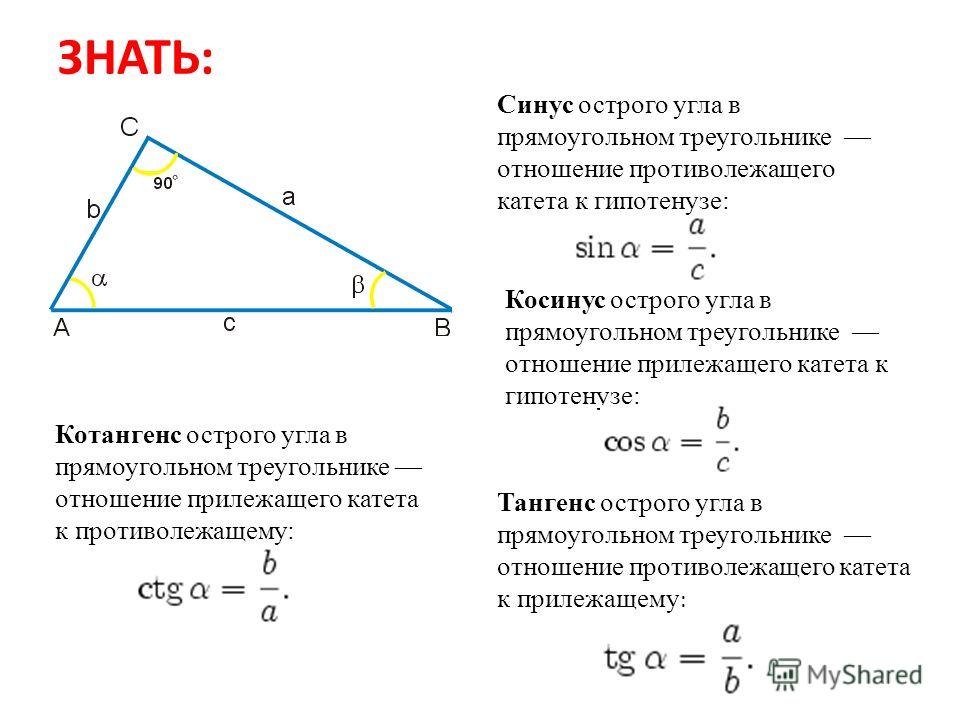
Сферическую геометрию можно рассматривать как модель геометрии, в которой некоторые обычные аксиомы геометрии не справедливы, то есть как простейшую модель неевклидовой геометрии.
Нужно отметить, что говоря о моделях геометрии, подразумевают некоторое множество точек, вместе с совокупностью выделенных подмножеств этого множества, называемых прямыми. Геометрические модели возникают при изучении геометрических свойств окружающего реального мира; при этом абстрагируются от всяких физических и прочих не геометрических свойств. Так, при изучении геометрии поверхности Земли на сравнительно небольших, «плоских», участках возникла обычная, так называемая евклидова геометрия (планиметрия).
Сравнение аксиом планиметрии и стереометрии представлено в таблице:
|
Планиметрия |
Сферическая геометрия |
|
Всякая прямая разбивает плоскость на две открытые полуплоскости — два непустых множества, таких, что для точек А и В, принадлежащих разным множествам, отрезок АВ пересекает данную прямую, а если А и В принадлежат одному множеству, то АВ не пересекает прямую. |
Совпадает. Большая окружность разбивает сферу на две открытые полусферы |
|
Каждая прямая есть множество точек |
Совпадает. Большие окружности суть множества точек |
|
Для любых двух точек А и В существует единственная содержащая эти точки прямая |
Совпадает если точки А и В сферы не являются диаметрально противоположными Но, для диаметрально противоположных точек А и В существует бесконечно много сферических прямых, содержащих эти точки: пересечение сферы с любой плоскостью, содержащей диаметр АВ, даст такую прямую. |
|
Исходя из поправки о диаметрально противоположных прямых формулируется следующая аксиома: Любые две различные прямые на сфере пересекаются в диаметрально противоположных точках сферы. |
|
|
Через любую точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну. |
Не существует, так как в сферической геометрии нет содержательного понятия параллельности — нет различных параллельных прямых. |
Сферический треугольник
Очень важная часть сферической геометрии – тема «Сферический треугольник». Этот простейший сферический многоугольник представляет особый интерес.
Этот простейший сферический многоугольник представляет особый интерес.
Свойства сферического треугольника (рис. 7.).
Рис. 7
Первым его ввёл в геометрический обиход и исследовал Менелай из Александрии (I в.). Его труд «Сферика» стал вершиной достижений треков в сферической геометрии. Менелай перенёс на сферу евклидову теорию плоских треугольников и вчисле прочего получил условие, при котором три точки на сторонах сферического треугольника или их продолжениях лежат на одной прямой. Интересно, что соответствующая теорема для плоскости в то время была уже широко известна, однако в историю геометрии она вошла именно как теорема Менелая.
Многие свойства сферического треугольника почти дословно повторяют свойства обычного треугольника. Среди них — неравенство треугольника, которое на языке трёхгранных углов гласит, что любой плоский угол трёхгранного угла меньше суммы двух других.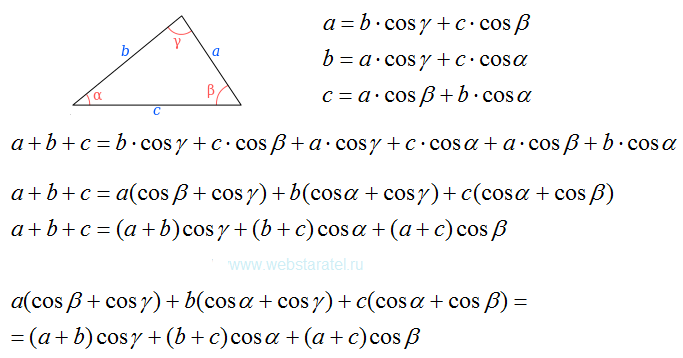
Для сферических треугольников справедливы три известных в планиметрии признака равенства: по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам, по трём сторонам.
На сфере справедлив ещё один признак равенства треугольников — по трём углам.
Подобных, но не равных между собой сферических треугольников не существует.
Понятно, что все планиметрические следствия упомянутых теорем вместе с их доказательствами остаются справедливыми на сфере. Так, множество точек, равноудалённых от концов отрезка, будет и на сфере перпендикурятной к нему прямой, проходящей через его середину, а отсюда следует, что серединные перпендикуляры к сторонам сферического треугольника АВС, биссектрисы внутренних углов, медианы и высоты имеют общую точку, точнее, две диаметрально противоположные общие точки Р и Р’, являющиеся полюсами его единственной описанной окружности. В стереометрии это означает, что около любого трёхгранного угла можно описать конус. Легко перенести на сферу и теорему о том, что биссектрисы треугольника пересекаются в центре его вписанной окружности.
В стереометрии это означает, что около любого трёхгранного угла можно описать конус. Легко перенести на сферу и теорему о том, что биссектрисы треугольника пересекаются в центре его вписанной окружности.
Теоремы о пересечении высот и медиан тоже остаются верными, но их обычные доказательства в планиметрии прямо или косвенно используют параллельность, которой, как мы знаем, на сфере нет, и поэтому проще доказать их заново, на языке стереометрии.
Равными треугольниками считаются те, которые могут быть совмещены после передвижения по сфере. Отсюда следует, что равные сферические треугольники имеют равные элементы и одинаковую ориентацию. Треугольники, имеющие равные элементы и различную ориентацию, называются симметричным.
Сравнение признаков Евклидова треугольника и сферического:
|
Треугольник на плоскости |
Сферический треугольник |
|
Признак неравенства треугольников: любой плоский угол трёхгранного угла меньше суммы двух других. |
|
|
Два треугольника называются равными, если их можно совместить наложением. |
Равными треугольниками считаются те, которые могут быть совмещены после передвижения по сфере. |
|
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны |
|
|
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны |
|
|
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны |
|
|
На сфере справедлив ещё один признак равенства треугольников — по трём углам. |
|
|
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны. |
Подобных, но не равных между собой сферических треугольников не существует. |
|
Если угол одного треугольника равен углу другого треугольника, а стороны, образующие этот угол, пропорциональны в равном отношении, то такие треугольники подобны. |
|
Сферическая тригонометрия.
Сферическая тригонометрия — математическая дисциплина, изучающая зависимости между углами и сторонами сферического треугольника.
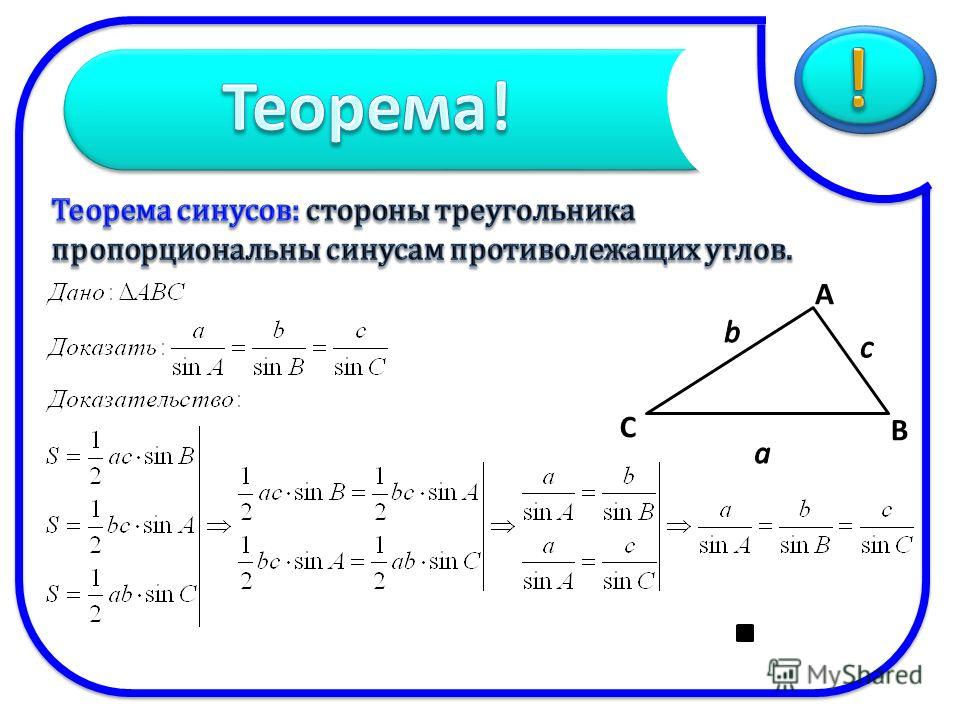
Сферическая теорема синусов
Теорема.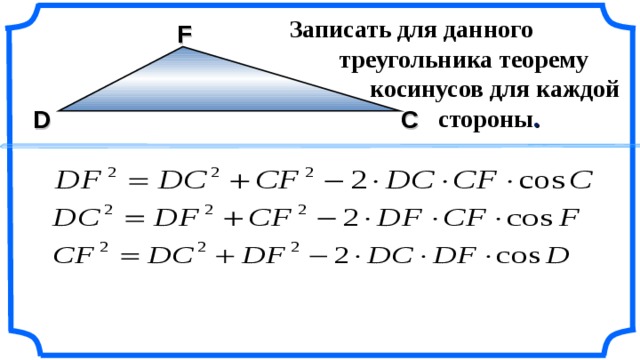 Синусы сторон сферического треугольника относятся как синусы противолежащих углов.
Синусы сторон сферического треугольника относятся как синусы противолежащих углов.
Пусть длины сторон сферического треугольника (рис. 14) равны а, b, с, а противолежащие им углы этого треугольника равны А, В, С соответственно, r- радиус сферы, тогда
Рис.8
Перейдем к теореме косинусов, которая гласит:
Косинус одной стороны сферического треугольника равняется произведению косинусов двух других его сторон плюс произведение синусов тех же сторон на косинус угла между ними:
cos
Просмотров работы: 478
КриссТал: Сферическая тригонометрия
КриссТал: Сферическая тригонометрия [Домашняя страница] [Введение в числа] [Отзывы читателей (математика)] [Язык] 7 Рекламная ссылка |
Сферическая тригонометрия имеет дело с треугольниками, нарисованными на сфере. Сюжет возник в исламских халифатах Ближнего Востока, Северной Африки и Испании в период с 8 по 14 века. Он возник для решения, казалось бы, простой задачи: В каком направлении находится Мекка?
Развитие этого предмета привело к совершенствованию искусства навигации, составлению звездных карт, составлению географических карт, определению положения восхода и захода солнца и усовершенствованию солнечных часов.
На рисунке выше треугольник ABC нарисован на сфере. Каждая линия треугольника представляет собой Большой круг . Это круги, нарисованные на сфере того же радиуса, что и сфера. Большие круги охватывают кратчайшее расстояние между двумя точками.
Заглавные буквы (A, B, C) обозначают углы между дугами большого круга треугольника, измеренные на поверхности сферы.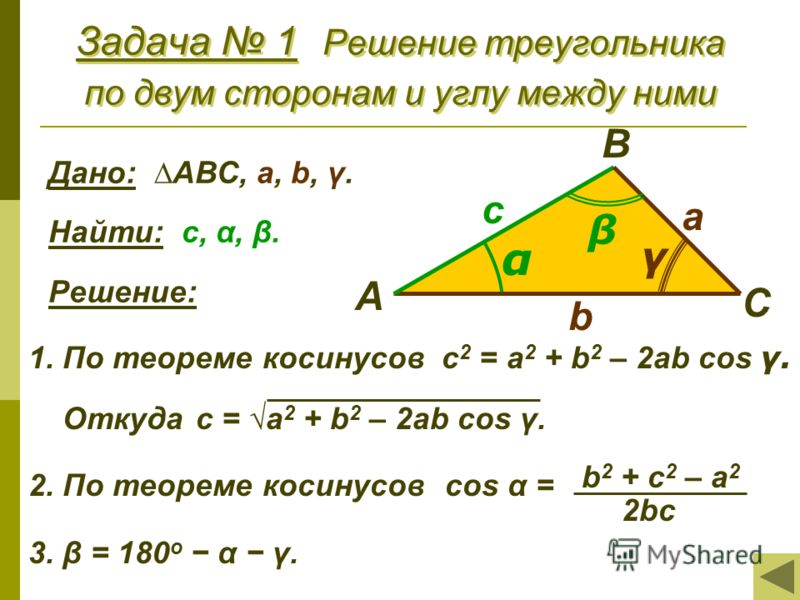 Меньшие последние (a, b, c) представляют длины дуг большого круга, измеренные как углы от центра сферы.
Меньшие последние (a, b, c) представляют длины дуг большого круга, измеренные как углы от центра сферы.
Сферический треугольник отличается от плоского треугольника тем, что сумма углов на больше , чем 180 градусов.
Правило косинусов
Существует правило косинусов для сферических треугольников: = Cos(a) × Cos(c) + Sin(a) × Sin(c) × Cos(B)Правило косинусов позволяет оценить длину одной из дуг сферического треугольника, если известны две другие дуги и угол, противоположный дуге.
Правило синусов
Правило синусов для сферических треугольников: Правило синусов можно использовать для нахождения угла, если известны две стороны и угол, ИЛИ для нахождения стороны, если известны два угла и сторона.Это таблица широт и долгот выбранных городов (в алфавитном порядке) для проработанных примеров.
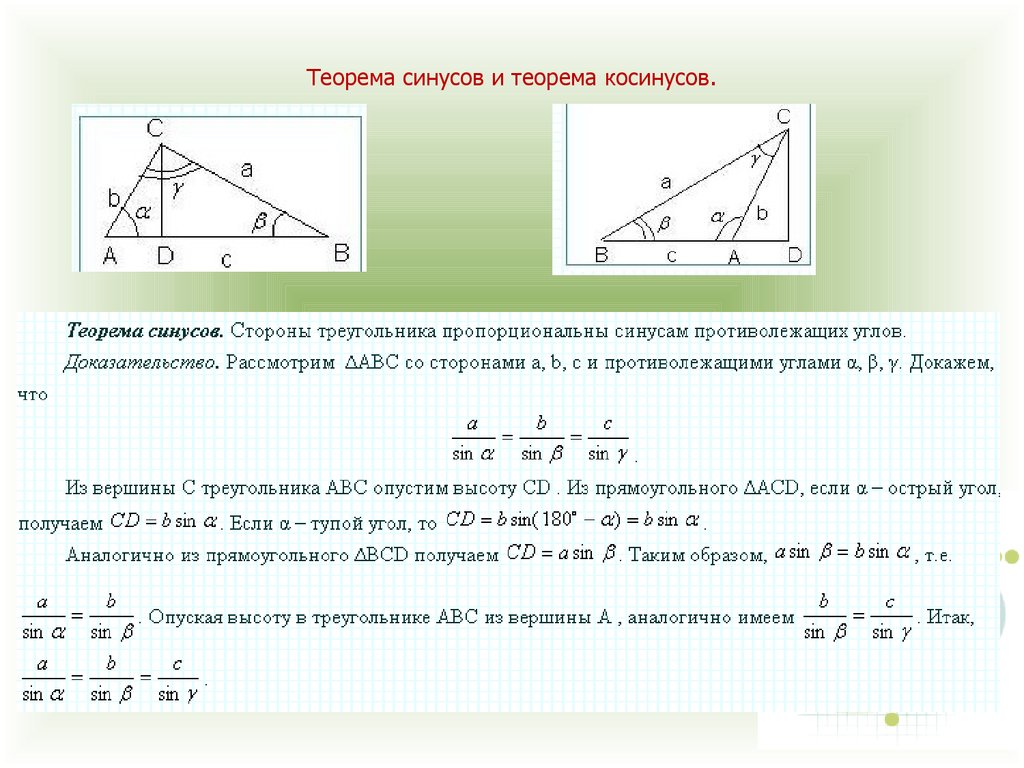
| Город | Страна | Широта | Долгота |
|---|---|---|---|
| Афины | Греция | 38.00°N | 23,44° в.д. |
| Багдад | Ирак | 33,20° с.ш. | 44,26° в.д. |
| Пекин | Китай | 39,55° с.ш. | 116,26° в. д. |
| Буэнос-Айрес | Аргентина | 34,40°ю.ш. | 58,30°з.д. |
| Кейптаун | Южная Африка | 33,56°ю.ш. | 18,28° в.д. |
| Чикаго | США | 41,50° с.ш. | 87,45°з.д. |
| Джакарта | Индонезия | 6,08°ю.ш. | 106,45° в. д. |
| Лондон | Великобритания | 51,30° с. ш. ш. | 0,10°з.д. |
| Мекка | Саудовская Аравия | 21,26° с.ш. | 39,49° в.д. |
| Мехико | Мексика | 19,25° с.ш. | 99,10°з.д. |
| Найроби | Кения | 1,17°ю.ш. | 36,50°E |
| Сидней | Австралия | 16,40°ю.ш. | 139,30° в. д. |
| Имя звезды | Склонение | Прямое восхождение |
|---|---|---|
| Альфа Центавра | -60,5° | 14ч 40м |
| Вега | +38,5° | 18ч 40м |
 Чтобы перевести километры в мили, разделите на 1,609.
Чтобы перевести километры в мили, разделите на 1,609.Определения
Правила косинуса и синуса могут быть использованы для решения основных задач навигации на поверхности Земли.На рисунке выше точки B и C — это две точки на поверхности Земли. Мы можем определить следующее:
- Точка А — это Северный полюс.
- Большой круг, соединяющий точки B и C, является кратчайшим расстоянием между ними.
- Большой круг (синий), соединяющий точки B’ и C’, — это экватор (0° широты).
- Большой круг (красный), соединяющий ABB’, является линией долготы. Это долгота Б.
- Большой круг, соединяющий АСС, — это еще одна линия Долготы. Это долгота C.
- Длина дуги большого круга B’B равна широте точки B. Дуга B’A равна 90° (от экватора до полюса).
- Длина дуги большого круга C’C равна широте точки C. Дуга C’A также равна 90°.
Широта (λ) измеряется в градусах (°) от экватора на север (отмечено N) или на юг (S). Широта Северного полюса составляет 90° северной широты, а широта Южного полюса составляет 90° южной широты. Южные широты считаются отрицательными (по соглашению). Экватор — это естественная линия на Земле, поскольку она представляет собой большой круг, делящий пополам ось вращения Земли.
Широта Северного полюса составляет 90° северной широты, а широта Южного полюса составляет 90° южной широты. Южные широты считаются отрицательными (по соглашению). Экватор — это естественная линия на Земле, поскольку она представляет собой большой круг, делящий пополам ось вращения Земли.
Долгота (L) измеряется в градусах восточной (E) или западной (W) линии долготы, проходящей через Гринвичскую обсерваторию в пригороде Лондона (Великобритания). Это называется нулевым меридианом Гринвичского меридиана . Это не естественная линия, выбранная условно.
Использование теоремы косинусов
Правило косинуса можно использовать для определения расстояния между точками B и C (дуга, a ) следующим образом:где
- A — угол, измеренный в градусах.
 Это разница в долготе между точками B и C.
Это разница в долготе между точками B и C. - Дуга большого круга, b , равна 90° минус широта C. Это называется полярным расстоянием .
- Дуга большого круга, c , равна 90° минус широта B.
Если мы используем диаграмму ниже, то B — это Лондон, а C — Багдад. Из таблицы выше Лондон имеет широту 51,30 ° северной широты и долготу 0,10 ° западной долготы. Багдад имеет широту 33,20 ° северной широты и долготу 44,26 ° восточной долготы.
- Мы ищем a , угловое расстояние по большому кругу между Лондоном и Багдадом. Это кратчайшее расстояние между этими двумя городами по поверхности Земли. На схеме он показан красным.
- A (разница в долготе между Лондоном и Багдадом) составляет 44,26°E + 0,10°W = 44,36°.
 Два города лежат по разные стороны Гринвичского меридиана (просто так), поэтому мы добавляем долготы.
Два города лежат по разные стороны Гринвичского меридиана (просто так), поэтому мы добавляем долготы. - b — полярное расстояние до Багдада, равное 90° минус широта Багдада (90° — 33,20° = 56,80°).
- c — полярное расстояние до Лондона: 90° минус широта Лондона (90° — 51,30° = 38,70°).
По правилу косинуса:
подставляя значения:
что дает:
 Следовательно, расстояние между Лондоном и Багдадом равно
Следовательно, расстояние между Лондоном и Багдадом равноПравило косинуса с широтами
В разделе о тригонометрии мы видели, что для любого угла X в градусахпоэтому мы можем переписать правило косинусов, чтобы использовать (более доступные) широты вместо полярных расстояний.
Существует две формы этого правила в зависимости от того, совпадают ли значения двух долгот. Если обе долготы находятся на одной стороне Гринвичского меридиана (т. е. обе E или обе W), формула задается следующим образом:
Если долготы находятся на разных сторонах Гринвичского меридиана (т. е. одна — E, а другая — W), формула задается следующим образом:
е. одна — E, а другая — W), формула задается следующим образом:
В любой форме:
- Dist BC — это угловое расстояние между B и C по дуге большого круга. Это кратчайшее расстояние между двумя точками.
- λ B — широта B (положительная для N, отрицательная для S).
- λ C — широта C (положительная для N, отрицательная для S).
- L B — долгота B.
- L C — долгота C.
Если мы установим B в Мехико, а C в Чикаго на диаграмме ниже и воспользуемся правилом косинуса с широтами:
- Dist BC — необходимое угловое расстояние между Мехико и Чикаго.
 Это и на диаграмме выше.
Это и на диаграмме выше. - λ B — широта Мехико (угол BB’ = 19,25°N).
- λ C — широта Чикаго ( CC’ = 41,50° северной широты).
- L B — долгота Мехико (99,10° западной долготы). Большой круг ABB’ и есть эта Долгота.
- L C — долгота Чикаго (87,45° западной долготы). Большой круг ACC’ .
Обе долготы находятся к западу от Гринвичского меридиана, поэтому мы используем следующее правило косинуса с широтами:
Подставив значения и взяв разницу между двумя долготами, мы имеем:
Это дает:
 э. ) = 0,6626 × 0,3297 + 0,7490 × 0,9441 × 0,9794 = 0,9110
э. ) = 0,6626 × 0,3297 + 0,7490 × 0,9441 × 0,9794 = 0,9110 Следовательно:
Расстояние между Чикаго и Мехико равно:
- Dist BC — необходимое угловое расстояние между Буэнос-Айресом и Афинами ( a ).
- λ B — широта Буэнос-Айреса ( B’B = 34,40°ю.ш.). Находясь к югу от экватора, это можно записать как -34,40 °.

- λ C — широта Афин ( CC’ = 38,00° северной широты).
- L B — долгота Буэнос-Айреса (58,30° западной долготы). Большой круг AB’B .
- L C — долгота Афин (23,44° в.д.). Большой круг ACC’ .
Две долготы находятся на разных сторонах Гринвичского меридиана, поэтому мы используем следующее правило косинуса с широтами:
Вставьте значения. Помните, что мы используем отрицательную широту для Буэнос-Айреса:
Из графиков синусов и косинусов в эссе «Тригонемтрические уравнения» мы знаем, что:
Следовательно,
Что дает:
Следовательно:
Расстояние между Буэнос-Айресом и Афинами равно:
Определения
В этом разделе мы рассмотрим направление между двумя точками.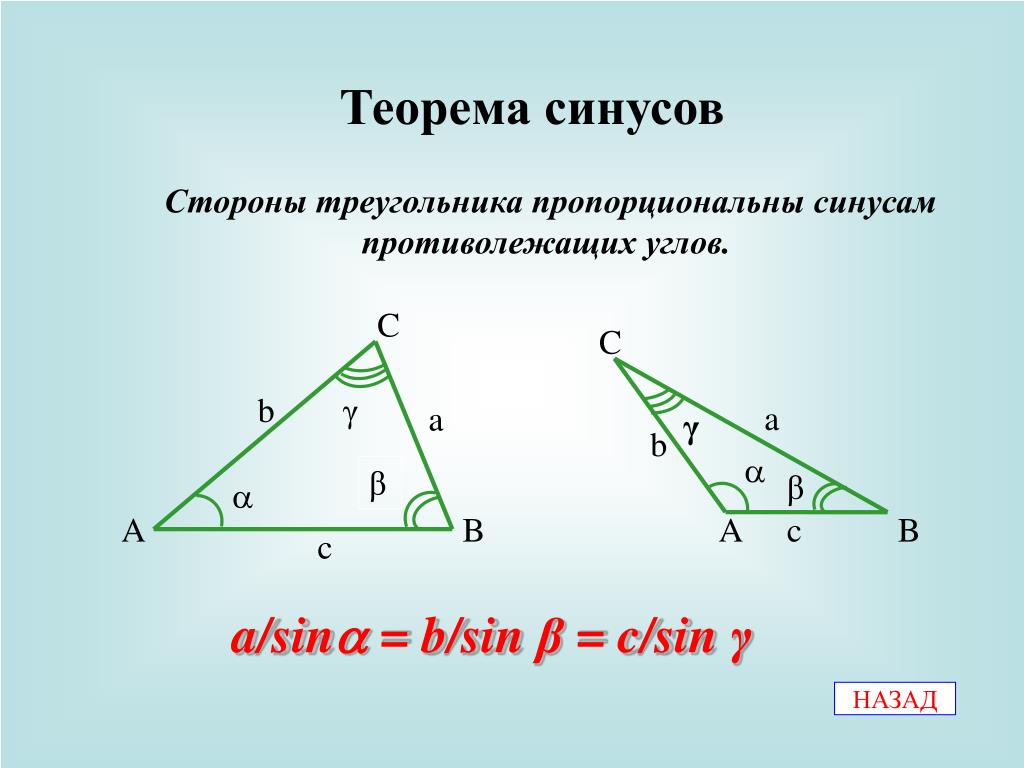 Если мы едем из B в C (на диаграмме ниже), то мы должны двигаться в определенном направлении, заданном углом ABC. Этот угол называется курсом или курсом и измеряется в градусах по часовой стрелке от севера.
Если мы едем из B в C (на диаграмме ниже), то мы должны двигаться в определенном направлении, заданном углом ABC. Этот угол называется курсом или курсом и измеряется в градусах по часовой стрелке от севера.Использование правила синусов
Правило синусов можно использовать для определения направления между точками B и C (угол B) следующим образом:0002 Грех(а) / Грех(А) = Грех(б) / Грех(В) = Грех(с) / Грех(С)где
- Строчные буквы ( a , b , c ) — это дуги больших кругов.
- Прописные буквы ( A , B , C ) — это углы между большими кругами, составляющими треугольник. Угол A представляет собой разницу в логитедах между точками В и С. Долготы складываются, если они находятся на разных сторонах Гринвичского меридиана, и вычитаются, если они находятся на одной стороне Гринвичского меридиана.

Используя диаграмму ниже, установите C для Джакарты и B для Мекки.
Дуги больших кругов ( c и b ) известны. Это просто полярные расстояния точек B и C соответственно (90° минус широта этих точек). Угол A также известен: это разница долгот между точками C и B. Правило синусов можно использовать только следующим образом:
Преобразование C дает
где
- C — требуемый угол.
 Это будет к западу от севера (угол ACB на схеме).
Это будет к западу от севера (угол ACB на схеме). - A — это разница долготы между Меккой и Джакартой. В данном случае значение равно 66,96°.
- c — полярное расстояние до Мекки (90° — 21,26° = 68,74°).
- a — это расстояние между Меккой и Джакартой. Это определяется с помощью правила косинуса и имеет значение 71,08 ° (соответствует расстоянию 7912 км).
По правилу синусов
что дает
Это дает значение угла C:
Чтобы повернуться лицом к Мекке из Джакарты, нужно повернуться лицом на север и повернуться против часовой стрелки на угол 65,04°.
Пример 5: Самолет должен лететь из Кейптауна в Южной Африке в Пекин в Китае. Если судно летит по прямой линии, какой курс должен следовать пилот.
Если судно летит по прямой линии, какой курс должен следовать пилот. Используя приведенную ниже диаграмму, установите B в Кейптаун, а C в Пекин.
Опять же, мы используем правило синусов:
Преобразование B дает
где
- B — требуемый угол. Это будет к востоку от севера. Курс измеряется по часовой стрелке от севера, поэтому этот угол и будет курсом.
- A — это разница долготы между Кейптауном и Пекином. В данном случае значение равно 97,98°.
- b — полярное расстояние до Пекина (90° — 39,55° = 50,45°).

- a — это расстояние между Кейптауном и Пекином. Это определяется с помощью правила косинусов и имеет значение 116,18 ° (соответствует расстоянию 12 933 км).
По правилу синусов
что дает
Это дает значение угла B:
Чтобы лететь из Кейптауна в Пекин, нужно держать курс 58,31°.
Определения
В эссе о системах координат было показано, что есть две местные координаты, которые можно использовать для определения положения звезды из определенного места. На схеме ниже точка O — наблюдатель и S — звезда:- Угол НЕ — это Азимут , α , (измеряется в градусах по часовой стрелке от севера).

- Угол TOS — это Высота , измеренная в градусах от горизонта. На практике проще измерить зенитное расстояние , z , которое равно 90° — высота над уровнем моря. Zenith — точка прямо над головой.
Карта звездного неба (или таблица положений звезд) — очень полезный помощник в навигации. Небесная Сфера имеет систему координат, аналогичную земной. прямое восхождение аналогично долготе на Земле. Он находится путем измерения времени и здесь обсуждаться не будет. Склонение звезды — это количество градусов к северу или югу от небесного экватора . Как только эти две координаты известны, звезда может быть точно нанесена на карту звездного неба или занесена в таблицу для использования в навигации.
Поиск отклонений
Если азимут звезды ( α ) и зенитное расстояние ( z ) измеряются одновременно из места, широта которого ( λ ) известна, то склонение звезды (данное символом δ ) может быть найдено с помощью приведенной ниже формулы склонения .
Звезды имеют фиксированное положение (в течение жизни человека), но такие объекты, как Солнце, Луна, планеты и кометы, меняют свое положение на небе, поэтому этот процесс также можно использовать для отслеживания их движения на фоне звезд и нанесения их траекторий на звездную карту. .
Пример 6: Новая комета обнаружена в Сиднее, Австралия. Его азимут ( α ) измеряется как 57,40 °, а его зенитное расстояние ( z ) составляет 83,70 °. Каково его склонение.Перед использованием формулы мы перечисляем значения, которые будут использоваться:
- Требуемое склонение ( δ ).
- Азимут ( α ) равен 57,40°.
- Зенитное расстояние ( z ) равно 83,70°.
- Широта Сиднея ( λ ) составляет 16,40 ° ю.ш. (что можно записать как -16,40 °).

Используя формулу склонения,
что дает
Помня, что Sin(-X) = -Sin(X) и Cos(-X) = Cos(X), это можно переписать как
Это дает
Следовательно,
На звездной карте комета находится на 33° южнее небесного экватора.
Поиск широты
Это обратная сторона поиска склонений. Однако необходимо использовать две звезды. Оба должны иметь известное склонение. Для определения широты навигатору требуется таблица склонений и инструмент для измерения зенитного расстояния и азимута выбранных звезд.
Метод заключается в одновременном измерении зенитного расстояния и азимута двух известных звезд. Формула длинная, поэтому она разбита ниже:
куда
а также
Символы определяются следующим образом:
- λ — требуемая Широта.
- z 1 , z 2 — зенитные расстояния двух выбранных звезд.
- α 1 , α 1 — азимуты двух выбранных звезд.
- δ 1 , δ 1 — Склонения выбранных звезд (из таблиц или звездной карты).

В следующем примере для краткости углы измеряются только с точностью до 1 знака после запятой.
В качестве примечания: долгота определяется путем знания местного времени и сравнения его со средним временем по Гринвичу . Каждая разница в один час соответствует разнице в 15° по долготе. Это не рассматривается в этом эссе.
Пример 7: На корабле производятся следующие измерения звезд Альфа Центавра (азимут: 183,0°; зенитное расстояние: 74,0°) и Вега (азимут: 51,0°; зенитное расстояние: 54,5°). Найдите широту.Сначала мы перечисляем элементы, необходимые для формулы.
- λ — требуемая Широта.
- z 1 , z 2 — зенитные расстояния Альфы Центавра (74,0°) и Веги (54,5°).
- α 1 , α 1 — азимуты Альфы Центавра (183,0°) и Веги (51,0°).
- δ 1 , δ 1 — это склонения Альфы Центавра (-60,5°) и Веги (38,5°), взятые из таблицы выше.

Теперь мы можем начать вставлять значения в формулу, начиная с P:
что дает
Теперь Q:
= Cos(74,0°) × Sin(54,5°) × Cos(51,0°) — Sin(74,0°) × Cos(54,5°) × Cos(183,0°)
что дает
Наконец,
Это дает нам значение Широты:
Определения
Склонение Солнца меняется в течение года от +23,5° 21 июня до -23,5° 21 декабря. Эти две даты называются солнцестояниями года. Это движение с севера от экватора к югу от экватора вызывает смену времен года. Он также меняет продолжительность светового дня и положение местных восходов и закатов в течение года.
Эти две даты называются солнцестояниями года. Это движение с севера от экватора к югу от экватора вызывает смену времен года. Он также меняет продолжительность светового дня и положение местных восходов и закатов в течение года.В дни равноденствий (21 марта и 23 сентября) склонение Солнца равно 0°, Солнце восходит точно на востоке (азимут 90°) и садится точно на западе (азимут 270°). В другое время года Солнце восходит и заходит к северу или югу от восточной или западной точки по мере изменения его склонения.
На приведенной выше диаграмме (в Северном полушарии) красная линия — это дневной путь Солнца в день равноденствия. Восходит на востоке (азимут = NOE ) проходит через Юг (когда он самый высокий) и заходит на Западе (Азимут = СЕЙЧАС ).
Синяя линия — это ежедневный путь Солнца во время декабрьского солнцестояния. Солнце восходит к югу от востока (азимут = NOR ), проходит через юг (ниже, чем в дни равноденствия) и заходит к югу от запада (азимут = НЕ ).
На диаграмме выше зеленая линия — это дневной путь Солнца во время июньского солнцестояния. Солнце восходит к северу от востока (азимут = NOR ), проходит через юг (выше, чем в дни равноденствий) и заходит к северу от запада (азимут = НЕ ).
Эта формула вычисляет точки восхода и захода Солнца (или любого другого объекта), если его склонение известно для данной Широты.
Символы определяются следующим образом:
- α — требуемый азимут.
- дельта — Склонение Солнца (или другого объекта).
- λ — Широта наблюдателя.
Сначала мы перечисляем значения, которые будут использоваться:
- α – требуемый азимут.

- δ — Склонение Солнца (0° 21 марта).
- λ — широта Лондона, Найроби или Сиднея. Эти значения 51,30° с. ш., 1,17° ю. ш. и 16,40° ю. ш. соответственно.
Используя формулу,
Понятно, что независимо от значения λ , когда δ = 0,
следовательно,
Это доказывает, что Солнце восходит и заходит строго на востоке и западе соответственно 21 марта для трех городов.
Пример 9: Найдите положение восхода солнца в Найроби 21 июня и 21 декабря.Сначала мы перечисляем значения, которые будут использоваться:
- α – требуемый азимут.
- δ — Склонение Солнца в эти два дня (+23,5° 21 июня; -23,5° 21 декабря).

- λ — широта Найроби (1,17° южной широты или -1,17°).
Используя формулу,
Для Найроби 21 июня
Для Найроби 21 декабря
Это дает две требуемые точки восхода солнца:
Найроби находится недалеко от экватора (λ = 1,17 ° ю.ш.). Разница в положении восхода солнца в два дня солнцестояния составляет 47 °, что является разницей в склонении Солнца между двумя датами.
Пример 10. Найдите положение восхода солнца в Лондоне 21 июня и 21 декабря.Сначала мы перечисляем значения, которые будут использоваться:
- α – требуемый азимут.

- δ — Склонение Солнца в эти два дня (+23,5° 21 июня; -23,5° 21 декабря).
- λ — широта Лондона (51,30° северной широты).
Используя формулу,
Для Лондона 21 июня:
Для Лондона 21 декабря
Это дает две требуемые точки восхода солнца:
Лондон находится далеко к северу от экватора (λ = 51,30° с.ш.). Разница в положении восхода солнца в два дня солнцестояния составляет более 79°.
История и описание
Самый ранний хронометрист был солнечные часы . Первоначально они состояли из палки (называемой гномон ), помещенной вертикально в землю. По положению тени можно было получить представление о времени суток. Простой гномон использовался всеми основными древними цивилизациями, включая вавилонян, египтян, жителей долины Инда, китайцев, греков и римлян.
По положению тени можно было получить представление о времени суток. Простой гномон использовался всеми основными древними цивилизациями, включая вавилонян, египтян, жителей долины Инда, китайцев, греков и римлян.
Одна проблема с вертикальным гномоном заключается в том, что склонение Солнца меняется в течение года. Это влияет на Солнце двумя способами:
- Солнце находится на разной высоте в определенное время дня и в разное время года.
- Видимый путь Солнца в небе меняется в течение года.
Эти два эффекта означают, что движение тени Солнца в течение дня в июне отличается от движения тени в декабре. Июньский час, измеренный от тени Солнца у подножия гномона, отличается по продолжительности от декабрьского часа. Для каждого месяца требуется своя шкала у подножия гномона для точного определения времени.
Современные солнечные часы
В 10 веке нашей эры мавританские правители Испании решили эту проблему, сделав солнечные часы под углом.
На приведенной выше диаграмме показаны мавританские солнечные часы, которые в настоящее время являются обычным украшением садов Великобритании.
Угол OQP равен широте места, где будут располагаться солнечные часы. Солнечные часы для Багдада не будут работать в Лондоне или Афинах. Солнечные часы расположены (в северном полушарии) так, что линия QP обращен к точке прямо над Северным полюсом в небе ( Северный небесный полюс ). Другими словами, солнечные часы выровнены по меридиану Север-Юг. Это делает линию QP параллельной оси вращения Земли.
Это простое изменение приводит к тому, что все часы, измеренные по тени Солнца, имеют одинаковую продолжительность в течение года, независимо от видимого пути Солнца по небу.
Тень Солнца в местный полдень будет направлена строго на север. На каждый час после местного полудня тень солнечных часов (называемая Shadow Angle и показанный на диаграмме OTQ ) будут смотреть в другом направлении.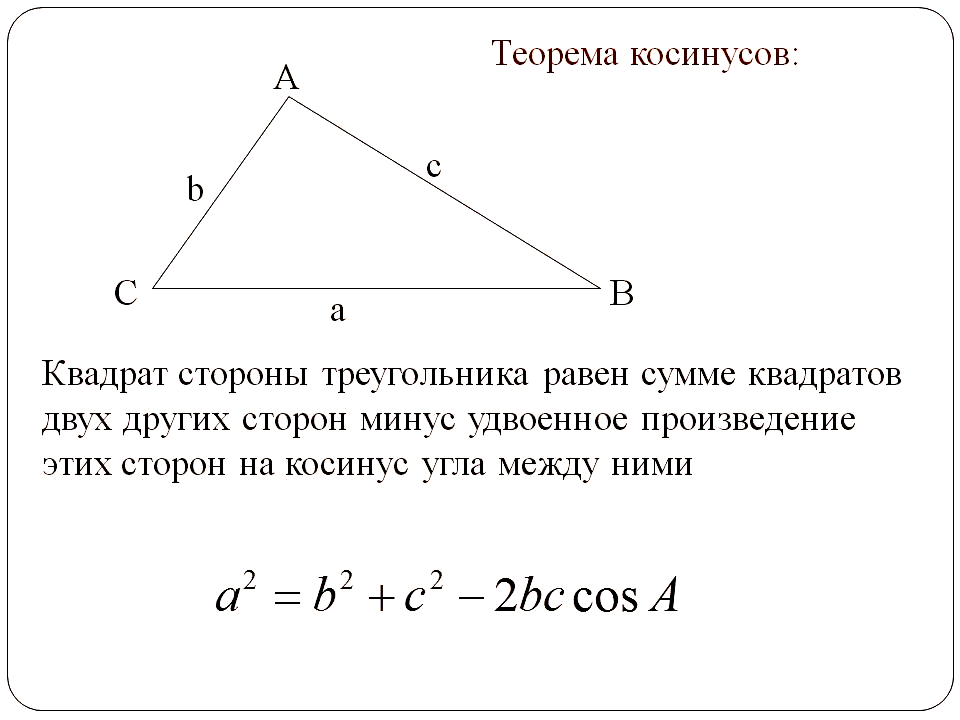 В каждую единицу времени будет происходить регулярное движение тени, и это можно рассчитать.
В каждую единицу времени будет происходить регулярное движение тени, и это можно рассчитать.
После того, как солнечные часы построены под правильным углом и правильно расположены, градуировка для измерения времени может быть найдена по следующей формуле.
где
- S — угол тени для заданного времени (скажем, 13:00). Угол тени измеряется в градусах от положения тени Солнца в местный полдень. Здесь на шкале у подножия солнечных часов будет стоять отметка этого времени.
- λ — широта солнечных часов (для правильной работы они должны равняться углу OQP ).
- H требуемый час. В формуле оно умножается на 15, потому что за полные 24-часовые солнечные сутки Солнце, кажется, делает один оборот вокруг Земли (360°). Это означает, что 360° эквивалентны 24 часам; 15° эквивалентно одному часу (360/24 = 15).

Необходимые значения:
- S (угол тени). Это то, что мы ищем.
- λ — широта Лондона (51,30°).
- H — требуемый час, в данном случае 2.
Используя формулу,
Это дает
Угол тени, ю.ш. , следовательно, равен
. Ежедневное движение Солнца — с востока на запад (если смотреть на юг, движение слева направо в северном полушарии). Поэтому тень Солнца будет двигаться от своего северного положения в местный полдень к востоку. Отметка 14:00 будет поставлена на 24,26° северной широты. Поскольку движение Солнца симметрично, отметка 10:00 (полдень минус 2 часа) также будет на 24,26°, но на западной стороне севера.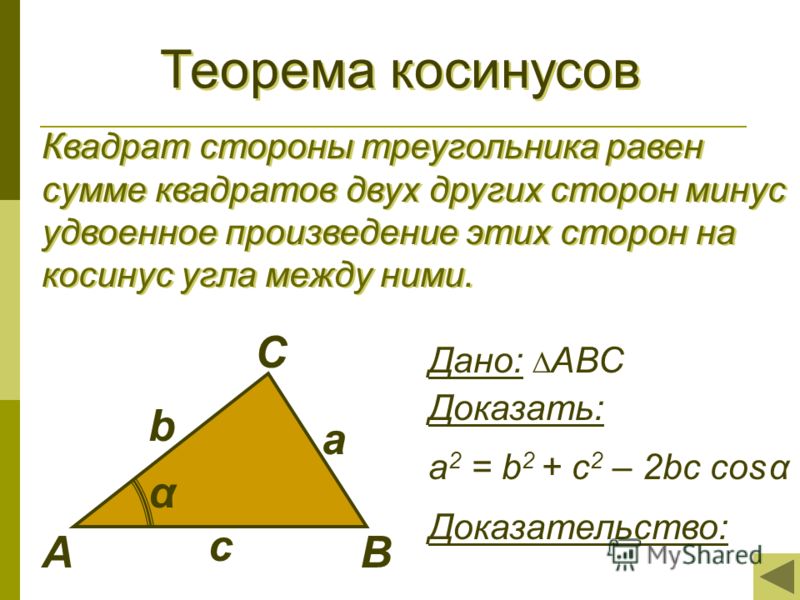
Таким образом, все часы (или полчаса, или даже четверть часа) могут быть отмечены на шкале солнечных часов.
Столы
Ниже приведена таблица углов тени от местного полудня (0 часов) до 5 часов вечера (5 часов) для солнечных часов в Лондоне (Великобритания), Афинах (Греция) и Мехико (Мексика), полученная из приведенной выше формулы. Конечно, те же углы можно использовать и с 7 утра до полудня по местному времени.| Время | Лондон (λ = 51,30°) | Афины (λ = 38,00°) | Мехико (λ = 19,25°) |
|---|---|---|---|
| 0h | 0° | 0° | 0° |
| 1ч | 11,81° | 9,37° | 5,05° |
| 2ч | 24,26° | 19,57° | 10,78° |
| 3 часа | 37,97° | 31,62° | 18,25° |
| 4ч | 53,51° | 46,84° | 29,73° |
| 5ч | 71,05° | 66,48° | 50,90° |

Из таблицы видно, что во всех трех городах угол тени равен 0° в местный полдень (0ч). Остальные углы все разные. Например, в Лондоне тень Солнца сдвинется на 37,39°.° между местным полуднем и 15:00. Это угол тени для 3 часов в таблице. В Афинах тот же период времени произведет движение тени на 31,62°. В Мехико этот показатель составит 18,25°. Чем ближе солнечные часы к экватору, тем меньше движение тени Солнца между местным полуднем и 15:00.
Корректировка солнечных часов
Прежде чем солнечные часы можно будет использовать для определения времени, необходимо внести три поправки в показания положения тени. На самом деле Солнце не является идеальным хранителем времени. Это связано с тем, что его движения имеют определенные неравномерности, из-за которых время, считываемое с солнечных часов, может отличаться от времени на часах до 17 минут. Коррекция должна быть сделана (называется Уравнение времени ) и вычитается из времени, считанного с солнечных часов, чтобы получить правильное время на часах. Эта коррекция зависит только от даты. Диаграмма показана ниже. Уравнение Времени равно нулю четыре дня в году.
Эта коррекция зависит только от даты. Диаграмма показана ниже. Уравнение Времени равно нулю четыре дня в году.
Большинство стран используют часовых поясов . Это полосы территории шириной обычно 15°. Время часов установлено на местное время в центре часового пояса. Если солнечные часы находятся точно в центре часового пояса, корректировка не требуется. Однако, если солнечные часы расположены на краю часового пояса, они могут быть на 7,5° от центра. Поскольку 1 час эквивалентен 15°, эта ошибка приведет к тому, что время на солнечных часах будет отставать от времени на часах до получаса. Эта поправка зависит от положения солнечных часов и всегда имеет постоянное значение. Он равен
где L S — долгота солнечных часов, а L T — долгота центра часового пояса.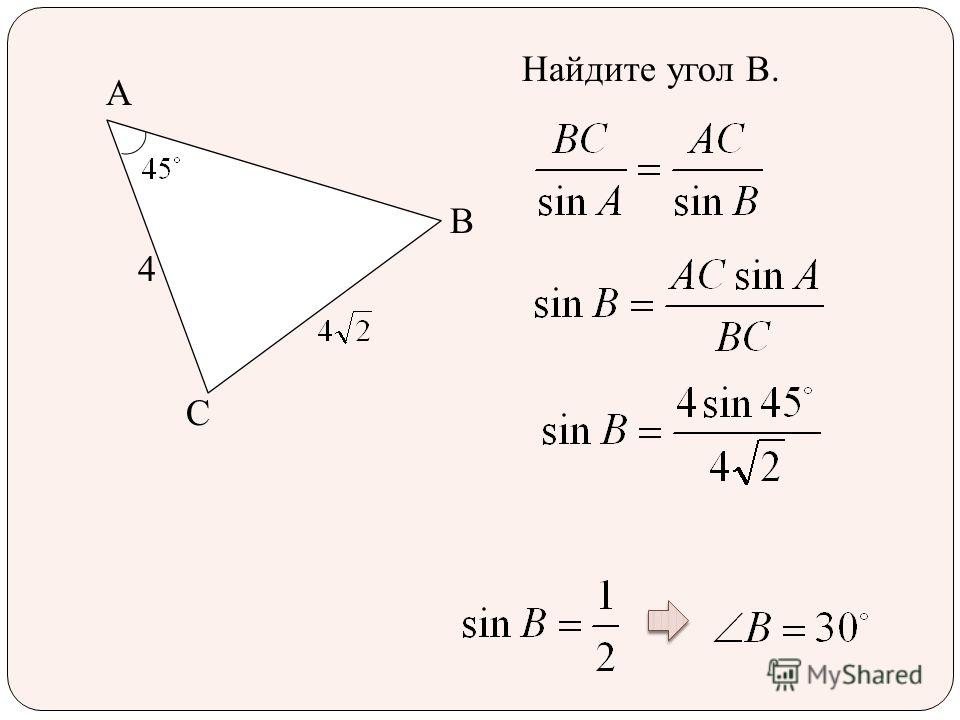 Если солнечные часы находятся к востоку от центра часового пояса, поправка вычитается, если к западу – добавляется.
Если солнечные часы находятся к востоку от центра часового пояса, поправка вычитается, если к западу – добавляется.
Третья поправка: Летнее время или Летнее время . Если это сила, то к времени на солнечных часах нужно добавить час, чтобы часы получили время. В каждой стране действуют разные правила, когда действует этот дополнительный час.
© 2004, 2009 КриссТал
Это эссе было вдохновлено британским политиком Робертом Килроем-Силком , который писал, что арабская цивилизация не принесла миру ничего примечательного.
Введение в различные системы координат, используемые в географии и астрономии. Прямоугольные треугольники. Синусы, косинусы и тангенсы. Тригонометрические расчеты, формулы и ряды. Сесекансы, косекансы и котангенсы. Тригонометрические тождества и тригонометрические графы. Решение уравнений, содержащих синусы, косинусы и тангенсы.
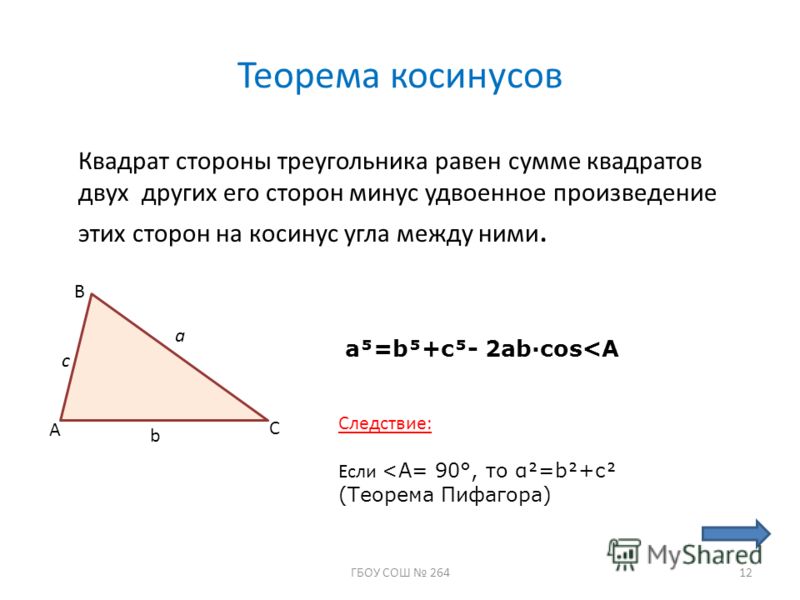 Что мы подразумеваем под словами день , неделя , месяц , год ? Кто изобрел наш календарь? Когда началось третье тысячелетие? Связь между временем и астрономией.
Что мы подразумеваем под словами день , неделя , месяц , год ? Кто изобрел наш календарь? Когда началось третье тысячелетие? Связь между временем и астрономией.тригонометрия | Определение, формулы, отношения и тождества
тригонометрические функции
Смотреть все СМИ
- Ключевые люди:
- Гиппарх Леонард Эйлер Региомонтан Абу аль-Вафах Франсуа Виет, сеньор де ла Биготьер
- Похожие темы:
- тригонометрическая таблица сферический треугольник плоская тригонометрия сферическая тригонометрия аналитическая тригонометрия
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
тригонометрия , раздел математики, связанный со специфическими функциями углов и их применением в вычислениях. В тригонометрии обычно используются шесть функций угла. Их названия и сокращения: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Эти шесть тригонометрических функций по отношению к прямоугольному треугольнику показаны на рисунке. Например, треугольник содержит угол А , а отношение стороны, противоположной А и стороны, противоположной прямому углу (гипотенузе), называется синусом А , или синусом А ; аналогично определяются другие тригонометрические функции. Эти функции являются свойствами угла A , не зависящими от размера треугольника, и вычисленные значения были сведены в таблицы для многих углов до того, как компьютеры сделали тригонометрические таблицы устаревшими. Тригонометрические функции используются для получения неизвестных углов и расстояний от известных или измеренных углов в геометрических фигурах.
Их названия и сокращения: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Эти шесть тригонометрических функций по отношению к прямоугольному треугольнику показаны на рисунке. Например, треугольник содержит угол А , а отношение стороны, противоположной А и стороны, противоположной прямому углу (гипотенузе), называется синусом А , или синусом А ; аналогично определяются другие тригонометрические функции. Эти функции являются свойствами угла A , не зависящими от размера треугольника, и вычисленные значения были сведены в таблицы для многих углов до того, как компьютеры сделали тригонометрические таблицы устаревшими. Тригонометрические функции используются для получения неизвестных углов и расстояний от известных или измеренных углов в геометрических фигурах.
Тригонометрия возникла из-за необходимости вычислять углы и расстояния в таких областях, как астрономия, составление карт, геодезия и дальномер артиллерийских орудий.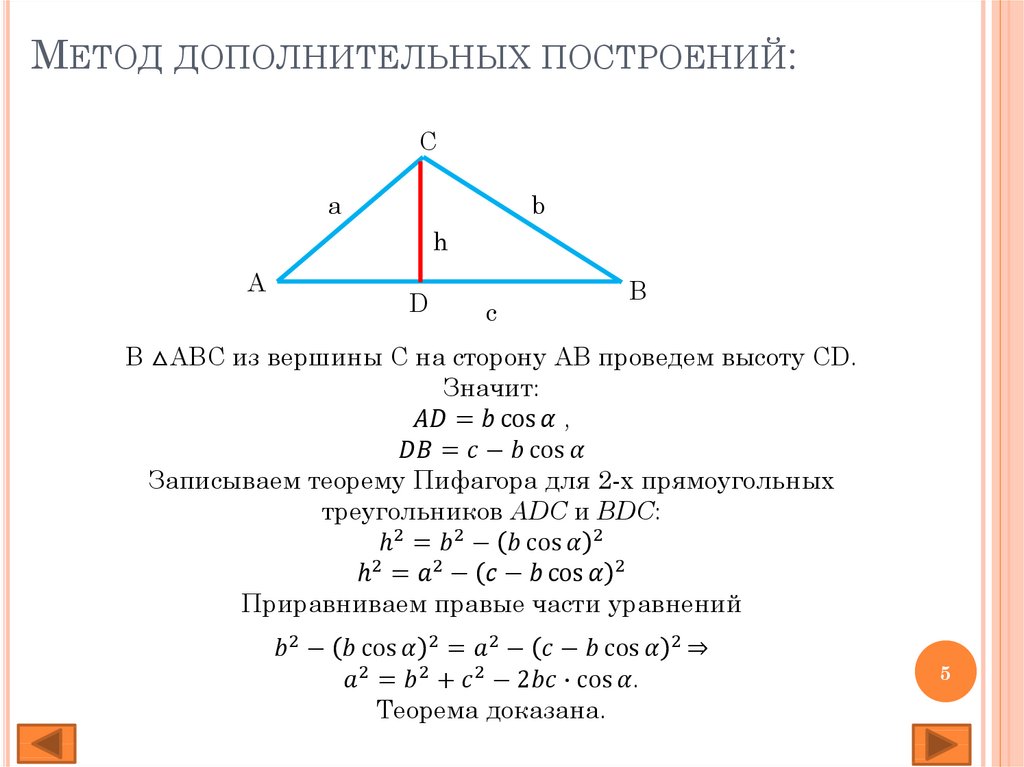 Задачи, связанные с углами и расстояниями в одной плоскости, рассматриваются в плоской тригонометрии. Приложения к подобным задачам более чем в одной плоскости трехмерного пространства рассматриваются в сферической тригонометрии.
Задачи, связанные с углами и расстояниями в одной плоскости, рассматриваются в плоской тригонометрии. Приложения к подобным задачам более чем в одной плоскости трехмерного пространства рассматриваются в сферической тригонометрии.
История тригонометрии
Классическая тригонометрия
Слово тригонометрия происходит от греческого слова тригонон («треугольник») и метрон («мерить»). Примерно до 16 века тригонометрия в основном занималась вычислением числовых значений отсутствующих частей треугольника (или любой формы, которую можно разбить на треугольники), когда были даны значения других частей. Например, если известны длины двух сторон треугольника и величина прилежащего к нему угла, можно вычислить третью сторону и два оставшихся угла. Такие вычисления отличают тригонометрию от геометрии, которая исследует главным образом качественные отношения. Конечно, это различие не всегда абсолютно: теорема Пифагора, например, представляет собой утверждение о длинах трех сторон прямоугольного треугольника и, таким образом, носит количественный характер. Тем не менее, в своем первоначальном виде тригонометрия в целом была потомком геометрии; только в 16 веке эти две науки стали отдельными разделами математики.
Тем не менее, в своем первоначальном виде тригонометрия в целом была потомком геометрии; только в 16 веке эти две науки стали отдельными разделами математики.
Древний Египет и Средиземноморье
Несколько древних цивилизаций — в частности, египетская, вавилонская, индуистская и китайская — обладали значительными познаниями в области практической геометрии, включая некоторые понятия, которые были прелюдией к тригонометрии. Папирус Райнда, египетский сборник из 84 задач по арифметике, алгебре и геометрии, датируемый примерно 1800 г. до н. э., содержит пять задач, касающихся секед . Тщательный анализ текста и сопровождающих его рисунков показывает, что это слово означает наклон склона — важное знание для крупных строительных проектов, таких как пирамиды. Например, в задаче 56 спрашивается: «Если высота пирамиды 250 локтей, а длина стороны ее основания 360 локтей, какова ее 9 локтей?1688 секедов ? Решение дается как 5 1 / 25 ладоней на локоть, и, поскольку один локоть равен 7 ладоням, эта дробь эквивалентна чистому отношению 18 / 25 .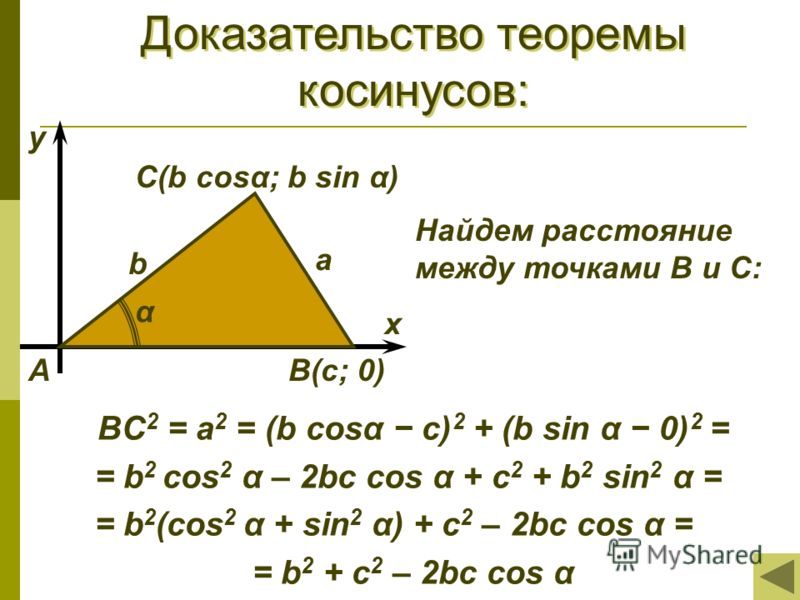 На самом деле это отношение «длины к высоте» рассматриваемой пирамиды — по сути, котангенс угла между основанием и гранью. Это показывает, что египтяне хотя бы немного знали числовые отношения в треугольнике, своего рода «прототригонометрию».
На самом деле это отношение «длины к высоте» рассматриваемой пирамиды — по сути, котангенс угла между основанием и гранью. Это показывает, что египтяне хотя бы немного знали числовые отношения в треугольнике, своего рода «прототригонометрию».
Британника Викторина
Числа и математика
A-B-C, 1-2-3… Если вы считаете, что считать числа — это то же самое, что читать алфавит, проверьте, насколько свободно вы владеете языком математики в этом тесте.
Тригонометрия в современном понимании началась с греков. Гиппарх ( г. ок. г., 190–120 гг. до н. э.) первым составил таблицу значений тригонометрической функции. Он рассматривал каждый треугольник — плоский или сферический — как вписанный в окружность, так что каждая сторона становится хордой (то есть прямой линией, соединяющей две точки на кривой или поверхности, как показано вписанным треугольником 9).1688 A B C на рисунке). Чтобы вычислить различные части треугольника, нужно найти длину каждой хорды как функцию центрального угла, который ее стягивает, или, что то же самое, длину хорды как функцию соответствующей ширины дуги.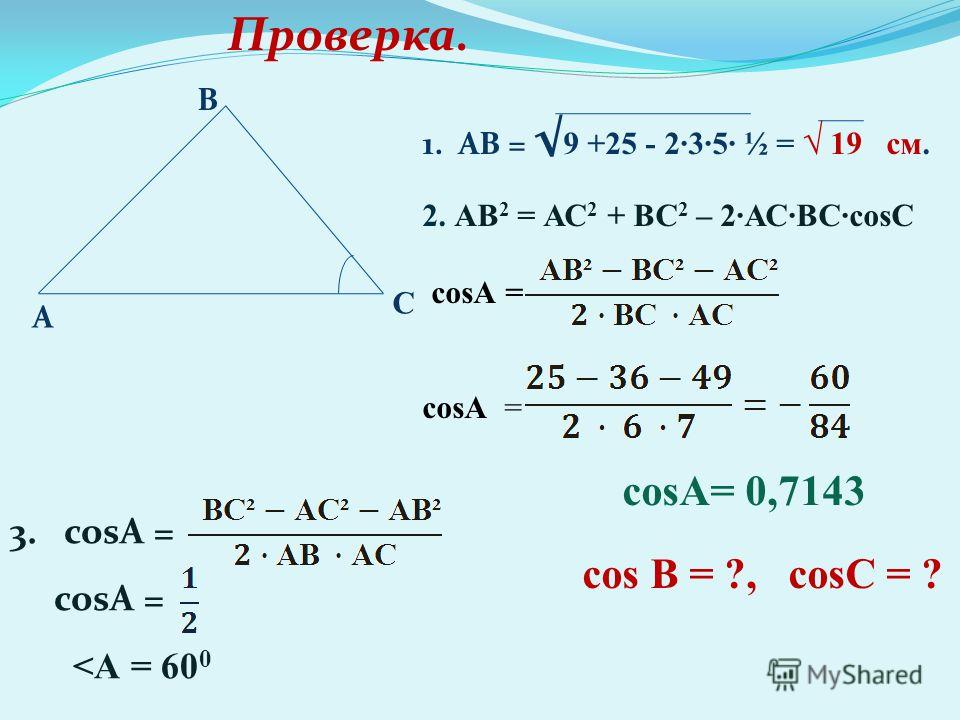 Это стало главной задачей тригонометрии на следующие несколько столетий. Как астронома Гиппарха в основном интересовали сферические треугольники, такие как воображаемый треугольник, образованный тремя звездами на небесной сфере, но он также был знаком с основными формулами плоской тригонометрии. Во времена Гиппарха эти формулы выражались в чисто геометрических терминах как отношения между различными хордами и углами (или дугами), которые их стягивают; современные символы для тригонометрических функций не вводились до 17 века.
Это стало главной задачей тригонометрии на следующие несколько столетий. Как астронома Гиппарха в основном интересовали сферические треугольники, такие как воображаемый треугольник, образованный тремя звездами на небесной сфере, но он также был знаком с основными формулами плоской тригонометрии. Во времена Гиппарха эти формулы выражались в чисто геометрических терминах как отношения между различными хордами и углами (или дугами), которые их стягивают; современные символы для тригонометрических функций не вводились до 17 века.
Изучите, как Птолемей пытался использовать деференты и эпициклы для объяснения ретроградного движения
Просмотреть все видео к этой статье Щелкните здесь, чтобы просмотреть таблицу в полном размереПервой крупной древней работой по тригонометрии, дошедшей до Европы в целости и сохранности после Средневековья, был Альмагест Птолемеем ( ок. 100–170 н.э.). Он жил в Александрии, интеллектуальном центре эллинистического мира, но больше о нем мало что известно.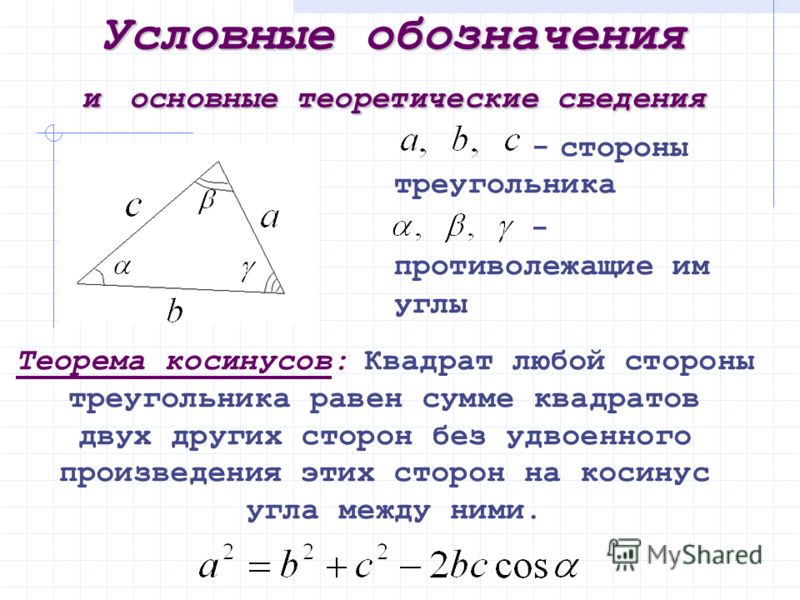 Хотя Птолемей написал работы по математике, географии и оптике, в основном он известен своими Альмагест , сборник из 13 книг по астрономии, который стал основой для картины мира человечества, пока гелиоцентрическая система Николая Коперника не начала вытеснять геоцентрическую систему Птолемея в середине 16 века. Чтобы развить эту картину мира, сущностью которой была неподвижная Земля, вокруг которой по круговым орбитам движутся Солнце, Луна и пять известных планет, Птолемею пришлось использовать некоторую элементарную тригонометрию. Главы 10 и 11 первой книги Альмагеста г. касаются построения таблицы хорд, в которой длина хорды в окружности дана как функция центрального угла, который ее стягивает, для углов в диапазоне от 0 ° до 180 ° с интервалами в полградуса. . По сути, это таблица синусов, которую можно увидеть, обозначив радиус r , дугу A и длину стягиваемой хорды c , чтобы получить c = 2 r sin А / 2 .
Хотя Птолемей написал работы по математике, географии и оптике, в основном он известен своими Альмагест , сборник из 13 книг по астрономии, который стал основой для картины мира человечества, пока гелиоцентрическая система Николая Коперника не начала вытеснять геоцентрическую систему Птолемея в середине 16 века. Чтобы развить эту картину мира, сущностью которой была неподвижная Земля, вокруг которой по круговым орбитам движутся Солнце, Луна и пять известных планет, Птолемею пришлось использовать некоторую элементарную тригонометрию. Главы 10 и 11 первой книги Альмагеста г. касаются построения таблицы хорд, в которой длина хорды в окружности дана как функция центрального угла, который ее стягивает, для углов в диапазоне от 0 ° до 180 ° с интервалами в полградуса. . По сути, это таблица синусов, которую можно увидеть, обозначив радиус r , дугу A и длину стягиваемой хорды c , чтобы получить c = 2 r sin А / 2 . Поскольку Птолемей использовал вавилонские шестидесятеричные числа и системы счисления (основание 60), он провел свои вычисления со стандартным кругом радиуса 9.1688 r = 60 единиц, так что c = 120 sin A / 2 . Таким образом, помимо коэффициента пропорциональности 120, это была таблица значений sin A / 2 и, следовательно (удвоение дуги) sin A . С помощью своей таблицы Птолемей усовершенствовал существующие геодезические меры мира и уточнил Гиппархову модель движения небесных тел.
Поскольку Птолемей использовал вавилонские шестидесятеричные числа и системы счисления (основание 60), он провел свои вычисления со стандартным кругом радиуса 9.1688 r = 60 единиц, так что c = 120 sin A / 2 . Таким образом, помимо коэффициента пропорциональности 120, это была таблица значений sin A / 2 и, следовательно (удвоение дуги) sin A . С помощью своей таблицы Птолемей усовершенствовал существующие геодезические меры мира и уточнил Гиппархову модель движения небесных тел.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Сферическая тригонометрия
Сферическая тригонометрия(Роберто Бигони)
1. Шары, геодезические, лунки.
Окружность, полученная путем пересечения сферической поверхности Σ радиуса R плоскостью, проходящей через ее центр,
т.е. одна из окружностей максимального радиуса, получаемая на сферической поверхности, называется геодезической .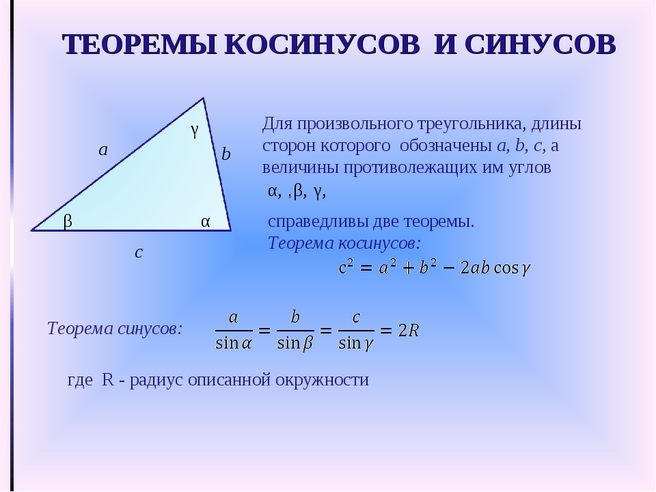 Секущую плоскость называют образующей плоскостью 9.1804 г. геодез.
Секущую плоскость называют образующей плоскостью 9.1804 г. геодез.
Например, предполагая, что Земля является идеальной сферой, все меридианы являются геодезическими, но единственная параллель, являющаяся геодезической, — это экватор.
Две разные геодезические пересекаются в двух диаметрально противоположных точках P и Q. Их образующие плоскости образуют две пары вертикально противоположных двугранников. Каждый двугранник с мерой λ образует на сферической поверхности область, ограниченную двумя полуокружностями с крайними точками P и Q, сказал lune , с вершинами P и Q и сторонами PAQ и PBQ. Точки P и Q являются вершинами двух сферических углов, оба измерения λ . Мы также можем сказать, что лунка PAQB — это лунка Λ с углом λ .
Отношение площади l лунки Λ с углом λ к поверхности Σ равно отношению между углом λ и 2π .
, затем
Множество всех геодезических, пересекающихся в одних и тех же точках P и Q, называется пучком геодезических с полюсами PQ.
Например, два земных меридиана пересекаются в географических полюсах N и S.
Множество всех меридианов представляет собой пучок геодезических с полюсами NS.
2. Сферические треугольники.
Если мы пересечем луну Λ α под углом α карандаша с полюсами AZ, с третьей геодезической, который не принадлежит одному и тому же пучку и, следовательно, пересекает стороны Λ α в точках B и C разделим лунку Λ α на две области с вершинами ABC и ZBC, называемые сферические треугольники .
Площадь треугольника ZBC получается вычитанием площади треугольника ABC из площади лунки Λ α .
Треугольник ABC является пересечением лунки Λ β с углом β и Λ γ .
с углом γ .
Таким образом, площадь объединения Λ β и Λ γ определяется суммой их площадей.
уменьшается на площадь треугольника ABC (которая в противном случае вычислялась бы дважды).
Кроме того, если мы соединим треугольник с вершинами в точках, диаметрально противоположных Z, B и C, конгруэнтного треугольнику ZBC с объединением лунок Λ β и Λ γ , получаем полусферу. Итак, если мы добавим площадь треугольника ZBC к площади объединения Λ β и Λ γ получаем площадь поверхности полушария.
Объединяя эти результаты, мы получаем
, значит, площадь сферического треугольника ABC равна:
.Поскольку площадь сферического треугольника должна быть положительной, мы заключаем, что сумма внутренних углов сферического треугольника больше прямого угла.
Этот результат очевиден на карандаше земных меридианов: два разных меридиана образуют прямые углы.
с экватором и, сходясь в полюсе, образуют угол, заданный абсолютной величиной разности их долгот.
Итак, на земной поверхности в сферическом треугольнике, ограниченном двумя разными меридианами и дугой экватора между ними,
сумма внутренних углов больше двух прямых углов.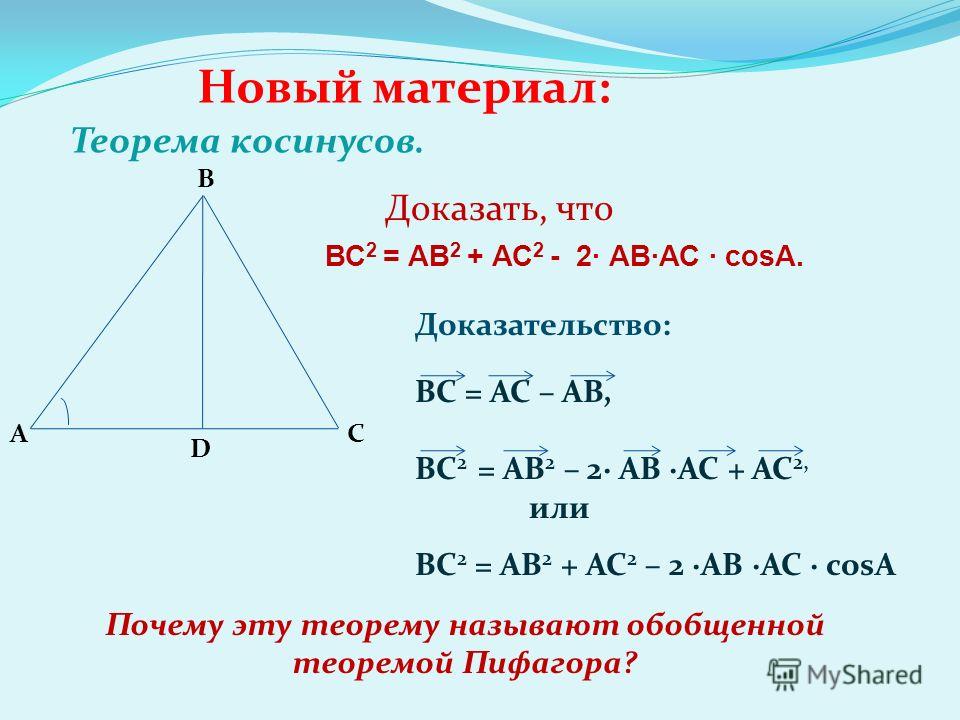
3. Формула Эйлера.
Рассмотрим выпуклый многогранник Π с треугольными гранями, и пусть F — число его граней, V — число его вершин и S количество его ребер. Пусть Σ — сферическая поверхность с радиусом R , содержащая многогранник Π и из точки P, расположенной внутри Π, спроецируем ребра самого Π на Σ. Каждой из граней Π будет соответствовать сферический треугольник, для каждого из ребер Π будет соответствующая сторона треугольника и для каждой вершины Π будет соответствующая точка, в которой сходятся стороны смежных треугольников.
Площадь каждого сферического треугольника равна произведению разности между суммой его внутренних углов и прямой угол, умноженный на квадрат радиуса.
Площадь сферической поверхности равна сумме площадей всех треугольников, то есть сумма всех углов треугольников уменьшилась на столько прямых углов, сколько граней.
Сумма внутренних углов равна количеству полных углов и вершин.
Поэтому
Поскольку каждая сторона является общей для двух смежных треугольников, число S сторон равно половине трехкратного числа F граней:
Поэтому
Если Π имеет многоугольные грани (поэтому не обязательно треугольные), его проекция на Σ будет сеткой
образованы сферическими многоугольниками, которые, если они имеют более трех сторон, можно разделить на треугольники, проследив их диагонали.
Для каждой построенной диагонали мы имеем увеличение на единицу как количества сторон, так и количества граней,
и соотношение между числами граней, ребер и вершин остается неизменным.
В общем получаем, что
в каждом многограннике сумма количества граней и вершин на два превышает количество ребер.
Этот результат является одним из самых известных среди полученных Л. Эйлер.
4. Теорема Пифагора.
Рассмотрим на сферической поверхности Σ радиуса R с центром O сферический треугольник с вершинами A, B и C,
так что внутренний угол ACB прямой. Пусть a, b и c — меры сторон соответственно противоположных
к А, В и С.
Пусть a, b и c — меры сторон соответственно противоположных
к А, В и С.
В этом случае мы можем выбрать ортогональную декартову систему отсчета с началом в центре O, такую, что плоскость O yz совпадает с образующей стороны AC, а плоскость O xz совпадает с образующей стороной BC.
Мы можем описать отрезки OA и OB как векторы длины R . Пусть α — мера угла AOC, β мера угла BOC и i , j и k — единичные векторы декартовых осей. Тогда:
Скалярное произведение двух векторов равно
.Мы можем записать скалярное произведение как произведение их модулей на косинус угла AOB с мерой γ :
Итак, у нас есть
Поскольку мера угла в центре окружности в радианах определяется отношением между дугой и радиусом,
Этот результат является обобщением теоремы Пифагора. На самом деле из
На самом деле из
получаем
Если мы увеличим до бесконечности сферическую поверхность, так что ограниченная область на ней станет неотличима от плоской области, мы должны вычислить предел этого равенства как . Получаем
но
Итак, до предела имеем
5. Длина дуги.
Пусть A и B — две точки на сферической поверхности Σ с радиусом R . Пусть С — точка экватора, принадлежащая к меридиану А. Если принять долготу А за 0, векторы ОА и ОВ можно выразить как
Скалярное произведение двух векторов равно
.и может быть записано также как
, затем
Длина дуги AB равна
В частности, если A и B — точки на поверхности Земли, и если мы предположим, что Земля — идеальная сфера, мы имеем
Пример: расчет расстояния (по прямой) между Нью-Йорком и Кейптауном.
| место | широта | долгота |
|---|---|---|
| Нью -Йорк | 40 ° 45’25 «N | 73 ° 59’10» W |
| Кейптаун | 33 ° 54 ’58 «S | 18 ° 25’19» E |
| place | latitude | longitude |
|---|---|---|
| New York | 40.757140° | -73.986053° |
| Cape Town | -33.6° | 18.422012° |
Мы вычисляем соответствующие радианы.
| place | latitude | longitude |
|---|---|---|
| New York | 0.711346 | -1.2 |
| Cape Town | -0.5 | 0.321525 |
We calculate the difference of longitude::
и мера угла γ :
Наконец, расстояние между Нью-Йорком и Кейптауном получается путем умножения средний радиус Земли на γ :
Измерения, полученные с
более сложные расчеты,
исходя из того, что Земля не идеальная сфера, а эллипсоид, дайте расстояние 12552 км.
Как видите, погрешность порядка 1 ‰.
Здесь расстояние между двумя точками на идеальной сферической поверхности вычисляется с помощью Javascript. Избегайте пар диаметрально противоположных точек.
Если ваш браузер не поддерживает iframe , вы можете напрямую открыть страницу приложения
6. Теорема косинусов.
Пусть A, B и C — три точки на сферической поверхности с единичным радиусом. У нас есть
Более того
Если мы подставим правые части этого тождества в уравнение
получаем
Это тождество выражает c как функцию косинуса угла образованные двумя другими сторонами. Итак, это сферическая версия известной теоремы косинуса плоской тригонометрии. Если угол ACB прямой, то получаем теорему Пифагора.
Из измерений сторон получаем косинусы внутренних углов треугольника:
Если сфера имеет радиус р у нас
, затем
7.
 Периметр и площадь треугольника.
Периметр и площадь треугольника.Дан треугольник ABC на сферической поверхности Σ с единичным радиусом и центром O, если мы знаем углы α , β e γ на приведенном выше рисунке (то есть широты и долготы A, B и C относительно подходящей системы отсчета на Σ), если a , b и c — размеры сторон, меры внутренних углов можно вывести из мер a , b и c с помощью теоремы косинусов. Площадь треугольника, как мы видели в разделе 2, получается вычитанием π из суммы внутренних углов. Мера этой площади совпадает с мерой в стерадианах телесного угла с вершиной в О и сторонами, определяемыми пересечения образующих полуплоскостей сторон треугольника.
Если Σ имеет радиус R , стерадиан необходимо умножить на R 2 .
Для решения сферического треугольника полезно реализовать расчет в электронной таблице или на последовательном языке программирования. Здесь мы предлагаем версию Javascript. Широта и долгота записываются как
шестидесятеричные градусы ( ggg°mm’ss» хотя бы с одним из трех разделителей) или в радианах (чистое десятичное число). Избегайте пар диаметрально противоположных точек.
Здесь мы предлагаем версию Javascript. Широта и долгота записываются как
шестидесятеричные градусы ( ggg°mm’ss» хотя бы с одним из трех разделителей) или в радианах (чистое десятичное число). Избегайте пар диаметрально противоположных точек.
Если ваш браузер не поддерживает тег iframe , вы можете напрямую открыть страницу приложения
8. Закон синусов.
Пусть A, B и C — вершины треугольника на сферической поверхности Σ с центром O и радиусом R . Проведем радиусы от O до вершин и пусть α , β и γ — углы между ними. Рассмотрим плоскость из С, перпендикулярную плоскости радиусов ОА и ОВ. и пусть A’ и B’ будут пересечениями этой плоскости с двумя радиусами. Рассмотрим треугольник CA’B’ и пусть CH высота этого треугольника относительно стороны A’B’. Пусть ч — мера СН.
Применяя известные формулы плоской тригонометрии, получаем
, затем
Углы при знаменателях совпадают с углами при вершинах сферического треугольника ABC; те, что в числителях
определяются отношением сторон ABC к радиусу R . Поэтому
Поэтому
Такую же конструкцию можно повторить на каждой из вершин треугольника, так что в общем случае
Если , это отношение сходится к закону синусов плоской тригонометрии.
последняя редакция: ноябрь 2018 г.
Закон косинусов и сферический Пифагор
Закон косинусов и сферический ПифагорГеометрия закона косинусов
В треугольнике ABC стороны равны a = BC, b = CA, c = AB. Смысл D — основание высоты, проходящей через B. Назовем угол ACB = t. Для каждого из этих цифр запишите CD, BD и AD в пересчете на триггерные функции т и а, б, с .
CD = стоимость | CD = стоимость (если CD считается отрицательным) |CD| = а |стоимость т| = -a cos t = a cos (180 — t) |
BD = a sin t | BD = a sin t |
AD = b — стоимость | н. |
- Используйте свою работу выше, чтобы записать теорему Пифагора для треугольника BDA в терминах тригонометрических функций от t и a, b и c. Упрощение с помощью триггерная личность
в 2 = а 2 + (б — а стоимость т) 2
в 2 = а 2 + б 2 — 2аб стоимость
тАлгебра закона косинусов
Предположим, что A = (a1, a2, a3), B = (b1, b2, b3), C = (0, 0, 0). Используйте алгебраический формула расстояния для вычисления:
- б 2 = |КА| 2 = (а1) 2 + (а2) 2 + (а3) 2
- a 2 = |CB| 2 = (b1) 2 + (б2) 2 + (б3) 2
- с 2 = |AB| 2 = (а1 — b1) 2 + (a2 — b2) 2 + (a3 — b3) 2
- Сравните результаты с приведенным выше законом косинусов и посмотрите, как триггерный член
можно вычислить алгебраически.

с 2 = |АВ| 2 = (a1 — b1) 2 + (a2 — b2) 2 + (a3 — b3) 2 =
( (а1) 2 + (а2) 2 + (а3) 2 ) + ( (б1) 2 + (б2) 2 + (b3) 2 ) — 2 (a1b1 + a2b2 + a3b3)
Напишите здесь, что мы узнали о скалярном произведении и косинусе
Переписывая последнее уравнение, мы даем имя выражению
(a1b1
+ а2б2 + а3б3)
и назовите его A . B, скалярное произведение A и B . Точка
произведение может быть определено в n-пространстве любой размерности. Для двух векторов умножьте
соответствующие записи, а затем добавить. В данном случае
в 2 = а 2 + б 2 — 2А . Б
Таким образом:
А .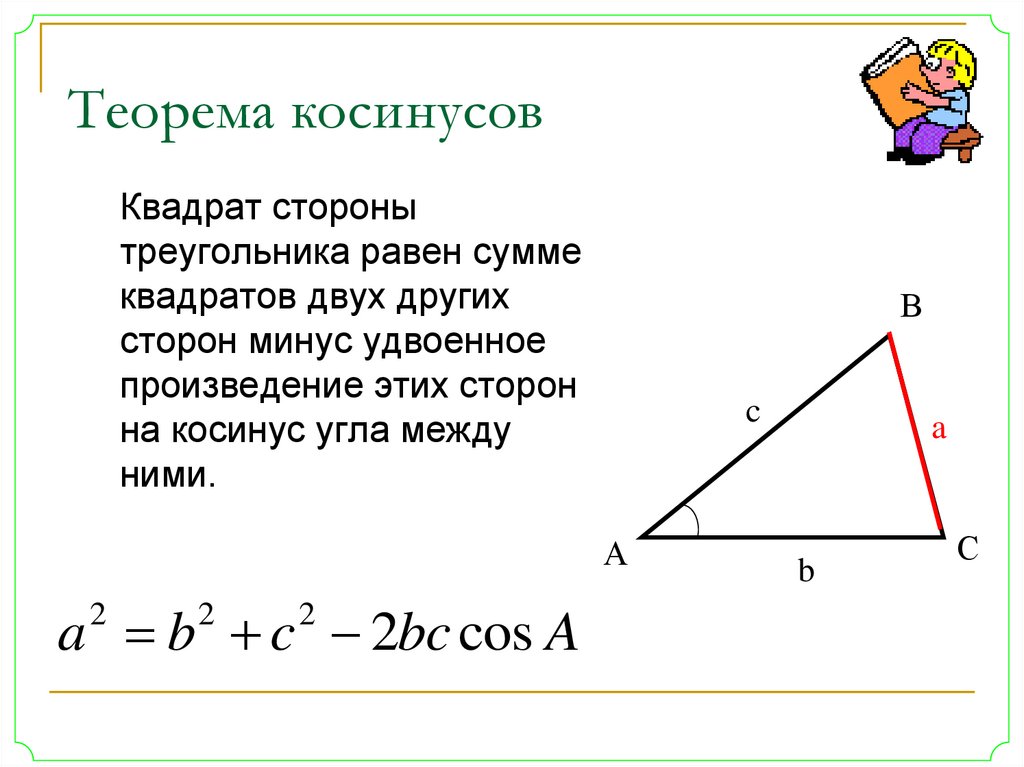 Б = |А| |Б| cos (AOB)
Б = |А| |Б| cos (AOB)
Обратите внимание, что квадрат длины также является скалярным произведением. вектора с самим собой, поэтому это уравнение можно записать так (с C = O с нулевыми координатами):
б 2 = |ОА| 2 = А . А; а 2 = |ОБ| 2 = В . Б; в 2 = |А — В| 2 = (А-В) . (А-Б)
Это приводит к наблюдению, что алгебраическая версия закона косинусов происходит из распределительного закона [ A . (Б+В) = А . Б+А . C] и коммутативный закон [ A . Б = В . A] для скалярного произведения:
(А-Б) . (А-В) = А . А — А . Б-Б . А + В . Б = А . А + В . Б — 2 А . Б
Теорема Пифагора о сфере
Предположим, что треугольник ABC является сферическим треугольником с прямым углом C. Мы можем выбрать пространственные координаты так, что C = K = (0,0,1), A находится в (x,0,z)
плоскости, а B находится в плоскости (0,y,z). Вот два сечения, где I =
(1, 0, 0) и J = (0, 1, 0).
Мы можем выбрать пространственные координаты так, что C = K = (0,0,1), A находится в (x,0,z)
плоскости, а B находится в плоскости (0,y,z). Вот два сечения, где I =
(1, 0, 0) и J = (0, 1, 0).
Сферические расстояния a = BC, b = CA и c = AB на самом деле являются мерами углов. Каковы углы в каждом случае?
- Сферическое расстояние a = угловая мера BOC,
- Сферическое расстояние b = угловая мера COA,
- Сферическое расстояние c = угловая мера AOB,
Используя углы a, b, c, каковы координаты A?
Используя углы a, b, c, каковы координаты точки B?
- A = (sin b , 0, cos b) = (sin b) I + (cos b) К
- B = (0, sin a, cos a) = (sin a) J + (cos a) К
Теперь используйте скалярное произведение для вычисления г., потому что ок. Это это «Теорема Пифагора для сферы».
Поскольку для измерения c мы измеряем угол AOB, мы можем найти
косинус этого угла от скалярного произведения, как объяснялось выше.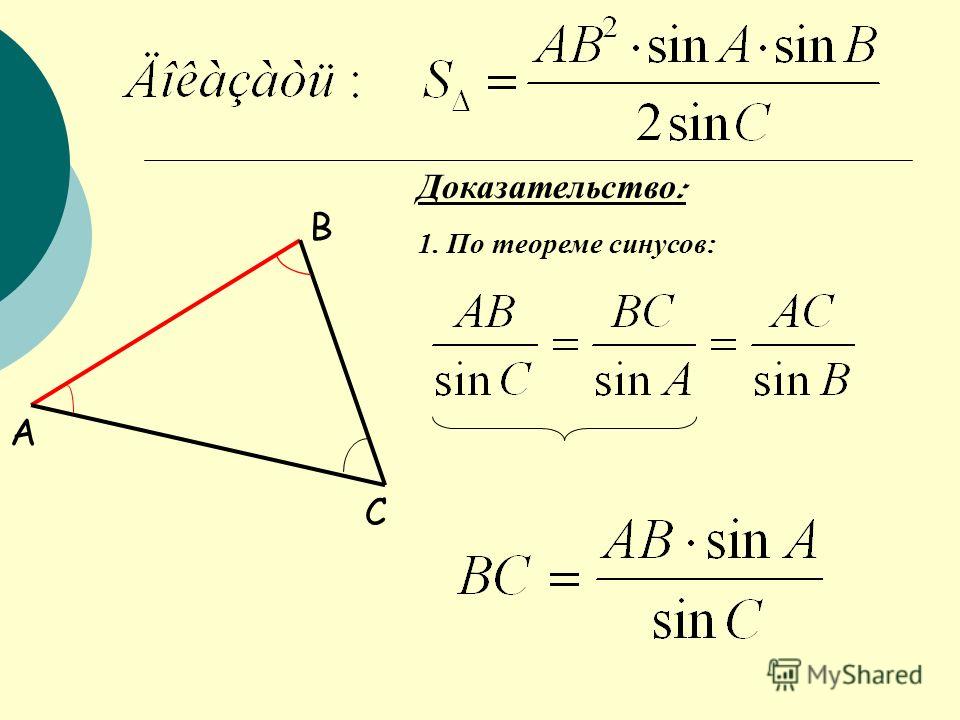
|A||B|cos c = A . Б
Но так как |A| = |В| = 1 (из геометрии или из формула), затем
потому что с = A . В = 0 + 0 + (cos а) (кос б)
Тогда для треугольника с прямым углом в C пифагорейская Теорема для сферы государства
cos c = (cos a) (cos b)
Примечание: Трудно распознать
обычная теорема Пифагора в этом, но для очень малых углов t стоимость t приблизительно равна
равно 1 — т 2 /2. Таким образом, это уравнение стало приближенным
уравнение
(1
— c 2 /2) «=» (1 — a 2 /2) (1 — b 2 /2) «=» 1
— (1/2)(а 2 + b 2 ), поэтому
в 2 «=» а 2 + б 2 (мы игнорируем a 2 б 2 срок и
Другой
члены четвертой степени после
они намного меньше, чем квадратичные члены). Таким образом, «в пределе»
сферический формальный согласуется с формулой для плоской плоскости.
Эти заметки касаются некоторых принципов сферической тригонометрии, которые имеют значение для практической навигации по земному шару. Сферическая тригонометрия отличается от плоской тригонометрии тем, что лежащие в основе треугольники расположены на поверхности сферы, а не на плоскости. В следующих примечаниях предполагается, что углы выражены в градусах. Также предполагается, что основные тригонометрические функции синус (sin(x)) и косинус (cos(x)) взять их аргумент (x) в градусах. Это также означает, что обратное функции Арксинус (asin(x)) и Арккосинус (acos(x)) возвращают значения угла в градусов. Некоторые калькуляторы принимают значения углов только в радианах. Значение угла «градус», выраженный в градусах, преобразуется в значение угла «араданы», выраженное в радианах следующее тождество: арадиан = градус *3,1415/360 [радиан/градус]. Наклонный сферический треугольник
Закон синусов:
Закон косинусов для сторон:
Закон косинусов для углов:
Примечание: Решение одного из приведенных выше уравнений для значения сторон
или углов сферического треугольника, потребуются обратные тригонометрические
функции Арксинус (asin(x)) и Арккосинус (acos(x)).
Закон касательных углов: Если возможно, следует сформулировать решение для углов или сторон
в виде функций тангенса (tan(x)). Функция арктангенса (atan(x))
возвращает значения от -90° до +90° и может использоваться для обработки
неоднозначность функций арксинуса и арккосинуса. С комбинацией «Закона косинусов для углов» и «Закона Sines» можно вывести следующие тождества:
Вычет будет объяснен для угла «a1». Объедините первое два уравнения «Закона косинуса для углов»: cos(a1) = -cos(a2)*cos(a3) + sin(a2)*sin(a3)*cos(S1) (1)с первыми двумя уравнениями «Закона синусов»: sin(a1) = sin(a3)*sin(S1) / sin(S3) (3) sin(a2) = sin(a3)*sin(S2) / sin(S3) (4)Сначала замените термины «sin(a2)» в уравнении (1) с уравнением (4) и термином «sin(a1)» в уравнении (2) с уравнением (3) .  затем
замените термин cos(a2) в уравнении (1) на
новый идентификатор (2) и решить это новое уравнение для «cos (a1)»: затем
замените термин cos(a2) в уравнении (1) на
новый идентификатор (2) и решить это новое уравнение для «cos (a1)»: cos(a1) = -cos(a3)*[-cos(a1)*cos(a3) + sin 2 (a3)*sin(S1)*cos(S2) / sin(S3)]
+ sin 2 (a3)*sin(S2)*cos(S1) / sin(S3)
соз(а1) = соз 2 (a3)*cos(a1) - cos(a3)*sin 2 (a3)*sin(S1)*cos(S2) / sin(S3)
+ sin 2 (a3)*sin(S2)*cos(S1) / sin(S3)
cos(a1)*[1 - cos 2 (a3)] = sin 2 (a3)*sin(S2)*cos(S1) / sin(S3)
- cos(a3)*sin 2 (a3)*sin(S1)*cos(S2) / sin(S3)
cos(a1)*sin 2 (a3) = sin 2 (a3)*[sin(S2)*cos(S1) - cos(a3)*sin(S1)*cos(S2)] / sin( С3)
cos(a1) = [sin(S2)*cos(S1)-cos(a3)*sin(S1)*cos(S2)] / sin(S3) Вместе с использованным ранее тождеством «Закон синусов»: sin(a1) = sin(a3)*sin(S1) / sin(S3)уравнение для тангенсов «a1» можно записать как: tan(a1) = sin(a1) / cos(a1)
= sin(a3)*sin(S1) / [cos(S1)*sin(S2) - cos(a3)*sin(S1)*cos(S2) ] Прямоугольный сферический треугольник Если один из углов a1,a2 или a3 является прямым углом (90°), вышеуказанное
отношения можно упростить. Правила Непера для прямоугольных сферических треугольников Дан прямоугольный треугольник на сфере со сторонами, обозначенными S1, S2 и S3. Пусть a1 — угол, противолежащий стороне S1, a2 — угол, противолежащий стороне S2, и a3 прямой угол, противоположный стороне S3. Для этого устройства Джон Нейпир (1550–1617) разработал следующие десять уравнений. отношение сторон и углов этого треугольника (в котором a3 не отображается, так как это фиксированный прямой угол):
Приведенные выше правила Нейпирса показывают только произведения и частные тригонометрических функций,
и поэтому очень подходят для логарифмических вычислений. |
Сферический закон косинусов — HandWiki
Из HandWiki
Пространства имен
- Страница
- Обсуждение
Еще
- Еще
- Языки
Действия со страницей
В сферической тригонометрии закон косинусов (также называемый правилом косинусов для сторон 1)72 связывает стороны 1 и [ углы сферических треугольников, аналогично обычному закону косинусов из плоской тригонометрии.
Сферический треугольник, решенный по закону косинусов.
Для единичной сферы «сферический треугольник» на поверхности сферы определяется большими окружностями, соединяющими три точки u , v и w на сфере (показано справа). Если длины этих трех сторон равны a (от u до v ), b (от u до w ) и c (от до v ) , а угол угла напротив c равен C , то (первый) сферический закон косинусов гласит: [2] [1]
- [math]\displaystyle{ \cos c = \cos a \cos b + \sin a \sin b \cos C\, }[/math]
Поскольку это единичная сфера, длины a , b и c просто равны углам (в радианах), образуемым этими сторонами из центра сферы. (Для неединичной сферы длины равны стягиваемым углам, умноженным на радиус, и формула остается в силе, если a , b и c интерпретировать как стягиваемые углы).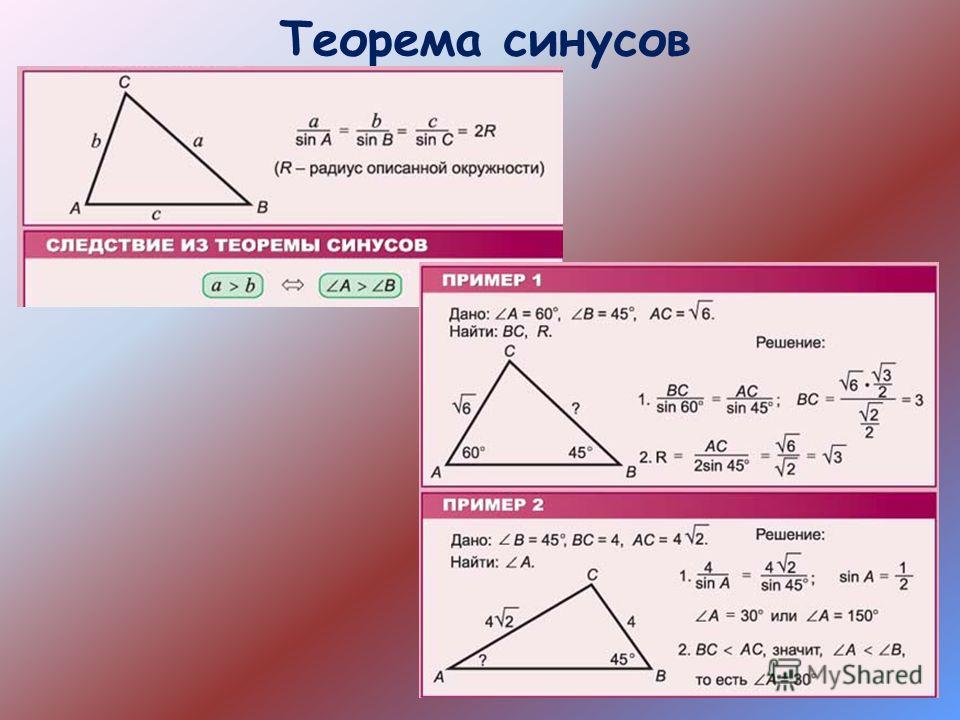 Как частный случай, для C = π/2, тогда cos C = 0, и получается сферический аналог теоремы Пифагора:
Как частный случай, для C = π/2, тогда cos C = 0, и получается сферический аналог теоремы Пифагора:
- [math]\displaystyle{ \cos c = \cos a \cos b\, }[/math]
ошибки округления при c невелики. В этом случае предпочтительнее альтернативная формулировка закона гаверсинусов. [3]
Вариант закона косинусов, второй сферический закон косинусов, [4] (также называемый правилом косинусов для углов [1] ) говорится:
- [math]\displaystyle{ \cos C = -\cos A \cos B + \sin A \sin B \cos c\, }[/math]
, где A и B углы углов, противоположных сторонам a и b соответственно. Его можно получить из рассмотрения двойственного заданному сферического треугольника.
Содержание
- 1 Пробы
- 1.1 Первое доказательство
- 1.2 Второе доказательство
- 2 Перестановки
- 3 Плоский предел: малые углы
- 4 См.
 также
также - 5 Примечания
Доказательства
Первое доказательство
Пусть u , v и w обозначают единичные векторы от центра сферы к этим углам треугольника. Углы и расстояния не изменяются при повороте системы координат, поэтому мы можем повернуть систему координат так, чтобы [math]\displaystyle{ \mathbf{u} }[/math] находилась на северном полюсе, а [math]\displaystyle { \mathbf{v} }[/math] находится где-то на нулевом меридиане (долгота 0). При таком вращении сферические координаты для [math]\displaystyle{ \mathbf{v} }[/math] равны [math]\displaystyle{ (r, \theta, \phi) = (1, a, 0) }[ /математика], где θ — это угол, измеренный от северного полюса, а не от экватора, а сферические координаты для [math]\displaystyle{ \mathbf{w} }[/math] равны [math]\displaystyle{ (r, \theta, \phi) = (1, b, C) }[/math]. Декартовы координаты для [math]\displaystyle{ \mathbf{v} }[/math] равны [math]\displaystyle{ (x, y, z) = (\sin a, 0, \cos a) }[/math ] и декартовы координаты для [math]\displaystyle{ \mathbf{w} }[/math] равны [math]\displaystyle{ (x, y, z) = (\sin b \cos C, \sin b \sin C, \cos b) }[/math]. Значение [math]\displaystyle{ \cos c }[/math] представляет собой скалярное произведение двух декартовых векторов, то есть [math]\displaystyle{ \sin a \sin b \cos C + \cos a \cos б }[/математика].
Значение [math]\displaystyle{ \cos c }[/math] представляет собой скалярное произведение двух декартовых векторов, то есть [math]\displaystyle{ \sin a \sin b \cos C + \cos a \cos б }[/математика].
Второе доказательство
Пусть u , v и w обозначают единичные векторы от центра сферы к этим углам треугольника. We have u · u = 1, v · w = cos c , u · v = cos a , and u · w = cos b . Векторы u × v и u × w имеют длины sin a и sin b соответственно, а угол между ними равен C , поэтому
- SIN A SIN B COS C = ( U × V ) · ( U × W ) · ( U × W ) = ( U × W ) = ( U × W ) = ( U × W ) = ( U × W ) = ( U × W ) = ( U ° W ) — ( U · V ) ( U · W ) = COS C — COS A COS B — COS A COS B — COS A COS B — COS A , COS B — COS A .



 1)
1)
 2.2) устанавливается зависимость между элементами А, m, В и а, то угол А и сторона а являются крайними, а угол В и сторона m – средними элементами, и тогда:
2.2) устанавливается зависимость между элементами А, m, В и а, то угол А и сторона а являются крайними, а угол В и сторона m – средними элементами, и тогда: 4)
4)
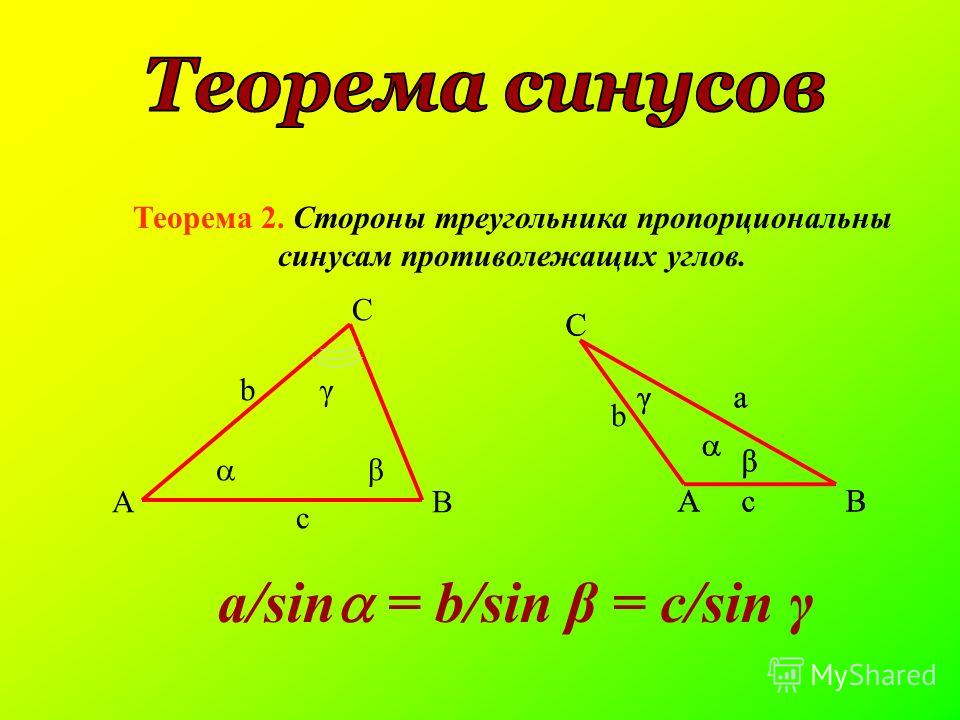 5)
5)
 ..
.. {\displaystyle \cos A=-\cos B\cos C+\sin B\sin C\cos a.}
{\displaystyle \cos A=-\cos B\cos C+\sin B\sin C\cos a.}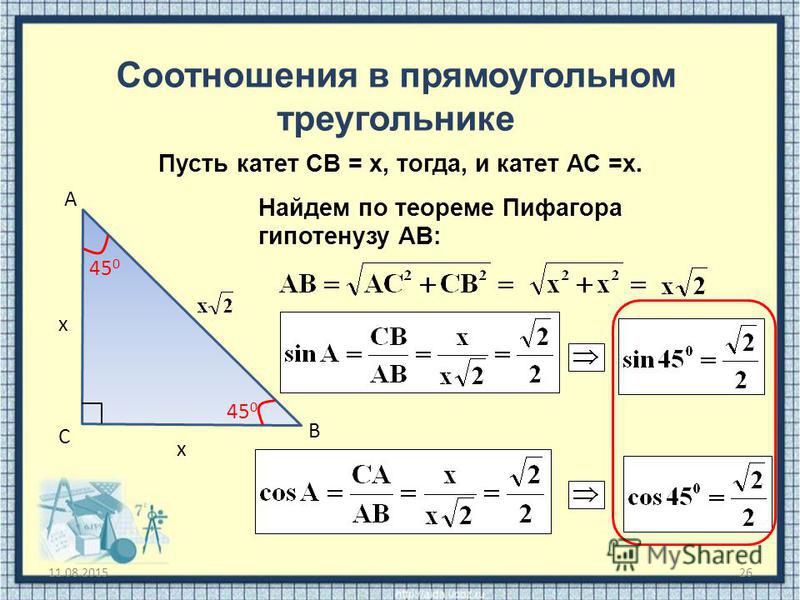 Позднее Средневековье. — Изд. 2-е. — М.: Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9.
Позднее Средневековье. — Изд. 2-е. — М.: Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9.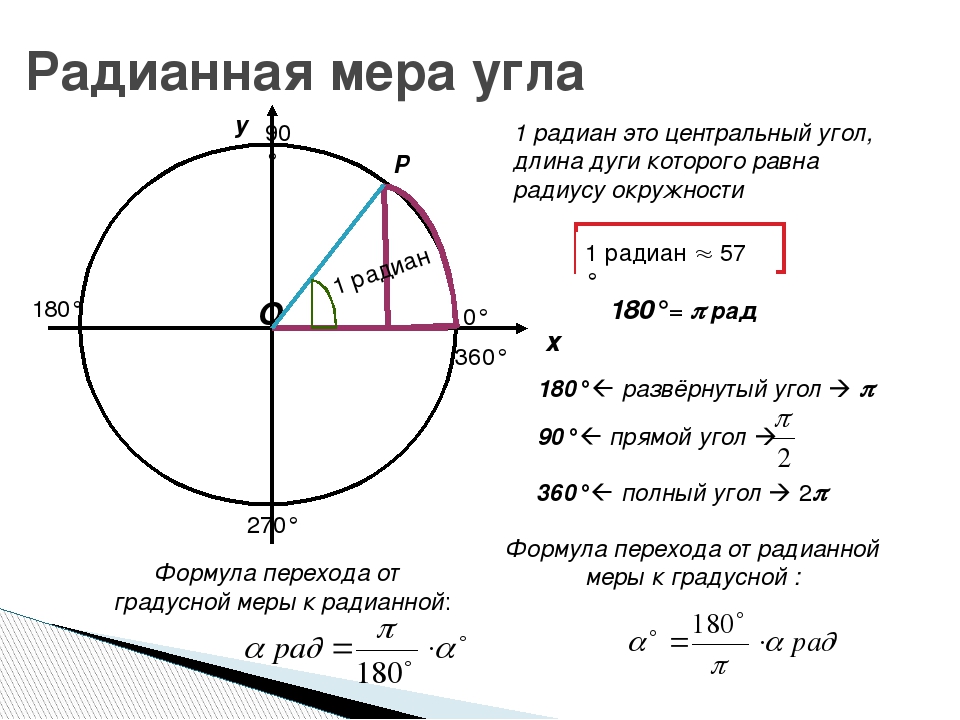

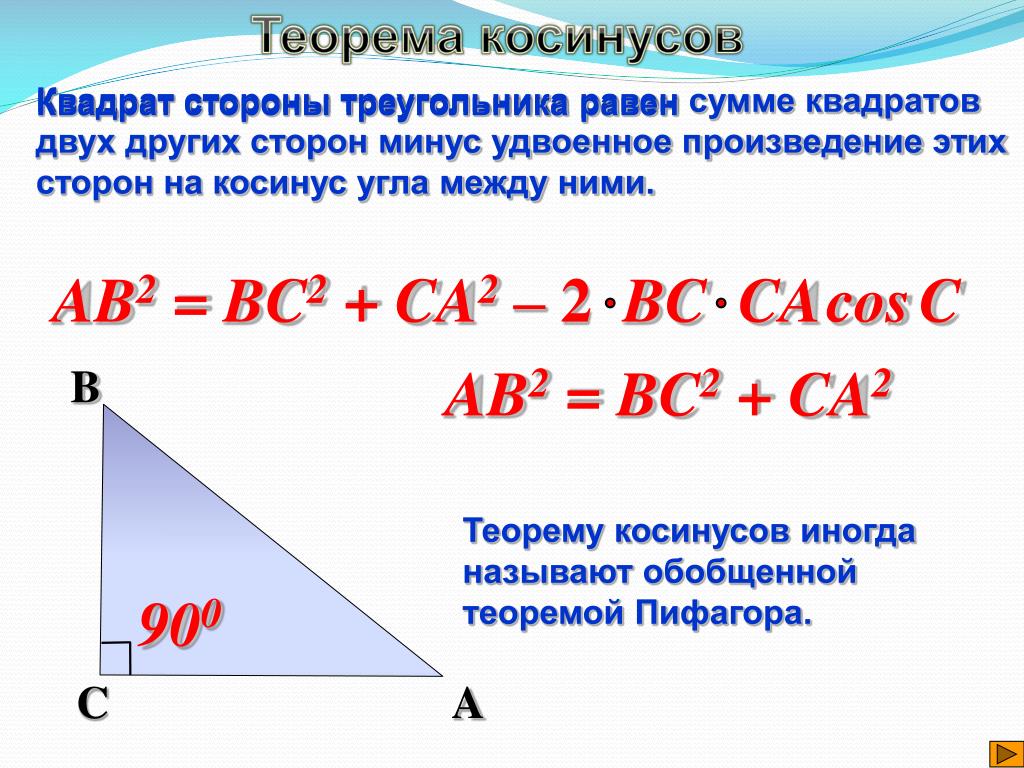
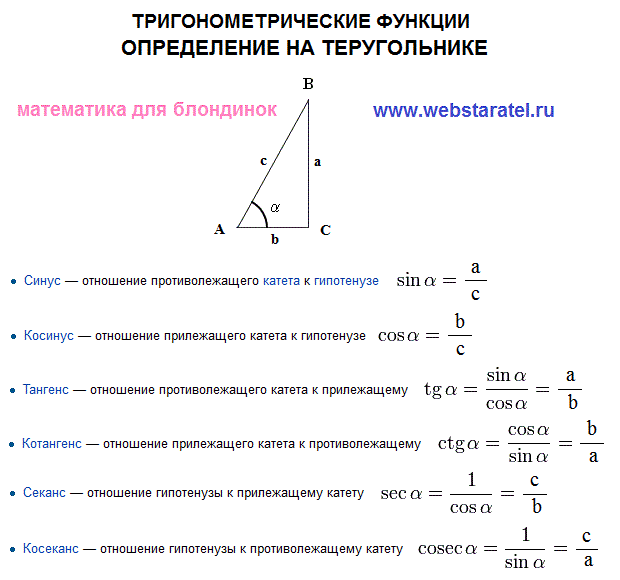

 Это разница в долготе между точками B и C.
Это разница в долготе между точками B и C.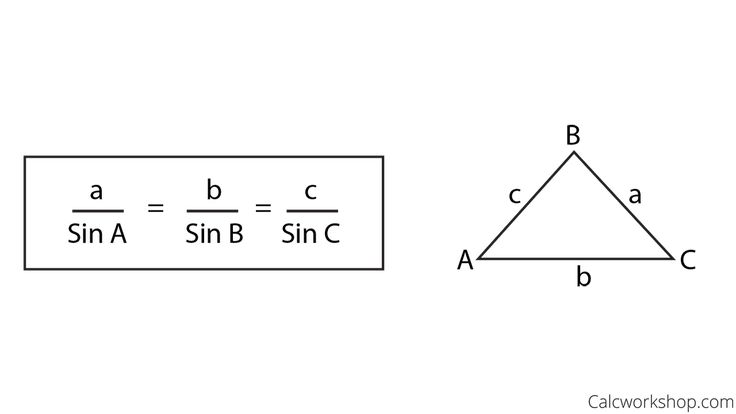 Два города лежат по разные стороны Гринвичского меридиана (просто так), поэтому мы добавляем долготы.
Два города лежат по разные стороны Гринвичского меридиана (просто так), поэтому мы добавляем долготы. Это и на диаграмме выше.
Это и на диаграмме выше.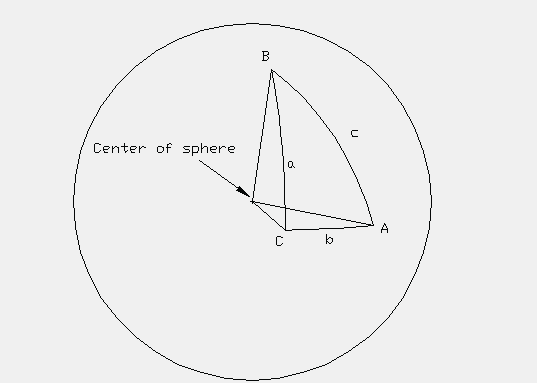

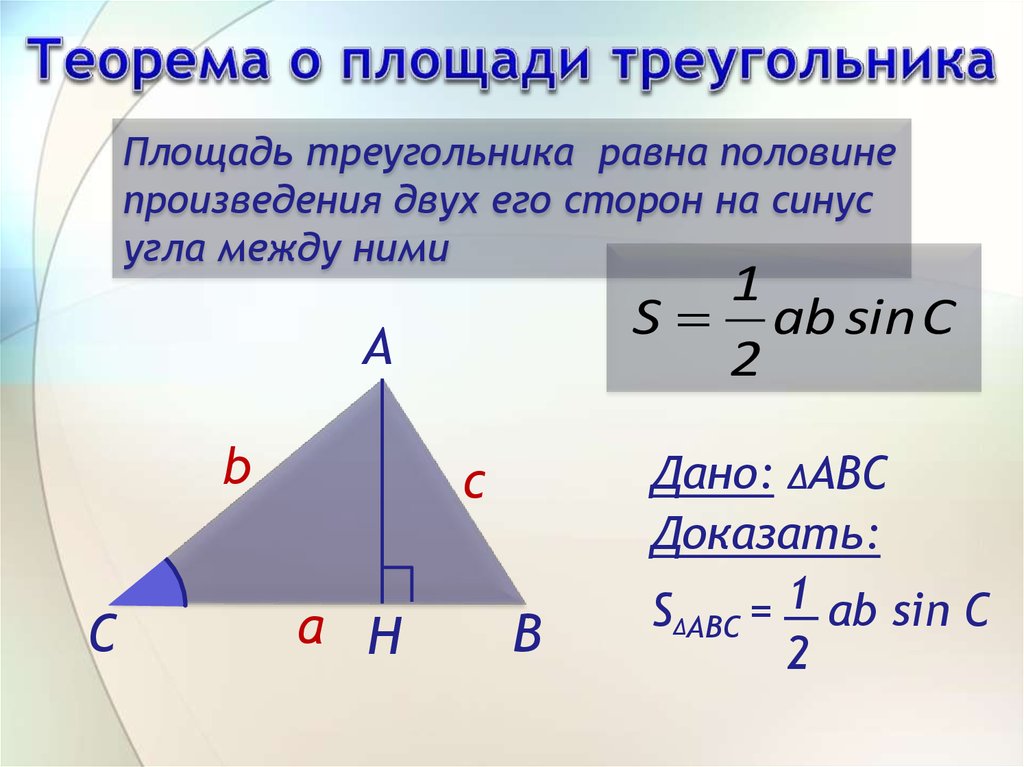 Это будет к западу от севера (угол ACB на схеме).
Это будет к западу от севера (угол ACB на схеме).
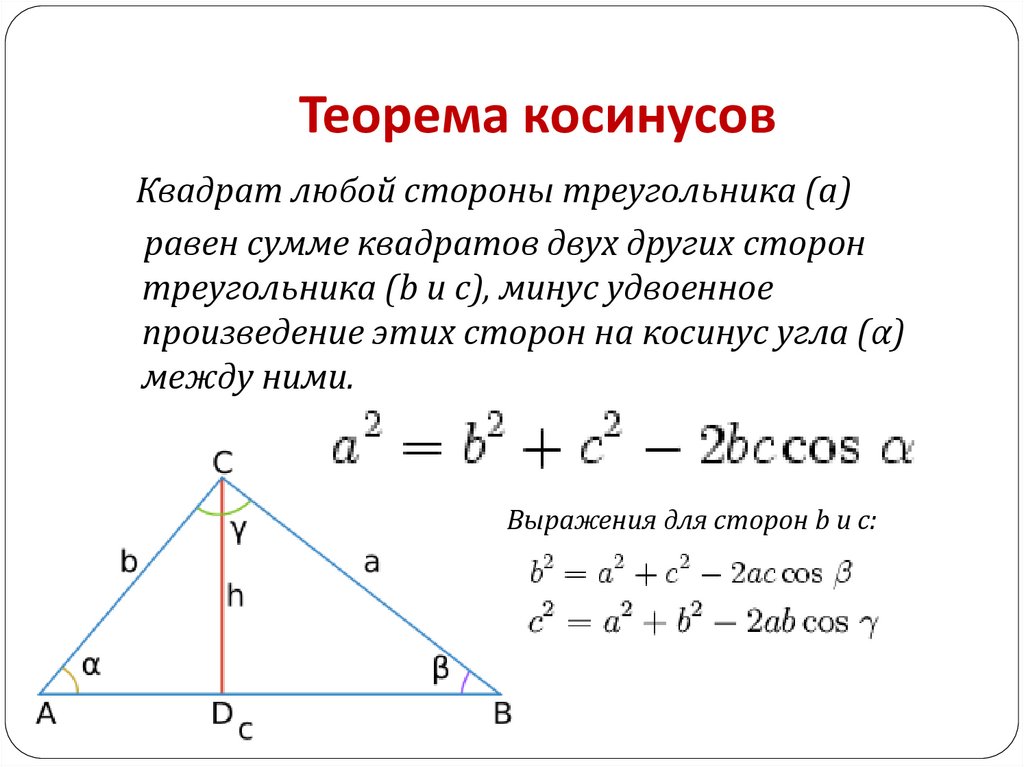

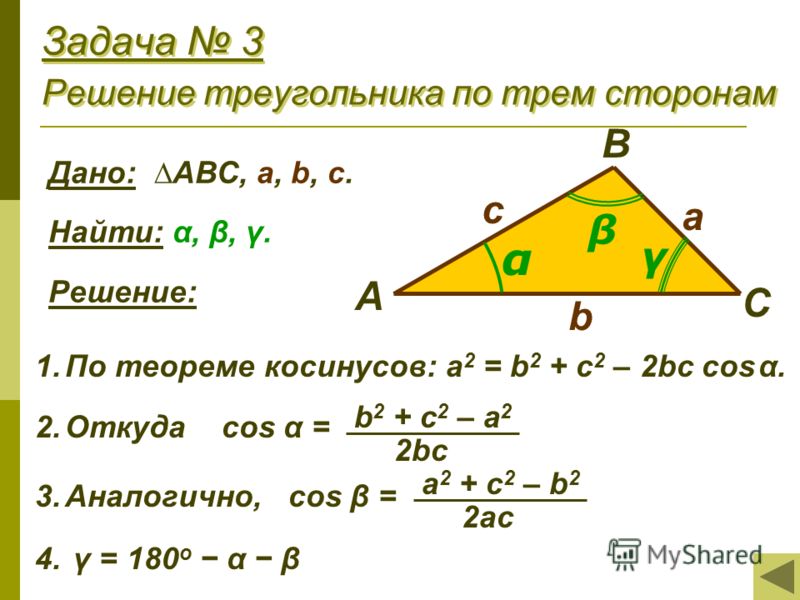
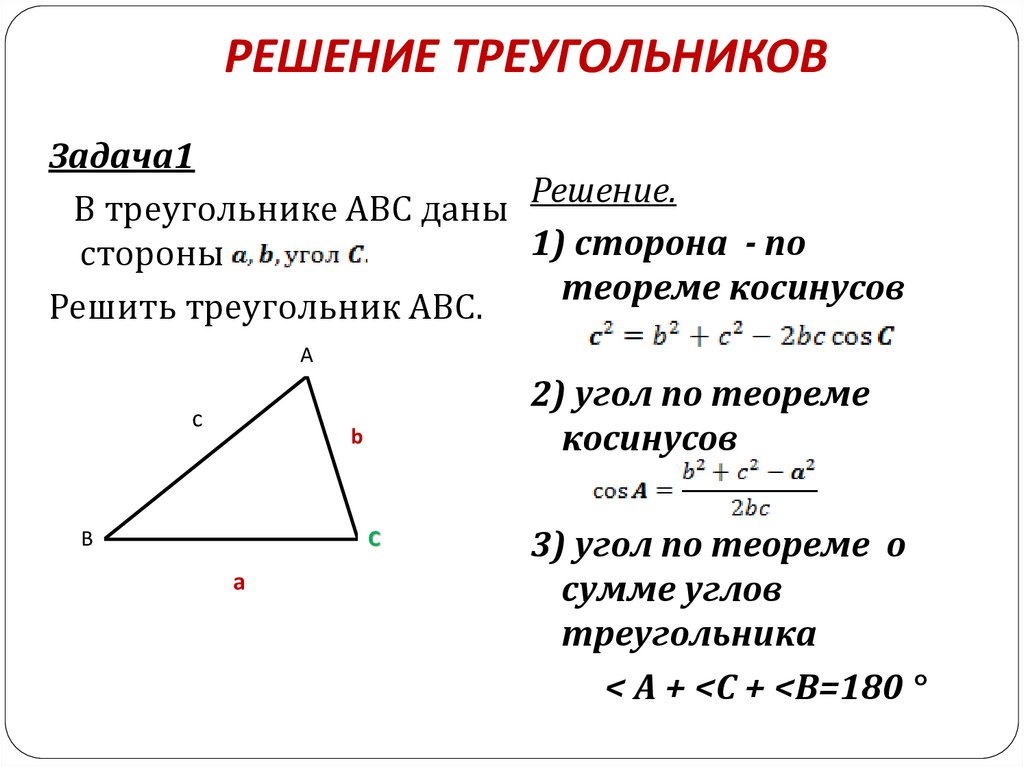




 э. = b + |CD| = b — стоимость t
э. = b + |CD| = b — стоимость t
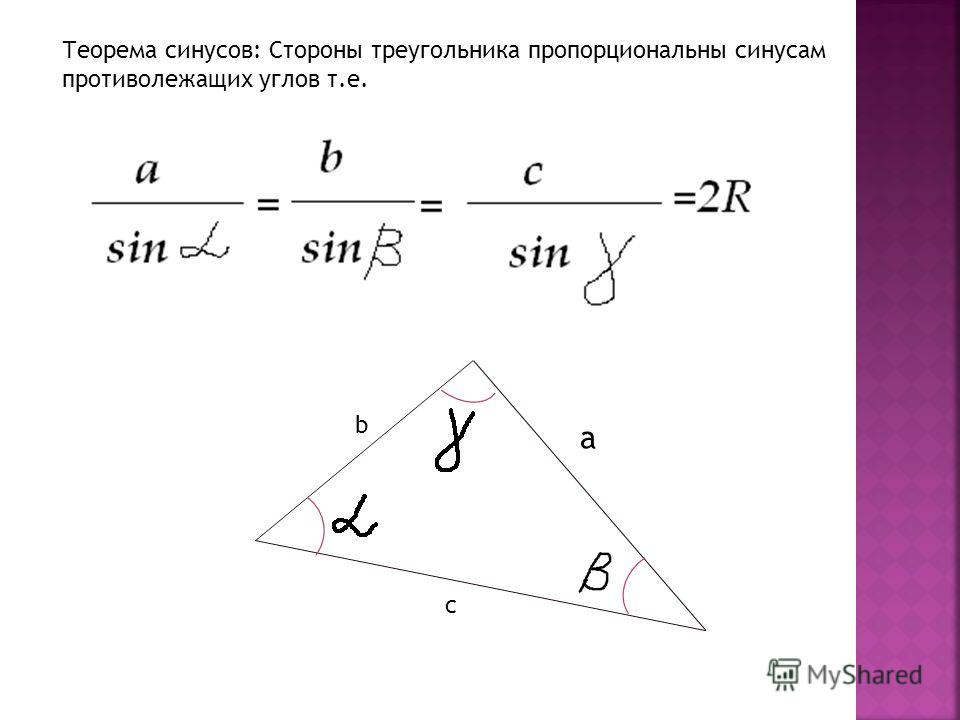
 Эти «Arcus»-функции
определяются однозначно только в ограниченном диапазоне результирующих углов. Этот
следует учитывать при применении этих функций:
Эти «Arcus»-функции
определяются однозначно только в ограниченном диапазоне результирующих углов. Этот
следует учитывать при применении этих функций: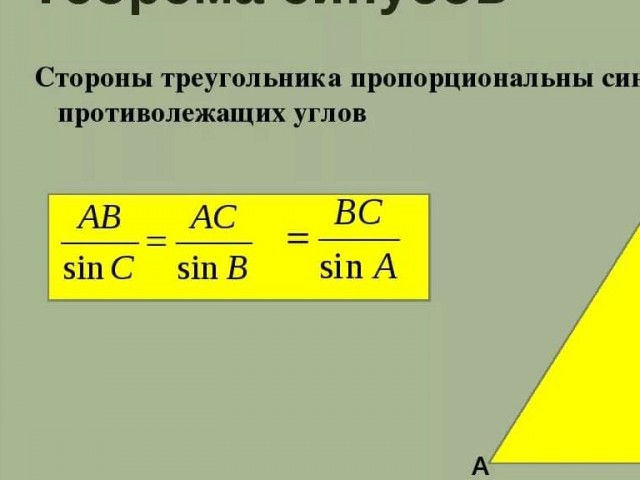
 Поскольку любой наклонный сферический треугольник можно описать как
сумма или разность двух прямоугольных сферических треугольников, эти упрощенные правила
также предоставить метод решения наклонных сферических треугольников.
Поскольку любой наклонный сферический треугольник можно описать как
сумма или разность двух прямоугольных сферических треугольников, эти упрощенные правила
также предоставить метод решения наклонных сферических треугольников.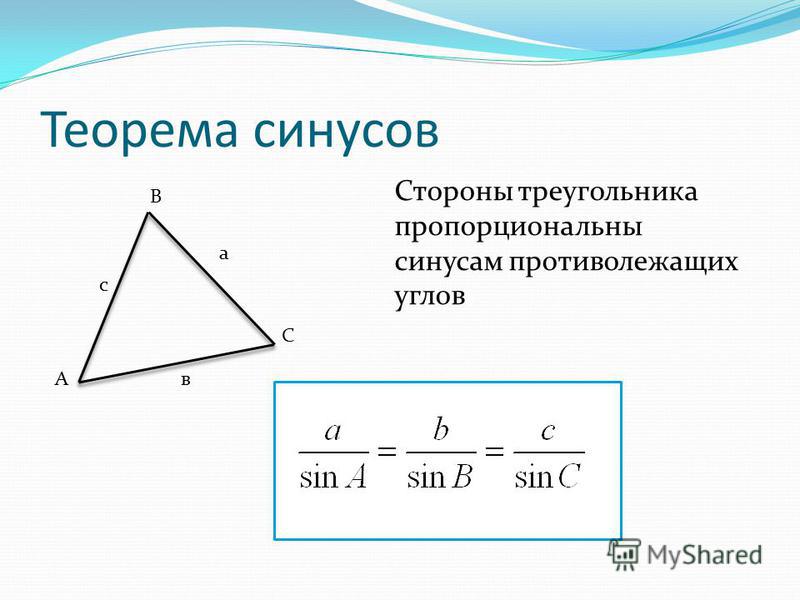 На самом деле, Джон Непер также был первым, кто разработал принцип логарифмов.
и его работа г. «Mirifici Logarithmorum Canonis Desciptio» от 1614 г. предоставил полный
практический набор инструментов для решения математических задач, связанных со сферическими треугольниками
возникающие напр. в навигации, астрономии и геодезии.
На самом деле, Джон Непер также был первым, кто разработал принцип логарифмов.
и его работа г. «Mirifici Logarithmorum Canonis Desciptio» от 1614 г. предоставил полный
практический набор инструментов для решения математических задач, связанных со сферическими треугольниками
возникающие напр. в навигации, астрономии и геодезии. также
также